Adsorption-Membrane Hybrid Approach for the Removal of Azithromycin from Water: An Attempt to Minimize Drug Resistance Problem
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Adsorbents
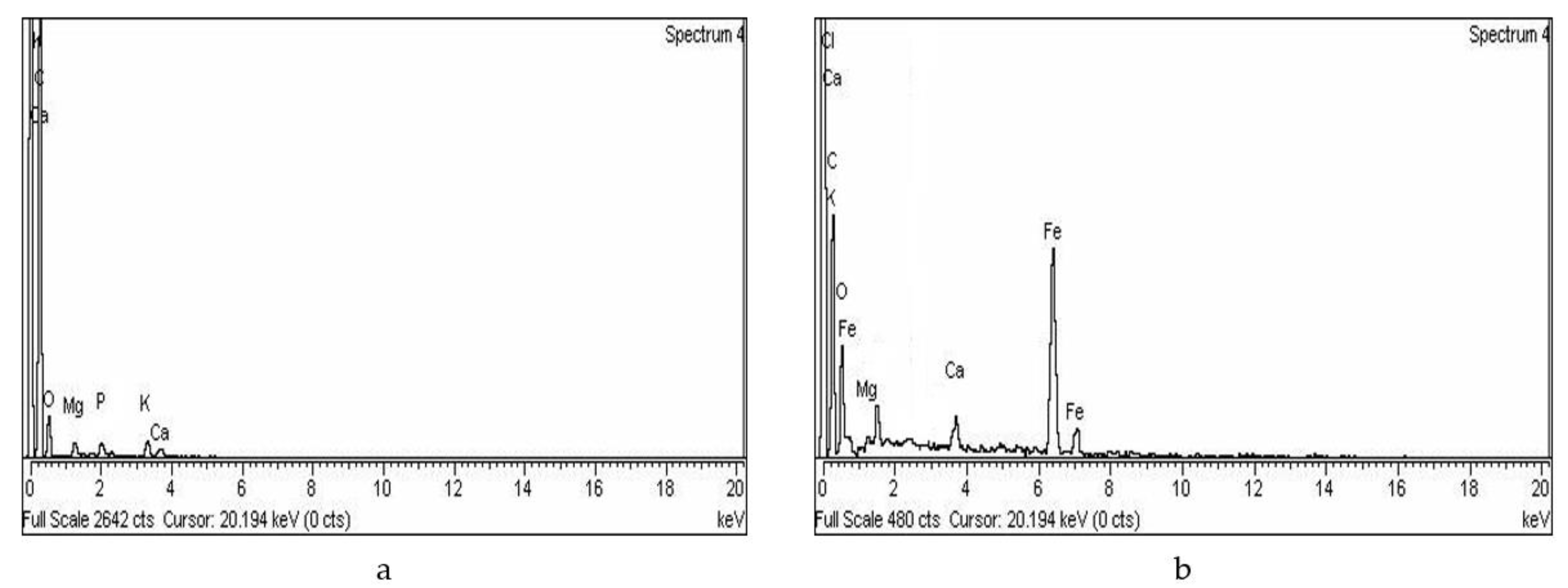
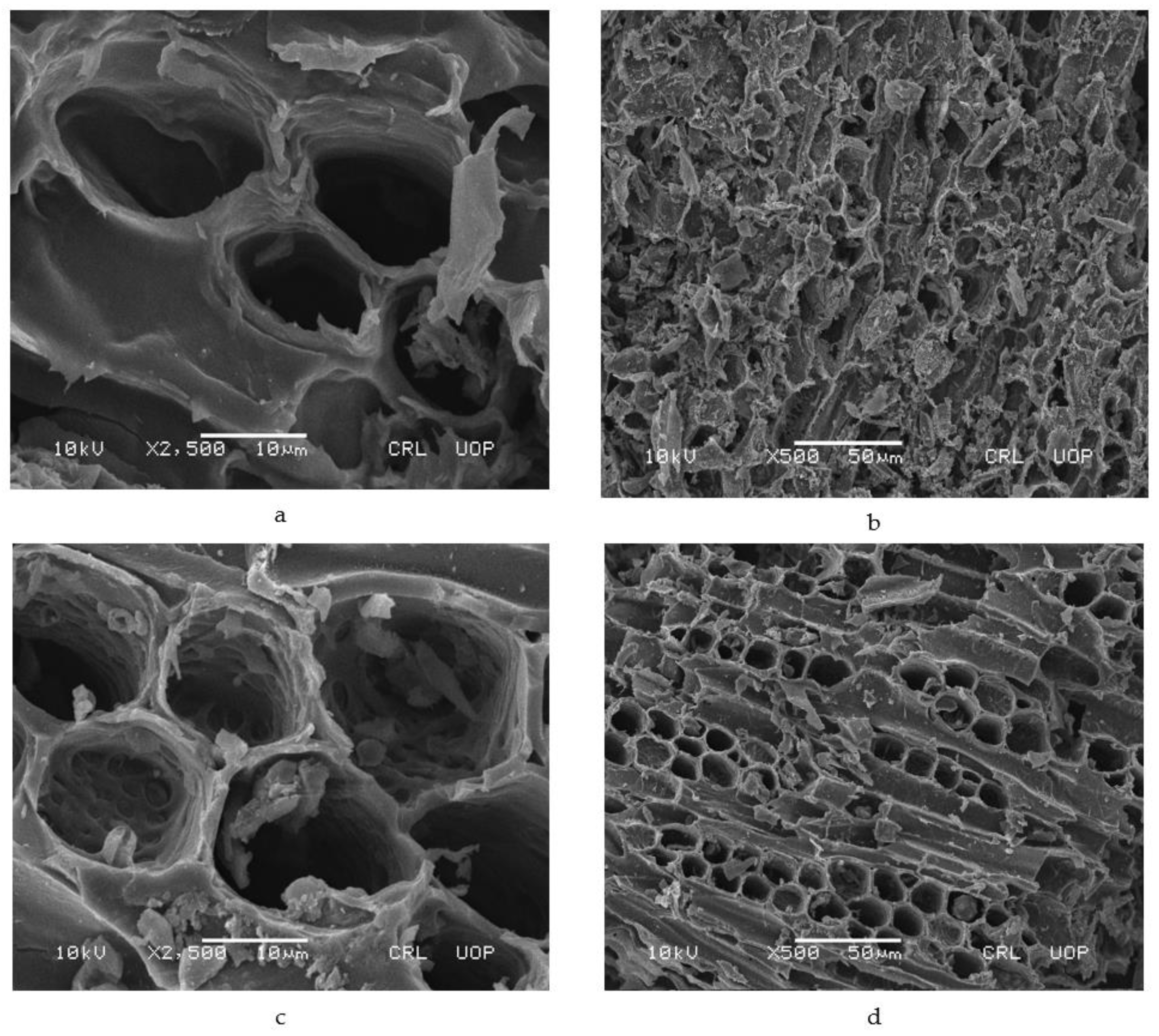
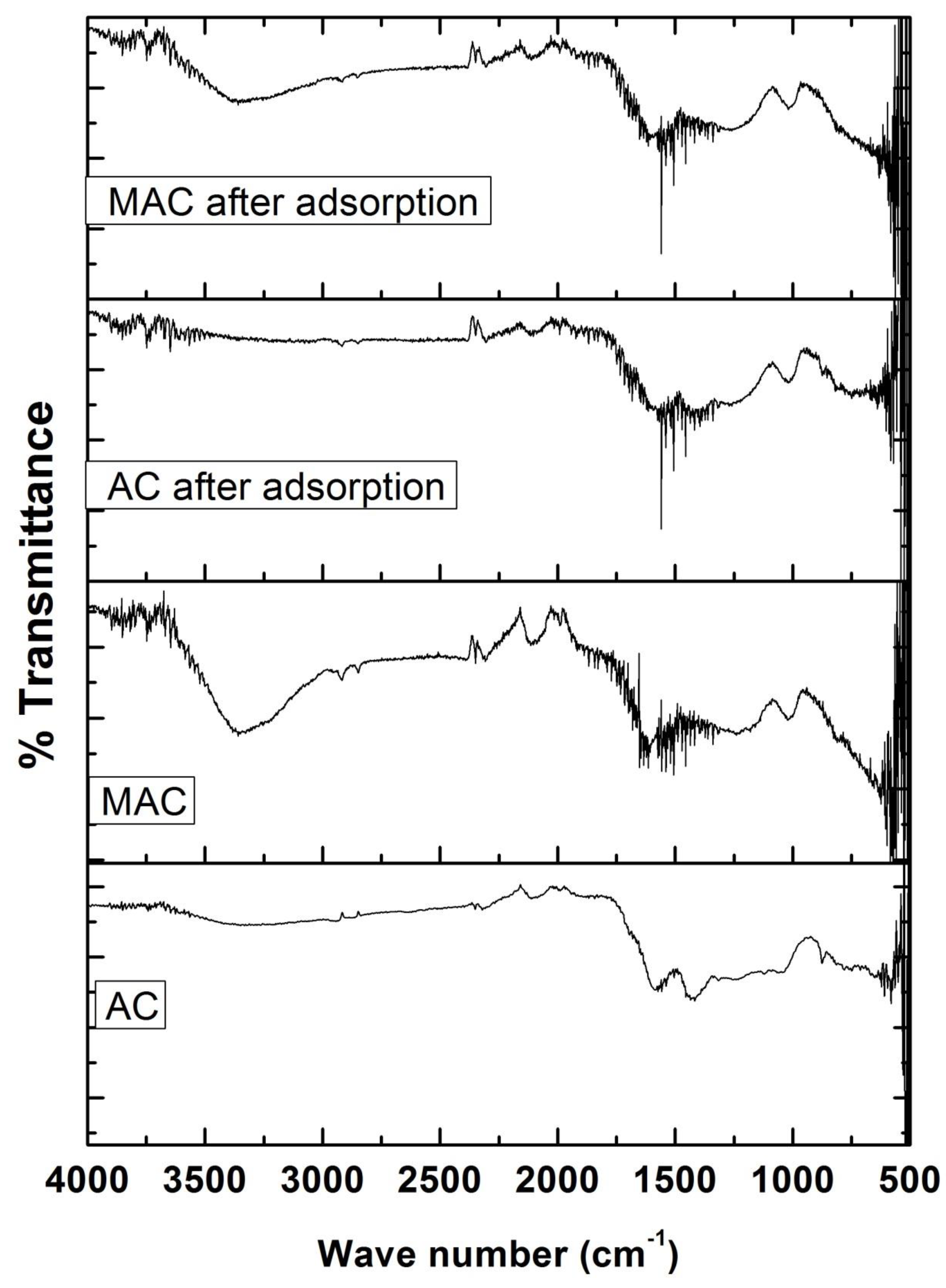
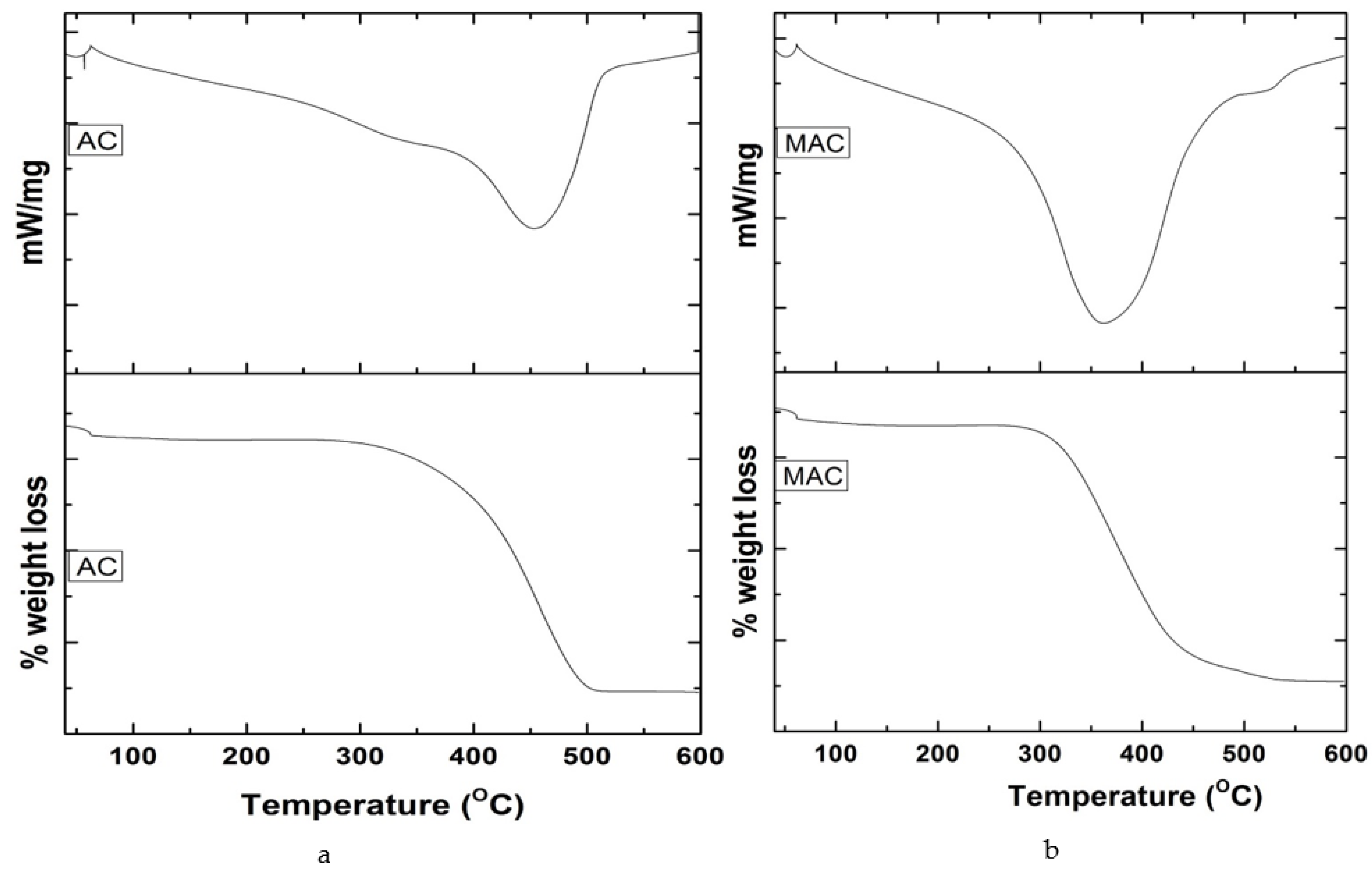
2.2. Characterization
2.3. Batch Adsorption Experiments
2.4. Isothermal Study
2.5. Kinetic Study
2.6. pH and Adsorbent Dosage Effect
2.7. Effect of Temperature
2.8. Removal of AZM by Membranes System
2.9. Pilot Plant Studies/Membranes Hybrid Technology
3. Result and Discussion
3.1. Characterization of Adsorbents
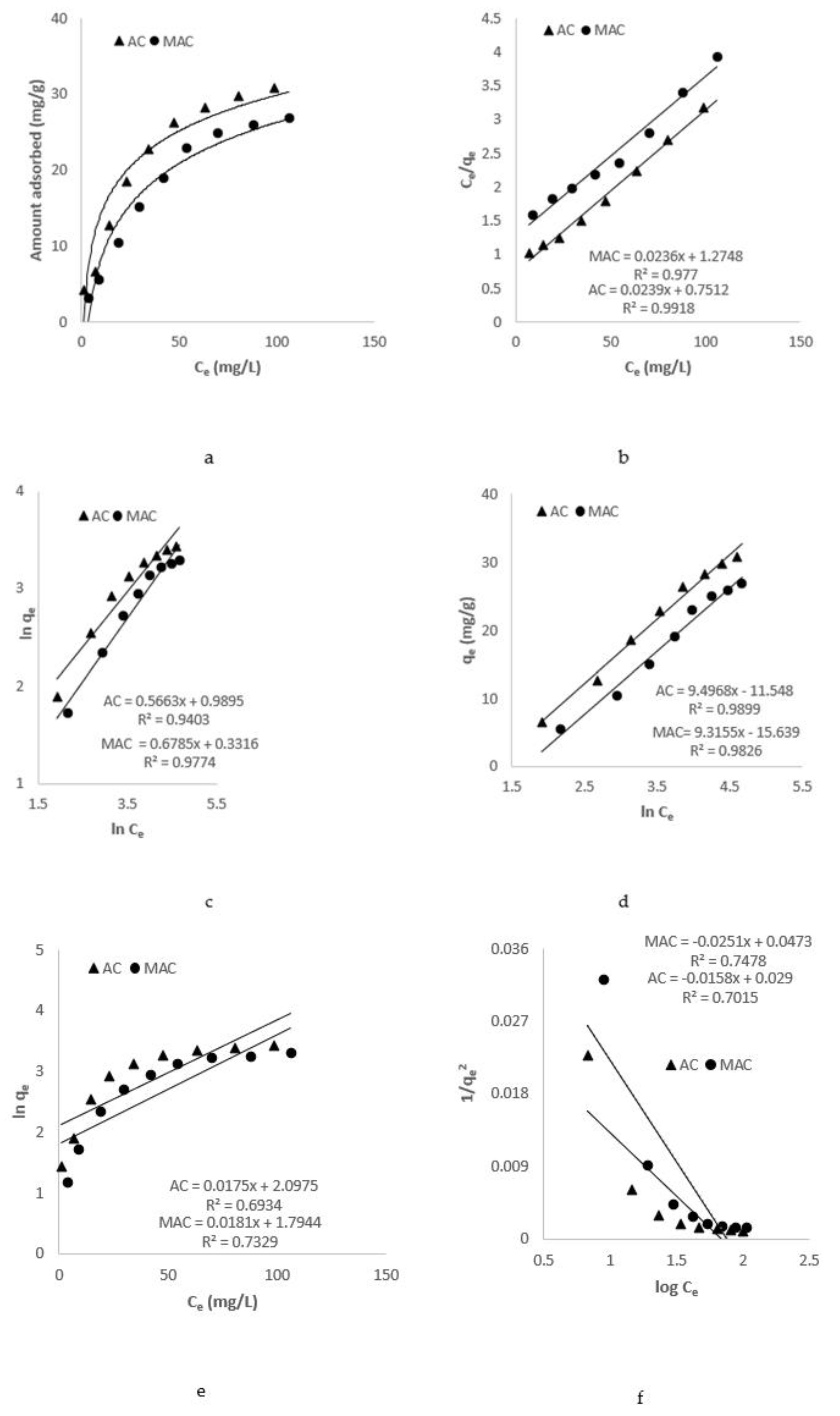
3.2. Isothermal Studies
3.2.1. Langmuir Isotherm Model
3.2.2. Freundlich Isotherm Model
3.2.3. Temkin Isotherm Model
3.2.4. Jovanovic Isotherm Model
3.2.5. Harkins–Jura Isotherm Model
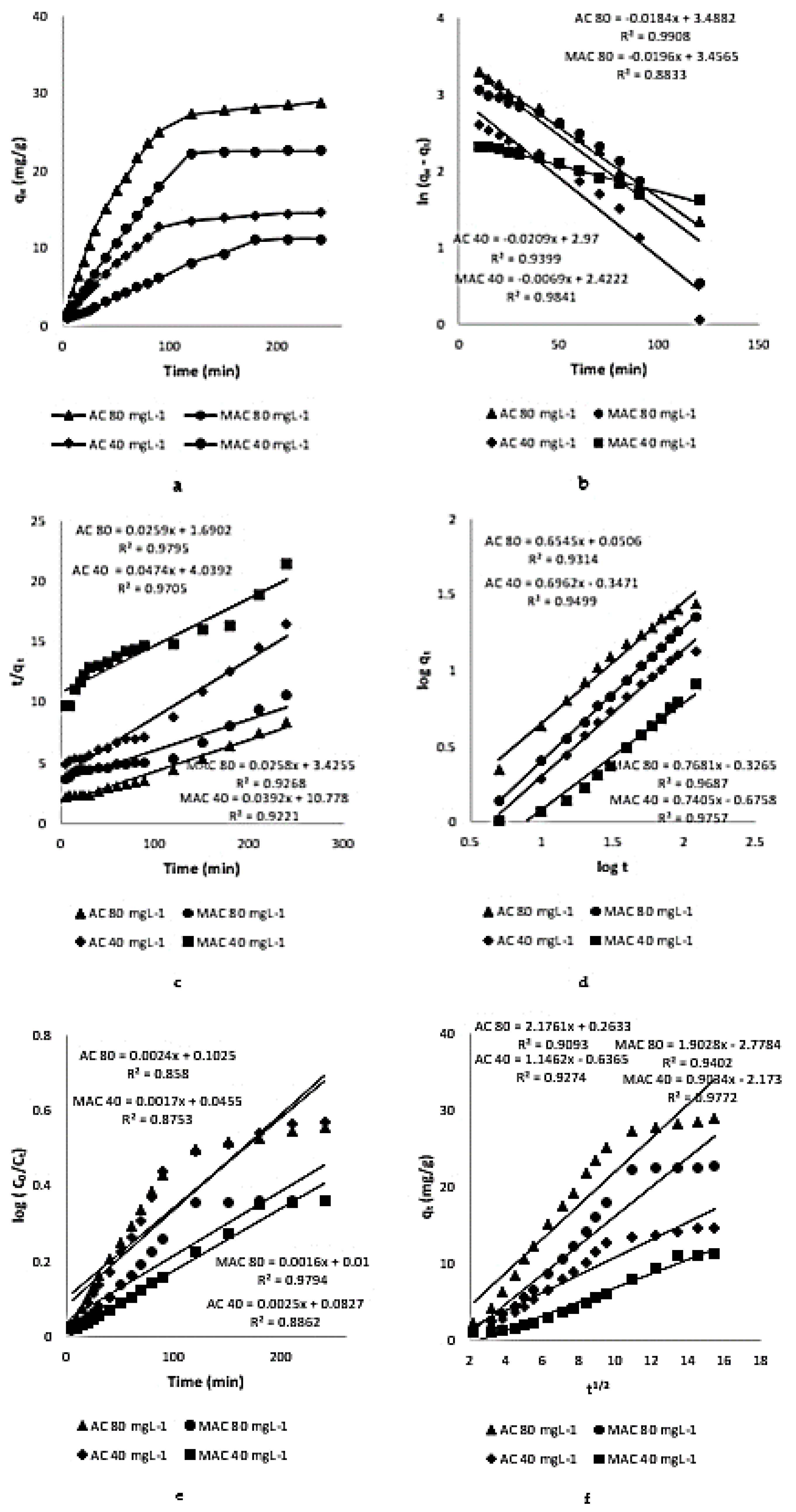
3.3. Kinetic Study
3.3.1. Pseudo-First-Order Kinetic Model
3.3.2. Pseudo-Second-Order Kinetic Model
3.3.3. Power Function Kinetic Model
3.3.4. Natarajan and Khalaf Kinetic Model
3.3.5. Intraparticle Diffusion Model
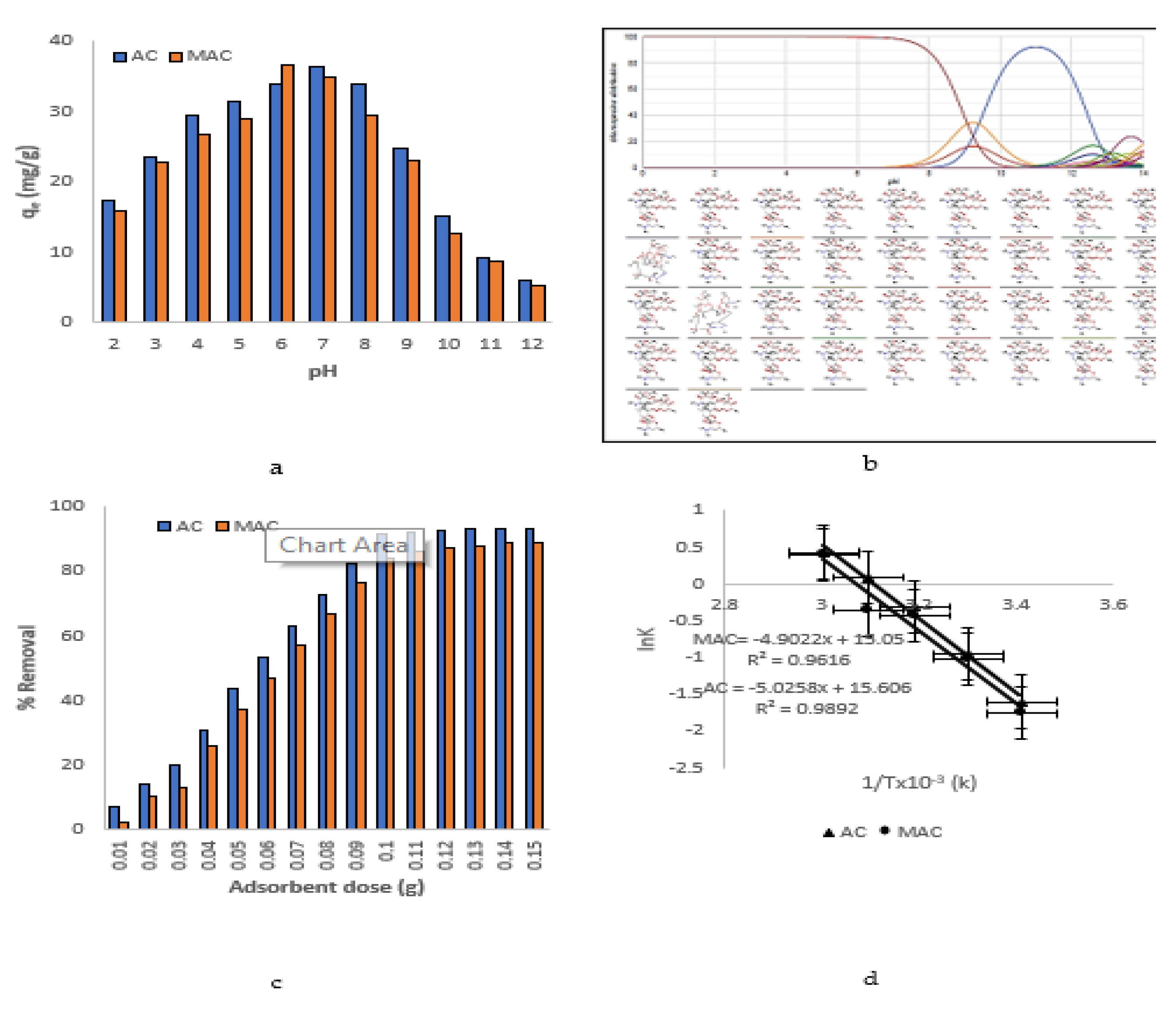
3.4. Effect of pH
3.5. Effect of Adsorbents Dosage
3.6. Thermodynamic Analysis
3.7. Comparison of Adsorption Capacities of Present Adsorbents with Those Reported in Literature
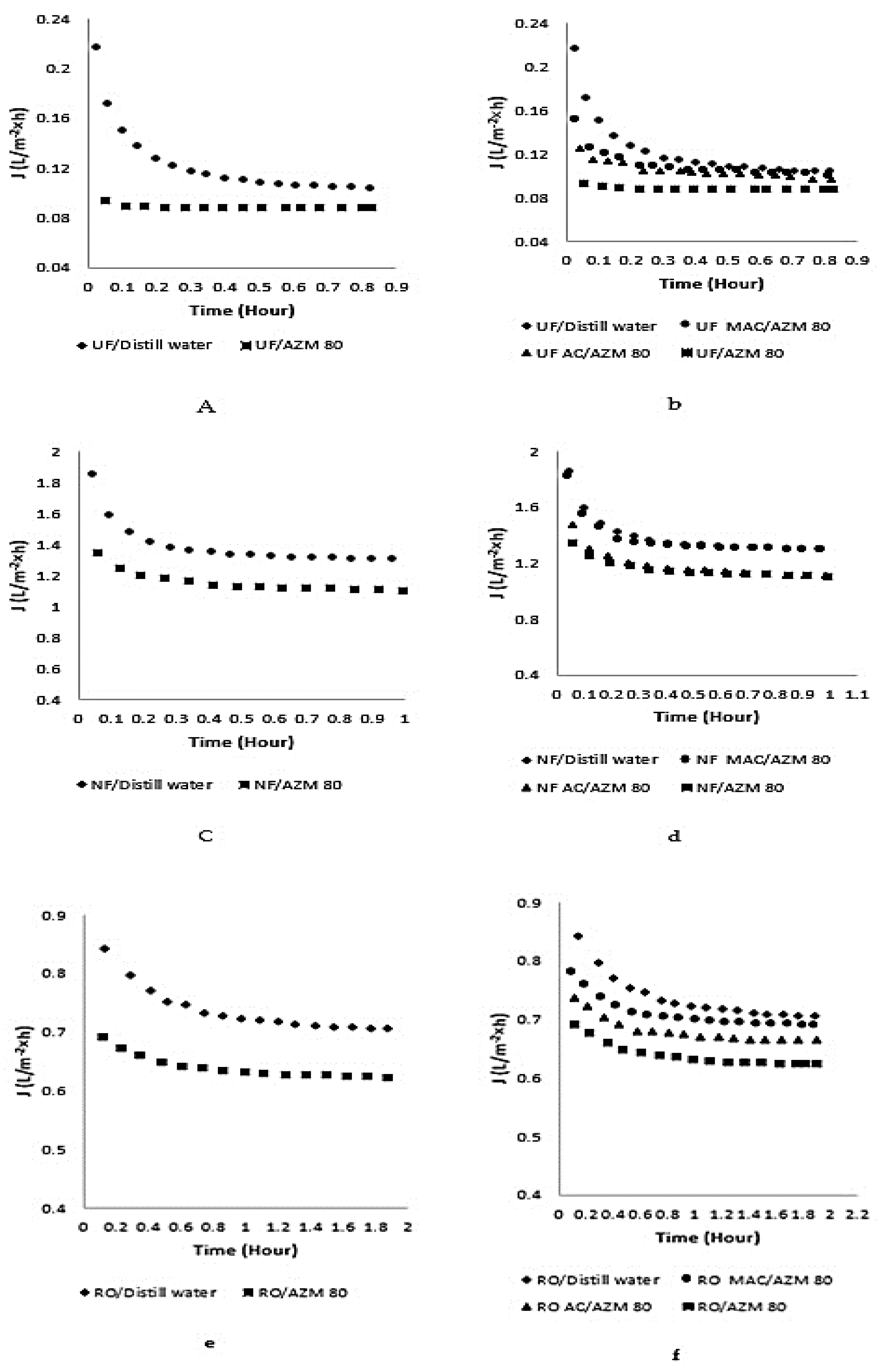
3.8. Effect of AZM on Permeate Flux and Their Improvement by AC and MAC through UF, NF and RO
3.9. Percent Retention of AZM by UF, NF and RO Membranes and Adsorption/Membranes Hybrid Technology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shikuku, V.O.; Zanella, R.; Kowenje, C.O.; Donato, F.F.; Bandeira, N.M.; Prestes, O.D. Single and binary adsorption of sulfonamide antibiotics onto iron-modified clay: Linear and nonlinear isotherms, kinetics, thermodynamics, and mechanistic studies. Appl. Water Sci. 2018, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Luke, D.R.; Foulds, G. Disposition of oral azithromycin in humans. Clin. Pharmacol. Ther. 1997, 61, 641–648. [Google Scholar] [CrossRef]
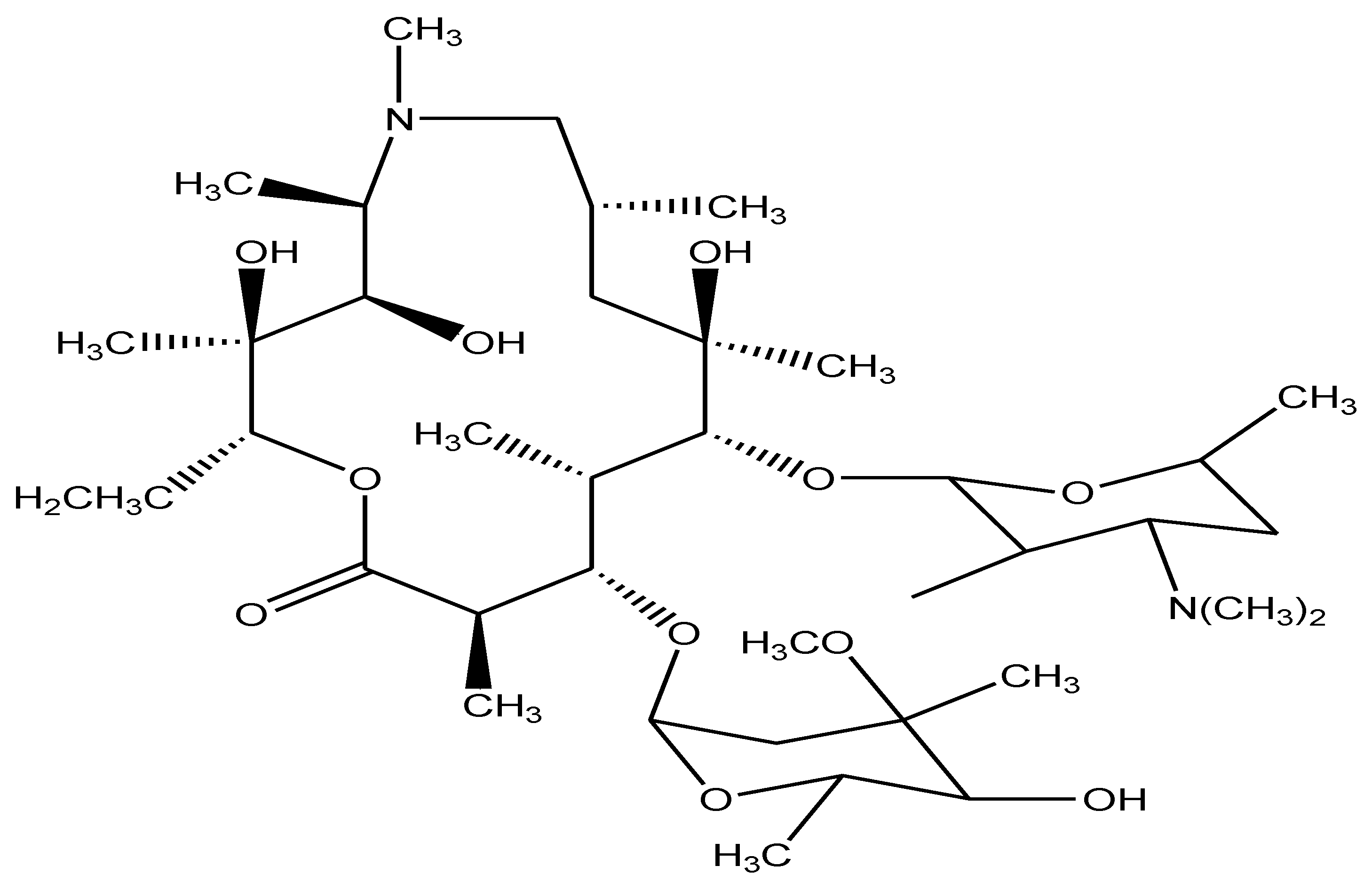
- Shoeb, M.; Alam, M.F.; Islam, M.M.; Parvin, N.; Islam, M.N.; Mamun, M.I.R. Assessment of Quality of Azithromycin, a Macrolide Antibiotic by NMR Spectroscopy. Bangladesh J. Pharmacol. 2021, 24, 37–44. [Google Scholar] [CrossRef]
- Al-Gheethi, A.A.; Ismail, N. Biodegradation of pharmaceutical wastes in treated sewage effluents by Bacillus subtilis 1556WTNC. Environ. Sci. Process. 2014, 1, 459–481. [Google Scholar] [CrossRef] [Green Version]
- Wolff-Hughes, D.L.; McClain, J.J.; Dodd, K.W.; Berrigan, D.; Troiano, R.P. Number of accelerometer monitoring days needed for stable group-level estimates of activity. Physiol. Meas. 2016, 37, 1447. [Google Scholar] [CrossRef] [PubMed]
- Febrianto, F.; Jang, J.H.; Lee, S.H.; Santosa, I.A.; Hidayat, W.; Kwon, J.H.; Kim, N.H. Effect of bamboo species and resin content on properties of oriented strand board prepared from steam-treated bamboo strands. BioResources 2015, 10, 2642–2655. [Google Scholar] [CrossRef]
- Yadanaparthi, S.K.R.; Graybill, D.; von Wandruszka, R. Adsorbents for the removal of arsenic, cadmium, and lead from contaminated waters. J. Hazard. Mater. 2009, 171, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Mehdi, K.; Lounis, M.; Bounceur, A.; Kechadi, T. Cupcarbon: A multi-agent and discrete event wireless sensor network design and simulation tool. In Proceedings of the 7th International ICST Conference on Simulation Tools and Techniques, Lisbon, Portugal, 18 August 2014; pp. 17–19. [Google Scholar]
- Hartmann, A.; Mudarra, M.; Andreo, B.; Marín, A.; Wagener, T.; Lange, J. Modeling spatiotemporal impacts of hydroclimatic extremes on groundwater recharge at a Mediterranean karst aquifer. Water Res. 2014, 50, 6507–6521. [Google Scholar] [CrossRef]
- Ahmed, M.B.; Zhou, J.L.; Ngo, H.H.; Guo, W. Adsorptive removal of antibiotics from water and wastewater: Progress and challenges. Sci. Total Environ. 2015, 532, 112–126. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, D.; Xu, Z.; Zheng, S. Adsorptive removal of pharmaceutical antibiotics from aqueous solution by porous covalent triazine frameworks. Environ. Pollut. 2017, 226, 379–384. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, J.H.; Lee, H.J.; Ahn, T.K.; Shin, H.S.; Park, J.S.; Kim, H.D. High mobility bottom gate InGaZnO thin film transistors with Si O x etch stopper. Appl. Phys. Lett. 2007, 90, 212114. [Google Scholar] [CrossRef]
- Watkinson, A.; Murby, E.; Kolpin, D.W.; Costanzo, S. The occurrence of antibiotics in an urban watershed: From wastewater to drinking water. Sci. Total Environ. 2009, 407, 2711–2723. [Google Scholar] [CrossRef] [PubMed]
- Radjenović, J.; Petrović, M.; Ventura, F.; Barceló, D. Rejection of pharmaceuticals in nanofiltration and reverse osmosis membrane drinking water treatment. Water Res. 2008, 42, 3601–3610. [Google Scholar] [CrossRef]
- Dolar, D.; Vuković, A.; Ašperger, D.; Košutić, K. Efficiency of RO/NF membranes at the removal of veterinary antibiotics. Water Sci. Technol. 2012, 65, 317–323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, M.; Keten, S.; Lueptow, R.M. Dynamics of water and solute transport in polymeric reverse osmosis membranes via molecular dynamics simulations. J. Membr. Sci. 2016, 506, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Zahoor, M.; Mahramanlioglu, M. Removal of 2, 4-D from water, using various adsorbents in combination with ultrafiltration. Fresenius Environ. Bull. 2011, 20, 2508–2513. [Google Scholar]
- Košutić, K.; Kaštelan-Kunst, L.; Kunst, B. Porosity of some commercial reverse osmosis and nanofiltration polyamide thin-film composite membranes. J. Membr. Sci. 2000, 168, 101–108. [Google Scholar] [CrossRef]
- Zahoor, M. Effect of granular activated carbon on percent retention of humic acid and permeate flux in GAC/UF membrane process. Desalin. Water Treat. 2016, 57, 23661–23665. [Google Scholar] [CrossRef]
- Tang, D.; Zheng, Z.; Lin, K.; Luan, J.; Zhang, J. Adsorption of p-nitrophenol from aqueous solutions onto activated carbon fiber. J. Hazard. Mater. 2007, 143, 49–56. [Google Scholar] [CrossRef]
- Fasoto, T.S.; Arawande, J.O.; Akinnusotu, A. Adsorption of zinc and chromium ions from aqueous solution onto sugarcane bagasse. Int. J. Chem. 2004, 6, 28–47. [Google Scholar]
- Wahaba, M.; Zahoorb, M.; Salmana, S.M. A novel approach to remove ofloxacin antibiotic from industrial effluent using magnetic carbon nanocomposite prepared from sawdust of Dalbergia sissoo by batch and membrane hybrid technology. Membr. Technol. 2019, 27, 28. [Google Scholar] [CrossRef]
- Diem, M. Modern Vibrational Spectroscopy and Micro-Spectroscopy: Theory, Instrumentation and Biomedical Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Jayamani, E.; Hamdan, S.; Rahman, M.R.; Bakri, M.K.B. Study of sound absorption coefficients and characterization of rice straw stem fibers reinforced polypropylene composites. Bioresour. Technol. 2015, 10, 3378–3392. [Google Scholar] [CrossRef] [Green Version]
- Araujo, J.; Ortíz, R.; Velásquez, W.; Ortega, J. Determination of Azithromycin in Pharmaceutical Formulations by Differential Pulse Voltammetry: Comparison with Fourier Transformed Infrared Spectroscopic Analysis. Port. Electrochim. Acta 2006, 24, 71–81. [Google Scholar] [CrossRef]
- Mallah, M.A.; Sherazi, S.; Mahesar, S.A.; Rauf, A. Assessment of azithromycin in pharmaceutical formulation by fourier-transform infrared (FT-IR) transmission spectroscopy. Pak. J. Anal. Environ. Chem. 2011, 12, 7. [Google Scholar]
- Mao, H.; Wang, S.; Lin, J.Y.; Wang, Z.; Ren, J. Modification of a magnetic carbon composite for ciprofloxacin adsorption. J. Environ. Sci. 2016, 49, 179–188. [Google Scholar] [CrossRef]
- Azmat, U.; Muhammad, Z.; Sultan, A. Removal of ciprofloxacin from water through magnetic nanocomposite/membrane hybrid processes.desalination. Water Treat. 2019, 137, 260–272. [Google Scholar]
- Wahab, M.; Zahoor, M.; Salman, S.M.; Naz, S. Effective removal of tetracycline from water by batch method using activated carbon, magnetic carbon nanocomposite, and membrane hybrid technology. Z. Phys. Chem. 2021, 1. ahead-of-print. [Google Scholar]
- LeVan, M.D.; Vermeulen, T. Binary Langmuir and Freundlich isotherms for ideal adsorbed solutions. Am. J. Phys. Chem. 1981, 85, 3247–3250. [Google Scholar] [CrossRef]
- Freundlich, H. Über die adsorption in lösungen. Z. Phys. Chem. 1907, 57, 385–470. [Google Scholar] [CrossRef]
- Park, J.C.; Joo, J.B.; Yi, J. Adsorption of acid dyes using polyelectrolyte impregnated mesoporous silica. Korean J. Chem. Eng. 2005, 22, 276–280. [Google Scholar] [CrossRef]
- Malkoc, E.; Nuhoglu, Y. Determination of kinetic and equilibrium parameters of the batch adsorption of Cr (VI) onto waste acorn of Quercus ithaburensis. Chem. Eng. Process. 2007, 46, 1020–1029. [Google Scholar] [CrossRef]
- Isotherms, T.A. Sorption Energies Estimation Using Dubinin-Radushkevich and. Life Sci. 2010, 7, 68–76. [Google Scholar]
- Panagiotis Zalmas, L.; Zhao, X.; Graham, A.L.; Fisher, R.; Reilly, C.; Coutts, A.S.; La Thangue, N.B. DNA-damage response control of E2F7 and E2F8. EMBO Rep. 2008, 9, 252–259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Podder, M.; Majumder, C. Studies on removal of As (III) and As (V) onto GAC/MnFe2O4 composite: Isotherm studies and error analysis. Compos. Interfaces 2016, 23, 327–372. [Google Scholar] [CrossRef]
- Lagergren, S.K. About the theory of so-called adsorption of soluble substances.K. Seven. Vetenskapsakad. Handl. 1898, 24, 1–39. [Google Scholar]
- Ho, Y.; Ng, J.; McKay, G. Kinetics of pollutant sorption by biosorbents. Sep. Purif. Methods 2000, 29, 189–232. [Google Scholar] [CrossRef]
- Riahi, K.; Chaabane, S.; Thayer, B.B. A kinetic modeling study of phosphate adsorption onto Phoenix dactylifera L. date palm fibers in batch mode. J. Saudi Chem. Soc. 2017, 21, S143–S152. [Google Scholar] [CrossRef] [Green Version]
- Cheung, W.; Ng, J.; McKay, G. Kinetic analysis of the sorption of copper (II) ions on chitosan. J. Chem. Technol. Biotechnol. J. Chem. Technol. Biot. 2003, 78, 562–571. [Google Scholar] [CrossRef]
- Srivastava, S.; Tyagi, R.; Pant, N. Adsorption of heavy metal ions on carbonaceous material developed from the waste slurry generated in local fertilizer plants. Water Res. 1989, 23, 1161–1165. [Google Scholar] [CrossRef]
- Tassone, L.; Notarangelo, L.D.; Bonomi, V.; Savoldi, G.; Sensi, A.; Soresina, A.; Notarangelo, L.D. Clinical and genetic diagnosis of warts, hypogammaglobulinemia, infections, and myelokathexis syndrome in 10 patients. Allergy Clin. Immunol. Pract. 2009, 123, 1170–1173. [Google Scholar] [CrossRef]
- Kara, S.; Aydiner, C.; Demirbas, E.; Kobya, M.; Dizge, N. Modeling the effects of adsorbent dose and particle size on the adsorption of reactive textile dyes by fly ash. Desalination 2007, 212, 282–293. [Google Scholar] [CrossRef]
- Falcoz, Q.; Gauthier, D.; Abanades, S.; Flamant, G.; Patisson, F. Kinetic rate laws of Cd, Pb, and Zn vaporization during municipal solid waste incineration. Environ. Sci. Technol. 2009, 43, 2184–2189. [Google Scholar] [CrossRef]
- Lima, E.C.; Hosseini-Bandegharaei, A.; Moreno-Piraján, J.C.; Anastopoulos, I. A critical review of the estimation of the thermodynamic parameters on adsorption equilibria. Wrong use of equilibrium constant in the Van’t Hoof equation for calculation of thermodynamic parameters of adsorption. J. Mol. Liq. 2019, 273, 425–434. [Google Scholar] [CrossRef]
- Salvestrini, S.; Leone, V.; Iovino, P.; Canzano, S.; Capasso, S. Considerations about the correct evaluation of sorption thermodynamic parameters from equilibrium isotherms. J. Chem.Thermodyn. 2014, 68, 310–316. [Google Scholar] [CrossRef]
- de Franco, M.A.E.; de Carvalho, C.B.; Bonetto, M.M.; de Pelegrini Soares, R.; Féris, L.A. Removal of amoxicillin from water by adsorption onto activated carbon in batch process and fixed bed column: Kinetics, isotherms, experimental design and breakthrough curves modelling. J. Clean. Prod. 2017, 161, 947–956. [Google Scholar] [CrossRef]
- Korzh, E.; Smolin, S.; Klymenko, N. Impact of characteristic of activated carbons on the efficiency of removal from water of pharmaceutical preparations of various chemical nature. J. Water. Chem. Technol. 2016, 38, 83–88. [Google Scholar] [CrossRef]
- Samarghandi, M.R.; Asgari, G.; Shokoohi, R.; Dargahi, A.; Arabkouhsar, A. Removing amoxicillin antibiotic from aqueous solutions by Saccharomyces cerevisiae bioadsorbent: Kinetic, thermodynamic and isotherm studies. Desalin. Water. Treat. 2019, 152, 306–315. [Google Scholar] [CrossRef]
- Badi, M.Y.; Azari, A.; Pasalari, H.; Esrafili, A.; Farzadkia, M. Modification of activated carbon with magnetic Fe3O4 nanoparticle composite for removal of ceftriaxone from aquatic solutions. J. Mol. Liq. 2018, 261, 146–154. [Google Scholar] [CrossRef]
- Kerkez-Kuyumcu, Ö.; Bayazit, Ş.S.; Salam, M.A. Antibiotic amoxicillin removal from aqueous solution using magnetically modified graphene nanoplatelets. J. Ind. Eng. Chem. 2016, 36, 198–205. [Google Scholar] [CrossRef]
- Dai, K.; Wang, F.; Jiang, W.; Chen, Y.; Mao, J.; Bao, J. Magnetic Carbon Microspheres as a Reusable Adsorbent for Sulfonamide Removal from Water. Nanoscal. Res. Lett. 2017, 12, 1–9. [Google Scholar] [CrossRef] [Green Version]
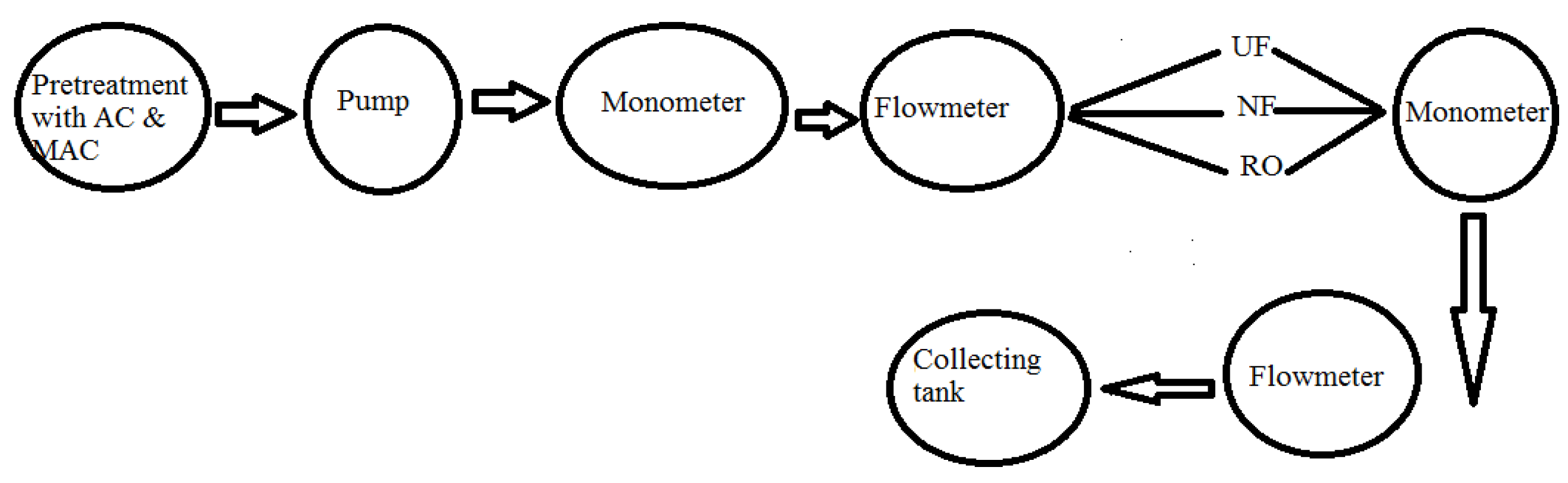


| UF Membrane | NF Membrane (Dow Film Tech 2.5 × 40) | RO Membrane (Dow Film Tech ECO PRO 400 i) | |||
|---|---|---|---|---|---|
| Parameters | Specification | Parameters | Specification | Parameters | Specification |
| Membrane type | Capillary multi bore × 7 | model | NF(270–2540) | model | RO(270–2540) |
| Surface area | 50 m2 | Surface area | 3.2 m2 | Surface area | 3.2 m2 |
| Maximum pressure | 109 psi | Maximum pressure | 100–1000 psi | Maximum pressure | 100–1000 psi |
| Membrane back wash pressure | 0.5–1 psi | Membrane back wash pressure | 50–800 psi | Membrane back wash pressure | 50–800 psi |
| MWCO | 100 KD | MWCO | 200–300 | MWCO | 200 |
| Stabilized salt rejection | 10–20% | Stabilized salt rejection | >97% | Stabilized salt rejection | 99.5% |
| Maximum temperature | 40 °C | Maximum temperature | 40–180 °C | Maximum temperature | 40–180 °C |
| pH operating range | 3–10 | pH operating range | 3–10 | pH operating range | 3–10 |
| Backwash pH range | 1–13 | Back wash pH range | 1–12 | Backwash pH range | 1–12 |
| Disinfection chemicals | Hypochlorite and Hydrogen peroxide | Disinfection chemicals | Hydrogen peroxide and peracetic acid | Disinfection chemicals | Hydrogen peroxide and peracetic acid |
| Pore size | 5–20 nm | Pore size | 5–20 nm | Pore size | 5–20 nm |
| Material | Polyethersulfone | Applied pressure | 4.8 bar | Membrane type | Thin film composite |
| Isotherm Models | Parameters | Adsorbents | |
|---|---|---|---|
| AC | MAC | ||
| Langmuir | qmax (mg/g) | 41.841 | 42.372 |
| KL (L/mg) | 0.0318 | 0.0185 | |
| R2 | 0.9918 | 0.977 | |
| Freundlich | KF (mg/g) | 2.69 | 1.393 |
| 1/n | 0.5663 | 0.6785 | |
| R2 | 0.9403 | 0.9774 | |
| Temkin | β | 9.4968 | 9.3155 |
| α | 3.374 | 5.36 | |
| b | 238.998 | 243.65 | |
| R2 | 0.9899 | 0.9826 | |
| Jovanovich | KJ (L/g) | 0.0175 | 0.0181 |
| qmax(mg/g) | 8.121 | 6.015 | |
| R2 | 0.6934 | 0.7329 | |
| Harkins–Jura | AH (g2/L) | 0.0633 | 0.0399 |
| BH (mg2/L) | 1.835 | 1.884 | |
| R2 | 0.7015 | 0.7478 | |
| Kinetic Model | Parameters | Adsorbents and Initial Concentrations | |||
|---|---|---|---|---|---|
| AC 80 mg/L | MAC 80 mg/L | AC 40 mg/L | MAC 40 mg/L | ||
| Pseudo-first-order | K1 (min−1) | 0.018 | 0.02 | 0.021 | 0.007 |
| qe (mg/g) | 32.727 | 31.705 | 19.492 | 11.271 | |
| R2 | 0.991 | 0.883 | 0.94 | 0.984 | |
| Pseudo-second-order | K2(g/mg × min) | 3.97 × 10−4 | 1.94 × 10−4 | 5.56 × 10−3 | 1.43 × 10−4 |
| qe (mg/g) | 38.61 | 38.76 | 21.097 | 25.51 | |
| R2 | 0.98 | 0.927 | 0.971 | 0.922 | |
| Power function | α | 1.124 | 2.121 | 4.968 | 4.74 |
| b | 0.655 | 0.768 | 0.696 | 0.741 | |
| R2 | 0.931 | 0.969 | 0.95 | 0.976 | |
| KN (min−1) | 5.53 × 10−3 | 3.69 × 10−3 | 5.76 × 10−3 | 3.92 × 10−3 | |
| R2 | 0.858 | 0.979 | 0.854 | 0.875 | |
| Intra-particle diffusion | Kdiff (mg/g × min1/2) | 2.861 | 2.686 | 1.279 | 1.128 |
| C | 4.544 | 0.45 | 2.399 | 0.14 | |
| R2 | 0.909 | 0.94 | 0.886 | 0.977 | |
| Adsorbents | ΔH (KJ/mol) | ΔS (J/mol⋅K) | ΔG (KJ/mol) | ||||
|---|---|---|---|---|---|---|---|
| 298 K | 303 K | 313 K | 323 K | 333 K | |||
| AC | −26.507 | 91.812 | −37.974 | −39.271 | −40.569 | −41.909 | −43.164 |
| MAC | −40.756 | 125.126 | −37.500 | −37.872 | −39.123 | 40.376 | −41.625 |
| Adsorbent | Adsorbate | Qmax (mg/g) | Reference |
|---|---|---|---|
| Activated carbon prepared from Dilbergia Sissoo | Azithromycin | 41.841 | This study |
| Activated carbon prepared from biomass | Amoxicillin | 4.4 | [47] |
| Activated carbon prepared from biomass | Sulfonamide | 31 | [48] |
| Activated carbon prepared from Saccharomyces cerevisiae | Amoxicillin | 6.27 | [49] |
| Magnetic activated carbon prepared from Dilbergia Sissoo | Azithromycin | 42.372 | This study |
| Activated carbon with magnetic Fe3O4 | Ceftriaxone | 28.93 | [50] |
| Magnetically modified graphene | Amoxicillin | 14.1 | [51] |
| Fe3O4 nanoparticles | Sulfonamide | 10.83 | [52] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahab, M.; Zahoor, M.; Muhammad Salman, S.; Kamran, A.W.; Naz, S.; Burlakovs, J.; Kallistova, A.; Pimenov, N.; Zekker, I. Adsorption-Membrane Hybrid Approach for the Removal of Azithromycin from Water: An Attempt to Minimize Drug Resistance Problem. Water 2021, 13, 1969. https://doi.org/10.3390/w13141969
Wahab M, Zahoor M, Muhammad Salman S, Kamran AW, Naz S, Burlakovs J, Kallistova A, Pimenov N, Zekker I. Adsorption-Membrane Hybrid Approach for the Removal of Azithromycin from Water: An Attempt to Minimize Drug Resistance Problem. Water. 2021; 13(14):1969. https://doi.org/10.3390/w13141969
Chicago/Turabian StyleWahab, Muhammad, Muhammad Zahoor, Syed Muhammad Salman, Abdul Waheed Kamran, Sumaira Naz, Juris Burlakovs, Anna Kallistova, Nikolai Pimenov, and Ivar Zekker. 2021. "Adsorption-Membrane Hybrid Approach for the Removal of Azithromycin from Water: An Attempt to Minimize Drug Resistance Problem" Water 13, no. 14: 1969. https://doi.org/10.3390/w13141969







