Prediction of the Cavitation over a Twisted Hydrofoil Considering the Nuclei Fraction Sensitivity at 4000 m Altitude Level
Abstract
:1. Introduction
2. Numerical Methods
2.1. Numerical Method for Turbulent Flow
2.2. Cavitation Model
2.3. Vapor Volume Fraction
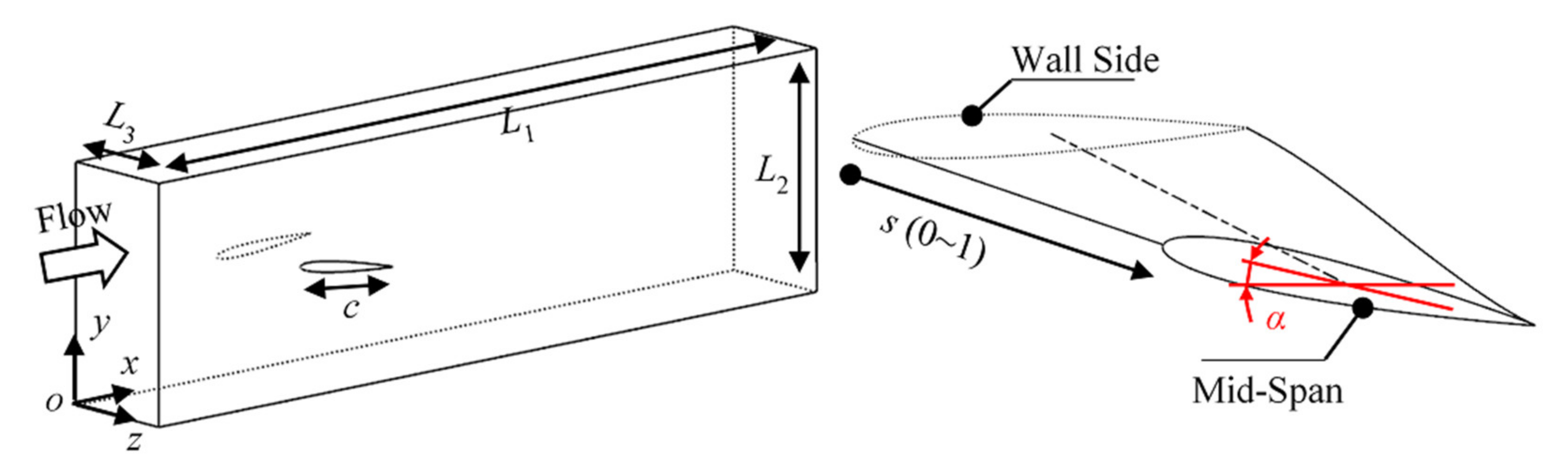
3. Case and Setup
3.1. Important Dimensionless Parameters
3.2. Flow Domain of Hydrofoil
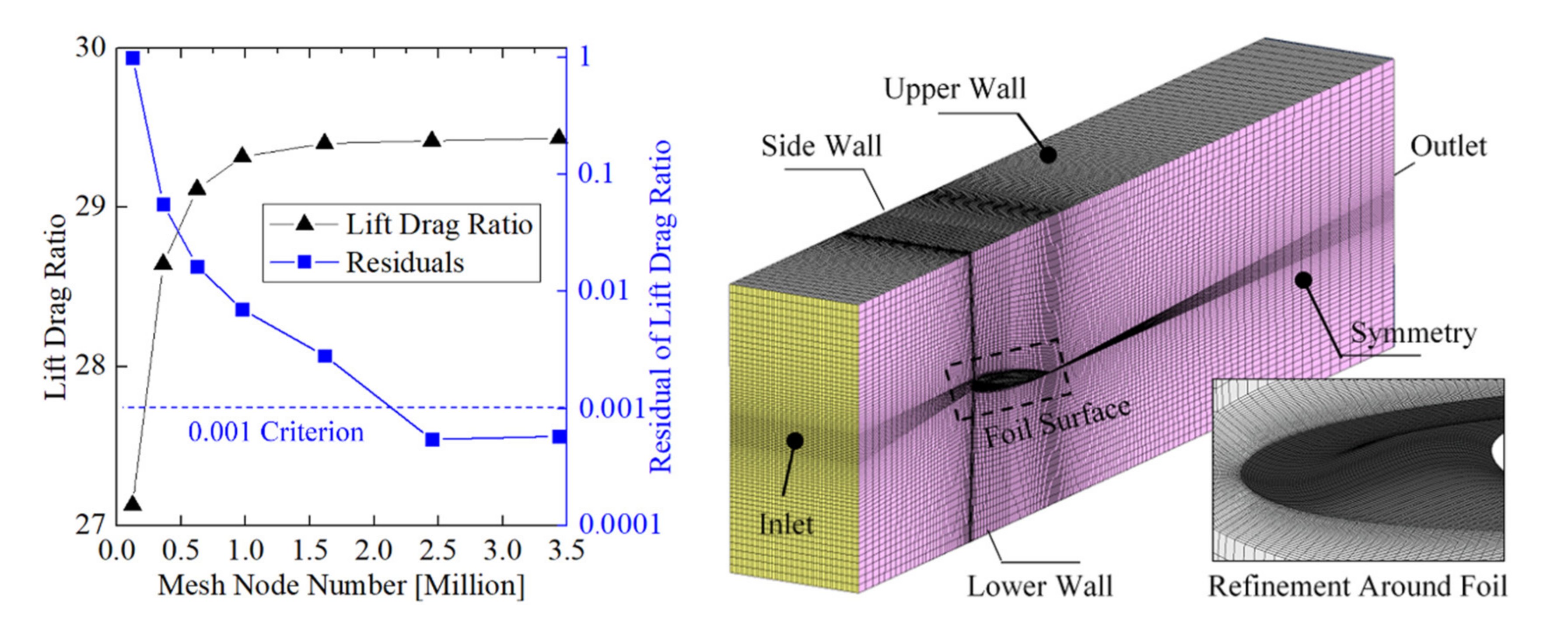
3.3. CFD Setup
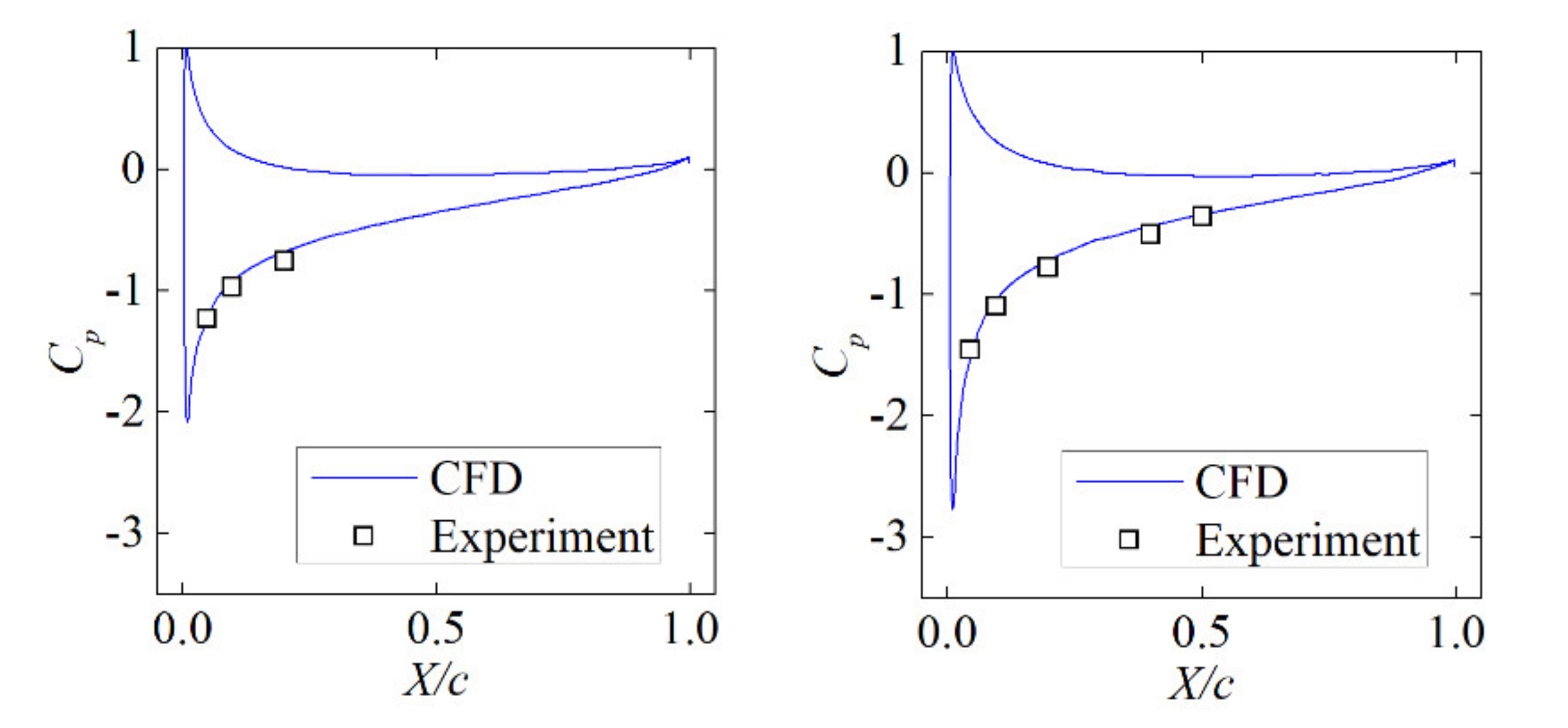
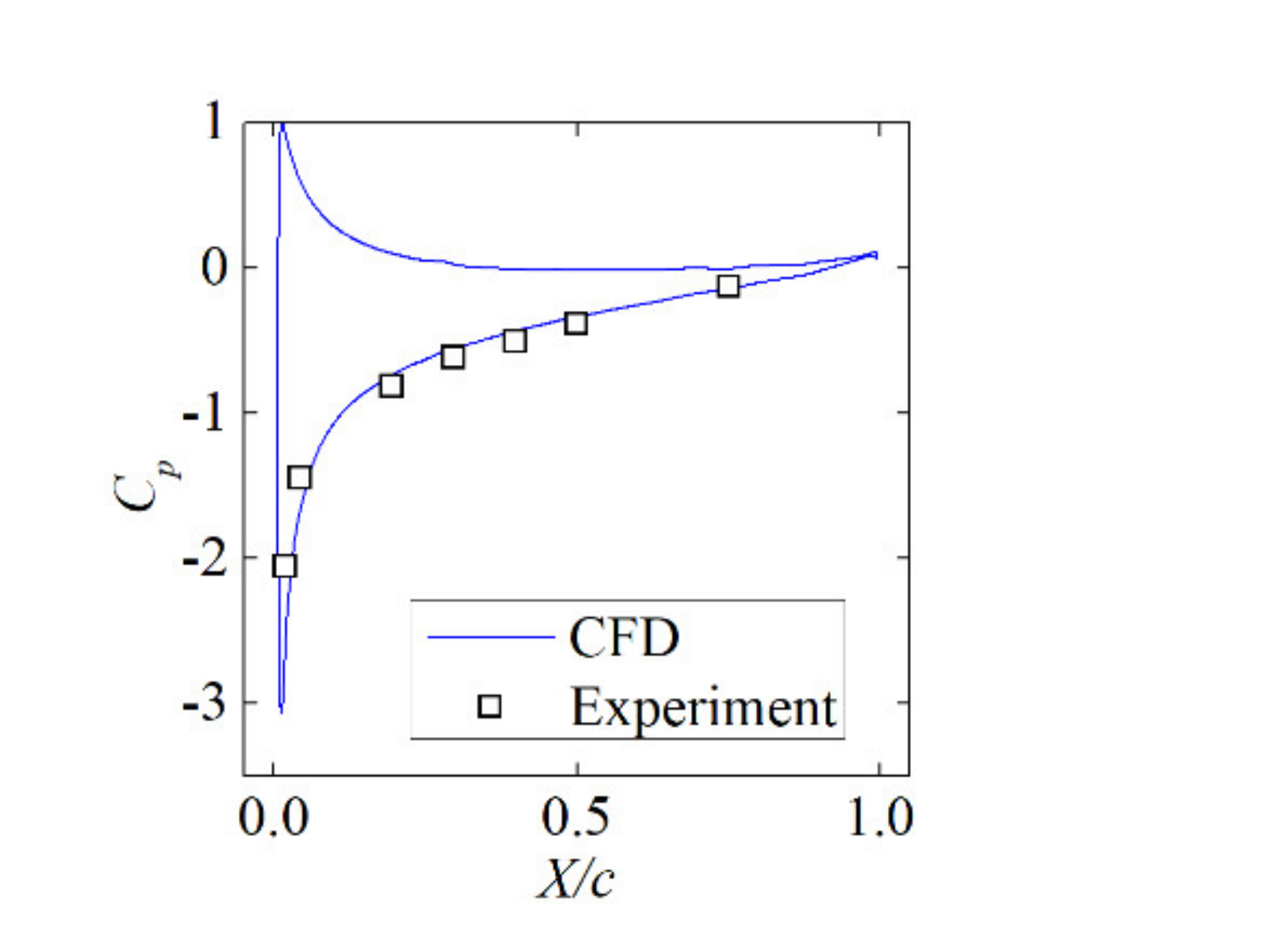
4. Numerical-Experimental Verification
5. Cavitation Vapor Proportion at Different Altitudes
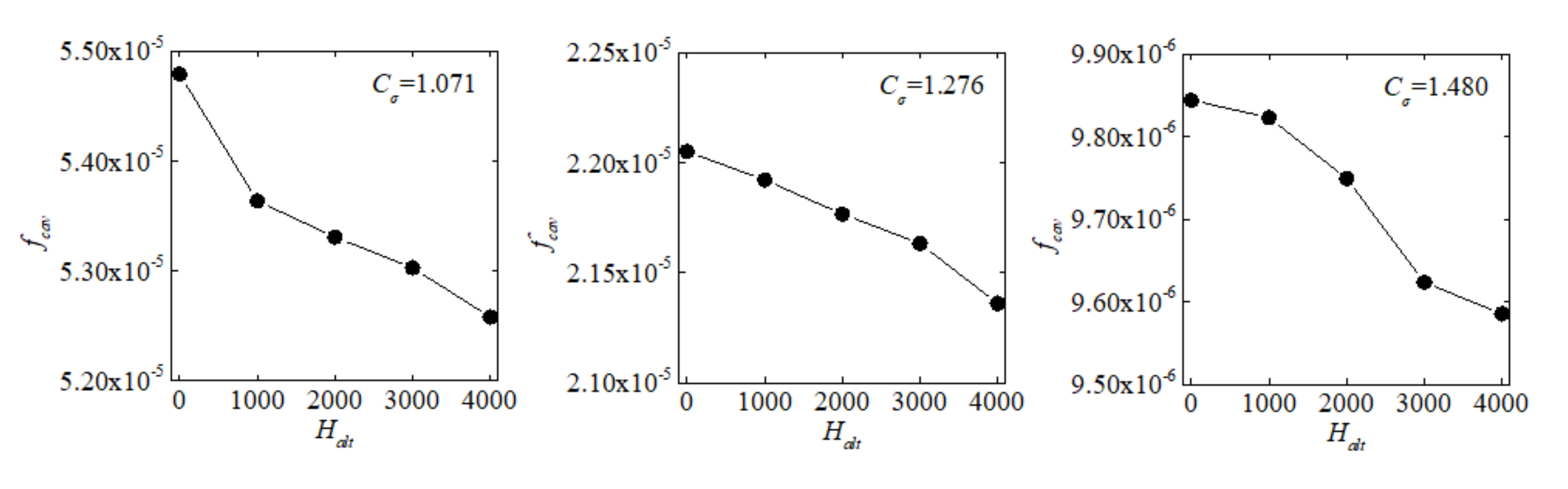
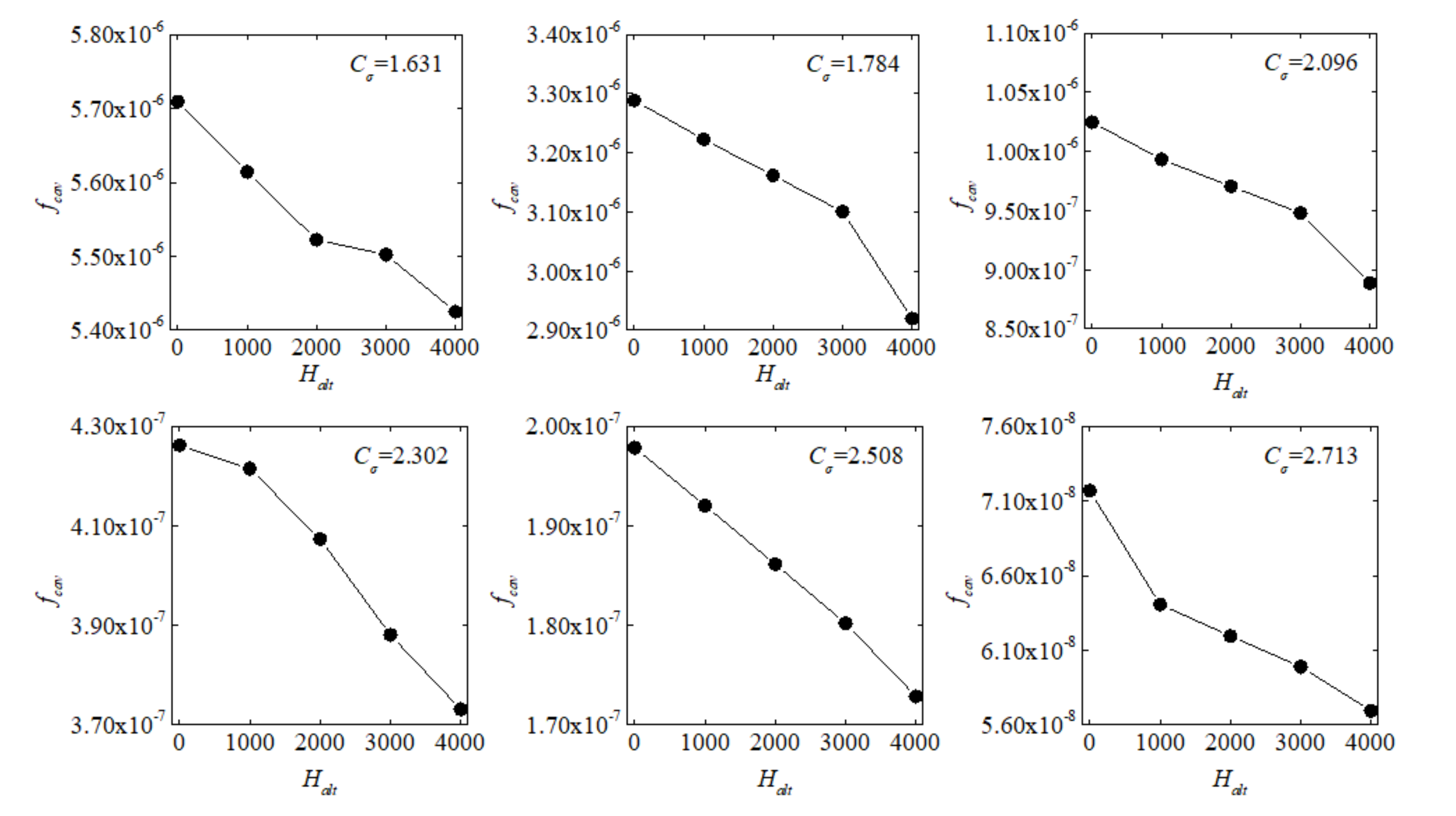
5.1. Variation Law
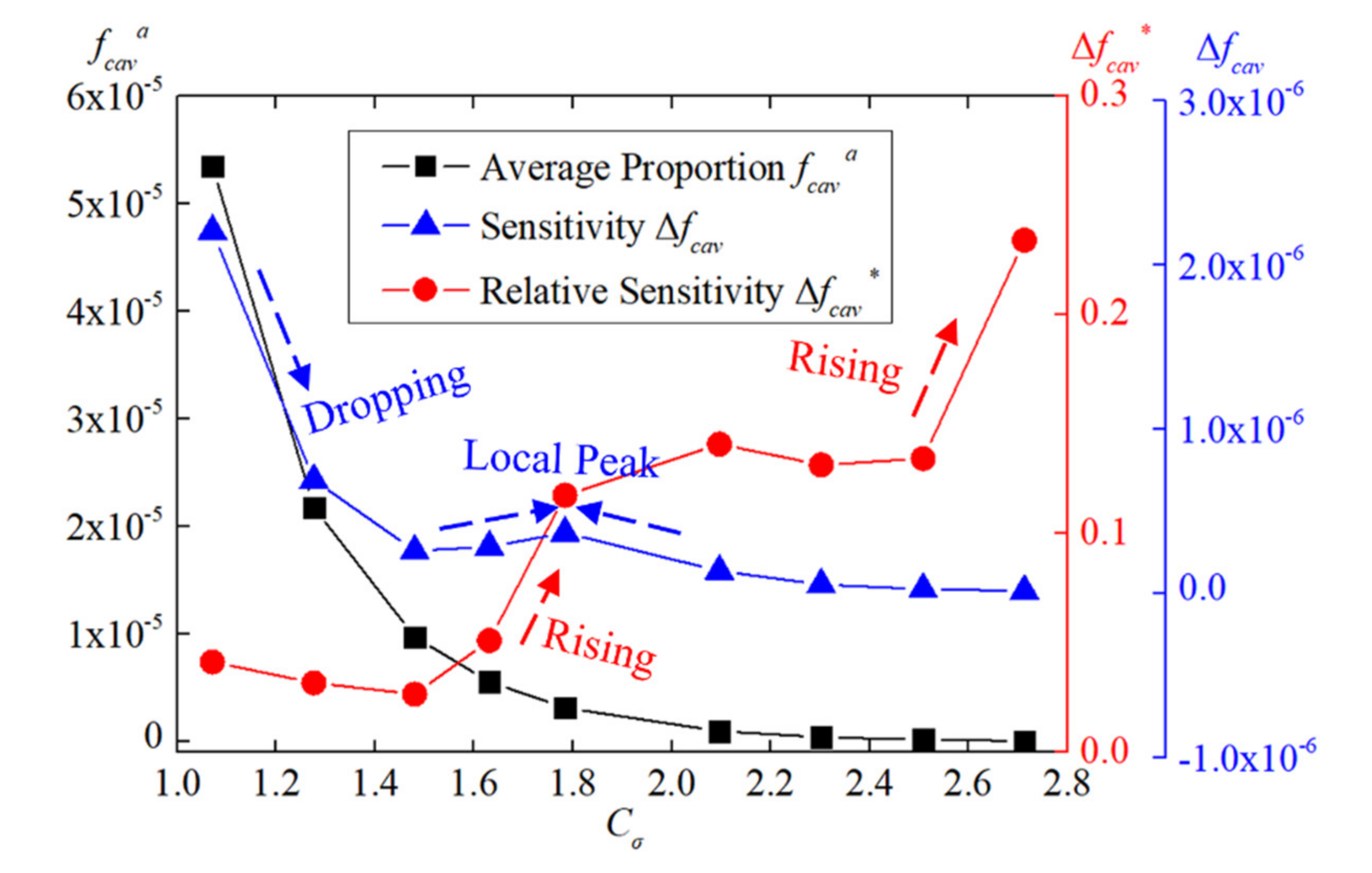
5.2. Sensitivity Analysis
6. Flow Behaviors Considering Altitude Level
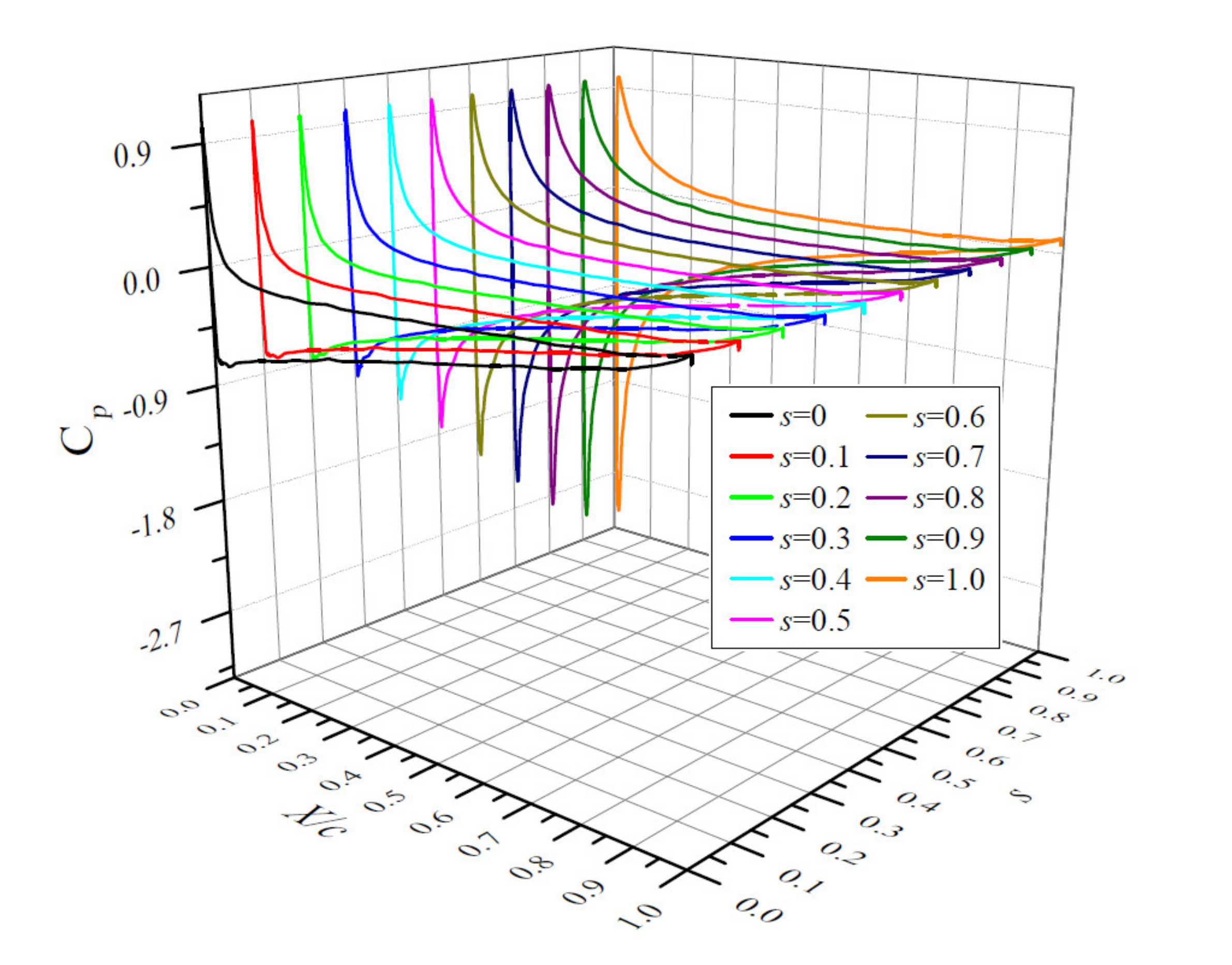
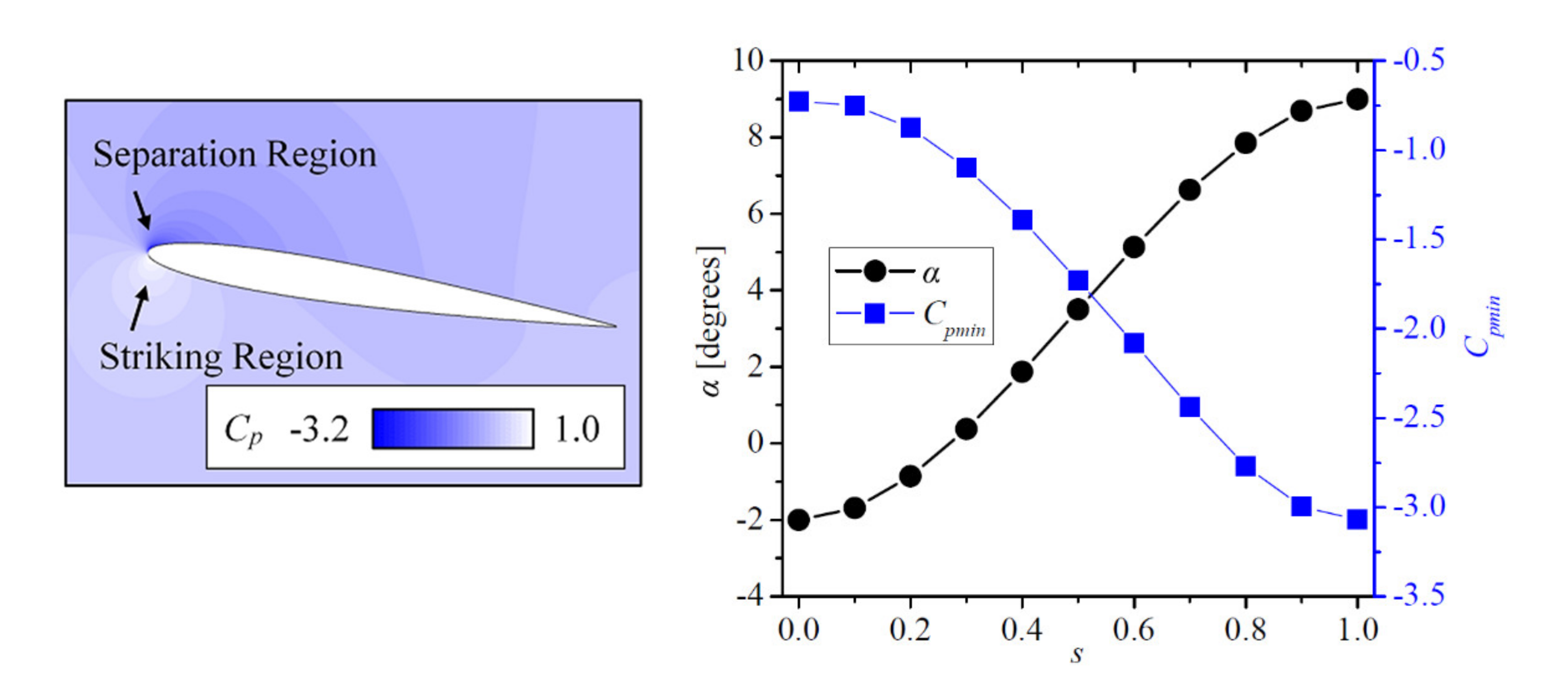
6.1. Pressure Distribution Law on Foil Surface
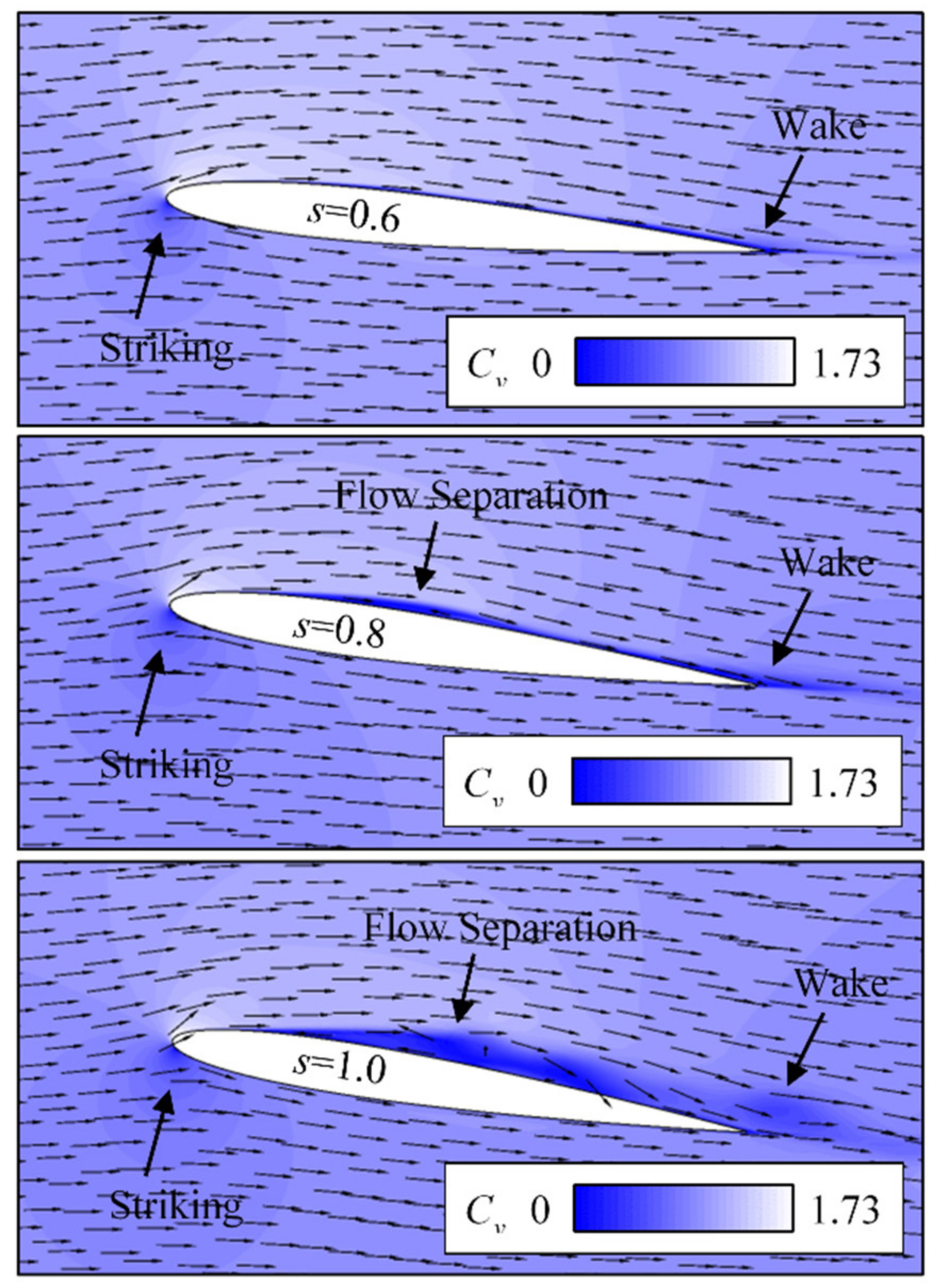
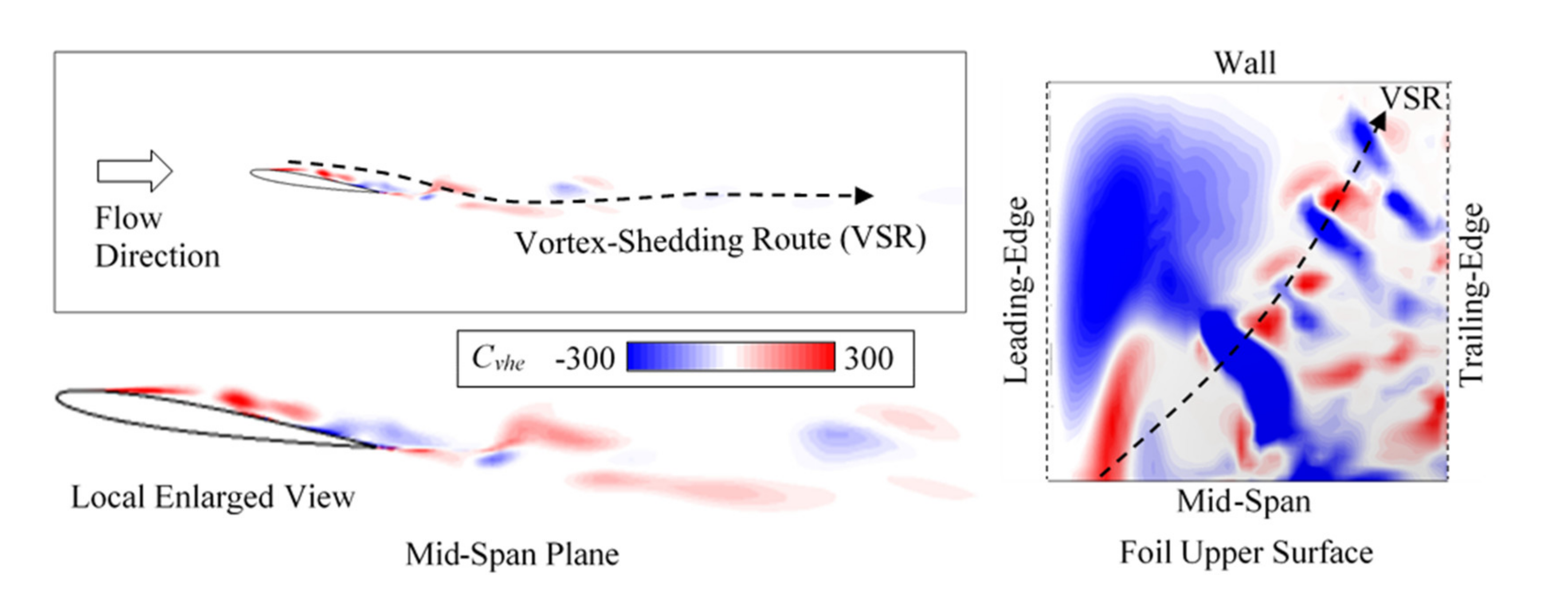
6.2. Turbulent Flow around Foil
6.3. Development of Cavitation at Halt- = 4000 m
7. Conclusions
- (1)
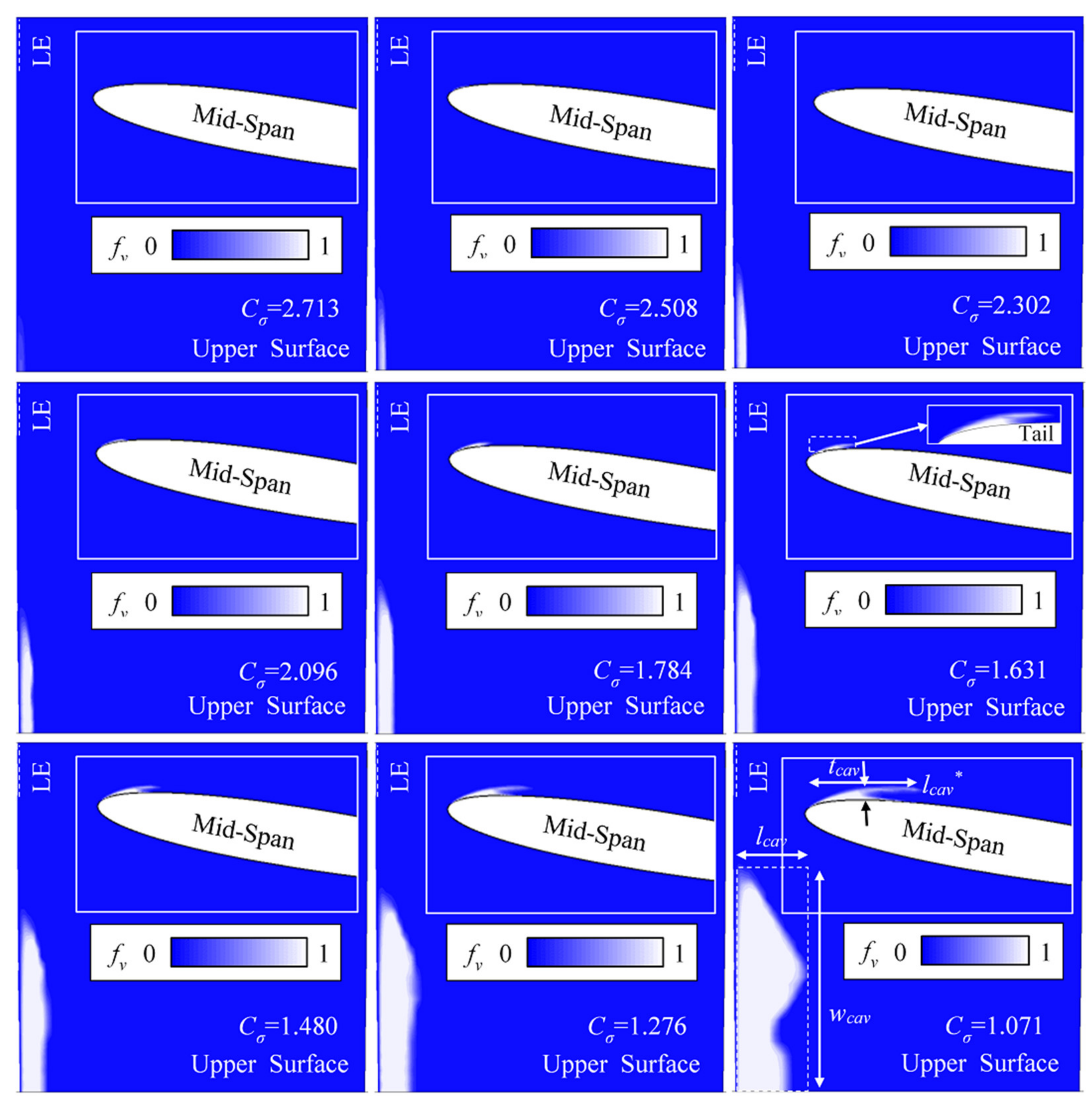
- With the decreasing of cavitation coefficient Cσ, the scale of cavitation continually increases and the increasing is quicker and quicker. The nuclei volume fraction fvnuc has obvious influence on cavitation. The size of cavitation is different at different altitude levels. If the altitude is higher within 0~4000 m, the fvnuc is lower and the size of cavitation is smaller. The difference of the size of cavitation among altitude levels is bigger when Cσ is small. That is, the sensitivity Δfcav is high. On the contrary, the relative sensitivity Δfcav*, which is the ratio between Δfcav and the absolute cavitation fraction fcav, is high when Cσ is large. When Cσ is 1.071, the Δfcav* between 0 m and 4000 m altitudes is about 4.6%. When Cσ increases to 2.713, the Δfcav* can be up to about 22.8%. It means that the cavitation volume fraction sensitivity should be considered in judging the inception cavitation of water pumps and hydro-turbines in the plateau environment.
- (2)
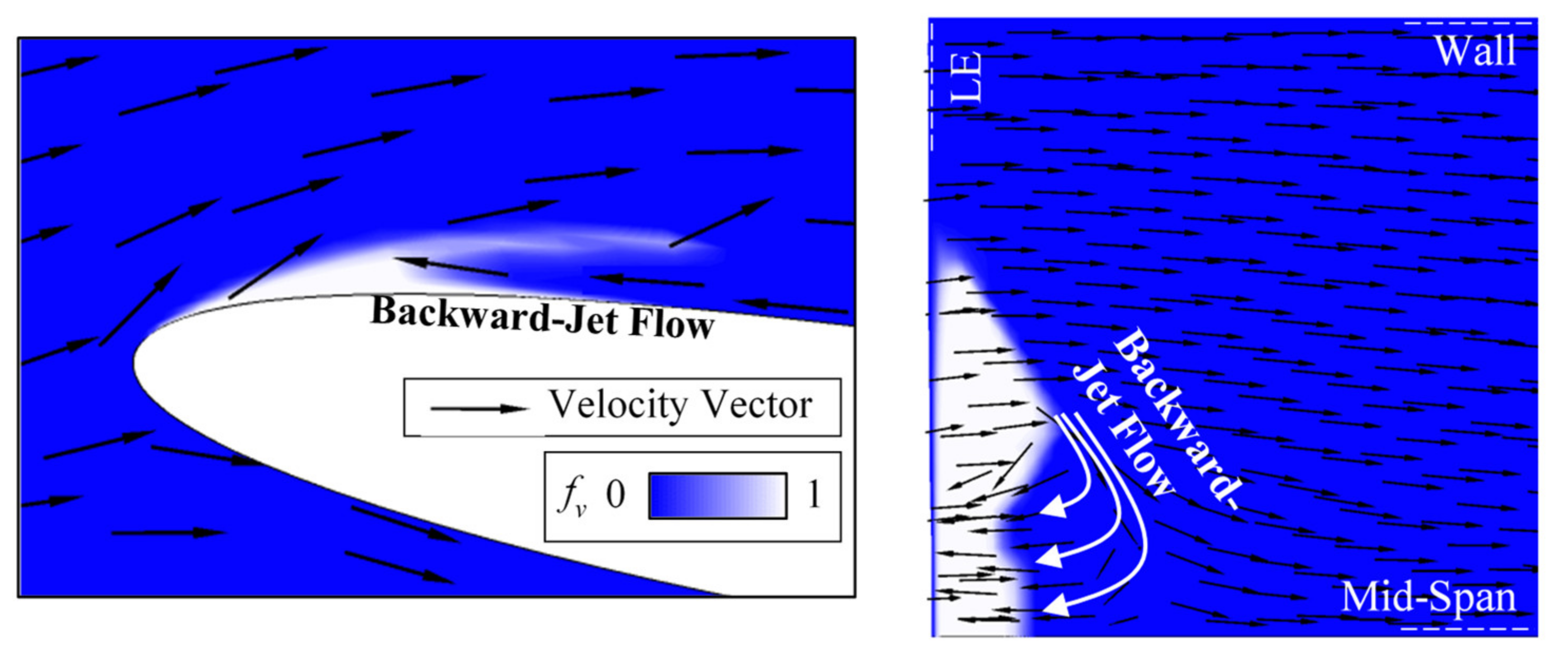
- For this twisted hydrofoil, the installation angle and flow incidence angle are different at different spans. The incoming flow will cause local high pressure on the lower surface of hydrofoil. There will be a local low pressure site on the foil upper surface due to flow separation. This low pressure will cause cavitation. From sidewall to mid-span, the installation angle increases and the minimum pressure decreases. With the decreasing of Cσ, the size of cavitation extends along the spanwise direction, streamwise direction and thickness direction. The growth rate is high in the spanwise (cavity width) and streamwise (cavity length) directions and low in thickness direction. When the size of cavitation is large enough, it will be broken by backflow-jet flow. A tail generates and the cavity becomes relatively unstable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dupont, P. Numerical prediction of cavitation-improving pump design. World Pumps 2001, 83, 26–28. [Google Scholar]
- Arndt, R.E.A. Cavitation in fluid machinery and hydraulic structures. Annu. Rev. Fluid Mech. 2003, 13, 273–326. [Google Scholar] [CrossRef]
- Roussopoulos, K.; Monkewitz, P.A. Measurements of tip vortex characteristics and the effect of an anti-cavitation lip on a model Kaplan turbine blade. Flow Turbul. Combust. 2012, 64, 119–144. [Google Scholar] [CrossRef]
- Čdina, M. Detection of cavitation phenomenon in a centrifugal pump using audible sound. Mech. Syst. Signal Process. 2003, 17, 1335–1347. [Google Scholar] [CrossRef]
- Ni, Y.; Yuan, S.; Pan, Z.; Yuan, J. Detection of cavitation in centrifugal pump by vibration methods. Chin. J. Mech. Eng. 2008, 5, 50–53. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, Z.; Stone, H.A.; Liu, S. Motion of a Free-Settling Spherical Particle Driven by a Laser-Induced Bubble. Phys. Rev. Lett. 2017, 119, 084501. [Google Scholar] [CrossRef] [PubMed]
- Arabnejad, M.H.; Amini, A.; Farhat, M.; Bensow, R.E. Hydrodynamic mechanisms of aggressive collapse events in leading edge cavitation. J. Hydrodyn. 2020, 32, 6–19. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Farhat, M. Effect of leading edge roughness on cavitation inception and development on thin hydrofoil. J. Drain. Irrig. Mach. Eng. 2017, 35, 921–926. [Google Scholar]
- Dreyer, M.; Decaix, J.; Münch-Alligné, C.; Farhat, M. Mind the gap: A new insight into the tip leakage vortex using stereo-PIV. Exp. Fluids 2014, 55, 1–13. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, L.; Wang, Z.; Liu, M.; Cheng, H. Numerical simulation for the tip leakage vortex cavitation. Ocean Eng. 2018, 151, 71–81. [Google Scholar] [CrossRef]
- Escaler, X.; Farhat, M.; Avellan, F.; Egusquiza, E. Cavitation erosion tests on a 2D hydrofoil using surface-mounted obstacles. Wear 2003, 254, 441–449. [Google Scholar] [CrossRef]
- Melissaris, T.; Bulten, N.; Terwisga, T.J.C. On the applicability of cavitation erosion risk models with a URANS solver. J. Fluids Eng. 2019, 141, 101104. [Google Scholar] [CrossRef] [Green Version]
- Arakeri, V.H.; Acosta, A.J. Viscous effects in the inception of cavitation on axisymmetric bodies. J. Fluids Eng. 1973, 95, 519–527. [Google Scholar] [CrossRef] [Green Version]
- Morgut, M.; Nobile, E.; Biluš, I. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil. Int. J. Multiph. Flow 2011, 37, 620–626. [Google Scholar] [CrossRef]
- Shi, S.; Wang, G.; Wang, F.; Deming, G. Experimental study on unsteady cavitation flows around three-dimensional hydrofoil. Chin. J. Appl. Mech. 2011, 28, 105–110. [Google Scholar]
- Sear, R.P. Nucleation: Theory and applications to protein solutions and colloidal suspensions. J. Phys. Condens. Matter 2007, 19, 033101. [Google Scholar] [CrossRef]
- Liu, Y.; He, L.; Nie, Q.; Yin, C. Impact of hydropower development on the landscape pattern of Yarlung Zangbo river basin. Water Power 2020, 46, 1–5. [Google Scholar]
- Jaber, J.O. Prospects and challenges of small hydropower development in Jordan. Jordan J. Mech. Ind. Eng. 2012, 6, 110–118. [Google Scholar]
- Feng, C. Monitor of Qinghai-Tibet plateau hydro-thermal circulation with heat pulse. Acta Geol. Sin. 2013, 87, 631–632. [Google Scholar]
- Ahn, S.-H.; Xiao, Y.; Wang, Z.; Zhou, X.; Luo, Y. Numerical prediction on the effect of free surface vortex on intake flow characteristics for tidal power station. Renew. Energy 2017, 101, 617–628. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Numerical and experimental evidence of the inter-blade cavitation vortex development at deep part load operation of a Francis turbine. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082005. [Google Scholar] [CrossRef]
- Ding, H.; Visser, F.; Jiang, Y.; Furmanczyk, M. Demonstration and validation of a 3D CFD simulation tool predicting pump performance and cavitation for industrial applications. J. Fluids Eng. 2011, 133, 011101. [Google Scholar] [CrossRef]
- Zhu, D.; Xiao, R.; Liu, W. Influence of leading-edge cavitation on impeller blade axial force in the pump mode of reversible pump-turbine. Renew. Energy 2021, 163, 939–949. [Google Scholar] [CrossRef]
- Lipej, A.; Mitruševski, D. Numerical Prediction of Inlet Recirculation in Pumps. Int. J. Fluid Mach. Syst. 2016, 9, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Brennen, C.E. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kubota, A.; Kato, H. Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling techniques. J. Fluids Eng. 1989, 111, 204–210. [Google Scholar] [CrossRef]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Sauer, J.; Schnerr, G.H. Unsteady cavitating flow-A new cavitation model based on a modified front capturing method and bubble dynamics. In Proceedings of the 2000 ASME Fluid Engineering Summer Conference, Boston, MA, USA, 11–15 June 2000. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Wang, F. Analysis Method of Flow in Pumps and Pumping Stations; China Water & Power Press: Beijing, China, 2020. [Google Scholar]
- Bensow, R.E. Simulation of the unsteady cavitation on the Delft Twist11 foil using RANS, DES and LES. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Liu, W.; Wei, W.L.; Tian, G.X.; Liu, J.; Liu, Q.H. Research on basic physiological principles of respirator used for plateau areas. Chin. Med. Equip. J. 2010, 31, 22–36. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Vaz, G.; Lloyds, T.; Gnanasundaram, A. Improved Modelling of Sheet Cavitation Dynamics on Delft Twist11 Hydrofoil. In Proceedings of the Seventh International Conference on Computational Methods in Marine Engineering, Nantes, France, 15–17 May 2017. [Google Scholar]
- Olshanskii, M.A.; Rebholz, L.G. Velocity–vorticity–helicity formulation and a solver for the Navier–Stokes equations. J. Comput. Phys. 2010, 229, 4291–4303. [Google Scholar] [CrossRef] [Green Version]


| Altitude Halt | Nuclei Volume Fraction fvnuc |
|---|---|
| 0 m | 5 × 10−4 |
| 1000 m | 4.38 × 10−4 |
| 2000 m | 3.88 × 10−4 |
| 3000 m | 3.48 × 10−4 |
| 4000 m | 3.01 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Tao, R. Prediction of the Cavitation over a Twisted Hydrofoil Considering the Nuclei Fraction Sensitivity at 4000 m Altitude Level. Water 2021, 13, 1938. https://doi.org/10.3390/w13141938
Luo H, Tao R. Prediction of the Cavitation over a Twisted Hydrofoil Considering the Nuclei Fraction Sensitivity at 4000 m Altitude Level. Water. 2021; 13(14):1938. https://doi.org/10.3390/w13141938
Chicago/Turabian StyleLuo, Hongying, and Ran Tao. 2021. "Prediction of the Cavitation over a Twisted Hydrofoil Considering the Nuclei Fraction Sensitivity at 4000 m Altitude Level" Water 13, no. 14: 1938. https://doi.org/10.3390/w13141938
APA StyleLuo, H., & Tao, R. (2021). Prediction of the Cavitation over a Twisted Hydrofoil Considering the Nuclei Fraction Sensitivity at 4000 m Altitude Level. Water, 13(14), 1938. https://doi.org/10.3390/w13141938






