A Comprehensive Evaluation Model of Ammonia Pollution Trends in a Groundwater Source Area along a River in Residential Areas
Abstract
:1. Introduction
2. Materials and Methods
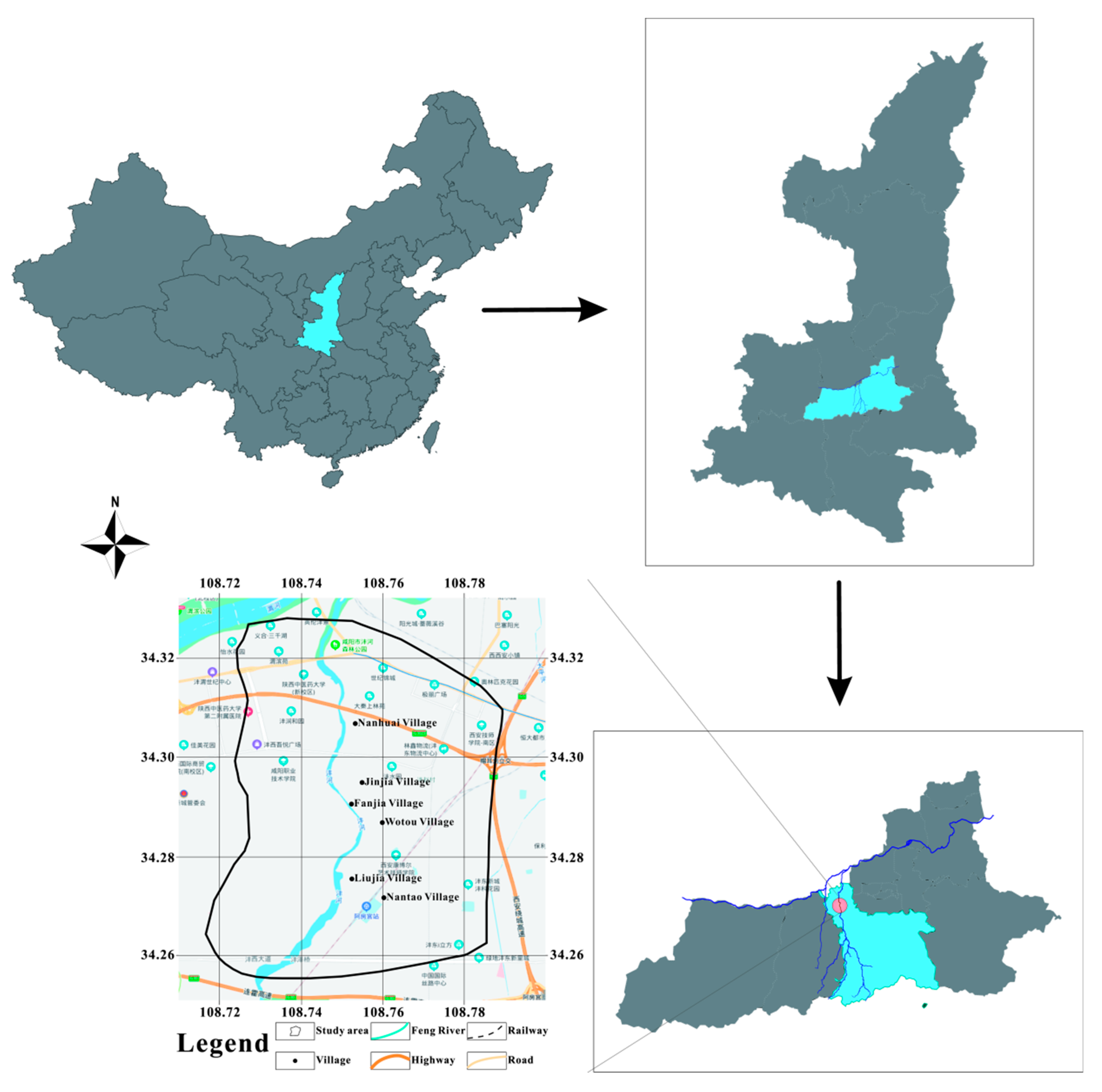
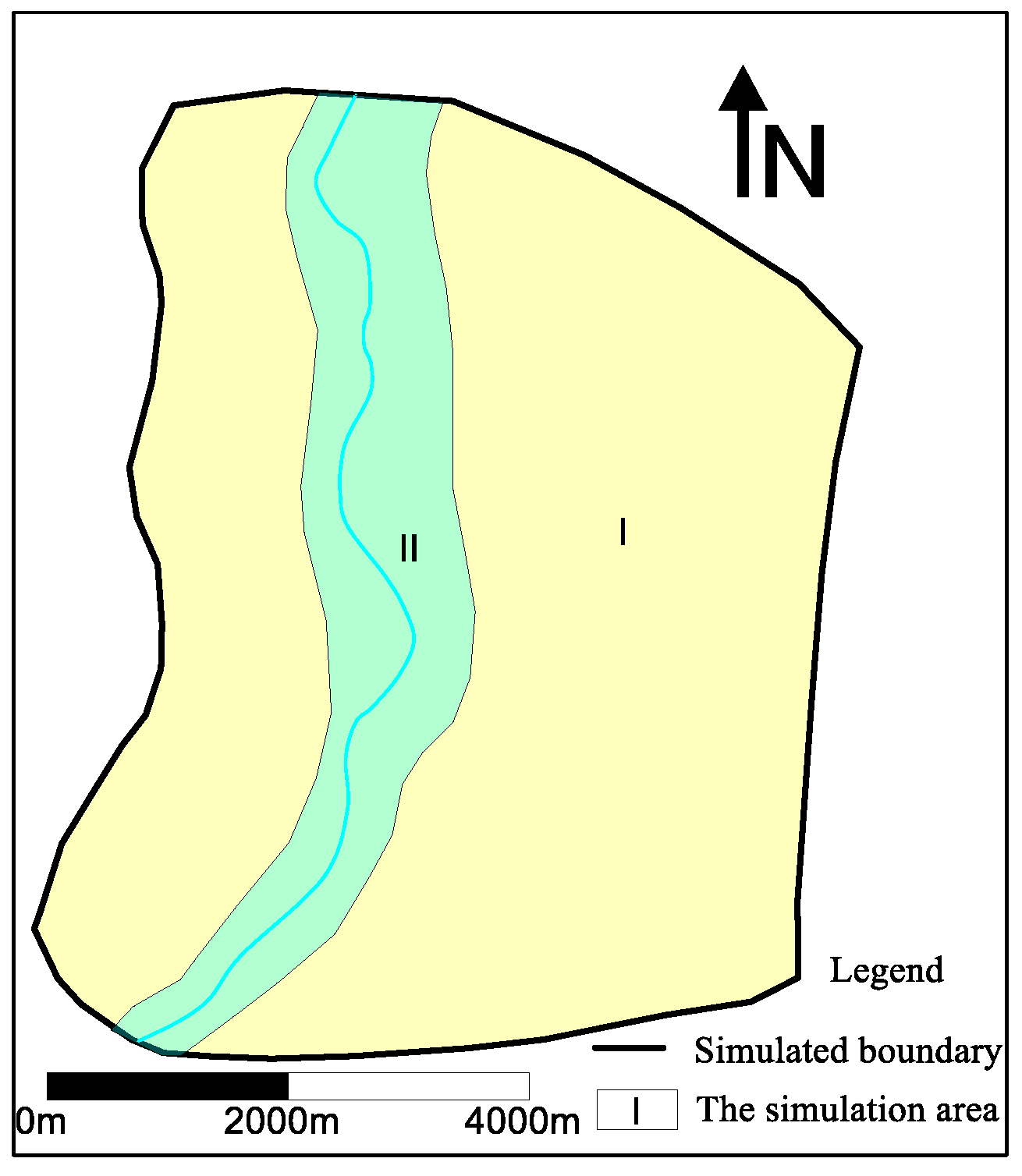
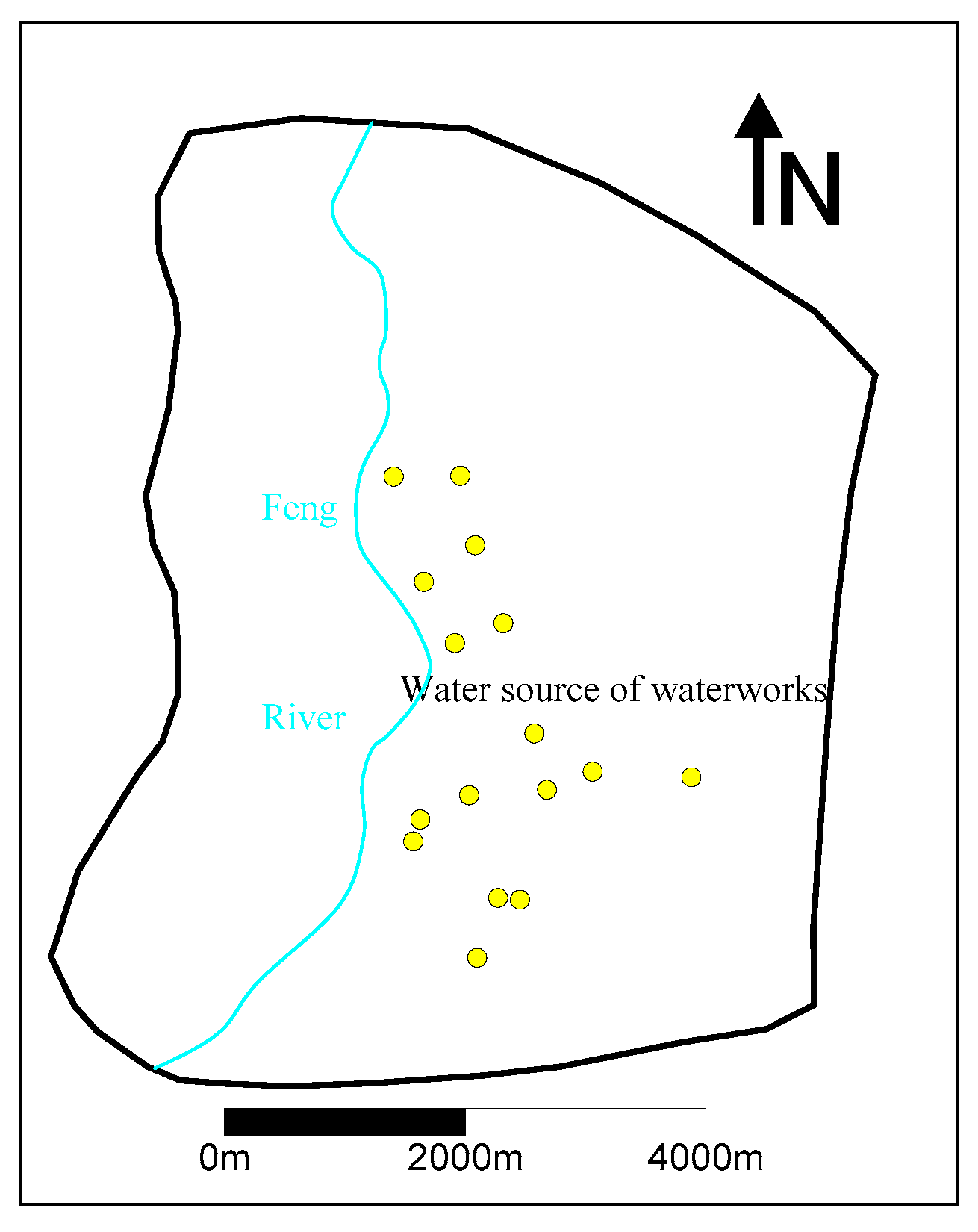
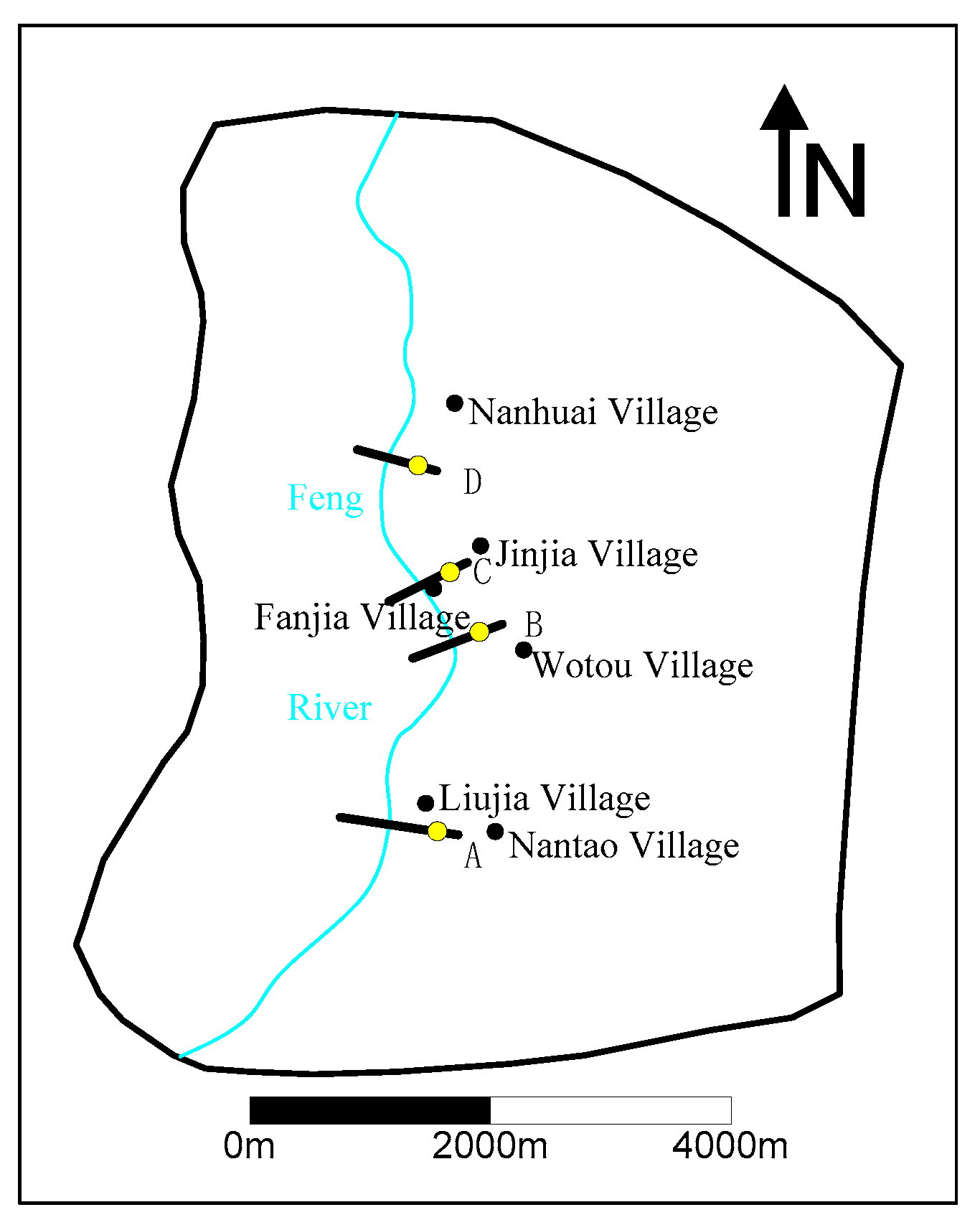
2.1. Study Area
2.2. Numerical Simulation of Groundwater Flow
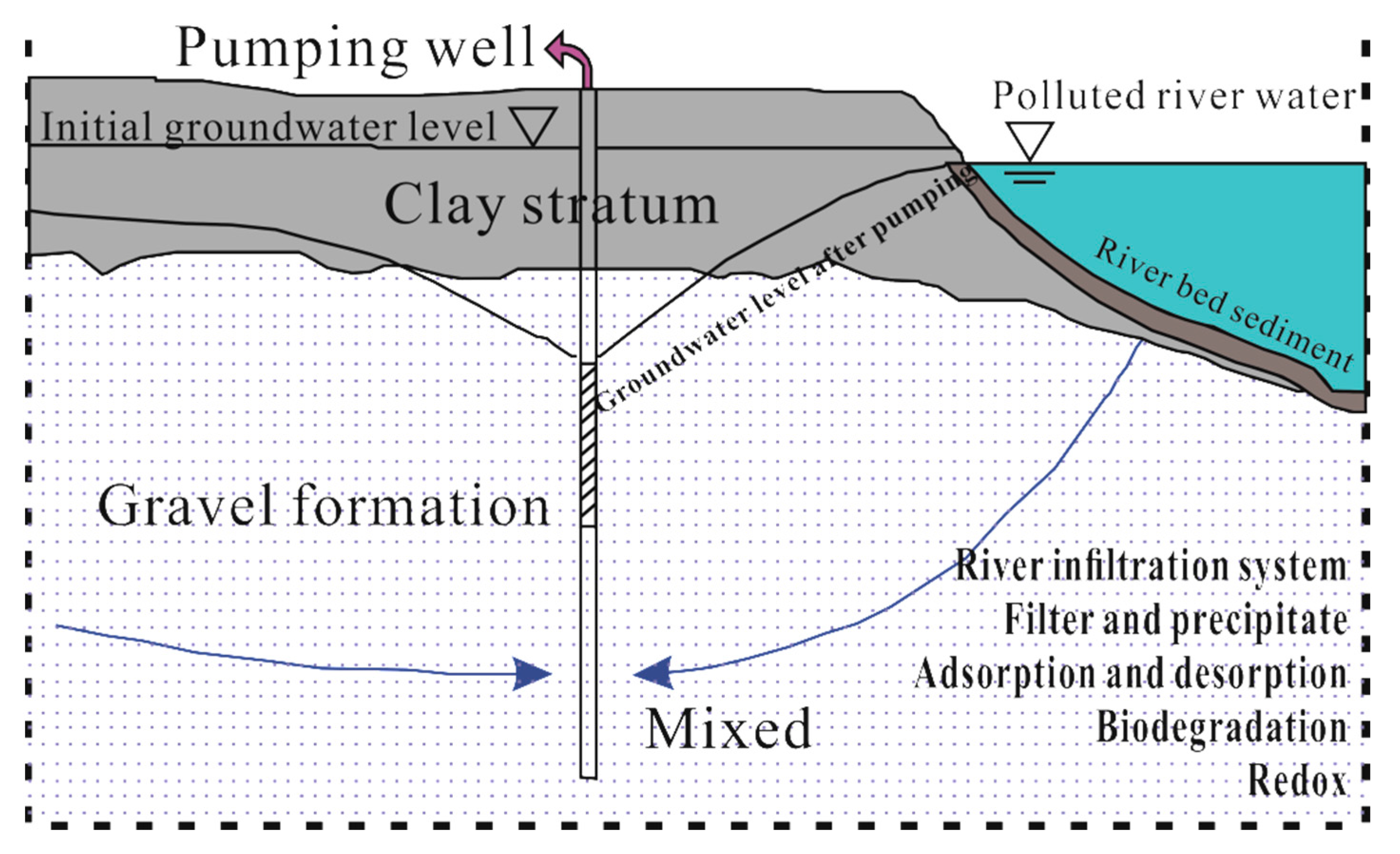
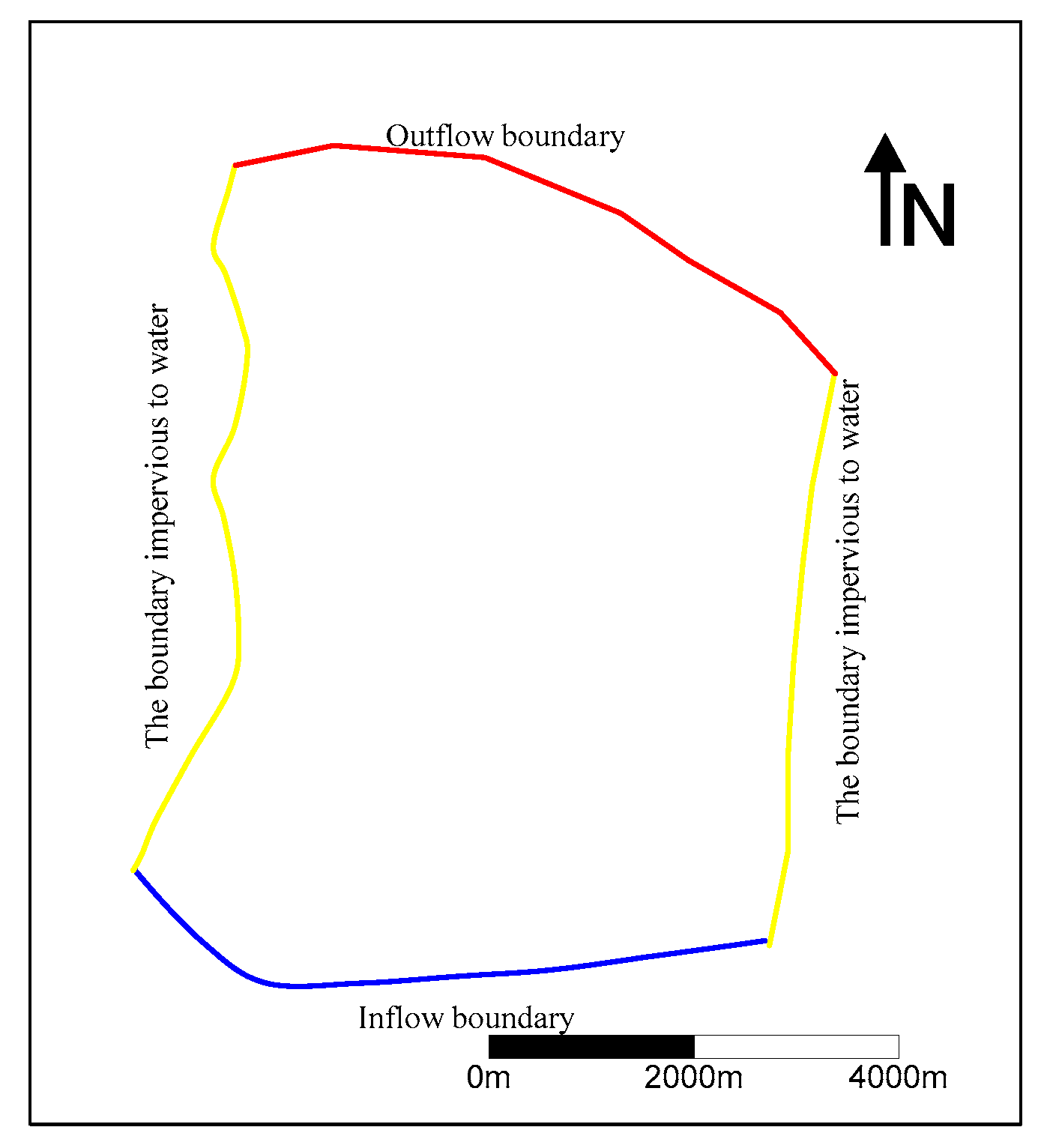
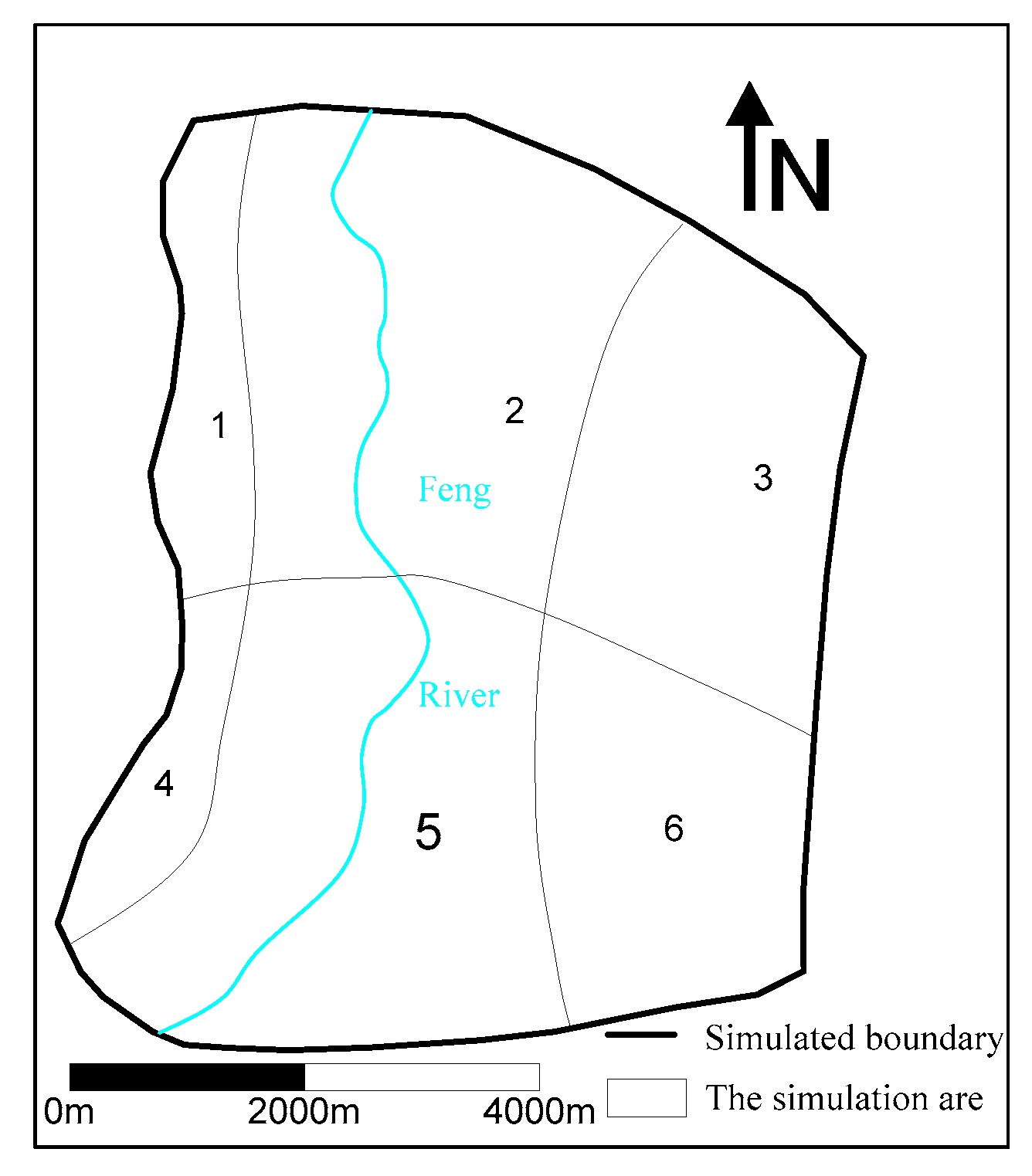
2.2.1. Generalization of Aquifers and Boundary Conditions
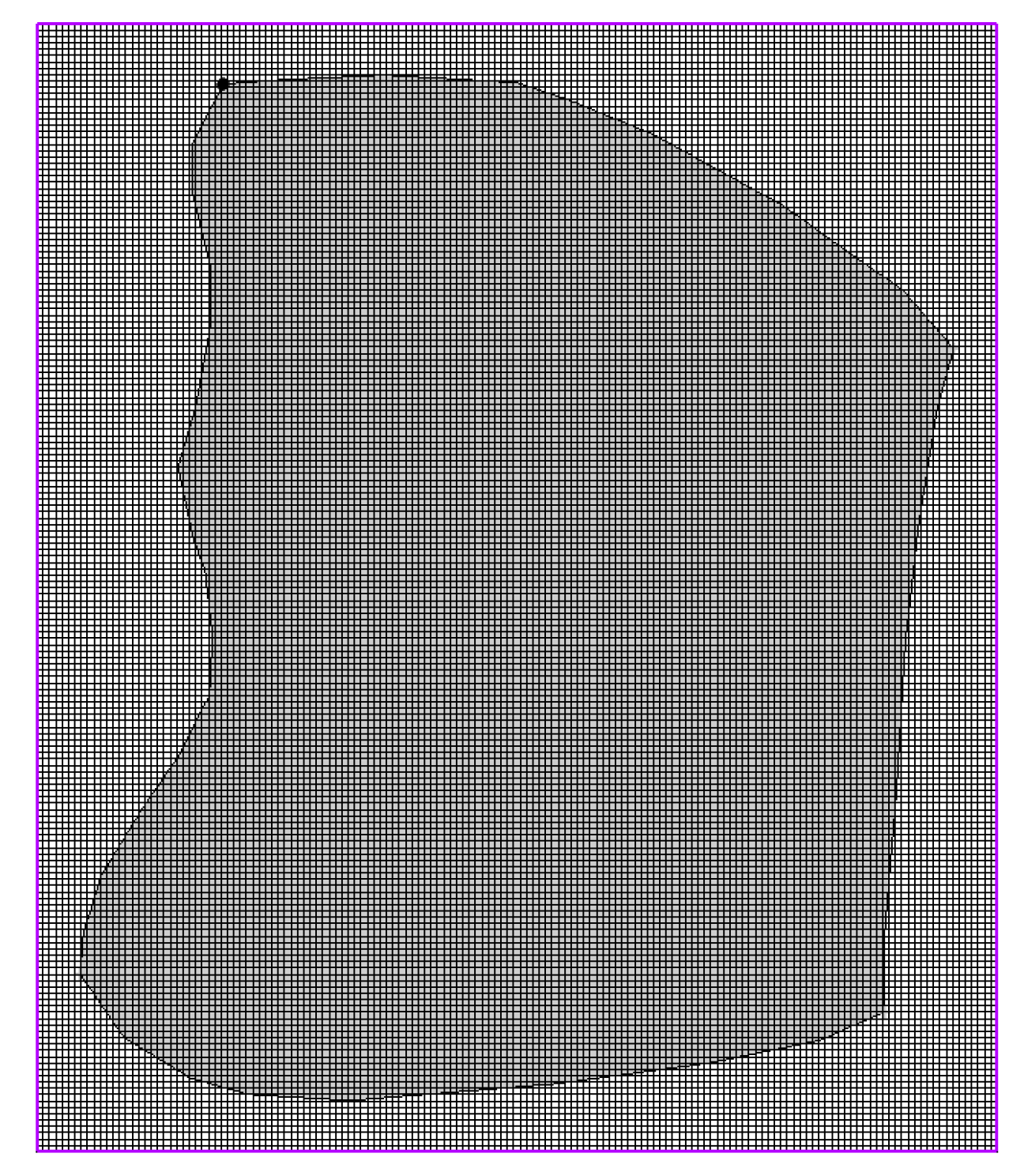
2.2.2. Meshing
2.2.3. Terms of Source and Sink
- —quantity of rain recharges (m3/d);
- —coefficient of rain infiltration of each calculation partition;
- —precipitation of each calculation partition (m/d); and
- —area of each calculation partition (m2).
- —quantity of river recharges (m3/d);
- K—coefficient of infiltration (m/d);
- B—length of the river in the study area (m);
- H—distance from the river level to the aquifer floor in the calculation interval (m);
- h—distance from the phreatic water level to the aquifer floor in the calculation interval (m); and
- b—width of the supply zone of the river (m).
- —quantity of lateral runoff recharges (m3/d);
- —coefficient of infiltration of the aquifer of part ;
- —normal hydraulic slope of the section of part ; and
- —area of the section of the aquifer of part (m2).
- —quantity of well irrigation return flow (104 m³/a);
- —quantity of agricultural extraction (104 m³/a); and
- —coefficient of well irrigation returns flow.
2.2.4. Hydrogeological Parameter
2.2.5. Mathematical Model
- Ω—vadose zone;
- H—height of the groundwater level (m);
- K—hydraulic conductivity of the aquifer in horizontal direction (m/d);
- H0—initial flow field (m);
- ε—terms of source and sink of the aquifer (m/d);
- Γ2—second-class boundary of the vadose zone;
- n—normal direction of the boundary surface;
- —derivative of H along the outer n (dimensionless);
- q—single-width flow on Γ2 (m2/d), with its inflow positive and its outflow negative; and
- —elevation of the aquifer floor (m).
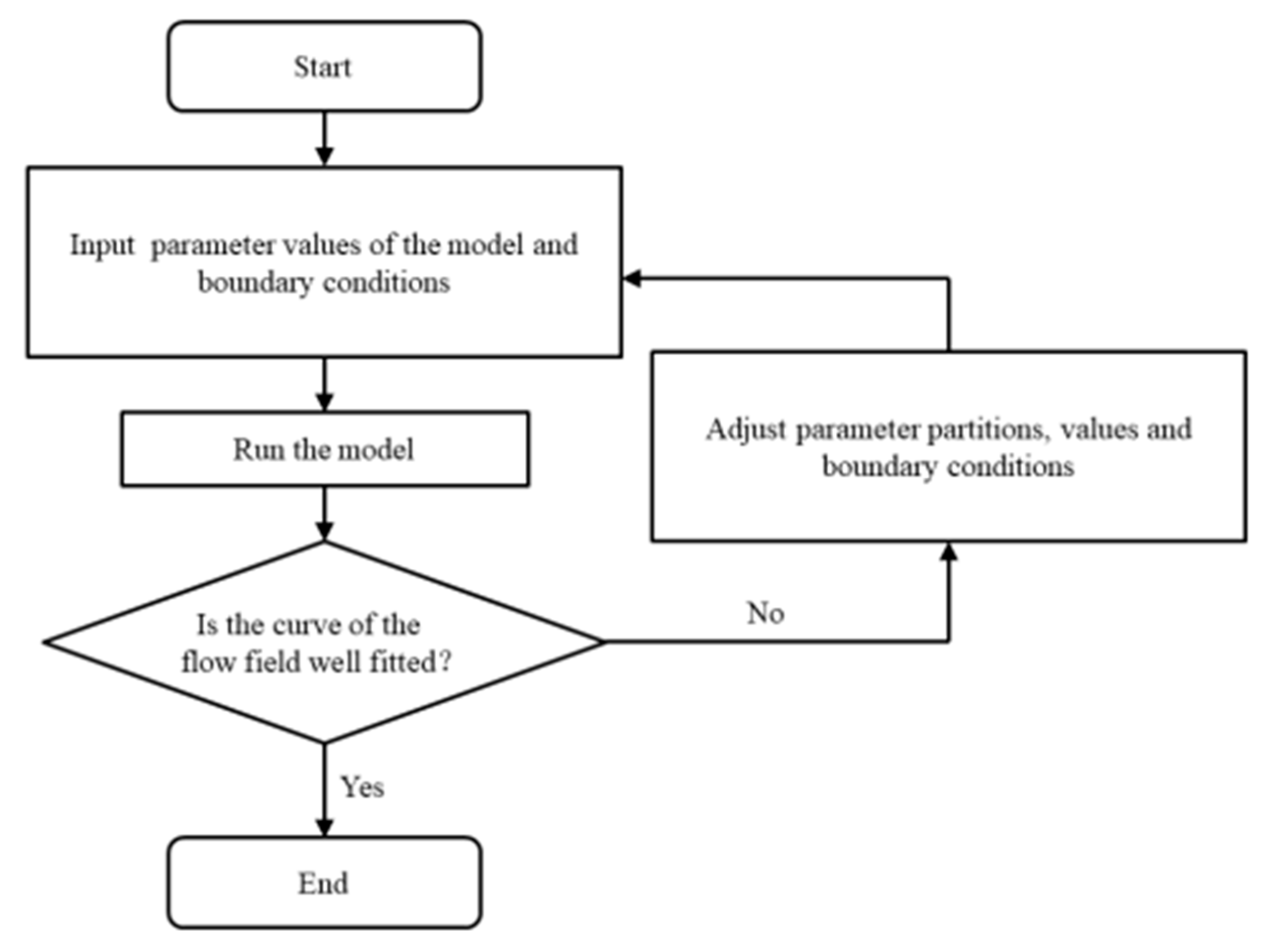
2.2.6. Solving Process
2.2.7. Temporal Discretization
2.2.8. Run the Model
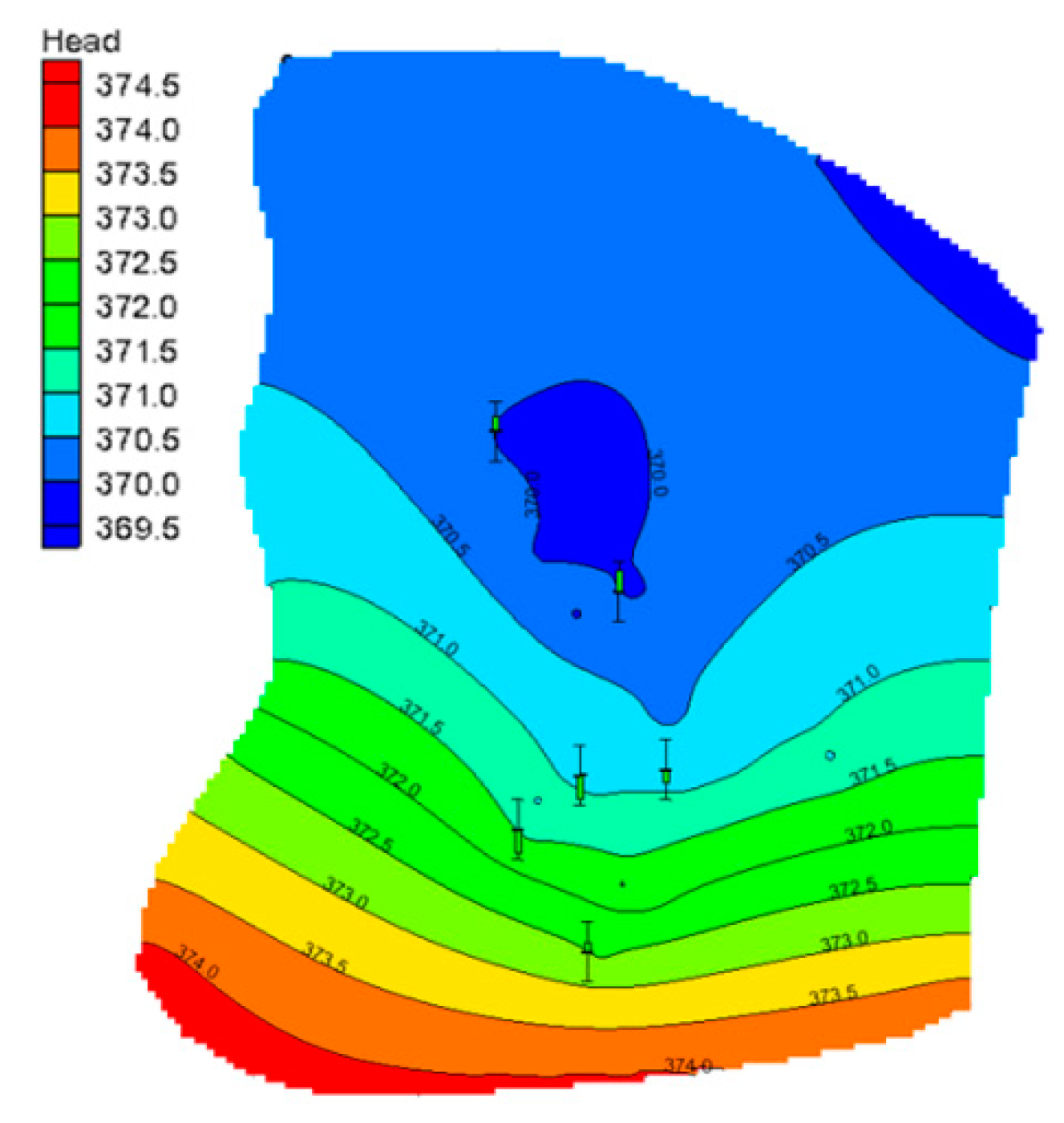
2.2.9. Model Identification and Validation
2.3. Model of Migration of Pollutants in the Groundwater
- C—concentration of the dissolved phase of the pollutants (ML−3);
- θ—porosity of the stratum medium (dimensionless);
- t—time (T);
- —distance along the axis of the rectangular coordinate system (L);
- —tensor of the coefficient of hydrodynamic dispersion (L2T−1);
- —actual flow rate of pore water on average (LT−1);
- —flow of the aquifer per unit volume, representing source (positive) and sink (negative) (T−1);
- —concentration of pollutants in a source or sink (ML−3);
- —term of chemical reaction (ML−3T−1); and
- Ω—overall simulation area.
2.3.1. Selection of Simulated Factors
2.3.2. Stress Period
3. Results
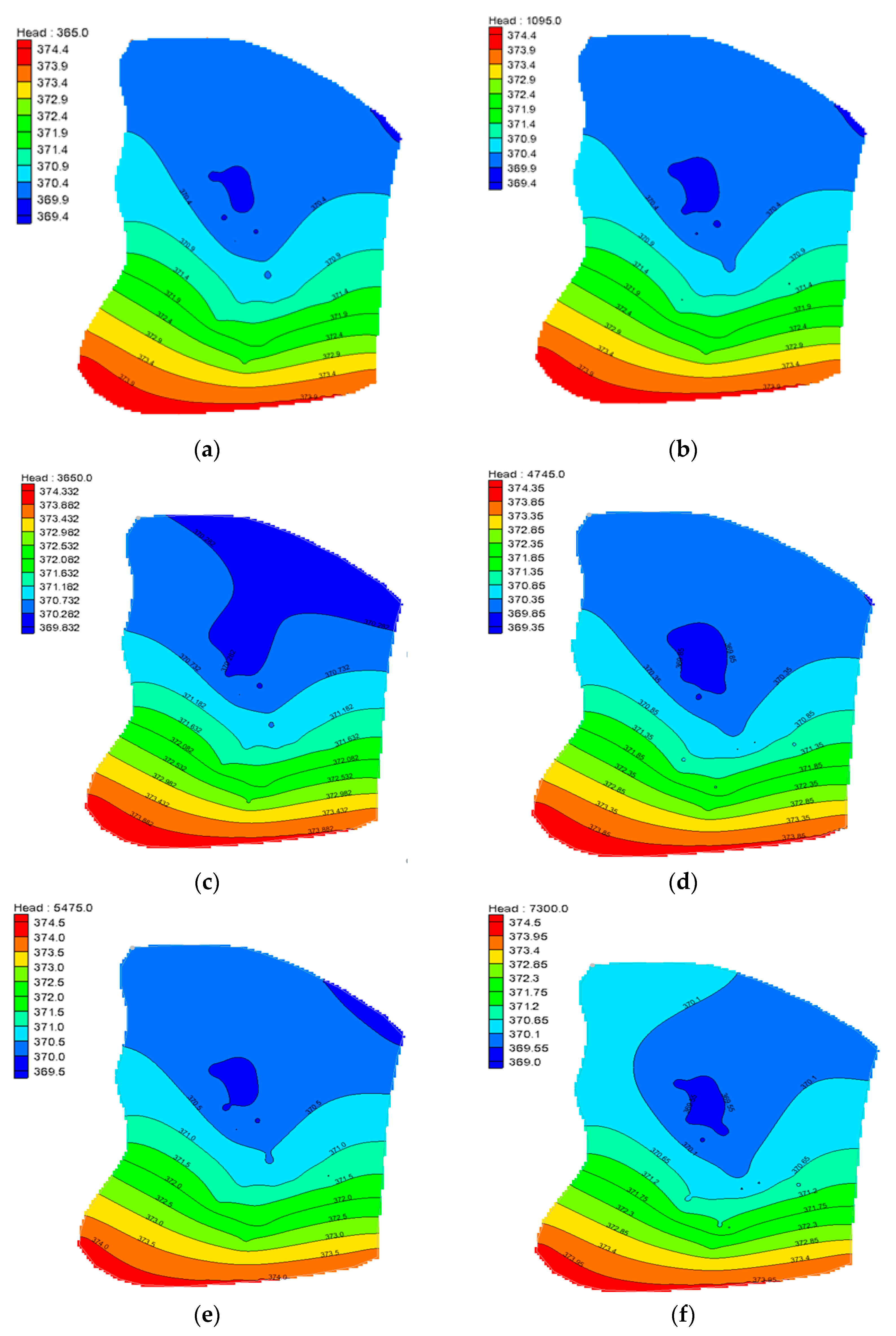
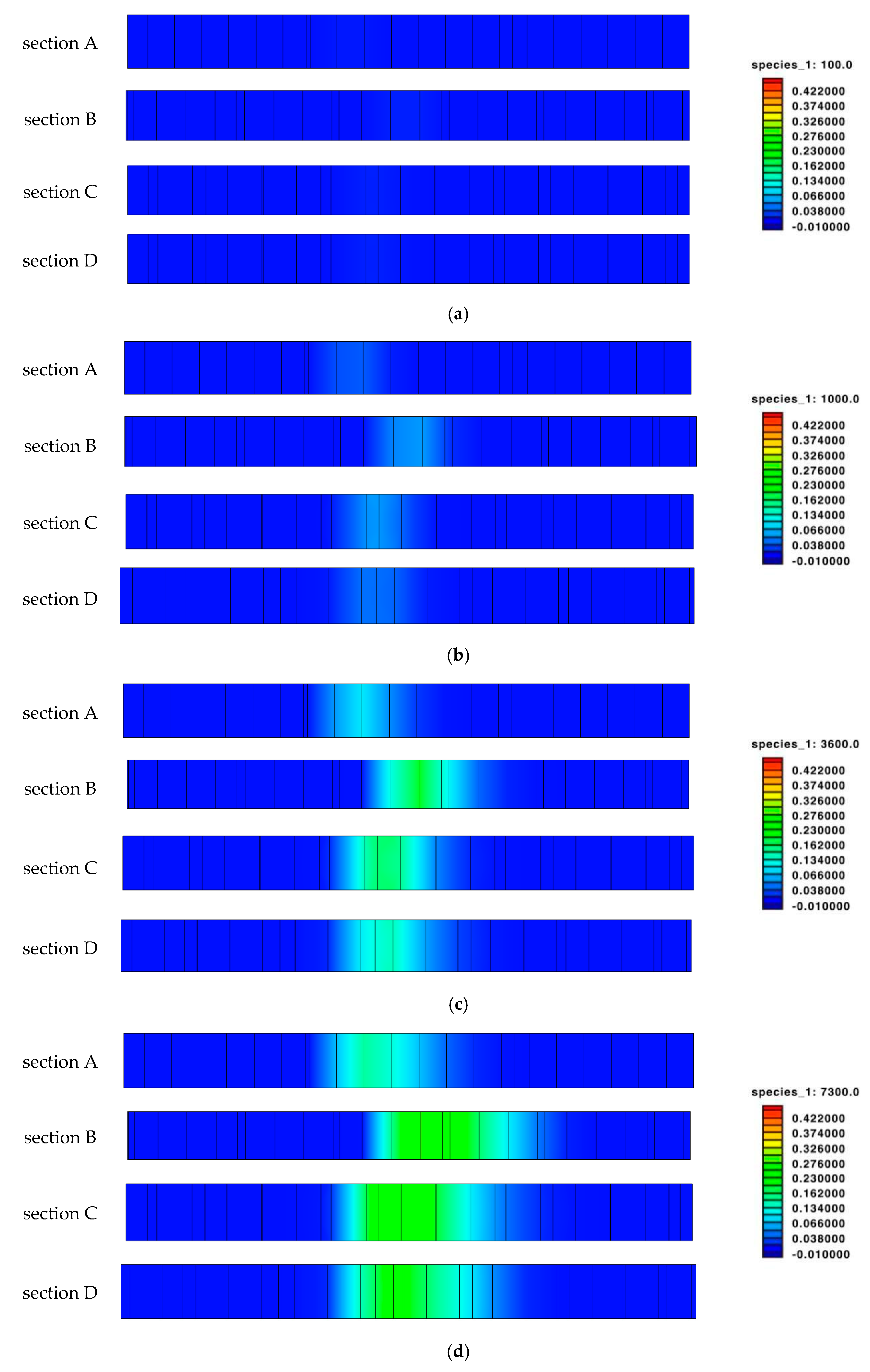
3.1. The Area of Influence of Ammonia
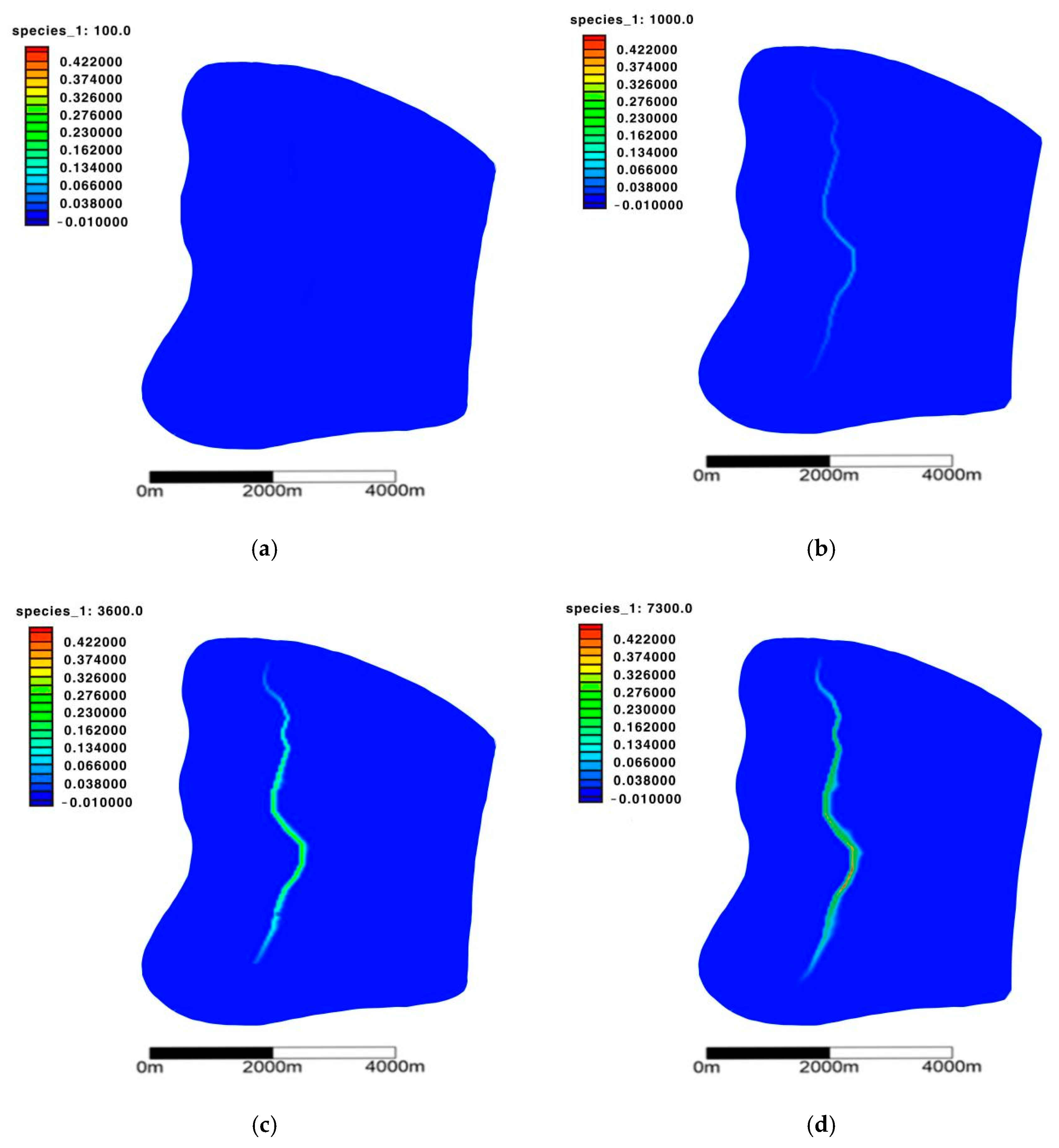
3.2. The Ammonia Pollution Plume
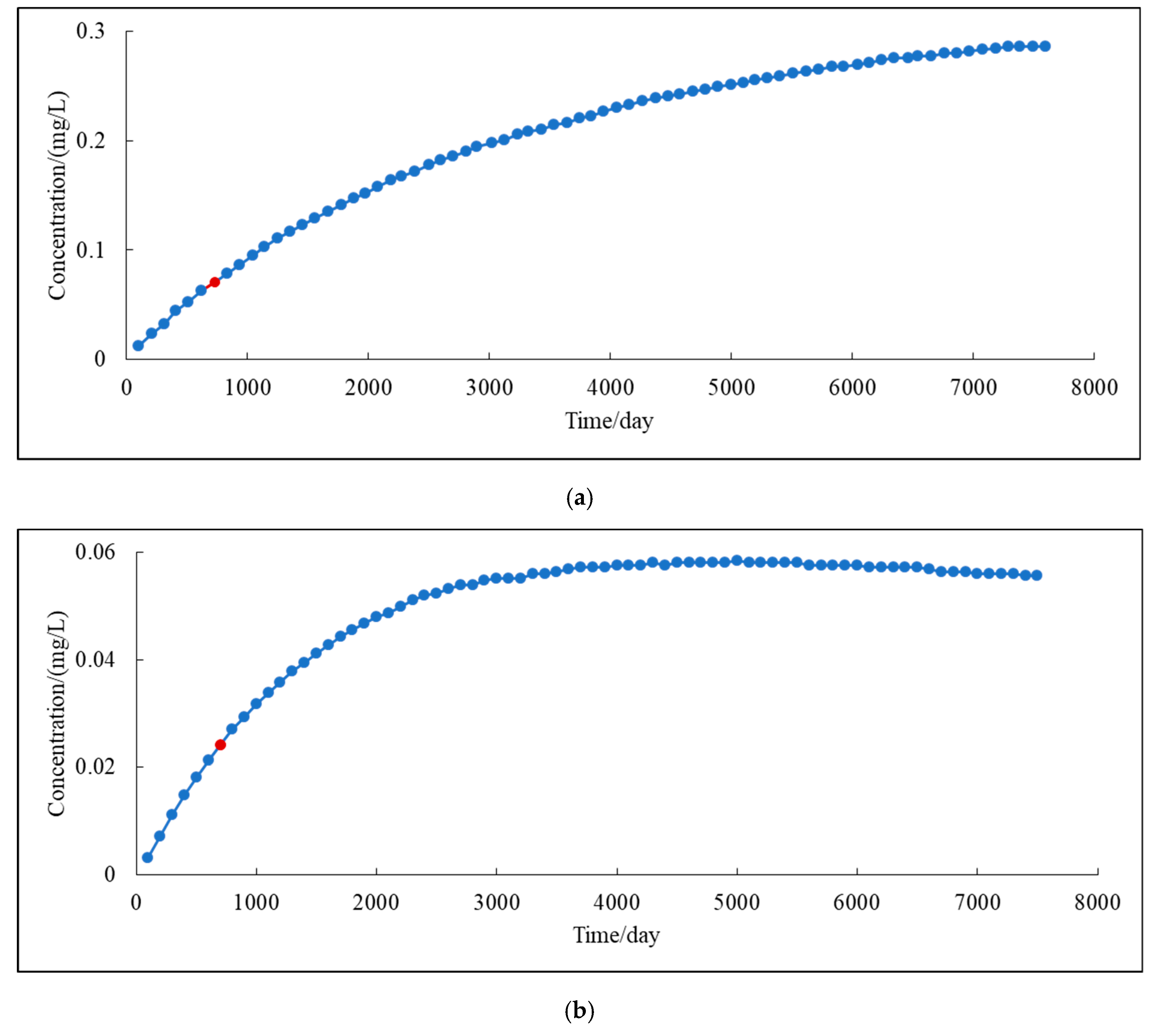
3.3. The Ammonia Content
4. Discussion
5. Conclusions
- (1)
- During this simulation, a field survey was conducted in the study area. Combined with the current hydrology and water quality of the study area, the hydrogeological conceptual model was converted into a numerical model of groundwater flow and solute transport. Additionally, by using ammonia as the simulation factor, the calibrated model was used to simulate the hydrology and water quality of the study area. It is concluded that the established hydrogeological conceptual model and numerical model are correct, and the selected parameters and calculated source and sink terms are reasonable, which conform to the actual groundwater conditions in the study area. Thus, the results of this study can be used for water flow field research and water source mining planning.
- (2)
- In this study, the GMS model was used to predict and analyze the diffusion process of pollutants in the study area and to simulate the migration trend for 20 years. Through the analysis of the GMS model, it is predicted that pollutants will gradually migrate eastward from the river to groundwater, with the impact of ammonia in the river water on groundwater remaining within an acceptable range, and the ammonia content at the intake well meets the Quality Standard for Ground Water class III [ammonia (GB/T14848-2017 (in Chinese))].
- (3)
- Using the GMS model to simulate and predict the hydrological and water quality status of groundwater is conducive to understanding the status of groundwater pollution and to adopting thoughtful treatment and maintenance measures. However, the speed of pollutant migration and the size of the diffusion range are closely related to the amount and intensity of groundwater extraction. Therefore, when predicting the migration of pollutants, the influencing factors should be taken into consideration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mercado, A.; Libhaber, M.; Soares, M.I.M. In situ Biological Groundwater Denitrification: Concepts and Preliminary Field Tests. Water Sci. Technol. 1988, 20, 197–209. [Google Scholar] [CrossRef]
- Darabi, H.; Torabi Haghighi, A.; Mohamadi, M.; Rashidpour, M.; Ziegler, A.; Hekmatzadeh, A.A.; Klöve, B. Urban flood risk mapping using data-driven geospatial techniques for a flood-prone case area in Iran. Hydrol. Res. 2019, 51, 127–142. [Google Scholar] [CrossRef] [Green Version]
- Junjie, J. A Study of the Grain Production and Fertilizer Application in China-From the Perspective of Peasant Households and Market. Master’s Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Arnold, J.; Moriasi, D.; Gassman, P.; Mikayilov, F.; White, M.; Srinivasan, R.; Santhi, C.; Harmel, R.; van Griensven, A.; Van Liew, M.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Beaujouan, V.; Durand, P.; Ruiz, L.; Aurousseau, P.; Cotteret, G. A hydrological model dedicated to topography-based simulation of nitrogen transfer and transformation: Rationale and application to the geomorphology—Denitrification relationship. Hydrol. Process. 2002, 16, 493–507. [Google Scholar] [CrossRef]
- He, J.; Li, A.; Tan, Z.; Xie, G.; Shi, H.; Yao, J.; Zhang, X.; Sun, W.; Du, P. Potential impact of water transfer policy implementation on lake eutrophication on the Shandong Peninsula: A difference-in-differences approach. Hydrol. Res. 2020, 51, 1063–1076. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Li, M.; Ji, R.; Dolf, R.; Gu, X. Water Quality Analysis of the Yangtze and the Rhine River: A Comparative Study Based on Monitoring Data from 2007 to 2018. Bull. Environ. Contam. Toxicol. 2021, 106, 825–831. [Google Scholar] [CrossRef]
- Yuepeng, L. Research on the Influence of Polluted River on Groundwater Quality and the Model of Protection and Rehabilitation. Ph.D. Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Rankinen, K.; Granlund, K.; Etheridge, R.; Seuri, P. Valuation of nitrogen retention as an ecosystem service on a catchment scale. Hydrol. Res. 2013, 45, 411–424. [Google Scholar] [CrossRef]
- De la Hoz, R.E.; Schlueter, D.P.; Rom, W.N. Chronic lung disease secondary to ammonia inhalation injury: A report on three cases. Am. J. Ind. Med. 1996, 29, 209–214. [Google Scholar] [CrossRef]
- Casal, L.; Durand, P.; Akkal-Corfini, N.; Benhamou, C.; Laurent, F.; Salmon-Monviola, J.; Ferrant, S.; Probst, A.; Probst, J.-L.; Vertès, F. Reduction of stream nitrate concentrations by land management in contrasted landscapes. Nutr. Cycl. Agroecosystems 2019, 114, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Wang, G.; Xue, B.; Xie, G.; Peng, Y. Identification of regional water security issues in China, using a novel water security comprehensive evaluation model. Hydrol. Res. 2020, 51, 854–866. [Google Scholar] [CrossRef]
- Ferrant, S.; Oehler, F.; Durand, P.; Ruiz, L.; Salmon-Monviola, J.; Justes, E.; Dugast, P.; Probst, A.; Probst, J.-L.; Sanchez-Perez, J.-M. Understanding nitrogen transfer dynamics in a small agricultural catchment: Comparison of a distributed (TNT2) and a semi distributed (SWAT) modeling approaches. J. Hydrol. 2011, 406, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Lyra, A.; Loukas, A.; Sidiropoulos, P.; Tziatzios, G.; Mylopoulos, N. An Integrated Modeling System for the Evaluation of Water Resources in Coastal Agricultural Watersheds: Application in Almyros Basin, Thessaly, Greece. Water 2021, 13, 268. [Google Scholar] [CrossRef]
- Evenson, G.R.; Golden, H.E.; Lane, C.R.; D’Amico, E. An improved representation of geographically isolated wetlands in a watershed-scale hydrologic model. Hydrol. Process. 2016, 30, 4168–4184. [Google Scholar] [CrossRef]
- Farjad, B.; Gupta, A.; Razavi, S.; Faramarzi, M.; Marceau, D.J. An Integrated Modelling System to Predict Hydrological Processes under Climate and Land-Use/Cover Change Scenarios. Water 2017, 9, 23. [Google Scholar] [CrossRef] [Green Version]
- Mabon, F.; Raimbault, T.; Moreau, P.; Devienne, S.; Delaby, L.; Durand, P.; Ruiz, L.; Vertes, F. Concilier efficacité technico-économique et environnementale des exploitations agricoles en zone vulnérable : Apport du diagnostic agraire. Fourrages 2009, 199, 373–388. [Google Scholar]
- Petry, J.; Soulsby, C.; Malcolm, I.A.; Youngson, A.F. Hydrological controls on nutrient concentrations and fluxes in agricultural catchments. Sci. Total Environ. 2002, 294, 95–110. [Google Scholar] [CrossRef]
- Ohte, N.; Tokuchi, N.; Katsuyama, M.; Hobara, S.; Asano, Y.; Koba, K. Episodic increases in nitrate concentrations in streamwater due to the partial dieback of a pine forest in Japan: Runoff generation processes control seasonality. Hydrol. Process. 2003, 17, 237–249. [Google Scholar] [CrossRef]
- Lapworth, D.J.; Shand, P.; Abesser, C.; Darling, W.G.; Haria, A.H.; Evans, C.D.; Reynolds, B. Groundwater nitrogen composition and transformation within a moorland catchment, mid-Wales. Sci. Total Environ. 2008, 390, 241–254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schubert, J. Hydraulic aspects of riverbank filtration—Field studies. J. Hydrol. 2002, 266, 145–161. [Google Scholar] [CrossRef]
- Balke, K.-D.; Zhu, Y. Natural water purification and water management by artificial groundwater recharge. J. Zhejiang Univ. Sci. B 2008, 9, 221–226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alvarez-Cobelas, M.; Angeler, D.G.; Sánchez-Carrillo, S. Export of nitrogen from catchments: A worldwide analysis. Environ. Pollut. 2008, 156, 261–269. [Google Scholar] [CrossRef] [PubMed]
- Johnsson, H.; Bergstrom, L.; Jansson, P.-E.; Paustian, K. Simulated nitrogen dynamics and losses in a layered agricultural soil. Agric. Ecosyst. Environ. 1987, 18, 333–356. [Google Scholar] [CrossRef]
- Vanclooster, M.; Viaene, P.; Diels, J.; Feyen, J. A deterministic evaluation analysis applied to an integrated soil-crop model. Ecol. Model. 1995, 81, 183–195. [Google Scholar] [CrossRef]
- Jabro, J.D.; Toth, J.D.; Dou, Z.; Fox, R.H.; Fritton, D.D. Evaluation of Nitrogen Version of Leachm for Predicting Nitrate Leaching. Soil Sci. 1995, 160, 209–217. [Google Scholar] [CrossRef]
- Knisel, W.G. CREAMS: A Field-Scale Model for Chemicals, Runoff and Erosion from Agricultural Management Systems; U.S. Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1980; p. 640.
- Medici, C.; Bernal, S.; Butturini, A.; Sabater, F.; Martin, M.; Wade, A.J.; Frances, F. Modelling the inorganic nitrogen behaviour in a small Mediterranean forested catchment, Fuirosos (Catalonia). Hydrol. Earth Syst. Sci. 2010, 14, 223–237. [Google Scholar] [CrossRef] [Green Version]
- Moharir, K.; Pande, C.; Patil, S. Inverse modelling of aquifer parameters in basaltic rock with the help of pumping test method using MODFLOW software. Geosci. Front. 2017, 8, 1385–1395. [Google Scholar] [CrossRef]
- Wang, R.; Liu, Z.; Yao, Z.; Lei, Y. Modeling the risk of nitrate leaching and nitrate runoff loss from intensive farmland in the Baiyangdian Basin of the North China Plain. Environ. Earth Sci. 2014, 72, 3143–3157. [Google Scholar] [CrossRef]
- Yousefi, H.; Zahedi, S.; Niksokhan, M.H.; Momeni, M. Ten-year prediction of groundwater level in Karaj plain (Iran) using MODFLOW2005-NWT in MATLAB. Environ. Earth Sci. 2019, 78, 343. [Google Scholar] [CrossRef]
- Rankinen, K.; Lehtonen, H.; Granlund, K. Assessing the Effects of Agricultural Change on Nitrogen Fluxes Using the Integrated Nitrogen CAtchment. In Proceedings of the 2nd International Congress on Environmental Modelling and Software, Osnabrück, Germany, 14–17 June 2004. [Google Scholar]
- Ferrant, S.; Durand, P.; Justes, E.; Probst, J.-L.; Sanchez-Perez, J.-M. Simulating the long term impact of nitrate mitigation scenarios in a pilot study basin. Agric. Water Manag. 2013, 124, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Bu, J.; Sun, Z.; Ma, R.; Liu, Y.; Gong, X.; Pan, Z.; Wei, W. Shallow Groundwater Quality and Its Controlling Factors in the Su-Xi-Chang Region, Eastern China. Int. J. Environ. Res. Public Health 2020, 17, 1267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El Idrysy, H.; De Smedt, F. Modelling groundwater flow of the Trifa aquifer, Morocco. Hydrogeol. J. 2006, 14, 1265–1276. [Google Scholar] [CrossRef]
- Sun, R.; Wang, Z.Z.; Chen, L.; Wang, W.W. Assessment of Surface Water Quality at Large Watershed Scale: Land-Use, Anthropogenic, and Administrative Impacts. J. Am. Water Resour. Assoc. 2013, 49, 741–752. [Google Scholar] [CrossRef]
- Junyan, Z.; Cuimei, L.; Jingxiong, H.; Song, X. Application of GMS Model in Hydrological and Water Quality Simulation. J. China Hydrol. 2019, 39, 56–73. [Google Scholar]
| Calculation Partition | Parameter Value | Calculation Partition | Parameter Value |
|---|---|---|---|
| I | 0.10 | II | 0.08 |
| Number | Horizontal Permeability Coefficient (m/d) | Specific Yield | Number | Horizontal Permeability Coefficient ((m/d) | Specific Yield |
|---|---|---|---|---|---|
| 1 | 45.2 | 0.2 | 4 | 6.4 | 0.2 |
| 2 | 38.3 | 0.2 | 5 | 16.1 | 0.3 |
| 3 | 35.2 | 0.2 | 6 | 7.8 | 0.3 |
| Profile Number | A | B | C | D |
|---|---|---|---|---|
| Concentration (mg/L) | 0.48 | 0.46 | 0.34 | 0.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhao, X.; Xie, T.; Wen, N.; Yao, J. A Comprehensive Evaluation Model of Ammonia Pollution Trends in a Groundwater Source Area along a River in Residential Areas. Water 2021, 13, 1924. https://doi.org/10.3390/w13141924
Wang Z, Zhao X, Xie T, Wen N, Yao J. A Comprehensive Evaluation Model of Ammonia Pollution Trends in a Groundwater Source Area along a River in Residential Areas. Water. 2021; 13(14):1924. https://doi.org/10.3390/w13141924
Chicago/Turabian StyleWang, Zhuoran, Xiaoguang Zhao, Tianyu Xie, Na Wen, and Jing Yao. 2021. "A Comprehensive Evaluation Model of Ammonia Pollution Trends in a Groundwater Source Area along a River in Residential Areas" Water 13, no. 14: 1924. https://doi.org/10.3390/w13141924
APA StyleWang, Z., Zhao, X., Xie, T., Wen, N., & Yao, J. (2021). A Comprehensive Evaluation Model of Ammonia Pollution Trends in a Groundwater Source Area along a River in Residential Areas. Water, 13(14), 1924. https://doi.org/10.3390/w13141924






