1. Introduction
Sanitary sewage collection systems, or simply speaking sewer networks, are essential parts of any modern city; they directly influence public health and are vital for environmental protection. Sewer networks have traditionally been designed and developed in the form of centralized networks to collect and transfer wastewater from homes and factories, preferably by gravity, to a centralized wastewater treatment plant located far enough from urban areas [
1,
2]. Increasing population growth and industrial and agricultural developments have added to the demand for water in societies. In addition to the pollution and scarcity of available water resources, the increasing water demands have introduced significant challenges. This issue is particularly critical in arid and semi-arid countries suffering from freshwater scarcity; hence, the need for the sustainable management and protection of water resources is striking.
The expansion, reconstruction, and rapid growth of cities and industries have resulted in fundamental challenges for developing and upgrading urban water systems. Due to rapid urbanization and increased costs on one hand and reduced budgets on the other hand, the construction, operation, maintenance, and rehabilitation of centralized sewer networks present severe challenges and obstacles. Additional concerns relate to the reliability and lack of resilience of centralized systems. In flat areas, particularly with high-level groundwater, poor geotechnical conditions for civil engineering activities, and with highly populated and fully urbanized cities, it is expensive or even unfeasible to install sewer lines of sufficiently large diameter and depth. As a result, in such areas sewers are often designed and constructed with minimum slopes. Although the minimum slope approach generally leads to a cost-effective sewer system, it causes operational problems such as increased sedimentation rates and risk of clogging due to a lack of proper flow velocity in sewers, which is required for self-cleaning. To compensate for a lack of natural ground slope, centralized networks serving large and flat areas mostly require pumping stations, which bring about additional costs, consume energy, and make the system fragile.
Recently, decentralized systems have been introduced to overcome the drawbacks mentioned above. Such approaches involve treating and reusing wastewater near the source using independent units [
3,
4,
5,
6]. In decentralized systems, it is expected that increasing the number of treatment plants will reduce operating costs by reducing the diameter of the sewers and the excavation volumes, as well as the number of pumping and lift stations. Furthermore, independent units (subnetworks and treatment packages) dramatically enhance the reliability and resilience of a sewer system. Decentralized urban water systems have recently received more attention in developing countries lacking reliable systems and financial resources to afford the high construction, operation, maintenance, and rehabilitation costs of centralized systems [
2,
7,
8,
9,
10,
11,
12,
13,
14].
It is also worth mentioning that advances in the design and operation of modern wastewater treatment processes such as sequencing batch reactors (SBRs), which are efficient, small in size, and suitable for urban environments, make these promising for use in decentralized urban sewer networks. Such systems have much more potential for recycling and reusing treated wastewater (e.g., for irrigation of urban green spaces) and are more efficient and cost-effective than centralized systems. Additionally, recent developments in network design and optimization algorithms have facilitated the design of decentralized sewer systems.
A literature review showed that despite many innovative methods being used for designing centralized wastewater collection networks [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28], only a few studies have proposed decentralized sewer networks [
2,
25,
29]. Overall, systematically generating feasible decentralized layouts is a bottleneck in optimizing decentralized sewer networks [
28]. Recently, several investigations have been published regarding decentralization aspects for stormwater networks. The layout generator algorithms [
9,
30], single-objective optimization algorithm [
9], multiobjective optimization algorithms [
12,
31,
32,
33,
34,
35,
36], and multicriteria decision-making algorithms [
11,
37,
38] are some of the main approaches investigated so far for decentralized stormwater systems.
In general, the design of a sewer network needs to solve two mathematically different subproblems: (1) generate feasible layouts employing algorithms from the graph theory; (2) measure the network’s components by solving the hydraulic governing equations concerning a set of design criteria. The latter includes calculating the sewer diameters and installation depths (or sewer slopes) and the pumping capacities. The subproblems are nonlinear and discrete, with many complex constraints from the hydraulics principles, technical criteria, and regional limitations [
16]. It is possible to simplify the sewer network design by separately solving the subproblems mentioned above. For this purpose, a near-optimum layout is first derived using engineering judgments or a simplified objective function and optimization. Then, for the layout at hand, the network is hydraulically designed [
39]; however, for the above subproblems, the layout and the hydraulic designs are highly interrelated. The layout can significantly affect the network hydraulic design characteristics and vice versa. This issue is particularly significant in flat and wide areas in which the layout alternatives are numerous. Additionally, the inter-relationship between the subproblems is much more critical when designing a decentralized sewer network.
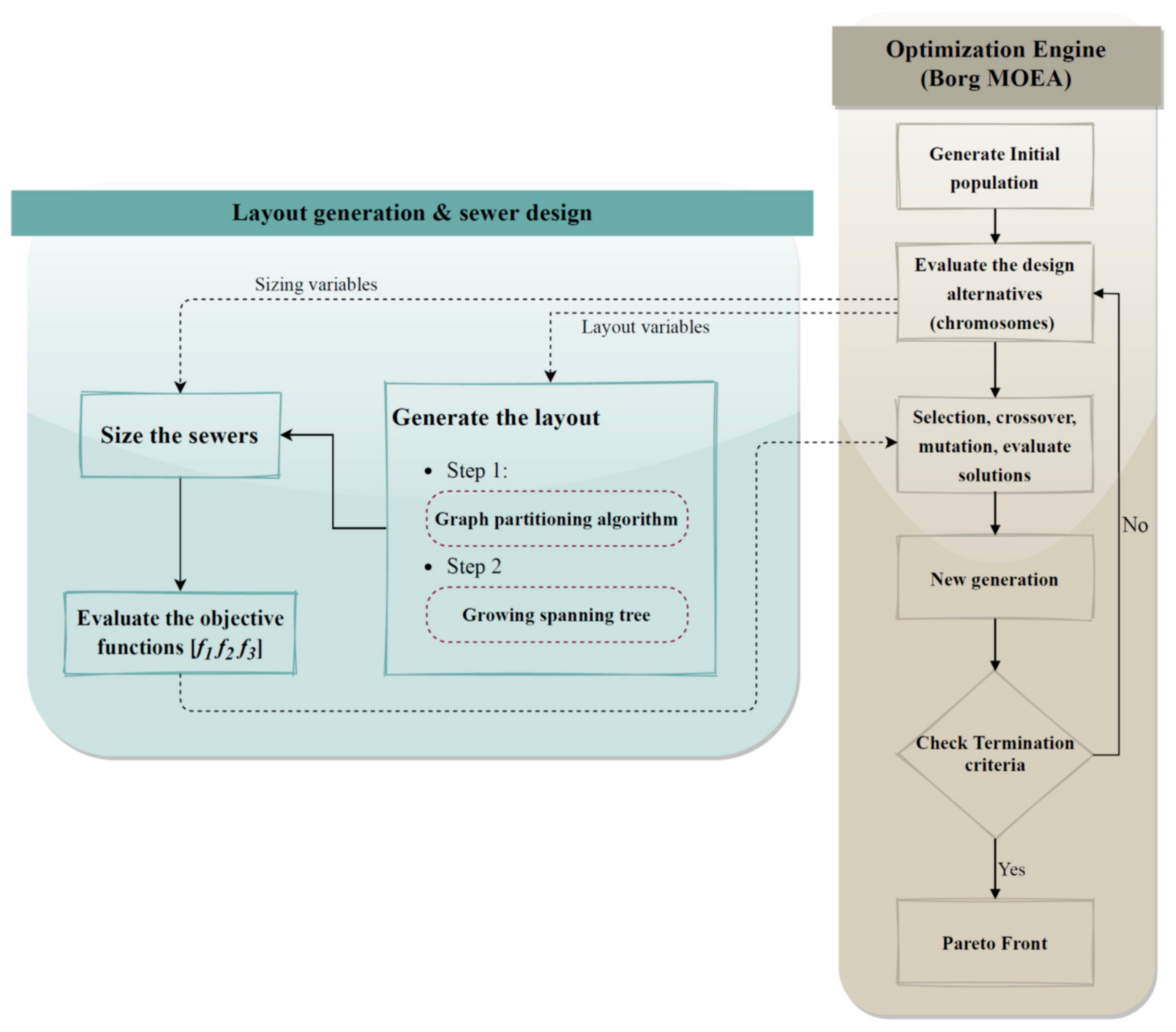
Consequently, the global optimum design of a sewer network can only be achieved when these two subproblems are solved implicitly and simultaneously. In this respect, the current study introduces a multiobjective optimization framework for decentralized sewer system design. The layout and hydraulic design subproblems are optimized implicitly using a coupled design package. The objective functions include the construction and operational costs of the network and the wastewater treatment plant(s), the structural resilience, and the degree of centralization. For this purpose, a systematic network layout generator and hydraulic simulation–design model are developed to produce all feasible network configurations with a vast degrees of centralization. The multiobjective optimization is used to drive the optimum trade-off between the aforementioned objective functions.
2. Materials and Methods
As mentioned earlier, in order to optimize a sewer collection network, the layout and hydraulic design subproblems must be solved simultaneously. Mathematically, a sewer network optimization problem can be expressed as follows:
where
represents the objective functions,
represents the annualized cost of construction and operation,
represents the structural resilience, and
represents the degree of network centralization. Additionally,
is the vector of decision variables, including the layout parameters; the number and locations of treatment plants; the depth of roots (outlets); and the hydraulic characteristics of the network, consisting of the sewer diameters and slopes and the locations of pumping (lift) stations. Additionally,
is an optimal solution and
is the feasible space of the problem. The above objective functions are optimized subject to a train of physical and technical constraints on the layout and hydraulic designs. For centralized sanitary sewer networks, the constraints and design criteria have usually been well explained in the previous investigations, especially in [
16,
39], which are adopted in this study. Subject to the constraints, the following objective functions are optimized together using the Borg multiobjective evolutionary algorithm (MOEA) [
40].
2.1. Cost Function ()
A sewer network cost function consists of the construction and operational costs of sewers (
), manholes (
), pressurized transmission pipelines (
), pumping and lift stations (
), and wastewater treatment plants (
). Accordingly, the total cost function of a sewer network design to be used as an objective function is defined as follows:
In which is the buried sewer depth or manhole installation depth, is the sewer diameter, is the sewer length, and is the pumping or treatment flow rate. For each particular case study, the above functions are estimated and derived through nonlinear regressions.
To establish the objective function
, the annual cash flow method is applied to the estimated cost
as the following:
where
is the interest rate;
is the design period, which can be different for each component of the design cost function;
is a parameter used to calculate the profit from selling the design, which can be different for each component during its design period;
is a parameter used to estimate the annual operation cost.
2.2. Structural Resilience Analysis ()
Structural resilience as an objective function is the network’s ability to minimize the frequency and magnitude of structural failures, such as clogging and sewer cracking or pump failure [
41]. The maximum structural resilience is obtained when clogging in the sewers has the least effect on the upstream parts [
42]. To quantify the clogging consequence in sewer networks, Bakhshipour et al. (2021) [
12] proposed a criterion, Equation (4), which uses layout design properties. The principle is that the lower the proportion of the population affected by sewer clogging, the more resilient the network will be.
where
is the area connected to
and
is the total area covered by the network. To account for the effects of DC (degree of centralization) on Equation (4), Bakhshipour et al., 2020 proposed Equation (5) to quantify the structural resilience:
in which
is the number of sewers with structural resilience of more than 90% and
is the number of sewers with structural resilience of less than 90%. SRI is zero when all sewers are connected to more than 10% percent of the total area
and 100% if each root (outlet) is connected to up to 10 % of the total area
. More details on this index are found in the given references.
2.3. Degree of Centralization ()
Despite the increasing attention being paid to decentralized urban water management, no explicit definitions have been proposed to measure the degree of centralization (DC) [
2]. The available definitions are mostly limited to fully centralized or fully decentralized systems; however, a wide range of solutions with different DCs is feasible. Eggimann et al. (2015) [
2] adopted a weighted DC by considering a continuum of possible facility sizes for wastewater management infrastructure. Following that idea, the present study introduces a weighted index to measure the DC based on the network’s layout and the sewer pipes’ accumulative flow (Equation (6)). The main idea behind this formulation is that “the more unbalanced the distribution of sewers and flow rates between the subgraphs, the more centralized the network will be”.
where
is the number of selected locations (sites) of the treatment plants,
is the number of candidate locations of the treatment plants, and
and
are calculated as follows:
where
is the flow received at each treatment plant,
is the number of sewers in each subgraph, and
is the total number of sewers in the network. Equation (6) considers both distributions of infrastructure (sewers and pumping facilities) and flow in different parts of the network by applying the coefficient
. The more balanced the distribution of wastewater flows between the subgraphs, the closer the
coefficient is to 1 and the lower the DC the network will have.
Based on Equation (6), the DC is 1 when the system is fully centralized and merely one treatment plant is selected from the candidate list. In contrast, the DC is almost zero when the system is fully decentralized, meaning that all candidate treatment plants are chosen. In decentralized cases, the network has two or more roots (treatment plant); according to the above formula, the DC is a function of both the number of roots (treatment plants) and the distribution of sewers and wastewater flows. In other words, for the same number of treatment plants, the flow distribution between the subgraphs governs the DC value.
2.4. Subproblem 1: Layout Generator Algorithm
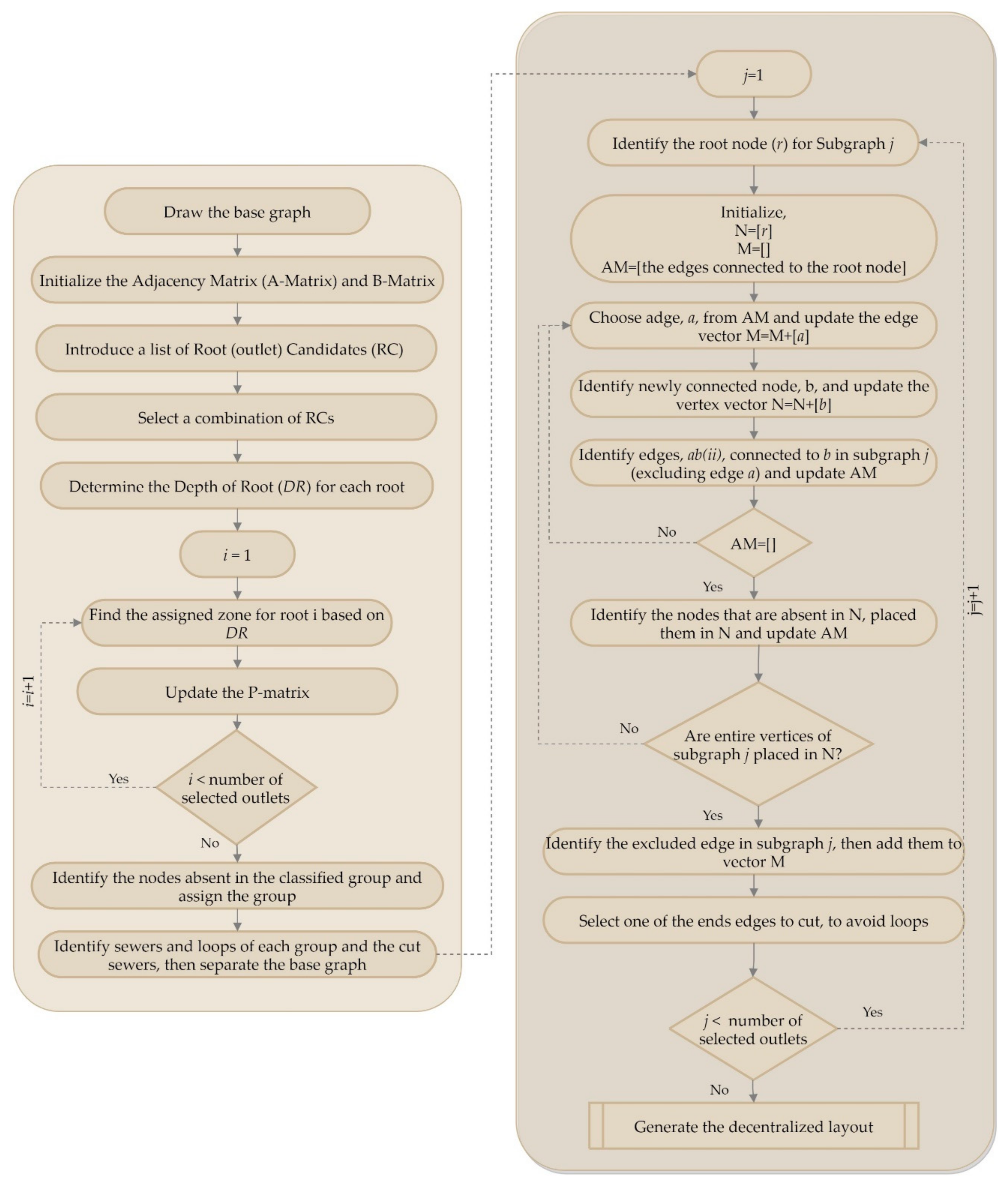
To generate a decentralized sewer layout, first the network’s base graph is drawn. In a base graph, all sewer possibilities are included so that manholes (vertices) and sewers (edges) constitute a connected cyclic graph. With respect to the street alignment, topology, barriers, watercourses, outlets, and existing sewers in the city, an undirected base graph can be drawn for the network [
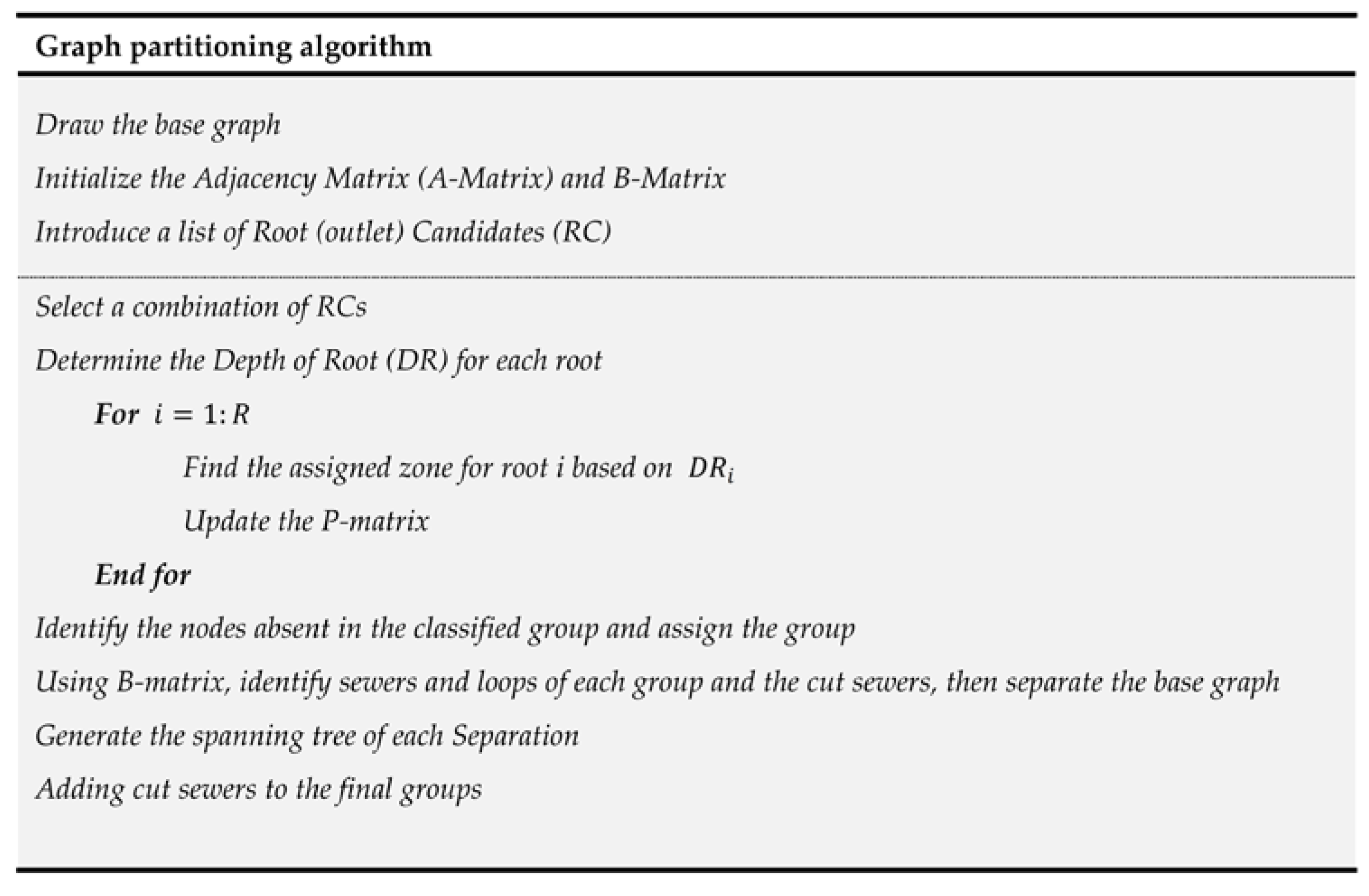
43]. To design feasible sewer layouts, an algorithm is developed to partition the base graph into several sub-base graphs and to extract spanning trees for each. The proposed algorithm used to generate decentralized layouts is described through the pseudocode in
Figure 1. The base graph partitioning algorithm consisting of three modules is described below by solving a simple example.
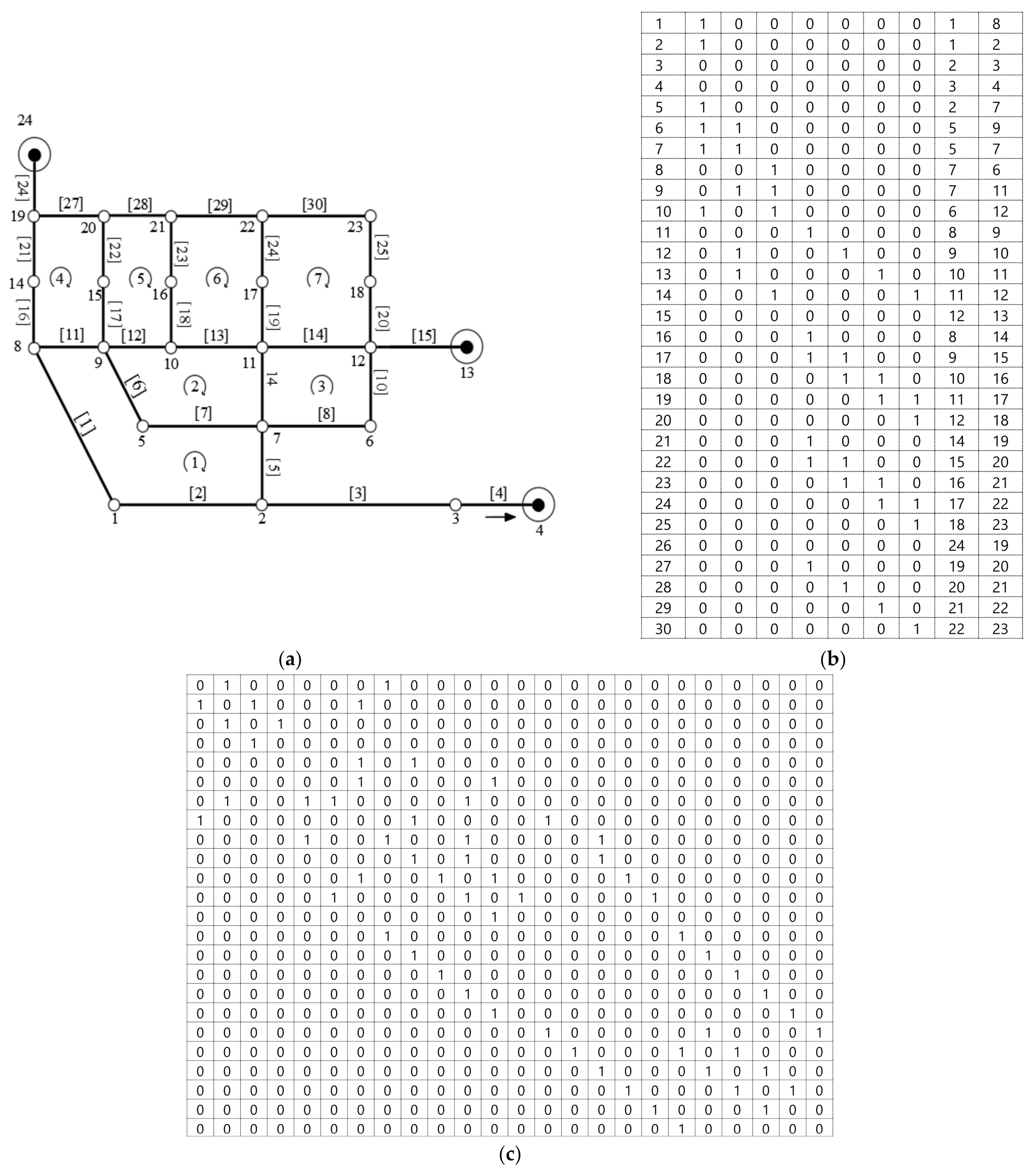
Figure 2a illustrates the base graph of a wastewater network. This graph is mathematically represented and introduced to the model by an adjacency matrix (A-Matrix,
Figure 2c) and an information matrix (B-Matrix,
Figure 2b) containing sewers and connections data. Let N be the number of nodes (manholes), M be the number of edges (sewers), and NL be the number of loops in the base graph. The B-Matrix involves M rows and NL+3 columns. Column 1 contains the sewer names from 1 to M, while columns 2 to NL+1 are sewer-in-loop indicators determining whether a sewer is in a loop (value 1) or not (value 0). Columns NL+2 and NL+3 include the sewer ends without any order, since the base graph is undirected. The adjacency matrix is an
with binary elements; element (i, j) is 1 if nodes i and j are connected and zero if they are not connected.
2.4.1. The Assigned Zone to Each Root
The first step is finding the assigned zone to each root (outlet) and partitioning the base graph according to the number and location of roots. To this end, a notion called the depth of root (
DR) is introduced here. Either engineering judgment or systematic optimization can determine a
DR. This study employs optimization by defining a decision variable
as follows:
where
is a real value number in the range of (0, 1), R is the number of roots in the base graph, and
is the path between the closest root and the desired root. The closest root to another root is the one with the shortest path. Finding the shortest path between two nodes is possible using the shortest path algorithms in the graph theory. Here, Dijkstra’s algorithm is adopted to calculate
. The calculation of
is performed based on the P-Matrix, which is initially equal to the adjacency matrix of the base graph A-Matrix.
For example, suppose nodes 4, 13, and 24 are potential roots in
Figure 2a; thus, R = ([4,13,24]) is the vector of roots. Once a
DR is found for a root, the nodes of the base graph whose shortest path to the root is smaller than the
DR are classified into a group. For instance, for the first root (node 4), node 13 with
is the closest root. Given that
and
, nodes 1, 2, 3, and 7 are classified into the group of root node 4 (
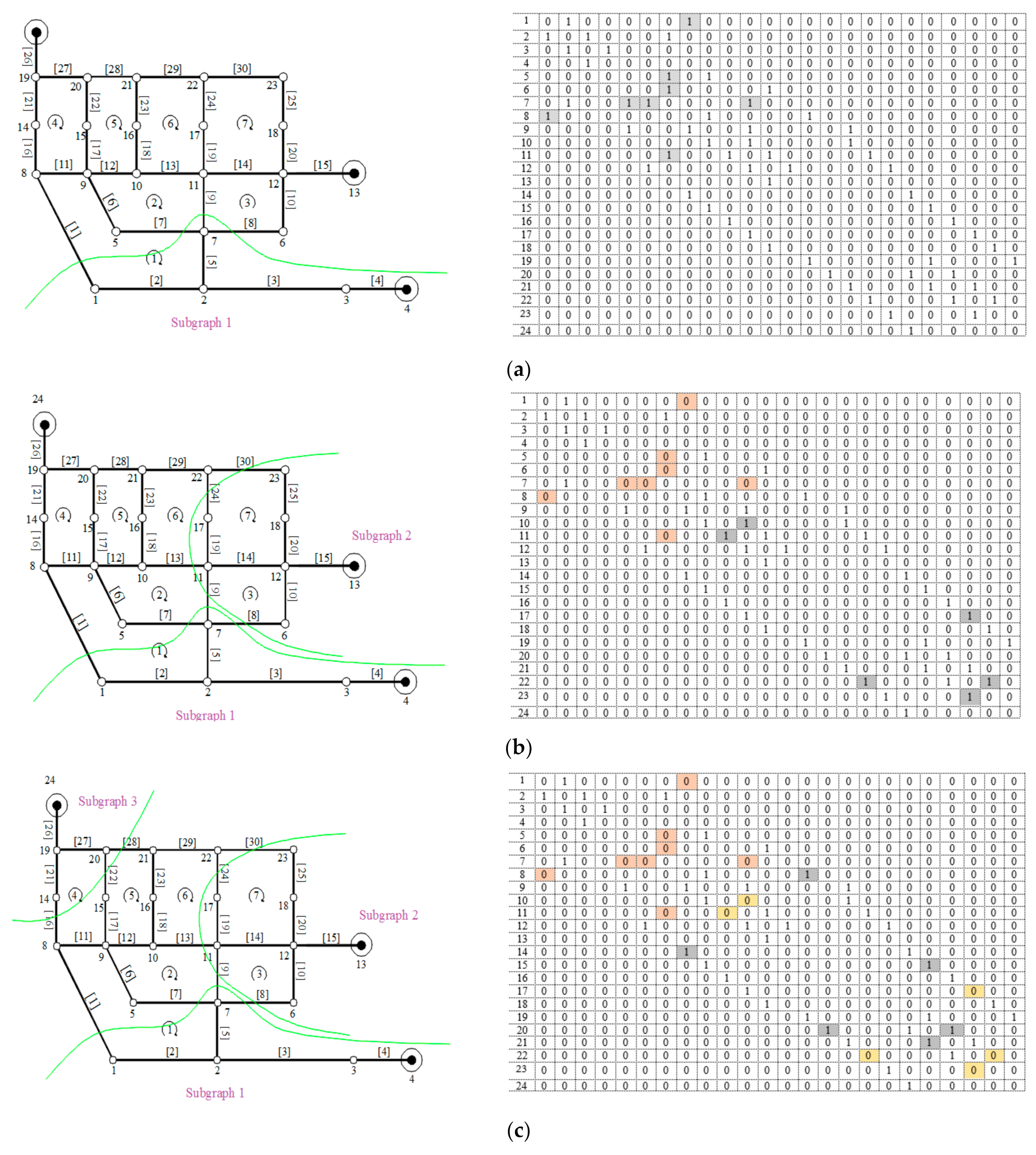
Figure 3a). After this, in order to identify the assigned zone of the next root, some modifications are required. Since Nodes 1, 2, 3, and 7 have already been assigned to node 4, they are excluded from the base graph’s node set N. As the subgraphs should remain connected with the nodes excluded from N, the paths including nodes 1, 2, 3, and 7 are no longer used for the shortest paths in the following stages. Accordingly, the P-Matrix needs to be modified to identify the assigned nodes of the next root, node 13. This is performed by disconnecting nodes 1, 2, 3, and 7 from the node set N by setting elements (7, 6), (7, 5), (7, 11), and (1, 8) to zero in the P-Matrix. The elements related to nodes 2 and 3 do not require modification as they are not connected to the node-set N. It is also worth noting that nodes 1 and 7 are now called upstream nodes. This approach is implemented step-by-step until all members of vector R are covered.
Figure 3 demonstrates a schematic of the proposed procedure on the base graph. Once the above procedure is implemented for all roots, the base graph vertices absent in the classified groups are identified and assigned to relevant groups. As mentioned, the subgraphs must remain connected; thus, the strategy selected for this purpose is based on the development of subgraphs through the upstream nodes. For example, to assign the nodes of set N to subgraphs, subgraph 1 develops through nodes 1 and 7; subgraph 2 develops through nodes 11, 17, and 23; and subgraph 3 develops through nodes 14 and 20. Using the adjacency matrix, the A-Matrix, the nodes connected to the upstream nodes of these subgraphs are identified and considered new upstream nodes of the corresponding group. It should be noted that set N needs to be updated at each node assignment step. These steps continue until the all nodes of set N are assigned to the subgraphs.
2.4.2. Base Graph Partitioning
Once the assigned zone for each root is determined, the base subgraphs are extracted through the following steps:
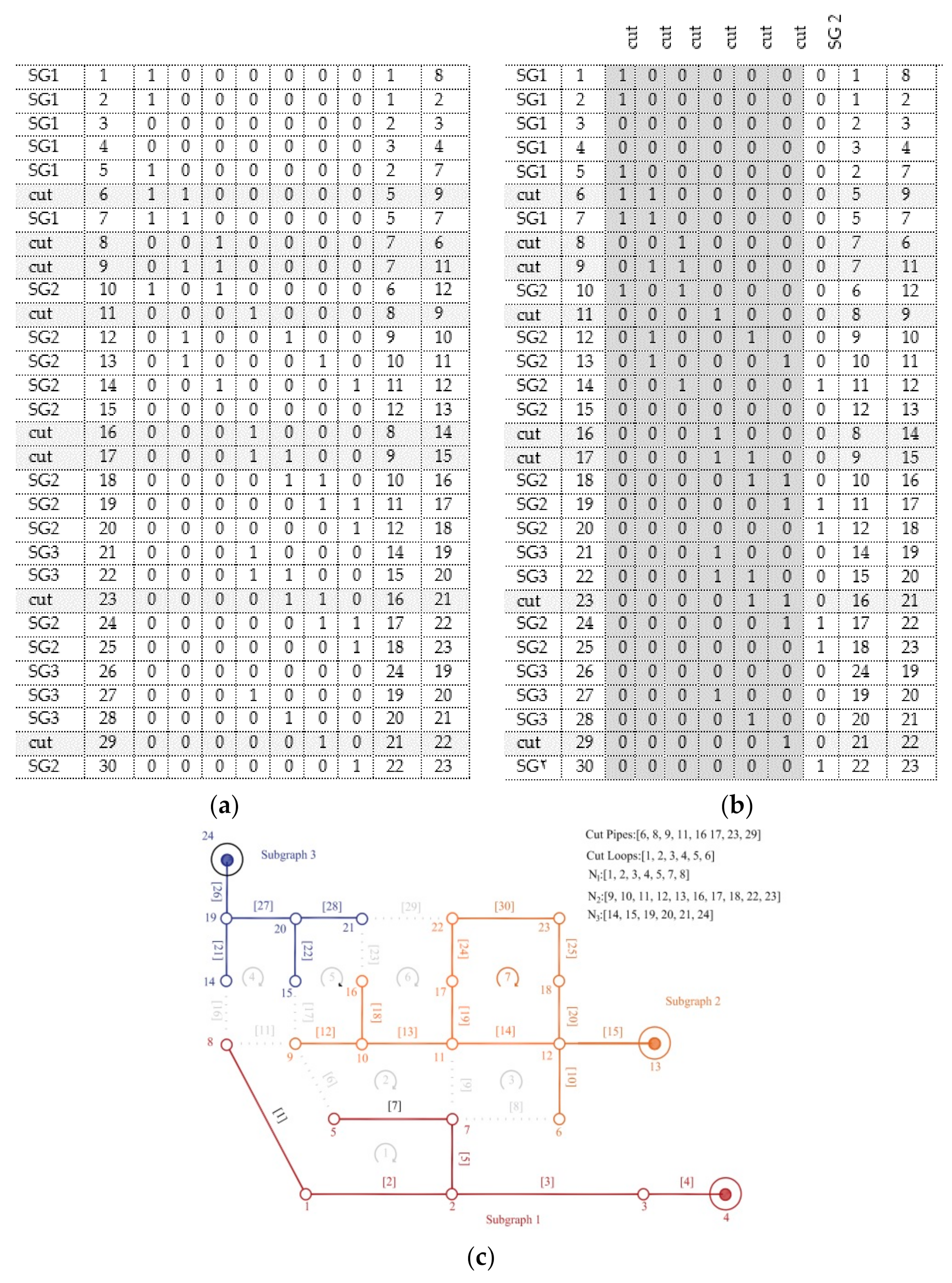
The sewers of each subgraph are identified. For each sewer in the B-Matrix, the upstream and downstream nodes are identified. If the nodes are in the same group, the corresponding sewer belongs to that group; otherwise, it is a cut sewer;
The loops of each subgraph are identified. For each loop in the B-Matrix, the corresponding sewers are placed. If there are cut sewers among the sewers of a loop, the loop is excluded; otherwise, the sewers of the loop indicate to which subgraph the loop belongs.
After the sewers and loops of each base subgraph are identified (
Figure 4), their corresponding B-Matrices are created.
2.4.3. Generating the Spanning Trees of Base Subgraphs
A feasible layout for a decentralized sewer network is a forest of spanning trees with roots each, including a treatment plant. The present study adopts the algorithm of growing spanning trees (Walters and Smith 1995) to extract the tree-like sewer network from the undirected looped base graphs. Through this approach, a sewer of each loop is cut rather than excluded. In the growing spanning tree method, each tree begins to grow from a root defining three growing vectors:
- (i)
Vector , consisting of the edges (sewers) of the growing tree;
- (ii)
Vector , consisting of the vertices (nodes or manholes) of the growing tree;
- (iii)
Vector , consisting of the base graph edges adjacent to the growing tree. Each of these edges may be considered a decision variable in order to construct another growing tree branch.
According to the above definitions, the spanning tree growth algorithm applied to the base graph includes the following steps:
The root node, root r, is identified;
The vector N is initialized with a single member . No edge has yet been selected, meaning ;
The AM vector is updated in each stage; in the beginning, only edges connected to the root are included, i.e., (the edges connected to the root node);
An edge from vector
is chosen through optimization. For this purpose, a decision variable
(
) in the range of (0, 1) is defined and
is the total number of vertices in the base graph. Let
be the current number of adjacent edges; the chosen edge number
from variable
is as follows, where
represents the sewer “a” in the network;
The edge vector is updated, ;
The selection of edge “a” adds a new vertex “b” to the growing tree; therefore, it is required to update the vertex vector, ;
All edges except “a” connected to vertex “b” are denoted as ;
Vector is updated by excluding edge “a” and adding edges . then contains all choices for the next edge of the growing tree. Before going to the next step, the following query should be applied to each new member of to make it feasible: Is already in or are both end nodes of present in ?
If yes, then edge is removed from , since its selection causes a loop in the growing tree; ; if no, vector is acceptable;
The algorithm goes back to step 5 and the tree continues growing until vector becomes empty. After this, a branch of the growing tree is generated, including vertices of the base graph and edges according to variables to ;
The vertices of the base graph that are not present in the vertex vector are identified. The number of these vertices is ;
A vertex absent in is selected and placed in and vector is updated accordingly. Then, the algorithm goes to step 5 and a new edge is identified using Equation (10);
This process continues until all absent vertices are placed in . The algorithm eventually generates a root-ending spanning tree based on the decision variables ; however, there are a number of excluded sewers—as many as the number of loops in the base graph. These sewers must be included in the final design of the sewer network. To meet this constraint, the following modification is applied;
Let be the number of edges in the base graph. The number of edges in the grown spanning tree at the end of the previous step is . The excluded edges are identified as and added to vector ;
Since the excluded edges are returned to the spanning tree, they should be cut to avoid loops. For this purpose, one of the ends of the edge is selected to be cut. This introduces another decision variable to the problem. A binary variable ) is used for this purpose. When , the edge is cut from its upstream, otherwise it is cut from the downstream. As an is cut, a new vertex appears at the truncation end, which is named . The process continues until all elements are cut.
Eventually, all excluded edges are added to the tree, while c new vertices (vertex n + 1 to n + c) are created in the network. Then, a feasible wastewater collection network is at hand, whose edges can be easily directed to the root node r as shown in
Figure 5.
The proposed algorithm is applied to all partitions of the base graph to extract the base graph’s spanning forest (decentralized layout).
Figure 6 explains this algorithm schematically.
2.5. Solving Subproblem 2: Hydraulic Design of the Network
After generating layouts, the second subproblem is the hydraulic design (sizing) of the sewer diameters (
d), slopes (
s), and pump stations (
p) for each layout directed to a root. This subproblem includes many complex constraints, which are nonlinear and discrete, and should be satisfied ordinarily. Handling such constraints introduces intractable challenges to the design of sewer systems. For this purpose, a hydraulic design algorithm proposed by Haghighi and Bakhshipour (2012) [
15] is adopted in this study. Employing this approach, the entire design criteria and constraints of wastewater collection networks are systematically satisfied through a self-adaptive step-by-step hydraulic design algorithm; therefore, there is no need to impose any penalty function on the objective functions used to handle the constraints. This capability is a significant relief for the optimization process and dramatically reduces blind searches to approach feasible decision spaces.
3. Case Study
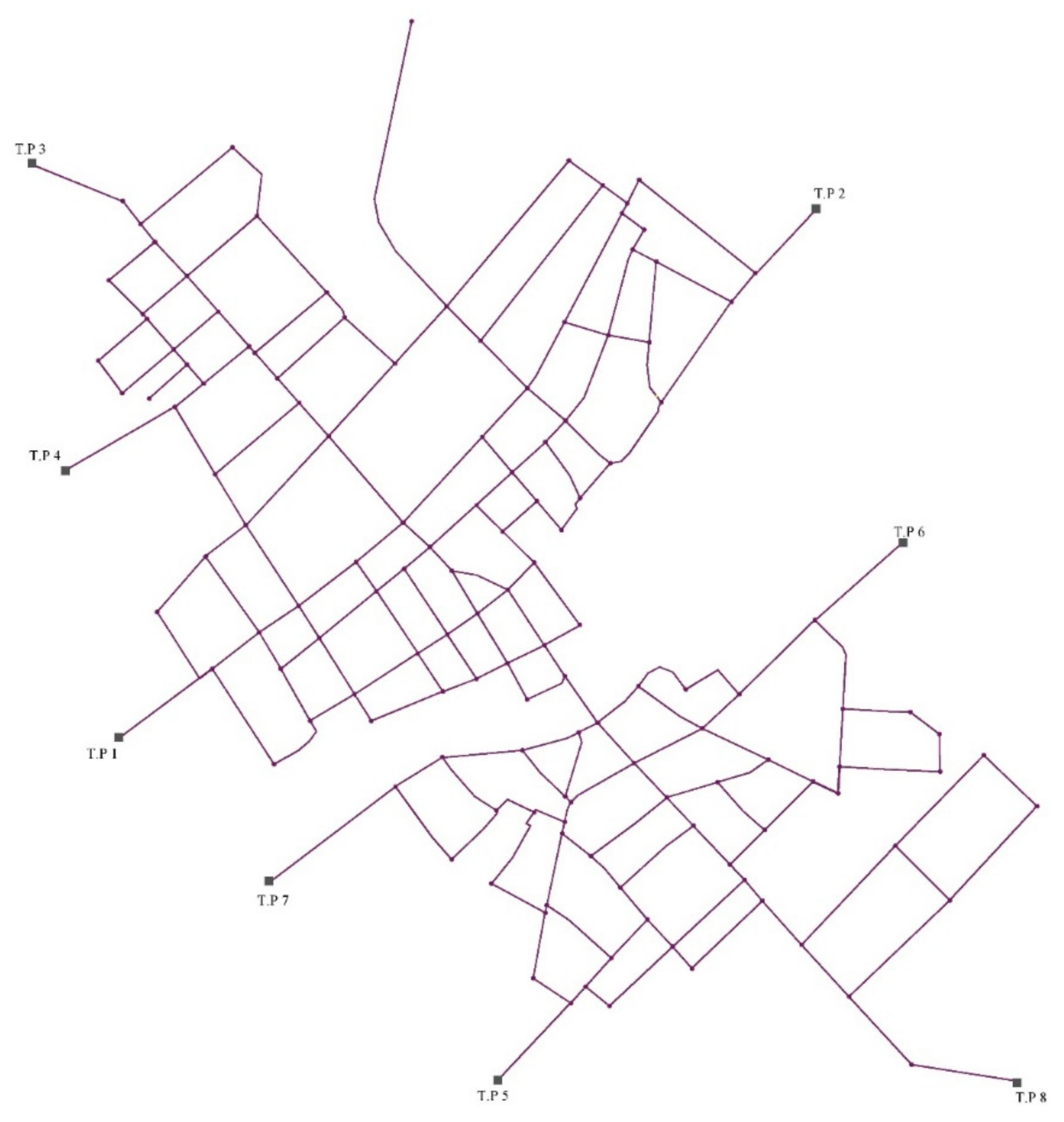
As a case study to investigate the proposed algorithms, the sewage collection network of Hendijan city, located in the southwest of Iran (
Figure 7), with about 700 hectares area and a population of 50,000, was designed. Some natural features of this city have made it a suitable candidate for developing a decentralized sewer network. The city crosses a large river dividing it into northern and southern parts, has high-level groundwater due to its proximity to the Persian Gulf, is fully flat in topography, and has poor geotechnical conditions, which are the main challenges for designing a fully centralized sewer network. In such a case, a feasibility study for decentralized systems is necessary.
The base graph (
Figure 8) of Hendijan city’s sewer network consists of 208 sewers, 64 loops, and 8 candidate locations for treatment plant installation (i.e., network roots).
Table 1 represents the hydraulic and other technical criteria and the constraints on the network design, while
Table 2 shows the problem’s decision variables. Due to lack of space and other regional limitations, only the treatment plant at candidate location T.P. 8 can treat 100% of the produced wastewater in this area. The treatment plant at location T.P. 3 can treat up to 75%, while the plants at the other candidate locations can treat 50% of the total wastewater at most.
To set up the optimization model, the number and locations of the roots (treatment plants) and layout and hydraulic design parameters are considered the decision variables. Then, to drive the optimum trade-off between the objective functions, the construction and operation costs (
Table 3), the network structural resilience (Equation (5)), and the degree of centralization (Equation (6)), the Borg multiobjective solver is applied.
According to the described framework, the optimization generates and optimizes the layouts and hydraulic design parameters simultaneously. In contrast, all physical constraints and design criteria for both subproblems (layout and hydraulic designs) are systematically satisfied in the algorithms. The process continues until the best Pareto front is achieved (
Figure 9).
It is also worth mentioning that for this case study, initially the costs of a wide range of sewer diameter sizes with different buried depths were estimated to derive the cost functions of sewers and manholes through mathematical regression (
Table 3). Similarly, the costs for a wide range of pumping stations and wastewater treatment plants (the sequential batch reactor process) with different flow rates and pumping heads were estimated to attain the corresponding cost functions in
Table 3. Although the derived cost functions may have uncertainty and errors, they help state the problem mathematically and facilitate automated optimization. In addition, since they are used in optimization to compare the design alternatives, the errors mentioned above would not play a significant role in the comparative nature of optimization.
4. Results and Discussion
After optimization, it was found that on average, 200,000 (de)centralized layouts were generated and hydraulically designed and evaluated during a multiobjective run. The computational time for solving the case study was estimated at around 15 h using a personal laptop with an Intel(R) Core i7-7700HQ CPU, 2.8 GHz quad-core CPU, and 16 GB random access memory (RAM).
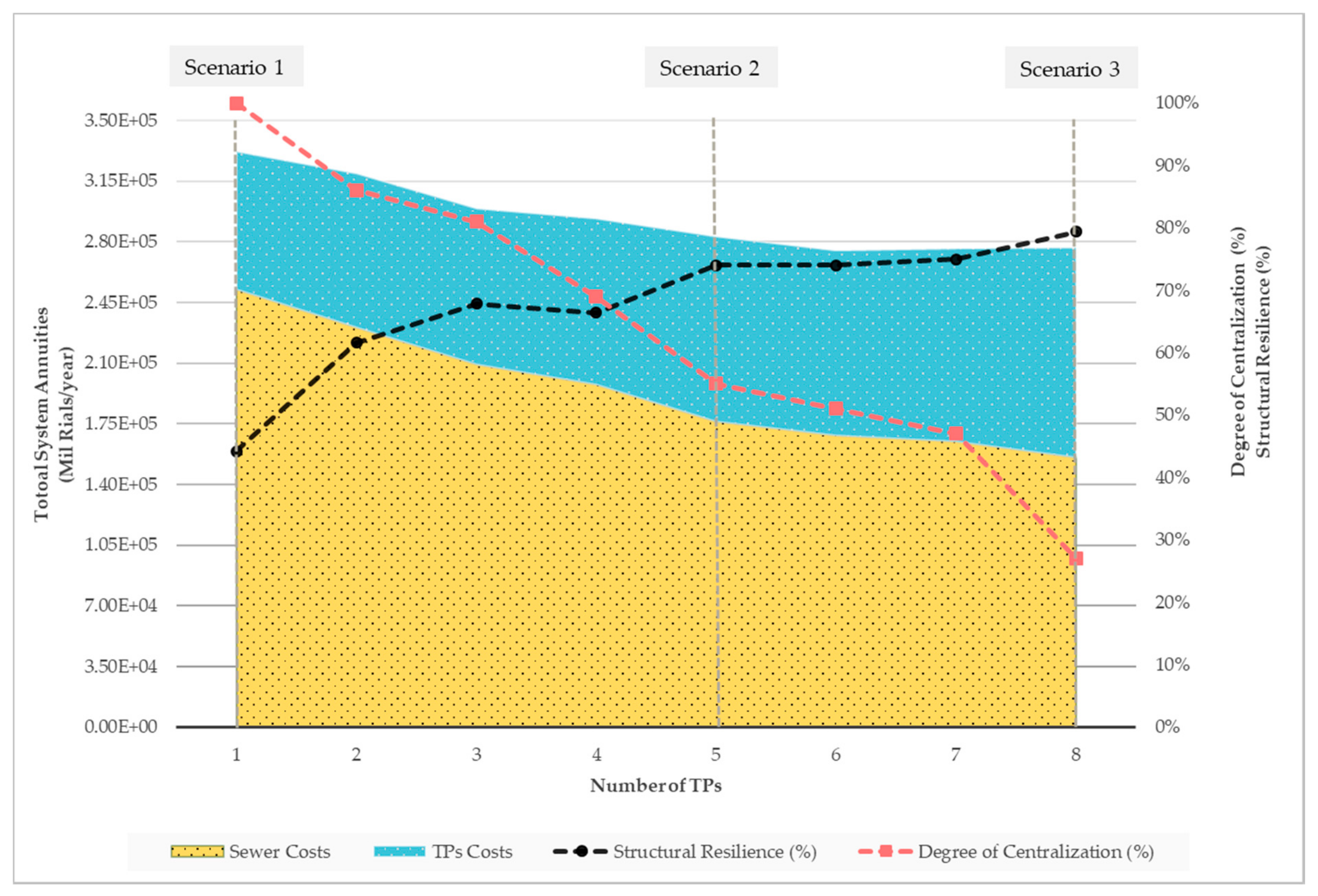
Certain optimum solutions with a different number of treatment plants were chosen from the obtained Pareto front for presentation in
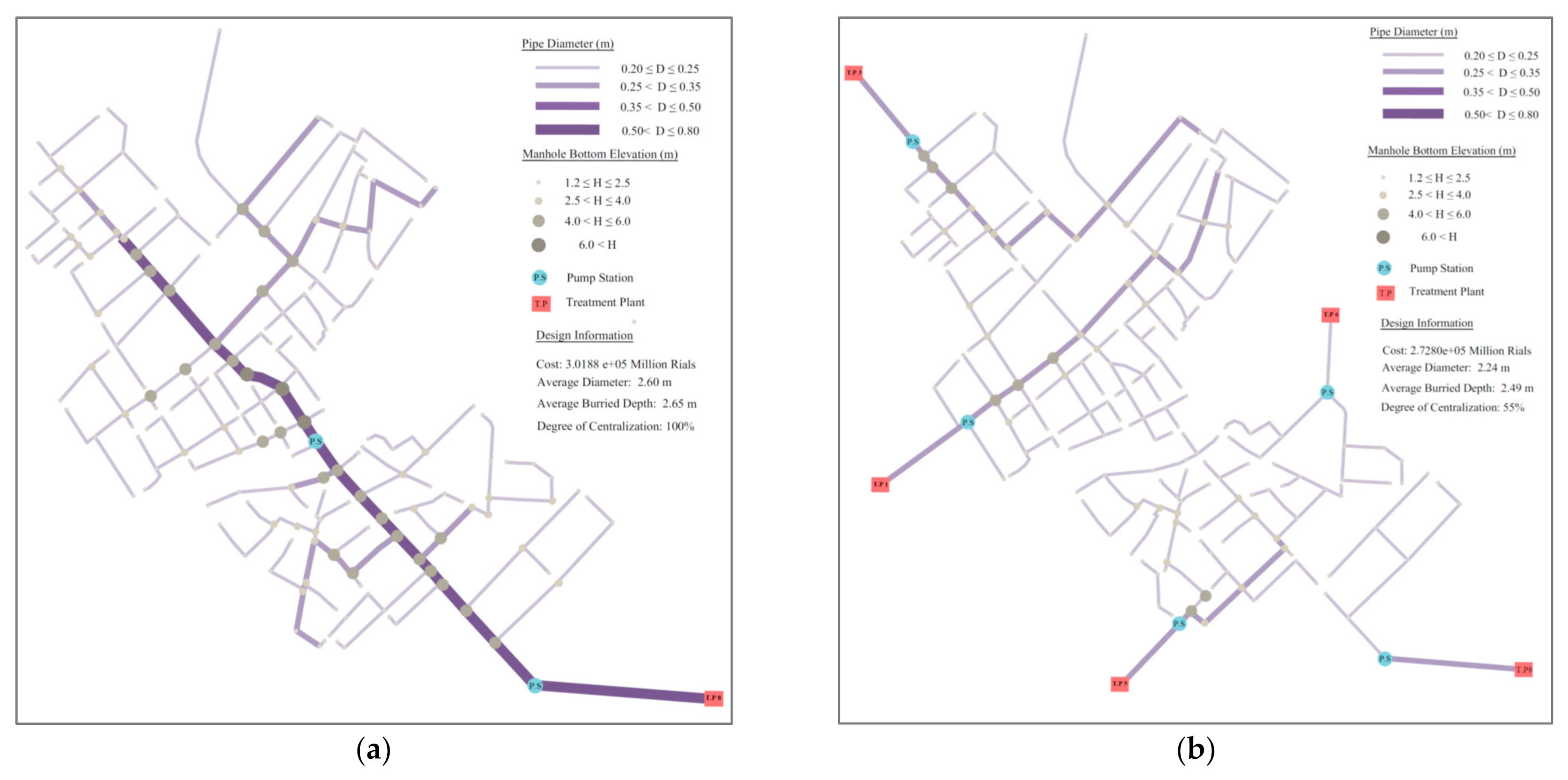
Figure 10 (8 optimum designs in total). Three designs among them were considered for further investigation through the following scenarios:
Scenario 1: The fully centralized design with only one treatment plant (
Figure 11a);
Scenario 2: A design with 5 treatment plants (
Figure 11b);
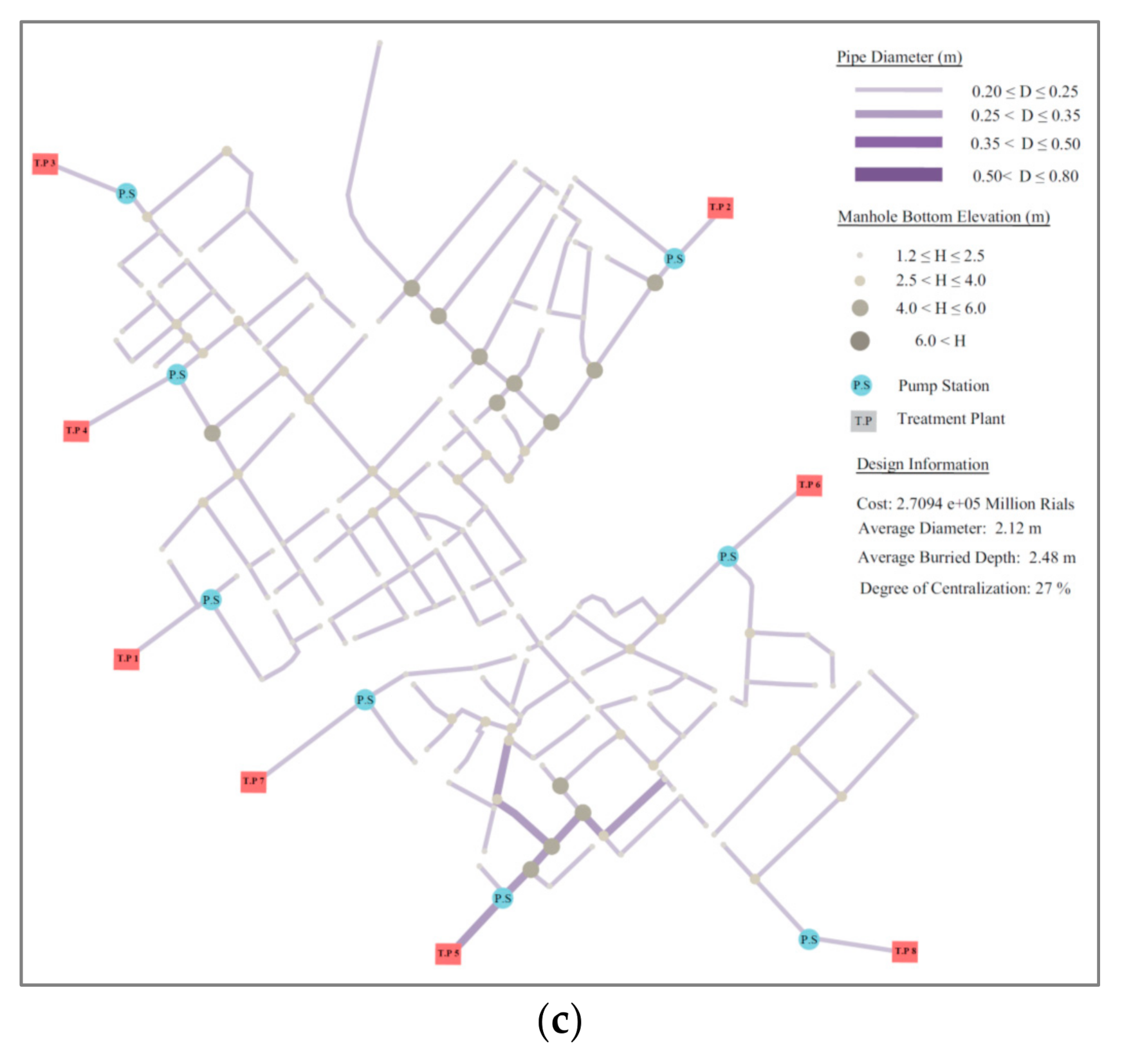
Scenario 3: The most decentralized design found via the optimization with 8 treatment plants (
Figure 11c).
The last scenario cannot be called a fully decentralized design, since by definition DC is a function of both the number of network roots and the sewage flow distribution between the network’s sublayouts. The minimum DC found for this case study is about 27%.
As expected, solving the case study revealed that most of the entire budget for constructing and operating a centralized sewage collection network is spent on the sewers. In scenario 1, around 24% of the total cost is spent on a single wastewater treatment plant (scenario 1). At the same time, in the most decentralized design with 8 treatment plants (scenario 3), the portion of total cost spent on treatment plants increases to about 44%. In other words, as the number of treatment plants increases, toward the more decentralized network, the cost of the sewer system decreases because of the reductions in excavation depths and sewer diameter sizes and the need for pumping energy. Conversely, the total costs for construction and operation of multiple small treatment facilities increase. Indeed, economies of scale are essential issues to consider when designing a decentralized urban water system. Multiobjective optimization is a helpful tool to investigate this importance, as applied to the case study.
Figure 10 shows that the total annuities of the system do not change significantly for DCs above 55%, corresponding to design alternatives with more than 5 treatment plants (scenario 2). In these cases, the other considerations and criteria might be used to differentiate the optimum designs.
Table 4 provides a comprehensive comparison between scenarios 1 to 3.
As shown in
Figure 10, decentralization strikingly increases the structural resilience by distributing the risk of system failure between multiple small subsystems. The structural resilience is increased from 44% in the fully centralized design in scenario 1 to 79% in the most decentralized system in scenario 3. According to
Figure 10, the structural resilience of the optimum design in scenario 2 with
is 74%, which is very close to the most decentralized system in scenario 3. In other words, it is concluded that the decentralization benefits in terms of the both the system costs and structural resilience do not improve dramatically for
. Obviously, this finding is case-dependent, and different results are expected for different case studies.
5. Summary and Conclusions
Wastewater management systems rely heavily on network-based infrastructure, traditionally designed and constructed with a high degree of centralization, conveying the whole collected sewage flow to a large treatment plant very far from urban areas. In general, centralized sewer networks are expensive in terms of construction, operation, maintenance, and upgrades. They also cause serious concerns regarding long-term sustainability, resilience, and adaptiveness to upcoming challenges such as rapid urbanization. The challenges associated with centralized sewer networks are much more significant in flat areas and when water recycling and reuse are of interest.
Recent studies have proposed a shift from centralized systems to decentralized ones to overcome the challenges mentioned above. The superiority of decentralized sewer systems over centralized systems is case-dependent, although they are generally found to be more cost-effective and resilient if their network configuration and degree of centralization are optimized. This requires sophisticated graph-based algorithms for layout design and multiobjective optimization.
The current study introduced a new algorithm to generate all feasible layouts of a decentralized sewer network, resulting in a wide range of degrees of centralization. The layout generator algorithm was coupled to a self-adaptive hydraulic design model to measure the network components hydraulically. A multiobjective optimization problem was introduced to find the optimum trade-off between the cost, resilience, and degree of centralization for the network at hand. The optimization problem is quite self-adaptive, without any penalty function. It optimizes the network’s layout and hydraulic components implicitly.
The proposed model was applied to a coastal city in Iran. The city is flat with a large river running through it, the groundwater level is high, and the geotechnical conditions are unfavorable, making the installation of deep and large sewers expensive. These issues made the case study a proper candidate for investigating the advantages of decentralized sewer networks. The results demonstrated the good performance of the proposed algorithms in generating decentralized layouts, with a wide range of degrees of centralization and with the algorithms finding near-optimum solutions. As expected, the decentralization increases the structural resilience by distributing the risk of system failure to multiple small subsystems. By deriving the optimal trade-offs between the system’s costs, structural resilience, and degree of centralization, one can decide on the best design depending on further considerations and limitations.
For this purpose, developing a multicriteria decision-making framework to be used as a post-processing model is suggested for further investigations in the future. This model would facilitate the stakeholders in picking the best solution from the derived optimum Pareto front.