Exploring the Spatial Impact of Green Infrastructure on Urban Drainage Resilience

Abstract

This paper explores the spatial impact of green infrastructure (GI) location on the resilience of urban drainage systems by the application of exploratory spatial data analysis (ESDA). A framework that integrates resilience assessment, location sensitivity analysis and ESDA is presented and applied to an urban catchment in the United Kingdom. Three types of GI, namely a bioretention cell, permeable pavement, and green roof, are evaluated separately and simultaneously. Resilience is assessed using stress-strain tests, which measure the system performance based on the magnitude and duration of sewer flooding and combined sewer overflows. Based on the results of a location sensitivity analysis, ESDA is applied to determine if there is spatial autocorrelation, spatial clusters, and spatial outliers. Results show a stronger spatial dependency using sewer flooding indicators. Different GI measures present differences in spatial autocorrelation and spatial cluster results, highlighting the differences in their underlying mechanisms. The finding of conflicting spatial clusters indicates that there are trade-offs in the placement of GI in certain locations. The proposed framework can be used as a tool for GI spatial planning, helping in the development of a systematic approach for resilience-performance orientated GI design and planning.

1. Introduction

The need to build resilience into urban drainage systems is increasingly recognised as vital, as systems need to adapt and recover from failure in face of deeply uncertain threats [1]. There is increasing pressure not just to plan for sustainability, but also to increase resilience [2]. A major strategy to enhance the resilience of urban drainage systems is the implementation and expansion of green infrastructure (GI) [3,4]. GI is on-site nature-based stormwater management measures that contribute to reversing hydrological and water quality impacts of urbanisation [5]. They are a promising alternative to traditional stormwater practices, as they not only increase the flexibility and diversity of the urban drainage systems but also bring multiple functions and benefits, such as water quality improvements, flood risk reduction, increased biodiversity, improved air quality and reduction of urban heat island effect [6,7,8,9]. GI has been promoted by government agencies and organisations, and adopted in various countries [10,11].

Despite their growing popularity, there are still various challenges associated with the application of GI [10]. Although they are suggested to have some resilient properties, they may or may not deliver resilience, depending on the systems’ framing or indicators used [2,7]. Previous research has demonstrated that GI can contribute to resilience [12], although this contribution may be small and not always guaranteed [7]. Additionally, GI interventions may result in trade-offs between different indicators, with the improvement in one indicator leading to the reduction in another [3,7]. There is a need for a systematic approach to understanding the key drivers of resilience performance and, in particular, a systematic exploration of the complex relationship between resilience performance impacts of GI.

Understanding the spatial impact of GI is key to develop their design and placement strategies. In literature, various frameworks have been developed for the implementation of GI based on various catchment characteristics and performance indicators. These include, for example, the regret-based approach [8], adaptation pathways [13] and real options [14]. However, only a few frameworks specifically link GI locations in the network to their impact on the performance of the sewer system [3,15,16,17,18]. Although there is some evidence suggesting spatial dependency of GI and their performance on the urban drainage system [12,17], there is a lack of understanding of the impacts of underlying spatial patterns of GI on the enhancement of resilience. This paper targets this gap through the application of spatial analysis methods.

Exploratory spatial data analysis (ESDA), often described as a subset of exploratory data analysis (EDA), is a collection of techniques that analyse spatial data to reveal spatial autocorrelation and heterogeneity [19]. More specifically, it allows description and visualisation of spatial distributions, identification of atypical locations or spatial outliers, and discovery of spatial patterns. It can help generate hypotheses for spatial regimes or other forms of spatial heterogeneity [19,20]. Originally applied in economic and social sciences [20,21,22], it has been extensively used in several other fields such as geography and environmental sciences [23,24,25,26].

This paper proposes the application of ESDA to understand the impact of GI location on resilience enhancement in urban drainage systems. Despite the multiple benefits of the GI, this study is centred on water quantity and water quality, through the study of the resilience to sewer flooding and combined sewer overflows (CSOs). The main questions to be answered are: (i) if there is spatial autocorrelation between the locations of GI in the system and its impact on resilience, and is such a relationship detected, (ii) if there are spatial clusters and spatial outliers of high and low resilience impact, and (iii) how these spatial relationships and spatial heterogeneities vary when using different types of GI and resilience indicators. Addressing these questions can help in the development of a resilience-performance orientated GI design and planning, as well as provide a systematic approach to revealing the link between resilient properties and resilience performance in urban drainage systems. To answer these questions, a framework that incorporates resilience assessment, location sensitivity analysis and exploratory spatial data analysis is presented. To test the competence and practical value of the proposed framework, a case study in the United Kingdom (UK) is used. The structure of this paper is as follows: the framework used is presented in Section 2, the results of the analysis are presented in Section 3, the implications of the findings are discussed in Section 4, along with the limitations and future research, and finally, the findings are summarised in Section 5, along with some concluding remarks.

2. Materials and Methods

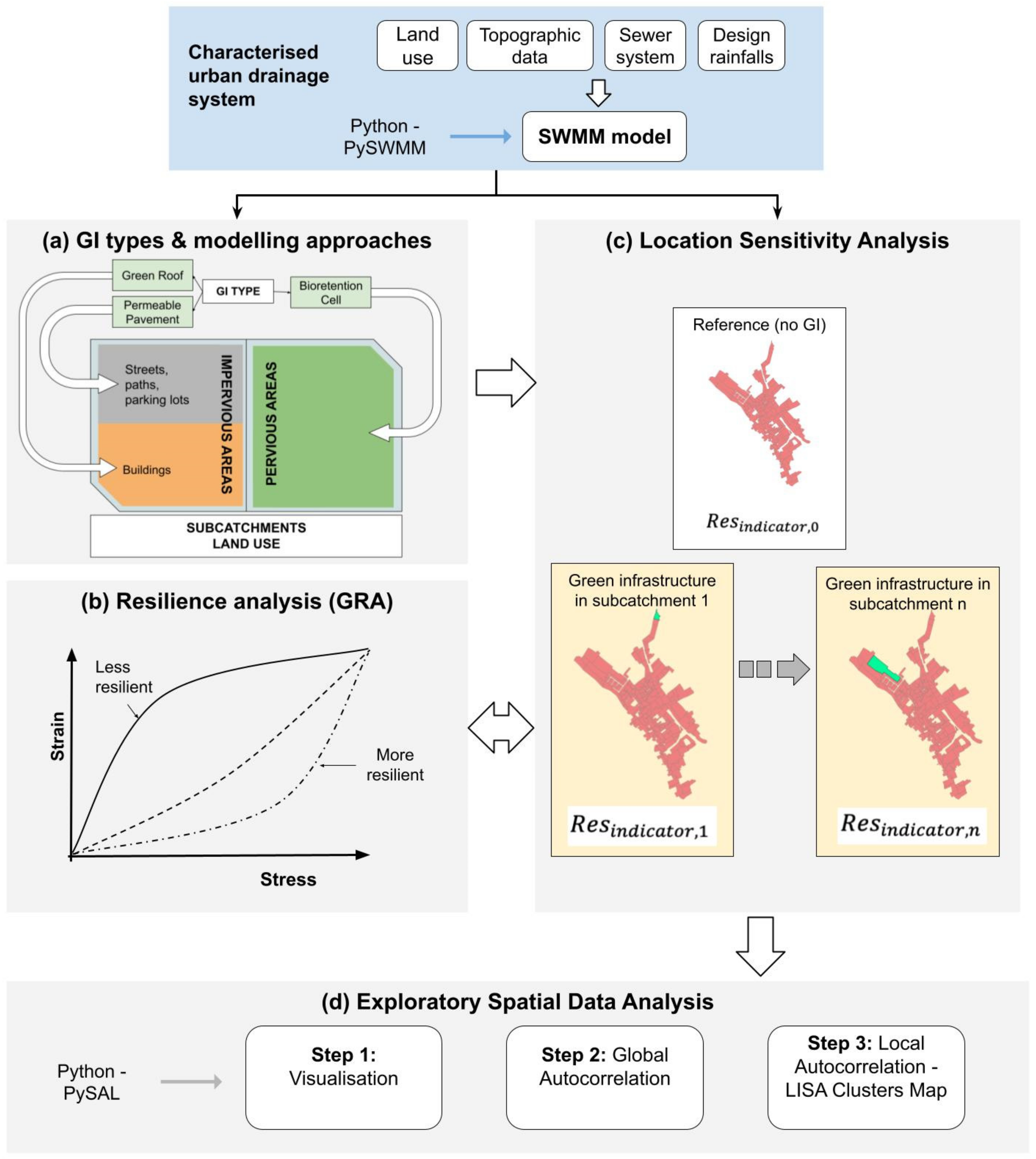
2.1. Overview

The proposed framework, illustrated in Figure 1, consists of four key elements: the GI types and modelling approaches, the resilience assessment, the location sensitivity analysis, and the exploratory spatial data analysis. The framework was implemented using Python and a combination of different open access packages. The hydrologic-hydraulic simulations were performed using the US EPA Stormwater Management Model (SWMM) [27], and the Python interface PySWMM [28]. All the spatial analysis methods used in the ESDA were performed using PySAL [29].

2.2. GI Types and Modelling Approaches

The impact of three types of GI were studied: bioretention cells, green roofs, and permeable pavements. These were selected as they are commonly used in practical applications, as well as in literature [30]. The interventions selected could be implemented in different parts of the catchment, namely, by retrofitting them in existing urban areas or in new developments. Their selection attempts to capture strategies that affect different urban area types (i.e., roofs, streets, pervious areas). Additionally, the differences in their functionality provide a wide scope on how different mechanisms interact with the performance of urban drainage systems [27,31]. Bioretention cells provide storage, infiltration and evaporation from direct rainfall and runoff captured from surrounding areas; green roofs convey rainfall off the roofs, also allowing evapotranspiration; and permeable pavements capture and convey rainfall to a storage zone and the native soil below [31].

There are two different approaches to simulate GI impacts within a subcatchment in the SWMM: either by incorporating the GI as a part of an existing subcatchment or by creating a new subcatchment composed only by the GI practice [27]. In this study, the first option is used, and the extent of the GI is determined by the different land uses in the subcatchment (Figure 1a). The maximum spatial extent for bioretention cells is capped by the pervious area available in each subcatchment. Similarly, for green roofs, the maximum spatial extent is delimited by the building area in the subcatchment. For permeable pavements, the maximum spatial extent is the total area of streets, pedestrian paths, and car parks in the subcatchment. The implementation of GI at the maximum spatial extent is unlikely to be met in practice, due to various limitations such as ownership of the land, building types, and characteristics of the catchment itself (i.e., soil types and groundwater level). However, this approach represents the best possible case at each subcatchment and serves as a benchmark to compare their effectiveness in the different locations in the catchment.

GI types selected in this study are represented using a unit processes-based approach, each containing a combination of different media, storage, and drainage layers [27]. The design variables that affect the performance of the GI include properties of the media (soil and gravel), the vertical depth of the media layers, the hydraulic capacity of any underdrain system used, and the surface area of the unit itself [31]. The parameter values used are typical values found in the literature [30,32,33] and are presented in

Table 1. Summary of GI characteristics. Typical values for all the parameters are based on the literature [30,32,33].

Layer	Parameter	Green Roof	Permeable Pavement	Bio-Retention Cell
Surface	Berm height (mm)	50	0	150
	Vegetation fraction (%)	0.5	0	0.1
	Roughness (Manning’s n)	0.4	0.012	0.1
	Surface slope (%)	0	1	1
Pavement	Thickness (mm)	-	150	-
	Void ratio (volume fraction)	-	0.15	-
	Fraction Imperviousness (%)	-	0	-
	Permeability (mm/h)	-	500	-
	Clogging factor	-	0	-
Soil	Thickness (mm)	150	-	600
	Porosity (volume fraction)	0.45	-	0.5
	Field capacity (volume fraction)	0.2	-	0.2
	Wilting point (volume fraction)	0.1	-	0.1
	Conductivity (mm/h)	650	-	250
	Conductivity slope (-)	5	-	12.5
	Suction head (mm)	49.5	-	50
Storage	Height (mm)	-	300	150
	Void ratio (-)	-	0.4	0.75
	Seepage factor (mm/h)	-	7.0	7
Drain	Coefficient (mm/h)	-	0.5	0.5
	Exponent (-)	-	0.5	0.5
	Offset height (mm)	-	100	150
	Delay (days)	-	0	0
Drain Mat	Thickness (mm)	75	-	-
	Void ration (volume fraction)	0.75	-	-
	Roughness (Manning’s n)	0.1	-	-

.

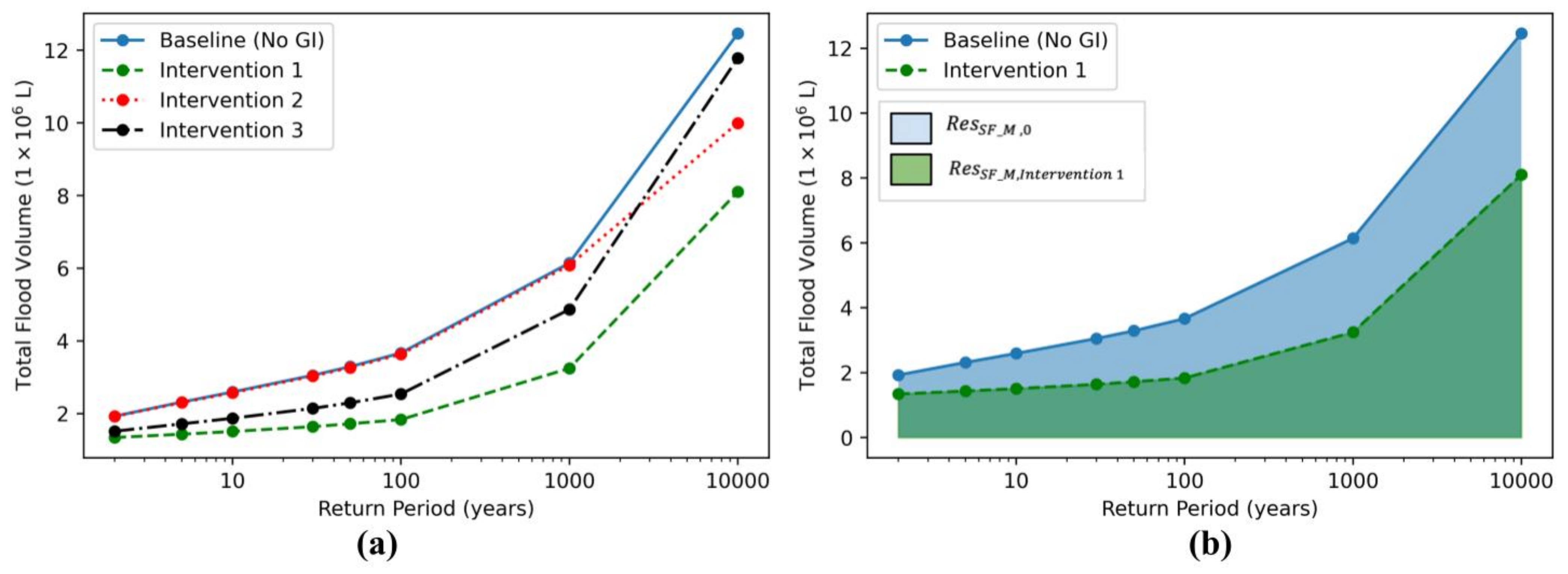
2.3. Resilience Assessment

In this study, resilience is defined as “the degree to which the system minimises the level of service failure magnitude and duration over its design life when subject to exceptional conditions” [2,7,34]. Therefore, the components of resilience are failure duration and failure magnitude, if they are unknown, resilience cannot be calculated [7]. In addition, under this definition, knowing the probability of the event causing the failure is not required [2,7,34].

The global resilience analysis (GRA) methodology is used for the resilience assessment [1,2,34], as illustrated in Figure 1b. This methodology was selected as it provides a performance-based and quantitative measurement of resilience, considering the effects of a wide range of potential system failure types and magnitudes without the need for scenario development or the need to identify the root of all failures, in accordance with the resilience definition used [2]. GRA calculates the system’s performance as a function of system failure magnitude, enabling the generation of response curves or “stress-strain” curves. These represent the performance under a range of stress magnitudes, where the “stress” is a measure of the load on the system and the “strain” is a measure of its impact on the system [2,34].

In this study, stress is modelled as an increase of the return period in the design rainfall event considered, which corresponds to an increase in the rainfall depth. A total of nine rainfall events are considered with different return periods (1 in 2-years, 1 in 5-years, 1 in 10-years, 1 in 30-years, 1 in 50-years, 1 in 100-years, 1 in 200-years, 1 in 1000-years and 1 in 10,000-years). The duration of the storms is the same across all the return periods, and it is determined by the critical storm duration for the system studied. Although this does not capture every possible rainfall event, it does represent a wide range of possibilities, including extreme events as necessary for the assessment of resilience. This includes the highly unlikely events of 1 in 1000-years storm and 1 in 10,000-years storms, whose magnitude are obtained based on extrapolation and fitting of the depth-duration-frequency models [35].

Under each rainfall, the resulting strain or loss of system functionality is quantified. A basic approach for the quantification of the effects of GI on water quantity and water quality in the system is by evaluating the reduction of sewer flooding (water quantity impacts) and the reduction of CSOs (water quality impacts). Thus, the system’s level of service loss is measured through the magnitude and duration of sewer flooding and CSOs (

Table 2. Level of service loss measures.

Level of Service Loss	Metric	Description	Calculation	Notations
Sewer flooding	Failure Magnitude	The total flood volume in the system	Summation of flood volume at the flooded nodes	SF_M
	Failure Duration	Time taken between the occurrence of flooding to the recovery of normal performance	Average of the duration of the flooding at the flooded nodes	SF_D
CSO (combined sewer overflows)	Failure Magnitude	The total CSO volume in the system	Summation of CSO volume at the outfall nodes	CSO_M
	Failure Duration	Time taken between the occurrence of CSO to the recovery of normal performance	Average of the duration of the CSO at the outfall nodes	CSO_D

). The sewer flooding magnitude and duration are computed for every node. To derive the metric for the system, the nodes’ values are summed to account for the failure magnitude and averaged for the failure duration. In the case of the CSO, the magnitude and duration are obtained from the outfall nodes in the system studied, and similarly to sewer flooding indicators, these are summed or averaged to obtain the whole network metric value.

An example of the resulting stress-strain curve obtained for different GI interventions is shown in Figure 2a. The area under each response curve provides a performance-based indicator of resilience to the corresponding system failure mode [36]. In this study, this is the area under the return period versus the system’s level of service loss (Figure 2b). The area is calculated using the trapezium rule, using a pre-defined function in Python. This does not intend to be an accurate representation of the absolute resilience of the system, but rather a proxy for comparing the effect of different GI types and their locations on the system’s failures, when subject to the same conditions.

A higher resilience is represented by a smaller area under the response curve, as it indicates a lower level of service failure over a range of conditions [36]. To compare the impact of different interventions the net change in resilience is calculated using

$$Netchang{e}_{indicator,j}=100\times \left(\frac{Re{s}_{indicator,0}-Re{s}_{indicator,j}}{Re{s}_{indicator,0}}\right)$$

(1)

where $Re{s}_{indicator , 0}$ corresponds to the baseline where no GI was installed in the system, and $Re{s}_{indicator, j}$ corresponds to the area under the curve for an intervention j. A positive net change implies that there is a positive impact on resilience, therefore a resilience enhancement. Similarly, a negative net change implies that the intervention caused a decrease in resilience.

2.4. Location Sensitivity Analysis

One simple approach to sensitivity analysis is the one-factor-at-a-time method, where only one model parameter is modified, the variation in the resulting modelling output is analysed. Such is the approach used in the GIS-based application of sensitivity analysis for sewer models [37], where the change in the system performance caused by the variation of a single parameter is spatially referenced at the location where the change has happened. This approach was previously used in literature to understand the sensitivity to the location in the effect of GI in the urban drainage system performance [17].

In this case, this technique is applied to determine the sensitivity to the location of GI in their impact on resilience (Figure 1c). The main steps in the implementation of the location sensitivity analysis are as follow,

• The system with no design or operational changes is used as the reference for system performance. GRA is used to evaluate the baseline (or no-GI case) resilience for the different indicators, and it is referred to as $Re{s}_{indicator,0}$.
• A single GI infrastructure with a consistent type is applied in each subcatchment at a time and simulated for resilience assessment. The GI size is determined by the maximum extent possible determined by the land use of the subcatchment.
• Assessment of resilience using GRA considering the different metrics. The impact of different GI types and their location in the system is reflected by a change in the response curve shape.
• The net change in the system’s resilience due to the placement of a GI in a subcatchment is calculated using Equation (1).

Steps 1–4 are repeated for each subcatchment in the urban drainage system considered.

The result of this analysis shows the net resilience in each subcatchment due to the installation of GI. This procedure is applied for each of the different level of service loss indicators (SF_M, SF_D, CSO_M, and CSO_D), as well as for each type of GI separately. Further, a combination of three types of GI is simultaneously applied to subcatchments, referred to as “all GI” in the rest of the paper.

2.5. Exploratory Spatial Data Analysis

In this section, we briefly describe the ESDA methods used (Figure 1d). This follows the methodology presented in [20].

2.5.1. Visualisation

To start the exploration of spatial data, an important aspect of ESDA is the visualisation of the data in maps. A standard tool for appreciating the spatial distribution of the values and detection of outliers is the choropleth map using a box classification. The box map is the mapped version of the box plot, where the “extreme” values or outliers are defined based on the interquartile range (IQR) [19,20]. It allows the separation of the range of values into six categories: the four quartiles (<25%, 25–50%, 50–75%, >75%), as well as the lower and upper outliers (Figure 3) [20]. The outliers are defined as values outside a cut-off value, set at one and a half times the IQR.

2.5.2. Global Spatial Autocorrelation

The phenomenon to which observations in spatial proximity present similar values is named spatial autocorrelation or spatial association, and it is the spatial counterpart to traditional autocorrelation [19]. There are two scales in the autocorrelation evaluation: global and local. Global spatial autocorrelation determines if there is spatial clustering in the values, meaning that the distribution of values in the space follows a pattern. A positive spatial autocorrelation indicates that similar values are in a similar location, and a negative spatial autocorrelation implies that similar values are further apart.

The Global Moran’s I statistics is used as a formal test of global spatial correlation and clustering, by testing the null hypothesis of random location. A spatial weight matrix W is for the incorporation of spatiality (Section 2.5.4), and the significance is based on a comparison to a reference distribution obtained by randomly permuting the observed values. Moran’s I is defined as below [38]

$$I=\frac{N}{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{w}_{ij}}\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{w}_{ij}\left(x_i-\overline{x}\right)\left(x_j-\overline{x}\right)}{{{\displaystyle \sum }}_i{\left(x_i-\overline{x}\right)}^2}$$

(2)

where N is the number of observations (in this case the number of subcatchments), $x_i$ and $x_j$ are the value of the indicator of interest at location i and j (in this case the different levels of service loss indicators), $\overline{x}$ is the sample mean, and $w_{ij}$ is the row-standardised values of the spatial weights from the spatial weights matrix W. Moran’s I test values ranges between 0 (perfect dispersion or a random spatial pattern) and 1 (perfect clustering).

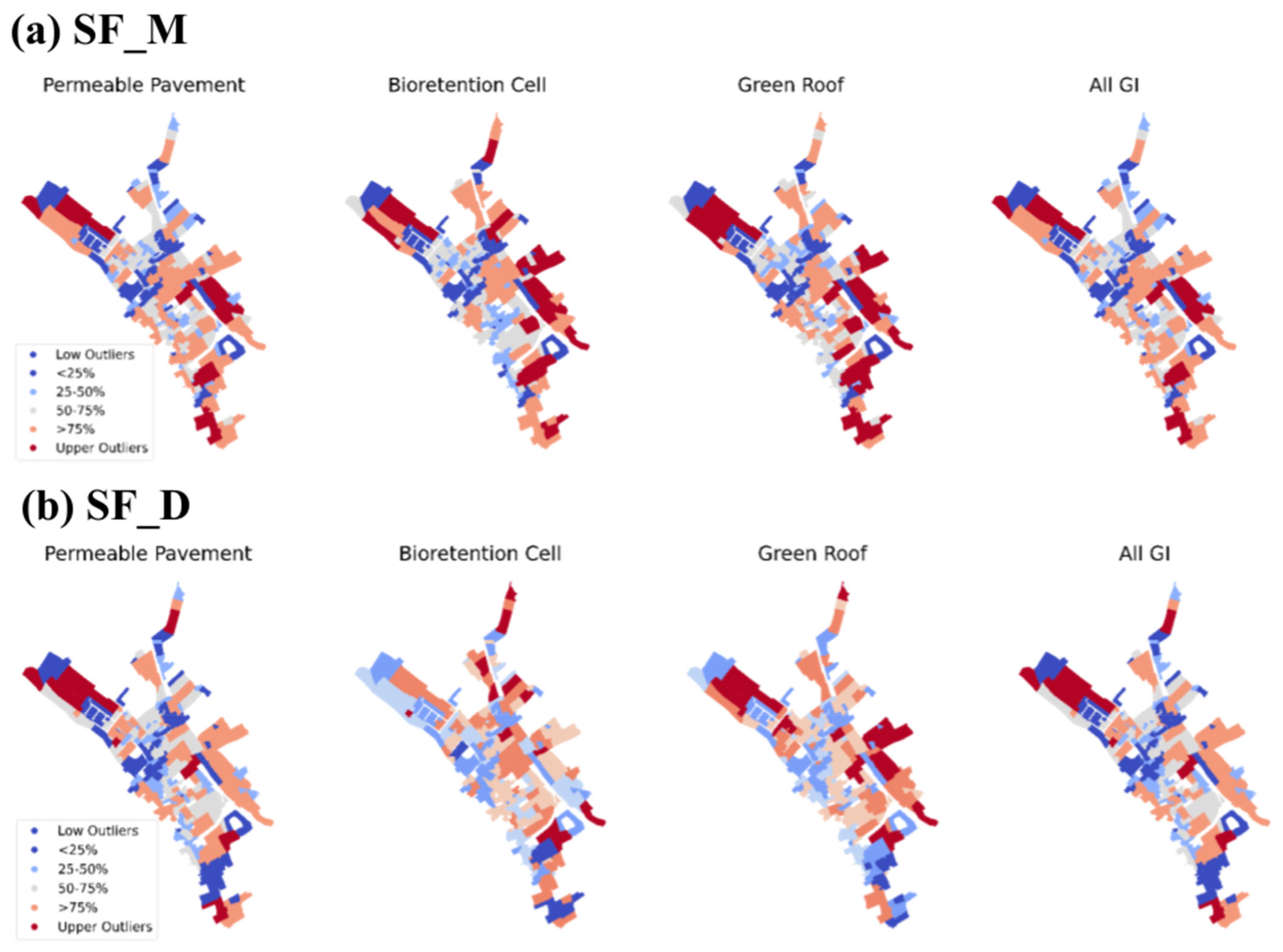
2.5.3. Local Spatial Autocorrelation

While Moran’s I test provides a measure of the overall clustering, it does not indicate where the clusters and outliers are located. Local spatial autocorrelation determines if there are specific parts of the space with an extraordinary concentration of similar/dissimilar values, highlighting pockets of spatial instability. The Local Indicator of Spatial Association (LISA) statistics, and local Moran’s I, are used for spatial cluster detection, by comparing the observed map with many randomly generated ones and evaluates how likely is to obtain the observed association for each location. The formal representation of the statistic is defined as below [39]

$$I_i=\frac{\left(x_i-\overline{x}\right)}{{\sigma }^2}{\displaystyle \sum }_j{w}_{ij}\left(x_j-\overline{x}\right)$$

(3)

where $x_i$ and $x_j$ are the value of the indicator of interest at location i and j (in this study, the net change in resilience in the different subcatchments), $\overline{x}$ is the sample mean, and $w_{ij}$ is the row-standardised value of spatial wights from the spatial weights matrix W. ${\sigma }^2$ is the variance of a given $x$.

The significance of the local Moran statistic is determined by generating reference distribution using 999 random permutations. This number of permutations is the usual practice, as it provides an acceptable balance between precision and processing times [39,40]. The nature of spatial autocorrelation can be categorised into four main groups: significant local clusters high-high (HH) or low-low (LL), and local spatial outliers high-low (HL) or low-high (LH), as explained below:

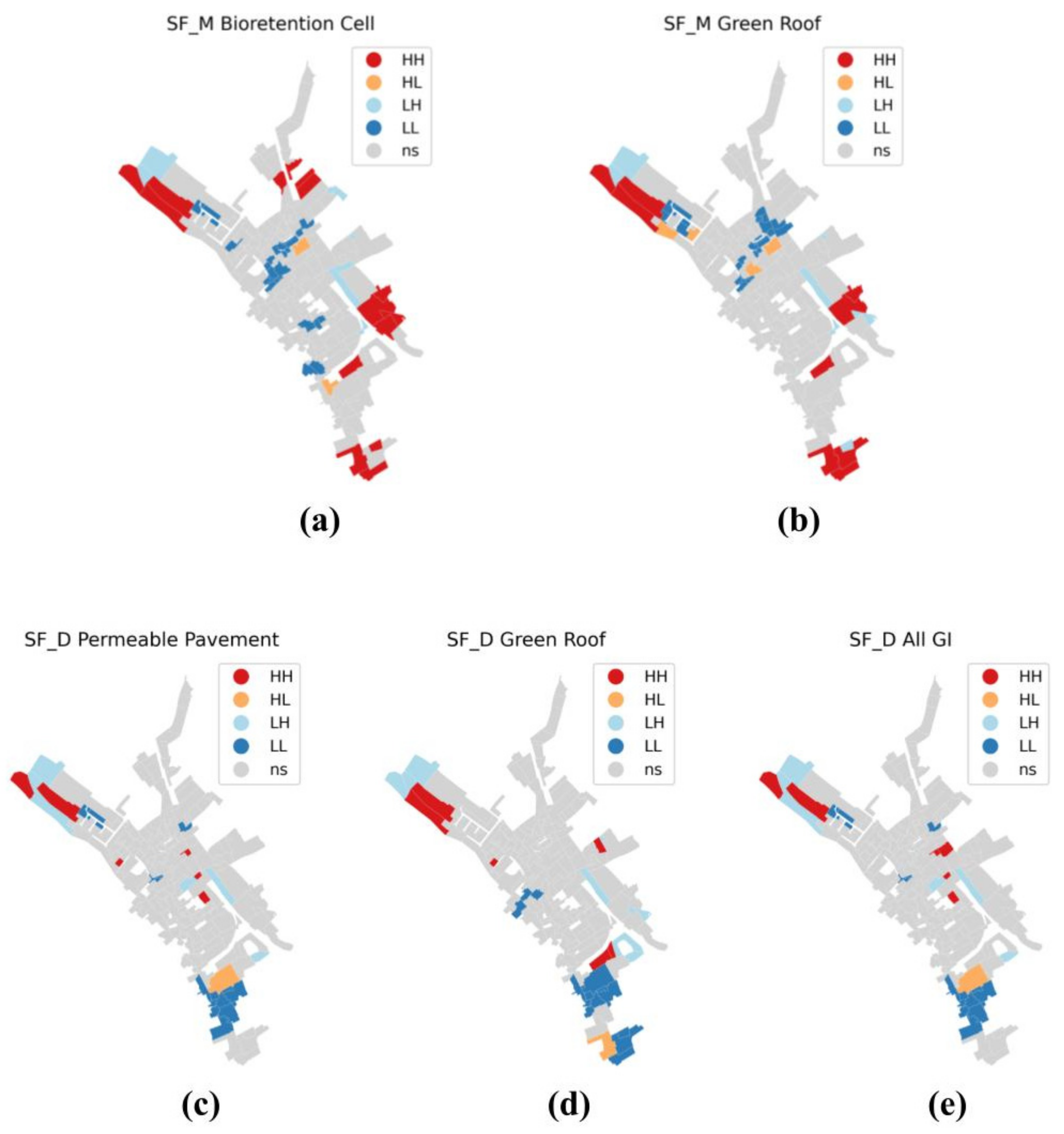
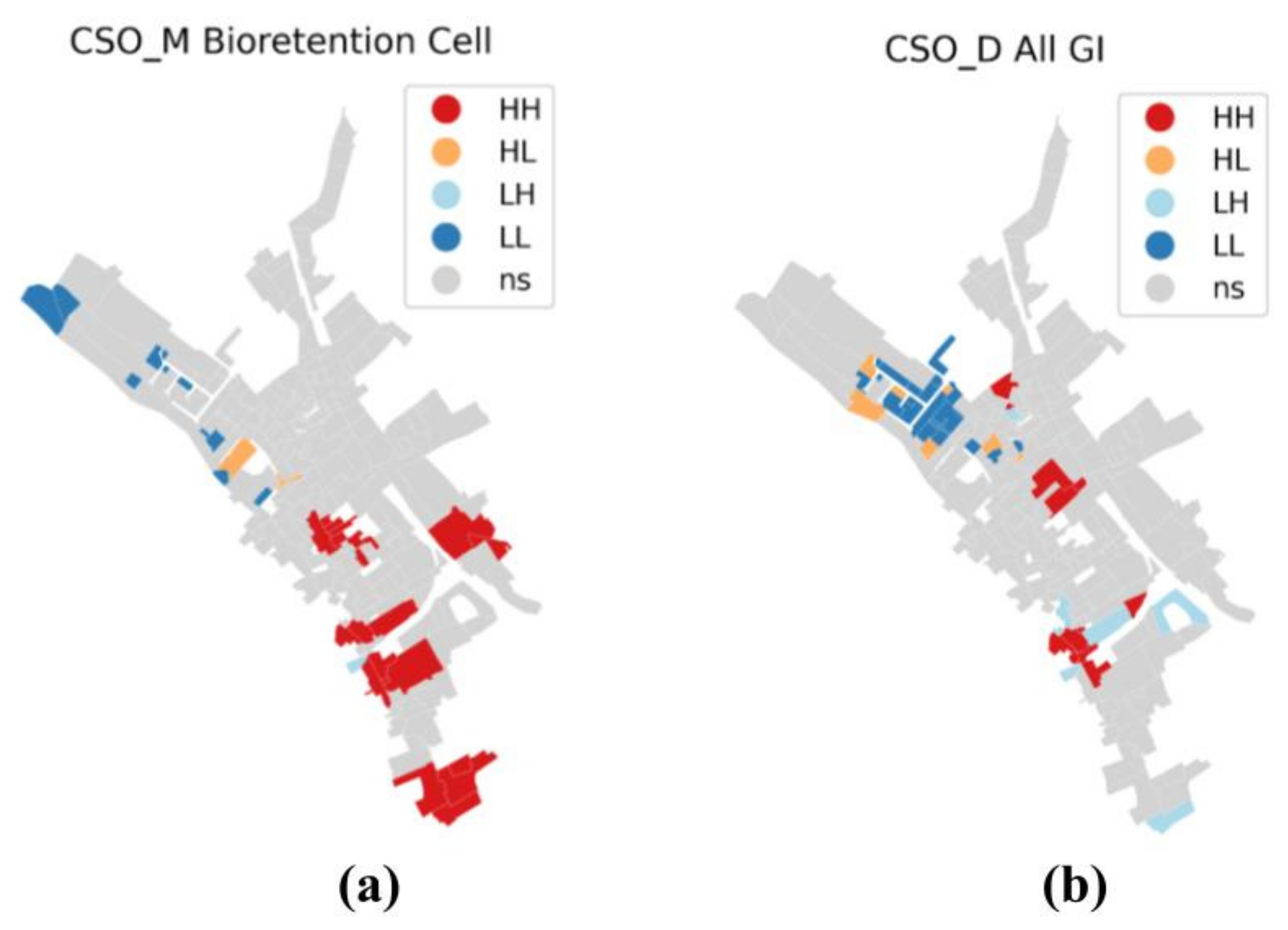
• High-high (HH): a high value of net change in resilience in a subcatchment, neighbouring subcatchments have high values of net change in resilience.
• Low-high (LH): a low value of net change in resilience in a subcatchment, neighbouring subcatchments have high values of net change in resilience.
• Low-low (LL): a low value of net change in resilience in a subcatchment, neighbouring subcatchments have low values of net change in resilience.
• High-low (HL): a high value of net change in resilience, neighbouring subcatchments have low values of net change in resilience.

The map showing the location of these categories is incorporated in the LISA cluster maps, where the information about the significance of the local spatial pattern [20]. The categories resulting in a spatial typology consist of the four categories mentioned (HH, LL, LH and HL), with the addition of the non-significant locations (ns). These maps allow the visualisation of the locations of the high and low net change in resilience, identifying areas of high interest and exhibiting spatial heterogeneity [20].

2.5.4. Spatial Weights Matrix

Measuring spatial clustering requires a spatial weight matrix W, as a mean to represent the spatial relationships and adjacencies [41]. There are many approaches to represent this matrix. As it is difficult to choose a single best option, the robustness of the results was tested using five different weight matrices,

• Queen contiguity: which reflects adjacency relationships as a binary indicator variable denoting whether a subcatchment shares an edge or a vertex with another polygon.
• Rook contiguity: which considers the subcatchment neighbours only when they are sharing an adjacent edge.
• K-nearest neighbours matrices (k = 4, 5, 6): the distances between a given subcatchment and the rest of the set are ranked, and the neighbours are defined as the k closest ones in the ranking [40].

Using these five different weight matrices allows the evaluation of the robustness towards different definitions of neighbourhood (contiguity versus distance-based), but also, the contemplation of how different k-neighbours (or distances bands) affect the spatial interactions.

The spatial contiguity matrices were row-normalised, normalising the impact of each neighbouring subcatchment and summing them to one.

2.6. Case Study

The case study used is a satellite town of Exeter, located in the South West of England, UK. The watershed consists of 220 sub-catchments with a total area of 73.3 ha, serving approximately 4000 inhabitants. The combined sewer system consists of 487 conduit links and junction nodes, 3 storage tanks, and one outfall node (Figure 4a). The dynamic wave theory is used for flow routing computations and the modified Horton method is used to simulate infiltration in pervious areas.

The model parametrisation was based on GIS data and recommended values from technical design guides, planning regulations and the literature [42,43,44,45,46,47]. In Figure 4b, the distribution and categorisation of different land uses can be visualised.

Different design rainfall events needed for the GRA were generated according to the FEH procedures [48], using a 50% summer profile. Various storm durations were simulated (30 min to 24 h) for each return period, allowing the determination of the critical storm duration. The critical storm duration chosen was 10 h for the catchment, determined by the duration which caused the highest total volume of sewer flooding and flood duration on average, when considering all the return periods.

3. Results

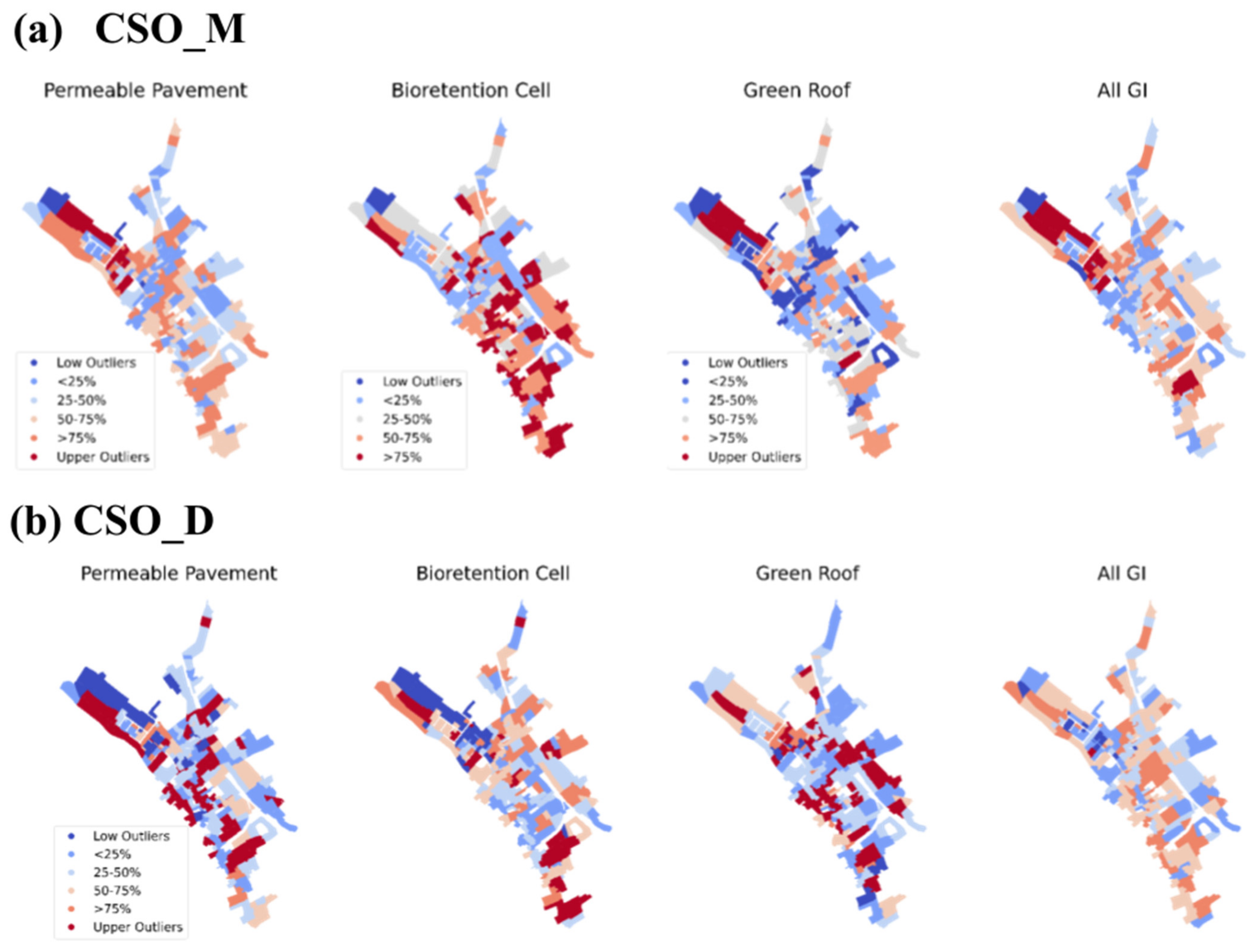
3.1. Visualisation

Figure 5 provides a summary of results obtained in the location sensitivity analysis for each type of GI separately and the “all GI” case. As explained in Section 2.3, a positive net change in resilience implies that the intervention increases resilience. Although the results show that the impact of a single GI at a system level is small for most of the locations, there is still a great variation presented in the results due to the placement of GI in different subcatchments. In addition, there are locations that produce the opposite effect, causing a decrease in resilience. This is the case for most of the locations and types of GI when considering CSO as level of service loss (Figure 5c,d), highlighting trade-offs on the benefits of GI placement in certain locations. These negative effects may be attributed to the synchronization of peak flows due to GI overflow at an unfavourable time, and the characteristics of the sewer system and catchment [7]. However, a conclusive hypothesis on the mechanistic reasons behind this performance requires further spatial and hydraulic-hydrological modelling, out of the scope of this paper.

To appreciate the spatial distribution and identify spatial outliers of high/low net change in resilience, Figure 6 and Figure 7 provide the box maps resulting from the analysis on sensitivity to location for GI in the enhancement of resilience. The spatial outliers are the most impactful locations and are of the highest interest in this analysis.

In Figure 6, where the level of service loss was measured using the sewer flooding flows, it can be observed that the overall spatial pattern is consistent when comparing different GI. The spatial patterns in the different maps are similar for both failure magnitude and failure duration, however, the spatial outliers are more prominent and more abundant in the case of bioretention cells and green roofs. Generally, the central subcatchments show lower values in the net change of resilience, whereas the most peripheral subcatchments show higher values.

In Figure 7, where the level of service loss was measured by the CSO, the spatial pattern and outliers are not consistent through the different infrastructure measures. In particular, the spatial pattern for failure magnitude in green roofs differs from the results of bioretention cells and permeable pavements. In addition, when accounting for the failure duration, both green roofs and permeable pavements show a significant number of upper outliers, differing with the results obtained for the bioretention cell and “all GI”.

3.2. Global Spatial Autocorrelation

The results for the Moran’s I test for spatial autocorrelation are given in

Table 3. Moran’s I and statistic for spatial autocorrelation in GI impact on resilience. The positive and significant spatial autocorrelation are highlighted in yellow.

		SF_M		SF_D		CSO_M		CSO_D
GI Type	Spatial Weights	Moran’s I	p-Value	Moran’s I	p-Value	Moran’s I	p-Value	Moran’s I	p-Value
Permeable Pavement	Queen Contiguity	0.015	0.354	0.110	0.020	−0.005	0.138	−0.011	0.430
	Rook Contiguity	0.012	0.346	0.111	0.011	−0.047	0.169	−0.006	0.487
	KNN–4	0.070	0.052	0.156	0.001	0.059	0.058	0.001	0.448
	KNN–5	0.088	0.024	0.152	0.001	0.048	0.074	0.003	0.397
	KNN–6	0.076	0.020	0.135	0.003	0.034	0.118	0.012	0.305
Bioretention Cell	Queen Contiguity	0.191	0.001	0.052	0.111	0.168	0.001	0.042	0.150
	Rook Contiguity	0.181	0.004	0.052	0.114	0.172	0.001	0.043	0.145
	KNN–4	0.200	0.002	0.087	0.022	0.199	0.001	0.039	0.146
	KNN–5	0.210	0.001	0.040	0.126	0.175	0.001	0.044	0.096
	KNN–6	0.215	0.001	0.041	0.086	0.160	0.001	0.043	0.087
Green Roof	Queen Contiguity	0.106	0.027	0.167	0.003	0.053	0.092	−0.060	0.122
	Rook Contiguity	0.101	0.022	0.164	0.001	0.053	0.111	−0.070	0.092
	KNN–4	0.170	0.002	0.193	0.001	0.107	0.006	−0.057	0.101
	KNN–5	0.165	0.001	0.159	0.001	0.088	0.017	−0.045	0.138
	KNN–6	0.167	0.001	0.135	0.001	0.059	0.033	−0.053	0.067
All GI	Queen Contiguity	0.015	0.289	0.110	0.012	−0.019	0.370	0.195	0.001
	Rook Contiguity	0.012	0.325	0.111	0.018	−0.018	0.404	0.198	0.001
	KNN–4	0.070	0.049	0.156	0.002	0.010	0.019	0.191	0.001
	KNN–5	0.087	0.016	0.151	0.002	0.059	0.058	0.195	0.001
	KNN–6	0.076	0.019	0.134	0.001	0.059	0.033	0.154	0.001

, along with the p-values based on permutation approaches. The spatial correlation is considered significant if the p-value is less than 0.05.

There is a significant and positive spatial correlation across all the spatial weights for the green roof when measuring SF_M and SF_D, and for the bioretention cell for the SF_M and CSO_M. For the SF_D and CSO_D, this is also the case when all the GI are simultaneously placed in the same subcatchment. In the case of the permeable pavement, positive spatial autocorrelation across all the weights was only found for the SF_D.

There are various cases where there is a positive and significant spatial correlation, but it is only for some of the spatial weights. In addition, these cases show a low Moran’s I.

3.3. Local Spatial Autocorrelation

The previous analysis suggested non-randomness in the overall spatial pattern in the net change of some of the different indicators used in the GRA. This section focuses on where the spatial heterogeneity is placed, identifying spatial clusters and outliers. Figure 8 and Figure 9 present the LISA Cluster maps for the net change in resilience due to GI placement. The results presented are using a k-nearest neighbours spatial weight matrix (k = 5), and only the indicators with significant global autocorrelation across all the weights considered were included.

In Figure 8a,b, the spatial pattern between the clusters obtained using a bioretention cell and green roofs is similar for the SF_M. The HH clusters are generally located upstream in the network, whereas the LL clusters are concentrated in the middle/low stream of the sewer network. The area where the LL values are situated in the area where all the ramifications of the sewer unite to flow towards the wastewater treatment plant and outfall (Figure 4a). The location of these clusters might indicate that the placement of GI upper stream on the network is generally more beneficial in the enhancement of resilience. There are some similarities between the failure magnitude clusters (Figure 8a,b) and failure duration (Figure 8c,e), however, the failure magnitude clusters seem more prominent and abundant.

In Figure 8c,e, the overall pattern for permeable pavements, green roofs and all the GI types simultaneously in the subcatchment for the SF_D is observed. There is a cluster of low values in the south extreme of the catchment, as well as in some areas in the middle of the catchment. These are conflicting clusters, as they were HH clusters for the SF_M, which may indicate trade-offs in the impact of resilience when considering different indicators. The HH clusters, which are the most interesting as they show areas of high resilience enhancement, are relatively small and placed upstream.

For CSO_M, only the bioretention cell shows a significant spatial correlation for the failure magnitude. Figure 9a shows HH clusters in the south extreme of the catchment and a LL cluster in the network’s outfall. The “all GI” was the only case where positive and significant global autocorrelation was detected for the CSO_D, and the clusters identified are shown in Figure 9b.

4. Discussion

4.1. GI location and Resilience Enhancement Spatial Relationships

The exploration of spatial patterns demonstrated the presence of significant spatial clusters of high and low performance, as well as some spatial outliers, in the resilience impact of GI. The inclusion of GI in the urban drainage systems seeks to enhance the system’s resilient properties such as flexibility, redundancy, and diversity, but their effect on resilience performance is not guaranteed and remains uncertain [1,2]. The application of the analysis framework proposed, and the detection of the spatial autocorrelation, spatial clusters and outliers helps establishing a spatial link between the resilient properties and resilience performance. This can be described and included in GI placement design and policy development, helping in the operationalisation of resilience in urban drainage systems.

The variations found in the spatial autocorrelations and spatial clusters detected in the analysis provide interesting insights. It must be highlighted that the results here presented are case-specific and not universal, however, they demonstrate the potential of this framework.

Firstly, there is a contrast between the sewer flooding indicators and CSO indicators. There is only positive and significant autocorrelation for the bioretention cell when considering CSO_M, and the “all GI” case for CSO_D. This implies that the location of GI in the network impacts the reduction of sewer flooding, but not necessarily the CSO.

Secondly, the difference among the GI types could help understand how these interact with the system’s resilience performance. The bioretention cells showed spatial autocorrelation for the magnitude but not duration, both for sewer flooding and CSO. Permeable pavements only showed spatial autocorrelation for sewer flooding duration. Green roofs showed a spatial relationship for sewer flooding indicators only. In the “all GI” case, global autocorrelation was found only for the duration measurements. These results highlight differences in their underlying working mechanisms, as well as providing insights for strategies in their placement in the catchment.

Thirdly, the LISA Cluster maps show some “conflicting” clusters, where subcatchments are a part of HH clusters for some GI and indicators and a part of LL for other GI types and indicators. This would indicate trade-offs in resilience enhancement, which need to be further considered in the analysis. This highlights the complexity of resilience enhancement. The “one-size-fits-all” approach to GI design and placement, may not be the most effective strategy for improving resilience in the system.

Finally, there is a disparity in the location of the HH and LL clusters. For the SF_M, HH clusters are located upstream in the network, whereas the LL clusters are concentrated in the middle/low stream of the sewer network. The location of these clusters might indicate that the placement of GI on peripheric areas of the network is generally more beneficial in the enhancement of resilience in this catchment.

4.2. ESDA and Implications in Urban Planning

This paper demonstrates that spatial analysis could be used for urban planning, as a first step to identify strategic areas where GI provides higher impacts on resilience. The prioritisation of the areas for the installation of the GI could narrow the areas for the implementation of these practices. The LISA Cluster maps could be used on their own, or for example, as a valuable map layer in a GIS multi-criteria analysis.

Spatial dependence may reflect variations in a wide range of factors, including sewer system characteristics and other topographical attributes of the subcatchment areas. We argue that spatial patterns provide opportunities for a planner to have a deeper insight and understanding of the characteristics of the catchment and can help bring a structured way to understand the relationships in these complex systems. The progression towards an ESDA framework is accordant with the expanding role of GIS-based approaches and frameworks in GI placement and design.

Focusing on the detection of patterns can be seen as an instrument for reducing the search space in urban planning, where trade-offs between indicators could be identified [20]. Additionally, this research provides a valuable reference basis for the GI implementation path, and for scientifically formulating urban planning policies, based on effectively identifying the link between resilient properties and resilience performance.

4.3. Limitations and Future Research

The application of the ESDA in this paper has various limitations. It must be highlighted that the specific results presented in this case study cannot be generalised, due to the unique characteristics of each sewer system. However, this study represents the first approach to spatial considerations of resilience and their relationship with GI placement. This could be used in other networks to enable a deeper understanding of spatial interactions between GI and resilience impacts in the network.

The framework can be applied to sewer systems of any scale. However, the level of detail could have an impact on the analysis results (i.e., resilience) of the green infrastructure effect. The integration of a greater level of detail at a subcatchment level could bring a higher granularity in the spatial analysis. However, this would imply higher simulation times.

Limitations in the GI modelling approach used could be used as a starting point for exploration in future research. Other types of GI could be considered to enrich the analysis. In addition, the urban form (i.e., land availability and land prices), soil information and groundwater table could be integrated for a more realistic GI placement strategy in the subcatchments.

GRA was chosen for the resilience assessment as it provides a performance-based, quantitative measure of resilience. Further research could contemplate other types of “stress” to the system, such as structural failure, base-flow characteristics, and groundwater table. This could be easily adapted to the criticalities of the sewer network studied. Furthermore, due to the multi-functional nature of GI, the analysis could include other “strain” parameters, such as water quality parameters and ecology impacts.

ESDA, as its name indicates, is an exploratory technique, and the methods used are indicative of possible hypotheses and relations [20]. Further spatial modelling is needed to confirm these relationships [19,20]. Future research could include the incorporation of spatial modelling using a greater variety of sewers to identify if certain characteristics of the sewer system or topological structures in the catchment, lead to certain spatial patterns in the impact of the GI in the system performance.

This study was performed using open-access programming language and packages, which makes this method accessible to everyone with a basic computer. All the simulations can be performed individually and independently, allowing the use of parallel computing, and diminishing simulation times. Even though the SWMM was chosen as the modelling platform, the authors would like to highlight that the methodology here presented could be applied using any other hydraulic/hydrological model that evaluates urban drainage performance (such as MUSIC or InfoWorks) with a combination of any other programming language (such as MATLAB).

5. Conclusions

This paper proposed the application of spatial analytical methods for understanding the relationship between GI location in the urban drainage systems and their impact on resilience. Applied to an urban catchment in the UK, the findings illustrated the potential of this framework to be used as a systematic approach to establishing the link between resilient properties and resilience performance.

The application of the framework has found a positive and significant spatial correlation between the GI location and resilience enhancement when considering sewer flooding as the level of service loss measurement for the system. When considering CSO as level of service loss, only the bioretention cell and the “all GI” case showed spatial autocorrelation for the magnitude and duration, respectively.

Spatial clusters and spatial outliers were detected in the urban catchment. There are significant differences between the different level of service loss measures chosen for the assessment of resilience, however, the spatial patterns remain generally similar when considering different GI using the same indicator. Conflicting clusters between the different indicators indicate that there might be trade-offs in the placement of GI in certain locations—while ameliorating an indicator, other indicators might be worsened.

The framework proposed could be used in urban planning as a starting point to develop resilience-based infrastructure development plans and stormwater alleviation schemes at an urban scale. Furthermore, the output of the framework is especially important to highlight the clusters of high performance in the system.