3D Numerical Simulation of Gravity-Driven Motion of Fine-Grained Sediment Deposits in Large Reservoirs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Features of Fine-Grained Sediment Deposition in Deep Reservoirs
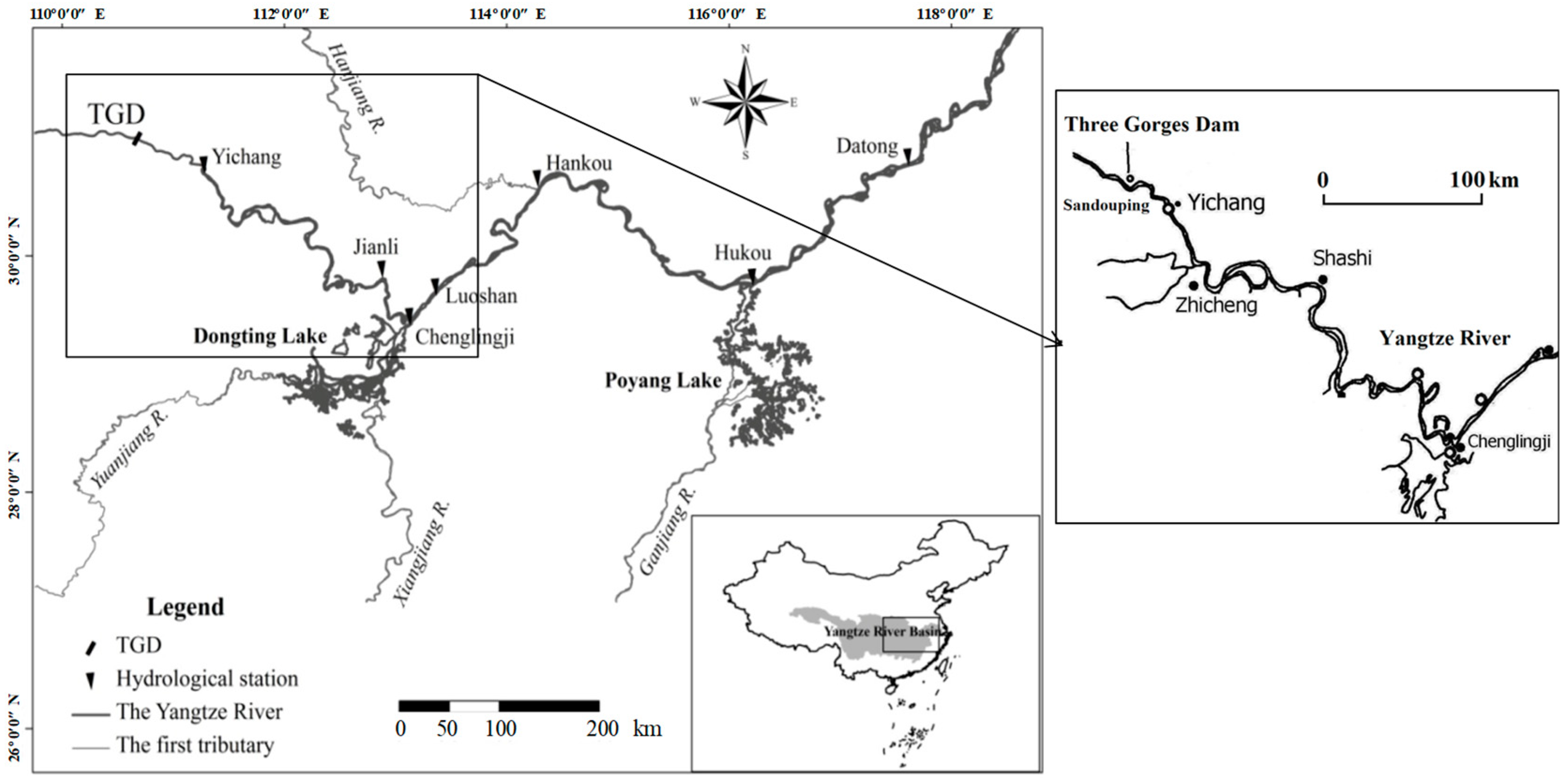
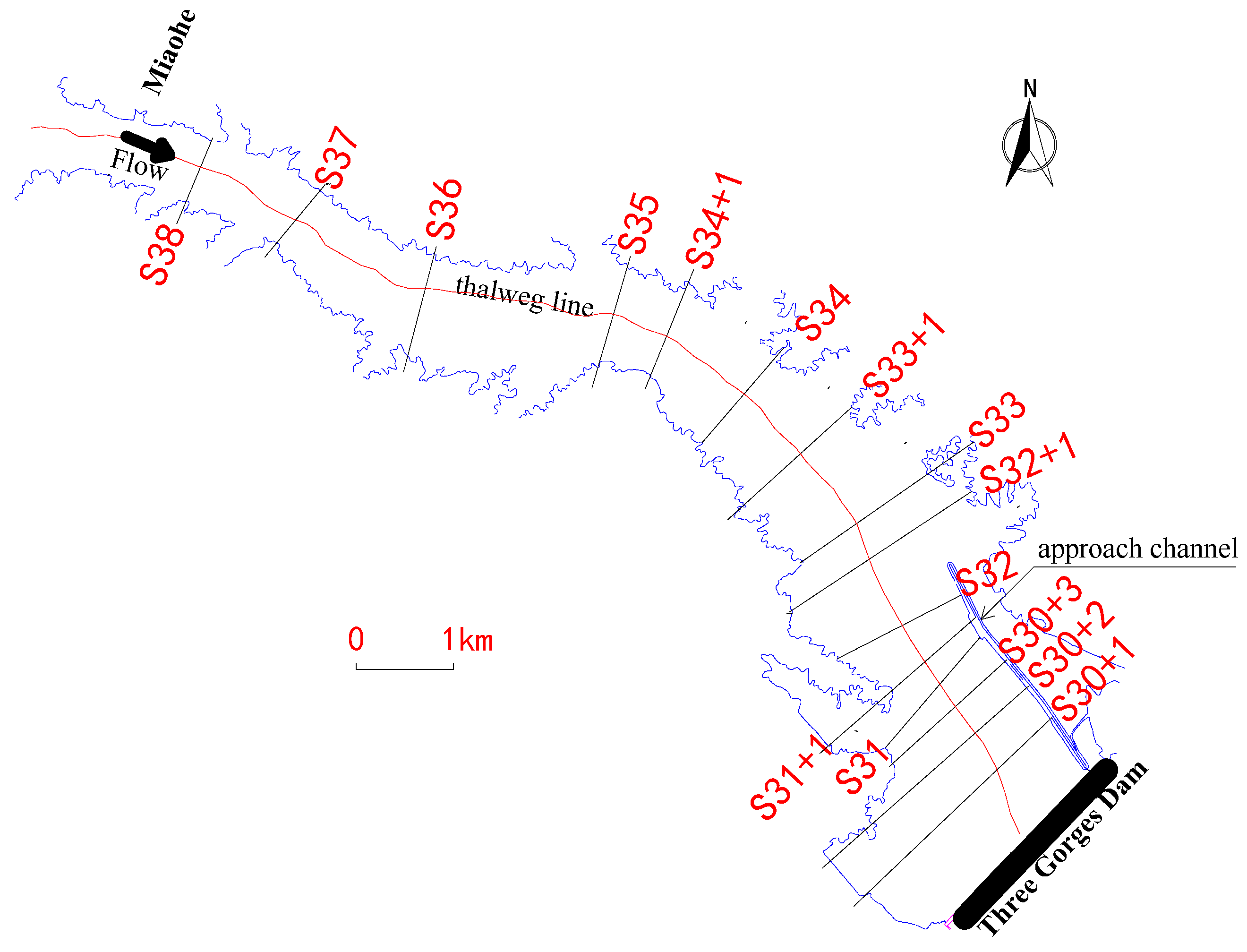
2.2. Numerical Simulation Method for Transport and Settlement of Fine-Grained Sediment
2.3. Numerical Simulation Method for Gravity-Driven Motion of Fine-Grained Sediment Deposits
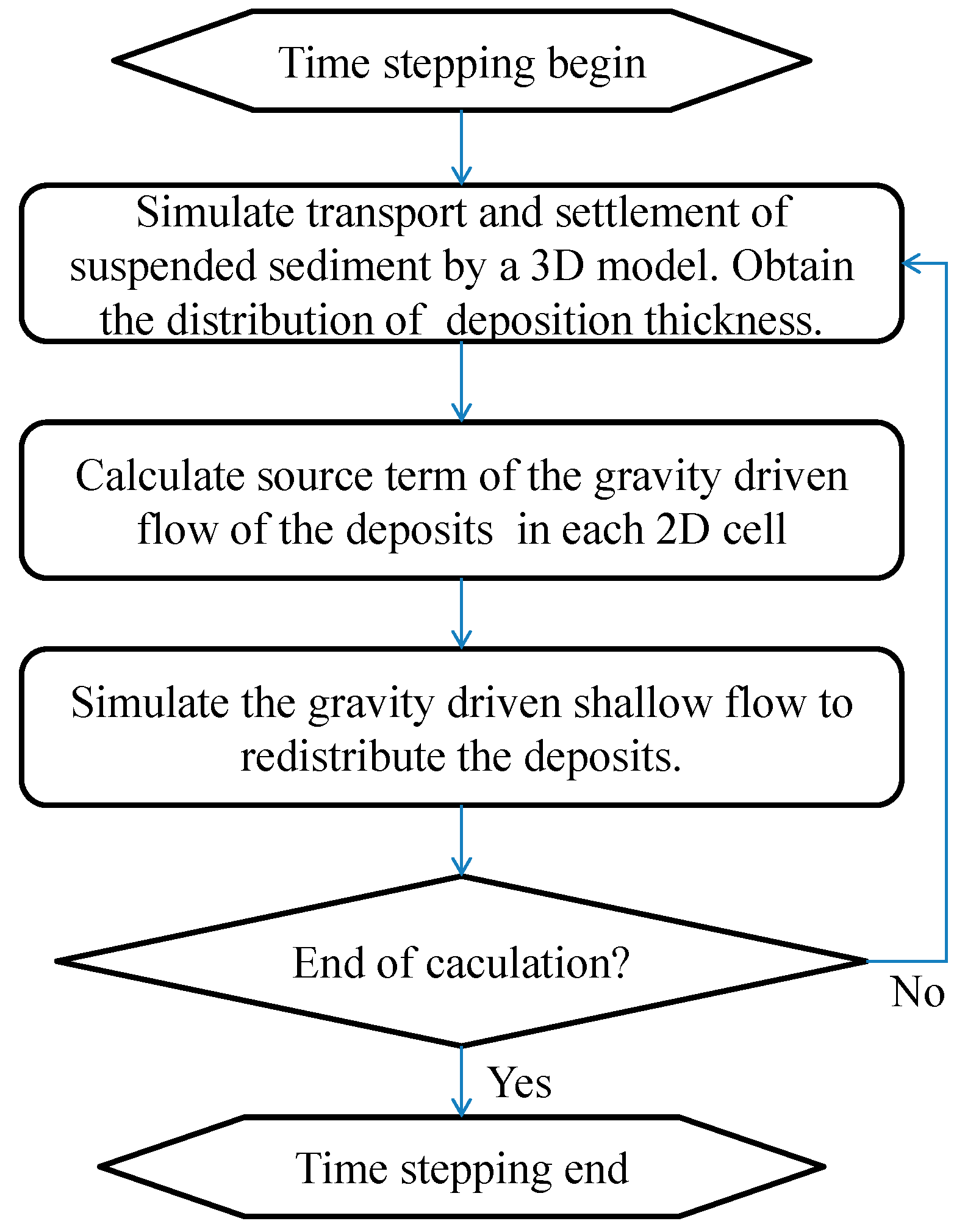
2.4. Numerical Simulation Procedure
3. Results
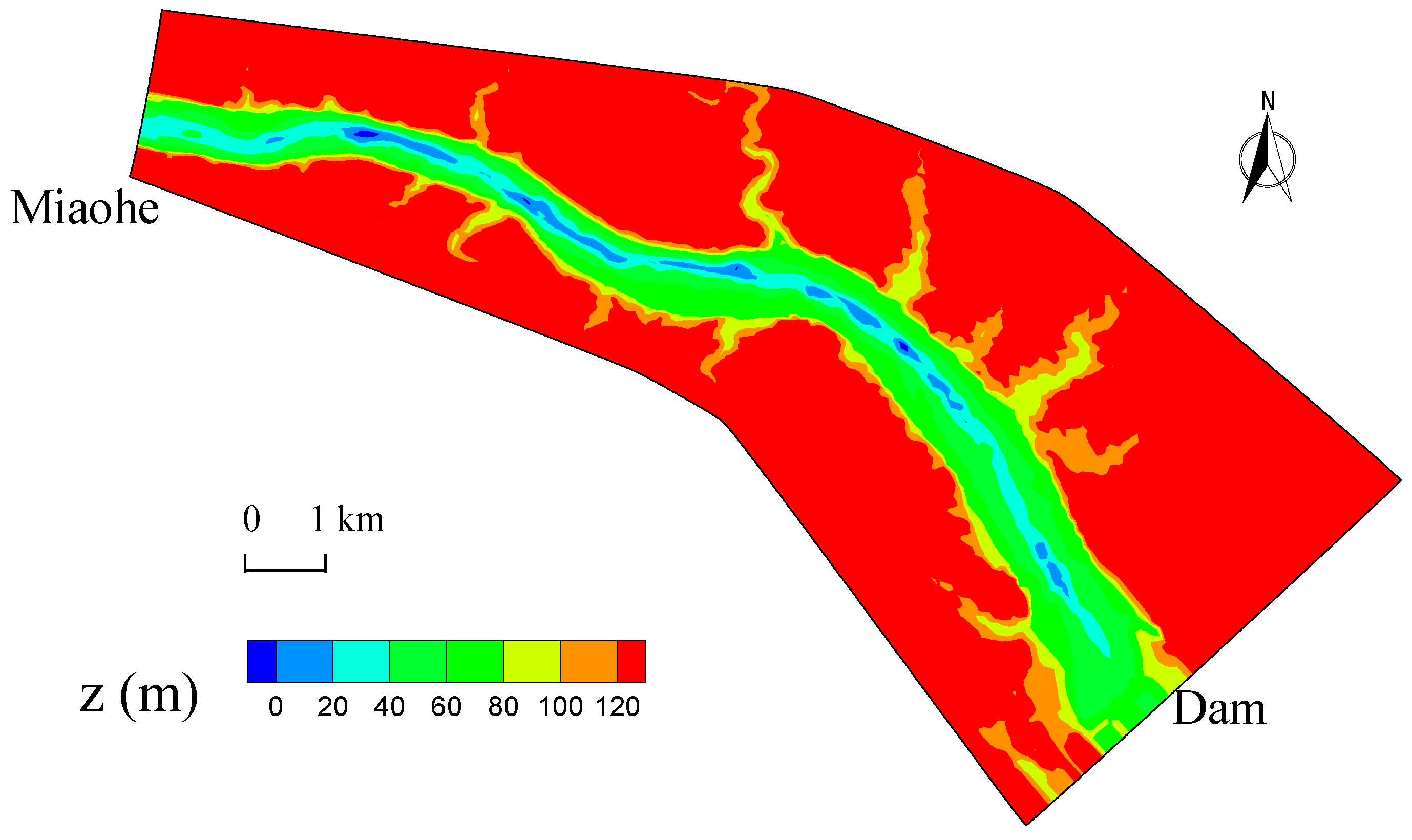
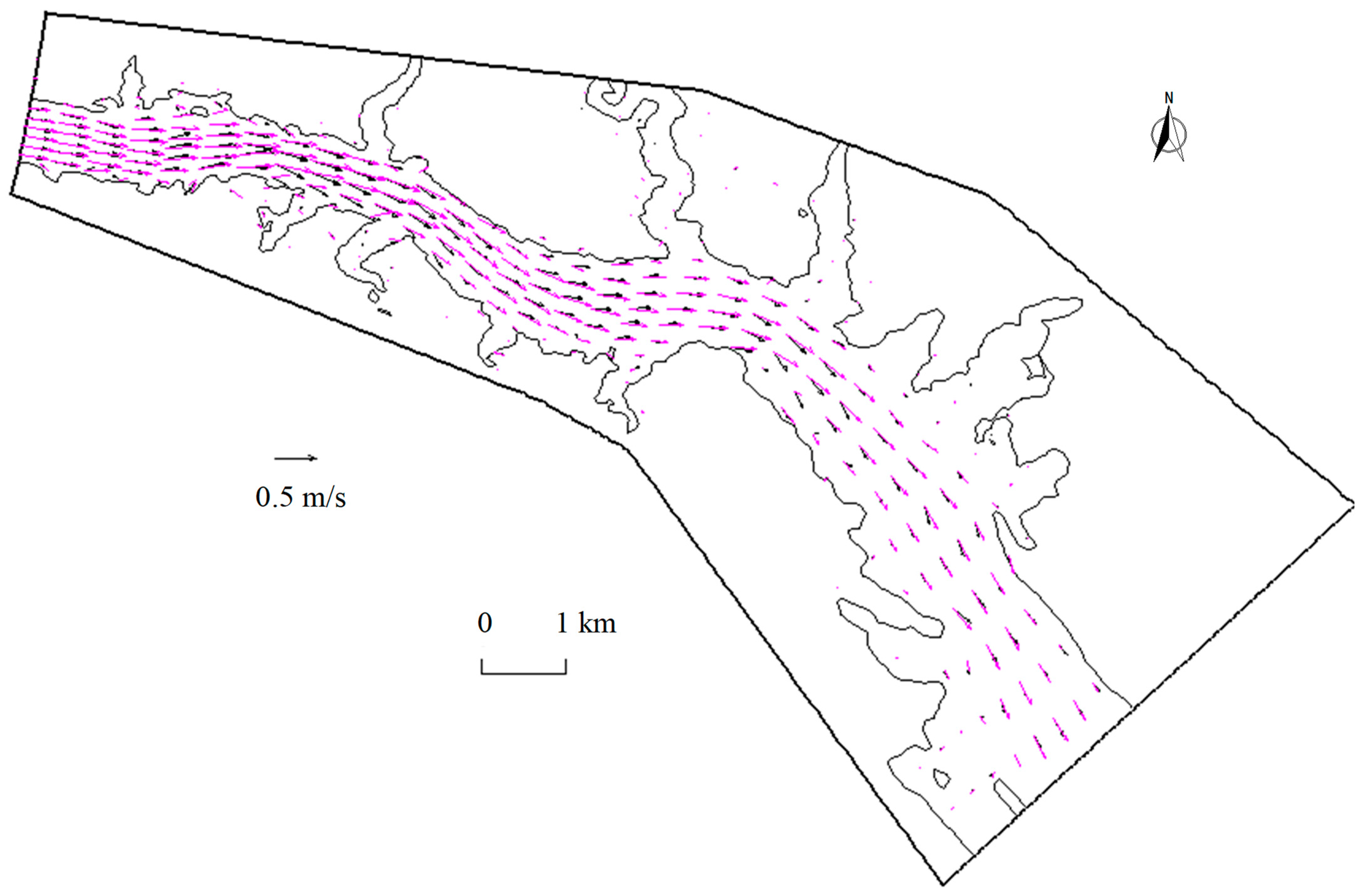
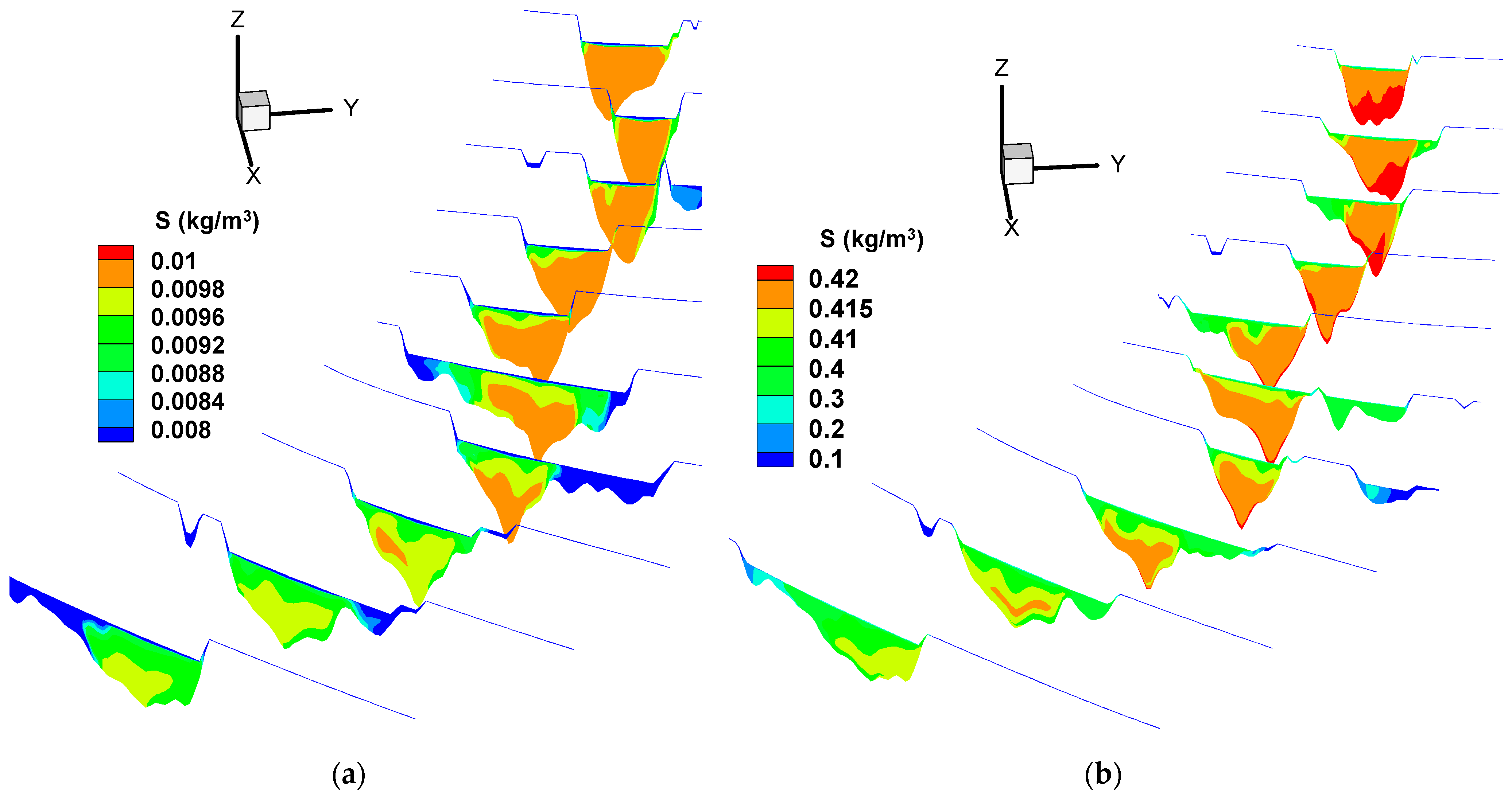
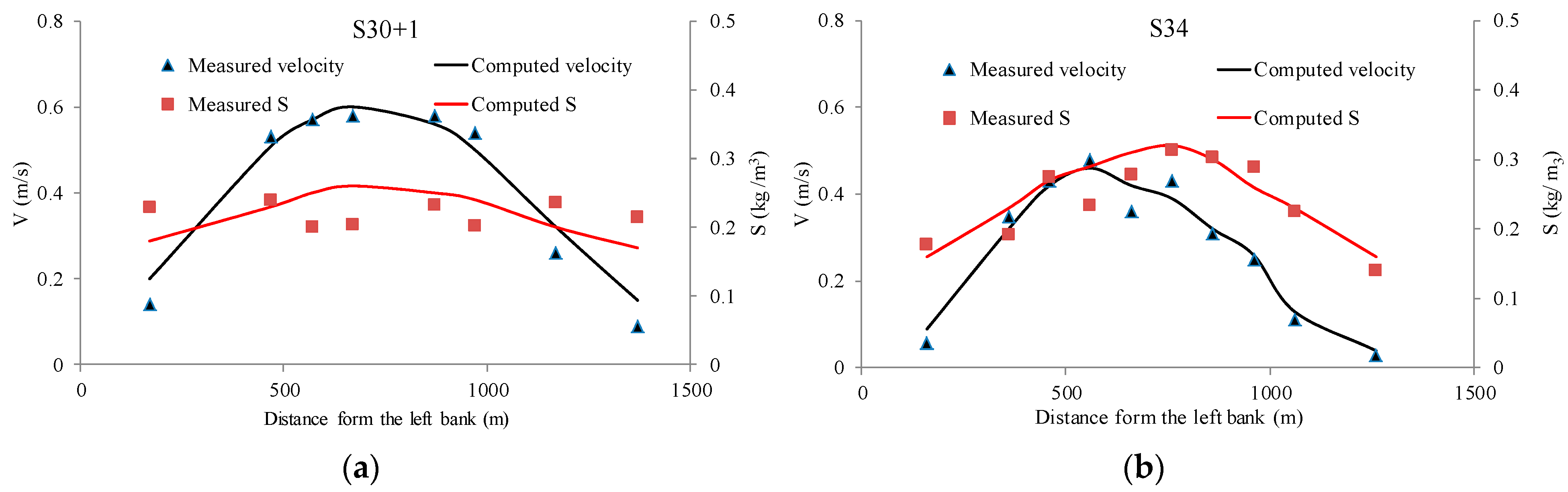
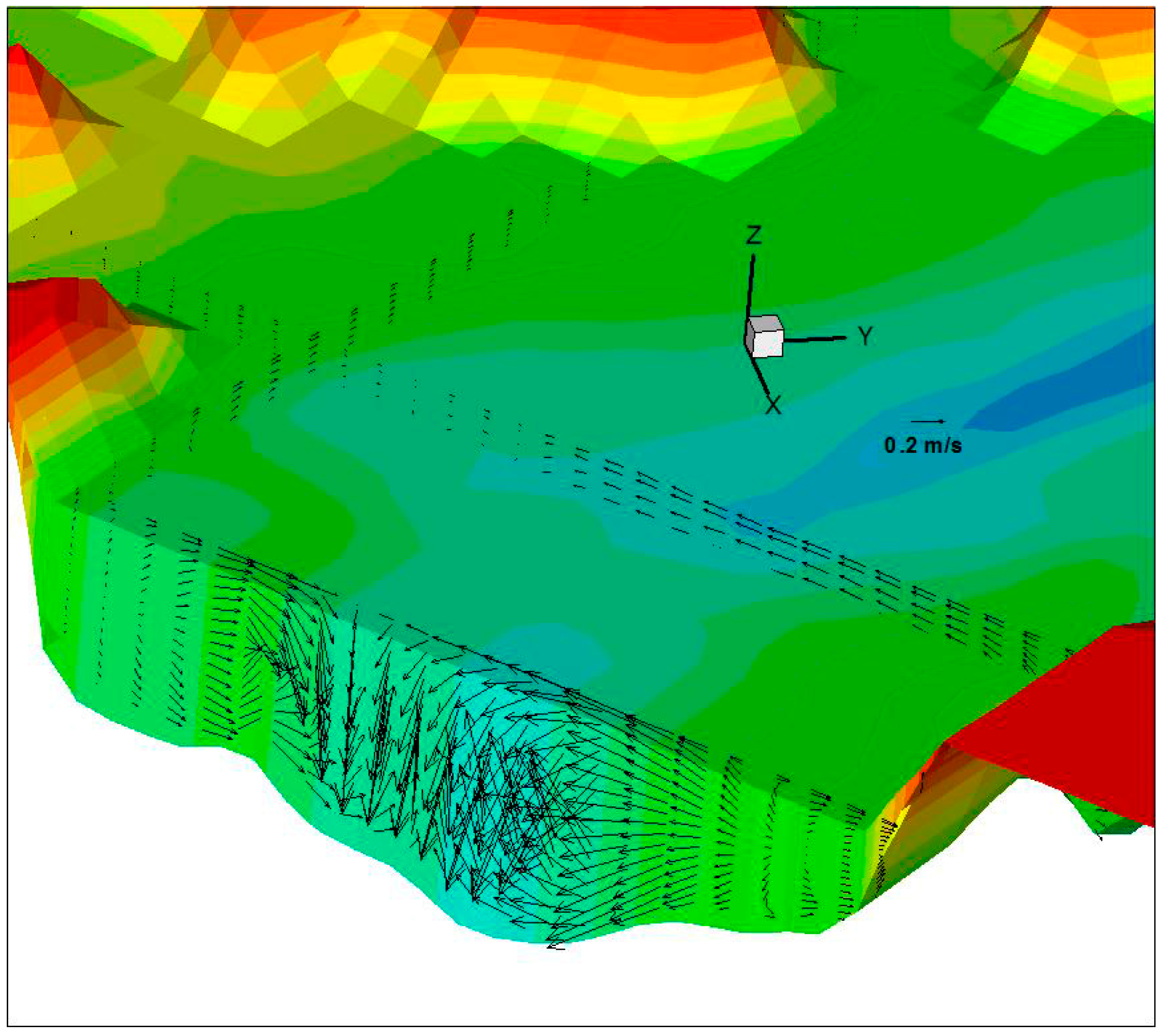
3.1. Flow Field and Suspended Sediment Concentration
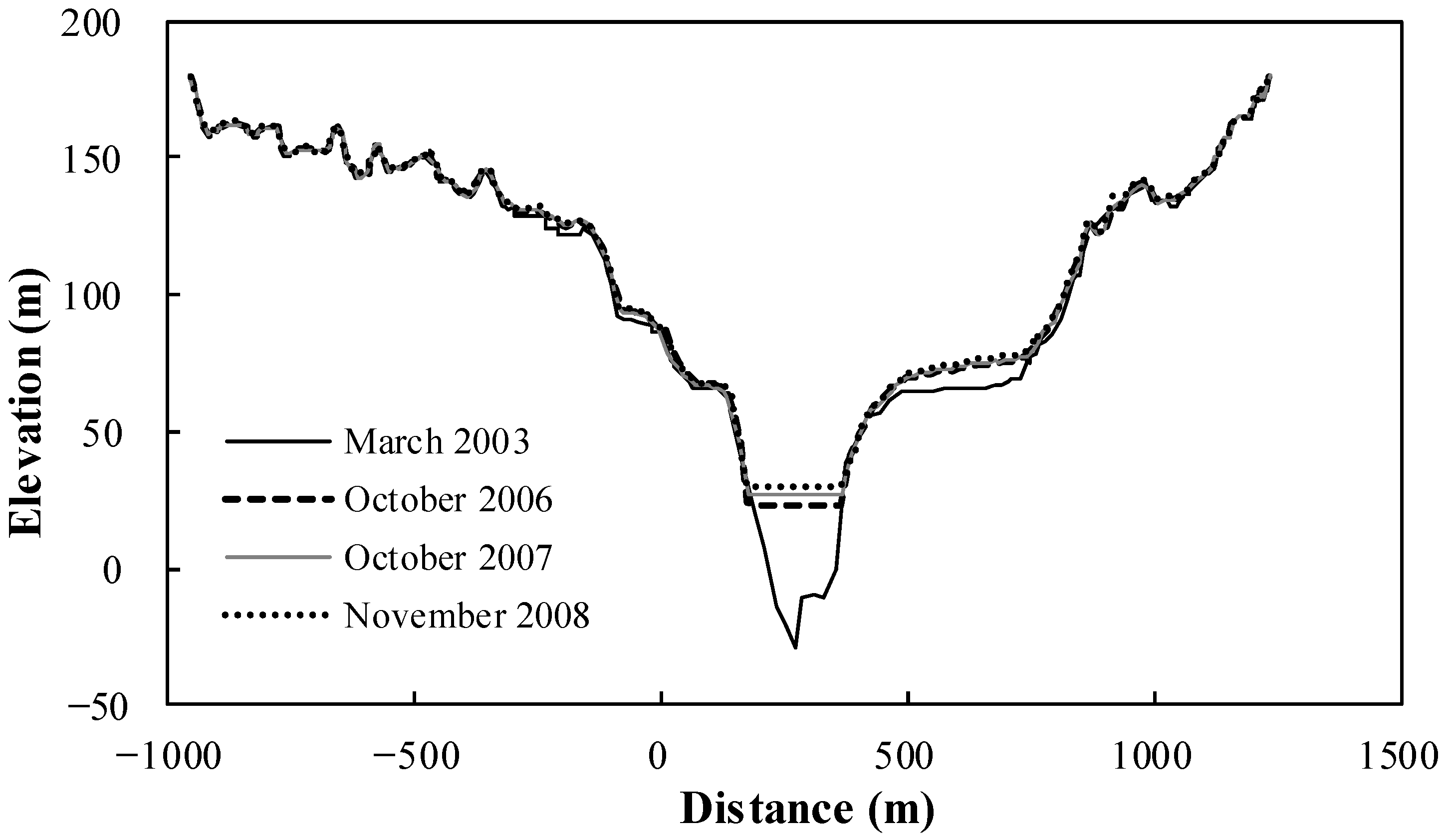
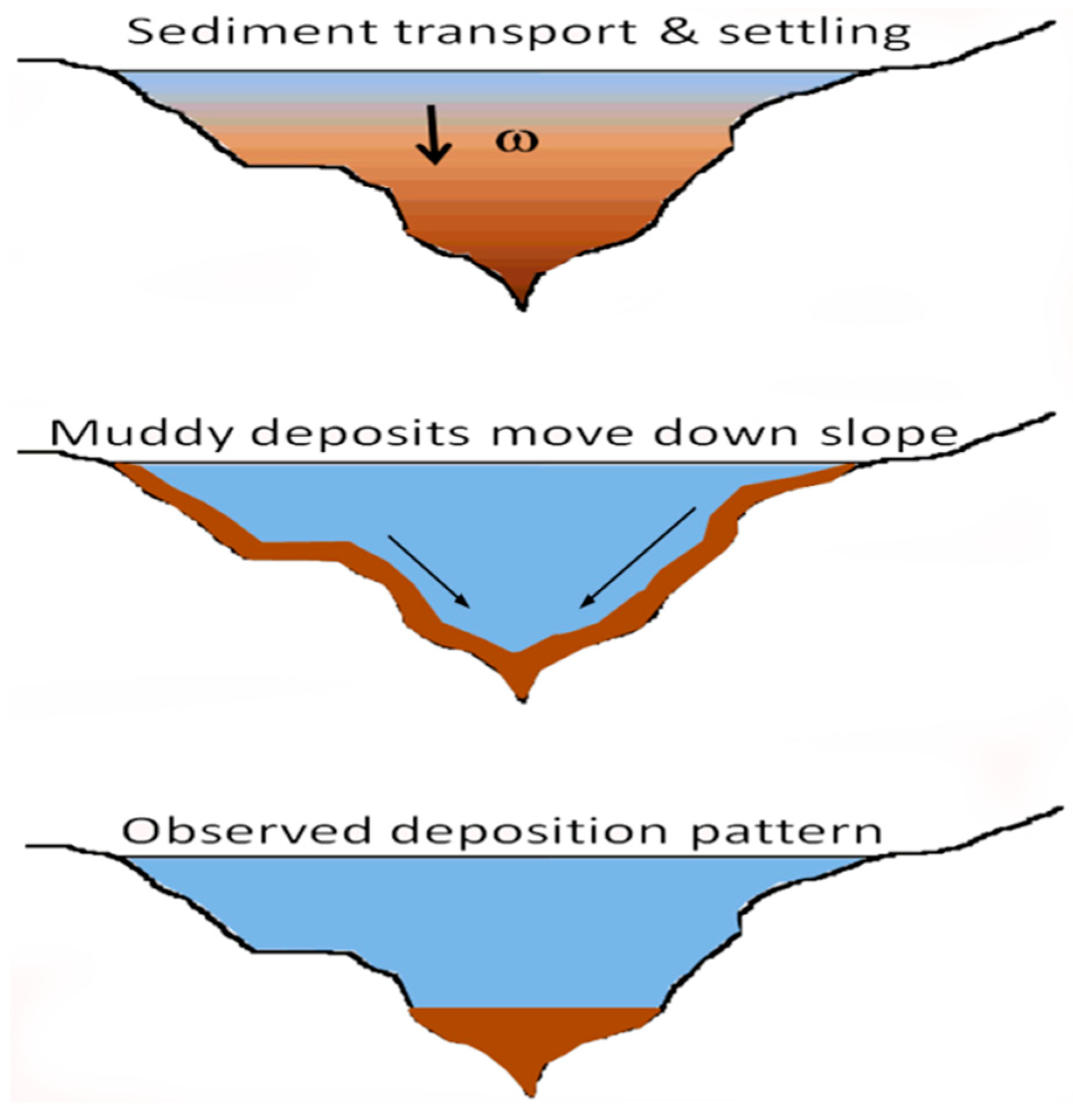
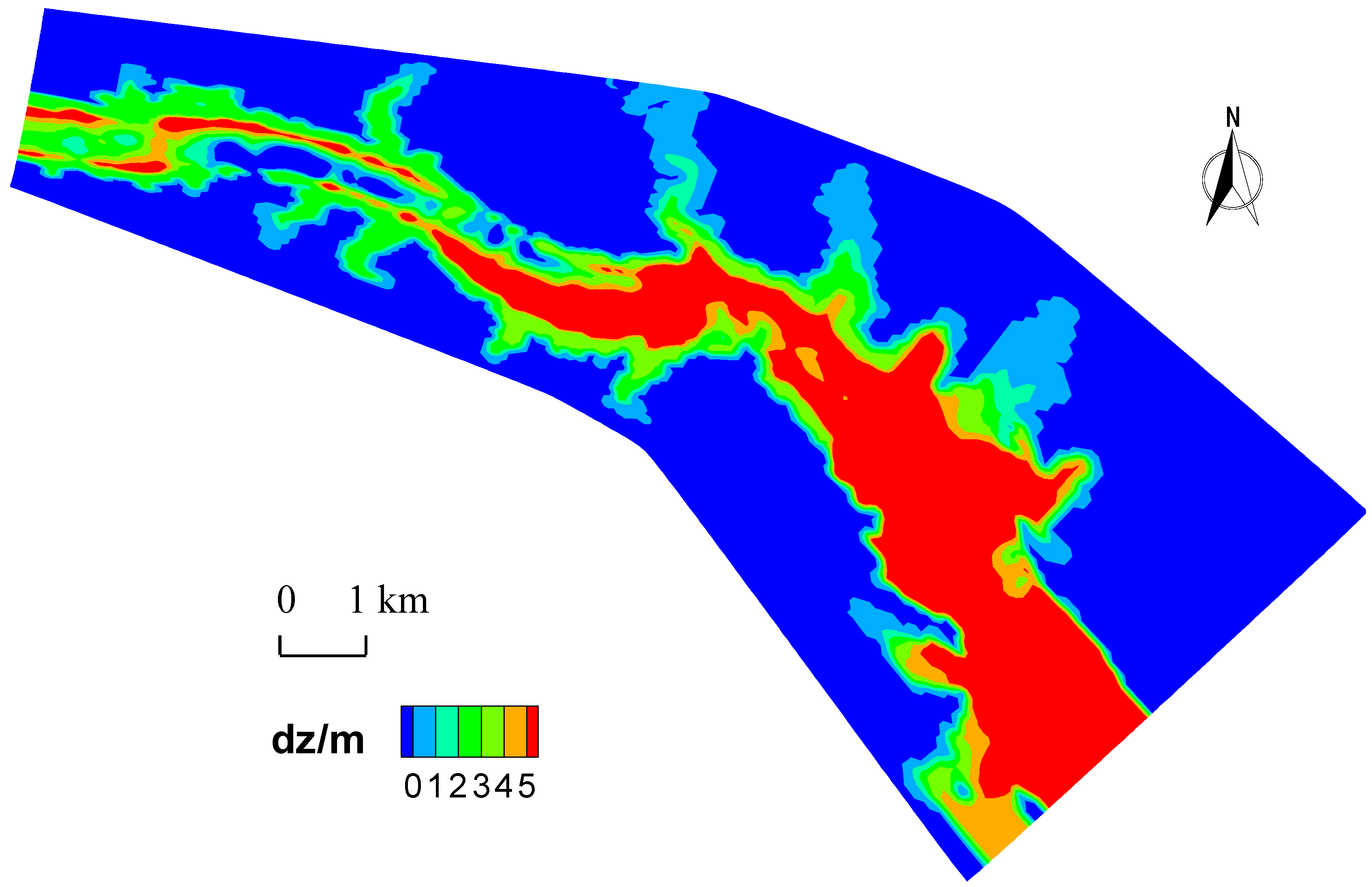
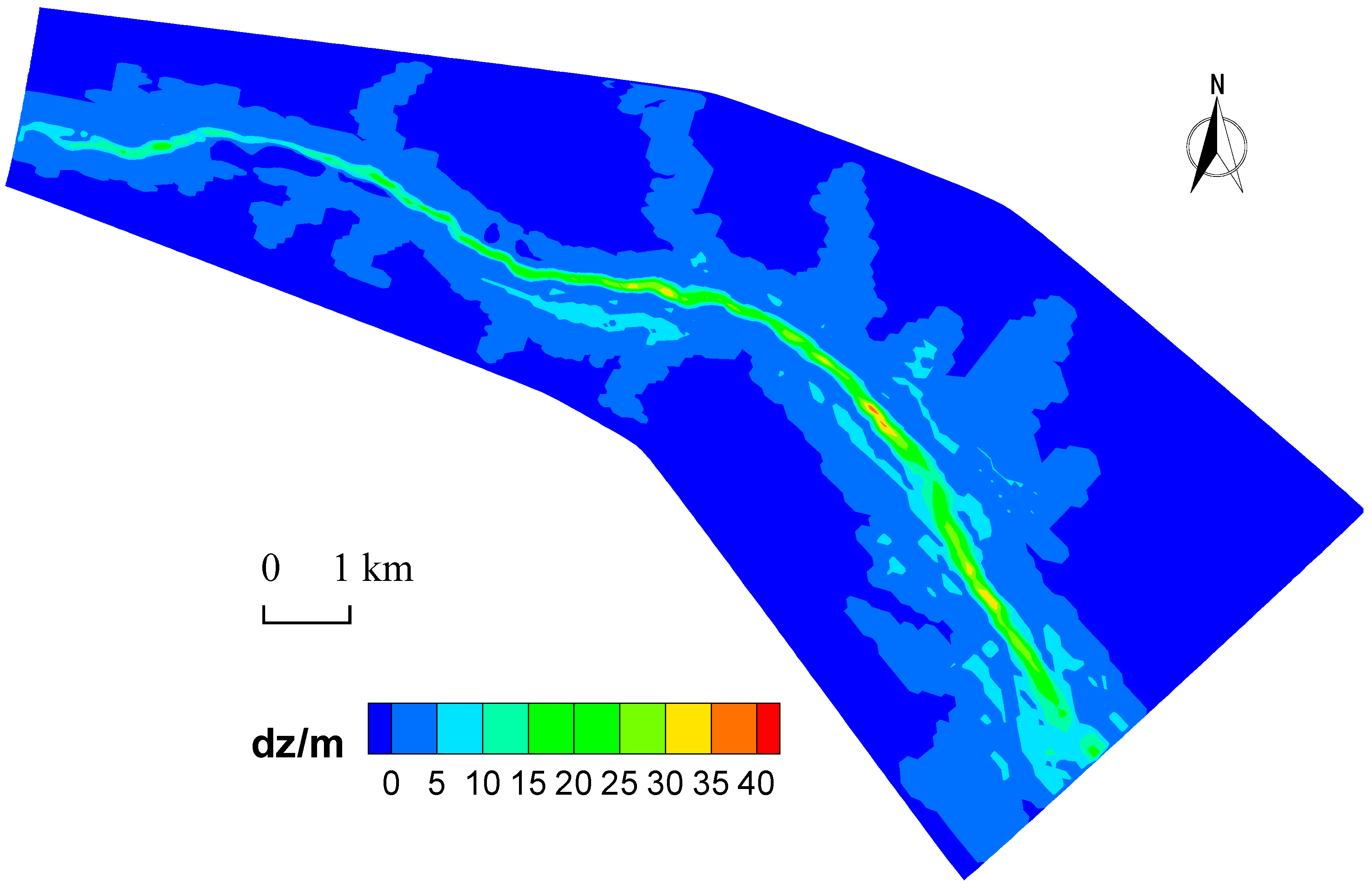
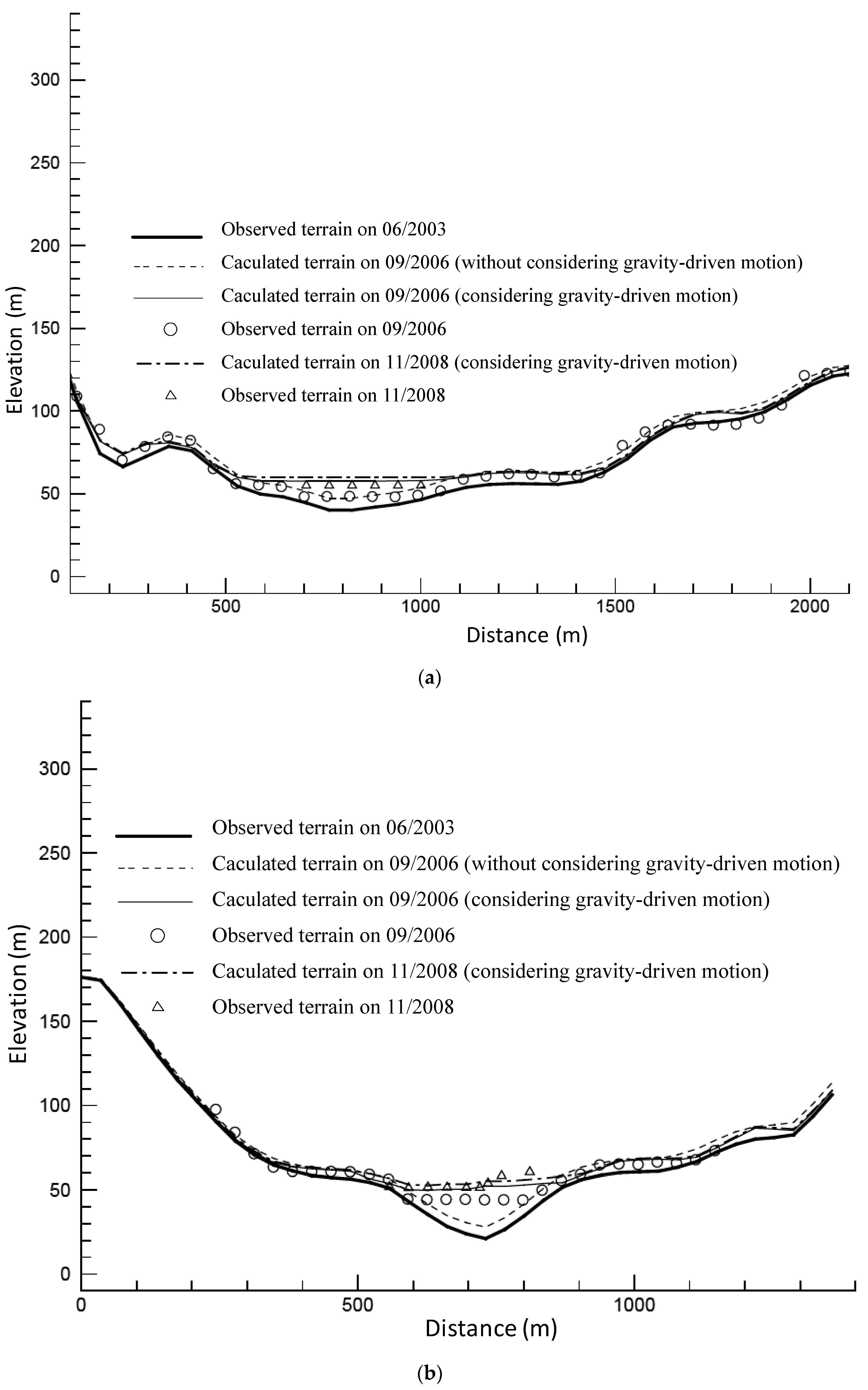
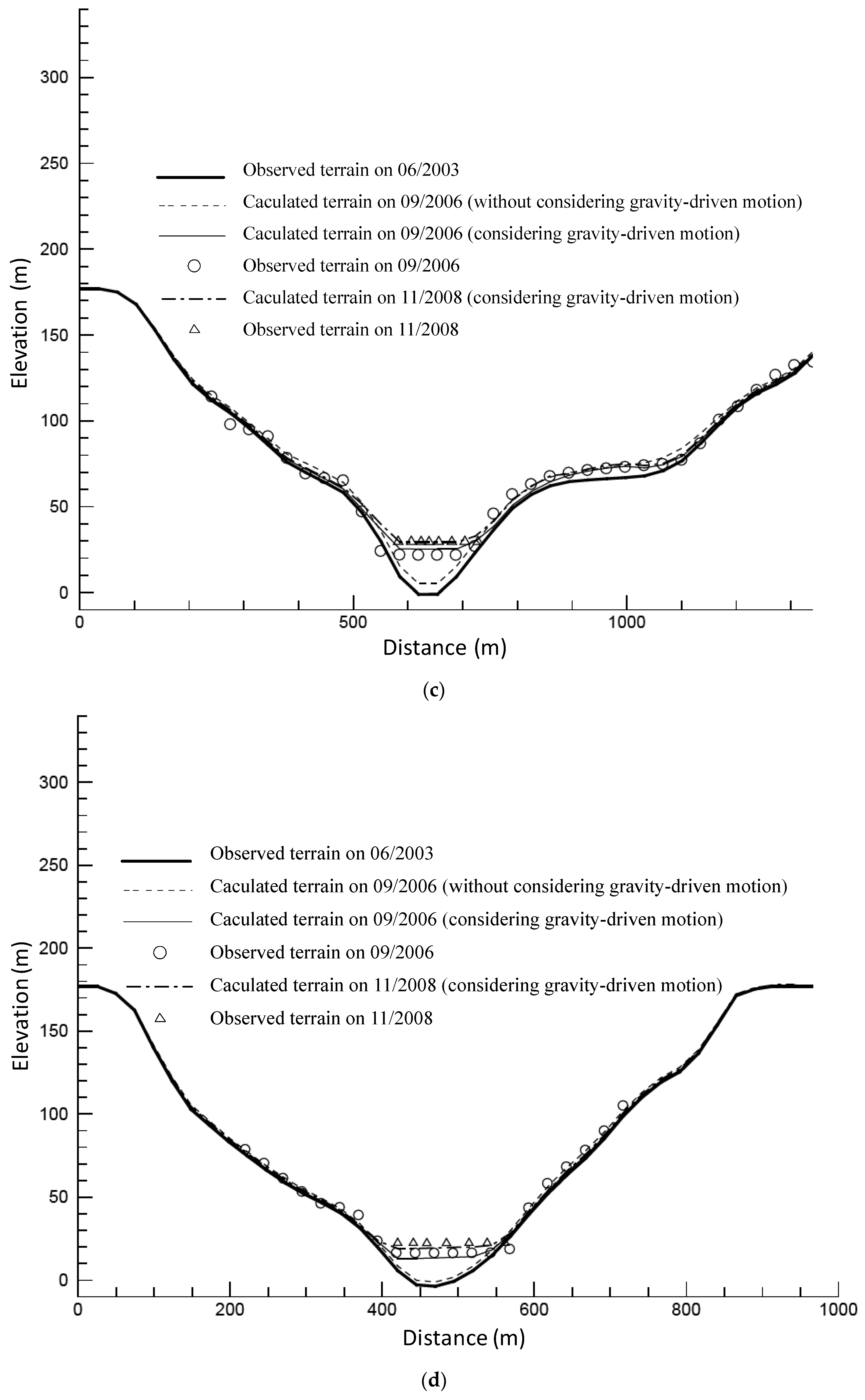
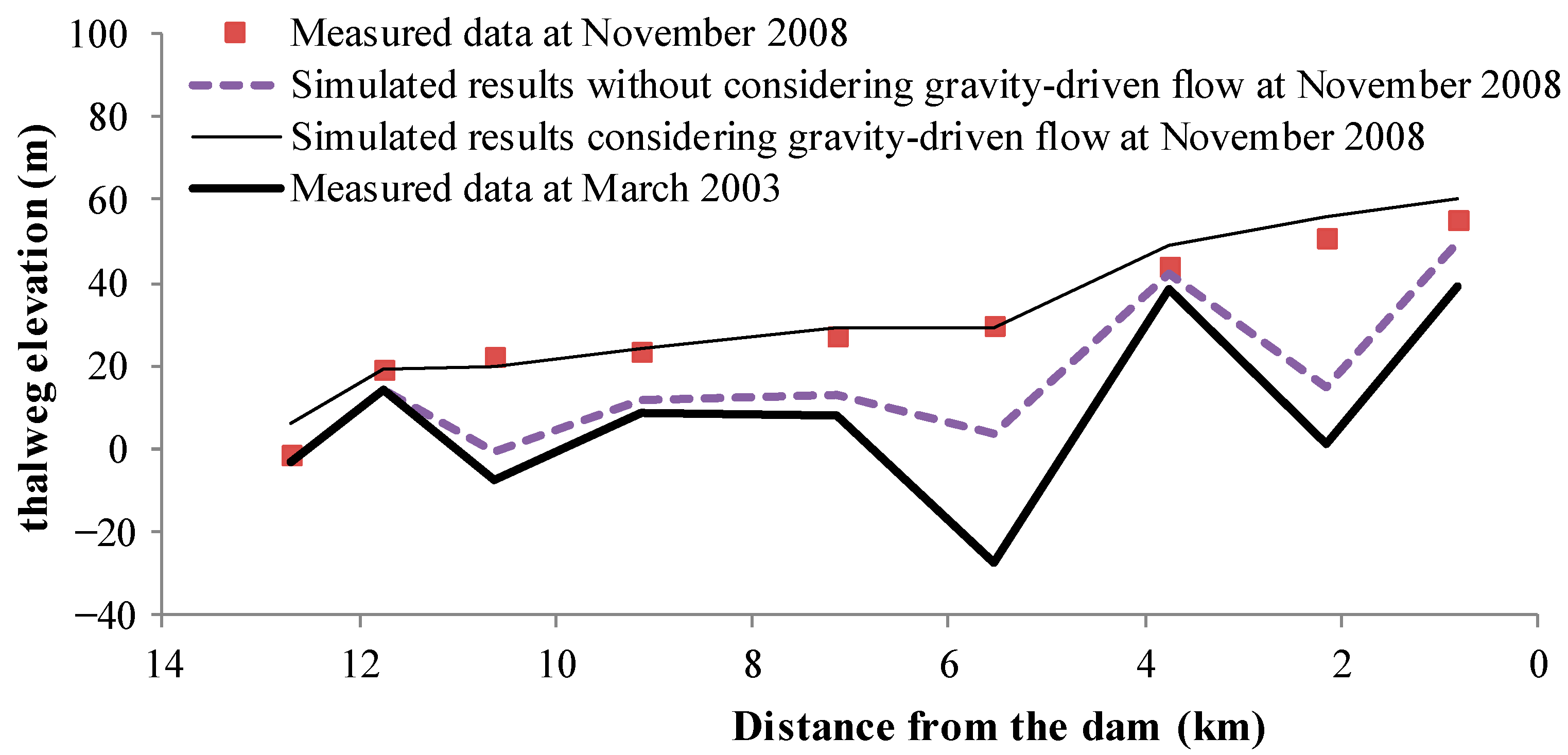
3.2. Features of Sedimentation Pattern
4. Discussion
4.1. Difference between Calculation and Measurement
4.2. Shortcomings of Present Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.J.; Zhang, M.; Cao, H.Q. Removing coarse sediment by sorting of reservoirs. Sci. China Technol. Sci. 2011, 41, 833–844. (In Chinese) [Google Scholar] [CrossRef]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, J.; Yang, M. Unexpected sedimentation patterns upstream and downstream of the Three Gorges Reservoir: Future risks. Int. J. Sediment. Res. 2019, 34, 108–117. [Google Scholar] [CrossRef]
- Faghihirad, S.; Lin, B.; Falconer, R. Application of a 3D Layer Integrated Numerical Model of Flow and Sediment Transport Processes to a Reservoir. Water 2015, 7, 5239–5257. [Google Scholar] [CrossRef] [Green Version]
- The Science and Technology Department of Ministry of Water Conservancy and Electric Power. Reports Collection on the Sediment Issues of the Three Gorges Reservoir; The Science and Technology Department of Ministry of Water Conservancy and Electric Power: Beijing, China, 1988. (In Chinese)
- State Council Three Gorges Project Construction Committee Executive Office Sediment Experts Group, China Three Gorges Project Corporation Sediment Experts Group. Sediment Research of the Three Gorges Project (1996–2000, Volume 8); Intellectual Property Press: Beijing, China, 2008; Chapter 3. (In Chinese)
- Li, W.J.; Yang, S.F.; Fu, X.H.; Xiao, Y. Study on the sedimentation characteristics in the Three Gorges Reservoir during the initial operation stage. Adv. Water Sci. 2015, 26, 676–685. (In Chinese) [Google Scholar]
- Chen, G.Y.; Yuan, J.; Xu, Q.X. On sediment diversion ratio after the impoundment of the Three Gorges Project. Adv. Water Sci. 2012, 23, 355–362. (In Chinese) [Google Scholar]
- Yang, C.R.; Deng, J.Y.; Qi, Y.M.; Wang, Y.X.; Lin, J.Y. Study on Long-term Impact of Small and medium-sized floods regulation on sedimentation of the Three Gorges Reservoir. Water Resour. Power 2020, 38, 34–37. (In Chinese) [Google Scholar]
- Bureau of Hydrology, Changjiang Water Resources Commission. Analysis of Sedimentation and Erosion in the Three Gorges Reservoir and the River Reach Between TGP and Gezhouba Project in 2007; Bureau of Hydrology, Changjiang Water Resources Commission: Wuhan, China, 2008. (In Chinese)
- Fang, H.W.; Rodi, W. Three-dimensional calculations of flow and suspended sediment transport in the neighborhood of the dam for the Three Gorges Project reservoir in the Yangtze River. J. Hydraul. Res. 2003, 41, 379–394. [Google Scholar] [CrossRef]
- Lu, Y.J.; Dou, G.R.; Han, L.X.; Shao, X.J.; Yang, X.H. 3D mathematical model for suspended load transport by turbulent flows and its applications. Sci. China. Ser. E. 2004, 47, 237–256. [Google Scholar] [CrossRef]
- Zhang, N.; Yi, D.R.; Dai, W.L. Analysis of scouring and silting in the reach from dam to Lidu town in the Three Gorges Reservoir. Yangtze River 2006, 37, 95–98. (In Chinese) [Google Scholar]
- Department of Hydraulic Engineering, Tsinghua University. Analysis of the Field Data of Reservoir Sedimentation in the Three Gorges Reservoir; Tsinghua University: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Hu, C. Analysis on sediment scouring and silting variation of Three Gorges Reservoir since 175 m trial impoundment for past ten years. Water Resour. Hydropower Eng. 2019, 50, 18–26. (In Chinese) [Google Scholar]
- Ren, S.; Zhang, B.; Wang, W.; Yuan, Y.; Guo, C. Sedimentation and its response to management strategies of the Three Gorges Reservoir, Yangtze River, China. Catena 2021, 199, 105096. [Google Scholar] [CrossRef]
- Han, Q.W. Reservoir Sedimentation; Science Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Jia, D.D.; Shao, X.J.; Zhang, X.N.; Zhou, J.Y. Preliminary analysis on the causes of reservoir sedimentation pattern in the vicinity of Three Gorges Project during its early filling. Adv. Water Sci. 2011, 22, 539–545. (In Chinese) [Google Scholar]
- Zhang, N.; Dai, W.; Zhu, H.; Li, J. Initial dry density of sediments in the Three Gorges Reservoir. Yangtze River 2006, 37, 59–61. (In Chinese) [Google Scholar]
- Jia, D.D.; Shao, X.J.; Zhang, X.N.; Ye, Y.T. Sedimentation patterns of fine-grained particles in the dam area of the Three Gorges Project: 3D numerical simulation. J. Hydraul. Eng-ASCE 2013, 139, 669–674. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Shao, X.J.; Jiang, L.; Jia, D.D. Gravity-driven transport of fine grained reservoir sediments. J. Zhejiang Univ. 2014, 48, 2254–2258. (In Chinese) [Google Scholar]
- Xiao, Y.; Yang, F.S.; Zhou, J.Y.; Chen, W.S. 1-D numerical modeling of the mechanics of gravity-driven transport of fine sediments in the Three Gorges Reservoir. Lake. Reserv. Manag. 2015, 31, 83–91. [Google Scholar] [CrossRef]
- Jiang, L.; Ban, X.; Wang, X.; Cai, X. Assessment of Hydrologic Alterations Caused by the Three Gorges Dam in the Middle and Lower Reaches of Yangtze River, China. Water 2014, 6, 1419–1434. [Google Scholar] [CrossRef] [Green Version]
- Chien, N.; Zhang, R.; Zhou, Z.D. Fluvial Processes; Science Press: Beijing, China, 1987. (In Chinese) [Google Scholar]
- Tang, L.; Zhang, W.; Wu, F.L. Study on sediment movement forms and mechanism causing mild slope on nearshore muddy coast. J. Sediment Res. 2016, 6, 66–73. (In Chinese) [Google Scholar]
- Imran, J.; Parker, G.; Locat, J.; Lee, H. 1D numerical model of muddy subaqueous and subaerial debris flows. J. Hydraul. Eng. 2001, 127, 959–968. [Google Scholar] [CrossRef]
- Laigle, D.; Coussot, P. Numerical modeling of mud flows. J. Hydraul. Eng. 1997, 123, 617–623. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, D.; Zhou, J.; Shao, X.; Zhang, X. 3D Numerical Simulation of Gravity-Driven Motion of Fine-Grained Sediment Deposits in Large Reservoirs. Water 2021, 13, 1868. https://doi.org/10.3390/w13131868
Jia D, Zhou J, Shao X, Zhang X. 3D Numerical Simulation of Gravity-Driven Motion of Fine-Grained Sediment Deposits in Large Reservoirs. Water. 2021; 13(13):1868. https://doi.org/10.3390/w13131868
Chicago/Turabian StyleJia, Dongdong, Jianyin Zhou, Xuejun Shao, and Xingnong Zhang. 2021. "3D Numerical Simulation of Gravity-Driven Motion of Fine-Grained Sediment Deposits in Large Reservoirs" Water 13, no. 13: 1868. https://doi.org/10.3390/w13131868
APA StyleJia, D., Zhou, J., Shao, X., & Zhang, X. (2021). 3D Numerical Simulation of Gravity-Driven Motion of Fine-Grained Sediment Deposits in Large Reservoirs. Water, 13(13), 1868. https://doi.org/10.3390/w13131868




