Abstract
Water level data obtained from telemetry stations typically contains large number of outliers. Anomaly detection and a data imputation are necessary steps in a data monitoring system. Anomaly data can be detected if its values lie outside of a normal pattern distribution. We developed a median-based statistical outlier detection approach using a sliding window technique. In order to fill anomalies, various interpolation techniques were considered. Our proposed framework exhibited promising results after evaluating with F1-score and root mean square error (RMSE) based on our artificially induced data points. The present system can also be easily applied to various patterns of hydrological time series with diverse choices of internal methods and fine-tuned parameters. Specifically, the Spline interpolation method yielded a superior performance on non-cyclical data while the long short-term memory (LSTM) outperformed other interpolation methods on a distinct tidal data pattern.
1. Introduction
An anomaly detection is an identification of data points that behave differently from normal patterns, see [1]. This process is essential as anomalous data can indicate changes in typical behaviors or technical malfunctions. After successfully detecting anomalies, a data imputation for substituting detected points or missing values is required. A significant amount of previous work has been performed in the area of the outlier detection for temporal data as thoroughly reviewed in [2,3,4,5,6,7,8]. In the context of time series, input data are generally either univariate, which is our focus in this work, or a multivariate type. Both statistical and machine learning approaches were regularly applied for detecting anomalies as broadly reviewed in [9,10,11,12].
Detecting anomalies based on a prediction interval constructed from standard deviations spanning over the mean is one of a common practice. Instead of using the mean as the outlier indicator, various median-based methods were alternatively proposed due to their robustness [13,14]. Particularly, robust statistical metrics, median, and median absolute deviation (MAD), were introduced to accurately detect anomalies in [15]. The MAD scale estimation is commonly used for the anomaly analysis due to its desirable performance. It is insensitive to a large dispersion of anomalous. Additionally, it is easy to implement and only a light computational effort is required [16]. Another important statistical-based method is the prediction confidence interval which relies on neighboring data to identify time series anomalies. An observed value is classified as anomalous if it falls outside of the range with upper and lower bounds of the interval [17]. Its main advantage includes a capability to provide an automatic threshold for differentiate between normal and abnormal groups. Due to contrasting data distributions among various sources, a parameter tuning and a threshold estimation of the interval are the main challenges where further studies are highly required.
In order to detect anomalous points in time series, a sliding window technique is one of the powerful method due to its applicability for a real-time detection. It is commonly employed to sequentially detect outliers within a specific focus range over the raw data. It can be utilized with various outlier prediction methods without extensive modification. For instance, Yu et al. [18] adopted the sliding window technique to segment the original hydrological time series into sub-sequences and further implemented an autoregressive prediction model with the prediction confidence interval to specify outlier points. Similar techniques were also applied in [19] to identify outliers which were further corrected on meteorological data efficiently. In addition, the moving window was seamlessly implemented with the MAD scale estimator, as proposed in [16]. According to the interpolation perspective, multiple data filling methods, such as a simple interpolation, a regression, an autoregressive and machine learning methods were introduced [20]. In recent years, a deep learning method has been successfully applied to various tasks in time series analysis. In particular, a recurrent neural network (RNN), a specific type of deep learning models known to work well with temporal sequence data, have widely been used for the data imputation [21]. Several studies also relied on a bidirectional RNN-based imputation to capture temporal information embedded in the original time series and further compute substituted values [22,23,24].
In a water management system, hydrological time series are automatically collected from sensors at telemetry stations. Many environmental factors in surroundings such as floating objects or human operations can interfere the recorded values. These situations consequently result in anomalous points in the collected water level data. Poor-quality data potentially leads to incorrect implications and misleading insights. Therefore, the anomaly detection and the data imputation of identified anomalies or missing values for time series data are the necessary processes for any application in the water management analytics. Previous studies applied several techniques to detect anomaly patterns in hydrological time series. Yu et al. [18] initially utilized the sliding window technique with an auto-regressive outlier prediction. Similarly, the ARIMA model with the confidence interval was employed with the moving window in [25]. Various machine learning models were extensively implemented for the anomaly detection, such as a density-based approach [26], SVM-based models [27,28], and the isolation forest algorithm [29,30]. The imputation methods for hydrological data processing, such as a simple infilling, a model-based deterministic, as well as machine learning methods were also explored [31,32]. With advanced deep learning models, Ren et al. [33] relied on LSTM to complete gaps in spatial-temporal hydrological data.
A quality control method for hydrological data which included two forecasting models and one statistical model was proposed [34]. Specifically, these proposed models were used to compute confidence intervals to detect potential outliers, as well as suggest proper values to fill suspicious and missing values. Bae and Ji [35] developed a statistical process for detecting and removing anomalous data points of water level data from ultrasonic sensors. The modified Z-scores based on the MAD formula was applied for the anomaly detection process. Moreover, the detected data were further smoothed by an exponentially weighted moving average (EWMA) method. These two studies, which are the main motivation of our work, proposed a framework for the anomaly detection and the interpolation in order to process hydrological time series data.
In this work, we focus on identifying data instances that deviated from normal data patterns. Technical anomalies based on an automatic sensor measurement are specifically considered both in terms of irregular quantities and frequency. We proposed a combination of MAD and the sliding window technique to capture irregular data behaviors in a specific time frame. Hence, anomaly points were detected locally over a specified window using the prediction interval. With a statistical characteristic of MAD, a superior performance was achieved especially with a large amount of data. In addition, missing values and anomalies were filled by various model predictions based on a sequence or an isolate point of anomalous data in the time window. Although the simple linear interpolation replaced missing values with a fitted linear line, the spline method relied on different polynomial sub-functions instead. Lastly, we employed the bidirectional LSTM model [21], a weighted combination of a forward and a backward LSTM model, with a capability of learning an ordered dependency among sequential data. A main contribution of this work is exploring anomaly detection and data imputation of the overall data monitoring system with diverse data behaviors.
This work is under the project titled “Data analytics for improving the efficiency of water management: phase I” initiated for improving the data quality control from telemetry stations in Thailand. We retrieved water level time series from hydro-informatics institute (HII) as a case study. In order to evaluate the proposed methods, test cases were specifically constructed based on 2-year data of 4 telemetry stations with relatively complete data. We artificially manipulated 10% of the second-year data of each station with anomalies. The proposed anomaly detection were evaluated based on the manually-created anomalous data with F1-score. The prediction accuracy of the data filling methods is further measured using RMSE. A comparison based on predictability of all presented methods was performed.
The paper is organized as follows. A main methodology regarding backgrounds, anomaly detection methods, and data filling methods are described in Section 2. Section 3 discusses an experimental analysis consisting of a data preparation for our case studies, parameters, training configurations, as well as evaluation metrics. Results and discussions are provided in Section 4 while the conclusion are summarized in Section 5.
2. Materials and Methods
Our proposed framework consists of two main parts which are anomaly detection methods and data filling methods. Prior to discussing the main methodology, we initially provide basic backgrounds utilized in the proposed methods. The median and MAD are explored in the anomaly detection part while the linear interpolation, the spline method and the LSTM-based model are utilized for the data filling step.
2.1. Backgrounds
2.1.1. MAD as a Robust Scale Estimator
Median absolute derivation (MAD) is a robust scale estimator since it is insensitive to large deviations of time series data, see [13,14]. It can be used to estimate the deviation from the median of the data. For instance, given the dataset , the value of MAD is defined as
where b is a specified constant. Under an assumption of Gaussian distribution associated with the data, the value of b can be derived as , see [14].
2.1.2. Bidirectional LSTM with Decreasing Weight Model
The bidirectional long short-term memory (LSTM) with decreasing weight model was proposed in [21]. It consists of two unidirectional LSTM structures which are the forward and the reverse LSTM. Its concept comes from weighting factors between forward and reverse results. For instance, at the index i in the sequence of time series data, if and are the predictive results from forward and reverse LSTM models, the improved prediction value can be obtained by
where and are two weighting factors given by = [1:0:s] and = [0:1:s]. Here s is the step value obtained from The main advantage of this method is that it improves the prediction value by considering both directions. The prediction over some small intervals is possible and it is relatively accurate.
2.1.3. An Architecture of Bidirectional LSTM Networks
Bidirectional LSTM networks [36] consist of two independent LSTM networks, which are connected together side-by-side. An input sequence is given to the first layer of the networks while a reverse sequence of the input is given to the second layer. With this approach, the bidirectional LSTM networks are able to learn both forward and backward information from the input sequences. They are widely used in many applications, see [37,38,39].
2.2. Anomaly Detection Methods
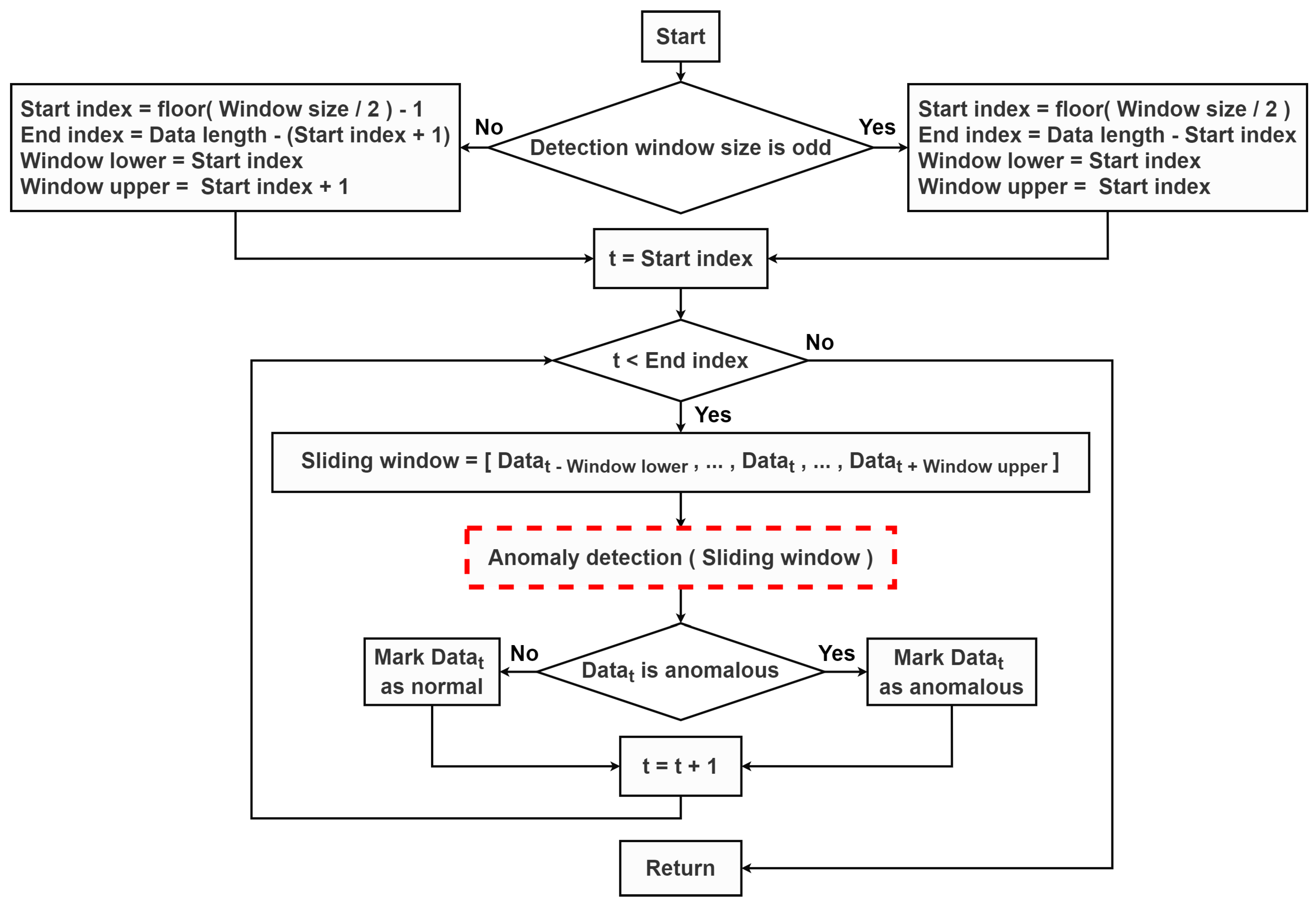
A flow chart of the anomaly detection process is summarized in Figure 1. A window size for the sliding window was initially identified. It was used to determine a start index, an end index, and a sliding window’s upper index and lower index. According to the anomaly detection method depicted as a red dash box in Figure 1, a middle point of the sliding window, defined as ,was detected as anomalous or not. Then, the sliding window was repeatedly moved to the subsequent data point until the end index was reached.
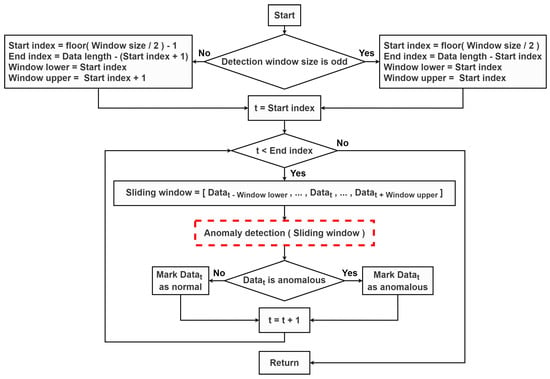
Figure 1.
A flow chart of the anomaly detection process.
In this work, two statistical-based anomaly detection methods depicted as the red dash box in Figure 1 were experimented. These two methods relied mainly on the median value of time series data within the sliding window. The prediction interval was further computed in order to identify anomalous points. Detailed explanations of these two methods are provided as follows.
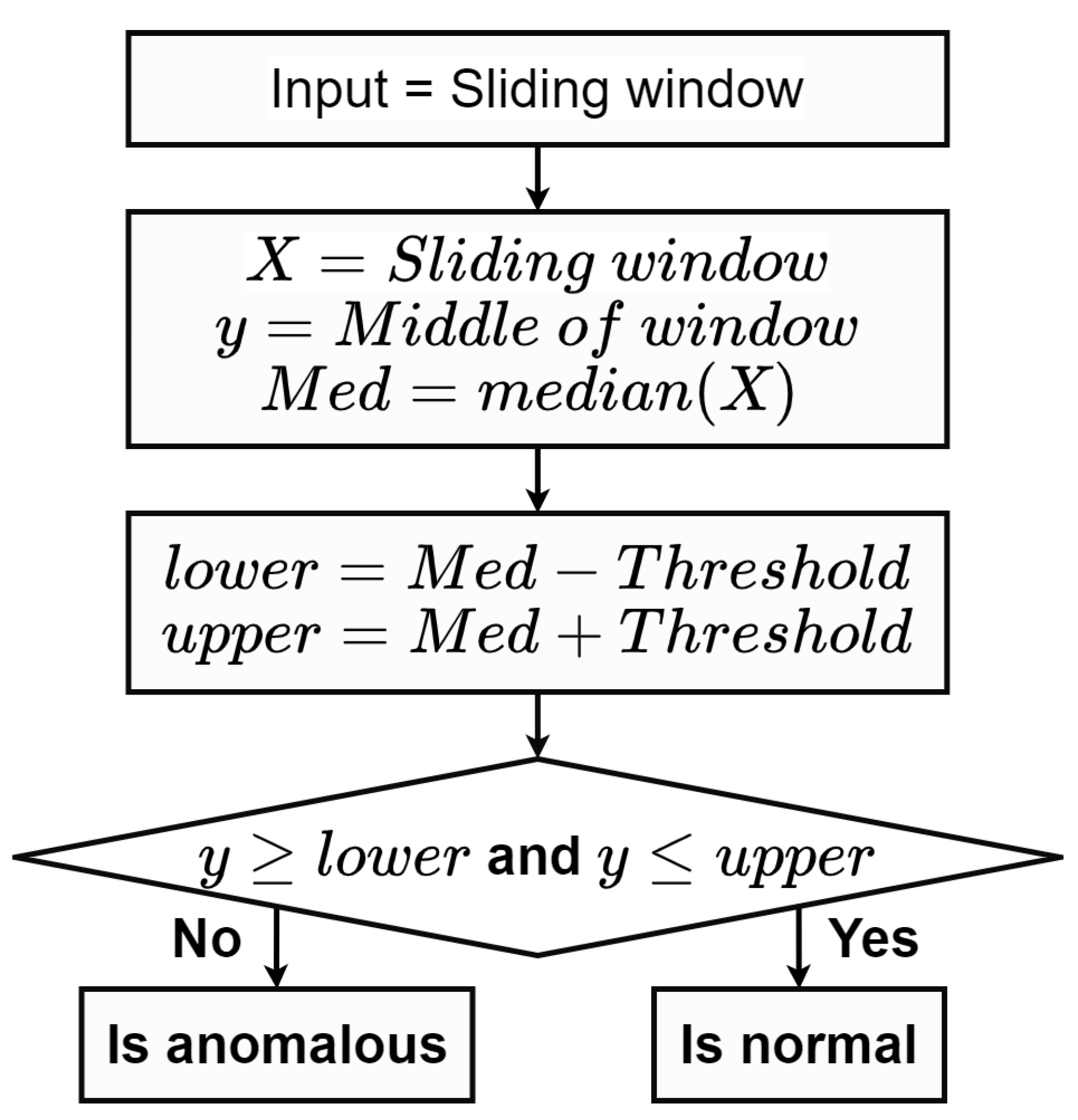
2.2.1. Median with Fixed Threshold
With predetermined , the median of data within the sliding window coupled with predefined were used to calculate the prediction interval (PI). A middle point of the sliding window, y, was detected as anomalous if it fell outside of the interval. In this method as shown in Figure 2, the parameters and need to be further fine-tuned using an exhaustive grid search.
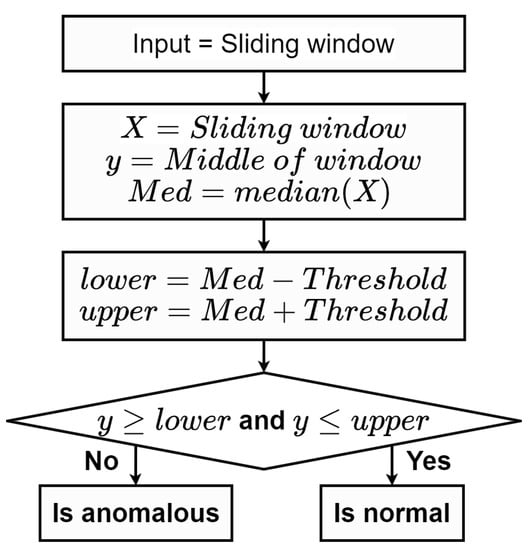
Figure 2.
A flow chart of the median with fixed threshold method.
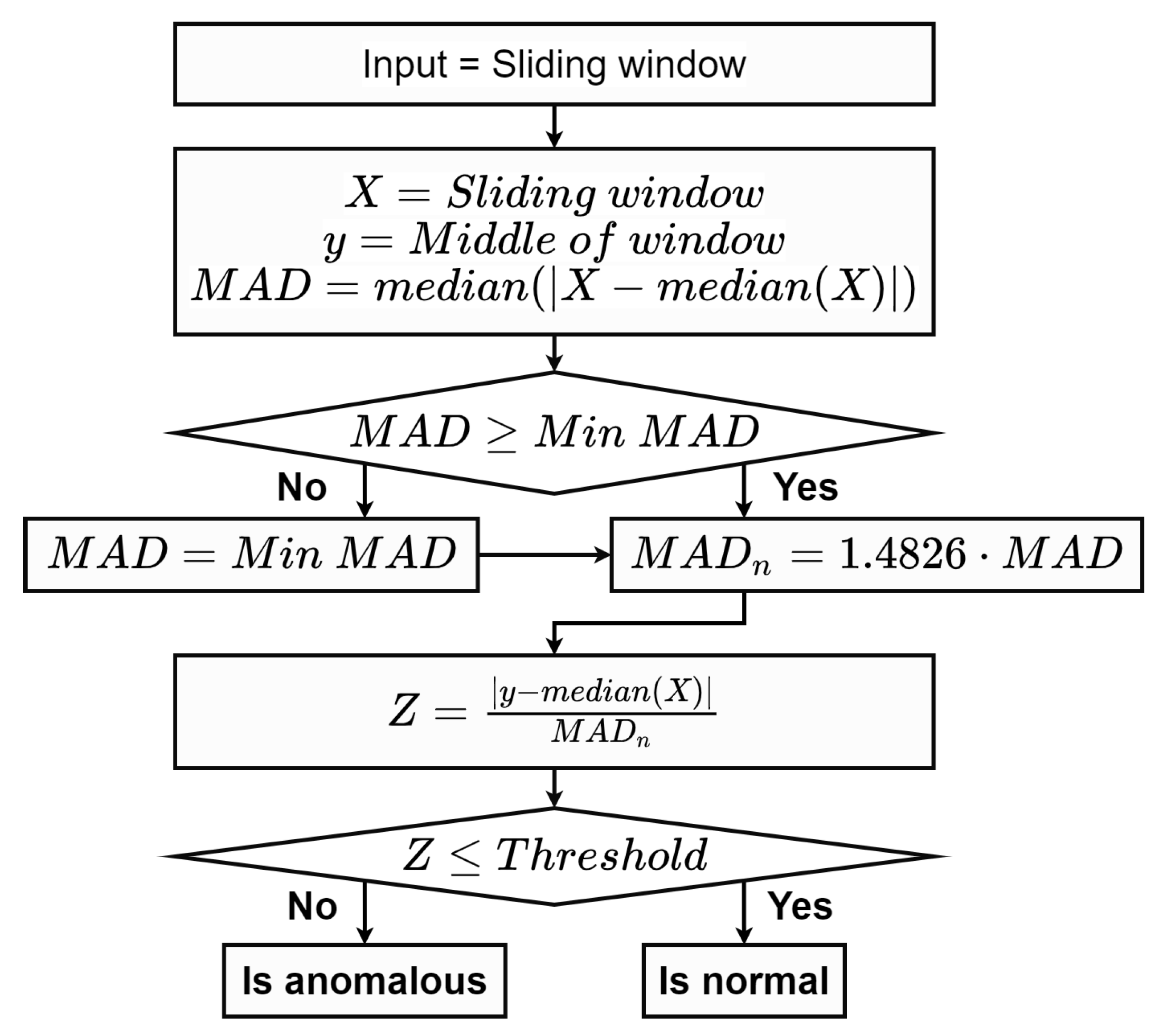
2.2.2. Median Absolute Deviation (MAD)
We initially defined three parameters including , and . The median absolute deviation, , of the sliding window was compared with . If calculated was smaller, was substituted with . A modified Z-score was then calculated using Equation (2). A middle point, y, of the sliding window, X, was classified as an anomaly if the computed Z-score exceeded . A flow chart of the proposed method is shown in Figure 3. An additional step is required to fine-tune all predefined parameters via the grid search.
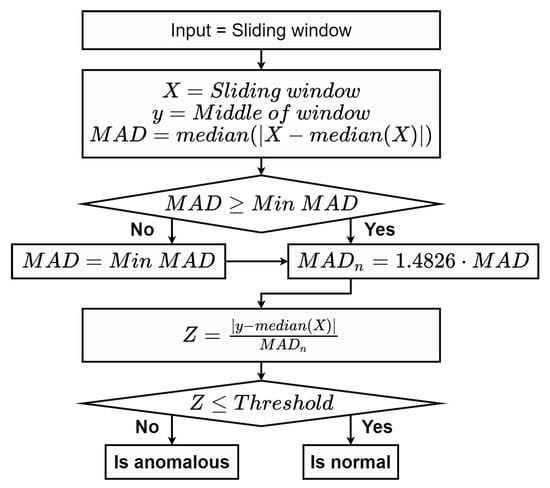
Figure 3.
A flow chart of the median absolute deviation (MAD) method.
2.3. Data Filling Methods
There are three various data filling methods utilized in this work. We applied the linear and the spline interpolation due to their simplicity. More advanced bidirectional LSTM with decreasing weight model was further considered. A comparison among these methods was performed on hydrological time series as our case studies.
2.3.1. Linear Interpolation
A simple linear function was implemented with respect to existing data points in order to fill missing data points. Specifically, a straight line was fitted between two adjacent points of each missing gap in order to estimate new values.
2.3.2. Spline
We relied on piece-wise functions using various polynomial sub-functions on subsets of the data. The function from the widely used SciPy python library was employed. According to this function, the degree of polynomials, k, identifies a specific type of relationship applied to the data. In addition, a smoothing function, s, specifies a smoothness of the fitted curve.
2.3.3. Bidirectional LSTM with Decreasing Weight Model
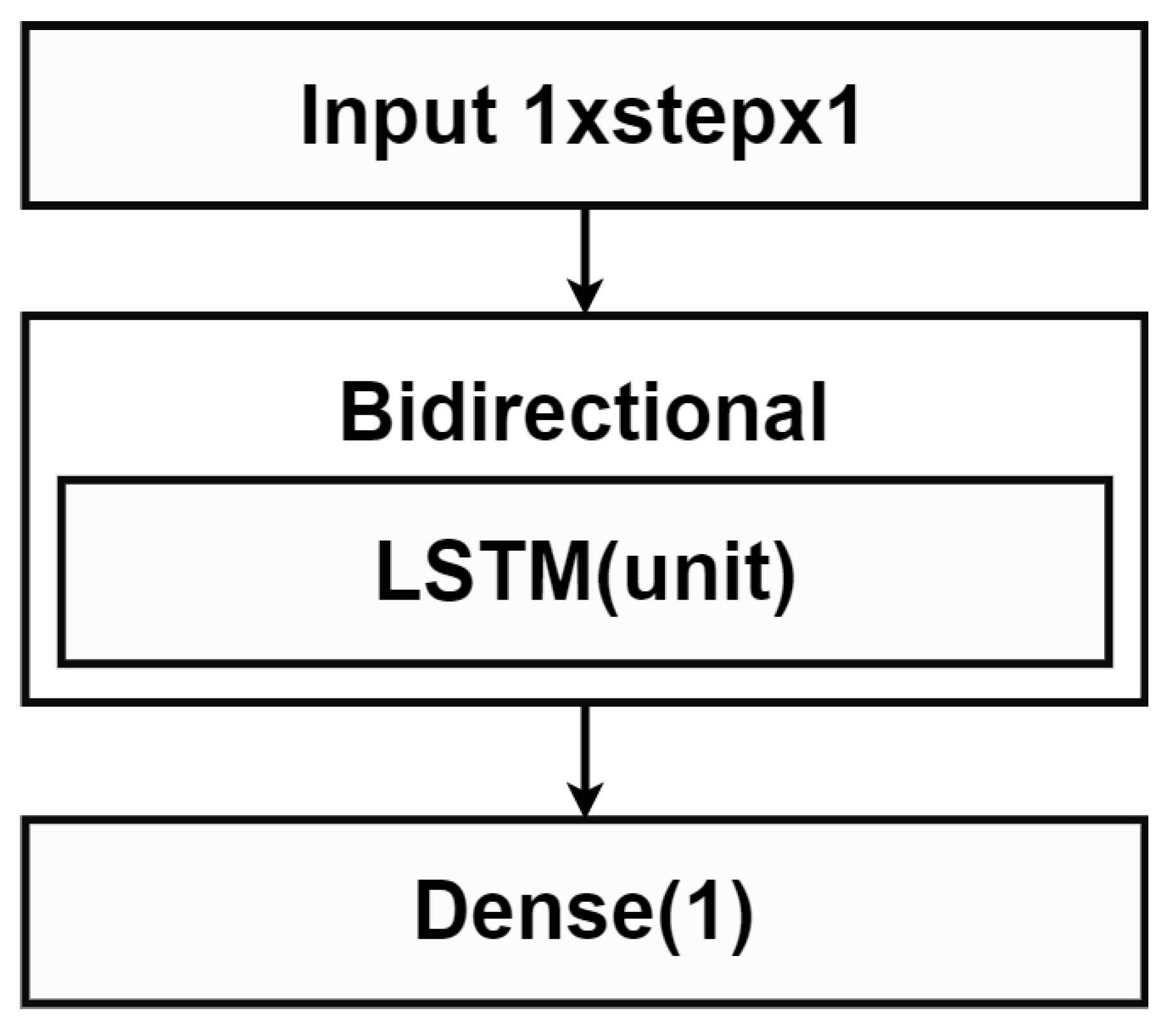
The method proposed in [21] consisted of forward and backward LSTM models to estimate the final prediction using Equation (3). An architecture of each LSTM model is shown in Figure 4. The orange shaded block in Figure 4 is the bidirectional LSTM network [36] as explained in Section 2.1.3. There are two parameters and involved in this model where is the amount of input data points, and is the amount of the LSTM layer units.
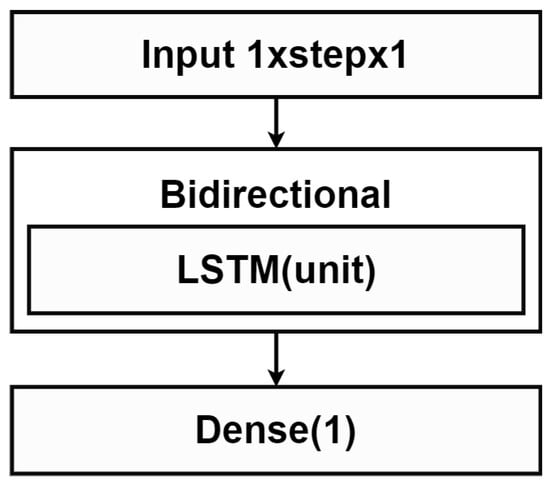
Figure 4.
LSTM model in Bidirectional LSTM.
3. Experimental Analysis
In this section, our case studies regarding hydrological time series are discussed. A data gathering and a test set generation process are further elaborated. We also indicate training configurations, fine-tuned parameters for the proposed methods and evaluation metrics.
3.1. Data Gathering and Pre-Processing Step
We received 10-min time series water level data during 2017 and 2020 gathered from telemetry stations across Thailand. There are 52,560 data points for the whole year. Missing values and anomalies are typically observed in the raw data due to malfunctioned sensors or unexpected circumstances. In response, a preliminary data pre-processing step is unavoidably required prior to any further analysis.
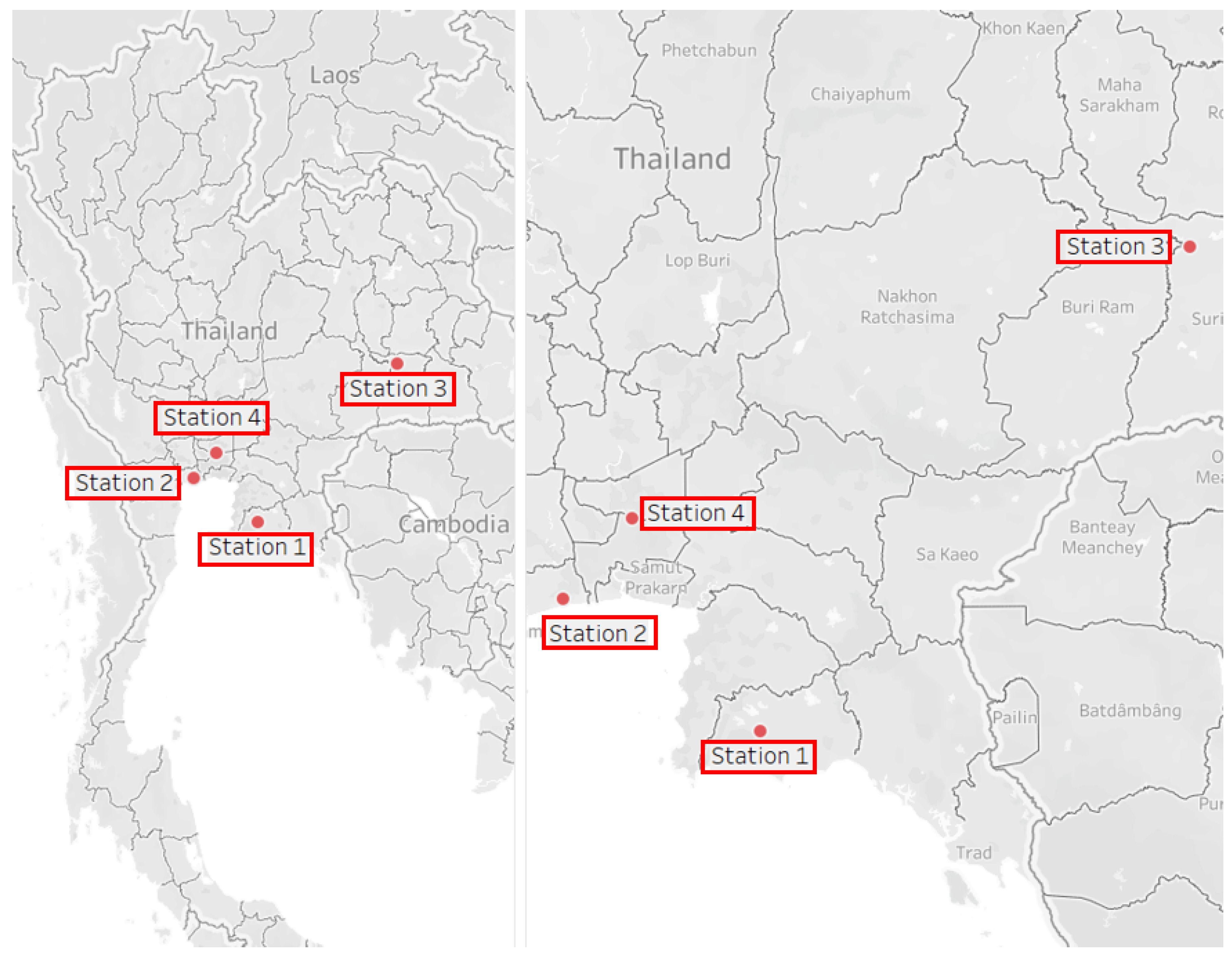
With an exploratory observation, more recent data typically contained less missing values or extremely incorrect values. Stations with overabundant missing values were initially eliminated. Among the remaining data, we removed extreme anomalies and initially imputed missing values with a simple interpolation function. To properly train and test the anomaly detection and data filling methods as our case studies, we selected 2-year data from particular 4 stations as representations of contrasting behaviors. Various locations with different associated basin were selected in order to verify a flexibility and a generalization of our proposed framework. Specifically, the same overall framework was applied to all data from these 4 stations while parameters corresponding to internal models were separately fine-tuned. Descriptions of these selected stations are summarized in Table 1 while their locations are depicted in Figure 5.

Table 1.
Descriptions of the selected stations.
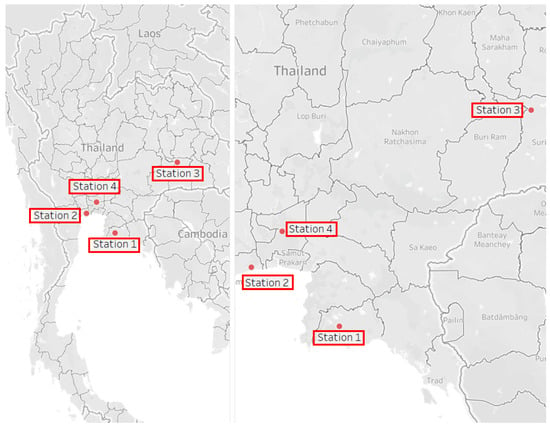
Figure 5.
Locations of the selected stations at a country level (left) and at a specific zoom-in level (right).
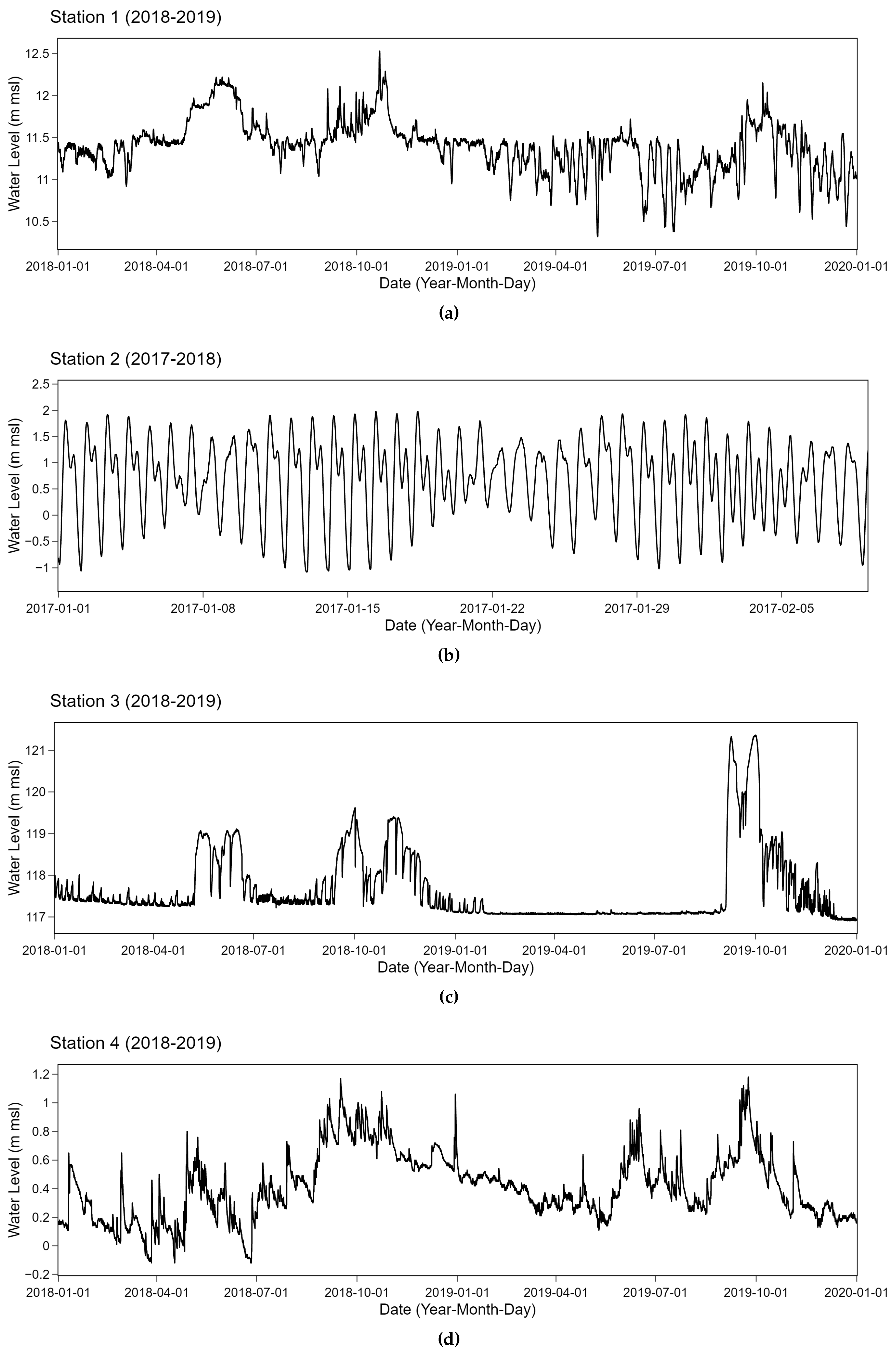
Two consecutive years of relatively complete data with very few missing values of no more than 5% corresponding to selected stations were collected from the original data. These retrieved time series of all 4 stations are depicted in Figure 6. Time series data from 2017 and 2018 were retrieved for station 2 while other stations relied on 2018 and 2019 data. These time series from specifically selected stations tend to have different behaviors. Strong periodic patterns due to external factors are observed in station 2 which is located near the mouth of the Chao Phraya River connecting to the ocean. A tide effect potentially plays an important role in an observed periodicity. On the contrary, station 3 which is located at a weir has relatively stable characteristics with small changes while abrupt spikes occur at particular points. Additionally, time series data obtained from station 1 and station 4 fluctuate around the mean with different swing behaviors. These inland stations tend to be less influenced by a coastal effect than the other two. More fluctuations are observed in station 4 with several upward and downward trends. These time series having different patterns were collected from telemetry stations. Types of anomalies in the water level data are naturally common. Highly unexpected outliers are rarely noticed. Anomalies types as classified in [40] in these data include constant offsets with sudden shifts. Clusters of spikes and small sudden spikes can also be observed.
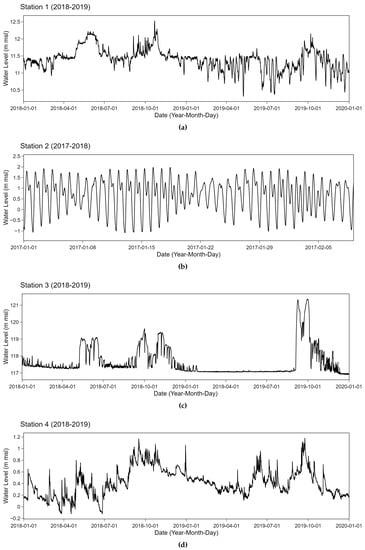
Figure 6.
Water level data at station 1, station 2, station 3 and station 4 (a–d).
In order to verify the performance of our proposed methods, we held out part of the whole data for evaluating purposes. In particular, the first-year data was used for training while the testing step was performed on the second-year data. As these datasets were collected from sensors without any annotation, annotated labels were required. In order to evaluate the proposed methods, we intentionally removed data points which were hold as the gold standard in our test sets. We separately constructed the test sets for anomaly detection and data filling methods. In these test sets, artificially-created labels were constructed to represent types of anomalies found in our water level data.
3.1.1. Test Data Generation for Anomaly Detection
In order to generate a test data for evaluating anomaly detection methods, 10% of the pre-processed data was converted to anomalies. We initially randomized an integer A from a range of 2000 to 4000. Then, A was used as an input for Dirichlet distribution to compute a probability vector B of length A that sums to 1. The vector B was used in Equation (4) to calculate K, the length of all intervals of anomalous data where the length of data l was given.
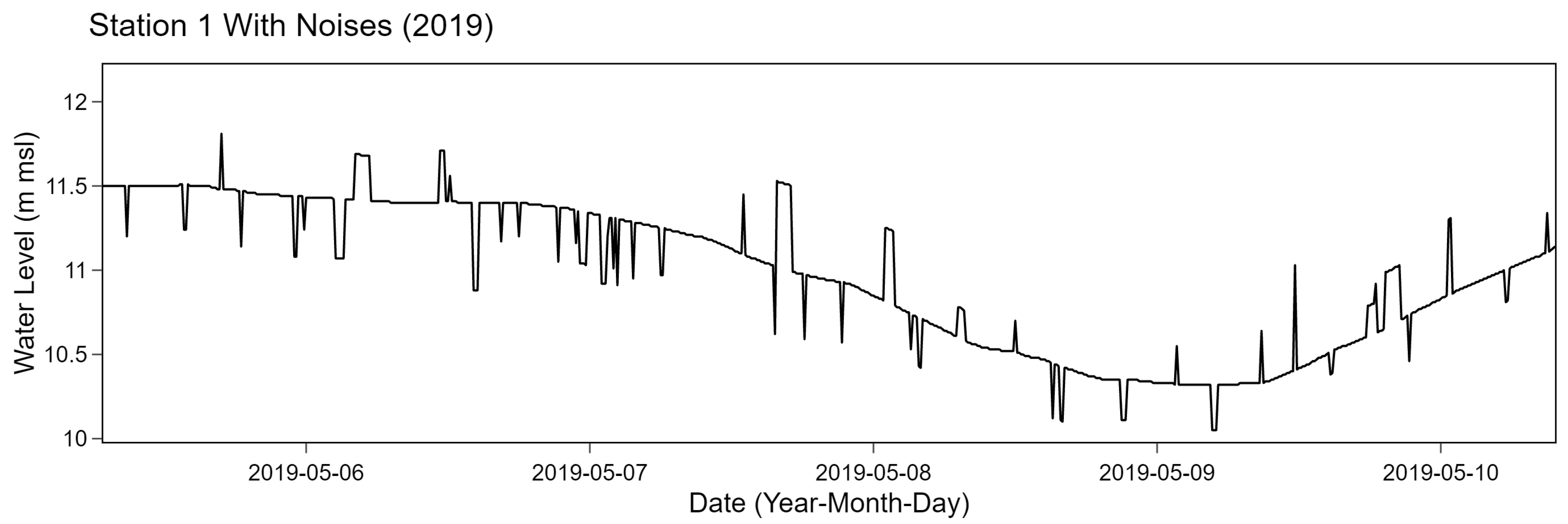
Positions of anomalous data intervals with lengths obtained from K were randomly selected on the time series data without any overlapping. After specifying the positions of all intervals, noises were added to existing values in the intervals. Noises were selected from the highest value from Gaussian random number generators. Particularly, the Gaussian distribution was implemented with of 0.2 for station 1, 3, and 4 while of 0.5 was used for station 2. We specified parameters to mimic the original data based on a manual observation. An example of result corresponding to station 1 after adding noises is shown in Figure 7.
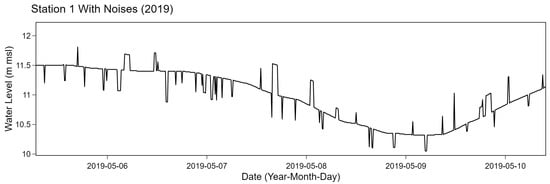
Figure 7.
Example of station 1 with noises.
3.1.2. Test Data Generation for Data Filling
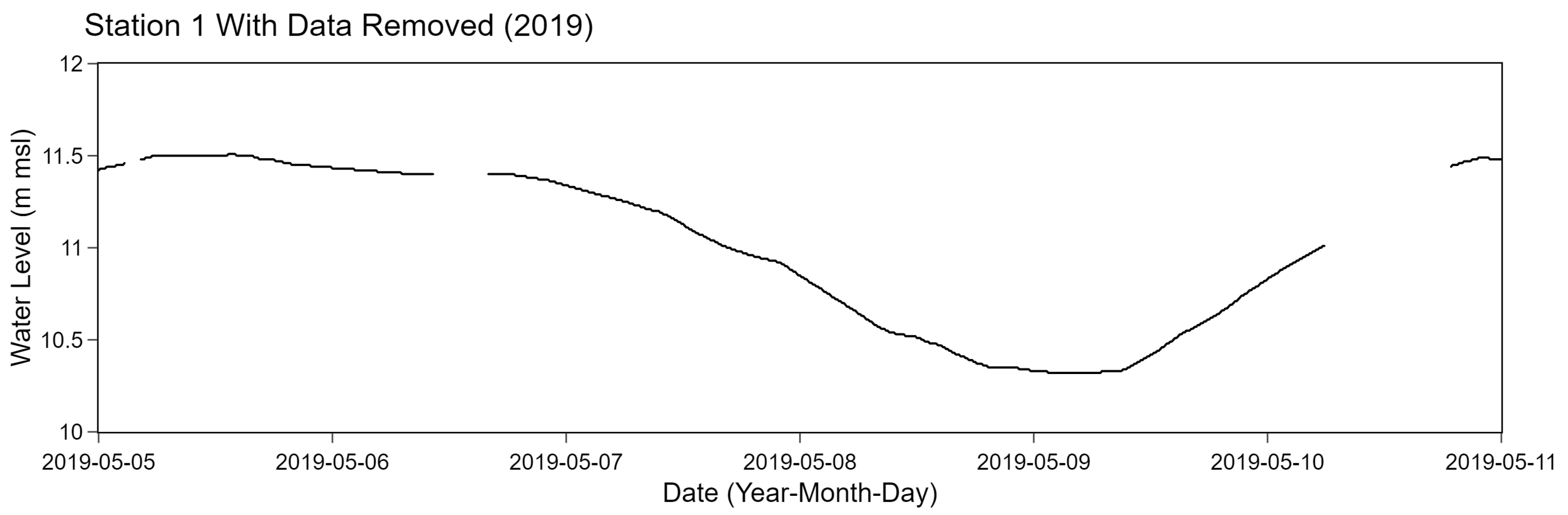
We generated a separate test data for evaluating data filling methods based on 10% of the whole data. A similar approach to generate the test data as discussed in Section 3.1.1 was also performed. Particularly, the Dirichlet distribution was also applied to compute K, a list of interval lengths, with a randomized integer A. Instead of adding noises to the original data, selected points were completely removed. An example of results of station 1 after removing selected data points is shown in Figure 8.
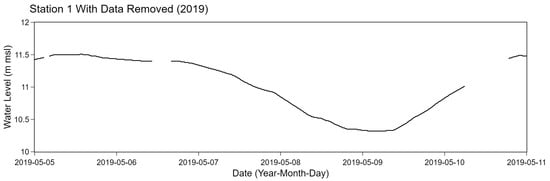
Figure 8.
Example of station 1 after removing data points.
3.2. Parameters and Training Configurations
Each time series data typically contains different patterns. In order for the proposed methods to work well with various data, associated parameters need to be adjusted accordingly. In particular, involved parameters were thoroughly explored in this work in order to fine-tune for appropriate values. For anomaly detection parameters, and were extensively fine-tuned for both median with fixed threshold and MAD methods. These parameters were experimented until superior performance of the proposed method was achieved. Additionally, we modified the original MAD method to include criteria. Regarding data filling parameters, k and s were examined in the spline method while bidirectional LSTM explored and parameters. After fine-tuning, all final experimented parameters in the anomaly detection and data filling methods are shown in Table 2.

Table 2.
Anomaly detection and data filling parameters.
In order to properly train LSTM models, all the data were divided into 80% training and 20% validating. Training and validation data were normalized using a min–max scaler. The mean absolute error (MAE) was used as the loss function with ADAM optimizer. A number of epochs, a batch size, min delta, and patience parameters were set to 200, 128, 0.0001, and 20, respectively. In the training step, GeForce GTX 1080 GPU was used in this work.
3.3. Evaluation Metrics
Two common evaluation metrics were utilized in this work. Specifically, F1-score, a harmonic mean of precision and recall, was employed for assessing the anomaly detection performance. The root mean square error (RMSE) comparing between predicted values and the ground truth was used to evaluate the data filling methods.
4. Results and Discussions
The anomaly detection methods with fine-tuned parameters as listed in Table 2 were evaluated using F1-score, as depicted in Table 3. Prior to obtain selected parameters, the fine-tuning step was performed. As an example, we further provided sensitivity of F1-score obtained from MAD method of station 1 as shown in Table 4. Specifically, the and were varied while holding another parameter fixed at specified value. Varying parameters utilized in these methods resulted in slight inferior F1-score compared to 0.9944 F1-score corresponding to the selected parameters.

Table 3.
F1-score resulting from anomaly detection methods.

Table 4.
F1-score sensitivity resulting from MAD method after varying and parameters for station 1.
A desirable performance with high F1-score was achieved as reported in Table 3. Our proposed method is able to estimate so flexible predictive interval that changes in the data are well-captured. Comparing between anomaly detection methods, an average F1-score of the median with fixed threshold was relatively higher than the MAD method. In particular, both methods provided superior performances on all stations except station 2. Considering only station 2 data, the median with fixed threshold method gave 0.8823 F1-score which is higher than 0.7804 F1-score of MAD.
Distinct behaviors of station 2 mostly due to tidal effects can be clearly observed as shown in Figure 6. Due to the periodicity of the water level data of station 2, we observed that have to be small enough to capture abrupt and frequent changes in the data. Utilizing large windows potentially relies on many irrelevant observations. As a result, inaccurate estimations due to abrupt changing trends resulting from these observations are observed. We identified the appropriate size of sliding window based on the exhaustive search. The was on the range of 25 to 55 depending on their variations and time frames. After fine-tuning, of 25 and 19 for median with fixed threshold and MAD were obtained for station 2. They were relatively smaller than those of other stations. The effect was less obvious in the MAD method as selected parameters were less deviated among stations. The was on the range of 0.05 to 3.5 depending on a strong variation at each data point.
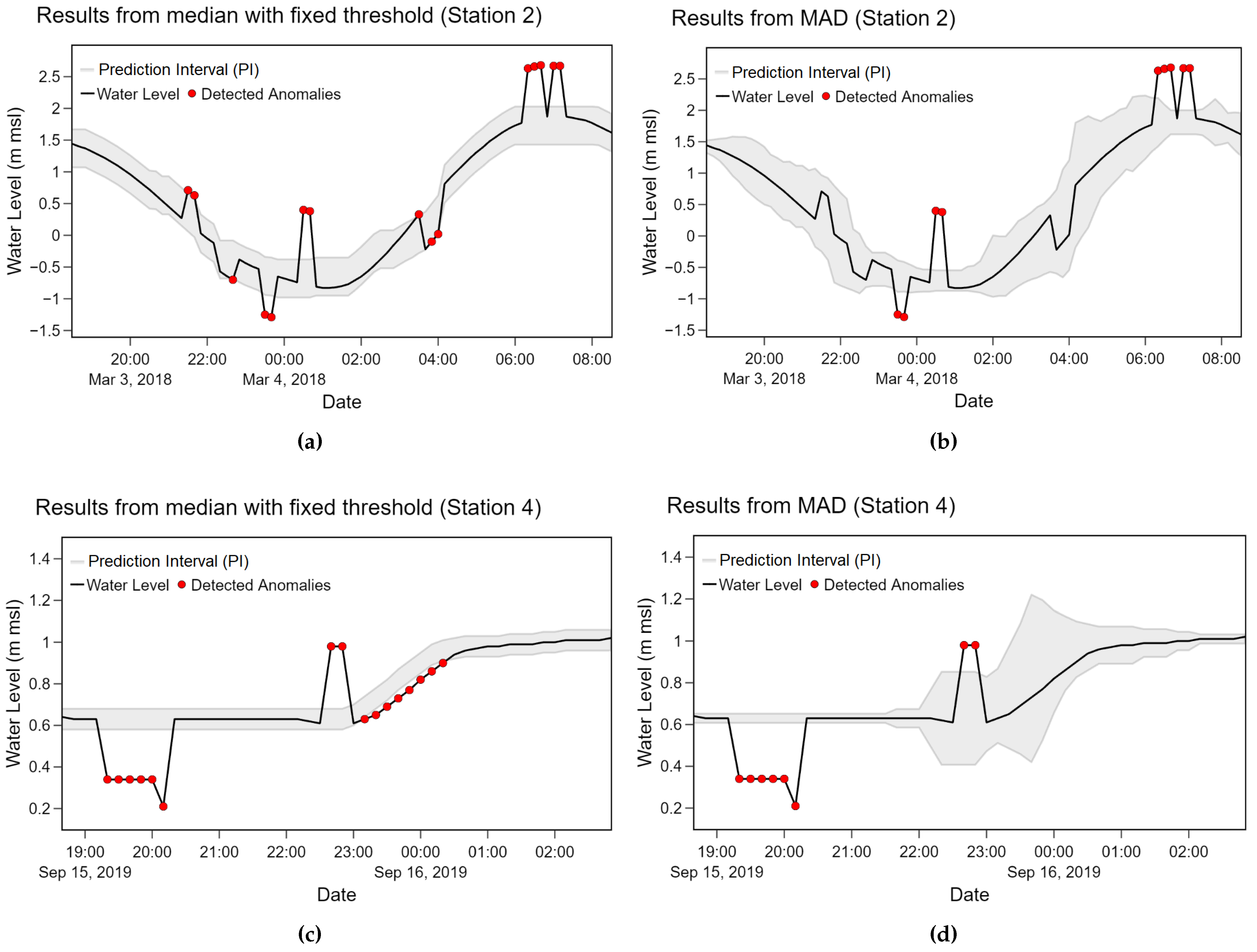
With the current experiment settings, anomalies in some cases were incorrectly identified as normal points in MAD method as shown in the second plot (b) of Figure 9. The median with fixed threshold method was less affected to such situation as shown in the first plot (a) of Figure 9. The prediction interval (PI) was calculated from upper and lower values for the median with fixed threshold method while it relied on the Z value for the MAD method, respectively. Based on our observation, the fixed threshold yields more stable PI which is more suitable for data with abrupt and frequent changes like station 2. However, in some situations, as shown in plots (c) and (d) of Figure 9, the MAD method was able to follow changes in water level better than the median with fixed threshold method. The prediction interval of the MAD method was expandable while the interval of the median with fixed threshold was constantly fixed. Another disadvantage of the fixed threshold can be observed from plot (c) of Figure 9 where several adjacent points were incorrectly detected as anomalies. When one point is incorrectly classified, subsequent points are likely to follow the same pattern.
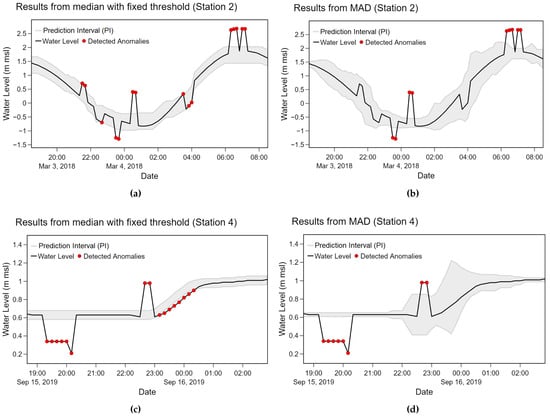
Figure 9.
A comparison between the median with fixed threshold and MAD (a) station 2 with median with fixed threshold; (b) station 2 with MAD. (c) station 4 with median with fixed threshold; (d) station 4 with MAD.
Regarding tidal effects, recurrent upward and downward trends are noticeable in station 2 data while infrequent changes with some peaks can be observed in non-cyclical data patterns. According to our observation from the experiments, the tidal effects yielded frequent changes with similar magnitudes in the data. The method with a constant threshold resulting in a fixed prediction interval consequently performed better in the data with tidal effects. On the other hand, the adaptive threshold method like MAD is more capable of dealing with infrequent and unexpected changes.
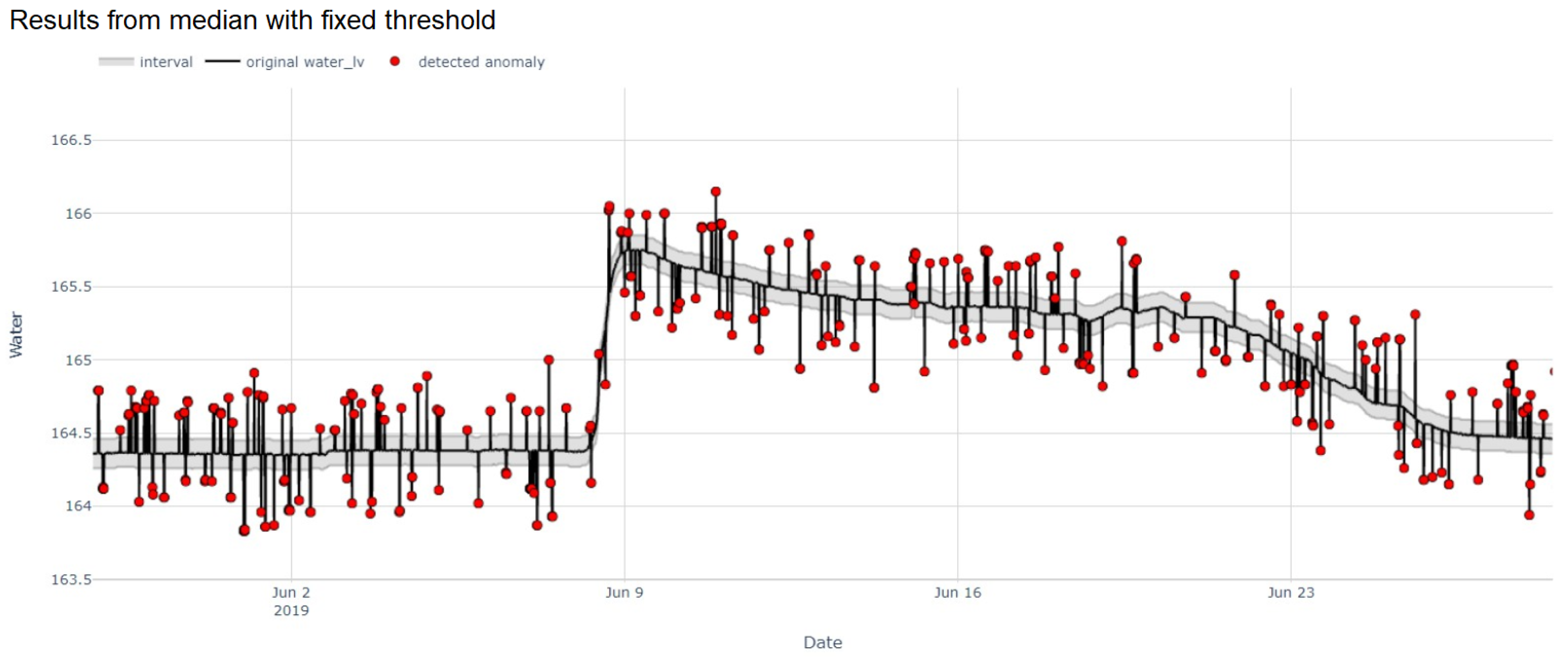
We further applied our proposed methods with additional data containing infrequent and anomalous step changes to verify their capability. The median with fixed threshold and MAD yielded 0.975 and 0.9693 F1-score as depicted in Figure 10. With respect to false detection rates, the median with fixed threshold yielded 0.2744 false positive rate (FPR) and 2.4923 false negative rate (FNR) while 0.3904 FPR and 2.5889 FNR were retrieved from MAD. Our proposed methods performed reasonably well even with some abrupt change points commonly found in water level data.
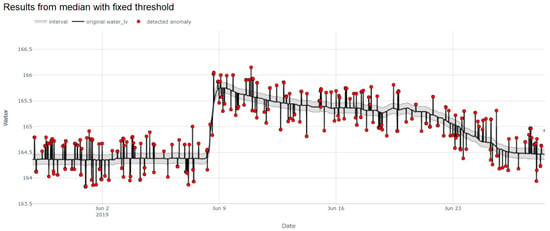
Figure 10.
Example of the median with fixed threshold applied on the additional data with anomalous step changes.
Due to the data imputation perspective, RMSE was employed to evaluate the performance of 3 methods as shown in Table 5. Considering all stations, the bidirectional LSTM model provided the best performance with 0.0291 average RMSE. However, this method actually performed worse than other methods on most stations except station 2. On the other hand, the spline method yielded desirable performance among station 1, 3, and 4 with 0.0038 RMSE while the linear interpolation yielded 0.004 RMSE.

Table 5.
RMSE resulting from data filling methods.
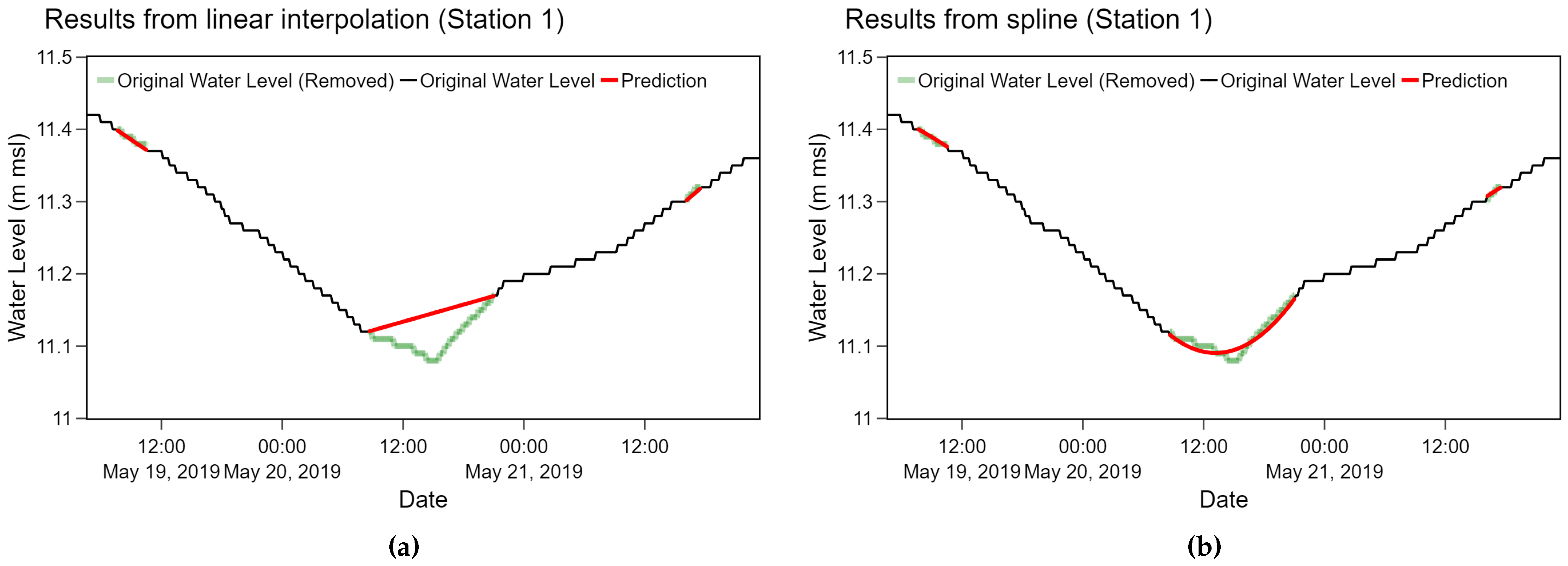
According to both overall average and the average among 3 stations, the spline and the linear interpolation method performed equally well. We observed that results from the spline method were relatively smoother than the linear interpolation as depicted in Figure 11 where both methods were applied on station 1 data. Even though the spline method is likely to yield a slight better performance at substituting water level data, fine-tuning for appropriate parameters is more time-consuming.
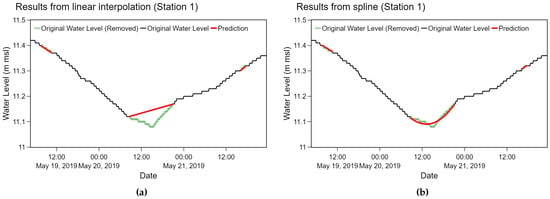
Figure 11.
A result comparison between (a) the linear interpolation and (b) the spline method applied on parts of time series obtained from station 1.
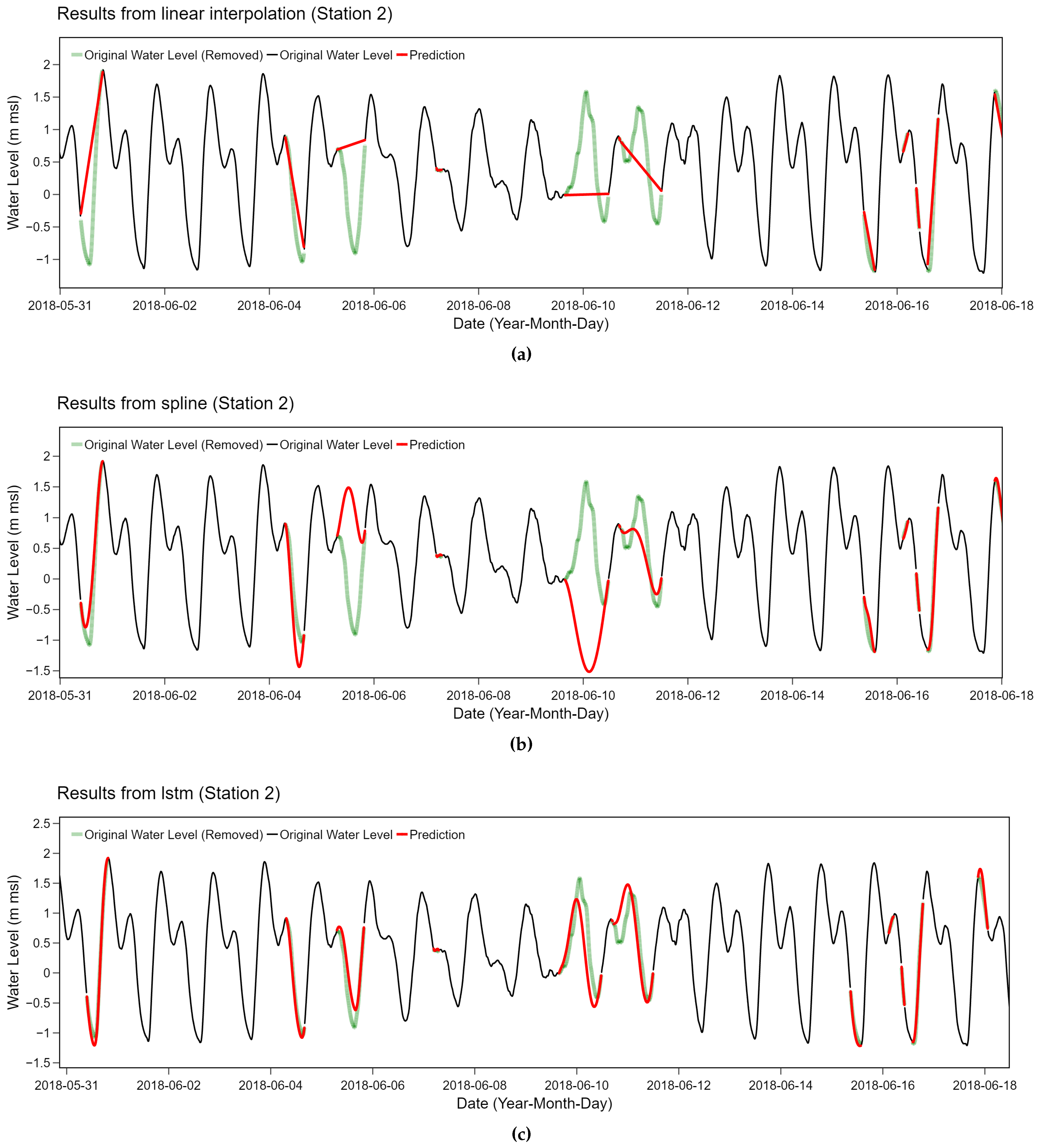
We performed a further analysis on the specific case of station 2. Periodic behaviors of water level at station 2 can be captured with LSTM-based method while the other two methods failed considerably. The utilized bidirectional LSTM model was trained on the input sequence and its reversed copy which preserved both past and future information of a specific time frame. With this advantage, the bidirectional LSTM model is able to understand the context better which is suitable for relatively complicated time series with frequent changes with tidal effects like station 2. According to our experiments, the linear relationship and polynomial functions utilized in the spline method were too naive to capture periodic behaviors, as shown in Figure 12. Due to the strong periodicity with frequent upward and downward changes, several red interpolation lines do not match with the original green line which has previously been removed. Comparing between these figures, both methods tend to behave similarly as they fail at the same particular points of the data. On the contrary, more complicated method like bidirectional LSTM is suitable for this situation as depicted in the bottom plot of Figure 12.
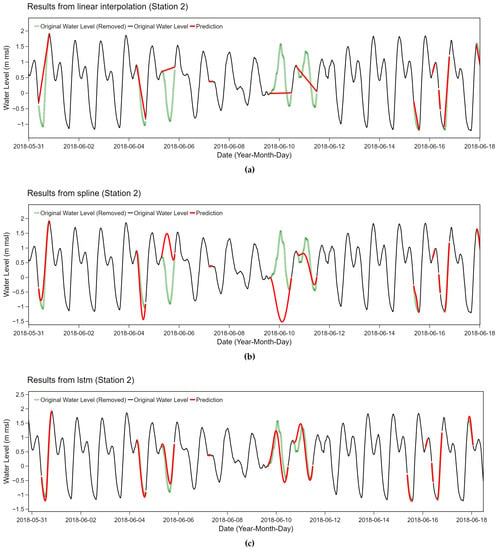
Figure 12.
A result comparison between (a) the linear interpolation method, (b) the spline method and (c) the bidirectional LSTM method for station 2.
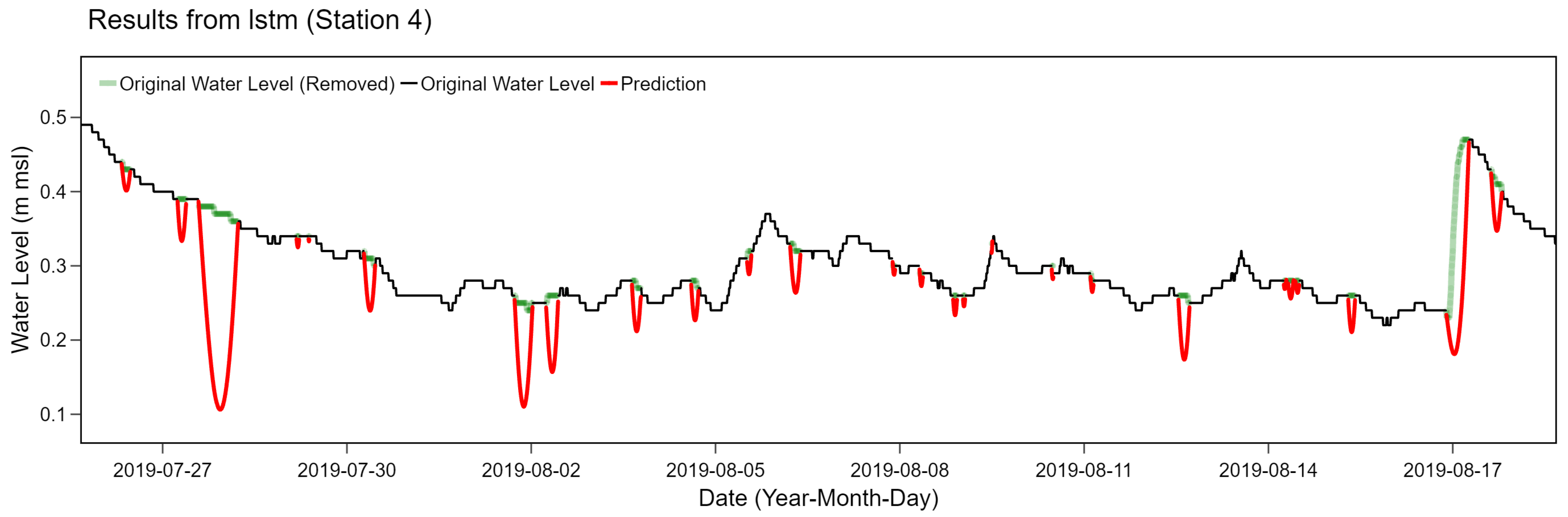
However, the bidirectional LSTM filling method may not provide the best performance in all scenarios. For example, time series of station 4 tend to have smoother patterns with much less seasonality due to tidal effects than station 2. According to our experiment on these data, the bidirectional LSTM method incorrectly estimated too fluctuated values compared to the original time series, as depicted in Figure 13. The LSTM model was prone to underestimate the ground truth for non-cyclical behaviors without frequent upward and downward trends. The bidirectional LSTM model considered both future and past directions when estimating the final prediction. When one point was incorrectly estimated, adjacent points tended to follow the same tendency. As a result, these errors were further accumulated over time resulting in distinct drop-down miscalculations.
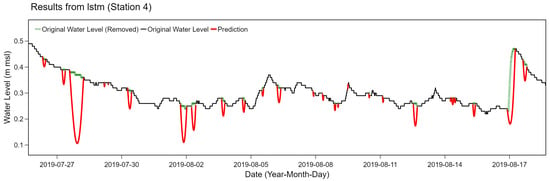
Figure 13.
Results from bidirectional LSTM filling method for station 4.
Our current LSTM model was trained with fine-tuned parameters without an over-fitting problem. Particularly, a particular part of the whole training data was intentionally held out for validating. Loss functions on the training and validating parts were observed to avoid the over-fitting phenomenon. The model was carefully trained until loss functions were flattened. We constructed this model based on 1-year time series while training complicated LSTM-based method typically requires large enough dataset to learn patterns. In order to justify the LSTM model performance, an additional experiment by varying a proportion of required training data was conducted. We selected non-cyclical data behaviors like station 1 as an example. Instead of using 80% training data, we reduced this number to 70% and 60% prior to repeating the same experiment for training the bidirectional LSTM model. These models were evaluated and compared with 0.0052 RMSE of current settings as previously reported in Table 5. According to our additional experiment, 0.0187 and 0.0206 RMSE were achieved from the LSTM models using 70% and 60% training data, respectively. The higher number of training data tends to reduce the model error considerably. Retrieving additional data potentially enhances the performance of our present LSTM model.
To sum up, both statistical-based anomaly detection methods are easy to implement, fast, and require light computation efforts. They tend to perform equally well in most situations. Regarding data imputation, the linear and spline interpolation work well with non-cyclical time series patterns while the bidirectional LSTM method is able to capture periodic behaviors. With the desirable performance as observed in our case studies, applying the proposed methods in an on-line framework for a real-time detection is promising with a slight modification. Particularly, the proposed real-time quality control framework for hydrological data consists of the anomaly detection part which screen out outliers from the data. The imputation method is further applied on detected data to substitute anomalies with appropriate values. Even though this study conducted experiments on the water level data only, the general proposed framework is intentionally designed to be applicable with other hydrological time series data. Additional steps of fine-tuning parameters for other data distributions or different data types are required.
A combination of methods and an application of the models distinguish our work from others. Our main contribution is combining both statistical-based anomaly detection methods under the prediction interval framework with a sliding window technique while implementing machine learning data imputation approaches as an overall system. Compared to previous work [35] with MAD outlier detection and EWMA smoothing, we utilized the similar approach to identify anomalies but we relied on relatively advanced bidirectional LSTM data filling method. Several works focused solely on the anomaly detection or the data imputation task while we developed the overall system with both components. Our present method allows an adaptive prediction interval, so it can capture anomalies from various data distributions with a small computational time requirement. This technique can be applied for both off-line and on-line detection which is suitable for a data monitoring system. To the best of our knowledge, none of prior works applied a similar framework on a dataset collected in Thailand. Our case studies consisted of time series data collected from several telemetry stations among various locations. We explored diverse data patterns especially the strong periodicity which required a specific treatment. We performed thorough experiments comparing between multiple data behaviors, such as cyclic and non-cyclic (with and without tidal effects), as well as infrequent abrupt changes.
To enhance the proposed quality control framework for time series data, applying machine learning algorithms, such as isolation forest or deep learning algorithms as the anomaly detection method with the sliding window technique is promising. Further integrating seasonality (e.g., wet and dry seasons) and change-point features in the proposed model to represent unexpected spikes commonly found in the water level data are an encouraging enhancement. Another direction of future work includes specifying groups of stations with pre-defined parameters without extensively fine-tuning. This will further improve the efficiency and practicality of the proposed framework. Instead of considering each individual station for the data filling method, a spatial-temporal relationship which relies on nearby stations is compelling. Finally, applying the proposed framework with other hydrological data extends the completeness and the generalizability of this work considerably.
5. Conclusions
This paper extensively performed experiments on statistical methods for an automated anomaly detection, as well as various data filling methods. Particularly, the median and the median absolute deviation (MAD) were implemented for detecting anomalies. Multiple data filling methods including the linear interpolation, the spline method and bidirectional long short-term memory (LSTM) were further explored in order to substitute detected anomaly or missing data. Developing an overall system consisting of both functionalities, as well as its application are our main contributions. Generally, our proposed methods provide desirable performance which can be practically applied in a real-time detection. According to our observation, both median-based statistical methods for anomaly detection coupled with the linear and the spline method for data filling provided promising results for non-cyclical data behaviors. On the other hand, the bidirectional LSTM performed relatively well on time series data with strong seasonality with drastic changes in a short period of time like tidal effects.
Author Contributions
Conceptualization, S.W., K.S. and S.B.-a.; methodology, L.K., C.C., M.M. and P.W.; software, L.K. and C.C.; validation, M.M. and P.W.; formal analysis, L.K.; investigation, C.C., M.M. and P.W.; data curation, S.W., K.S. and S.B.-a.; writing—original draft preparation, L.K.; writing—review and editing, M.M. and P.W.; visualization, L.K.; supervision, C.C., M.M. and P.W.; project administration, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
No applicable.
Data Availability Statement
Data available on request due to restrictions, e.g., privacy. The data presented in this study are available on request from the Hydro Informatics Institute (HII) authors.
Acknowledgments
This research was partially supported by Kasetsart University Research and Development Institute under the “FF(KU)25.64” project (to P.W. and M.M. authors). We are also grateful to Hydro Informatics Institute (HII), Thailand for providing the water level data used in this work and for advice about in-depth knowledge of the water level behaviors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Gupta, M.; Gao, J.; Aggarwal, C.C.; Han, J. Outlier detection for temporal data: A survey. IEEE Trans. Knowl. Data Eng. 2013, 26, 2250–2267. [Google Scholar] [CrossRef]
- Ahmad, S.; Purdy, S. Real-time anomaly detection for streaming analytics. arXiv 2016, arXiv:1607.02480. [Google Scholar]
- Thakkar, P.; Vala, J.; Prajapati, V. Survey on outlier detection in data stream. Int. J. Comput. Appl. 2016, 136, 13–16. [Google Scholar] [CrossRef]
- Mishra, S.; Chawla, M. A comparative study of local outlier factor algorithms for outliers detection in data streams. In Emerging Technologies in Data Mining and Information Security; Springer: Singapore, 2019; pp. 347–356. [Google Scholar]
- Park, C.H. Outlier and anomaly pattern detection on data streams. J. Supercomput. 2019, 75, 6118–6128. [Google Scholar] [CrossRef]
- Zhang, M.; Guo, J.; Li, X.; Jin, R. Data-Driven Anomaly Detection Approach for Time-Series Streaming Data. Sensors 2020, 20, 5646. [Google Scholar] [CrossRef]
- Alghushairy, O.; Alsini, R.; Soule, T.; Ma, X. A Review of Local Outlier Factor Algorithms for Outlier Detection in Big Data Streams. Big Data Cogn. Comput. 2021, 5, 1. [Google Scholar]
- Braei, M.; Wagner, S. Anomaly detection in univariate time-series: A survey on the state-of-the-art. arXiv 2020, arXiv:2004.00433. [Google Scholar]
- Gao, C.; Chen, Y.; Wang, Z.; Xia, H.; Lv, N. Anomaly detection frameworks for outlier and pattern anomaly of time series in wireless sensor networks. In Proceedings of the 2020 International Conference on Networking and Network Applications (NaNA), Haikou, China, 10–13 December 2020; pp. 229–232. [Google Scholar]
- Safaei, M.; Asadi, S.; Driss, M.; Boulila, W.; Alsaeedi, A.; Chizari, H.; Abdullah, R.; Safaei, M. A systematic literature review on outlier detection in wireless sensor networks. Symmetry 2020, 12, 328. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on Outlier/Anomaly Detection in Time Series Data. ACM Comput. Surv. 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Croux, C. Alternatives to the median absolute deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef] [Green Version]
- Hochenbaum, J.; Vallis, O.S.; Kejariwal, A. Automatic anomaly detection in the cloud via statistical learning. arXiv 2017, arXiv:1704.07706. [Google Scholar]
- Mehrang, S.; Helander, E.; Pavel, M.; Chieh, A.; Korhonen, I. Outlier detection in weight time series of connected scales. In Proceedings of the 2015 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Washington, DC, USA, 9–12 November 2015; pp. 1489–1496. [Google Scholar]
- Hill, D.J.; Minsker, B.S. Anomaly detection in streaming environmental sensor data: A data-driven modeling approach. Environ. Model. Softw. 2010, 25, 1014–1022. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, Y.; Li, S.; Wan, D. Time series outlier detection based on sliding window prediction. Math. Probl. Eng. 2014, 2014, 10–1155. [Google Scholar] [CrossRef]
- Ma, L.; Gu, X.; Wang, B. Correction of outliers in temperature time series based on sliding window prediction in meteorological sensor network. Information 2017, 8, 60. [Google Scholar] [CrossRef] [Green Version]
- Lepot, M.; Aubin, J.B.; Clemens, F.H. Interpolation in time series: An introductive overview of existing methods, their performance criteria and uncertainty assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Gao, C.; Zhao, Y.; Zhao, Y. A Time Series Data Filling Method Based on LSTM—Taking the Stem Moisture as an Example. Sensors 2020, 20, 5045. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Wang, D.; Li, J.; Zhou, H.; Li, L.; Li, Y. Brits: Bidirectional recurrent imputation for time series. arXiv 2018, arXiv:1805.10572. [Google Scholar]
- Suo, Q.; Yao, L.; Xun, G.; Sun, J.; Zhang, A. Recurrent Imputation for Multivariate Time Series with Missing Values. In Proceedings of the 2019 IEEE International Conference on Healthcare Informatics (ICHI), Xi’an, China, 10–13 June 2019; pp. 1–3. [Google Scholar]
- Yang, S.; Dong, M.; Wang, Y.; Xu, C. Adversarial Recurrent Time Series Imputation. IEEE Trans. Neural Netw. Learn. Syst. 2020. [Google Scholar] [CrossRef]
- Ye, F.; Liu, Z.; Liu, Q.; Wang, Z. Hydrologic Time Series Anomaly Detection Based on Flink. Math. Probl. Eng. 2020, 2020, 3187697. [Google Scholar] [CrossRef]
- Sun, J.; Lou, Y.; Ye, F. Research on anomaly pattern detection in hydrological time series. In Proceedings of the 2017 14th Web Information Systems and Applications Conference (WISA), Liuzhou, China, 11–12 November 2017; pp. 38–43. [Google Scholar]
- Sun, J.; Lou, Y.; Chen, Y. Outlier detection of hydrological time series based on ARIMA-SVR model. Comput. Digit. Eng. 2018, 2, 225–230. [Google Scholar]
- Tan, F.H.S.; Park, J.R.; Jung, K.; Lee, J.S.; Kang, D.K. Cascade of One Class Classifiers for Water Level Anomaly Detection. Electronics 2020, 9, 1012. [Google Scholar] [CrossRef]
- Qin, Y.; Lou, Y. Hydrological time series anomaly pattern detection based on isolation forest. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1706–1710. [Google Scholar]
- Shao, P.; Ye, F.; Liu, Z.; Wang, X.; Lu, M.; Mao, Y. Improving iForest for Hydrological Time Series Anomaly Detection. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, New York, NY, USA, 2–4 October 2020; pp. 170–183. [Google Scholar]
- Gao, Y.; Merz, C.; Lischeid, G.; Schneider, M. A review on missing hydrological data processing. Environ. Earth Sci. 2018, 77, 1–12. [Google Scholar] [CrossRef]
- Hamzah, F.B.; MohdHamzah, F.; Razali, S.F.M.; Jaafar, O.; AbdulJamil, N. Imputation methods for recovering streamflow observation: A methodological review. Cogent Environ. Sci. 2020, 6, 1745133. [Google Scholar] [CrossRef]
- Ren, H.; Cromwell, E.; Kravitz, B.; Chen, X. Using deep learning to fill spatio-temporal data gaps in hydrological monitoring networks. Hydrol. Earth Syst. Sci. Discuss. 2019. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Zhu, Y.; Wan, D.; Yu, Y.; Cheng, X. Research on the Data-Driven quality control method of hydrological time series data. Water 2018, 10, 1712. [Google Scholar] [CrossRef] [Green Version]
- Bae, I.; Ji, U. Outlier detection and smoothing process for water level data measured by ultrasonic sensor in stream flows. Water 2019, 11, 951. [Google Scholar] [CrossRef] [Green Version]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Graves, A.; Jaitly, N.; Mohamed, A.R. Hybrid speech recognition with deep bidirectional LSTM. In Proceedings of the 2013 IEEE Workshop on Automatic Speech Recognition and Understanding, Olomouc, Czech Republic, 8–12 December 2013; pp. 273–278. [Google Scholar]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Deep bidirectional and unidirectional LSTM recurrent neural network for network-wide traffic speed prediction. arXiv 2018, arXiv:1801.02143. [Google Scholar]
- Romphet, P.; Kajkamhaeng, S.; Chantrapornchai, C. Hand Writing Recognition Model Enhancement Exploration Based on Skipped Connections. In Proceedings of the 2020 17th International Joint Conference on Computer Science and Software Engineering (JCSSE), Bangkok, Thailand, 4–6 November 2020; pp. 122–127. [Google Scholar]
- Leigh, C.; Alsibai, O.; Hyndman, R.J.; Kandanaarachchi, S.; King, O.C.; McGree, J.M.; Neelamraju, C.; Strauss, J.; Talagala, P.D.; Turner, R.D.; et al. A framework for automated anomaly detection in high frequency water-quality data from in situ sensors. Sci. Total Environ. 2019, 664, 885–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).