4.1. Data Base Construction
The existing seven pressure–head sensors and flowrate meters installed in Quinta do Lago WDS are mainly located near the upstream storage tank, at the inlet of the network, not being widely nor adequately spread throughout the network to allow the pipe burst location based on pressure and flowrate measurements. A detailed analysis of the collected data confirmed that relevant pressure variations were not registered in these sensors, when pipe bursts occurred far from the upstream tank, it not being possible to use collected data during the occurrence of pipe bursts to train the ANN to detect leaks and ruptures This corresponds to the most common situation in real networks.
The solution to the lack of real pipe burst data is to artificially generate pipe burst scenarios using a reliable and calibrated network model. This model can be developed in EPANET, a public domain software applied to WDS modeling, and pipe burst scenarios systematically simulated with the support of any programming tool, such as the MATLAB library (as used in this research). This procedure is applied herein and the artificially generated database is composed of sets of pressure–head data at different locations during a 24–hour period, with a 10–minute interval. Simulated scenarios correspond to six burst sizes, randomly located at different network nodes, starting at different times during the 24–hour period and with a constant 4–hour duration.
The InfraQuinta network model is composed of 4448 nodes. Many of these nodes are very close to each other, corresponding to upstream/downstream nodes of open valves and containing small diameter service connections. Considering all these nodes as potential burst locations would significantly increase the search space and, consequently, the complexity of the burst location and sizing problem. In these cases, search space reduction (SSR) is recommended [
19]; this can be carried out based on simple topological analysis. Firstly, every downstream node of the service connection is eliminated from the set of potential burst locations, as its sensitivity is similar to that of the upstream node. This allows a significant reduction of the number of potential burst nodes (from 4448 to 3116 nodes). A second reduction is carried out by removing the downstream node of every valve and nodes with only two connected pipes (except nodes with the service connections). With both simplifications, the number of burst simulated scenarios to train and to test the ANN is reduced to approximately 90%, as the final number of nodes is 276, increasing the efficiency of the search method, as the number of scenarios is significantly lower, with the same expected results.
Six different single burst scenarios are simulated for each of the 276 nodes, described by the emitter law incorporated in EPANET, Q = CH
α, where C is the emitter coefficient (m
3−α/h), H is the pressure–head (m) and α is the emitter exponent. Germanopoulos [
33] has carried out an extensive study in a real WDN, calibrating the emitter exponent to α = 1.18; since then, this value has been widely used by the technical and scientific community [
34,
35,
36], the reason why it is also adopted herein. Six emitter coefficients (0.05, 0.10, 0.50, 1.0, 1.5 and 2.0) are considered for simulating mean burst sizes between approximately 0.5 and 30 L/s. Each simulated single burst scenario has a constant duration of 4 h and contains the nodal pressure–head and flow rate, with a time step of 10 min, located at one of the 3116 possible locations – these are the nodes obtained after the first SSR. Hence, 18,696 (6 × 3116) different scenarios are simulated, each one with the corresponding pressure–head and flowrate time series, burst starting time, location (represented by the X–Y Cartesian coordinates) and emitter coefficient.
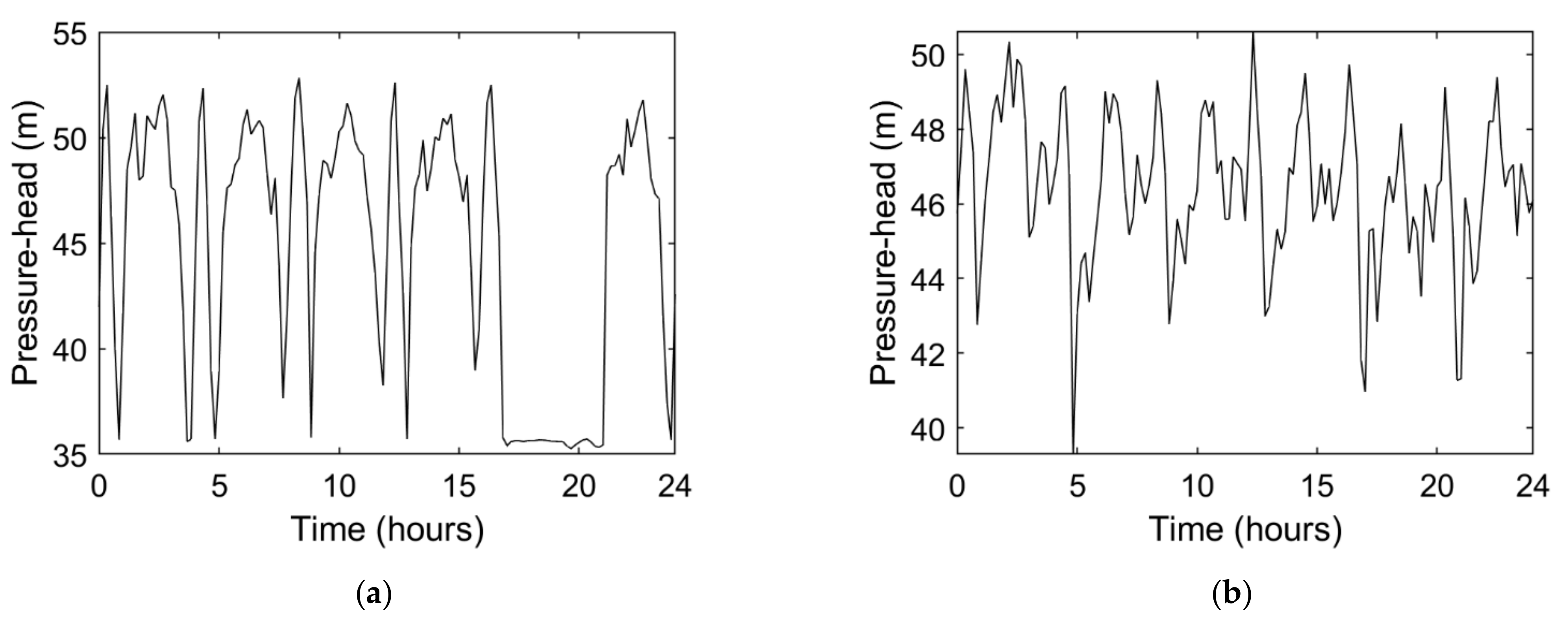
Figure 4 depicts examples of the daily pressure–head time series at two different locations for the scenario corresponding to the burst mean flowrate 25 L/s, located at node 2812, starting at 17 h. Comparing both graphs,
Figure 4a shows a clear pressure–head drop at 17 h, whereas, in
Figure 4b, the pressure–head hardly shows any variation caused by the burst (the burst effect does not reach the pressure head at the node); this is because the burst occurred closer to the former node (node 1000) than to the latter (node 2000). These graphs highlight the importance of having pressure–head sensors uniformly distributed throughout the WDS, so that bursts located at any node can be captured by, at least, one sensor. The location of these nodes (nodes 1000, 2000 and 2812) is presented in
Figure 5a.
A set of 21 pressure–head sensors (Set I), uniformly distributed throughout the network, is considered as the basis of the analysis. This set corresponds, on average, to one sensor per 3.7 km of pipes, which is considered reasonable for burst detection. The determination of the optimal number and location of pressure sensors is not in the scope of the current paper. Set I is considered, herein, the reference sensor location.
Figure 5a depicts the location of the 21 pressure sensors and of the 276 possible burst locations (after the second SSR).
At a second stage, a sensitivity analysis is carried out to assess the effect of the number of sensors and their location on the success and accuracy of burst location and quantification. Thus, a second set of sensors (Set II) is analyzed;
Figure 5b depicts the location of the Set II sensors.
The burst database used to train the ANN is composed of six bursts with 4–hour duration, located at each one of the 276 nodes, leading to a total of 1656 burst scenarios (6 sizes×276 nodes). Each scenario is characterized by 21 records of hourly–determined pressure–head over one day and the characteristics of the bursts, namely the burst location in Cartesian coordinates (X and Y), the burst size, described by the discharge coefficient C, and the burst starting time. Data series with 1 h time step are used herein, instead of 10 min as originally generated by the hydraulic simulator, in order to reduce the ANN training computational time.
4.2. Problem Formulation and ANN Architecture Definition
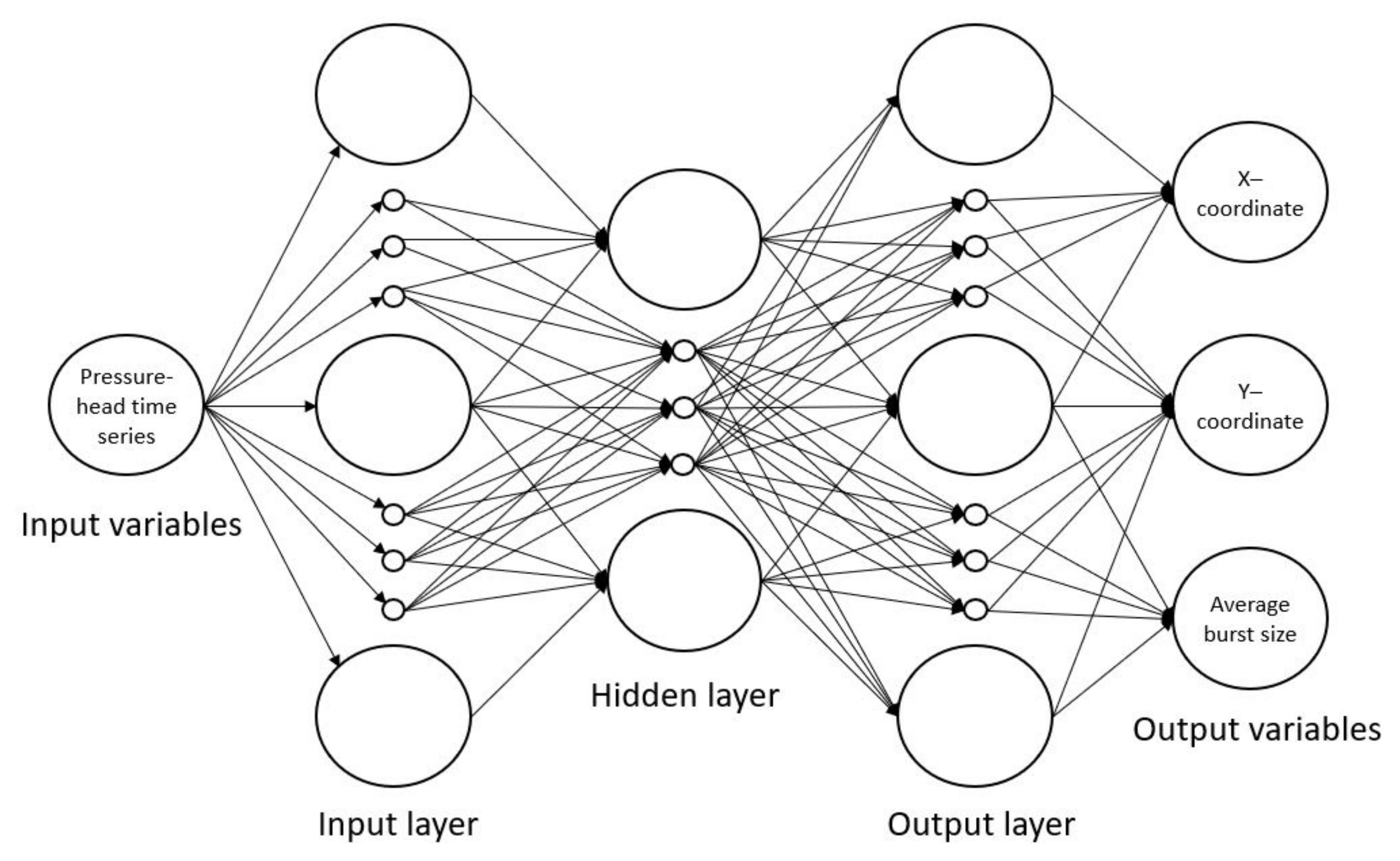
The problem formulation requires the establishment of the input and output variables of the ANN. After preliminary tests in which several combinations of variables of the ANN are analyzed, the configuration with the best results is the one in which the input variables are the pressure–head time series at the 21 sensors corresponding to Set I and the output variables are the node location described by the Cartesian X and Y coordinates and the average burst discharge.
The architecture of an ANN is defined by the input and output data, the number of hidden layers and the number of neurons at each layer. In this paper, the ANN used is of the class Multi–Layer Perceptron (MLP) with three layers, one of which is hidden. Different number of neurons for these three layers are analyzed to determine the configuration that provides the best compromise between lower errors during the training process and better results after testing, along with a reasonable computing time. This process is called herein sensitivity analysis of neurons’ number. This analysis considers different numbers of neurons, but maintains the same neuron arrangement of the following type (5k + 5, 5k, 5k + 5) with k ranging from 1 to 9.
Figure 6 represents a scheme of the ANN, emphasizing the architecture and the input and output variables.
For the ANN development, the burst scenarios are divided in two groups: one with 90% of the scenarios for training the ANN and the other with 10% for testing the ANN. It is guaranteed that every possible leak location had, at least, one of six burst scenarios being used for ANN training. This avoids a given burst location being tested, but not having been trained with any burst, which would significantly decrease the location hit percentage.
The analysis of the ANN configuration is carried out using data from 21 sensors (set I) and 1656 burst scenarios, whose results are presented in
Table 2 in terms of the statistical parameters obtained in the training process for three ANN configurations, namely the mean square error (MSE) and the correlation coefficient (R
2). These results show that as the number of neurons increases, the MSE diminishes and the R
2 increases, highlighting that the more neurons are added, the better the accuracy of the ANN achieved; however, the improvement attained from the ANN with (45, 40, 45) to the (50, 45, 50) are minimum and the computational time significantly increases, the configuration (45, 40, 45) being the one with the best compromise between time and accuracy.
A sensitivity analysis for the number of sensors in the networks is also carried out to assess the effect of the number of sensors in the final results. For this purpose, three ANN are trained with data from different groups of sensors considering Set I: 21 sensors (the reference sensor location), 14 sensors and 7 sensors, each having 1656, 1242 (3/4 of 1656) and 828 (half of 1656) burst scenarios. In terms of the ANN architecture, changing the number of sensors leads to a change in the size of input dataset. Additionally, these results are compared to the results of considering a 2nd set of sensors (Set II) with different locations to emphasize the importance of having a good sensor location uniformly distributed in the WDS.
Table 3 presents the statistical parameters, namely the mean square error (MSE) and the correlation coefficient (R
2) for the multiple ANN analyzed with the reference configuration (45, 40, 45). These results show that the decrease of the number of sensors and of the burst scenarios used to train the ANN results in the MSE increase and in the R
2 decrease, highlighting that the more sensors and the more burst scenarios are used, the better is the obtained accuracy of the ANN. Results from these analysis in the test phase are further discussed in
Section 4.3.
4.3. ANN Training and Testing and Sensitivity Analyses
4.3.1. Main Results for the Reference ANN
Results presented herein correspond to those obtained for: a three–layer ANN with (45, 40, 45) neurons in each layer, trained and tested with a database composed of 1656 burst scenarios. The input data are composed of hourly pressure–head at the 21 sensors of the Set I (reference set) and the output data are the burst size, described by the burst coefficient C, and the burst location, described by the Cartesian coordinates X and Y. This ANN is considered the reference case and is used for comparison with other results in the sensitivity analysis.
Results from the training phase have been presented in
Table 2.
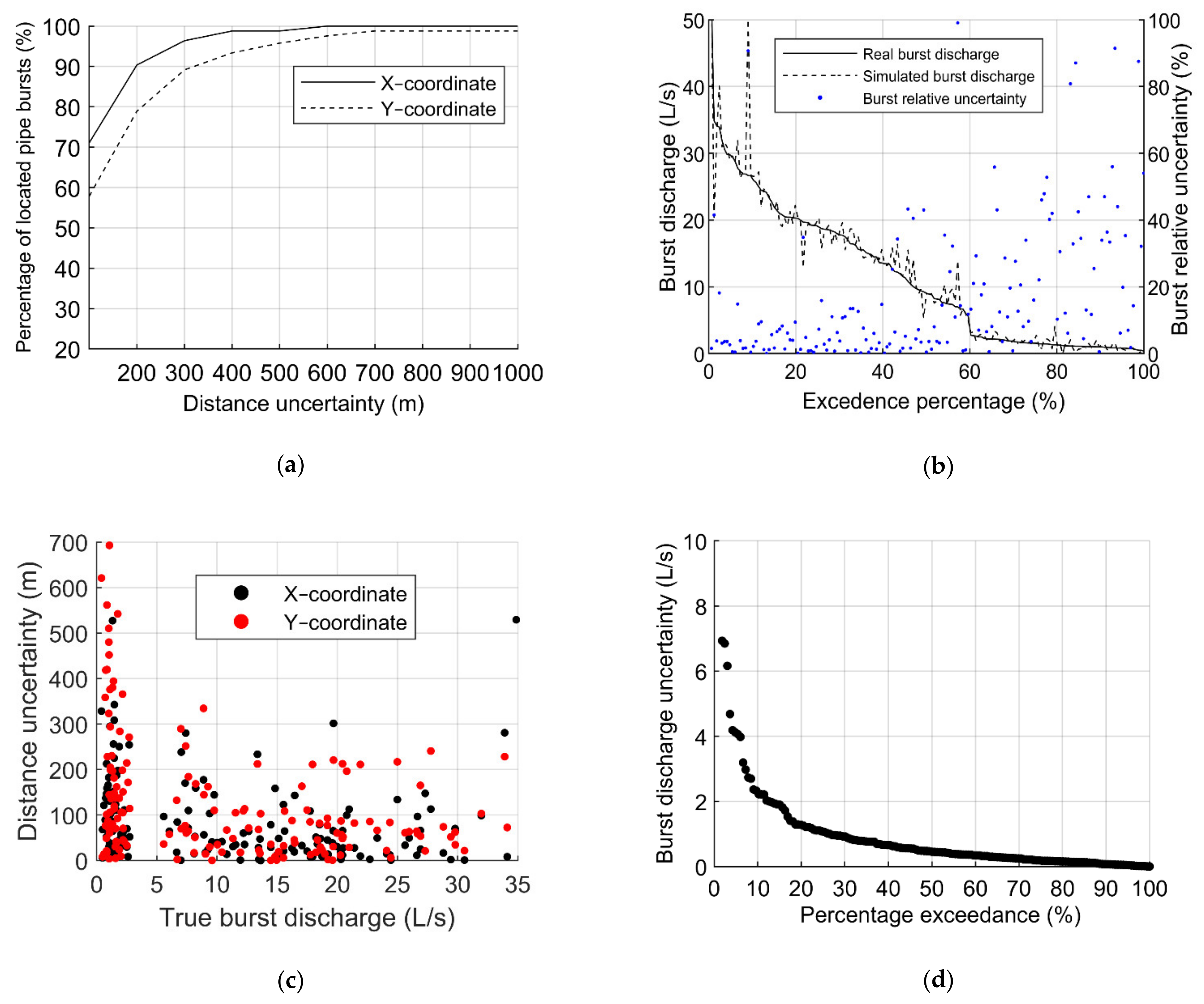
Figure 7 presents the results obtained in the testing phase, in terms of (a) the percentage of located pipe bursts regarding the distance uncertainties in X–coordinate and Y–coordinate, (b) the true burst discharge distribution and the respective estimated bursts and burst size relative uncertainty, given by the ratio between the true and the estimated burst size and the true burst size, (c) the distance uncertainty as a function of the true burst discharge, and (d) burst discharge uncertainty.
Regarding the burst location, the higher the distance uncertainty is, the higher the number of located pipe bursts becomes (
Figure 7a). The ANN locates the bursts in 98% of the cases with a maximum uncertainty of 400 m in terms of the X–coordinate and 700 m in the Y–coordinate. However, the ANN can only locate bursts in 60% and 70% of the cases, for the coordinates Y and X, respectively, with uncertainties of 100 m. This 10% difference between the hit percentage on both coordinates results from the fact that the InfraQuinta network is five times longer in the Y–direction than in the X–direction, thus, increasing the search space at the Y–coordinate, decreasing the accuracy of the results.
Concerning the burst size,
Figure 7b–d) shows that the highest burst relative uncertainties occur for smaller burst discharges: true burst discharges higher than 15 L/s have size uncertainties lower than 20%, whereas burst sizes below 2.5 L/s have relative uncertainties up to 90–100%. Additionally, for true burst discharges higher than 2.5 L/s, the ANN can successfully predict the burst location with distance uncertainties lower than 250 m (
Figure 7c), whereas for lower than 2.5 L/s burst, the distance uncertainty varies between 0 and 700 m. This shows that higher size burst are more effectively located by the ANN than the smaller bursts (as expected).
A sensitivity analysis is carried out, in the following sections, to assess the effect of the ANN configuration in terms of the number of neurons, the number of sensors, the number of burst scenarios used in the training and testing processes and the location of the sensors on the successful burst location and sizing.
4.3.2. Effect of the ANN Configuration
Different tested ANN configurations have been analyzed, namely configurations of the type (5k + 5, k, 5k + 5), with k ranging from 1 to 9. The ANN obtained for k = 7, 8, 9 corresponded to those with the highest hit percentage results. The higher the number of neurons in each layer is, the better the results are expected to be, despite increasing considerably the computational time to train the ANN. Thus, a compromise between training time and expected results must be considered.
Results from the training phase have been presented in
Table 2. The ANN configuration (50, 45, 50) presents slightly better results than those obtained for the reference configuration (45, 40, 45); however, it requires excessive time to train (ca. 1.5 days in a Ryzen R9 computed with 32MB RAM), making it impractical to apply in a daily basis in a real WDS. Its results will not be presented herein.
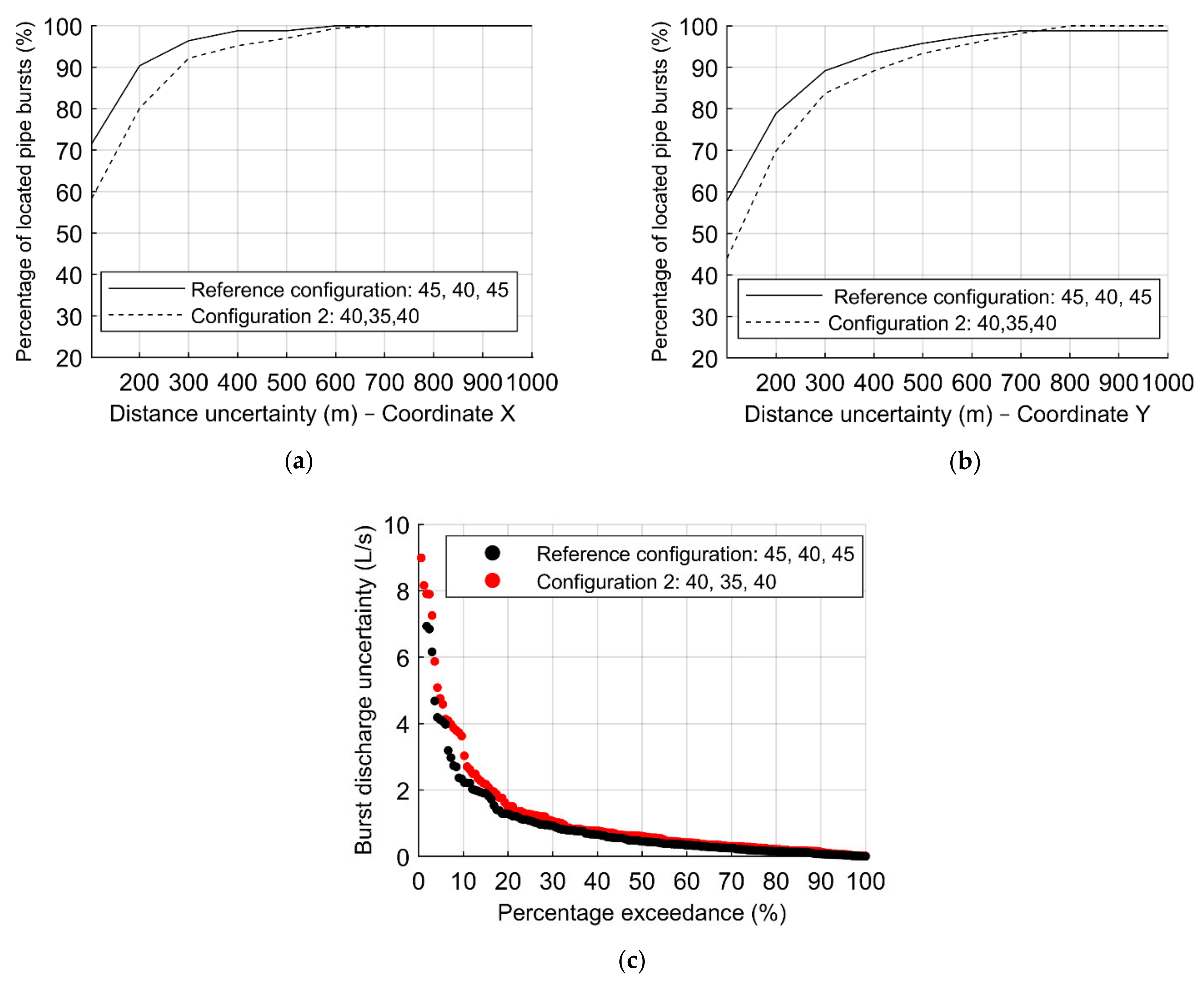
Obtained results from the testing phase of the ANN configuration (40, 35, 40) are compared with those from the reference configuration in
Figure 8, in terms of the percentage of located bursts for each distance uncertainty in X and Y directions (i.e., distance between the estimated burst location and the real one). Both ANN have been trained with the same number of burst scenarios (1656) and the same set of sensors (Set I).
Figure 8a,b depicts the distance uncertainties of the X and Y–coordinate.
Figure 8c represents the percentage exceedance associated with the absolute error in the burst discharge (i.e., the difference between the estimated size of the burst and its real size).
The results for configuration (40, 35, 40) in the prediction of the burst locations (
Figure 8a,b) are quite similar to those from configuration (45, 40, 45), with a lower hit percentage of approximately 10% for lower uncertainties. For the minimum distance uncertainty of 100 m, the hit percentage is, on average, 50%, with variations between both coordinates of 15%, being higher in the Y–coordinate.
Figure 8c presents similar burst discharge uncertainties for both configurations. Thus, despite the differences between the configuration (40, 35, 40) and the reference case being minor, the latter (45, 40, 45) provides better overall results.
4.3.3. Effect of the Number of Sensors
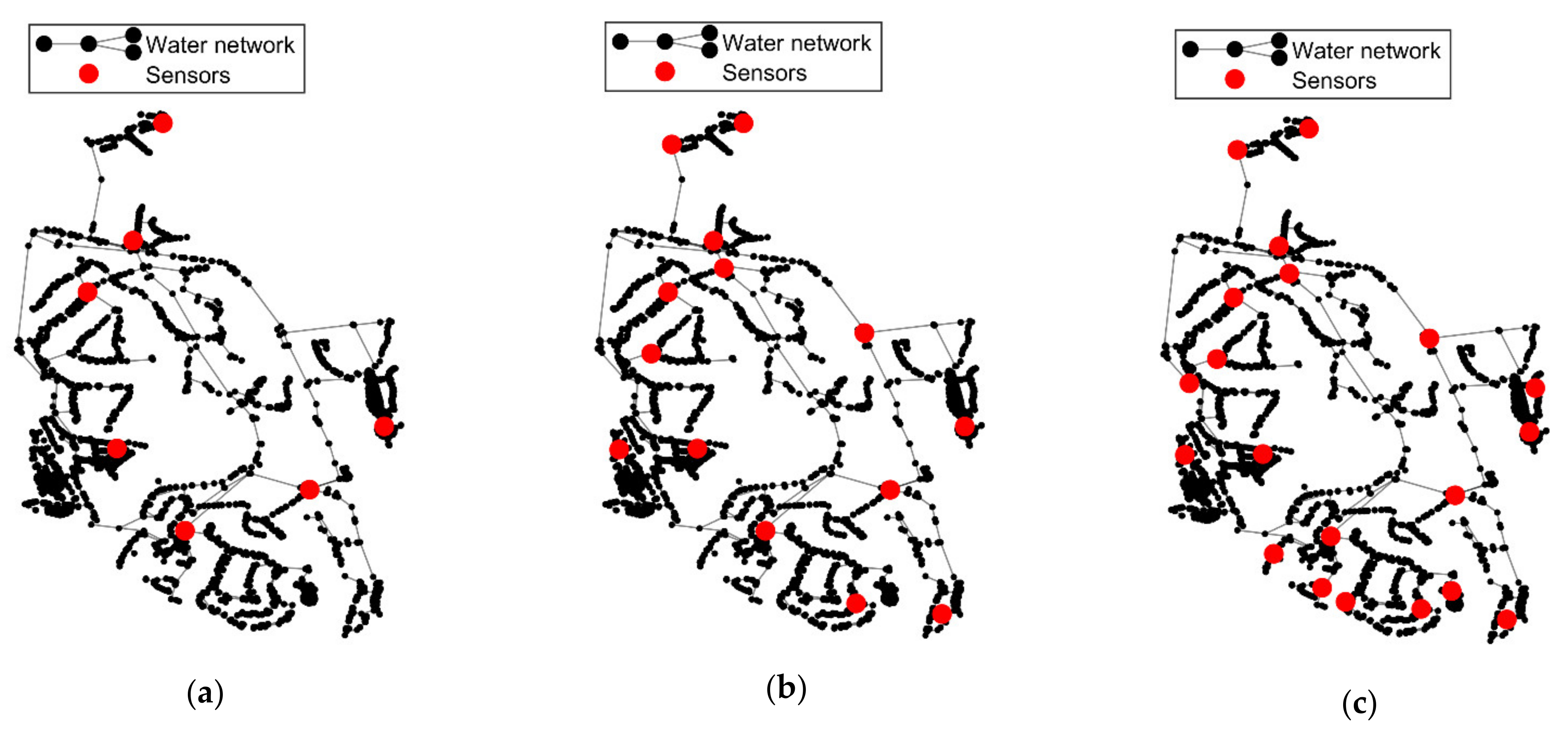
The analysis of the effect of the number of sensors on leak location is carried out herein. For this purpose, the Set I of sensors is divided into three groups comprised of 7, 14 and 21 sensors, equally distributed in the network. Once again, the reference configuration is used as a basis to carry out this analysis.
Figure 9 presents the location of the three groups of sensors in the WDS.
Results from the training phase have been presented in
Table 3.
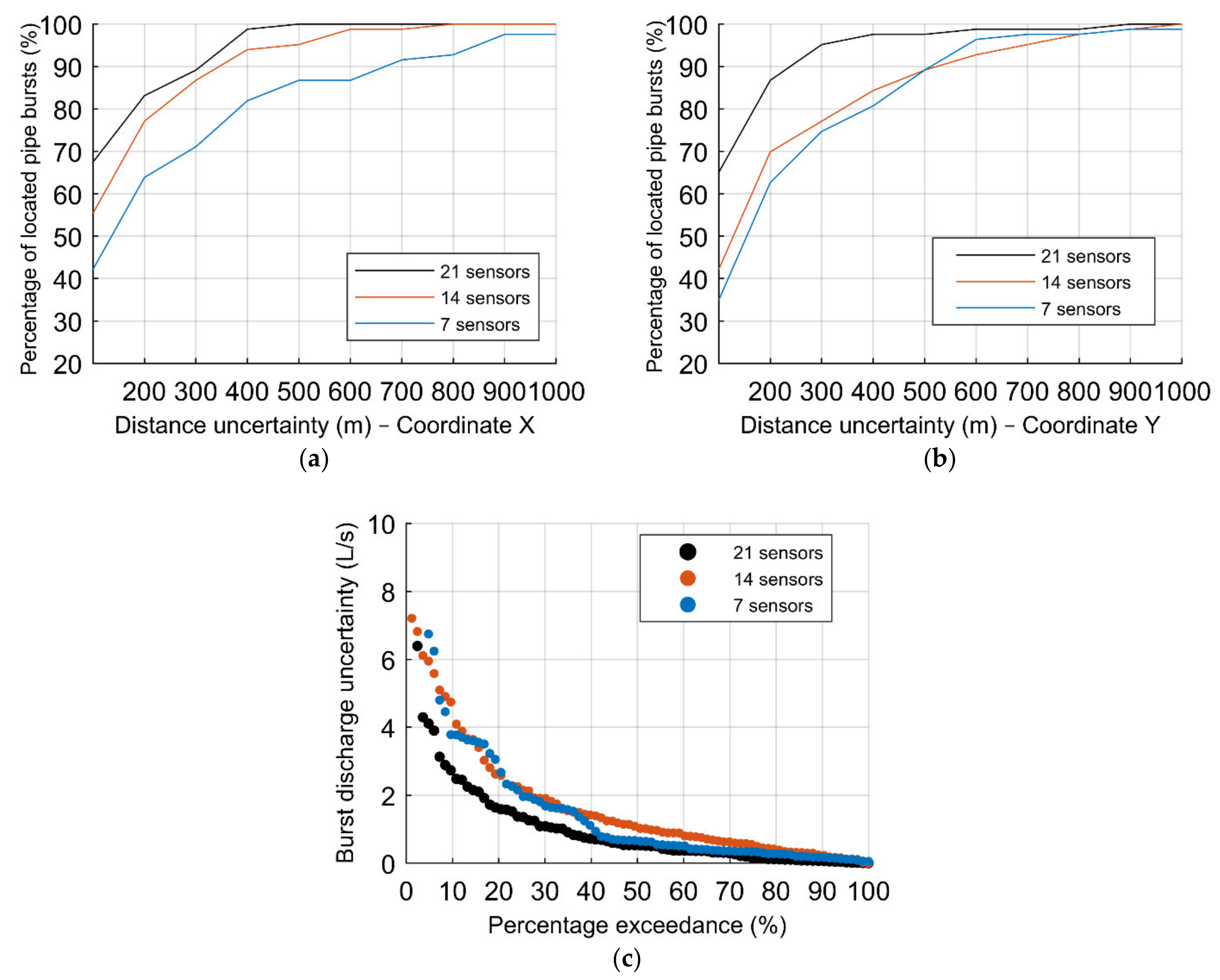
Figure 10 depicts the results from the testing phase, in terms of the percentage of located pipe bursts regarding (a,b) the distance uncertainties in the X–coordinate and Y–coordinate, comparing the hit percentage results concerning the three groups of sensors and (c) the burst discharge uncertainty distribution, for the reference ANN configuration. As observed in the training phase
Table 3, there is a noticeable reduction of the percentage of located pipe bursts, especially within the smaller distances (100–300 m), with the decreasing number of sensors considered. The same reduction applies to the burst sizing, as the 21 sensors, considered in the reference case, present fewer burst discharge uncertainties when compared to 14 and 7 sensors. This analysis demonstrates that the higher the number of sensors spread throughout the WDS is, the more successful the ANN can be in the location and quantification of pipe bursts. In the current case, the set with 21 sensors leads to the best location and sizing results.
4.3.4. Effect of the Number of Burst Scenarios Considered
A sensitivity analysis was carried out on the effect of the size of the database, that is the number of burst scenarios considered, for the reference ANN configuration and the number of sensors. For this purpose, three different burst scenarios have been analyzed (828, 1242 and 1656). Results from the training phase have been presented in
Table 3 and from the testing phase in
Figure 11 in terms of the percentage of located pipe bursts according to the (a–b) distance uncertainty of X and Y coordinates, comparing the hit percentage results concerning the three burst scenarios (828, 1242 and 1656), and the (c) percentage exceedance associated with the absolute error in the burst discharge.
The ANN trained with 90% of the 828 burst scenarios presents the best results for the location of the pipe bursts concerning the coordinate Y, for the lower distance uncertainty (
Figure 11b), contrarily to the results obtained for the coordinate X (
Figure 11a), in which it presents the least percentage of located pipe bursts. The reference burst scenario (1656) and 1242 burst scenarios present very similar results with small differences lower than 2% both in terms of pipe location and size.
The results of 828 scenario might seem contradictory, as these present the best results of located pipe bursts on the Y–coordinate. This can be explained by the scenario selection process. Since the scenario location of the bursts is carried out by a random process, selected scenarios turned out to be, by chance, quite well representative along the Y–coordinate. On the other hand, this is, as expected, the group with the higher uncertainties in locating the burst in the X–coordinate, confirming the good representativity it has along the Y–coordinate. Thus, since the WDS varies less in the X–coordinate than the Y–coordinate, the larger the database is, the better the results become (i.e., lower distance uncertainties are attained).
4.3.5. Effect of the Number of Sensors in the Burst Scenarios Considered
After assessing the effect of the number of sensors and of the number of considered scenarios on the burst location and sizing accuracy, it is necessary to carry out a sensitivity analysis on the combined effect of the number of sensors in the different burst scenarios.
Thereby,
Figure 12 presents the obtained results from the testing phase on the effect of the number of sensors in the 2nd group of scenarios, comprised of 1242 burst scenarios, with the percentage of located pipe bursts according to the distance uncertainty of the (a) X and (b) Y–coordinate, respectively, comparing the hit percentage results concerning the groups of sensors, and the (c) percentage exceedance associated with the absolute error in the burst discharge. The reference ANN configuration (21 sensors) is used for comparison.
There is a noticeable reduction regarding the percentage of located pipe bursts, especially within the smaller considered distances (100–300 m) on both coordinates, with the decreasing number of sensors considered (
Figure 12a,b). The results between considering 21 and 14 sensors are similar in locating the burst. However, as for quantifying the burst discharge, the ANN trained with data from 21 sensors presents leads to lower size uncertainties than that trained with 14 sensor data (
Figure 12c). Considering seven sensors, for the higher precision considered of 100 m, the results are approximately 25% lower than both other groups of sensors.
In addition,
Figure 13 depicts the results of the simulations to assess the effect of the number of sensors to the third group of scenarios, composed of 828 burst scenarios, with the percentage of located pipe bursts according to the distance uncertainty of the (a) X and (b) Y–coordinates, respectively, comparing the hit percentage results between the multiple groups of sensors, and the (c) percentage exceedance associated with the absolute error in the burst discharge. The reference ANN configuration is used in all three graphs.
Considering an even smaller database, there is a more evident reduction of well–located pipe bursts for the smaller groups of sensors, especially when considering higher precisions, i.e., smaller distances, for both X and Y coordinates (
Figure 13a,b). For the minimum distance of 100 m in the X coordinate, there is a reduction on the percentage of located pipe bursts of 10% and 20%, comparing to the reference group of 21 sensors with 14 and 7 sensors, respectively; considering the Y coordinate, the reduction in the percentage of located pipe bursts is 20% and 30%. The importance of the number of sensors is also visible in quantifying the burst discharge, as the reference group presents the lower burst discharge uncertainties, depicted in
Figure 13c.
Thus, smaller databases used to train the ANN need to be compensated with a large number of pressure–head sensors spread throughout the entire WDS to achieve the same results. Overall, the ANN need data to be trained: these data can be provided by fewer burst scenarios but with more measurement locations or by more burst scenarios and fewer sensors.
4.3.6. Effect of the Location of Sensors
The effect of the location of the sensors on the ANN successfully detecting bursts is assessed by comparing results obtained for the two sets of sensors, Sets I and II (see the location in
Figure 5b).
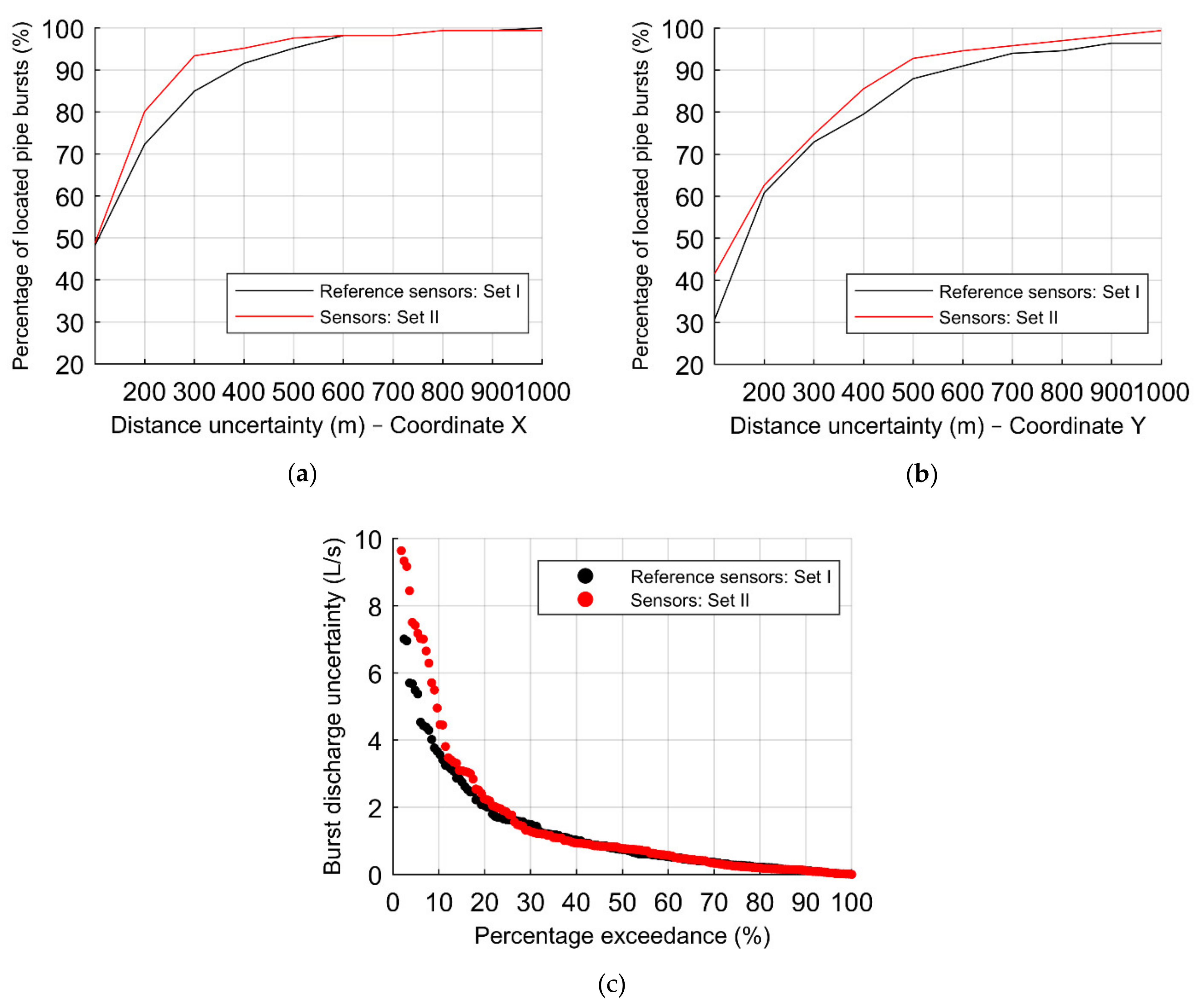
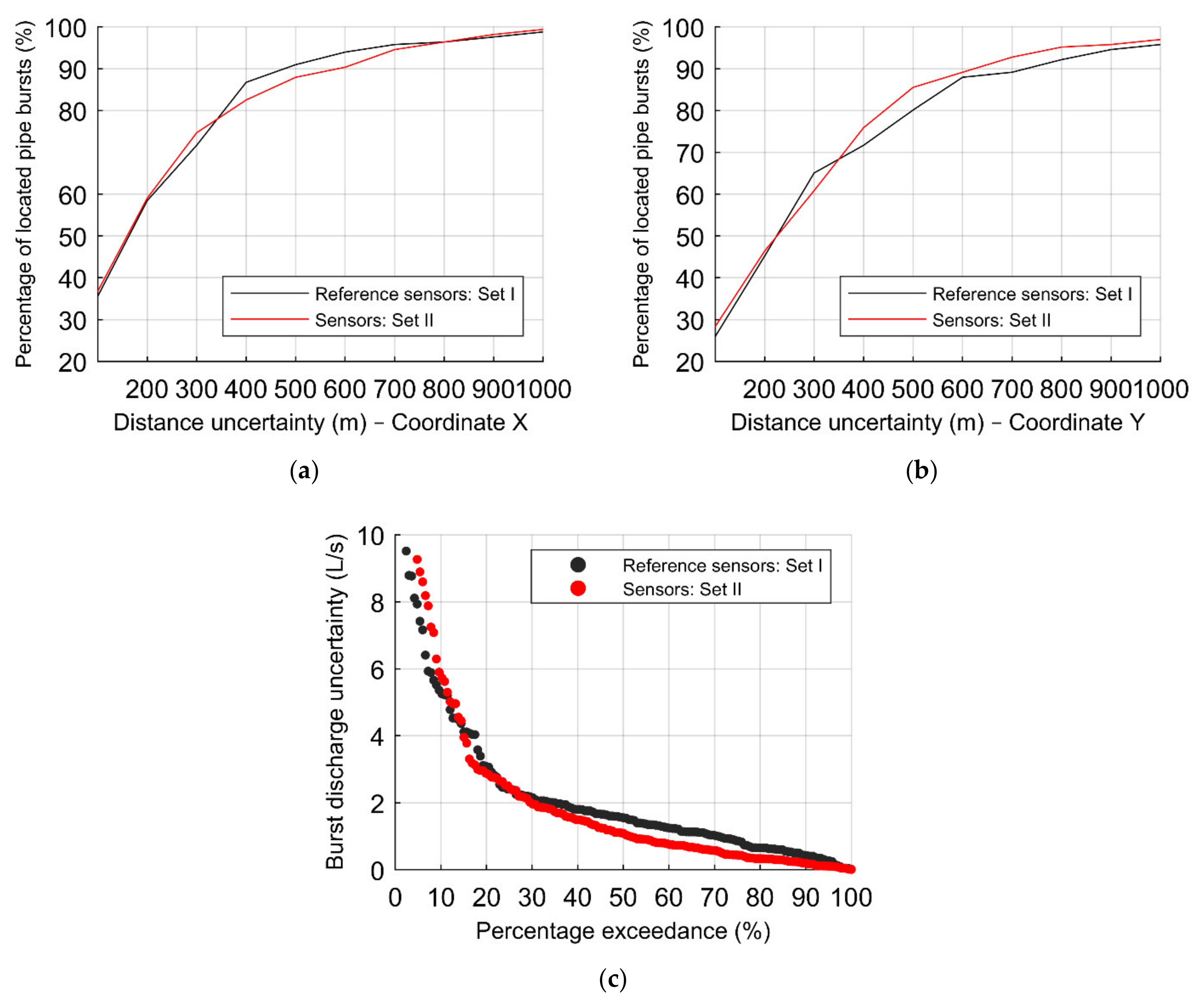
Figure 14 presents the results of both sets of sensors, each comprised of 21 sensors, considering the reference ANN configuration and 1656 burst scenarios, with the percentage of located pipe bursts according to the distance uncertainties of the (a) X–coordinate, and (b) Y–coordinate, and the (c) percentage exceedance associated with the absolute error in the burst discharge. The reference set of sensors, Set I, leads to better results in the location of the pipe bursts in both X and Y coordinates with ca. 5% and 10% higher precision than Set II (see
Figure 14a,b).
Figure 14c also shows the lower uncertainties considering the Set I, regarding the burst discharge uncertainties. These results are obtained due to the wider spread of the reference set of sensors, throughout the WDS.
Additionally, to better assess the effect of considering a different set of sensors, simulations are also carried out for 14 sensors.
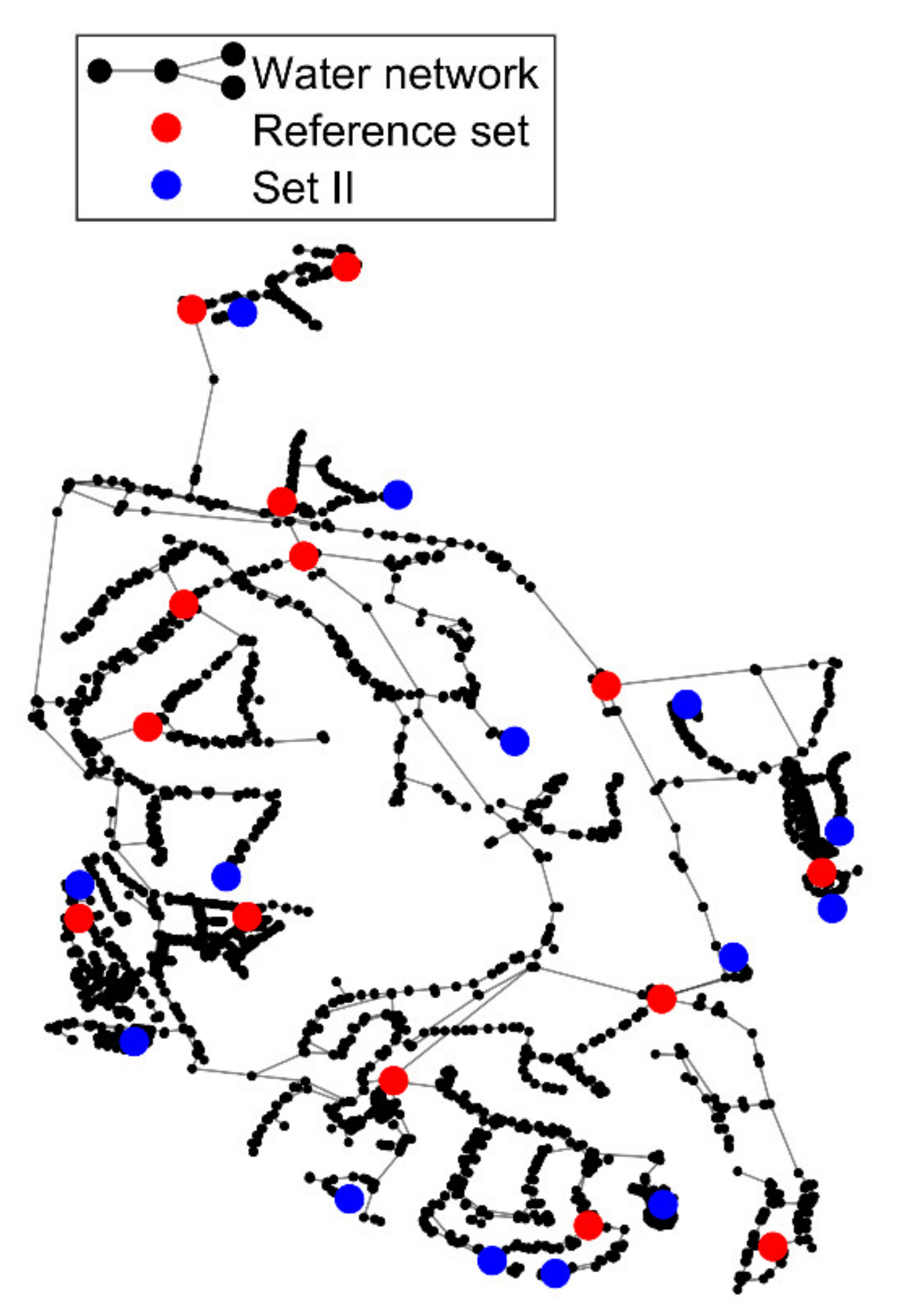
Figure 15 depicts the percentage of located pipe bursts according to the distance uncertainties of the (a) X–coordinate, and (b) Y–coordinate, as well as the (c) percentage exceedance associated with the absolute error in the burst discharge. See the location of these sets in
Figure 16. These results show that, when considering 14 sensors, ANN trained with Set II is more sensible to burst locations. The percentage of located pipe bursts, for Set II, is higher both for the X and the Y–coordinates (see
Figure 15a,b). This higher sensitivity to locate the pipe bursts is explained by the location of the 14 sensors; in fact, the 14 sensors of Set II are located at the downstream sections of the WDS (more sensible nodes), whereas the 14 sensors of the reference set are mostly located in intermediate nodes of the water network. Both sets present approximately the same burst discharge uncertainty for 90% of the considered pipe burst scenarios.
Figure 16 presents the location of the 14 sensors of both sets, with the reference set (Set I) depicted in red and the Set II in blue.
To conclude the assessment of the effect of considering a different set of sensors, the same analysis is carried out for 7 sensors.
Figure 17 depicts the results of both sets, considering the reference configuration and the 1st group of scenarios, composed of 1656 burst scenarios, with the percentage of located pipe bursts according to the distance uncertainties of the (a) X–coordinate, and (b) Y–coordinate, and the (c) percentage exceedance associated with the absolute error in the burst discharge.
Both sets present identical percentages of detected pipe bursts according to X and Y coordinates (see
Figure 17a,b). Considering 7 sensors, the different location of the sensors seems to become less relevant in comparison with previous cases (14 or 21 sensors), in which there is a clear uniform difference regarding the percentages of located pipe bursts. However, to quantify the size of the burst, the Set II presents better overall results, with lower uncertainties for approximately 85% of the total scenarios. The accuracy of the ANN to estimate the size and location of pipe bursts is highly sensitive to the location (and number) of the sensors. Thus, for future applications, an optimization regarding the location and number of the sensors should be carried out, complementary to this study.