The Influence of Drying-Wetting Cycles on the Suction Stress of Compacted Loess and the Associated Microscopic Mechanism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Drying-Wetting Cycles
2.4. Microstructural Investigation
2.4.1. NMR Test
2.4.2. SEM Test
2.5. SWCC Test
3. Results and Discussion
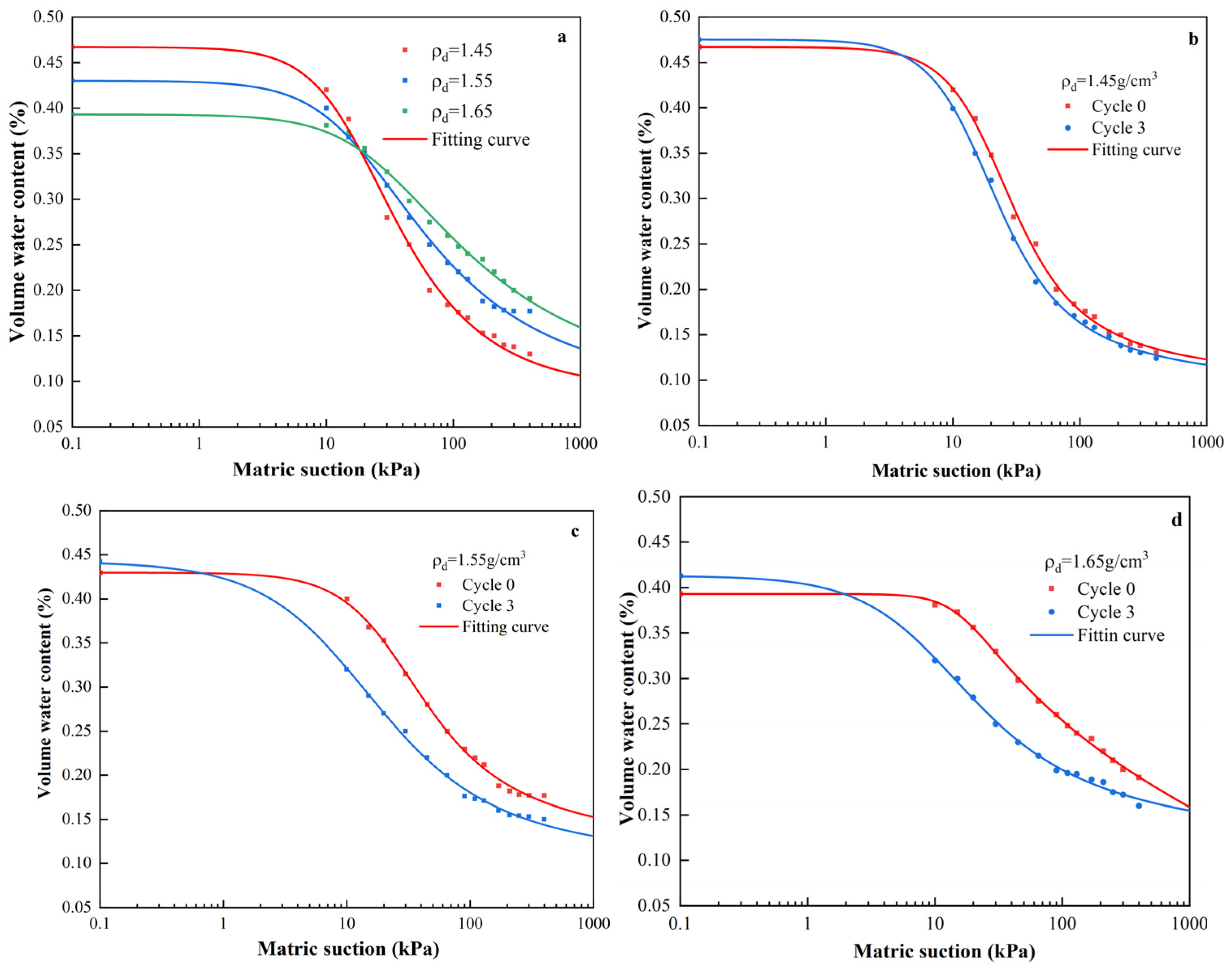
3.1. SWCC
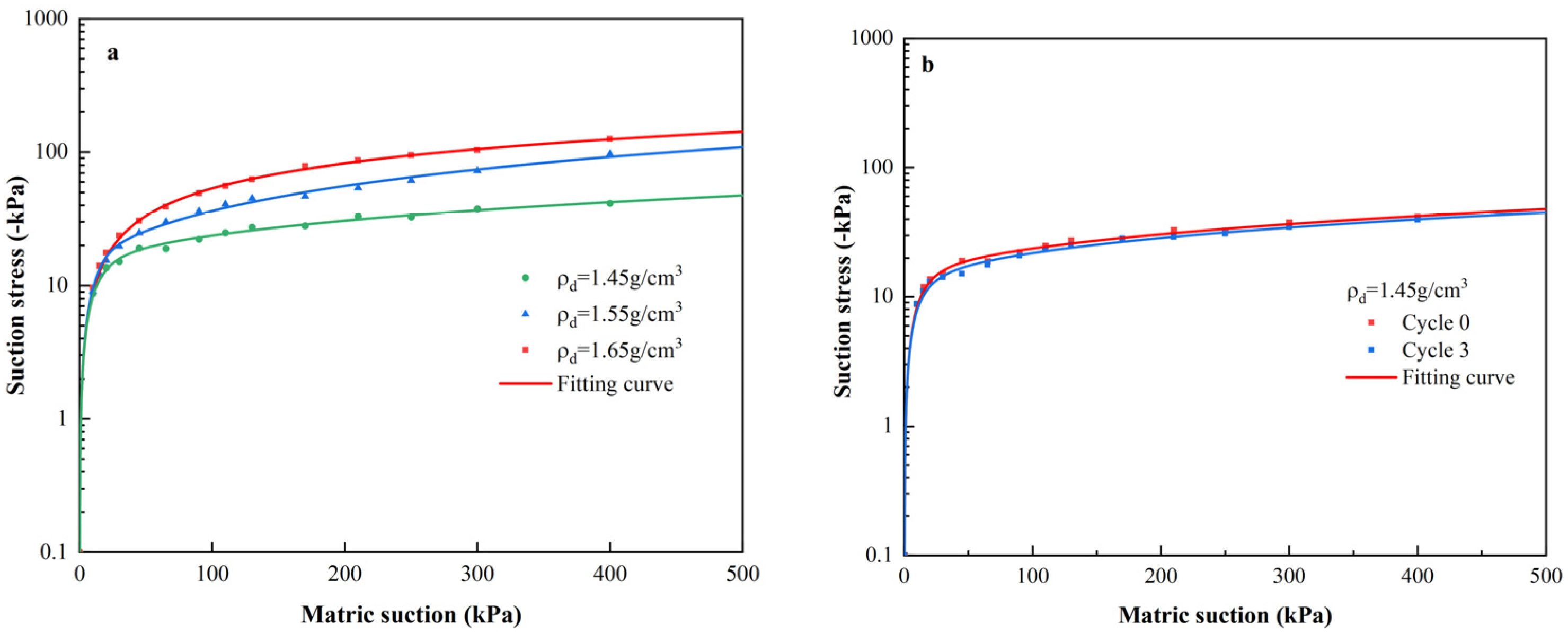
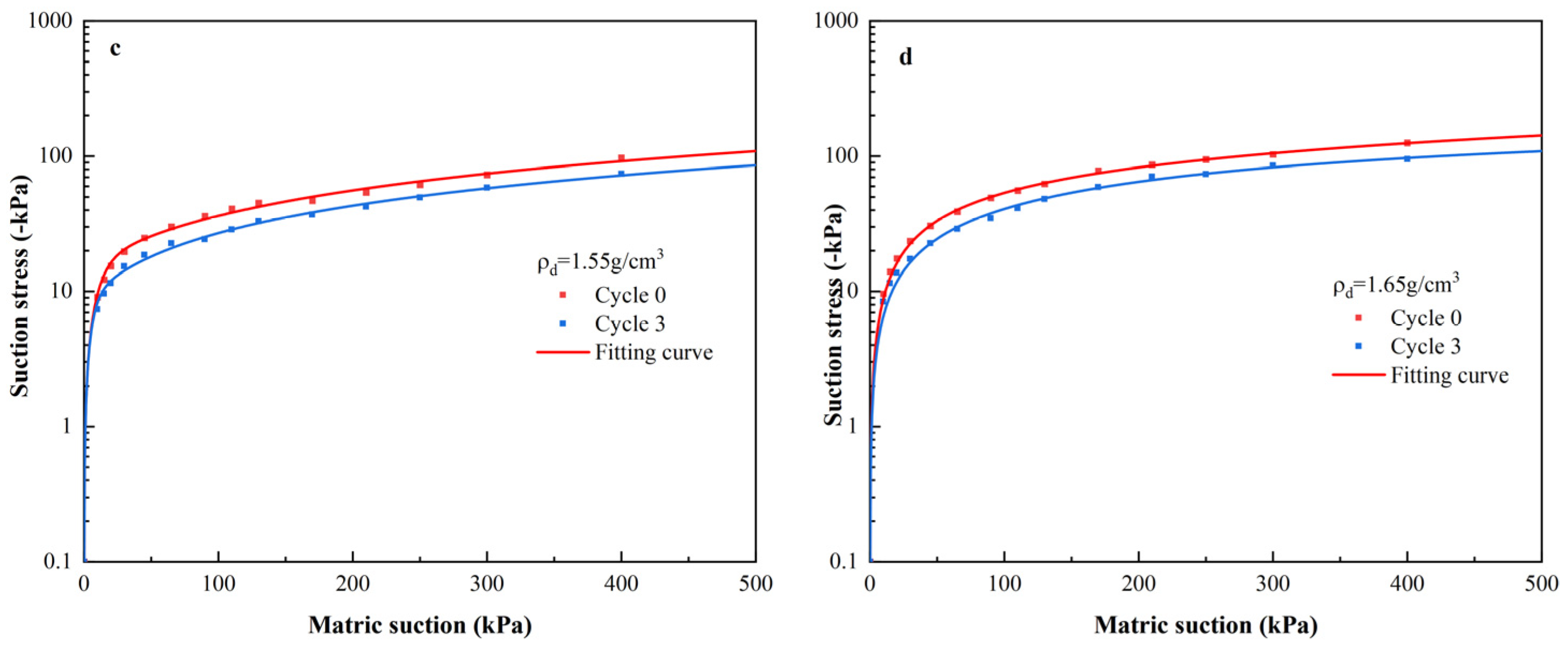
3.2. SSCC
3.3. Microscopic Analysis of Changes in the Suction Stress of Compacted Loess Samples
3.3.1. SEM Observations
3.3.2. NMR Analysis
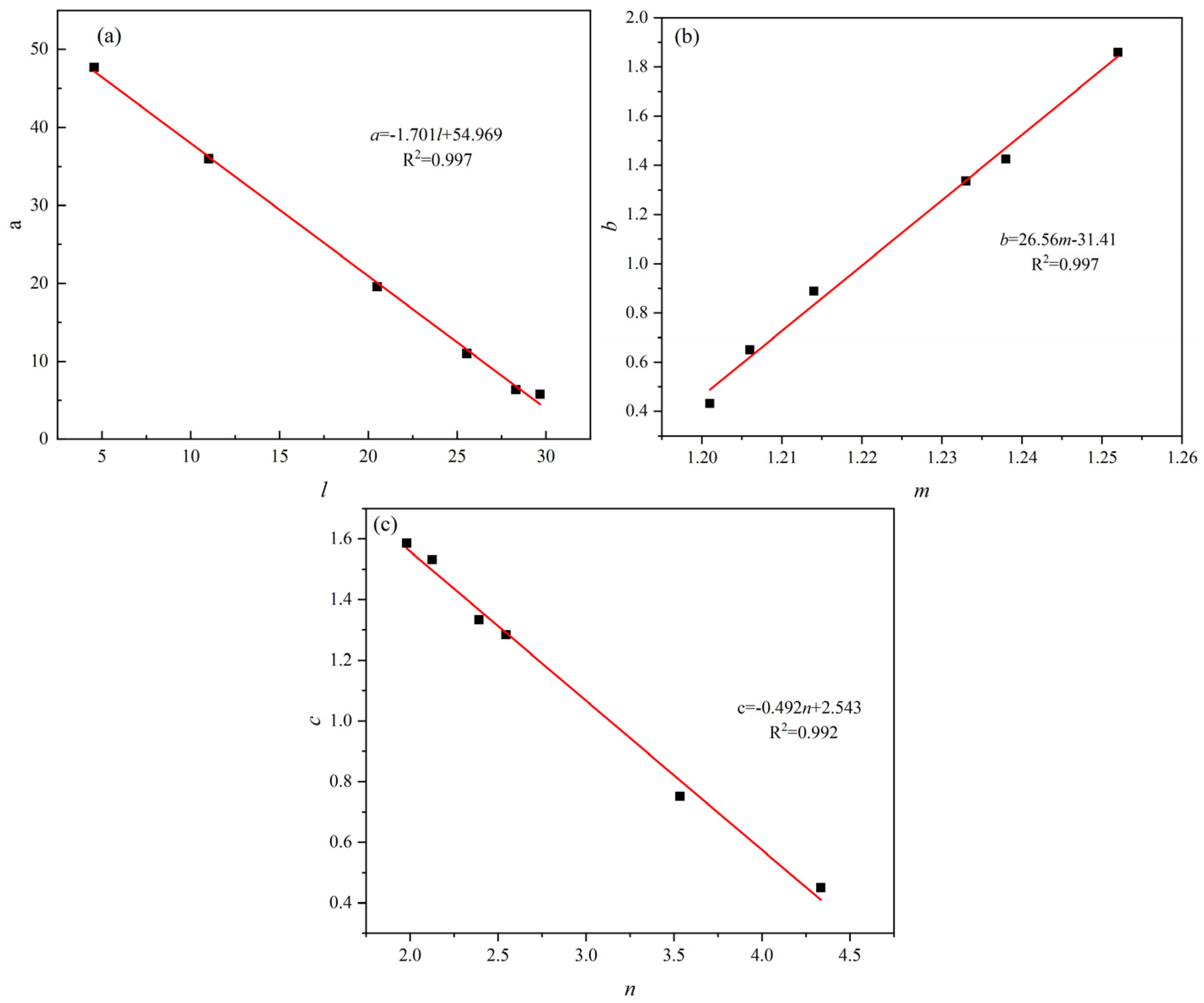
3.4. Suction Stress Calculation Model Based on PSD Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, J.; Wang, G.; Wang, Q.; Zhang, F. Shear wave velocity imaging of landslide debris deposited on an erodible bed and possible movement mechanism for a loess landslide in Jingyang, Xi’an, China. Landslides 2017, 14, 1503–1512. [Google Scholar] [CrossRef]
- Peng, J.; Qi, S.; Williams, A.; Dijkstra, T.A. Preface to the special issue on “Loess engineering properties and loess geohazards”. Eng. Geol. 2018, 236, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Derbyshire, E. Landslides in the Thick Loess Terrain of North-West China; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Feng, S.; Du, F.; Shi, Z.; Shui, W.; Tan, K. Field study on the reinforcement of collapsible loess using dynamic compaction. Eng. Geol. 2015, 185, 105–115. [Google Scholar] [CrossRef]
- Luo, H.; Wu, F.; Chang, J.; Xu, J. Microstructural constraints on geotechnical properties of Malan Loess: A case study from Zhaojiaan landslide in Shaanxi province, China. Eng. Geol. 2017, 236, 60–69. [Google Scholar] [CrossRef]
- Ni, W.; Yuan, K.; Lu, X.; Yuan, Z. Comparison and quantitative analysis of microstructure parameters between original loess and remoulded loess under different wetting-drying cycles. Sci. Rep. 2020, 10. [Google Scholar] [CrossRef]
- Qin, P.; Liu, Y.; Song, Z.; Ma, F.; Wang, Y.; Zhang, X.; Miao, C.; Dong, X. An Electrical Resistivity Method of Characterizing Hydromechanical and Structural Properties of Compacted Loess During Constant Rate of Strain Compression. Sensors 2020, 20, 4783. [Google Scholar] [CrossRef]
- Kong, L.; Sayem, H.M.; Tian, H. Influence of drying–wetting cycles on soil-water characteristic curve of undisturbed granite residual soils and microstructure mechanism by nuclear magnetic resonance (NMR) spin-spin relaxation time (T2) relaxometry. Can. Geotech. J. 2017, 55, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Wang, F.; Ma, W.; Fortier, R.; Mu, Y.; Mao, Y.; Hou, X. Variations in strength and deformation of compacted loess exposed to wetting-drying and freeze-thaw cycles. Cold Reg. Sci. Technol. 2018, 151, 159–167. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, C.; Loureno, S.D.N.; Dong, S.; Jiang, Y. Factors affecting the soil–water retention curve of Chinese loess. Bull. Eng. Geol. Environ. 2020. [Google Scholar] [CrossRef]
- Schnellmann, R.; Busslinger, M.; Schneider, H.R.; Rahardjo, H. Effect of rising water table in an unsaturated slope. Eng. Geol. 2010, 114, 71–83. [Google Scholar] [CrossRef]
- Lourenço, S.D.N.; Wang, G.H.; Kamai, T. Processes in model slopes made of mixtures of wettable and water repellent sand: Implications for the initiation of debris flows in dry slopes. Eng. Geol. 2015, 196, 47–58. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Collins, B.D.; Znidarcic, D. Stability Analyses of Rainfall Induced Landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some Aspects of Effective Stress in Saturated and Partly Saturated Soils. Géotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R. Stress state variables for unsaturated soils. J. Geotech. Eng. Div. 1978, 103. [Google Scholar]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Khalili, N.; Khabbaz, M.H. A unique relationship for χ for the determination of the shear strength of unsaturated soils. Géotechnique 2015, 52, 477–478. [Google Scholar] [CrossRef]
- Bishop, A.W. The Principle of Effective Stress. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- Ning, L.; Likos, W.J. Suction Stress Characteristic Curve for Unsaturated Soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.S.; Hwang, W.K.; Jung, S.J.; Kim, T.H. A comparative study of suction stress between sand and silt under unsaturated conditions. Eng. Geol. 2012. [Google Scholar] [CrossRef]
- Song, Y.S. Suction stress in unsaturated sand at different relative densities. Eng. Geol. 2014, 176, 1–10. [Google Scholar] [CrossRef]
- Oh, S.; Lu, N.; Yun, K.K.; Lee, S.J.; Lee, S.R. Relationship between the Soil-Water Characteristic Curve and the Suction Stress Characteristic Curve: Experimental Evidence from Residual Soils. J. Geotech. Geoenviron. Eng. 2012, 138, 47–57. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.; Ning, L.; Kim, T.K.; Lee, Y.H. Experimental Validation of Suction Stress Characteristic Curve from Nonfailure Triaxial K0 Consolidation Tests. J. Geotech. Geoenviron. Eng. 2013, 139, 1490–1503. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, W.; Wang, G.; Sun, G.; Zhang, F. Influence of initial dry density and water content on the soil–water characteristic curve and suction stress of a reconstituted loess soil. Bull. Eng. Geol. Environ. 2016, 76. [Google Scholar] [CrossRef]
- Song, Y.S.; Hong, S. Effect of clay minerals on the suction stress of unsaturated soils. Eng. Geol. 2020, 269, 105571. [Google Scholar] [CrossRef]
- ASTM. Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2006. [Google Scholar]
- Al-Homoud, A.S.; Basma, A.A.; Husein Malkawi, A.I.; Al Bashabsheh, M.A. Cyclic Swelling Behavior of Clays. J. Geotech. Eng. 1995, 121, 562–565. [Google Scholar] [CrossRef]
- Liu, T.C. Desiccation and cracking behaviour of clay layer from slurry state under wetting–drying cycles. Geoderma 2011. [Google Scholar] [CrossRef] [Green Version]
- Tian, H.; Wei, C.; Wei, H.; Yan, R.; Pan, C. An NMR-Based Analysis of Soil–Water Characteristics. Appl. Magn. Reson. 2014, 45, 49–61. [Google Scholar] [CrossRef]
- Kleinberg, R.L. Deep sea NMR: Methane hydrate growth habit in porous media and its relationship to hydraulic permeability, deposit accumulation, and submarine slope stability. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- ASTM. Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Leong, E.C.; Rahardjo, H. Review of Soil-Water Characteristic Curve Equations. J. Geotech. Geoenviron. Eng. 1997, 123, 1106–1117. [Google Scholar] [CrossRef] [Green Version]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Gallage, C.; Uchimura, T. Effects of dry density and grain size distribution on soil-water characteristic curves of sandy soils. Soils Found. 2010, 50, 161–172. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Q.; Rahardjo, H. Determination of soil–water characteristic curve variables. Comput. Geotech. 2012, 42, 37–43. [Google Scholar] [CrossRef]
- Xie, X.; Li, P.; Hou, X.; Li, T.; Zhang, G. Microstructure of Compacted Loess and Its Influence on the Soil-Water Characteristic Curve. Adv. Mater. Sci. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Burger, C.A.; Shackelford, C.D. Evaluating dual porosity of pelletized diatomaceous earth using bimodal soil-water characteristic curve functions. Can. Geotech. J. 2001, 38, 53–66. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Ning, L.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Azizi, A.; Musso, G.; Jommi, C. Effects of repeated hydraulic loads on microstructure and hydraulic behaviour of a compacted clayey silt. Can. Geotech. J. 2019. [Google Scholar] [CrossRef]
- Yao, Z.; Zaiqiang, H.; Lei, L.; Zahijia, X. Improving the structure and mechanical properties of loess by acid solutions—An experimental study. Eng. Geol. 2018, 244, 132–145. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Mu, Q.Y.; Zhou, C. Effects of specimen preparation method on the volume change of clay under cyclic thermal loads. Geotechnique 2019, 69, 146–150. [Google Scholar] [CrossRef]
- Delage, P.; Audiguier, M.; Cui, Y.J.; Howat, M.D. Microstructure of a compacted silt. Can. Geotech. J. 1996, 33, 150–158. [Google Scholar] [CrossRef]
- Hu, C.; Yuan, Y.; Mei, Y.; Wang, X.; Liu, Z. Comprehensive strength deterioration model of compacted loess exposed to drying-wetting cycles. Bull. Eng. Geol. Environ. 2020, 79, 383–398. [Google Scholar] [CrossRef]
- Day and Robert, W. Swell-Shrink Behavior of Compacted Clay. J. Geotech. Eng. 1994, 120, 618–623. [Google Scholar] [CrossRef]
- Baker, R.; Frydman, S. Unsaturated soil mechanics Critical review of physical foundations. Eng. Geol. 2009, 106, 26–39. [Google Scholar] [CrossRef]
- Washburn, E.W. Note on a Method of Determining the Distribution of Pore Sizes in a Porous Material. Proc. Natl. Acad. Sci. USA 1921, 7, 115–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, P.; Li, T.; Vanapalli, S.K. Prediction of soil–water characteristic curve for Malan loess in Loess Plateau of China. J. Cent. South Univ. 2018, 25, 432–447. [Google Scholar] [CrossRef]


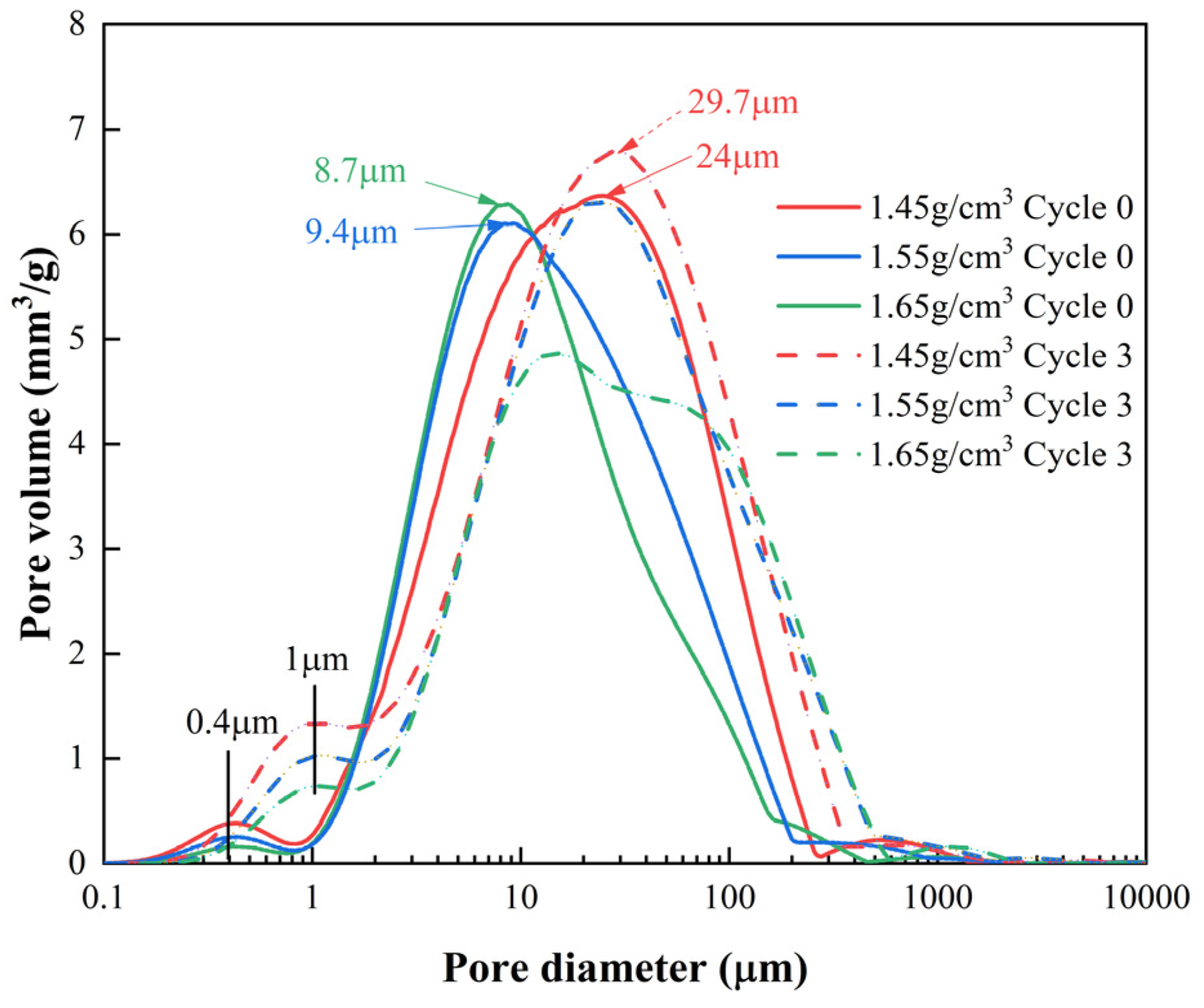
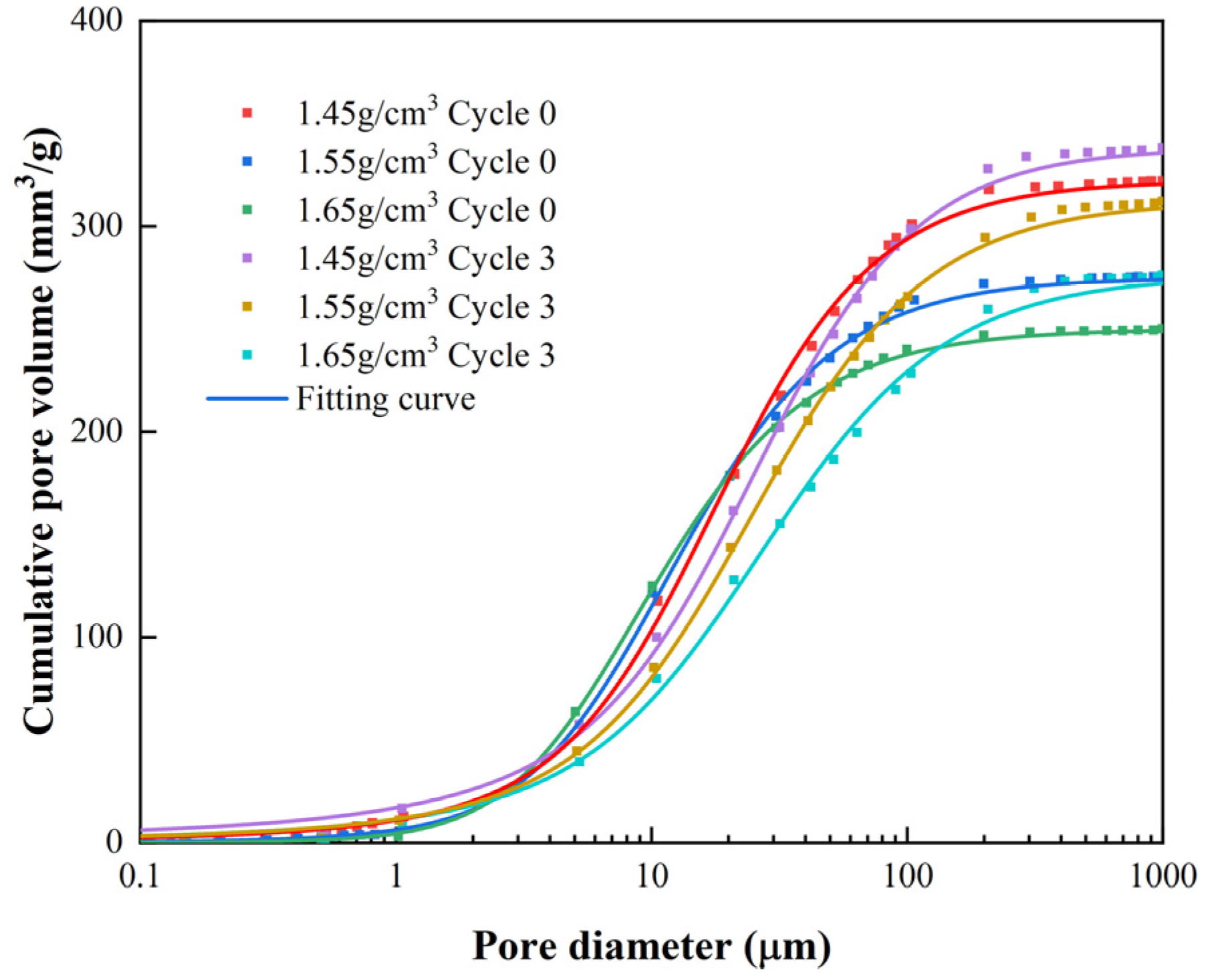

| Maximum Dry Density (g/cm3) | Optimal Water Content (%) | Specific Gravity | Liquid Limit (%) | Plastic Limit (%) | Grain Size Fractions (%) | ||
|---|---|---|---|---|---|---|---|
| <0.005 mm | 0.005–0.075 mm | >0.075 mm | |||||
| 1.69 | 14.11 | 2.72 | 28.9 | 16.1 | 9.96 | 82.22 | 7.82 |
| The Sample | a | b | c | AEV (kPa) | R2 |
|---|---|---|---|---|---|
| 1.45 Cycle 0 | 17.996 | 1.911 | 1.105 | 6.59 | 0.998 |
| 1.45 Cycle 3 | 13.578 | 1.843 | 1.214 | 5.66 | 0.998 |
| 1.55 Cycle 0 | 18.937 | 1.601 | 0.888 | 14.8 | 0.998 |
| 1.55 Cycle 3 | 8.724 | 1.016 | 1.404 | 5.89 | 0.997 |
| 1.65 Cycle 0 | 26.08 | 1.684 | 0.715 | 17.01 | 0.999 |
| 1.65 Cycle 3 | 7.406 | 1.202 | 0.957 | 6.04 | 0.998 |
| The Sample | a | b | c | R2 |
|---|---|---|---|---|
| 1.45 Cycle 0 | 19.564 | 1.425 | 1.532 | 0.991 |
| 1.45 Cycle 3 | 5.771 | 1.337 | 1.585 | 0.991 |
| 1.55 Cycle 0 | 35.971 | 1.859 | 0.752 | 0.989 |
| 1.55 Cycle 3 | 11.007 | 0.651 | 1.333 | 0.996 |
| 1.65 Cycle 0 | 47.719 | 0.889 | 0.45 | 0.998 |
| 1.65 Cycle 3 | 6.36 | 0.432 | 1.284 | 0.995 |
| The Sample | l | m | n | R2 |
|---|---|---|---|---|
| 1.45 Cycle 0 | 20.499 | 1.238 | 2.126 | 0.999 |
| 1.45 Cycle 3 | 29.667 | 1.233 | 1.981 | 0.998 |
| 1.55 Cycle 0 | 11.007 | 1.252 | 3.534 | 0.999 |
| 1.55 Cycle 3 | 25.541 | 1.206 | 2.392 | 0.998 |
| 1.65 Cycle 0 | 4.561 | 1.214 | 4.334 | 0.999 |
| 1.65 Cycle 3 | 28.31 | 1.201 | 2.545 | 0.997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Ni, W.; Li, X.; Wang, H.; Yuan, K.; Guo, Y.; Tuo, W. The Influence of Drying-Wetting Cycles on the Suction Stress of Compacted Loess and the Associated Microscopic Mechanism. Water 2021, 13, 1809. https://doi.org/10.3390/w13131809
Nie Y, Ni W, Li X, Wang H, Yuan K, Guo Y, Tuo W. The Influence of Drying-Wetting Cycles on the Suction Stress of Compacted Loess and the Associated Microscopic Mechanism. Water. 2021; 13(13):1809. https://doi.org/10.3390/w13131809
Chicago/Turabian StyleNie, Yongpeng, Wankui Ni, Xiangning Li, Haiman Wang, Kangze Yuan, Yexia Guo, and Wenxin Tuo. 2021. "The Influence of Drying-Wetting Cycles on the Suction Stress of Compacted Loess and the Associated Microscopic Mechanism" Water 13, no. 13: 1809. https://doi.org/10.3390/w13131809
APA StyleNie, Y., Ni, W., Li, X., Wang, H., Yuan, K., Guo, Y., & Tuo, W. (2021). The Influence of Drying-Wetting Cycles on the Suction Stress of Compacted Loess and the Associated Microscopic Mechanism. Water, 13(13), 1809. https://doi.org/10.3390/w13131809





