“One Out–All Out” Principle in the Water Framework Directive 2000—A New Approach with Fuzzy Method on an Example of Greek Lakes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Biological Assessment Methods
- (a)
- OOAO: the lowest EQR of BQEs was attributed for the whole waterbody;
- (b)
- average: the arithmetic average of the EQRs for all BQEs was calculated and rounded to the nearest class; and
- (c)
- median: the median of EQRs for all BQEs was calculated and rounded to the nearest class.
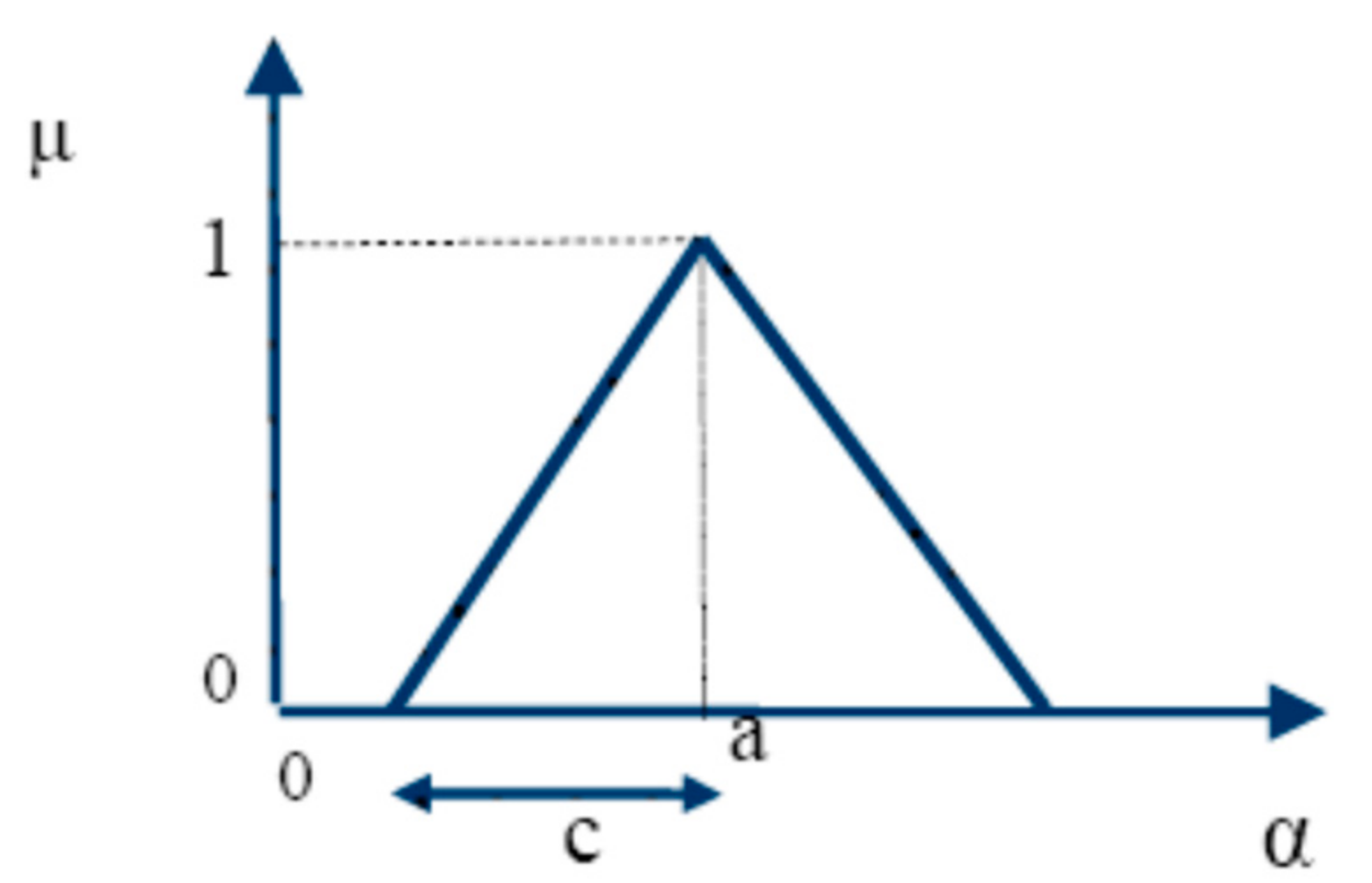
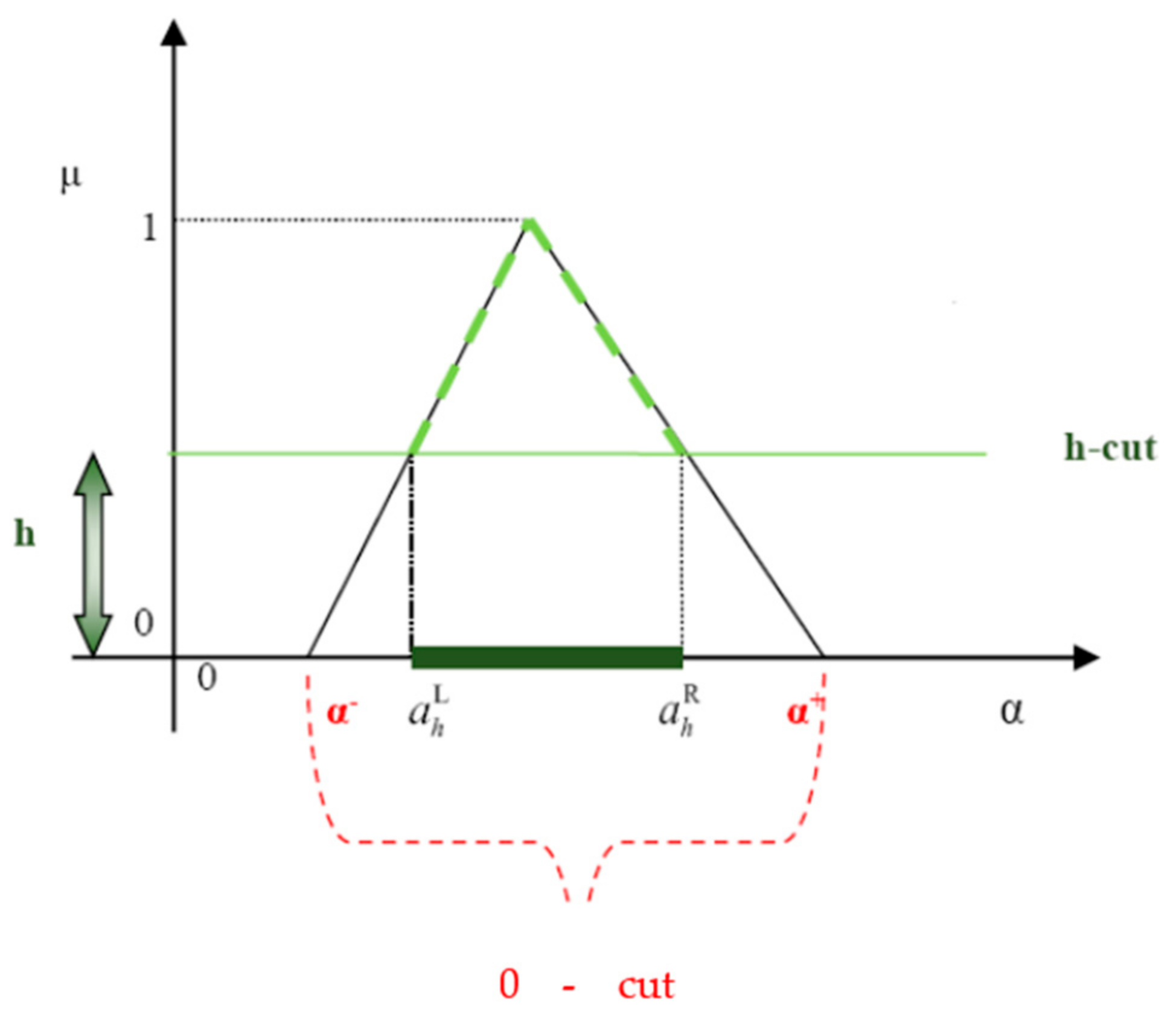
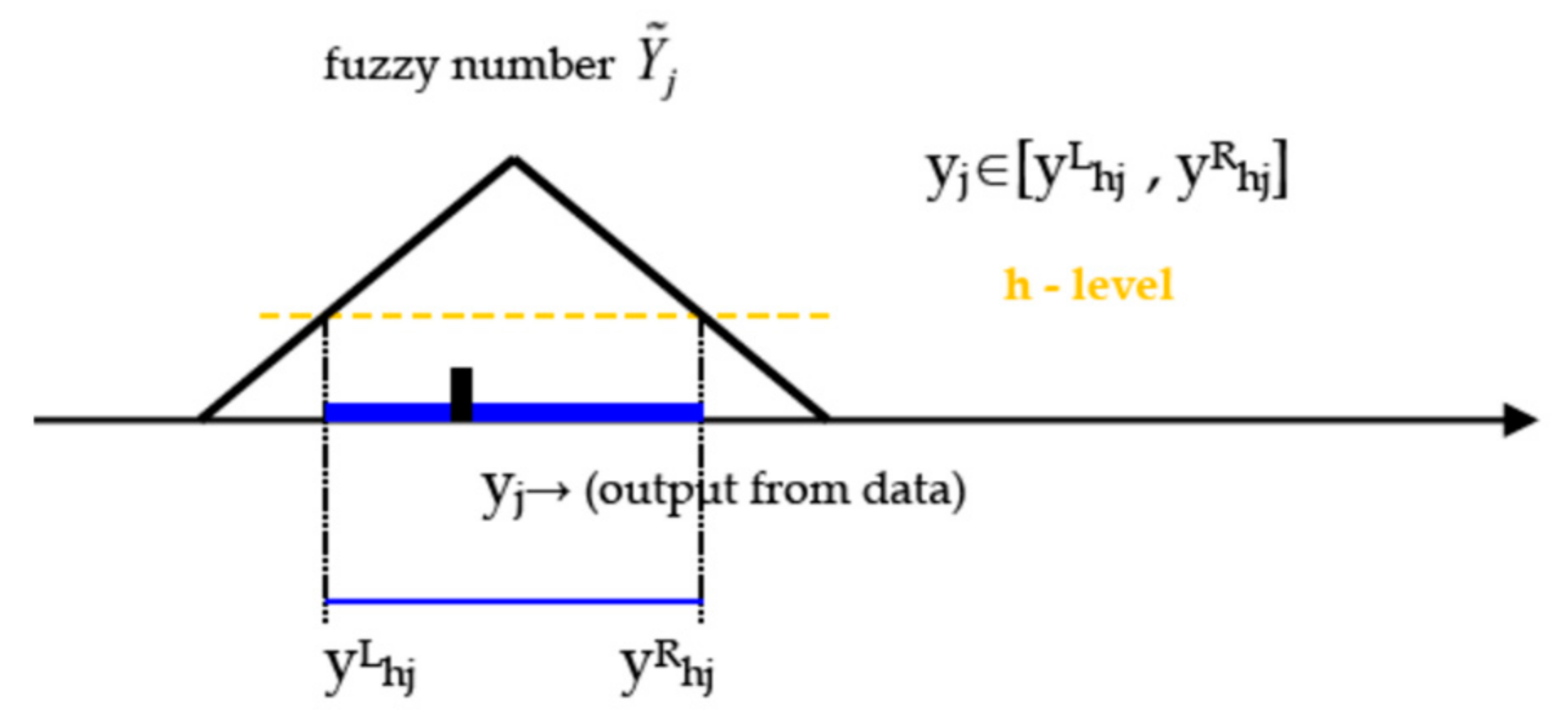
2.3. The Proposed Fuzzy Regression Model
2.4. Tested Scenarios and Basic Interpretation
3. Results
3.1. BQEs Comparison and Status Classification Approaches
3.2. Implementation of the Proposed Methodology
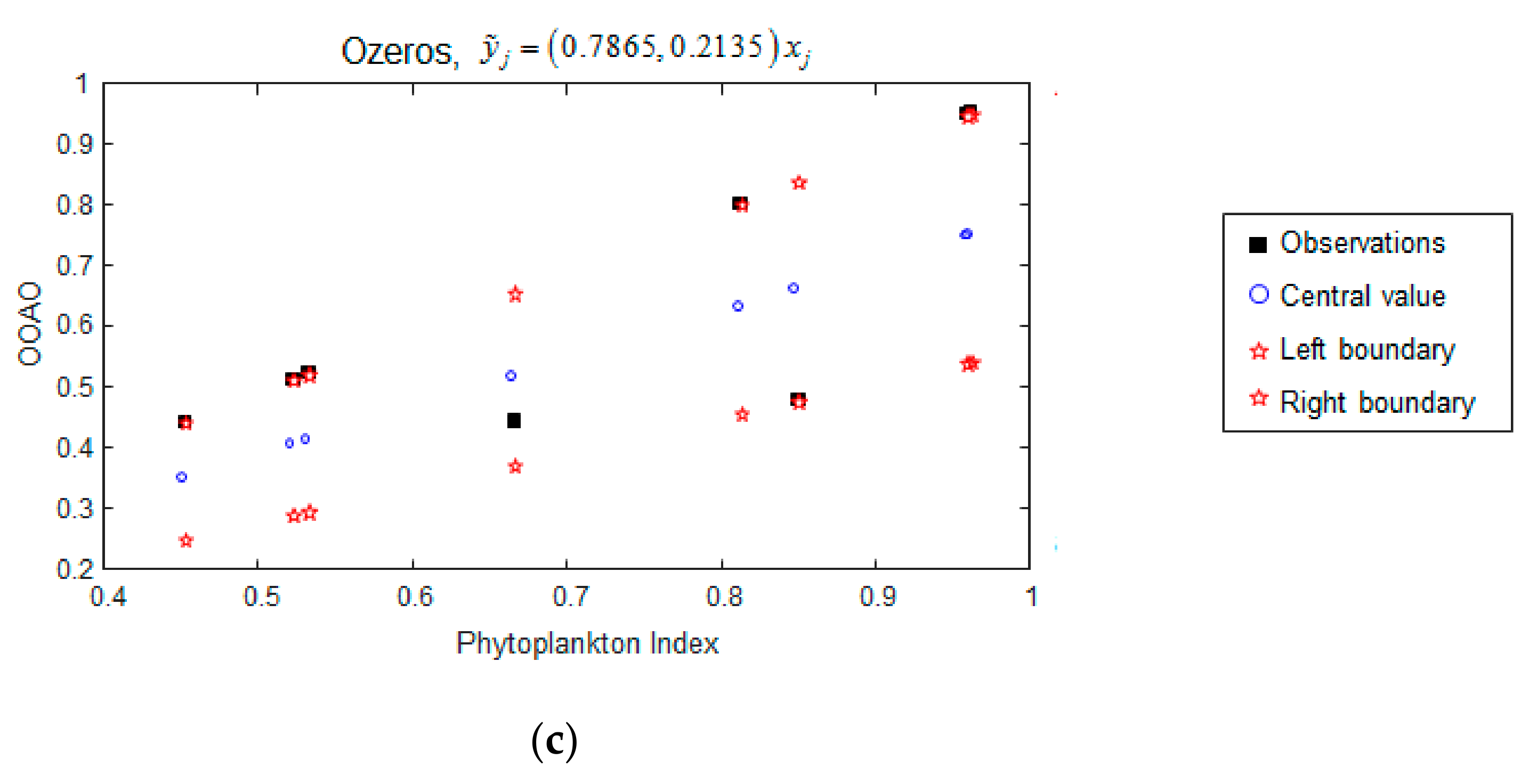
3.2.1. Fuzzy Regression Scenario A
3.2.2. Fuzzy Regression Scenario B
4. Discussion
5. Conclusions
- The inclusion of a fuzzy regression among the frequently monitored BQE (phytoplankton) and the outcome of OOAO (determined by the comparison of four BQE indices) application in lakes encompasses the uncertainty and the possibility to broaden the acceptable final EQR based on the character and status of each lake;
- The fuzzy OOAO is an approach that seems to allow a better understanding of the WFD implementation and case-specific evaluation, including the uncertainty in classification as an asset;
- It offers a deeper understanding through self-learning processes based on the existing datasets;
- As for the progress reporting of individual BQEs, this requires a more complete dataset to apply a statistically solid fuzzy regression.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Index | Metrics | Lake Type GR-DNL | Lake Type GR-SNL |
|---|---|---|---|
| HeLPhy | Total Phytoplankton Biovolume (mm3 L−1) | 1.29 | 0.74 |
| Cyanobacteria Biovolume (mm3 L−1) | 0.01 | 0.01 | |
| modNygaard Index | 1.03 | 1.11 | |
| Chlorophyll a (μg L−1) | 1.56 | 3.59 | |
| HeLM | TIHelm | 7.14 | 7.14 |
| Cmax (m) | 12.2 | 6.1 | |
| HeLLBI | ASPT | 5.47 | 5.47 |
| Odonata (% AC) | 16.67 | 16.67 | |
| Simpson | 0.80 | 0.80 |
References
- European Community. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for com-munity action in the field of water policy. Eur. Dir. 2000, L327, 1–72. [Google Scholar]
- Moe, S.; Couture, R.-M.; Haande, S.; Lyche Solheim, A.; Jackson-Blake, L. Predicting Lake Quality for the Next Generation: Impacts of Catchment Management and Climatic Factors in a Probabilistic Model Framework. Water 2019, 11, 1767. [Google Scholar] [CrossRef] [Green Version]
- European Community. Directive 2008/105/EC of the European Parliament and of the Council of 16 December 2008 on environmental quality standards in the field of water policy, amending and subsequently repealing Council Directives 82/176/EEC, 83/513/EEC, 84/156/EEC, 84/491/EEC, 86/280/EEC and amending Directive 2000/60/EC of the European Parliament and of the Council. Eur. Dir. 2008, L348, 84–97. [Google Scholar]
- European Community. Directive 2006/118/EC of the European Parliament and of the Council of 12 December 2006 on the protection of groundwater against pollution and deterioration. Eur. Dir. 2006, L372, 19–31. [Google Scholar]
- European Community. Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the assessment and management of flood risks (Text with EEA relevance). Eur. Dir. 2007, L288, 27–34. [Google Scholar]
- Kristensen, P.; Whalley, C.; Zal, F.N.N.; Christiansen, T. European Waters Assessment of Status and Pressures 2018; European Environment Agency: Copenhagen, Denmark, 2018; p. 85. [Google Scholar]
- European Commission. Fitness check of the Water Framework Directive, Groundwater Directive, Environmental Quality Standards Directive and Floods Directive; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Kagalou, I.; Latinopoulos, D. Filling the Gap between Ecosystem Services Concept and River Basin Management Plans: The Case of Greece in WFD 20+. Sustainability 2020, 12, 7710. [Google Scholar] [CrossRef]
- Prato, S.; La Valle, P.; De Luca, E.; Lattanzi, L.; Migliore, G.; Morgana, J.G.; Munari, C.; Nicoletti, L.; Izzo, G.; Mistri, M. The “one-out, all-out” principle entails the risk of imposing unnecessary restoration costs: A study case in two Mediterranean coastal lakes. Mar. Pollut. Bull. 2014, 80, 30–40. [Google Scholar] [CrossRef]
- Moe, S.J.; Lyche Solheim, A.; Soszka, H.; Gołub, M.; Hutorowicz, A.; Kolada, A.; Picińska-Fałtynowicz, J.; Białokoz, W. Integrated assessment of ecological status and misclassification of lakes: The role of uncertainty and index combination rules. Ecol. Indic. 2015, 48, 605–615. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, L.; Mackay, E.B.; Cardoso, A.C.; Baattrup-Pedersen, A.; Birk, S.; Blackstock, K.L.; Borics, G.; Borja, A.; Feld, C.K.; Ferreira, M.T.; et al. Protecting and restoring Europe’s waters: An analysis of the future development needs of the Water Framework Directive. Sci. Total Environ. 2019, 658, 1228–1238. [Google Scholar] [CrossRef]
- Birk, S.; Chapman, D.; Carvalho, L.; Spears, B.M.; Andersen, H.E.; Argillier, C.; Auer, S.; Baattrup-Pedersen, A.; Banin, L.; Beklioglu, M.; et al. Impacts of multiple stressors on freshwater biota across spatial scales and ecosystems. Nat. Ecol. Evol. 2020, 4, 1060–1068. [Google Scholar] [CrossRef]
- Hering, D.; Borja, A.; Carstensen, J.; Carvalho, L.; Elliott, M.; Feld, C.K.; Heiskanen, A.S.; Johnson, R.K.; Moe, J.; Pont, D.; et al. The European Water Framework Directive at the age of 10: A critical review of the achievements with recommendations for the future. Sci. Total Environ. 2010, 408, 4007–4019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reid, A.J.; Carlson, A.K.; Creed, I.F.; Eliason, E.J.; Gell, P.A.; Johnson, P.T.J.; Kidd, K.A.; MacCormack, T.J.; Olden, J.D.; Ormerod, S.J.; et al. Emerging threats and persistent conservation challenges for freshwater biodiversity. Biol. Rev. 2019, 94, 849–873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carvalho, L.; Poikane, S.; Lyche Solheim, A.; Phillips, G.; Borics, G.; Catalan, J.; De Hoyos, C.; Drakare, S.; Dudley, B.J.; Järvinen, M.; et al. Strength and uncertainty of phytoplankton metrics for assessing eutrophication impacts in lakes. Hydrobiologia 2013, 704, 127–140. [Google Scholar] [CrossRef] [Green Version]
- Clarke, R.T.; Hering, D. Errors and uncertainty in bioassessment methods—major results and conclusions from the STAR project and their application using STARBUGS. Hydrobiologia 2006, 566, 433–439. [Google Scholar] [CrossRef]
- Kelly, M.; Bennion, H.; Burgess, A.; Ellis, J.; Juggins, S.; Guthrie, R.; Jamieson, J.; Adriaenssens, V.; Yallop, M. Uncertainty in ecological status assessments of lakes and rivers using diatoms. Hydrobiologia 2009, 633, 5–15. [Google Scholar] [CrossRef]
- Thackeray, S.J.; Nõges, P.; Dunbar, M.J.; Dudley, B.J.; Skjelbred, B.; Morabito, G.; Carvalho, L.; Phillips, G.; Mischke, U.; Catalan, J.; et al. Quantifying uncertainties in biologically-based water quality assessment: A pan-European analysis of lake phytoplankton community metrics. Ecol. Indic. 2013, 29, 34–47. [Google Scholar] [CrossRef] [Green Version]
- Kolada, A. The use of aquatic vegetation in lake assessment: Testing the sensitivity of macrophyte metrics to anthropogenic pressures and water quality. Hydrobiologia 2010, 656, 133–147. [Google Scholar] [CrossRef]
- Kuczyńska-Kippen, N. The use of bdelloids in reference to rotifer biocoenotic indices as an indicator of the ecological state of small field water bodies: The effect of macrophytes, shading and trophic state of water. Ecol. Indic. 2018, 89, 576–583. [Google Scholar] [CrossRef]
- Borja, A.; Rodriguez, J.G. Problems associated with the ‘one-out, all-out’ principle, when using multiple ecosystem components in assessing the ecological status of marine waters. Mar. Pollut. Bull. 2010, 60, 1143–1146. [Google Scholar] [CrossRef]
- Moss, B. The Water Framework Directive: Total environment or political compromise? Sci. Total Environ. 2008, 400, 32–41. [Google Scholar] [CrossRef]
- Borja, A.; Ranasinghe, A.; Weisberg, S.B. Assessing ecological integrity in marine waters, using multiple indices and ecosystem components: Challenges for the future. Mar. Pollut. Bull. 2009, 59, 1–4. [Google Scholar] [CrossRef]
- Hering, D.; Johnson, R.K.; Kramm, S.; Schmutz, S.; Szoszkiewicz, K.; Verdonschot, P.F.M. Assessment of European streams with diatoms, macrophytes, macroinvertebrates and fish: A comparative metric-based analysis of organism response to stress. Freshw. Biol. 2006, 51, 1757–1785. [Google Scholar] [CrossRef]
- McFarland, B.; Carse, F.; Sandin, L. Littoral macroinvertebrates as indicators of lake acidification within the UK. Aquat. Conserv. Mar. Freshw. Ecosyst. 2010, 20, S105–S116. [Google Scholar] [CrossRef]
- Urbanič, G. A Littoral Fauna Index for assessing the impact of lakeshore alterations in Alpine lakes. Ecohydrology 2014, 7, 703–716. [Google Scholar] [CrossRef]
- Poikane, S.; Johnson, R.K.; Sandin, L.; Schartau, A.K.; Solimini, A.G.; Urbanic, G.; Arbaciauskas, K.; Aroviita, J.; Gabriels, W.; Miler, O.; et al. Benthic macroinvertebrates in lake ecological assessment: A review of methods, intercalibration and practical recommendations. Sci. Total Environ. 2016, 543, 123–134. [Google Scholar] [CrossRef]
- Poikane, S.; Ritterbusch, D.; Argillier, C.; Bialokoz, W.; Blabolil, P.; Breine, J.; Jaarsma, N.G.; Krause, T.; Kubecka, J.; Lauridsen, T.L.; et al. Response of fish communities to multiple pressures: Development of a total anthropogenic pressure intensity index. Sci. Total Environ. 2017, 586, 502–511. [Google Scholar] [CrossRef]
- Tsiaousi, V.; Zervas, D.; Tsiripidis, I. Report on the Development of the National Method for the Assessment of the Ecological Status of Natural Lakes in Greece, Using the Biological Quality Element “Phytoplankton”, 1st ed.; Greek Biotope/Wetland Centre and Special Secretariat for Waters, Ministry of Environment: Thermi, Greece, 2017; p. 17.
- Zervas, D.; Tsiaoussi, V.; Tsiripidis, I. HeLM: A macrophyte-based method for monitoring and assessment of Greek lakes. Environ. Monit. Assess. 2018, 190, 326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petriki, O.; Lazaridou, M.; Bobori, D.C. A fish-based index for the assessment of the ecological quality of temperate lakes. Ecol. Indic. 2017, 78, 556–565. [Google Scholar] [CrossRef]
- Ntislidou, C.; Lazaridou, M.; Tsiaoussi, V.; Bobori, D.C. A new multimetric macroinvertebrate index for the ecological assessment of Mediterranean lakes. Ecol. Indic. 2018, 93, 1020–1033. [Google Scholar] [CrossRef]
- Mavromati, E.K.D.; Tsiaoussi, V.; Lazaridou, M. Report on the Development of the National Method for the Assessment of Ecological Status of Natural Lakes in Greece, with the Use of Littoral Benthic Invertebrates; Greek Biotope/Wetland Centre and Special Secretariat for the Natural Environment and Waters, Ministry of Environment and Energy: Thermi, Greece, 2020; p. 11.
- Salski, A. Ecological applications of fuzzy logic. In Ecological Informatics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 3–14. [Google Scholar]
- Prato, T. A fuzzy logic approach for evaluating ecosystem sustainability. Ecol. Model. 2005, 187, 361–368. [Google Scholar] [CrossRef]
- Pouw, F.A.; Kwiatkowska, M. An overview of fuzzy-logic based approaches to ecology: Addressing uncertainty. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 540–545. [Google Scholar]
- Spiliotis, M.; Panagiotou, L.; Kagalou, I.; Latinopoulos, D. A Fuzzified Multicriteria Outranking Method for Water Framework Directive Implementation in a Heavily Modified Urban Lake (Pamvotis, Greece). Water Resour. Manag. 2020, 34, 4491–4510. [Google Scholar] [CrossRef]
- Ganoulis, J. Engineering Risk Analysis of Water Pollution Probabilities and Fuzzy Sets; Verlagsgesellschaft: Weinheim, Germany, 1994; p. 306. [Google Scholar]
- Kitsikoudis, V.; Spiliotis, M.; Hrissanthou, V. Fuzzy Regression Analysis for Sediment Incipient Motion under Turbulent Flow Conditions. Environ. Process. 2016, 3, 663–679. [Google Scholar] [CrossRef]
- Spiliotis, M.; Hrissanthou, V. Fuzzy and crisp regression analysis between sediment transport rates and stream discharge in the case of two basins in northeastern Greece. Conv. Fuzzy Regres. Theory Eng. Appl. 2018, 1, 49. [Google Scholar]
- Spiliotis, M.; Angelidis, P.; Papadopoulos, B. Assessment of annual hydrological drought based on fuzzy estimators. In Proceedings of the 4th IAHR Europe Congress, “Sustainable hydraulics in the era of global change”, Liege, Belgium, 27–29 July 2016. [Google Scholar]
- Papadopoulos, B.K.; Sirpi, M.A. Similarities in fuzzy regression models. J. Optim. Theory Appl. 1999, 102, 373–383. [Google Scholar] [CrossRef]
- Spiliotis, M.; Bellos, C. Flooding risk assessment in mountain rivers. In Proceedings of the Water resources management in a changing World: Challenges and opportunities, Instabul, Turkey, 10–13 June 2015. [Google Scholar]
- Tanaka, H. Fuzzy data analysis by bossibilistic linear models. Fuzzy Sets Syst. 1987, 24, 262–375. [Google Scholar] [CrossRef]
- Tanaka, H.; Uejima, S.; Asai, K. Linear regression analysis with fuzzy model. IEEE Trans. Syst. Man. Cybern. 1982, 12, 903–907. [Google Scholar]
- Tsakiris, G.; Tigkas, D.; Spiliotis, M. Assessment of interconnection between two adjacent watersheds using deterministic and fuzzy approaches. Eur. Water 2006, 15, 15–22. [Google Scholar]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Ыall: Hoboken, NJ, USA, 1995; p. 574. [Google Scholar]
- Tanaka, H.; Hayashi, I.; Watada, J. Possibilistic linear regression analysis for fuzzy data. Eur. J. Oper. Res. 1989, 40, 389–396. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, K.; Papadopoulos, B. Fuzzy regression with applications in hydrology. Int. J. Eng. Innov. Technol. 2016, 5, 69–75. [Google Scholar]
- Papadopoulos, B.K.; Sirpi, M.A. Similarities and distances in fuzzy regression modeling. Soft Comput. 2004, 8, 556–561. [Google Scholar] [CrossRef]
- Profillidis, V.A.; Papadopoulos, B.K.; Botzoris, G.N. Similarities in fuzzy regression models and application on transportation. Fuzzy Econ. Rev. 1999, 4, 4. [Google Scholar] [CrossRef]
- Caroni, R.; Bund, W.; Clarke, R.T.; Johnson, R.K. Combination of multiple biological quality elements into waterbody assessment of surface waters. Hydrobiologia 2013, 704, 437–451. [Google Scholar] [CrossRef]
- Lyche-Solheim, A.; Feld, C.K.; Birk, S.; Phillips, G.; Carvalho, L.; Morabito, G.; Mischke, U.; Willby, N.; Søndergaard, M.; Hellsten, S.; et al. Ecological status assessment of European lakes: A comparison of metrics for phytoplankton, macrophytes, benthic invertebrates and fish. Hydrobiologia 2013, 704, 57–74. [Google Scholar] [CrossRef] [Green Version]
- Poikane, S.; Portielje, R.; Denys, L.; Elferts, D.; Kelly, M.; Kolada, A.; Maemets, H.; Phillips, G.; Sondergaard, M.; Willby, N.; et al. Macrophyte assessment in European lakes: Diverse approaches but convergent views of ‘good’ ecological status. Ecol. Indic. 2018, 94, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Alahuhta, J.; Vuori, K.-M.H.; Olin, M.; Rask, M.; Palomäki, A. Defining the ecological status of small forest lakes using multiple biological quality elements and palaeolimnological analysis. Fundam. Appl. Limnol. 2009, 175, 203–216. [Google Scholar] [CrossRef]
- European Commission. Draft Technical Report on Water Quality Indicators. Available online: https://circabc.europa.eu/ui/group/9ab5926d-bed4-4322-9aa7-9964bbe8312d/library/0d521a5a-2f8e-49b6-a011-204ceb144960/details (accessed on 25 March 2021).
- Wiering, M.; Boezeman, D.; Crabbé, A. The Water Framework Directive and Agricultural Diffuse Pollution: Fighting a Running Battle? Water 2020, 12, 1447. [Google Scholar] [CrossRef]
- Tsakiris, G. The Status of the European Waters in 2015: A Review. Environ. Process. 2015, 2, 543–557. [Google Scholar] [CrossRef] [Green Version]
- Lyche Solheim, A.; Globevnik, L.; Austnes, K.; Kristensen, P.; Moe, S.J.; Persson, J.; Phillips, G.; Poikane, S.; Van de Bund, W.; Birk, S. A new broad typology for rivers and lakes in Europe: Development and application for large-scale environmental assessments. Sci. Total Environ. 2019, 697, 134043. [Google Scholar] [CrossRef]
- European Commission. Commission Staff Working Document. Report on the Implementation of the Water Framework Directive (2000/60/EC) and the Floods Directive (2007/60/EC)—Second River Basin Management Plans and First Flood Risk Management Plans; Report from the Commission to the European Parliament and the Council; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Zacharias, I.; Liakou, P.; Biliani, I. A Review of the Status of Surface European Waters Twenty Years after WFD Introduction. Environ. Process. 2020, 7, 1023–1039. [Google Scholar] [CrossRef]
- Voulvoulis, N.; Arpon, K.D.; Giakoumis, T. The EU Water Framework Directive: From great expectations to problems with implementation. Sci. Total Environ. 2017, 575, 358–366. [Google Scholar] [CrossRef] [Green Version]
- Poikane, S.; Várbíró, G.; Kelly, M.G.; Birk, S.; Phillips, G. Estimating river nutrient concentrations consistent with good ecological condition: More stringent nutrient thresholds needed. Ecol. Indic. 2021, 121, 107017. [Google Scholar] [CrossRef]
- Poikane, S.; Kelly, M.G.; Salas Herrero, F.; Pitt, J.A.; Jarvie, H.P.; Claussen, U.; Leujak, W.; Lyche Solheim, A.; Teixeira, H.; Phillips, G. Nutrient criteria for surface waters under the European Water Framework Directive: Current state-of-the-art, challenges and future outlook. Sci. Total Environ. 2019, 695, 133888. [Google Scholar] [CrossRef] [PubMed]
- Moss, B. Climate change, nutrient pollution and the bargain of Dr Faustus. Freshw. Biol. 2010, 55, 175–187. [Google Scholar] [CrossRef]
- Kelly, M.G.; Birk, S.; Willby, N.J.; Denys, L.; Drakare, S.; Kahlert, M.; Karjalainen, S.M.; Marchetto, A.; Pitt, J.A.; Urbanic, G.; et al. Redundancy in the ecological assessment of lakes: Are phytoplankton, macrophytes and phytobenthos all necessary? Sci. Total Environ. 2016, 568, 594–602. [Google Scholar] [CrossRef] [PubMed]
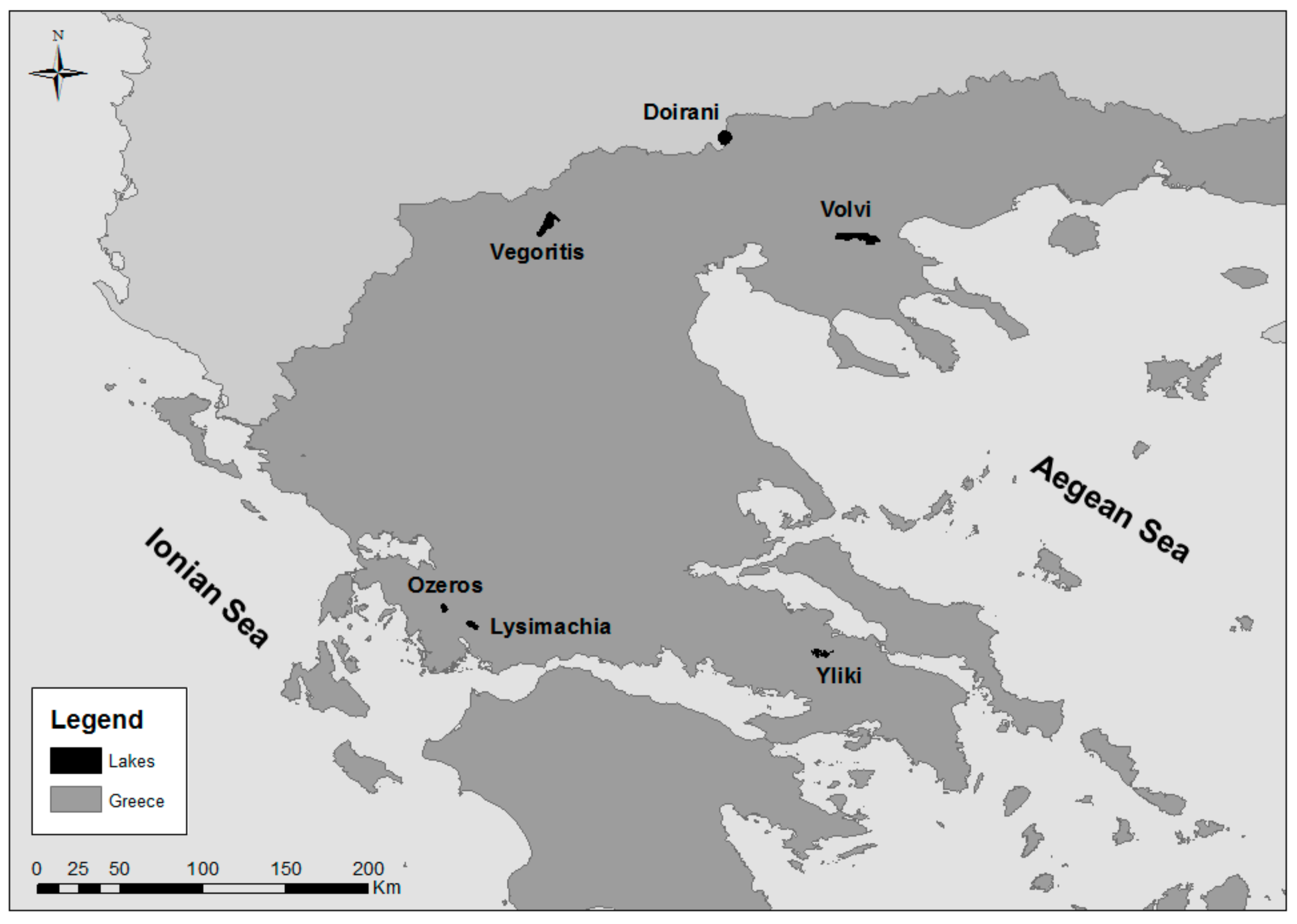
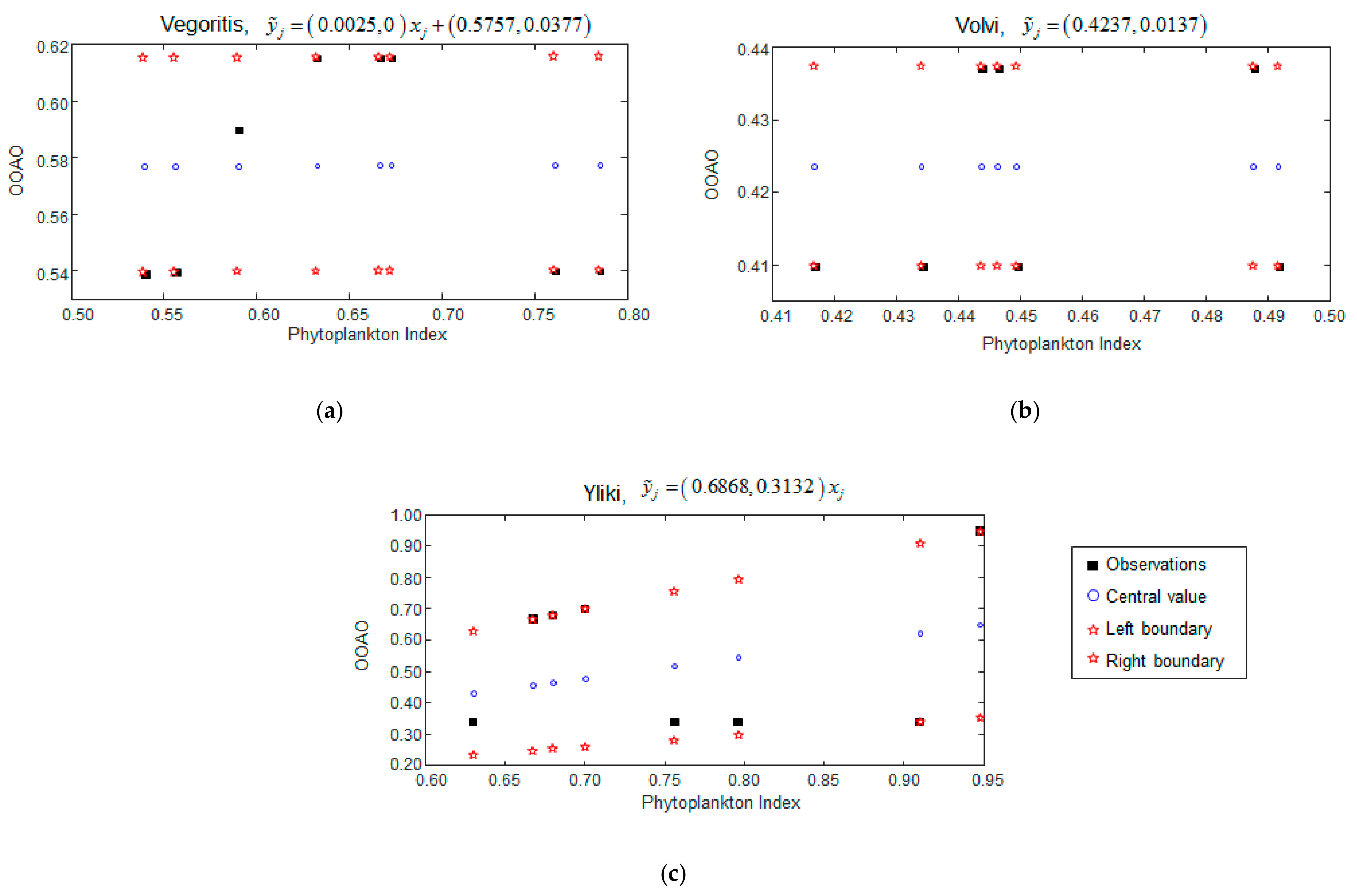
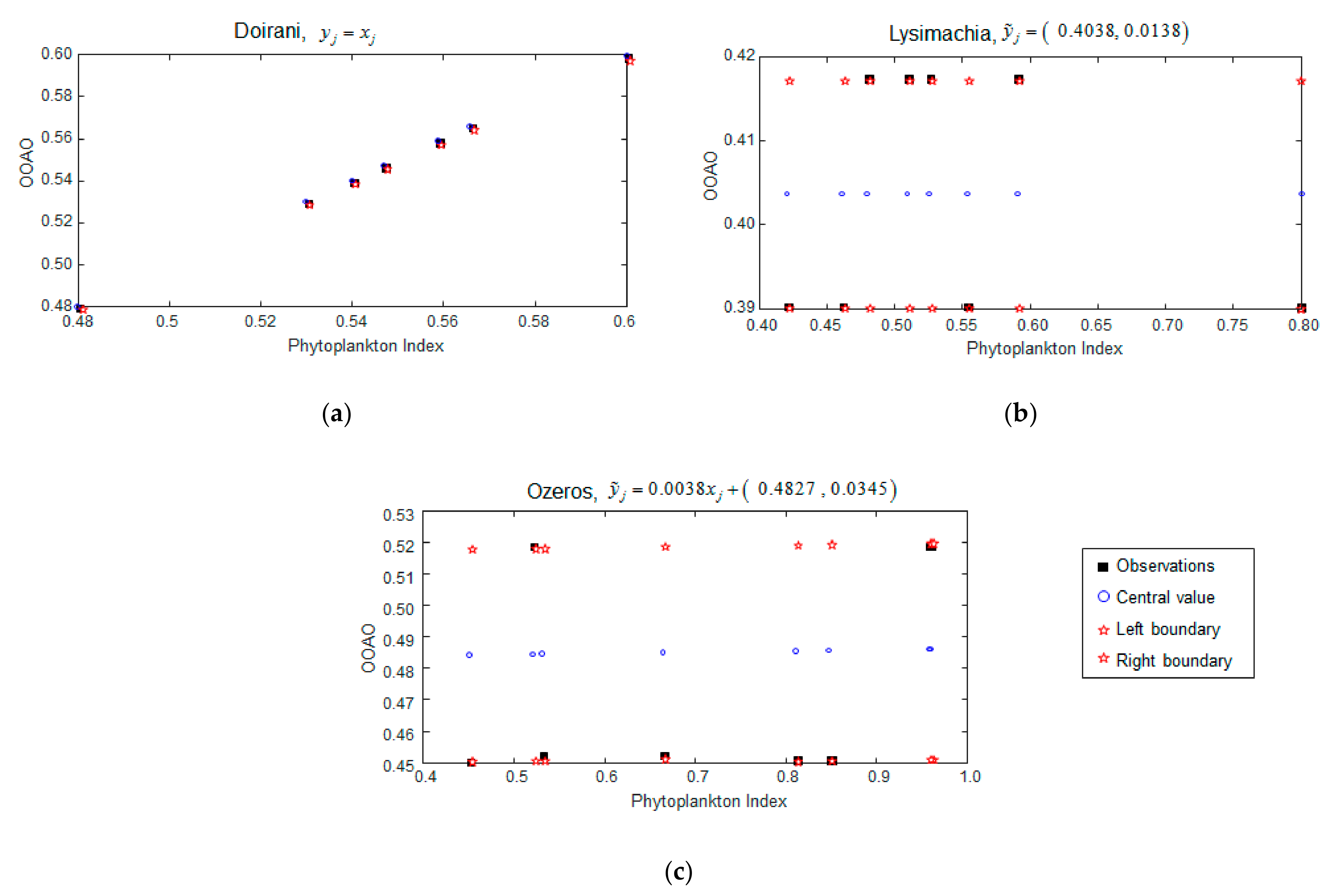
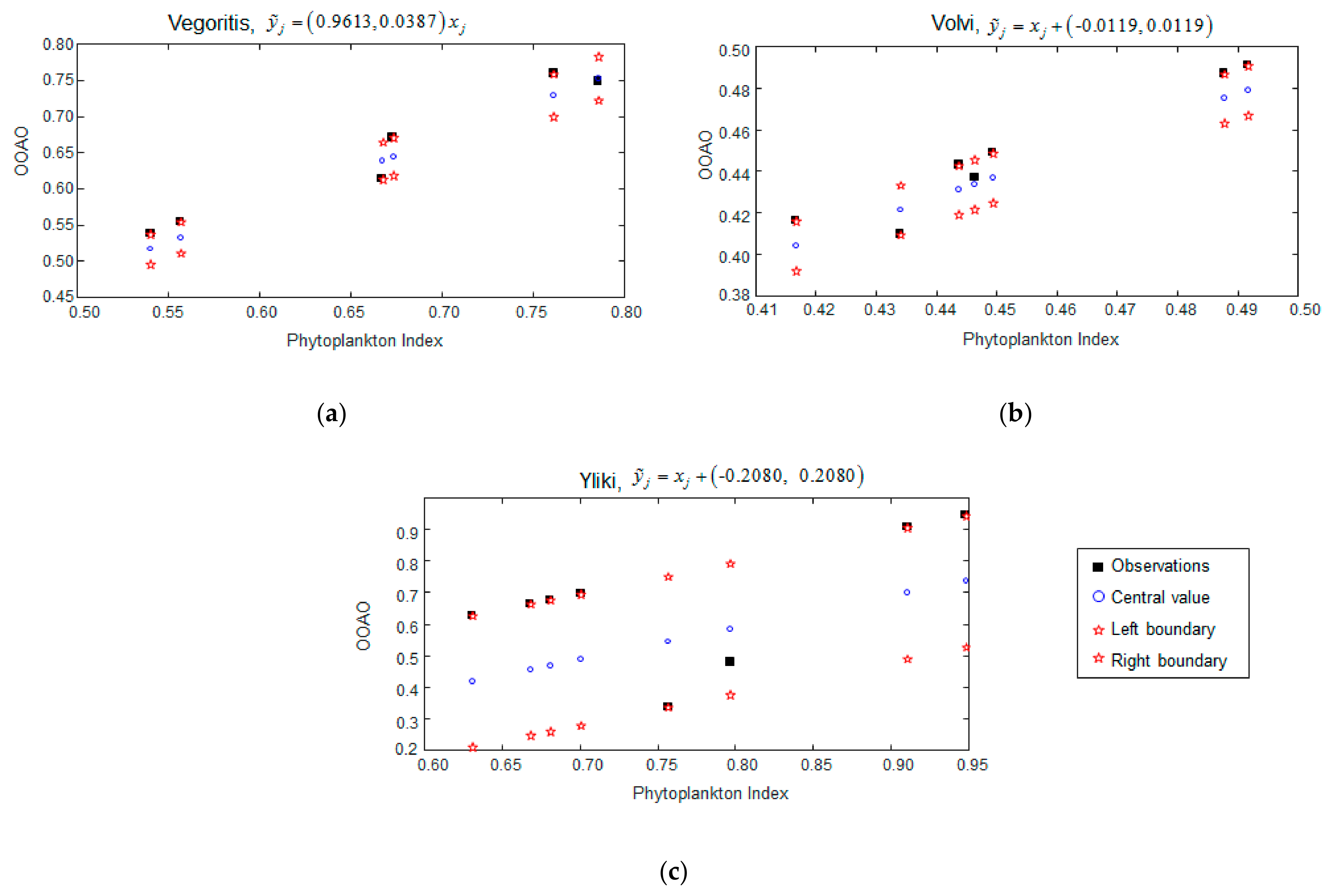
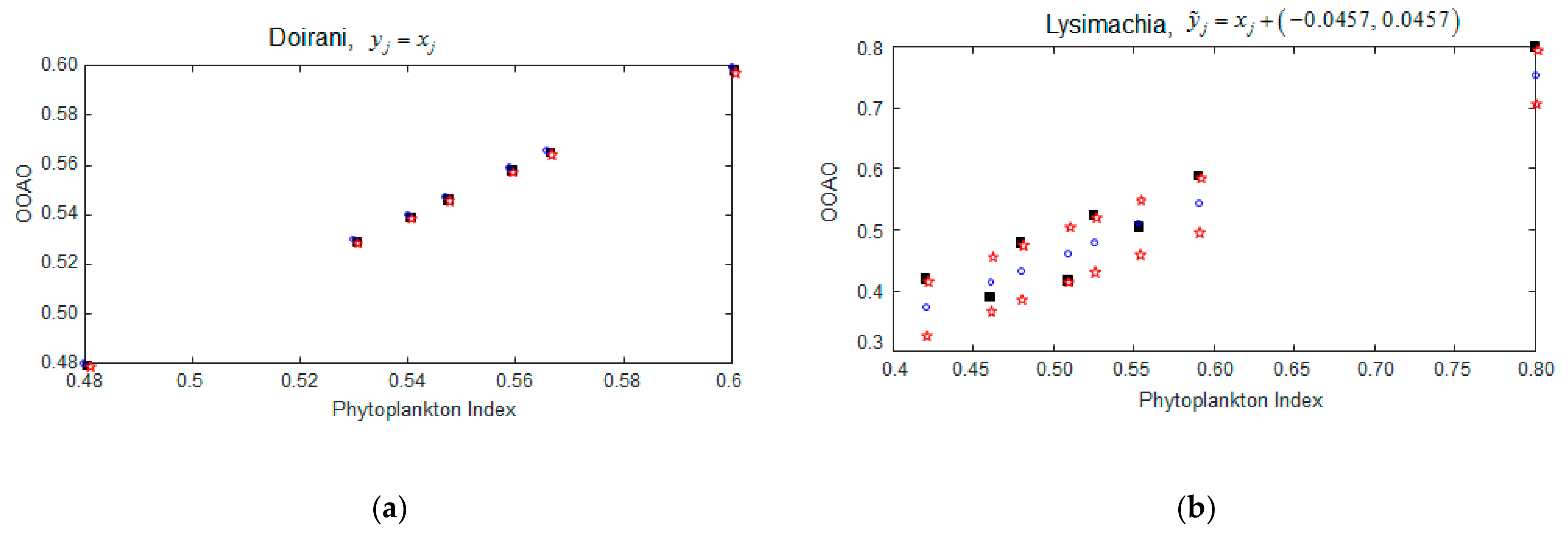
| Lake | Altitude (m.a.s.l.) | Mean Depth (m) a | Maximum Depth (m) a | Lake Area (km2) a | Trophic Status |
|---|---|---|---|---|---|
| Doirani | 142 | 4.5 | 5.5 | 32.4 * | ET |
| Lysimachia | 16 | 3.5 | 7.7 | 13.0 | ET |
| Ozeros | 22 | 3.8 | 6.1 | 10.4 | ET |
| Vegoritis | 510 | 26.1 | 52.4 | 47.4 | MT-ET |
| Volvi | 37 | 12.5 | 27.3 | 72.9 | ET |
| Yliki | 80 | 20.9 | 38.5 | 21.6 | OL-MT |
| Lake | 1st Monitoring Period | 2nd Monitoring Period | ||||||
|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
| Doirani | P | P, M | P, B-SP | P | P, M | P | P | |
| Lysimachia | P | P | P, M, B-SP | P, B-L | P | P, M | P, B-L | P |
| Ozeros | P | P | P, M, B-SP | P, B-L | P | P, B-L | P | P |
| Vegoritis | P | P, M | P, B-SP | P | P, M | P | P, B-L | P |
| Volvi | P | P, M | P, B-SP | P | P, M | P, B-L | P | |
| Yliki | P | P | P, M, B-SP | P, B-L | P | P | P | P |
| Lake Type | Lake | Monitoring Period | P | M | B-SP | B-L | OOAO | Median | Average |
|---|---|---|---|---|---|---|---|---|---|
| Deep | Vegoritis | 1st (2012–2015) | 0.66 | 0.75 | 0.54 | 0.54 | 0.66 | 0.65 | |
| 2nd (2016–2019) | 0.64 | 0.62 | 0.69 | 0.62 | 0.64 | 0.65 | |||
| Volvi | 1st (2012–2015) | 0.45 | 0.70 | 0.41 | 0.41 | 0.45 | 0.52 | ||
| 2nd (2016–2019) | 0.46 | 0.71 | 0.44 | 0.44 | 0.46 | 0.53 | |||
| Yliki | 1st (2012–2015) | 0.77 | 0.69 | 0.34 | 0.48 | 0.34 | 0.59 | 0.57 | |
| 2nd (2016–2019) | 0.75 | 0.75 | 0.75 | 0.75 | |||||
| Shallow | Doirani | 1st (2012–2015) | 0.56 | 0.77 | 0.69 | 0.56 | 0.69 | 0.68 | |
| 2nd (2016–2019) | 0.57 | 0.77 | 0.57 | 0.67 | 0.67 | ||||
| Lysimachia | 1st (2012–2015) | 0.59 | 0.59 | 0.39 | 0.51 | 0.39 | 0.53 | 0.51 | |
| 2nd (2016–2019) | 0.53 | 0.42 | 0.63 | 0.42 | 0.53 | 0.52 | |||
| Ozeros | 1st (2012–2015) | 0.71 | 0.45 | 0.53 | 0.49 | 0.45 | 0.51 | 0.55 | |
| 2nd (2016–2019) | 0.72 | 0.62 | 0.52 | 0.52 | 0.62 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latinopoulos, D.; Spiliotis, M.; Ntislidou, C.; Kagalou, I.; Bobori, D.; Tsiaoussi, V.; Lazaridou, M. “One Out–All Out” Principle in the Water Framework Directive 2000—A New Approach with Fuzzy Method on an Example of Greek Lakes. Water 2021, 13, 1776. https://doi.org/10.3390/w13131776
Latinopoulos D, Spiliotis M, Ntislidou C, Kagalou I, Bobori D, Tsiaoussi V, Lazaridou M. “One Out–All Out” Principle in the Water Framework Directive 2000—A New Approach with Fuzzy Method on an Example of Greek Lakes. Water. 2021; 13(13):1776. https://doi.org/10.3390/w13131776
Chicago/Turabian StyleLatinopoulos, Dionissis, Mike Spiliotis, Chrysoula Ntislidou, Ifigenia Kagalou, Dimitra Bobori, Vasiliki Tsiaoussi, and Maria Lazaridou. 2021. "“One Out–All Out” Principle in the Water Framework Directive 2000—A New Approach with Fuzzy Method on an Example of Greek Lakes" Water 13, no. 13: 1776. https://doi.org/10.3390/w13131776
APA StyleLatinopoulos, D., Spiliotis, M., Ntislidou, C., Kagalou, I., Bobori, D., Tsiaoussi, V., & Lazaridou, M. (2021). “One Out–All Out” Principle in the Water Framework Directive 2000—A New Approach with Fuzzy Method on an Example of Greek Lakes. Water, 13(13), 1776. https://doi.org/10.3390/w13131776












