Assessment of the Climatic Variability of the Kunhar River Basin, Pakistan
Abstract
:1. Introduction
2. Data and Methods
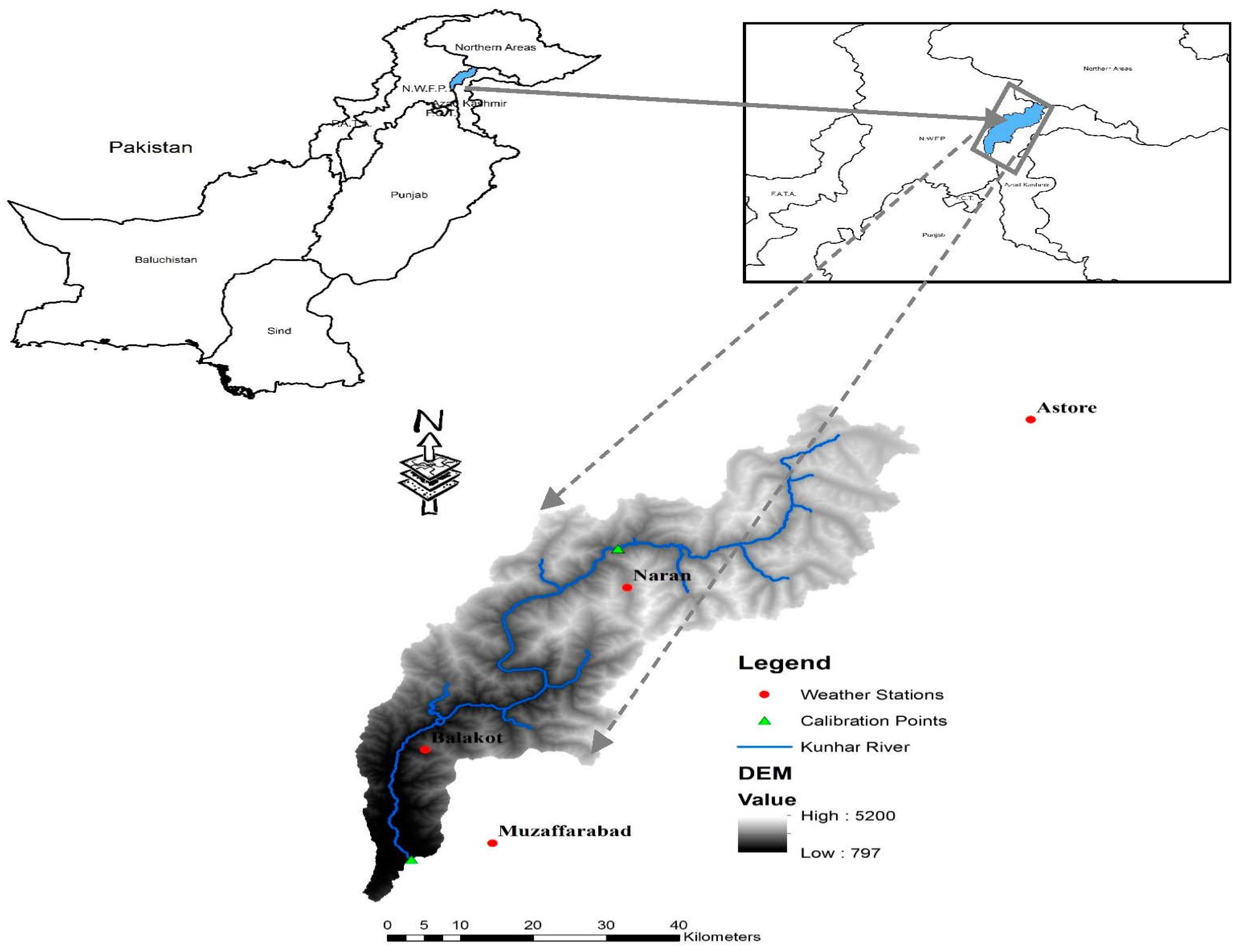
2.1. Study Area Description and Data Sources
2.1.1. Kunhar River Basin
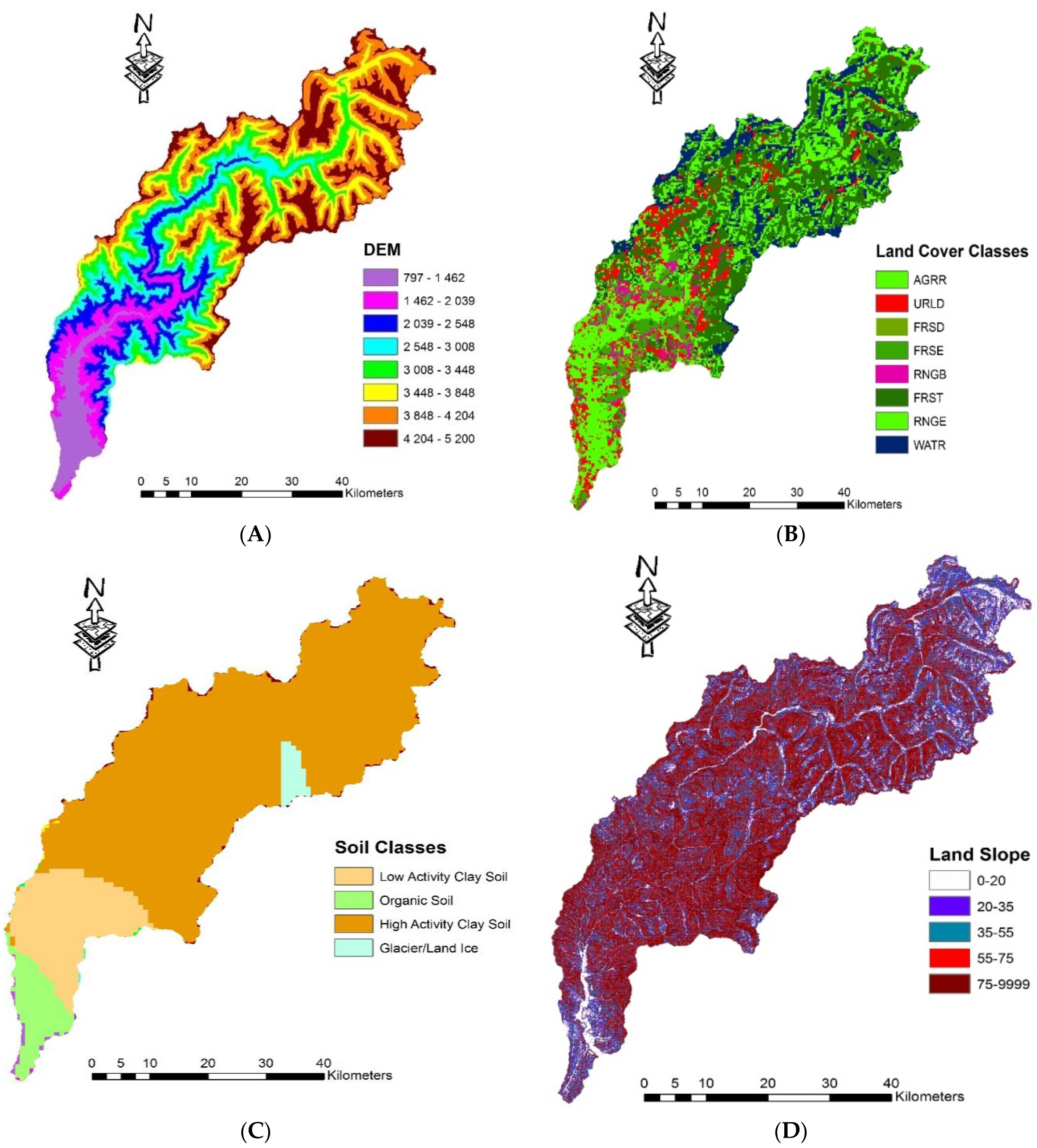
2.1.2. Data
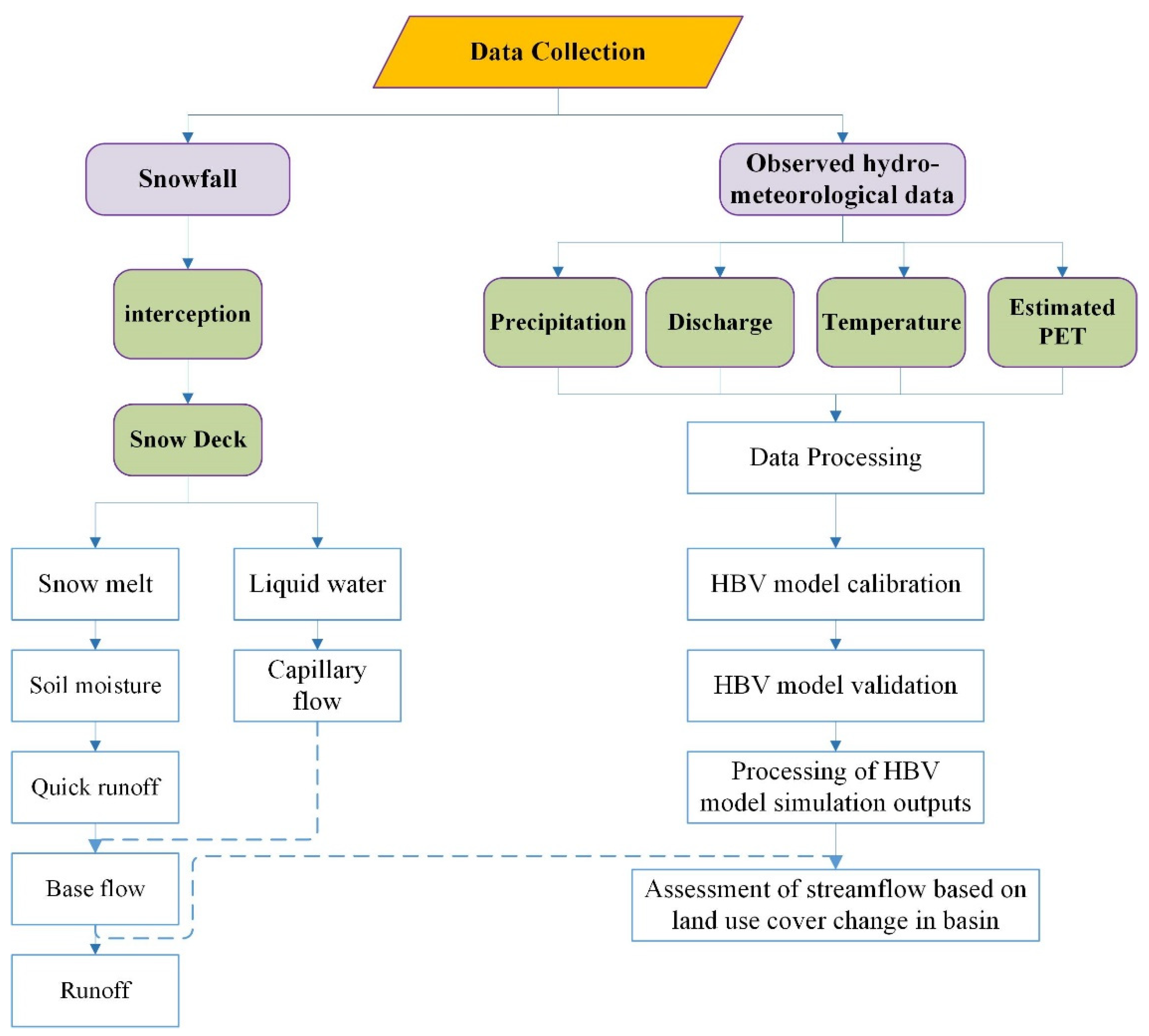
2.2. Methods
HBV Model and Input Data
2.3. Hydrological Modeling Method
2.3.1. Snowmelt and Snow Accumulation Module
2.3.2. Concept of the Ice Module
2.3.3. Efficient Subcritical Rainfall
2.3.4. Evapotranspiration Module
2.3.5. Application of Runoff
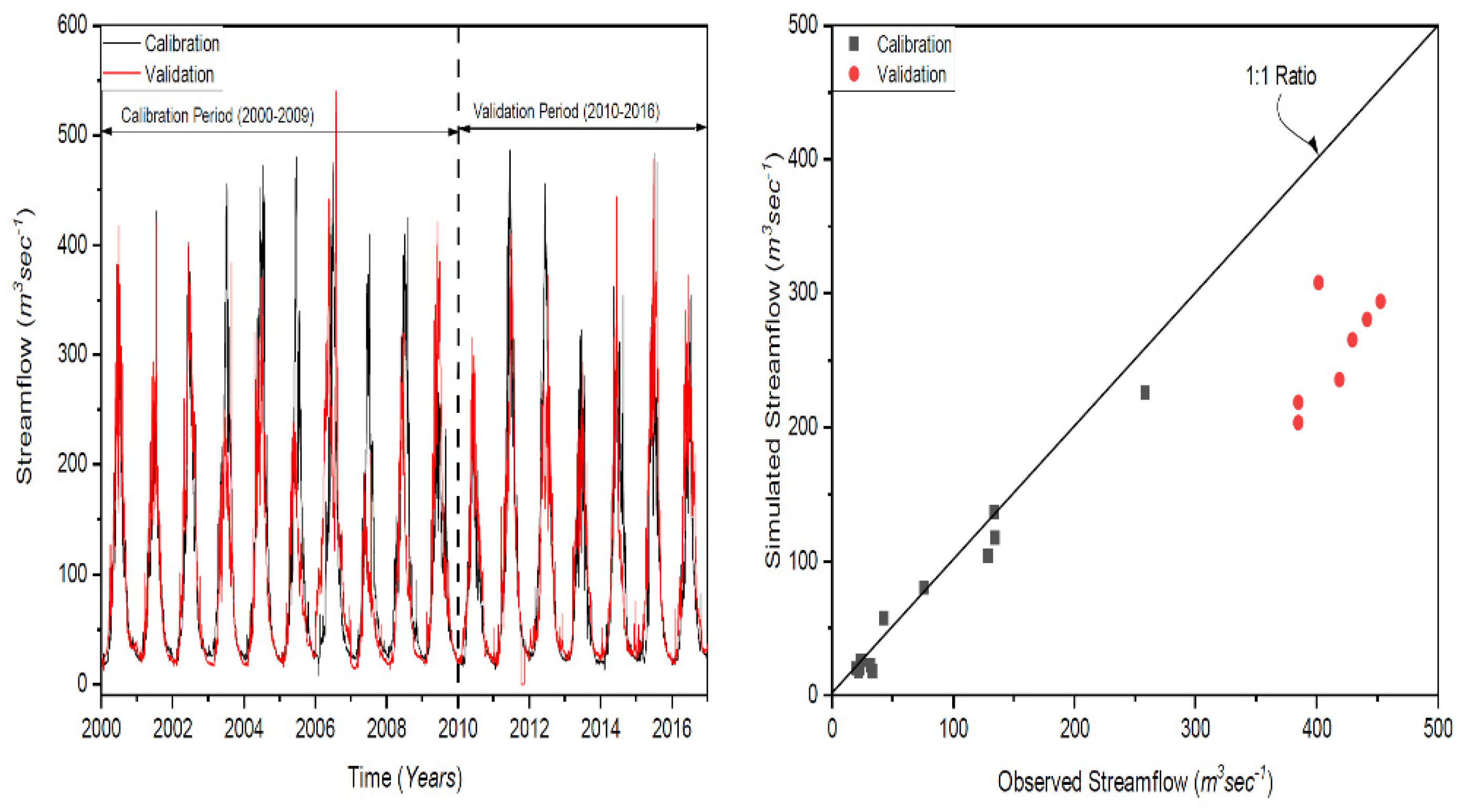
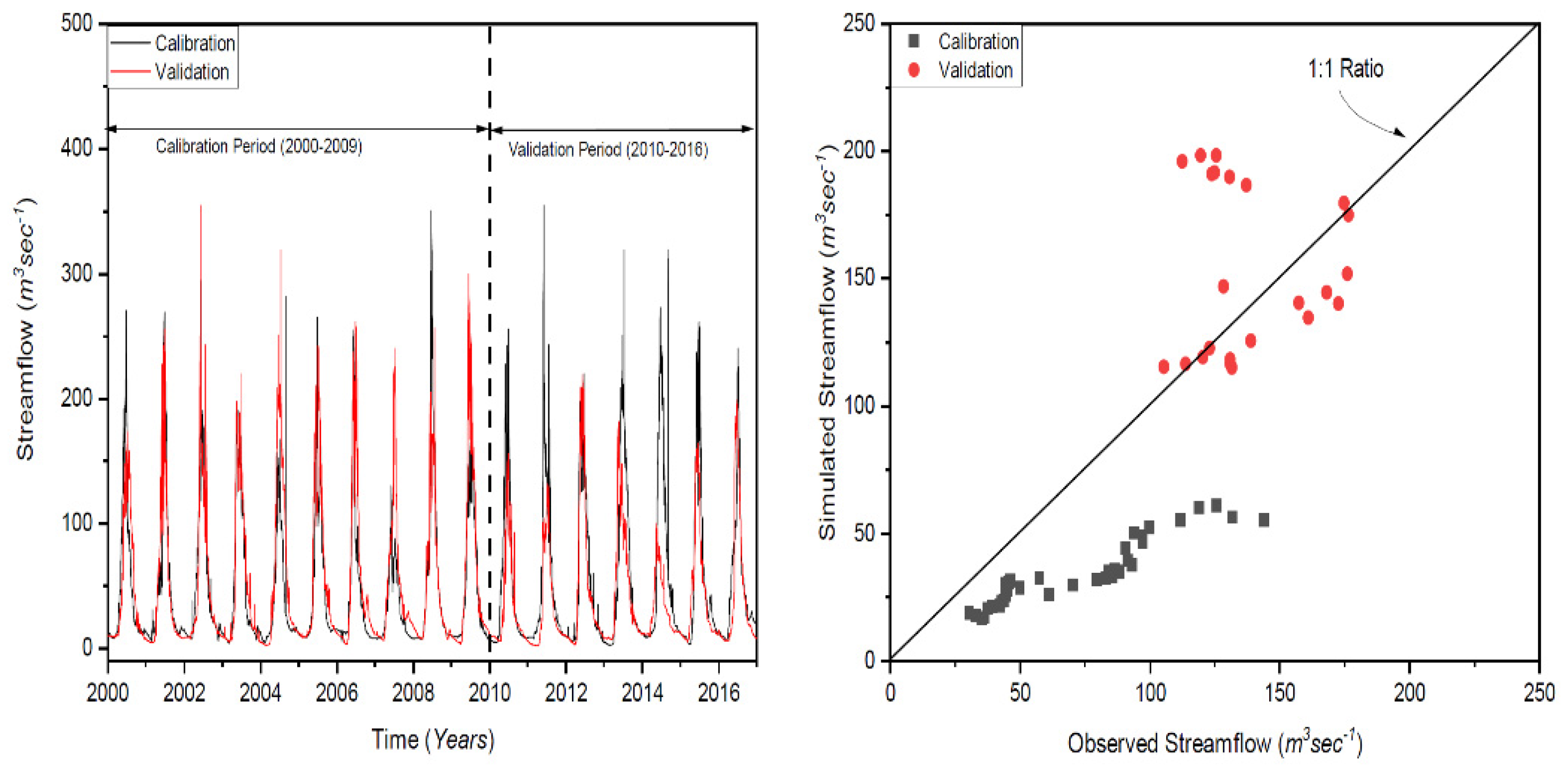
2.4. Calibration and Validation of the HBV Model in the Kunhar River Basin
2.5. Comparison in Each Time Scale (Daily/Monthly/Seasonal)
3. Results
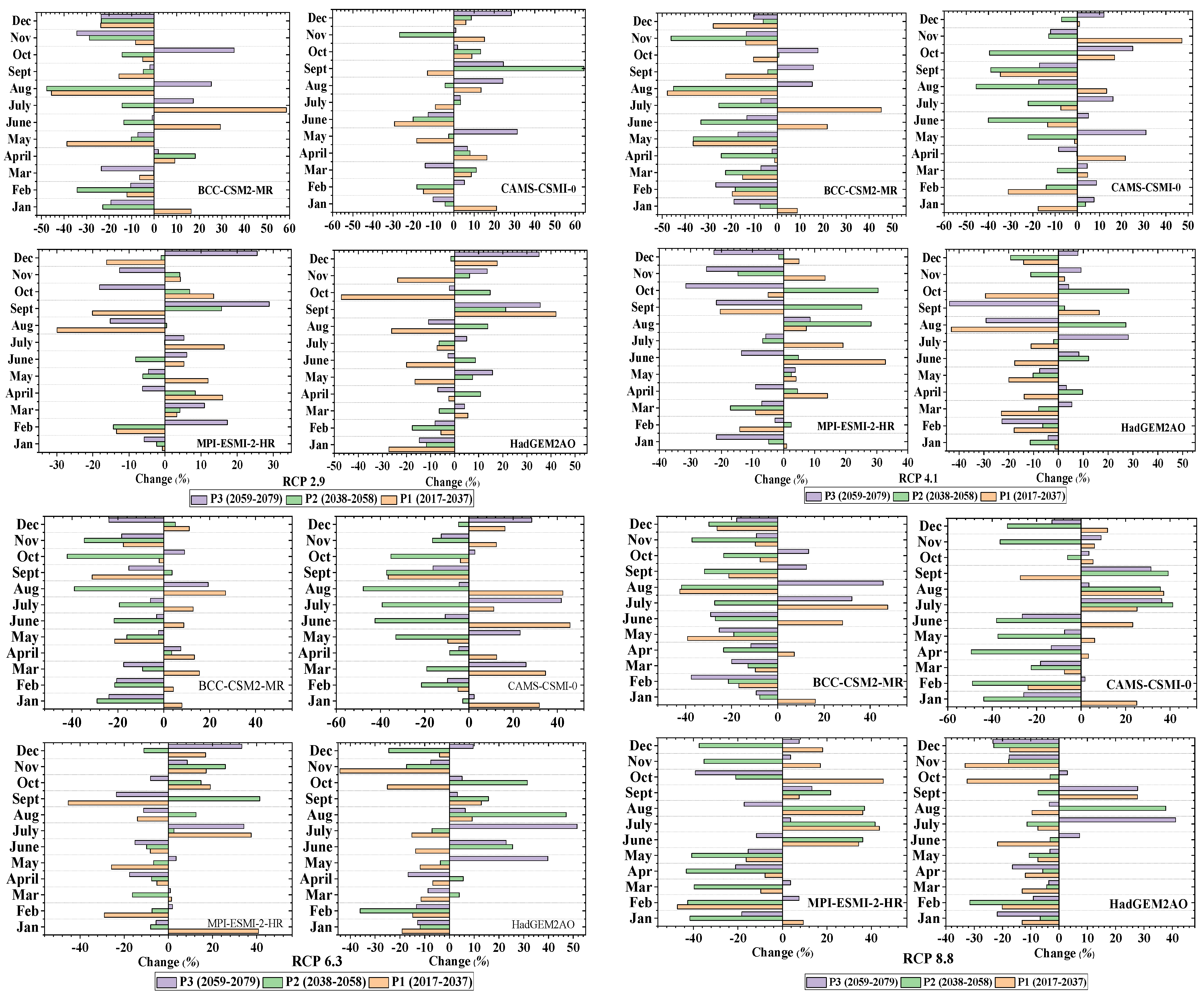
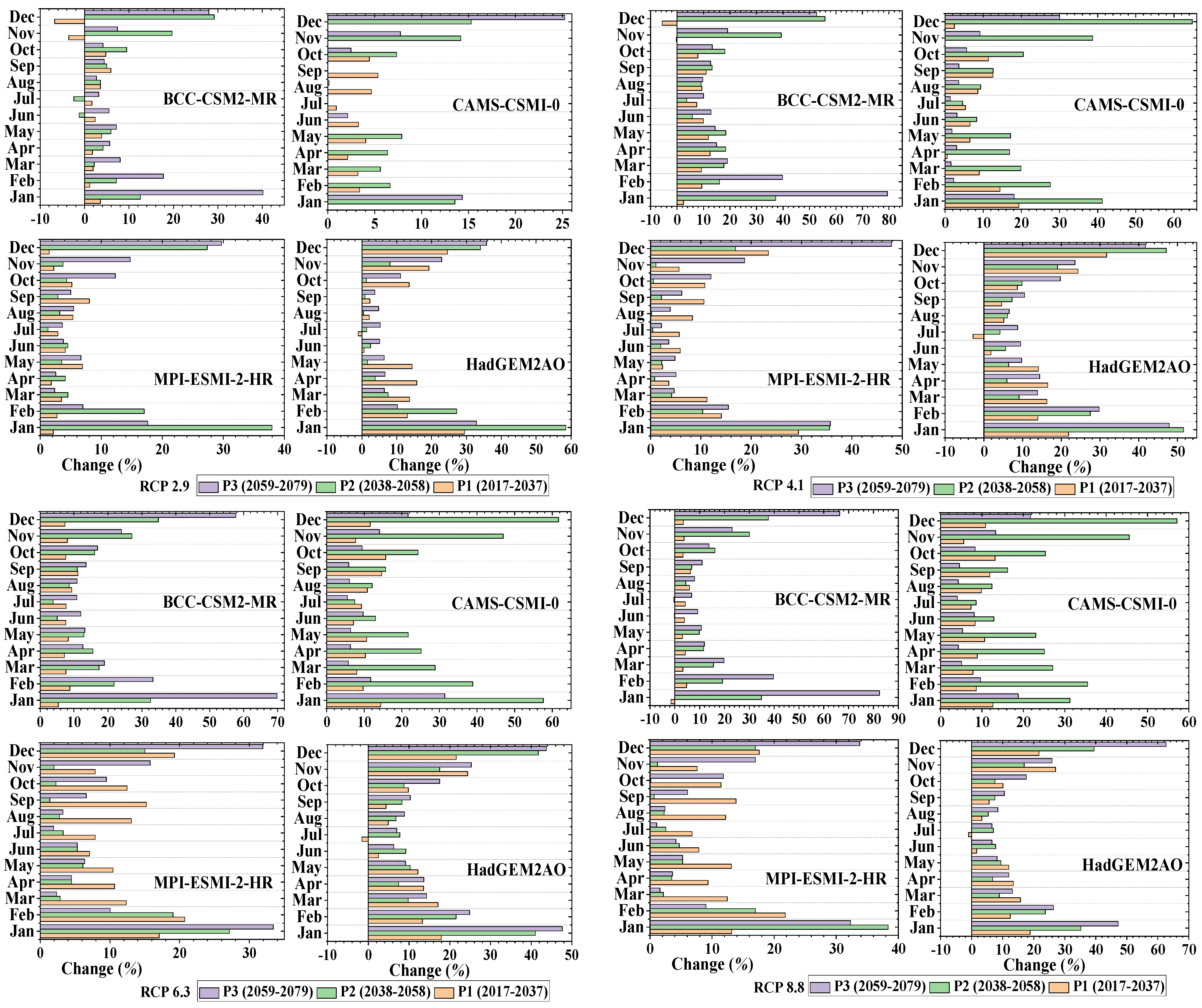
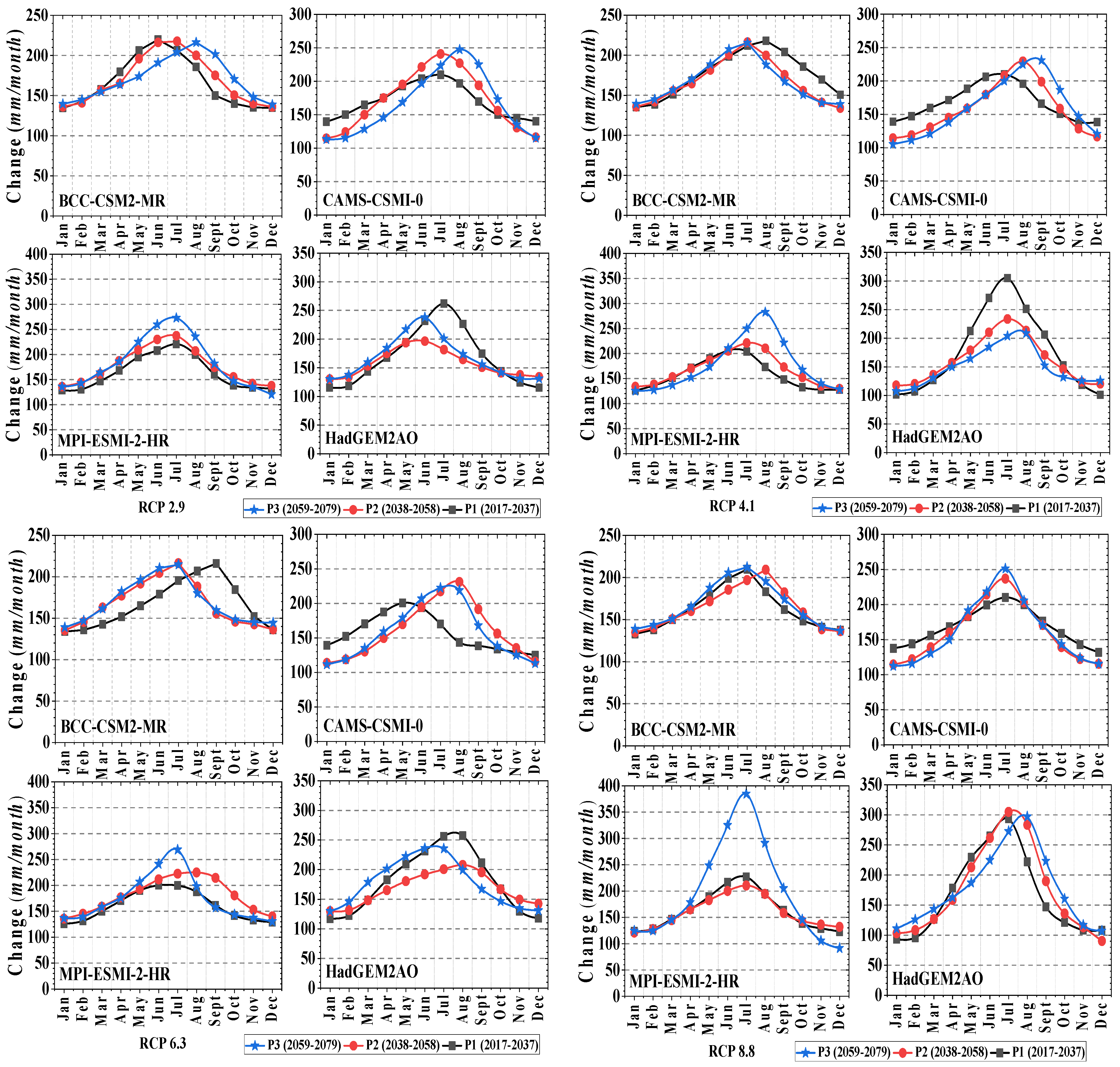
3.1. Projected Changes in Precipitation
3.2. Projected Changes in Temperature
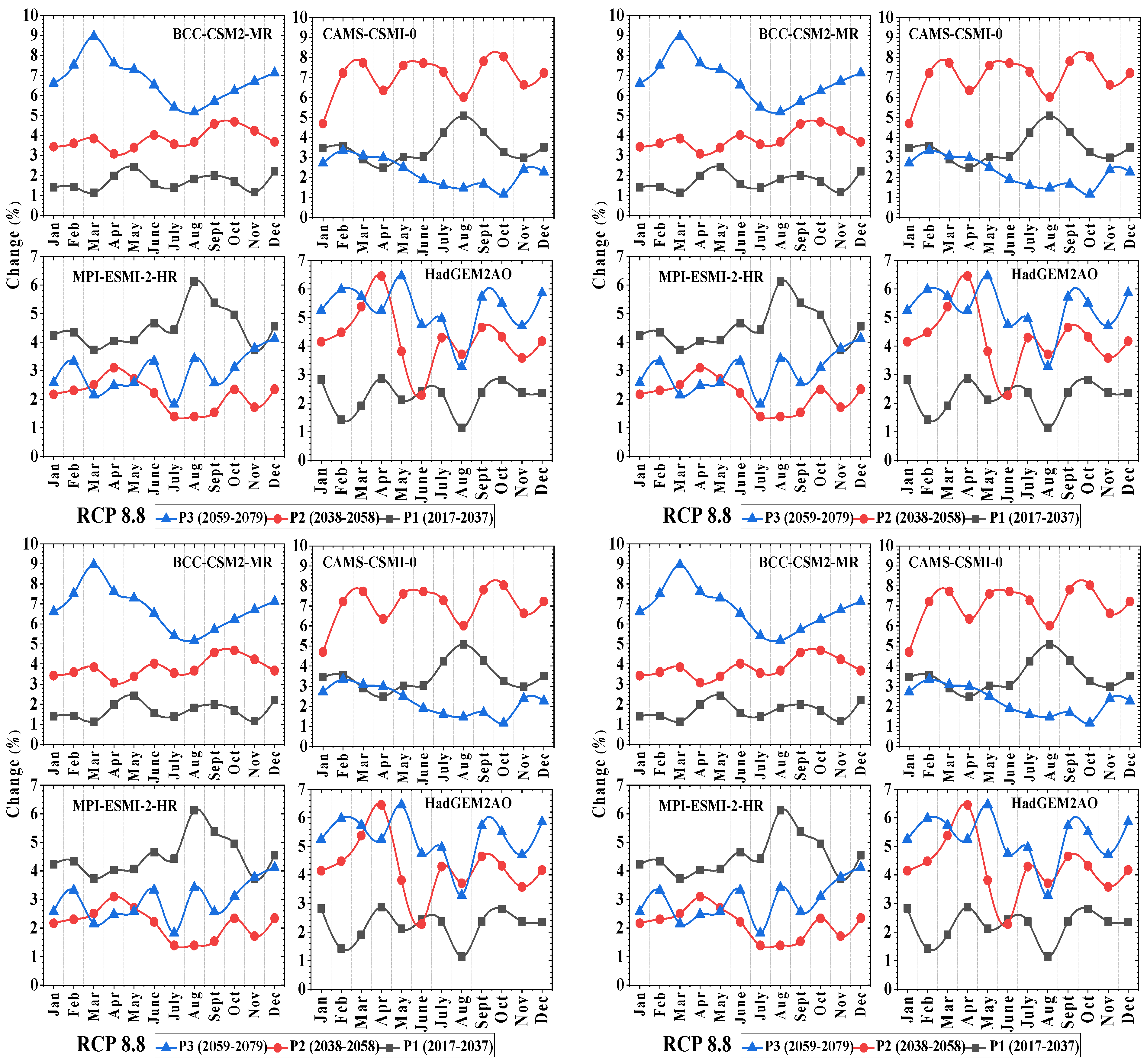
3.3. Projected Changes in Evapotranspiration
3.4. Projected Changes in Stream Flow
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ludwig, F.; van Slobbe, E.; Cofino, W. Climate change adaptation and Integrated Water Resource Management in the water sector. J. Hydrol. 2014, 518, 235–242. [Google Scholar] [CrossRef]
- Naeem, U.A.; Hashmi, H.N.; Shakir, A.S. Flow trends in river Chitral due to different scenarios of glaciated extent. KSCE J. Civ. Eng. 2013, 17, 244–251. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–332. [Google Scholar] [CrossRef] [Green Version]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef] [Green Version]
- Goderniaux, P.; Brouyère, S.; Fowler, H.J.; Blenkinsop, S.; Therrien, R.; Orban, P.; Dassargues, A. Large scale surface-subsurface hydrological model to assess climate change impacts on groundwater reserves. J. Hydrol. 2009, 373, 122–138. [Google Scholar] [CrossRef]
- Eckhardt, K.; Ulbrich, U. Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Dahri, Z.H.; Querner, E.P.; Khan, A.; Hofstra, N. Impact of climate change on flood frequency and intensity in the Kabul River Basin. Geosciences 2018, 8, 114. [Google Scholar] [CrossRef] [Green Version]
- Akhtar, M.; Ahmad, N.; Booij, M.J. The impact of climate change on the water resources of Hindukush–Karakorum–Himalaya region under different glacier coverage scenarios. J. Hydrol. 2008, 355, 148–163. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.; Deb, P.; Kumari, N. Multi-Model Approach to Assess the Dynamics of Hydrologic Components in a Tropical Ecosystem. Water Resour. Manag. 2020, 34, 327–341. [Google Scholar] [CrossRef]
- Paul, P.K.; Kumari, N.; Panigrahi, N.; Mishra, A.; Singh, R. Implementation of cell-to-cell routing scheme in a large scale conceptual hydrological model. Environ. Model. Softw. 2018, 101, 23–33. [Google Scholar] [CrossRef]
- Langsholt, E.; Lawrence, D.; Wong, W.; Andjelic, M.; Ivkovic, M.; Vujadinovic, M. Effects of Climate Change in the Kolubara and Toplica Catchments, Serbia; Norwegian Water Resources and Energy Directorate: Oslo, Norway, 2013. [Google Scholar]
- Shiwakoti, S. Hydrological modeling and climate change impact assessment using HBV light model: A case study of Karnali River basin. Iran. J. Energy Environ. 2017, 8, 296–304. [Google Scholar]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Kay, A.; Davies, H.; Bell, V.; Jones, R. Comparison of uncertainty sources for climate change impacts: Flood frequency in England. Clim. Chang. 2009, 92, 41–63. [Google Scholar] [CrossRef]
- Konz, M.; Seibert, J. On the value of glacier mass balances for hydrological model calibration. J. Hydrol. 2010, 385, 238–246. [Google Scholar] [CrossRef] [Green Version]
- Hay, L.E.; Wilby, R.L.; Leavesley, G.H. A comparison of delta change and downscaled GCM scenarios for three mountainous basins in the United States 1. J. Am. Water Resour. Assoc. 2000, 36, 387–397. [Google Scholar] [CrossRef]
- Wilby, R.L.; Hay, L.E.; Gutowski, W.J., Jr.; Arritt, R.W.; Takle, E.S.; Pan, Z.; Leavesley, G.H.; Clark, M.P. Hydrological responses to dynamically and statistically downscaled climate model output. Geophys. Res. Lett. 2000, 27, 1199–1202. [Google Scholar] [CrossRef] [Green Version]
- Chu, J.; Xia, J.; Xu, C.-Y.; Singh, V. Statistical downscaling of daily mean temperature, pan evaporation and precipitation for climate change scenarios in Haihe River, China. Theor. Appl. Climatol. 2010, 99, 149–161. [Google Scholar] [CrossRef]
- Thompson, J.; Green, A.; Kingston, D.; Gosling, S. Assessment of uncertainty in river flow projections for the Mekong River using multiple GCMs and hydrological models. J. Hydrol. 2013, 486, 1–30. [Google Scholar] [CrossRef]
- Mahmood, R.; Babel, M.S. Evaluation of SDSM developed by annual and monthly sub-models for downscaling temperature and precipitation in the Jhelum basin, Pakistan and India. Theor. Appl. Climatol. 2013, 113, 27–44. [Google Scholar] [CrossRef]
- Houben, G.; Tünnermeier, T.; Eqrar, N.; Himmelsbach, T. Hydrogeology of the Kabul Basin (Afghanistan), part II: Groundwater geochemistry. Hydrogeol. J. 2009, 17, 935–948. [Google Scholar] [CrossRef]
- Sarwar, S. Reservoir Life Expectancy in Relation to Climate and Land-Use Changes: Case Study of the Mangla Reservoir in Pakistan. Ph.D. Thesis, University of Waikato, Hamilton, New Zealand, 2013. [Google Scholar]
- Ali, S.; Li, D.; Congbin, F.; Khan, F. Twenty first century climatic and hydrological changes over Upper Indus Basin of Himalayan region of Pakistan. Environ. Res. Lett. 2015, 10, 014007. [Google Scholar] [CrossRef]
- Hewitt, K.; Young, G. Snow and ice hydrology project: Upper Indus basin. Overall Rep. Can. Cent. 1990, 4, 203–232. [Google Scholar]
- Irmak, S.; Irmak, A.; Allen, R.; Jones, J. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates. J. Irrig. Drain. Eng. 2003, 129, 336–347. [Google Scholar] [CrossRef]
- Bocchiola, D.; Diolaiuti, G.; Soncini, A.; Mihalcea, C.; D’agata, C.; Mayer, C.; Lambrecht, A.; Rosso, R.; Smiraglia, C. Prediction of future hydrological regimes in poorly gauged high altitude basins: The case study of the upper Indus, Pakistan. Hydrol. Earth Syst. Sci. 2011, 15, 2059–2075. [Google Scholar] [CrossRef] [Green Version]
- Meenu, R.; Rehana, S.; Mujumdar, P. Assessment of hydrologic impacts of climate change in Tunga–Bhadra river basin, India with HEC-HMS and SDSM. Hydrol. Process. 2013, 27, 1572–1589. [Google Scholar] [CrossRef]
- Verma, A.K.; Jha, M.K.; Mahana, R.K. Evaluation of HEC-HMS and WEPP for simulating watershed runoff using remote sensing and geographical information system. Paddy Water Environ. 2010, 8, 131–144. [Google Scholar] [CrossRef]
- Khalid, S.; Rehman, S.U.; Shah, S.M.A.; Naz, A.; Saeed, B.; Alam, S.; Ali, F.; Gul, H. Hydro-meteorological characteristics of Chitral River basin at the peak of the Hindukush range. Nat. Sci. 2013, 5, 987–992. [Google Scholar] [CrossRef] [Green Version]
- Darbandsari, P.; Coulibaly, P. Inter-comparison of lumped hydrological models in data-scarce watersheds using different precipitation forcing data sets: Case study of Northern Ontario, Canada. J. Hydrol. Reg. Stud. 2020, 31, 100730. [Google Scholar] [CrossRef]
- Dinh, K.D.; Anh, T.N.; Nguyen, N.Y.; Bui, D.D.; Srinivasan, R. Evaluation of grid-based rainfall products and water balances over the Mekong river Basin. Remote Sens. 2020, 12, 1858. [Google Scholar] [CrossRef]
- Mondal, Y.; Chiang, J.C.; Koo, M. Statistical Downscaling of Last Glacial Maximum and mid-Holocene climate simululations over the Continental United States. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014; p. IN21A-3689. [Google Scholar]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.; Shrestha, A.B.; Bierkens, M.F. Climate change impacts on the upper indus hydrology: Sources, shifts and extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Pomeroy, J.W. Snowmelt runoff sensitivity analysis to drought on the Canadian prairies. Hydrol. Process. Int. J. 2007, 21, 2594–2609. [Google Scholar] [CrossRef]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef] [Green Version]
- Beniston, M. Climate Variability and Change in High Elevation Regions: Past, Present & Future; Springer: Dordrecht, The Netherlands, 2003; Volume 59, pp. 1–4. [Google Scholar]
- Beniston, M.; Diaz, H.; Bradley, R. Climatic change at high elevation sites: An overview. Clim. Chang. 1997, 36, 233–251. [Google Scholar] [CrossRef]
- Ahmad, S.; Israr, M.; Liu, S.; Hayat, H.; Gul, J.; Wajid, S.; Ashraf, M.; Baig, S.U.; Tahir, A.A. Spatio-temporal trends in snow extent and their linkage to hydro-climatological and topographical factors in the Chitral River Basin (Hindukush, Pakistan). Geocarto Int. 2020, 35, 711–734. [Google Scholar] [CrossRef]
- Archer, D.; Fowler, H. Seasonal forecasting of runoff on the River Jhelum, Pakistan, using meteorological data. J. Hydrol. 2008, 361, 10–23. [Google Scholar] [CrossRef]
- Khalida, K.; Muhammad, Y.; Yasir, L.; Ghulam, N. Detection of river flow trends and variability analysis of Upper Indus Basin, Pakistan. Sci. Int. (Lahore) 2015, 27, 1261–1270. [Google Scholar]
- Hock, R.; Holmgren, B. A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden. J. Glaciol. 2005, 51, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Larson, J.W. Visualizing climate variability with time-dependent probability density functions, detecting it using information theory. Procedia Comput. Sci. 2012, 9, 917–926. [Google Scholar] [CrossRef] [Green Version]
- Krol, M.; Jaeger, A.; Bronstert, A.; Güntner, A. Integrated modelling of climate, water, soil, agricultural and socio-economic processes: A general introduction of the methodology and some exemplary results from the semi-arid north-east of Brazil. J. Hydrol. 2006, 328, 417–431. [Google Scholar] [CrossRef]
- Minville, M.; Brissette, F.; Leconte, R. Uncertainty of the impact of climate change on the hydrology of a nordic watershed. J. Hydrol. 2008, 358, 70–83. [Google Scholar] [CrossRef]
- Ahmad, Z.; Hafeez, M.; Ahmad, I. Hydrology of mountainous areas in the upper Indus Basin, Northern Pakistan with the perspective of climate change. Environ. Monit. Assess. 2012, 184, 5255–5274. [Google Scholar] [CrossRef] [PubMed]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef] [Green Version]
- Vervoort, R.W.; Florke, M.; Hattermann, F.F.; Huang, S.; Koch, H.; Krysanova, V.; Pechlivanidis, I.G.; Plotner, S.; Reinhardt, J.; Seidou, O. Evaluation of sources of uncertainty in projected hydrological changes under climate change in 12 large-scale river basins. Clim. Chang. 2017, 141, 419–433. [Google Scholar]
- Immerzeel, W.W.; Droogers, P.; De Jong, S.; Bierkens, M. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.P.; Bierkens, M.F. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef]
- Seibert, J. Multi-criteria calibration of a conceptual runoff model using a genetic algorithm. Hydrol. Earth Syst. Sci. 2000, 4, 215–224. [Google Scholar] [CrossRef] [Green Version]
- Seibert, J.; Vis, M.J.P.P. Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrol. Earth Syst. Sci. 2012, 16, 3315–3325. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Teukolsky, S.A.; Vettering, W.T.; Flannery, B.P. Numerical Recipes the Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; ISBN 9788578110796. [Google Scholar]
- Burhan, A.; Waheed, I.; Syed, A.; Rasul, G.; Shreshtha, A.; Shea, J. Generation of high-resolution gridded climate fields for the upper Indus River Basin by downscaling CMIP5 outputs. J. Earth Sci. Clim. Chang. 2015, 6, 1. [Google Scholar]
- Bokhari, S.A.A.; Ahmad, B.; Ali, J.; Ahmad, S.; Mushtaq, H.; Rasul, G. Future climate change projections of the Kabul River Basin using a multi-model ensemble of high-resolution statistically downscaled data. Earth Syst. Environ. 2018, 2, 477–497. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Kopec, E.G.; Lemma, M.; Connor, S.J. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model: Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrkoping, Sweden, 1992. [Google Scholar]
- Arnell, N. Climate-change impacts on river flows in Britain: The UKCIPO2 scenarios. Water Environ. J. 2004, 18, 112–117. [Google Scholar] [CrossRef]
- Sudheer, K.; Chaubey, I.; Garg, V.; Migliaccio, K.W. Impact of time-scale of the calibration objective function on the performance of watershed models. Hydrol. Process. Int. J. 2007, 21, 3409–3419. [Google Scholar] [CrossRef]
- Shakir, A.S.; Ehsan, S. Climate change impact on river flows in Chitral watershed. Pak. J. Eng. Appl. Sci. 2016, 7, 12–22. [Google Scholar]
- Nyeko, M. Land Use Changes in Aswa Basin-Northern Uganda: Opportunities and Constrains to Water Resources Management; Università Degli Studi di Napoli Federico ii: Naples, Italy, 2010. [Google Scholar]
- Hill, A.F.; Minbaeva, C.K.; Wilson, A.M.; Satylkanov, R. Hydrologic Controls and Water Vulnerabilities in the Naryn River Basin, Kyrgyzstan: A Socio-Hydro Case Study of Water Stressors in Central Asia. Water 2017, 9, 325. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Li, W.; Xu, J.; Li, L. Extreme precipitation indices over China in CMIP5 models. Part I: Model evaluation. J. Clim. 2015, 28, 8603–8619. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Cracknell, A.P. Assessment of three long-term gridded climate products for hydro-climatic simulations in tropical river basins. Water 2017, 9, 229. [Google Scholar] [CrossRef] [Green Version]
- Roth, V.; Lemann, T. Comparing CFSR and conventional weather data for discharge and soil loss modelling with SWAT in small catchments in the Ethiopian Highlands. Hydrol. Earth Syst. Sci. 2016, 20, 921–934. [Google Scholar] [CrossRef] [Green Version]
- Su, B.; Huang, J.; Gemmer, M.; Jian, D.; Tao, H.; Jiang, T.; Zhao, C. Statistical downscaling of CMIP5 multi-model ensemble for projected changes of climate in the Indus River Basin. Atmos. Res. 2016, 178, 138–149. [Google Scholar] [CrossRef]
- Xue, L.; Zhu, B.; Yang, C.; Wei, G.; Meng, X.; Long, A.; Yang, G. Study on the characteristics of future precipitation in response to external changes over arid and humid basins. Sci. Rep. 2017, 7, 15148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Smith, P.K. Hydrological Modeling of Highly Glacierized Basins (Andes, Alps, and Central Asia). Water 2017, 9, 111. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Wang, X.; Piao, S.; Sun, L.; Ciais, P.; Zhang, Y.; Ma, C.; Gan, R.; He, C. Contrasting streamflow regimes induced by melting glaciers across the Tien Shan–Pamir–North Karakoram. Sci. Rep. 2018, 8, 16470. [Google Scholar] [CrossRef]
- Lutz, A.; Immerzeel, W.; Shrestha, A.; Bierkens, M. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587. [Google Scholar] [CrossRef] [Green Version]
- You, Q.; Min, J.; Kang, S. Rapid warming in the Tibetan Plateau from observations and CMIP5 models in recent decades. Int. J. Climatol. 2016, 36, 2660–2670. [Google Scholar] [CrossRef]
- Tabari, H.; Willems, P. Seasonally varying footprint of climate change on precipitation in the Middle East. Sci. Rep. 2018, 8, 4435. [Google Scholar] [CrossRef] [PubMed]
- Ozturk, T.; Turp, M.T.; Türkeş, M.; Kurnaz, M.L. Projected changes in temperature and precipitation climatology of Central Asia CORDEX Region 8 by using RegCM4. 3.5. Atmos. Res. 2017, 183, 296–307. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J. Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China. Atmos. Res. 2016, 178, 521–534. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, F.; Hao, Z.; Xu, C.; Yu, Z.; Wang, L.; Tong, K. Impact of projected climate change on the hydrology in the headwaters of the Yellow River basin. Hydrol. Process. 2015, 29, 4379–4397. [Google Scholar] [CrossRef]
- Folini, D.; Wild, M. The effect of aerosols and sea surface temperature on China’s climate in the late twentieth century from ensembles of global climate simulations. J. Geophys. Res. Atmos. 2015, 120, 2261–2279. [Google Scholar] [CrossRef]
- Bollasina, M.A.; Ming, Y.; Ramaswamy, V. Anthropogenic aerosols and the weakening of the South Asian summer monsoon. Science 2011, 334, 502–505. [Google Scholar] [CrossRef] [Green Version]
- Xin, J.; Gong, C.; Wang, S.; Wang, Y. Aerosol direct radiative forcing in desert and semi-desert regions of northwestern China. Atmos. Res. 2016, 171, 56–65. [Google Scholar] [CrossRef]
- Siegfried, T.; Bernauer, T.; Guiennet, R.; Sellars, S.; Robertson, A.W.; Mankin, J.; Bauer-Gottwein, P.; Yakovlev, A. Will climate change exacerbate water stress in Central Asia? Clim. Chang. 2012, 112, 881–899. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Liu, J.; Ahmad, I.; Ijaz, M.W.; Khan, M.I. Quantification of spatial temporal variability of snow cover and hydro-climatic variables based on multi-source remote sensing data in the Swat watershed, Hindukush Mountains, Pakistan. Meteorol. Atmos. Phys. 2019, 131, 467–486. [Google Scholar] [CrossRef]
- Luo, K.; Tao, F.; Moiwo, J.P.; Xiao, D. Attribution of hydrological change in Heihe River Basin to climate and land use change in the past three decades. Sci. Rep. 2016, 6, 33704. [Google Scholar] [CrossRef] [Green Version]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Reddy, V.; Smith, P.K. Impacts of climate change on the glacier melt runoff from five river basins. Trans. ASABE 2016, 59, 829–848. [Google Scholar]
- Garee, K.; Chen, X.; Bao, A.; Wang, Y.; Meng, F. Hydrological modeling of the upper indus basin: A case study from a high-altitude glacierized catchment Hunza. Water 2017, 9, 17. [Google Scholar] [CrossRef] [Green Version]
- Pendergrass, A.G.; Knutti, R.; Lehner, F.; Deser, C.; Sanderson, B.M. Precipitation variability increases in a warmer climate. Sci. Rep. 2017, 7, 17966. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Chen, Y.; Fang, G.; Li, Y. Multivariate assessment and attribution of droughts in Central Asia. Sci. Rep. 2017, 7, 1316. [Google Scholar] [CrossRef]
- Meng, X.; Long, A.; Wu, Y.; Yin, G.; Wang, H.; Ji, X. Simulation and spatiotemporal pattern of air temperature and precipitation in Eastern Central Asia using RegCM. Sci. Rep. 2018, 8, 3639. [Google Scholar] [CrossRef] [Green Version]
- Sorg, A.; Bolch, T.; Stoffel, M.; Solomina, O.; Beniston, M. Climate change impacts on glaciers and runoff in Tien Shan (Central Asia). Nat. Clim. Chang. 2012, 2, 725. [Google Scholar] [CrossRef]
- Olsson, O.; Gassmann, M.; Wegerich, K.; Bauer, M. Identification of the effective water availability from streamflows in the Zerafshan river basin, Central Asia. J. Hydrol. 2010, 390, 190–197. [Google Scholar] [CrossRef]
- Liu, J.; Luo, M.; Liu, T.; Bao, A.; De Maeyer, P.; Feng, X.; Chen, X. Local climate change and the impacts on hydrological processes in an arid alpine catchment in Karakoram. Water 2017, 9, 344. [Google Scholar] [CrossRef] [Green Version]
- Babur, M.; Babel, M.; Shrestha, S.; Kawasaki, A.; Tripathi, N. Assessment of climate change impact on reservoir inflows using multi climate-models under RCPs—The case of Mangla Dam in Pakistan. Water 2016, 8, 389. [Google Scholar] [CrossRef] [Green Version]
| Parameter | Explanation | Unit | Span | Value | |
|---|---|---|---|---|---|
| Meteorological data | P Calt | Gradient of precipitation | %/100 m | 12 | 12 |
| T Calt | Gradient of temperature | °C/100 m | 0.58 | 0.58 | |
| Snow and glacier routine | TT | Threshold temperature | °C | −5 | −1.48 |
| DDF | Degree-day factor of snow | mm/(°C_day) | 3 | 3 | |
| SCF | Snowfall correction factor | - | 0–2 | 0.76 | |
| CC | Coefficient of cooling | - | 0.03 | 0.03 | |
| CCW | Capacity to contain water | - | 0.14 | 0.14 | |
| Cg | Factor of increased melt office | - | 0.98 | 0.98 | |
| Ca | Factor of increased melting from the south slope to north slope | - | 1–2.5 | 1.2 | |
| Soil routine | FC | Maximum of SM (storage in the soil) | mm | 100–380 | 347.3 |
| LP | Threshold for reduction of evaporation (SM/FC) | - | 0.4–1 | 0.84 | |
| BETA | Shape coefficient | - | 1–4 | 2.3 | |
| Response routine | MFULB | Maximal flow from upper to lower G-W box | mm/day | 1–7 | 4.1 |
| RCUS | Recession coefficient (upper storage) | /day | 1–2 | 1.03 | |
| RCLS | Recession coefficient (lower storage) | /day | 0.01–0.6 | 0.08 | |
| Routing routine | MAX-BAX | Routing length of weighting function | /day | 2 | 1.3 |
| Data Type | Origin | Level of Precision | Explanation |
|---|---|---|---|
| Topography | USGS National Elevation Dataset | 30 × 30 m | DEM (Elevation) |
| Land-use data | European Space Agency (ESA) Global Land Cover http://ionia1.esrin.esa.int/ Access date: 3 August 2020 | 300 × 300 m | Classified land use, such as forests, agriculture, crops, water, etc. |
| Soil data | FAO–UNESCO global soil map http://www.fao.org/nr/land/soils/ Access date: 8 September 2020 | 5 km | Classified soil and physical properties, such as sand, silt, clay, bulk density, etc. |
| Climatic data | Pakistan Metrological Department (PMD) | Daily | Precipitation, temperature, solar radiation, wind speed; Balakot, Naran, Muzaffarabad, and Astore stations (2000–2016) |
| Sr. No. | Information | Area (km2) | % Area | HBV Land-Use Symbol |
|---|---|---|---|---|
| 1 | Agricultural croplands | 432.21 | 13.08 | AGRR |
| 2 | Urban areas | 271.85 | 11.26 | URLD |
| 3 | Deciduous forests | 15.67 | 0.49 | FRSD |
| 4 | Evergreen forests | 238.21 | 6.47 | FRSE |
| 5 | Rangeland | 73.21 | 32.06 | RNGB |
| 6 | Mixed forests | 708.46 | 3.95 | FRST |
| 7 | Grasslands | 568.42 | 18.3 | RNGE |
| 8 | Water Bodies | 410.57 | 14.39 | WATR |
| Total | - | 2718.6 | 100 | - |
| Sr. No. | Elevation (m) | Vegetation Zone (km2) | Barren Land Zone (km2) | Glaciation Zone (km2) | Total Area (km2) |
|---|---|---|---|---|---|
| 1 | 2160 | 482 | 122.75 | 5 | 662 |
| 2 | 3420 | 2750 | 450.16 | 2 | 2843 |
| 3 | 4750 | 4855 | 369.20 | 28.23 | 4675 |
| 4 | 5530 | 5328 | 40.186 | 720 | 5912 |
| 5 | 6380 | 2370 | 4.64 | 689 | 2431 |
| 6 | 7240 | 1542 | 2.48 | 123 | 467 |
| 7 | 8430 | 239 | 2.3 | 24.78 | 45 |
| Parameters | Units | Yearly | |
|---|---|---|---|
| Calibration | Validation | ||
| Coefficient of determination (R2) | 0.95 | 0.94 | |
| Nash–Sutcliffe efficiency (NS) | 0.88 | 0.85 | |
| Percentage bias (PBIAS) | % | 0.47 | 14.61 |
| Correlation coefficient (CC) | 0.95 | 0.94 | |
| Average error (AE) | Cumec | 0.01 | 0.24 |
| Average absolute error (AAE) | Cumec | 0.4 | 0.45 |
| Standard error (SE) | Cumec | 0.69 | 0.68 |
| Time Scale | GCMs | Mean (mm) | Correlation Coefficient (CC) | Average Error (AE) | Average Absolute Error (AAE) | PBIAS (%) |
|---|---|---|---|---|---|---|
| Daily | BCC-CSM2-MR | 8.02 4.83 | 0.39 0.48 | 7.3 5.8 | 14.3 16.4 | 97.1 −15.24 |
| Monthly | CAMS-CSMI-0 | 258.34 113.7 | 0.78 0.64 | 165.33 65.31 | 156.12 82.41 | 98.4 −17.25 |
| Rainy Season | MPI-ESMI-2-HR | 2675.4 1328.3 | 0.5 0.3 | 1568.7 342.3 | 471.5 181.5 | 113.1 −7.3 |
| Dry Season | HadGEM2AO | 421.2 165.1 | 0.7 0.8 | 289 119.4 | 107 83.4 | −52.7 −39.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soomro, S.-e.-h.; Hu, C.; Boota, M.W.; Wu, Q.; Soomro, M.H.A.A.; Zhang, L. Assessment of the Climatic Variability of the Kunhar River Basin, Pakistan. Water 2021, 13, 1740. https://doi.org/10.3390/w13131740
Soomro S-e-h, Hu C, Boota MW, Wu Q, Soomro MHAA, Zhang L. Assessment of the Climatic Variability of the Kunhar River Basin, Pakistan. Water. 2021; 13(13):1740. https://doi.org/10.3390/w13131740
Chicago/Turabian StyleSoomro, Shan-e-hyder, Caihong Hu, Muhammad Waseem Boota, Qiang Wu, Mairaj Hyder Alias Aamir Soomro, and Li Zhang. 2021. "Assessment of the Climatic Variability of the Kunhar River Basin, Pakistan" Water 13, no. 13: 1740. https://doi.org/10.3390/w13131740
APA StyleSoomro, S.-e.-h., Hu, C., Boota, M. W., Wu, Q., Soomro, M. H. A. A., & Zhang, L. (2021). Assessment of the Climatic Variability of the Kunhar River Basin, Pakistan. Water, 13(13), 1740. https://doi.org/10.3390/w13131740






