Hillslope Contribution to the Clark Instantaneous Unit Hydrograph: Application to the Seolmacheon Basin, Korea
Abstract
1. Introduction
2. Analytical Evaluation of the Clark IUH with Different Channel and Hillslope Velocities
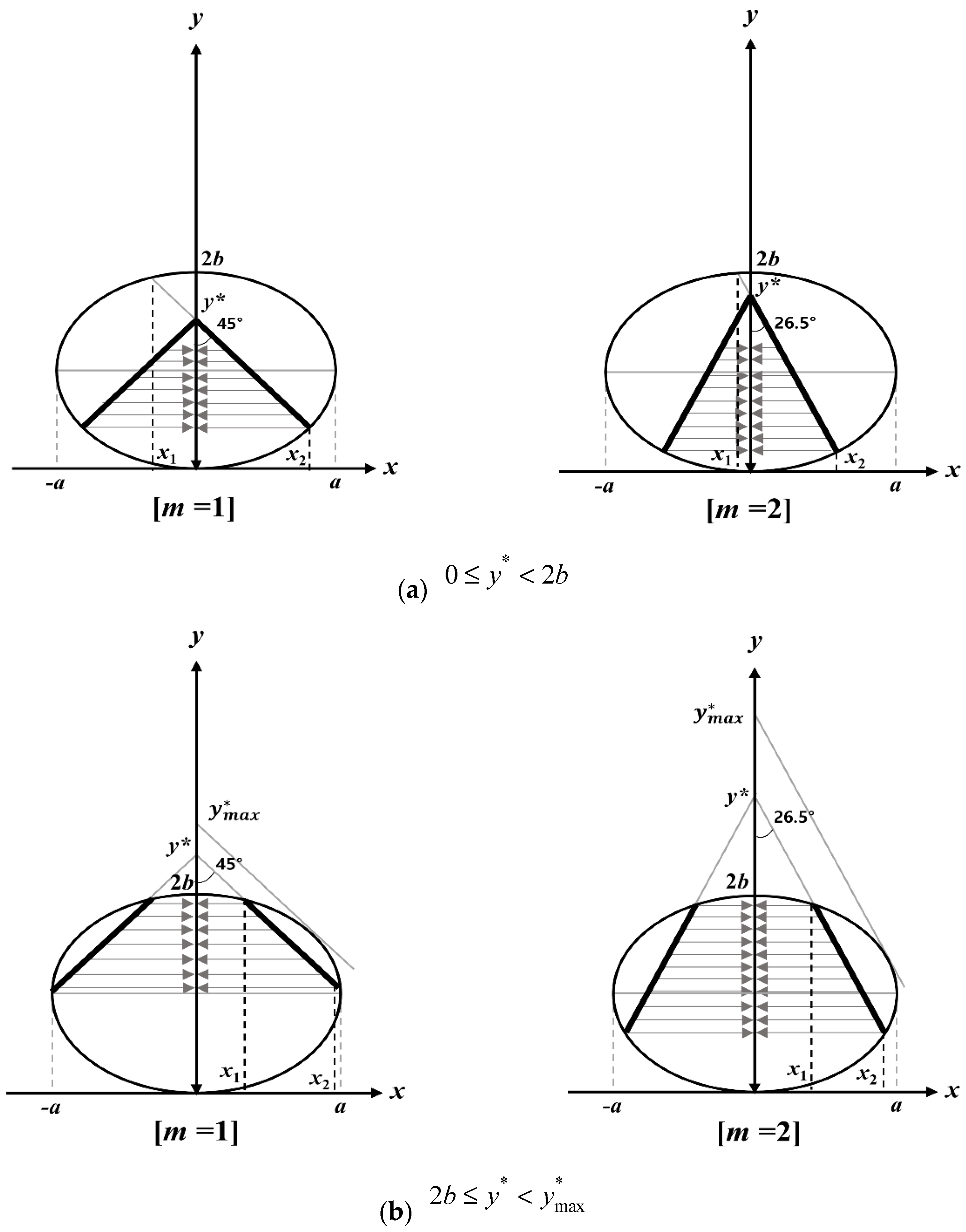
2.1. Time–Area Curve of an Ellipse
2.2. Clark IUH of an Ellipse
2.3. Application to an Elliptical Basin
3. Study Basin and Rainfall Events
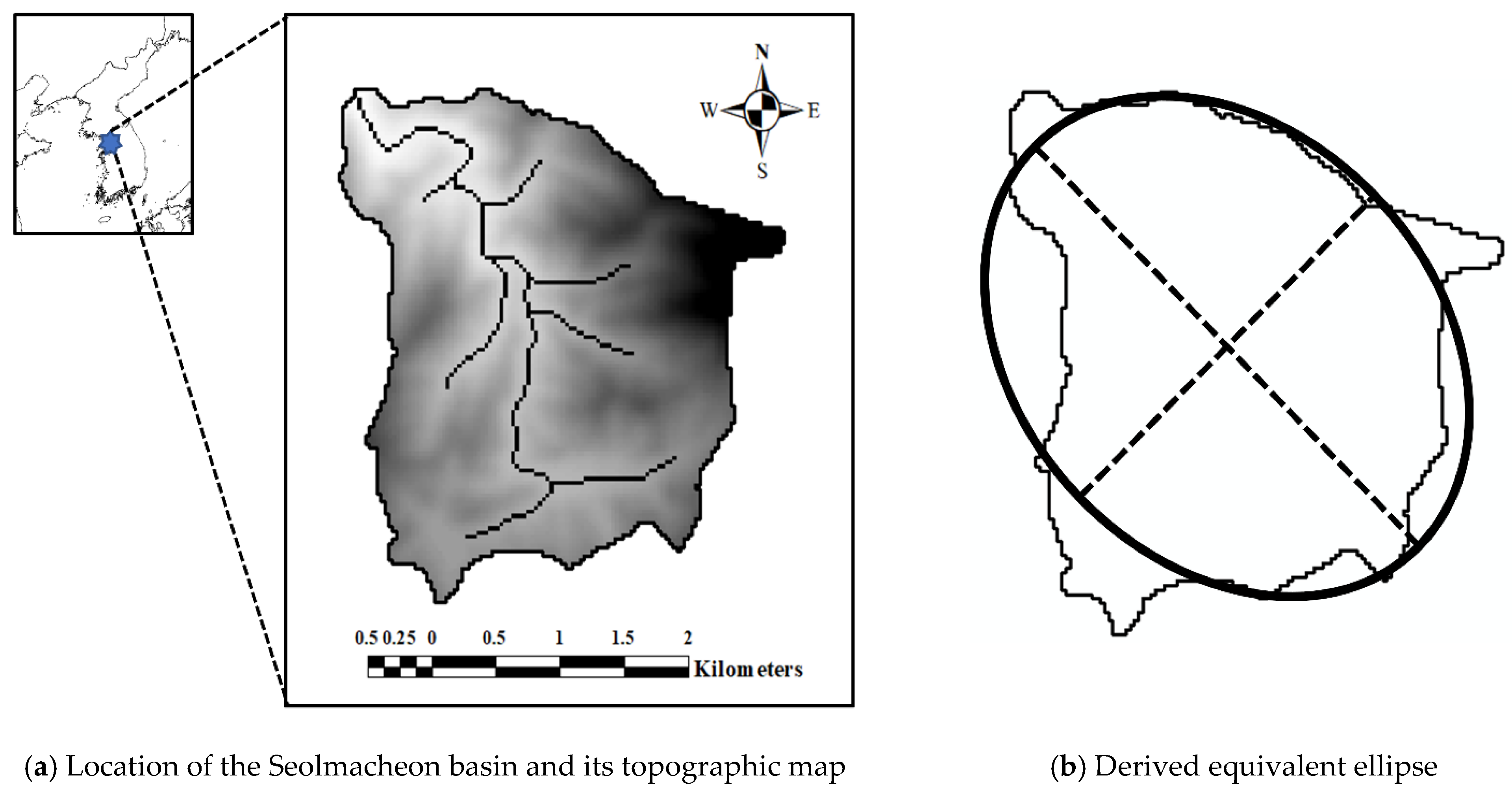
3.1. Study Basin
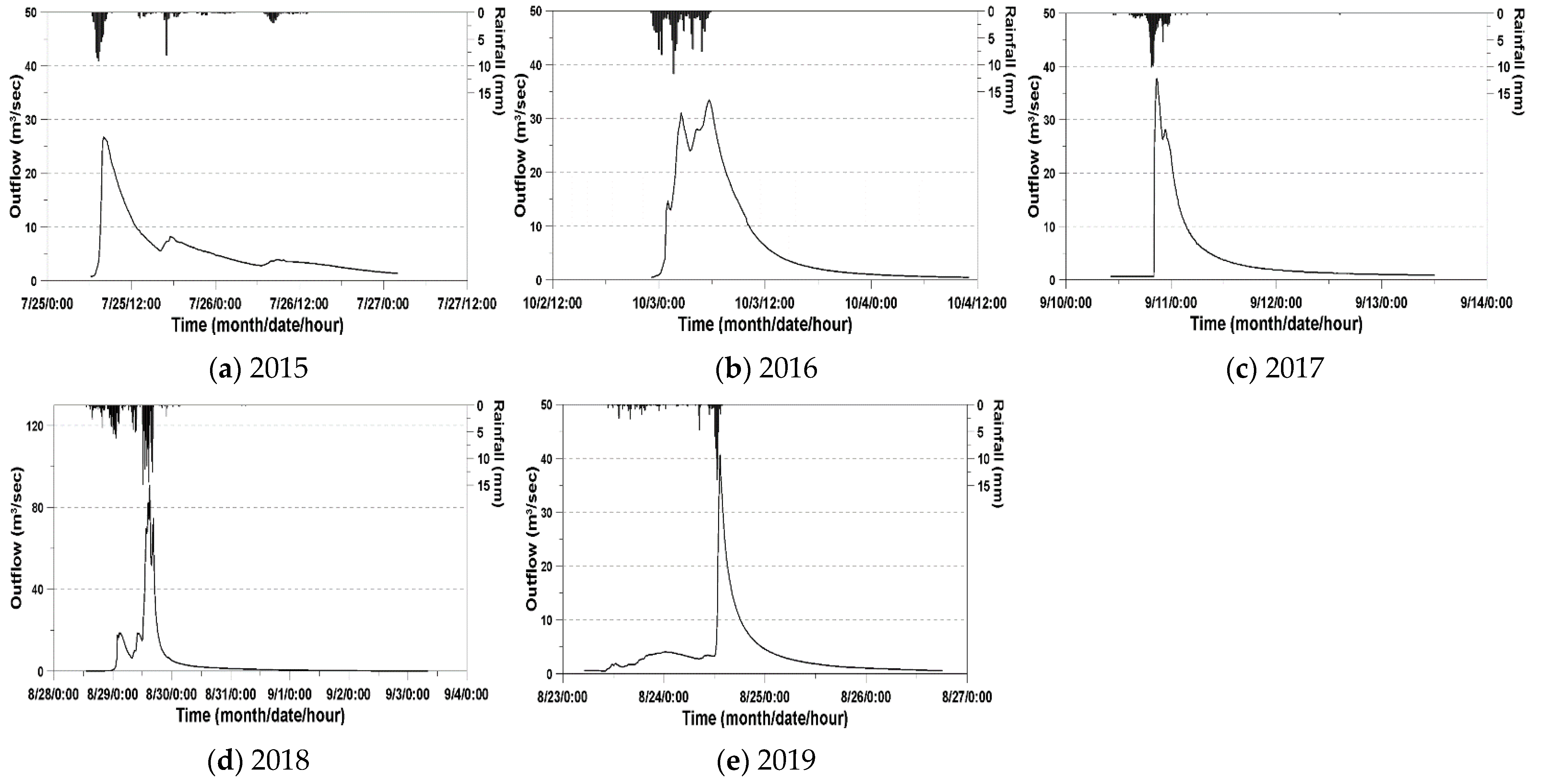
3.2. Rainfall Events
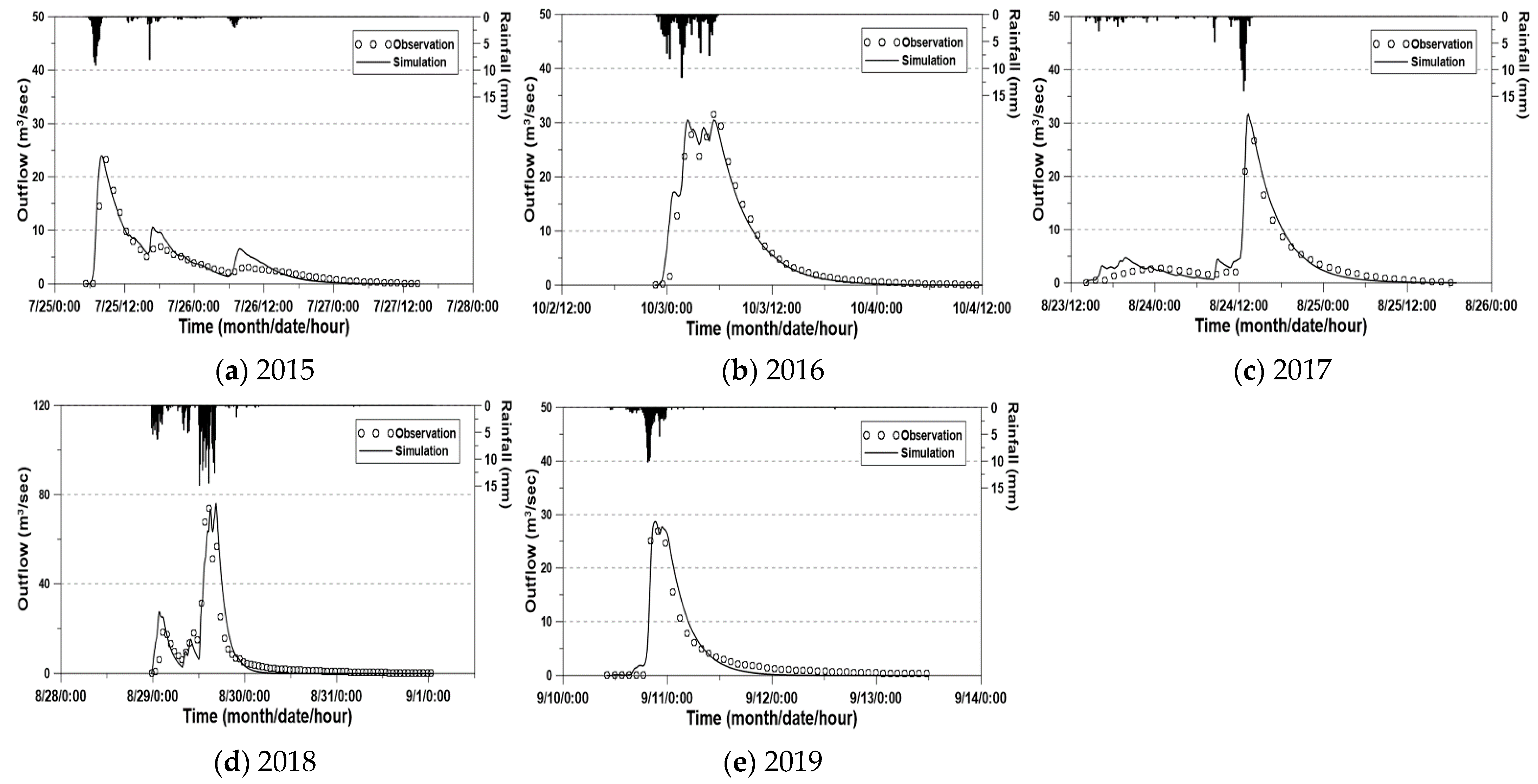
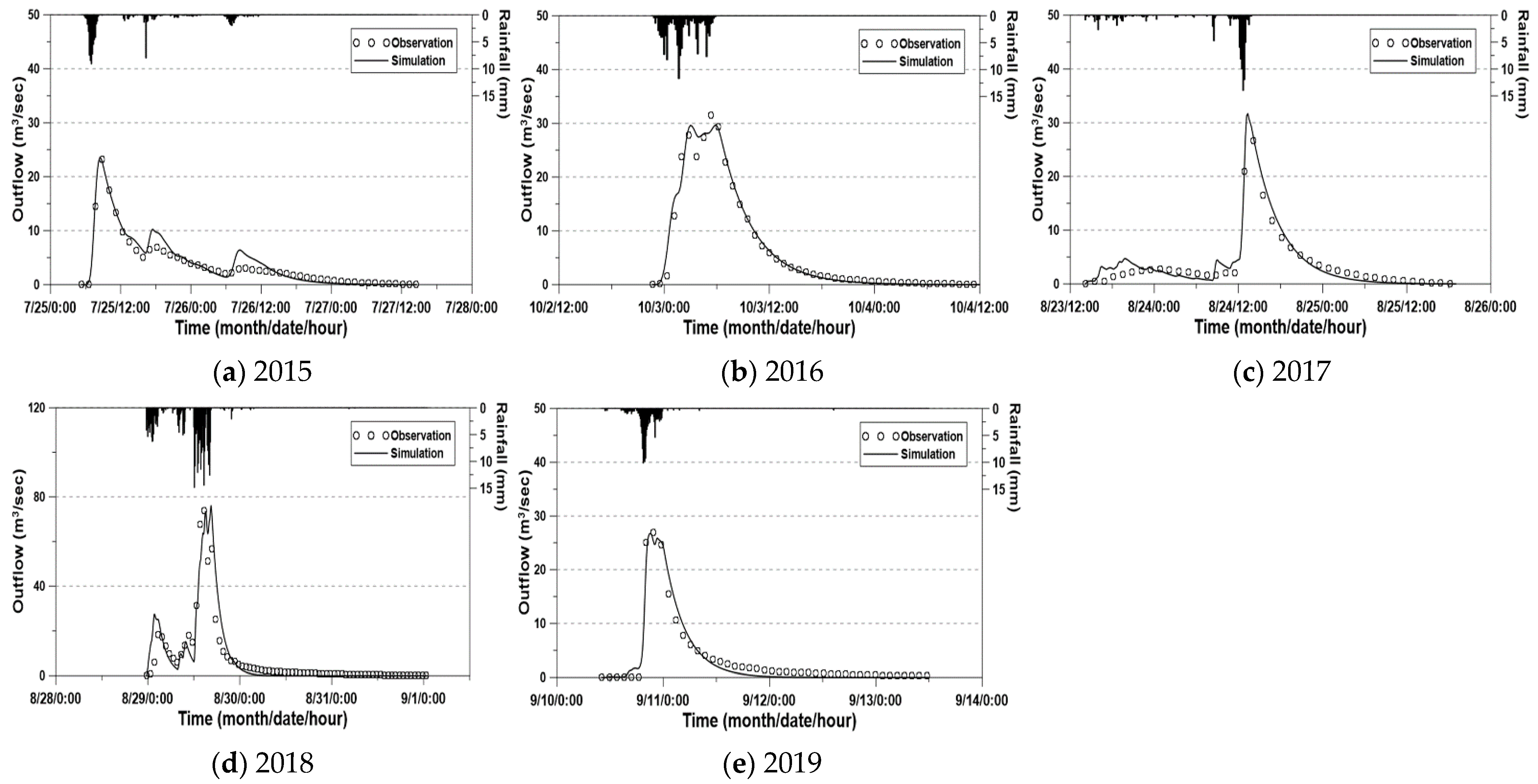
4. Results and Discussions
4.1. Clark IUH for Uniform Velocity Case (Baseline Case)
4.2. Clark IUH for Different Velocity Case (Consideration of the Hillslope Velocity)
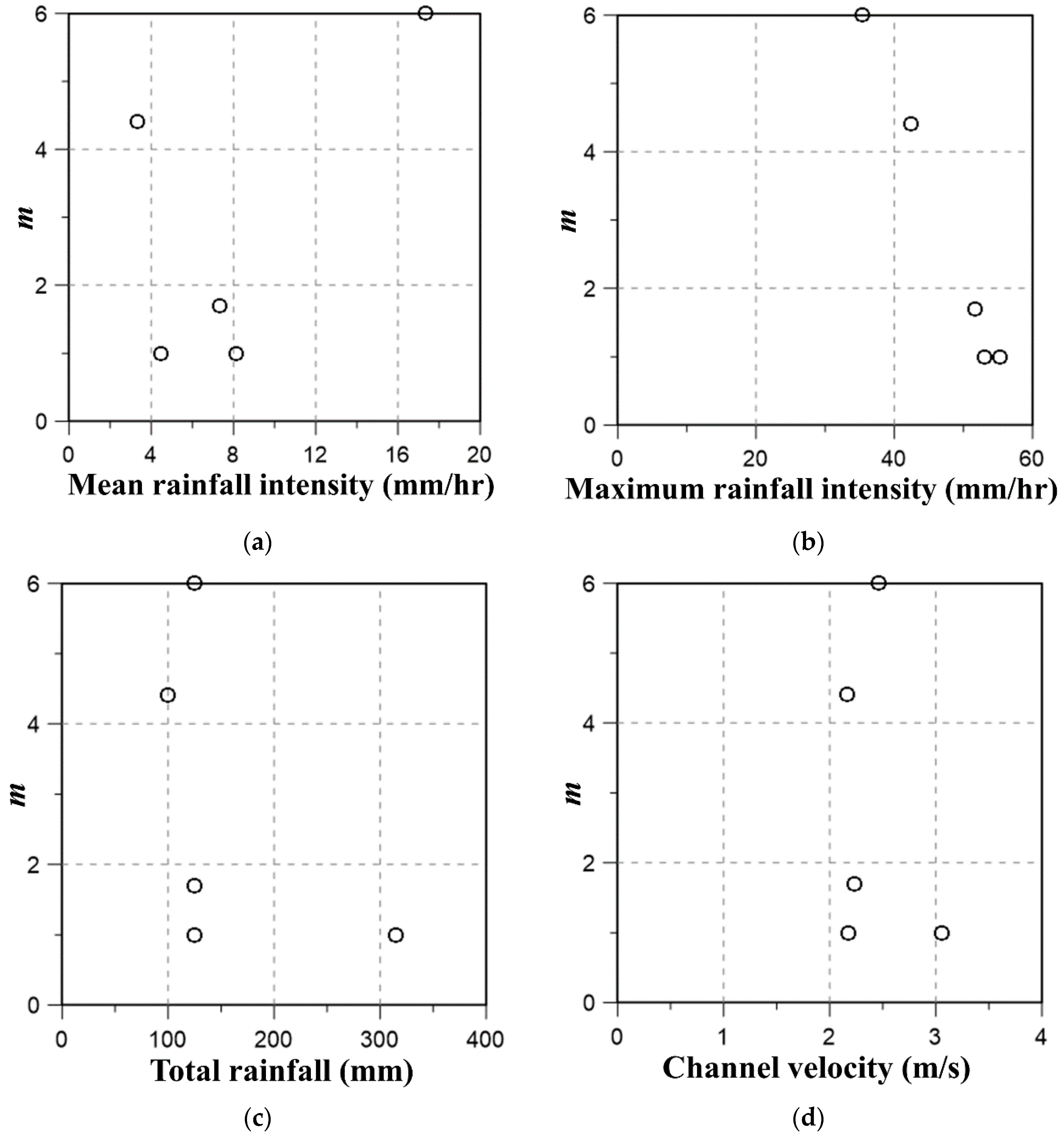
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- D’Odorico, P.; Rigon, R. Hillslope and channel contributions to the hydrologic response. Water Resour. Res. 2003, 39, WR001708. [Google Scholar] [CrossRef]
- Van der Tak, L.D.; Bras, R.L. Incorporating hillslope effects into the geomorphological instantaneous unit hydrograph. Water Resour. Res. 1990, 26, 2393–2400. [Google Scholar] [CrossRef]
- Robinson, J.S.; Sivapalan, M.; Snell, J.D. On the relative roles of hillslope processes, channel routing, and network morphology in the hydrologic response of natural catchments. Water Resour. Res. 1995, 31, 3089–3101. [Google Scholar] [CrossRef]
- Rinaldo, A.; Vogel, G.K.; Rigon, R.; Rodriguez-Iturbe, I. Can one gauge the shape of a basin? Water Resour. Res. 1995, 31, 1119–1127. [Google Scholar] [CrossRef]
- Snell, J.D.; Sivapalan, M. On geomorphological dispersion in natural catchments and the geomorphological unit hydrograph. Water Resour. Res. 1994, 30, 2311–2323. [Google Scholar] [CrossRef]
- Maidment, D.R.; Olivera, F.; Calver, A.; Eatherall, A.; Fraczek, W. Unit hydrograph derived from a spatially distributed velocity field. Hydrol. Process. 1996, 10, 831–844. [Google Scholar] [CrossRef]
- Muzik, I. Flood modelling with GIS-derived distributed unit hydrographs. Hydrol. Process. 1996, 10, 1401–1409. [Google Scholar] [CrossRef]
- Rodriguez, F.; Andrieu, H.; Creutin, J.D. Surface runoff in urban catchments: Morphological identification of unit hydrographs from urban databanks. J. Hydrol. 2003, 283, 146–168. [Google Scholar] [CrossRef]
- Pilgrim, D.H. Travel times and nonlinearity of flood runoff from tracer measurements on a small watershed. Water Resour. Res. 1976, 12, 487–496. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Alonso, G.; Nardi, F. Flow time estimation with spatially variable hillslope velocity in ungauged basins. Adv. Water Resour. 2010, 33, 1216–1223. [Google Scholar] [CrossRef]
- Sahoo, B.; Chatterjee, C.; Raghuwanshi, N.S.; Singh, R.; Kumar, R. Flood estimation by GIUH-based Clark and Nash models. J. Hydrol. Eng. 2006, 11, 515–525. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; González-Sanabria, M.; Bras, R.L. A geomorphoclimatic theory of the instantaneous unit hydrograph. Water Resour. Res. 1982, 18, 877–886. [Google Scholar] [CrossRef]
- Rinaldo, A.; Marani, A.; Rigon, R. Geomorphological dispersion. Water Resour. Res. 1991, 27, 513–525. [Google Scholar] [CrossRef]
- Kumar, R.; Chatterjee, C.; Singh, R.D.; Lohani, A.K.; Kumar, S. Runoff estimation for an ungauged catchment using geomorphological instantaneous unit hydrograph (GIUH) models. Hydrol. Process. 2007, 21, 1829–1840. [Google Scholar] [CrossRef]
- Clark, C.O. Storage and the unit hydrograph. Trans. Am. Soc. Civil Eng. 1945, 110, 1419–1446. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y.; De Troch, F.P.; Troch, P.A. A dynamic hillslope response model in a geomorphology based rainfall-runoff model. J. Hydrol. 1996, 178, 1–18. [Google Scholar] [CrossRef]
- Yang, D.; Herath, S.; Musiake, K. A hillslope-based hydrological model using catchment area and width functions. Hydrol. Sci. J. 2002, 47, 49–65. [Google Scholar] [CrossRef]
- Di Lazzaro, M. Regional analysis of storm hydrographs in the rescaled width function framework. J. Hydrol. 2009, 373, 352–365. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Nardi, F. A parsimonious geomorphological unit hydrograph for rainfall–runoff modelling in small ungauged basins. Hydrol. Sci. J. 2012, 57, 73–83. [Google Scholar] [CrossRef]
- Zhang, H.L.; Wang, Y.J.; Wang, Y.Q.; Li, D.X.; Wang, X.K. The effect of watershed scale on HEC-HMS calibrated parameters: A case study in the Clear Creek watershed in Iowa, US. Hydrol. Earth Syst. Sci. 2013, 17, 2735–2745. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Volk, M.; Williams, J.R.; Bosch, D.D. Assessment of different representations of spatial variability on SWAT model performance. Trans. ASABE 2010, 53, 1433–1443. [Google Scholar] [CrossRef]
- Rathjens, H.; Oppelt, N.; Bosch, D.D.; Arnold, J.G.; Volk, M. Development of a grid-based version of the SWAT landscape model. Hydrol. Process. 2015, 29, 900–914. [Google Scholar] [CrossRef]
- Hoang, L.; Schneiderman, E.M.; Moore, K.E.; Mukundan, R.; Owens, E.M.; Steenhuis, T.S. Predicting saturation-excess runoff distribution with a lumped hillslope model: SWAT-HS. Hydrol. Process. 2017, 31, 2226–2243. [Google Scholar] [CrossRef]
- Bouraoui, F.; Dillaha, T.A. ANSWERS-2000: Runoff and sediment transport model. J. Environ. Eng. 1996, 122, 493–502. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L. Gridded Surface Subsurface Hydrological Analysis (GSSHA) User’s Manual; Version 1.43 for Watershed Modeling System 6.1; Engineer Research and Development Center, U.S. Army Corps of Engineers: Washington, DC, USA, 2006. [Google Scholar]
- Zhang, Y.; Shuster, W. The Comparative Accuracy of Two Hydrologic Models in Simulating Warm-Season Runoff for Two Small, Hillslope Catchments. J. Am. Water Resour. Assoc. 2014, 50, 434–447. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, J. Assessment of the effects of DEM gridding on the predictions of basin runoff using MIKE SHE and a modelling resolution of 600 m. J. Hydrol. 2007, 334, 73–87. [Google Scholar] [CrossRef]
- Noh, S.J.; An, H.; Kim, S.; Kim, H. Simulation of soil moisture on a hillslope using multiple hydrologic models in comparison to field measurements. J. Hydrol. 2015, 523, 342–355. [Google Scholar] [CrossRef]
- Loritz, R.; Hassler, S.K.; Jackisch, C.; Allroggen, N.; Schaik, L.V.; Wienhöfer, J.; Zehe, E. Picturing and modeling catchments by representative hillslopes. Hydrol. Earth Syst. Sci. 2017, 21, 1225–1249. [Google Scholar] [CrossRef]
- Heerdegen, R.G.; Reich, B.M. Unit hydrographs for catchments of different sizes and dissimilar regions. J. Hydrol. 1974, 22, 143–153. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Littlewood, I.G.; Whitehead, P.G. Computation of the instantaneous unit hydrograph and identifiable component flows with application to two small upland catchments. J. Hydrol. 1990, 117, 275–300. [Google Scholar] [CrossRef]
- Cleveland, T.G.; He, X.; Asquith, W.H.; Fang, X.; Thompson, D.B. Instantaneous unit hydrograph evaluation for rainfall-runoff modeling of small watersheds in north and south central Texas. J. Irrig. Drain. Eng. 2006, 132, 479–485. [Google Scholar] [CrossRef]
- Chow, V.T. Applied Hydrology; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Ahmad, M.M.; Ghumman, A.R.; Ahmad, S. Estimation of Clark’s instantaneous unit hydrograph parameters and development of direct surface runoff hydrograph. Water Resour. Manag. 2009, 23, 2417–2435. [Google Scholar] [CrossRef]
- Seong, K.W.; Lee, Y.H. A practical estimation of Clark IUH parameters using root selection and linear programming. Hydrol. Process. 2011, 25, 3676–3687. [Google Scholar] [CrossRef]
- Osman, S.; Abustan, I. Estimating the Clark Instantaneous Unit Hydrograph parameters for selected gauged catchments in the west Coast of Peninsular Malaysia. ASEAN Eng. J. 2011, 1, 126–141. [Google Scholar]
- Yoo, C.; Lee, J.; Park, C.; Jun, C. Method for estimating concentration time and storage coefficient of the Clark model using rainfall-runoff measurements. J. Hydrol. Eng. 2014, 19, 626–634. [Google Scholar] [CrossRef]
- Kar, K.K.; Yang, S.K.; Lee, J.H. Assessing unit hydrograph parameters and peak runoff responses from storm rainfall events: A case study in Hancheon Basin of Jeju Island. J. Environ. Sci. Int. 2015, 24, 437–447. [Google Scholar] [CrossRef][Green Version]
- Hemmati, M.; Shahnazi, M.; Ahmadi, H.; Salarjazi, M. Flood Peak Flow Simulation and Determination of Flood Source Area in the QARANQU Watershed Using Hydrological Mod-Clark Model and GIS. Irrig. Water Eng. 2017, 7, 65–80. [Google Scholar]
- Cho, Y.; Engel, B.A.; Merwade, V.M. A spatially distributed Clark’s unit hydrograph based hybrid hydrologic model (Distributed-Clark). Hydrol. Sci. J. 2018, 63, 1519–1539. [Google Scholar] [CrossRef]
- Moradi, H.R.; Asadi, H.; Sadeghi, S.H.; Telvari, A. Evaluation of Time-Area Accuracy in Developing IUH. J. Range Watershed Manag. 2015, 68, 647–656. [Google Scholar]
- Sabzevari, T. Runoff prediction in ungauged catchments using the gamma dimensionless time-area method. Arab. J. Geosci. 2017, 10, 131. [Google Scholar] [CrossRef]
- Fariborzi, H.; Sabzevari, T.; Noroozpour, S.; Mohammadpour, R. Prediction of the subsurface flow of hillslopes using a subsurface time-area model. Hydrogeol. J. 2019, 27, 1401–1417. [Google Scholar] [CrossRef]
- Jun, C.; Yoo, C. Relative roles of time-area curve and storage coefficient on the shape of Clark’s instantaneous unit hydrograph: An analytical approach. J. Hydrol. Eng. 2021, 26, 06021001. [Google Scholar] [CrossRef]
- Moussa, R. On morphometric properties of basins, scale effects and hydrological response. Hydrol. Process. 2003, 17, 33–58. [Google Scholar] [CrossRef]
- USACE (United States Army Corps of Engineers). Hydrologic Modeling System HEC-HMS: User’s Manual; US Army Corps of Engineers: Washington, DC, USA, 2016. [Google Scholar]
- Langbein, W.B. Topographic Characteristics of Drainage Basins; U.S. Geological Survey: Reston, VA, USA, 1947. [Google Scholar]
- Taylor, A.B.; Schwarz, H.E. Unit hydrograph lag and peak flow related to basin characteristics. Eos Trans. Am. Geophys. Union. 1952, 33, 235–246. [Google Scholar] [CrossRef]
- Wu, I.P. Design hydrographs for small watershed in Indiana. J. Hydraul. Division. 1963, 89, 36–65. [Google Scholar] [CrossRef]
- Kim, J.C.; Jung, K.S.; Kim, J.H. The correlation analysis between new catchment shape descriptor and the lag time of Nash model. J. Korea Water Resour. Assoc. 2004, 37, 1065–1074. [Google Scholar] [CrossRef]
- McCuen, R.H. Hydrologic Analysis and Design, 3rd ed.; Prentice Hall: New Jersey, NJ, USA, 2005. [Google Scholar]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Hansen, E.M.; Schreiner, L.C.; Miller, J.F. Application of Probable Maximum Precipitation Estimates—United States East of the 105th Meridian, Hydrometeorological Report No. 52; National Weather Service: Washington, DC, USA, 1982. [Google Scholar]
- Suyanto, A.; O’Connell, P.E.; Metcalfe, A.V. The influence of storm characteristics and catchment conditions on extreme flood response: A case study based on the Brue river basin. U.K. Surv. Geophys. 1995, 16, 201–225. [Google Scholar] [CrossRef]
- USACE (United States Army Corps of Engineers). Hydrologic Modeling System HEC-HMS Technical Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2000. [Google Scholar]
- Singh, S.K. Clark’s and Espey’s unit hydrographs vs. the gamma unit hydrograph. Hydrol. Sci. J. 2005, 50, 1053–1067. [Google Scholar]
- Quinn, P.F.B.J.; Beven, K.; Chevallier, P.; Planchon, O. The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
- Onda, Y.; Tsujimura, M.; Tabuchi, H. The role of subsurface water flow paths on hillslope hydrological processes, landslides and landform development in steep mountains of Japan. Hydrol. Process. 2004, 18, 637–650. [Google Scholar] [CrossRef]
- Tarolli, P.; Dalla Fontana, G. Hillslope-to-valley transition morphology: New opportunities from high resolution DTMs. Geomorphology 2009, 113, 47–56. [Google Scholar] [CrossRef]
- Sabzevari, T.; Noroozpour, S. Effects of hillslope geometry on surface and subsurface flows. Hydrogeol. J. 2014, 22, 1593–1604. [Google Scholar] [CrossRef]
- Scaini, A.; Hissler, C.; Fenicia, F.; Juilleret, J.; Iffly, J.F.; Pfister, L.; Beven, K. Hillslope response to sprinkling and natural rainfall using velocity and celerity estimates in a slate-bedrock catchment. J. Hydrol. 2018, 558, 366–379. [Google Scholar] [CrossRef]
- Wacha, K.M.; Papanicolaou, A.N.; Giannopoulos, C.P.; Abban, B.K.; Wilson, C.G.; Zhou, S.; Hatfield, J.L.; Filley, T.R.; Hou, T. The role of hydraulic connectivity and management on soil aggregate size and stability in the Clear Creek Watershed, Iowa. Geosciences 2018, 8, 470. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Valdes, J.B. The geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.C.; Wang, C.T. A representation of an instantaneous unit hydrograph from geomorphology. Water Resour. Res. 1980, 16, 855–862. [Google Scholar] [CrossRef]
- Ascough, J.C., II; Baffaut, C.; Nearing, M.A.; Liu, B.Y. The WEPP watershed model: I. Hydrology and erosion. Trans. ASAE 1997, 40, 921–933. [Google Scholar] [CrossRef]
- Broda, S.; Larocque, M.; Paniconi, C. Simulation of distributed base flow contributions to streamflow using a hillslope-based catchment model coupled to a regional-scale groundwater model. J. Hydrol. Eng. 2014, 19, 907–917. [Google Scholar] [CrossRef]
- Hallema, D.W.; Moussa, R. A model for distributed GIUH-based flow routing on natural and anthropogenic hillslopes. Hydrol. Process. 2014, 28, 4877–4895. [Google Scholar] [CrossRef]
- Hallema, D.W.; Moussa, R.; Sun, G.; McNulty, S.G. Surface storm flow prediction on hillslopes based on topography and hydrologic connectivity. Ecol. Process. 2016, 5, 1–13. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications: North Hempstead, NY, USA, 1970. [Google Scholar]
- KICT (Korea Institute of Civil Engineering and Building Technology). Operation and Research on the Hydrologic Characteristics of the Experimental Catchment; Korea Institute of Civil Engineering and Building Technology: Goyang, Korea, 2004. [Google Scholar]
- KICT (Korea Institute of Civil Engineering and Building Technology). Hydrological Survey for the Water Disaster Prevention Response; Korea Institute of Civil Engineering and Building Technology: Goyang, Korea, 2018. [Google Scholar]
- O’Kelly, J.J. The employment of unit hydrographs to determine the flows of irish arterial drainage channels. Proc. Inst. Civ. Eng. 1955, 4, 365–412. [Google Scholar]
- Wilson, B.N.; Brown, J.W. Development and evaluation of a dimensionless unit hydrograph. J. Am. Water Resour. Assoc. 1992, 28, 397–408. [Google Scholar] [CrossRef]
- Hydrologic Engineering Center (HEC). Hydrologic Modeling System HEC-HMS: Technical Reference Manual; Hydrologic Engineering Center, Corps of Engineers, US Army: Washington, DC, USA, 2000. [Google Scholar]
- Rodríguez-Iturbe, I.; Devoto, G.; Valdés, J.B. Discharge response analysis and hydrologic similarity: The interrelation between the geomorphologic IUH and the storm characteristics. Water Resour. Res. 1979, 15, 1435–1444. [Google Scholar] [CrossRef]
- Bhaskar, N.R.; Parida, B.P.; Nayak, A.K. Flood estimation for ungauged catchments using the GIUH. J. Water Resour. Plan. Manag. 1997, 123, 228–238. [Google Scholar] [CrossRef]
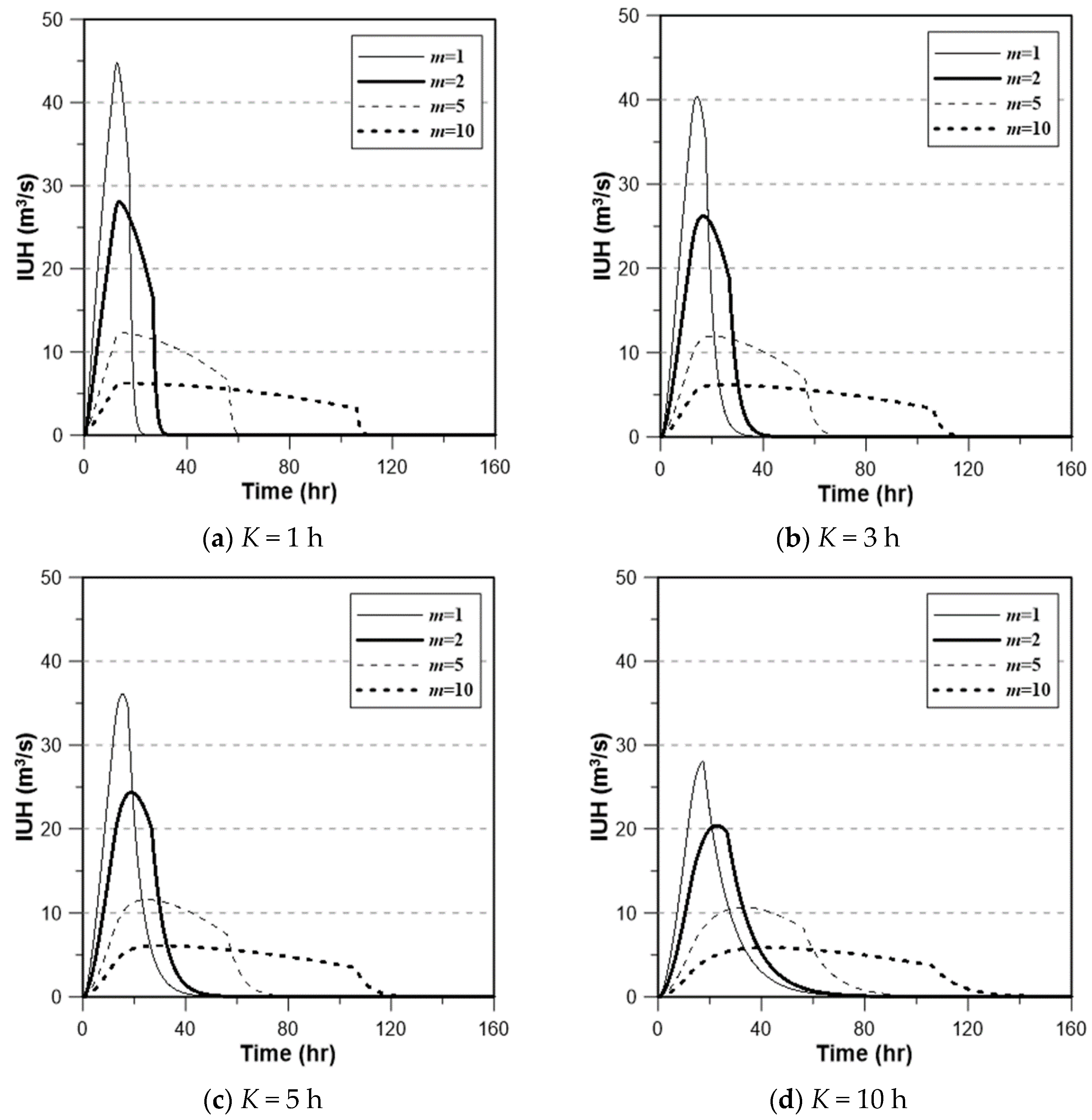
| m | Tc (h) | K = 1 h | K = 3 h | K = 5 h | K = 10 h | ||||
|---|---|---|---|---|---|---|---|---|---|
| Tp (h) | Qp (m3/s) | Tp (h) | Qp (m3/s) | Tp (h) | Qp (m3/s) | Tp (h) | Qp (m3/s) | ||
| 1 | 17.63 | 12.80 | 44.72 | 14.26 | 40.35 | 15.48 | 36.07 | 17.27 | 27.97 |
| 2 | 27.09 | 13.72 | 28.04 | 16.63 | 26.20 | 18.93 | 24.32 | 22.78 | 20.37 |
| 5 | 56.51 | 15.25 | 12.27 | 20.63 | 11.95 | 25.04 | 11.58 | 33.13 | 10.66 |
| 10 | 106.23 | 16.48 | 6.24 | 24.01 | 6.17 | 30.35 | 6.09 | 42.75 | 5.85 |
| Year | Duration | Total Rainfall (mm) | Maximum Rainfall Intensity (mm/h) | Peak Discharge (m3/s) | Maximum Channel Velocity (m/s) |
|---|---|---|---|---|---|
| 2015 | 7/25 05:50–7/26 11:40 (30.0 h) | 99.6 | 42.5 | 26.71 | 2.16 |
| 2016 | 10/02 22:50–10/03 05:50 (7.2 h) | 124.8 | 35.4 | 33.46 | 2.46 |
| 2017 | 8/23 09:50–8/24 13:50 (28.2 h) | 125.4 | 55.3 | 40.70 | 2.18 |
| 2018 | 8/28 13:10–8/30 03:40 (38.7 h) | 315.1 | 53.0 | 90.78 | 3.06 |
| 2019 | 9/10 10:50–9/11 03:40 (17.0 h) | 124.8 | 51.7 | 37.76 | 2.23 |
| Year | Vc (m/s) | Vh (m/s) | m | Tc (h) |
|---|---|---|---|---|
| 2015 | 2.16 | 0.49 | 4.4 | 1.11 |
| 2016 | 2.46 | 0.41 | 6.0 | 1.24 |
| 2017 | 2.18 | 2.18 | 1.0 | 0.53 |
| 2018 | 3.06 | 3.06 | 1.0 | 0.38 |
| 2019 | 2.23 | 1.31 | 1.7 | 0.61 |
| Year | RMSE (m3/s) | R2 | ||
|---|---|---|---|---|
| Uniform Velocity | Different Velocity | Uniform Velocity | Different Velocity | |
| 2015 | 1.748 | 1.268 | 0.887 | 0.942 |
| 2016 | 2.009 | 1.374 | 0.958 | 0.980 |
| 2017 | 1.439 | 1.439 | 0.947 | 0.947 |
| 2018 | 5.706 | 5.706 | 0.877 | 0.877 |
| 2019 | 2.141 | 2.086 | 0.912 | 0.917 |
| Year | Concentration Time Tc (h) | ||
|---|---|---|---|
| Yoo et al. (2014) | Uniform Velocity Case | Considering both the Channel and Hillslope Velocity Case | |
| 2015 | 1.17 | 0.53 | 1.11 |
| 2016 | 1.42 | 0.47 | 1.24 |
| 2017 | 0.50 | 0.53 | 0.53 |
| 2018 | 0.22 | 0.38 | 0.38 |
| 2019 | 0.91 | 0.52 | 0.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, C.; Doan, H.P.; Jun, C.; Na, W. Hillslope Contribution to the Clark Instantaneous Unit Hydrograph: Application to the Seolmacheon Basin, Korea. Water 2021, 13, 1707. https://doi.org/10.3390/w13121707
Yoo C, Doan HP, Jun C, Na W. Hillslope Contribution to the Clark Instantaneous Unit Hydrograph: Application to the Seolmacheon Basin, Korea. Water. 2021; 13(12):1707. https://doi.org/10.3390/w13121707
Chicago/Turabian StyleYoo, Chulsang, Huy Phuong Doan, Changhyun Jun, and Wooyoung Na. 2021. "Hillslope Contribution to the Clark Instantaneous Unit Hydrograph: Application to the Seolmacheon Basin, Korea" Water 13, no. 12: 1707. https://doi.org/10.3390/w13121707
APA StyleYoo, C., Doan, H. P., Jun, C., & Na, W. (2021). Hillslope Contribution to the Clark Instantaneous Unit Hydrograph: Application to the Seolmacheon Basin, Korea. Water, 13(12), 1707. https://doi.org/10.3390/w13121707









