Copula-Based Infilling Methods for Daily Suspended Sediment Loads
Abstract
1. Introduction
2. Methodology
2.1. Copula-Based Joint Probability Distribution of Sediment and Discharge
2.2. Copula-Based Conditional Distribution of Sediment
2.3. Copula-Based Single-Value Sediment Imputation Methods
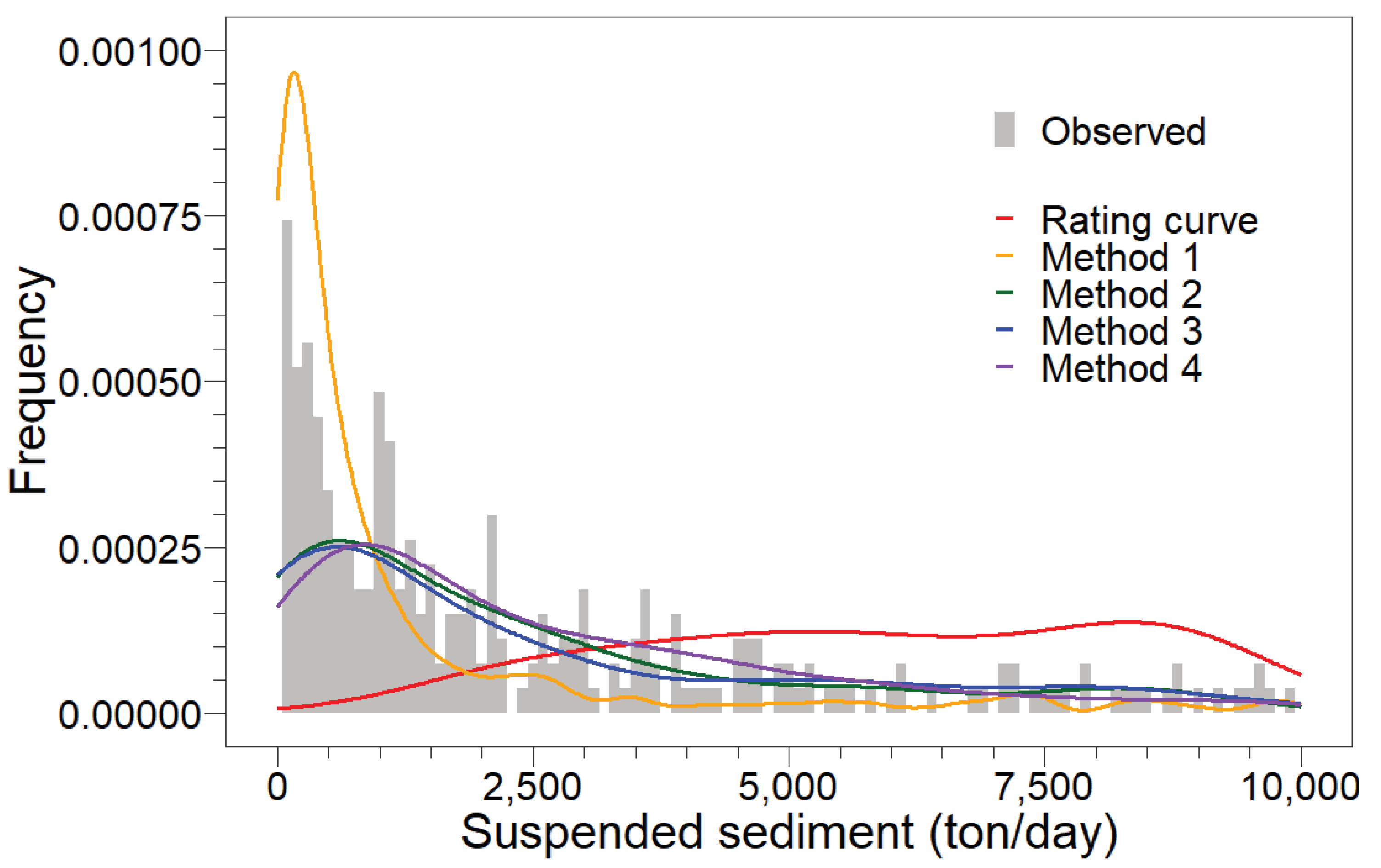
- Method 1. The most natural thought to obtain the imputed data is the mode of the CPDF, which represents the most likely value (i.e., the quantile with the highest CPDF value).
- Method 2. Di Lascio et al. [5] proposed the Hit or Miss Monte Carlo method to estimate missing data, which uses the CPDF and random numbers. The following steps are used to estimate the imputed sediment data.
- Method 3. Peng et al. [52] used the CCDF and a random number to infill the missing sediment data.
- Method 4. Bezak et al. [18] used a similar procedure in Method 3, but with 10,000 generations, to have 10,000 imputed values, and selected the median of these 10,000 data as the imputed sediment data.
3. Data Used
3.1. Suspended Sediment Load and Streamflow Discharge Data
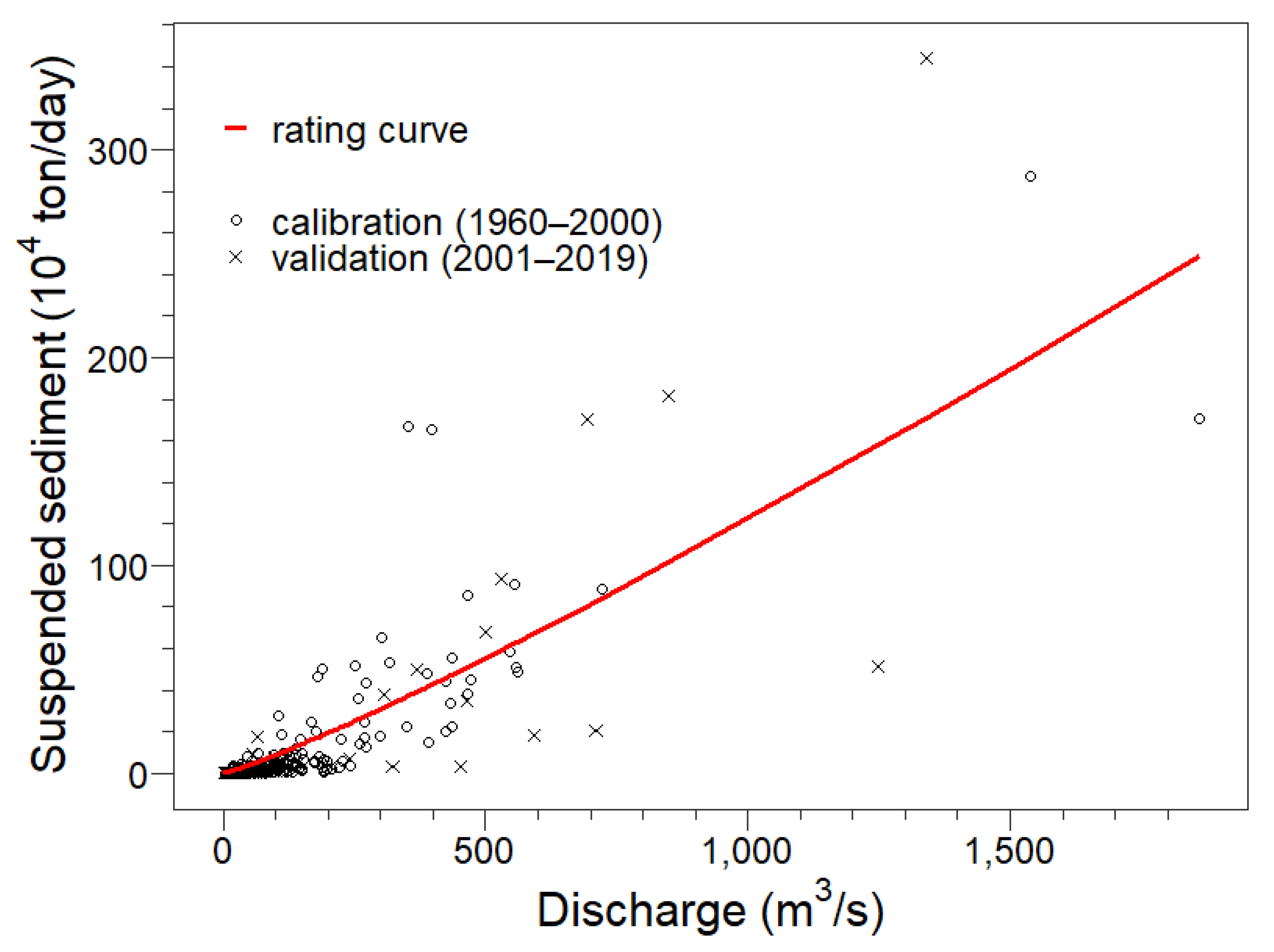
3.2. Empirical Sediment Rating Curve
4. Results and Discussion
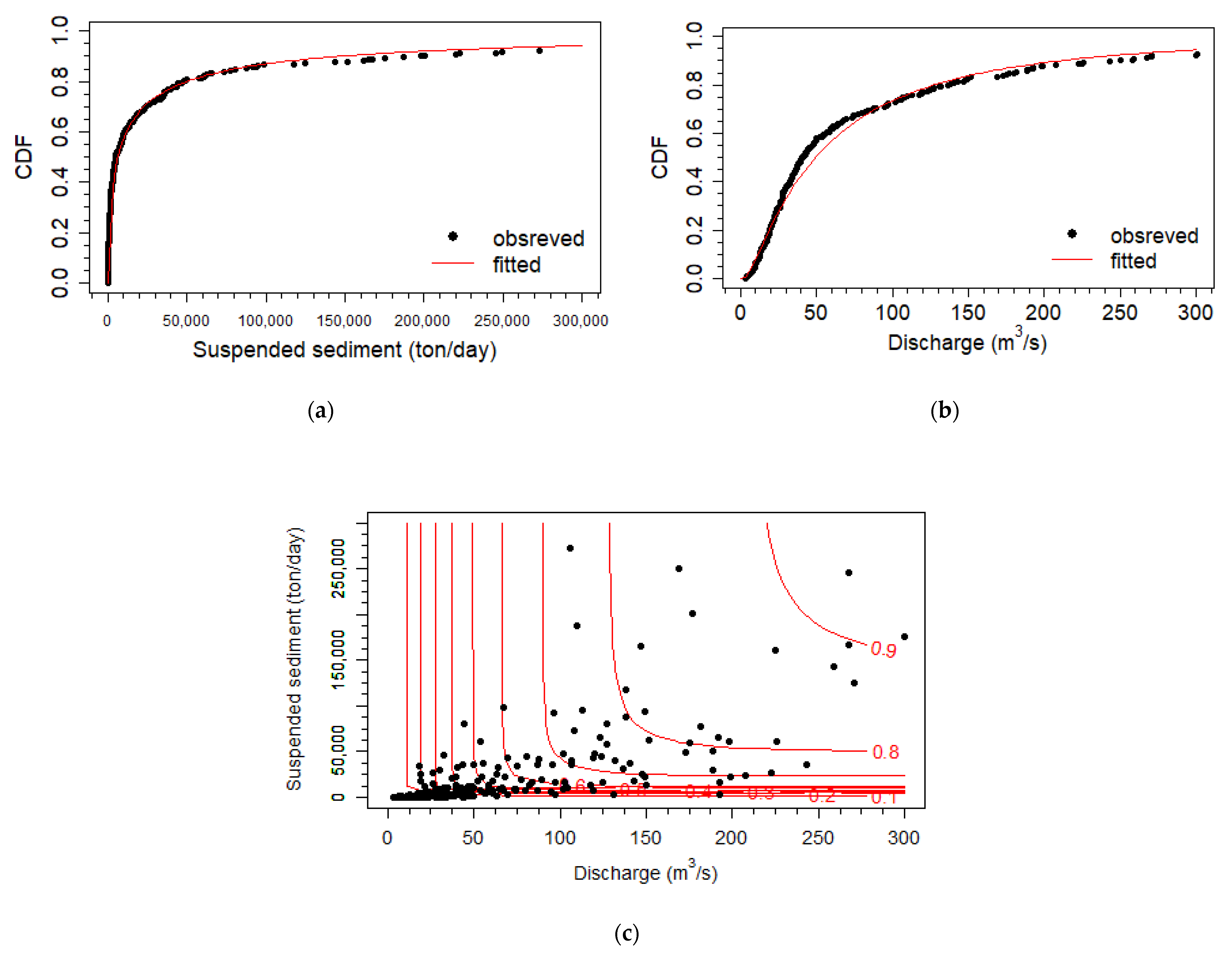
4.1. The Best-Fitted Marginal Distributions and Copulas
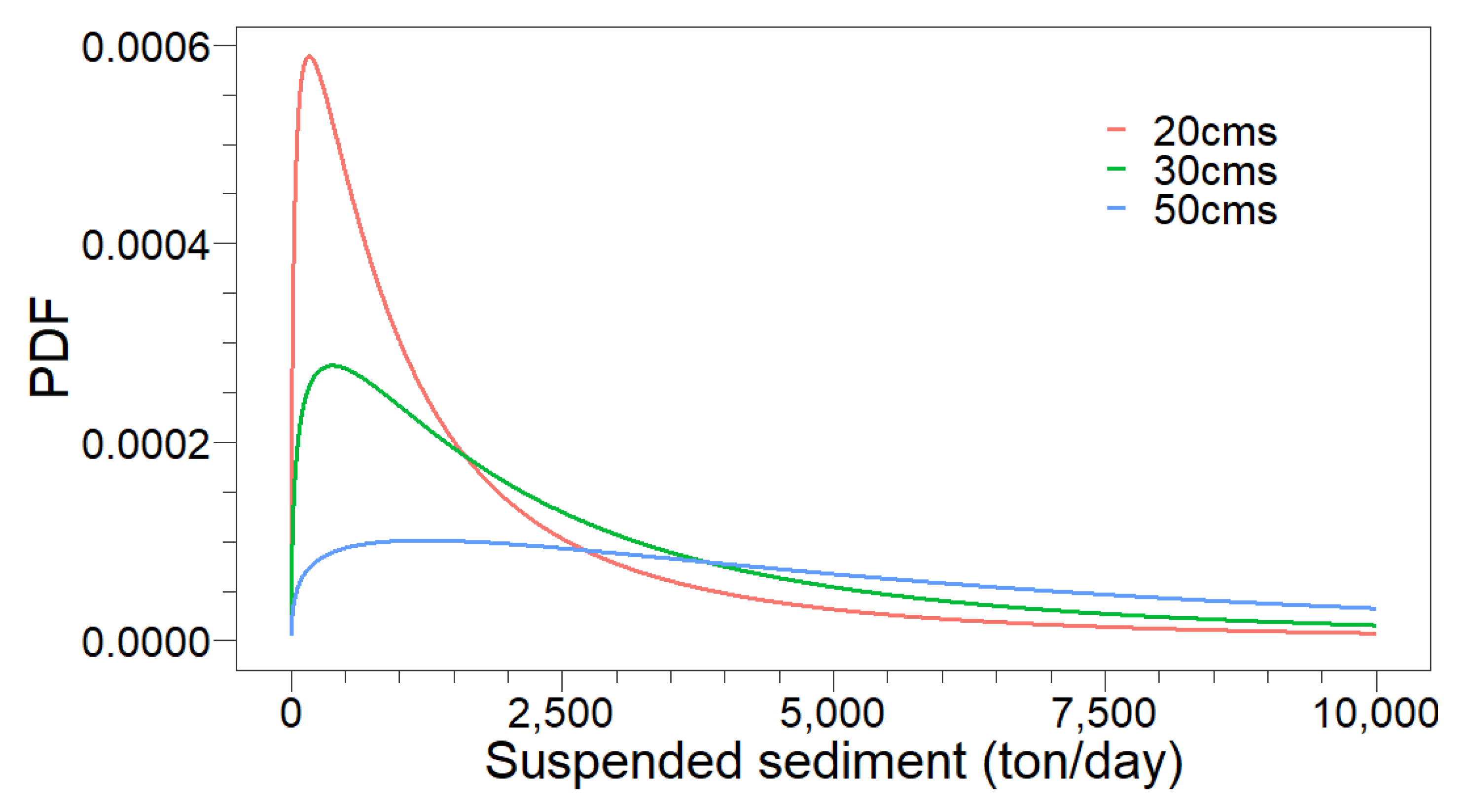
4.2. Probabilistic Sediment Estimations Using Copula-Based Conditional Probability Density Function
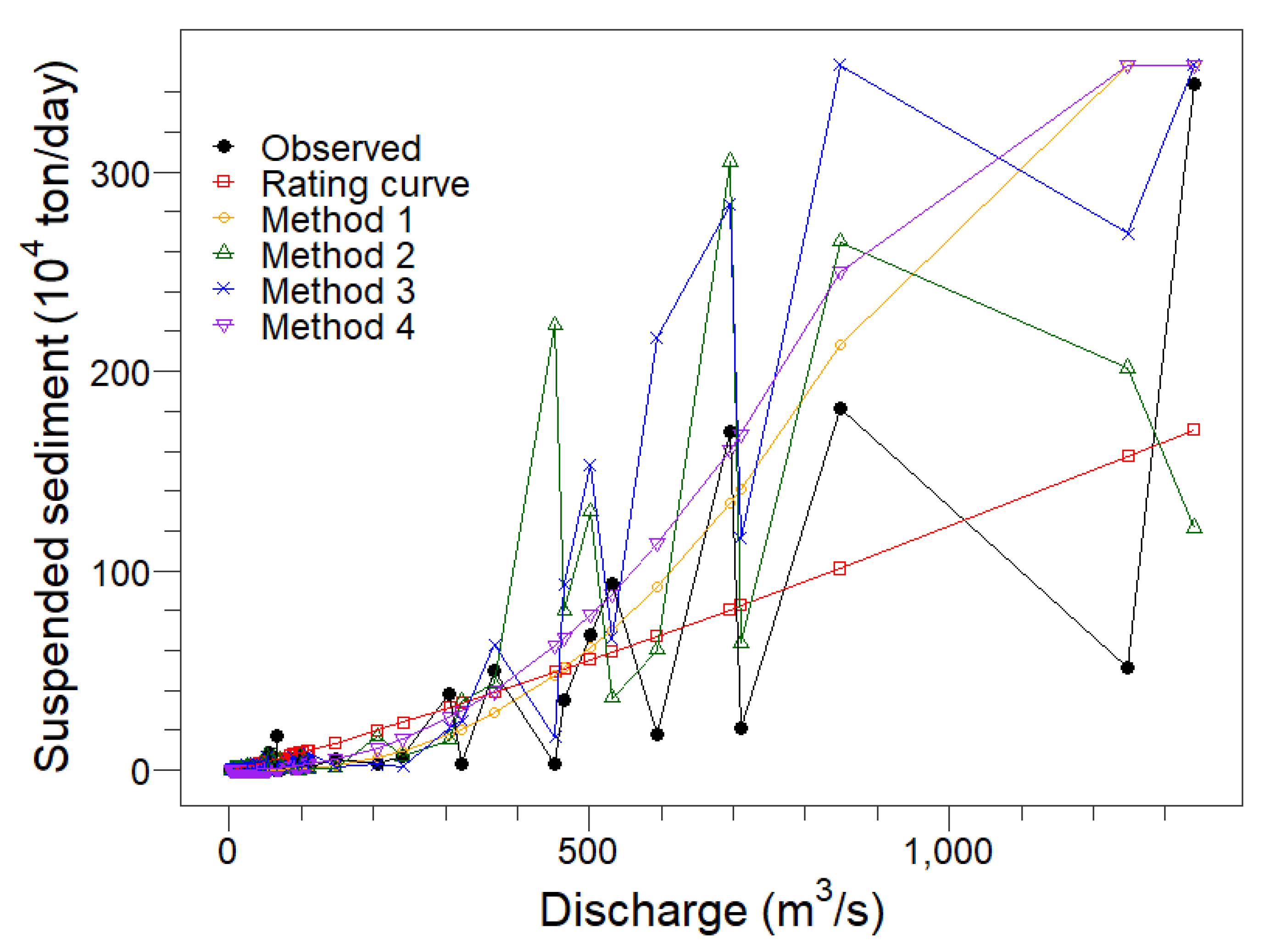
4.3. Single-Value Sediment Estimations
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bárdossy, A.; Pegram, G. Infilling missing precipitation records—A comparison of a new copula-based method with other techniques. J. Hydrol. 2014, 519, 1162–1170. [Google Scholar] [CrossRef]
- Kalteh, A.M.; Hjorth, P. Imputation of missing values in a precipitation—runoff process database. Hydrol. Res. 2009, 40, 420–432. [Google Scholar] [CrossRef]
- Ben Aissia, M.A.; Chebana, F.; Ouarda, T.B.M.J. Multivariate missing data in hydrology—Review and applications. Adv. Water Resour. 2017, 110, 299–309. [Google Scholar] [CrossRef]
- Käärik, E.; Käärik, M. Modeling dropouts by conditional distribution, a copula-based approach. J. Stat. Plan. Inference 2009, 139, 3830–3835. [Google Scholar] [CrossRef]
- Di Lascio, F.M.L.; Giannerini, S.; Reale, A. Exploring copulas for the imputation of complex dependent data. Stat. Methods Appl. 2015, 24, 159–175. [Google Scholar] [CrossRef]
- Hamzah, F.B.; MohdHamzah, F.; Razali, S.F.M.; Jaafar, O.; AbdulJamil, N. Imputation methods for recovering streamflow observation: A methodological review. Cogent Environ. Sci. 2020, 6, 1745133. [Google Scholar] [CrossRef]
- Yang, C.T. Sediment Transport Theory and Practice; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Walling, D.E. Human impact on land-ocean sediment transfer by the world’s rivers. Geomorphology 2006, 79, 192–216. [Google Scholar] [CrossRef]
- Shojaeezadeh, S.A.; Nikoo, M.R.; McNamara, J.; AghaKouchak, A.; Sadegh, M. Stochastic modeling of suspended sediment load in alluvial rivers. Adv. Water Resour. 2018, 119, 188–196. [Google Scholar] [CrossRef]
- Walling, D.E. Assessing the accuracy of suspended sediment rating curves for a small basin. Water Resour. Res. 1977, 13, 531–538. [Google Scholar] [CrossRef]
- Jain, S.K. Development of integrated sediment rating curves using ANNs. J. Hydraul. Eng. 2001, 127, 30–37. [Google Scholar] [CrossRef]
- Kişi, Ö. Suspended sediment estimation using neuro-fuzzy and neural network approaches. Hydrol. Sci. J. 2005, 50, 683–696. [Google Scholar] [CrossRef]
- Çimen, M. Estimation of daily suspended sediments using support vector machines. Hydrol. Sci. J. 2008, 53, 656–666. [Google Scholar] [CrossRef]
- Vigiak, O.; Bende-Michl, U. Estimating bootstrap and Bayesian prediction intervals for constituent load rating curve. Water Resour. Res. 2013, 49. [Google Scholar] [CrossRef]
- Kitsikoudis, V.; Sidiropoulos, E.; Hrissanthou, V. Machine learning utilization for bed load transport in gravel-bed rivers. Water Resour. Manag. 2014, 28, 3727–3743. [Google Scholar] [CrossRef]
- Shiau, J.T.; Chen, T.J. Quantile regression-based probabilistic estimation scheme for daily and annual suspended sediment loads. Water Resour. Manag. 2015, 29, 2805–2818. [Google Scholar] [CrossRef]
- Kisi, O.; Zounemat-Kermani, M. Suspended sediment modeling using neuro-fuzzy embedded fuzzy c-means clustering techniques. Water Resour. Manag. 2016, 30, 3979–3994. [Google Scholar] [CrossRef]
- Bezak, N.; Rusjan, S.; Fijavž, M.K.; Mikoš, M.; Šraj, M. Estimation of suspended sediment loads using copula functions. Water 2017, 9, 628. [Google Scholar] [CrossRef]
- Mirakhorlo, M.S.; Rahimzadegan, M. Application of sediment rating curves to evaluate efficiency of EPM and MPSIAC using RS and GIS. Environ. Earth Sci. 2018, 77, 723. [Google Scholar] [CrossRef]
- Al-Mukhtar, M. Random forest, support vector machine, and neural networks to modelling suspended sediment in Tigris River-Baghdad. Environ. Monit. Assess. 2019, 191, 673. [Google Scholar] [CrossRef]
- Tao, H.; Keshtegar, B.; Yaseen, Z.M. The feasibility of integrative radial basis M5Tree predictive model for river suspended sediment load simulation. Water Resour. Manag. 2019, 33, 4471–4490. [Google Scholar] [CrossRef]
- Salih, S.Q.; Sharafati, A.; Khosravi, K.; Faris, H.; Kisi, O.; Tao, H.; Ali, M.; Yaseen, Z.M. River suspended sediment load prediction based on river discharge information: Application of newly developed data mining models. Hydrol. Sci. J. 2020, 65, 624–637. [Google Scholar] [CrossRef]
- Hazarika, B.B.; Gupta, D.; Berlin, M. Modeling suspended sediment load in a river using extreme learning machine and twin support vector regression with wavelet conjunction. Environ. Earth Sci. 2020, 79, 234. [Google Scholar] [CrossRef]
- Sharafati, A.; Asadollah, S.B.H.S.; Motta, D.; Yaseen, Z.M. Application of newly developed ensemble machine learning models for daily suspended sediment load prediction and related uncertainty analysis. Hydrol. Sci. J. 2020, 65, 2022–2042. [Google Scholar] [CrossRef]
- Yadav, A.; Chatterjee, S.; Equeenuddin, S.M. Suspended sediment yield modeling in Mahanadi River, India by multi-objective optimization hybridizing artificial intelligence algorithm. Int. J. Sediment Res. 2021, 36, 76–91. [Google Scholar] [CrossRef]
- Idrees, M.B.; Jehanzaib, M.; Kim, D.; Kim, T.W. Comprehensive evaluation of machine learning models for suspended sediment load inflow prediction in a reservoir. Stoch. Environ. Res. Risk Assess. 2021. [Google Scholar] [CrossRef]
- Gupta, D.; Hazarika, B.B.; Berlin, M.; Sharma, U.M.; Mishra, K. Artificial intelligence for suspended sediment load prediction: A review. Environ. Earth Sci. 2021, 80, 346. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Lee, T.; Salas, J.D. Copula-based stochastic simulation of hydrological data applied to Nile River flows. Hydrol. Res. 2011, 42, 318–330. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Application of copulas for derivation of drought severity-duration-frequency curves. Hydrol. Process. 2012, 26, 1672–1685. [Google Scholar] [CrossRef]
- Shiau, J.T.; Hsiao, Y.Y. Water-deficit-based drought risk assessment in Taiwan. Nat. Hazards 2012, 64, 237–257. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.M.J.; Duong, T.C. Testing for multivariate trends in hydrologic frequency analysis. J. Hydrol. 2013, 486, 519–530. [Google Scholar] [CrossRef]
- Callau Ponduje, A.C.; Belli, A.; Haberlandt, U. Dam risk assessment based on univariate versus bivariate statistical approaches: A case study for Argentina. Hydrol. Sci. J. 2014, 59, 2216–2232. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A.; Archetti, R. Coastal flooding: A copula based approach for estimating the joint probability of water levels and waves. Coast. Eng. 2015, 97, 37–52. [Google Scholar] [CrossRef]
- Requena, A.I.; Flores, I.; Mediero, L.; Garrote, L. Extension of observed flood series by combining a distributed hydro-meteorological model and a copula-based model. Stoch. Environ. Res. Risk Assess. 2016, 30, 1363–1378. [Google Scholar] [CrossRef][Green Version]
- Dodangeh, E.; Shahedi, K.; Shiau, J.T.; Mirakbari, M. Spatial hydrological drought characteristics in Karkheh River basin, southwest Iran using copulas. J. Earth Syst. Sci. 2017, 126, 80. [Google Scholar] [CrossRef]
- Qian, L.; Wang, H.; Dang, S.; Wang, C.; Jiao, Z.; Zhao, Y. Modelling bivariate extreme precipitation distribution for data-scare regions using Gumbel-Hougaard copula with maximum entropy estimation. Hydrol. Process. 2018, 32, 212–227. [Google Scholar] [CrossRef]
- Mazdiyasni, O.; Sadegh, M.; Chiang, F.; AghaKouchak, A. Heat wave intensity duration frequency curve: A multivariate approach for hazard and attribution analysis. Sci. Rep. 2019, 9, 14117. [Google Scholar] [CrossRef] [PubMed]
- Dondangeh, E.; Shahedi, K.; Solaimani, K.; Shiau, J.T.; Abraham, J. Data-based bivariate uncertainty assessment of extreme rainfall-runoff using copulas: Comparison between annual maximum series (AMS) and peaks over threshold (POT). Environ. Monit. Assess. 2019, 191, 67. [Google Scholar] [CrossRef]
- Ben Nasr, I.; Chebana, F. Homogeneity testing of multivariate hydrological records, using multivariate copula L-moments. Adv. Water Resour. 2019, 134, 103449. [Google Scholar] [CrossRef]
- Bushra, N.; Trepanier, J.C.; Rohli, R.C. Joint probability risk modeling of storm surge and cyclone wind along the coast of Bay of Bengal using a statistical copula. Int. J. Climatol. 2019, 39, 4206–4217. [Google Scholar] [CrossRef]
- Tahroudi, M.N.; Ramezani, Y.; De Michele, C.; Mirabbasi, R. Analyzing the conditional behavior of rainfall deficiency and groundwater level deficiency signatures by using copula functions. Hydrol. Res. 2020, 51, 1332–1348. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; Adeola, A.M.; de Wit, J.P.; Ncongwane, K.P.; Zwane, N.N. Drought risk analysis in the Eastern Cape Province of South Africa: The copula lens. Water 2020, 12, 1938. [Google Scholar] [CrossRef]
- Singh, H.; Pirani, F.J.; Najafi, M.R. Characterizing the temperature and precipitation covariability over Canada. Theor. Appl. Climatol. 2020, 139, 1543–1558. [Google Scholar] [CrossRef]
- Uttarwar, S.B.; Barma, S.D.; Mahesha, A. Bivariate modeling of hydroclimatic variables in humid tropical coastal region using Archimedean copulas. J. Hydrol. Eng. 2020, 25, 05020026. [Google Scholar] [CrossRef]
- Zhong, M.; Zeng, T.; Jiang, T.; Wu, H.; Chen, X.H.; Hong, Y. A copula-based multivariate probability analysis for flash flood risk under the compound effect of soil moisture and rainfall. Water Resour. Manag. 2021, 35, 83–98. [Google Scholar] [CrossRef]
- Sajeev, A.; Barma, D.; Mahesha, A.; Shiau, J.T. Bivariate drought characterization of two contrasting climatic regions in India using copula. J. Irrig. Drain. Eng. 2021, 147, 05020005. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; You, J. The joint probability distribution of runoff and sediment and its change characteristics with multi-time scales. J. Hydrol. Hydromech. 2014, 62, 218–225. [Google Scholar] [CrossRef]
- Bezak, N.; Mikoš, M.; Šraj, M. Trivariate frequency analyses of peak discharge, hydrograph volume and suspended sediment concentration data using copulas. Water Resour. Manag. 2014, 28, 2195–2212. [Google Scholar] [CrossRef]
- Guo, A.; Chang, J.; Wang, Y.; Huang, Q. Variations in the runoff-sediment relationship of the Weihe River basin based on the copula function. Water 2016, 8, 223. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G. Copula-based identification of the non-stationarity of the relation between runoff and sediment load. Int. J. Sediment Res. 2017, 32, 221–230. [Google Scholar] [CrossRef]
- Peng, Y.; Yu, X.; Yan, H.; Zhang, J. Stochastic simulation of daily suspended sediment concentration using multivariate copulas. Water Resour. Manag. 2020, 34, 3913–3932. [Google Scholar] [CrossRef]
- Peng, Y.; Shi, Y.; Yan, H.; Zhang, J. Multivariate frequency analysis of annual maxima suspended sediment concentrations and floods in the Jinsha River China. J. Hydrol. Eng. 2020, 25, 05020029. [Google Scholar] [CrossRef]
- Sklar, K. Fonctions de repartition à n dimensions et leura marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Joe, H. Multivariate Models and Dependence Concepts; Chapman and Hall: New York, NY, USA, 1997. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Genest, C.; Remillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Asselman, N.E.M. Fitting and interpretation of sediment rating curve. J. Hydrol. 2000, 234, 228–248. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual model part I—A discussion of principle. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of goodness-of-fit measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
| Name | Copula | Copula Density | Range of Parameter |
|---|---|---|---|
| Clayton | |||
| Frank | |||
| Gumbel-Hougaard |
| Station | River | Catchment Area (km2) | Data Length | Number of Sediment Data | Number of Discharge Data | Percentage (%) | Sediment (104 ton/day) | Discharge (m3/s) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | |||||||
| Jenshou | Hualian | 425.9 | 1960–2019 | 21,898 | 21.28 | 65.2 | ||||
| 1960–2019 | 427 | 427 | 1.9 | 8.55 | 30.9 | 99.96 | 187.9 | |||
| Station | Sediment Load | Discharge | Copula | |||||
|---|---|---|---|---|---|---|---|---|
| Dist. | Parameters | Dist. | Parameters | Dist. | Parameter | |||
| Jenshou | LNO | μ = 8.753 | σ = 2.456 | LNO | μ = 3.898 | σ = 1.134 | Gumbel-Hougaard | θ = 2.97 |
| Index | Calibration (1960–2000) | Validation (2001–2019) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rating Curve | Method 1 | Method 2 | Method 3 | Method 4 | Rating Curve | Method 1 | Method 2 | Method 3 | Method 4 | |
| RMSE | 146,424.5 a | 182,177.6 | 179,157.3 | 254,951.8 | 184,142.6 | 226,631.6 a | 298,106.7 | 268,855.1 | 311,492.7 | 316,581.9 |
| MAPE | 3033.9 | 119.3 a | 12,154.6 | 1338.9 | 352.8 | 1365.4 | 94.8 a | 341.2 | 270.0 | 120.5 |
| NSE | 0.7068 a | 0.5465 | 0.5611 | 0.1111 | 0.5363 | 0.6445 a | 0.3848 | 0.4996 | 0.3284 | 0.3062 |
| MNSE | 0.5044 | 0.5856 a | 0.5016 | 0.4292 | 0.5640 | 0.4826 | 0.5872a | 0.4724 | 0.5120 | 0.5593 |
| Period | Flow State | Index | Rating Curve | Method 1 | Method 2 | Method 3 | Method 4 |
|---|---|---|---|---|---|---|---|
| 1960–2000 (calibration) | Low | RMSE | 101,77.7 | 5266.4 | 4976.7 a | 5397.8 | 4982.3 |
| MAPE | 3145.4 | 77.2 a | 508.1 | 760.1 | 160.8 | ||
| NSE | −3.3041 | −0.1524 | −0.0291 a | −0.2106 | −0.0314 | ||
| MNSE | −3.0301 | 0.1549 | 0.1138 | −0.0031 | 0.2743 a | ||
| Moderate | RMSE | 29,913.6 | 17,904.8 | 18,300.2 | 18,751.7 | 15,627.2 a | |
| MAPE | 4953.7 | 174.3 a | 1718.6 | 858.3 | 624.2 | ||
| NSE | −2.7236 | −0.3340 | −0.3936 | −0.4632 | −0.0162 a | ||
| MNSE | −1.6813 | 0.0558 | −0.0014 | −0.0939 | 0.2323 a | ||
| High | RMSE | 265,144.2 a | 332,168.8 | 480,711 | 364,901 | 335,106.5 | |
| MAPE | 361.9 | 86.6 a | 235.0 | 194.9 | 149.3 | ||
| NSE | 0.64490 a | 0.44268 | −0.16722 | 0.32744 | 0.43278 | ||
| MNSE | 0.43362 | 0.44188a | 0.16033 | 0.33467 | 0.40119 | ||
| 2001–2019 (validation) | Low | RMSE | 6464.6 | 1091.5 | 1716.0 | 1081.8 | 887.8 a |
| MAPE | 2276.0 | 82.8 a | 214.1 | 221.0 | 93.6 | ||
| NSE | −50.0076 | −0.4542 | −2.5942 | −0.4284 | 0.0379 a | ||
| MNSE | −8.6240 | −0.0542 | −0.5792 | −0.2131 | 0.2138 a | ||
| Moderate | RMSE | 21,132.1 | 5410.8 | 9133.0 | 5898.9 | 4016.8 a | |
| MAPE | 1398.4 | 74.0 a | 271.4 | 181.7 | 101.0 | ||
| NSE | −22.4377 | −0.5366 | −3.3778 | −0.8263 | 0.1532 a | ||
| MNSE | −5.0707 | −0.0363 | −0.6552 | −0.1649 | 0.2493 a | ||
| High | RMSE | 412,452 a | 543,548 | 564,287 | 606,548.2 | 577,797.3 | |
| MAPE | 450.6 | 134.4 a | 178.5 | 175.2 | 176.0 | ||
| NSE | 0.5973 a | 0.3007 | 0.2463 | 0.1292 | 0.2098 | ||
| MNSE | 0.4262 | 0.4879 a | 0.4007 | 0.3527 | 0.4488 | ||
| 1960–2019 | Low | RMSE | 10,012.78 | 4984.5 | 6582.7 | 4881.4 | 4641.2 a |
| MAPE | 2614.2 | 79.2 a | 393.2 | 298.1 | 129.9 | ||
| NSE | −3.6745 | −0.1584 | −1.0204 | −0.1110 | −0.0044 a | ||
| MNSE | −2.9390 | 0.1617 | −0.1682 | 0.0424 | 0.2954 a | ||
| Moderate | RMSE | 32,243.5 | 22,044.2 | 53,492.3 | 23,257.7 | 19,783.2 a | |
| MAPE | 3930.0 | 146.5 a | 21,830.5 | 2208.8 | 503.0 | ||
| NSE | −1.6099 | −0.2199 | −6.1834 | −0.3579 | 0.0175 a | ||
| MNSE | −1.6147 | 0.0882 | −0.8592 | −0.0841 | 0.2658 a | ||
| High | RMSE | 338,540.2 a | 436,071.9 | 405,494.7 | 531,516.1 | 453,425.8 | |
| MAPE | 349.9 | 105.5 a | 199.2 | 233.7 | 164.1 | ||
| NSE | 0.6112 a | 0.3549 | 0.4422 | 0.0416 | 0.3025 | ||
| MNSE | 0.4172 | 0.4394 a | 0.3475 | 0.2599 | 0.3945 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiau, J.-T.; Lien, Y.-C. Copula-Based Infilling Methods for Daily Suspended Sediment Loads. Water 2021, 13, 1701. https://doi.org/10.3390/w13121701
Shiau J-T, Lien Y-C. Copula-Based Infilling Methods for Daily Suspended Sediment Loads. Water. 2021; 13(12):1701. https://doi.org/10.3390/w13121701
Chicago/Turabian StyleShiau, Jenq-Tzong, and Yu-Cheng Lien. 2021. "Copula-Based Infilling Methods for Daily Suspended Sediment Loads" Water 13, no. 12: 1701. https://doi.org/10.3390/w13121701
APA StyleShiau, J.-T., & Lien, Y.-C. (2021). Copula-Based Infilling Methods for Daily Suspended Sediment Loads. Water, 13(12), 1701. https://doi.org/10.3390/w13121701






