Note on the Application of Transient Wave Packets for Wave–Ice Interaction Experiments
Abstract
1. Introduction
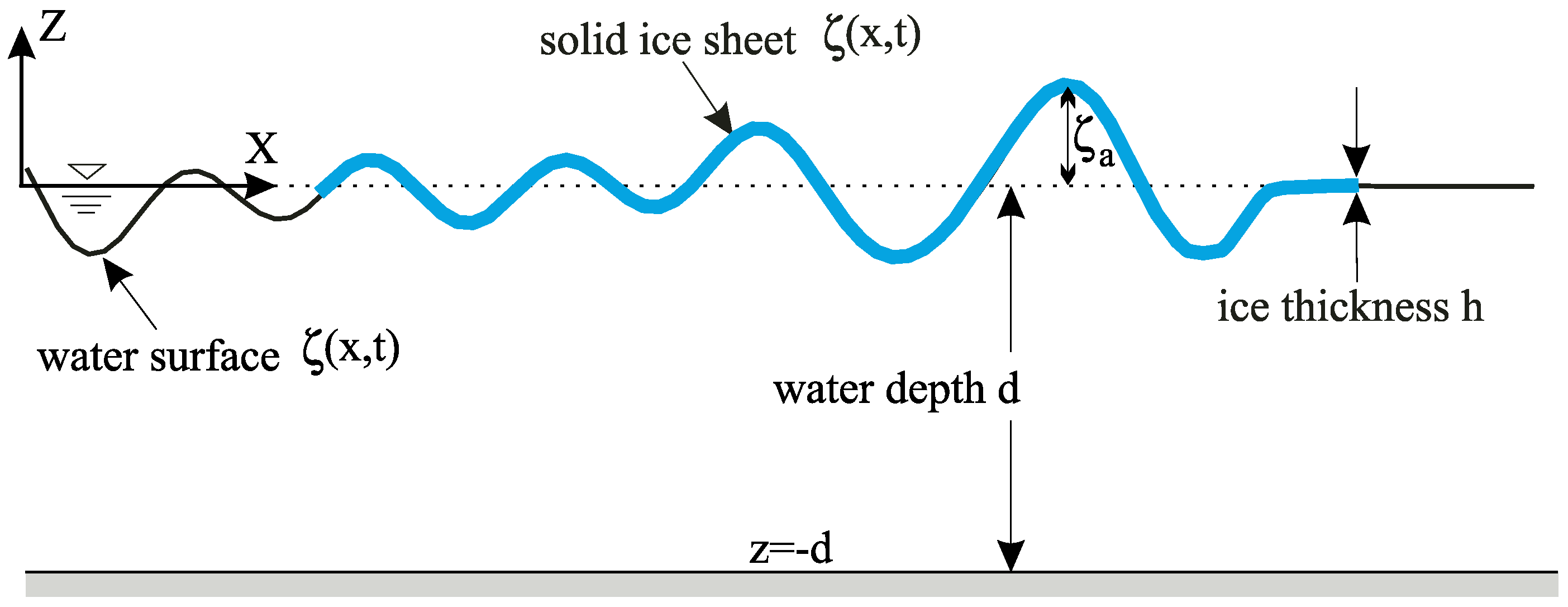
2. Theoretical Basis
2.1. Open Water Waves
2.2. Ice-Covered Waves
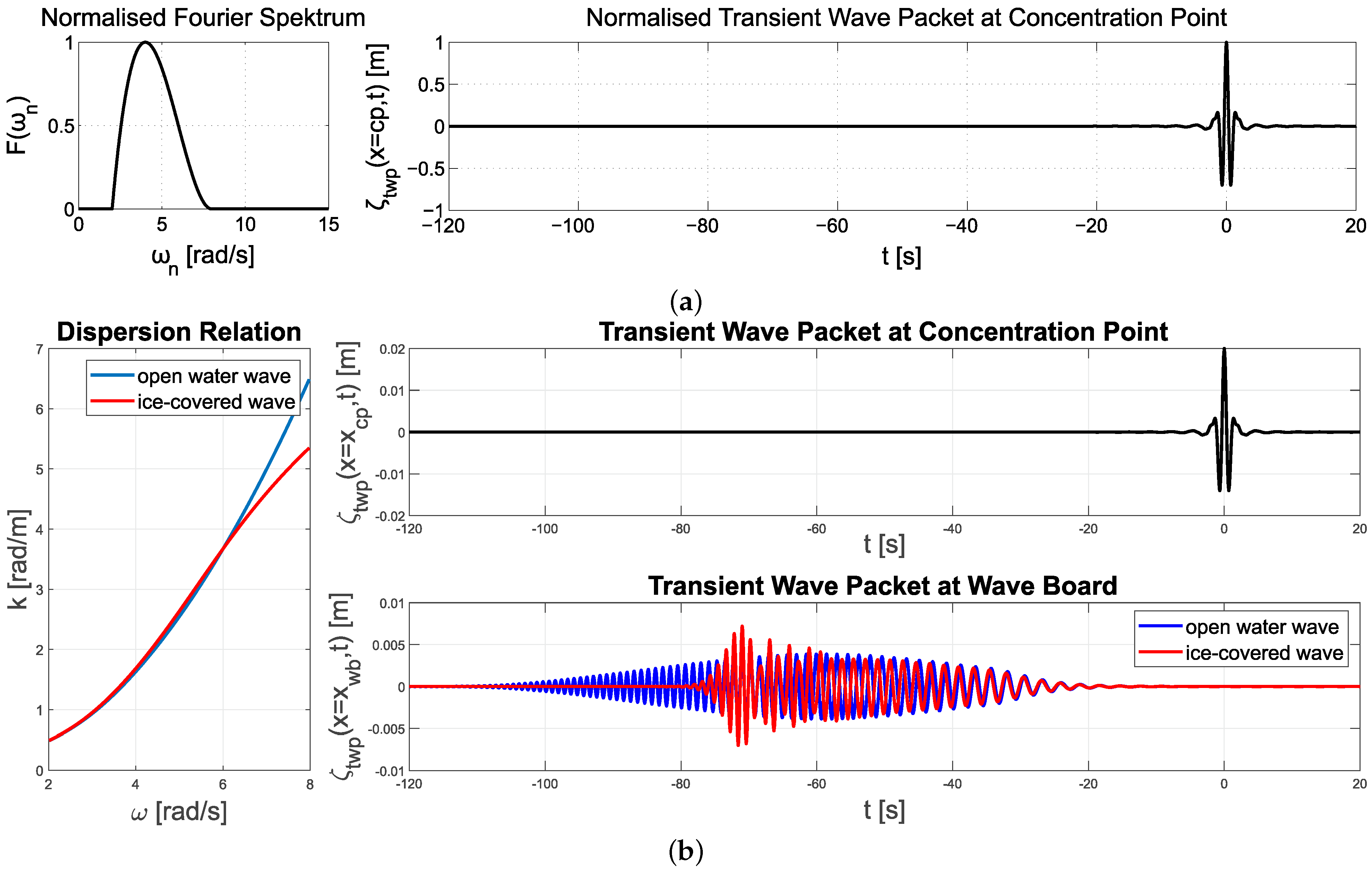
2.3. Transient Wave Packets
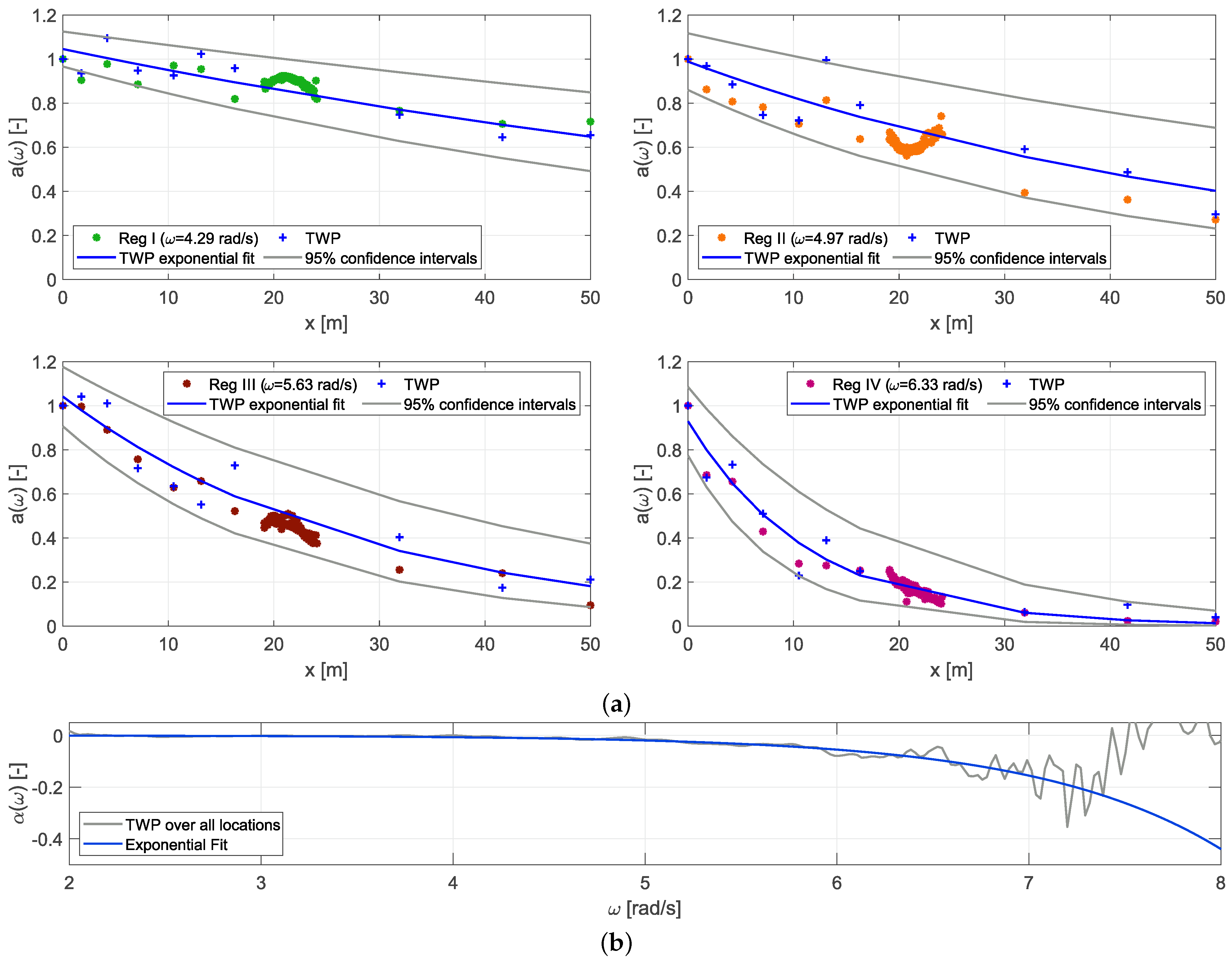
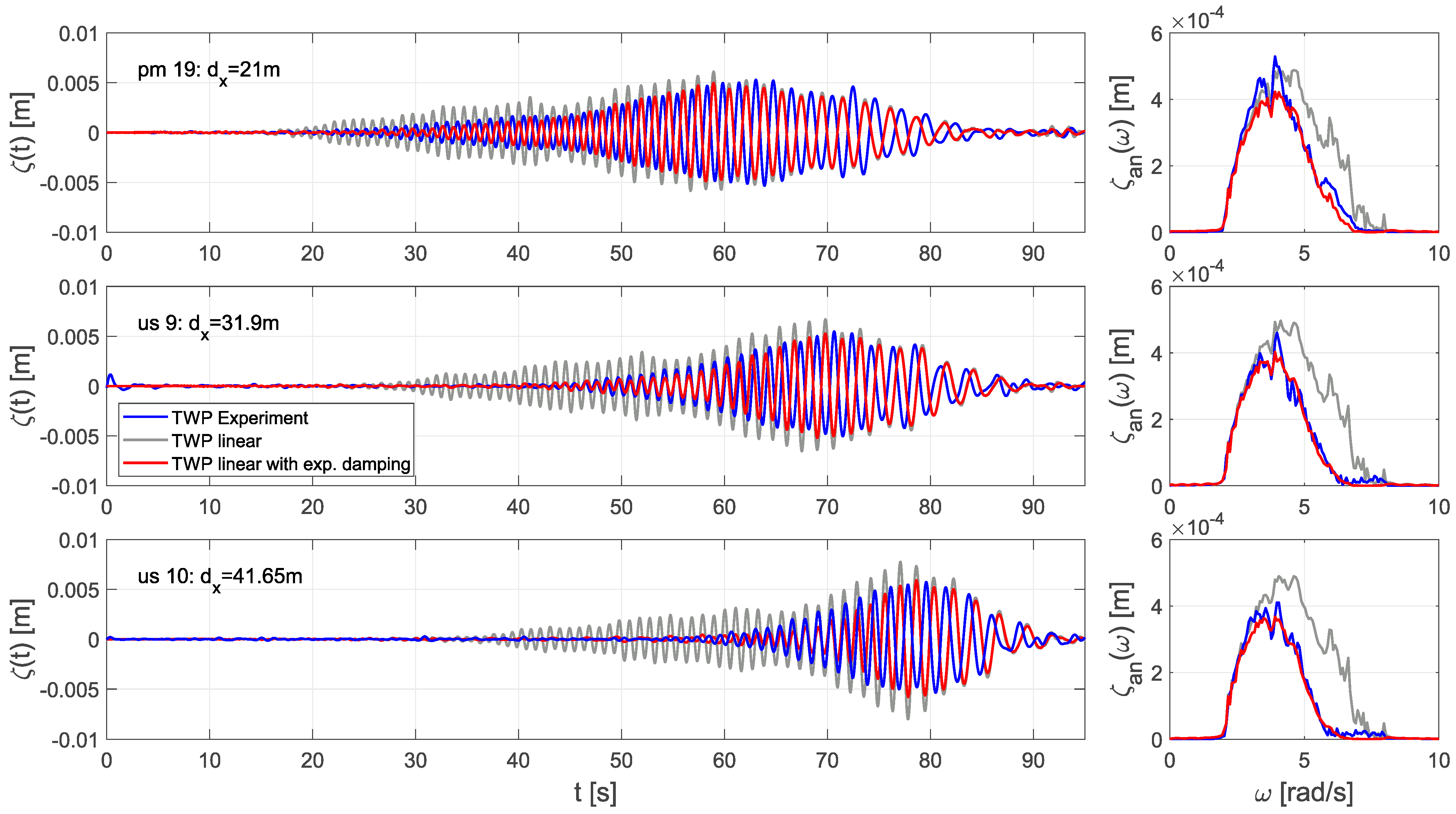
2.4. Wave Damping
3. Experiment
3.1. Model Ice
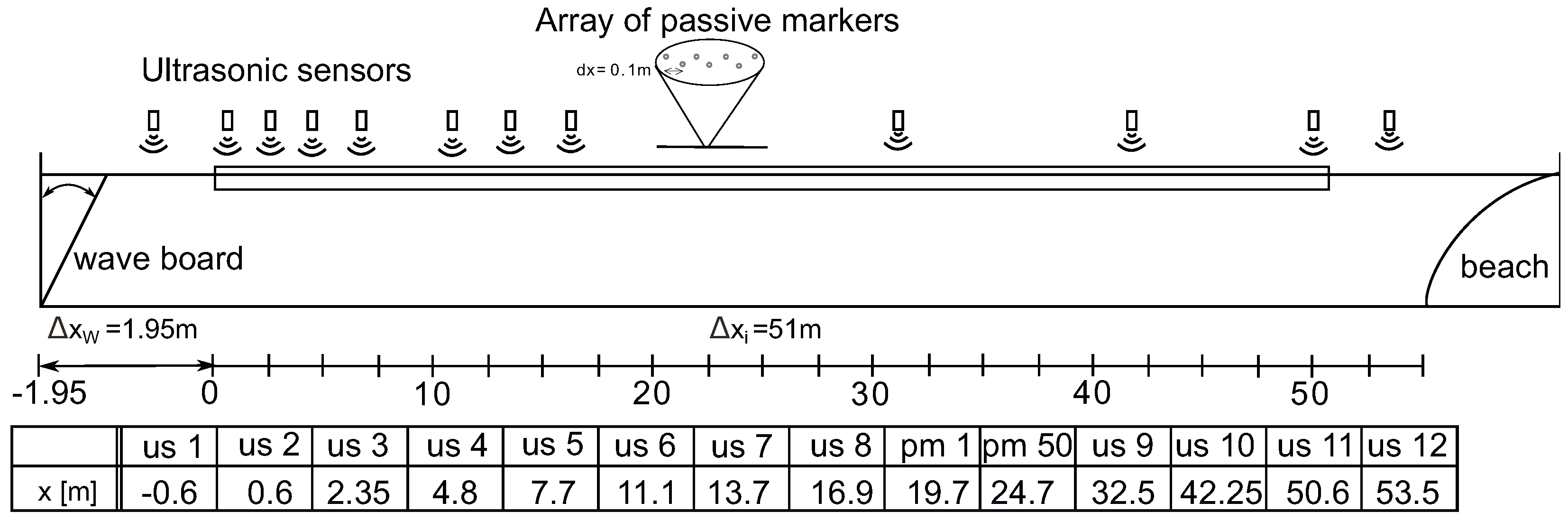
3.2. Experimental Setup
3.3. Experimental Programme
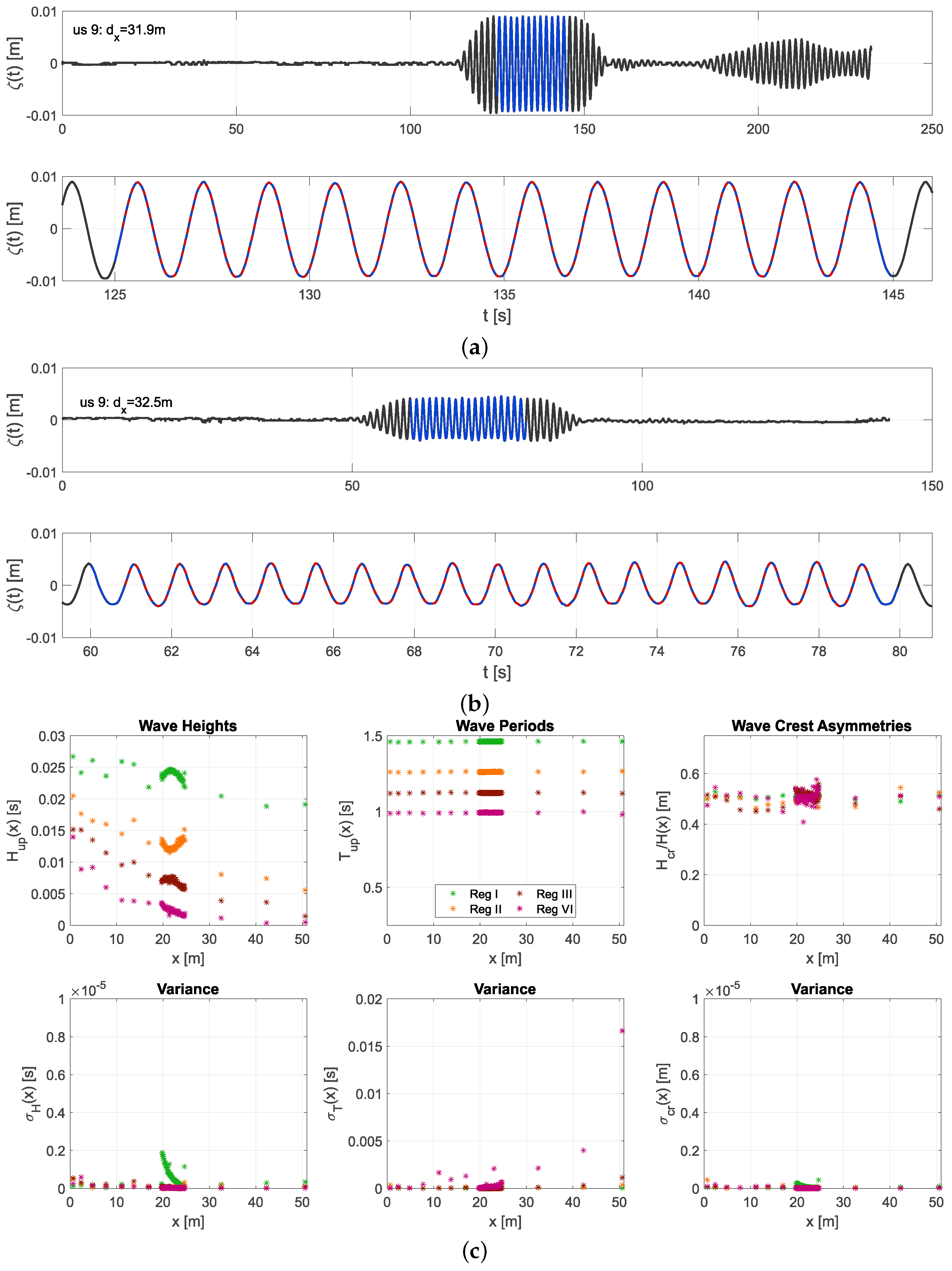
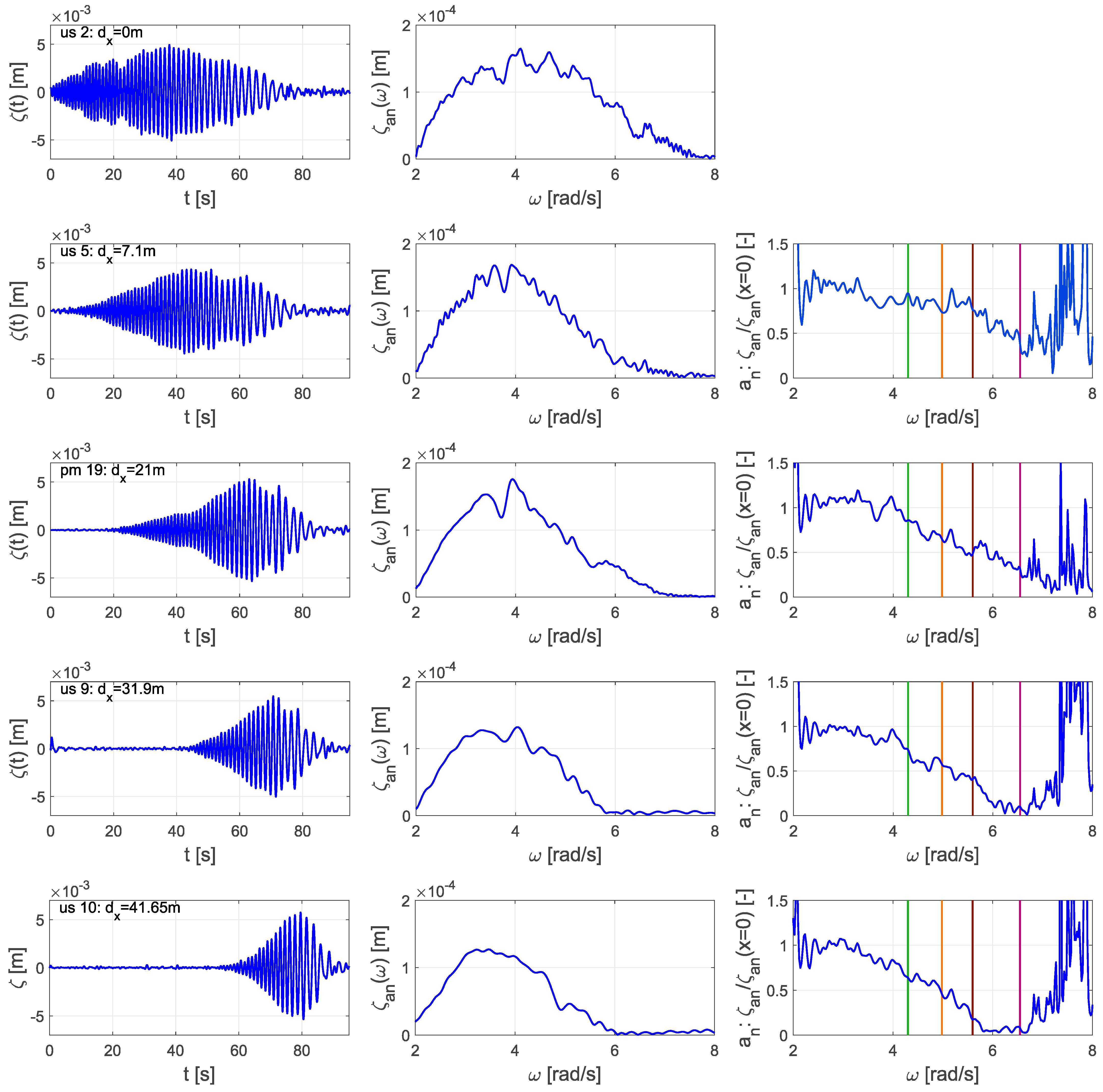
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A
| Ultralab USS 30250 | Ultralab USS 2001300 | |
|---|---|---|
| Blind area | ||
| Working range | ||
| Techn. resolution | ||
| Reproducibility |
References
- Squire, V.A.; Wadhams, P. Some Wave Attenuation Results from MIZEX-West; CRREL Spec. Rep. 85-06; CRREL: Hanover, NH, USA, 1985.
- Squire, V. Of ocean waves and sea-ice revisited. Cold Reg. Sci. Technol. 2007, 49, 110–133. [Google Scholar] [CrossRef]
- Doble, M.J.; Bidlot, J.R. Wave buoy measurements at the Antarctic sea ice edge compared with an enhanced ECMWF WAM: Progress towards global waves-in-ice modelling. Ocean. Model. 2013, 70, 166–173. [Google Scholar] [CrossRef]
- Montiel, F.; Squire, V.A.; Doble, M.; Thomson, J.; Wadhams, P. Attenuation and Directional Spreading of Ocean Waves During a Storm Event in the Autumn Beaufort Sea Marginal Ice Zone. J. Geophys. Res. Ocean. 2018, 123, 5912–5932. [Google Scholar] [CrossRef]
- Frankenstein, S.; Loset, S.; Shen, H.H. Wave-Ice Interactions in Barents Sea Marginal Ice Zone. J. Cold Reg. Eng. 2001, 15, 91–102. [Google Scholar] [CrossRef]
- Squire, V.A.; Moore, S. Direct measurement of the attenuation of ocean waves by pack ice. Nature 1980, 283, 365–368. [Google Scholar] [CrossRef]
- Wadhams, P.; Squire, V.A.; Goodman, D.J.; Cowan, A.M.; Moore, S.C. The attenuation rates of ocean waves in the marginal ice zone. J. Geophys. Res. Ocean. 1988, 93, 6799–6818. [Google Scholar] [CrossRef]
- Wadhams, P. Ice in the Ocean; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Liu, A.K.; Mollo-Christensen, E. Wave Propagation in a Solid Ice Pack. J. Phys. Oceanogr. 1988, 18, 1702–1712. [Google Scholar] [CrossRef]
- Kohout, A.L.; Williams, M.J.M.; Dean, S.M.; Meylan, M.H. Storm-induced sea-ice breakup and the implications for ice extent. Nature 2014, 509, 604–607. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.K.; Vachon, P.W.; Peng, C.Y.; Bhogal, A. Wave attenuation in the marginal ice zone during LIMEX. Atmos. Ocean 1992, 30, 192–206. [Google Scholar] [CrossRef]
- Fox, C.; Haskell, T.G. Ocean wave speed in the Antarctic marginal ice zone. Ann. Glaciol. 2001, 33, 350–354. [Google Scholar] [CrossRef]
- Wadhams, P.; Parmiggiani, F.; de Carolis, G. The Use of SAR to Measure Ocean Wave Dispersion in Frazil-Pancake Icefields. J. Phys. Oceanogr. 2002, 32, 1721–1746. [Google Scholar] [CrossRef]
- Collins, C.O., III; Rogers, W.E.; Marchenko, A.; Babanin, A.V. In situ measurements of an energetic wave event in the Arctic marginal ice zone. Geophys. Res. Lett. 2015, 42, 1863–1870. [Google Scholar] [CrossRef]
- Squire, V.; Allan, A. Propagation of Flexural Gravity Waves in Sea Ice. 1980. Available online: http://hydrologie.org/redbooks/a124/iahs_124_0327.pdf (accessed on 19 March 2021).
- Newyear, K.; Martin, S. A comparison of theory and laboratory measurements of wave propagation and attenuation in grease ice. J. Geophys. Res. Ocean. 1997, 102, 25091–25099. [Google Scholar] [CrossRef]
- Wang, R.; Shen, H.H. Gravity waves propagating into an ice-covered ocean: A viscoelastic model. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Zhao, X.; Shen, H.H. Wave propagation in frazil/pancake, pancake, and fragmented ice covers. Cold Reg. Sci. Technol. 2015, 113, 71–80. [Google Scholar] [CrossRef]
- Sutherland, G.; Rabault, J. Observations of wave dispersion and attenuation in landfast ice. J. Geophys. Res. Ocean. 2016, 121, 1984–1997. [Google Scholar] [CrossRef]
- Vance, G. A Scaling System for Vessels Modelled in Ice. In Proceedings of the Society of Naval Architects and Marine Engineers (SNAME) Ice Tech Symposium, Montreal, QC, Canada, 9–11 April 1975. [Google Scholar]
- Schwarz, J. New developments in modeling ice problems. In Proceedings of the 4th International Conference on Port and Ocean Engineering under Arctic Conditions, POAC 77, St. John’s, NB, Canada, 26–30 September 1977; pp. 45–61. [Google Scholar]
- Enkvist, E.; Mäkinen, S. A Fine-Grain Model Ice. In Proceedings of the International Association for Hydro-Environment Engineering and Research (IAHR) on Ice Symposium, Hamburg, Germany, 27–31 August 1984. [Google Scholar]
- Evers, K.; Jochman, P. An Advanced Technique to Improve the Mechanical Properties of Model Ice Developed at the HSVA Ice Tank. In Proceedings of the Conference on Port and Ocean Engineering under Arctic Conditions (POAC), Hamburg, Germany, 17–20 August 1993. [Google Scholar]
- Von Bock und Polach, R. The Mechanical Behavior of Model-Scale Ice: Experiments, Numerical Modeling and Scalability. Ph.D. Thesis, Aalto University, Helsinki, Finnland, 2016. [Google Scholar]
- Von Block und Polach, R.U.F.; Gralher, S.; Ettema, R.; Kellner, L.; Stender, M. The non-linear behavior of aqueous model ice in downward flexure. Cold Reg. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Von Bock und Polach, R.U.F. Numerical analysis of the bending strength of model-scale ice. Cold Reg. Sci. Technol. 2015, 118, 91–104. [Google Scholar] [CrossRef]
- von Bock Und Polach, R.U.F.; Ziemer, G.; Klein, M.; Hartmann, M.C.N.; Toffoli, A.; Monty, J. Case based scaling: Recent developments in ice model testing technology. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE: Virtual Conference, Online, 3–7 August 2020; Volume 7. [Google Scholar] [CrossRef]
- Squire, V.A. A theoretical, laboratory, and field study of ice-coupled waves. J. Geophys. Res. Ocean. 1984, 89, 8069–8079. [Google Scholar] [CrossRef]
- Shen, H.H.; Ackley, S.F.; Yuan, Y. Limiting diameter of pancake ice. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Cheng, S.; Tsarau, A.; Li, H.; Herman, A.; Evers, K.U.; Shen, H. Loads on Structure and Waves in Ice (LS-WICE) Project, Part 1: Wave Attenuation and Dispersion in Broken Ice Fields. In Proceedings of the 24th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC 2017), Busan, Korea, 11–16 June 2017. [Google Scholar]
- Herman, A.; Tsarau, A.; Evers, K.U.; Li, H.; Shen, H. Loads on Structure and Waves in Ice (LS-WICE) Project, Part 2: Sea Ice Breaking by Waves. In Proceedings of the 24th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC 2017), Busan, Korea, 11–16 June 2017. [Google Scholar]
- Rabault, J.; Sutherland, G.; Jensen, A.; Christensen, K.; Marchenko, A. Experiments on wave propagation in grease ice: Combined wave gauges and particle image velocimetry measurements. J. Fluid Mech. 2019, 864, 876–898. [Google Scholar] [CrossRef]
- Yu, J.; Rogers, W.E.; Wang, D.W. A Scaling for Wave Dispersion Relationships in Ice-Covered Waters. J. Geophys. Res. Ocean. 2019, 124, 8429–8438. [Google Scholar] [CrossRef]
- Marchenko, A.; Haase, A.; Jensen, A.; Lishman, B.; Rabault, J.; Evers, K.; Shortt, M.; Thiel, T. Elasticity and viscosity of ice measured in the experiment on wave propagation below the ice in HSVA ice tank. In Proceedings of the 25th IAHR International Symposium on Ice; The International Association for Hydro-Environment Engineering and Research (IAHR): Virtual Conference, Online, 23–25 November 2020. [Google Scholar]
- Damping of Regular Waves in Model Ice, Volume 7: Polar and Arctic Sciences and Technology. Int. Conf. Offshore Mech. Arct. Eng. 2020. [CrossRef]
- Marchenko, A.; Haase, A.; Jensen, A.; Lishman, B.; Rabault, J.; Evers, K.; Shortt, M.; Thiel, T. Laboratory Investigations of the Bending Rheology of Floating Saline Ice and Physical Mechanisms of Wave Damping In the HSVA Hamburg Ship Model Basin Ice Tank. Water 2021, 13, 1080. [Google Scholar] [CrossRef]
- Clauss, G.F.; Bergmann, J. Gaussian wave packets – a new approach to seakeeping tests of ocean structures. Appl. Ocean. Res. 1986, 8, 190–206. [Google Scholar] [CrossRef]
- Clauss, G.; Kühnlein, W. Seakeeping Tests in Transient Wave Packets. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Kopenhagen, Denmark, 18–22 June 1995. [Google Scholar]
- Clauss, G.; Kühnlein, W. A new tool for seakeeping tests—Nonlinear transient wave packets. In Proceedings of the 8th International Conference on the Behaviour of Offshore Structures (BOSS), Delft, The Netherlands, 7–10 July 1997; pp. 269–285. [Google Scholar]
- Davis, M. Testing ship models in transient waves. In Proceedings of the 5th Symposium on Naval Hydrodynamics, Bergen, Norway, 10–12 September 1964. [Google Scholar]
- Takezawa, S.; Hirayama, T. Advanced experimental techniques for test-ing ship models in transient water waves. Part II: The controlled transientwater waves for using in ship motion tests. In Proceedings of the 11th Symposium on Naval Hy-drodynamics: Unsteady Hydrodynamics of Marine Vehicles, London, UK, 28 March–2 April 1976. [Google Scholar]
- Mansard, E.; Funke, E. A new approach to transient wave generation. Coast. Eng. Proc. 1982, 1, 45. [Google Scholar] [CrossRef]
- Grigoropoulos, G.; Florios, N.; Loukakis, T. Transient waves for ship and floating structure testing. Appl. Ocean. Res. 1994, 16, 71–85. [Google Scholar] [CrossRef]
- Airy, G. Tides and Waves. Encycl. Metrop. 1845, 3, 241–396. [Google Scholar]
- Newman, J. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Mei, C. The Applied Dynamics of Ocean Surface Waves; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Chakrabarti, S.K. Hydrodynamics of Offshore Structures; Springer: Berlin/Heidelberg, Germany, 1987; ISBN 3-540-17319-6. [Google Scholar]
- Clauss, G.; Lehmann, E.; Östergaard, C. Offshore Structures; Conceptual Design and Hydrodynamics; Springer: London, UK, 1992; Volume 1. [Google Scholar]
- Fox, C.; Squire, V.A. On the oblique reflexion and transmission of ocean waves at shore fast sea ice. Philos. Trans. R. Soc. London. Ser. A Phys. Eng. Sci. 1994, 347, 185–218. [Google Scholar] [CrossRef]
- Rabault, J. An Investigation into the Interaction between Waves and Ice. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2018. [Google Scholar]
- Clauss, G.F.; Steinhagen, U. Numerical simulation of nonlinear transient waves and its validation by Laboratory data. In Proceedings of the 9th International Offshore and Polar Engineering Conference (ISOPE), Brest, France, 30 May–4 June 1999; Volume III, pp. 368–375. [Google Scholar]
- Kühnlein, W.L.; Clauss, G.F.; Hennig, J. Tailor made freak waves within irregular seas. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, 23–28 June 2002; Volume 36142, pp. 759–768. [Google Scholar]
- Clauss, G.F.; Klein, M.; Dudek, M. Influence of the Bow Shape on Loads in High and Steep Waves. In Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010. [Google Scholar] [CrossRef]
- Hennig, J. Generation and Analysis of Harsh Wave Environments. Doctoral Thesis, Technische University, Berlin, Germany, 2005. [Google Scholar]
- Clauss, G.F.; Stuppe, S.; Dudek, M. Transient Wave Packets: New Application in CFD-Methods, Volume 8B: Ocean Engineering. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar] [CrossRef]
- ITTC. Ice Property Measurements, 7.5-02-04-02; ITTC: Zürich Switzerland, 2014. [Google Scholar]
- Von Bock und Polach, R.U.F.; Molyneux, D. Model ice: A review of its capacity and identification of knowledge gaps. In Proceedings of the ASME 2017 36st International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; p. 9. [Google Scholar]
- Zufelt, J.E.; Ettema, R. Model Ice Properties; Technical Report CRREL Report 96-1; U.S. Army Corps of Engineers; Cold Regions Research and Engineering Laboratory (CRREL): Hanover, NH, USA, 1996.
| Parameter | Test Conditions |
|---|---|
| Water density | |
| Ice density | |
| Ice thickness | |
| Ice sheet length | |
| Bending strength | – |
| Effective strain modulus | – |
| Wave ID | ||
|---|---|---|
| Reg I | ||
| Reg II | ||
| Reg III | ||
| Reg IV |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klein, M.; Hartmann, M.; von Bock und Polach, F. Note on the Application of Transient Wave Packets for Wave–Ice Interaction Experiments. Water 2021, 13, 1699. https://doi.org/10.3390/w13121699
Klein M, Hartmann M, von Bock und Polach F. Note on the Application of Transient Wave Packets for Wave–Ice Interaction Experiments. Water. 2021; 13(12):1699. https://doi.org/10.3390/w13121699
Chicago/Turabian StyleKlein, Marco, Moritz Hartmann, and Franz von Bock und Polach. 2021. "Note on the Application of Transient Wave Packets for Wave–Ice Interaction Experiments" Water 13, no. 12: 1699. https://doi.org/10.3390/w13121699
APA StyleKlein, M., Hartmann, M., & von Bock und Polach, F. (2021). Note on the Application of Transient Wave Packets for Wave–Ice Interaction Experiments. Water, 13(12), 1699. https://doi.org/10.3390/w13121699








