A Numerical Study on Impacts of Sediment Erosion/Deposition on Debris Flow Propagation
Abstract
1. Introduction
2. Mathematical Formulations
2.1. Numerical Models That Will Be Used in This Paper
2.2. Governing Equations
2.3. Empirical Relations
2.4. Numerical Method
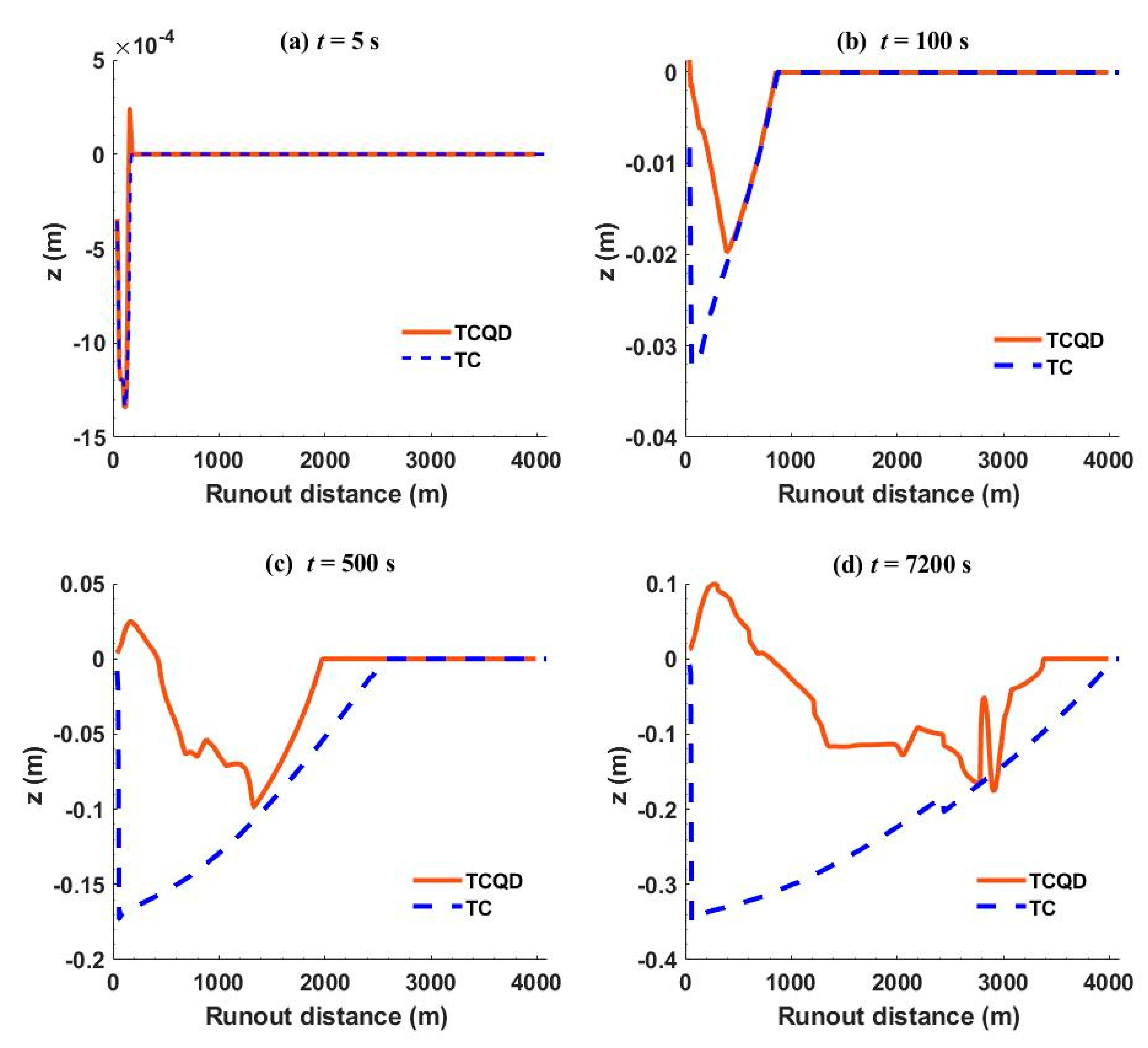
3. Model Validation
3.1. Experimental Data Description
3.2. Verification with One-Dimensional Laboratory Test (Subaerial)
3.3. Verification with One-Dimensional Laboratory Test
4. Model Application
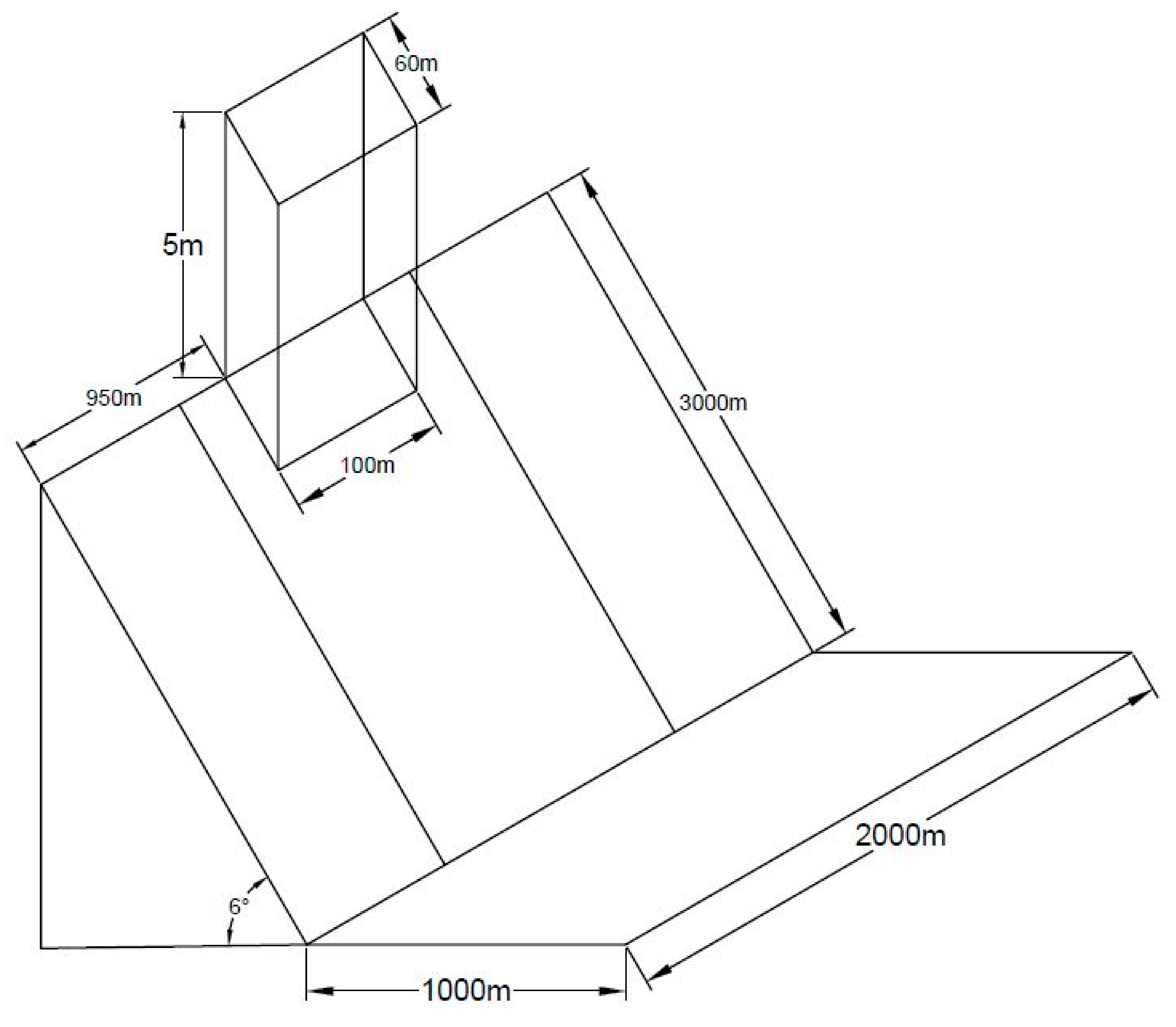
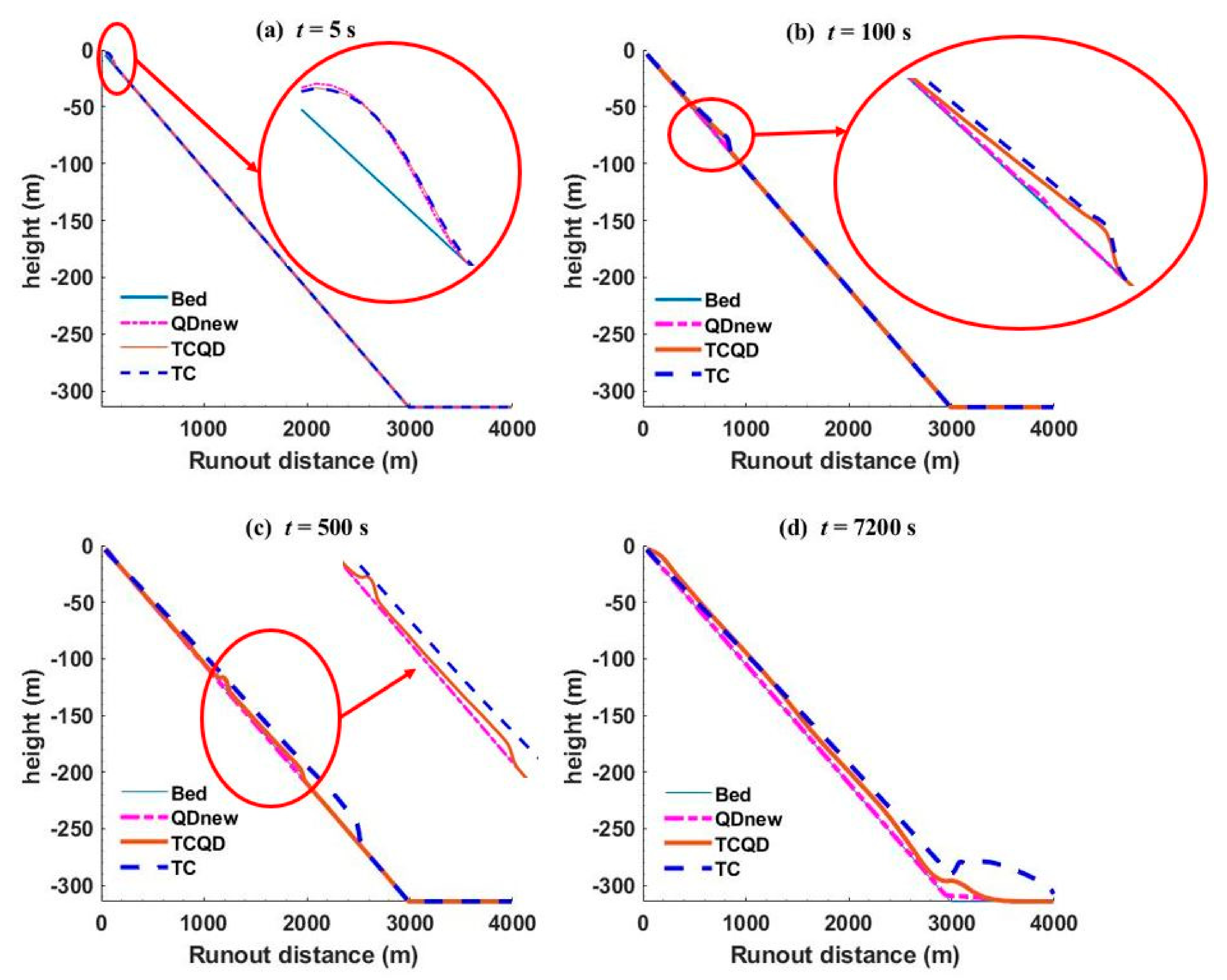
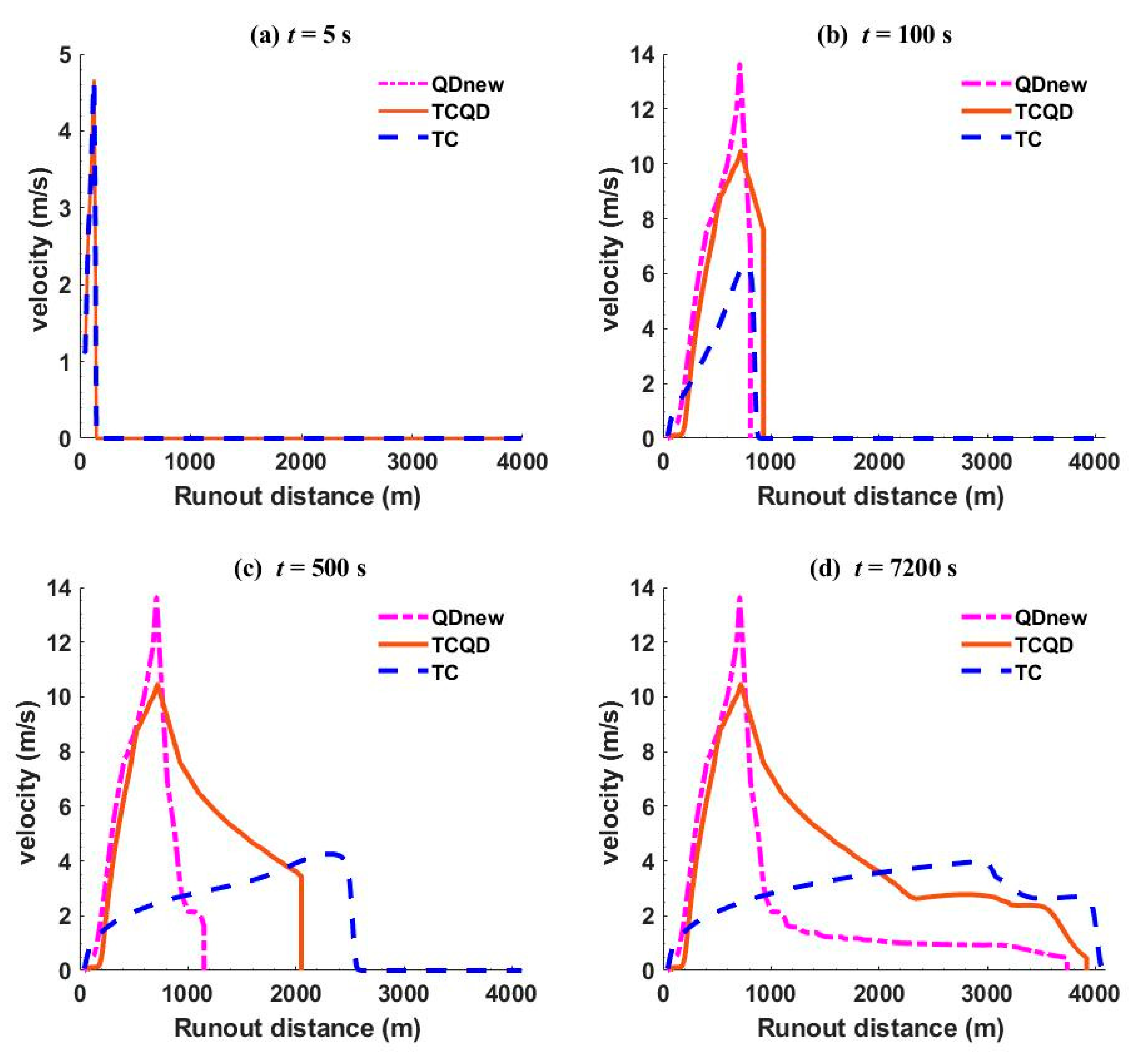
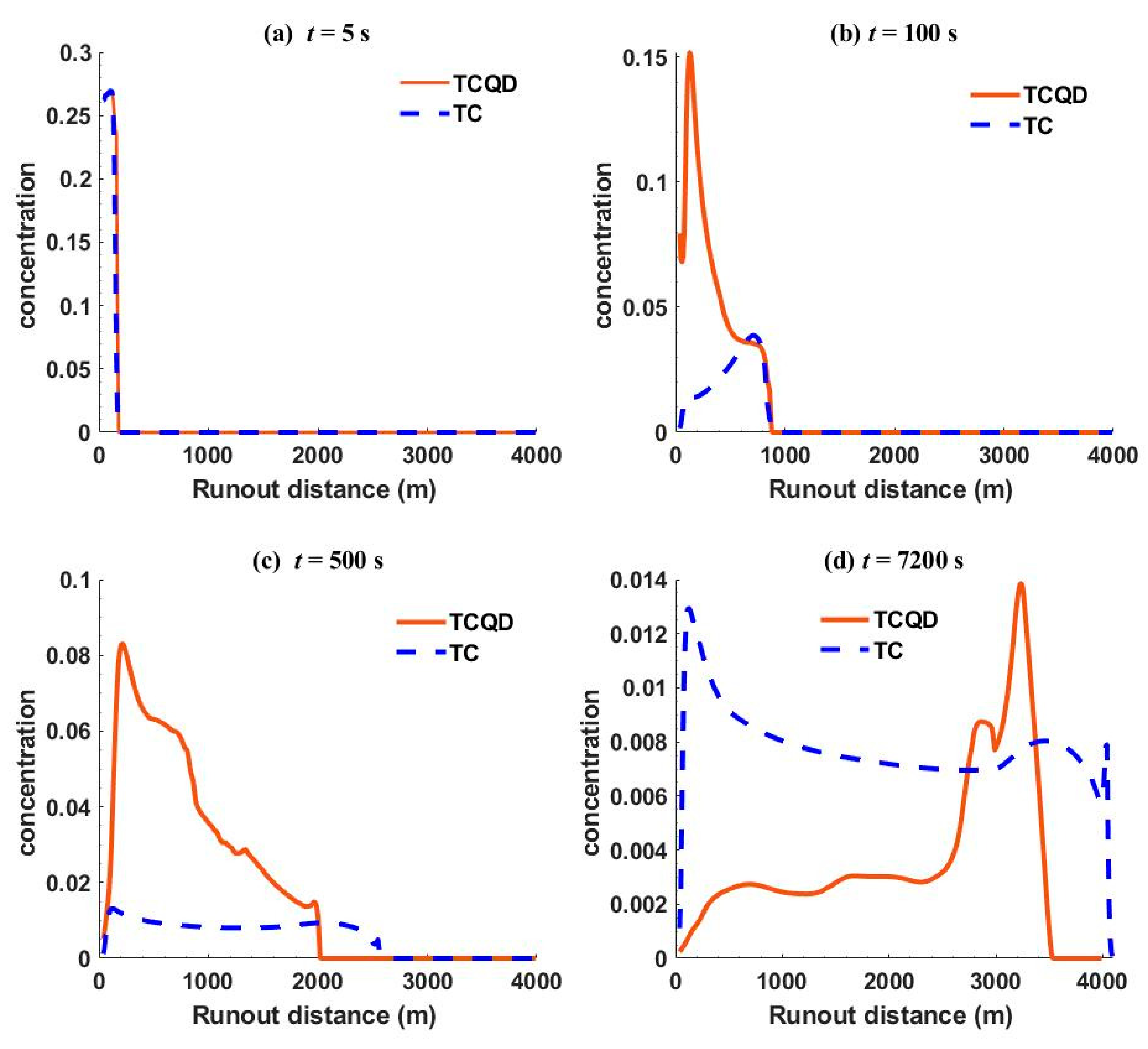
4.1. Application to Debris Flow over a Continental Shelf that Leads to Deep Sea
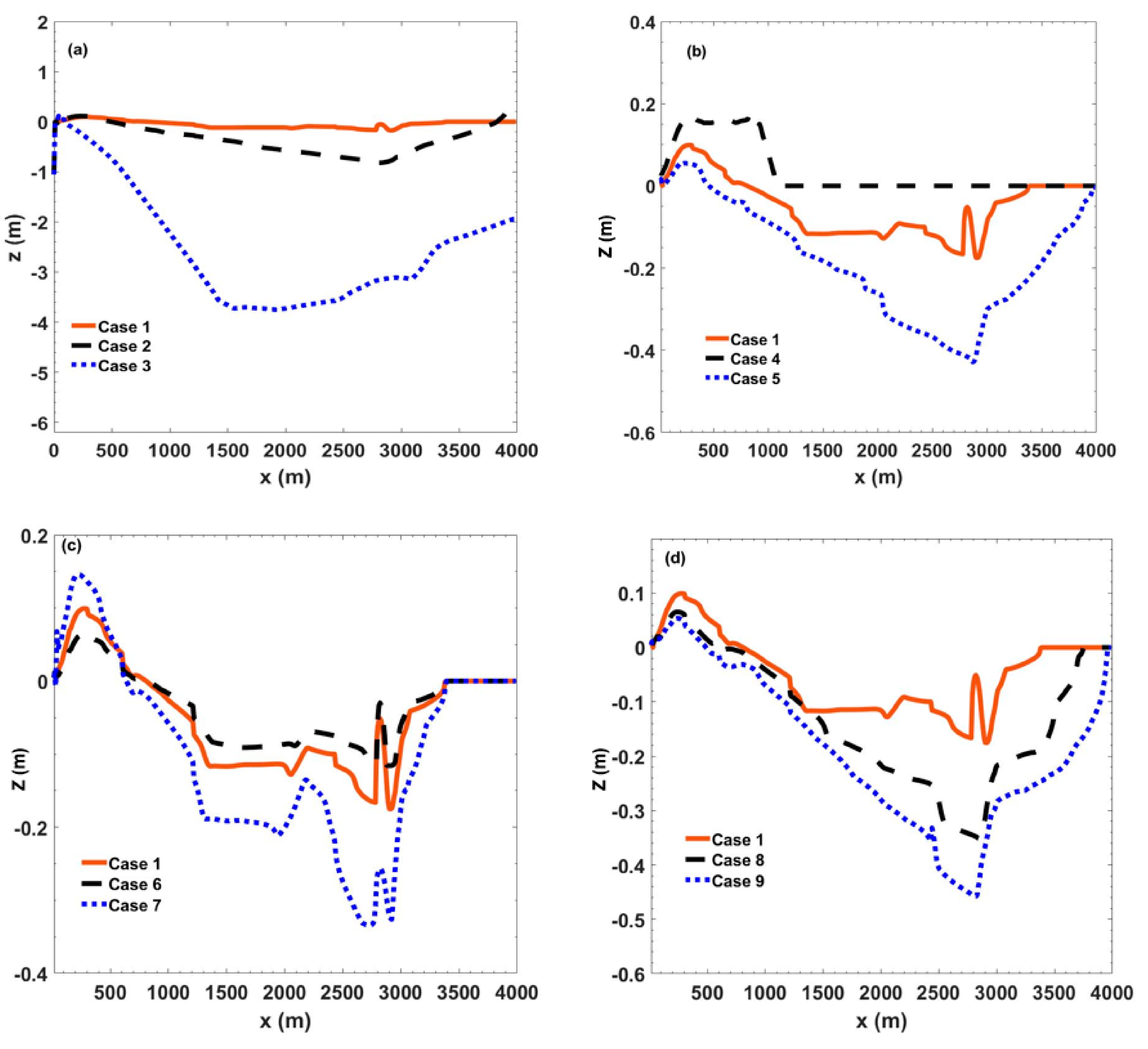
4.2. Sensitivity Analyses
4.2.1. Impact of Sediment Size and Bed Slope Angle on Bed Thickness
4.2.2. Impact of Bed Porosity and Debris Concentration on Bed Thickness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qian, X.; Xu, J.; Das, H.S.; Wang, D.; Bai, Y. Improved Modeling of Subaerial and Subaqueous Muddy Debris Flows. J. Hydraul. Eng. 2020, 146, 06020007. [Google Scholar] [CrossRef]
- De Blasio, F.V. Hydroplaning and submarine debris flows. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Imran, J.; Parker, G.; Locat, J.; Lee, H. 1D numerical model of muddy subaqueous and subaerial debris flows. J. Hydraul. Eng. 2001, 27, 717–729. [Google Scholar] [CrossRef]
- Kim, J.; Løvholt, F.; Issler, D.; Forsberg., C.F. Landslide material control on tsunami genesis—The Storegga Slide and tsunami (8,100 years BP). J. Geophys. Res. Oceans 2019, 124, 3607–3627. [Google Scholar] [CrossRef]
- McDougall, S.; Hungr, O. A model for the analysis of rapid landslide motion across three-dimensional terrain. Can. Geotech. J. 2004, 41, 1084–1097. [Google Scholar] [CrossRef]
- Pastor, M.; Quecedo, M.; González, E.; Herreros, I.; Fernández Merodo, J.A.; Mira, P. A simple approximation to bottom friction for Bingham fluid depth integrated models. J. Hydraul. Eng. 2004, 130, 149–155. [Google Scholar] [CrossRef]
- Qian, X.; Das, H.S. Modeling Subaqueous and Subaerial Muddy Debris Flows. J. Hydraul. Eng. 2019, 145, 04018083. [Google Scholar] [CrossRef]
- Huang, X.; García, M.H.; Huang, X.; García, M.H. A Perturbation Solution for Bingham-Plastic Mudflows. J. Hydraul. Eng. 1997, 123, 986–994. [Google Scholar] [CrossRef]
- Pastor, M.; Blanc, T.; Haddad, B.; Petrone, S.; Sanchez Morles, M.; Drempetic, V.; Issler, D.; Crosta, G.B.; Cascini, L.; Sorbino, G.; et al. Application of a SPH depth-integrated model to landslide run-out analysis. Landslides 2004, 11, 793–812. [Google Scholar] [CrossRef]
- Pudasaini, S.P. A general two-phase debris flow model. J. Geophys. Res. Earth Surf. 2012, 117, F03010. [Google Scholar] [CrossRef]
- Meng, X.; Wang, Y. Investigations of Gravity-Driven Two-Phase Debris Flows. In Recent Advances in Modeling Landslides and Debris Flows; Springer Series in Geomechanics and Geoengineering; Wu, W., Ed.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Wang, W.; Chen, G.; Han, Z.; Zhou, S.; Zhang, H.; Jing, P. 3D numerical simulation of debris-flow motion using SPH method incorporating non-Newtonian fluid behavior. Nat Hazards 2016, 81, 1981–1998. [Google Scholar] [CrossRef]
- Braun, A.; Cuomo, S.; Petrosino, S.; Wang, X.; Zhang, L. Numerical SPH analysis of debris flow run-out and related river damming scenarios for a local case study in SW China. Landslides 2018, 15, 535–550. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P.; Ghilardi, P.; Natale, L.; Savi, F. 1D mathematical modeling of debris flow. J. Hydraul. Res. 2000, 38, 435–446. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Du, J.; Song, D. Numerical study of granular debris flow run-up against slit dams by discrete element method. Landslides 2020, 17, 585–595. [Google Scholar] [CrossRef]
- Lu, P.; Yang, X.; Xu, F.; Hou, T.; Zhou, J. An Analysis of the Entrainment Effect of Dry Debris Avalanches on Loose Bed Materials; SpringerPlus: Cham, Switzerland, 2016; pp. 1–15. [Google Scholar]
- Toniolo, H.; Harff, P.; Marr, J.; Paola, C.; Parker, G. Experiments on reworking by successive unconfined subaqueous and subaerial muddy debris flows. J. Hydraul. Eng. 2004, 130, 38–48. [Google Scholar] [CrossRef]
- Takebayashi, H.; Fujita, M. Numerical Simulation of a Debris Flow on the Basis of a Two-Dimensional Continuum Body Model. Geosciences 2020, 10, 45. [Google Scholar] [CrossRef]
- Ali, S.Z.; Dey, S. Origin of the scaling laws of sediment transport. Proc. R. Soc. A 2017, 473, 20160785. [Google Scholar] [CrossRef]
- Ali, S.Z.; Dey, S. Impact of phenomenological theory of turbulence on pragmatic approach to fluvial hydraulics. Phys. Fluids 2018, 30, 045105. [Google Scholar] [CrossRef]
- Venditti, J.G.; Church, M.; Bennett, S.J. On interfacial instability as a cause of transverse subcritical bed forms. Water Resour. Res. 2006, 42, W07423. [Google Scholar] [CrossRef]
- Dey, S. Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena; Springer: Berlin, Germany, 2014. [Google Scholar]
- Naqshband, S.; Ribberink, J.S.; Hurther, D.; Hulscher, S.J.M.H. Bed load and suspended load contributions to migrating sand dunes in equilibrium. J. Geophys. Res. Earth Surf. 2014, 119, 1043–1063. [Google Scholar] [CrossRef]
- Ourmières, Y.; Chaplin, J.R. Visualizations of the disturbed-laminar waveinduced flow above a rippled bed. Exp. Fluids 2004, 36, 908–918. [Google Scholar] [CrossRef]
- Recking, A.; Bacchi, V.; Naaim, M.; Frey, P. Antidunes on steep slopes. J. Geophys. Res. Earth Surf. 2009, 114, F04025. [Google Scholar] [CrossRef]
- Eekhout, J.P.C.; Hoitink, A.J.F.; Mosselman, E. Field experiment on alternate bar development in a straight sand-bed stream. Water Resour. Res. 2013, 49, 8357–8369. [Google Scholar] [CrossRef]
- Li, J.; Cao, Z.; Pender, G.; Liu, Q. A double layer-averaged model for dam-break flows over mobile bed. J. Hydraul. Res. 2013, 51, 518–534. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Julien, P.J.; Fullerton, W.T. Two-dimensional water flood and mudflow simulation. J. Hyd. Eng. 1993, 119, 244. [Google Scholar] [CrossRef]
- Egashira, S.; Miyamoto, K.; Takahiro, I. Constitutive Equations of Debris Flows and Their Applicability. In Debris Flow Hazard Mitigation: Mechanics, Prediction and Assessment; ASCE: New York, NY, USA, 1997; pp. 340–349. [Google Scholar]
- Takahashi, T. Debris Flow. Annu. Rev. Fluid Mech. 1981, 13, 57–77. [Google Scholar] [CrossRef]
- Armanini, A.; Fraccarollo, L. Critical Conditions for Debris Flow. In Debris Flow Hazard Mitigation: Mechanics, Prediction, and Assessment; ASCE: New York, NY, USA, 1997; pp. 434–443. [Google Scholar]
- Hirano, M.; Harada, T.; Banihabib, M.E.; Kawahara, K. Estimation of Hazard Area Due to Debris Flow”, Debris Flow Hazard Mitigation: Mechanics, Prediction and Assessment; ASCE: San Francisco, CA, USA, 1997; pp. 697–706. [Google Scholar]
- Hu, P.; Cao, Z.; Pender, G. Well-balanced two-dimensional coupled modelling of submarine turbidity currents. In Maritime Engineering, Proceedings of the Institute of Civil Engineers; ICE Publishing: London, UK, 2012; Volume 165, pp. 169–188. [Google Scholar]
- Wright, V.; Krone, R.B. Laboratory and Numerical Study of Mud and Debris Flow; Rep. 1 and 2; Department of Civil Engineering, University of California: Davis, CA, USA, 1987. [Google Scholar]
- Mohrig, D.; Elverhøi, A.; Parker, G. Experiments on the relative mobility of muddy subaqueous and subaerial debris flows, and their capacity to remobilize antecedent deposits. Mar. Geol. 1999, 154, 117–129. [Google Scholar] [CrossRef]
- Hu, P.; Cao, Z.; Pender, G.; Tan, G. Numerical modelling of turbidity currents in the Xiaolangdi reservoir, Yellow River, China. J. Hydrol. 2012, 464–465, 41–53. [Google Scholar] [CrossRef]
- Hu, P.; Li, Y. Numerical modeling of the propagation and morphological of turbidity currents using a cost-saving strategy of solution updating. Int. J. Sed. Res. 2020, 35, 587–599. [Google Scholar] [CrossRef]
- Fukushima, Y.; Parker, G.; Pantin, H.M. Prediction of ignitive turbidity currents in Scripps Submarine Canyon. Mar. Geol. 1985, 67, 55–81. [Google Scholar] [CrossRef]
- Parker, G.; Fukushima, Y.; Pantin, H.M. Self-accelerating turbidity currents. J. Fluid Mech. 1986, 171, 145–181. [Google Scholar] [CrossRef]
- Zhang, R.J.; Xie, J.H. Sedimentation Research in China-Systematic Selections; China Water and Power Press: Beijing, China, 1993. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen (Measuring the consistency of rubber benzene solution). Kolloid Z. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Marr, J.G.; Elverhoi, A.; Harbitz, C.; Imran, J.; Harff, P. Numerical simulation of mud-rich subaqueous debris flows on the glacially active margins of the Svalbard-Barents Sea. Mar. Geol. 2002, 188, 351–364. [Google Scholar] [CrossRef]
- Parsons, J.D.; Friedrichs, C.T.; Traykovski, P.A.; Mohrig, D.; Imran, J.; Syvitski, J.P.M.; Parker, G.; Puig, P.; Buttles, J.L.; García, M.H. The mechanics of marine sediment gravity flows. In Continental Margin Sedimentation: From Sediment Transport to Sequence Stratigraphy; Nittrouer, C.A., Austin, J.A., Field, M.E., Kravitz, J.H., Syvitski, J.P.M., Wiberg, P.L., Eds.; Blackwell Publishing: Oxford, UK, 2007. [Google Scholar]
- Hu, P.; Cao, Z.X. Fully coupled mathematical modeling of turbidity currents over erodible bed. Adv. Water Res. 2009, 32, 1–15. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. A weighted surface-depth gradient method for the numerical integration of the 2D shallow-water equations with topography. Adv. Water Res. 2008, 31, 962–974. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Lan, C. Assessment of depth-averaged method in analysing runout submarine landslide. Landslides 2019, 17, 543–555. [Google Scholar] [CrossRef]
- Gauer, P.; Issler, D. Possible erosion mechanisms in snow avalanches. Ann. Glaciol. 2004, 38, 384–392. [Google Scholar] [CrossRef]
- Davies, T.R.; McSaveney, M.J. Runout of dry granular avalanches. Can. Geotech. J. 1999, 36, 313–320. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nat. Geosci. 2011, 4, 116–121. [Google Scholar] [CrossRef]
- Reid, M.E.; Iverson, R.M.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Entrainment of bed sediment by debris flows: Results from large-scale experiments. In Proceedings of the Fifth International Conference on debris flow hazards mitigation, mechanics, prediction and assessment, Padua, Italy, 14–17 June 2011; pp. 367–374. [Google Scholar]
- Hungr, O.; Evans, S.G. Entrainment of debris in rock avalanches: An analysis of a long run-out mechanism. Geol. Soc. Am. Bull. 2004, 116, 1240–1252. [Google Scholar] [CrossRef]
- Wang, G.; Sassa, K.; Fukuoka, H. Downslope volume enlargement of a debris slide-debris flow in the 1999 Hiroshima, Japan, rainstorm. Eng. Geol. 2003, 69, 309–330. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Fischer, J.T. A New Two-Phase Erosion-Deposition Model for Mass Flows; Geophysical Research Abstract: Vienna, Austria, 2016; Volume 18, EGU2016-4424. [Google Scholar]
- Liu, W.; He, S.; Chen, Z.; Yan, S.; Deng, Y. Effect of viscosity changes on the motion of debris flow by considering entrainment. J. Hydraul. Res. 2020, 59, 1–16. [Google Scholar] [CrossRef]
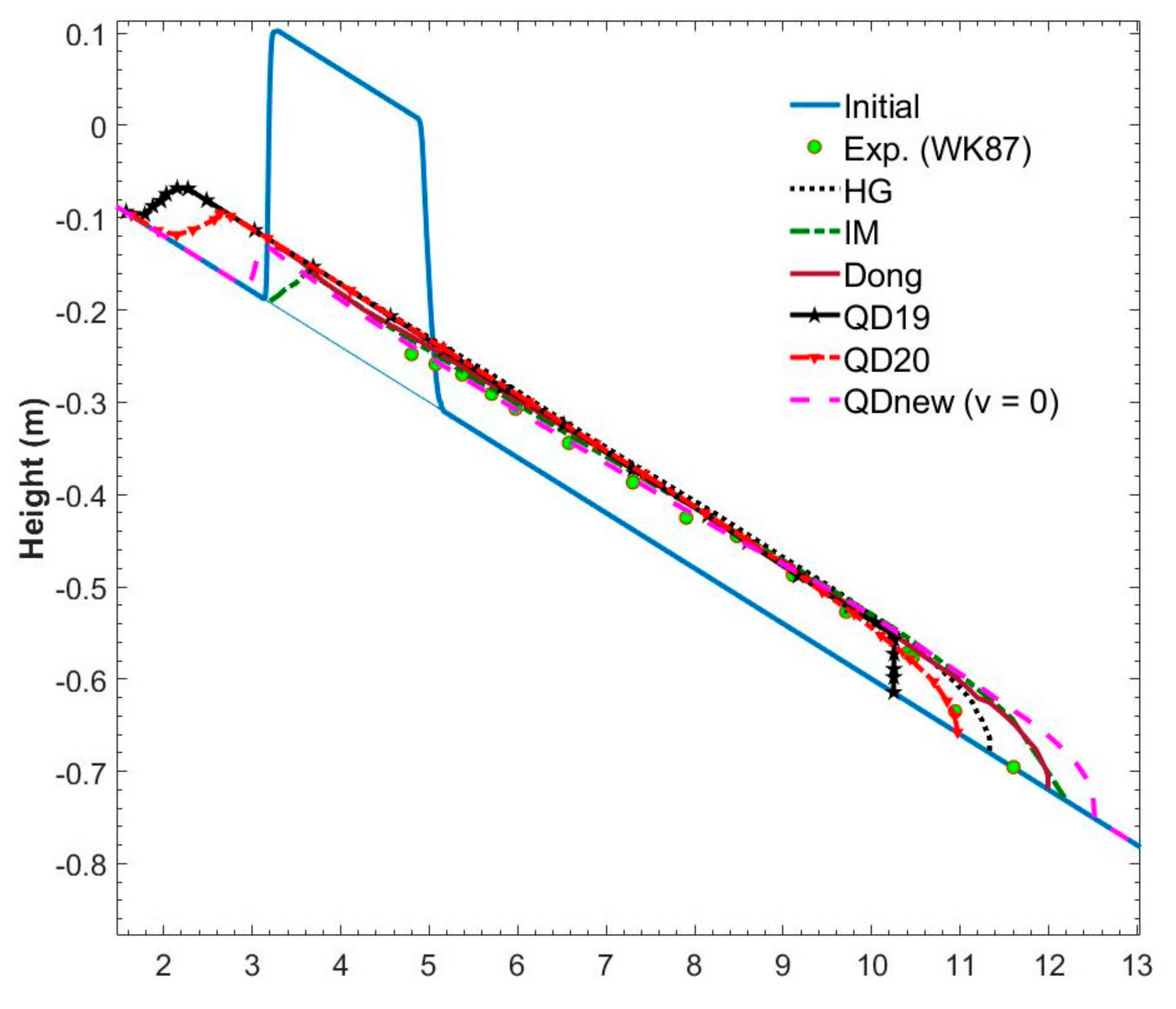
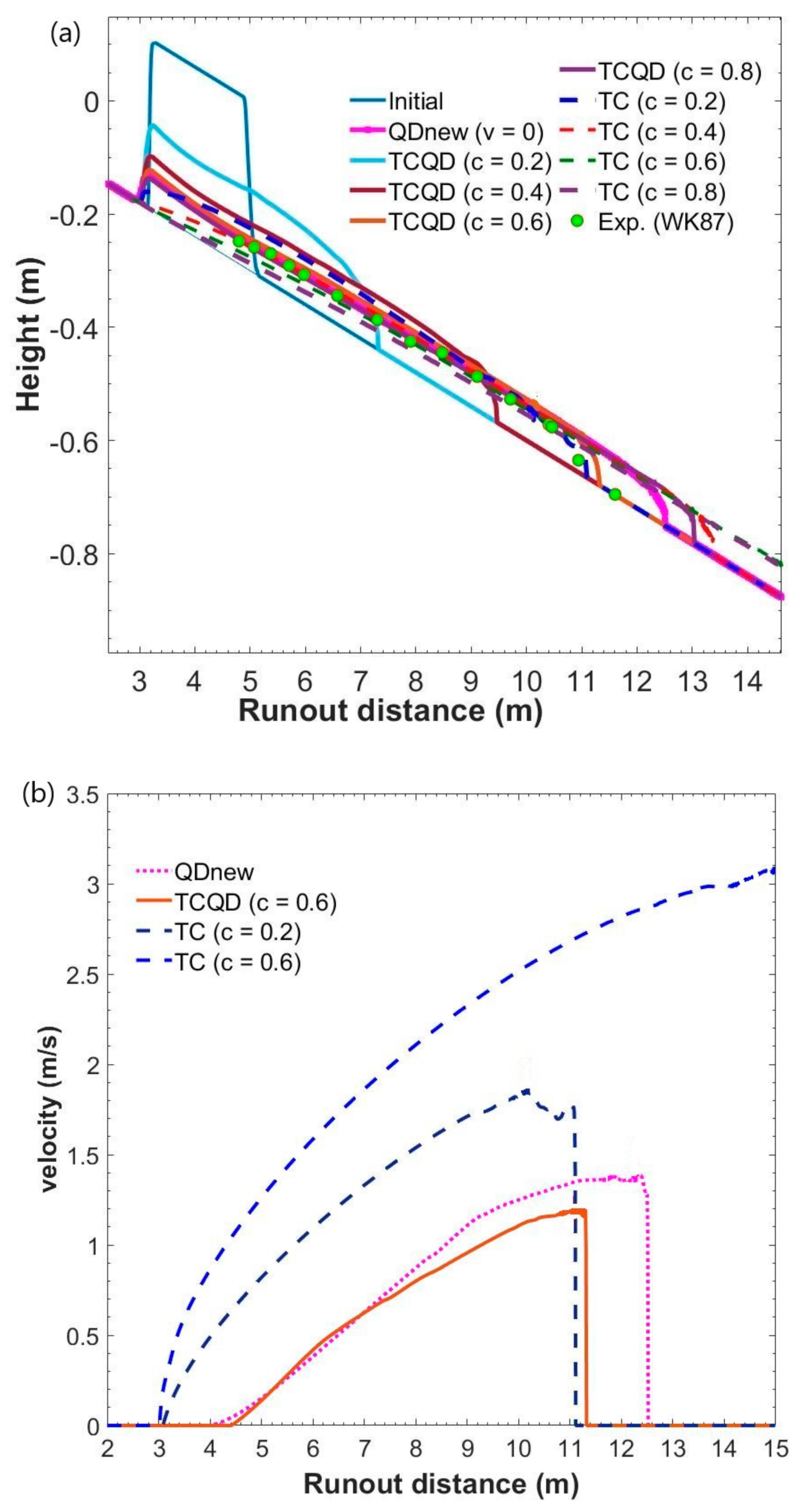
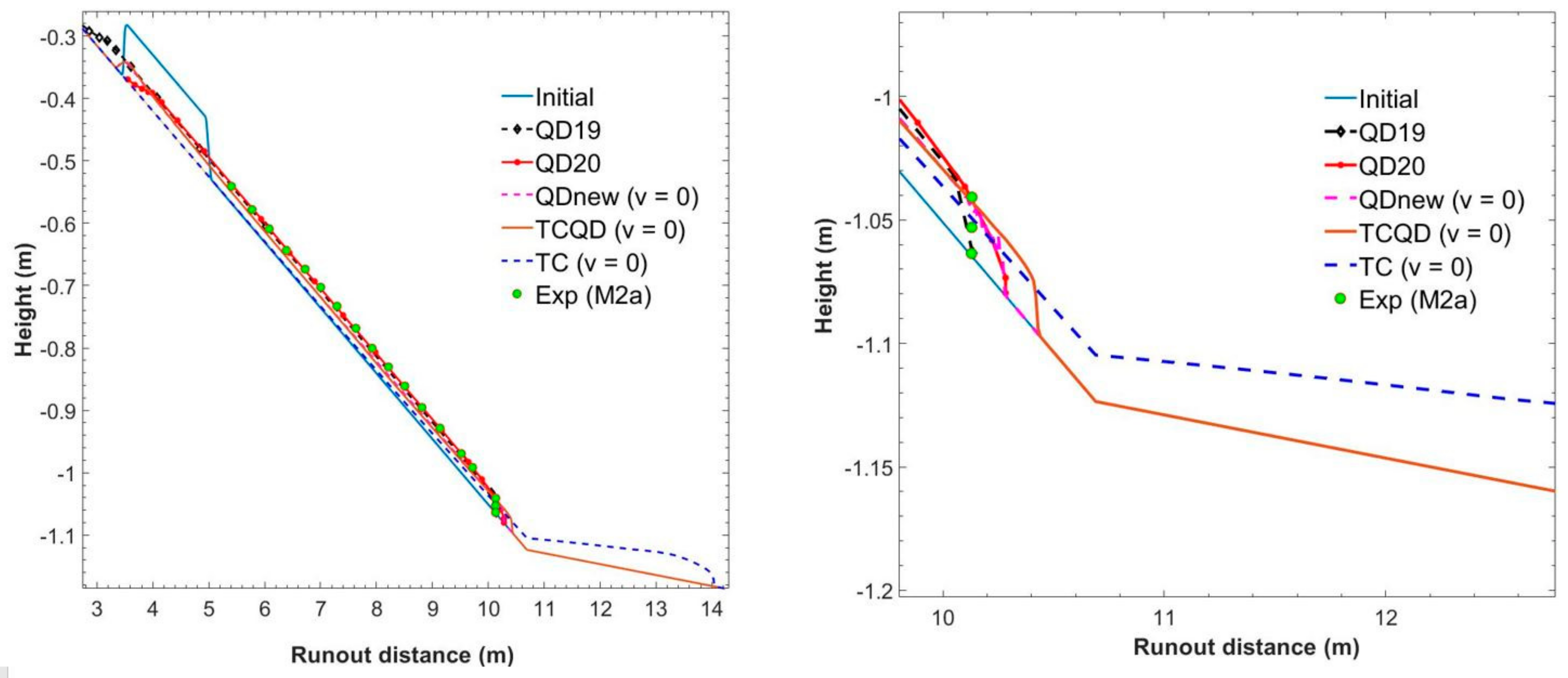
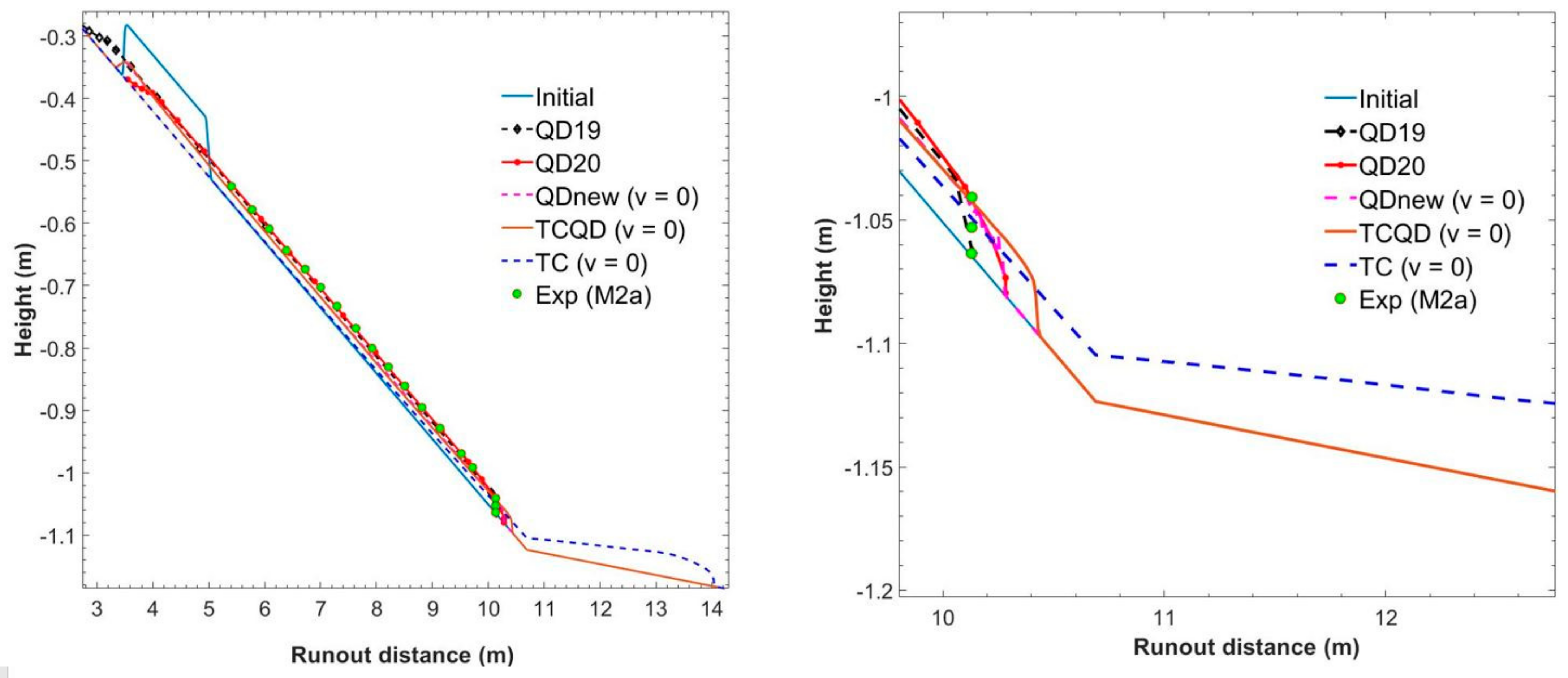
| Cases | Models | Estimation (%) |
|---|---|---|
| WK87 | QDnew | 7.9 |
| TCQD | −2.4 | |
| TC | 29.3 | |
| M2a | QDnew | 1.48 |
| TCQD | 3.06 | |
| TC | 38.7 | |
| M3a | QDnew | −4.2 |
| TCQD | −2.4 | |
| TC | 12.9 |
| Case No. | d (µm) | Porosity | c | (Pa.s) | Remarks | ||
|---|---|---|---|---|---|---|---|
| 1 | 37 | 6 | 0.5 | 0.27 | 100 | 20 | Reference case |
| 2 | 50 | 6 | 0.5 | 0.27 | 100 | 20 | Impact of sediment size |
| 3 | 100 | 6 | 0.5 | 0.27 | 100 | 20 | |
| 4 | 37 | 3 | 0.5 | 0.27 | 100 | 20 | Impact of bed slope angle |
| 5 | 37 | 9 | 0.5 | 0.27 | 100 | 20 | |
| 6 | 37 | 6 | 0.2 | 0.27 | 100 | 20 | Impact of bed porosity |
| 7 | 37 | 6 | 0.7 | 0.27 | 100 | 20 | |
| 8 | 37 | 6 | 0.5 | 0.5 | 100 | 20 | Impact of concentration/mass/density |
| 9 | 37 | 6 | 0.5 | 0.8 | 100 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adebiyi, A.A.; Hu, P. A Numerical Study on Impacts of Sediment Erosion/Deposition on Debris Flow Propagation. Water 2021, 13, 1698. https://doi.org/10.3390/w13121698
Adebiyi AA, Hu P. A Numerical Study on Impacts of Sediment Erosion/Deposition on Debris Flow Propagation. Water. 2021; 13(12):1698. https://doi.org/10.3390/w13121698
Chicago/Turabian StyleAdebiyi, Abiola Abraham, and Peng Hu. 2021. "A Numerical Study on Impacts of Sediment Erosion/Deposition on Debris Flow Propagation" Water 13, no. 12: 1698. https://doi.org/10.3390/w13121698
APA StyleAdebiyi, A. A., & Hu, P. (2021). A Numerical Study on Impacts of Sediment Erosion/Deposition on Debris Flow Propagation. Water, 13(12), 1698. https://doi.org/10.3390/w13121698







