How Well Can Machine Learning Models Perform without Hydrologists? Application of Rational Feature Selection to Improve Hydrological Forecasting
Abstract
1. Introduction
- Can rational (e.g., manual, based on empirical knowledge) feature selection improve the performance of an ML model of future streamflow runoff, compared to models with automatically selected features?
- Can this effect be retained in different ML model types and structures, including the DL model?
- Can the stochastic shuffling of input streamflow runoff time series for building training and test sets improve the overall model accuracy?
2. Materials and Methods
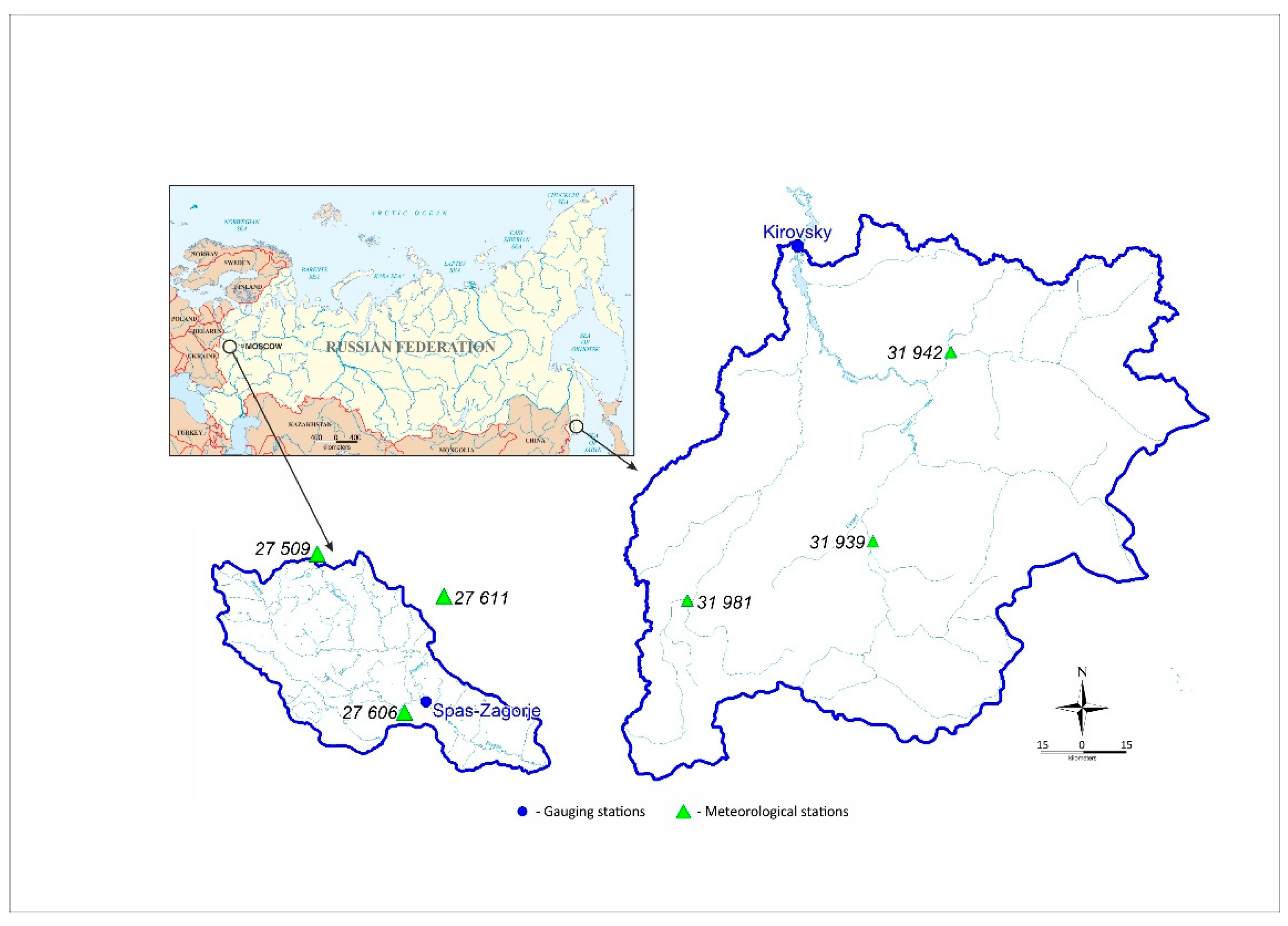
2.1. Case Study Catchments
2.2. ML Models
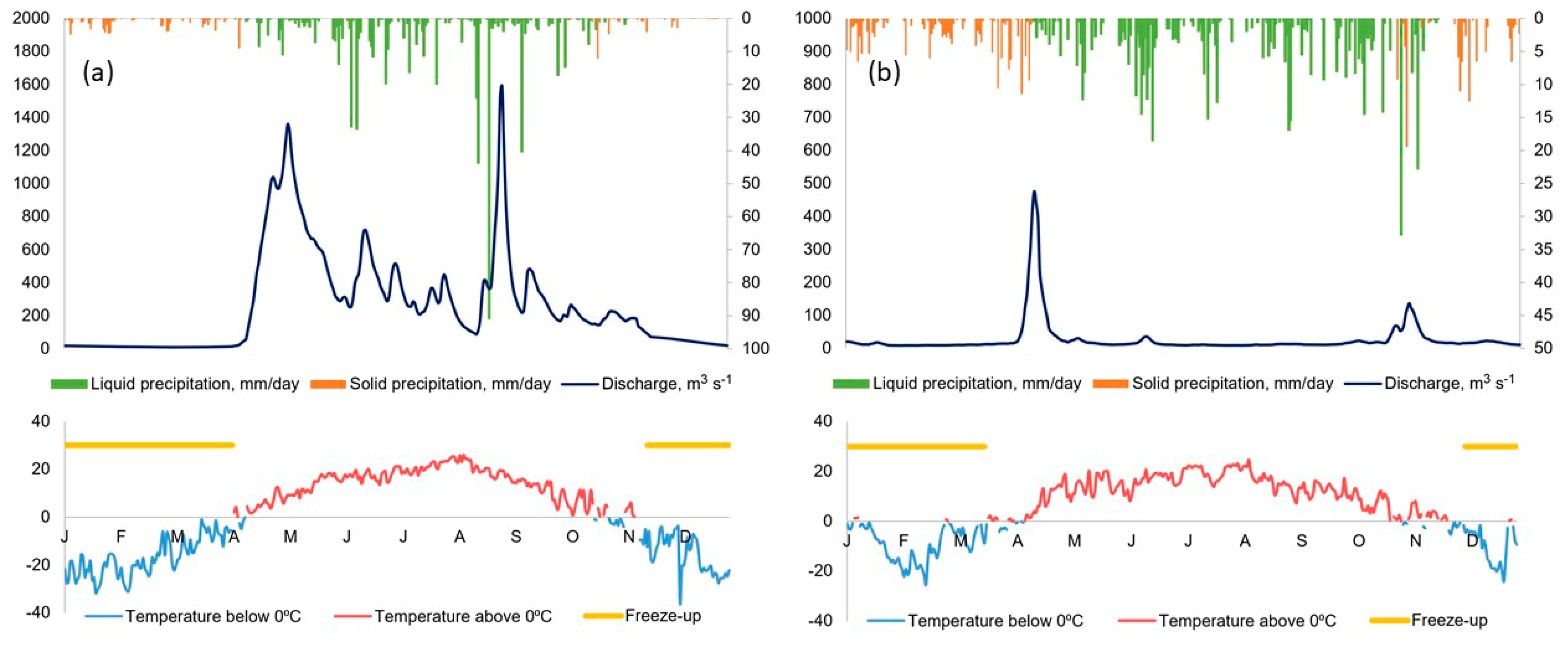
2.3. Initial Data Description
- Streamflow discharge at the basin outlet at current day and 7 days before , τ = 1, …, 7;
- Maximum streamflow discharge spread in the preceding period of 2 to 7 days , τ = 2, …, 7;
- Daily precipitation amount at individual weather stations for each day in the preceding 7 day period ;
- Basin-averaged daily precipitation amount for each day in the preceding 7 day period ;
- Accumulated precipitation for the preceding period of 2 to 7 days ;
- Accumulated daily temperatures from the beginning of the warm period above three thresholds 0, +2 и +5 °С ;
- Preceding moisture content index [27], calculated from the basin-averaged precipitation of the preceding 60 days as
- Accumulated potential evaporation from the beginning of the warm period, calculated as [28]:where is the daily potential evaporation amount, in mm, Re it the incoming solar irradiance, in W, T is the mean daily air temperature, in °С.
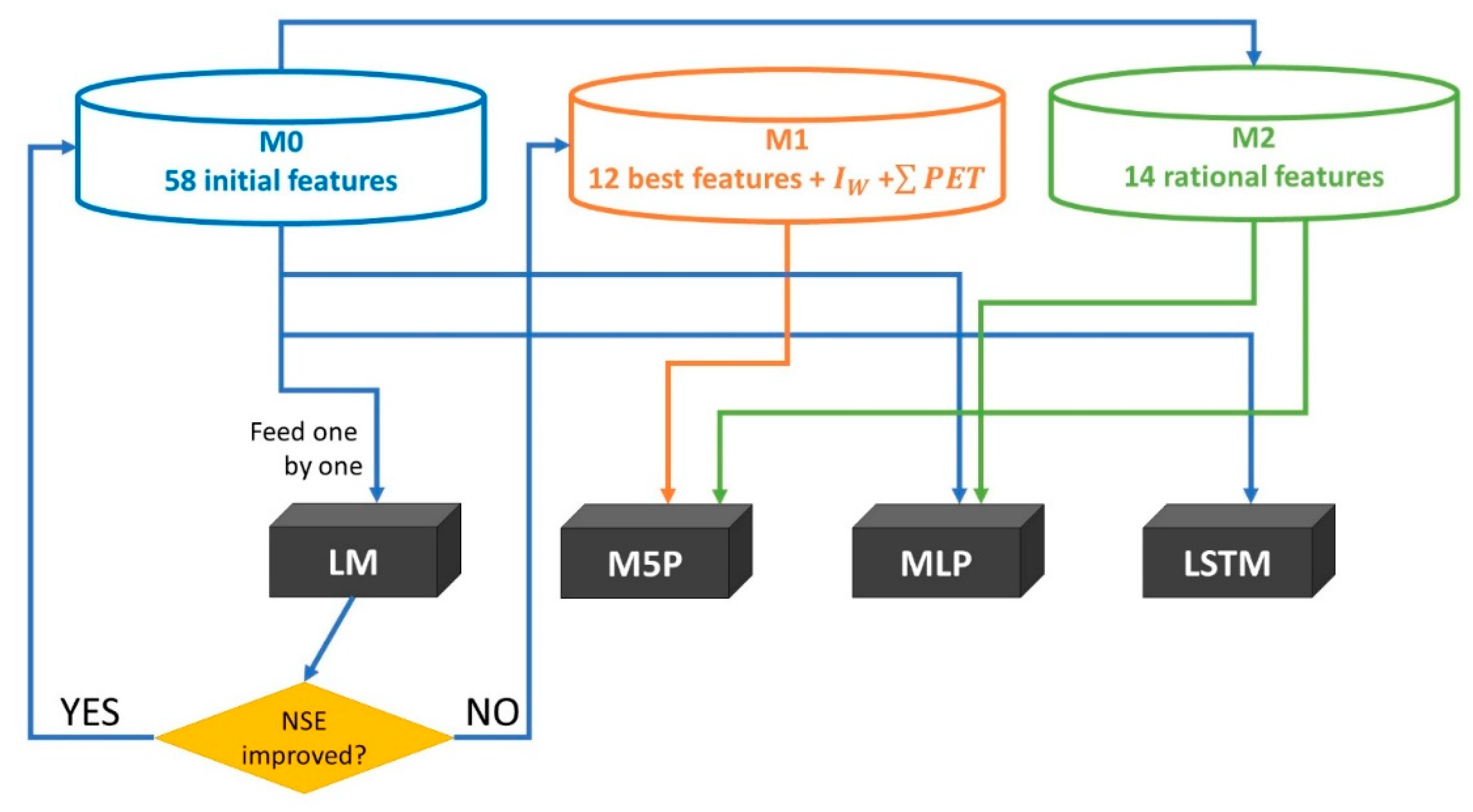
2.4. Feature Selection and Experimental Design
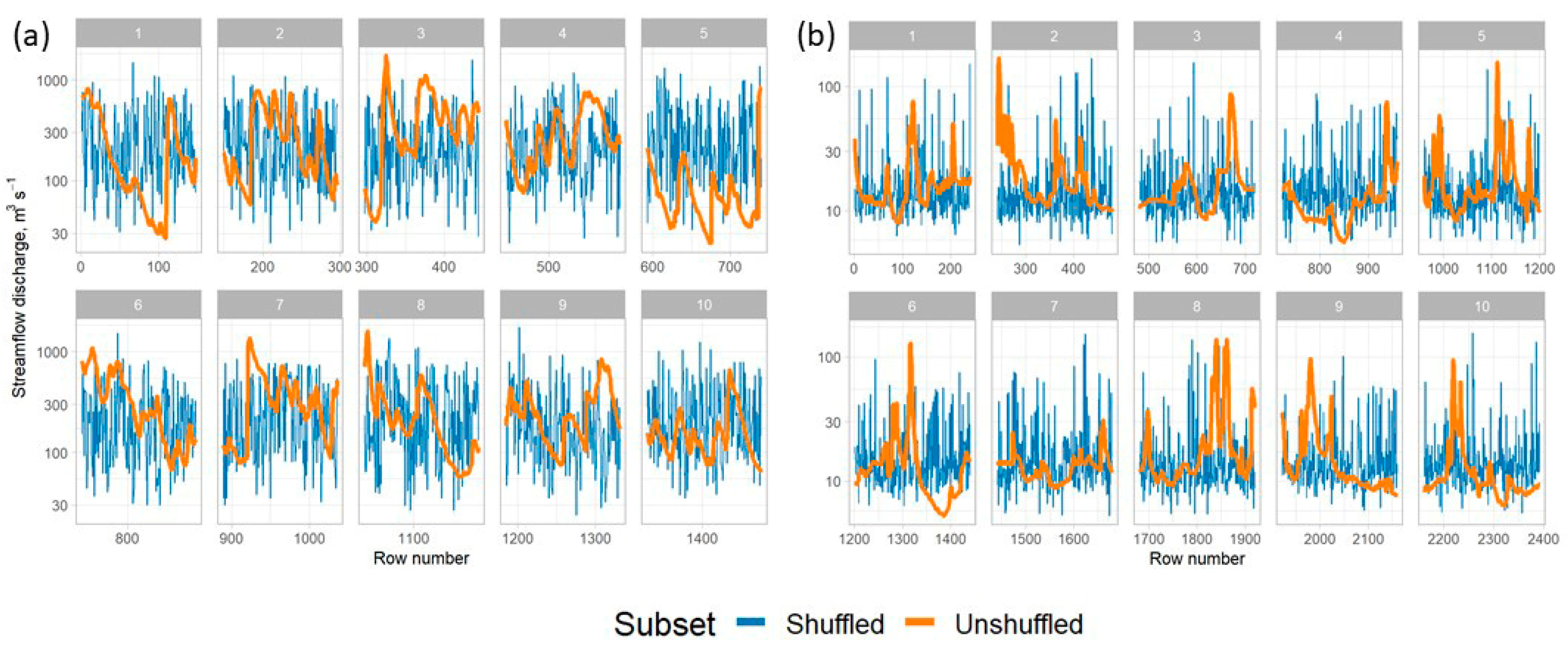
2.5. Model Training and Testing Methodology
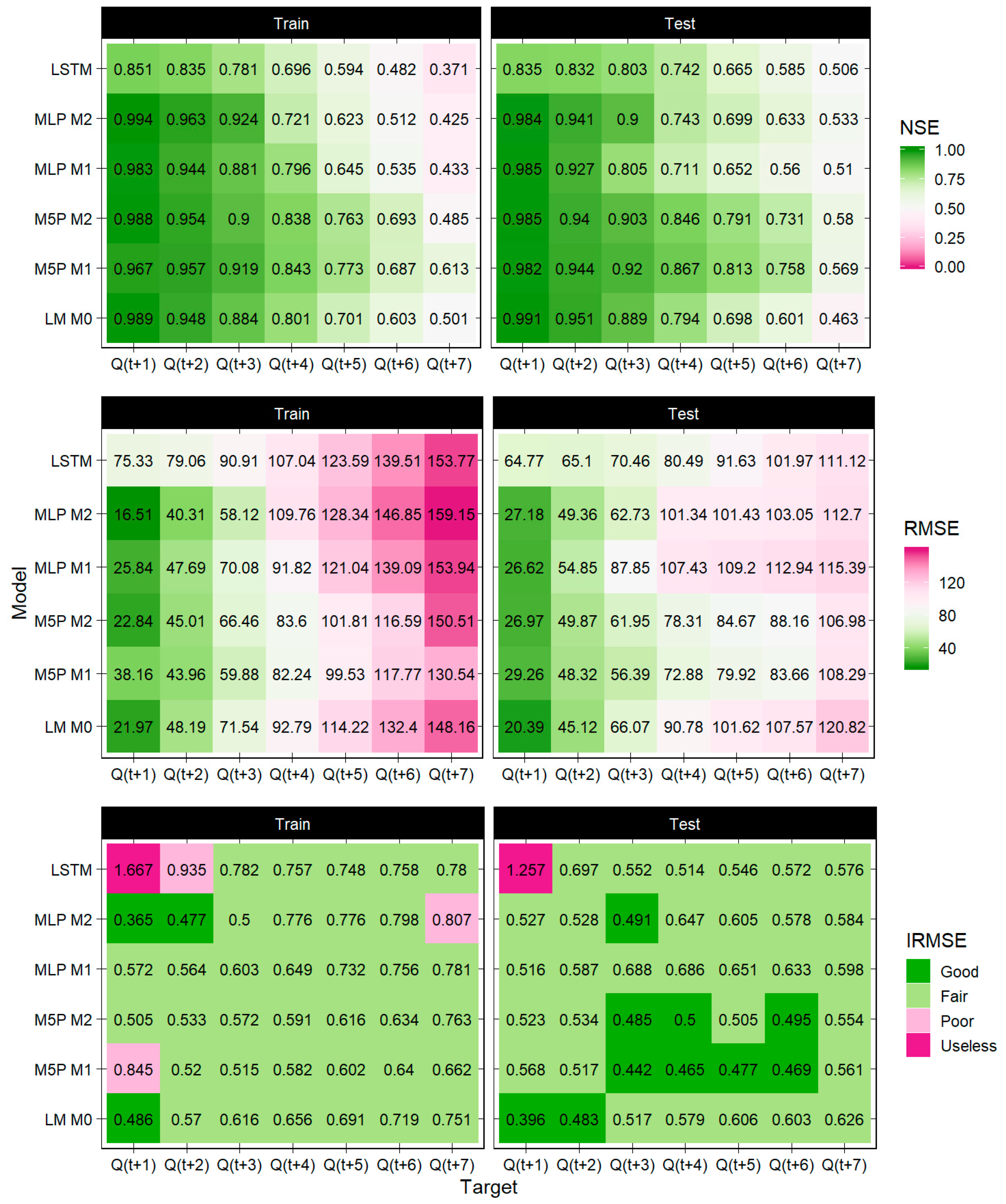
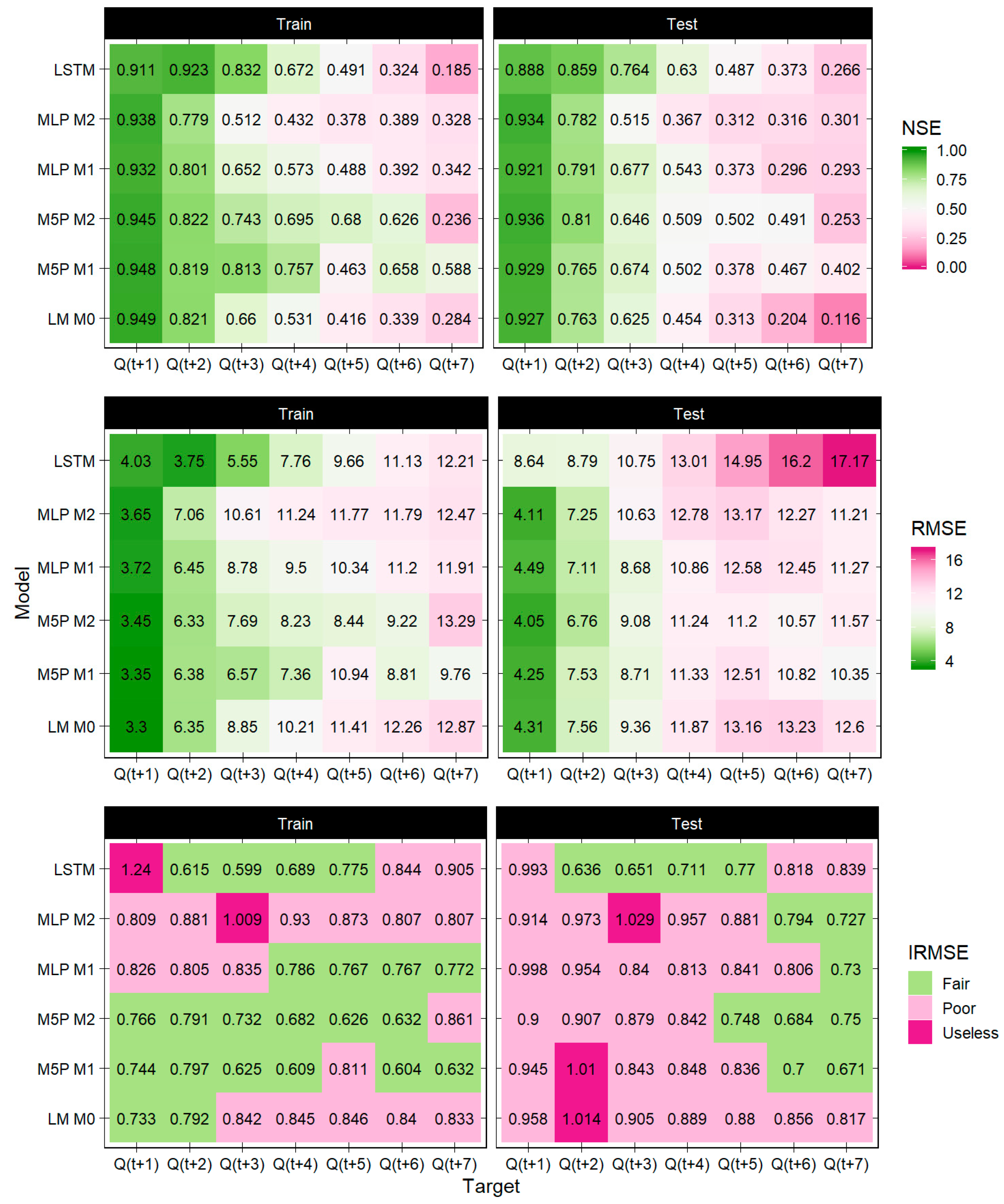
3. Results
Model Performance Evaluation
4. Discussion and Conclusions
- Overall, the models’ performance for the selected period of rainfall floods was better and more stable for the Ussuri river catchment than for the Protva river catchment;
- Deterioration of forecasting accuracy was more rapid and pronounced for Protva than for Ussuri; the “predictability threshold” was reached in 5 days of lead time for Protva, yet extended to more than 7 days for Ussuri;
- For both catchments, the LM and (piece-wise linear) M5P models outperformed ANNs on all lead times; however, the LSTM model was also effective on both training and test samples;
- For Ussuri, the performance of M5P M1 and M5P M2 was similar, yet this was not observed for Protva;
- The MLP M1 and MLP M2 models showed contrasting results for different catchments, with the MLP M2 performing better than the MLP M1 for Ussuri, while the opposite was observed for Protva.
5. Further Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pappenberger, F.; Pagano, T.C.; Brown, J.D.; Alfieri, L.; Lavers, D.A.; Berthet, L.; Bressand, F.; Cloke, H.L.; Cranston, M.; Danhelka, J.; et al. Hydrological Ensemble Prediction Systems Around the Globe. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H.L., Schaake, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–35. [Google Scholar]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Sood, A.; Smakhtin, V. Global hydrological models: A review. Hydrol. Sci. J. 2015, 60, 549–565. [Google Scholar] [CrossRef]
- Beven, K. Deep learning, hydrological processes and the uniqueness of place. Hydrol. Process. 2020, 34, 3608–3613. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.; Mount, N.J.; See, L.M.; Shamseldin, A.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Prog. Phys. Geogr. Earth Environ. 2012, 36, 480–513. [Google Scholar] [CrossRef]
- Dibike, Y.; Solomatine, D. River flow forecasting using artificial neural networks. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2001, 26, 1–7. [Google Scholar] [CrossRef]
- Halff, A.H.; Halff, H.M.; Azmoodeh, M. Predicting runoff from rainfall using neural networks. In Engineering Hydrology, Proceedings of the Symposium sponsored by the Hydraulics Division of ASCE, San Francisco, CA, 25–30 July 1993; Kuo, C.Y., Ed.; ASCE: New York, NY, USA, 1993; pp. 760–765. [Google Scholar]
- Jain, A.; Sudheer, K.P.; Srinivasulu, S. Identification of physical processes inherent in artificial neural network rainfall runoff models. Hydrol. Process. 2004, 18, 571–581. [Google Scholar] [CrossRef]
- See, L.M.; Jain, A.; Dawson, C.W.; Abrahart, R.J. Visualisation of Hidden Neuron Behaviour in a Neural Network Rainfall-Runoff Model. In Practical Hydroinformatics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Schmidt, L.; Heße, F.; Attinger, S.; Kumar, R. Challenges in Applying Machine Learning Models for Hydrological Inference: A Case Study for Flooding Events Across Germany. Water Resour. Res. 2020, 56, e2019WR025924. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Solomatine, D. Improving AI System Awareness of Geoscience Knowledge: Symbiotic Integration of Physical Approaches and Deep Learning. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 1: Concepts and methodology. Hydrol. Earth Syst. Sci. 2010, 14, 1931–1941. [Google Scholar] [CrossRef]
- Amaranto, A.; Munoz-Arriola, F.; Solomatine, D.P.; Corzo, G. A Spatially Enhanced Data-Driven Multimodel to Improve Semiseasonal Groundwater Forecasts in the High Plains Aquifer, USA. Water Resour. Res. 2019, 55, 5941–5961. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model with LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Time of concentration: A paradox in modern hydrology. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef]
- Beven, K.J. A history of the concept of time of concentration. Hydrol. Earth Syst. Sci. 2020, 24, 2655–2670. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D. Machine learning in sedimentation modelling. Neural Netw. 2006, 19, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An evaluation framework for input variable selection algorithms for environmental data-driven models. Environ. Model. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Australia, 16–18 November 1992; World Scientific: Singapore, 1992; Volume 92, pp. 343–348. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines. Pearson Prentice Hall New Jersey USA 936 pLinks (Vol. 3). 2009. Available online: https://cours.etsmtl.ca/sys843/REFS/Books/ebook_Haykin09.pdf (accessed on 1 May 2021).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; Cournapeau, D.; Pedregosa, F.; Varoquaux, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Frank, E.; Hall, M.A.; Witten, I.H. The WEKA Workbench. In Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”, 4th ed.; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Loginov, V.F.; Volchek, A.A.; Shelest, T.A. Analysis and simulation of rain flood hydrographs in Belarus rivers. Water Resour. 2015, 42, 292–301. [Google Scholar] [CrossRef]
- Oudin, L.; Michel, C.; Anctil, F. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 1—Can rainfall-runoff models effectively handle detailed potential evapotranspiration inputs? J. Hydrol. 2005, 303, 275–289. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Dominguez, E.; Dawson, C.W.; Ramirez, A.; Abrahart, R. The search for orthogonal hydrological modelling metrics: A case study of 20 monitoring stations in Colombia. J. Hydroinform. 2010, 13, 429–442. [Google Scholar] [CrossRef]
- Borsch, S.; Simonov, Y. Operational Hydrologic Forecast System in Russia. In Flood Forecasting; Elsevier: Amsterdam, The Netherlands, 2016; pp. 169–181. Available online: https://linkinghub.elsevier.com/retrieve/pii/B9780128018842000074 (accessed on 20 April 2021).
- Germann, U.; Zawadzki, I. Scale-Dependence of the Predictability of Precipitation from Continental Radar Images. Part I: Description of the Methodology. Mon. Weather Rev. 2002, 130, 2859–2873. [Google Scholar] [CrossRef]
| Variable | Column | Ussuri | Protva |
|---|---|---|---|
| Predictands | |||
| Future streamflow discharge | 2–8 | , τ = 1, …, 7 | |
| ”Dynamic” predictors | |||
| Current and past streamflow discharge | 9–16 | , τ = 1, …, 7 | |
| Maximum discharge spread | 17–23 | , τ = 2, …, 7 | |
| Daily precipitation amount at each weather station | 24–47 | , τ = 1, …, 7, j = 31,939, 31,942, 31,981 | , τ = 1, …, 7, j = 27,509, 27,606, 27,611 |
| Basin-averaged daily precipitation amount | 48–55 | , τ = 1, …, 7 | |
| Accumulated precipitation for the preceding period | 56–61 | τPτ, τ = 2, …, 7 | |
| ”Inertial” predictors | |||
| Preceding moisture content index | 62 | ||
| Accumulated daily temperatures from the beginning of the warm period above thresholds 0, +2 и +5 °C | 63–65 | T0, T+2, T+5 | |
| Accumulated potential evaporation from the beginning of the warm period | 66 | ||
| River | М1 | М2 |
|---|---|---|
| Ussuri | ||
| Protva |
| River | Feature Set | LM | M5P | MLP | LSTM |
|---|---|---|---|---|---|
| Ussuri | M0 | + | + | + | |
| M1 | + | ||||
| M2 | + | + | |||
| Protva | M0 | + | + | + | |
| M1 | + | ||||
| M2 | + | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreido, V.; Gartsman, B.; Solomatine, D.P.; Suchilina, Z. How Well Can Machine Learning Models Perform without Hydrologists? Application of Rational Feature Selection to Improve Hydrological Forecasting. Water 2021, 13, 1696. https://doi.org/10.3390/w13121696
Moreido V, Gartsman B, Solomatine DP, Suchilina Z. How Well Can Machine Learning Models Perform without Hydrologists? Application of Rational Feature Selection to Improve Hydrological Forecasting. Water. 2021; 13(12):1696. https://doi.org/10.3390/w13121696
Chicago/Turabian StyleMoreido, Vsevolod, Boris Gartsman, Dimitri P. Solomatine, and Zoya Suchilina. 2021. "How Well Can Machine Learning Models Perform without Hydrologists? Application of Rational Feature Selection to Improve Hydrological Forecasting" Water 13, no. 12: 1696. https://doi.org/10.3390/w13121696
APA StyleMoreido, V., Gartsman, B., Solomatine, D. P., & Suchilina, Z. (2021). How Well Can Machine Learning Models Perform without Hydrologists? Application of Rational Feature Selection to Improve Hydrological Forecasting. Water, 13(12), 1696. https://doi.org/10.3390/w13121696







