Overland Flow Resistance Law under Sparse Stem Vegetation Coverage
Abstract
1. Introduction
2. Methods and Material
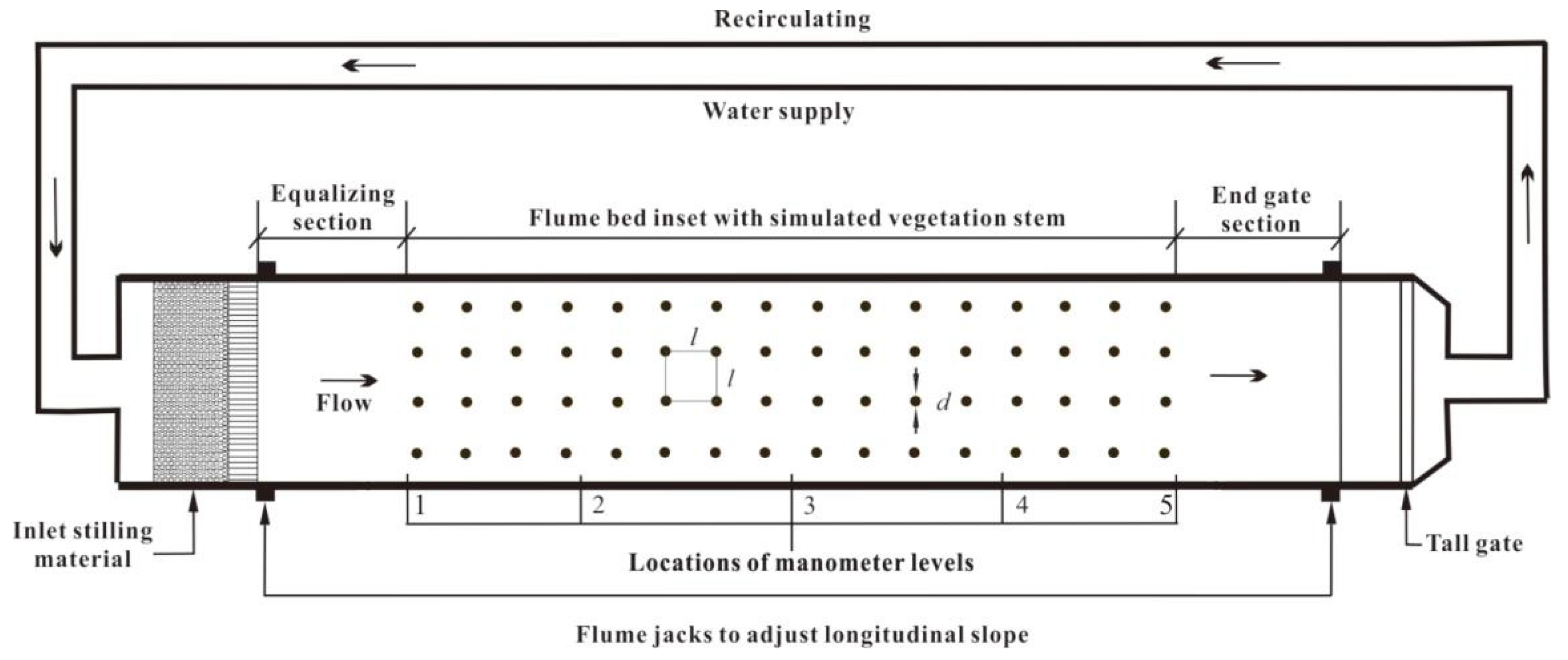
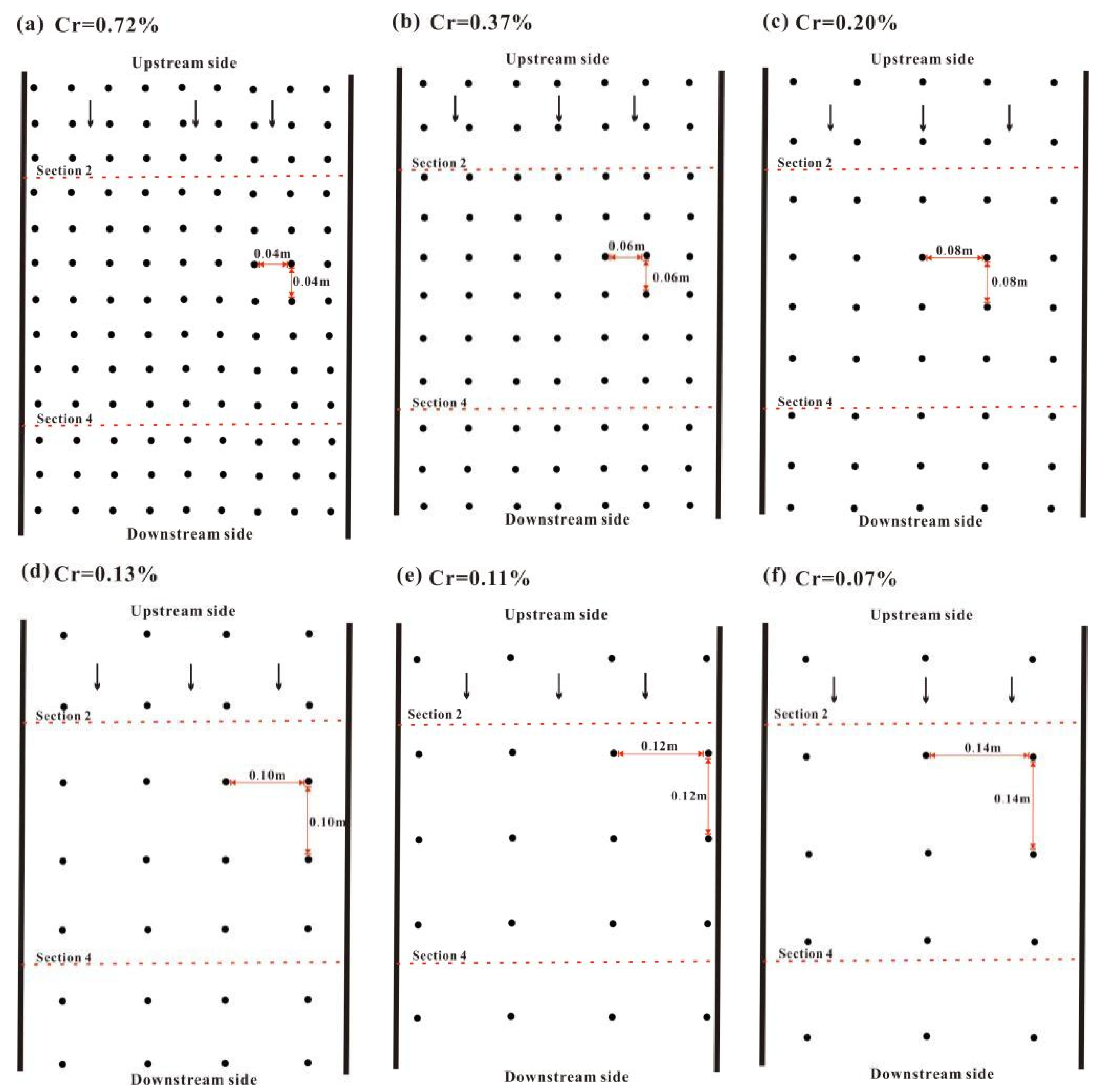
2.1. Experimental Structure
2.2. Data Analysis
3. Results and Discussion
3.1. Statistical Analysis
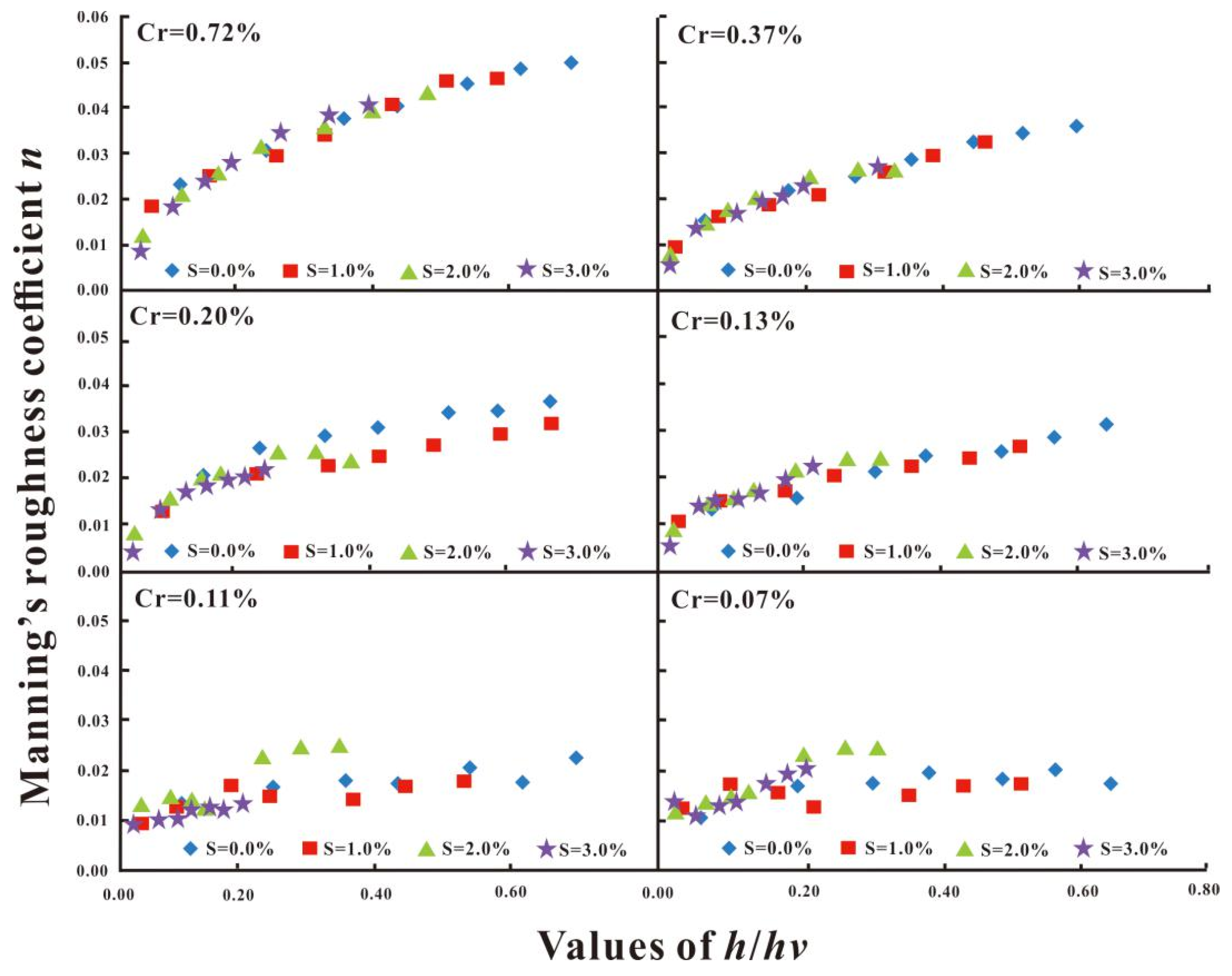
3.2. The Relationship between n and h/hv under Different Density and Slope Conditions
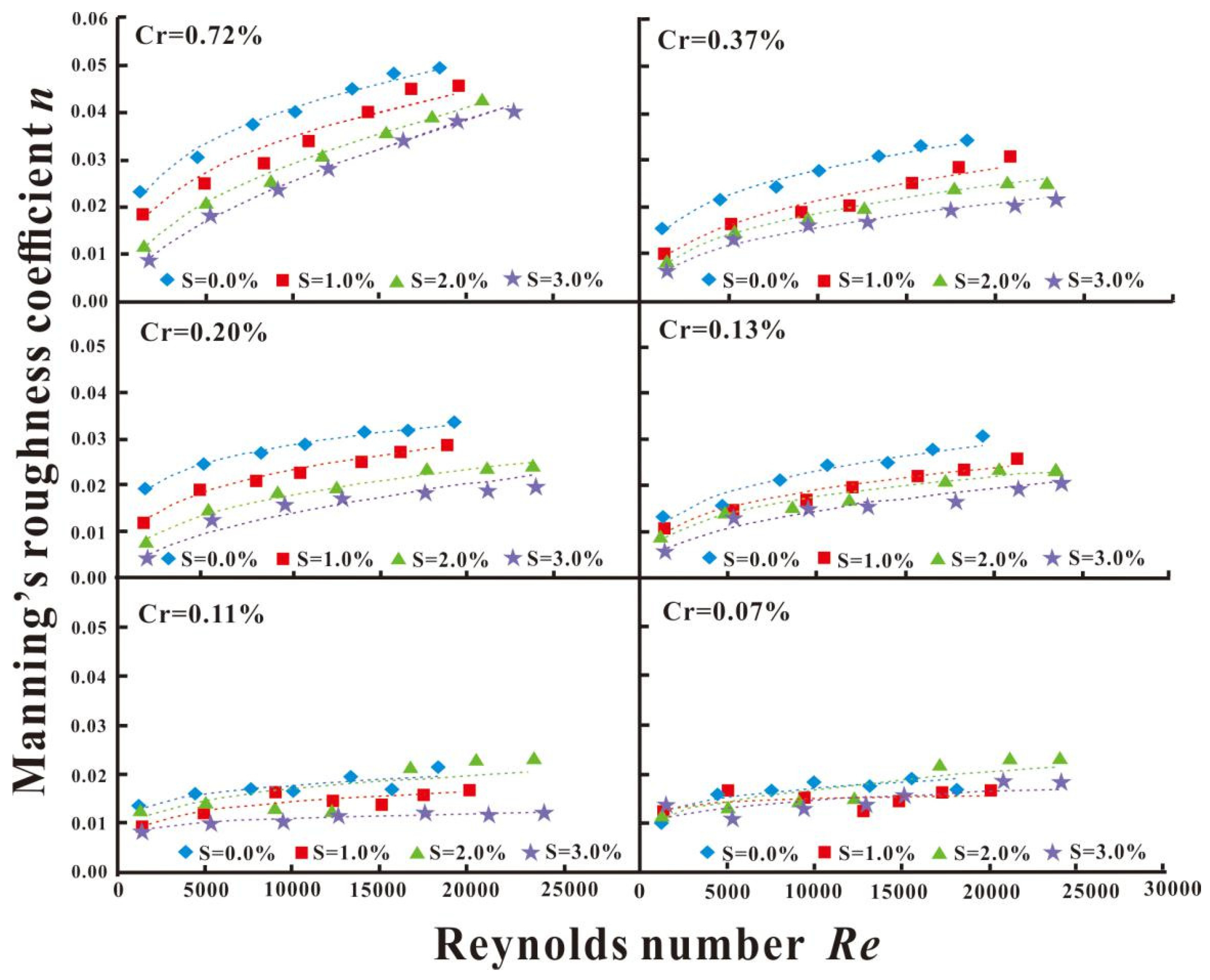
3.3. The Relationship between n and Re under Different Density and Slope Conditions
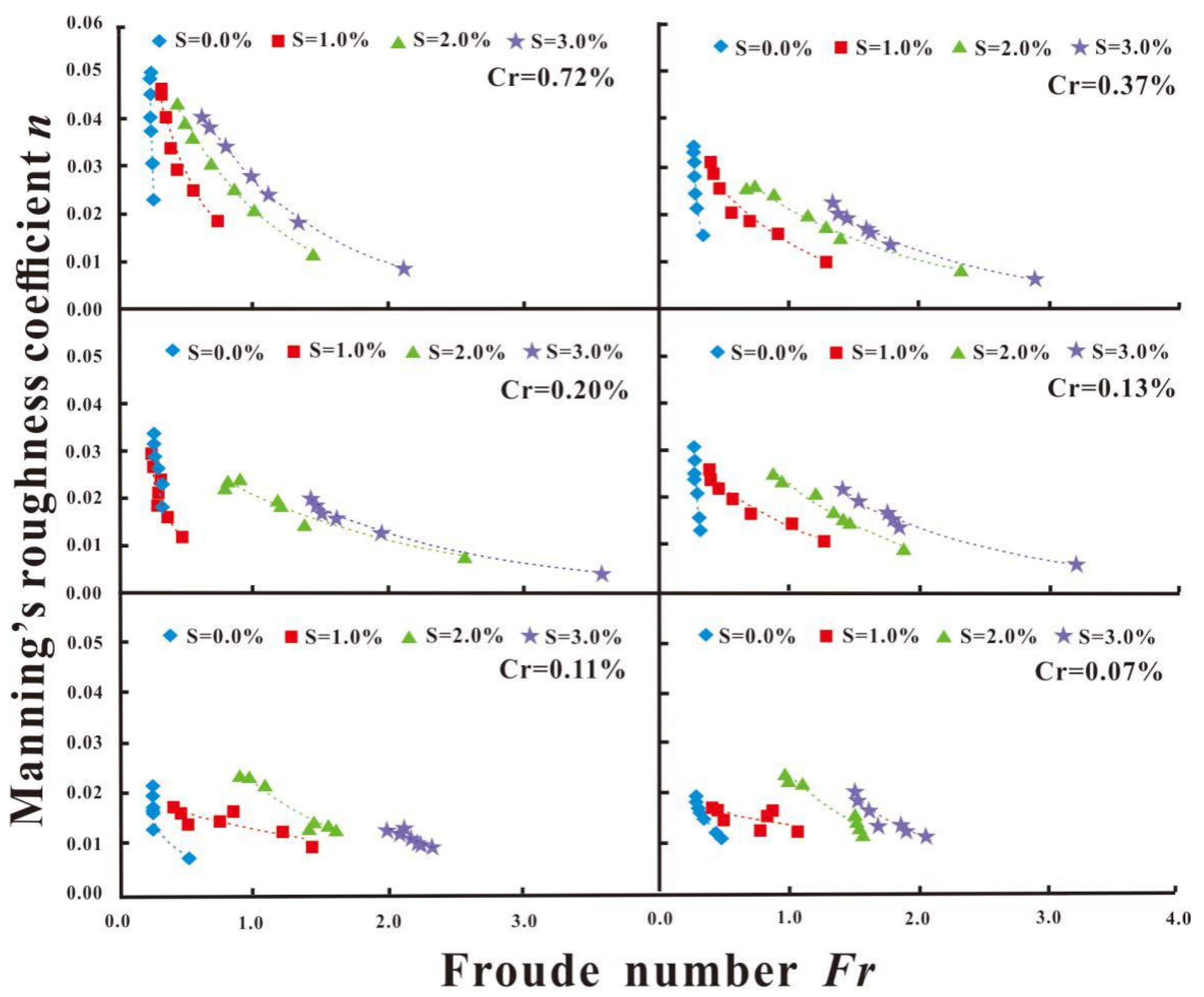
3.4. The Relationship between n and Fr under Different Density and Slope Conditions
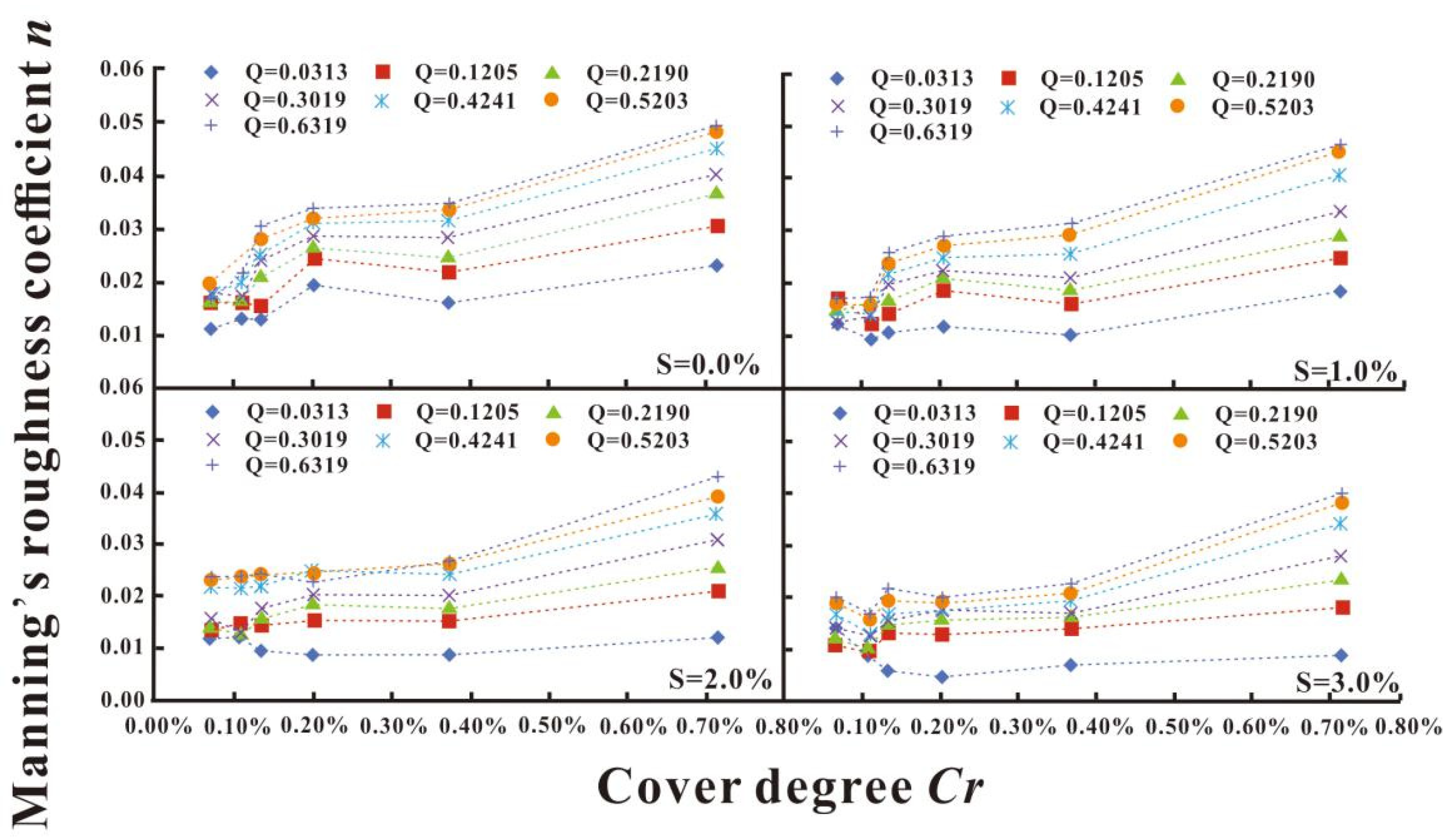
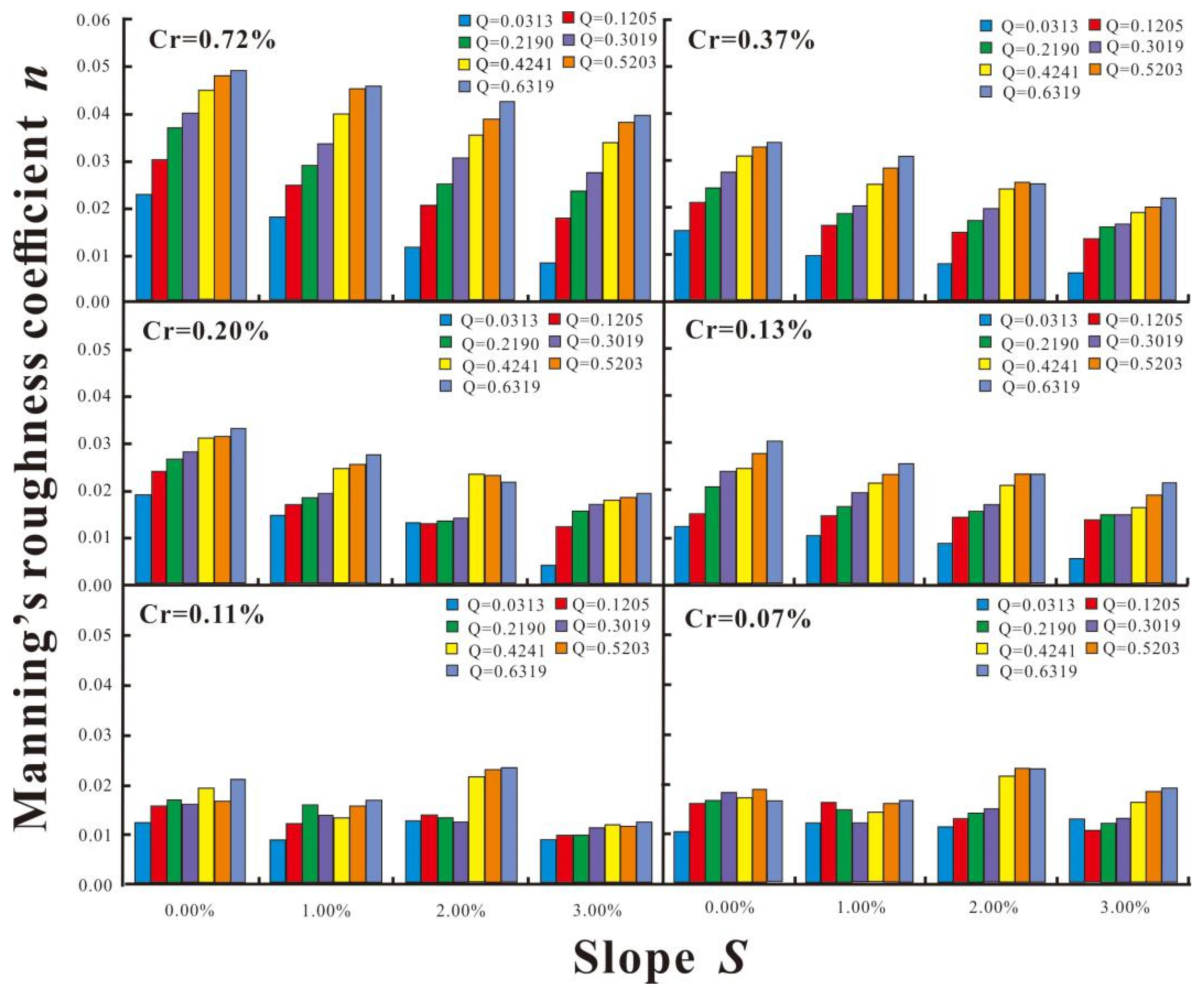
3.5. The Relationship between n and Cr and S under Different Flow Discharge Conditions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, N.S.; Nguyen, H.T.; Tan, S.K.; Shao, S.D. Scaling of velocity profiles for depth-limited open channel flows over simulated rigid vegetation. J. Hydraul. Eng. 2012, 138, 673–683. [Google Scholar] [CrossRef]
- Zhang, K.D.; Wang, G.Q.; Sun, X.M.; Wang, J.J. Hydraulic characteristic of overland flow under different vegetation coverage. Adv. Water Sci. 2014, 25, 825–834. [Google Scholar]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth Surf. Proc. Land. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Zhu, H.C.; Zhao, Y.P.; Liu, H.Y. Scale characters analysis for gully structure in the watersheds of loess landforms based on digital elevation models. Front. Earth Sci. Pro. 2018, 12, 431–443. [Google Scholar] [CrossRef]
- Dunkerley, D.L. Flow threads in surface runoff: Implications for the assessment of flow properties and friction coefficients in soil erosion and hydraulics investigations. Earth Surf. Proc. Land. 2004, 29, 1012–1026. [Google Scholar] [CrossRef]
- Ali, M.; Sterk, G.; Seeger, M. Effect of flow discharge and median grain size on mean flow velocity under overland flow. J. Hydrol. 2012, 337, 150–160. [Google Scholar] [CrossRef]
- Wang, W.J.; Huai, W.X.; Zeng, Y.H.; Zhou, J.F. Analytical solution of velocity distribution for flow through submerged large deflection flexible vegetation. Appl. Math. Mech. 2015, 36, 107–120. [Google Scholar] [CrossRef]
- Ding, W.F.; Li, M. Effects of grass coverage and distribution patterns on erosion and overland flow hydraulic characteristics. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Mohammadiun, S.; Neyshabouri, S.A.A.S.; Naser, G.; Vahabi, H. Numerical investigation of submerged vane effects on flow pattern in a 90 junction of straight and bend open channels. Iran J. Sci. Technol. Trans. Civ. Eng. 2016, 40, 1–17. [Google Scholar] [CrossRef]
- Yasi, M.; Ashori, M. Environmental flow contributions from inbasin rivers and dams for saving Urmia lake. Iran J. Sci. Technol. Trans. Civ. Eng. 2017, 41, 1–10. [Google Scholar] [CrossRef]
- Zhang, S.T.; Zhang, J.Z.; Liu, Y.; Liu, Y.C. Effects of farmland vegetation row direction on overland flow hydraulic characteristics. Hydrol. Res. 2018, 49, 1991–2001. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Chen, L.; Li, B.; Liu, T. Macrobenthic assemblage characteristics under stressed waters and ecological health assessment using AMBI and M-AMBI: A case study at the Xin’an River Estuary, Yantai, China. Acta Oceanol. Sin. 2018, 37, 77–86. [Google Scholar] [CrossRef]
- Turner, A.K.; Chanmeesri, N. Shallow flow of water through non-submerged vegetation. Agric. Water Manag. 1984, 8, 375–385. [Google Scholar] [CrossRef]
- Weltz, M.A.; Arsland, A.B.; Lane, L.J. Hydraulic roughness coefficients for native rangelands. J. Irrig. Drain. Eng. 1992, 118, 776–790. [Google Scholar] [CrossRef]
- Gilley, J.E.; Kottwitz, E.R. Darcy-Weisbach roughness coefficients for selected crops. Trans. ASAE 1994, 37, 467–471. [Google Scholar] [CrossRef]
- Wu, F.S. Characteristics of flow resistance in open channels with non-submerged rigid vegetation. J. Hydrodyn. Ser. B 2008, 20, 239–245. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, G.; Tang, K.; Luo, R. Experiment on the effect of simulated surface cover on the overland flow velocity. J. Mt. Sci. 2011, 29, 654–659. [Google Scholar]
- Fathi-Moghadam, M.; Drikvandi, K. Manning roughness coefficient for rivers and flood plains with non-submerged vegetation. Int. J. Hydraulic. Eng. 2012, 1, 1–4. [Google Scholar]
- Zhao, C.; Gao, J.; Huang, Y.; Wang, G.; Zhang, M. Effects of vegetation stems on hydraulics of overland flow under varying water discharges. Land Degrad. Dev. 2016, 27, 748–757. [Google Scholar] [CrossRef]
- Abrahams, A.D.; Parsons, A.J.; Wainwright, J. Resistance to overland flow on semiarid grassland and shrubland hillslopes, Walnut Gulch, southern Arizona. J. Hydrol. 1994, 156, 431–446. [Google Scholar] [CrossRef]
- Järvelä, J. Effect of Submerged Flexible Vegetation on Flow Structure and Resistance. J. Hydrol. 2005, 307, 233–241. [Google Scholar] [CrossRef]
- Gabarròn-Galeote, M.A.; Mart ınez-Murillo, J.F.; Quesada, M.A.; Ruiz-Sinoga, J.D. Seasonal Changes in the Soil Hydrological and Erosive Response Depending on Aspect, Vegetation Type and Soil Water Repellency in Different Mediterranean Micro Environments. Solid Earth 2013, 4, 497–509. [Google Scholar] [CrossRef]
- Xia, J.H.; Nehal, L. Hydraulic features of flow through emergent bending aquatic vegetation in the riparian zone. Water 2013, 5, 2080–2093. [Google Scholar] [CrossRef]
- Okamoto, T.A.; Nezu, I. Turbulence structure and “Monami” phenomena in flexible vegetated open-channel flows. J. Hydraul. Res. 2009, 47, 798–810. [Google Scholar] [CrossRef]
- Jin, C.X.; Römkens, M.J.M.; Griffioen, F. Estimating Manning’s roughness coefficient for shallow overland flow in non-submerged vegetative filter strips. Trans. ASAE 2000, 43, 1459–1466. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 48, 829–830. [Google Scholar] [CrossRef]
- Kowobary, T.S.; Rice, C.E.; Garton, J.E. Effect of roughness elements on hydraulic resistance for overland flow. Trans. ASAE 1972, 15, 979–984. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Termini, D. Flow resistance law in channels with flexible submerged vegetation. J. Hydraul. Eng. 2005, 131, 554–564. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. The structure of the shear layer in flows over rigid and flexible canopies. Environ. Fluid Mech. 2006, 6, 277–301. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Ferro, V. Assessing flow resistance law in vegetated channels by dimensional analysis and self-similarity. Flow Meas. Instrum. 2020, 69, 101610. [Google Scholar] [CrossRef]
- Chiew, Y.M.; Tan, S.K. Frictional resistance of overland flow on tropical turfed slope. J. Hydraul. Eng. 1992, 118, 92–97. [Google Scholar] [CrossRef]
- Pan, C.Z.; Shangguan, Z.P. Runoff Hydraulic Characteristics and Sediment Generation in Sloped Grassplots under Simulated Rainfall Conditions. J. Hydrol. 2006, 331, 178–185. [Google Scholar] [CrossRef]
- Wu, S.F.; Wu, P.T.; Feng, H.; Merkley, G.P. Effects of alfalfa coverage on runoff, erosion and hydraulic characteristics of overland flow on loess slope plots. Front. Environ. Sci. Eng. 2011, 5, 76–83. [Google Scholar] [CrossRef]
- Salman, M.; Manochehr, G.; Ali, J. Effect of rock fragments cover on distance of rill erosion initiation and overland flow hydraulics. Int. J. Soil Sci. 2012, 7, 100–107. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 36, 1985–1986. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Y. Drag coefficient for rigid vegetation in subcritical open channel. Procedia Eng. 2016, 154, 1124. [Google Scholar] [CrossRef]
- Wu, F.C.; Shen, H.W.; Chou, Y.J. Variation of roughness coefficient for unsubmerged and submerged vegetation. J. Hydraulic. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent Flow through Idealized Emergent Vegetation. J. Hydraulic. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Sun, W.; Shao, Q.; Liu, J. Soil erosion and its response to the changes of precipitation and vegetation cover on the Loess Plateau. J. Geogr. Sci. 2013, 23, 1091–1106. [Google Scholar] [CrossRef]
- Fu, S.H.; Mu, H.L.; Liu, B.Y.; Yu, X.J.; Liu, Y.G. Effect of plant basal cover on velocity of shallow overland flow. J. Hydrol. 2019, 577, 123947. [Google Scholar] [CrossRef]
- Babalola, O.; Oshunsanya, S.O.; Are, K. Effects of vetiver grass (Vetiveria nigritana) strips, vetiver grass mulch and an organomineral fertilizer on soil, water and nutrient losses and maize (Zea mays, L.) yields. Soil Till. Res. 2007, 96, 6–18. [Google Scholar] [CrossRef]
- Deletic, A. Sediment transport in urban runoff over grassed areas. J. Hydrol. 2005, 301, 108–122. [Google Scholar] [CrossRef]
- Ghadiri, H.; Rose, C.W.; Hogarth, W.L. The influence of grass and porous barrier strips on runoff hydrology and sediment transport. Trans. ASAE 2001, 44, 259–268. [Google Scholar] [CrossRef]
- Hussein, J.; Ghadiri, H.; Yu, B.; Rose, C. Sediment retention by a stiff grass hedge under subcritical flow conditions. Soil Sci. Soc. Am. J. 2007, 71, 1516–1523. [Google Scholar] [CrossRef]
- Pan, C.Z.; Ma, L.; Shangguan, Z.P. Effectiveness of grass strips in trapping suspended sediments from runoff. Earth Surf. Proc. Land. 2010, 35, 1006–1013. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, Q.H.; Wu, J.Y.; Huang, C.W.; Yu, D.F. Protective function of narrow grass hedges on soil and water loss on sloping croplands in Northern China. Agric. Ecosyst. Environ. 2010, 139, 653–664. [Google Scholar] [CrossRef]
- Zhou, Z.C.; Gan, Z.T.; Shangguan, Z.P. Sediment trapping from hyperconcentrated flow as affected by grass filter strips. Pedosphere 2013, 23, 372–375. [Google Scholar] [CrossRef]
- Xin, Z.; Xu, J.; Zheng, W. Spatiotemporal variations of vegetation cover on the Chinese Loess Plateau (1981–2006): Impacts of climate changes and human activities. Sci. China Ser. D 2008, 51, 67–78. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, P.; Zhao, X.; Wang, Y.; Gao, X. Changes in vegetation condition in areas with different gradients (1980–2010) on the Loess Plateau, China. Environ. Earth Sci. 2013, 68, 2427–2438. [Google Scholar] [CrossRef]
- Ma, L.; Pan, C.Z.; Teng, Y.G.; Shangguan, Z.P. The performance of grass filter strips in controlling high-concentration suspended sediment from overland flow under rainfall/non-rainfall conditions. Earth Surf. Proc. Land. 2013, 38, 1523–1534. [Google Scholar] [CrossRef]
- Braud, I.; Vich, A.I.J.; Zuluaga, J.; Fornero, L.; Pedrani, A. Vegetation influence on runoff and sediment yield in the Andes region: Observation and modelling. J. Hydrol. 2001, 254, 124–144. [Google Scholar] [CrossRef]
- Michaelides, K.; Lister, D.; Wainwright, J.; Parsons, A.J. Vegetation controls on small-scale runoff and erosion dynamics in a degrading dryland environment. Hydrol. Process. 2009, 23, 1617–1630. [Google Scholar] [CrossRef]
- Xu, Q.X.; Wang, T.W.; Cai, C.F.; Li, Z.X.; Shi, Z.H.; Fang, R.J. Responses of runoff and soil erosion to vegetation removal and tillage on steep lands. Pedosphere 2013, 23, 532–541. [Google Scholar] [CrossRef]
- Zhou, Z.C.; Shangguan, Z.P. The effects of ryegrass roots and shoots on loess erosion under simulated rainfall. Catena 2007, 70, 350–355. [Google Scholar] [CrossRef]
- Zhou, Z.C.; Shangguan, Z.P. Effect of ryegrasses on soil runoff and sediment control. Pedosphere 2008, 18, 131–136. [Google Scholar] [CrossRef]
- Hsieh, T. Resistance of cylinder piers in open-channel flow. J. Hydraul. Div. 1964, 90, 161–173. [Google Scholar] [CrossRef]
- Li, R.M.; Shen, H.W. Effect of tall vegetation on flow and sediment. J. Hydraul. Div. 1973, 99, 793–814. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.C.M.; Hulscher, S.J.M.H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43, 129–148. [Google Scholar] [CrossRef]
- Yagci, O.; Tschiesche, U.; Kabdasli, M.S. The role of different forms of natural riparian vegetation on turbulence and kinetic energy characteristics. Adv. Water Resour. 2010, 33, 601–614. [Google Scholar] [CrossRef]
- Abrahams, A.D.; Li, G.; Krishnan, C.; Atkinson, J.F. A sediment transport equation for interrill overland flow on rough surfaces. Earth Surf. Proc. Land. 2001, 26, 1443–1459. [Google Scholar] [CrossRef]
- Stone, B.M.; Shen, H.T. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraulic. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Zhang, S.T.; Li, G.B. Effect of partially submerged vegetation distribution directions on flood flow resistance. Environ. Earth Sci. 2019, 36, 1147–1155. [Google Scholar] [CrossRef]
- Zhang, S.T.; Liu, Y.C.; Zhang, J.Z.; Liu, Y.; Wang, Z.K. Study of the impact of vegetation direction and slope on drag coefficient. Iran J. Sci. Technol. Trans. Civ. Eng. 2018, 42, 381–390. [Google Scholar] [CrossRef]
- Juha, J. Flow resistance of flexible and still vegetation: A flume study with natural vegetations. J. Hydrol. 2002, 269, 44–54. [Google Scholar]
- Roche, N.; Daıän, J.F.; Lawrence, D.S.L. Hydraulic modeling of runoff over a rough surface under partial inundation. Water Resour. Res. 2007, 43, 8410–8420. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liu, Y.H.; Wang, X.H. Experimental investigation of hydrodynamic characteristics of overland flow with geocell. J. Hydrodyn. Ser. B 2012, 24, 737–743. [Google Scholar] [CrossRef]
- Jeon, H.S.; Obana, M.; Tsujimoto, T. Concept of bed roughness boundary layer and its application to bed load transport in flow with non-submerged vegetation. J. Water Res. Prot. 2014, 6, 881–887. [Google Scholar] [CrossRef]
- James, C.S.; Goldbeck, U.K.; Patini, A.; Jordanova, A.A. Influence of foliage on flow resistance of emergent vegetation. J. Hydraul. Res. 2008, 46, 536–542. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Zhao, X.; Huang, E.; Liu, X.; Cao, S. Flexible and rigid vegetation overland flow resistance. Trans. ASAE 2013, 56, 919–926. [Google Scholar]
- Zhang, G.H.; Liu, G.B.; Yi, L.; Zhang, P.C. Effects of patterned Artemisia capillaris on overland flow resistance under varied rainfall intensities in the Loess Plateau of China. J. Hydrol. Hydromech. 2014, 62, 334–342. [Google Scholar] [CrossRef]
- Zhang, S.T.; Liu, Y. Experimental study on anisotropic attributes of surface roughness in watersheds. J. Hydrol. Eng. 2017, 22, 6017005. [Google Scholar] [CrossRef]
- Pan, C.; Ma, L.; Wainwright, J.; Shangguan, Z. Overland flow resistances on varying slope gradients and partitioning on grassed slopes under simulated rainfall. Water Resour. Res. 2016, 52, 2490–2512. [Google Scholar] [CrossRef]
- Wang, J.J.; Zhang, K.D.; Gong, J.G.; Yang, F.; Dong, X. Overland flow resistance law under different vegetation coverage. J. Soil Water Conserv. 2015, 25, 1–6. [Google Scholar]
- Pan, C.Z.; Shangguan, Z.P. Infuence of forage grass on hydrodynamic characteristics of slope erosion. J. Hydraulic. Eng. 2005, 36, 371–377. [Google Scholar]
- Zhang, K.D.; Wang, G.Q.; Wang, Z.L.; Liu, J.E.; Lv, H.X. Experiments on hydraulic characteristics of roll wave for sheet flow with artificial rough bed. Trans. CSAE 2011, 27, 25–30. [Google Scholar]
| Slope S (%) | Stem Cover Cr (%) | Q (m3/min) | Parameter | |||||
|---|---|---|---|---|---|---|---|---|
| Water Depth of the Measure Section | haverage (m) | Re | Fr | n | ||||
| h2 (m) | h4 (m) | |||||||
| 0.0% | 0.72% | 0.0313 | 0.0148 | 0.0119 | 0.0134 | 1218 | 0.2756 | 0.0215 |
| 0.1205 | 0.0351 | 0.0311 | 0.0331 | 3847 | 0.2692 | 0.0266 | ||
| 0.2190 | 0.0536 | 0.0485 | 0.0511 | 6041 | 0.2552 | 0.0311 | ||
| 0.3019 | 0.0660 | 0.0601 | 0.0630 | 7634 | 0.2562 | 0.0325 | ||
| 0.4241 | 0.0832 | 0.0759 | 0.0796 | 9626 | 0.2540 | 0.0354 | ||
| 0.5203 | 0.0961 | 0.0879 | 0.0920 | 10,962 | 0.2505 | 0.0371 | ||
| 0.6319 | 0.1081 | 0.0990 | 0.1036 | 12,483 | 0.2547 | 0.0375 | ||
| 0.37% | 0.0313 | 0.0125 | 0.0102 | 0.0113 | 1254 | 0.3511 | 0.0147 | |
| 0.1205 | 0.0320 | 0.0296 | 0.0308 | 4145 | 0.2982 | 0.0197 | ||
| 0.2190 | 0.0479 | 0.0450 | 0.0464 | 6803 | 0.2930 | 0.0221 | ||
| 0.3019 | 0.0609 | 0.0575 | 0.0592 | 8687 | 0.2803 | 0.0247 | ||
| 0.4241 | 0.0759 | 0.0716 | 0.0738 | 11,264 | 0.2833 | 0.0272 | ||
| 0.5203 | 0.0875 | 0.0826 | 0.0850 | 13,039 | 0.2807 | 0.0286 | ||
| 0.6319 | 0.1000 | 0.0947 | 0.0974 | 14,916 | 0.2783 | 0.0294 | ||
| 0.20% | 0.0313 | 0.0116 | 0.0262 | 0.0189 | 1458 | 0.1894 | 0.0187 | |
| 0.1205 | 0.0250 | 0.0381 | 0.0316 | 4664 | 0.2999 | 0.0234 | ||
| 0.2190 | 0.0401 | 0.0527 | 0.0464 | 7641 | 0.2980 | 0.0254 | ||
| 0.3019 | 0.0522 | 0.0646 | 0.0584 | 9841 | 0.2887 | 0.0267 | ||
| 0.4241 | 0.0686 | 0.0804 | 0.0745 | 12,752 | 0.2805 | 0.0290 | ||
| 0.5203 | 0.0798 | 0.0915 | 0.0856 | 14,862 | 0.2787 | 0.0292 | ||
| 0.6319 | 0.0919 | 0.1030 | 0.0975 | 17,141 | 0.2782 | 0.0306 | ||
| 0.13% | 0.0313 | 0.0125 | 0.0112 | 0.0119 | 1330 | 0.3246 | 0.0126 | |
| 0.1205 | 0.0305 | 0.0290 | 0.0297 | 4619 | 0.3137 | 0.0149 | ||
| 0.2190 | 0.0473 | 0.0450 | 0.0462 | 7723 | 0.2949 | 0.0201 | ||
| 0.3019 | 0.0586 | 0.0557 | 0.0571 | 10,103 | 0.2952 | 0.0230 | ||
| 0.4241 | 0.0744 | 0.0715 | 0.0730 | 13,220 | 0.2873 | 0.0235 | ||
| 0.5203 | 0.0861 | 0.0825 | 0.0843 | 15,463 | 0.2839 | 0.0263 | ||
| 0.6319 | 0.0975 | 0.0931 | 0.0953 | 17,967 | 0.2868 | 0.0287 | ||
| 0.11% | 0.0313 | 0.0137 | 0.0128 | 0.0133 | 5106 | 0.2736 | 0.0125 | |
| 0.1205 | 0.0334 | 0.0323 | 0.0328 | 17,976 | 0.2704 | 0.0156 | ||
| 0.2190 | 0.0490 | 0.0478 | 0.0484 | 30,625 | 0.2745 | 0.0165 | ||
| 0.3019 | 0.0603 | 0.0591 | 0.0597 | 40,371 | 0.2762 | 0.0159 | ||
| 0.4241 | 0.0755 | 0.0739 | 0.0747 | 53,611 | 0.2770 | 0.0187 | ||
| 0.5203 | 0.0869 | 0.0857 | 0.0863 | 63,102 | 0.2736 | 0.0160 | ||
| 0.6319 | 0.0988 | 0.0968 | 0.0978 | 73,698 | 0.2757 | 0.0202 | ||
| 0.07% | 0.0313 | 0.0105 | 0.0079 | 0.0092 | 1286 | 0.4814 | 0.0106 | |
| 0.1205 | 0.0302 | 0.0285 | 0.0294 | 4382 | 0.3191 | 0.0159 | ||
| 0.2190 | 0.0458 | 0.0443 | 0.0451 | 7396 | 0.3053 | 0.0164 | ||
| 0.3019 | 0.0577 | 0.0560 | 0.0568 | 9676 | 0.2970 | 0.0181 | ||
| 0.4241 | 0.0729 | 0.0714 | 0.0721 | 12,753 | 0.2919 | 0.0170 | ||
| 0.5203 | 0.0840 | 0.0822 | 0.0831 | 14,980 | 0.2894 | 0.0185 | ||
| 0.6319 | 0.0955 | 0.0941 | 0.0948 | 17,407 | 0.2885 | 0.0162 | ||
| Slope S (%) | Stem Cover Cr (%) | Q (m3/min) | Parameter | |||||
|---|---|---|---|---|---|---|---|---|
| Water Depth of the Measure Section | haverage (m) | Re | Fr | n | ||||
| h2 (m) | h4 (m) | |||||||
| 1.0% | 0.72% | 0.0313 | 0.0071 | 0.0064 | 0.0068 | 1297 | 0.7529 | 0.0176 |
| 0.1205 | 0.0181 | 0.0223 | 0.0202 | 4360 | 0.5676 | 0.0227 | ||
| 0.2190 | 0.0318 | 0.0387 | 0.0353 | 6897 | 0.4478 | 0.0254 | ||
| 0.3019 | 0.0437 | 0.0497 | 0.0467 | 8622 | 0.4031 | 0.0285 | ||
| 0.4241 | 0.0602 | 0.0642 | 0.0622 | 10,778 | 0.3668 | 0.0328 | ||
| 0.5203 | 0.0734 | 0.0760 | 0.0747 | 12,160 | 0.3417 | 0.0361 | ||
| 0.6319 | 0.0850 | 0.0878 | 0.0864 | 13,743 | 0.3339 | 0.0358 | ||
| 0.37% | 0.0313 | 0.0050 | 0.0045 | 0.0047 | 1376 | 1.2956 | 0.0097 | |
| 0.1205 | 0.0136 | 0.0154 | 0.0145 | 4898 | 0.9263 | 0.0155 | ||
| 0.2190 | 0.0216 | 0.0310 | 0.0263 | 8360 | 0.7107 | 0.0176 | ||
| 0.3019 | 0.0322 | 0.0433 | 0.0377 | 10,554 | 0.5626 | 0.0189 | ||
| 0.4241 | 0.0482 | 0.0579 | 0.0530 | 13,323 | 0.4680 | 0.0228 | ||
| 0.5203 | 0.0601 | 0.0687 | 0.0644 | 15,264 | 0.4277 | 0.0255 | ||
| 0.6319 | 0.0722 | 0.0802 | 0.0762 | 17,372 | 0.4029 | 0.0272 | ||
| 0.20% | 0.0313 | 0.0109 | 0.0078 | 0.0094 | 1342 | 0.4751 | 0.0117 | |
| 0.1205 | 0.0318 | 0.0298 | 0.0308 | 4417 | 0.2985 | 0.0183 | ||
| 0.2190 | 0.0480 | 0.0459 | 0.0469 | 7342 | 0.2882 | 0.0197 | ||
| 0.3019 | 0.0599 | 0.0575 | 0.0587 | 9526 | 0.2838 | 0.0212 | ||
| 0.4241 | 0.0725 | 0.0693 | 0.0709 | 12,621 | 0.3004 | 0.0232 | ||
| 0.5203 | 0.0877 | 0.0844 | 0.0860 | 14,455 | 0.2754 | 0.0251 | ||
| 0.6319 | 0.0997 | 0.0960 | 0.0979 | 16,692 | 0.2757 | 0.0265 | ||
| 0.13% | 0.0313 | 0.0038 | 0.0061 | 0.0049 | 1457 | 1.2748 | 0.0105 | |
| 0.1205 | 0.0132 | 0.0138 | 0.0135 | 5054 | 1.0237 | 0.0144 | ||
| 0.2190 | 0.0205 | 0.0343 | 0.0274 | 8996 | 0.6878 | 0.0163 | ||
| 0.3019 | 0.0318 | 0.0437 | 0.0377 | 11,335 | 0.5640 | 0.0191 | ||
| 0.4241 | 0.0479 | 0.0600 | 0.0539 | 14,549 | 0.4578 | 0.0210 | ||
| 0.5203 | 0.0604 | 0.0723 | 0.0664 | 16,797 | 0.4095 | 0.0225 | ||
| 0.6319 | 0.0713 | 0.0823 | 0.0768 | 19,452 | 0.3985 | 0.0246 | ||
| 0.11% | 0.0313 | 0.0038 | 0.0051 | 0.0044 | 1356 | 1.4426 | 0.0092 | |
| 0.1205 | 0.0110 | 0.0130 | 0.0120 | 4909 | 1.2245 | 0.0123 | ||
| 0.2190 | 0.0176 | 0.0298 | 0.0237 | 8839 | 0.8582 | 0.0160 | ||
| 0.3019 | 0.0222 | 0.0420 | 0.0321 | 11,973 | 0.7746 | 0.0139 | ||
| 0.4241 | 0.0413 | 0.0581 | 0.0497 | 14,481 | 0.5251 | 0.0133 | ||
| 0.5203 | 0.0534 | 0.0687 | 0.0611 | 16,684 | 0.4669 | 0.0154 | ||
| 0.6319 | 0.0662 | 0.0810 | 0.0736 | 19,110 | 0.4267 | 0.0163 | ||
| 0.07% | 0.0313 | 0.0048 | 0.0060 | 0.0054 | 1303 | 1.0671 | 0.0123 | |
| 0.1205 | 0.0124 | 0.0184 | 0.0154 | 4868 | 0.8715 | 0.0163 | ||
| 0.2190 | 0.0168 | 0.0339 | 0.0253 | 9052 | 0.8173 | 0.0150 | ||
| 0.3019 | 0.0208 | 0.0450 | 0.0329 | 12,247 | 0.7793 | 0.0122 | ||
| 0.4241 | 0.0445 | 0.0605 | 0.0525 | 14,118 | 0.4808 | 0.0142 | ||
| 0.5203 | 0.0562 | 0.0713 | 0.0638 | 16,374 | 0.4368 | 0.0160 | ||
| 0.6319 | 0.0683 | 0.0832 | 0.0757 | 18,872 | 0.4081 | 0.0163 | ||
| Slope S (%) | Stem Cover Cr (%) | Q (m3/min) | Parameter | |||||
|---|---|---|---|---|---|---|---|---|
| Water Depth of the Measure Section | haverage (m) | Re | Fr | n | ||||
| h2 (m) | h4 (m) | |||||||
| 2.0% | 0.72% | 0.0313 | 0.0062 | 0.0032 | 0.0047 | 1475 | 1.4638 | 0.0114 |
| 0.1205 | 0.0127 | 0.0145 | 0.0136 | 4637 | 1.0204 | 0.0195 | ||
| 0.2190 | 0.0209 | 0.0241 | 0.0225 | 7714 | 0.8731 | 0.0230 | ||
| 0.3019 | 0.0285 | 0.0364 | 0.0325 | 9779 | 0.7019 | 0.0269 | ||
| 0.4241 | 0.0411 | 0.0526 | 0.0468 | 12,201 | 0.5698 | 0.0301 | ||
| 0.5203 | 0.0517 | 0.0640 | 0.0578 | 13,746 | 0.5073 | 0.0321 | ||
| 0.6319 | 0.0644 | 0.0764 | 0.0704 | 15,269 | 0.4570 | 0.0344 | ||
| 0.37% | 0.0313 | 0.0026 | 0.0039 | 0.0033 | 1447 | 2.3332 | 0.0080 | |
| 0.1205 | 0.0105 | 0.0115 | 0.0110 | 5024 | 1.4012 | 0.0145 | ||
| 0.2190 | 0.0154 | 0.0192 | 0.0173 | 8774 | 1.3014 | 0.0167 | ||
| 0.3019 | 0.0218 | 0.0245 | 0.0231 | 11,498 | 1.1527 | 0.0187 | ||
| 0.4241 | 0.0267 | 0.0447 | 0.0357 | 15,588 | 0.8989 | 0.0224 | ||
| 0.5203 | 0.0350 | 0.0583 | 0.0466 | 17,774 | 0.7367 | 0.0232 | ||
| 0.6319 | 0.0425 | 0.0683 | 0.0554 | 20,319 | 0.6853 | 0.0228 | ||
| 0.20% | 0.0313 | 0.0022 | 0.0042 | 0.0032 | 1522 | 2.5853 | 0.0078 | |
| 0.1205 | 0.0114 | 0.0107 | 0.0110 | 4983 | 1.3902 | 0.0144 | ||
| 0.2190 | 0.0179 | 0.0185 | 0.0182 | 8650 | 1.1918 | 0.0179 | ||
| 0.3019 | 0.0198 | 0.0257 | 0.0227 | 11,769 | 1.1987 | 0.0188 | ||
| 0.4241 | 0.0252 | 0.0466 | 0.0359 | 16,326 | 0.9156 | 0.0226 | ||
| 0.5203 | 0.0302 | 0.0582 | 0.0442 | 19,304 | 0.8319 | 0.0224 | ||
| 0.6319 | 0.0345 | 0.0701 | 0.0523 | 22,758 | 0.7992 | 0.0207 | ||
| 0.13% | 0.0313 | 0.0042 | 0.0032 | 0.0037 | 1416 | 1.8839 | 0.0089 | |
| 0.1205 | 0.0097 | 0.0116 | 0.0107 | 5176 | 1.4743 | 0.0142 | ||
| 0.2190 | 0.0154 | 0.0169 | 0.0161 | 9061 | 1.4273 | 0.0152 | ||
| 0.3019 | 0.0195 | 0.0221 | 0.0208 | 12,184 | 1.3474 | 0.0167 | ||
| 0.4241 | 0.0210 | 0.0381 | 0.0295 | 17,558 | 1.2180 | 0.0206 | ||
| 0.5203 | 0.0284 | 0.0525 | 0.0404 | 20,401 | 0.9368 | 0.0227 | ||
| 0.6319 | 0.0332 | 0.0617 | 0.0475 | 23,928 | 0.8961 | 0.0226 | ||
| 0.11% | 0.0313 | 0.0042 | 0.0047 | 0.0044 | 1330 | 1.4198 | 0.0127 | |
| 0.1205 | 0.0107 | 0.0106 | 0.0107 | 4916 | 1.4591 | 0.0139 | ||
| 0.2190 | 0.0154 | 0.0148 | 0.0151 | 8717 | 1.5694 | 0.0132 | ||
| 0.3019 | 0.0195 | 0.0172 | 0.0184 | 11,838 | 1.6228 | 0.0124 | ||
| 0.4241 | 0.0250 | 0.0361 | 0.0305 | 15,999 | 1.0961 | 0.0212 | ||
| 0.5203 | 0.0284 | 0.0487 | 0.0386 | 19,462 | 0.9845 | 0.0227 | ||
| 0.6319 | 0.0332 | 0.0605 | 0.0469 | 22,991 | 0.9078 | 0.0228 | ||
| 0.07% | 0.0313 | 0.0038 | 0.0045 | 0.0042 | 1305 | 1.5701 | 0.0115 | |
| 0.1205 | 0.0103 | 0.0102 | 0.0103 | 4829 | 1.5414 | 0.0131 | ||
| 0.2190 | 0.0148 | 0.0160 | 0.0154 | 8554 | 1.5287 | 0.0143 | ||
| 0.3019 | 0.0182 | 0.0202 | 0.0192 | 11,574 | 1.5183 | 0.0149 | ||
| 0.4241 | 0.0235 | 0.0381 | 0.0308 | 16,096 | 1.1061 | 0.0214 | ||
| 0.5203 | 0.0268 | 0.0520 | 0.0394 | 19,772 | 0.9872 | 0.0227 | ||
| 0.6319 | 0.0302 | 0.0620 | 0.0461 | 23,620 | 0.9655 | 0.0227 | ||
| Slope S (%) | Stem Cover Cr (%) | Q (m3/min) | Parameter | |||||
|---|---|---|---|---|---|---|---|---|
| Water Depth of the Measure Section | haverage (m) | Re | Fr | n | ||||
| h2 (m) | h4 (m) | |||||||
| 3.0% | 0.72% | 0.0313 | 0.0059 | 0.0021 | 0.0040 | 1733 | 2.1338 | 0.0083 |
| 0.1205 | 0.0136 | 0.0094 | 0.0115 | 4980 | 1.3546 | 0.0170 | ||
| 0.2190 | 0.0202 | 0.0177 | 0.0189 | 8167 | 1.1312 | 0.0217 | ||
| 0.3019 | 0.0261 | 0.0246 | 0.0253 | 10,553 | 1.0050 | 0.0248 | ||
| 0.4241 | 0.0338 | 0.0389 | 0.0363 | 13,485 | 0.8250 | 0.0295 | ||
| 0.5203 | 0.0403 | 0.0547 | 0.0475 | 15,326 | 0.6898 | 0.0322 | ||
| 0.6319 | 0.0483 | 0.0657 | 0.0570 | 17,344 | 0.6380 | 0.0329 | ||
| 0.37% | 0.0313 | 0.0035 | 0.0022 | 0.0029 | 1471 | 2.9053 | 0.0062 | |
| 0.1205 | 0.0098 | 0.0088 | 0.0093 | 5097 | 1.7923 | 0.0131 | ||
| 0.2190 | 0.0152 | 0.0145 | 0.0148 | 8851 | 1.6196 | 0.0154 | ||
| 0.3019 | 0.0189 | 0.0181 | 0.0185 | 11,866 | 1.6071 | 0.0157 | ||
| 0.4241 | 0.0248 | 0.0247 | 0.0248 | 15,916 | 1.4560 | 0.0179 | ||
| 0.5203 | 0.0291 | 0.0292 | 0.0292 | 18,926 | 1.3955 | 0.0189 | ||
| 0.6319 | 0.0311 | 0.0371 | 0.0341 | 22,372 | 1.3525 | 0.0206 | ||
| 0.20% | 0.0313 | 0.0034 | 0.0017 | 0.0026 | 1534 | 3.6021 | 0.0041 | |
| 0.1205 | 0.0091 | 0.0086 | 0.0088 | 5055 | 1.9421 | 0.0122 | ||
| 0.2190 | 0.0159 | 0.0140 | 0.0149 | 8859 | 1.6079 | 0.0154 | ||
| 0.3019 | 0.0204 | 0.0180 | 0.0192 | 11,885 | 1.5234 | 0.0166 | ||
| 0.4241 | 0.0242 | 0.0238 | 0.0240 | 16,162 | 1.5243 | 0.0174 | ||
| 0.5203 | 0.0280 | 0.0279 | 0.0279 | 19,369 | 1.4884 | 0.0181 | ||
| 0.6319 | 0.0324 | 0.0324 | 0.0324 | 22,929 | 1.4490 | 0.0187 | ||
| 0.13% | 0.0313 | 0.0032 | 0.0021 | 0.0026 | 1460 | 3.1964 | 0.0056 | |
| 0.1205 | 0.0086 | 0.0097 | 0.0092 | 5198 | 1.8405 | 0.0135 | ||
| 0.2190 | 0.0132 | 0.0146 | 0.0139 | 9187 | 1.7905 | 0.0148 | ||
| 0.3019 | 0.0164 | 0.0176 | 0.0170 | 12,417 | 1.8144 | 0.0148 | ||
| 0.4241 | 0.0204 | 0.0232 | 0.0218 | 17,027 | 1.7675 | 0.0161 | ||
| 0.5203 | 0.0255 | 0.0293 | 0.0274 | 20,274 | 1.5401 | 0.0187 | ||
| 0.6319 | 0.0287 | 0.0375 | 0.0331 | 24,155 | 1.4269 | 0.0211 | ||
| 0.11% | 0.0313 | 0.0031 | 0.0033 | 0.0032 | 1336 | 2.3287 | 0.0090 | |
| 0.1205 | 0.0090 | 0.0072 | 0.0081 | 5048 | 2.2281 | 0.0098 | ||
| 0.2190 | 0.0137 | 0.0107 | 0.0122 | 8992 | 2.2080 | 0.0098 | ||
| 0.3019 | 0.0161 | 0.0145 | 0.0153 | 12,029 | 2.1365 | 0.0113 | ||
| 0.4241 | 0.0194 | 0.0186 | 0.0190 | 16,522 | 2.1598 | 0.0118 | ||
| 0.5203 | 0.0235 | 0.0210 | 0.0222 | 19,966 | 2.1012 | 0.0115 | ||
| 0.6319 | 0.0271 | 0.0249 | 0.0260 | 23,738 | 2.0127 | 0.0125 | ||
| 0.07% | 0.0313 | 0.0033 | 0.0048 | 0.0040 | 1344 | 1.6988 | 0.0131 | |
| 0.1205 | 0.0095 | 0.0076 | 0.0086 | 4932 | 2.0548 | 0.0109 | ||
| 0.2190 | 0.0145 | 0.0121 | 0.0133 | 8701 | 1.9099 | 0.0124 | ||
| 0.3019 | 0.0178 | 0.0156 | 0.0167 | 11,741 | 1.8746 | 0.0131 | ||
| 0.4241 | 0.0238 | 0.0223 | 0.0230 | 15,920 | 1.6200 | 0.0162 | ||
| 0.5203 | 0.0268 | 0.0278 | 0.0273 | 19,103 | 1.5359 | 0.0182 | ||
| 0.6319 | 0.0295 | 0.0331 | 0.0313 | 22,817 | 1.5259 | 0.0191 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, S.; Chen, S.; Liu, M.; Xu, X.; Zhou, J.; Wang, W.; Ma, L.; Wang, C. Overland Flow Resistance Law under Sparse Stem Vegetation Coverage. Water 2021, 13, 1657. https://doi.org/10.3390/w13121657
Zhang J, Zhang S, Chen S, Liu M, Xu X, Zhou J, Wang W, Ma L, Wang C. Overland Flow Resistance Law under Sparse Stem Vegetation Coverage. Water. 2021; 13(12):1657. https://doi.org/10.3390/w13121657
Chicago/Turabian StyleZhang, Jingzhou, Shengtang Zhang, Si Chen, Ming Liu, Xuefeng Xu, Jiansen Zhou, Wenjun Wang, Lijun Ma, and Chuantao Wang. 2021. "Overland Flow Resistance Law under Sparse Stem Vegetation Coverage" Water 13, no. 12: 1657. https://doi.org/10.3390/w13121657
APA StyleZhang, J., Zhang, S., Chen, S., Liu, M., Xu, X., Zhou, J., Wang, W., Ma, L., & Wang, C. (2021). Overland Flow Resistance Law under Sparse Stem Vegetation Coverage. Water, 13(12), 1657. https://doi.org/10.3390/w13121657





