2.1. Problem Description and Generalization
In the case that the WDN layout has been determined, the annual cost and reliability of the WDN can be optimized by taking the pipe diameter as the variable. Therefore, in the model, only the connection between the pump station and the water demand nodes were considered, and the position of tank was not considered.
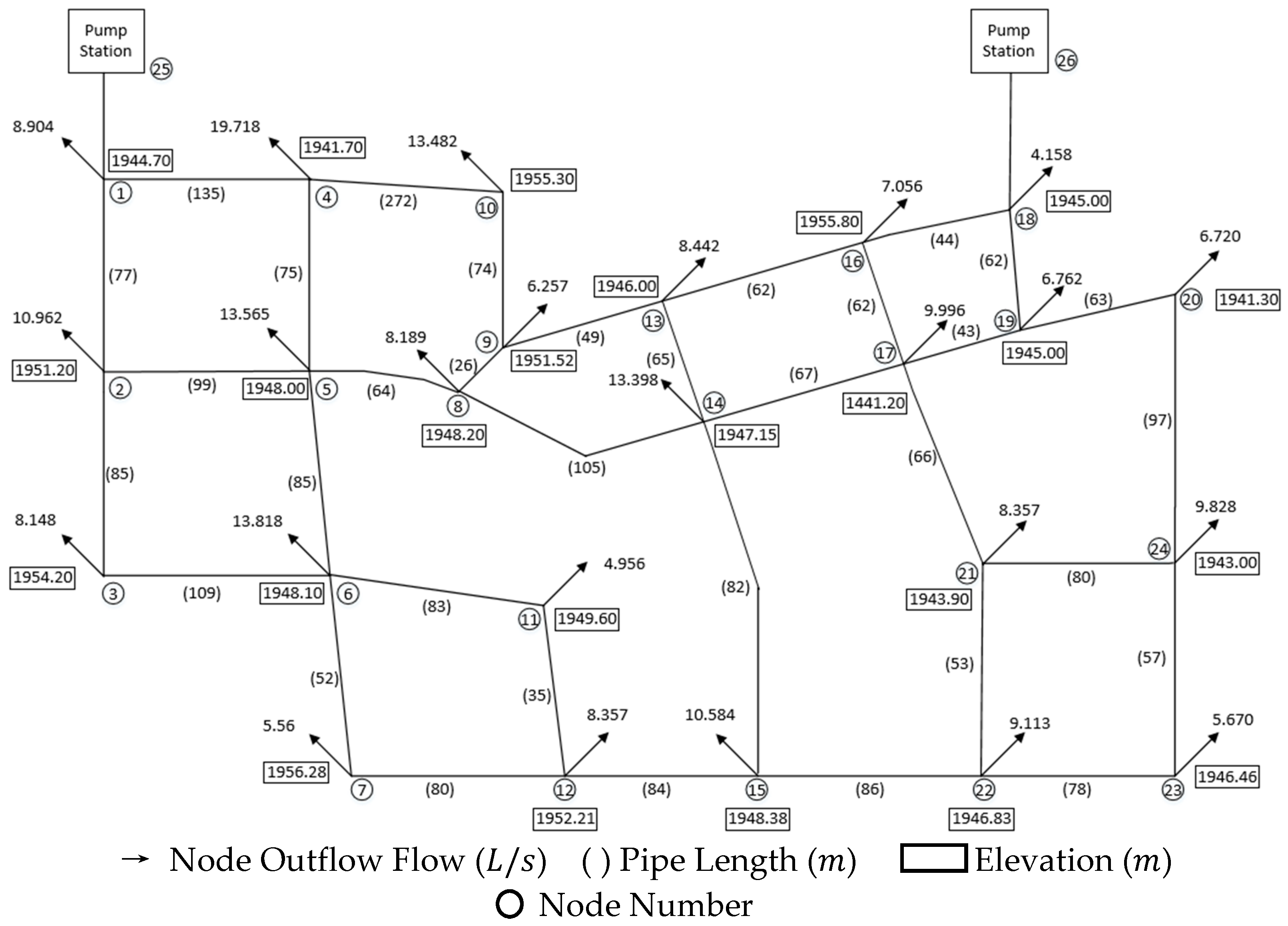
One or more pump stations can be used for water supply in a WDN. For convenience, the WDN of only a single pump station was briefly described, as the WDN of multi-pump stations is similar.
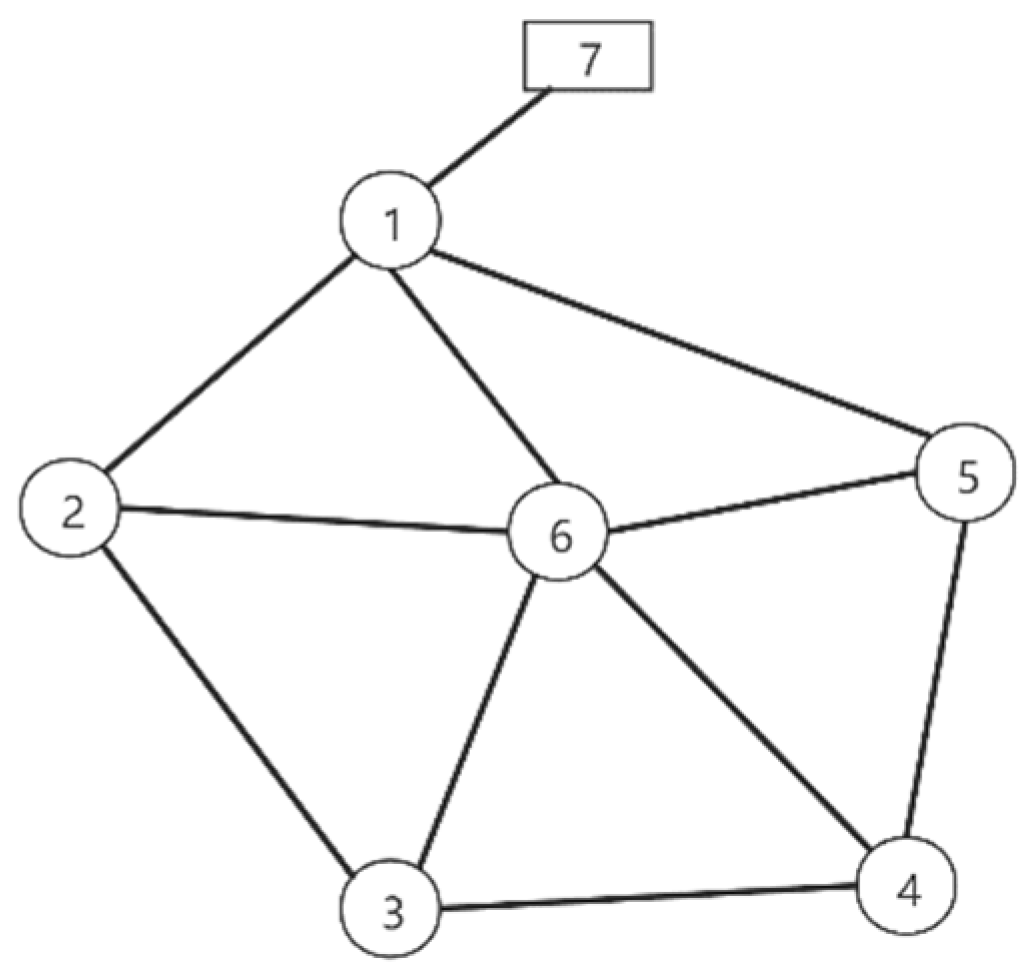
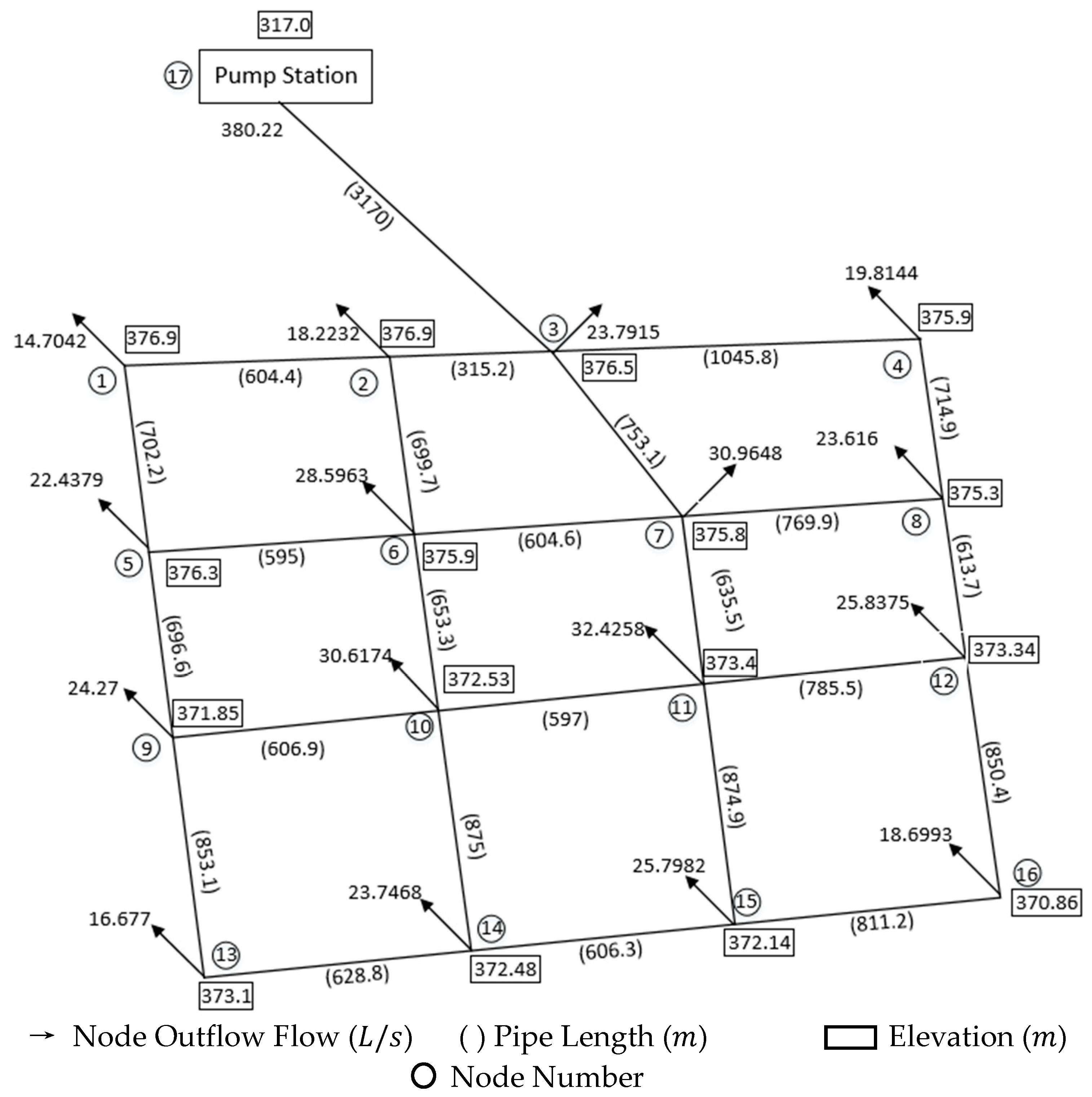
Figure 1 shows a typical WDN. In the figure, Nodes 1–6 are the water output nodes in the WDN, where each node has a different elevation. Node 7 is the pump station that provides water for the whole WDN. According to the design requirements, the quantity of the water supply provided by the pump station is
. The quantity of water output by the node
is
where
denotes a node number in the WDN, and each node must meet the flow balance.
The pipe section should be suspended in case of accident conditions, such as a pipe burst, whereas the other sections of the WDN must continue to operate. The two adjacent nodes of the burst section are supplied by other sections. The water supply should be maintained at a certain proportion of the normal condition, which is generally 70%. In addition, the water pressure should also meet the pressure requirements so that a continuous flow is provided to the outflow nodes.
2.2. Mathematical Optimization Model
The purpose of this paper is to meet the practical requirements of the system, reduce the operation cost as much as possible and improve the operation reliability. Objective functions and constraints are provided in this section.
2.2.1. Objective Function
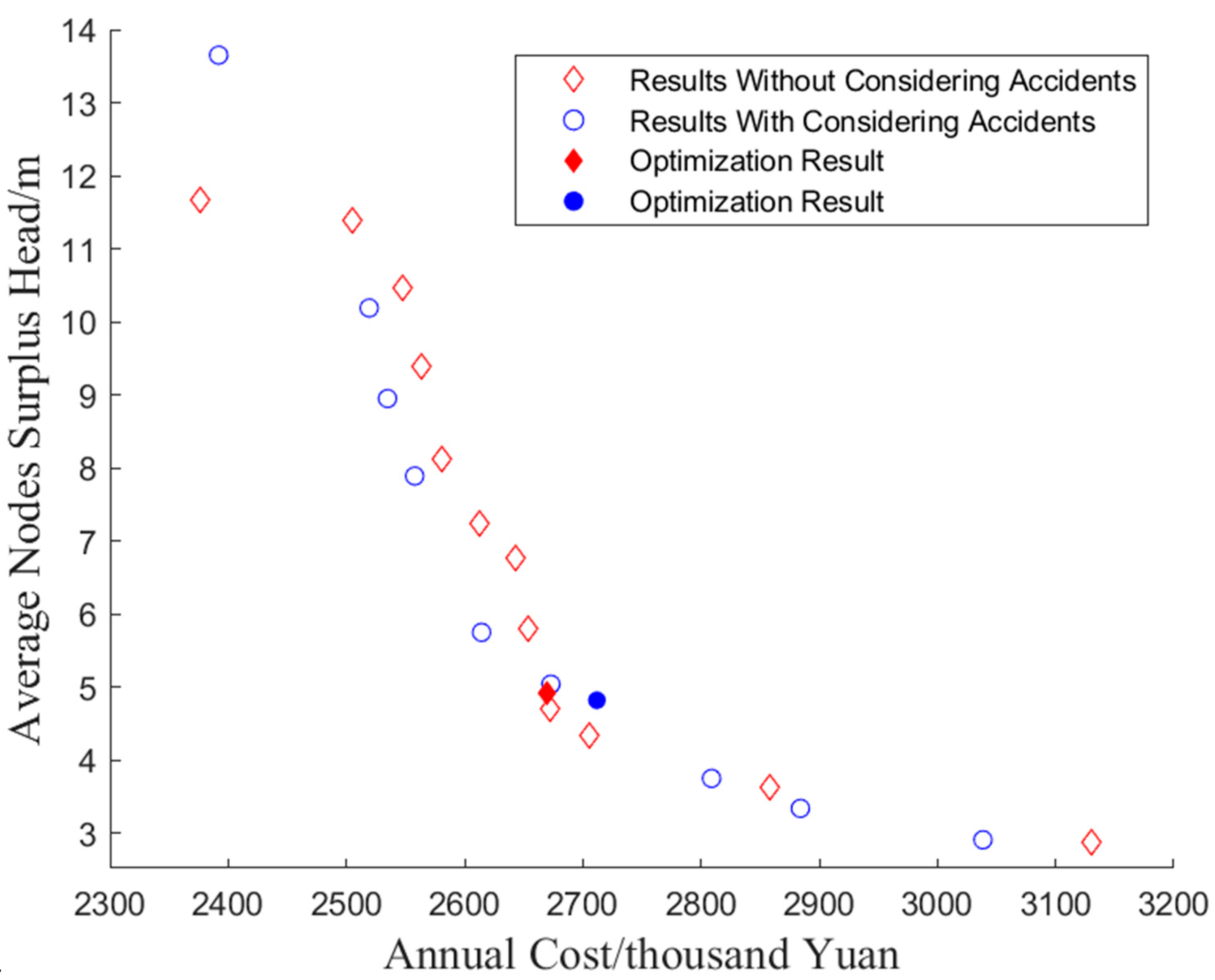
In the design of the WDNs layout, it is necessary to consider not only the relatively low annual cost, but also the reliability of WDNs operation. The accidents will cause unstable operation of the WDN and waste of water, which will increase the cost of the WDN. In order to ensure the reliability of its operation, the head pressure of each node should not be too high, which can prevent the occurrence of accidents such as a pipe burst. The node surplus head can be used to analyze the reliability of pipe network operation. Therefore, in this paper, annual cost as economic objective and weighted average value of the node surplus head as reliability objective were selected as the two objective functions of multi-objective optimization.
The economic objective is the first consideration in the optimal design of WDN. This objective is the annual cost composed of depreciation, and the annual energy cost of the pumping station. The annual cost is shown in Equation (1), which is the only equation considered for single-objective optimization. However, for the multi-objective optimization, the reliability objective of WDN should also be considered. The objective function considering reliability is defined by the average surplus head, shown by Equation (2).
In Equation (1), and are the annual average cost and the depreciation cost rate, respectively, with the units in , is the payback period with the unit of , is the diameter of the pipe section between nodes and given in mm, is the pipe unit price corresponding to given in and is the length of pipe section between nodes and in . The water supply energy change parameter within the specified time is represented by , is the electricity tariff given in , is the water density in 1000 is gravitational acceleration in 9.8 , is the efficiency coefficient of the pumping station with the value in the range of 0.55–0.85, is the node head of the pump in and is the flow of the pump station in . In Equation (2), is the weighted average value of the node surplus head in , is the outflow of node given in , is the head of node and is the minimum water head required by each node.
2.2.2. Constraints
Node flow continuity constraints. Any node
should be consistent with the same inflow and outflow, i.e., the inflow should be equal to the outflow. The following Equation is composed of a total of
Equations:
where
is the water inflow of the pipe segment connected to node
and
is the output of node
.
In case of accident conditions, such as a pipe burst, pipe rupture, etc., the node water supply should be maintained at a certain proportion of the normal water supply requirements, which is represented by
and is generally between 0.5–0.8. It is shown by Equation (4) as follows:
In Equation (4), represents the water supply required by node . The value of is 1 under normal water supply conditions. Its value is taken between 0.5–0.8 when an accident occurs.
Water pressure balance constraints. The head loss between any two nodes
and
should satisfy Equation (5), given as follows:
where
is the head loss between any two adjacent nodes
and
,
is the expansion coefficient considering the local head loss, and generally has a value of 1.1,
is the friction head loss coefficient,
is the pipe flow between nodes
and
, while
and
are the coefficients related to the pipe type.
Water pressure constraints. The constraints of water pressure must meet the following conditions shown by Equation (6):
where
is the minimum required water pressure and
is the maximum water pressure that can be tolerated by the node. Considering the economy optimization, the design water pressure of the WDN does not exceed the upper limit. Therefore, the calculations here only require the lower limit of the water pressure.
Velocity constraints. Pipe diameter and velocity constraints are shown by Equation (7) as follows:
where
and
represent the velocity and maximum velocity in each section, respectively.
The possibility of pipe bursts increases if the flow is too fast. Therefore, we needed to specify the upper limit of velocity. As the water demand time of each node during the water supply process is random, the flow between each node occurs naturally and, therefore, the lower limit of flow rate was not considered.
2.3. Optimization Algorithm for Solving the Model
Obviously, this is a single-objective or a multi-objective optimization problem with multiple constraints. This paper mainly uses the genetic algorithm based on infeasibility and the NSGA-II algorithm. The genetic algorithm based on infeasibility was used for single-objective optimization, and the NSGA-II algorithm was used for multi-objective optimization. To obtain the pressure of each node in WDN, the LM algorithm can be used for solving nonlinear equations.
2.3.1. Genetic Algorithm Based on Infeasibility
The genetic algorithm (GA) is a heuristic algorithm with strong robustness and global search ability [
16,
17,
18], and has been widely used in many fields [
19,
20,
21,
22]. For this paper, the genetic algorithm was used as a single-objective optimization algorithm. The model proposed in this paper involves many constraints that must be satisfied. The GA generally deals with constraints using the penalty function method [
23]. However, this method is difficult to use to guarantee the characteristics of the objective function. Thus, it performs poorly for highly constrained or nonconvex constrained optimization problems [
24]. Therefore, the genetic algorithm based on the infeasibility degree was used to deal with the constraints. This method attempts to maintain a fixed proportion of infeasible individuals and increase their diversity in the population, prevent convergence to a local optimum and compare the advantages of individuals according to the defined comparison rules. The specific steps of this method are as follows:
Firstly, we calculated the deviation value (
) according to Equation (8), which represents the degree of each individual violating all constraints in the model. These constraints are given by Equation (9) [
16].
In Equation (8), is the value of individual , and are the numbers of inequalities and equalities, respectively, and and are the inequality and equality constraints, respectively. The value of is 0 if all constraints are satisfied.
The proportion of infeasible individuals (
) in the present population was calculated in the genetic algorithm. Subsequently, the upper threshold (
) was adjusted according to Equation (10). In the Equation, the value of the fixed proportion (
) is generally taken as 0.25 [
16].
The following rules were used to select individuals in each GA selection operation: First, multiple pairs of individuals are randomly selected. For each pair, the individual with the best fitness value is selected if both individuals are feasible. Otherwise, the individual with a lower is selected. If only one individual is feasible, and if the of the infeasible individual is less than , then the individual with the best fitness value is selected. Otherwise, the feasible individual is selected.
2.3.2. Non-Dominated Sorting Genetic Algorithm-II Handling Constraints
For this paper, the NSGA-II algorithm was used to solve the multi-objective optimization problem, while considering the value of each objective. In this study, the economic objective, i.e., the annual cost, and safety objective, i.e., average surplus water head, were mutually restricted, and each objective had its own weight. Thus, allocation of these weights was an important problem. Therefore, we mainly studied scientific selection of decision variables, and encoding and decoding NSGA-II, so as to provide a general method to solve the multi-objective optimization problem.
The NSGA-II algorithm is one of the most popular multi-objective genetic algorithms [
15,
25,
26,
27,
28] and was proposed based on the NSGA [
29]. It has the advantages of speed and a good convergence of the solution set. It adopts a fast non-dominant sorting algorithm, which significantly reduces the computational complexity. It also enables individuals in the Pareto domain to extend over the whole Pareto domain and distribute evenly, thus maintaining the population diversity. In addition, an elite strategy was introduced in this algorithm to expand the sampling space, preventing the loss of the best individual and improving the robustness. The NSGA-II algorithm finally obtained a set of Pareto solutions, and the set of optimal solutions of the objective function was called the Pareto optimal solutions.
The NSGA-II deals with constraints by using binary tournament selection [
29]. It chooses the better solution out of two randomly selected solutions in the population. In the presence of constraints, each solution can be either feasible or infeasible. When both solutions are feasible, the crowded-comparison operator is used to select the solution having a better objective function value. On the other hand, the feasible solution is directly selected when one solution is feasible and the other is not. When both solutions are not feasible, the solution with the lower total constraint violation is selected. Finally, the dominant relationship between the two selected solutions is defined such that any feasible solution has a better nondominated rank compared to any infeasible solution. The degree of non-dominance of the objective function value is used to rank all feasible solutions. For the two infeasible solutions, the one with a lower constraint violation has a better rank.
2.3.3. Levenberg-Marquardt Algorithm for Solving Nonlinear Equations
During the WDN optimization process, the pressure of each node under the determined section diameter is calculated when the layout, pump station pressure and water consumption of each node are known. As Equation (5) is nonlinear, this paper uses the LM algorithm to calculate the pressure of each water supply node under a certain level of accuracy [
30,
31].
The LM method is a least squares estimation method for obtaining regression parameters in nonlinear regression [
32]. It is a combination of the steepest descent and linearization (Taylor series) methods. The combination of the two methods can quickly find the optimal value.
2.4. Generalization of Pressure and Flow Calculation for WDN
The first step in the optimization algorithm is to carry out coding design. The diameter of each pipe segment is determined through the intelligent algorithms of screening, crossover, replication and decoding. The pressure of each node and the flow and velocity of each pipe segment are calculated under the condition of known diameter, and the fitness and constraint conditions of each chromosome are determined. Subsequently, the optimization results are obtained through a continuous optimization process. In the calculation process, the generalization of Equations (3) and (4) is an important issue in order to ensure the universality of the program according to the situation of complex WDN.
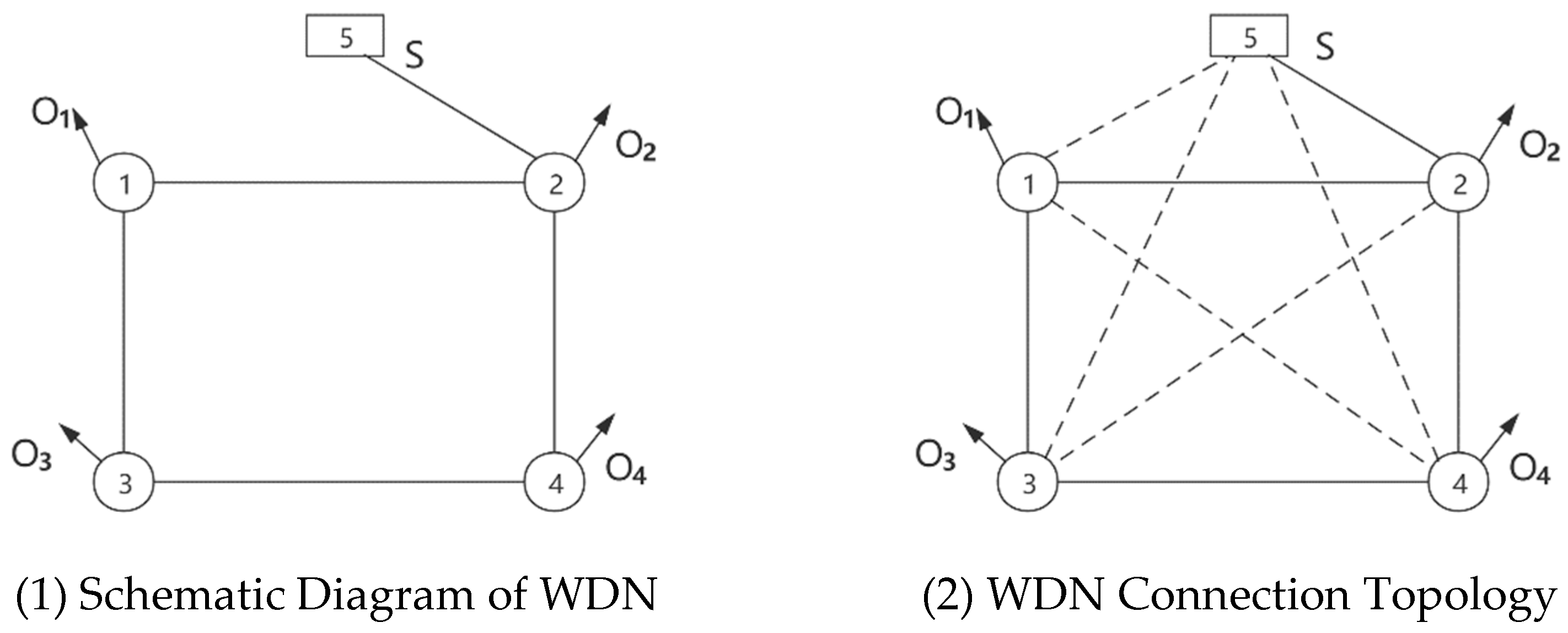
In order to ensure the generality of the algorithm, a simplified WDN connection and its topological diagram shown in
Figure 2 are used to illustrate the transformation of the flow relationship of Equation (3) into a general Equation expressed by Equation (11). The node connection matrix
, the WDN flow matrix
, the construction matrix
, the outflow node flow matrix
and the flow matrix of pump station
are given by Equations (12), (16)–(19), respectively. The Equations can be used for general calculation. The WDN model for a single pump station and
outlet nodes is described by
Figure 2, and the multi-pump stations model is similar.
Matrix
shown in Equation (12) represents the connection between two nodes. All values of the matrix consist of 1, 0 and −1. Furthermore, 1 and −1 represent the flow direction of the connected nodes, and 0 represents the absence of a connection between two nodes.
Matrix
is the WDN connection matrix, which represents the connection of each node in the WDN. The values of the matrix elements are assigned according to Equations (13)–(15). In these Equations,
represents the connection of outflow nodes in the WDN, and
and
represent the connection between the pump stations and outflow nodes, respectively.
The element
belongs to the matrix of size
, where
is the number of outflow nodes in the WDN.
The element
belongs to the connection matrix between the pump stations and the outflow nodes. The size of the matrix is
.
The element
belongs to the connection matrix between the pump station and the WDN nodes. The size of the vector is
, as shown in Equation (15).
If the node is connected to the node , is calculated according to Equation (20); otherwise, the value of is 0.
For the convenience of calculation, the matrix
is a (
) construction matrix, shown in Equation (17). In this matrix, the first
elements are 1 and the rest are 0.
The node flow matrix
is of size (
, and the matrix elements from
to
represent the rated water demand of each node. The remaining element is equal to 0. The matrix is shown by Equation (18).
The pump station inflow vector
is a column vector of size (n + 1). The matrix elements from the first row to the nth row are all equal to 0, and the (n + 1) row is equal to the inflow flow
of the pump station. It is given by Equation (19) as follows:
In Equation (16),
is an implicit function of the hydraulic pressure difference between two adjacent nodes, which can be calculated as follows:
Equations (11)–(19) constitute the general equations of the water flow pressure balance equation. Under the condition that the elevation and water supply quantity of the pump station, and the pipeline length and the water output of each node are known, the pressure
of each node can be calculated. Equation (20) can be substituted into Equation (11), and the Equation group
composed of (n + 1) Equations can be obtained as follows:
Obviously, this is a nonlinear system of Equations, which can be solved using the LM algorithm. When the water pressure at the pump station (), pipe length (), pipe diameter (), water output () of each node and the node water supply () are known, the pressure () of each node can be obtained using the LM algorithm.
In the case of a single pump station model, the initial pressure of the outflow node connected to the pump station is assumed to be equal to the water pressure (
) of the pump station, which ensures the robustness of the calculations. In the case of the multiple pump stations model, first one pump station (
,
) is selected as the main pump station, while the other pump station only converts its own flow into adjacent outflow nodes. The issue is transformed into a single water supply algorithm model by changing negative flow values at the nodes connected to the other pump station. The LM algorithm is used to calculate the water pressure of the outflow nodes connected at the pump stations, and invert the water flow and pressure at the corresponding pump station.
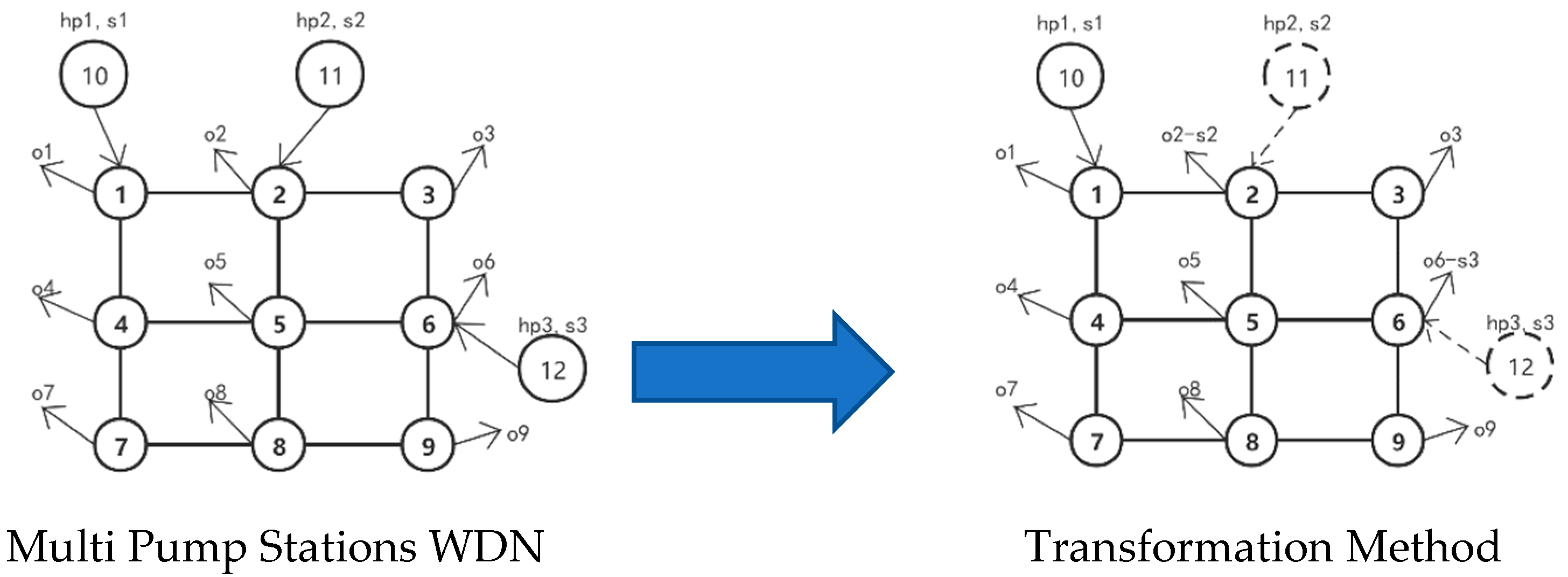
Figure 3 shows the schematic diagram of the method.
In
Figure 3, nodes 1–9 and 10–12 represent the outflow nodes in the WDN, and the pump stations, respectively. The flow of pump stations 10, 11 and 12 are denoted by
,
and
, respectively. The outflow of nodes 1, 2 and 6 adjacent to the pump station are
,
and
, respectively. Assume that the pump station 10 with flow
and water pressure
is the main pump station. In this case, the outflow of node 2 is converted to (
), and the water flow of node 6 is converted to (
).
In the calculation, the Equation group
in Equation (21) is always 0, which is not easy to calculate. Therefore, according to the actual implementation, the equation group
can be changed to be less than a fixed value. In this paper,
was selected, therefore Equation (21) can be converted to Equation (22) as follows:
The flow of the pipe section between the nodes can be determined using Equation (20) after determining the pressure of each node. The flow of the pipe section can be calculated using the flow and the diameter of the pipe section to ensure that the flow velocity of the pipe section meets the flow velocity constraints shown in Equation (7).
2.5. Algorithm Implementation
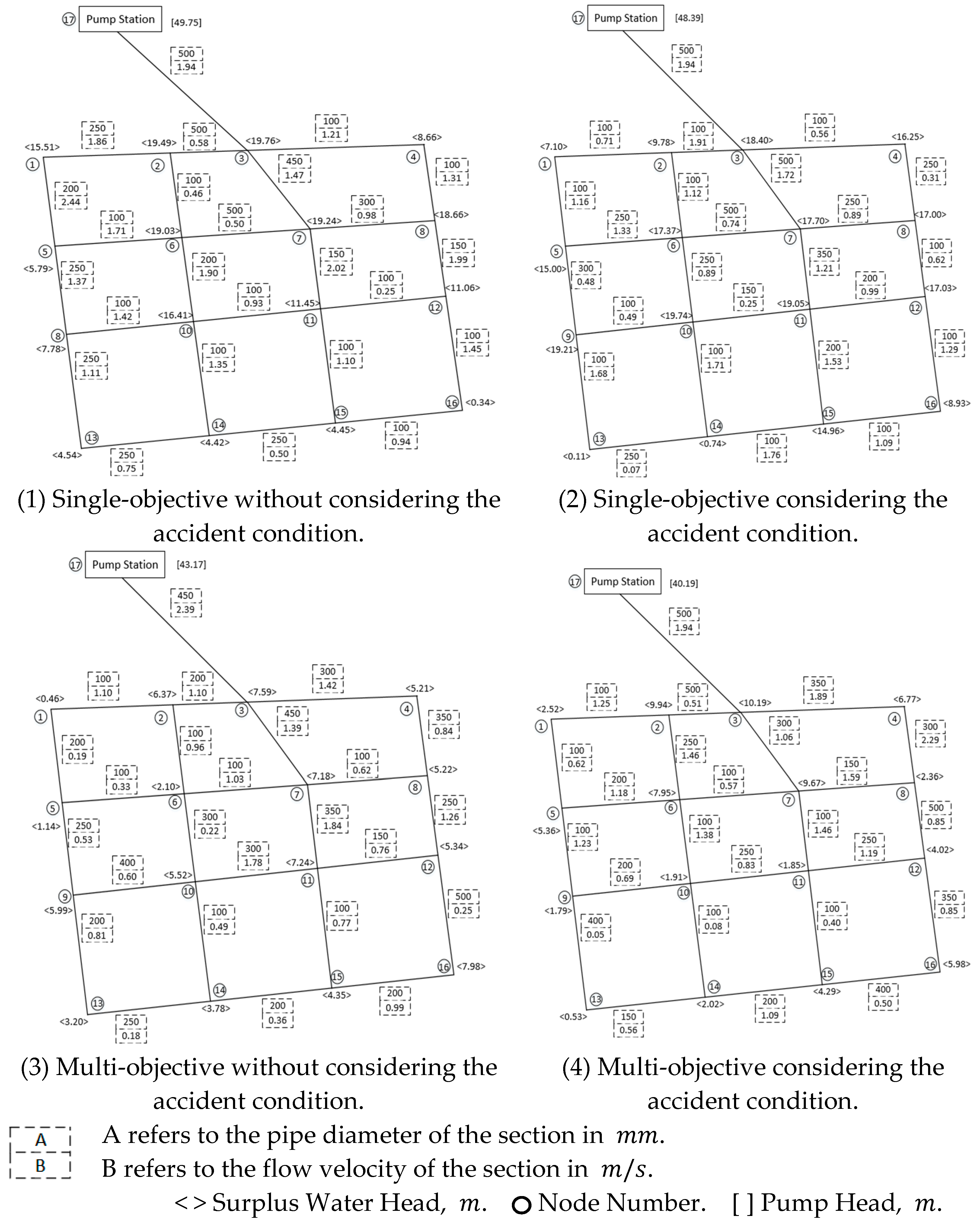
Coding design. The solution of the single-objective optimization problem is based on the genetic algorithm and the LM algorithm. In addition, the solution of the multi-objective optimization problem is based on the NSGA-II algorithm and the LM algorithm. In this paper, integer coding is used for the section diameter () in order to prevent non-standard pipe diameter in the optimization results. Furthermore, binary coding is used for the pressure of pump stations ().
Decoding and calculation of nodes pressure () and section velocity (). In the algorithm, each chromosome is decoded and its fitness value is calculated, respectively. The nodes pressure () and the flow velocity of each section are calculated, which are then used as the basis for subsequent processing of constraint conditions.
Fitness function. The economic objective of WDN is mainly considered for single-objective optimization. Therefore, the minimum annual cost given by in Equation (1) is used as the fitness function. In addition, the multi-objective optimization needs to comprehensively consider the economic and reliability objectives of the WDN. Therefore, the minimum annual cost and the weighted average surplus water head, given by in Equation (2) are used together as the fitness function.
Treatment of constraint conditions. The value of water pressure at each node of the WDN must be between the minimum and maximum water pressure values, as shown in Equation (6). The flow velocity in each section cannot be higher than the maximum flow velocity given by Equation (8). In the case of an accident condition, the outflow of each node needs to reach 70% of the normal condition, as shown by Equation (4), in addition to satisfying the two aforementioned constraints.
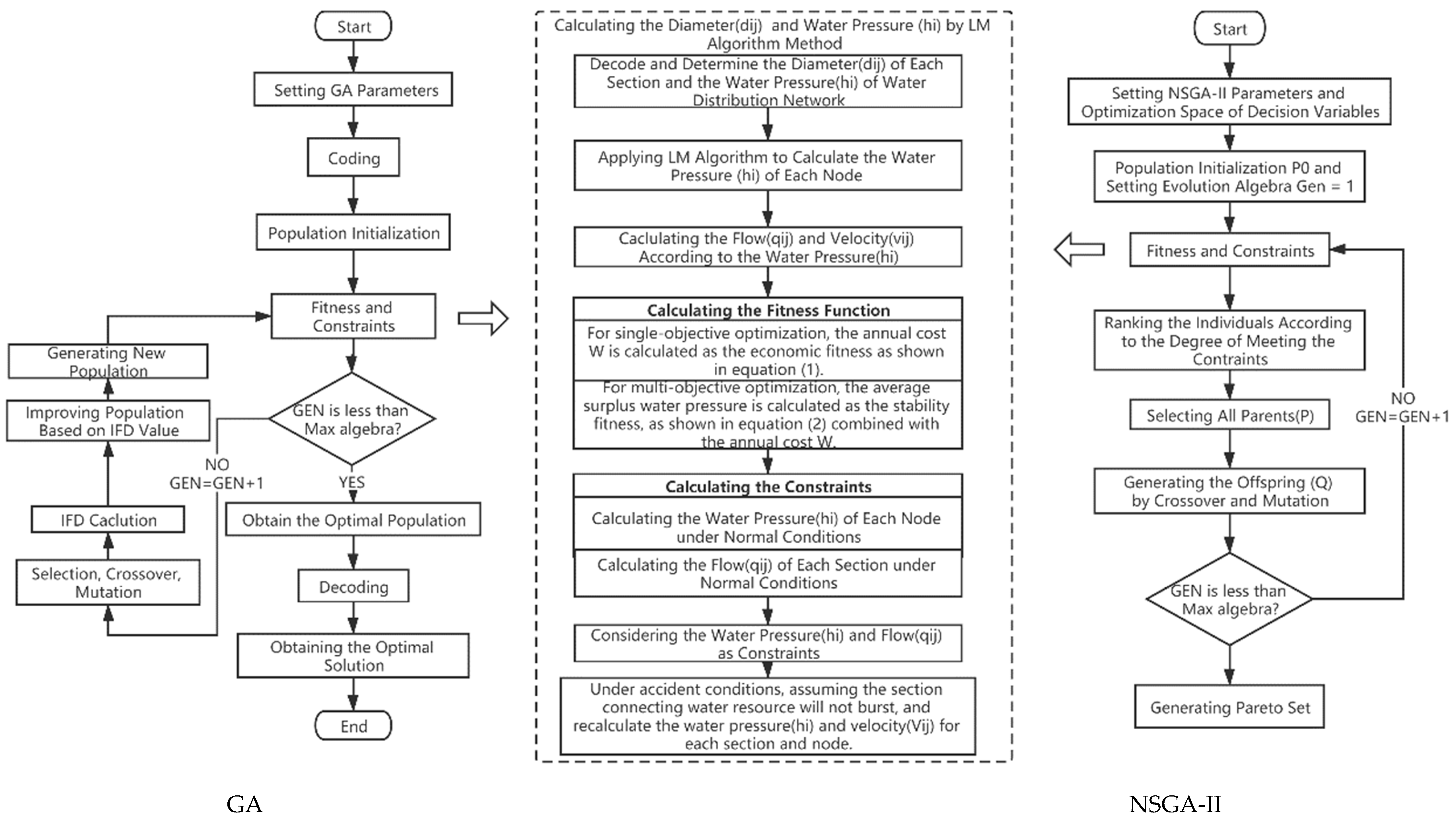
The detailed flow chart of the optimization solution model involving the genetic algorithm for single-objective optimization, and the NSGA-II for multi-objective optimization is shown in
Figure 4.