1. Introduction
Internet of Things (IoT) is a relatively new computing paradigm that enables the connectivity and synchronization of large numbers of heterogeneous devices, i.e., things, to perform complex tasks without the direct involvement of human agents. Due to the growth in popularity of IoT networks, the data collected over time from these networks reached very large volumes. These observations are recorded in a time orderly fashion and are structured as time series. We focus our work on analyzing time series for water resource management and network distribution.
Water resource management is an essential field of study that has been the focus of both researchers and practitioners. Reduction of water consumption is an issue that requires the improvement of the water distribution network in order to minimize both non-revenue and demand by taking into account several parameters: (i) current state of the distribution network, (ii) changing demands, and (iii) consumption required. To improve the management of this resource and to minimize water consumption and losses, there is a current need for new automated and intelligent decision support systems that employ machine and deep learning to analyze in real-time the utilization of this resource and alert users of any anomalies that appear in the water distribution system. In order to obtain accurately detect anomalies, we need systems that manage to distinguish automatically between normal and abnormal behavior before sending alerts to users. Using as motivation the current need of preserving water consumption, the main focus of this paper is to propose a system that works on real-world data to minimizing water losses. Thus, we propose a novel automated and intelligent rule-based decision support system that enhances anomaly detection for time series data with change point detection, with a focus on water data collected by sensors from the Internet of Things. Furthermore, the proposed system alerts end-users in real-time of any changes in the water distribution network in order to employ effective procedures that enable predictive [
1] and proactive maintenance [
2]. Predictive and proactive maintenance is a solution used to alleviate the costs related to loss of resources when water distribution networks encounter defects and the equipment breaks down. Predictive maintenance is used to make assessments regarding the well functioning of the water distribution network and consumption using real-time data to detect anomalies and change points and historical data to predict future failures. Proactive maintenance concentrates on monitoring and correcting the root causes of failures within the network using real-time anomaly detection.
Anomaly (or outlier) detection is the identification of events, items, or observations that do not correspond to normal behavior. Anomaly detection is an essential task in solving different problems in IoT networks, e.g., detecting structural defects due to various reasons such as lack of maintenance, edge cases that can generate critical situations, intrusions. Recently, anomaly detection has been successfully used to detect malicious activities by analyzing the data transferred between the IoT devices, modeling good behavior, and detecting tamper data and malicious activities as anomalies. While anomaly detection based approaches can potentially detect more attacks, current systems suffer from high false positive rates. Additionally, in the current literature, there are many studies that underline the importance of outlier detection in the water management domain [
3,
4].
Along with anomaly detection, change point detection plays an important part in time series analysis. It indicates an unexpected and significant change in the analyzed time series stream that represents a normal behavior and not an anomaly.
Currently, many anomaly detection systems need a lot of human interaction to interpret the generated data. This process becomes more and more complex as the number of interconnected devices grows exponentially. Furthermore, many anomaly detection algorithms have high false positive rates, as they tend to label the change points as outliers. Thus, a method that distinguishes between them is required to increase the accuracy of anomaly detection systems and alleviate the decision process. By automating the matching process between anomalies and change points, the required human interaction and interpretation can be reduced only to rare cases. This process can be improved by using a rule-based decision system that manages to discriminate between a change point and an anomaly with high confidence.
We identified the following shortcomings in the current literature. Firstly, none of the proposed methods remove change points from the points detected as anomalies to minimize the detection of false positives, a challenge that still remains unresolved [
5]. Secondly, none of the current methods enable both predictive and proactive maintenance using a rule-based decision support system for water management and network distribution systems. Although both maintenance methods have been discussed separably [
6,
7] from the point of view of anomaly detection applications, they have not been taken into consideration change point detection.
Given these shortcomings in the current literature, the main research questions we want to answer are:
Can we minimize the water consumption and losses using a rule-based decision system that alerts users in real-time?
Can we enhance anomaly detection techniques using change point detection?
Can we remove the false positives that anomaly detection techniques find using change point detection?
Can we enable predictive and proactive maintenance using a rule-based decision support system for water management?
To answer the four research questions, in this paper, we propose a novel rule-based decision system that enhances anomaly detection using change point detection for IoT time series. The architecture uses a pipeline that automatically manages to detect real anomalies and remove the false positives introduced by change points. We use five anomaly detection algorithms: Gaussian Distribution (GD), K-Means, Isolation Forest (IF), OC-SVM (One-Class Support Vector Machine), and Autoencoders (AEs). For change point detection, we also use five algorithms: window-based segmentation (WinSeg), binary segmentation (BinSeg), bottom-up segmentation (BottonUp), Pruned Exact Linear Time (PELT), and exact segmentation dynamic programming model (OPT). We propose a new confidence metric based on the support for a point to be an anomaly and the support for a point to be a change point. We propose a novel rule-based decision module based on support and confidence metrics to alleviate human intervention and improve the decision process by automating some of the most frequent cases that arise during detecting false positives. In our experiments, we use a large real-world dataset containing multivariate time series about water consumption collected from smart meters. The experimental results strengthen our assumption that anomaly detection can be improved by determining and removing change points as well as validates the correctness of our proposed rules in real-world scenarios.
Thus, the main contributions of this paper are:
- (C1)
A new rule-based decision system for anomaly detection in IoT time series in order to answer ;
- (C2)
A new confidence metric based on the support for a point to be an anomaly and the support for a point to be a change point to remove false positives in order to answer ;
- (C3)
A new pipeline that automatically manages to detect real anomalies and remove the false positives introduced by change point using the confidence score in order to answer ;
- (C4)
Extensive experiments on real-world multivariate time series using five anomaly detection and five change point detection algorithms in order to enable predictive and proactive maintenance and answer .
The solution proposed in this paper is a continuation of a work initiated within the Datat4Water—Excellence in Smart Data and Services for Supporting Water Management (
https://data4water.pub.ro—accessed on 3 May 2021) H2020 Twinning project [
8].
This paper is structured as follows.
Section 2 presents current research methods, models, and strategies used for anomaly detection.
Section 3 discusses the algorithms used to implement our solution. In
Section 4, we present our pipeline used for enhancing anomaly detection using change points. We present the experimental setup and the results in
Section 5, and we provide a final discussion of our findings in
Section 6. Finally, we summarize our findings and hint at future research directions in
Section 7.
2. Related Work
There are multiple research solutions for solving the anomaly detection problem in IoT networks. These solutions imply using different heuristics rules or machine learning algorithms. From the perspective of the learning models, there are three main categories: unsupervised [
9,
10], supervised [
11,
12], and semi-supervised anomaly detection [
13,
14]. As we apply unsupervised methods, our focus in this section is going to be only on these techniques.
The unsupervised solutions detect anomalies using unlabeled datasets and consider that the majority of collected items are normal. They are a better fit for scenarios where, due to large streams of heterogeneous data from different sensors, it is impractical to label the dataset. Kieu et al. [
9] propose a solution to improve outlier detection in time series based on sparsely-connected recurrent Autoencoder ensembles. They argue that by combining multiple Autoencoders, the overall detection accuracy is improved, as these ensembles tend to reduce the effects of overfitting for some Autoencoders. To test their idea, they build two types of frameworks. The first proposed framework trains multiple recurrent Autoencoders independently, while the second one trains the Autoencoders jointly. For the experiments, they use two relatively small datasets. The first dataset consists of 120 univariate time series, each time series having 2000 to 5000 observations. The second dataset has seven 3-dimensional time series, each time series between 3750–5400 observations. They compared their solutions both with classical machine learning and deep learning approaches. In most of the cases, their ensembles solutions outperform the individual methods. Current literature argues that ensemble methods do not fully avoid the overfitting issue, as sometimes they do not generate a sufficient level of diversity [
15].
Vishwakarma et al. [
10] present another deep learning unsupervised approach. The proposed solution uses Feed Forward neural networks, and it is limited to univariate time series. The input data are transformed into a bivariate series using a robust measure of location and the dispersion matrix. One of the primary issues of their solution is that they use simulated data. Although the obtained results are promising, it is a known fact that there is a significant gap between simulated and real datasets and we cannot rely solely on synthetic data to judge the performance of anomaly detection techniques [
16], which can impact the discrimination sensitivity of Neural Networks.
Recurrent Neural Networks (RNN) have been used successfully for analyzing time series in prediction [
17], change point detection [
18], and anomaly detection tasks [
19,
20]. Saurav et al. [
19] propose a temporal model based on RNNs for time series anomaly detection considering sudden or regular changes in the normal behavior. The proposed model can automatically adapt to various types of changes and uses RNN based multi-step prediction and local normalization over a window to deal with non-stationary time series. The traditional RNN network suffers from the vanishing gradient problem [
21]. Thus, a new class of recurrent networks was designed, Long Short-Term Memory (LSTM) [
22]. LSTM based solutions were widely used for analyzing time series and especially for the task of anomaly detection. Maleki et al. [
20] present an LSTM-based Autoencoders architecture for unsupervised anomaly detection. The proposed solution provides online detection by using a sliding window to iteratively update the algorithm’s parameters.
Munir et al. [
23] tackle the impact of Convolutional Neural Networks (CNN) on detecting periodic and seasonality related point anomalies in unlabeled streaming data. The presented CNN based solution, i.e.,
DeepAnT, consists of two modules: a time series predictor (using CNNs) and an anomaly detector. Each predicted value is passed to the anomaly detector module that tags the corresponding timestamp as normal or not. The solution is evaluated using 10 datasets containing a total of 433 real and synthetic univariate or multivariate time series.
DeepAnT is compared with 15 other algorithms using F-score as the metric. One important conclusion of this study is that although LSTM based solutions are performant on temporal data due to the LSTM’s ability to extract long-term trends, CNN is a good alternative because of its parameter efficiency. Thus,
DeepAnT is equally applicable to big and small datasets, as opposed to LSTM architectures that require large learning datasets.
Kieu et al. [
24] propose an advanced framework that uses deep neural networks and enriched multivariate time series for outlier detection. The proposed framework uses Autoencoders, in particular, a 2D convolutional neural network-based Autoencoder (2DCNN-AE) and a long short term memory-based Autoencoder (LSTM-AE). The Autoencoders are compared with two non-Deep Learning baselines, i.e., Local Outlier Factor and One-Class Support Vector Machines. After analyzing the results, the authors concluded that LSTM based method always obtains the best metrics, i.e., Precision, Recall, and F1, in the case of a large dataset (S5 dataset that contains 371 time series). Although, Recall and F1 remain the best for LSTM-AE even for smaller datasets, in most of the cases the Support Vector Machines method has a better Precision.
Some authors argue that using a preprocessing step that does a preliminary screen of the data is very important and can have a major influence on the accuracy of the detection task. Zhang et al. [
25] propose a solution that consists of a three-level hybrid model, i.e., a preprocessing, a prediction, and an outlier detection level. In the preprocessing step, the input data is analyzed, and obvious outliers, such as sudden extremes, are removed. During second level prediction, the authors (i) decompose the preprocessed data into new and stationary intrinsic mode functions, and (ii) apply classification, regression tree, autoregression to obtain predicted values. To detect outliers in the predicted data, they use an exponential weighted moving average method. A relatively small real dataset from a hydrometeorological observation network was used in the experiments. Based on the obtained results, the authors believe that the first two levels of the proposed model improve its accuracy and robustness.
In the recent literature, there are also many interesting unsupervised non-Deep Learning methods for time series outlier detection [
26,
27]. Kant et al. [
26] use an enhanced K-means Clustering algorithm in combination with PSO (Particle Swarm Optimization). The Enhanced K-Means combines the traditional K-means algorithm with the Weight-based centre approach. The results show that the proposed algorithm finds the largest number of outliers compared with the traditional K-Means or PSO algorithms. Another unsupervised non-Deep Learning approach is
Pbad (pattern-based anomaly detection) [
27]. The proposal method (i) mines for the frequent itemsets and sequential patterns, (ii) it calculates their distance-weighted similarity, and (iii) constructs a pattern-based embedding of time series. The embedding is used to construct the anomaly detection classifier.
Pbad uses as a classifier an ensemble of decision trees, i.e., the Isolation Forest algorithm. The proposed solution is compared with other state-of-the-art pattern-based anomaly detection methods, e.g., Matrix profile (MP) [
28] an anomaly detection technique based on all-pairs similarity-search. In the majority of the cases, it outperforms all the other methods for both Univariate and Multivariate time series datasets. The methods are evaluated by computing the area under the receiver operating characteristic (AUROC) and average precision (AP). A solution for anomaly detection in water consumption is proposed by Gonzalez-Vidal et al. [
5]. The authors analyze the data collected by smart meters using an ARIMA-based framework anomaly detection and conclude that removing the false positive from the picture is still a challenge.
As an overall impression, after analyzing the current literature, we consider that even if some of the current solutions propose interesting new pipelines, many of them are not thoroughly tested using large real time-series datasets. Additionally, to the best of our knowledge, there is no current anomaly detection solution that uses change point algorithms to lower the false positive rate, which is highly desired for the anomaly detection task.
3. Methodology
A time series is a set of observations recorded at a specific point in time. Time series can be seen as discrete (i.e., each observation is measured at fixed points in time) or continuous (i.e., the values of measurements are recorded continuously for a window of time) [
29]. In this section, we define a time series and then discuss some of the models used in our architecture to correlate outliers with change points.
3.1. Time Series Definition
A statistical mathematical model that describes a sequence of data points recorded over a specified period of time is called a time series [
30]. A time series can be described as a sequence of random continuous or discrete variables
, where
t denotes the time point when a value was measured and
is the cardinality of
X. Moreover, the sequence
X is a stochastic process meaning that it can be defined as a family of random continuous or discrete variables.
A time series can be univariate or multivariate. A univariate time series is a series with a single time dependent variable. A multivariate time series has at least two time dependent variables, i.e., . Each of these variables depends on both its past values and the other variables.
A time series data point is described by three components:
- (i)
: the trend component represents variations of low frequency and can be determined by the moving averages or spectral smoothing methods;
- (ii)
: the seasonal component is a function that represents normal fluctuations that are more or less stable after a known period (or lag) h;
- (iii)
: the noise (residual) are used to check if a analysis model has correctly determined the information in the data points and can help to predict future values [
31].
These components are used to decompose the time series as an additive decomposition function (i.e., ), or a multiplicative decomposition function (i.e., ).
The seasonal and trend components indicate if a time series X is autocorrelated, i.e., determines if X is linearly related to a lagged version of itself. Thus, given the autocovariance function at a lag h as , where is the covariance function, then the autocorrelation is .
A time series X is stationary if its properties are similar to a h time shifted time series. Thereby, X is stationary if its mean () is independent of t and its covariance () is independent of t for each h. Usually, the trend and seasonality components are eliminated to get stationary residuals.
3.2. Time Series Outlier Detection
An outlier or an anomaly is a data point that significantly differs from other observations in a time series. Outliers can appear due to an experimental error or an anomaly in the measurement. Such suspicious points in the time series data must be identified and interpreted separately in order not to interfere with the analysis step and lead to wrong conclusions.
The outlier detection problem implies ranking the data points of a time series X using an outlier score , such that higher values of mean that is more likely to be an outlier.
3.2.1. Gaussian Distribution
Gaussian Distribution (GD) or normal distribution is a probabilistic statistical approach used in detecting outliers. To determine that the data points are normally distributed, the probability density function (PDF) is used to model the sample’s distribution space. Equation (
1) gives the general form of the probability density function for a GD, where
is the sample standard deviation, and
is the sample mean.
In the case of GD, an outlier is a data point that has a significant distance from the mean, i.e., the point lies many standard deviations (
) away from the mean (
). One approach for detecting the distance is to fit a covariance estimate to the data by utilizing an ellipse to center the data points. The Mahalanobis distances are used to estimate if a point is an outlier and determine the ellipse. All the points that are outside the center of the ellipse are considered anomalies. Equation (
2) presents the Mahalanobis distances between two data point
and
, where
is the standard deviation of the
i-th dimension over the sample.
3.2.2. K-Means
K-Means is an unsupervised machine learning algorithm that creates
k similar clusters of data points [
32]. Using the K-Means, the data points that do not belong to any clusters are marked as anomalies. The algorithm detects in an iterative way (i) the
k center points, i.e., centroids, (ii) the points closest to the centroids using a distance function. K-Means stopping criteria is either when the centroids do not change from one iteration to another, or a predefined number of iterations is reached. As this algorithm is unsupervised, the number of clusters is either known or is determined using a heuristic, e.g., Elbow Method, Silhouette Coefficient, etc. We chose the Elbow method to determine the optimal number of clusters. Furthermore, to avoid inaccurate clustering results by choosing the initial centroids at random, we use K-Means++, which minimizes the intra-cluster variance. The Euclidean distance (Equation (
3)) is used to measure the membership of a data point point
to a centroid
in an
M-dimensional space.
3.2.3. Isolation Forest
Isolation Forest (IF) is an unsupervised anomaly detection algorithm based on Random Forest [
33]. The algorithm trains multiple Isolation Trees using sub-samples with random attributes constructed using Bagging (Bootstrap aggregating). The Isolation Tree splits the sub-sample points using a randomly selected attribute value between its minimum and maximum value. The partitioning of the data produces trees with shorter paths for anomalies as attributes values that better represent the data are more likely to be separated in early splits. After multiple Isolation Trees are constructed, the algorithm scores the data points to quantify its potential of being an anomaly. As anomalies are closer to the root of the Isolation Tree, the score is a function of path length. Equation (
4) presents the score function, where
n is the size of the dataset,
measures the number of edges traversed from the root to a data point
,
is the average of
, and
is the average path length of unsuccessful search in Binary Search Tree.
3.2.4. One-Class Support Vector Machine
One-Class Support Vector Machine (OC-SVM) is an unsupervised machine learning algorithm trained on a dataset containing elements from one class [
34], i.e., the “normal” points. The OC-SVM models a function that estimates the support for the entire dataset. This approach is used to detect the representative points in a dataset and isolate the anomalies that are very few. Equation (
5) presents the OC-SVM function, where
is the sign function,
w are the equation coefficients that need to be determined in order to minimize the margin, i.e.,
, between the two hyperplanes
and
created by the two classes
,
b is the bias terms that ensures the function does not go through the origin, and
is a transformation function in an upper dimensional space in the case the data points are not linearly separable.
When using OC-SVM, a kernel function is needed to transform the input data into the required form for processing. A widely used kernel function is RTF (Radial Basis Function). The RTF kernel function is , where the kernel coefficient and is the squared Euclidean distance.
3.2.5. Autoencoders
An Autoencoder (AE) is a neural network that reproduces an input time series of
by an output vector
in an unsupervised manner [
24]. Each vector
is expected to approximate the input
. Both
and
have the same size
M. The architecture of this network contains two components: an encoder and a decoder. The encoder (
) maps the input
X to an intermediate
dimensional space
, i.e.,
where
is the weight vector,
is the bias, and
is an activation function (signoid, ReLU, etc.). The decoder (
) maps
to the output
, i.e.,
where
is the weight vector,
is the bias, and
is another activation function. The aim of the network is to estimate for each data point
which minimizes
.
3.3. Time Series Change Point Detection
The problem of change point detection in time series data deals with finding the point in time when the properties (e.g., mean, variance, etc.) of the time series change abruptly [
35].
A change point is a transition point between different states in the time series data. A continuous state is defined as a segment. For a given time series X and a set of indexes , a segmentation is defined by or simply , where the dummy indexes and are implicitly available and K is the number of change points.
The change point detection methods are dependent on prior knowledge about the number of change points K. Thus they are either supervised (i.e., the K is known) or unsupervised (i.e., the K is unknown). The change point detection problem is formulated as detecting the best possible segmentation for a time series X according to a criterion function . The criterion function is the sum of costs of all the segments that define the segmentation . The “best segmentation” is the minimize of the criterion function .
Depending on the approach, i.e., supervised and unsupervised, the entire problem is reduced to solving an optimization problem. For a known number of change points K, the change point detection problem consists in solving , while for an unknown number of change points it consists in solving where is a measurement that balances out over-fitting when small change amplitudes are detected. Therefore, the search method is how the discrete optimization problem is solved. Its constraints are defined by the number of change points to detect.
In the literature, the cost functions are either parametric (e.g., maximum likelihood estimation models [
36], multiple linear model [
37,
38], mahalanobis-type seminorm model [
39]) or non-parametric models (e.g., non-parametric maximum likelihood model [
40], rank-based detection model [
41], kernel-based detection model [
42], etc.).
The search methods use either optimal detection models, i.e., finds the exact solution to the optimization problem, or approximate detection models, i.e., solves the optimization problem yielding an approximate result. Approximate detection models are used when it is desired to reduce the computational complexity.
3.3.1. Window-Based Segmentation Model
The Window-based segmentation (WinSeg) [
43,
44] algorithm computes the discrepancies between two adjacent time windows that slide along the data point of a time series
in order to detect change points. A discrepancy is a value calculated for each index of time
t between the immediate past, i.e., the left window, and the immediate future, i.e., the right window. Using this method, the algorithm detects peaks, i.e., large values, when two windows cover dissimilar segments and compute the discrepancy curve. The change point indexes are determined using a peak detection procedure on the curve.
3.3.2. Binary Segmentation Model
Binary segmentation (BinSeg) [
45,
46] is a greedy sequential algorithm that searches for the change point that minimizes the sum of costs. The time series is then split into two at the index of the determined first change point and restarts the computation on the new sub-series. The algorithm stops when either the required number of required change points are found or when a stopping criterion is met.
3.3.3. Bottom-up Segmentation Model
Bottom-up segmentation (BottonUp) [
47,
48] is a sequential approach used to perform fast signal segmentation that starts with many change points and successively deletes the less significant ones. Thus, the time series is divided into many segments along a regular grid, and then, the contiguous segments are successively merged according to a measure of how similar they are. Moreover, bottom-up segmentation can extend any single change point detection method to detect multiple changes points.
3.3.4. Pruned Exact Linear Time Model
When the number of change points is unknown, then the optimal solution can be computed using exact segmentation to minimize the penalization function. The model Pruned Exact Linear Time (PELT) [
49] finds the exact solution when the penalty is linear. PELT considers each time series data sample sequential. The explicit pruning rule tests if each sample point and determine if it is a potential change point. PELT works under the assumption that each region’s length is randomly drawn from a uniform distribution.
3.3.5. Exact Segmentation Dynamic Programming Model
When the number of change points is known then the optimal solution can be computed using the exact segmentation dynamic programming model (OPT) [
50]. The OPT algorithm solves the problem recursively by using the additive nature of the objective function
. Under these observations the optimal partitions with
elements of all sub-series of
are known, thus the first change point of the optimal segmentation can be computed. Using recursively, the complete segmentation is then computed.
4. Proposed Solution
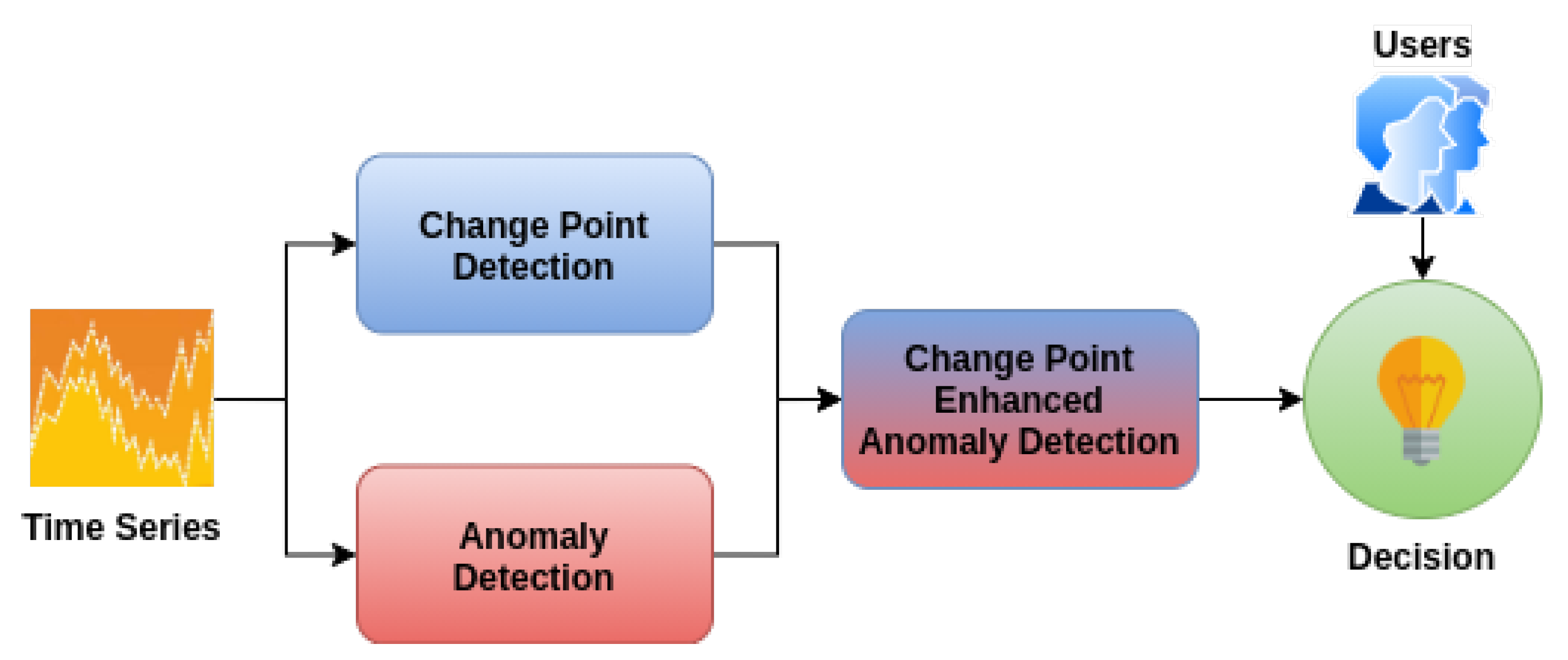
The architecture of our proposed solution contains four modules (
Figure 1). The Anomaly Detection Module uses specialized unsupervised Machine Learning algorithms to detect outliers from an input time series. The Change Point Detection Module uses different techniques to detect change points within the same input time series. The Change Point Enhanced Anomaly Detection Module takes the output from the previous two modules, compares the results, and calculates a confidence score of each point to be an outlier. These results are analyzed by the Decision Module using a set of rules. The system either takes an automated action or alert users to make an informed decision. The code is freely available online on GitHub at the following link
https://github.com/cipriantruica/iot-ts-cpd-ad.
4.1. Anomaly Detection Module
Gaussian Distribution: in our implementation, we use the Elliptical Envelope as the covariance function for GD. We initialize the proportion of outliers to 0.01.
K-Means: we initialized the K-Means centroids using the K-Mean++ algorithm, thus removing the problem of detecting poor clusters due to the initial values chosen for the centroid. To minimize the number of dimensions and remove the curse of dimensionality from which clustering algorithms suffers when dealing with data points that have a large number of attributes [
51], we use the PCA (Principal Component Analysis) to extract only the attributes that better describe the data points. To get the optimal number of clusters for the K-Means algorithm, we used the Elbow Method. Any point that has a distance from the closest centroid of over a given threshold is considered an anomaly.
Isolation Forest: for IF, we used 100 Isolation Trees trained on subsamples with replacement using Bootstrap. For each time series, the proportion of outliers should be determined using Cross-Validation. We found that a good default value for our dataset is 0.01.
One-Class Support Vector Machine: we initialized the kernel function to RTF. Using Cross-Validation, we set the upper bound on the fraction of training errors to 0.01.
Autoencoder: we used the PyOD (
https://pyod.readthedocs.io/en/latest/) Python package that uses Keras and Tensorflow to implement an Autoencoder network. We model a network containing 13 fully connected hidden layers having the following number of perceptrons:
, where
M is the number of dimensions in the time series. We set the maximum number of training epochs to 100.
4.2. Change Point Detection Module
The Change Point Detection Module uses the algorithm presented in
Section 3.3 to detect change points. The algorithms are implemented in Python using the latest version of the Ruptures (
https://centre-borelli.github.io/ruptures-docs/) package. For all the employed change point detection algorithms, we use the same parameter configuration: the model is initialized using the
-norm, and the minimum segment and length between two change points is set to 2. PELT determines the optimal number of points before stopping automatically. For the other algorithms, i.e., WinSeg, BinSeg, BottomUp, and OPT, we set as the optimal number of breakpoints the value computed with PELT.
4.3. Change Point Enhanced Anomaly Detection Module
The Change Point Enhanced Anomaly Detection Module computes the confidence for a data point to be an outlier. Equation (
6) presents the
score, where
is the support for the data point
x to be an anomaly, i.e., the number of times the point is marked as an anomaly (
) divided by the number of algorithms employed for this task (
), and
is the support of the same data point
x to be a change point, i.e., the number of times the point is marked as a change point (
) divided by the number of algorithms used for detecting change points (
). The proposed confidence function ensures that if
, then its score is equal to 1. Furthermore, in the case that
, then
, leaving the decision to be taken by the user.
When a data point is both labeled as an anomaly and a change point, the function can remove the obvious false positives introduced by change point. In case the decision is felt to the human operator, then the function helps in taking an informed decision. This function also enables the performance of effective predictive and proactive maintenance. By assessing the values of the function, predictive maintenance is achieved in time by determining if the system is functioning correct. Thus, if we mark anomalies as change points means that the system works normally. While, if we only determine anomalies we can assume with a high confidence that the system is faulty. Proactive maintenance concentrates on monitoring and correcting the root causes of failure. Thus, if the system determines with a high confidence that there are anomalies within the water distribution network, then the human operator can in-time correct any errors. While, if there is a high confidence that the data points are only change points, the human operator can conclude that this behaviour is normal and no maintenance is required.
4.4. Decision Module
The Decision Module uses rules to determine if a human operator should be alerted or if the system can take an automatic decision. Frequent cases are also the easiest to interpret by the system and give an automatic response. Rare or ambiguous cases require human interpretation. Thus, the system needs to alert an operator and let him make an informed decision.
The system can take automatic decisions for the following frequent cases:
When the support for anomaly detection is high, and there is no or low support for change point detection, then the system automatically marks the point as an anomaly.
When the support for change point detection is high, and there is no or low support for anomaly detection, the system marks the point as a change point and not an anomaly.
When the support for change point detection is low, and there is no support for anomaly detection, the system marks the point as a change point and not an anomaly.
Human intervention is still required for the following very rare cases:
When the anomaly support is low and no change point is detected or the change point support is low, regardless if or .
When both the anomaly support and change point support are high, regardless if or .
When the anomaly support is equal to the change point support, regardless if both are high or low.
For , , and , the human operator should analyze the data point and take an informed decision, whether the data point is an anomaly or a change point.
Based on the use cases, we propose the decision rules presented in
Table 1 either for automatic resolve or to alert a human operator. These rules enable human operators that manage the water distribution network to perform effectively predictive and proactive maintenance.
6. Discussion
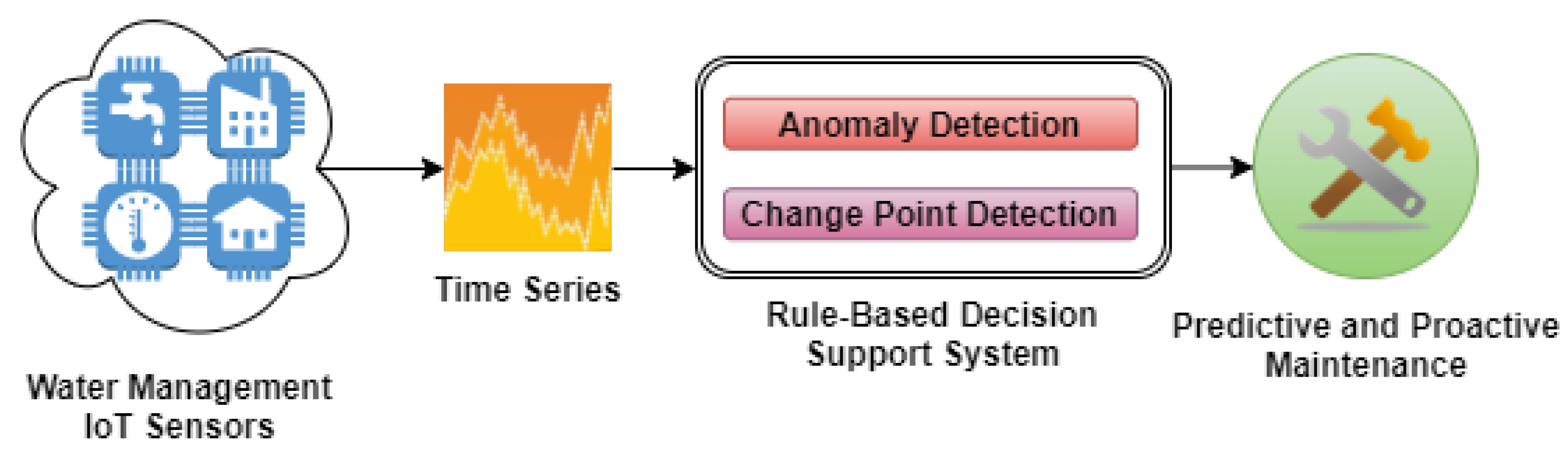
As new devices have been developed to monitors water installations, there is a need for self-learning solutions that employ machine and deep learning algorithms to automatically generate alerts and predict anomalies. These devices are required to save the world’s scarce water resources using edge computing sensors that are tightly integrated with artificial intelligence in the cloud. Thus, for early identification of real-time abnormal behaviour and to avoid the waste of resources, these sensors, together with machine learning models, are used to extract knowledge and identify patterns in the flow of water consumption. Furthermore, using cloud-enabled analytic tools with data collected from IoT sensors, end-users are alerted in real-time of any changes in the water distribution network in order to employ effective procedures that will enhance the decision-making process and enable predictive and proactive maintenance.
Predictive and proactive maintenance are performed continuously when the water distribution network operates efficiently for long periods. When the system starts to show disruptions signs in the provided services, then human operators and users must be alert to make informed decisions. To enable these novel types of maintenance that lowers costs [
52], close monitoring of each network device is needed using intelligent rule-based decision support systems. Anomaly detection and change-point detection algorithms that can scale with the volume of data are needed to create systems that can enable human operators and end-users to take advantage of these two types of maintenance procedures (
Figure 4) and make informed decisions regarding the status of the water distribution network.
Anomaly detection in time series is a complex task that requires large datasets to accurately discriminate between points that present a normal and abnormal behavior. Thus, the experiments need to be conducted on real data to create accurate models. In our experiments, we used a real-world dataset containing 119 multivariate time series, each collected over a period of 6 to 24 months at intervals of 5 s. The total size of the dataset is over 4.8 GB. Using such a large dataset, we manage to fine-tune our models. Furthermore, we observe that there is a shortage of real-world large multivariate time series dataset for anomaly detection in the current literature [
9,
25].
The proposed architecture uses five different anomaly detection algorithms, i.e., Gaussian Distribution (GD), K-Means, Isolation Forest (IF), OC-SVM (One-Class Support Vector Machine), and the state of the art Deep Neural Networks Autoencoders. We observe that, on average, OC-SVM has the overall best performance, managing to discriminate between normal and anomaly points. We observe that the algorithms manage to determine anomalies accurately in the same window of time. Furthermore, the employed Autoencoder algorithm needs more hyperparameter tuning to obtain better results and decrease the number of points marked as anomalies.
Using the decision rules proposed in
Table 1, the proposed enhancement of anomaly detection by using change point detection manages to reduce the human intervention for all the cases. Thus, automating the process of detecting abnormal behavior in time series. We can conclude that for frequent cases, human intervention is not required, and based on the rules we propose, the system automatically makes an accurate decision. In the less frequent cases, when human intervention is needed, the system sends alerts that describe the situation based on the proposed rules as soon as possible. Thus, our system manages to enable users to make informed decisions regarding the status of the water distribution network and perform effectively predictive and proactive maintenance.
7. Conclusions
In this paper, we present a change point enhanced anomaly detection architecture for IoT time series data. We propose an architecture that uses five distinct anomaly detection algorithms to detect outliers and then compute an agreement between them using a support function to determine if a data point in the time series is actually an outlier. Then, on the same time series, we detect change points using five distinct algorithms and compute a change point support to determine if a data point in the time series is actually such a point. Using the two support scores, we compute a confidence score that helps the rule-based decision system to automatically take a decision or determine if there is a need to alert a human operator. Furthermore, we experiment on a large dataset containing real-world time series regarding customer water consumption collected from smart meters. The results show that the proposed method manages to automate the decision process when dealing with anomaly detection, thus helping the decision process.
In conclusion, through this work, we address the identified shortcomings in the current literature and answer our research question as follows. To answer , we propose a new rule-based decision system for anomaly detection in IoT time series data with a focus on water resources management and distribution systems. To answer both and , we propose a new confidence metric based on the support for a point to be an anomaly and the support for a point to be a change point to remove false positives and enable human operators to perform efficiently predictive and proactive maintenance. To compute the proposed confidence metric, we developed a novel pipeline that automatically manages to detect real anomalies and remove the false positives introduced by change points using the confidence score. Finally, to prove the efficiency of our solution and to answer , we perform extensive experiments on real-world multivariate water consumption time series data using five anomaly detection and five change point detection algorithms.
In future research, we plan to investigate and enhance with change point detection other anomaly detection methods, i.e., Gaussian Processes, ARIMA, and other Autoencoders. We also plan to propose our own Deep Neural Network Architectures that employ attention and convolutional layers.