An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches
Abstract
1. Introduction
2. Governing Equations
2.1. Full-Form 1D Equations
2.2. Simplified Equations
2.3. Finite Volume Method
2.4. Two-Dimensional Flows
3. MOC Schemes
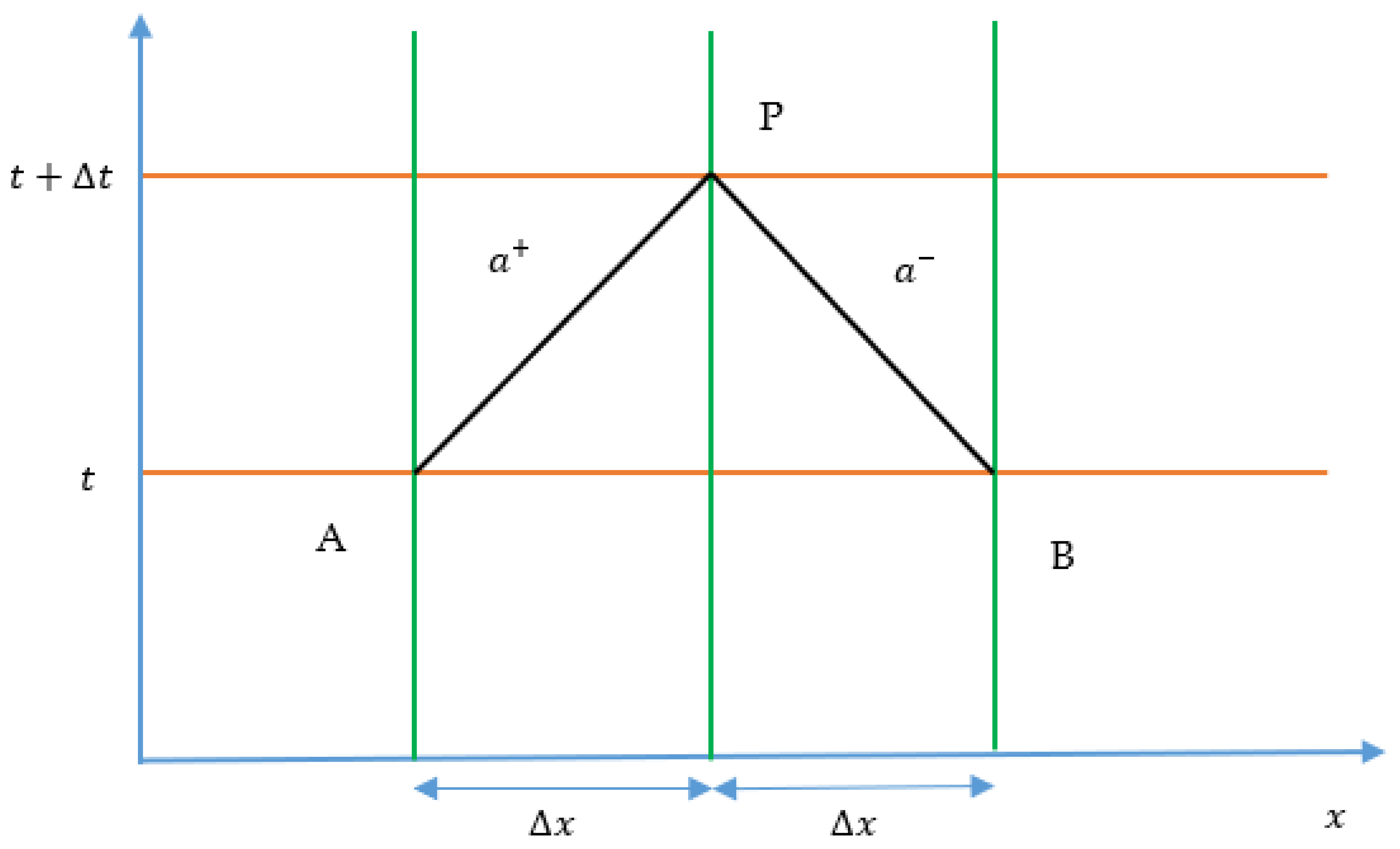
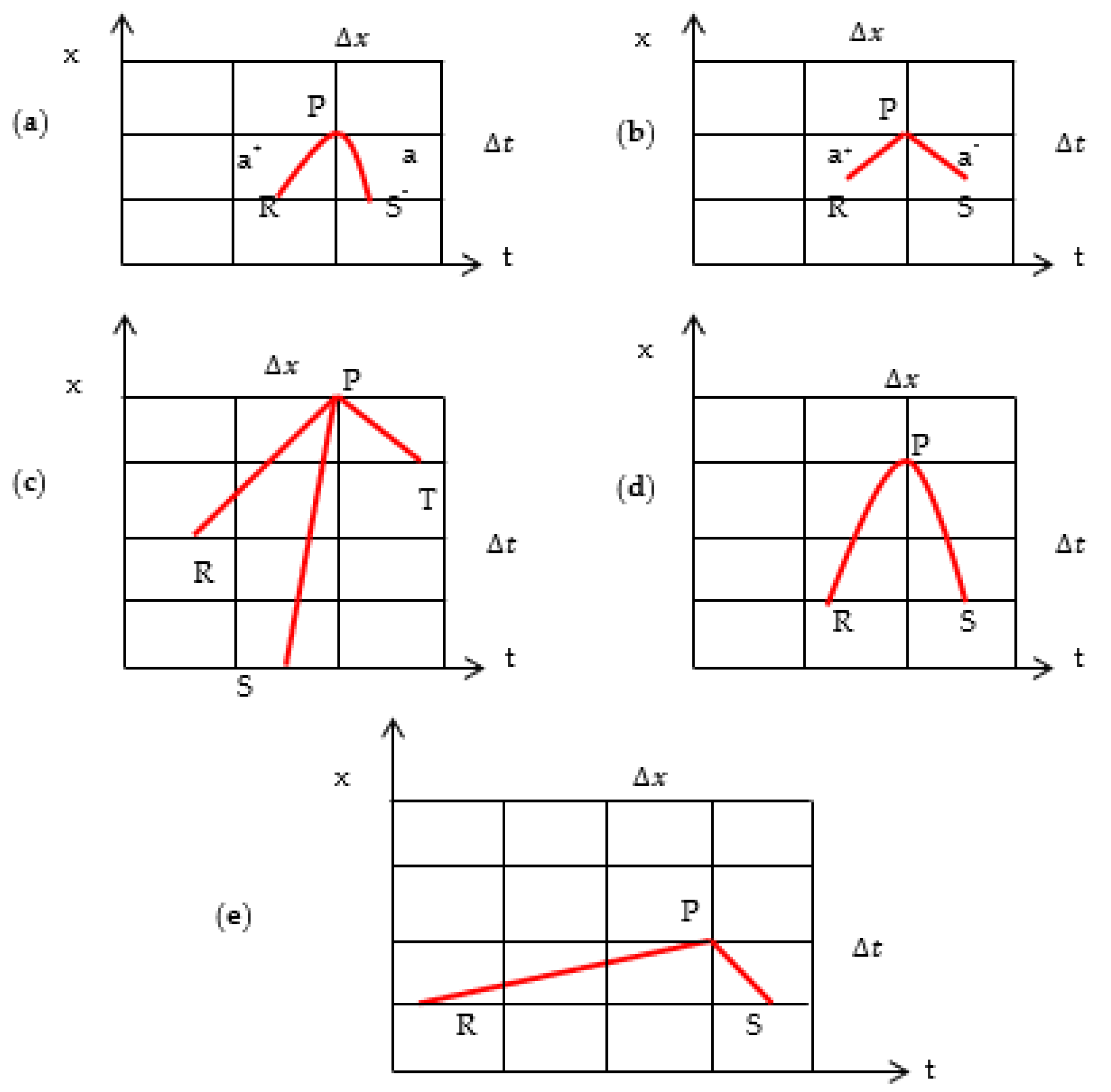
3.1. Limitations of MOC
- The MOC makes it difficult to include the convective acceleration term—a reality that can occasionally induce errors, particularly when the objective is to find a solution with = 1 [47].
- Conservation of momentum and mass cannot be ensured even if interpolation is not required.
- Overall, the MOC approach is best suited to systems with invariant celerity, since a condition of = 1 can be met.
- For = 1, explicit schemes are easy to program, and provide simpler solutions, whereas implicit schemes are more complex and computationally demanding to both code and execute [43]. The application of the explicit scheme is conditionally stable because of the source term, as discussed in Section 4.1, whereas the implicit scheme is unconditionally stable. Despite the popularity of explicit and implicit schemes, such approaches are often computationally inaccurate when used with larger spatial steps or conduits with variable cross-sectional areas [43].
3.2. Need for Improved Numerical Methods
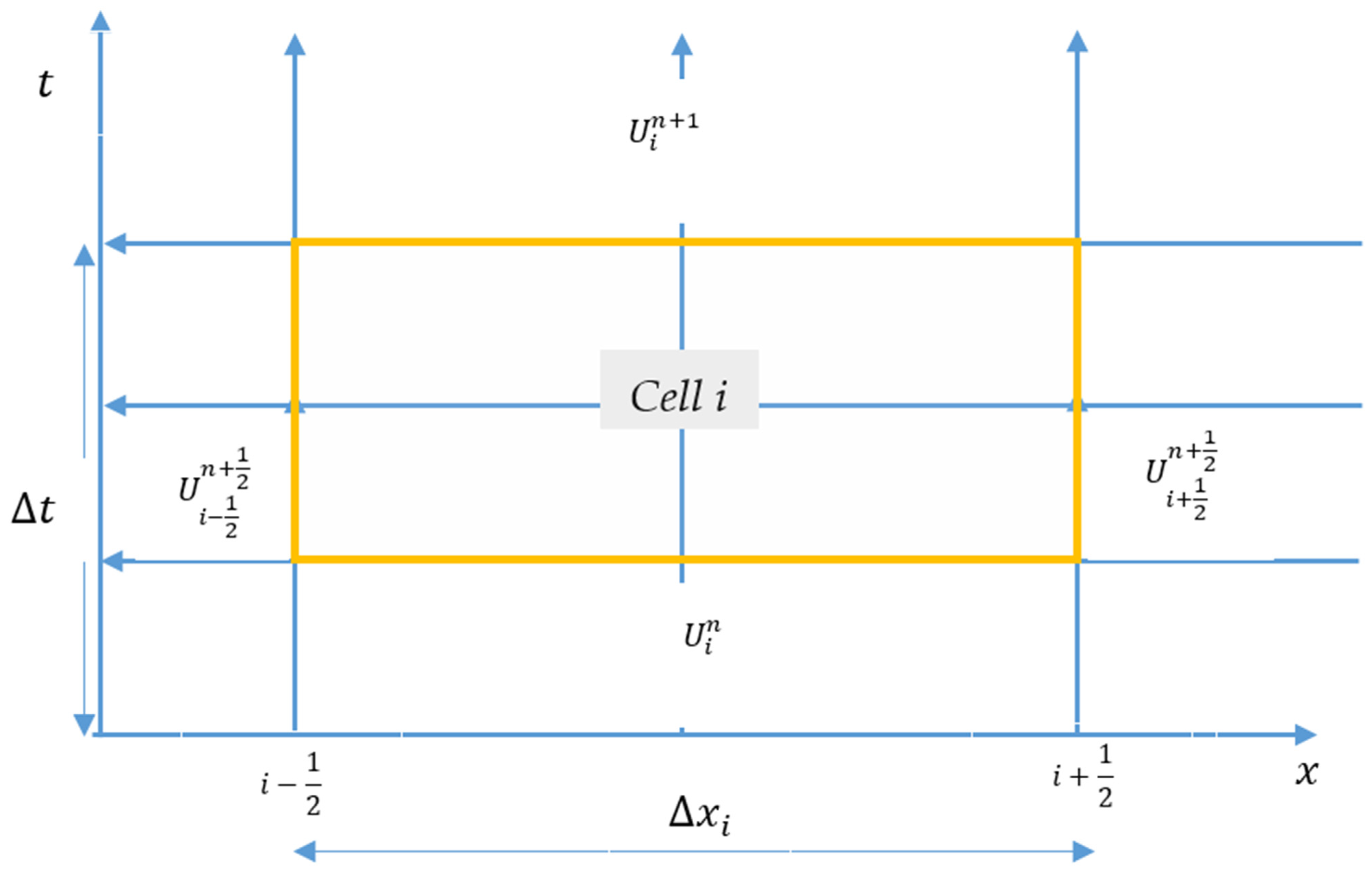
4. The Finite Volume Method (FVM)
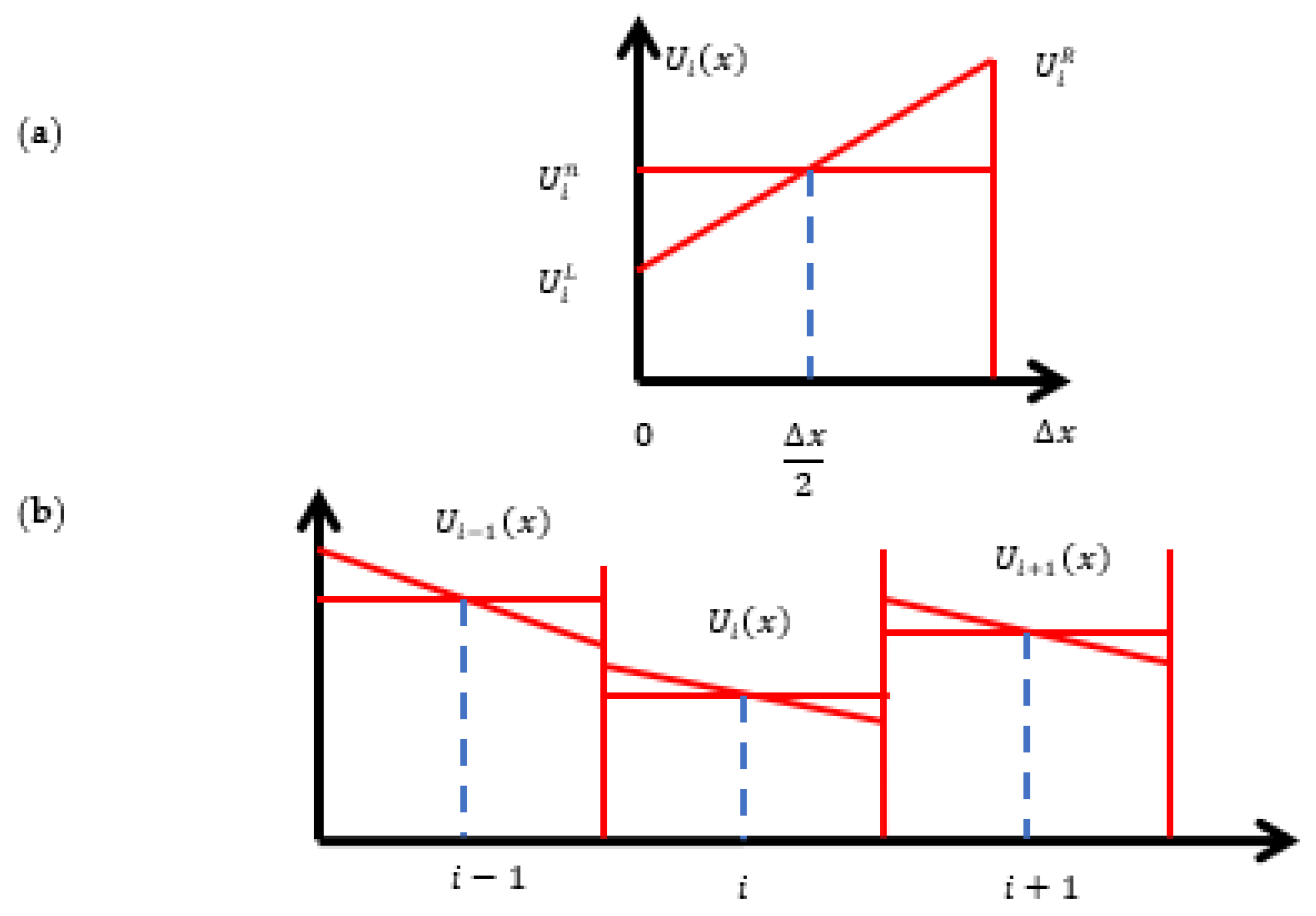
4.1. Finite Volume Method (FVM) Numerical Procedure
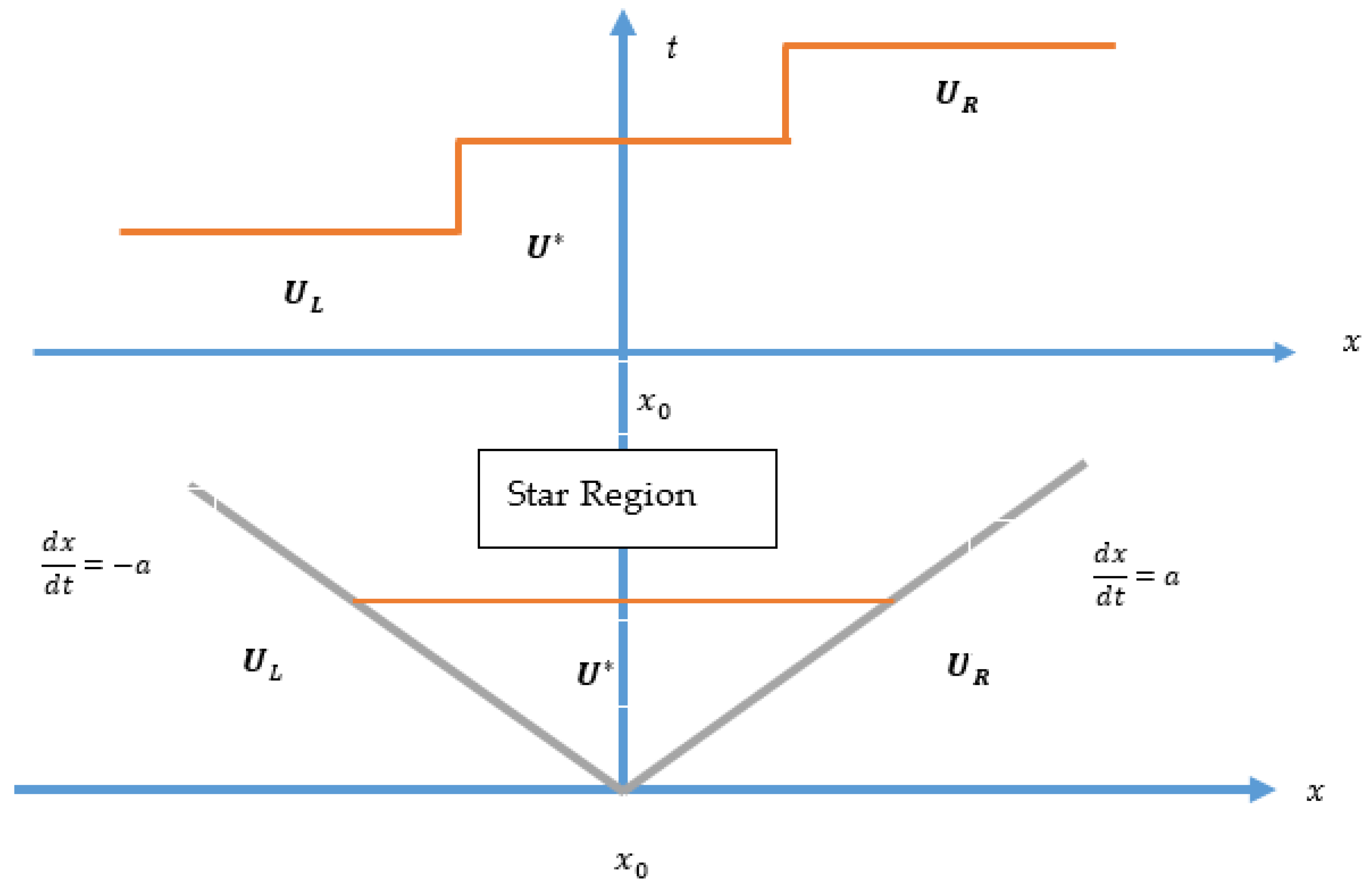
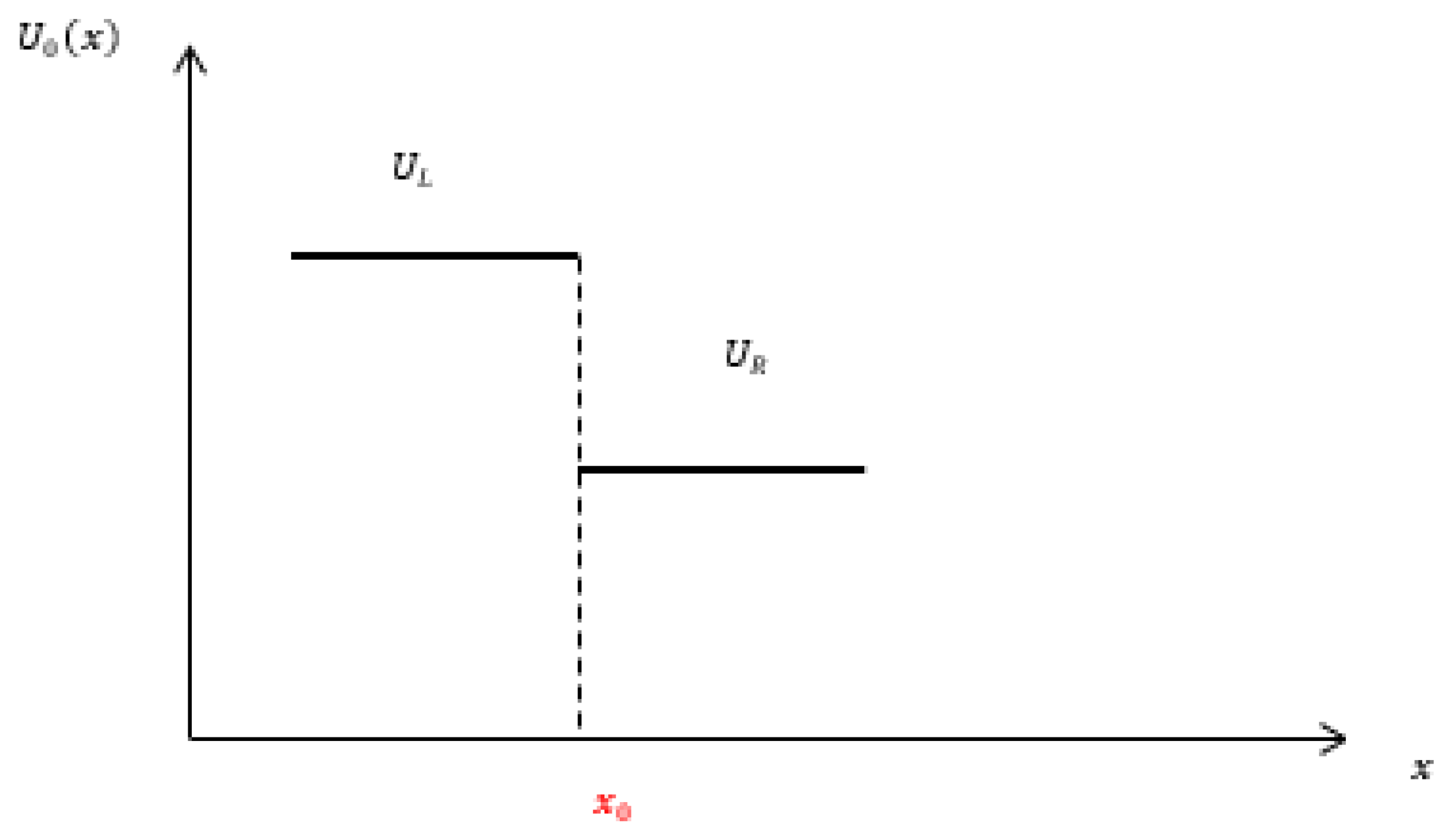
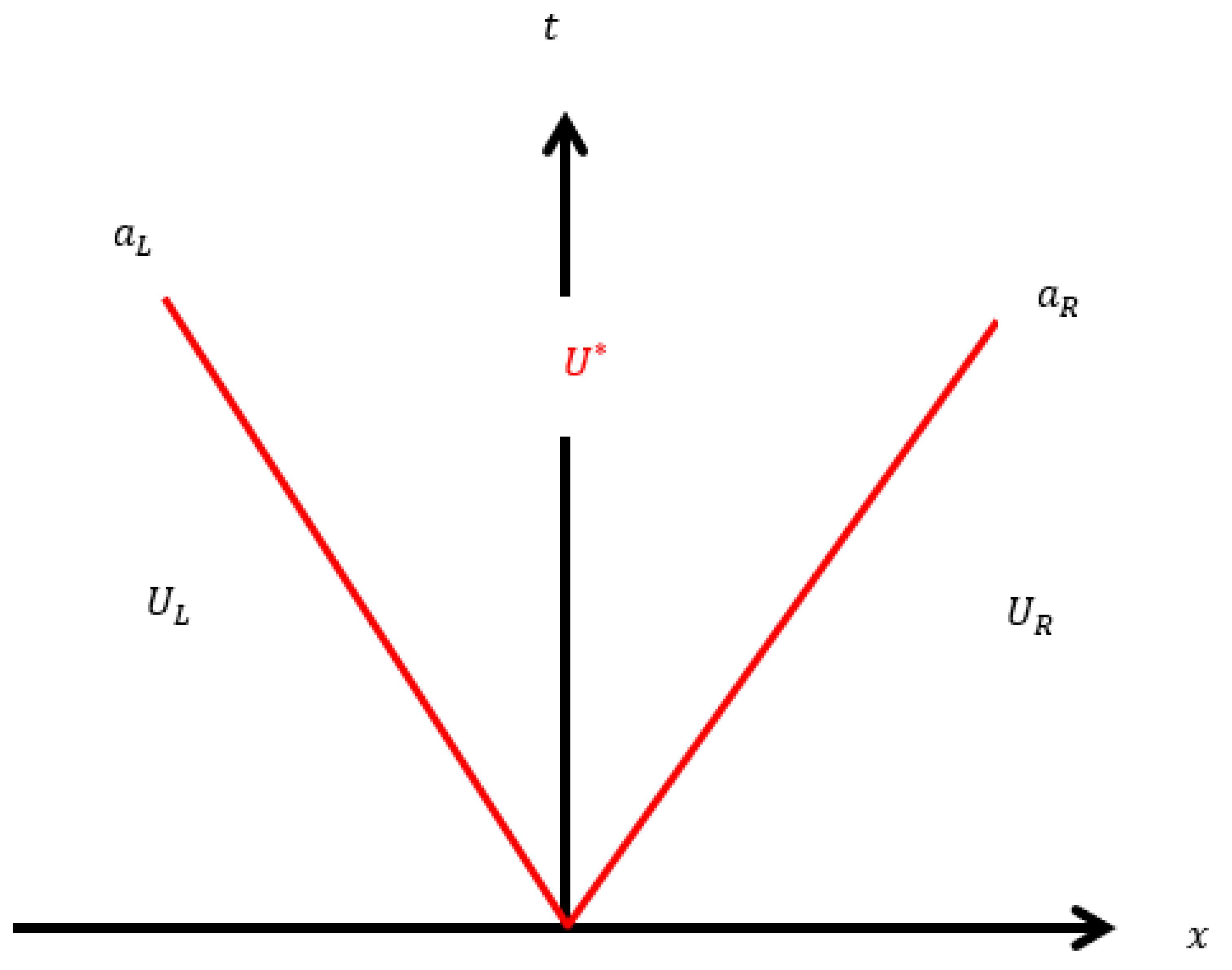
4.1.1. Approximate Riemann Solvers
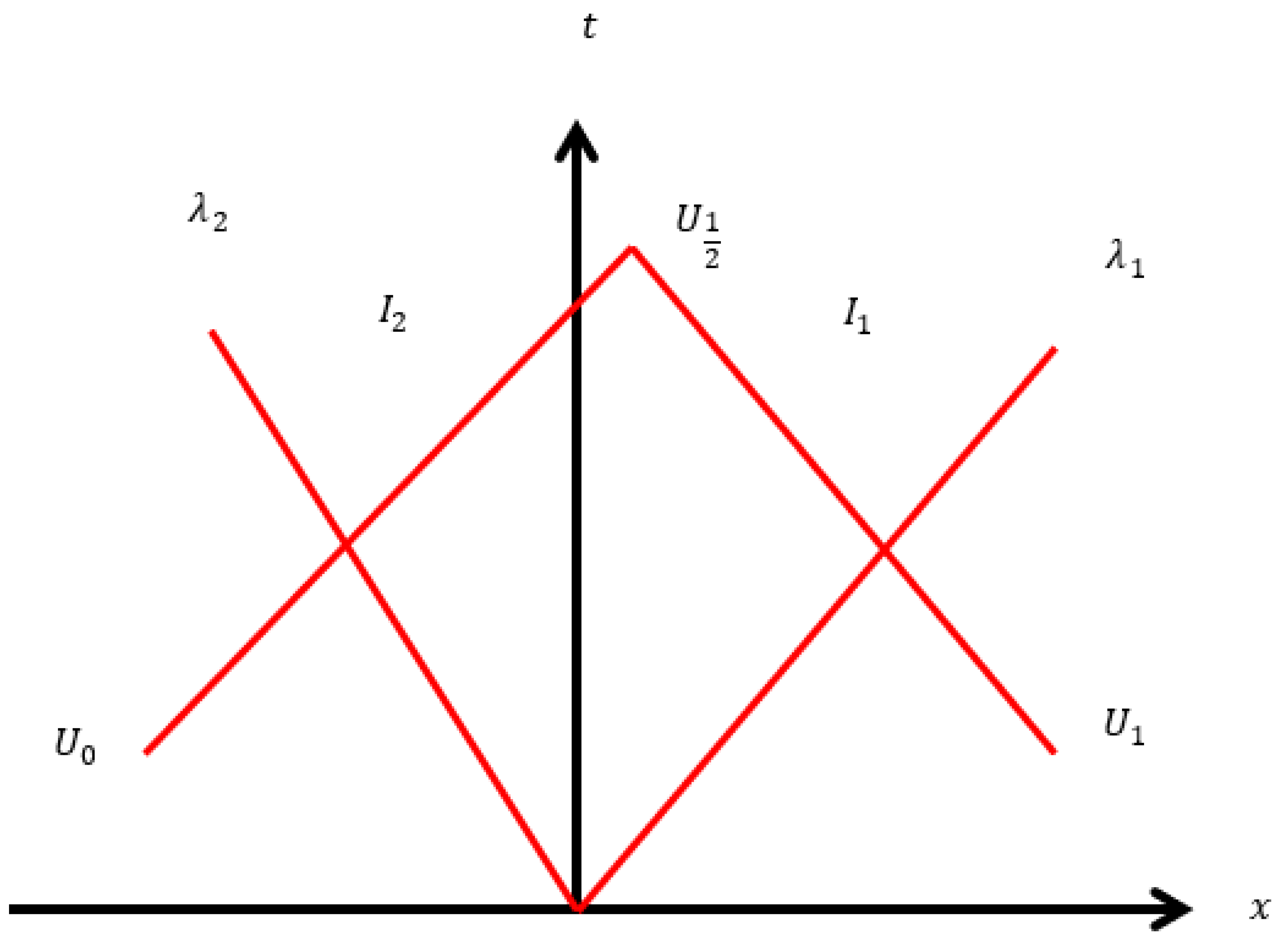
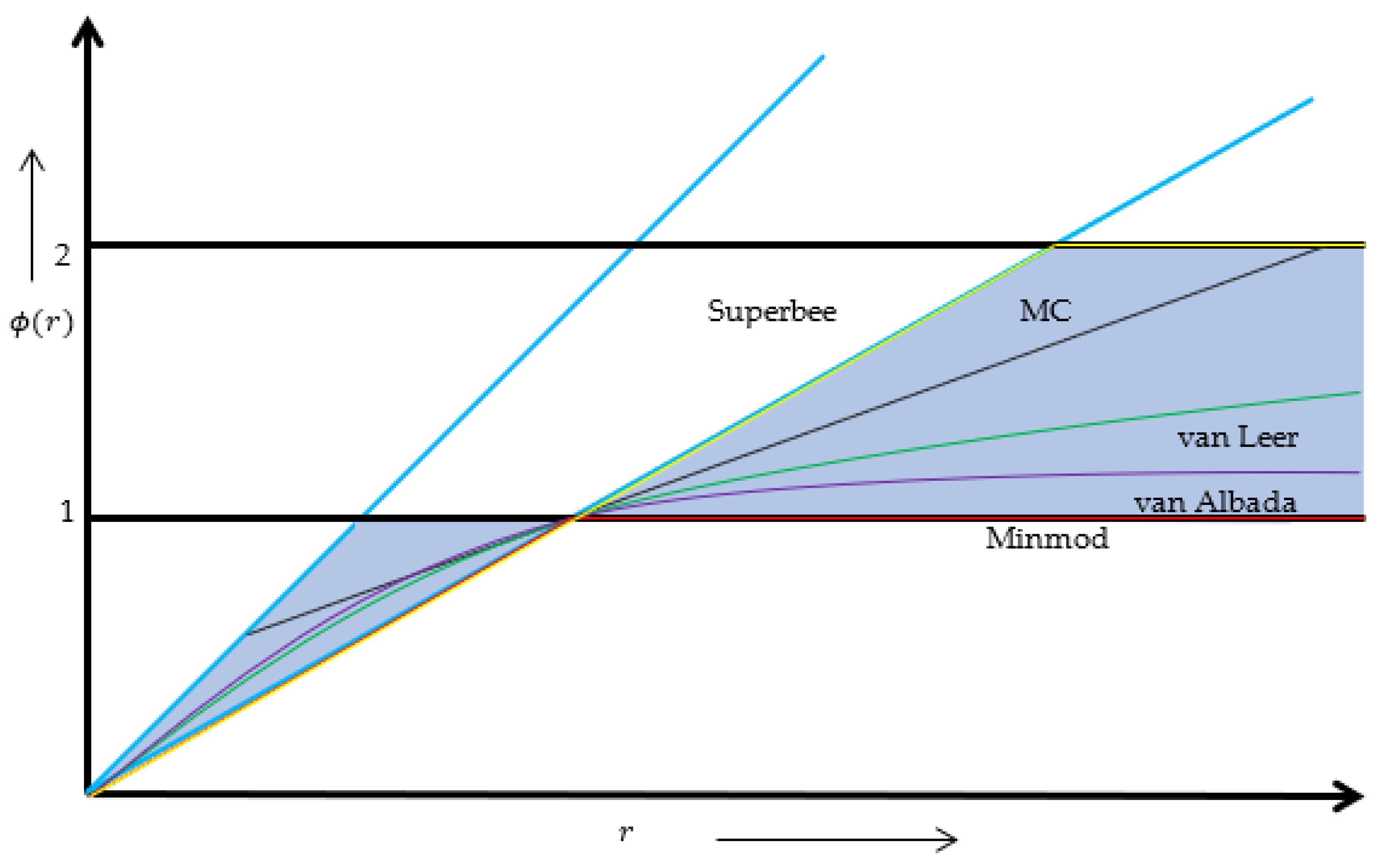
Limiters
4.1.2. Flux Vector Splitting (Boltzmann Approach)
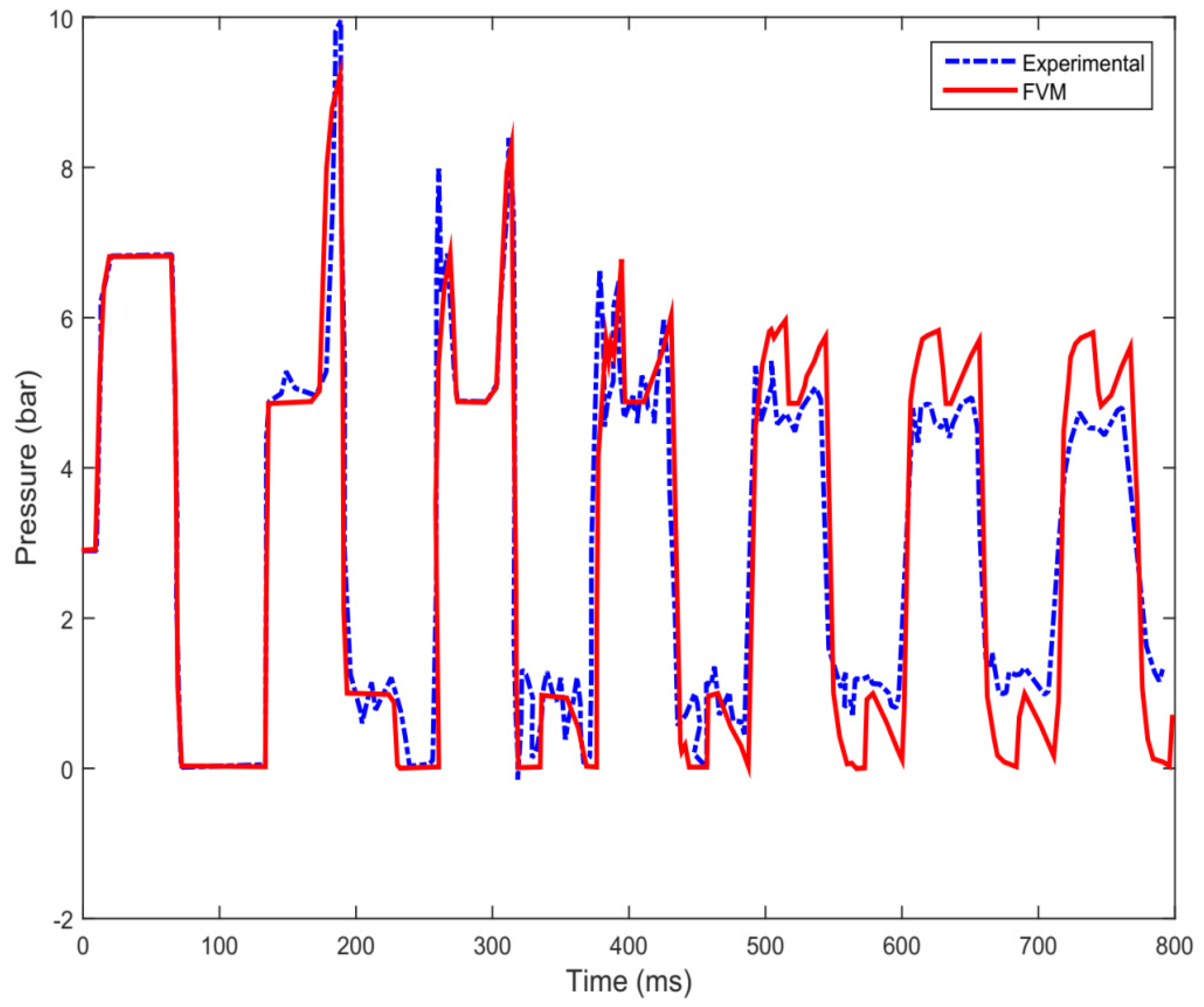
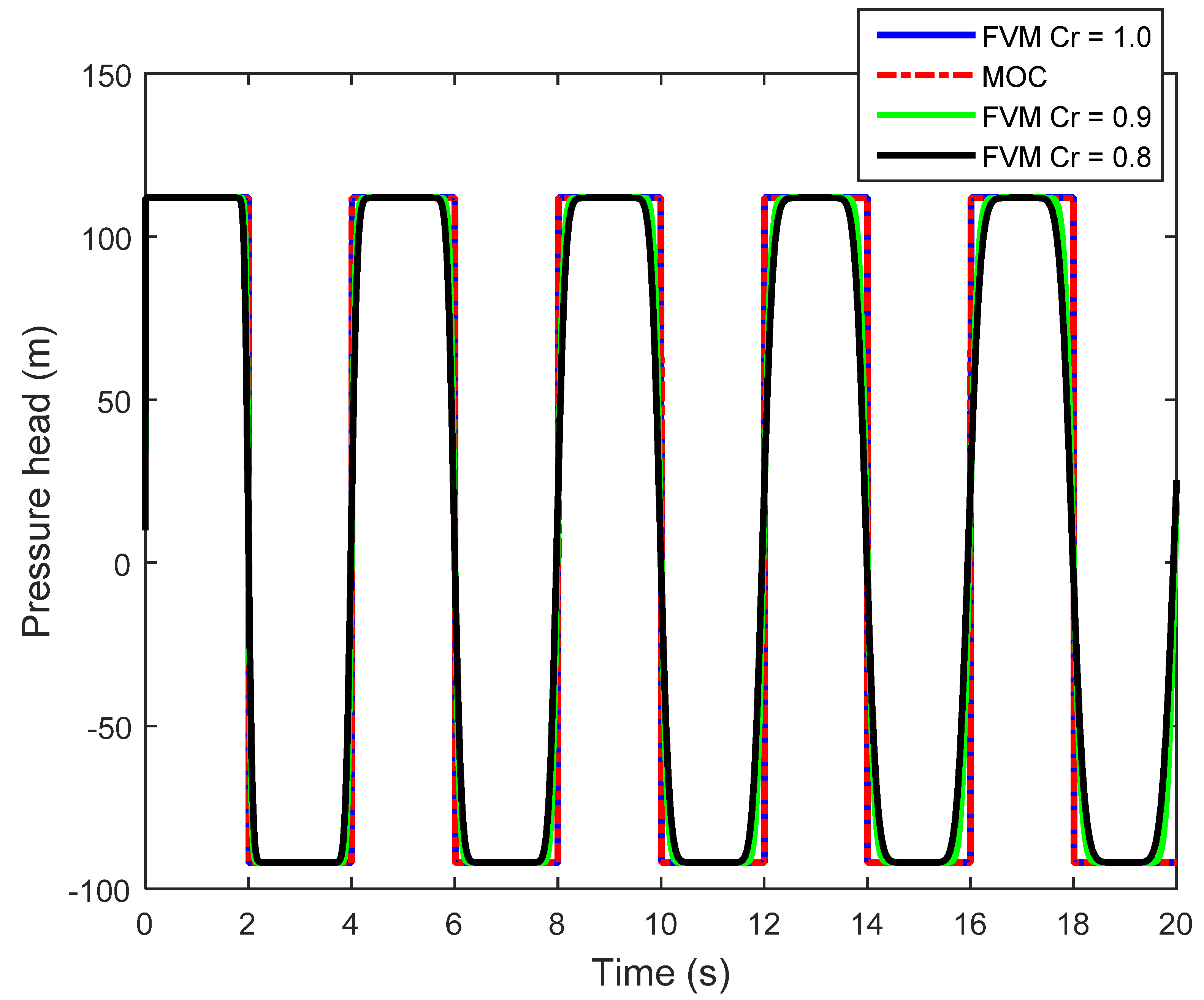
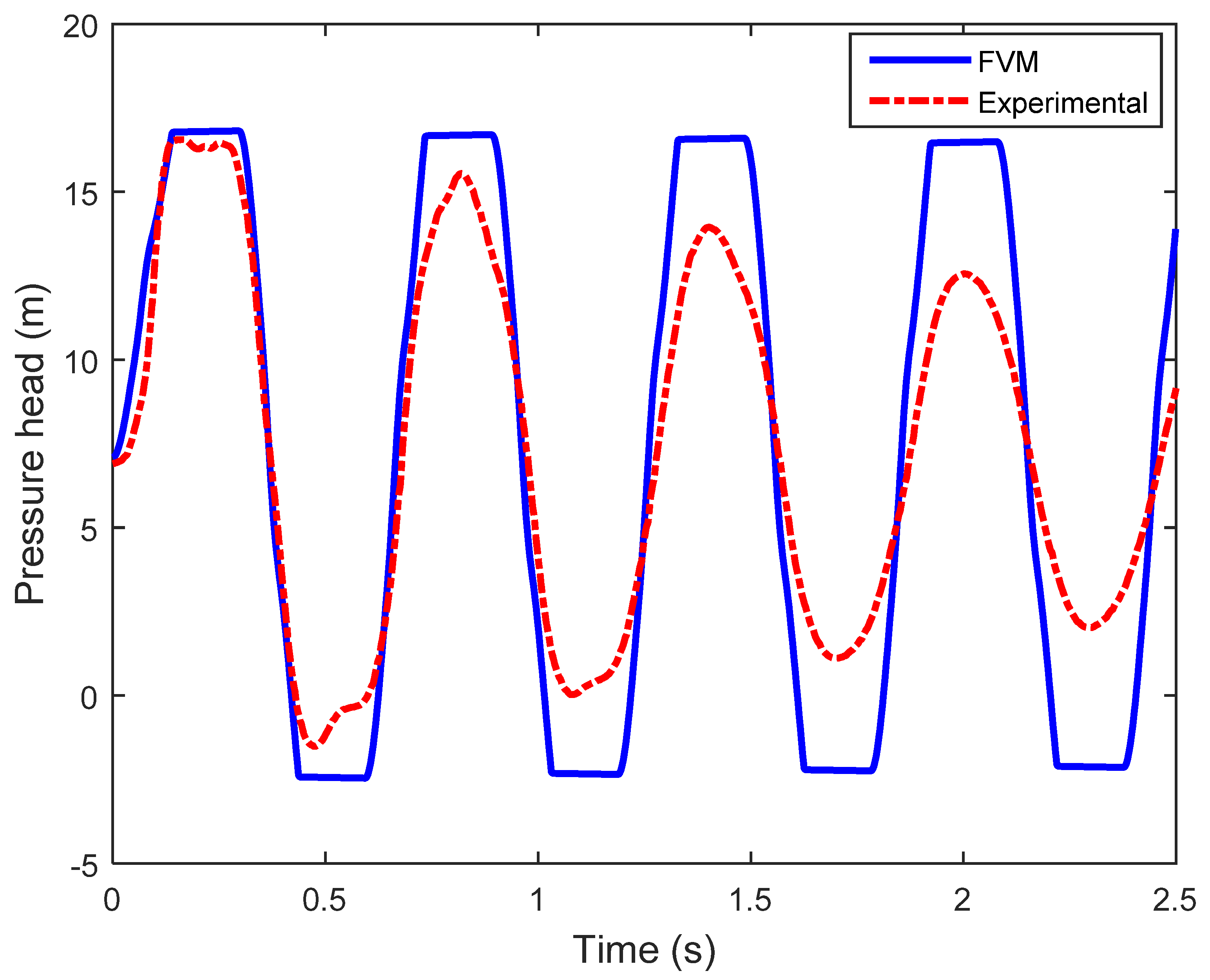
4.2. Finite Volume Method (FVM) Applications
5. Two-Phase Flow
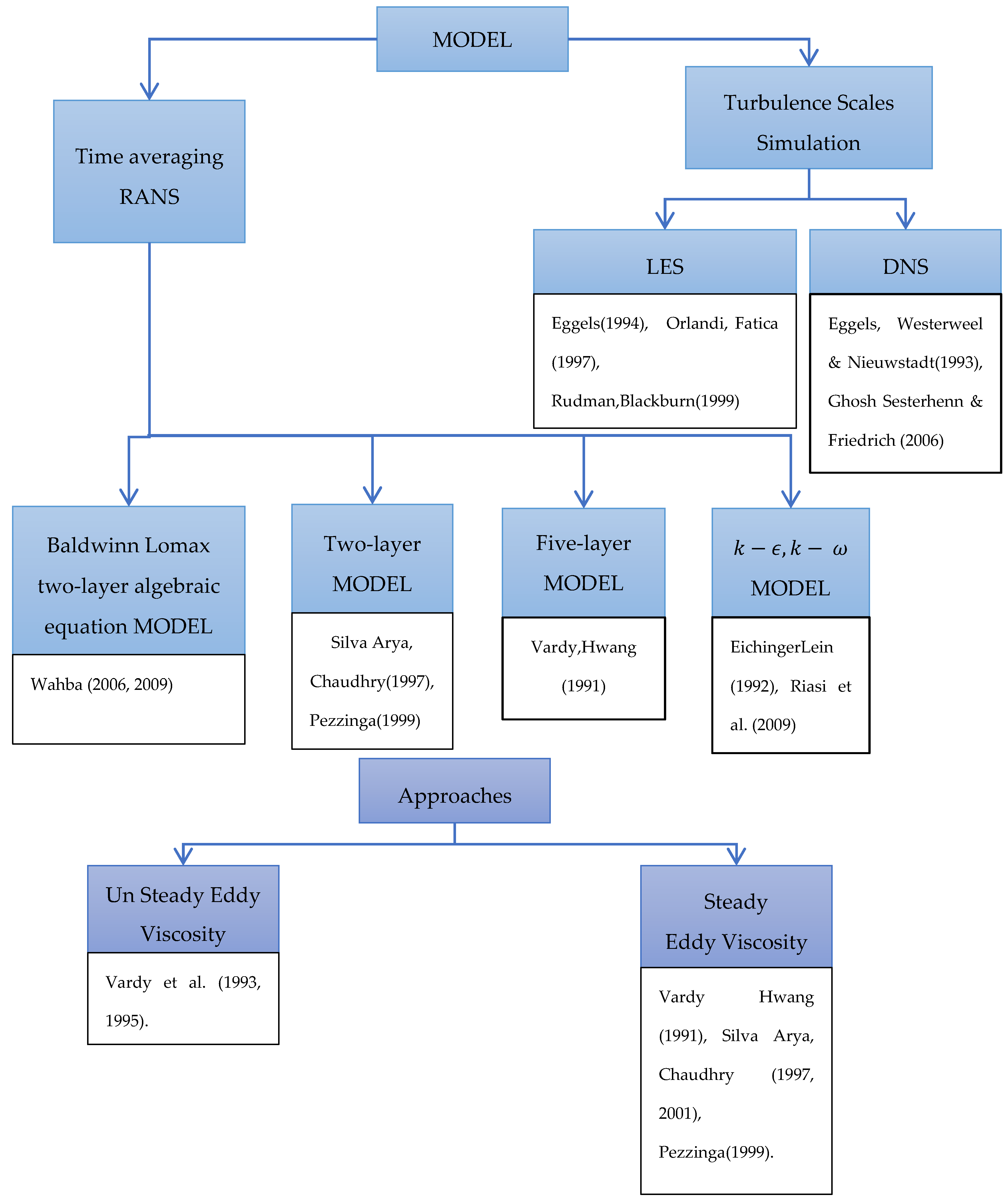
6. Development of Other Approaches
6.1. CFD Schemes
6.2. Lagrangian-Based Numerical Methods
6.3. Two-Dimensional Numerical Schemes
6.4. Modelling of Unsteady Flows in Pipe Networks
7. Future Research Directions for Water Hammer Modelling
8. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin, Germany, 1997. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Chaudhry, H.M. Applied Hydraulic Transients; Springer: New York, NY, USA, 2014. [Google Scholar]
- Joukowsky, N. Über den hydraulischen Stoss in Wasserleitungsro¨hren. (On the hydraulic hammer in water supply pipes.), Me´moires de l’Acade´mie Impe´riale des Sciences de St.-Petersbourg. 1900. Available online: https://www.win.tue.nl/analysis/reports/rana06-08.pdf (accessed on 1 June 2021).
- Allievi, L. General theory of pressure variation in Pipes. Ann. d. Ing. Archit. 1902, 17, 285–325. [Google Scholar]
- Streeter, V.L.; Lai, C. Water-Hammer Analysis Including Fluid Friction. J. Hydraul. Div. 1962, 88, 79–112. [Google Scholar] [CrossRef]
- Fox, J.A. Hydraulic Analysis and Unsteady Flow in Pipe Networks; MacMillan Press: London, UK, 1977. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Guinot, V. Riemann solvers for water hammer simulations by Godunov method. Int. J. Numer. Methods Eng. 2000, 49, 851–870. [Google Scholar] [CrossRef]
- Guinot, V. Wave Propagation in Fluids: Models and Numerical Techniques; ISTE Ltd.: London, UK; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; ISBN 978-1-84821-213-8. [Google Scholar]
- Guinot, V. Numerical simulation of two-phase flow in pipes using Godunov method. Int. J. Numer. Methods Eng. 2001, 50, 1169–1189. [Google Scholar] [CrossRef]
- Vardy, A.E.; Hwang, K.-L. A characteristics model of transient friction in pipes. J. Hydraul. Res. 1991, 29, 669–684. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Inc.: La Canada, CA, USA, 1998. [Google Scholar]
- Pezzinga, G. Quasi-2D Model for Unsteady Flow in Pipe Networks. J. Hydraul. Eng. 1999, 125, 676–685. [Google Scholar] [CrossRef]
- Duan, H.-F.; Pan, B.; Wang, M.; Chen, L.; Zheng, F.; Zhang, Y. State-of-the-art review on the transient flow modeling and utilization for urban water supply system (UWSS) management. J. Water Supply Res. Technol. 2020, 69, 858–893. [Google Scholar] [CrossRef]
- Hanmaiahgari, P.R.; Maji, S. Eddy Viscosity Turbulence Model for Incompressible Fluid Flow in Closed Conduits. In Proceedings of the 19th IAHR-APD Congress, Hanoi, Vietnam, 21–24 September 2014. [Google Scholar]
- Silva-Araya, W.F.; Chaudhry, M.H. Computation of Energy Dissipation in Transient Flow. J. Hydraul. Eng. 1997, 123, 108–115. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rohani, M. Water hammer simulation by implicit method of characteristic. Int. J. Press. Vessel. Pip. 2008, 85, 851–859. [Google Scholar] [CrossRef]
- Gray, C.A.M. The Analysis of the Dissipation of Energy in Water Hammer. Proc. ASCE 1953, 79, 1176. [Google Scholar]
- Lister, M. The numerical solutions of hyperbolic partial differential equations by the method of characteristics. In Mathematical Methods for Digital Computers; Ralston, A., Wild, H.S., Eds.; John Wiley: New York, NY, USA, 1960; pp. 165–179. [Google Scholar]
- Lai, C. A Study of Water Hammer Including Effect of Hydraulic Losses. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 1961. [Google Scholar]
- Streeter, V.L. Valve Stroking to Control Water Hammer. J. Hydraul. Div. 1963, 89, 39–66. [Google Scholar] [CrossRef]
- Perkins, F.E.; Tedrow, A.C.; Eagleson, P.S.; Ippen, A.T. Hydro-Power Plant Transients, Part II; Report No. 71; Department of Civil Engineering, School of Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 1964. [Google Scholar]
- Vardy, A.E. On the use of the method of characteristics for the solution of unsteady flows in networks. In Proceedings of the 2nd International Conference on Pressure Surges, BHRA Fluid Engineering, City University, London, UK, 22–24 September 1976. [Google Scholar]
- Wiggert, D.C.; Sundquist, M.J. Fixed-Grid Characteristics for Pipeline Transients. J. Hydraul. Div. 1977, 103, 1403–1416. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Wylie, E.B. Characteristics method using time-line interpolation. J. Hydraul. Eng. 1983, 109, 670–683. [Google Scholar] [CrossRef]
- Lai, C. Comprehensive Method of Characteristics Models for Flow Simulation. J. Hydraul. Eng. 1988, 114, 1074–1097. [Google Scholar] [CrossRef]
- Sibetheros, I.A.; Holley, E.R.; Branski, J.M. Spline Interpolations for Water Hammer Analysis. J. Hydraul. Eng. 1991, 117, 1332–1351. [Google Scholar] [CrossRef]
- Ames, W.F. Numerical Methods for Partial Differential Equations, 3rd ed.; eBook; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 9780080571300. [Google Scholar]
- Ghidaoui, M.S.; Karney, B.W. Equivalent Differential Equations in Fixed?Grid Characteristics Method. J. Hydraul. Eng. 1994, 120, 1159–1175. [Google Scholar] [CrossRef]
- Karney, B.W.; Ghidaoui, M.S. Flexible Discretization Algorithm for Fixed-Grid MOC in Pipelines. J. Hydraul. Eng. 1997, 123, 1004–1011. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Karney, B.W.; McInnis, D.A. Energy Estimates for Discretization Errors in Water Hammer Problems. J. Hydraul. Eng. 1998, 124, 384–393. [Google Scholar] [CrossRef]
- Shimada, M.; Brown, J.; Leslie, D.; Vardy, A. Time-Line Interpolation Errors in Pipe Networks. J. Hydraul. Eng. 2006, 132, 294–306. [Google Scholar] [CrossRef]
- Shimada, M.; Brown, J.M.B.; Vardy, A.E. Estimating friction errors in MOC analysis of unsteady pipe flows. Comput. Fluids 2007, 36, 1235–1246. [Google Scholar] [CrossRef]
- Shimada, M.; Brown, J.M.B.; Vardy, A.E. Interpolation errors in rectangular and diamond characteristic grids. J. Hyd. Eng. 2008, 134, 1480–1490. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A Review of Water Hammer Theory and Practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Tian, W.; Su, G.; Wang, G.; Qiu, S.; Xiao, Z. Numerical simulation and optimization on valve-induced water hammer characteristics for parallel pump feedwater system. Ann. Nucl. Energy 2008, 35, 2280–2287. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vítkovský, J.P.; Covas, D.I.; Simpson, A.R.; Lambert, M.F. Parameters affecting water-hammer wave attenuation, shape and timing- part 1. J. Hydraul. Res. 2008, 46, 373–381. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vítkovský, J.P.; Covas, D.I.; Simpson, A.R.; Lambert, M.F. Parameters affecting water-hammer wave attenuation, shape and timing-part 2. J. Hydraul. Res. 2008, 46, 382–391. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R. Interface model for transient cavitating flow in pipelines. In Unsteady Flow and Fluid Transients; IAHR: Graz, Austria, 1992; pp. 333–342. [Google Scholar]
- Bergant, A.; Simpson, A.R. Cavitation inception in pipeline column separation. In Proceedings of the 28th IAHR Congress, Graz, Austria, 22–27 August 1999; p. 7. [Google Scholar]
- Sadafi, M.; Riasi, A.; Nourbakhsh, S.A. Cavitating flow during water hammer using a generalized interface vaporous cavitation model. J. Fluids Struct. 2012, 34, 190–201. [Google Scholar] [CrossRef]
- Wang, C.; Yang, J.-D. Water Hammer Simulation Using Explicit–Implicit Coupling Methods. J. Hydraul. Eng. 2015, 141, 04014086. [Google Scholar] [CrossRef]
- Jang, T.U.; Wu, Y.; Xu, Y.; Newman, J.; Sun, Q. Efficient Quasi-Two-Dimensional Water Hammer Model on a Characteristic Grid. J. Hydraul. Eng. 2016, 142, 06016019. [Google Scholar] [CrossRef]
- Li, C.W.; Yu, T.S. Conservative Characteristics?Based Schemes for Mass Transport. J. Hydraul. Eng. 1994, 120, 1089–1099. [Google Scholar] [CrossRef]
- Guinot, V. Boundary Condition Treatment in 2 × 2 Systems of Propagation Equations. Int. J. Numer. Methods Eng. 1998, 42, 647–666. [Google Scholar] [CrossRef]
- Zhang, B.; Wan, W.; Shi, M. Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment. Water 2018, 10, 928. [Google Scholar] [CrossRef]
- Godunov, S.K. A difference method for numerical calculation of discontinuous solutions of the equations of hydrodynamics. Mat. Sb. (N.S.) 1959, 47, 271–306. [Google Scholar]
- Guinot, V. Godunov-Type Schemes: An Introduction for Engineers; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley Ltd.: Chichester, UK, 2001. [Google Scholar]
- Zhao, M.; Ghidaoui, M.S. Godunov-Type Solutions for Water Hammer Flows. J. Hydraul. Eng. 2004, 130, 341–348. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Guo, S. Godunov-Type Solutions with Discrete Gas Cavity Model for Transient Cavitating Pipe Flow. J. Hydraul. Eng. 2018, 144, 04018017. [Google Scholar] [CrossRef]
- Pal, S.; Hanmaiahgari, P.R.; Lambert, M.F. Efficient approach toward the application of the Godunov method to hydraulic transients. J. Hydroinformatics 2020, 22. [Google Scholar] [CrossRef]
- Riemann, B. Über die Fortpflanzung Ebener Luftwellen von Endlicher Schwingungsweite. Abhandlungen der Königlichen Gesellschaft der Wissen-schaften in Göttingen 1860, 8, 43–66. Available online: http://eudml.org/doc/135717 (accessed on 2 June 2021).
- Toro, E.F. A Linearised Riemann Solver for the Time-Dependent Euler Equations of Gas Dynamics. Proc. Roy Soc. Lond. 1991, A434, 683–693. [Google Scholar]
- Toro, E.F. Direct Riemann solvers for the time-dependent Euler equations. Shock. Waves 1995, 5, 75–80. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; Van Leer, B. On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock. Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Roe, P.L.; Pike, J. Efficient Construction and Utilisation of Approximate Riemann Solutions. In Proc. of the Sixth Int’l. Symposium on Computing Methods in Applied Science and Engineering; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Engquist, B.; Osher, S. One-Sided Difference Approximations for Nonlinear Conservation Laws. Math. Comput. 1981, 36, 321–351. [Google Scholar] [CrossRef]
- Osher, S.; Solomon, F. Upwind Difference Schemes for Hyperbolic Systems of Conservation Laws. Math. Comput. 1982, 38, 339–374. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme III. Upstream–Centered Finite Difference Schemes for Ideal Compressible Flow. J. Comput. Phys. 1977, 23, 263–275. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme IV. A New Approach to Numerical Convection. J. Comput. Phys. 1977, 23, 276–299. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme V. A Second-Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Van Leer, B. On the Relation Between the Upwind–Differencing Schemes of Godunov, Enguist-Osher and Roe. SIAM J. Sci. Stat. Comput. 1985, 5, 1–20. [Google Scholar] [CrossRef]
- Sweby, P.K. High Resolution Schemes Using Flux Limiters for Hyperbolic Conservation Laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Woodward, P.; Colella, P. The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comput. Phys. 1984, 54, 115–173. [Google Scholar] [CrossRef]
- Colella, P.; Woodward, P.R. The Piecewise Parabolic Method (PPM) for Gas Dynamical Simulation. J. Comput. Phys. 1984, 54, 174–201. [Google Scholar] [CrossRef]
- Rajamäki, M.; Saarinen, M. Numerical study of withdrawal and return of water following a volcanic eruption at sea. Commun. Numer. Methods Eng. 1994, 10, 461–468. [Google Scholar] [CrossRef]
- Coquel, F.; Postel, M.; Tran, Q.N. Convergence of time-space adaptive algorithms for nonlinear conservation laws. IMA J. Numer. Anal. 2012, 32, 1440–1483. [Google Scholar] [CrossRef]
- Boris, J.P.; David, L. Flux-corrected transport, I: SHASTA, a fluid transport algorithm that works. J. Comp. Phys. 1973, 11, 38. [Google Scholar] [CrossRef]
- Hwang, Y.-H.; Chung, N.-M. A fast Godunov method for the water-hammer problem. Int. J. Numer. Methods Fluids 2002, 40, 799–819. [Google Scholar] [CrossRef]
- Szydlowski, M. Two Dimensional Shallow Water Model for Rapidly and Gradually Varied Flow. Hydro-Eng. Environ. Mech. 2001, 48, 35–61. [Google Scholar]
- Szydlowski, M. Finite Volume Method for Water Hammer Simulation; TiASWiK’02; Gdańsk–Sobieszewo: Gdańsk, Poland, 2002; pp. 159–165. [Google Scholar]
- Sanders, R.H.; Prendergast, K.H. On the Origin the Three Kiloparsec. Arm. Astrophys. J. 1974, 18, 489–500. [Google Scholar] [CrossRef]
- Steger, J.L.; Warming, R. Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods. J. Comput. Phys. 1981, 40, 263–293. [Google Scholar] [CrossRef]
- Van Leer, B. Flux–Vector Splitting for the Euler Equations. In Technical Report ICASE 82–30; NASA Langley Research Center: Hampton, VA, USA, 1982. [Google Scholar]
- Van Leer, B. Flux Vector Splitting for the Euler Equations. In Proceedings of the 8th International Conference on Numerical Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1982; pp. 507–512. [Google Scholar]
- Zhao, M.; Ghidaoui, M.S. Efficient Quasi-Two-Dimensional Model for Water Hammer Problems. J. Hydraul. Eng. 2003, 129, 1007–1013. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Karney, B.; Cheng, Y.; Liu, D. Godunov-Type Solutions for Transient Pipe Flow Implicitly Incorporating Brunone Unsteady Friction. J. Hydraul. Eng. 2021, 147, 04021021. [Google Scholar] [CrossRef]
- Yazdi, S.R.S.; Mastorakis, N.E.; Abbasi, A. Water hammer modelling by Godunov type finite Volume Method. Int. J. Math. Com. Sim. 2007, 1, 350–355. [Google Scholar]
- León, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. Efficient Second-Order Accurate Shock-Capturing Scheme for Modeling One- and Two-Phase Water Hammer Flows. J. Hydraul. Eng. 2008, 134, 970–983. [Google Scholar] [CrossRef]
- León, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. Application of Godunov-type schemes to transient mixed flows. J. Hydraul. Res. 2009, 47, 147–156. [Google Scholar] [CrossRef]
- Kerger, F.; Archambeau, P.; Erpicum, S.; Dewals, B.; Pirotton, M. An exact Riemann solver and a Godunov scheme for simulating highly transient mixed flows. J. Comput. Appl. Math. 2011, 235, 2030–2040. [Google Scholar] [CrossRef]
- Preissmann, A. Propagation des intumescences dans les canaux et rivieres. In Proceedings of the 1st Congress of the French Association for Computation, Grenoble, France, 14–16 September 1961; pp. 433–442. [Google Scholar]
- Daude, F.S.; Tijsseling, A.S.; Galon, P. Numerical investigations of water-hammer with column-separation induced by vaporous cavitation using a one-dimensional Finite-Volume approach. J. Fluids Struct. 2018, 83, 91–118. [Google Scholar] [CrossRef]
- Reddy, H.P.; Silva-Araya, W.F.; Chaudhry, M.H. Estimation of Decay Coefficients for Unsteady Friction for Instantaneous, Acceleration-Based Models. J. Hydraul. Eng. 2012, 138, 260–271. [Google Scholar] [CrossRef]
- Prosperetti, A.; Tryggvason, G. Computational Methods for Multiphase Flow; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Taitel, Y.; Shoham, O.; Brill, J. Simplified transient solution and simulation of two-phase flow in pipelines. Chem. Eng. Sci. 1989, 44, 1353–1359. [Google Scholar] [CrossRef]
- Minami, K.; Shoham, O. Transient two-phase flow behaviour in pipelines-experiment and modelling. Int. J. Multiph. 1994, 20, 739–752. [Google Scholar] [CrossRef]
- Li, M. Transient Two-Phase Flow Modeling. In 76th Semi-Annual Advisory Board Meeting Brochure and Presentation; Tulsa University Fluid Flow Projects: Oklahoma, OK, USA, 2010. Available online: https://www.bsee.gov/sites/bsee.gov/files/tap-technical-assessment-program//302ah.pdf (accessed on 1 June 2021).
- Choi, J.; Pereyra, E.; Sarica, C.; Lee, H.; Jang, I.S.; Kang, J. Development of a fast transient simulator for gas–liquid two-phase flow in pipes. J. Pet. Sci. Eng. 2013, 102, 27–35. [Google Scholar] [CrossRef]
- Oloruntoba, O.; Kara, F. Simplified transient two-phase model for pipe flow. Int. J. Modn. Eng. 2017, 17, 5–12, Spring/Summer 2017. [Google Scholar]
- Cheung, H.S.; Khan, H.J.; Rothagi, U.S. Simulation of SBWR Start-Up Transient and Stability. 1998. BNL-65535. Available online: https://digital.library.unt.edu/ark:/67531/metadc702243/ (accessed on 1 June 2021).
- Elicson, G.T.; Henry, R.E.; Hammersley, R.J.; Burelbach, J.P. Dynamic Benchmarking of TREMOLO--A Program for Pipe Line TwoPhase Flow Transient Analysis. In Proceedings of the 9th International Topical Meeting on Nuclear Reactor Thermal-Hydraulics (NURETH-9), San Francisco, CA, USA, 3–8 October 1999. [Google Scholar]
- Tiselj, I.; Cerne, G. Some Comments on the behaviour of RELAP5 numerical scheme at very small time step. Nucl. Sci. Eng. 2000, 134, 3. [Google Scholar] [CrossRef]
- Marcel, C.P.; Rohde, M.; Van Der Hagen, T. Experimental and numerical investigations on flashing-induced instabilities in a single channel. Exp. Therm. Fluid Sci. 2009, 33, 1197–1208. [Google Scholar] [CrossRef]
- Lakshmanan, S.; Pandey, M.; Kumar, P.P.; Iyer, K.N. Study of startup transients and power ramping of natural circulation boiling systems. Nucl. Eng. Des. 2009, 239, 1076–1083. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Z.; Lei, W. Capability of RELAP5 code to simulate the thermal-hydraulic characteristics of open natural circulation. Ann. Nucl. Energy 2017, 109, 612–625. [Google Scholar] [CrossRef]
- Lyczkowski, R.W.; Gidaspow, D.; Solbrig, C.W.; Hughes, E.D. Characteristics and Stability Analyses of Transient One-Dimensional Two-Phase Flow Equations and Their Finite Difference Approximations. Nucl. Sci. Eng. 1978, 66, 378–396. [Google Scholar] [CrossRef]
- Tiselj, I.; Petelin, S. Modelling of two-phase flow with second-order accurate scheme. J. Comput. Phys. 1997, 136, 503–521. [Google Scholar] [CrossRef]
- Melikhov, O.; Melikhov, V.; Parfenov, Y.; Davydov, M. Modeling of Water Hammer in a Vertical Tube with WAHA code. In Proceedings of the International Conference Nuclear Energy for New Europe, Portorož, Slovenia, 11 September 2008; pp. 1–7. [Google Scholar]
- Gale, J.; Tiselj, I.; Horvat, A. Two-fluid model of the Waha code for simulations of water hammer transients. Multiph. Sci. Technol. 2008, 20, 291–322. [Google Scholar] [CrossRef]
- Wood, D.J.; Lingireddy, S.; Boulos, P.F.; Karney, B.W.; McPherson, D.L. Numerical methods for modeling transient flow in distribution systems. J. Am. Water Work. Assoc. 2005, 97, 104–115. [Google Scholar] [CrossRef]
- Verwey, A.; Yu, J.H. A space-compact high-order implicit scheme for water hammer simulations. In Proceedings of the XXVth IAHR, Tokyo, Japan, 30 August–9 September 1993; pp. 363–370. [Google Scholar]
- Chen, T.; Ren, Z.; Xu, C.; Loxton, R. Optimal Boundary Control for Water Hammer Suppression in Fluid Transmission Pipelines. Comput. Math. Appl. 2015, 69, 275–290. [Google Scholar] [CrossRef]
- Szymkiewicz, R.; Mitosek, M. Analysis of unsteady pipe flow using the modified finite element method. Commun. Numer. Methods Eng. 2004, 21, 183–199. [Google Scholar] [CrossRef]
- Ruprecht, A.; Helmrich, T. Simulation of the water hammer in a hydropower plant caused by draft tube surge. In Proceedings of the 4th ASME/JSME Joint Fluids Engineering Conference, Honolulu, HI, USA, 6–10 July 2003. [Google Scholar]
- Yuan, Y.-F.; Fan, H.G.; Li, F.C. Study on three-dimensional flow in surge tank with consideration of pipeline property. J. Hydroelect. Eng. 2012, 31, 168–172. (In Chinese) [Google Scholar]
- Fan, S.; Lakshminarayana, B.; Barnett, M. Low-Reynolds-number k-epsilon model for unsteady turbulent boundary-layer flows. AIAA J. 1993, 31, 1777–1784. [Google Scholar] [CrossRef]
- Wu, D.; Liu, Q.; Wu, P. Simulations on dynamic characteristics of pump and pipe system during pumps and valves adjusting process. In Proceedings of the 26th IAHR, Symposium on Hydraulic Machinery and Systems, Beijing, China, 19–23 August 2012. [Google Scholar]
- Zhang, X.; Cheng, Y.G. Simulation of hydraulic transients in hydropower systems using the 1-D-3-D coupling approach. J. Hydrodyn. 2012, 24, 595–604. [Google Scholar] [CrossRef]
- Yan, J.; Koutnik, J.; Seidel, U.; Hübner, B. Compressible simulation of rotor-stator interaction in pump-turbines. In Proceedings of the 25th IAHR Symposium on Hydraulic Machinery and Systems, Timisoara, Romania, 20–24 September 2010. [Google Scholar]
- Yin, J.; Wang, D.; Wang, L.; Wu, Y. Effects of water compressibility on the pressure fluctuation prediction in pump turbine. In Proceeding of the 26th IAHR Symposium on Hydraulic Machinery and Systems, Beijing, China, 19–23 August 2012. [Google Scholar]
- Zhang, X.-X.; Cheng, Y.-G.; Yang, J.-D.; Xia, L.-S.; Lai, X. Simulation of the load rejection transient process of a francis turbine by using a 1-D-3-D coupling approach. J. Hydrodyn. 2014, 26, 715–724. [Google Scholar] [CrossRef]
- Cheng, Y.-G.; Zhang, S.-H.; Chen, J.-Z. Water hammer simulation by the Lattice Boltzmann method’, transactions of the Chinese hydraulic engineering society. J. Hydraul. Eng. 1998, 6, 25–31. (In Chinese) [Google Scholar]
- Wu, Y.; Chi, L.; Zhang, H. Study of resistance distribution and numerical modelling of water hammer in a long-distance water supply pipeline. In Proceedings of the 10th Annual Water Distribution Systems Analysis Conference, Kruger National Park, Limpopo and Mpumalanga, South Africa, 17–20 August 2008; American Society of Civil Engineers: Reston, VA, USA, 2008. [Google Scholar]
- Budinski, L. Application of the LBM with adaptive grid on water hammer simulation. J. Hydroinform. 2016, 18, 687–701. [Google Scholar] [CrossRef]
- Louati, M.; Tekitek, M.M.; Ghidaoui, M.S. On the dissipation mechanism of lattice Boltzmann method when modeling 1-d and 2-d water hammer flows. Comput. Fluids 2019, 193, 103996. [Google Scholar] [CrossRef]
- Hou, Q.; Zhang, L.X.; Tijsseling, A.; Kruisbrink, A. Rapid filling of pipelines with the SPH particle method. Procedia Eng. 2012, 31, 38–43. [Google Scholar] [CrossRef]
- Hou, D.Q.; Kruisbrink, A.C.H.; Tijsseling, A.S.; Keramat, A. Simulating Water Hammer with Corrective Smoothed Particle Method; CASA: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hou, D.Q.; Wang, A.C.; Kruisbrink, H.; Tijsseling, A.S. Lagrangian modelling of fluid transients in pipelines with entrapped air. In Proceedings of the 12th International conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015. BHR Group. [Google Scholar]
- Eichinger, P.; Lein, G. The Influence of Friction on Unsteady Pipe Flow. In Bettess and Watts; Balkema: Rotterdam, The Netherlands, 1992; pp. 41–50. [Google Scholar]
- Silva-Araya, W.F.; Chaudhry, M.H. Unsteady Friction in Rough Pipes. J. Hydraul. Eng. 2001, 127, 607–618. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Mansour, S.G.S.; Zhao, M. Applicability of Quasisteady and Axisymmetric Turbulence Models in Water Hammer. J. Hydraul. Eng. 2002, 128, 917–924. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M. Transient, turbulent, smooth pipe friction. J. Hydraul. Res. 1995, 33, 435–456. [Google Scholar] [CrossRef]
- Vardy, A.; Brown, J. Transient turbulent friction in smooth pipe flows. J. Sound Vib. 2003, 259, 1011–1036. [Google Scholar] [CrossRef]
- Zhao, M.; Ghidaoui, M. Investigation of turbulence behavior in pipe transient using a k–ε model. J. Hydraul. Res. 2006, 44, 682–692. [Google Scholar] [CrossRef]
- Wahba, E.M. Runge–Kutta time-stepping schemes with TVD central differencing for the water hammer equations. Int. J. Numer. Methods Fluids 2006, 52, 571–590. [Google Scholar] [CrossRef]
- Wahba, E. Turbulence modeling for two-dimensional water hammer simulations in the low Reynolds number range. Comput. Fluids 2009, 38, 1763–1770. [Google Scholar] [CrossRef]
- Riasi, A.; Nourbakhsh, P.A.; Raisee, A.P.M. Unsteady turbulent pipe flow due to water hammer using k–θ turbulence model. J. Hydraul. Res. 2009, 47, 429–437. [Google Scholar] [CrossRef]
- Eggels, J.G.M. Direct and Large Eddy Simulation of Turbulent Flow in a Cylindrical Pipe Geometry. Ph.D. Dissertation, Delft University of Technology, Delft, The Netherlands, 1994. [Google Scholar]
- Eggels, J.G.M.; Westerweel, J.; Nieuwstadt, F.T.M.; Adrian, R.J. Direct numerical simulation of turbulent pipe flow. Flow Turbul. Combust. 1993, 51, 319–324. [Google Scholar] [CrossRef]
- Ghosh, S.; Sesterhenn, J.; Friedrich, R. DNS and LES of compressible turbulent pipe flow with isothermal wall. In Direct and Large-Eddy Simulation VI; Lamballais, E., Friedrich, R., Geurts, B.J., Métais, O., Eds.; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Riedelmeier, S.; Becker, S.; Schlücker, E. Damping of water hammer oscillations - comparison of 3D CFD and 1D calculations using two selected models for pipe friction. PAMM 2014, 14, 705–706. [Google Scholar] [CrossRef]
- Yang, J.-C.; Hsu, E.-L. On the use of the reach-back characteristics method for calculation of dispersion. Int. J. Numer. Methods Fluids 1991, 12, 225–235. [Google Scholar] [CrossRef]
- Yang, S.; Wu, D.; Lai, Z.; Du, T. Three-dimensional computational fluid dynamics simulation of valve-induced water hammer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 2263–2274. [Google Scholar] [CrossRef]
- Mahdizadeh, H. Numerical modelling of one- and two-dimensional water hammer problems using a modified wave propagation algorithm and turbulence model. J. Hydraul. Res. 2018, 57, 374–385. [Google Scholar] [CrossRef]
- Mandair, S.; Magnan, R.; Morissette, J.-F.; Karney, B. Energy-Based Evaluation of 1D Unsteady Friction Models for Classic Laminar Water Hammer with Comparison to CFD. J. Hydraul. Eng. 2020, 146, 04019072. [Google Scholar] [CrossRef]
- Orlandi, P.; Fatica, M. Large-eddy simulations of neutral-static-stability planetary boundary layer. Q. J. R. Meterol. Soc. 1997, 113, 413–443. [Google Scholar]
- Rudman, M.; Blackburn, H.M. Large Eddy Simulation of Turbulent pipe flow. In Proceedings of the 2nd International Conference CFD Minerals Process Industries, CSIRO, Melbourne, Australia, 6–8 December 1999. [Google Scholar]
- Karney, B.W.; McInnis, D. Transient Analysis of Water Distribution Systems. J. Am. Water Work. Assoc. 1990, 82, 62–70. [Google Scholar] [CrossRef]
- Karney, B.W.; McInnis, D. Efficient Calculation of Transient Flow in Simple Pipe Networks. J. Hydraul. Eng. 1992, 118, 1014–1030. [Google Scholar] [CrossRef]
- Cabrera, E.; García-Serra, J.; Iglesias, P.L. Modelling water distribution networks: From steady flow to water hammer. In Improving Efficiency and Reliability in Water Distribution Systems; Cabrera, E., Vela, J., Eds.; Springer-Science Business Media, B.V.: Valencia, Spain, 1995; pp. 3–32. [Google Scholar]
- Ani, H.M.V.S.; Khayatzadeh, A. Transient flow in pipe networks. J. Hydraul. Res. 2002, 40, 637–644. [Google Scholar] [CrossRef]
- Gad, A.A.M.; I Mohammed, H. Impact of pipes networks simplification on water hammer phenomenon. Sadhana 2014, 39, 1227–1244. [Google Scholar] [CrossRef]
- Nault, J.D.; Karney, B.W. Adaptive Hybrid Transient Formulation for Simulating Incompressible Pipe Network Hydraulics. J. Hydraul. Eng. 2016, 142, 04016050. [Google Scholar] [CrossRef]
- Nault, J.D.; Karney, B.W. Improved Rigid Water Column Formulation for Simulating Slow Transients and Controlled Operations. J. Hydraul. Eng. 2016, 142, 04016025. [Google Scholar] [CrossRef]
- Todini, E. Extending the global gradient algorithm to unsteady flow extended period simulations of water distribution systems. J. Hydroinform. 2010, 13, 167–180. [Google Scholar] [CrossRef]
- Shimada, M. Graph-Theoretical Model for Slow Transient Analysis of Pipe Networks. J. Hydraul. Eng. 1989, 115, 1165–1183. [Google Scholar] [CrossRef]
- Onizuka, K. System Dynamics Approach to Pipe Network Analysis. J. Hydraul. Eng. 1986, 112, 728–749. [Google Scholar] [CrossRef]
- Holloway, M.B. Dynamic Pipe Network Computer Model. Ph.D. Thesis, Washington State University, Pullman, WA, USA, 1985. [Google Scholar]
- Ahmed, I. Application of the Gradient Method for the Analysis of Unsteady Flow in Water Networks. Master’s Thesis, The University of Arizona, Tucson, AZ, USA, 1997. [Google Scholar]
- Islam, M.R.; Chaudhry, M.H. Modeling of Constituent Transport in Unsteady Flows in Pipe Networks. J. Hydraul. Eng. 1998, 124, 1115–1124. [Google Scholar] [CrossRef]
- Todini, E.; Rossman, L.A. Unified Framework for Deriving Simultaneous Equation Algorithms for Water Distribution Networks. J. Hydraul. Eng. 2013, 139, 511–526. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B. A practical overview of unsteady pipe flow modeling: From physics to numerical solutions. Urban Water J. 2016, 14, 502–508. [Google Scholar] [CrossRef]
- Nault, J.D.; Karney, B.W.; Jung, B.-S. Generalized Flexible Method for Simulating Transient Pipe Network Hydraulics. J. Hydraul. Eng. 2018, 144, 04018031. [Google Scholar] [CrossRef]
- Nault, J.D.; Karney, B.W. Comprehensive adaptive modelling of 1-D unsteady pipe network hydraulics. J. Hydraul. Res. 2021, 59, 263–279. [Google Scholar] [CrossRef]
- Tang, K.W.; Karney, B.W.; Brunone, B. Leak detection using inverse transient calibration and GA-some early successes and future challenges. In Proceedings of the Sixth International Conference on Computing and Control in the Water Industry (CCWI), Leicester, UK, 3–5 September 2001; ISBN 0863802737. [Google Scholar]
- Wu, J.; Cheng, Y.; Zhou, W.; Zhang, C.; Diao, W. GPU acceleration of FSI simulations by the immersed boundary-lattice Boltzmann coupling scheme. Comput. Math. Appl. 2019, 78, 1194–1205. [Google Scholar] [CrossRef]
- Bonelli, F.; Tuttafesta, M.; Colonna, G.; Cutrone, L.; Pascazio, G. An MPI-CUDA approach for hypersonic flows with detailed state-to-state air kinetics using a GPU cluster. Comput. Phys. Commun. 2017, 219, 178–195. [Google Scholar] [CrossRef]
- Zhang, C.-Z.; Cheng, Y.-G.; Wu, J.-Y.; Diao, W. Lattice Boltzmann simulation of the open channel flow connecting two cascaded hydropower stations. J. Hydrodyn. 2016, 28, 400–410. [Google Scholar] [CrossRef]
- Griebel, M.; Zaspel, P. A multi-GPU accelerated solver for the three-dimensional two-phase incompressible Navier-Stokes equations. Comput. Sci. Res. Dev. 2010, 25, 65–73. [Google Scholar] [CrossRef]
- Meng, W.; Cheng, Y.; Wu, J.; Yang, Z.; Zhu, Y.; Shang, S. GPU Acceleration of Hydraulic Transient Simulations of Large-Scale Water Supply Systems. Appl. Sci. 2018, 9, 91. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, S.; Hanmaiahgari, P.R.; Karney, B.W. An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water 2021, 13, 1597. https://doi.org/10.3390/w13111597
Pal S, Hanmaiahgari PR, Karney BW. An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water. 2021; 13(11):1597. https://doi.org/10.3390/w13111597
Chicago/Turabian StylePal, Susovan, Prashanth Reddy Hanmaiahgari, and Bryan W. Karney. 2021. "An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches" Water 13, no. 11: 1597. https://doi.org/10.3390/w13111597
APA StylePal, S., Hanmaiahgari, P. R., & Karney, B. W. (2021). An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water, 13(11), 1597. https://doi.org/10.3390/w13111597