Air–Water Properties in Rectangular Free-Falling Jets
Abstract
1. Introduction
2. Previous Studies
3. Materials and Methods
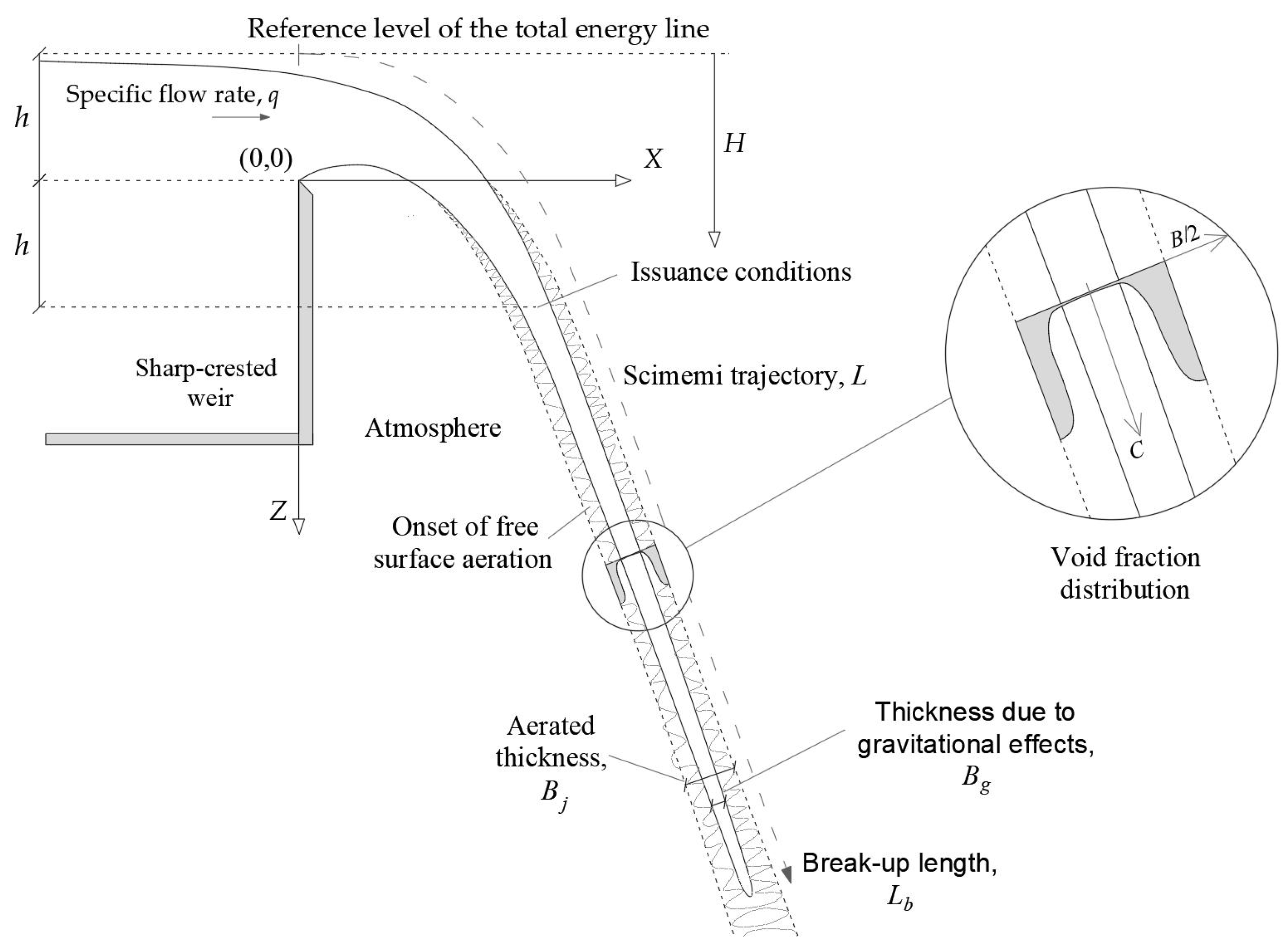
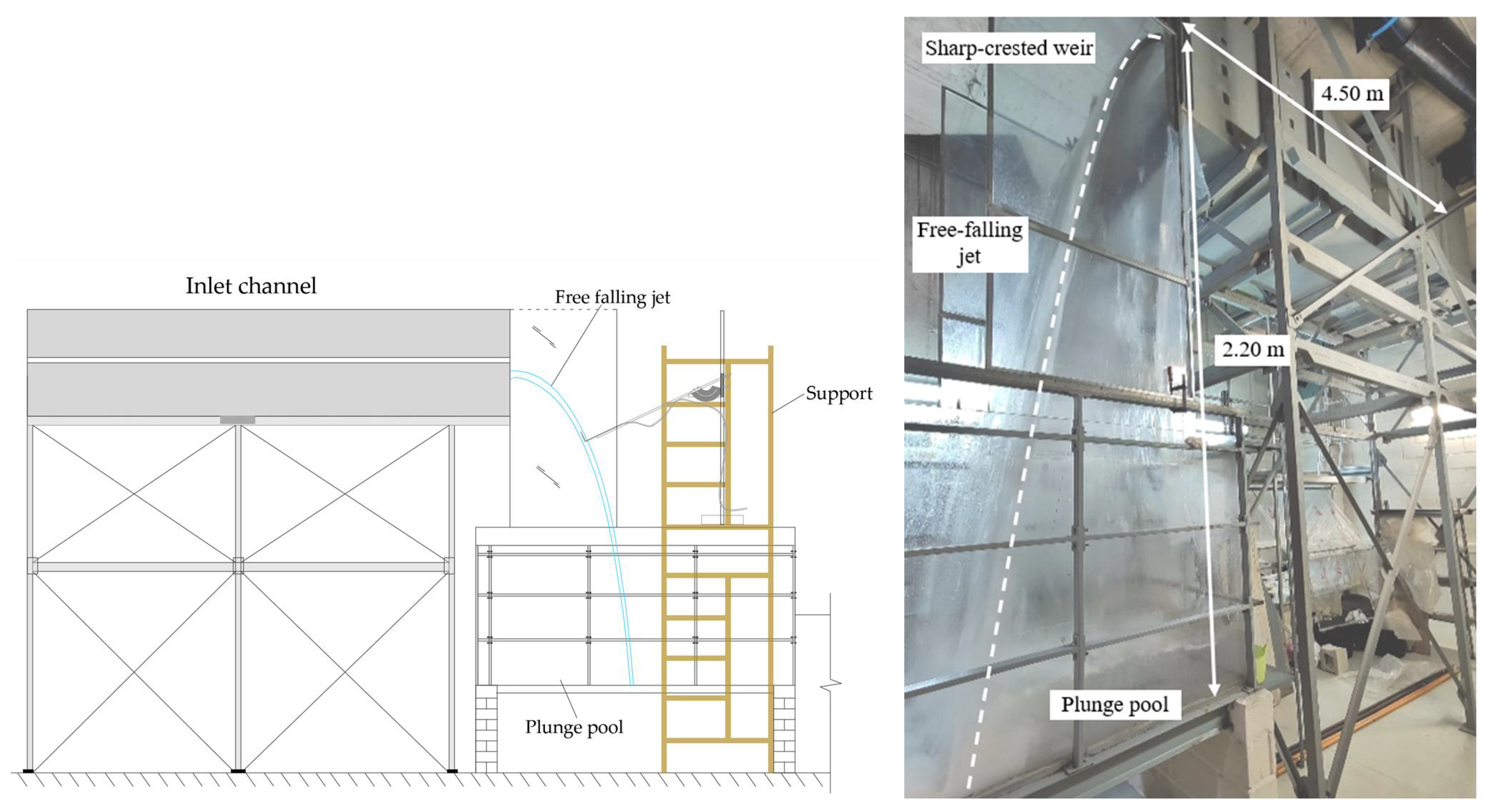
3.1. Experimental Setup
3.2. Instrumentation
3.2.1. Conductivity Phase-Detection Probe
3.2.2. Back-Flushing Pitot Tube
3.3. Experimental Tests and Flow Conditions
4. Results and Discussion
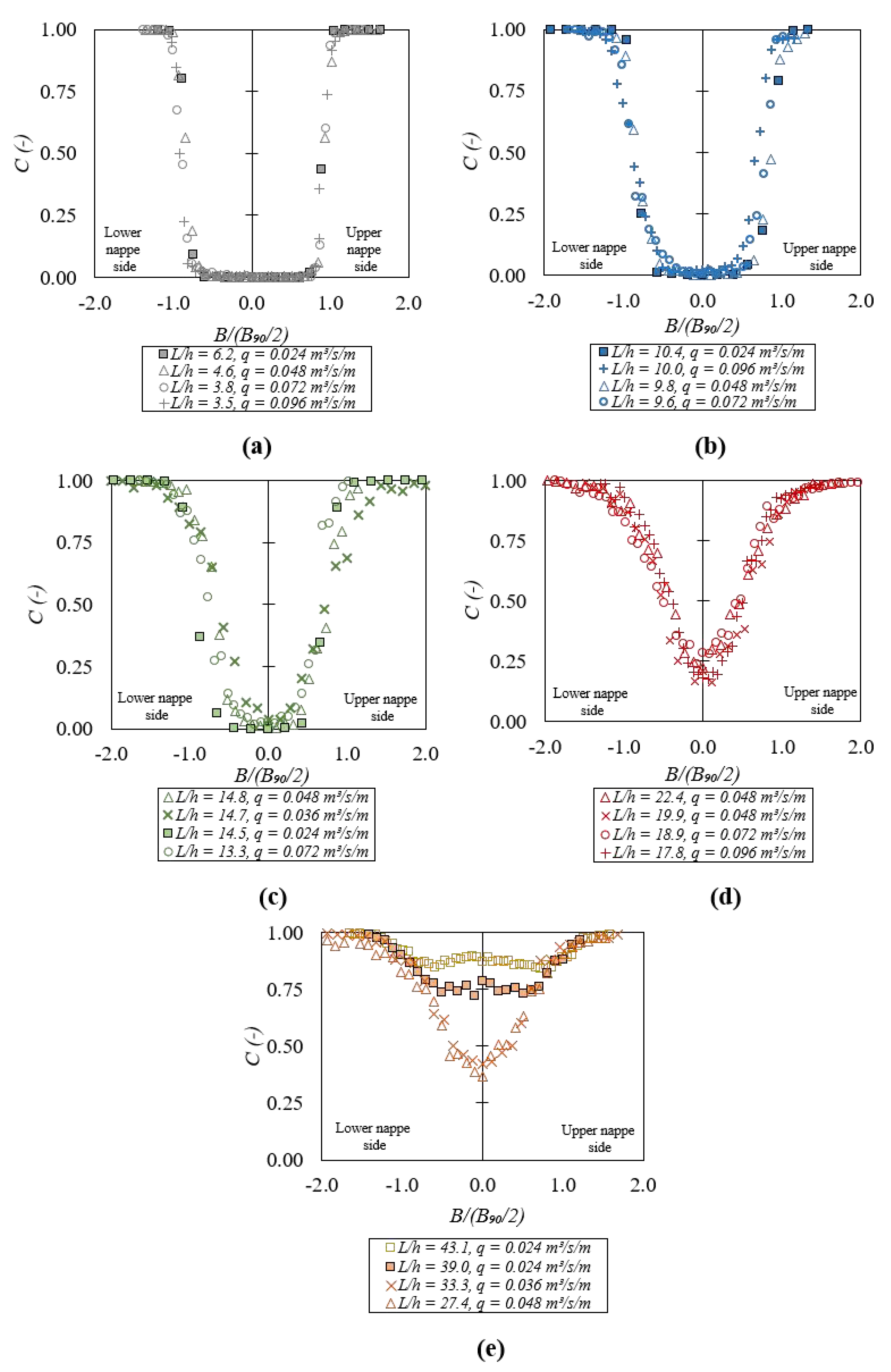
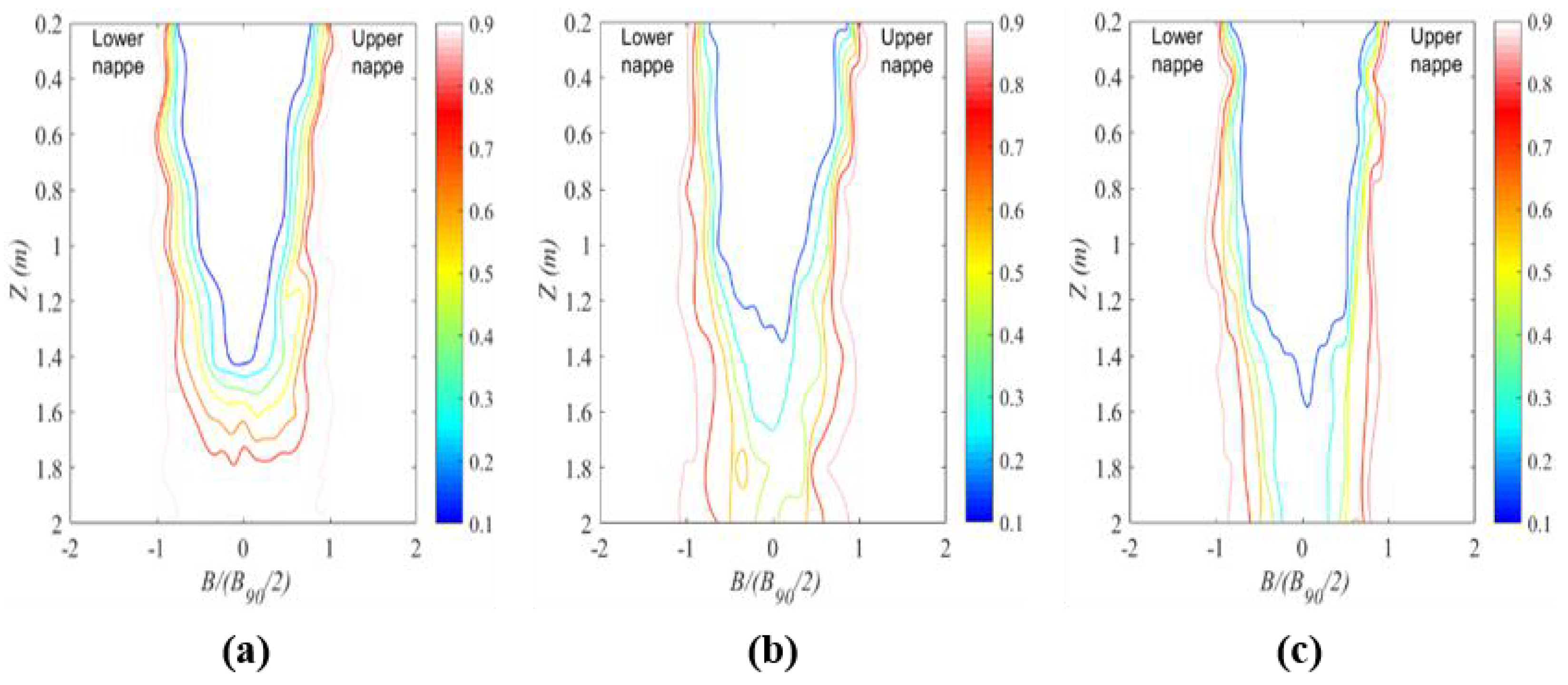
4.1. Void Fraction Distributions
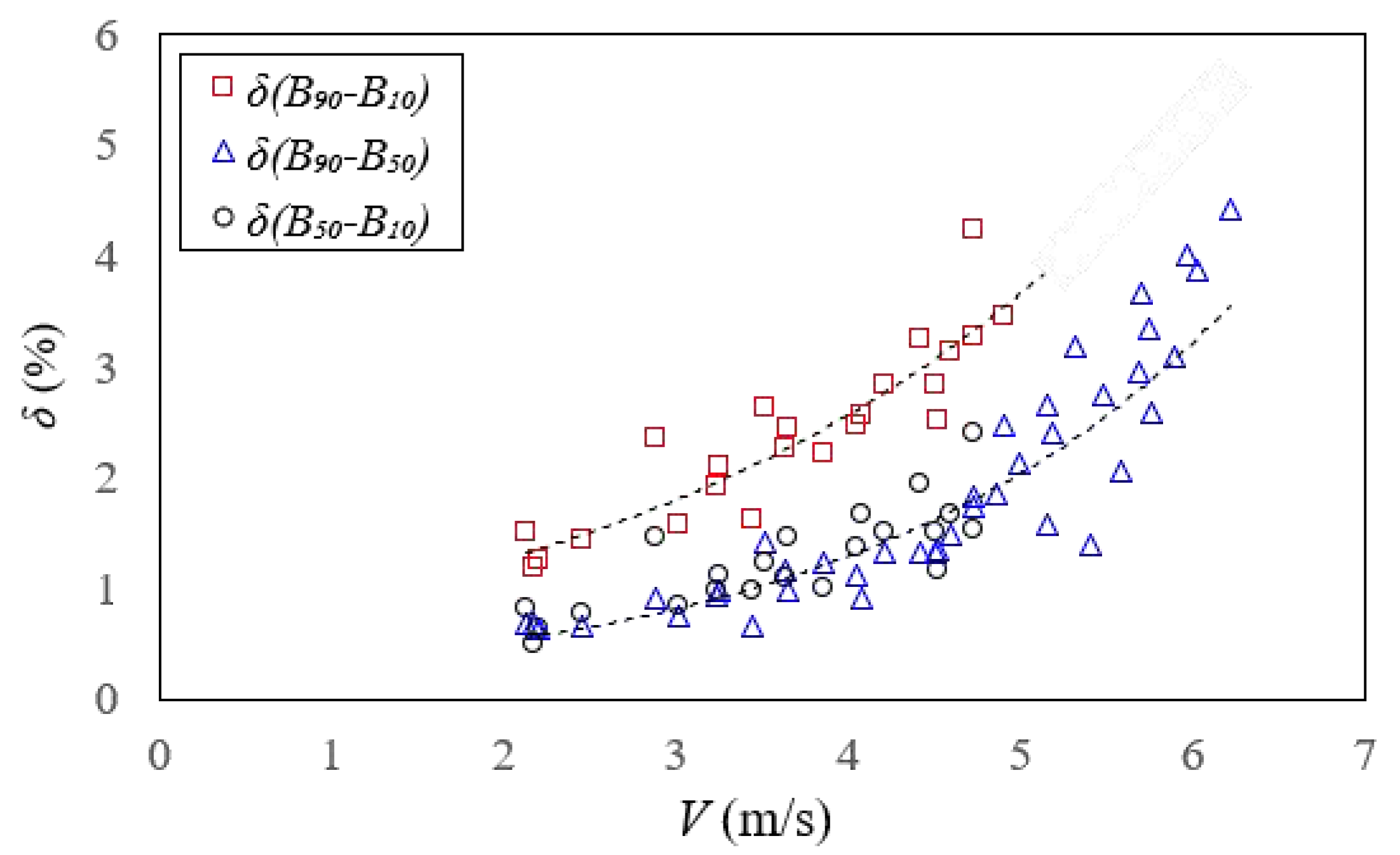
4.2. Jet Thickness and Spread
4.3. Air–Water Phase Change
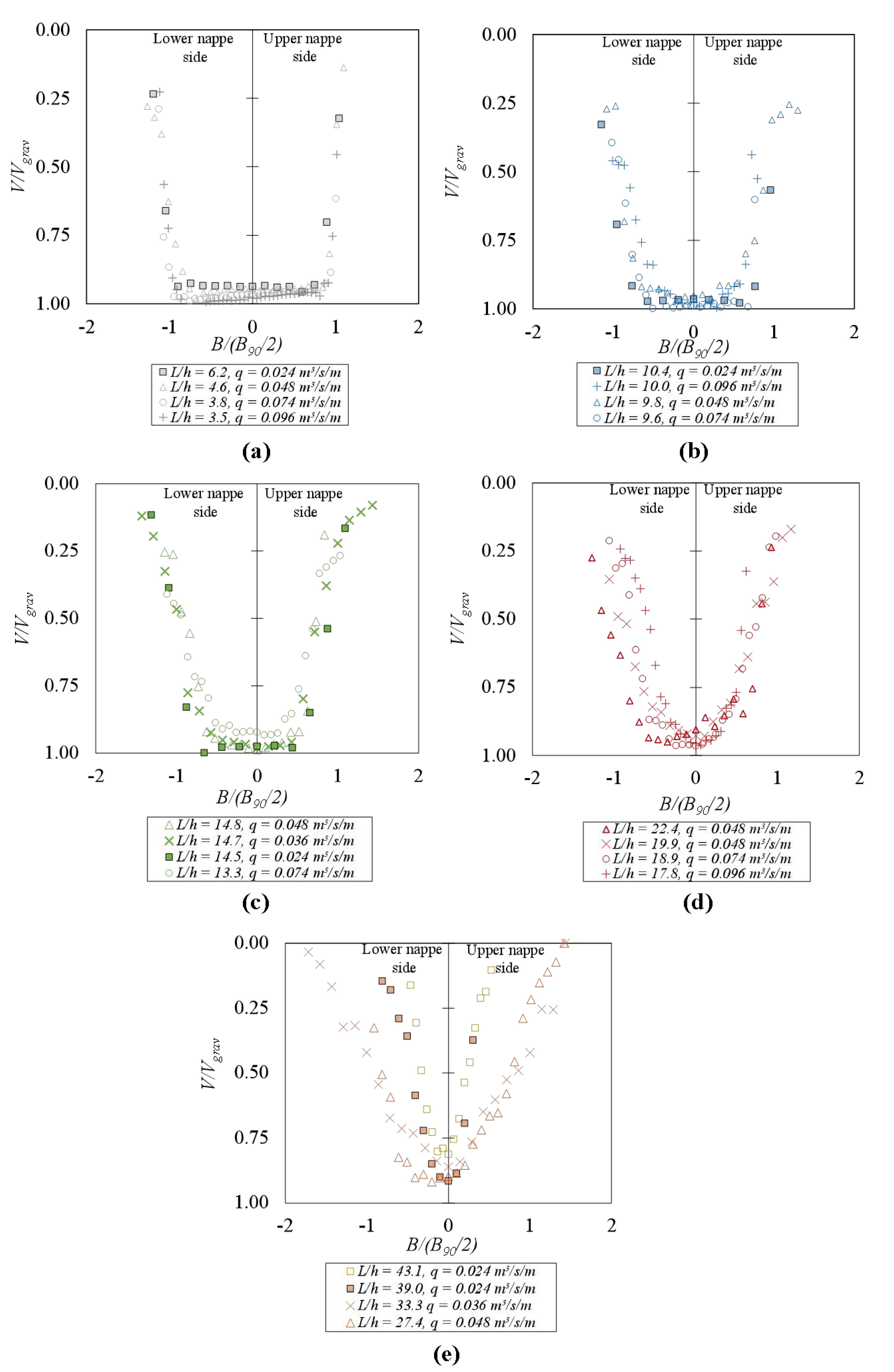
4.4. Velocity Distributions
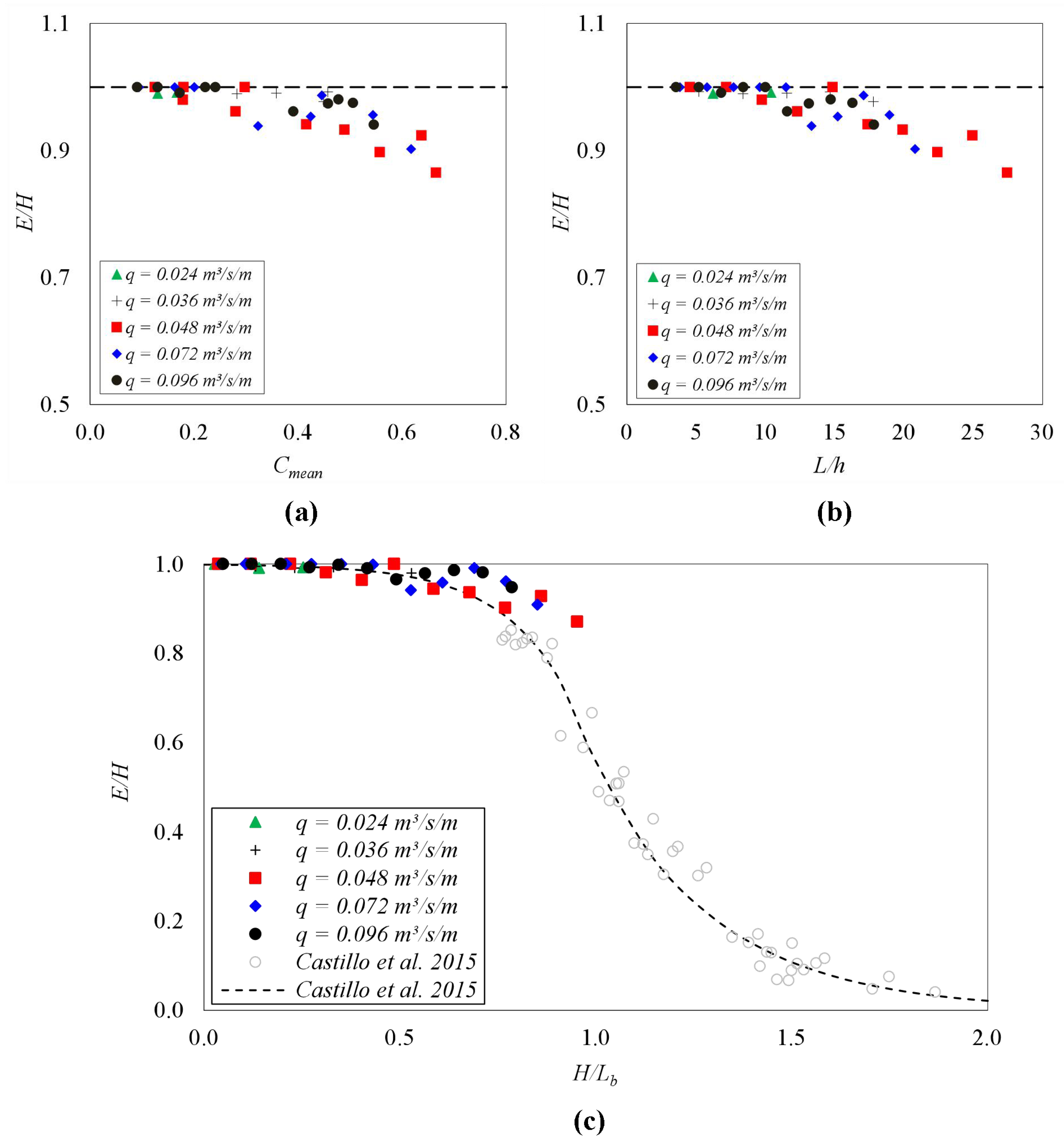
4.5. Energy Dissipation
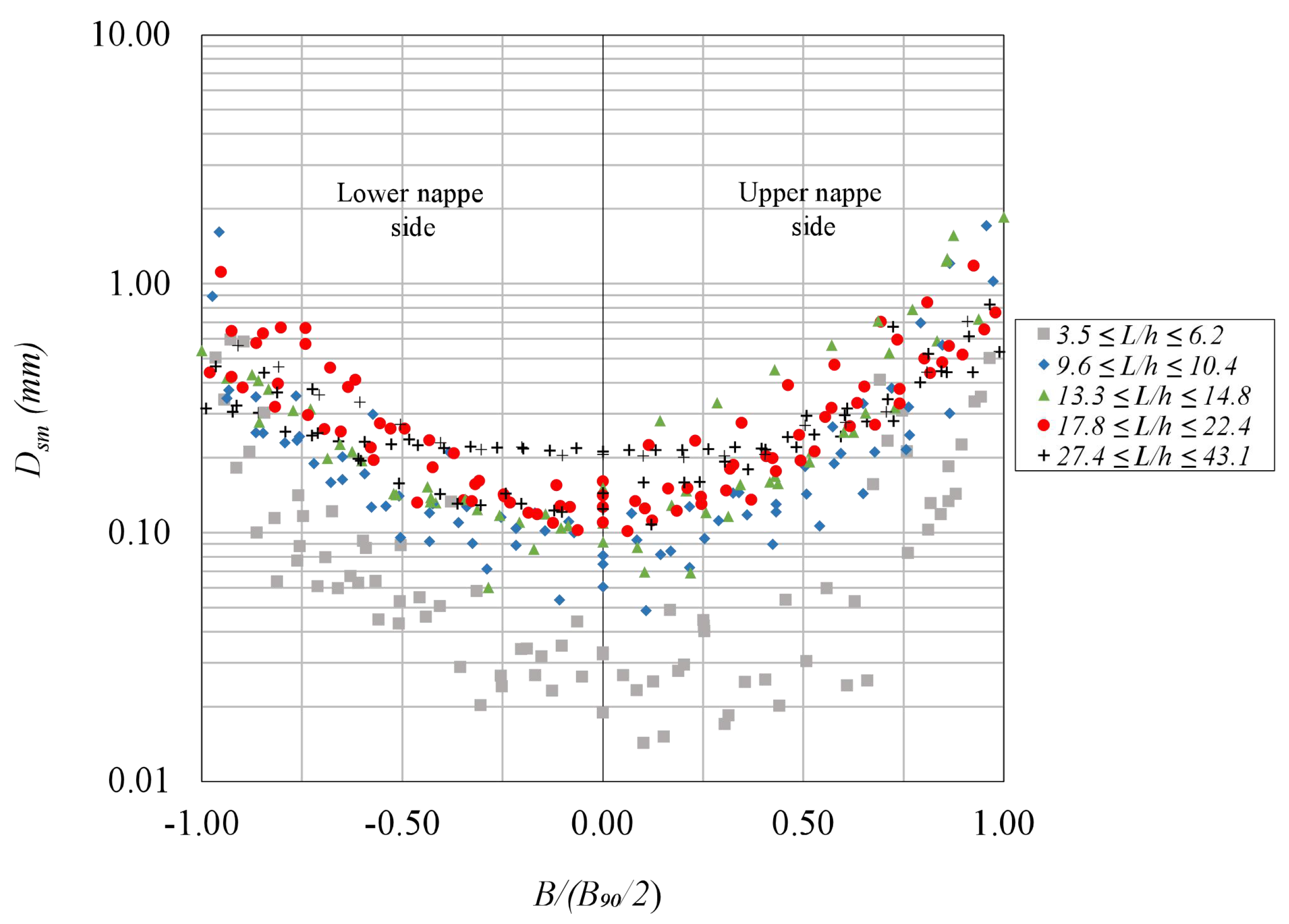
4.6. Sauter Mean Bubble Diameter
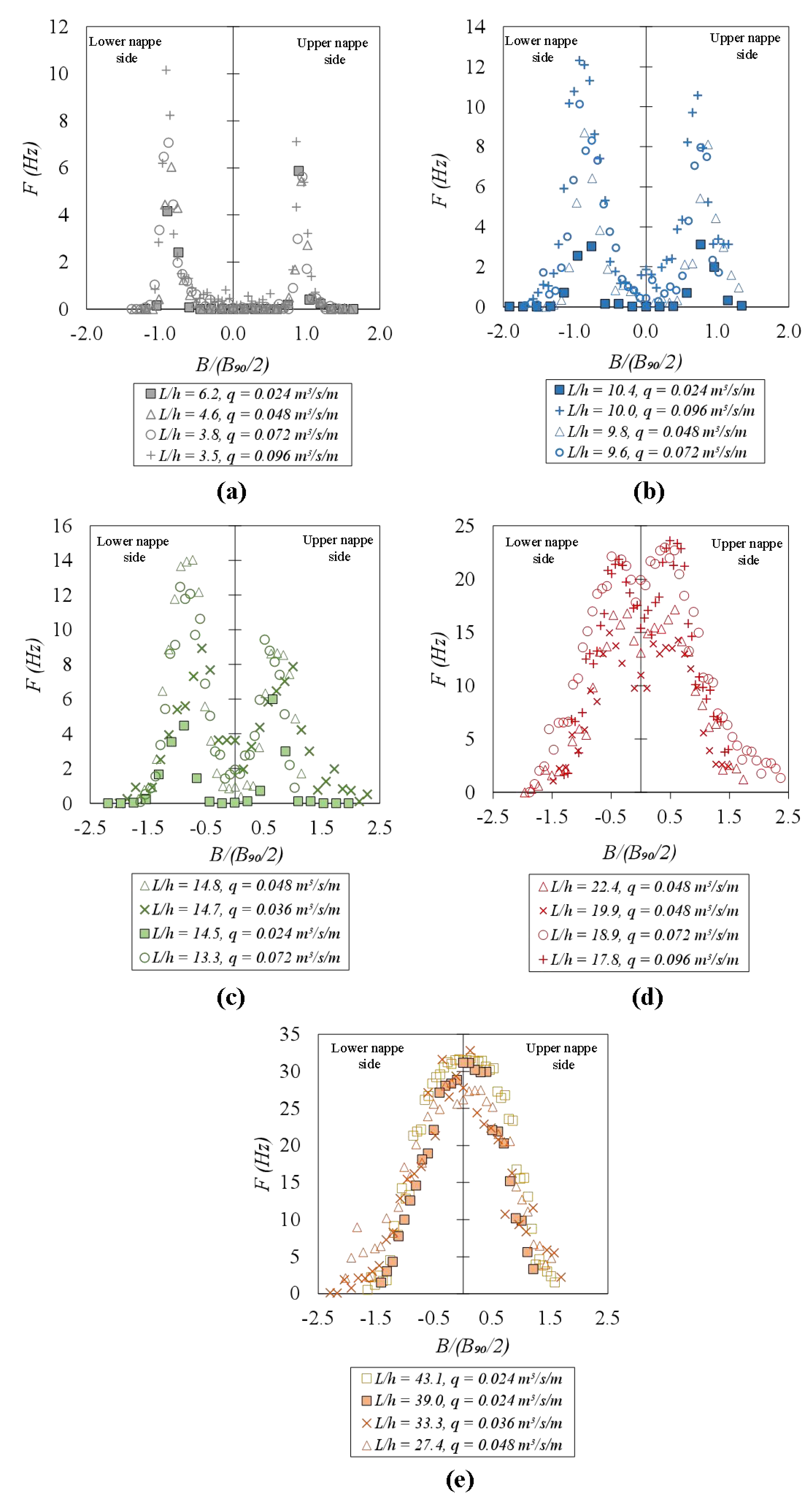
4.7. Air–Water Chord Length
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| B | jet thickness in the analyzed cross-section |
| Bg | jet thickness due to gravitational effects |
| Bi | jet thickness at the issuance conditions |
| Bj | jet thickness |
| B90 | jet thickness with void fraction C |
| B50 | jet thickness with void fraction C |
| B10 | jet thickness with void fraction C |
| C | local void fraction |
| Cd | discharge coefficient for sharp weir crest |
| Ch | bubble chord length |
| Cmean | mean void fraction |
| Dsm | Sauter mean diameter |
| E | energy at the analyzed cross-section |
| F | air–water phase count rate |
| Fi | Froude number at the issuance conditions |
| Fmax | maximum air–water phase count rate |
| Fr | Froude number |
| g | gravitational acceleration |
| h | total energy head over the weir crest |
| H | vertical distance between the reference level of the total energy line and the analyzed cross-section |
| IC | initial conditions |
| K | non-dimensional coefficient |
| Kφ | experimental term of the turbulence parameter φ |
| L | jet trajectory distance |
| Lb | jet break-up length |
| probability density function | |
| q | specific flow rate or water discharge per unit width |
| Re | Reynolds number |
| Tu | turbulent intensity at the issuance conditions |
| Tu* | turbulence intensity |
| t | time-averaged void fraction |
| tch | chord time |
| V | local mean velocity |
| Vgrav | gravitational velocity |
| root-mean-square of the velocity fluctuation | |
| Vi | mean velocity at the issuance conditions |
| We | Weber number |
| X | horizontal axis |
| Z | vertical axis |
| ΔP | difference between the total pressure head and the static pressure head |
| Σti | total recorded time |
| δ | spread angle |
| ξ | lateral spread |
| λ | tapping coefficient for the non-homogeneous behavior of the air–water flow |
| ν | kinematic viscosity |
| µ | dynamic viscosity |
| ρ | density of fluid |
| ρw | density of water |
| σ | surface tension |
| Ø | probe diameter and |
| φ | turbulence parameter in nappe flow. |
References
- Federal Emergency Management Agency. FEMA. P-1015 Technical Manual: Overtopping Protection for Dams; US Department of Homeland Security: Denver, CO, USA, 2014. Available online: https://www.fema.gov/es/media-library/assets/documents/97888 (accessed on 15 March 2021).
- Wahl, T.L.; Frizell, K.H.; Cohen, E.A. Computing the trajectory of free jets. J. Hydraul. Eng. 2008, 134, 256–260. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Phase-detection probe measurements in high-velocity free-surface flows including a discussion of key sampling parameters. Exp. Therm. Fluid Sci. 2014, 61, 66–78. [Google Scholar] [CrossRef]
- Ervine, D.A.; Falvey, H. Behaviour of turbulent jets in the atmosphere and plunge pools. P. I. Civil Eng. 1987, 83, 295–314. [Google Scholar] [CrossRef]
- Castillo, L.; Carrillo, J.M.; Blázquez, A. Plunge pool mean dynamic pressures: A temporal analysis in nappe flow case. J. Hydraul. Res. 2015, 53, 101–118. [Google Scholar] [CrossRef]
- Bertola, N.; Wang, H.; Chanson, H. A physical study of air-water flow in planar plunging water jet with large inflow distance. Int. J. Multiph. Flow 2017, 100, 155–171. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Ortega, P.R.; Castillo, L.G.; García, J.T. Air entrainment in rectangular free falling jets. In Proceedings of the 8th IAHR Int. Symp. on Hydraulic Structures, Santiago, Chile, 12–15 May 2020. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Ortega, P.R.; Castillo, L.G.; García, J.T. Experimental Characterization of Air Entrainment in Rectangular Free Falling Jets. Water 2020, 12, 1773. [Google Scholar] [CrossRef]
- Anderson, A.A.; Tullis, B.P. Finite crest length weir nappe oscillation. J. Hydraul. Eng. 2018, 144, 04018020. [Google Scholar] [CrossRef]
- Lodomez, M.; Tullis, B.; Dewals, B.; Archambeau, P.; Kitsikoudis, V.; Pirotton, M.; Erpicum, S. Nappe oscillations on free-overfall structures: Size scale effects. J. Hydraul. Eng. 2019, 145, 04018022. [Google Scholar]
- Horeni, P. Disintegration of a Free Jet of Water in Air; Byzkumny ustav vodohospodarsky prace a studie; VÝCHODOĆESKÉ MUZEUM V PARDUBICÍCH: Praha, Czech Republic, 1956. (In Czech) [Google Scholar]
- Castillo, L. Aerated jets and pressure fluctuation in plunge pools. In Proceedings of the Seventh International Conference on Hydroscience and Engineering, M. Piasecki and College of Engineering, Drexel University, Philadelphia, PA, USA, 10–13 September 2006; pp. 1–23. [Google Scholar]
- Carrillo, J.M. Metodología Numérica y Experimental Para el Diseño de los Cuencos de Disipación en el Sobrevertido de Presas de Fábrica. PhD Thesis, Universidad Politécnica de Cartagena, Cartagena, Spain, 2014. Available online: https://repositorio.upct.es/handle/10317/4038 (accessed on 10 June 2014). (In Spanish).
- Castillo, L.G.; Carrillo, J.M.; Sordo-Ward, A. Simulation of overflow nappe impingement jets. J. Hydroinform. 2014, 16, 922–940. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Castillo, L.G.; Marco, F.; García, J.T. Experimental and numerical analysis of two-phase flows in plunge pools. J. Hydraul. Eng. 2020, 146, 04020044. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Marco, F.; Castillo, L.G.; García, J.T. Experimental study of submerged hydraulic jumps generated downstream of rectangular plunging jets. Int. J. Multiph. Flow 2021, 137, 103579. [Google Scholar] [CrossRef]
- Chanson, H. Air Bubble Entrainment in Free-Surface Turbulent Shear Flows, 1st ed.; Academic Press: London, UK, 1997. [Google Scholar]
- Chanson, H. Air bubble entrainment in open channels. Flow structure and bubble size distributions. Int. J. Multiph. Flow 1997, 23, 193–203. [Google Scholar] [CrossRef]
- Chanson, H. Air-water Flows in Water Engineering and Hydraulic Structures. Basic Processes and Metrology. In Proceedings of the Hydraulics of Dams and River Structures; Yazdandoost, F., Attari, J., Eds.; CRC Press: London, UK, 2004; p. 50. [Google Scholar]
- Matos, J.; Frizell, K.H.; André, S.; Frizell, K.W. On the performance of velocity measurement techniques in air-water flows. In Hydraulic Measurements and Experimental Methods; ASCE: Minneapolis, MN, USA, 2002; pp. 130–140. [Google Scholar]
- Ortega, P.R.; Carrillo, J.M.; Castillo, L.G.; García, J.T. Análisis experimental de flujos bifásicos en resaltos hidráulicos. In Proceedings of the Jornadas de Ingeniería del Agua, Toledo, Spain, 23–24 October 2019. (In Spanish). [Google Scholar]
- Felder, S.; Pfister, M. Comparative analysis of phase-detective intrusive probes in high-velocity air-water flows. Int. J. Multiph. Flow 2017, 90, 88–101. [Google Scholar] [CrossRef]
- Kramer, M.; Hohermuth, B.; Valero, D.; Felder, S. Best practices for velocity estimations in highly aerated flows with dual-tip phase-detection probes. Int. J. Multiph. Flow 2020, 126, 103228. [Google Scholar] [CrossRef]
- Matos, J.; Frizell, K.H. Air concentration and velocity measurements on self-aerated flow down stepped chutes. In Proceedings of the Joint Conf. on Water Resources Engineering and Water Resources Planning & Management, ASCE, Minneapolis, MN, USA, 30 July–2 August 2000. [Google Scholar]
- Wood, I.R. Uniform region of self-aerated flow. J. Hydraul. Div. ASCE 1983, 109, 447–461. [Google Scholar] [CrossRef]
- Chamani, M.R.; Rajaratnam, N. Characteristics of skimming flow over stepped spillways. J. Hydraul. Eng. 1999, 105, 361–368. [Google Scholar] [CrossRef]
- Scimemi, E. Sulla forma delle vene tracimanti. L’Energia Elettr. 1931, 7, 293–305. (In Italian) [Google Scholar]
- Chanson, H. Turbulent air-water flows in hydraulic structures: Dynamic similarity and scale effects. Environ. Fluid Mech 2009, 9, 125–142. [Google Scholar] [CrossRef]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Scale effects in microscopic air-water flow properties in high-velocity free-surface flows. Exp. Therm. Fluid Sci. 2016, 83, 19–36. [Google Scholar] [CrossRef]
- Chanson, H. Velocity measurements within high velocity air-water jets. J. Hydraul. Res. 1993, 31, 365–382. [Google Scholar] [CrossRef]
- Toombes, L.; Chanson, H. Free-surface aeration and momentum exchange at a bottom outlet. J. Hydraul. Res. 2007, 45, 100–110. [Google Scholar] [CrossRef]
- Pfister, M.; Schwindt, S. Air concentration distribution in deflector jets. In Proceedings of the 5th IAHR International Symposium on Hydraulic Structures, Brisbane, Australia, 25–27 June 2014. [Google Scholar]
- André, S.; Boillat, J.L.; Schleiss, A.J. Two-phase flow characteristics of stepped spillways’. J. Hydraul. Eng. 2005, 131, 423–427. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Aeration and Air–Water Mass Transfer on Stepped Chutes with Embankment Dam Slopes. Environ. Fluid Mech. 2015, 15, 695–710. [Google Scholar] [CrossRef]
- Toombes, L. Experimental Study of Air-Water Flow Properties on Low-Gradient Stepped Cascades. Ph.D. Thesis, School of Civil Engineering, The University of Queensland, Brisbane, Australia, 2002. Available online: https://espace.library.uq.edu.au/view/UQ:9270 (accessed on 20 July 2020).
- Brattberg, T.; Toombes, L.; Chanson, H. Developing air-water shear layers of two-dimensional water jets discharging into air. In Proceedings of the ASME Fluids Engineering Division Summer Meeting (FEDSM’98), Washington, DC, USA, 21–25 June 1998. [Google Scholar]
- Matos, J. Discussion of the “Characteristics of skimming flow over stepped spillways”. J. Hydraul. Eng. 2000, 126, 865–869. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Academic Press: New York, NY, USA, 1978; p. 380. [Google Scholar]
- Chanson, H.; Carosi, G. Advanced post-processing and correlation analyses in high-velocity air-water flows. Environ. Fluid Mech 2007, 7, 495–508. [Google Scholar] [CrossRef]
- Felder, S. Air-Water Flow Properties on Stepped Spillways for Embankment Dams: Aeration, Energy Dissipation and Turbulence On Uniform, Non-Uniform and Pooled Stepped Chutes. Ph.D. Thesis, School of Civil Engineering, The University of Queensland, Brisbane, Australia, 2013. Available online: https://espace.library.uq.edu.au/view/UQ:301329 (accessed on 11 May 2019).





| q (m3/s/m) | h (m) | Vi (m/s) | Re (-) | We (-) | Lb (m) | Maximum L (m) | Maximum L/h(-) |
|---|---|---|---|---|---|---|---|
| 0.024 | 0.050 | 1.40 | 24,021 | 464 | 1.78 | 2.13 | 43.1 |
| 0.036 | 0.065 | 1.60 | 35,561 | 789 | 2.01 | 2.17 | 33.3 |
| 0.048 | 0.080 | 1.78 | 47,148 | 1162 | 2.19 | 2.21 | 27.4 |
| 0.072 | 0.109 | 2.07 | 70,721 | 2029 | 2.48 | 2.27 | 20.8 |
| 0.096 | 0.129 | 2.25 | 94,202 | 2940 | 2.71 | 2.34 | 17.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrillo, J.M.; Ortega, P.R.; Castillo, L.G.; García, J.T. Air–Water Properties in Rectangular Free-Falling Jets. Water 2021, 13, 1593. https://doi.org/10.3390/w13111593
Carrillo JM, Ortega PR, Castillo LG, García JT. Air–Water Properties in Rectangular Free-Falling Jets. Water. 2021; 13(11):1593. https://doi.org/10.3390/w13111593
Chicago/Turabian StyleCarrillo, José M., Patricio R. Ortega, Luis G. Castillo, and Juan T. García. 2021. "Air–Water Properties in Rectangular Free-Falling Jets" Water 13, no. 11: 1593. https://doi.org/10.3390/w13111593
APA StyleCarrillo, J. M., Ortega, P. R., Castillo, L. G., & García, J. T. (2021). Air–Water Properties in Rectangular Free-Falling Jets. Water, 13(11), 1593. https://doi.org/10.3390/w13111593








