An Optimal Water Resource Allocation Mechanism Based on Ex-Post Verification and Reward in Huangbai River
Abstract
1. Introduction
2. Literature Review
3. The Model
3.1. Event Timeline
3.1.1. Timeline of the Mechanism from the Governor’s Perspective
3.1.2. Timeline of the Mechanism from the Governor’s Perspective
3.2. Basic Information about the Model
3.2.1. Predetermined Mechanism Analysis
3.2.2. Self-Report Information Analysis
3.2.3. Quota-Based Allocation Rule Analysis
3.2.4. Ex Post Verification and Reward Mechanism Analysis
3.3. The Objective Function of the Mechanism
4. Case Study
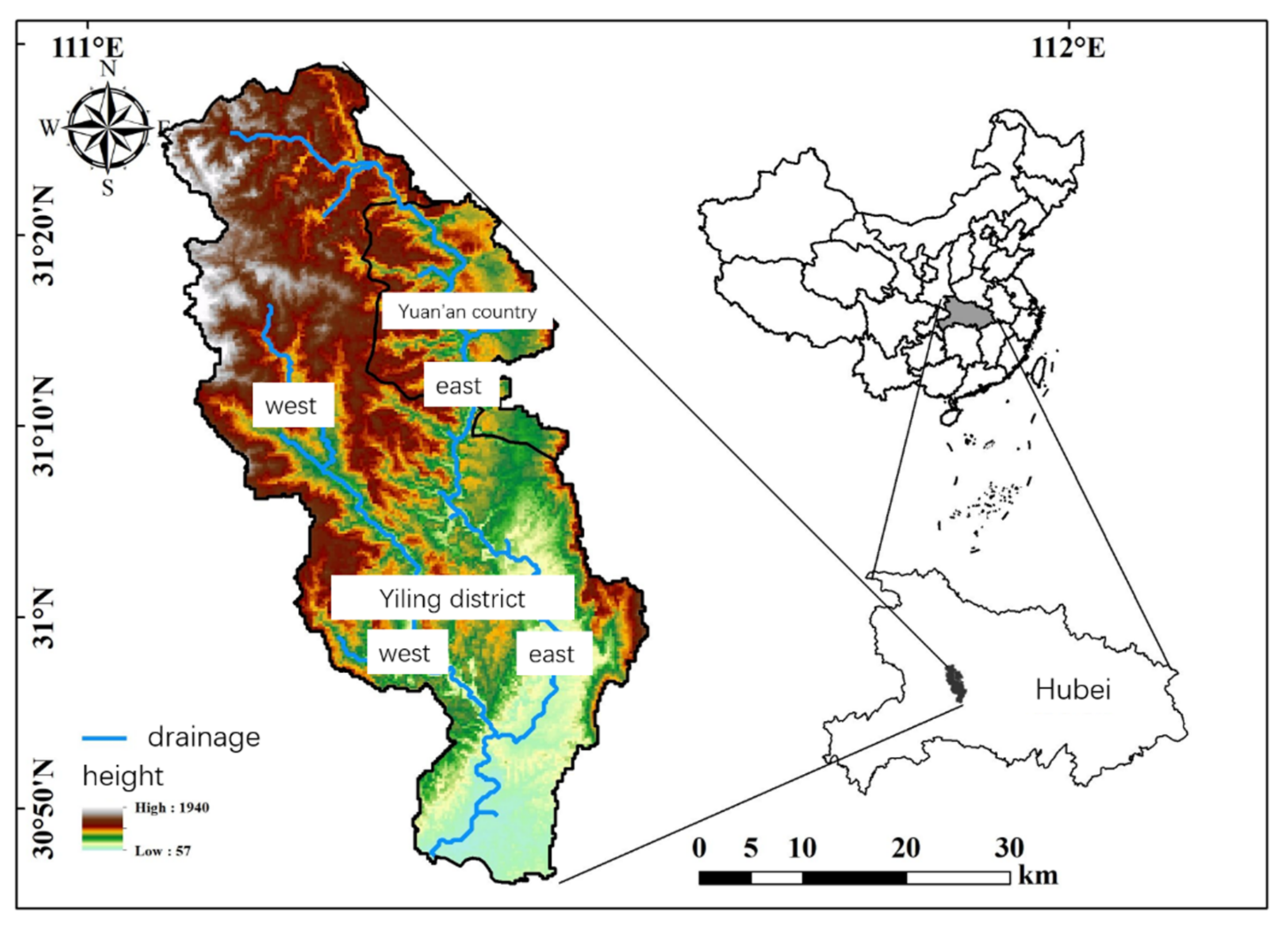
4.1. Study Area
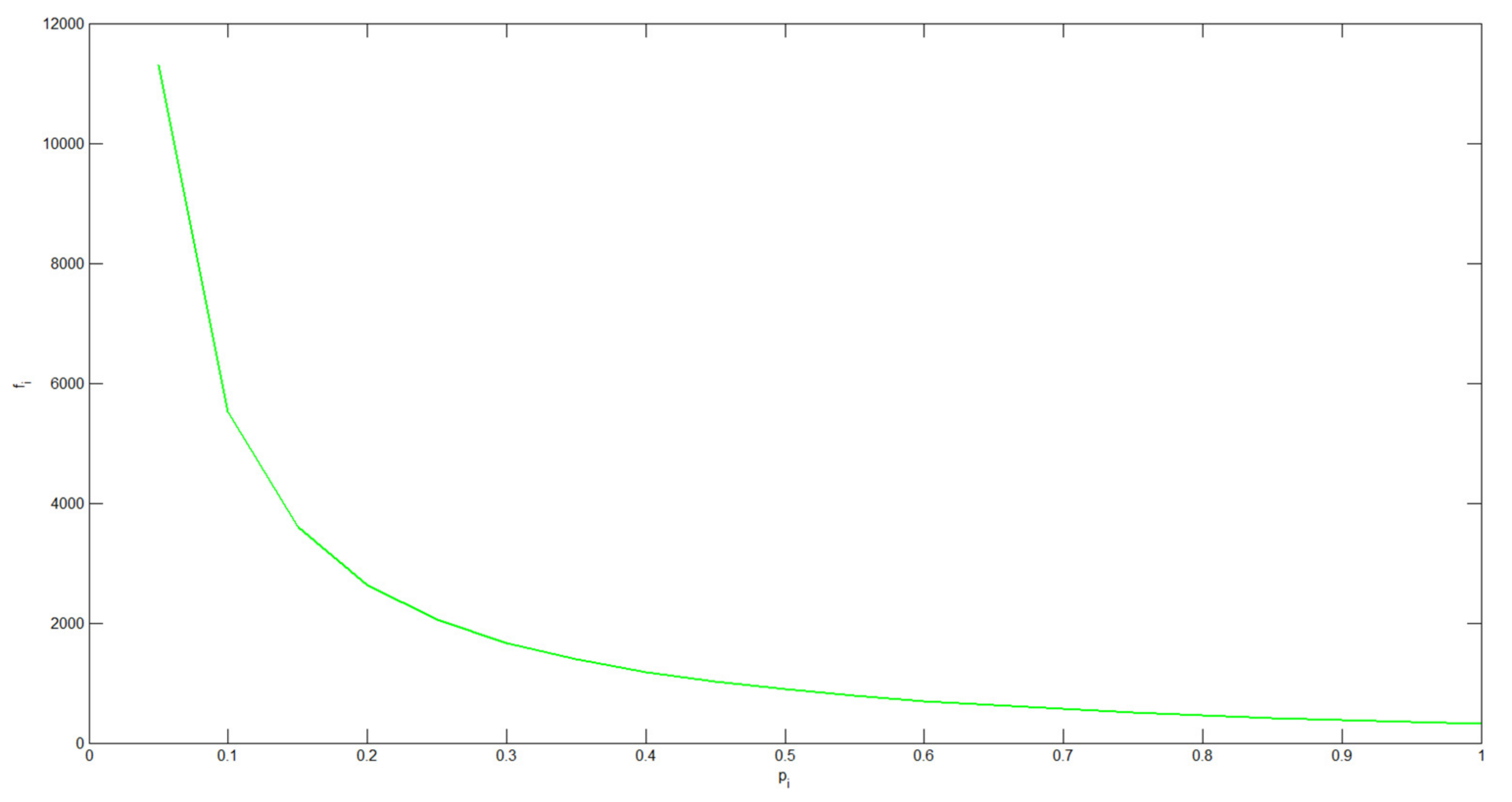
4.2. The Optimal Mechanism Analysis
5. Conclusions and Discussion
5.1. Conclusions
5.2. Disussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MWR (Ministry of Water Resources, P.R. China). The 11th Five-Year Plan of National Water Resources Development. In Gazette of the Ministry of Water Resources of the P.R. China; MWR: Beijing, China, 2016; pp. 34–48. [Google Scholar]
- Fuentes, E.; Arce, L.; Salom, J. A review of domestic hot water consumption profiles for application in systems and buildings energy performance analysis. Renew. Sustain. Energy Rev. 2017, 81, 1530–1547. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, X.; Wang, Z. Comparing administered and market-based water allocation systems through a consistent agent-based modeling framework. J. Environ. Manag. 2013, 123, 120–130. [Google Scholar] [CrossRef] [PubMed]
- Kling, C.L. Economic Incentives to Improve Water Quality in Agricultural Landscapes: Some New Variations on Old Ideas. Am. J. Agric. Econ. 2011, 93, 297–309. [Google Scholar] [CrossRef]
- Kahn, M.E.; Li, P.; Zhao, D. Water Pollution Progress at Borders: The Role of Changes in China’s Political Promotion Incentives. Am. Econ. J. Econ. Policy 2015, 7, 223–242. [Google Scholar] [CrossRef]
- Ørum, J.E.; Boesen, M.V.; Jovanovic, Z.; Pedersen, S.M. Farmers’ incentives to save water with new irrigation systems and water taxation—A case study of Serbian potato production. Agric. Water Manag. 2010, 98, 465–471. [Google Scholar] [CrossRef]
- Malik, A.S. Self-Reporting and the Design of Policies for Regulating Stochastic Pollution. J. Environ. Econ. Manag. 1993, 24, 241–257. [Google Scholar] [CrossRef]
- Ben-Porath, E.; Dekel, E.; Lipman, B.L. Optimal allocation with costly verification. Am. Econ. Rev. 2014, 104, 3779–3813. [Google Scholar] [CrossRef]
- Mylovanov, T.; Zapechelnyuk, A. Optimal allocation with ex post verification and limited penalties. Am. Econ. Rev. 2017, 107, 2666–2694. [Google Scholar] [CrossRef]
- Li, Y. Mechanism design with costly verification and limited punishments. J. Econ. Theory 2020, 186, 105000. [Google Scholar] [CrossRef]
- Inalhan, G.; Stipanovic, D.M.; Tomlin, C.J. Decentralized optimization with application to multiple aircraft coordination. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002. [Google Scholar]
- Yang, Y.-C.E.; Cai, X.; Stipanovic, D.M. A decentralized optimization algorithm for multiagent system-based watershed management. Water Resour. Res. 2009, 45, W08430. [Google Scholar] [CrossRef]
- Cai, Y.P.; Lin, X.; Yue, W.C.; Zhang, P.P. Inexact fuzzy chance-constrained programming for community-scale urban storm water management. J. Clean. Prod. 2018, 182, 937–945. [Google Scholar] [CrossRef]
- Su, X.; Li, J.; Singh, V.P. Optimal Allocation of Agricultural Water Resources Based on Virtual Water Subdivision in Shiyang River Basin. Water Resour. Manag. 2014, 28, 2243–2257. [Google Scholar] [CrossRef]
- Li, M.; Guo, P. A multi-objective optimal allocation model for irrigation water resources under multiple uncertainties. Appl. Math. Model. 2014, 38, 4897–4911. [Google Scholar] [CrossRef]
- Bourque, K.; Schiller, A.; Angosto, C.L.; McPhail, L.; Bagnasco, W.; Ayres, A.; Larsen, A. Balancing agricultural production, groundwater management, and biodiversity goals: A multi-benefit optimization model of agriculture in Kern County, California. Sci. Total. Environ. 2019, 670, 865–875. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Wang, F.; Huang, K.; Zhang, H.; Yu, J.; Han, A.Y. System Dynamics-Multiple Objective Optimization Model for Water Resource Management: A Case Study in Jiaxing City, China. Water 2021, 13, 671. [Google Scholar] [CrossRef]
- Mianabadi, H.; Mostert, E.; Zarghami, M.; van de Giesen, N. A new bankruptcy method for conflict resolution in water resources allocation. J. Environ. Manag. 2014, 144, 152–159. [Google Scholar] [CrossRef]
- Li, S.; He, Y.; Chen, X.; Zheng, Y. The improved bankruptcy method and its application in regional water resource allocation. J. Hydro-Environ. Res. 2020, 28, 48–56. [Google Scholar] [CrossRef]
- Janjua, S.; Hassan, I. Transboundary water allocation in critical scarcity conditions: A stochastic bankruptcy approach. J. Water Supply Res. Technol. AQUA 2020, 69, 014–029. [Google Scholar] [CrossRef]
- Janjua, S.; Hassan, I. Use of bankruptcy methods for resolving interprovincial water conflicts over transboundary river: Case study of Indus River in Pakistan. River Res. Appl. 2020, 36, 1334–1344. [Google Scholar] [CrossRef]
- Hatcher, A. Non-compliance and the quota price in an ITQ fishery. J. Environ. Econ. Manag. 2005, 49, 427–436. [Google Scholar] [CrossRef]
- Bruno, E.M.; Sexton, R.J. The Gains from Agricultural Groundwater Trade and the Potential for Market Power: Theory and Application. Am. J. Agric. Econ. 2020, 102, 884–910. [Google Scholar] [CrossRef]
- Cui, X.; Zhao, T.; Wang, J. Allocation of carbon emission quotas in China’s provincial power sector based on entropy method and ZSG-DEA. J. Clean. Prod. 2021, 284, 124683. [Google Scholar] [CrossRef]
- Huang, Q.; Xu, J. Bi-level multi-objective programming approach for carbon emission quota allocation towards co-combustion of coal and sewage sludge. Energy 2020, 211, 118729. [Google Scholar] [CrossRef]
- Wang, Y.Z. A comparative study on the balance between the water demand and the maximal quota of water consumption in water allocation of waterscape of Beijing’s Chaoyang Park. Geogr. Res. 2011, 11, 26–29. [Google Scholar]
- Townsend, R.M. Optimal contracts and competitive markets with costly state verification. J. Econ. Theory 1979, 21, 265–293. [Google Scholar] [CrossRef]
- Gale, D.; Hellwig, M. Incentive-compatible debt contracts: The one-period problem. Rev. Econ. Stud. 1985, 52, 647–663. [Google Scholar] [CrossRef]
- Li, Y. Mechanism Design with Financially Constrained Agents and Costly Verification. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwid7JDmnP3wAhVfzIsBHduZCvIQFjACegQIBBAD&url=https%3A%2F%2Fecontheory.org%2F%3Ff%3D3907&usg=AOvVaw1bm2lbf_T_uakc50VeS1F5 (accessed on 3 June 2021).
- Patel, R.; Urgun, C. Costly Inspection and Money Burning in Internal Capital Markets. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwi04I7Umv3wAhUKM94KHWwDBDsQFjABegQIBBAD&url=https%3A%2F%2Fscholar.princeton.edu%2Fsites%2Fdefault%2Ffiles%2Fcurgun%2Ffiles%2F2017-04-23-inspectionmodel_submitted.pdf&usg=AOvVaw3b13RejC6_p0RDl41RRoVV (accessed on 3 June 2021).
- Wang, G.; Lin, N.; Zhou, X.; Li, Z.; Deng, X. Three-Stage Data Envelopment Analysis of Agricultural Water Use Efficiency: A Case Study of the Heihe River Basin. Sustainability 2018, 10, 568. [Google Scholar] [CrossRef]
- Rolfe, J.; Windle, J. Using auction mechanisms to reveal costs for water quality improvements in Great Barrier Reef catchments in Australia. Agric. Water Manag. 2011, 98, 493–501. [Google Scholar] [CrossRef]
- Yao, L.; Xu, Z.; Chen, X. Sustainable water allocation strategies under various climate scenarios: A case study in China. J. Hydrol. 2019, 574, 529–543. [Google Scholar] [CrossRef]
- Xu, J.; Lv, C.; Yao, L.; Hou, S. Intergenerational equity based optimal water allocation for sustainable development: A case study on the upper reaches of Minjiang River, China. J. Hydrol. 2018, 568, 835–848. [Google Scholar] [CrossRef]
- Crase, L.; Pagan, P.; Dollery, B. Water markets as a vehicle for reforming water resource allocation in the Murray-Darling Basin of Australia. Water Resour. Res. 2004, 40, 196–212. [Google Scholar] [CrossRef]
- Abed-Elmdoust, A.; Kerachian, R. Water Resources Allocation Using a Cooperative Game with Fuzzy Payoffs and Fuzzy Coalitions. Water Resour. Manag. 2012, 26, 3961–3976. [Google Scholar] [CrossRef]
- Ichihashi, S. Limiting Sender’s Information in Bayesian Persuasion. Games Econ. Behav. 2019, 117, 276–288. [Google Scholar] [CrossRef]
- Mierendorff, K. Optimal dynamic mechanism design with deadlines. J. Econ. Theory 2016, 161, 190–222. [Google Scholar] [CrossRef]


| District | Town | Different Hydrological Conditions | Reported Water Demand, ui (Unit: Million m3) | Water Resource Contribution, ai (Unit: Mil-lion m3) | GDP Contribution, Ii (Unit: Trillion CNY) |
|---|---|---|---|---|---|
| Yiling district | Zhangcunping | annual average | 615 | 86 | 65.2 |
| 95% | 588 | ||||
| Wuduhe | annual average | 1036 | 153 | 85.8 | |
| 95% | 954 | ||||
| Fenxiang | annual average | 1128 | 33,040 | 104.9 | |
| 95% | 1038 | ||||
| Haunghua | annual average | 1009 | 951 | 96.2 | |
| 95% | 1019 | ||||
| Xiaoxita Jieban | annual average | 1789 | 16,619 | 332.5 | |
| 95% | 1722 | ||||
| Yuan’an | Luozu | annual average | 1295 | 5875 | 67.6 |
| 95% | 1346 |
| District | Town | Different Hydrological Conditions | Water Allocation, Xi (Unit: Million m3) | |
|---|---|---|---|---|
| Yiling district | Zhangcunping | annual average | 615 | 0 |
| 95% | 519.83 | 68.17 | ||
| Wuduhe | annual average | 1036 | 0 | |
| 95% | 843.39 | 110.61 | ||
| Fenxiang | annual average | 1128 | 0 | |
| 95% | 917.65 | 120.35 | ||
| Haunghua | annual average | 1009 | 0 | |
| 95% | 900.85 | 118.15 | ||
| Xiaoxita Jieban | annual average | 1789 | 0 | |
| 95% | 1522.34 | 199.66 | ||
| Yuan’an | Luozu | annual average | 1295 | 0 |
| 95% | 1189.94 | 150.06 |
| District | Town | Frequency | Water Allocation (Unit: Million m3) | |
|---|---|---|---|---|
| Yiling district | Zhangcunping | annual average | 985.8223 | 370.8223 |
| 95% | 844.5535 | 324.7287 | ||
| Wuduhe | annual average | 1020.234 | −15.7659 | |
| 95% | 868.7122 | 25.32297 | ||
| Fenxiang | annual average | 1577.539 | 449.5387 | |
| 95% | 1346.109 | 428.459 | ||
| Haunghua | annual average | 1016.615 | 7.615078 | |
| 95% | 877.1251 | −23.7278 | ||
| Xiaoxita Jieban | annual average | 1090.796 | −698.204 | |
| 95% | 933.972 | −588.372 | ||
| Yuan’an | Luozu | annual average | 1179.994 | −115.006 |
| 95% | 1023.528 | −166.411 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, J. An Optimal Water Resource Allocation Mechanism Based on Ex-Post Verification and Reward in Huangbai River. Water 2021, 13, 1588. https://doi.org/10.3390/w13111588
Zhang H, Li J. An Optimal Water Resource Allocation Mechanism Based on Ex-Post Verification and Reward in Huangbai River. Water. 2021; 13(11):1588. https://doi.org/10.3390/w13111588
Chicago/Turabian StyleZhang, Hui, and Jiaying Li. 2021. "An Optimal Water Resource Allocation Mechanism Based on Ex-Post Verification and Reward in Huangbai River" Water 13, no. 11: 1588. https://doi.org/10.3390/w13111588
APA StyleZhang, H., & Li, J. (2021). An Optimal Water Resource Allocation Mechanism Based on Ex-Post Verification and Reward in Huangbai River. Water, 13(11), 1588. https://doi.org/10.3390/w13111588






