Comparison of Forecasting Models for Real-Time Monitoring of Water Quality Parameters Based on Hybrid Deep Learning Neural Networks
Abstract
1. Introduction
2. Materials and Methods
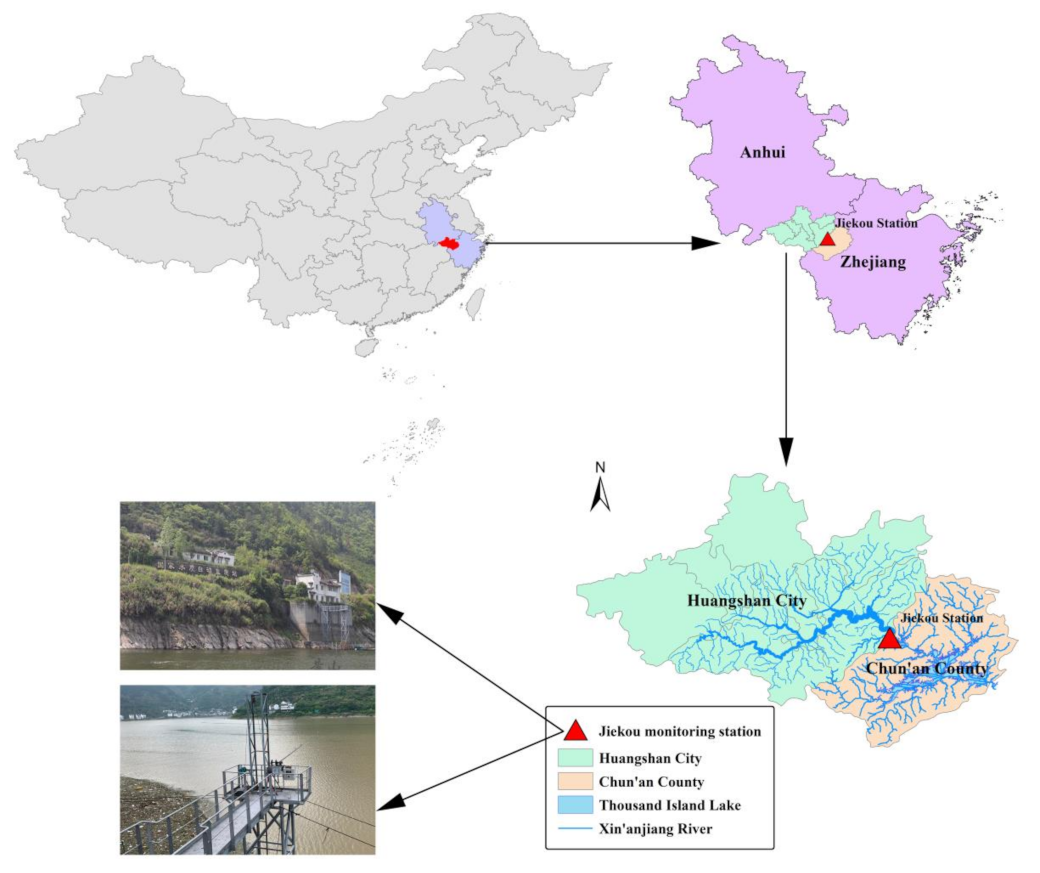
2.1. Study Area and Data Description
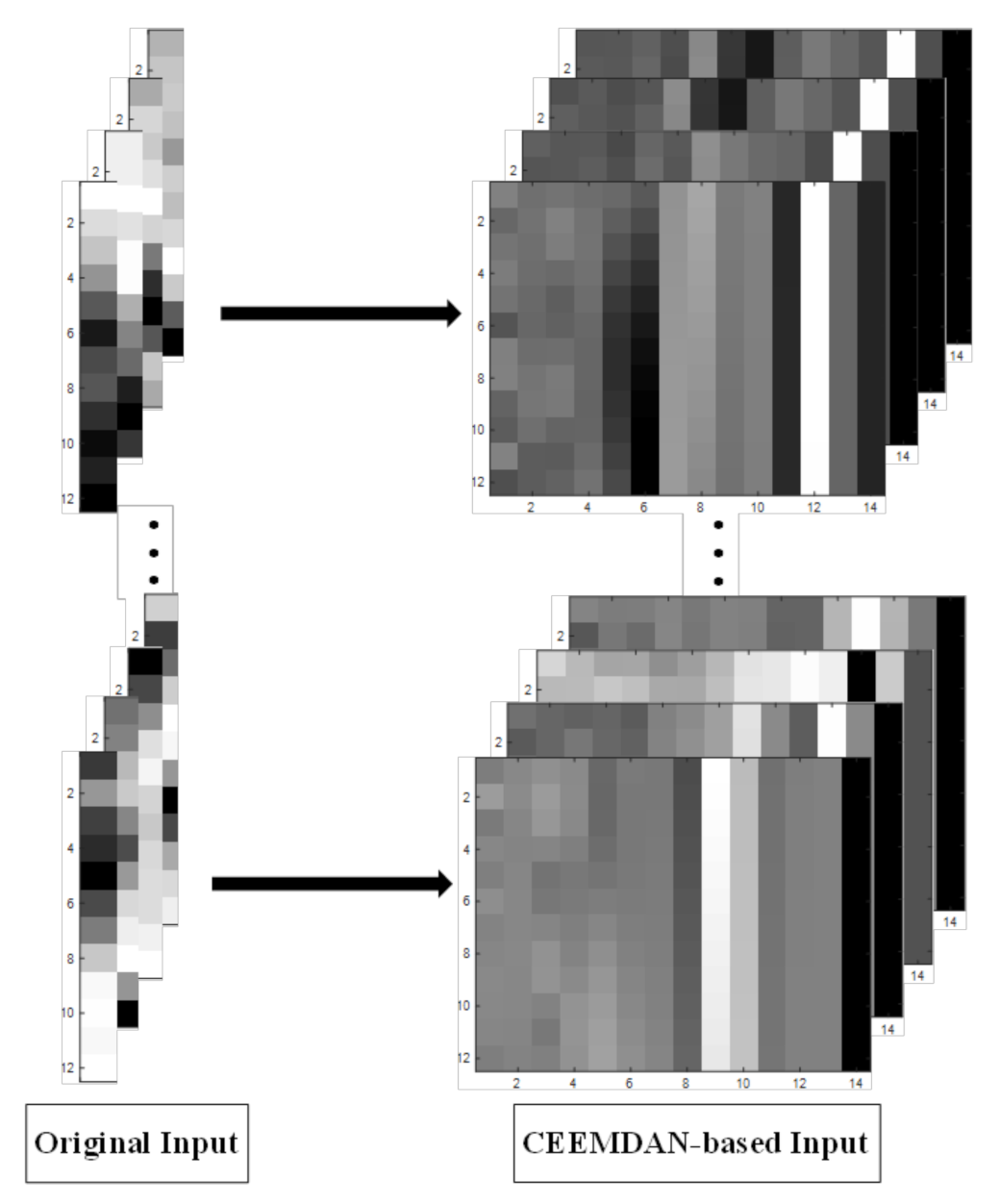
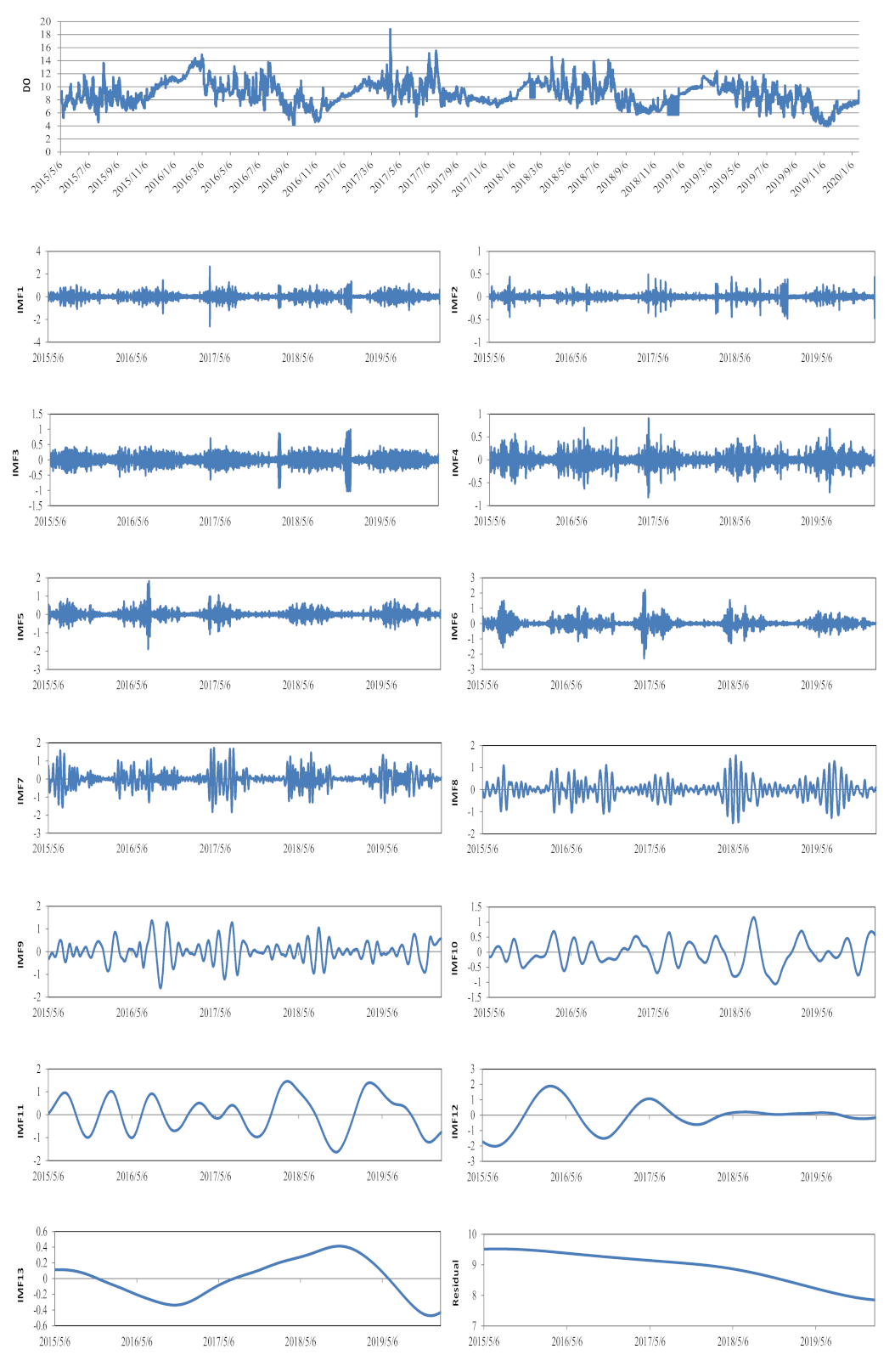
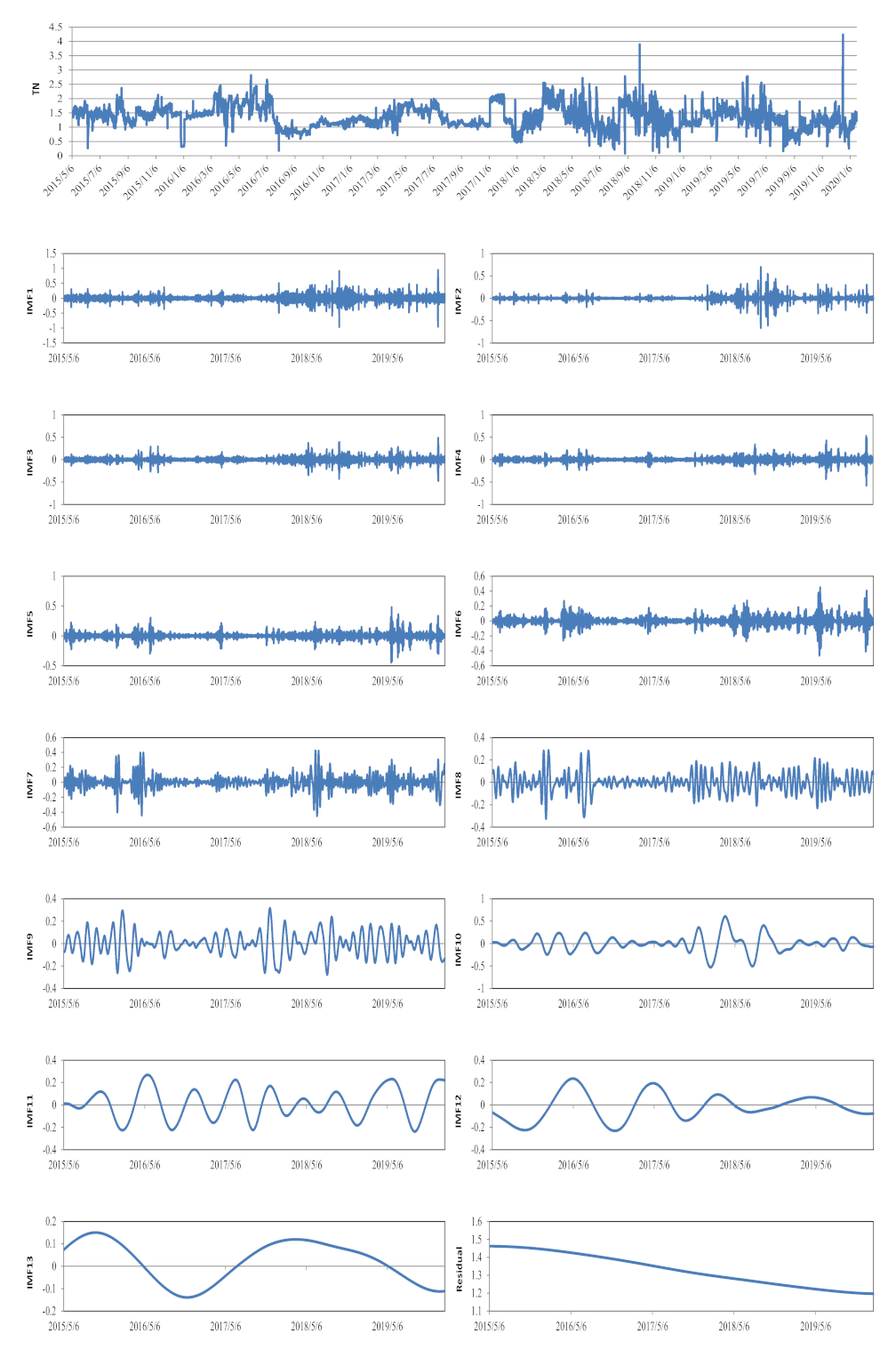
2.2. Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise
2.3. Convolutional Neural Network
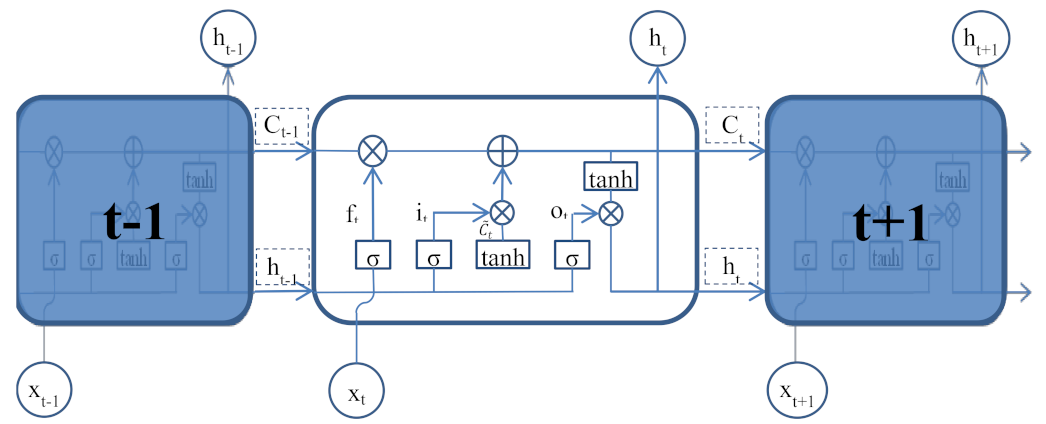
2.4. Long Short-Term Memory Neural Network
2.5. The Hybrid Forecasting Models Development
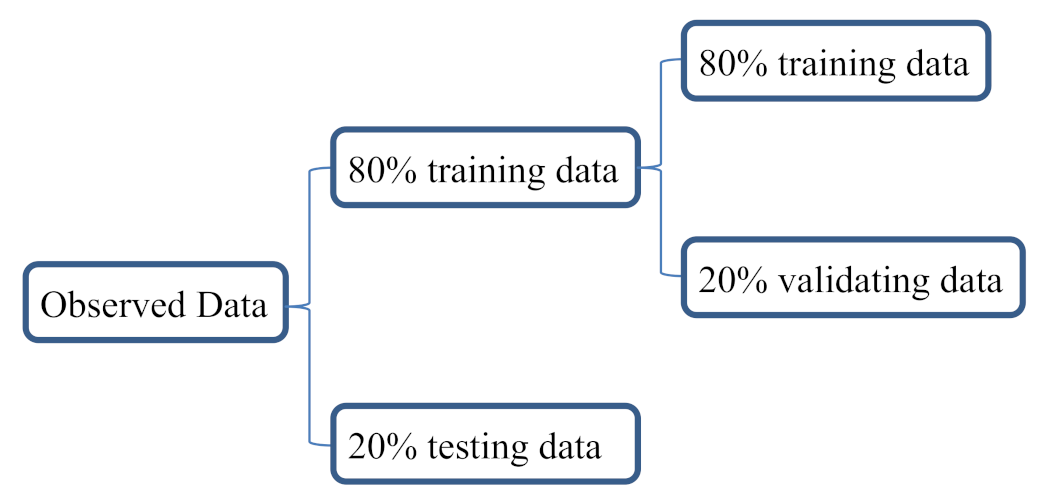
2.6. Evaluation Criteria
3. Results and Discussion
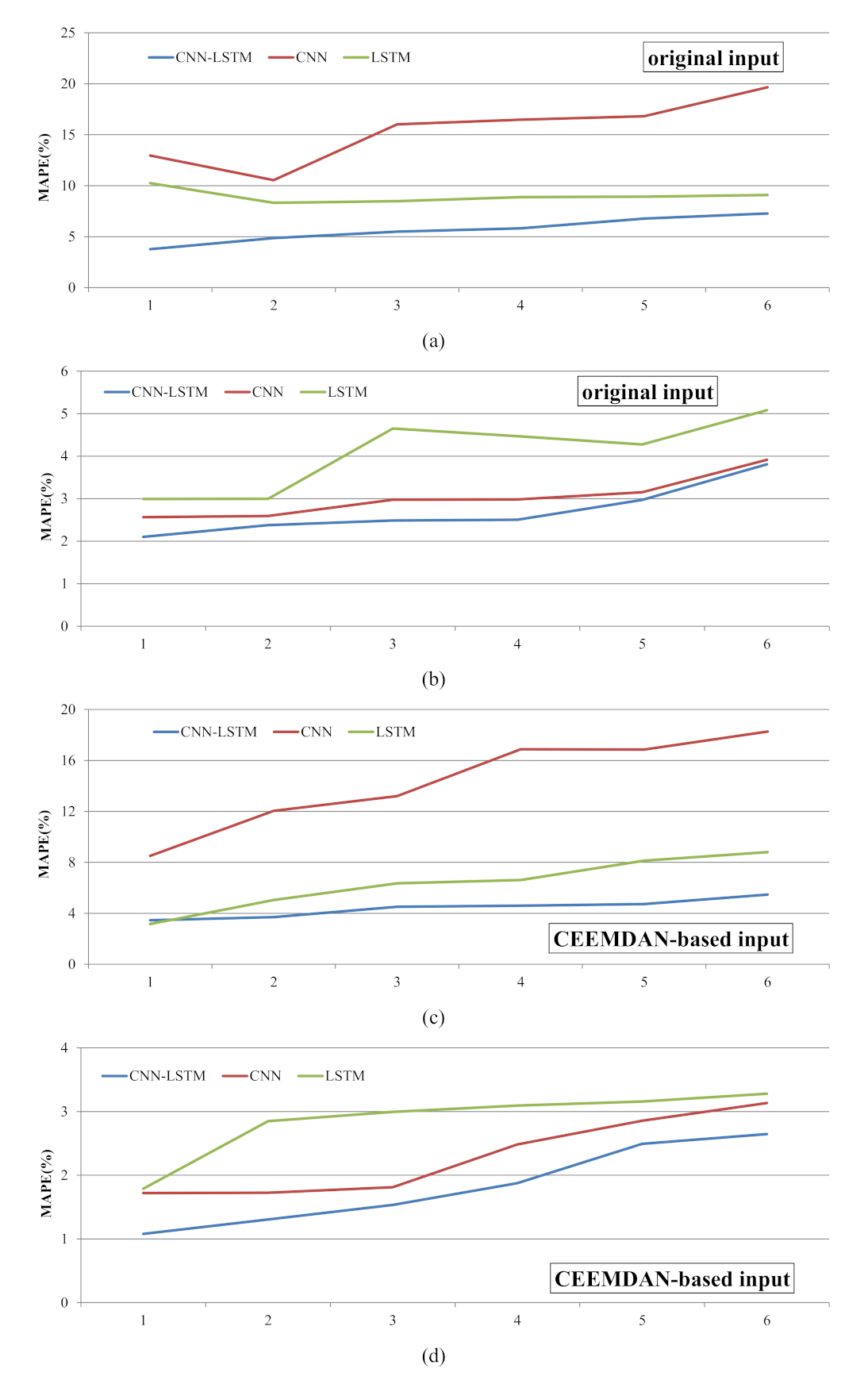
3.1. Results of DO Data Series
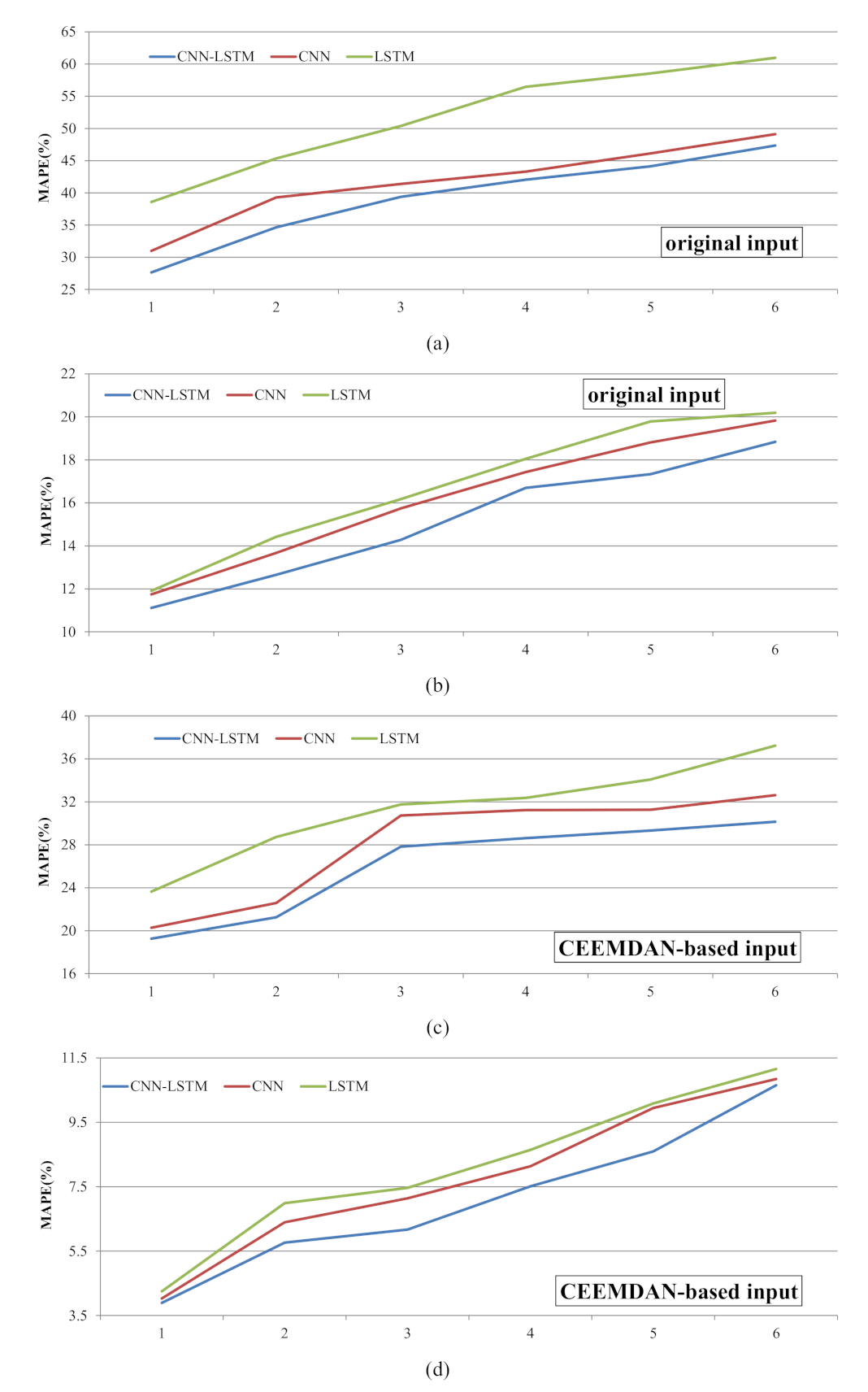
3.2. Results of TN Data Series
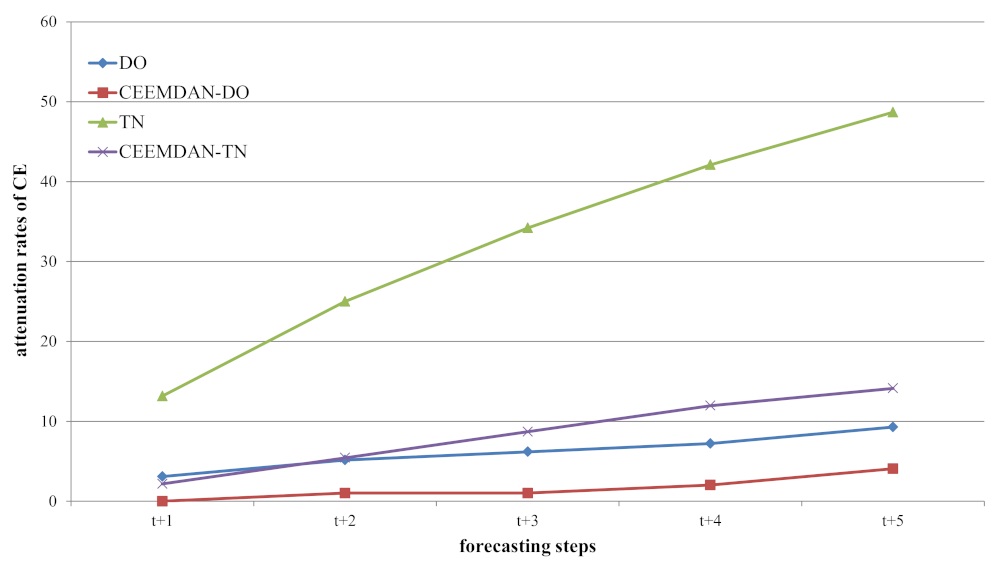
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, J.; Tang, S.; Han, D.; Fu, G.; Solomatine, D.; Zheng, Y. A comprehensive review on the design and optimization of surface water quality monitoring networks. Environ. Model. Softw. 2020, 132, 104792. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Z.; Wu, G.; Wu, Q.; Zhang, F.; Niu, Z.; Hu, H.-Y. Characteristics of water quality of municipal wastewater treatment plants in China: Implications for resources utilization and management. J. Clean. Prod. 2016, 131, 1–9. [Google Scholar] [CrossRef]
- Fijani, E.; Barzegar, R.; Deo, R.; Tziritis, E.; Skordas, K. Design and implementation of a hybrid model based on two-layer decomposition method coupled with extreme learning machines to support real-time environmental monitoring of water quality parameters. Sci. Total Environ. 2019, 648, 839–853. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef] [PubMed]
- Bucolo, M.; Fortuna, L.; Nelke, M.; Rizzo, A.; Sciacca, T. Prediction models for the corrosion phenomena in Pulp & Paper plant. Control Eng. Pract. 2002, 10, 227–237. [Google Scholar]
- Li, X.; Sha, J.; Li, Y.-M.; Wang, Z.-L. Comparison of hybrid models for daily streamflow prediction in a forested basin. J. Hydroinform. 2018, 20, 191–205. [Google Scholar] [CrossRef]
- Mohammadi, B.; Linh, N.T.T.; Pham, Q.B.; Ahmed, A.N.; Vojteková, J.; Guan, Y.; Abba, S.; El-Shafie, A. Adaptive neuro-fuzzy inference system coupled with shuffled frog leaping algorithm for predicting river streamflow time series. Hydrol. Sci. J. 2020, 65, 1738–1751. [Google Scholar] [CrossRef]
- Tabbussum, R.; Dar, A.Q. Performance evaluation of artificial intelligence paradigms—artificial neural networks, fuzzy logic, and adaptive neuro-fuzzy inference system for flood prediction. Environ. Sci. Pollut. Res. 2021, 1–18. [Google Scholar] [CrossRef]
- Raj, R.J.S.; Shobana, S.J.; Pustokhina, I.V.; Pustokhin, D.A.; Gupta, D.; Shankar, K. Optimal feature selection-based medical image classification using deep learning model in internet of medical things. IEEE Access 2020, 8, 58006–58017. [Google Scholar] [CrossRef]
- Jin, Y.; Wen, B.; Gu, Z.; Jiang, X.; Shu, X.; Zeng, Z.; Zhang, Y.; Guo, Z.; Chen, Y.; Zheng, T. Deep-Learning-Enabled MXene-Based Artificial Throat: Toward Sound Detection and Speech Recognition. Adv. Mater. Technol. 2020, 5, 2000262. [Google Scholar] [CrossRef]
- Wang, S.; Zha, Y.; Li, W.; Wu, Q.; Li, X.; Niu, M.; Wang, M.; Qiu, X.; Li, H.; Yu, H. A fully automatic deep learning system for COVID-19 diagnostic and prognostic analysis. Eur. Respir. J. 2020, 56. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Z.; Demir, I. Distributed long-term hourly streamflow predictions using deep learning—A case study for State of Iowa. Environ. Model. Softw. 2020, 131, 104761. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- An, L.; Hao, Y.; Yeh, T.-C.J.; Liu, Y.; Liu, W.; Zhang, B. Simulation of karst spring discharge using a combination of time–frequency analysis methods and long short-term memory neural networks. J. Hydrol. 2020, 589, 125320. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Liu, G.; He, W.; Cai, S. Seasonal Variation of Dissolved Oxygen in the Southeast of the Pearl River Estuary. Water 2020, 12, 2475. [Google Scholar] [CrossRef]
- Zhang, X.; Yi, Y.; Yang, Z. Nitrogen and phosphorus retention budgets of a semiarid plain basin under different human activity intensity. Sci. Total Environ. 2020, 703, 134813. [Google Scholar] [CrossRef]
- Li, X.; Feng, J.; Wellen, C.; Wang, Y. A Bayesian approach of high impaired river reaches identification and total nitrogen load estimation in a sparsely monitored basin. Environ. Sci. Pollut. Res. 2017, 24, 987–996. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Rahimpour, A.; Amanollahi, J.; Tzanis, C.G. Air quality data series estimation based on machine learning approaches for urban environments. Air Qual. Atmos. Health 2021, 14, 191–201. [Google Scholar] [CrossRef]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Harbola, S.; Coors, V. One dimensional convolutional neural network architectures for wind prediction. Energy Convers. Manag. 2019, 195, 70–75. [Google Scholar] [CrossRef]
- Wang, H.-Z.; Li, G.-Q.; Wang, G.-B.; Peng, J.-C.; Jiang, H.; Liu, Y.-T. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving monsoon precipitation prediction using combined convolutional and long short term memory neural network. Water 2019, 11, 977. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Niu, H.; Xu, K.; Wang, W. A hybrid stock price index forecasting model based on variational mode decomposition and LSTM network. Appl. Intell. 2020, 50, 4296–4309. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y.; Adamowski, J.F. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Appl. Energy 2018, 217, 422–439. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Yin, Z.; Yang, L.; Singh, V.P. Two-phase extreme learning machines integrated with the complete ensemble empirical mode decomposition with adaptive noise algorithm for multi-scale runoff prediction problems. J. Hydrol. 2019, 570, 167–184. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, K.; Luo, Y.; Shang, C. Spatial-temporal process simulation and prediction of chlorophyll-a concentration in Dianchi Lake based on wavelet analysis and long-short term memory network. J. Hydrol. 2020, 582, 124488. [Google Scholar] [CrossRef]
- Dai, S.; Niu, D.; Li, Y. Daily peak load forecasting based on complete ensemble empirical mode decomposition with adaptive noise and support vector machine optimized by modified grey wolf optimization algorithm. Energies 2018, 11, 163. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Si, J. Wavelet analysis–artificial neural network conjunction models for multi-scale monthly groundwater level predicting in an arid inland river basin, northwestern China. Hydrol. Res. 2017, 48, 1710–1729. [Google Scholar] [CrossRef]
| Descriptive Statistics | Unit | DO | TN | ||||
|---|---|---|---|---|---|---|---|
| T 1 | V 2 | T 3 | T 1 | V 2 | T 3 | ||
| Min. | mg/L | 4.12 | 5.7 | 3.95 | 0.18 | 0.08 | 0.16 |
| Mean | mg/L | 9.13 | 8.5 | 8.18 | 1.4 | 1.24 | 1.24 |
| Median | mg/L | 8.87 | 8.39 | 8.15 | 1.38 | 1.15 | 1.26 |
| Max. | mg/L | 18.85 | 14.14 | 12.42 | 2.82 | 3.9 | 4.24 |
| Standard deviation | mg/L | 1.79 | 1.69 | 1.91 | 0.37 | 0.42 | 0.37 |
| Skewness | dimensionless | 0.41 | 0.49 | −0.2 | 0.2 | 0.478 | 0.85 |
| Kurtosis | dimensionless | 0.27 | −0.25 | −0.8 | 0.12 | 0.61 | 0.36 |
| Target | Input1 | Input2 | Input3 | … | Input 11 | Input 12 |
|---|---|---|---|---|---|---|
| DOt | DOt−1 | DOt−2 | DOt−3 | … | DOt−11 | DOt−12 |
| DOt+1 | DOt−1 | DOt−2 | DOt−3 | … | DOt−11 | DOt−12 |
| DOt+2 | DOt−1 | DOt−2 | DOt−3 | … | DOt−11 | DOt−12 |
| DOt+3 | DOt−1 | DOt−2 | DOt−3 | … | DOt−11 | DOt−12 |
| DOt+4 | DOt−1 | DOt−2 | DOt−3 | … | DOt−11 | DOt−12 |
| DOt+5 | DOt−1 | DOt−2 | DOt−3 | … | DOt−11 | DOt−12 |
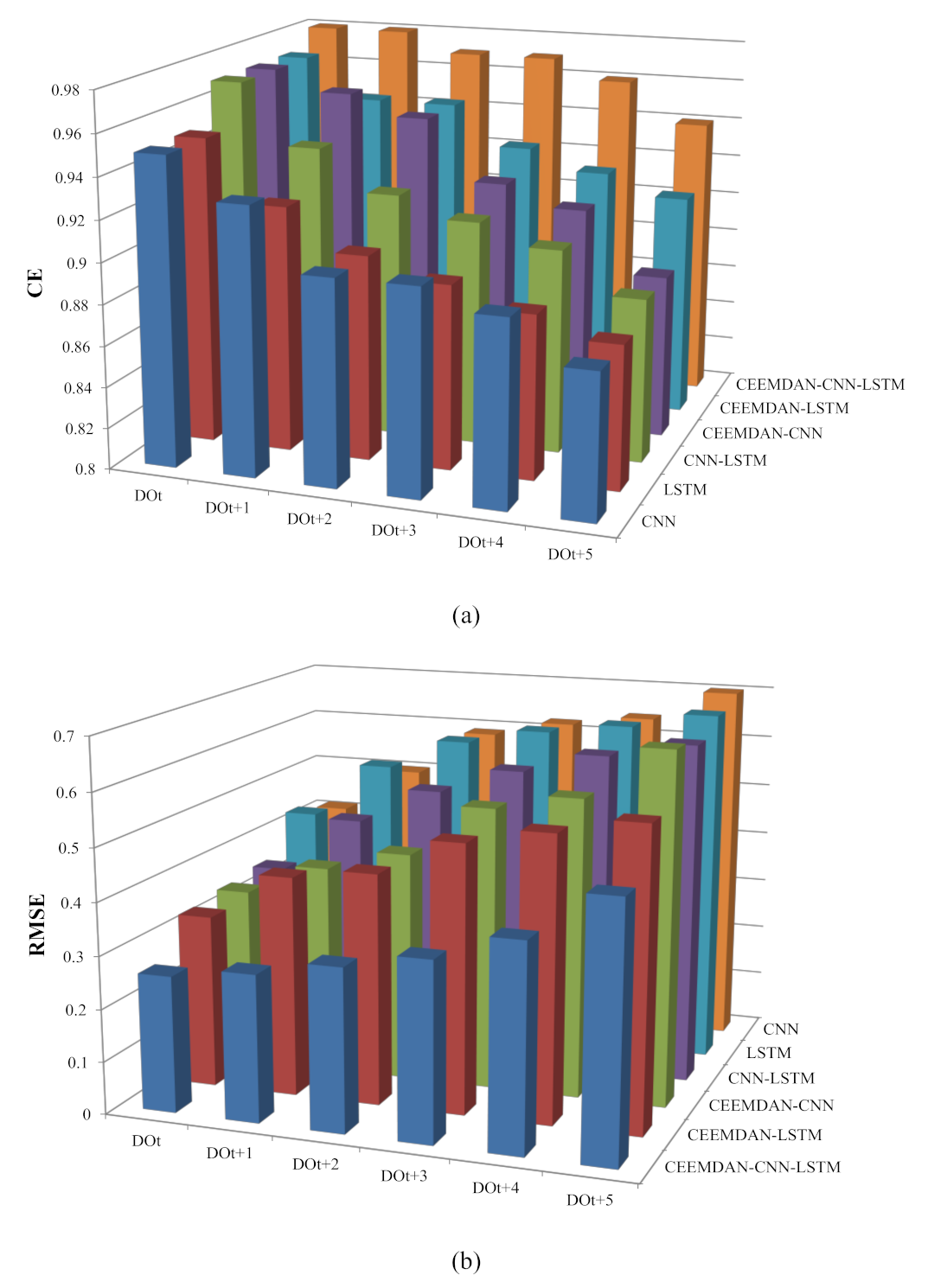
| Target | Models | CE | RMSE | MAPE |
|---|---|---|---|---|
| DOt | CNN | 0.95 | 0.41 | 4.17 |
| LSTM | 0.95 | 0.43 | 4.29 | |
| CNN–LSTM | 0.97 | 0.35 | 3.06 | |
| CEEMDAN–CNN | 0.97 | 0.34 | 4.02 | |
| CEEMDAN–LSTM | 0.97 | 0.33 | 3.23 | |
| CEEMDAN–CNN–LSTM | 0.98 | 0.26 | 2.55 | |
| DOt+1 | CNN | 0.93 | 0.50 | 4.68 |
| LSTM | 0.92 | 0.54 | 5.13 | |
| CNN–LSTM | 0.94 | 0.46 | 4.06 | |
| CEEMDAN–CNN | 0.96 | 0.40 | 4.92 | |
| CEEMDAN–LSTM | 0.95 | 0.42 | 4.32 | |
| CEEMDAN–CNN–LSTM | 0.98 | 0.28 | 2.79 | |
| DOt+2 | CNN | 0.90 | 0.59 | 6.03 |
| LSTM | 0.90 | 0.60 | 5.68 | |
| CNN–LSTM | 0.92 | 0.53 | 4.65 | |
| CEEMDAN–CNN | 0.95 | 0.44 | 5.37 | |
| CEEMDAN–LSTM | 0.95 | 0.44 | 4.62 | |
| CEEMDAN–CNN–LSTM | 0.97 | 0.31 | 3.00 | |
| DOt+3 | CNN | 0.90 | 0.62 | 6.21 |
| LSTM | 0.89 | 0.63 | 5.87 | |
| CNN–LSTM | 0.91 | 0.58 | 5.14 | |
| CEEMDAN–CNN | 0.92 | 0.54 | 6.66 | |
| CEEMDAN–LSTM | 0.93 | 0.51 | 5.24 | |
| CEEMDAN–CNN–LSTM | 0.97 | 0.34 | 3.30 | |
| DOt+4 | CNN | 0.89 | 0.64 | 6.34 |
| LSTM | 0.88 | 0.65 | 5.94 | |
| CNN–LSTM | 0.90 | 0.62 | 5.42 | |
| CEEMDAN–CNN | 0.91 | 0.57 | 7.02 | |
| CEEMDAN–LSTM | 0.92 | 0.54 | 5.76 | |
| CEEMDAN–CNN–LSTM | 0.96 | 0.39 | 3.65 | |
| DOt+5 | CNN | 0.87 | 0.70 | 6.96 |
| LSTM | 0.87 | 0.68 | 5.96 | |
| CNN–LSTM | 0.88 | 0.65 | 5.67 | |
| CEEMDAN–CNN | 0.88 | 0.67 | 8.38 | |
| CEEMDAN–LSTM | 0.91 | 0.57 | 6.24 | |
| CEEMDAN–CNN–LSTM | 0.94 | 0.48 | 4.56 |
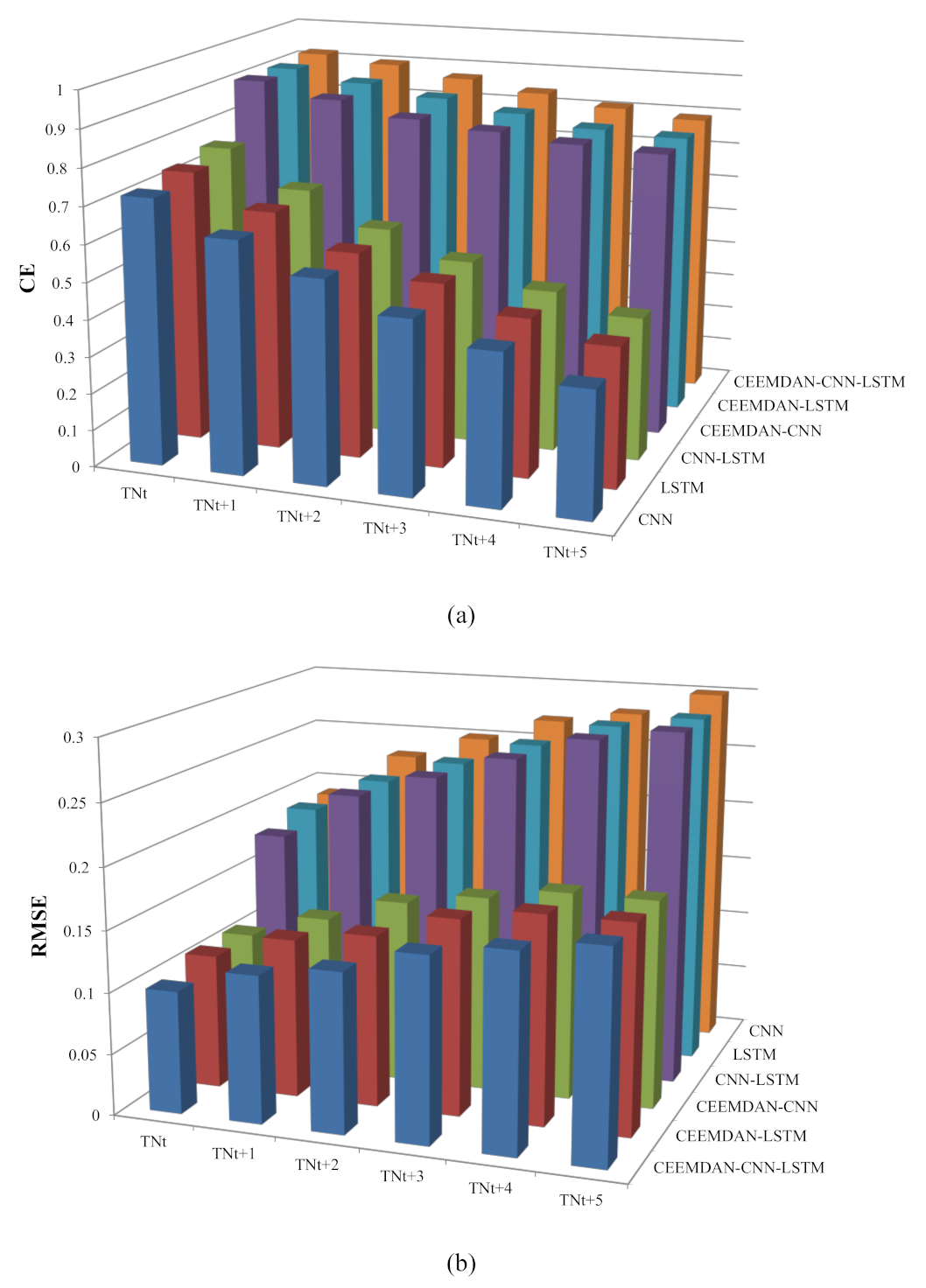
| Target | Models | CE | RMSE | MAPE |
|---|---|---|---|---|
| TNt | CNN | 0.72 | 0.19 | 10.79 |
| LSTM | 0.74 | 0.19 | 11.21 | |
| CNN–LSTM | 0.76 | 0.18 | 10.06 | |
| CEEMDAN–CNN | 0.91 | 0.11 | 6.68 | |
| CEEMDAN–LSTM | 0.91 | 0.11 | 7.41 | |
| CEEMDAN–CNN–LSTM | 0.92 | 0.10 | 6.63 | |
| TNt+1 | CNN | 0.63 | 0.23 | 12.71 |
| LSTM | 0.65 | 0.22 | 12.86 | |
| CNN–LSTM | 0.66 | 0.22 | 11.86 | |
| CEEMDAN–CNN | 0.87 | 0.13 | 7.95 | |
| CEEMDAN–LSTM | 0.88 | 0.13 | 8.64 | |
| CEEMDAN–CNN–LSTM | 0.90 | 0.12 | 7.71 | |
| TNt+2 | CNN | 0.55 | 0.25 | 13.48 |
| LSTM | 0.56 | 0.24 | 14.01 | |
| CNN–LSTM | 0.57 | 0.24 | 13.07 | |
| CEEMDAN–CNN | 0.83 | 0.15 | 10.27 | |
| CEEMDAN–LSTM | 0.85 | 0.14 | 9.65 | |
| CEEMDAN–CNN–LSTM | 0.87 | 0.13 | 8.71 | |
| TNt+3 | CNN | 0.47 | 0.27 | 14.37 |
| LSTM | 0.50 | 0.26 | 15.18 | |
| CNN–LSTM | 0.50 | 0.26 | 13.75 | |
| CEEMDAN–CNN | 0.81 | 0.16 | 10.88 | |
| CEEMDAN–LSTM | 0.82 | 0.16 | 10.03 | |
| CEEMDAN–CNN–LSTM | 0.84 | 0.15 | 9.12 | |
| TNt+4 | CNN | 0.41 | 0.28 | 15.24 |
| LSTM | 0.43 | 0.28 | 15.95 | |
| CNN–LSTM | 0.44 | 0.28 | 14.61 | |
| CEEMDAN–CNN | 0.79 | 0.17 | 10.68 | |
| CEEMDAN–LSTM | 0.79 | 0.17 | 10.66 | |
| CEEMDAN–CNN–LSTM | 0.81 | 0.16 | 9.37 | |
| TNt+5 | CNN | 0.34 | 0.30 | 15.86 |
| LSTM | 0.38 | 0.29 | 16.60 | |
| CNN–LSTM | 0.39 | 0.29 | 15.41 | |
| CEEMDAN–CNN | 0.78 | 0.17 | 10.55 | |
| CEEMDAN–LSTM | 0.78 | 0.17 | 11.13 | |
| CEEMDAN–CNN–LSTM | 0.79 | 0.17 | 9.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, J.; Li, X.; Zhang, M.; Wang, Z.-L. Comparison of Forecasting Models for Real-Time Monitoring of Water Quality Parameters Based on Hybrid Deep Learning Neural Networks. Water 2021, 13, 1547. https://doi.org/10.3390/w13111547
Sha J, Li X, Zhang M, Wang Z-L. Comparison of Forecasting Models for Real-Time Monitoring of Water Quality Parameters Based on Hybrid Deep Learning Neural Networks. Water. 2021; 13(11):1547. https://doi.org/10.3390/w13111547
Chicago/Turabian StyleSha, Jian, Xue Li, Man Zhang, and Zhong-Liang Wang. 2021. "Comparison of Forecasting Models for Real-Time Monitoring of Water Quality Parameters Based on Hybrid Deep Learning Neural Networks" Water 13, no. 11: 1547. https://doi.org/10.3390/w13111547
APA StyleSha, J., Li, X., Zhang, M., & Wang, Z.-L. (2021). Comparison of Forecasting Models for Real-Time Monitoring of Water Quality Parameters Based on Hybrid Deep Learning Neural Networks. Water, 13(11), 1547. https://doi.org/10.3390/w13111547






