Comparative Analysis of Runoff and Evaporation Assessment Methods to Evaluate Wetland–Groundwater Interaction in Mediterranean Evaporitic-Karst Aquatic Ecosystem
Abstract
1. Introduction
2. Geological and Hydrological Settings

3. Methods
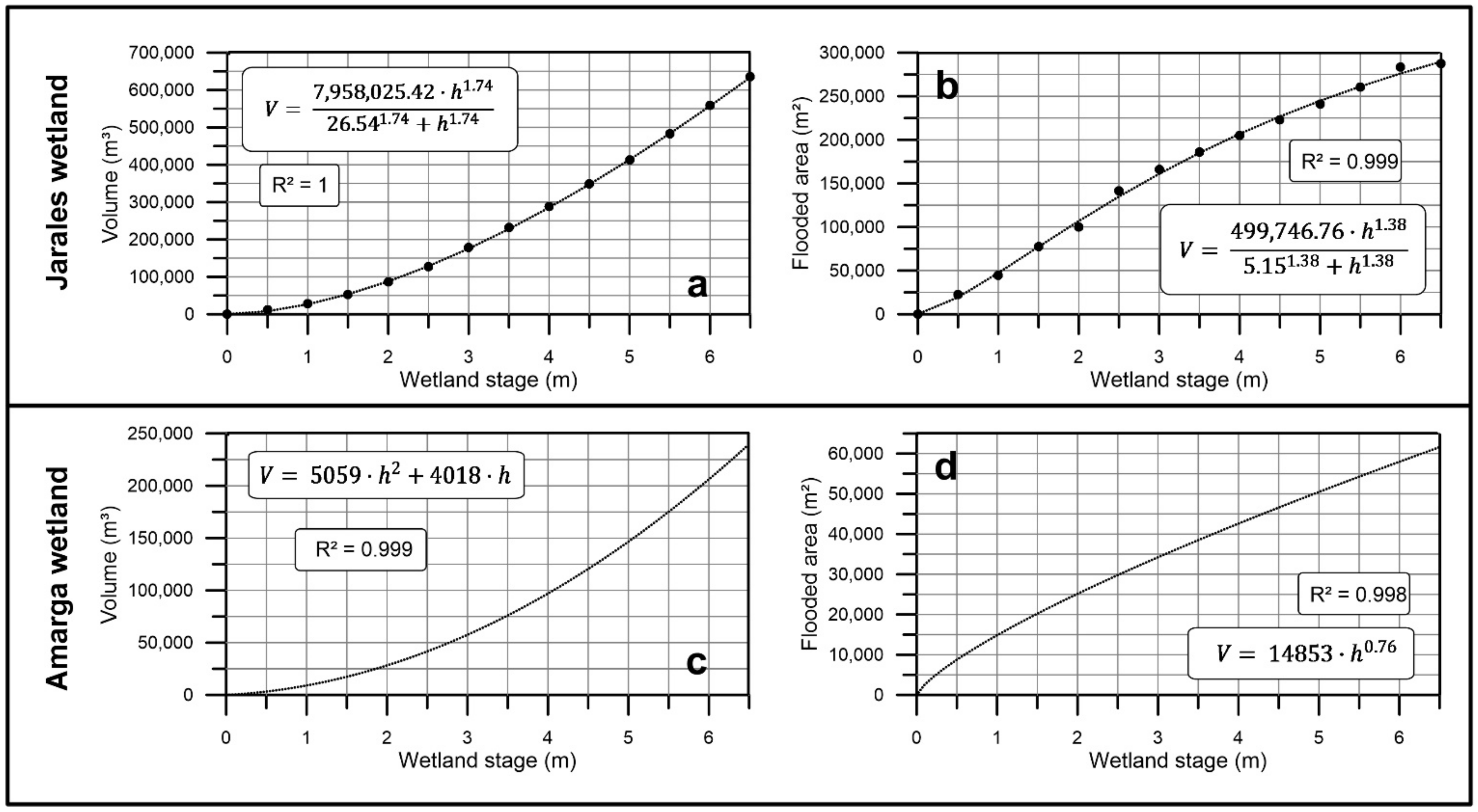
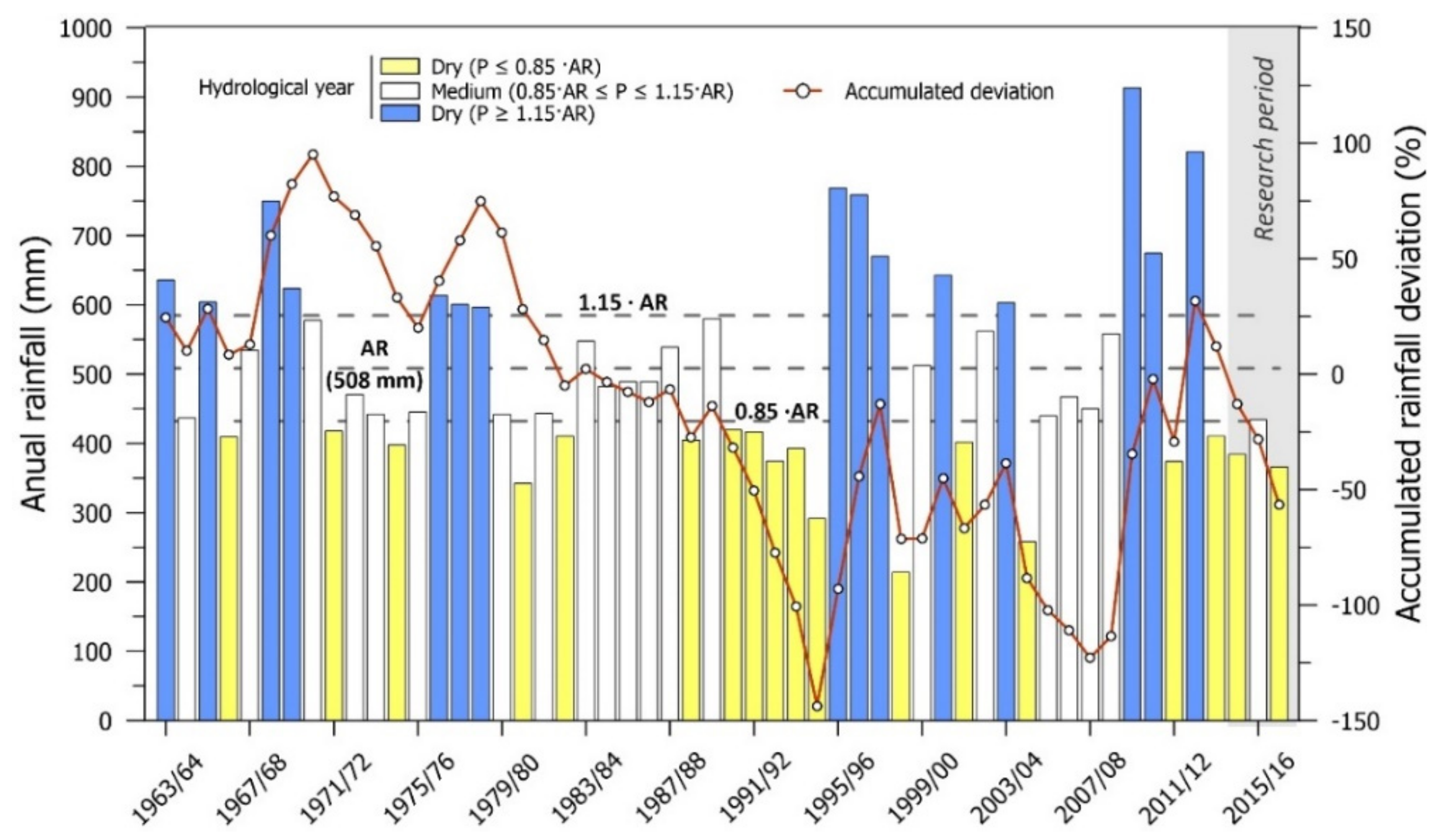
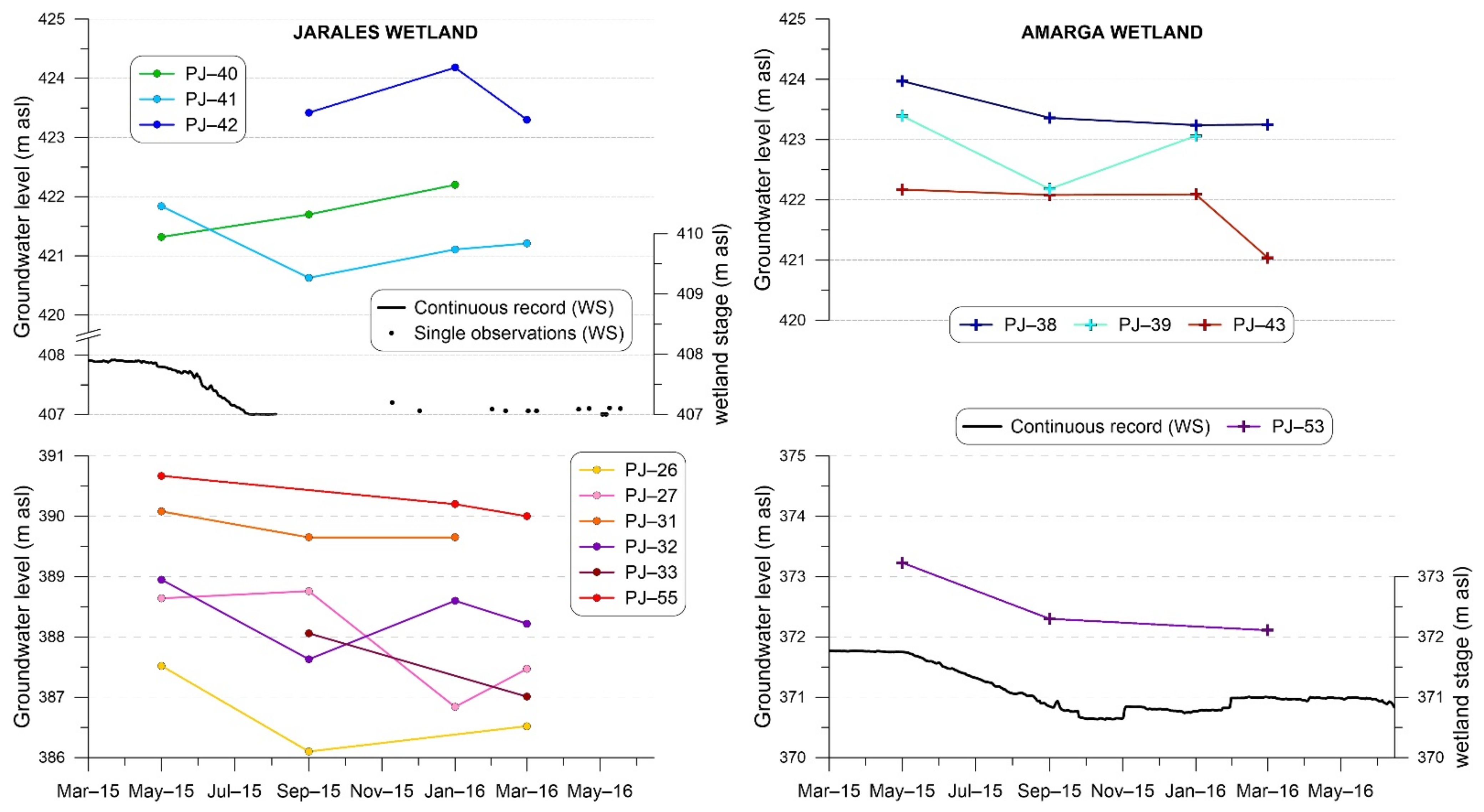
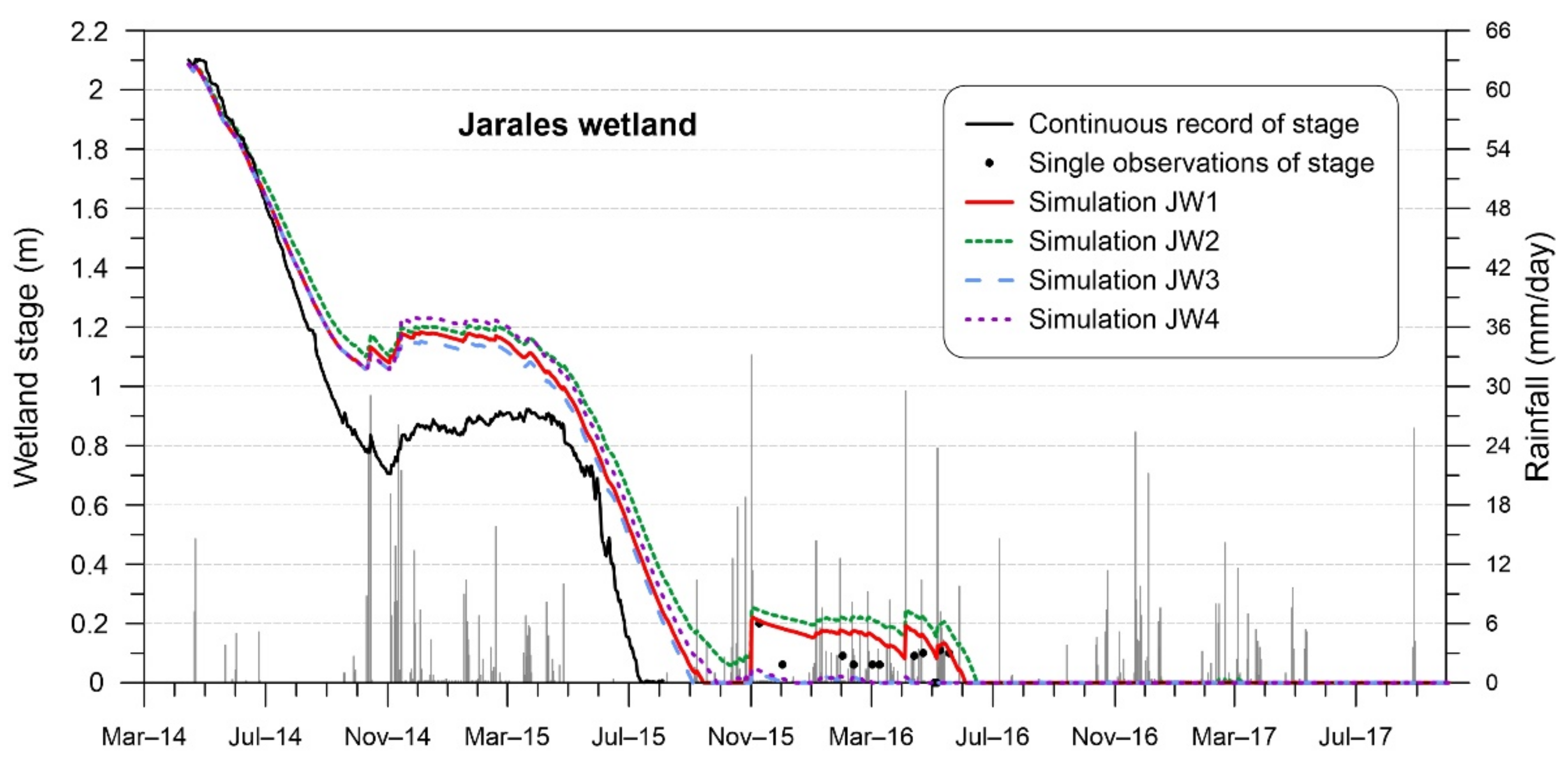
4. Results

5. Discussion
5.1. Choosing the Runoff and Evaporation Equations for the Limnimetric Simulation
5.2. Integrating the Results into a Hydrogeological Conceptual Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mitsch, W.J.; Gosselink, J.G. Wetlands, 5th ed.; Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 9788578110796. [Google Scholar]
- National Research Council. Wetlands: Characteristics and Boundaries; National Academy Press: Washington, DC, USA, 1995; ISBN 0309051347.
- Millenium Ecosystem Assessment. Ecosystems and Humanwell-Being: Wetlands and Water Syntesys; World Resources Institute: Washington, DC, USA, 2005. [Google Scholar]
- LePage, B.A. Wetlands; LePage, B.A., Ed.; Springer: Dordrecht, The Netherlands, 2011; ISBN 9789400705500. [Google Scholar]
- Jolly, I.D.; McEwan, K.L.; Holland, K.L. A review of groundwater–surface water interactions in arid/semi-arid wetlands and the consequences of salinity for wetland ecology. Ecohydrology 2008, 1, 43–52. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Winter, T.C. Dynamics of water-table fluctuations in an upland between two prairie-pothole wetlands in North Dakota. J. Hydrol. 1997, 191, 266–289. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O.; Labaugh, J.W. Where Does the Ground Water in Small Watersheds Come From? GroundWater 2003, 41, 989–1000. [Google Scholar] [CrossRef]
- House, A.R.; Thompson, J.R.; Acreman, M.C. Projecting impacts of climate change on hydrological conditions and biotic responses in a chalk valley riparian wetland. J. Hydrol. 2016, 534, 178–192. [Google Scholar] [CrossRef]
- Mitchell, J.; Jawitz, J.W. Wetland Water Budgets. In Methods in Biogeochemistry of Wetlands; DeLaune, R.D., Reddy, K.R., Richardson, C.J., Megonigal, J.P., Eds.; SSSA: Madison, WI, USA, 2013; pp. 919–936. [Google Scholar]
- Rosenberry, D.O.; Hayashi, M. Assesing and measuring wetland hydrology. In Wetland Techniques. Vol. 1: Foundations; Anderson, J.T., Davis, C.A., Eds.; Springer Sciences Business Media: Dordrecht, The Netherlands, 2013; pp. 87–225. [Google Scholar]
- Walton, R.; Chapman, R.S.; Davis, J.E. Development and application of the wetlands dynamic water budget model. Wetlands 1996, 16, 347–357. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, M.; Fernández, A.; Moral, F. Hydrological regime and modeling of three ponds of the Mediterranean area (south of Córdoba, Spain). Hydrobiologia 2016, 782, 155–168. [Google Scholar] [CrossRef]
- Rimmer, A.; Gal, G. Estimating the saline springs component in the solute and water balance of Lake Kinneret, Israel. J. Hydrol. 2003, 284, 228–243. [Google Scholar] [CrossRef]
- O′Driscoll, M.A.; Parizek, R.R. The hydrologic catchment area of a chain of karst wetlands in central Pennsylavania, USA. Wetlands 2003, 23, 171–179. [Google Scholar] [CrossRef]
- Min, J.H.; Perkins, D.B.; Jawitz, J.W. Wetland-groundwater interactions in subtropical depressional wetlands. Wetlands 2010, 30, 997–1006. [Google Scholar] [CrossRef]
- McKillop, R.; Kouwen, N.; Soulis, E.D. Modeling the rainfall-runoff response of a headwater wetland. Water Resour. Res. 1999, 35, 1165–1177. [Google Scholar] [CrossRef]
- Hood, J.L.; Roy, J.W.; Hayashi, M. Importance of groundwater in the water balance of an alpine headwater lake. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Castañeda, C.; García-Vera, M.Á. Water balance in the playa-lakes of an arid environment, Monegros, NE Spain. Hydrogeol. J. 2008, 16, 87–102. [Google Scholar] [CrossRef]
- Ludwig, A.L.; Hession, W.C. Groundwater influence on water budget of a small constructed floodplain wetland in the Ridge and Valley of Virginia, USA. J. Hydrol. Reg. Stud. 2015, 4, 699–712. [Google Scholar] [CrossRef][Green Version]
- Hayashi, M.; Van Der Kamp, G. Simple equations to represent the volume-area-depth relations of shallow wetlands in small topographic depressions. J. Hydrol. 2000, 237, 74–85. [Google Scholar] [CrossRef]
- Los Huertos, M.; Smith, D. Wetland bathymetry and mapping. In Wetland Techniques. Vol. 1: Foundations; Anderson, J.T., Davis, C.A., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 49–86. [Google Scholar]
- Ray, A.M.; Sepulveda, A.J.; Irvine, K.M.; Wilmoth, S.K.C.; Thoma, D.P.; Patla, D.A. Wetland drying linked to variations in snowmelt runoff across Grand Teton and Yellowstone national parks. Sci. Total Environ. 2019, 666, 1188–1197. [Google Scholar] [CrossRef]
- Keijman, J.Q.; Koopmans, R.W.R. A comparison of several methods of estimating the evaporation of Lake Flevo. Int. Assoc. Hydrol. Sci. 1973, 109, 225–232. [Google Scholar]
- Rosenberry, D.O.; Winter, T.C.; Buso, D.C.; Likens, G.E. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. J. Hydrol. 2007, 340, 149–166. [Google Scholar] [CrossRef]
- Yao, H. Long-Term Study of Lake Evaporation and Evaluation of Seven Estimation Methods: Results from Dickie Lake, South-Central Ontario, Canada. J. Water Resour. Prot. 2009, 1, 59–77. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, M.; Moral, F.; Benavente, J.; Beltrán, M. Developing hydrological indices in semi-arid playa-lakes by analyzing their main morphometric, climatic and hydrochemical characteristics. J. Arid Environ. 2010, 74, 1478–1486. [Google Scholar] [CrossRef]
- Vera, J.A.; Martín-Algarra, A. Cordillera Bética. In Geología de España; Vera, J.A., Ed.; IGME-SGE: Madrid, Spain, 2004; pp. 345–464. [Google Scholar]
- CHG. Definición del Contexto Hidrogeológico de Humedales de la Campiña Andaluza Central; Confederación Hidrográfica del Guadalquivir: Seville, Spain, 2008. [Google Scholar]
- CMA. Definición del Contexto Hidrogeológico de Humedales Andaluces; Conserjería de Medio Ambiente de la Junta de Andalucía: Málaga, Spain, 2005. [Google Scholar]
- Aljibe-Consultores. Estudio Hidrogeológico de las Lagunas del sur de Córdoba: Lagunas de Rincón y Santiago, Lagunas Amarga y Dulce; Junta de Andalucía: Córdoba, Spain, 2005. [Google Scholar]
- Moral, F.; Rodríguez-Rodríguez, M.; Beltrán, M.; Benavente, J.; Cifuentes, V.J. Water Regime of Playa Lakes from Southern Spain: Conditioning Factors and Hydrological Modeling. Water Environ. Res. 2013, 85, 632–642. [Google Scholar] [CrossRef]
- Martín-Serrano, A. Mapa Geológico de la Hoja no 1006 (Benamejí). Mapa Geológico de España, E. 1:50.000. Segunda Serie (MAGNA), Primera Edición; IGME: Madrid, Spain, 1986. [Google Scholar]
- Gil-Márquez, J.M.; Andreo, B.; Mudarra, M. Combining hydrodynamics, hydrochemistry, and environmental isotopes to understand the hydrogeological functioning of evaporite-karst springs. An example from southern Spain. J. Hydrol. 2019, 576, 299–314. [Google Scholar] [CrossRef]
- Gil-Márquez, J.M. Caracterización Hidrogeológica de Humedales y Manantiales Salinos Asociados a Acuíferos Kársticos Evaporíticos del Sector Central del Subbético; Universidad de Granada: Granada, Spain, 2018. [Google Scholar]
- Gil-Márquez, J.M.; Barberá, J.A.; Mudarra, M.; Andreo, B.; Prieto-Mera, J.; Sánchez, D.; Rizo-Decelis, L.D.; Argamasilla, M.; Nieto, J.M.; De la Torre, B. Karst development of an evaporitic system and its hydrogeological implications inferred from GIS-based analysis and tracing techniques. Int. J. Speleol. 2017, 46, 219–235. [Google Scholar] [CrossRef][Green Version]
- Miller, V.C. A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area Virginia and Tennessee (Proj. NR 389-402, Technical Report 3); Columbia University: New York, NY, USA, 1953. [Google Scholar]
- Schumm, S.A. Geological Society of America Bulletin Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage-basin characteristics. Trans. Am. Geophys. Union 1932, 13, 350. [Google Scholar] [CrossRef]
- IGN Plan Nacional de Ortofotografía Aerea. Available online: https://pnoa.ign.es/el-proyecto-pnoa-lidar (accessed on 1 March 2021).
- García-Ferrer, A.; Recio Espejo, J.M.; Sánchez de la Orden, M. Medidas morfométricas y batimétricas de las lagunas Amarga y del Rincón (Córdoba). Boletín la Estac. Cent. Ecol. 1983, 12, 51–55. [Google Scholar]
- Voldseth, R.A.; Johnson, W.C.; Gilmanov, T.; Guntenspergen, G.R.; Millett, B.V. Model estimation of land-use effects on water levels of northern prairie wetlands. Ecol. Appl. 2007, 17, 527–540. [Google Scholar] [CrossRef]
- Gurrieri, J.T.; Furniss, G. Estimation of groundwater exchange in alpine lakes using non-steady mass-balance methods. J. Hydrol. 2004, 297, 187–208. [Google Scholar] [CrossRef]
- Krasnostein, A.L.; Oldham, C.E. Predicting wetland water storage. Water Resour. Res. 2004, 40, 1–12. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Mockus, V. Estimation of direct runoff from storm rainfall. In SCS, National Engineering Handbook; USDA Soil Conservation Services: Washington DC, USA, 1964; p. 30. [Google Scholar]
- Públicas, M.d.O. Cálculo Hidrometeorológico de Caudales Máximos en Pequeñas Cuencas Naturales; Ministerio de Obras Públicas: Madrid, Spain, 1987. [Google Scholar]
- Thornthwaite, C.W.; Mather, J.R. The water balance. Publ. Climatol. 1955, 8, 86. [Google Scholar]
- Thornthwaite, C.W. An approach toward rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Areas from Climatological and Irrigation Data. Technical Report-96; USDA: Washington, DC, USA, 1950. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar]
- Souch, C.; Grimmond, C.S.B.; Wolfe, C.P. Evapotranspiration rates from wetlands with different disturbance histories: Indiana Dunes National Lakeshore. Wetlands 1998, 18, 216–229. [Google Scholar] [CrossRef]
- Finch, J.W. A comparison between measured and modelled open water evaporation from a reservoir in south-east England. Hydrol. Process. 2001, 15, 2771–2778. [Google Scholar] [CrossRef]
- Wossenu, A. Evaporation Estimation for Lake Okeechobee in South Florida. J. Irrig. Drain. Eng. 2001, 127, 140–147. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Morin, R.H. Use of an Electromagnetic Seepage Meter to Investigate Temporal Variability in Lake Seepage. Ground Water 2004, 42, 68–77. [Google Scholar] [CrossRef]
- Kohler, M.A.; Parmele, L.H. Generalized estimates of free-water evaporation. Water Resour. Res. 1967, 3, 997–1005. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and surface temperature. Q. J. R. Meteorol. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Morton, F.I. Practical estimates of lake evaporation. J. Clim. Appl. Meteorol. 1986, 25, 371–387. [Google Scholar] [CrossRef]
- Fennessey, N.M. Estimating average monthly lake evaporation in tile northeast united states. J. Am. Water Resour. Assoc. 2000, 36, 759–769. [Google Scholar] [CrossRef]
- McJannet, D.L.; Webster, I.T.; Stenson, M.P.; Sherman, B.S. Estimating Open Water Evaporation for the Murray-Darling Basin: A Report to the Australian Government from the CSIRO Murray-Darling Basin Sustainable Yields Project; CSIRO: Canbera, Australia, 2008; Volume 50. [Google Scholar]
- Vardavas, I.M.; Fountoulakis, A. Estimation of lake evaporation from standard meteorological measurements: Application to four Australian lakes in different climatic regions. Ecol. Modell. 1996, 84, 139–150. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Finch, J.; Calver, A. Methods for the Quantification of Evaporation from Lakes. Available online: http://nora.nerc.ac.uk/id/eprint/14359/1/wmoevap_271008.pdf (accessed on 1 March 2021).
- Andreo, B.; Gil-Márquez, J.M.; Mudarra, M.; Linares, L.; Carrasco, F. Hypothesis on the hydrogeological context of wetland areas and springs related to evaporitic karst aquifers (Málaga, Córdoba and Jaén provinces, Southern Spain). Environ. Earth Sci. 2016, 75, 1–19. [Google Scholar] [CrossRef]
- Doss, P.K. The nature of a dynamic water table in a system of non-tidal, freshwater coastal wetlands. J. Hydrol. 1993, 141, 107–126. [Google Scholar] [CrossRef]
- Moya, J.L. Hidrología de las Zonas Húmedas del sur de la Provincia de Córdoba; Universidad de Córdoba: Córdoba, Spain, 1988. [Google Scholar]
- Gil-Márquez, J.M.; Sültenfuß, J.; Andreo, B.; Mudarra, M. Groundwater dating tools (3H, 3He, 4He, CFC-12, SF6) coupled with hydrochemistry to evaluate the hydrogeological functioning of complex evaporite-karst settings. J. Hydrol. 2020, 580, 124263. [Google Scholar] [CrossRef]
- Valiente, N.; Gil-Márquez, J.M.; Gómez-Alday, J.J.; Andreo, B. Unraveling groundwater functioning and nitrate attenuation in evaporitic karst systems from southern Spain: An isotopic approach. Appl. Geochem. 2020, 123, 104820. [Google Scholar] [CrossRef]
- Cameron, C.R.; Hancock, M.C.; Carr, D.W.; Hurst, M.K.; Campbell, D.E.; Venning, T.J.; Tara, P.D.; Holzwart, K.R. Hydroperiods of Cypress Domes in West-Central Florida, USA. Wetlands 2020, 40, 2225–2234. [Google Scholar] [CrossRef]
- Montgomery, J.S.; Hopkinson, C.; Brisco, B.; Patterson, S.; Rood, S.B. Wetland hydroperiod classification in the western prairies using multitemporal synthetic aperture radar. Hydrol. Process. 2018, 32, 1476–1490. [Google Scholar] [CrossRef]
- Hayashi, M.; van der Kamp, G.; Rosenberry, D.O. Hydrology of Prairie Wetlands: Understanding the Integrated Surface-Water and Groundwater Processes. Wetlands 2016, 36, 237–254. [Google Scholar] [CrossRef]
- Tóth, Á.; Havril, T.; Simon, S.; Galsa, A.; Monteiro Santos, F.A.; Müller, I.; Mádl-Szőnyi, J. Groundwater flow pattern and related environmental phenomena in complex geologic setting based on integrated model construction. J. Hydrol. 2016, 539, 330–344. [Google Scholar] [CrossRef]
- Manzano, M.; Custodio, E. Relationships between weltands and the Doñana coastal aquifer (SW Spain). In Groundwater and Ecosystems; IAH, Ed.; CRC Press: London, UK, 2013; pp. 169–182. ISBN 978-1-138-00033-9. [Google Scholar]
- Bryant, R.G.; Rainey, M.P. Investigation of flood inundation on playas within the Zone of Chotts, using a time-series of AVHRR. Remote Sens. Environ. 2002, 82, 360–375. [Google Scholar] [CrossRef]
- Brooks, R.T. Potential impacts of global climate change on the hydrology and ecology of ephemeral freshwater systems of the forests of the northeastern United States. Clim. Chang. 2009, 95, 469–483. [Google Scholar] [CrossRef]
- Ma, J.Z.; Ding, Z.; Gates, J.B.; Su, Y. Chloride and the environmental isotopes as the indicators of the groundwater recharge in the Gobi Desert, northwest China. Environ. Geol. 2008, 55, 1407–1419. [Google Scholar] [CrossRef]
- Su, M.; Stolte, W.J.; Van Der Kamp, G. Modelling Canadian prairie wetland hydrology using a semi-distributed streamflow model. Hydrol. Process. 2000, 14, 2405–2422. [Google Scholar] [CrossRef]
- Hayashi, M.; Rosenberry, D.O. Effects of Ground Water Exchange on the Hydrology and Ecology of Surface Water. Ground Water 2002, 40, 309–316. [Google Scholar] [CrossRef]
- Acreman, M. Wetlands and Hydrology; Crivelli, J.A., Albert, J., Eds.; Station Biologuique de la Tour du Valat: Arles, France, 2000; ISBN 2-910368-32-7. [Google Scholar]
- Euliss, N.H.; Labaugh, J.W.; Fredrickson, L.H.; Mushet, D.M.; Laubhan, M.K.; Swanson, G.A.; Winter, T.C.; Rosenberry, D.O.; Nelson, R.D. the Wetland Continuum: A Conceptual Framework for Interpreting Biological Studies. Wetlands 2004, 24, 448–458. [Google Scholar] [CrossRef]
- Smith, A.J.; Townley, L.R. Influence of regional setting on the interaction between shallow lakes and aquifers. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Neff, B.P.; Rosenberry, D.O.; Leibowitz, S.G.; Mushet, D.M.; Golden, H.E.; Rains, M.C.; Brooks, J.R.; Lane, C.R. A Hydrologic Landscapes Perspective on Groundwater Connectivity of Depressional Wetlands. Water 2019, 12, 50. [Google Scholar] [CrossRef]

| JARALES WETLAND | |||||||
|---|---|---|---|---|---|---|---|
| Shape | Slope | Height | |||||
| Surface | 90.4 ha | Circularity Ratio (Rc) a | 0.33 | Maximum | 11.4% | Maximum | 464.5 m asl |
| Perimeter | 5857 m | Elongation Ratio (Re) b | 0.62 | Average | 3.6% | Minimum | 406.6 m asl |
| Maximum Length | 1736 m | Form Factor (Ff) c | 0.30 | Difference | 50.6 m | ||
| AMARGA WETLAND | |||||||
| Shape | Slope | Height | |||||
| Surface | 256.9 ha | Circularity Ratio (Rc) a | 0.34 | Maximum | 30.2% | Maximum | 440.4 m asl |
| Perimeter | 9730 m | Elongation Ratio (Re) b | 0.79 | Average | 3.8% | Minimum | 370.1 m asl |
| Maximum Length | 2280 m | Form Factor (Ff) c | 0.49 | Difference | 70.3 m | ||
| Month/Hydrol. Year | V0a | Pb | Rc | Ed | Simulated Vf e | Simulated ΔV f | Actual V f | Actual ΔV | ΔG g |
|---|---|---|---|---|---|---|---|---|---|
| Monthly water budget | |||||||||
| May 2014 | 94.8 | 0.4 | 0.0 | 14.6 | 80.6 | −14.2 | 77.6 | −17.2 | −3.0 |
| June 2014 | 77.6 | 0.7 | 0.0 | 14.5 | 63.8 | −13.8 | 61.2 | −16.3 | −2.5 |
| July 2014 | 61.2 | 0.0 | 0.0 | 14.5 | 46.7 | −14.5 | 42.4 | −18.8 | −4.4 |
| August 2014 | 42.4 | 0.0 | 0.0 | 11.2 | 31.2 | −11.2 | 27.0 | −15.4 | −4.2 |
| September 2014 | 27.0 | 0.3 | 0.0 | 5.4 | 22.0 | −5.1 | 19.2 | −7.8 | −2.7 |
| October 2014 | 19.2 | 2.5 | 1.1 | 3.5 | 19.3 | 0.1 | 14.4 | −4.8 | −4.9 |
| November 2014 | 14.4 | 4.8 | 0.5 | 1.6 | 18.1 | 3.7 | 20.8 | 6.4 | 2.7 |
| December 2014 | 20.8 | 0.8 | 0.0 | 1.2 | 20.4 | −0.5 | 19.8 | −1.0 | −0.6 |
| January 2015 | 19.8 | 1.7 | 0.0 | 1.5 | 20.0 | 0.2 | 22.0 | 2.2 | 2.0 |
| February 2015 | 22.0 | 1.2 | 0.0 | 2.1 | 21.1 | −0.9 | 22.4 | 0.4 | 1.4 |
| March 2015 | 22.4 | 1.4 | 0.0 | 4.1 | 19.7 | −2.8 | 22.0 | −0.4 | 2.3 |
| April 2015 | 22.0 | 1.2 | 0.0 | 5.5 | 17.6 | −4.4 | 18.2 | −3.8 | 0.6 |
| May 2015 | 18.2 | 0.0 | 0.0 | 7.4 | 10.8 | −7.4 | 12.2 | −5.9 | 1.5 |
| June 2015 | 12.2 | 0.0 | 0.0 | 6.8 | 5.5 | −6.8 | 1.0 | −11.2 | −4.4 |
| July 2015 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | −1.0 | 0.0 | −1.0 | 0.0 |
| August 2015 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| September 2015 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Annual water budget | |||||||||
| 2014/15 | 19.2 | 13.5 | 1.6 | 34.9 | 0 | −19.8 | 0 | −19.2 | 0.6 |
| Month/Hydrol. Year | V0 a | Pb | Rc | Ed | Simulated Vf e | Simulated ΔV f | Actual V f | Actual ΔV | ΔG g |
|---|---|---|---|---|---|---|---|---|---|
| Monthly water budget | |||||||||
| December 2014 | 187.98 | 1.10 | 0.00 | 2.40 | 186.69 | −1.30 | 187.13 | −0.85 | 0.45 |
| January 2015 | 187.13 | 2.46 | 0.00 | 2.94 | 186.65 | −0.48 | 188.58 | 1.44 | 1.93 |
| February 2015 | 188.58 | 1.61 | 0.00 | 2.60 | 187.59 | −0.99 | 188.62 | 0.04 | 1.03 |
| March 2015 | 188.62 | 1.96 | 0.00 | 4.63 | 185.95 | −2.67 | 188.25 | −0.36 | 2.31 |
| April 2015 | 188.25 | 1.69 | 0.00 | 6.69 | 183.26 | −5.00 | 187.57 | −0.68 | 4.31 |
| May 2015 | 187.57 | 0.00 | 0.00 | 10.52 | 177.05 | −10.52 | 177.12 | −10.45 | 0.07 |
| June 2015 | 177.12 | 0.02 | 0.00 | 12.01 | 165.14 | −11.99 | 163.27 | −13.85 | −1.86 |
| July 2015 | 163.27 | 0.00 | 0.00 | 13.02 | 150.25 | −13.02 | 149.39 | −13.89 | −0.87 |
| August 2015 | 149.39 | 0.05 | 0.00 | 10.42 | 139.02 | −10.36 | 138.19 | −11.20 | −0.83 |
| September 2015 | 138.19 | 0.95 | 0.00 | 7.84 | 131.30 | −6.89 | 127.93 | −10.26 | −3.37 |
| October 2015 | 127.93 | 3.33 | 0.00 | 4.67 | 126.59 | −1.34 | 127.83 | −0.10 | 1.24 |
| November 2015 | 127.83 | 2.38 | 4.66 | 2.75 | 132.12 | 4.29 | 135.72 | 7.88 | 3.59 |
| December 2015 | 135.72 | 0.13 | 0.00 | 2.75 | 133.10 | −2.62 | 133.78 | −1.94 | 0.68 |
| January 2016 | 133.78 | 4.01 | 5.16 | 2.03 | 140.93 | 7.15 | 145.24 | 11.47 | 4.32 |
| February 2016 | 145.24 | 2.10 | 0.00 | 2.83 | 144.52 | −0.72 | 146.04 | 0.80 | 1.52 |
| March 2016 | 146.04 | 1.22 | 0.00 | 4.42 | 142.85 | −3.19 | 143.49 | −2.55 | 0.65 |
| April 2016 | 143.49 | 2.85 | 2.67 | 4.82 | 144.19 | 0.69 | 145.13 | 1.64 | 0.94 |
| May 2016 | 145.13 | 3.27 | 0.58 | 7.61 | 141.37 | −3.76 | 143.39 | −1.75 | 2.01 |
| June 2016 | 143.39 | 0.00 | 0.00 | 10.97 | 132.42 | −10.97 | 131.76 | −11.63 | −0.67 |
| July 2016 | 131.76 | 0.81 | 0.00 | 12.05 | 120.51 | −11.24 | 123.72 | −8.04 | 3.21 |
| August 2016 | 123.72 | 0.02 | 0.00 | 11.67 | 112.07 | −11.65 | 112.98 | −10.74 | 0.91 |
| September 2016 | 112.98 | 0.18 | 0.00 | 7.62 | 105.55 | −7.43 | 108.07 | −4.91 | 2.52 |
| October 2016 | 108.07 | 1.59 | 0.00 | 5.15 | 104.52 | −3.55 | 109.59 | 1.52 | 5.08 |
| November 2016 | 109.59 | 3.30 | 1.01 | 2.78 | 111.12 | 1.53 | 121.92 | 12.33 | 10.80 |
| December 2016 | 121.92 | 2.39 | 0.13 | 2.24 | 122.19 | 0.27 | 128.82 | 6.90 | 6.63 |
| January 2017 | 128.82 | 0.30 | 0.00 | 2.25 | 126.86 | −1.96 | 124.57 | −4.24 | −2.29 |
| February 2017 | 124.57 | 2.04 | 0.00 | 2.09 | 124.52 | −0.06 | 127.04 | 2.46 | 2.52 |
| March 2017 | 127.04 | 2.19 | 0.00 | 3.68 | 125.54 | −1.49 | 127.64 | 0.61 | 2.10 |
| April 2017 | 127.64 | 1.07 | 0.00 | 6.19 | 122.52 | −5.12 | 122.34 | −5.31 | −0.18 |
| May 2017 | 122.34 | 0.70 | 0.00 | 7.77 | 115.27 | −7.06 | 116.58 | −5.76 | 1.31 |
| June 2017 | 116.58 | 0.00 | 0.00 | 10.22 | 106.36 | −10.22 | 105.72 | −10.86 | −0.64 |
| July 2017 | 105.72 | 0.01 | 0.00 | 9.59 | 96.14 | −9.58 | 95.48 | −10.24 | −0.66 |
| August 2017 | 95.48 | 1.42 | 1.14 | 8.11 | 89.93 | −5.55 | 96.20 | 0.71 | 6.27 |
| September 2017 | 96.20 | 0.00 | 0.00 | 6.60 | 89.60 | −6.60 | 91.66 | −4.54 | 2.06 |
| Annual water budget | |||||||||
| 2015/16 | 127.9 | 20.3 | 13.1 | 74.2 | 87.1 | −40.8 | 108.1 | −19.9 | 20.9 |
| 2016/17 | 108.1 | 15.0 | 2.3 | 66.7 | 58.7 | −49.4 | 91.7 | −16.4 | 33.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-Márquez, J.M.; Andreo, B.; Mudarra, M. Comparative Analysis of Runoff and Evaporation Assessment Methods to Evaluate Wetland–Groundwater Interaction in Mediterranean Evaporitic-Karst Aquatic Ecosystem. Water 2021, 13, 1482. https://doi.org/10.3390/w13111482
Gil-Márquez JM, Andreo B, Mudarra M. Comparative Analysis of Runoff and Evaporation Assessment Methods to Evaluate Wetland–Groundwater Interaction in Mediterranean Evaporitic-Karst Aquatic Ecosystem. Water. 2021; 13(11):1482. https://doi.org/10.3390/w13111482
Chicago/Turabian StyleGil-Márquez, José Manuel, Bartolomé Andreo, and Matías Mudarra. 2021. "Comparative Analysis of Runoff and Evaporation Assessment Methods to Evaluate Wetland–Groundwater Interaction in Mediterranean Evaporitic-Karst Aquatic Ecosystem" Water 13, no. 11: 1482. https://doi.org/10.3390/w13111482
APA StyleGil-Márquez, J. M., Andreo, B., & Mudarra, M. (2021). Comparative Analysis of Runoff and Evaporation Assessment Methods to Evaluate Wetland–Groundwater Interaction in Mediterranean Evaporitic-Karst Aquatic Ecosystem. Water, 13(11), 1482. https://doi.org/10.3390/w13111482






