A Novel Thin-Film Technique to Improve Accuracy of Fluorescence-Based Estimates for Periphytic Biofilms
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Evaluation of Bias and Precision
2.1.1. The Model
2.1.2. Generation of Synthetic Data
2.1.3. Numerical Simulations for Bias and Precision
2.2. Empirical Evaluation of Bias and Precision
2.2.1. Data Collection
2.2.2. Statistical Analysis
3. Results
3.1. Theoretical Evaluation of Bias and Precision
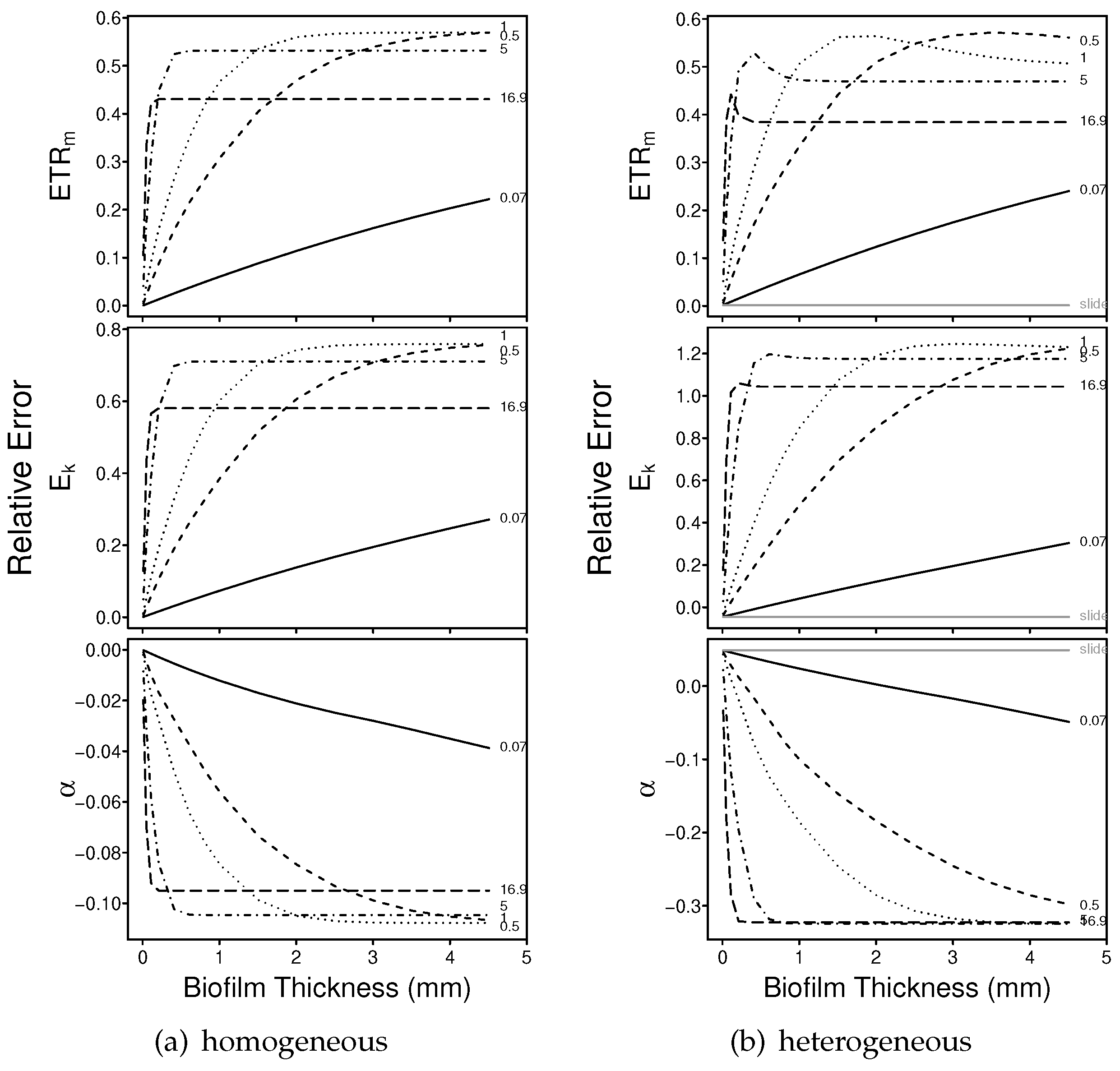
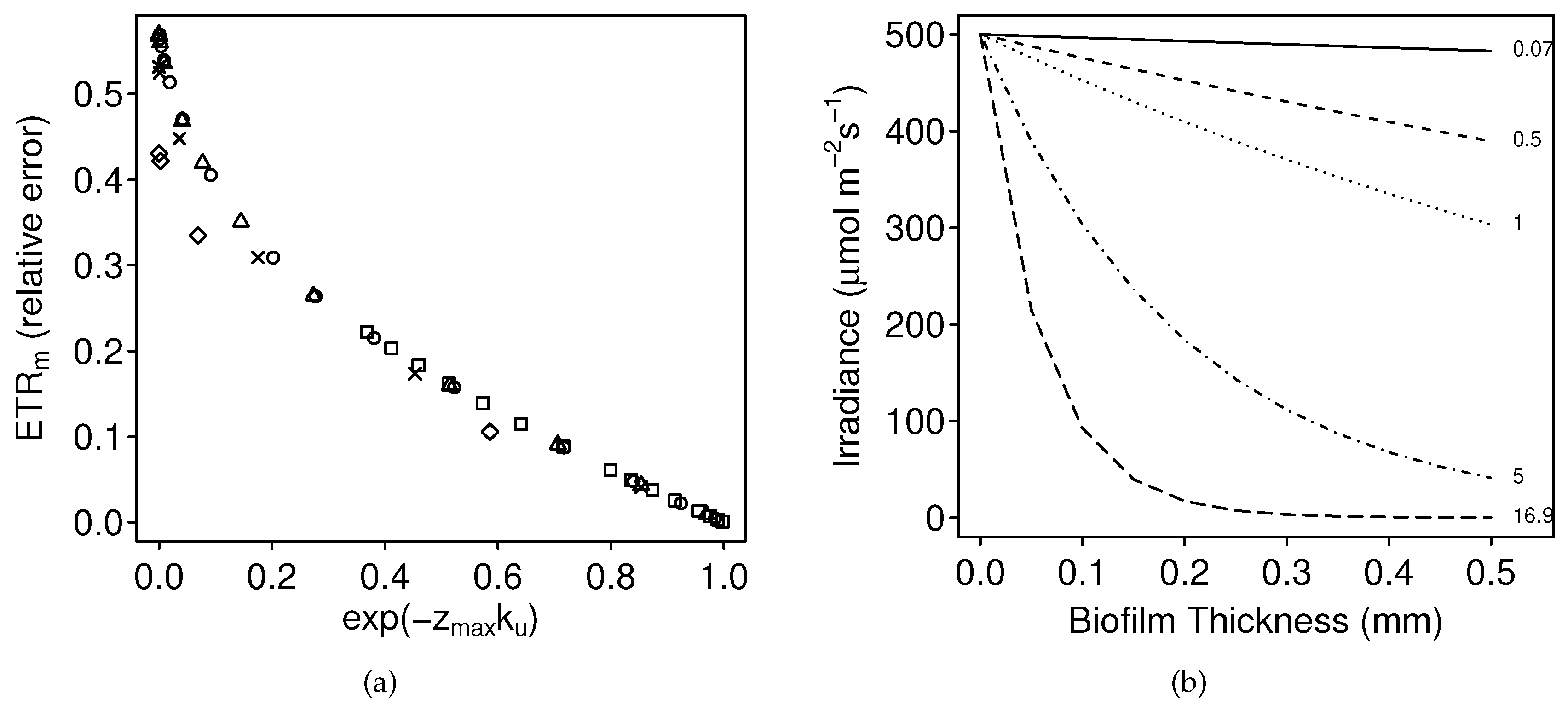
3.1.1. Numerical Simulations: Bias
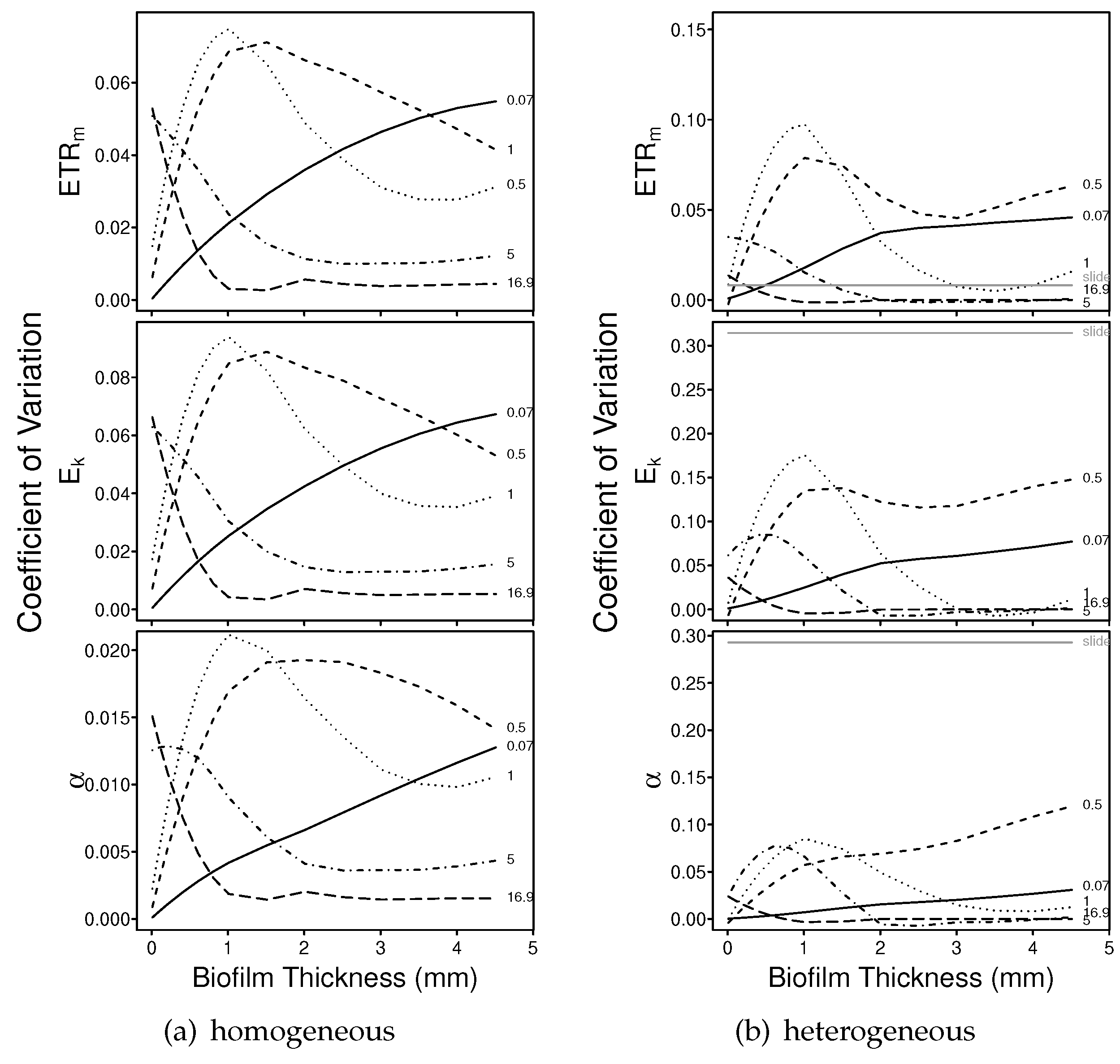
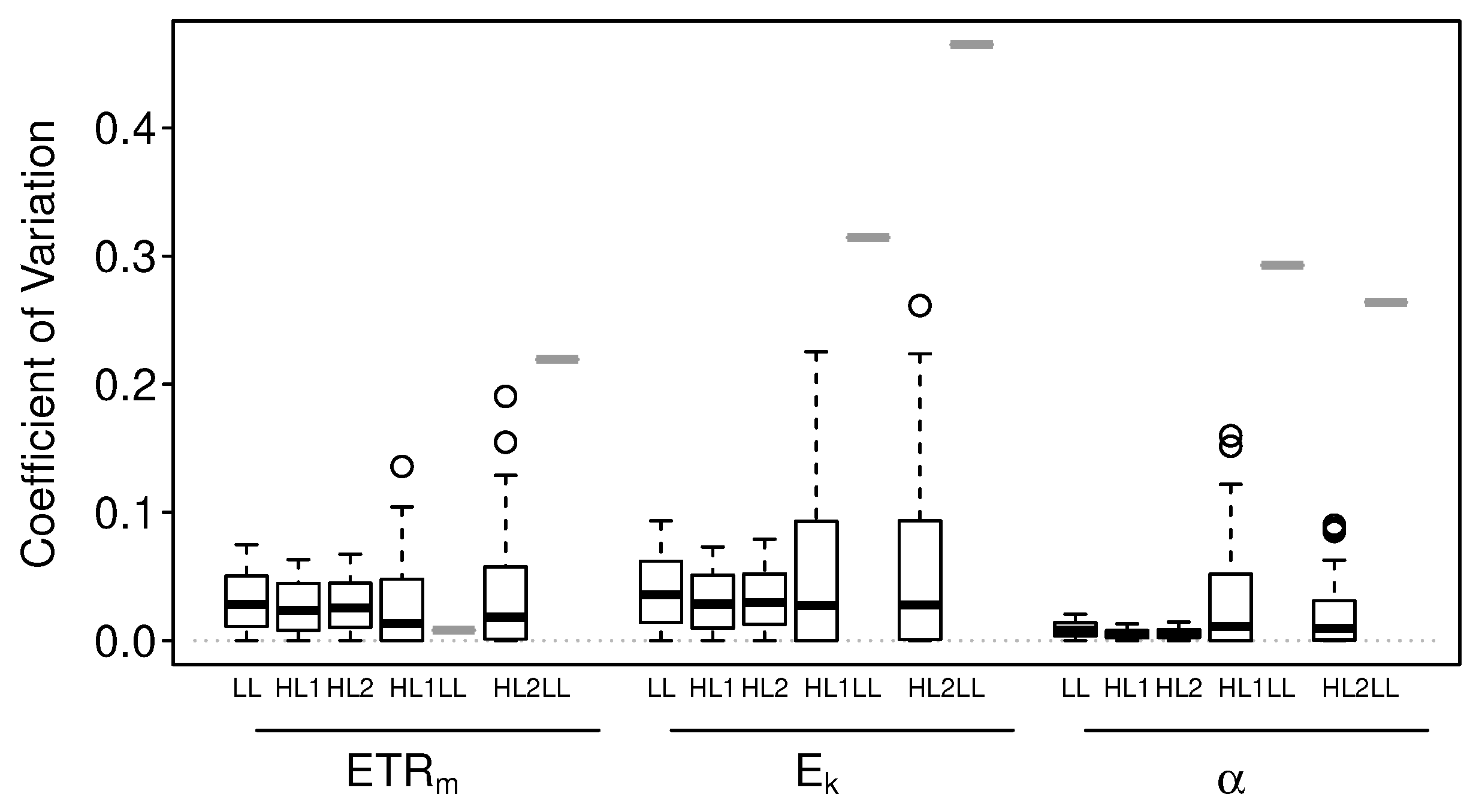
3.1.2. Numerical Simulations: Precision
3.2. Empirical Evaluation of Bias and Precision
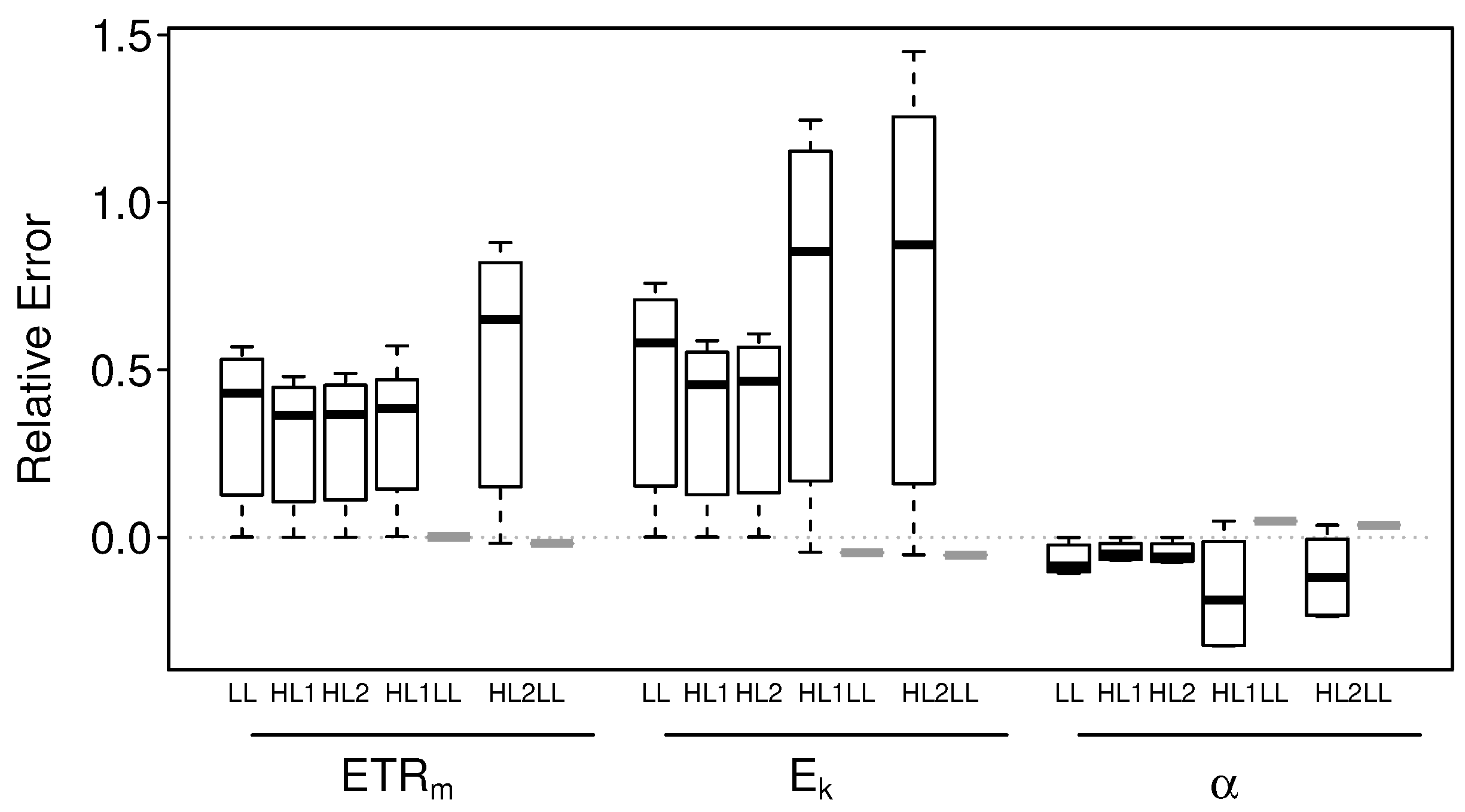
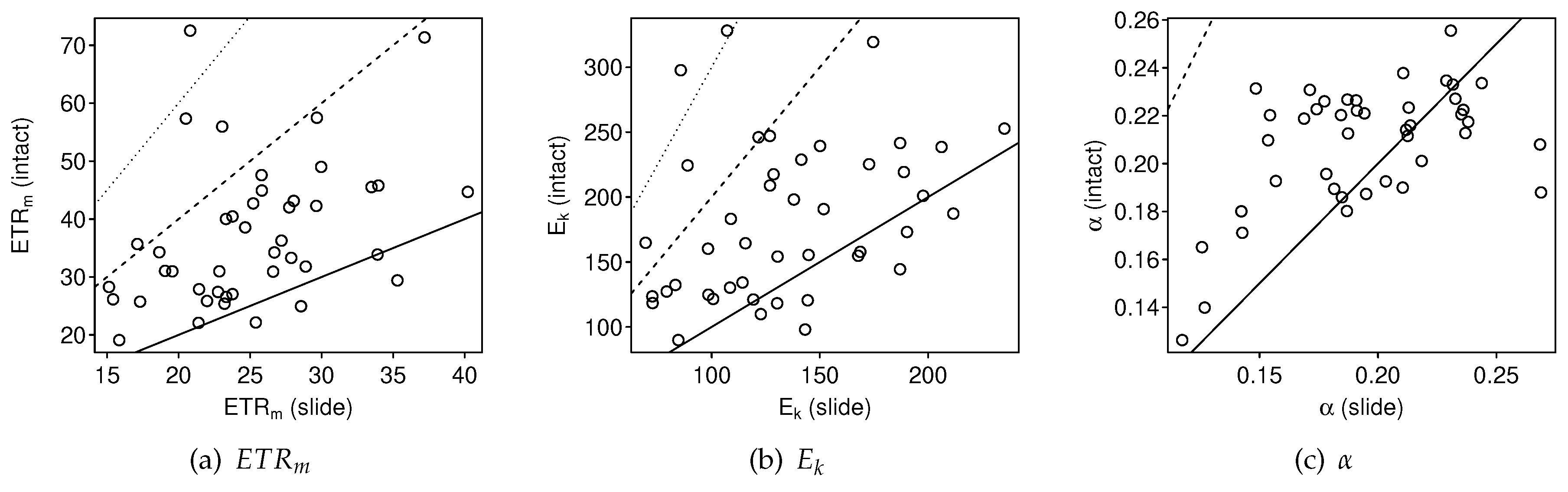
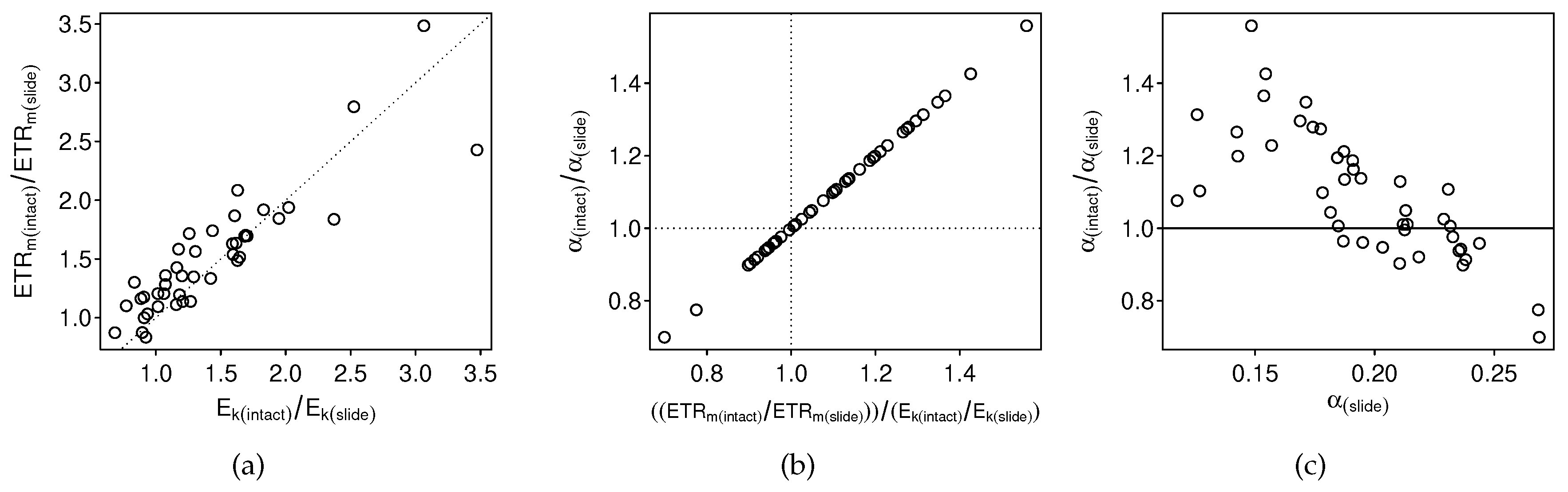
3.2.1. Intact-Biofilm-Method vs. Slide-Method: Bias
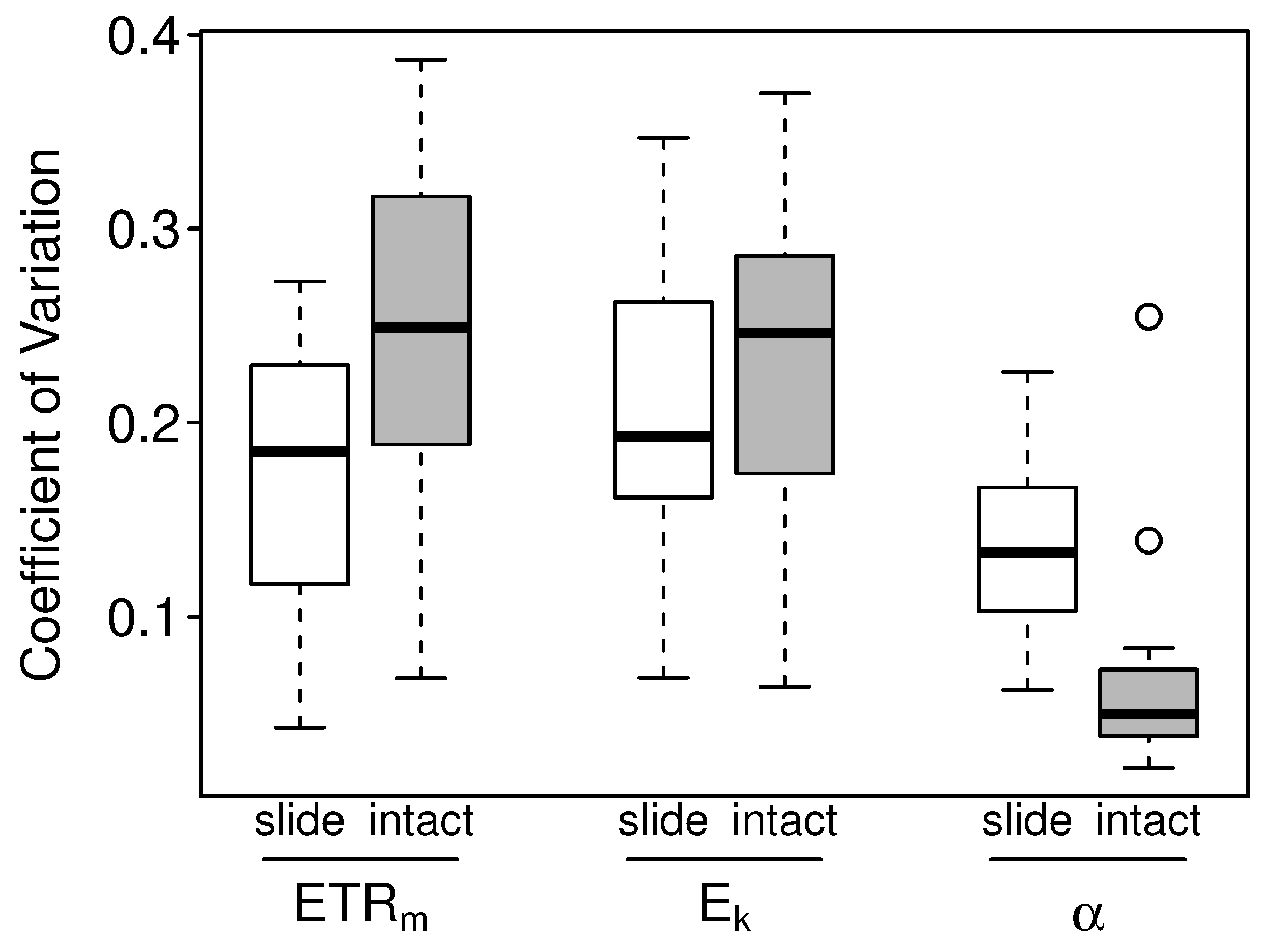
3.2.2. Intact-Biofilm-Method vs. Slide-Method: Precision
4. Discussion
4.1. Bias
4.2. Precision
4.3. The Problem with
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Photosynthetic efficiency | |
| CV | Coefficient of variation |
| E | Surface irradiance |
| Minimum saturating irradiance | |
| ESF | USEPA Experimental Stream Facility |
| Maximum electron transport rate | |
| F | Minimum fluorescence yield |
| Maximum fluorescence yield | |
| HL | High light |
| Downwelling attenuation coefficient | |
| Upwelling attenuation coefficient | |
| LL | Low light |
| PAM | Pulse-amplitude modulated |
| P–E | Photosynthesis–irradiance |
| Effective quantum yield | |
| rETR | Relative electron transport rate |
| RLC | Rapid light curve |
| SD | Standard deviation |
| Critical depth or effective biofilm thickness | |
| Total thickness of biofilm |
References
- Schreiber, U. Pulse-Amplitude-Modulation (PAM) Fluorometry and Saturation Pulse Method: An Overview. In Chlorophyll a Fluorescence: A Signature of Photosynthesis; Papageorgiou, G.C., Govindjee, Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 279–319. [Google Scholar]
- Consalvey, M.; Perkins, R.G.; Paterson, D.M.; Underwood, G.J.C. PAM Fluorescence: A Beginners Guide For Benthic Diatomists. Diatom Res. 2005, 20, 1–22. [Google Scholar] [CrossRef]
- Ralph, P.J.; Gademann, R. Rapid light curves: A powerful tool to assess photosynthetic activity. Aquat. Bot. 2005, 82, 222–237. [Google Scholar] [CrossRef]
- Serôdio, J. Analysis of variable chlorophyll fluorescence in microphytobenthos assemblages: Implications of the use of depth-integrated measurements. Aquat. Microb. Ecol. 2004, 36, 137–152. [Google Scholar] [CrossRef]
- Forster, R.M.; Kromkamp, J.C. Modelling the effects of chlorophyll fluorescence from subsurface layers on photosynthetic efficiency measurements in microphytobenthic algae. Mar. Ecol. Prog. Ser. 2004, 284, 9–22. [Google Scholar] [CrossRef]
- Vieira, S.; Ribeiro, L.; Jesus, B.; Cartaxana, P.; Marques da Silva, J. Photosynthesis Assessment in Microphytobenthos Using Conventional and Imaging Pulse Amplitude Modulation Fluorometry. Photochem. Photobiol. 2013, 89, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Lichtenberg, M.; Trampe, E.C.L.; Vogelmann, T.C.; Kühl, M. Light Sheet Microscopy Imaging of Light Absorption and Photosynthesis Distribution in Plant Tissue. Plant Physiol. 2017, 175, 721–733. [Google Scholar] [CrossRef]
- Johnson, R.E.; Tuchman, N.C.; Peterson, C.G. Changes in the Vertical Microdistribution of Diatoms within a Developing Periphyton Mat. J. N. Am. Benthol. Soc. 1997, 16, 503–519. [Google Scholar] [CrossRef]
- Dodds, W.K.; Biggs, B.J.F.; Lowe, R.L. Photosynthesis-irradiance patterns in benthic microalgae: Variations as a function of assemblage thickness and community structure. J. Phycol. 1999, 35, 42–53. [Google Scholar] [CrossRef]
- Barranguet, C.; van den Ende, F.P.; Rutgers, M.; Breure, A.M.; Greijdanus, M.; Sinke, J.J.; Admiraal, W. Copper-induced modifications of the trophic relations in riverine algal-bacterial biofilms. Environ. Toxicol. Chem. 2003, 22, 1340–1349. [Google Scholar] [CrossRef]
- Corcoll, N.; Bonet, B.; Leira, M.; Guasch, H. Chl-a fluorescence parameters as biomarkers of metal toxicity in fluvial biofilms: An experimental study. Hydrobiologia 2011, 673, 119–136. [Google Scholar] [CrossRef]
- Tiam, S.K.; Laviale, M.; Feurtet-Mazel, A.; Jan, G.; Gonzalez, P.; Mazzella, N.; Morin, S. Herbicide toxicity on river biofilms assessed by pulse amplitude modulated (PAM) fluorometry. Aquat. Toxicol. 2015, 165, 160–171. [Google Scholar] [CrossRef] [PubMed]
- Whorley, S.B.; Francoeur, S.N. Active fluorometry improves nutrient-diffusing substrata bioassay. Freshw. Sci. 2013, 32, 108–115. [Google Scholar] [CrossRef][Green Version]
- Bouma-Gregson, K.; Power, M.E.; Furey, P.C.; Huckins, C.J.; Vadeboncoeur, Y. Taxon-specific photosynthetic responses of attached algal assemblages to experimental translocation between river habitats. Freshw. Sci. 2021, 40, 175–190. [Google Scholar] [CrossRef]
- Schreiber, U.; Kühl, M.; Klimant, I.; Reising, H. Measurement of chlorophyll fluorescence within leaves using a modified PAM Fluorometer with a fiber-optic microprobe. Photosynth. Res. 1996, 47, 103–109. [Google Scholar] [CrossRef] [PubMed]
- Lichtenberg, M.; Larkum, A.W.D.; Kühl, M. Photosynthetic Acclimation of Symbiodinium in hospite Depends on Vertical Position in the Tissue of the Scleractinian Coral Montastrea curta. Front. Microbiol. 2016, 7, 230. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Oxborough, K.; Hanlon, A.R.M.; Underwood, G.J.C.; Baker, N.R. In vivo estimation of the photosystem II photochemical efficiency of individual microphytobenthic cells using high-resolution imaging of chlorophyll a fluorescence. Limnol. Oceanogr. 2000, 45, 1420–1425. [Google Scholar] [CrossRef]
- Jorgensen, B.B.; Des Marais, D.J. Optical properties of benthic photosynthetic communities: Fiber-optic studies of cyanobacterial mats. Limnol. Oceanogr. 1988, 33, 99–113. [Google Scholar] [CrossRef]
- Jassby, A.D.; Platt, T. Mathematical formulation of the relationship between photosynthesis and light for phytoplankton. Limnol. Oceanogr. 1976, 21, 540–547. [Google Scholar] [CrossRef]
- Webb, W.L.; Newton, M.; Starr, D. Carbon dioxide exchange of Alnus rubra. Oecologia 1974, 17, 281–291. [Google Scholar] [CrossRef]
- Platt, T.; Gallegos, C.L.; Harrison, W.G. Photoinhibition of photosynthesis in natural assemblages of marine phytoplankton. J. Mar. Res. 1980, 38, 687–701. [Google Scholar]
- Krause-Jensen, D.; Sand-Jensen, K. Light attenuation and photosynthesis of aquatic plant communities. Limnol. Oceanogr. 1998, 43, 396–407. [Google Scholar] [CrossRef]
- Li, T.; Piltz, B.; Podola, B.; Dron, A.; de Beer, D.; Melkonian, M. Microscale profiling of photosynthesis-related variables in a highly productive biofilm photobioreactor. Biotechnol. Bioeng. 2016, 113, 1046–1055. [Google Scholar] [CrossRef]
- Irving, T.E.; Allen, D.G. Species and material considerations in the formation and development of microalgal biofilms. Appl. Microbiol. Biotechnol. 2011, 92, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Latham, M.; Brown, D.S.; Nietch, C.T. Experimental Stream Facility: Design and Research; Technical Report EPA/600/F-11/004; U.S. Environmental Protection Agency: Washington, DC, USA, 2011.
- Nietch, C.T.; Quinlan, E.L.; Lazorchak, J.M.; Impellitteri, C.A.; Raikow, D.; Walters, D. Effects of a chronic lower range of triclosan exposure on a stream mesocosm community. Environ. Toxicol. Chem. 2013, 32, 2874–2887. [Google Scholar] [CrossRef] [PubMed]
- Taulbee, W.K.; Nietch, C.T.; Brown, D.; Ramakrishnan, B.; Tompkins, M.J. Ecosystem Consequences of Contrasting Flow Regimes in an Urban Effects Stream Mesocosm Study. J. Am. Water Resour. Assoc. 2009, 45, 907–927. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Blackman, F.F. Optima and limiting factors. Ann. Bot. 1905, 19, 281–295. [Google Scholar] [CrossRef]
- Perry, M.J.; Talbot, M.C.; Alberte, R.S. Photoadaption in marine phytoplankton: Response of the photosynthetic unit. Mar. Biol. 1981, 62, 91–101. [Google Scholar] [CrossRef]
- Roberts, S.; Sabater, S.; Beardall, J. Benthic microalgal colonization in streams of differing riparian cover and light availability. J. Phycol. 2004, 40, 1004–1012. [Google Scholar] [CrossRef]
- Peterson, D.H.; Perry, M.J.; Bencala, K.E.; Talbot, M.C. Phytoplankton productivity in relation to light intensity: A simple equation. Estuar. Coast. Shelf Sci. 1987, 24, 813–832. [Google Scholar] [CrossRef]
- Frenette, J.J.; Demers, S.; Legendre, L.; Dodson, J. Lack of agreement among models for estimating the photosynthetic parameters. Limnol. Oceanogr. 1993, 38, 679–687. [Google Scholar] [CrossRef]
| LL | 100.6 | 164 | 0.61 |
| HL1 | 100.5 | 301 | 0.33 |
| HL2 | 155.3 | 428 | 0.36 |
| HL1LL | 99.0 | 215 | 0.46 |
| HL2LL | 123.9 | 281 | 0.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katona, L.; Vadeboncoeur, Y.; Nietch, C.T.; Hossler, K. A Novel Thin-Film Technique to Improve Accuracy of Fluorescence-Based Estimates for Periphytic Biofilms. Water 2021, 13, 1464. https://doi.org/10.3390/w13111464
Katona L, Vadeboncoeur Y, Nietch CT, Hossler K. A Novel Thin-Film Technique to Improve Accuracy of Fluorescence-Based Estimates for Periphytic Biofilms. Water. 2021; 13(11):1464. https://doi.org/10.3390/w13111464
Chicago/Turabian StyleKatona, Leon, Yvonne Vadeboncoeur, Christopher T. Nietch, and Katie Hossler. 2021. "A Novel Thin-Film Technique to Improve Accuracy of Fluorescence-Based Estimates for Periphytic Biofilms" Water 13, no. 11: 1464. https://doi.org/10.3390/w13111464
APA StyleKatona, L., Vadeboncoeur, Y., Nietch, C. T., & Hossler, K. (2021). A Novel Thin-Film Technique to Improve Accuracy of Fluorescence-Based Estimates for Periphytic Biofilms. Water, 13(11), 1464. https://doi.org/10.3390/w13111464








