Analysis of Drought Characteristics in Northern Shaanxi Based on Copula Function
Abstract
:1. Introduction
2. Study Area and Data
3. Methodology
3.1. Standardized Precipitation Index
3.2. Drought Feature Recognition
- 1
- Set three truncation levels R0, R1 and R2. In this study, the threshold of drought index was determined by trial-and-error method. R0 = 0, R1 = −0.3, R2 = −0.5. By setting the truncation level to identify drought events, the results were consistent with the actual drought situation of China Meteorological Disasters (Shaanxi volume);
- 2
- Identify potential drought events. If SPI of a month is less than or equal to R1, the month is regarded as a potential drought month, and a continuous potential drought month is regarded as a potential drought event. As shown in Figure 2, there are five potential drought events a, b, c1, c2 and d;
- 3
- Determine drought events and their duration and intensity. If the potential drought event lasts for one month, when its SPI is greater than R2, this potential drought event will be eliminated (a in Figure 2). When its SPI is less than or equal to R2, it is determined as a drought event (b in Figure 2). A potential dry event is defined as a drought event if it lasts for more than a month (d in Figure 2). If the time interval between two drought events occurs is 1 and the SPI for the month is less than or equal to R0, the two drought events are combined into one drought event (c1 and c2 in Figure 2).
3.3. Construct the Marginal Distribution Function of Characteristic Variables
3.4. Construction of Copula Joint Distribution Function
3.5. Calculation of Return Periods
4. Results
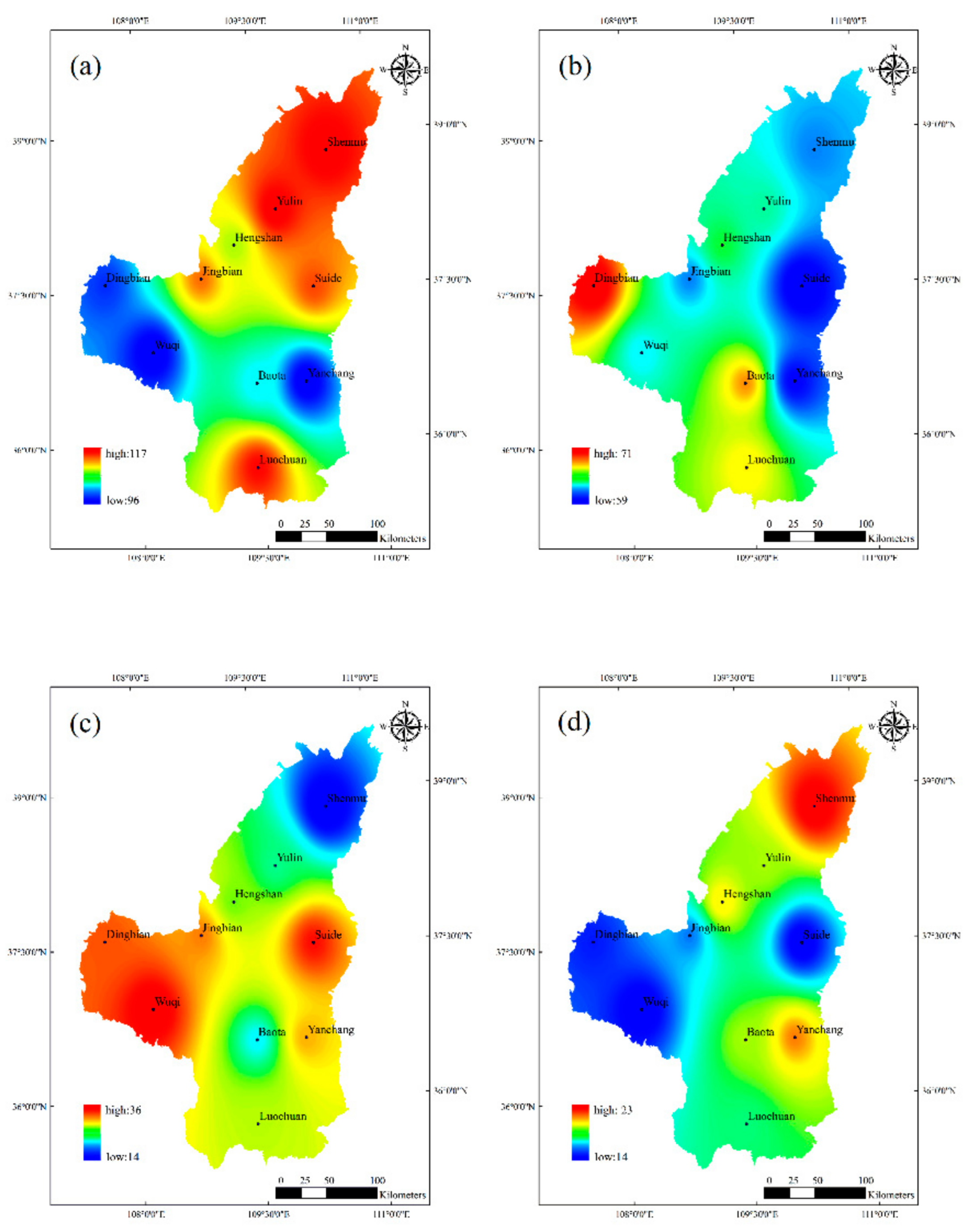
4.1. Spatial Distribution of Drought Frequency
4.2. Determination of Copula
4.2.1. Correlation Analysis of Characteristics of Drought Variables
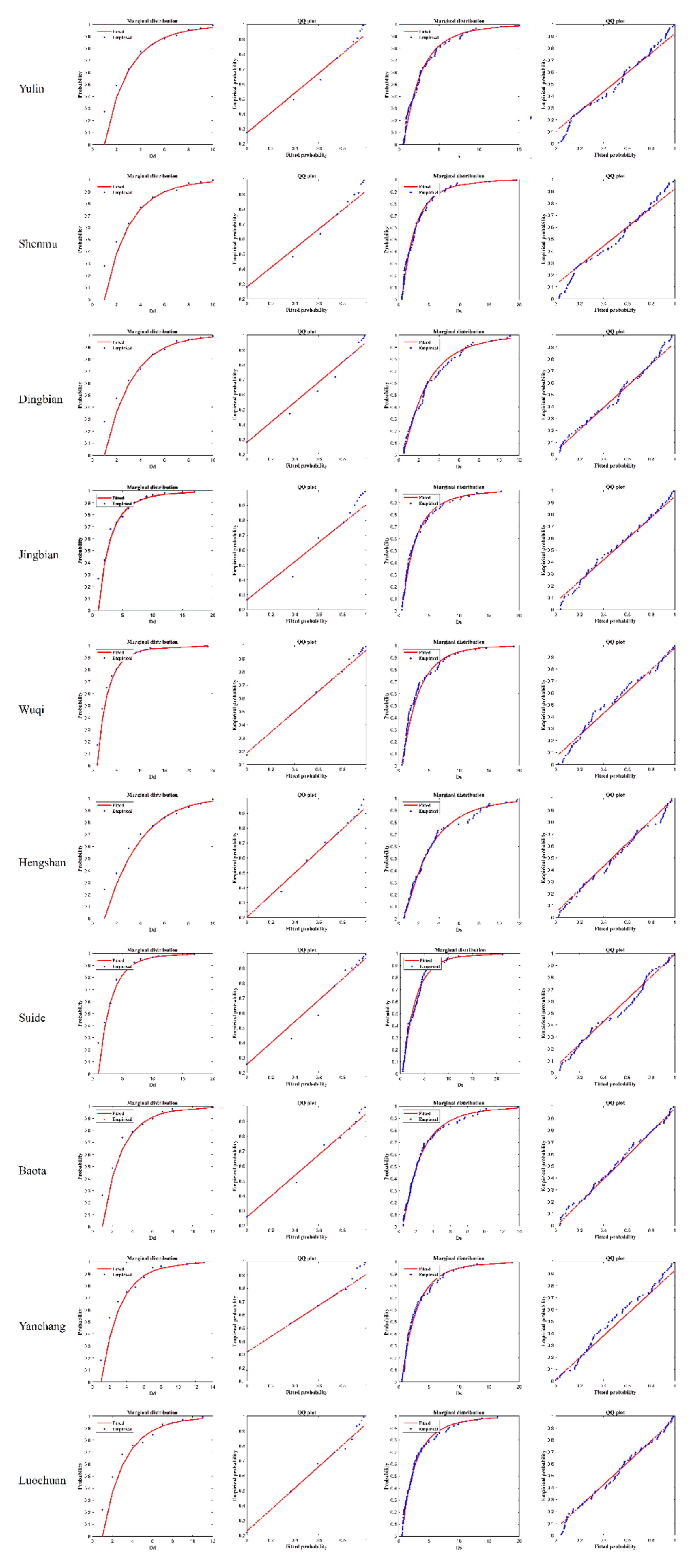
4.2.2. Determine the Appropriate Marginal Distribution Function
4.2.3. Determine the Appropriate Copula
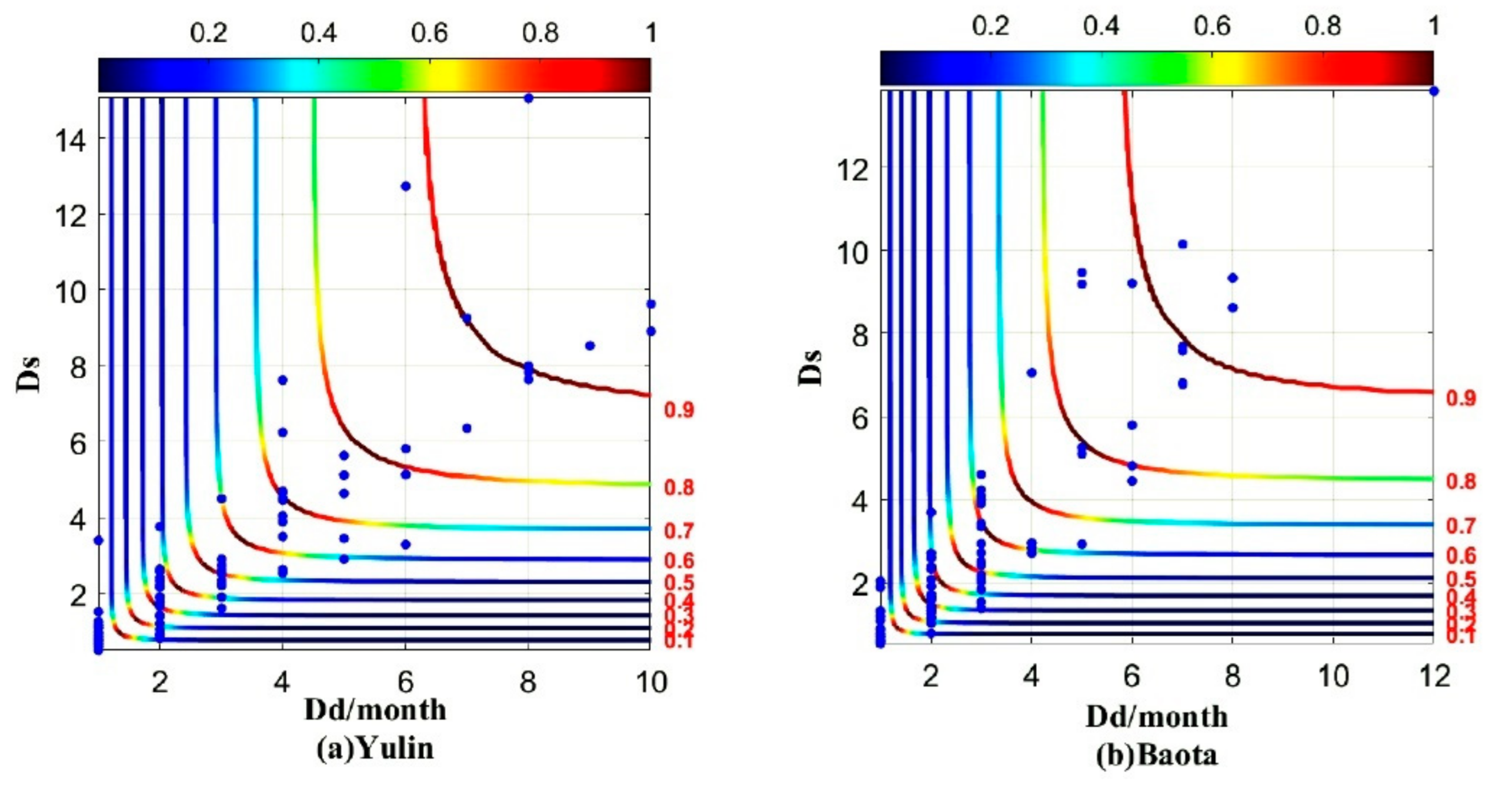
4.3. Drought Risk Probability Assessment
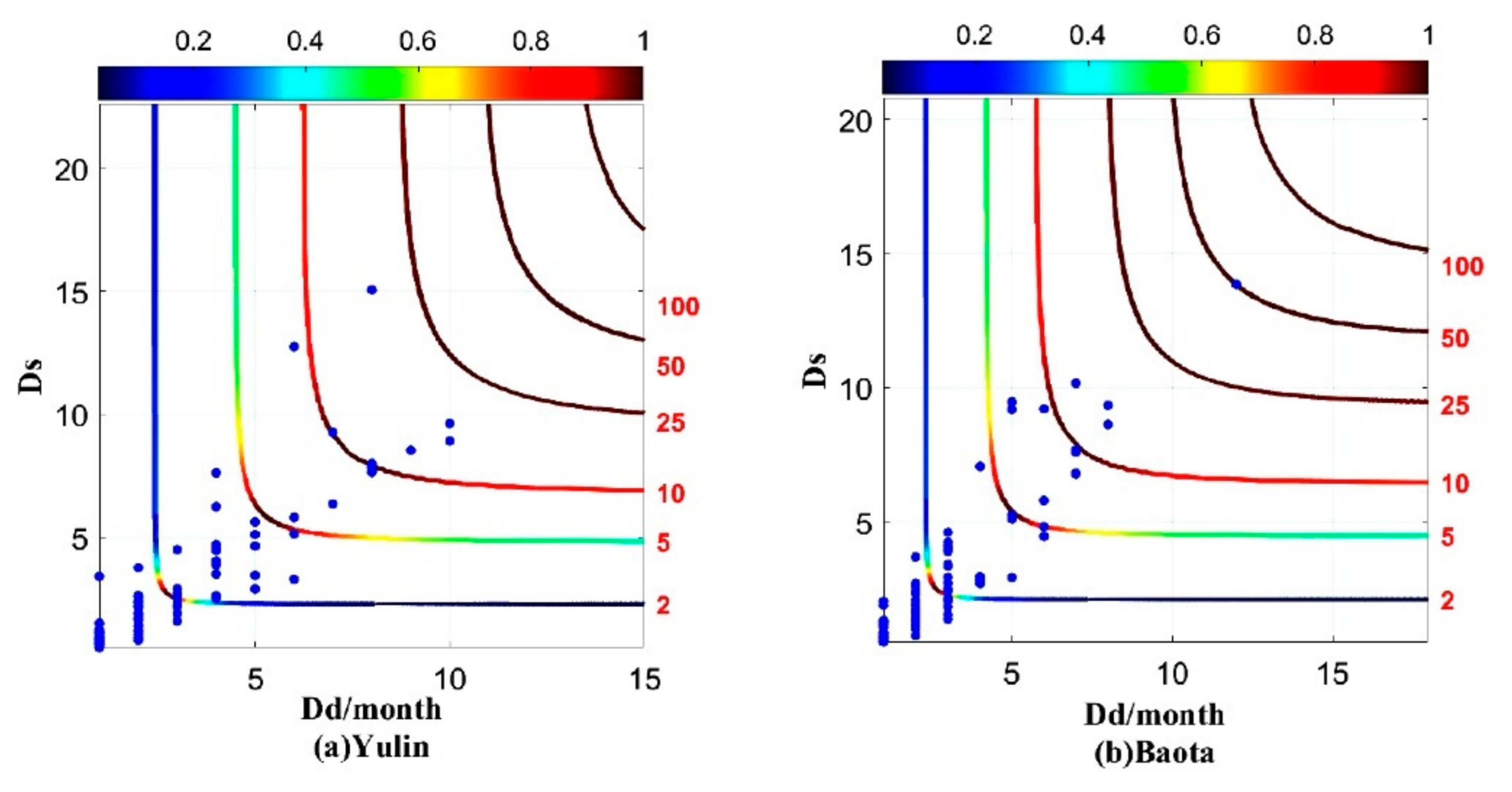
4.4. Joint Return Period
4.5. Application of Joint Return Period
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Jang, E.; Rhee, J. Drought assessment and monitoring through blending of multi-sensor indices using machine learning approaches for different climate regions. Agric. For. Meteorol. 2016, 216, 157–169. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Bernstein, L.; Bosch, P.; Canziani, O.; Chen, Z.; Christ, R.; Riahi, K. Climate Change 2007: Synthesis Report; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- Xu, Z.; Fan, K.; Wang, H. Role of sea surface temperature anomalies in the tropical Indo-Pacific region in the northeast Asia severe drought in summer 2014: Month-to-month perspective. Clim. Dyn. 2016, 49, 1631–1650. [Google Scholar] [CrossRef]
- Lu, E.; Luo, Y.; Zhang, R.; Wu, Q.; Liu, L. Regional atmospheric anomalies responsible for the 2009–2010 severe drought in China. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Wambuaraphael, M. Analysis of spatial and temporal drought variability in a tropical river basin using Palmer Drought Se-verity Index (PDSI). Int. J. Water Res. Environ. Eng. 2017, 9, 178–190. [Google Scholar]
- Yan, H.; Wang, S.Q.; Wang, J.B.; Lu, H.Q.; Guo, A.H.; Zhu, Z.C.; Myneni, R.B.; Shugart, H.H. Assessing spatiotemporal variation of drought in China and its impact on agriculture during 1982–2011 by using PDSI indices and agriculture drought survey data. J. Geophys. Res. Atmos. 2016, 121, 2283–2298. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wu, J.; Xu, Y. Investigating the effects of precipitation on drought in the Hanjiang River Basin using SPI. J. Water Clim. Chang. 2018, 10, 977–992. [Google Scholar] [CrossRef]
- Pham, Q.B.; Yang, T.-C.; Kuo, C.-M.; Tseng, H.-W.; Yu, P.-S. Coupling Singular Spectrum Analysis with Least Square Support Vector Machine to Improve Accuracy of SPI Drought Forecasting. Water Resour. Manag. 2021, 35, 847–868. [Google Scholar] [CrossRef]
- Pandey, R.P.; Ramasastri, K.S. Incidence of droughts in different climatic regions. Hydrol. Sci. J. 2002, 47, S31–S40. [Google Scholar] [CrossRef]
- Qianfeng, W.; Jingyu, Z.; Junyu, Q.; Xuesong, Z.; Yue, Z.; Wei, S.; Zhanghua, X.; Rongrong, Z.; Xiaoping, W.; Jiang, C. A multi-scale daily SPEI dataset for drought characterization at observation stations over mainland China from 1961 to 2018. Earth Syst. Sci. Data 2021, 13, 331–341. [Google Scholar]
- Wu, Z.; Yu, L.; Du, Z.; Zhang, H.; Fan, X.; Lei, T. Recent changes in the drought of China from 1960 to 2014. Int. J. Climatol. 2020, 40, 3281–3296. [Google Scholar] [CrossRef]
- Bravo, R.Z.B.; Cunha, A.P.M.D.A.; Leiras, A.; Oliveira, F.L.C. A new approach for a drought composite index. Nat. Hazards 2021, 1–19. [Google Scholar] [CrossRef]
- Saghafian, B.; Sanginabadi, H. Multivariate groundwater drought analysis using copulas. Hydrol. Res. 2020, 51, 666–685. [Google Scholar] [CrossRef]
- Seyedabadi, M.; Kavianpour, M.; Moazami, S. Multivariate drought risk analysis based on copula functions: A case study. Water Supply 2020, 20, 2375–2388. [Google Scholar] [CrossRef]
- Soumia, M.; Doudja, S.G. Spatio-temporal analysis of maximum drought severity using Copulas in Northern Algeria. J. Water Clim. Chang. 2020, 11, 68–84. [Google Scholar]
- Wang, R.; Zhao, C.; Zhang, J.; Guo, E.; Li, D.; Alu, S.; Ha, S.; Dong, Z. Bivariate copula function-based spatial–temporal characteristics analysis of drought in Anhui Province, China. Theor. Appl. Clim. 2018, 131, 1341–1355. [Google Scholar] [CrossRef]
- Moyé, L.A.; Kapadia, A.S. Predictions of drought length extreme order statistics using run theory. J. Hydrol. 1995, 169, 95–110. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Wang, S.; Salahou, M.K.; Fang, Y. Analysis and Application of Drought Characteristics Based on Theory of Runs and Copulas in Yunnan, Southwest China. Int. J. Environ. Res. Public Health 2020, 17, 4654. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, J.; Bao, Y.; Guo, E. Run Theory and Copula-Based Drought Risk Analysis for Songnen Grassland in Northeastern China. Sustainability 2019, 11, 6032. [Google Scholar] [CrossRef] [Green Version]
- Herbst, P.; Bredenkamp, D.; Barker, H. A technique for the evaluation of drought from rainfall data. J. Hydrol. 1966, 4, 264–272. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Feng, X.; Feng, Y.; Xue, Y.; Pan, N. Analysis and application of drought characteristics based on run theory and Copula function. Trans. CSAE 2017, 33, 206–214. [Google Scholar]
- Zhang, B.; Wang, S.; Wang, Y. Copula-Based Convection-Permitting Projections of Future Changes in Multivariate Drought Characteristics. J. Geophys. Res. Atmos. 2019, 124, 7460–7483. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Gürbüz, F.; Ispirli, M.N. Multivariate modeling of flood characteristics using Vine copulas. Environ. Earth Sci. 2020, 79, 1–21. [Google Scholar] [CrossRef]
- Feng, Y.; Li, Y.; Zhang, Z.; Gong, S.; Liu, M.; Peng, F. Multi-factor joint return period of rainstorms and its agricultural risk analysis in Liaoning Province, China. Geomat. Nat. Hazards Risk 2019, 10, 1988–2008. [Google Scholar] [CrossRef] [Green Version]
- Sklar, M. Fonctions de Répartition À N Dimensions Et Leurs Marges, 1st ed.; Publications de l’Institut de statistique de l’Université de Paris: Paris, France, 1960; pp. 229–231. [Google Scholar]
- Hui-Mean, F.; Yusof, F.; Yusop, Z.; Suhaila, J. Trivariate copula in drought analysis: A case study in peninsular Malaysia. Theor. Appl. Clim. 2019, 138, 657–671. [Google Scholar] [CrossRef]
- Liu, N.; Liu, Y.; Zhou, Q.; Bao, G. Droughts and broad-scale climate variability reflected by temperature-sensitive tree growth in the Qinling Mountains, central China. Int. J. Biometeorol. 2012, 57, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Bai, H.; Sarukkalige, R.; Fu, G.; Jia, W.; Zhang, C. Annual and seasonal precipitation trends and their attributions in the Qinling Mountains, a climate transitional zone in China. Theor. Appl. Clim. 2021, 144, 401–413. [Google Scholar] [CrossRef]
- Zhao, T.; Bai, H.; Yuan, Y.; Deng, C.; Qi, G.; Zhai, D. Spatio-temporal differentiation of climate warming (1959–2016) in the middle Qinling Mountains of China. J. Geogr. Sci. 2020, 30, 657–668. [Google Scholar] [CrossRef]
- Yi, Z.; Xue, L.; Feng, Y.; Yang, L.; Bin, W. Characteristics and influencing factors of proximity distance index on the northern Shaanxi Loess Plateau in China. J. Mt. Sci. 2019, 16, 2844–2855. [Google Scholar]
- Yixing, Y.; Lijuan, Z.; Xiaojun, W.; Wucheng, X.; Wenjun, Y.; Ye, Z. Meteorological Drought Changes and Related Circulation Characteristics in Yulin City of the Northern Shaanxi from 1961 to 2015. Atmos 2020, 11, 1196. [Google Scholar]
- Yudan, W.; Yunfeng, K.; Hao, C.; Yongjian, D. Spatial-temporal characteristics of drought detected from meteorological data with high resolution in Shaanxi Province, China. J. Arid Land 2020, 12, 561–579. [Google Scholar]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. AMS Conf. Appl. Climatol. 1993, 17, 179–184. [Google Scholar]
- Rahman, M.R.; Lateh, H. Meteorological drought in Bangladesh: Assessing, analysing and hazard mapping using SPI, GIS and monthly rainfall data. Environ. Earth Sci. 2016, 75, 1–20. [Google Scholar] [CrossRef]
- Ekanayake, E.M.R.S.B.; Perera, K. Analysis of Drought Severity and Duration Using Copulas in Anuradhapura, Sri Lanka. Br. J. Environ. Clim. Chang. 2014, 4, 312–327. [Google Scholar] [CrossRef]
- Abdi, A.; Hassanzadeh, Y.; Talatahari, S.; Fakheri-Fard, A.; Mirabbasi, R. Parameter estimation of copula functions using an optimization-based method. Theor. Appl. Clim. 2016, 129, 21–32. [Google Scholar] [CrossRef]
- Tosunoğlu, F.; Onof, C. Joint modelling of drought characteristics derived from historical and synthetic rainfalls: Application of Generalized Linear Models and Copulas. J. Hydrol. Reg. Stud. 2017, 14, 167–181. [Google Scholar] [CrossRef]
- Shiau, J.T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Filho, J.D.P.; Filho, F.D.A.S.; Martins, E.S.P.R.; Studart, T.M.D.C. Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil. Water 2020, 12, 834. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; AghaKouchak, A. Multivariate Standardized Drought Index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Amirataee, B.; Montaseri, M.; Rezaie, H. Regional analysis and derivation of copula-based drought Severity-Area-Frequency curve in Lake Urmia basin, Iran. J. Environ. Manag. 2018, 206, 134–144. [Google Scholar] [CrossRef]
- Rashid, M.; Beecham, S. Characterization of meteorological droughts across South Australia. Meteorol. Appl. 2019, 26, 556–568. [Google Scholar] [CrossRef] [Green Version]
- Sina, N.; Ahmad, S.; Mundher, Y.Z.; Shamsuddin, S. Copula based assessment of meteorological drought characteristics: Regional investigation of Iran. Agric. For. Meteorol. 2019, 276–277, 107611. [Google Scholar]
- Yang, M.; Mou, Y.; Meng, Y.; Liu, S.; Peng, C.; Zhou, X. Modeling the effects of precipitation and temperature patterns on agricultural drought in China from 1949 to 2015. Sci. Total Environ. 2020, 711, 135139. [Google Scholar] [CrossRef]


| SPI | Drought Level |
|---|---|
| >−0.5 | No drought |
| >−1.0~−0.5 | Light drought |
| >−1.5~−1.0 | Moderate drought |
| >−2.0~−1.5 | Severe drought |
| ≤−2.0 | Extreme drought |
| Copula Type | Copula Formula | Parameter Range |
|---|---|---|
| Clayton | ||
| Gumbel | ||
| Frank |
| Station | Kendall | Spearman | Pearson |
|---|---|---|---|
| Yulin | 0.7809 | 0.9054 | 0.8691 |
| Shenmu | 0.7814 | 0.9064 | 0.8566 |
| Dingbian | 0.8070 | 0.9336 | 0.8848 |
| Jingbian | 0.8083 | 0.9288 | 0.9367 |
| Wuqi | 0.7740 | 0.8973 | 0.9339 |
| Hengshan | 0.7452 | 0.8972 | 0.8599 |
| Suide | 0.7762 | 0.9078 | 0.9125 |
| Baota | 0.7596 | 0.8912 | 0.9082 |
| Yanchang | 0.7659 | 0.8940 | 0.9181 |
| Luochuan | 0.8019 | 0.9198 | 0.9213 |
| Station | Variable | Function | Parameter | Value |
|---|---|---|---|---|
| Yulin | Ds | Generalized Pareto | k | 0.0775 |
| sigma | 2.5133 | |||
| theta | 0.5100 | |||
| Dd | Generalized Pareto | k | 0.1215 | |
| sigma | 1.9607 | |||
| theta | 1.0000 | |||
| Shenmu | Ds | Generalized Pareto | k | 0.3788 |
| sigma | 1.7001 | |||
| theta | 0.5000 | |||
| Dd | Generalized Pareto | k | 25.1696 | |
| sigma | 0.0000 | |||
| theta | 1.0000 | |||
| Dingbian | Ds | Generalized Pareto | k | −0.1231 |
| sigma | 3.5957 | |||
| theta | 0.5000 | |||
| Dd | Generalized Extreme Value | k | 5.0868 | |
| sigma | 1.1733 | |||
| mu | 1.2306 | |||
| Jingbian | Ds | Generalized Pareto | k | 0.2465 |
| sigma | 2.2171 | |||
| theta | 0.5500 | |||
| Dd | Generalized Pareto | k | 0.2509 | |
| sigma | 1.9400 | |||
| theta | 1.0000 | |||
| Wuqi | Ds | Inverse Gaussian | mu | 3.5858 |
| lambda | 3.5500 | |||
| Dd | Generalized Pareto | k | 0.2044 | |
| sigma | 2.1046 | |||
| theta | 1.0000 | |||
| Hengshan | Ds | Generalized Pareto | k | −0.0794 |
| sigma | 3.2528 | |||
| theta | 0.5400 | |||
| Dd | Generalized Pareto | k | −0.1274 | |
| sigma | 3.0244 | |||
| theta | 1.0000 | |||
| Suide | Ds | Generalized Pareto | k | 0.1146 |
| sigma | 2.5609 | |||
| theta | 0.5400 | |||
| Dd | Generalized Pareto | k | 0.1229 | |
| sigma | 2.0815 | |||
| theta | 1.0000 | |||
| Baota | Ds | Generalized Pareto | k | 0.1355 |
| sigma | 2.1991 | |||
| theta | 0.5200 | |||
| Dd | Generalized Pareto | k | 0.0982 | |
| sigma | 1.8302 | |||
| theta | 1.0000 | |||
| Yanchang | Ds | Inverse Gaussian | mu | 3.4530 |
| lambda | 3.3911 | |||
| Dd | Generalized Pareto | k | 0.0708 | |
| sigma | 2.1494 | |||
| theta | 1.0000 | |||
| Luochuan | Ds | Generalized Pareto | k | 0.3055 |
| sigma | 2.0336 | |||
| theta | 0.5400 | |||
| Dd | Generalized Pareto | k | 0.0937 | |
| sigma | 2.1356 | |||
| theta | 1.0000 |
| Station | Copula | RMSE | NSE |
|---|---|---|---|
| Yulin | Clayton | 1.4031 | 0.6921 |
| Gumbel | 1.0875 | 0.8150 | |
| Frank | 0.8544 | 0.8858 | |
| Shenmu | Clayton | 1.0606 | 0.8309 |
| Gumbel | 1.0178 | 0.8443 | |
| Frank | 1.0513 | 0.8339 | |
| Dingbian | Clayton | 1.7848 | 0.4041 |
| Gumbel | 1.4929 | 0.5831 | |
| Frank | 1.4258 | 0.6197 | |
| Jingbian | Clayton | 1.4386 | 0.6613 |
| Gumbel | 1.0857 | 0.8071 | |
| Frank | 0.8101 | 0.8926 | |
| Wuqi | Clayton | 1.4781 | 0.6551 |
| Gumbel | 0.9978 | 0.8428 | |
| Frank | 0.6613 | 0.9310 | |
| Hengshan | Clayton | 1.3488 | 0.6665 |
| Gumbel | 1.0037 | 0.8153 | |
| Frank | 0.7321 | 0.9018 | |
| Suide | Clayton | 1.2932 | 0.7203 |
| Gumbel | 0.9627 | 0.8450 | |
| Frank | 0.7569 | 0.9042 | |
| Baota | Clayton | 1.4380 | 0.6807 |
| Gumbel | 1.0677 | 0.8240 | |
| Frank | 0.8125 | 0.8981 | |
| Yanchang | Clayton | 1.4534 | 0.6448 |
| Gumbel | 0.9237 | 0.8566 | |
| Frank | 0.6602 | 0.9267 | |
| Luochuan | Clayton | 1.4826 | 0.6506 |
| Gumbel | 1.0271 | 0.8323 | |
| Frank | 0.7026 | 0.9215 |
| Year | Drought Grade | Drought Duration | Return Period | ||
|---|---|---|---|---|---|
| Actual | Theoretical | Actual | Theoretical | ||
| 1995 | Light drought | 5 | 6 | 2 | 2.2 |
| 1996 | Moderate drought | 8 | 8 | 2.9 | 3.0 |
| 1997 | Light drought | 5 | 6 | 2 | 2.2 |
| 1998 | Moderate drought | 6 | 7 | 4.1 | 3.9 |
| 1999 | Moderate drought | 8 | 8 | 2.9 | 3.2 |
| 2000 | Severe drought | 8 | 9 | 7.5 | 7.7 |
| 2001 | Light drought | 3 | 3 | 1.8 | 1.6 |
| 2002 | Moderate drought | 6 | 7 | 4.1 | 3.9 |
| 2003 | Light drought | 3 | 3 | 1 | 1.1 |
| 2004 | Light drought | 3 | 3 | 1.1 | 1.2 |
| 2005 | Severe drought | 8 | 8 | 4.2 | 4.4 |
| 2006 | Light drought | 5 | 5 | 2.1 | 2.3 |
| 2007 | Severe drought | 8 | 8 | 5.3 | 5.5 |
| 2008 | Light drought | 3 | 3 | 1.2 | 1.1 |
| 2009 | Severe drought | 8 | 9 | 4.3 | 4.2 |
| 2010 | Light drought | 4 | 4 | 1.5 | 1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Rong, G.; Li, K.; Zhang, J. Analysis of Drought Characteristics in Northern Shaanxi Based on Copula Function. Water 2021, 13, 1445. https://doi.org/10.3390/w13111445
Wang J, Rong G, Li K, Zhang J. Analysis of Drought Characteristics in Northern Shaanxi Based on Copula Function. Water. 2021; 13(11):1445. https://doi.org/10.3390/w13111445
Chicago/Turabian StyleWang, Junhui, Guangzhi Rong, Kaiwei Li, and Jiquan Zhang. 2021. "Analysis of Drought Characteristics in Northern Shaanxi Based on Copula Function" Water 13, no. 11: 1445. https://doi.org/10.3390/w13111445
APA StyleWang, J., Rong, G., Li, K., & Zhang, J. (2021). Analysis of Drought Characteristics in Northern Shaanxi Based on Copula Function. Water, 13(11), 1445. https://doi.org/10.3390/w13111445






