Analytical Formula for the Mean Velocity Profile in a Pipe Derived on the Basis of a Spatial Polynomial Vorticity Distribution
Abstract
1. Introduction
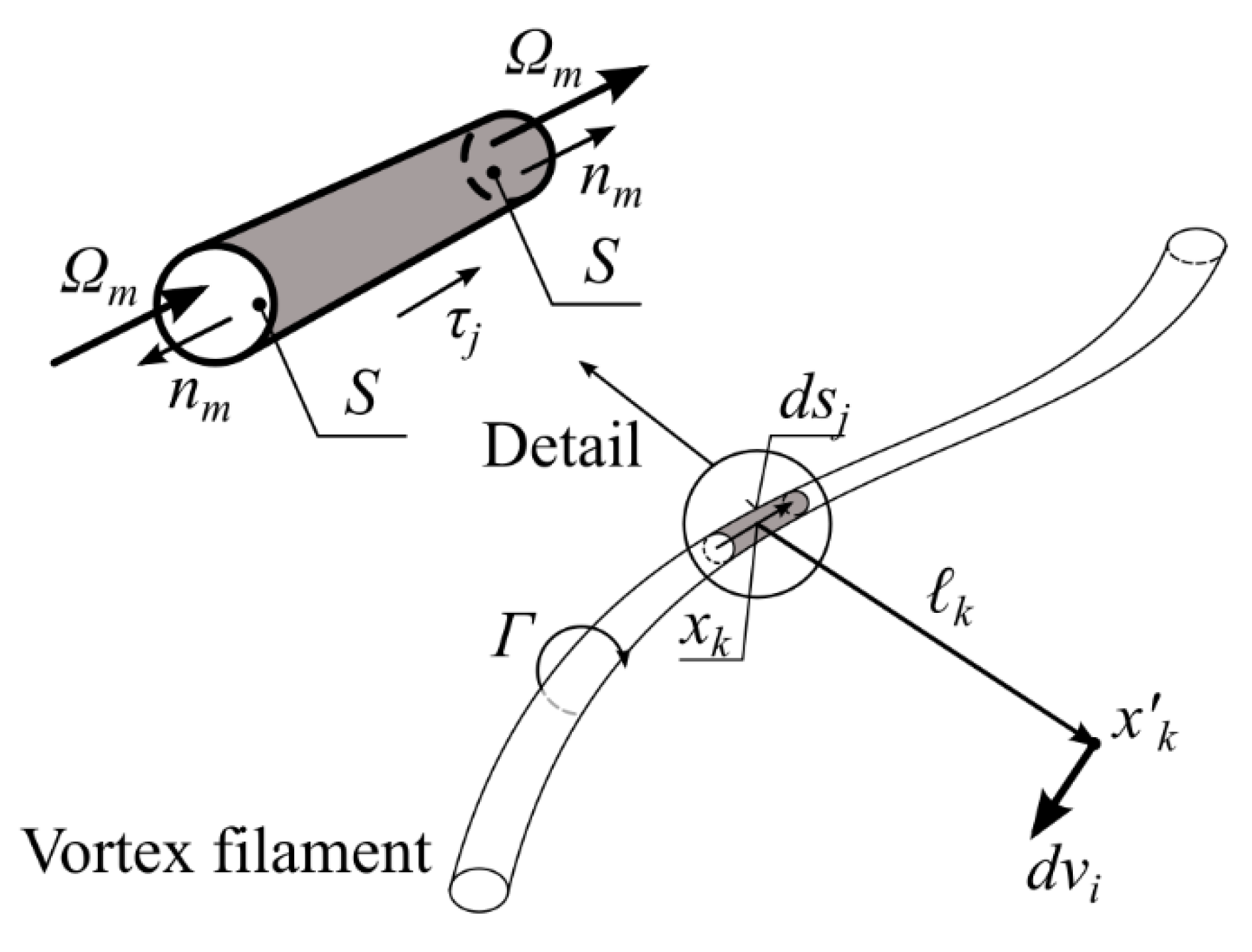
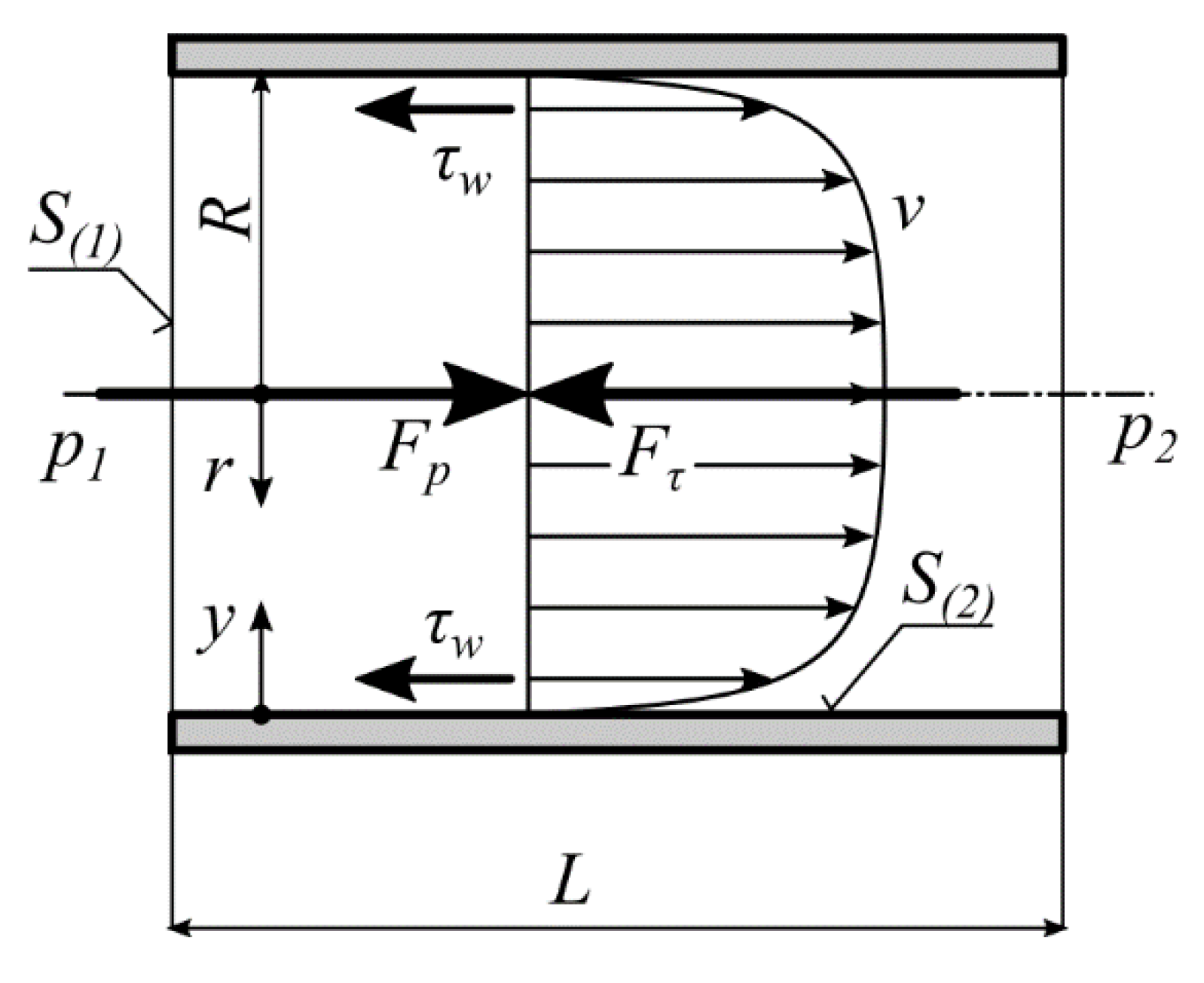
2. Backgrounds
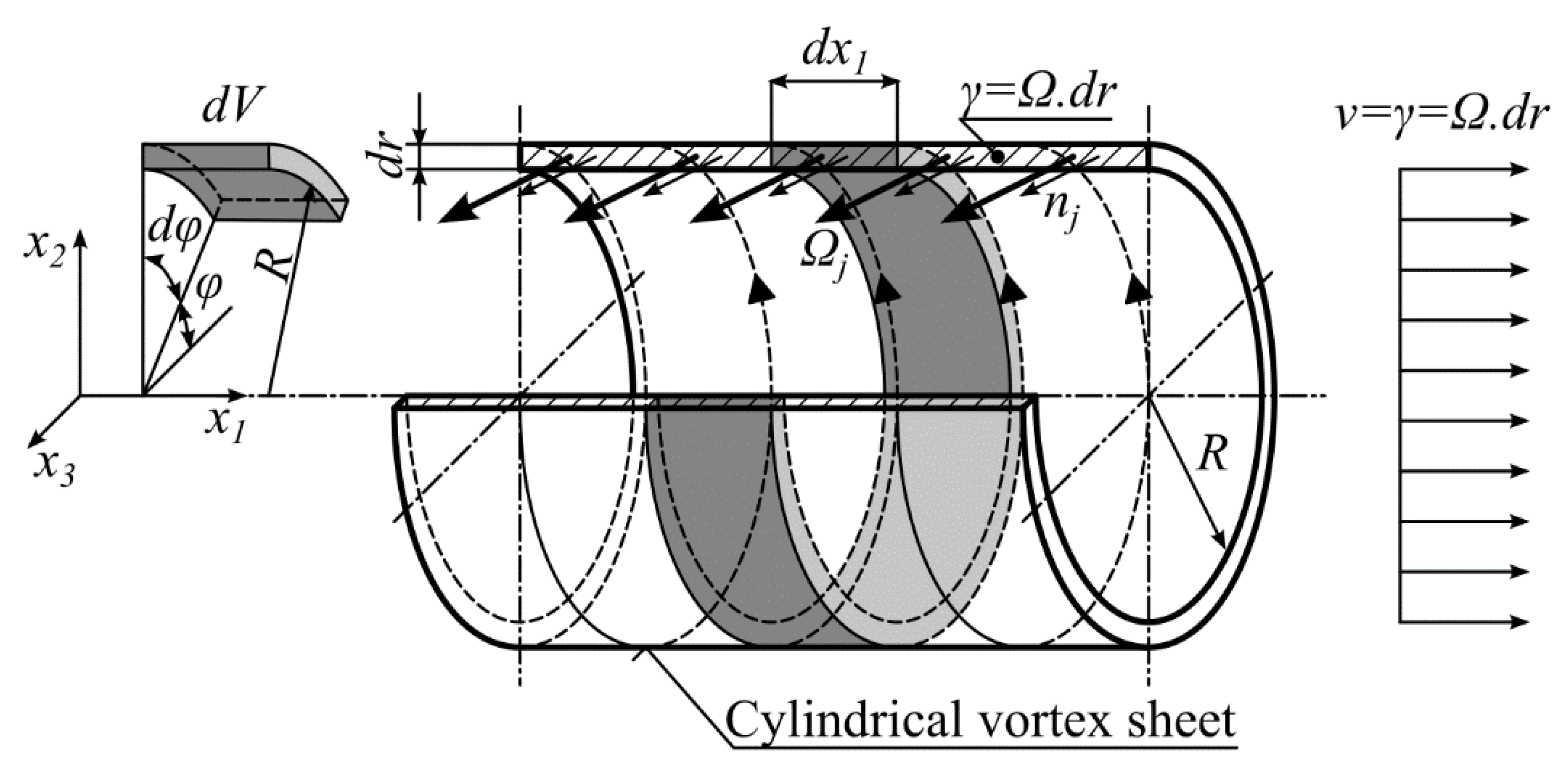
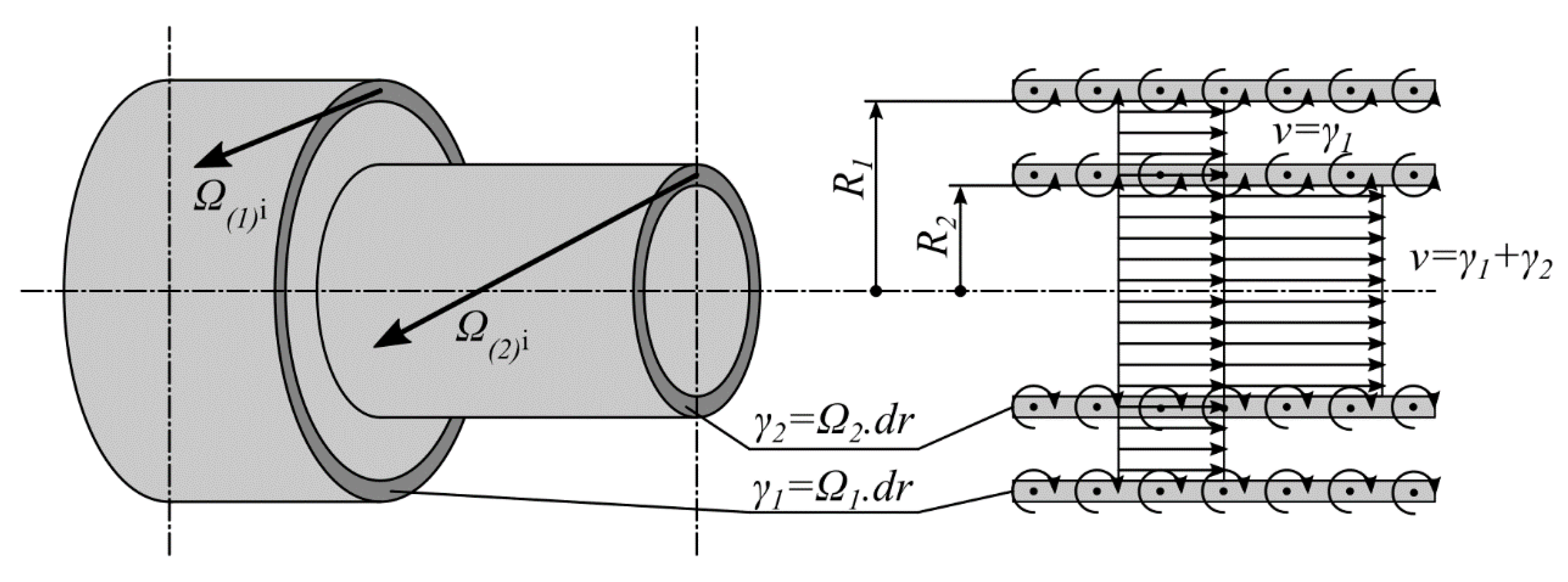
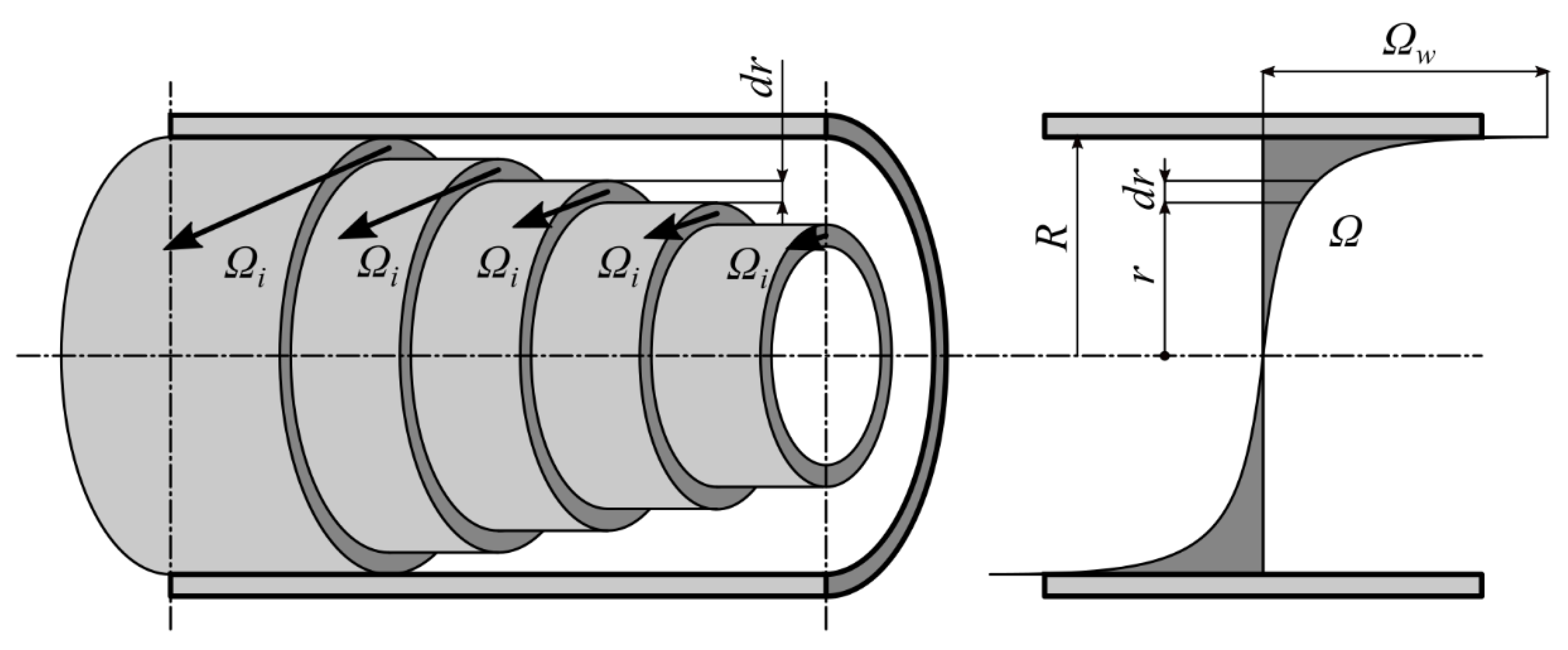
3. Basic Idea of Velocity Profile Derivation
4. Available Conditions for Free Coefficients Determining
- Zero velocity at the wall.
- Vorticity at the wall Ωw. This condition corresponds to the condition of pressure drop in the pipe.
- Zero value of the vorticity Ω in the pipe axis. This corresponds to the smoothness condition of the first velocity profile derivative in the pipe axis.
- The first vorticity derivative in the pipe axis. This condition corresponds to the curvature radius.
- Maximal velocity in the pipe axis.
- The knowledge of flow rate in pipe.
- The knowledge of radius where the velocity is the same as the average velocity.
- All conditions are explained in detail in the next chapters.
4.1. Zero Velocity at the Wall
4.2. Vorticity Value at the Wall Ωw
4.3. Zero Value of the Vorticity Ω in the Pipe Axis
4.4. The First Derivative of the Vorticity Function Ω in the Pipe Axis
4.5. Maximal Velocity in the Pipe Axis
4.6. The Knowledge of Flow Rate in Pipe
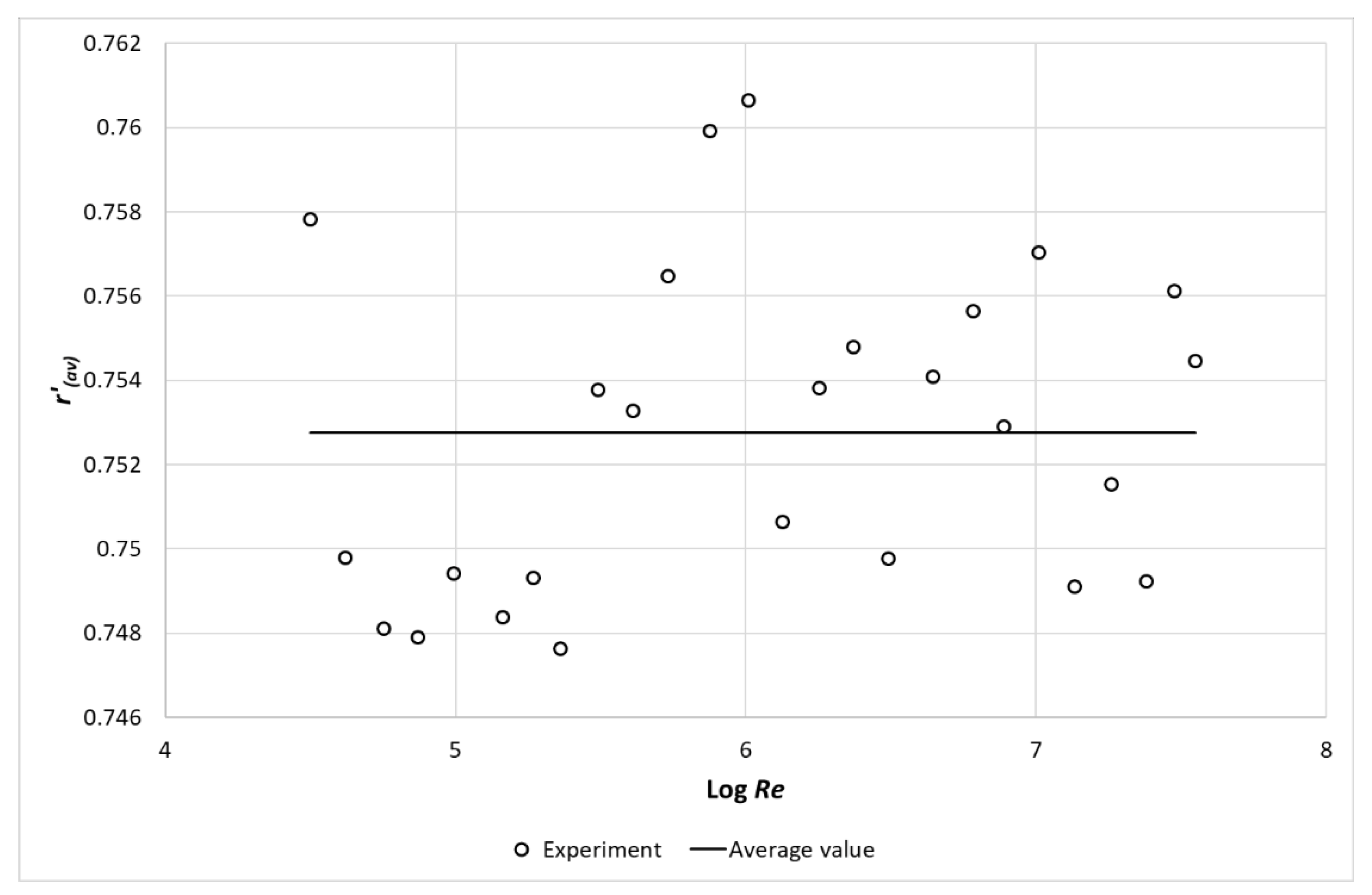
4.7. The Radius of the Average Velocity
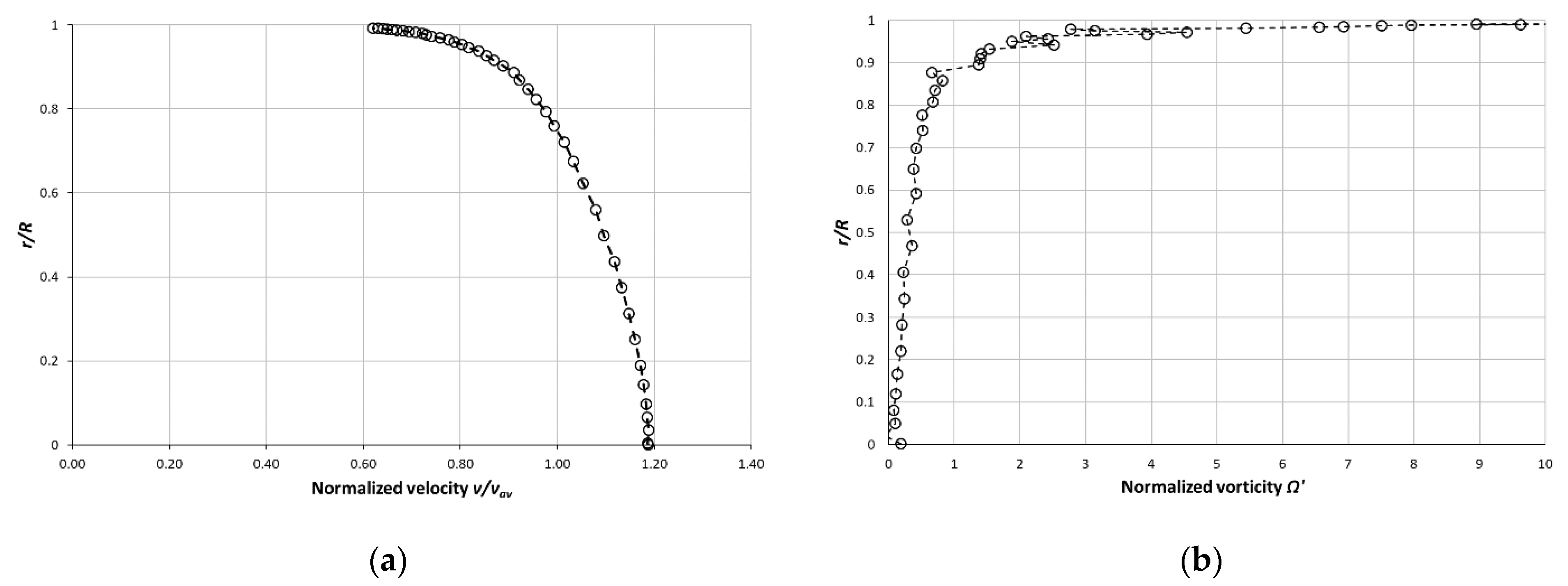
5. Mean Velocity Profile Formula Derivation
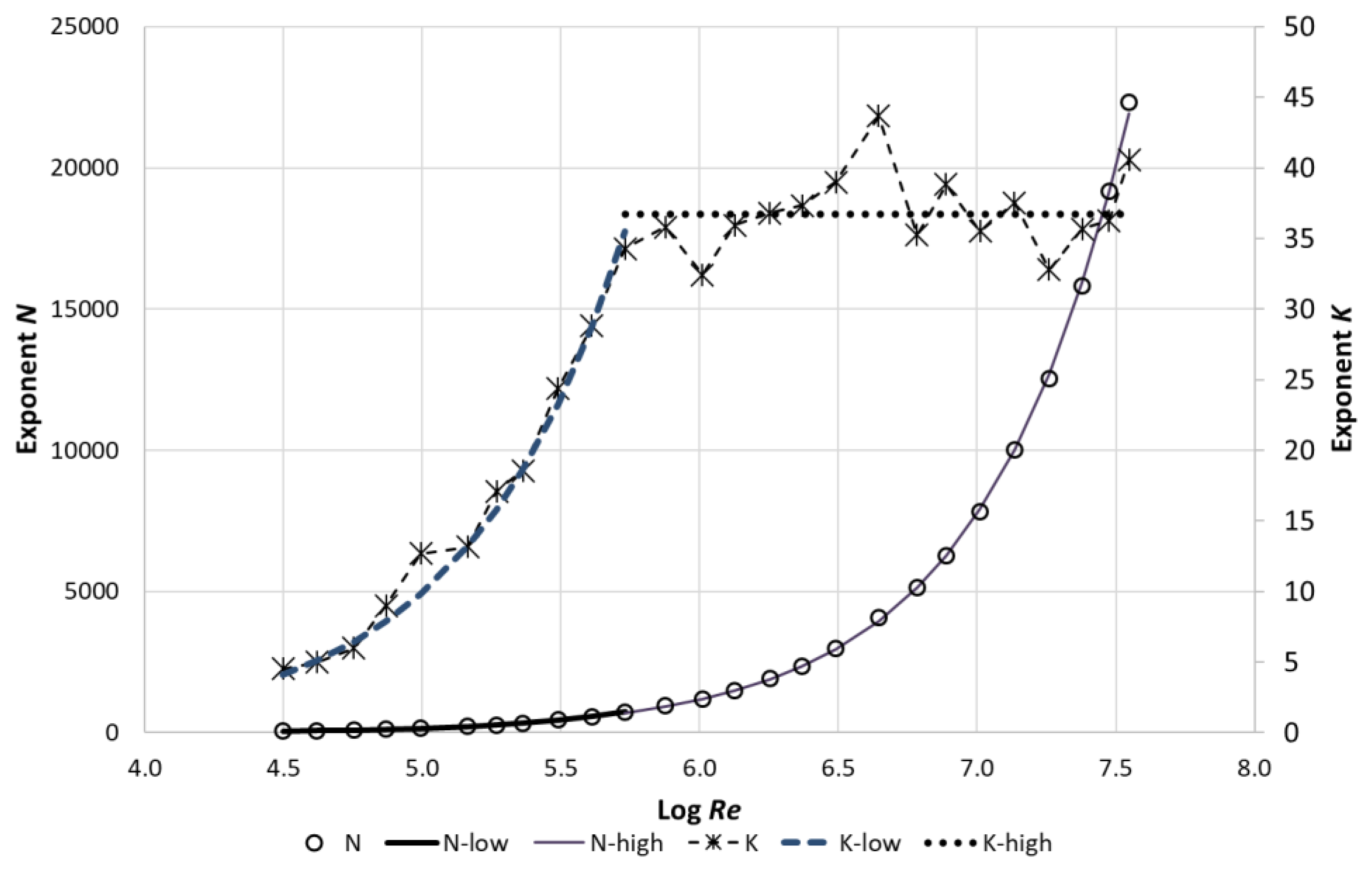
6. Exponents Determination
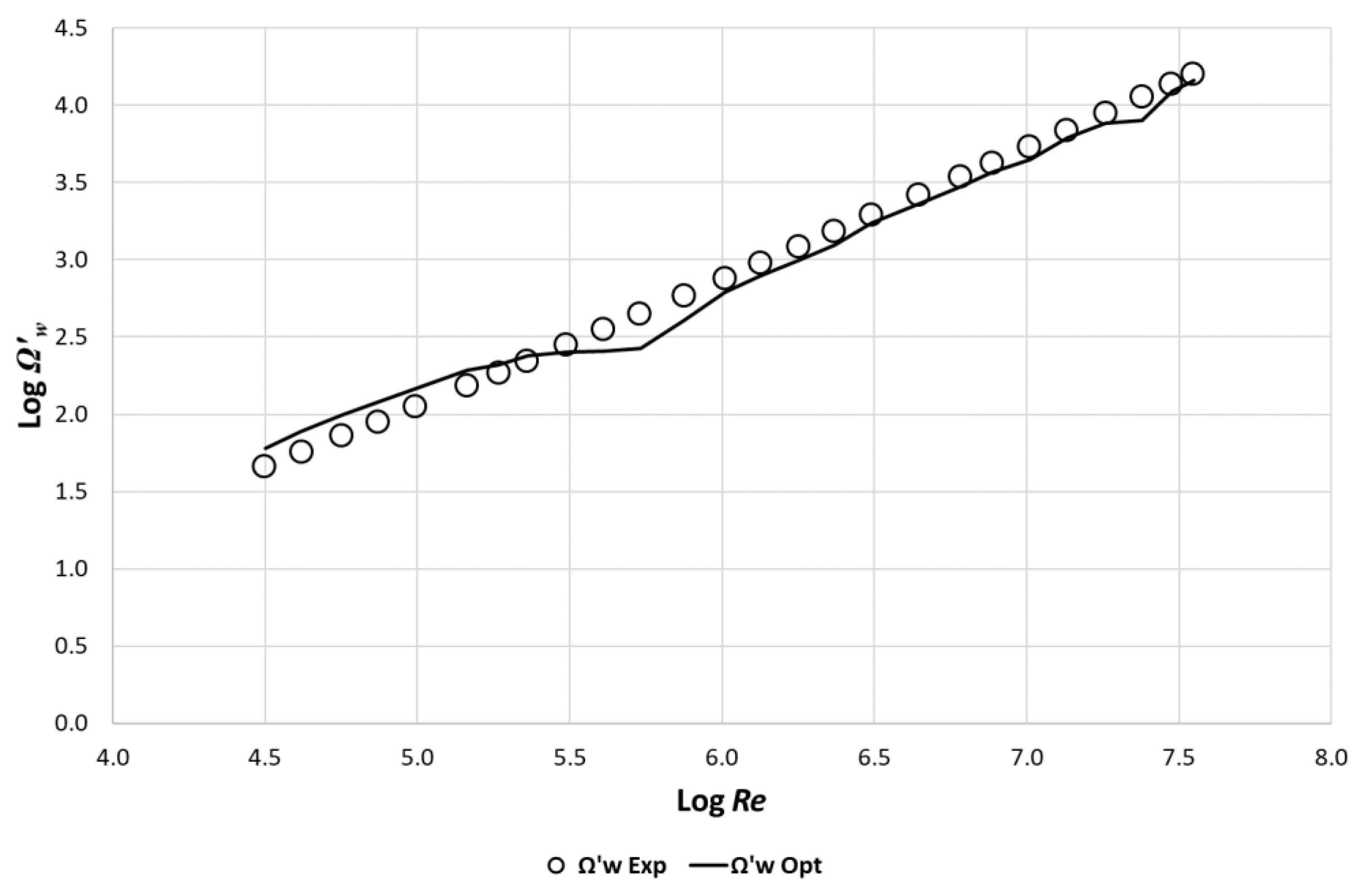
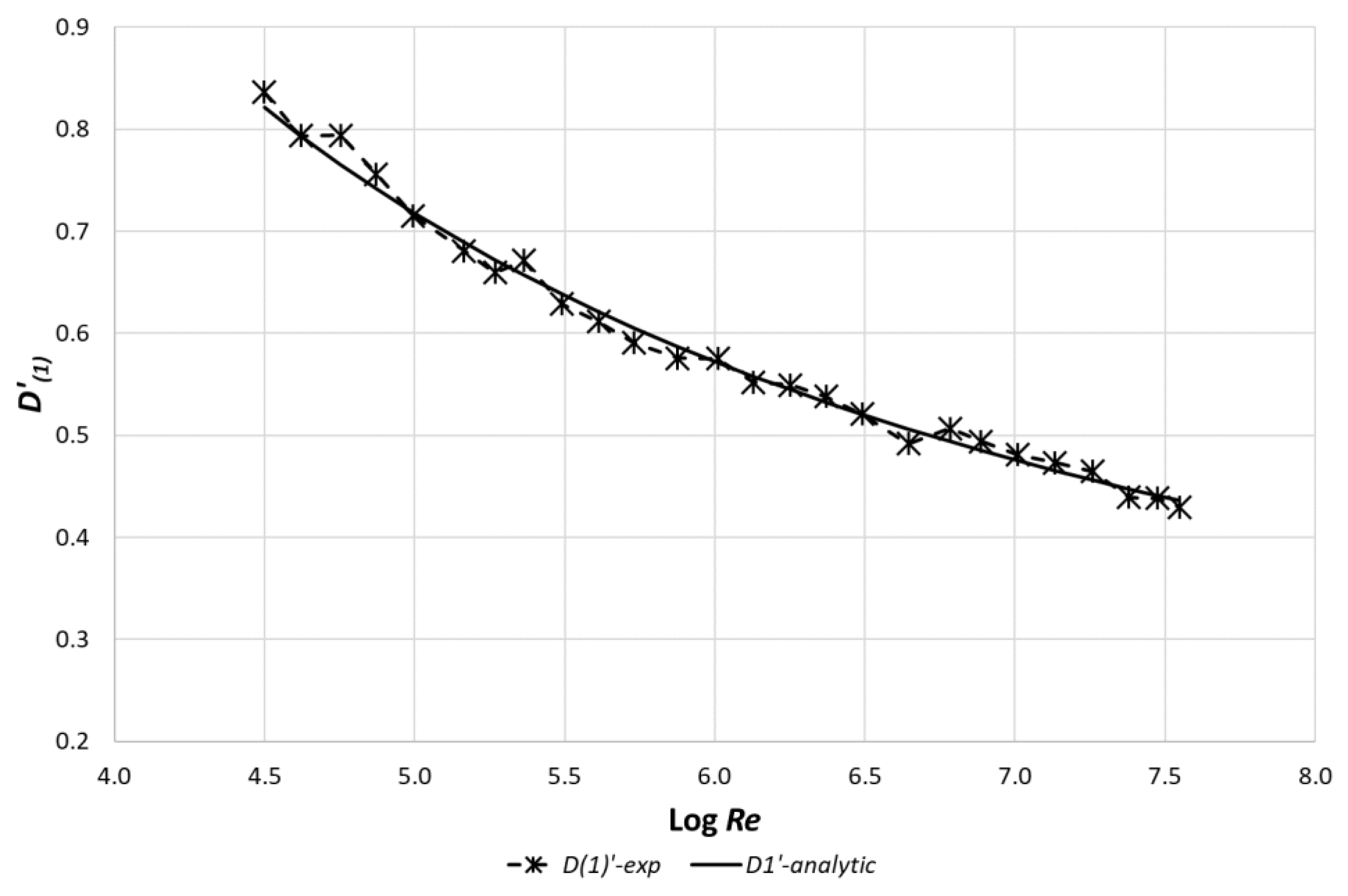
7. Normalized Wall Vorticity Ω′(w) as a Function of Re
8. The Dependence of the First Vorticity Derivative at the Pipe Axis on Re
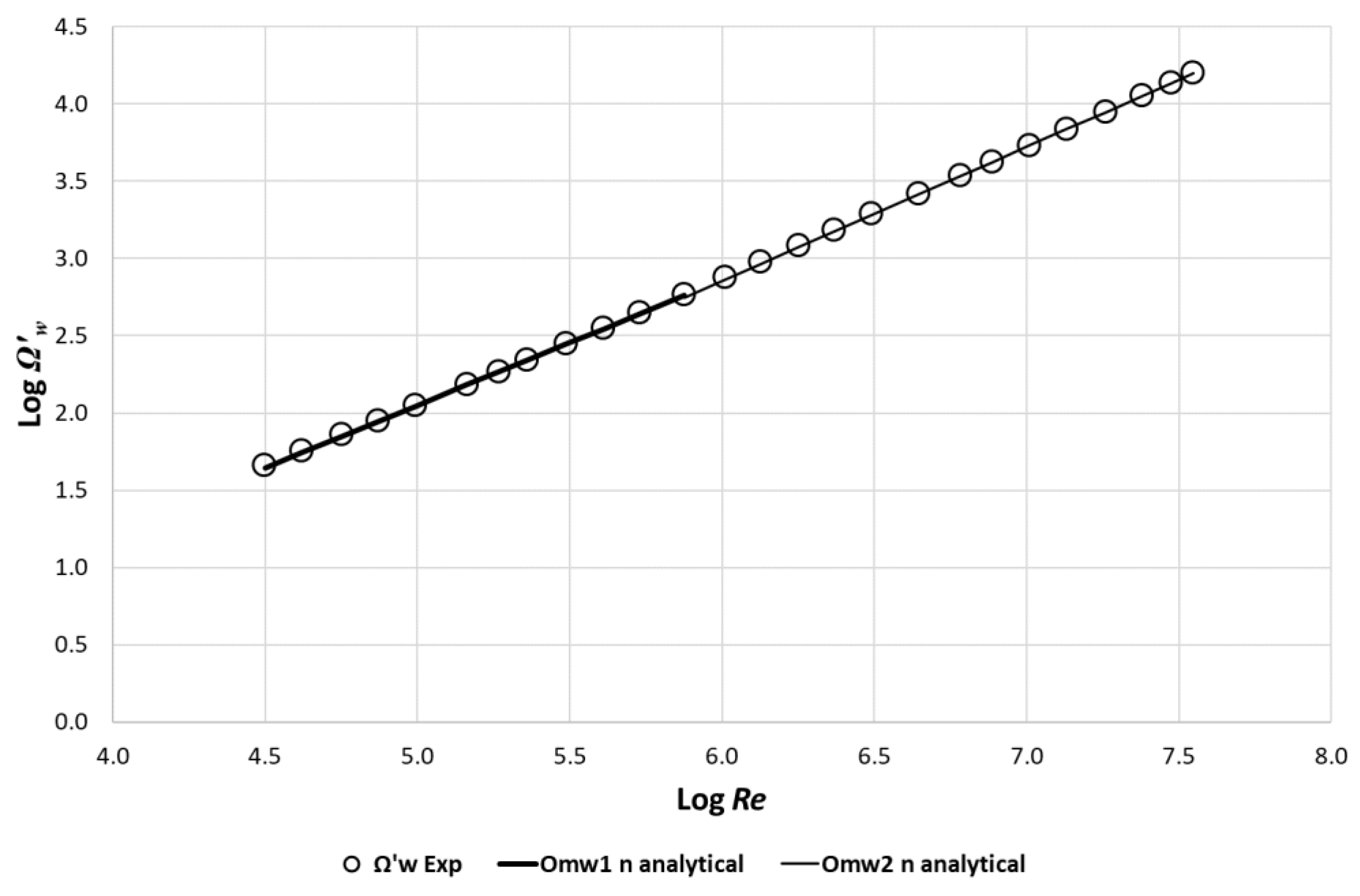
9. The Dependence of Exponents K and N on the Re
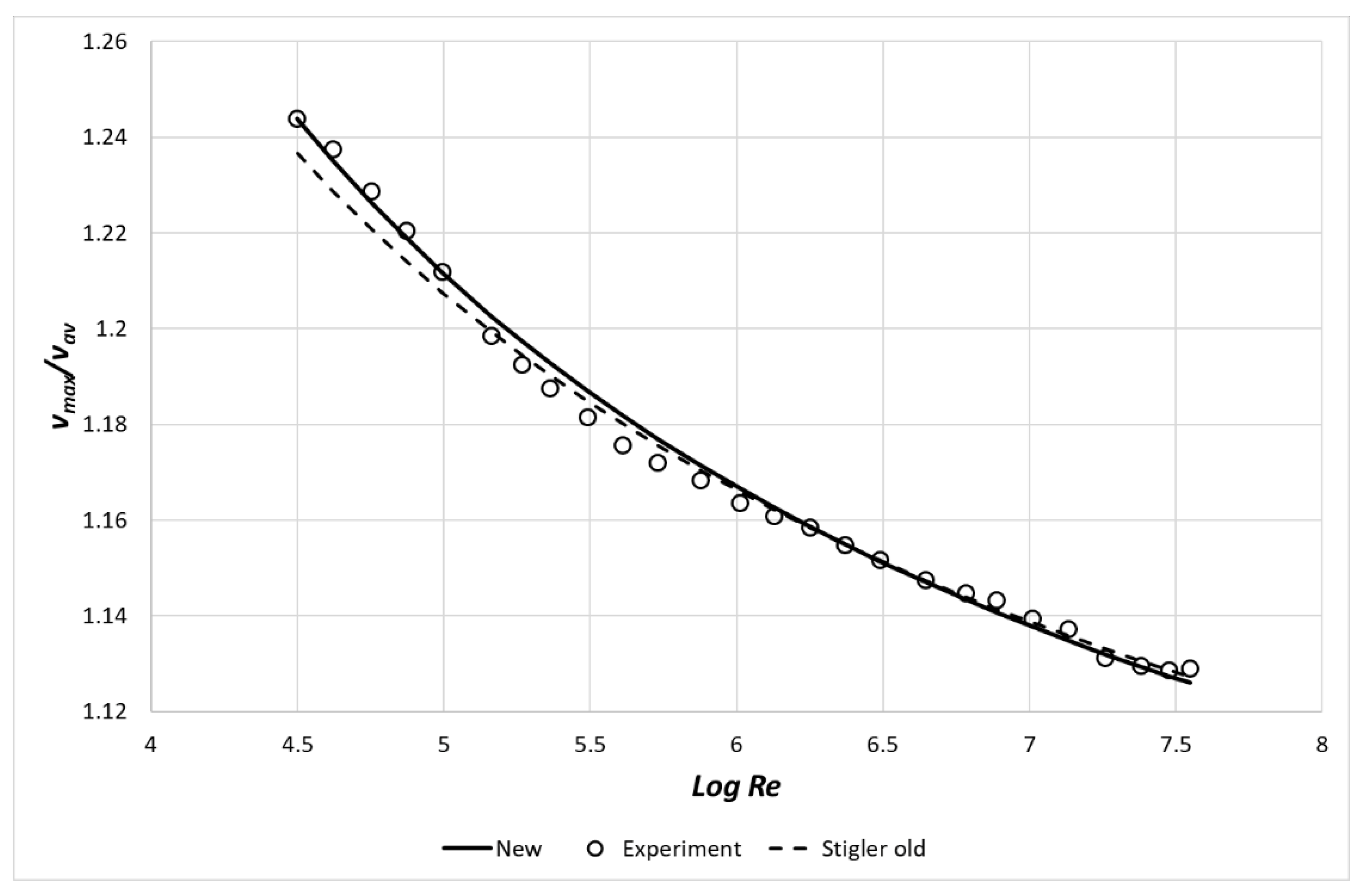
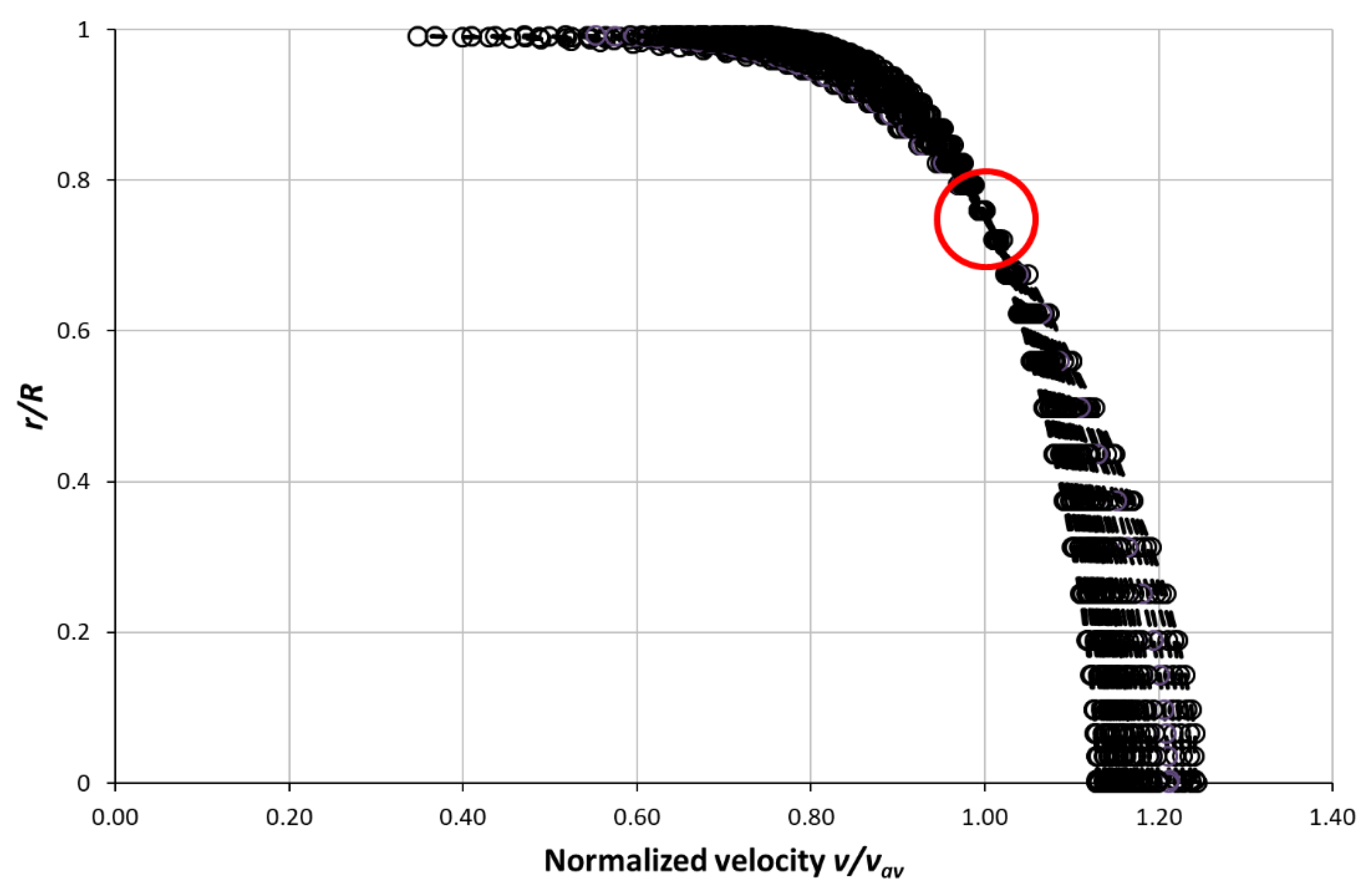
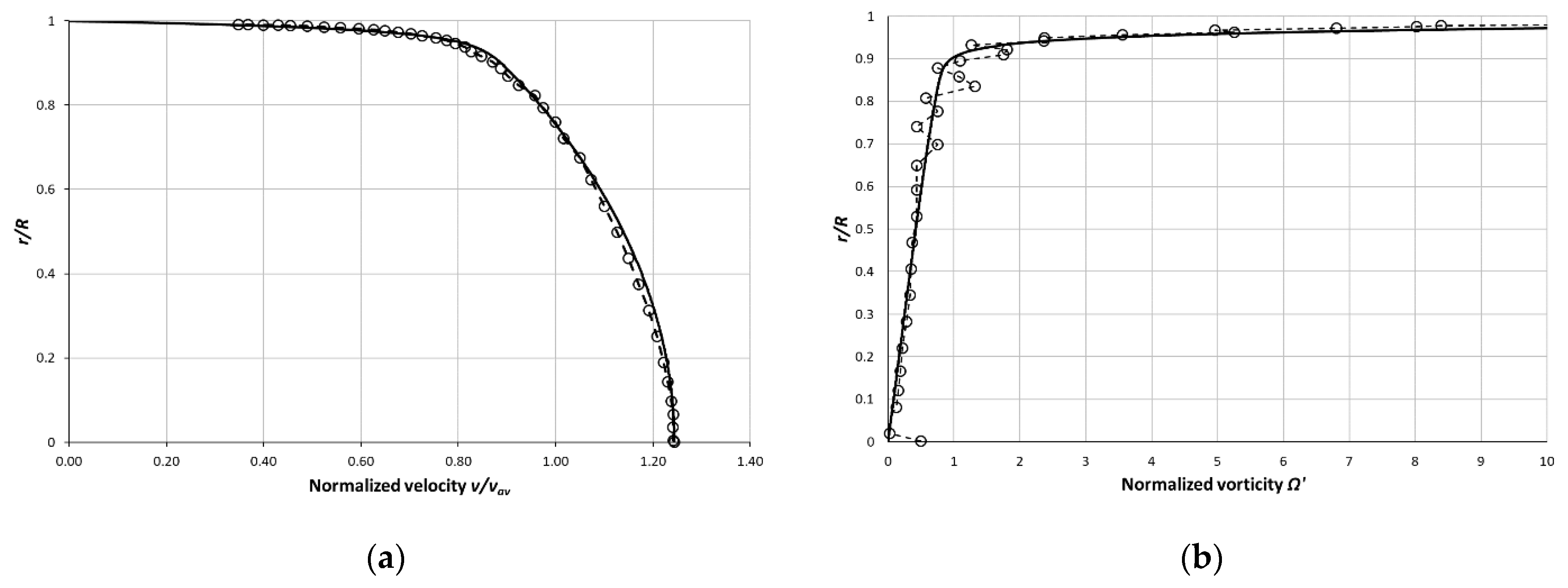
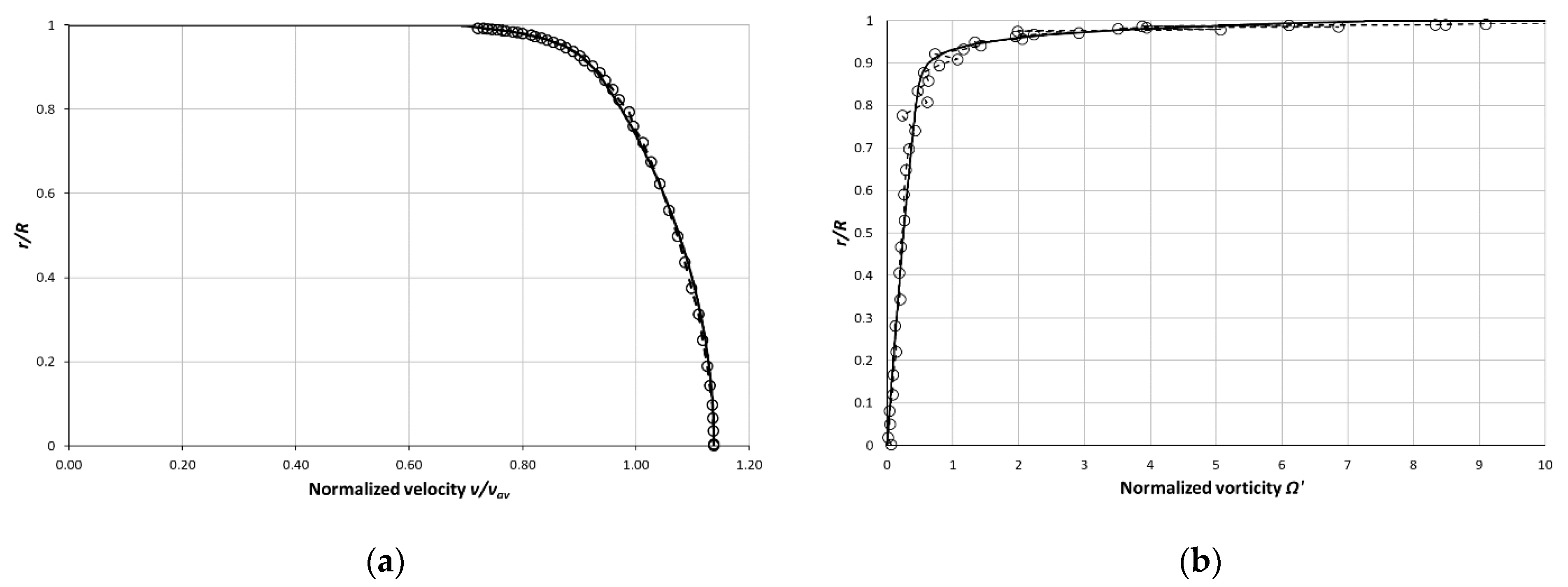
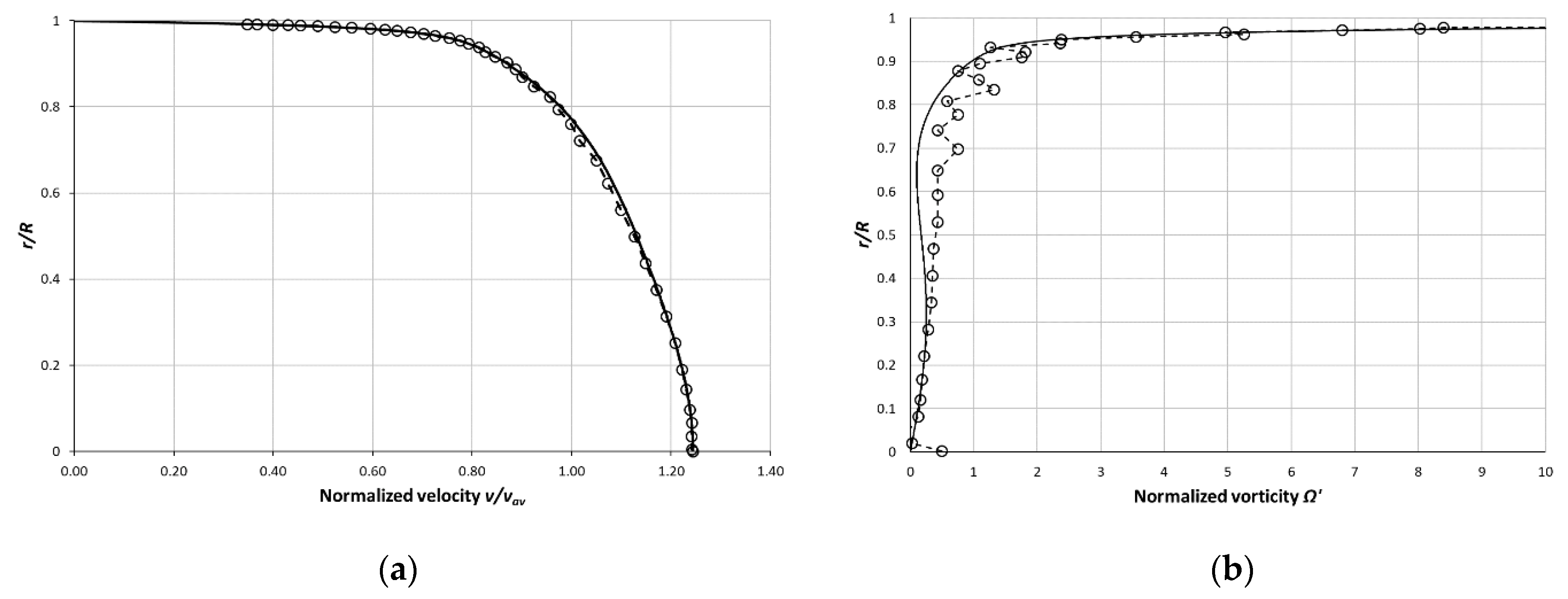
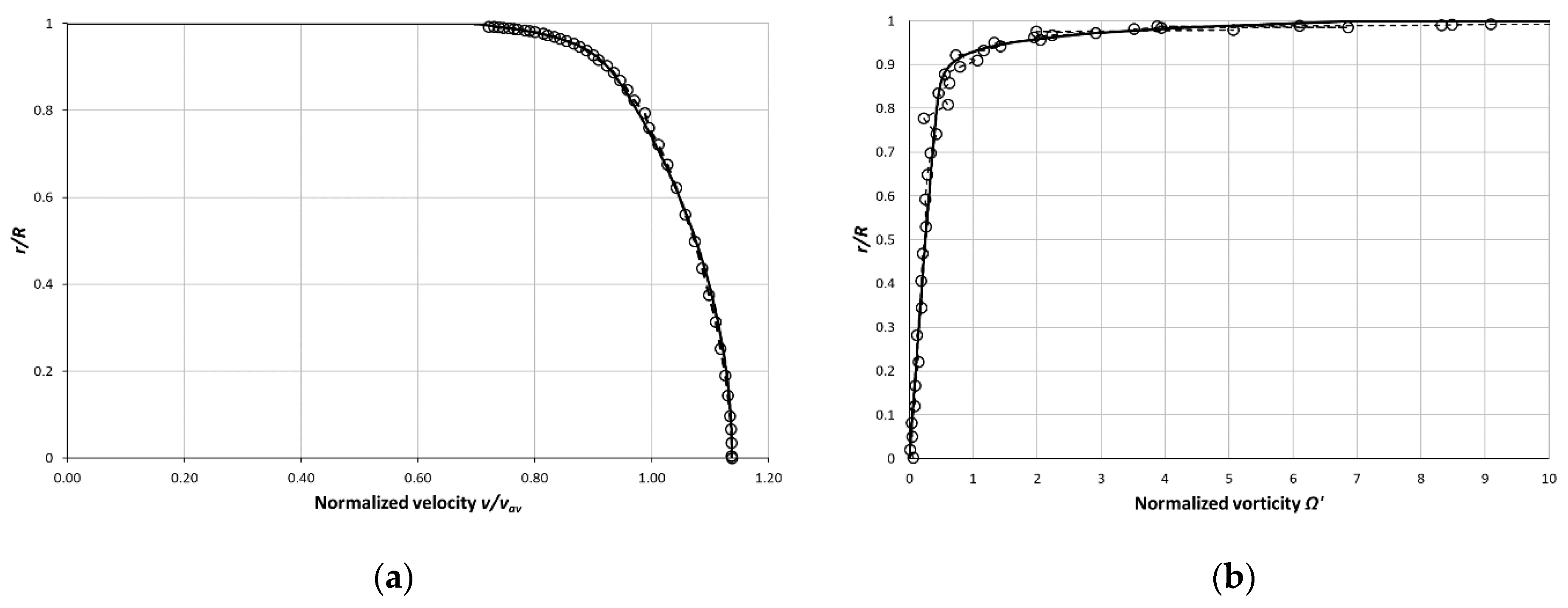
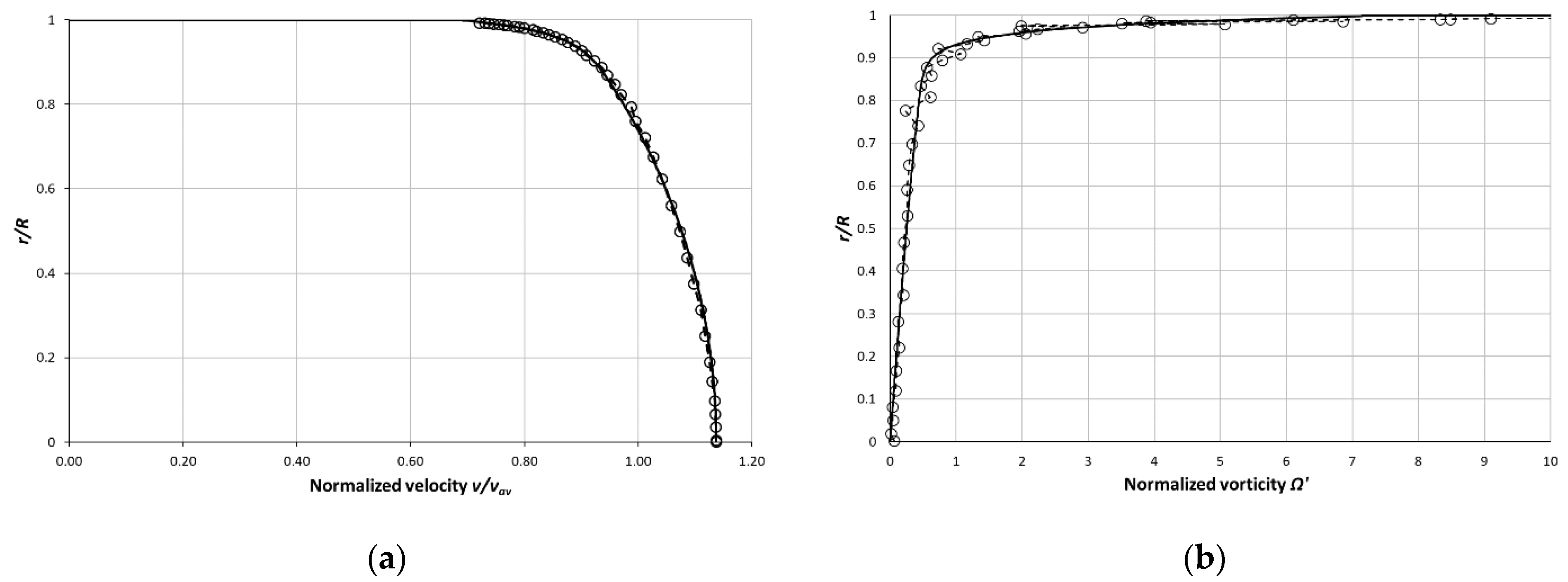
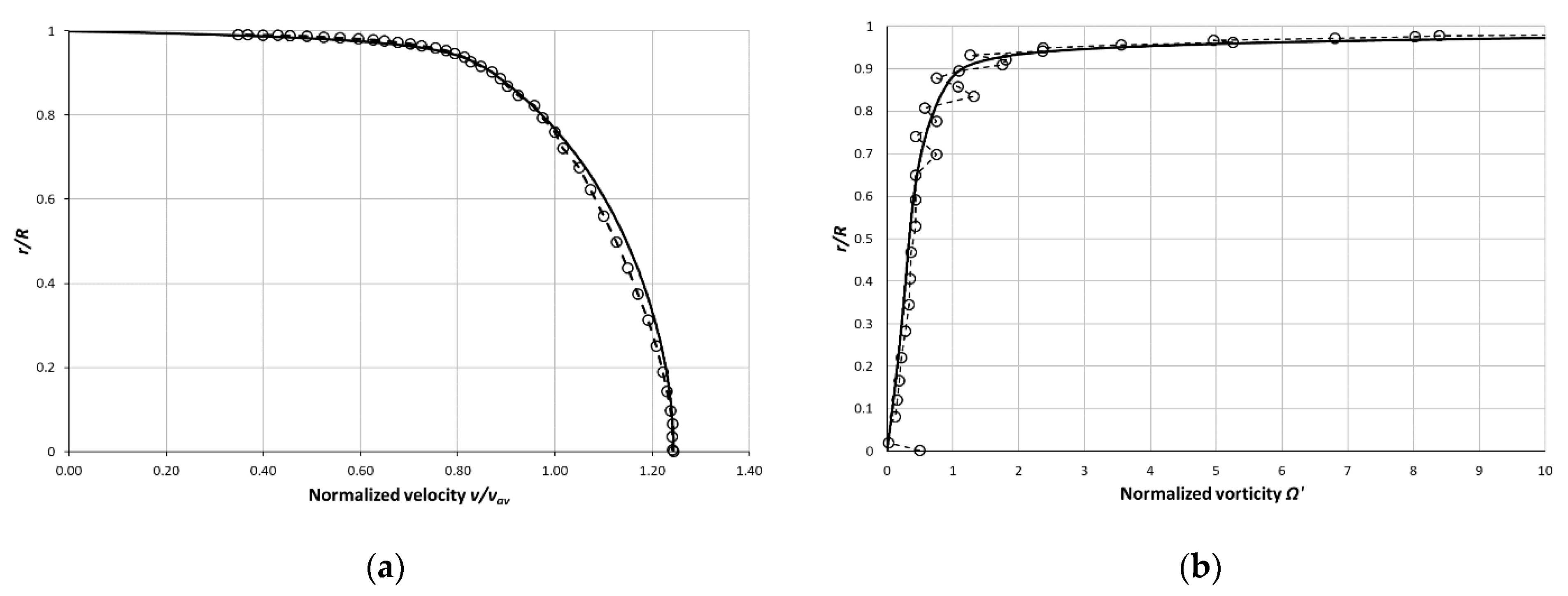
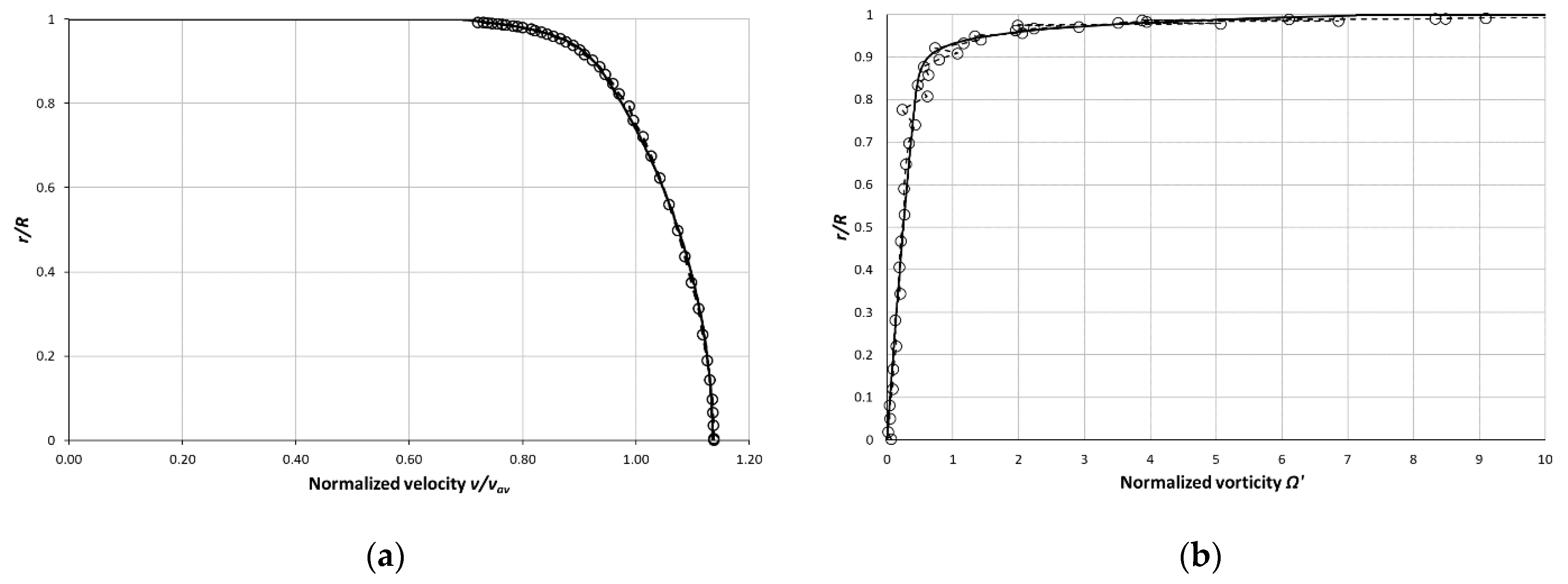
10. Mean Velocity Profile Prediction
11. Conclusions
12. Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Munson, B.R.; Young, D.F.; Okiishi, T.H. Fundamentals of Fluid Mechanics, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006; ISBN 978-0-471-67582-2. [Google Scholar]
- Matas, R.; Cibera, V.; Syka, T.; Vít, T. Modelling of flow in pipes and ultrasonic flowmeter bodies. EPJ Web. Conf. 2014, 67, 6. [Google Scholar] [CrossRef]
- Zagarola, M.V.; Smits, A.J. Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 1998, 373, 33–79. [Google Scholar] [CrossRef]
- Cantwell, B.J. A universal velocity profile for smooth wall pipe flow. J. Fluid Mech. 2019, 878, 834–874. [Google Scholar] [CrossRef]
- Field, M.S.; Schiesser, W.E. Modeling solute reactivity in a phreatic solution conduit penetrating a karst aquifer. J. Contam. Hydrol. 2018, 217, 52–70. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J. Calculus: Early Transcendentals, 7th ed.; Brooks/Cole Cengage Learning: Belmont, CA, USA, 2012; ISBN 978-0-538-49790-9. [Google Scholar]
- Alekseenko, S.V.; Kuibin, P.A.; Okulov, V.L. Theory of Concentrated Vortices: An Introduction; Springer: New York, NY, USA, 2007; ISBN 978-3-540-73375-1. [Google Scholar]
- Štigler, J. Contribution to investigation of turbulent mean-flow velocity profile in pipe of circular cross-section. In Proceedings of the 35th Meeting of Departments of Fluid Mechanics and Thermomechanics; AIP Publishing: Šamorín, Slovak Republic, 2016; pp. 1–13. [Google Scholar] [CrossRef]
- Soukup, L. Analysis of the Fluid Flow in Pipes Circular and not Circular Cross-Section with the Methods Using Distribution of the Vorticity Density. Ph.D. Thesis, Faculty of Mechanical Engineering, Energy Institute, Brno University of Technology, Brno, Czech Republic, December 2016. [Google Scholar]
- Bartková, T. Fluid Flow in Narrow gap Between two Cylinders Induced by Pressure Gradient. Master’s Thesis, Faculty of Mechanical Engineering, Energy institute, Brno University of Technology, Brno, Czech Republic, July 2020. [Google Scholar]
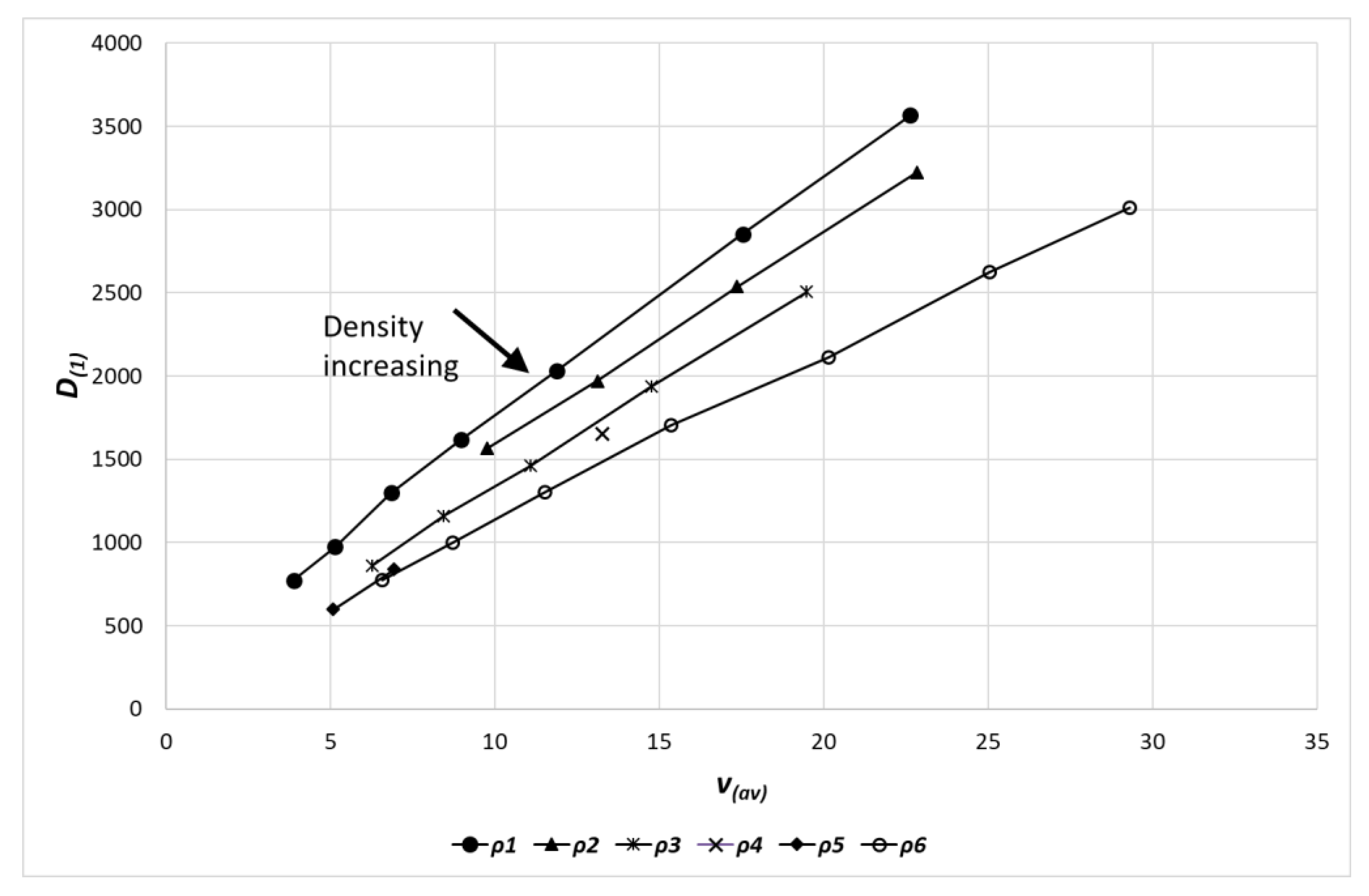


| p.n. | Re [1] | v(av) [m.s−1] | v(max) [m.s−1] | Ω(w) [s−1] | D(1) [m−1.s−1] | N [-] | K [-] | Ω′(w) [1] | D‘(1) [1] | v‘(max) [1] |
|---|---|---|---|---|---|---|---|---|---|---|
| 01 | 31,577 | 3.876 | 4.821 | 2748 | 775 | 55.3 | 4.5 | 45.9 | 0.8363 | 1.2439 |
| 02 | 41,727 | 5.132 | 6.351 | 4523 | 974 | 71.5 | 5.0 | 57.0 | 0.7939 | 1.2374 |
| 03 | 56,677 | 6.845 | 8.410 | 7639 | 1299 | 95.7 | 6.0 | 72.2 | 0.7941 | 1.2287 |
| 04 | 74,293 | 8.952 | 10.926 | 12,288 | 1618 | 120.9 | 9.0 | 88.8 | 0.7562 | 1.2204 |
| 05 | 98,811 | 11.896 | 14.404 | 20,447 | 2032 | 159.9 | 12.7 | 111.3 | 0.7151 | 1.2118 |
| 06 | 145,790 | 17.532 | 21.011 | 41,029 | 2853 | 223.5 | 13.1 | 151.4 | 0.6808 | 1.1984 |
| 07 | 185,430 | 22.623 | 26.976 | 64,189 | 3567 | 280.5 | 17.1 | 183.5 | 0.6596 | 1.1924 |
| 08 | 230,460 | 9.751 | 11.58 | 32,974 | 1565 | 340.1 | 18.6 | 218.7 | 0.6715 | 1.1875 |
| 09 | 309,500 | 13.110 | 15.489 | 56,885 | 1971 | 449.8 | 24.4 | 280.7 | 0.6289 | 1.1815 |
| 10 | 409,290 | 17.357 | 20.405 | 94,436 | 2537 | 575.6 | 28.8 | 351.9 | 0.6116 | 1.1756 |
| 11 | 539,090 | 22.840 | 26.768 | 156,752 | 3225 | 737.3 | 34.3 | 443.9 | 0.5908 | 1.1720 |
| 12 | 751820 | 6.271 | 7.327 | 56,744 | 863 | 955.1 | 35.8 | 585.2 | 0.5757 | 1.1683 |
| 13 | 1,023,800 | 8.440 | 9.820 | 98,752 | 1161 | 1208.0 | 32.4 | 756.9 | 0.5754 | 1.1636 |
| 14 | 1,340,400 | 11.071 | 12.851 | 162,559 | 1461 | 1504.3 | 35.9 | 949.7 | 0.5519 | 1.1608 |
| 15 | 1,787,500 | 14.769 | 17.110 | 276,184 | 1940 | 1915.6 | 36.8 | 1209.5 | 0.5495 | 1.1585 |
| 16 | 2,345,000 | 19.478 | 22.493 | 456,420 | 2506 | 2354.0 | 37.3 | 1515.6 | 0.5382 | 1.1548 |
| 17 | 3,098,100 | 13.268 | 15.280 | 395,546 | 1652 | 2974.4 | 39.0 | 1928.2 | 0.5208 | 1.1516 |
| 18 | 4,420,300 | 5.081 | 5.830 | 205,830 | 597 | 4064.6 | 43.7 | 2620.3 | 0.4920 | 1.1474 |
| 19 | 6,072,700 | 6.928 | 7.931 | 368,398 | 839 | 5126.3 | 35.2 | 3439.3 | 0.5068 | 1.1447 |
| 20 | 7,714,700 | 6.580 | 7.523 | 427,544 | 777 | 6262.6 | 38.8 | 4202.4 | 0.4941 | 1.1432 |
| 21 | 10,249,000 | 8.703 | 9.917 | 719,643 | 1001 | 7815.3 | 35.5 | 5348.3 | 0.4810 | 1.1395 |
| 22 | 13,598,000 | 11.504 | 13.083 | 1,220,866 | 1302 | 10,002.3 | 37.5 | 6864.2 | 0.4733 | 1.1373 |
| 23 | 18,196,000 | 15.345 | 17.358 | 2,093,107 | 1705 | 12,541.5 | 32.8 | 8822.6 | 0.4647 | 1.1312 |
| 24 | 23,977,000 | 20.149 | 22.758 | 3,499,514 | 2115 | 15,818.9 | 35.7 | 11,233.7 | 0.4391 | 1.1295 |
| 25 | 29,927,000 | 25.043 | 28.265 | 5,295,477 | 2623 | 19,157.9 | 36.3 | 13,676.9 | 0.4382 | 1.1287 |
| 26 | 35,259,000 | 29.306 | 33.087 | 7,180,224 | 3010 | 22,306.5 | 40.6 | 15,847.2 | 0.4297 | 1.1290 |
| p.n. | Re [1] | v(av) [m.s−1] | v(max) [m.s−1] | Ω(w) [s−1] | D(1) [m−1.s−1] | N [-] | K [-] | Ω′(w) [1] | D′(1) [1] | v′(max) [1] |
|---|---|---|---|---|---|---|---|---|---|---|
| 01 | 31,577 | 3.876 | 4.821 | 3606 | 1156 | 82.2 | 4.0 | 60.2 | 1.2475 | 1.2439 |
| 02 | 41,727 | 5.132 | 6.351 | 6183 | 1420 | 109.9 | 5.1 | 77.9 | 1.1579 | 1.2374 |
| 03 | 56,677 | 6.845 | 8.410 | 10,480 | 1560 | 146.8 | 10.0 | 99.0 | 0.9532 | 1.2287 |
| 04 | 74,293 | 8.953 | 10.926 | 16,677 | 1881 | 180.1 | 11.0 | 120.5 | 0.8789 | 1.2204 |
| 05 | 98,811 | 11.886 | 14.404 | 27,207 | 1969 | 229.3 | 19.7 | 148.1 | 0.6929 | 1.2118 |
| 06 | 145,790 | 17.532 | 21.011 | 52,502 | 2654 | 307.2 | 22.7 | 193.7 | 0.6332 | 1.1984 |
| 07 | 185,430 | 22.623 | 26.976 | 73,314 | 3313 | 329.6 | 22.2 | 209.6 | 0.6126 | 1.1924 |
| 08 | 230,460 | 9.752 | 11.580 | 36,037 | 1353 | 382.3 | 26.2 | 239.0 | 0.5805 | 1.1875 |
| 09 | 309,500 | 13.110 | 15.489 | 51,500 | 1825 | 400.6 | 25.2 | 254.1 | 0.5824 | 1.1815 |
| 10 | 409,290 | 17.357 | 20.405 | 68,893 | 2310 | 401.3 | 27.1 | 256.7 | 0.5567 | 1.1756 |
| 11 | 539,090 | 22.840 | 26.768 | 94,562 | 3076 | 422.1 | 30.3 | 267.8 | 0.5634 | 1.1720 |
| 12 | 751,820 | 6.271 | 7.327 | 39,572 | 815 | 660.0 | 37.2 | 408.1 | 0.5440 | 1.1683 |
| 13 | 1,023,800 | 8.439 | 9.820 | 80,881 | 1133 | 994.2 | 34.9 | 619.9 | 0.5615 | 1.1636 |
| 14 | 1,340,400 | 11.071 | 12.851 | 135,828 | 1456 | 1254.0 | 35.8 | 793.5 | 0.5502 | 1.1608 |
| 15 | 1,787,500 | 14.769 | 17.110 | 226,335 | 1952 | 1563.6 | 35.8 | 991.2 | 0.5528 | 1.1585 |
| 16 | 2,345,000 | 19.478 | 22.493 | 374,371 | 2527 | 1926.3 | 36.7 | 1,243.2 | 0.5427 | 1.1548 |
| 17 | 3,098,100 | 13.268 | 15.280 | 353,477 | 1658 | 2652.4 | 38.6 | 1,723.2 | 0.5227 | 1.1516 |
| 18 | 4,420,300 | 5.081 | 5.830 | 181,425 | 617 | 3554.7 | 40.9 | 2,309.6 | 0.5084 | 1.1474 |
| 19 | 6,072,700 | 6.928 | 7.931 | 318,384 | 835 | 4427.3 | 35.3 | 2,972.4 | 0.5044 | 1.1447 |
| 20 | 7,714,700 | 6.580 | 7.523 | 375,852 | 781 | 5501.9 | 38.5 | 3,694.3 | 0.4963 | 1.1432 |
| 21 | 10,249,000 | 8.703 | 9.917 | 597,357 | 1010 | 6495.2 | 35.6 | 4,439.5 | 0.4853 | 1.1395 |
| 22 | 13,598,000 | 11.504 | 13.083 | 1,104,237 | 1332 | 8983.2 | 34.6 | 6,208.5 | 0.4844 | 1.1373 |
| 23 | 18,196,000 | 15.345 | 17.358 | 1,812,336 | 1669 | 10,839.6 | 32.7 | 7,639.1 | 0.4550 | 1.1312 |
| 24 | 23,977,000 | 20.149 | 22.758 | 2,476,268 | 2041 | 11,258.8 | 40.3 | 7,949.0 | 0.4238 | 1.1295 |
| 25 | 29,927,000 | 25.043 | 28.265 | 4,757,948 | 2661 | 17,202.4 | 35.5 | 12,288.6 | 0.4446 | 1.1287 |
| 26 | 35,259,000 | 29.306 | 33.087 | 6,549,529 | 3293 | 20,042.4 | 31.9 | 14,455.2 | 0.4701 | 1.1290 |
| Analytical Velocity Profile | δ [% of v(av)] | |
|---|---|---|
| Re = 31,577 | Re = 13,598,000 | |
| Minimization variables K, and N | 2.183 | 0.364 |
| Minimization variables Ω(w), D(1), K, and N | 0.494 | 0.362 |
| The first prediction way | 2.210 | 0.377 |
| The second prediction way | 2.783 | 0.339 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Štigler, J. Analytical Formula for the Mean Velocity Profile in a Pipe Derived on the Basis of a Spatial Polynomial Vorticity Distribution. Water 2021, 13, 1372. https://doi.org/10.3390/w13101372
Štigler J. Analytical Formula for the Mean Velocity Profile in a Pipe Derived on the Basis of a Spatial Polynomial Vorticity Distribution. Water. 2021; 13(10):1372. https://doi.org/10.3390/w13101372
Chicago/Turabian StyleŠtigler, Jaroslav. 2021. "Analytical Formula for the Mean Velocity Profile in a Pipe Derived on the Basis of a Spatial Polynomial Vorticity Distribution" Water 13, no. 10: 1372. https://doi.org/10.3390/w13101372
APA StyleŠtigler, J. (2021). Analytical Formula for the Mean Velocity Profile in a Pipe Derived on the Basis of a Spatial Polynomial Vorticity Distribution. Water, 13(10), 1372. https://doi.org/10.3390/w13101372






