Multi-Gene Genetic Programming Regression Model for Prediction of Transient Storage Model Parameters in Natural Rivers
Abstract
1. Introduction
2. Models and Methods
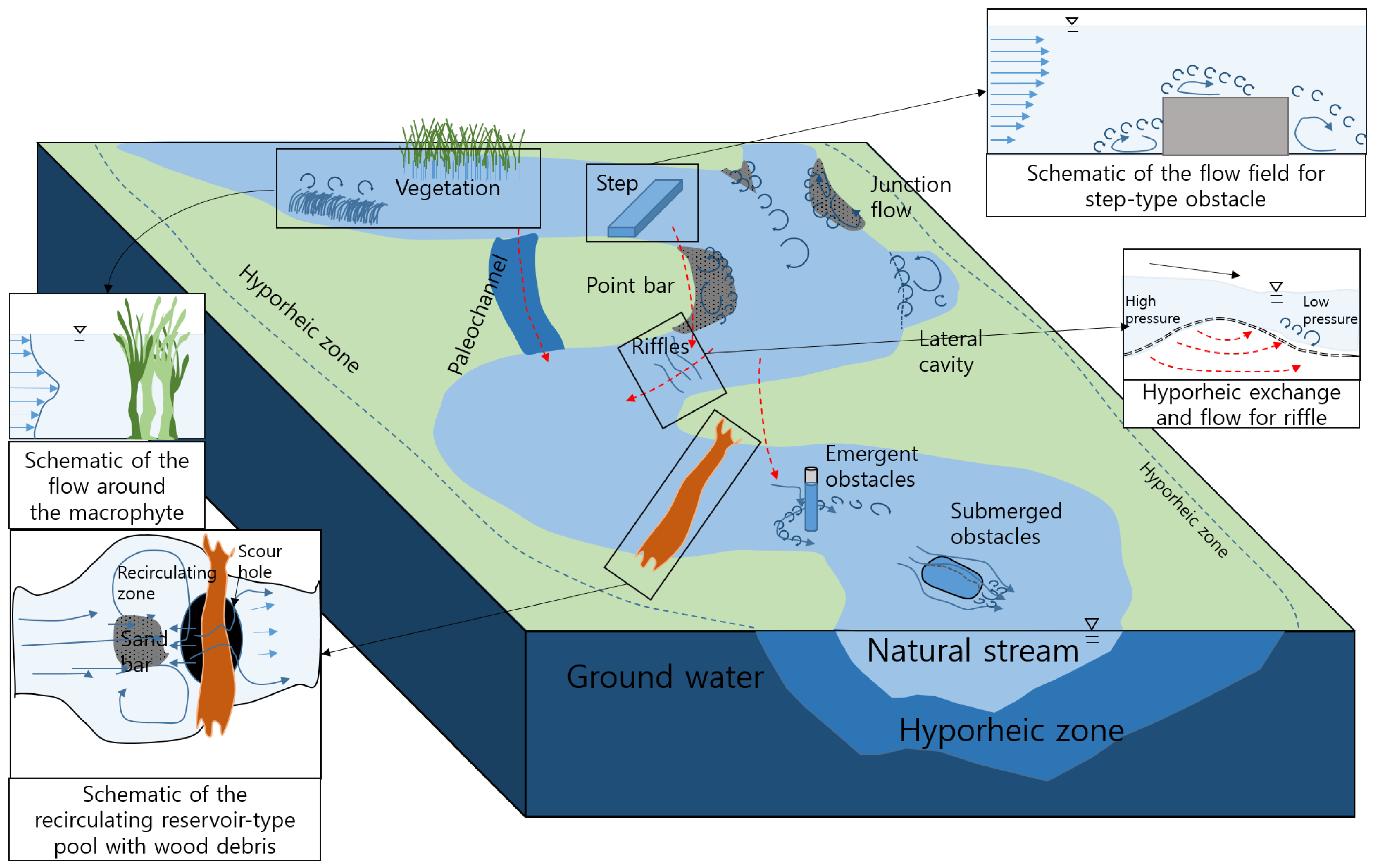
2.1. Transient Storage Model
Remarks for the TSM
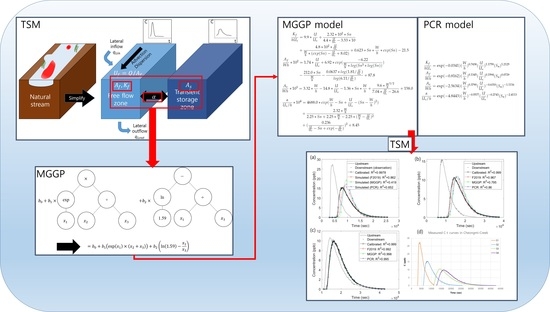
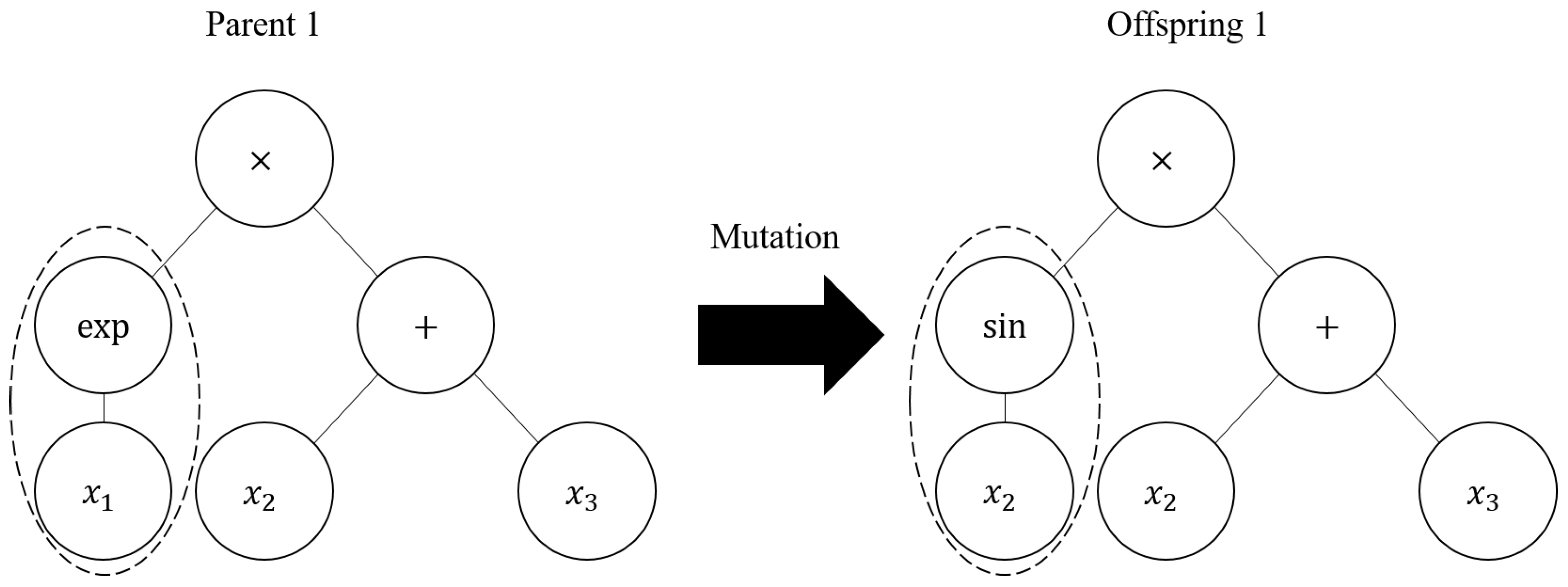
2.2. Multi-Gene Genetic Programming
3. Formulation of Empirical Equations
3.1. Dimensional Analysis and Data Collection
3.2. Formulated Equations
3.2.1. Formulation by MGGP
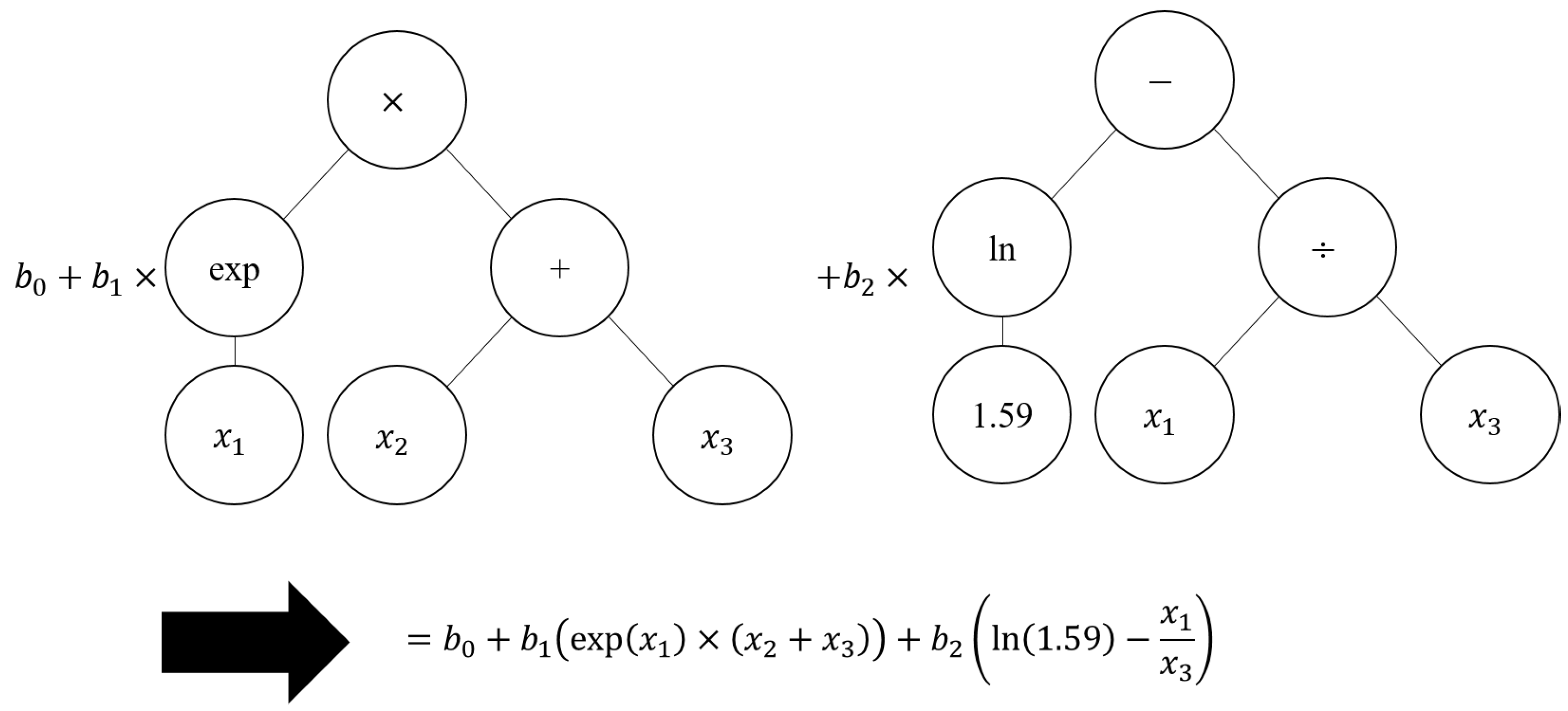
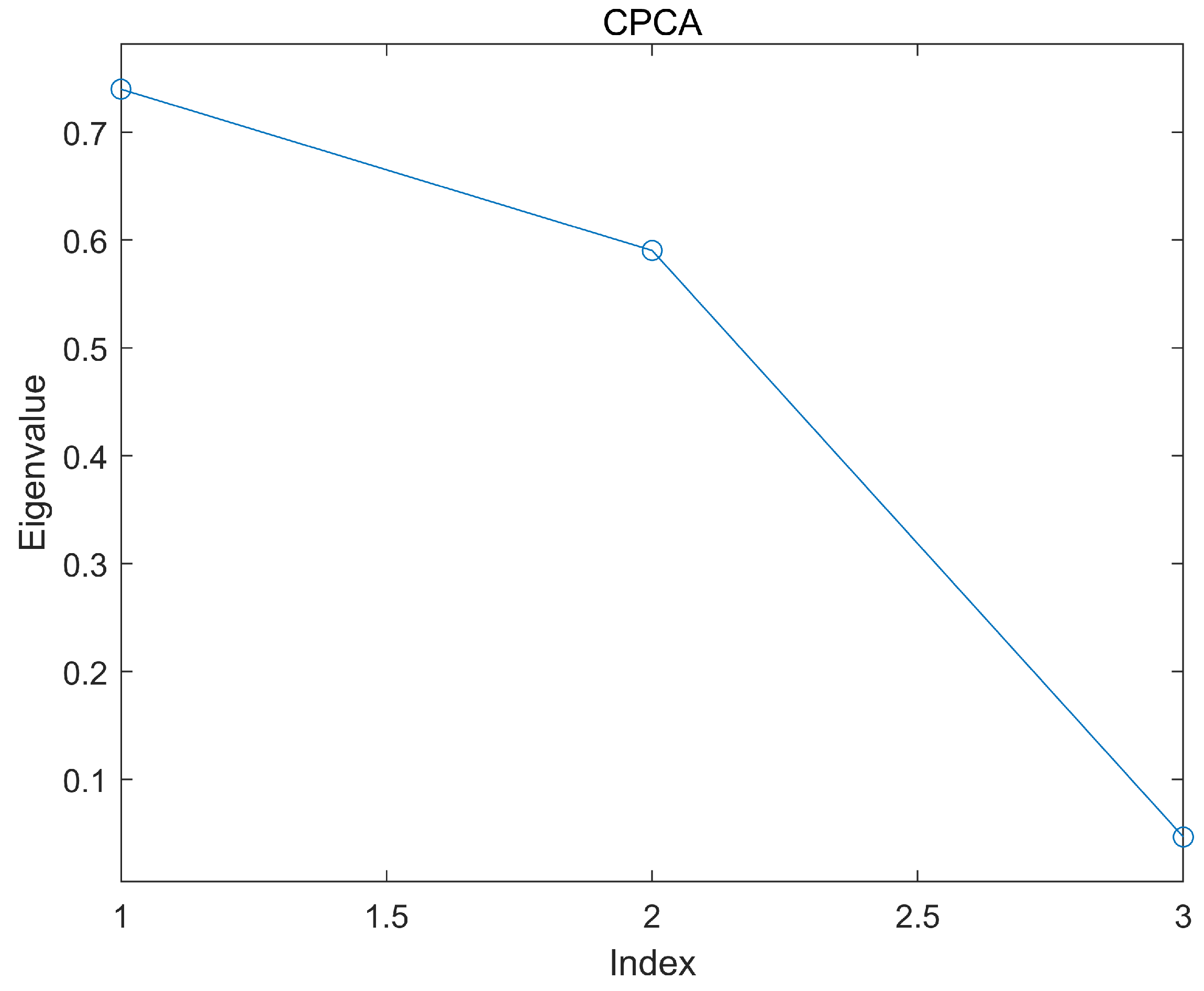
3.2.2. Formulation by PCR-Based Regression
3.3. Statistical Performance of the Models
4. In-Stream Application
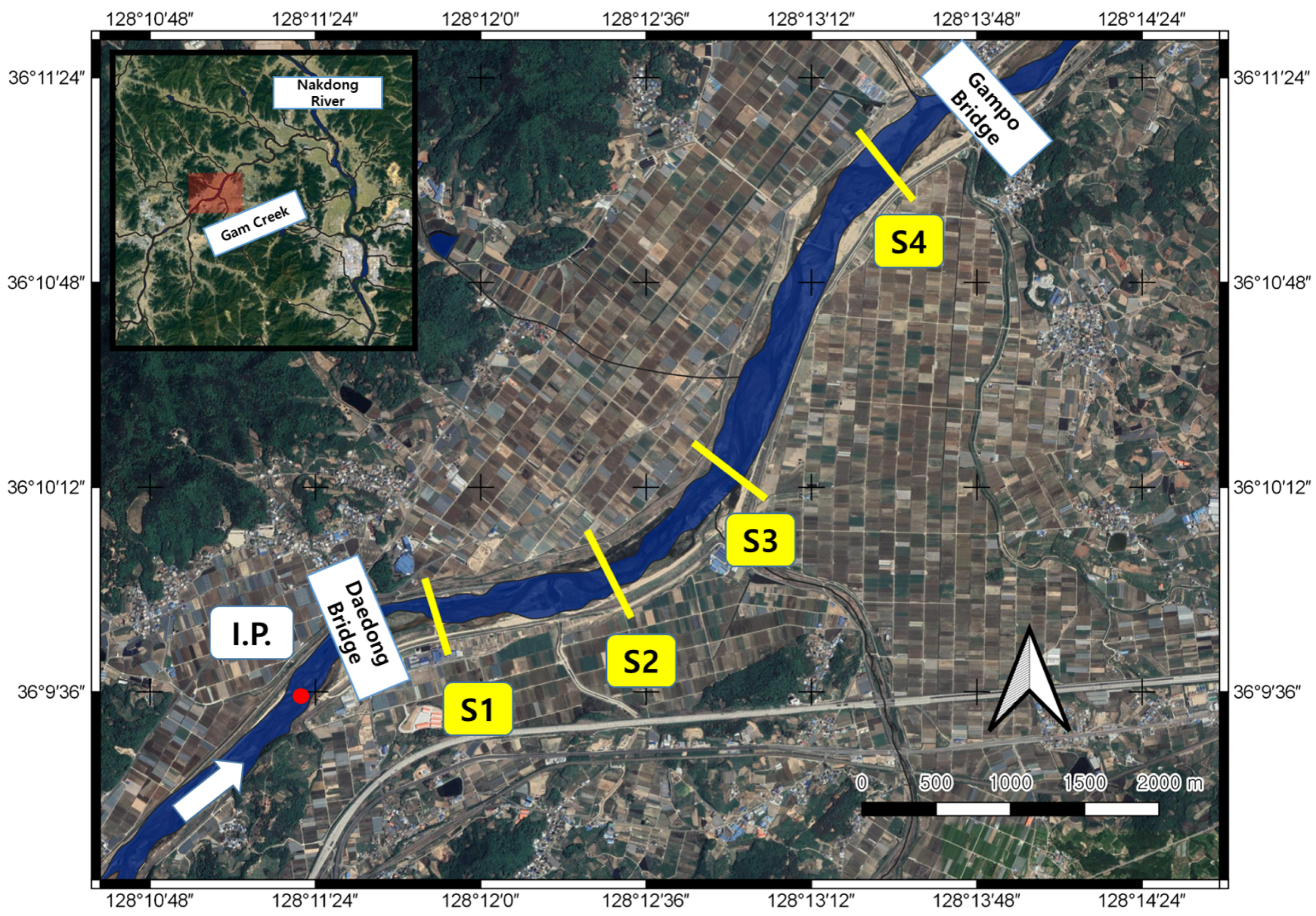
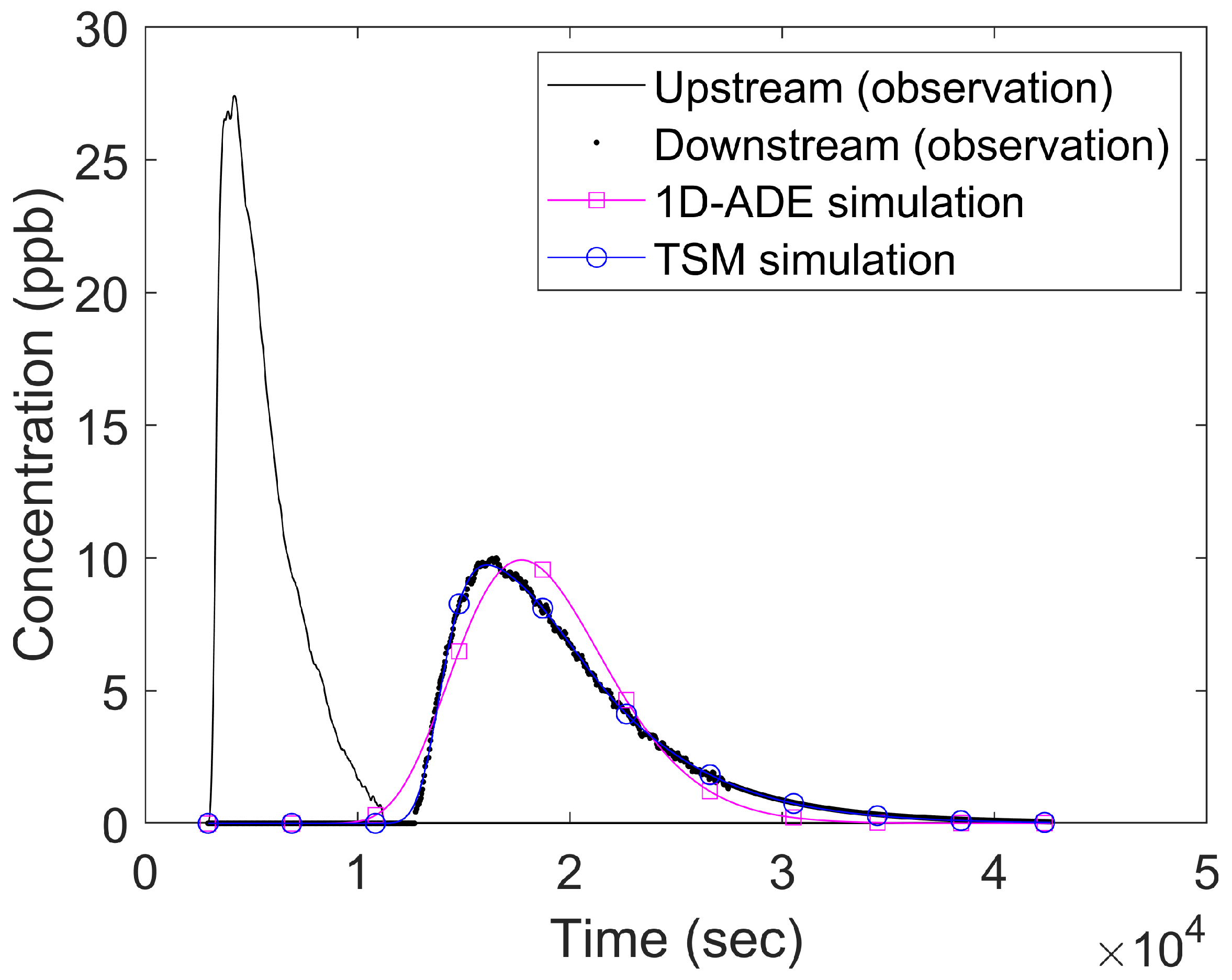
4.1. Tracer Test Description
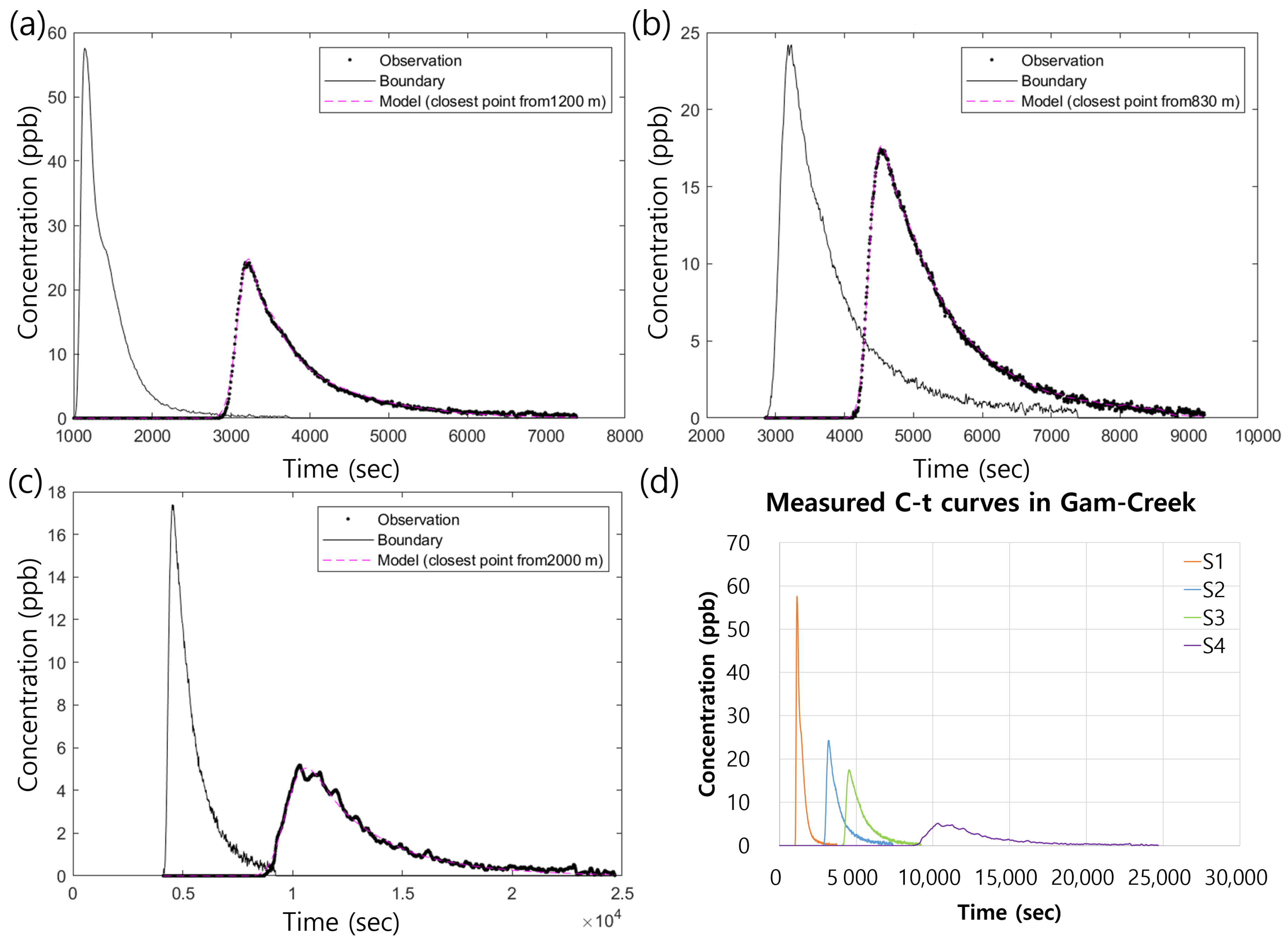
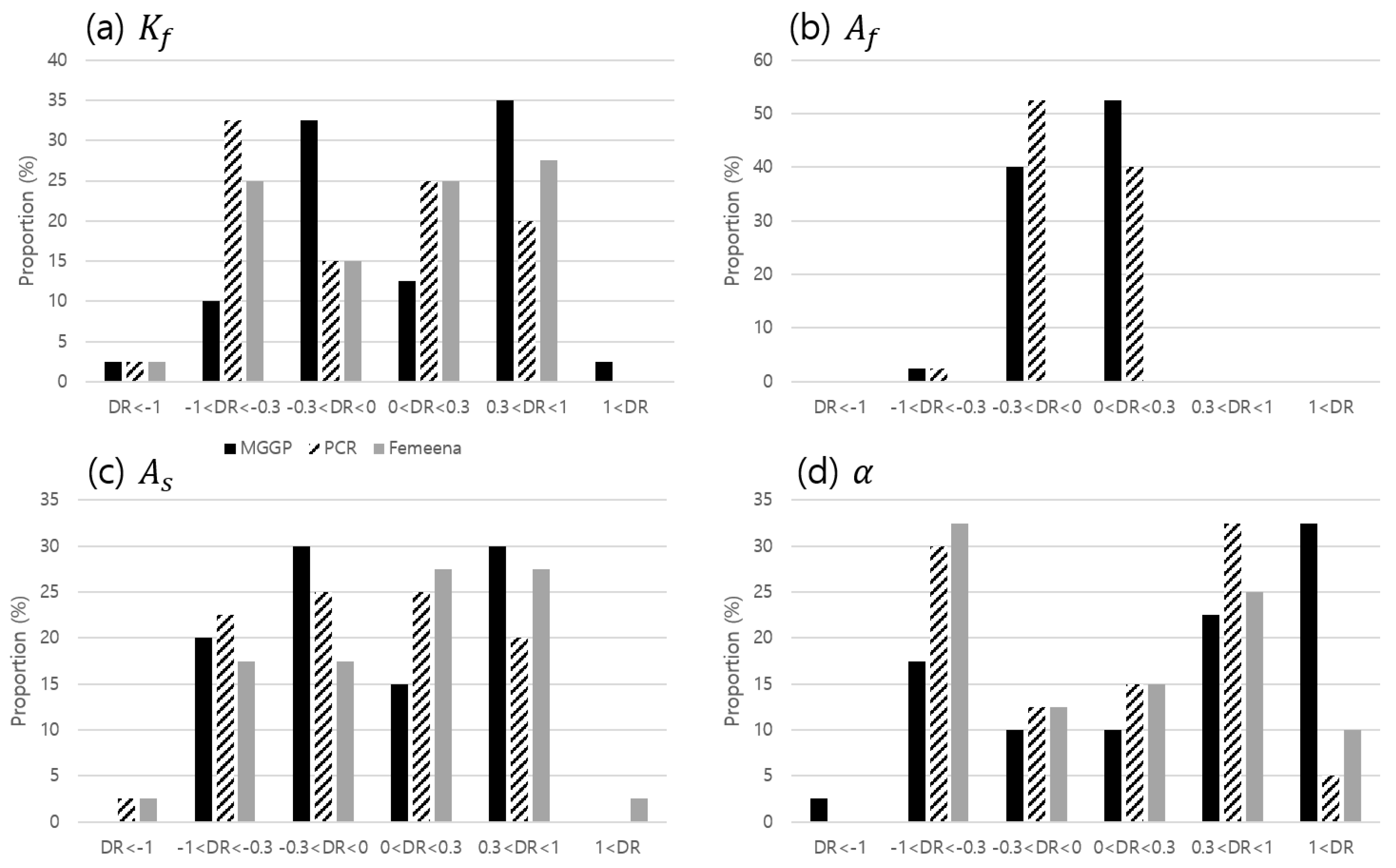
4.2. Simulation Results
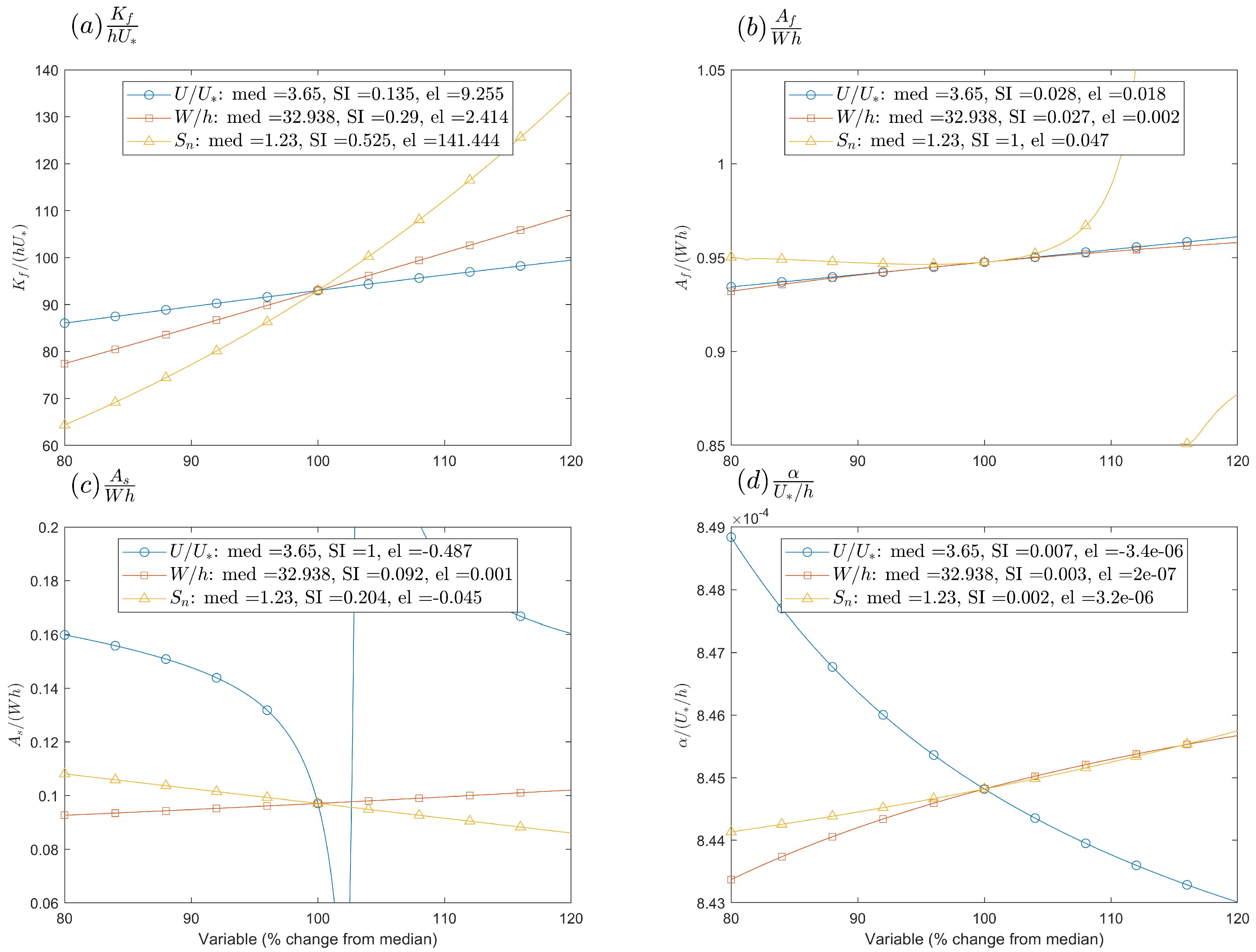
5. Sensitivity Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D-ADE | 1-Dimension Advection-Dispersion Equation |
| BTC | Breakthrough Curve |
| DR | Discrepancy Ratio |
| GA | Genetic Algorithm |
| GP | Genetic Programming |
| HTS | Hyporheic Transient Storage |
| MGGP | Multi-Gene Genetic Programming |
| MSE | Mean Squared Error |
| MSL | Mean Sea Level |
| OAT | One-At-a-Time |
| OTIS | One-Dimensional Transport with Inflow and Storage |
| PCR | Principal Components Regression |
| RMSE | Root Mean Squared Error |
| RTD | Residence Time Distribution |
| RWT | Rhodamine WT |
| SC-SAHEL | Shuffled Complex-Self Adaptive EvoLution |
| SCE-UA | Shuffled Complex Evolution-University of Arizona |
| SI | Sensitivity Index |
| STS | Surface Transient Storage |
| TSM | Transient Storage Model |
| VIF | Variance Inflation Factor |
Appendix A. Description of the Gam-Creek Tracer Test
| Variables | Reach | |||
|---|---|---|---|---|
| S1-S2 | S2-S3 | S3-S4 | ||
| Hydraulic Features | (m) | 1200 | 830 | 2000 |
| Q (cms) | 11.06 | 11.06 | 11.06 | |
| W (m) | 57.36 | 58.86 | 53.00 | |
| h (m) | 0.36 | 0.36 | 0.43 | |
| 0.0007 | 0.0024 | 0.0007 | ||
| (m/s) | 0.53 | 0.52 | 0.48 | |
| 1.082 | 1.028 | 1.078 | ||
| TSM Parameters | 0.568 | 0.596 | 4.926 | |
| 18.279 | 17.175 | 31.135 | ||
| 4.1473 | 2.6932 | 10.4883 | ||
| (1/s) | 3.758 | 2.920 | 1.533 | |
Appendix B. Derived PCR Equations Using Total Dataset
References
- Fischer, H.B.; Brooks, N.H. Longitudinal Dispersion in Laboratory and Natural Streams; Tecnical Report No. KH-R-12; California Institute of Technology, W. M. Keck Laboratory of Hydraulics and Water Resources: Pasadena, CA, USA, 1966. [Google Scholar]
- Hays, J.R. Mass Transport Mechanisms in Open Channel Flow. Ph.D. Thesis, Vanderbilt University, Nashville, TN, USA, 1967. [Google Scholar]
- Day, T.J. Longitudinal dispersion in natural channels. Water Resour. Res. 1975, 11, 909–918. [Google Scholar] [CrossRef]
- Pederson, F. Prediction of Longitudinal Dispersion in Natural Streams; Technical Report Series Paper 14; Technical University of Denmark: Lyngby, Denmark, 1977. [Google Scholar]
- Beltaos, S.; Day, T. A field study of longitudinal dispersion. Can. J. Civ. Eng. 1978, 5, 572–585. [Google Scholar] [CrossRef]
- Sabol, G.V.; Nordin, C.F. Dispersion in rivers as related to storage zones. J. Hydraul. Div. 1978, 104, 695–708. [Google Scholar]
- Liu, H.; Cheng, A.H. Modified Fickian model for predicting dispersion. J. Hydraul. Div. 1980, 106, 1021–1040. [Google Scholar]
- Chatwin, P.C. Presentation of longitudinal dispersion data. J. Hydraul. Div. 1980, 106, 71–83. [Google Scholar]
- Beer, T.; Young, P.C. Longitudinal dispersion in natural streams. J. Environ. Eng. 1983, 109, 1049–1067. [Google Scholar] [CrossRef]
- Bencala, K.E. Simulation of solute transport in a mountain pool-and-riffle stream with a kinetic mass transfer model for sorption. Water Resour. Res. 1983, 19, 732–738. [Google Scholar] [CrossRef]
- Abbe, T.B.; Montgomery, D.R. Large woody debris jams, channel hydraulics and habitat formation in large rivers. Regul. Rivers Res. Manag. 1996, 12, 201–221. [Google Scholar] [CrossRef]
- Abbe, T.B.; Montgomery, D.R. Patterns and processes of wood debris accumulation in the Queets river basin, Washington. Geomorphology 2003, 51, 81–107. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. Hyporheic exchange in mountain rivers I: Mechanics and environmental effects. Geogr. Compass 2009, 3, 1063–1086. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Jackson, T.R.; Haggerty, R.; Apte, S.V. A fluid-mechanics based classification scheme for surface transient storage in riverine environments: Quantitatively separating surface from hyporheic transient storage. Hydrol. Earth Syst. Sci. 2013, 17, 2747–2779. [Google Scholar] [CrossRef]
- Noh, H.; Baek, D.; Seo, I.W. Analysis of the applicability of parameter estimation methods for a transient storage model. J. Korea Water Resour. Assoc. 2019, 52, 681–695. [Google Scholar]
- Boano, F.; Harvey, J.W.; Marion, A.; Packman, A.I.; Revelli, R.; Ridolfi, L.; Wörman, A. Hyporheic flow and transport processes: Mechanisms, models, and biogeochemical implications. Rev. Geophys. 2014, 52, 603–679. [Google Scholar] [CrossRef]
- Choi, J.; Harvey, J.W.; Conklin, M.H. Characterizing multiple timescales of stream and storage zone interaction that affect solute fate and transport in streams. Water Resour. Res. 2000, 36, 1511–1518. [Google Scholar] [CrossRef]
- Deng, Z.Q.; Singh, V.P.; Bengtsson, L. Numerical solution of fractional advection-dispersion equation. J. Hydraul. Eng. 2004, 130, 422–431. [Google Scholar] [CrossRef]
- Singh, S.K. Treatment of stagnant zones in riverine advection-dispersion. J. Hydraul. Eng. 2003, 129, 470–473. [Google Scholar] [CrossRef]
- Haggerty, R.; McKenna, S.A.; Meigs, L.C. On the late-time behavior of tracer test breakthrough curves. Water Resour. Res. 2000, 36, 3467–3479. [Google Scholar] [CrossRef]
- Wörman, A.; Packman, A.I.; Johansson, H.; Jonsson, K. Effect of flow-induced exchange in hyporheic zones on longitudinal transport of solutes in streams and rivers. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Boano, F.; Packman, A.; Cortis, A.; Revelli, R.; Ridolfi, L. A continuous time random walk approach to the stream transport of solutes. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Marion, A.; Zaramella, M. A residence time model for stream-subsurface exchange of contaminants. Acta Geophys. Pol. 2005, 53, 527. [Google Scholar]
- Davis, P.; Atkinson, T. Longitudinal dispersion in natural channels: 3. An aggregated dead zone model applied to the River Severn, UK. Hydrol. Earth Syst. SC 2000, 4, 373–381. [Google Scholar] [CrossRef]
- Runkel, R.L. One-Dimensional Transport with Inflow and Storage (OTIS): A Solute Transport Model for Streams and Rivers; US Department of the Interior, US Geological Survey: Washington, DC, USA, 1998; Volume 98.
- Kelleher, C.; Wagener, T.; McGlynn, B.; Ward, A.; Gooseff, M.; Payn, R. Identifiability of transient storage model parameters along a mountain stream. Water Resour. Res. 2013, 49, 5290–5306. [Google Scholar] [CrossRef]
- Ward, A.S.; Kelleher, C.A.; Mason, S.J.; Wagener, T.; McIntyre, N.; McGlynn, B.; Runkel, R.L.; Payn, R.A. A software tool to assess uncertainty in transient-storage model parameters using Monte Carlo simulations. Freshw. Sci. 2017, 36, 195–217. [Google Scholar] [CrossRef]
- Wagner, B.J.; Harvey, J.W. Experimental design for estimating parameters of rate-limited mass transfer: Analysis of stream tracer studies. Water Resour. Res. 1997, 33, 1731–1741. [Google Scholar] [CrossRef]
- Choi, S.Y.; Seo, I.W.; Kim, Y.O. Parameter uncertainty estimation of transient storage model using Bayesian inference with formal likelihood based on breakthrough curve segmentation. Environ. Model. Softw. 2020, 123, 104558. [Google Scholar] [CrossRef]
- Wallis, S.; Manson, R. Sensitivity of optimized transient storage model parameters to spatial and temporal resolution. Acta Geophys. 2019, 67, 951–960. [Google Scholar] [CrossRef]
- Boano, F.; Revelli, R.; Ridolfi, L. Source identification in river pollution problems: A geostatistical approach. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Ghane, A.; Mazaheri, M.; Samani, J.M.V. Location and release time identification of pollution point source in river networks based on the backward probability method. J. Environ. Manag. 2016, 180, 164–171. [Google Scholar] [CrossRef]
- Zhang, S.P.; Xin, X.K. Pollutant source identification model for water pollution incidents in small straight rivers based on genetic algorithm. Appl. Water Sci. 2017, 7, 1955–1963. [Google Scholar] [CrossRef]
- Thackston, E.L.; Schnelle, K.B. Predicting effects of dead zones on stream mixing. J. Sanit. Eng. Div. 1970, 96, 319–331. [Google Scholar]
- Seo, I.W.; Yu, D.Y. Characterization of pool-riffle sequences in solute transport modeling of streams. Water Eng. Res. 2000, 1, 171–185. [Google Scholar]
- Cheong, T.S.; Seo, I.W. Parameter estimation of the transient storage model by a routing method for river mixing processes. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Cheong, T.S.; Younis, B.A.; Seo, I.W. Estimation of key parameters in model for solute transport in rivers and streams. Water Resour. Manag. 2007, 21, 1165–1186. [Google Scholar] [CrossRef]
- Sahay, R.R. Predicting transient storage model parameters of rivers by genetic algorithm. Water Resour. Manag. 2012, 26, 3667–3685. [Google Scholar] [CrossRef]
- Femeena, P.; Chaubey, I.; Aubeneau, A.; McMillan, S.; Wagner, P.; Fohrer, N. Simple regression models can act as calibration-substitute to approximate transient storage parameters in streams. Adv. Water Resour. 2019, 123, 201–209. [Google Scholar] [CrossRef]
- Riahi-Madvar, H.; Dehghani, M.; Seifi, A.; Singh, V.P. Pareto Optimal Multigene Genetic Programming for Prediction of Longitudinal Dispersion Coefficient. Water Resour. Manag. 2019, 33, 905–921. [Google Scholar] [CrossRef]
- Taylor, G.I. The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1954, 223, 446–468. [Google Scholar]
- Elder, J. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- McQuivey, R.S.; Keefer, T.N. Simple method for predicting dispersion in streams. J. Environ. Eng. Div. 1974, 100, 997–1011. [Google Scholar]
- Fischer, H.B.; List, J.E.; Koh, C.R.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Seo, I.W.; Cheong, T.S. Predicting longitudinal dispersion coefficient in natural streams. J. Hydraul. Eng. 1998, 124, 25–32. [Google Scholar] [CrossRef]
- Kashefipour, S.M.; Falconer, R.A. Longitudinal dispersion coefficients in natural channels. Water Res. 2002, 36, 1596–1608. [Google Scholar] [CrossRef]
- Disley, T.; Gharabaghi, B.; Mahboubi, A.; McBean, E. Predictive equation for longitudinal dispersion coefficient. Hydrol. Process. 2015, 29, 161–172. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Ahmadyar, D.; Afghantoloee, A. Improvement on the existing equations for predicting longitudinal dispersion coefficient. Water Resour. Manag. 2017, 31, 1777–1794. [Google Scholar] [CrossRef]
- Mehr, A.D.; Kahya, E. A Pareto-optimal moving average multigene genetic programming model for daily streamflow prediction. J. Hydrol. 2017, 549, 603–615. [Google Scholar] [CrossRef]
- Valencia-Ramírez, J.M.; Raya, J.A.; Cedeno, J.R.; Suárez, R.R.; Escalante, H.J.; Graff, M. Comparison between Genetic Programming and full model selection on classification problems. In Proceedings of the 2014 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 5–7 November 2014; pp. 1–6. [Google Scholar]
- Gandomi, A.H.; Sajedi, S.; Kiani, B.; Huang, Q. Genetic programming for experimental big data mining: A case study on concrete creep formulation. Autom. Constr. 2016, 70, 89–97. [Google Scholar] [CrossRef]
- Chatwin, P.; Allen, C. Mathematical models of dispersion in rivers and estuaries. Annu. Rev. Fluid Mech. 1985, 17, 119–149. [Google Scholar] [CrossRef]
- Valentine, E.M.; Wood, I.R. Longitudinal dispersion with dead zones. J. Hydraul. Div. 1977, 103, 975–990. [Google Scholar]
- Hart, D.R. Parameter estimation and stochastic interpretation of the transient storage model for solute transport in streams. Water Resour. Res. 1995, 31, 323–328. [Google Scholar] [CrossRef]
- Bottacin-Busolin, A.; Marion, A.; Musner, T.; Tregnaghi, M.; Zaramella, M. Evidence of distinct contaminant transport patterns in rivers using tracer tests and a multiple domain retention model. Adv. Water Resour. 2011, 34, 737–746. [Google Scholar] [CrossRef]
- Haggerty, R.; Wondzell, S.M.; Johnson, M.A. Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Gooseff, M.N.; Wondzell, S.M.; Haggerty, R.; Anderson, J. Comparing transient storage modeling and residence time distribution (RTD) analysis in geomorphically varied reaches in the Lookout Creek basin, Oregon, USA. Adv. Water Resour. 2003, 26, 925–937. [Google Scholar] [CrossRef]
- Jonsson, K.; Johansson, H.; Wörman, A. Hyporheic exchange of reactive and conservative solutes in streams—Tracer methodology and model interpretation. J. Hydrol. 2003, 278, 153–171. [Google Scholar] [CrossRef]
- Jonsson, K.; Johansson, H.; Wörman, A. Sorption behavior and long-term retention of reactive solutes in the hyporheic zone of streams. J. Environ. Eng. 2004, 130, 573–584. [Google Scholar] [CrossRef]
- Gooseff, M.N.; Hall, R.O., Jr.; Tank, J.L. Relating transient storage to channel complexity in streams of varying land use in Jackson Hole, Wyoming. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Harvey, J.W.; Conklin, M.H.; Koelsch, R.S. Predicting changes in hydrologic retention in an evolving semi-arid alluvial stream. Adv. Water Resour. 2003, 26, 939–950. [Google Scholar] [CrossRef]
- Ensign, S.H.; Doyle, M.W. In-channel transient storage and associated nutrient retention: Evidence from experimental manipulations. Limnol. Oceanogr. 2005, 50, 1740–1751. [Google Scholar] [CrossRef]
- Bukaveckas, P.A. Effects of channel restoration on water velocity, transient storage, and nutrient uptake in a channelized stream. Environ. Sci. Technol. 2007, 41, 1570–1576. [Google Scholar] [CrossRef]
- Rowiński, P.M.; Guymer, I.; Kwiatkowski, K. Response to the slug injection of a tracer—A large-scale experiment in a natural river/Réponse à l’injection impulsionnelle d’un traceur—Expérience à grande échelle en rivière naturelle. Hydrol. Sci. J. 2008, 53, 1300–1309. [Google Scholar] [CrossRef]
- Stofleth, J.M.; Shields, F.D., Jr.; Fox, G.A. Hyporheic and total transient storage in small, sand-bed streams. Hydrol. Process. Int. J. 2008, 22, 1885–1894. [Google Scholar] [CrossRef]
- Guecker, B.; Boechat, I.G.; Giani, A. Impacts of agricultural land use on ecosystem structure and whole-stream metabolism of tropical Cerrado streams. Freshw. Biol. 2009, 54, 2069–2085. [Google Scholar] [CrossRef]
- Claessens, L.; Tague, C.L.; Groffman, P.M.; Melack, J.M. Longitudinal assessment of the effect of concentration on stream N uptake rates in an urbanizing watershed. Biogeochemistry 2010, 98, 63–74. [Google Scholar] [CrossRef][Green Version]
- Claessens, L.; Tague, C.L.; Groffman, P.M.; Melack, J.M. Longitudinal and seasonal variation of stream N uptake in an urbanizing watershed: Effect of organic matter, stream size, transient storage and debris dams. Biogeochemistry 2010, 98, 45–62. [Google Scholar] [CrossRef]
- Stonedahl, S.H.; Harvey, J.W.; Detty, J.; Aubeneau, A.; Packman, A.I. Physical controls and predictability of stream hyporheic flow evaluated with a multiscale model. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Johnson, Z.C.; Warwick, J.J.; Schumer, R. Factors affecting hyporheic and surface transient storage in a western US river. J. Hydrol. 2014, 510, 325–339. [Google Scholar] [CrossRef]
- Mueller Price, J.; Baker, D.; Bledsoe, B. Effects of passive and structural stream restoration approaches on transient storage and nitrate uptake. River Res. Appl. 2016, 32, 1542–1554. [Google Scholar] [CrossRef]
- TT Le, A.; Kasahara, T.; Vudhivanich, V. Seasonal Variation and Retention of Ammonium in Small Agricultural Streams in Central Thailand. Environments 2018, 5, 78. [Google Scholar] [CrossRef]
- Bohrman, K.J.; Strauss, E.A. Macrophyte-driven transient storage and phosphorus uptake in a western Wisconsin stream. Hydrol. Process. 2018, 32, 253–263. [Google Scholar] [CrossRef]
- Naeini, M.R.; Yang, T.; Sadegh, M.; AghaKouchak, A.; Hsu, K.l.; Sorooshian, S.; Duan, Q.; Lei, X. Shuffled Complex-Self Adaptive Hybrid EvoLution (SC-SAHEL) optimization framework. Environ. Model. Softw. 2018, 104, 215–235. [Google Scholar] [CrossRef]
- Searson, D.P. GPTIPS 2: An open-source software platform for symbolic data mining. In Handbook of Genetic Programming Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 551–573. [Google Scholar]
- Verboven, S.; Hubert, M. LIBRA: A MATLAB library for robust analysis. Chemom. Intell. Lab. Syst. 2005, 75, 127–136. [Google Scholar] [CrossRef]
- Memarzadeh, R.; Zadeh, H.G.; Dehghani, M.; Riahi-Madvar, H.; Seifi, A.; Mortazavi, S.M. A novel equation for longitudinal dispersion coefficient prediction based on the hybrid of SSMD and whale optimization algorithm. Sci. Total. Environ. 2020, 716, 137007. [Google Scholar] [CrossRef] [PubMed]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; Water-Resource Paper 2339; U.S. Geological Survey: Washington, DC, USA, 1989.
- Kilpatrick, F.A.; Wilson, J.F. Measurement of Time of Travel in Streams by Dye Tracing; Chapter A9, USGS Techniques of Water-Resources Investigations; U.S. Geological Survey: Washington, DC, USA, 1989; Volume 3.
- Jin, L.; Siegel, D.I.; Lautz, L.K.; Otz, M.H. Transient storage and downstream solute transport in nested stream reaches affected by beaver dams. Hydrol. Process. Int. J. 2009, 23, 2438–2449. [Google Scholar] [CrossRef]
- Smart, P.; Smith, D. Water tracing in tropical regions, the use of fluorometric techniques in Jamaica. J. Hydrol. 1976, 30, 179–195. [Google Scholar] [CrossRef]
- Zarnetske, J.P.; Gooseff, M.N.; Brosten, T.R.; Bradford, J.H.; McNamara, J.P.; Bowden, W.B. Transient storage as a function of geomorphology, discharge, and permafrost active layer conditions in Arctic tundra streams. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Seo, I.W.; Jung, Y.J. Velocity distribution of secondary currents in curved channels. J. Hydrodyn. Ser. B 2010, 22, 617–622. [Google Scholar] [CrossRef]
- Han, E.J.; Kim, Y.D.; Baek, K.O.; Seo, I.W. Relation between transverse dispersion and diffusion at meandering channel in two-dimensional mixing based on tracer tests. Environ. Earth Sci. 2019, 78, 712. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W.; Jeong, S.J. Evaluation of dispersion coefficients in meandering channels from transient tracer tests. J. Hydraul. Eng. 2006, 132, 1021–1032. [Google Scholar] [CrossRef]



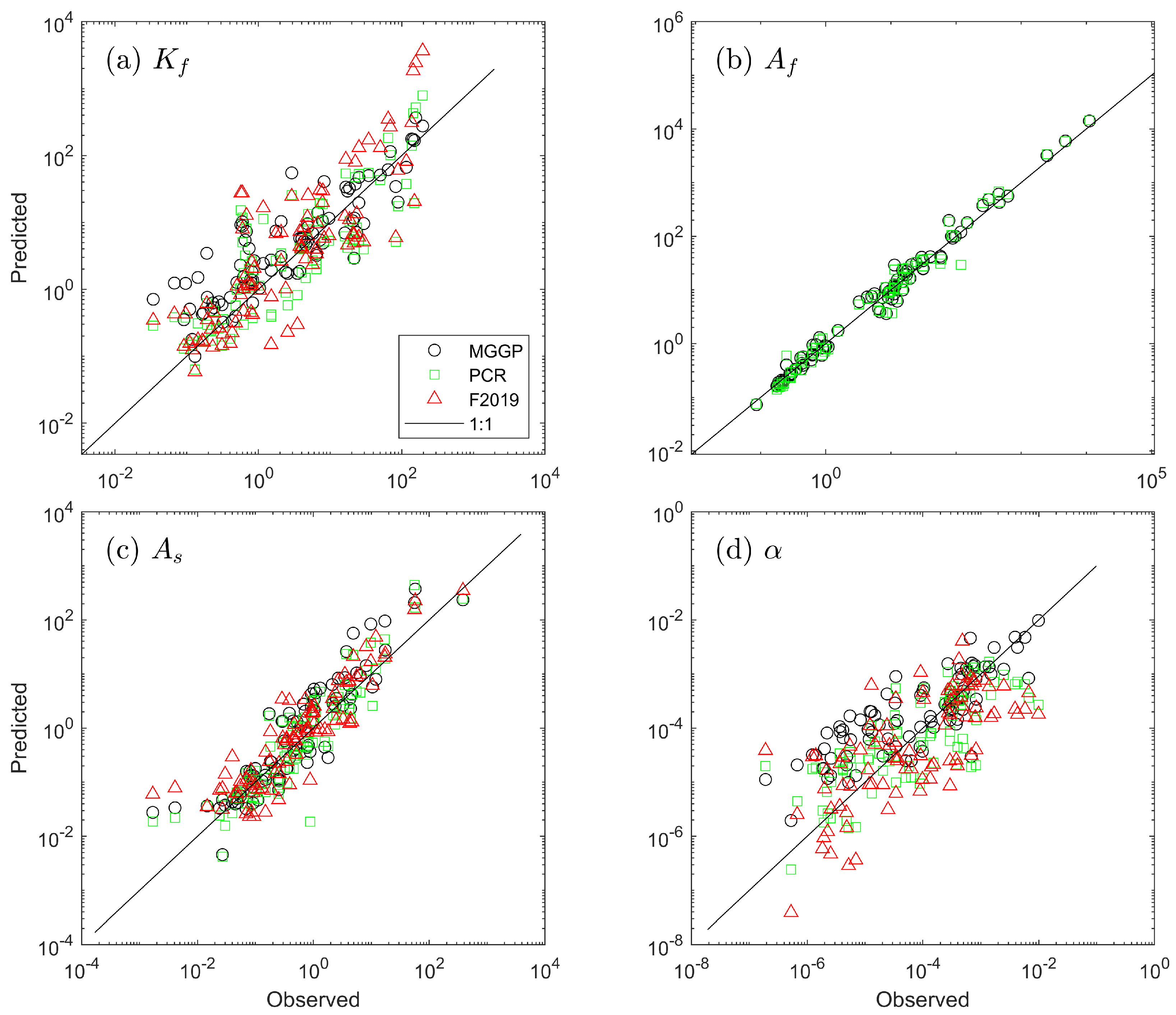
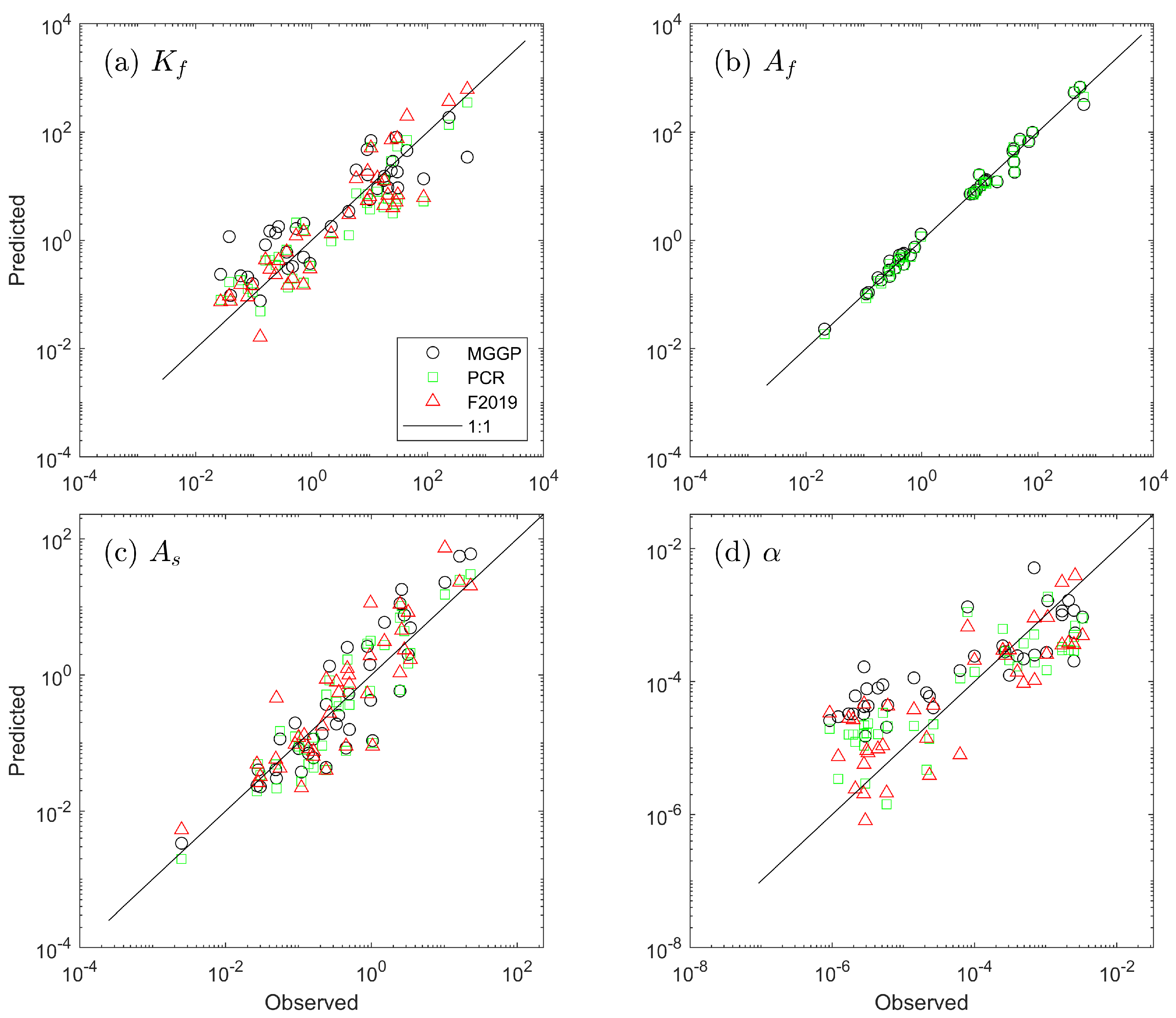
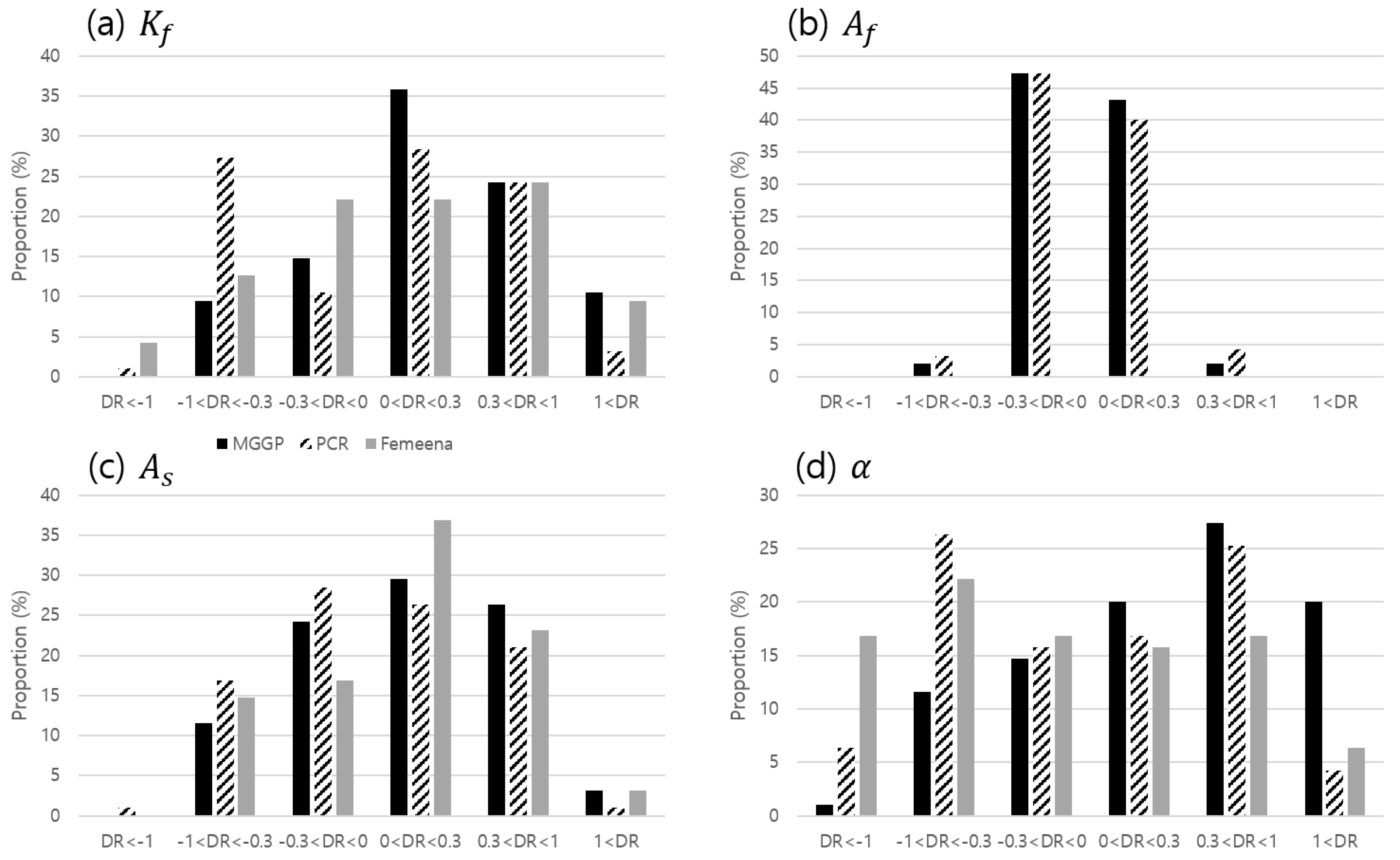

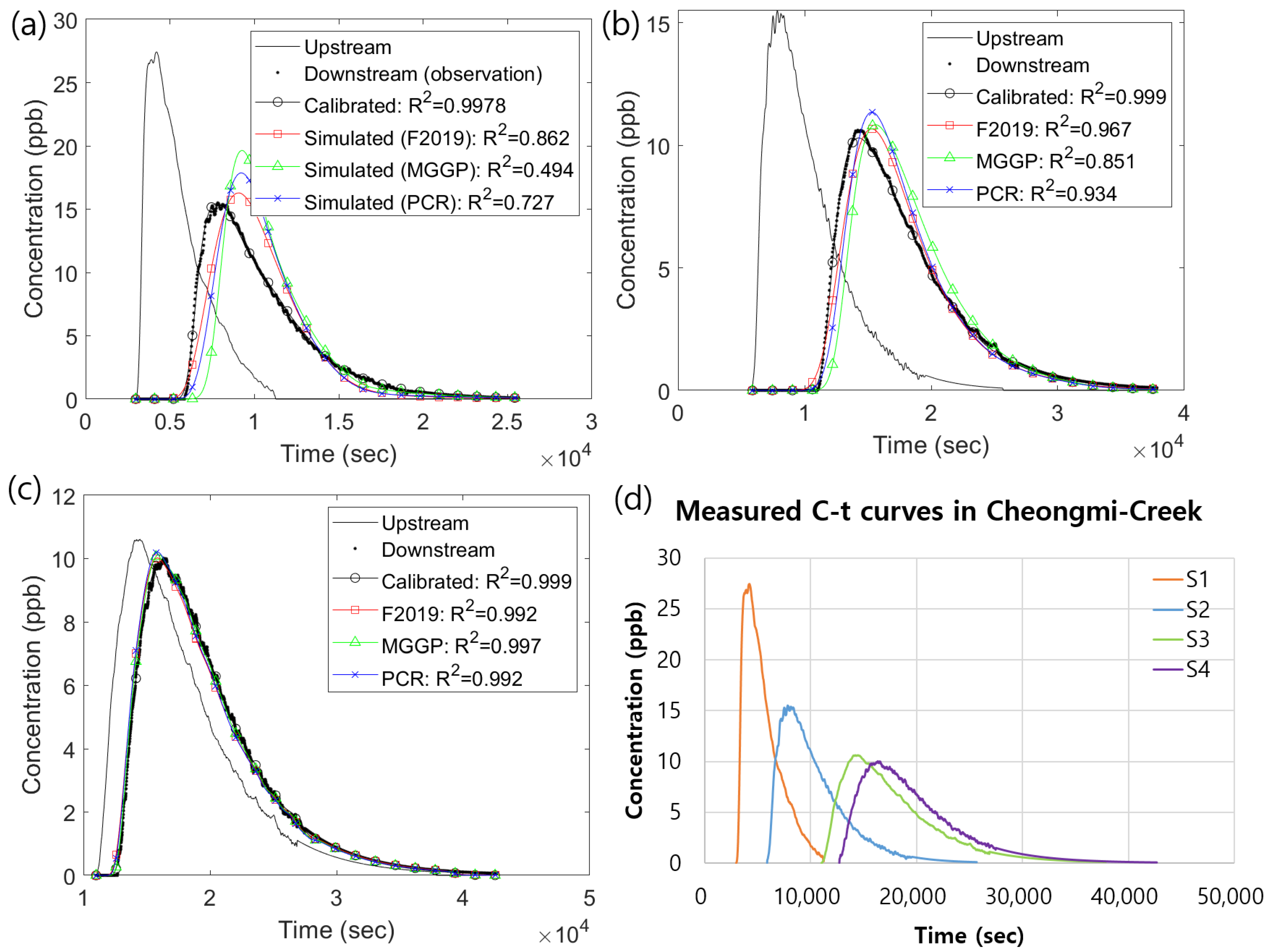
| Parameter | Training Set (90 Sets) | Test Set (38 Sets) | ||||
|---|---|---|---|---|---|---|
| Mean | Minimum | Maximum | Mean | Minimum | Maximum | |
| 46.83 | 3.80 | 331.86 | 36.51 | 3.80 | 114.51 | |
| 5.07 | 1.02 | 17.59 | 5.20 | 1.02 | 15.58 | |
| 1.36 | 1.00 | 2.27 | 1.34 | 1.00 | 2.00 | |
| 335.26 | 0.60 | 5558.20 | 295.79 | 3.42 | 1841.00 | |
| 1.02 | 0.26 | 7.00 | 1.01 | 0.47 | 2.78 | |
| 0.22 | 0.00 | 3.09 | 0.14 | 0.01 | 0.44 | |
| 19.50 | 0.04 | 256.80 | 14.14 | 0.34 | 164.99 | |
| Parameter | Settings |
|---|---|
| Function set | , square, cube, exp, tanh, power |
| Population size | 500 |
| Number of generations | 500 |
| Runs | over 200 |
| Maximum number of genes allowed in an individual | 4 |
| Maximum tree depth | 6 |
| Tournament size | 15 |
| Elitism | 0.01 % of population |
| Crossover events | 0.84 |
| High level crossover | 0.2 |
| Low level crossover | 0.8 |
| Mutation events | 0.14 |
| Sub-tree mutation | 0.9 |
| Replacing input terminal with another random terminal | 0.05 |
| Criteria | TSM Parameter | Training Set (90 Sets) | Test Set (38 Sets) | ||||
|---|---|---|---|---|---|---|---|
| MGGP | PCR | F2019 | MGGP | PCR | F2019 | ||
| Accuracy (%) | 53.33 | 41.11 | 46.67 | 47.37 | 42.11 | 42.11 | |
| 95.56 | 92.22 | - | 97.37 | 97.37 | - | ||
| 56.67 | 57.78 | 56.67 | 47.37 | 52.63 | 47.37 | ||
| 36.67 | 34.44 | 34.44 | 21.05 | 28.95 | 28.95 | ||
| RMSE | 28.20 | 83.04 | 475.91 | 75.83 | 32.00 | 43.80 | |
| 345.60 | 391.75 | - | 56.92 | 44.86 | - | ||
| 41.96 | 44.80 | 21.43 | 9.54 | 2.60 | 10.58 | ||
| 8.52 | 14.63 | 15.74 | 10.34 | 8.67 | 8.46 | ||
| 0.49 | −3.42 | −144.06 | 0.20 | 0.86 | 0.73 | ||
| 0.93 | 0.91 | - | 0.84 | 0.90 | - | ||
| −0.07 | −0.21 | 0.72 | −3.34 | 0.68 | −4.34 | ||
| 0.67 | 0.04 | −0.11 | −0.29 | 0.09 | 0.14 | ||
| 0.89 | 0.78 | 0.74 | 0.47 | 0.96 | 0.96 | ||
| 0.99 | 0.99 | - | 0.92 | 0.96 | - | ||
| 0.62 | 0.61 | 0.89 | 0.97 | 0.97 | 0.62 | ||
| 0.83 | 0.32 | 0.08 | 0.35 | 0.48 | 0.55 | ||
| Station | (m) | W (m) | h (m) | U (m/s) | (m/s) |
|---|---|---|---|---|---|
| I.P | 0 | 17.1 | 0.72 | 0.19 | 0.023 |
| U1 | 380 | 32.5 | 0.45 | 0.15 | 0.020 |
| S1 | 940 | 17.5 | 0.33 | 0.39 | 0.055 |
| U2 | 1300 | 32.6 | 0.53 | 0.13 | 0.017 |
| S2 | 1690 | 31.7 | 0.63 | 0.11 | 0.014 |
| U3 | 2050 | 34 | 0.59 | 0.11 | 0.014 |
| U4 | 2410 | 16.5 | 0.35 | 0.39 | 0.055 |
| U5 | 2730 | 34.6 | 0.18 | 0.37 | 0.057 |
| S3 | 3080 | 14.1 | 0.39 | 0.41 | 0.056 |
| S4 | 3550 | 24.25 | 0.36 | 0.26 | 0.036 |
| Average | 1810 | 25.48 | 0.42 | 0.21 | 0.028 |
| Sub-Reach | Methods | TSM Parameters | |||||
|---|---|---|---|---|---|---|---|
| (m2/s) | (m2) | (m2) | (1/s) | ||||
| S1-S2 | Calibrated | 1.3335 | 9.6377 | 5.4298 | 2.4187 | 2.1467 | 0.5634 |
| F2019 | 5.7524 | 14.6009 | 1.0905 | 0.1282 | 0.8939 | 0.0747 | |
| MGGP | 1.1441 | 15.1014 | 2.3081 | 0.4206 | 1.5898 | 0.1528 | |
| PCR | 3.2945 | 15.4021 | 1.5045 | 0.1633 | 0.9379 | 0.0977 | |
| S2-S3 | Calibrated | 1.2135 | 9.0384 | 2.9589 | 1.2481 | 2.8132 | 0.3274 |
| F2019 | 7.2714 | 11.1621 | 1.2463 | 0.2499 | 1.7079 | 0.1117 | |
| MGGP | 2.1512 | 11.5136 | 2.0088 | 0.8116 | 3.8688 | 0.1745 | |
| PCR | 4.3786 | 11.9084 | 1.2275 | 0.2918 | 2.2867 | 0.1031 | |
| S3-S4 | Calibrated | 2.0850 | 7.5056 | 1.5380 | 1.5573 | 1.4293 | 0.2049 |
| F2019 | 5.9005 | 7.1906 | 1.2024 | 0.4659 | 0.4863 | 0.1672 | |
| MGGP | 1.6943 | 7.3859 | 1.0414 | 1.0338 | 1.2850 | 0.1410 | |
| PCR | 4.3206 | 7.4839 | 0.6643 | 0.3746 | 0.7151 | 0.0888 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, H.; Kwon, S.; Seo, I.W.; Baek, D.; Jung, S.H. Multi-Gene Genetic Programming Regression Model for Prediction of Transient Storage Model Parameters in Natural Rivers. Water 2021, 13, 76. https://doi.org/10.3390/w13010076
Noh H, Kwon S, Seo IW, Baek D, Jung SH. Multi-Gene Genetic Programming Regression Model for Prediction of Transient Storage Model Parameters in Natural Rivers. Water. 2021; 13(1):76. https://doi.org/10.3390/w13010076
Chicago/Turabian StyleNoh, Hyoseob, Siyoon Kwon, Il Won Seo, Donghae Baek, and Sung Hyun Jung. 2021. "Multi-Gene Genetic Programming Regression Model for Prediction of Transient Storage Model Parameters in Natural Rivers" Water 13, no. 1: 76. https://doi.org/10.3390/w13010076
APA StyleNoh, H., Kwon, S., Seo, I. W., Baek, D., & Jung, S. H. (2021). Multi-Gene Genetic Programming Regression Model for Prediction of Transient Storage Model Parameters in Natural Rivers. Water, 13(1), 76. https://doi.org/10.3390/w13010076