Abstract
Karst cavities and caves are often present along fractures in limestone reservoirs and are of significance for oil and gas exploration. Understanding the formation and evolution of caves in fractured carbonate rocks will enhance oil and gas exploration and development. Herein, a reactive transport model was established considering both the matrix and fractures. Different factors affecting the dissolution along fractures were considered in the simulation of matrix–fracture carbonate rocks, including the magnitude and characteristic length of the matrix porosity heterogeneity, intersecting fractures, and complex fracture network. The results show that a strong heterogeneity of the matrix porosity significantly affects the cave formation along the fracture and the existence of fractures increases the heterogeneity due to the high permeability as well as the dissolution area. The characteristic length of the matrix porosity heterogeneity affects the cave location and shape. The larger permeability of intersecting fractures or the matrix greatly increases the cave size, leading to the formation of large, connected cave areas. A complex fracture network leads to more developed karst dissolution caves. The topology of the fracture network and preferential flow dominate the distribution of caves and alleviate the effect of the matrix heterogeneity.
1. Introduction
Carbonate rocks often contain karst cavities and caves, which form large aquifers as well as huge oil and gas reservoirs [1,2]. Large fracture–cave carbonate reservoirs have been reported worldwide [3,4,5]. The Tahe Oilfield in China has attracted attention because of its massive hydrocarbon reserves in the fracture–cave carbonate reservoirs [6,7,8]. Although the distribution patterns of fractures and caves vary in the Tahe Oilfield, caves that related to fractures reportedly represent one of the most common patterns [9,10,11]. Fractured caves can connect with each other vertically or horizontally through a string/fracture, and several individual bead–string units form a string–bead complex [12,13]. This pattern has also been reported as “beads-on-a-string” cave pattern in the Bahamas and Marianas [14]. Understanding the formation and evolution of the cavities in fractured carbonate rocks will help us to determine the karst evolution mechanism and enhance oil and gas exploration and development.
The dissolution process and cave formation patterns in carbonate rocks have been widely studied in laboratory experiments using digital reconstruction approaches such as X-ray computed tomography and magnetic resonance imaging [15,16,17]. Experimental studies can be used to directly observe the evolution of pores and fractures in carbonate rocks, which are fundamental for the development of mathematical models. However, they are often limited by the complexity of the rock samples and spatial resolution of the observation technique [18]. Therefore, many numerical models have been established to simulate the dissolution process and formation of caves; the results of many studies showed that the evolution of caves is governed by fluid convection, solute diffusion, and geochemical reaction mechanisms, which can be represented by the Pećlet and Damköhler numbers [19,20,21,22,23,24,25,26].
Many numerical models of cave formation have been established for carbonate rocks. Some studies simplify the carbonate rocks as porous medium, with high permeability within the fractures and faults position [27,28]. This method cannot highlight the preferential effects of fractures. Some other scholars simulate the karst evolution with dissolutional widening of fractures [29]. Deng et al. [30] and Hill et al. [31] investigated the reactive transport process using a single fracture model, which considers only one fracture. However, the dissolution process of a real fractured rock is different. Dong et al. [32] adopted a fracture network model to describe the dissolution process. In the model, multiple fractures were considered, but the matrix was ignored. Similarly, Dreybrodt et al. [33,34] and Gabrovšek et al. [35,36] described karstification by simulating dissolutional widening of orthogonal fracture network. However, few studies have considered the evolution of caves in fractured carbonates, which is very different due to the coexistence of seepage flow in matrix and preferential flow in fractures [37,38]. Kaufmann and his collaborators [39,40,41,42,43] developed a program package named KARSTAQUIFER, which can simulate the reactive transport process in karst aquifers, and tried to take the effects of matrix flow into consideration. Liu et al. [18,44] developed a continuum model by combining a two-scale continuum model with a discrete fracture network model. The model was used to study wormhole formation in cases with single and multiple fractures including characteristics, such as the fracture orientation, pattern, and aperture.
The main aim of this study was to establish a reactive transport model considering both matrix and fractures in carbonate rocks, which can be used to simulate and analyze the formation of fractured caves in fractured carbonate rocks. The impacts of heterogeneity caused by coexistence of matrix and fractures on the formation of cavities is the focus of this paper. The remainder of this paper is organized as follows. The mathematical models of the fluid flow, solute transport, and chemical reactions are presented in Section 2, for both the matrix and fractures. Detailed numerical simulation scenarios and model setups are presented in Section 3. The results of the simulations are presented in Section 4 and the effects of the matrix heterogeneity and fracture complexity on the formation of fractured caves in fractured carbonate rocks are discussed in Section 5. Finally, the conclusions are summarized in Section 6.
2. Mathematical Models
2.1. Fluid Flow
Based on Darcy’s law, the net flux across the face of a porous surface is:
where u is the Darcy velocity or specific discharge vector (m/s); κ is the permeability of the porous medium (m2); μ is the fluid’s dynamic viscosity (Pa·s), p is the fluid pressure (Pa), ρ is fluid density (kg/m3), g is the magnitude of gravitational acceleration (m/s2); and ∇D is a unit vector in the direction of the gravitational force. The permeability, κ, represents the resistance to flow over a representative volume consisting of many solid grains and pores.
The continuity equation of the fluid flow is as follows:
where is the porosity, and is a mass source term (kg/(m3·s)). Porosity is defined as the fraction of the control volume occupied by pores.
Based on the cubic law, the permeability in fractures can be obtained:
where is the fracture permeability (m2), g is the acceleration due to gravity (m/s2), is the kinematic viscosity coefficient of water (0.01 cm2/s), and is the aperture of fracture (m).
Fracture flow is available as a boundary condition in Darcy’s law interface. The physics interface uses the tangential version of Darcy’s law:
where is the volume flow rate per unit length in the fracture (m2/s), is the fluid’s dynamic viscosity (Pa·s), is the thickness of the fracture (m), ∇T denotes the gradient operator restricted to the fracture’s tangential plane, and D represents the vertical coordinate (m).
The variable represents the volume flow rate per unit length of the fracture. The mean fluid velocity within the fracture (· (m/s)) is:
The combination of Equation (3) with the material properties, and the continuity equation integrated over the fracture cross-section leads to a single equation for the pressure:
where is the fracture porosity and is the mass source term (kg/(m3·s)). The thickness varies along the fracture and therefore appears on both sides of the equation (m).
2.2. Solute Transport
The main physical processes of solute transport are convection, molecular diffusion, and mechanical dispersion. Therefore, the migration equation of Ca2+ in limestone can be expressed as follows:
The first three terms on the left-hand side of Equation (7) correspond to the accumulation of species within liquid, solid, and gas phases, whereas the last term describes the convection due to the velocity field u (m/s).
In Equation (7), denotes the concentration of species i in the liquid (mol/m3), is the amount adsorbed to (or desorbed from) solid particles (moles per unit dry weight of the solid), and is the concentration of species i in the gas phase.
The equation balances the mass transport throughout the porous medium using the porosity , liquid volume fraction θ, bulk (or drained) density (kg/m3), and solid phase density (kg/m3), and .
In saturated porous media, the liquid volume fraction θ is equal to the porosity . However, in partially saturated porous media, these parameters are related through the saturation s as: . The resulting gas volume fraction is .
The first term on the right-hand side of Equation (7) introduces the spreading of species due to mechanical mixing as well as diffusion and volatilization to the gas phase. The parameter is the tensor (m2/s) and is the effective diffusion (m2/s). The last two terms on the right-hand side of Equation (7) describe the production or consumption of species. The parameter is the reaction rate considering the reactions in the liquid, solid, or gas phase (mol/(m3·s)) and is an arbitrary source term, for example, related to a fluid flow source or sink (mol/(m3·s)).
2.3. Chemical Reaction
Groves et al. [45] pointed out that the dissolution rate of limestone is mainly controlled by the surface reaction and diffusion migration. Because the solute transport module includes diffusion and migration control, only the dissolution rate controlled by the surface reaction is considered here.
The dissolution rate of soluble components on the mineral surface is controlled by the surface reaction kinetics. The dissolution rate of general minerals is related to their relative saturation:
where R is the dissolution rate of limestone (mol/m2·s), is the kinetic constant (mol/m2·s) and is the equilibrium concentration of Ca2+ (mol/m3).
Note that, although the dissolution of most minerals satisfies the linear form of the abovementioned equation, it is not suitable for carbonate rocks, such as limestone, because limestone is corroded by groundwater. When the solution state is far from the equilibrium, the reaction conforms to the abovementioned equation. However, when the solution is in the saturated equilibrium state, the reaction rate on the test surface will sharply decrease and the relationship between reaction rate and relative saturation will become nonlinear, generating a “kinetic trigger” effect:
where and are the kinetic reaction constants (mol/m2 s); and are exponents, where is generally 1 and ranges from 3 to 6; and is the concentration of the inflection point, which generally is 0.7 Ceq–0.9 Ceq.
The equilibrium concentration of Ca2+ depends on the weathering and dissolution process of limestone on the surface and underground. The equilibrium concentration of a H2O–CO2–CaCO3 system with respect to calcite can be calculated as follows Dreybrodt and Buhmann [46]:
The and values are related to the temperature and can be obtained from Plummer and Busenberg [47].
The amount of calcite dissolution can be calculated based on the general form of the partial differential equation and limestone dissolution rate R [35]:
where is the damping (mass) coefficient, which is 1; is the dissolution amount of calcite (mol); is the source term (mol/s).
The matrix porosity evolves as follows [48]:
where is the current porosity, is the initial porosity, and is the initial calcite mass (mol).
The variation of the matrix permeability with the changing porosity can be represented as follows:
where is the current permeability (m2); is the initial permeability (m2); is an index whose value is set to 5, and is the matrix permeability factor (m2).
In order to prove the validity of the mathematical models listed above when describing the dissolution of carbonate rocks, the validation is conducted and the detailed statements are contained in Appendix A.
3. Numerical Models
3.1. Scenarios
Multiple scenarios were used in this study to investigate the factors influencing the dissolution and cavities of matrix–fracture carbonate rocks including the magnitude of the porosity heterogeneity, characteristic length of the matrix porosity heterogeneity, intersecting fractures, and complex fracture network.
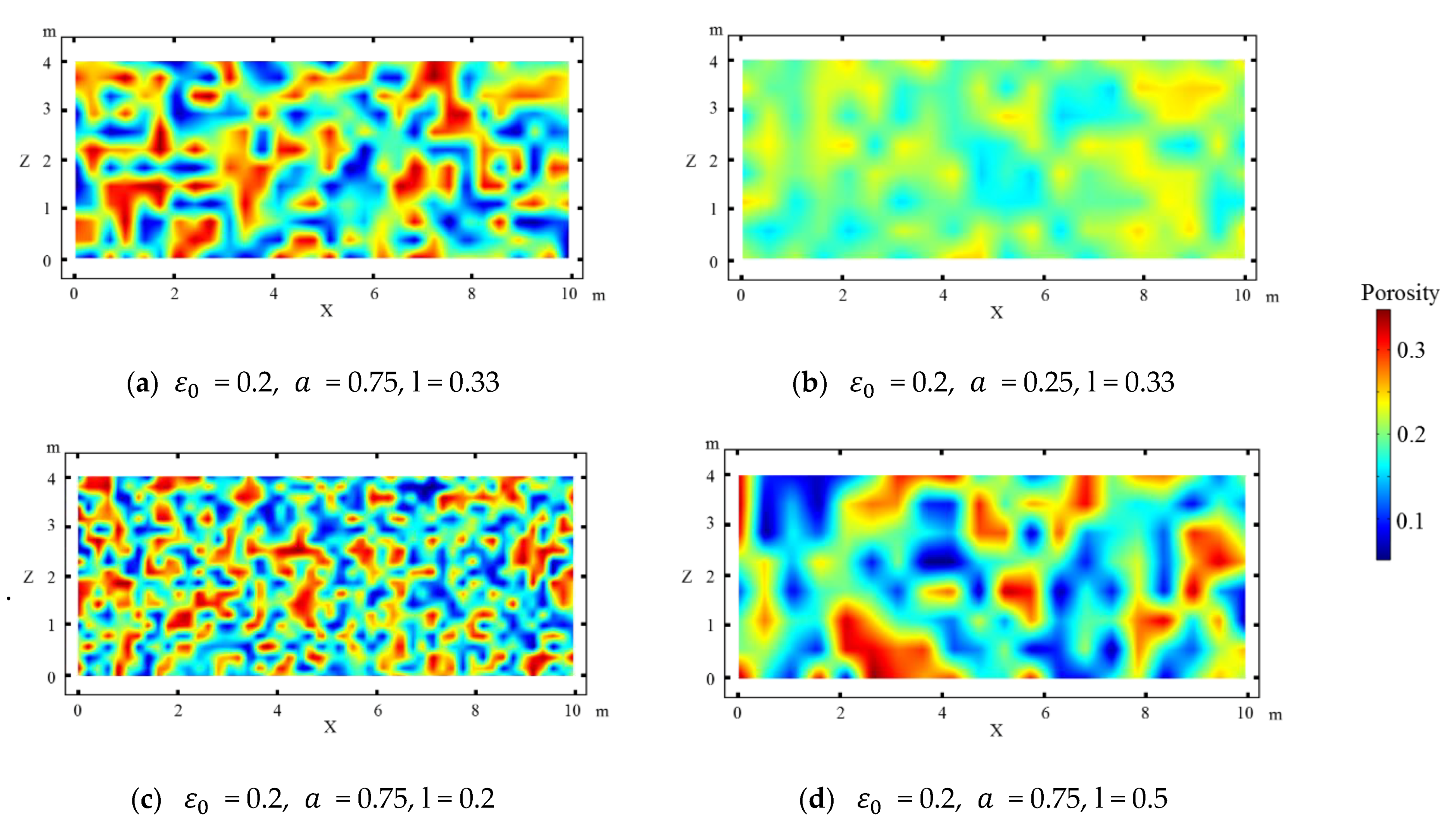
Initial porosity values were generated using the equation , where is the mean value of the porosity and is a random number that is uniformly distributed in the interval []. The magnitude of the porosity heterogeneity is defined as . In this study, was 0.2. was used as large heterogeneity and was used as small heterogeneity. The permeability values were calculated using the Carman–Kozeny equation [44,49]. Parameter l was used to represent the characteristic length of the porosity heterogeneity. Unless stated otherwise, l was used as the grid size for the model generating the initial porosity distribution. Figure 1 shows the porosity distribution with different magnitude of the heterogeneity and characteristic lengths.
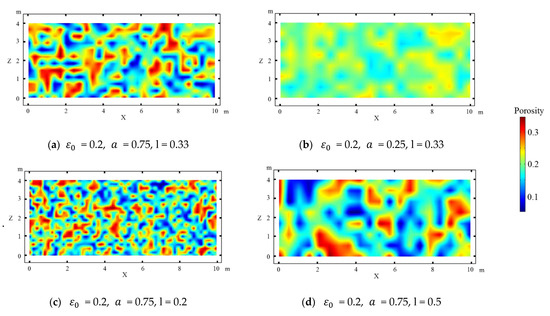
Figure 1.
Initial porosity distribution under different scenarios.
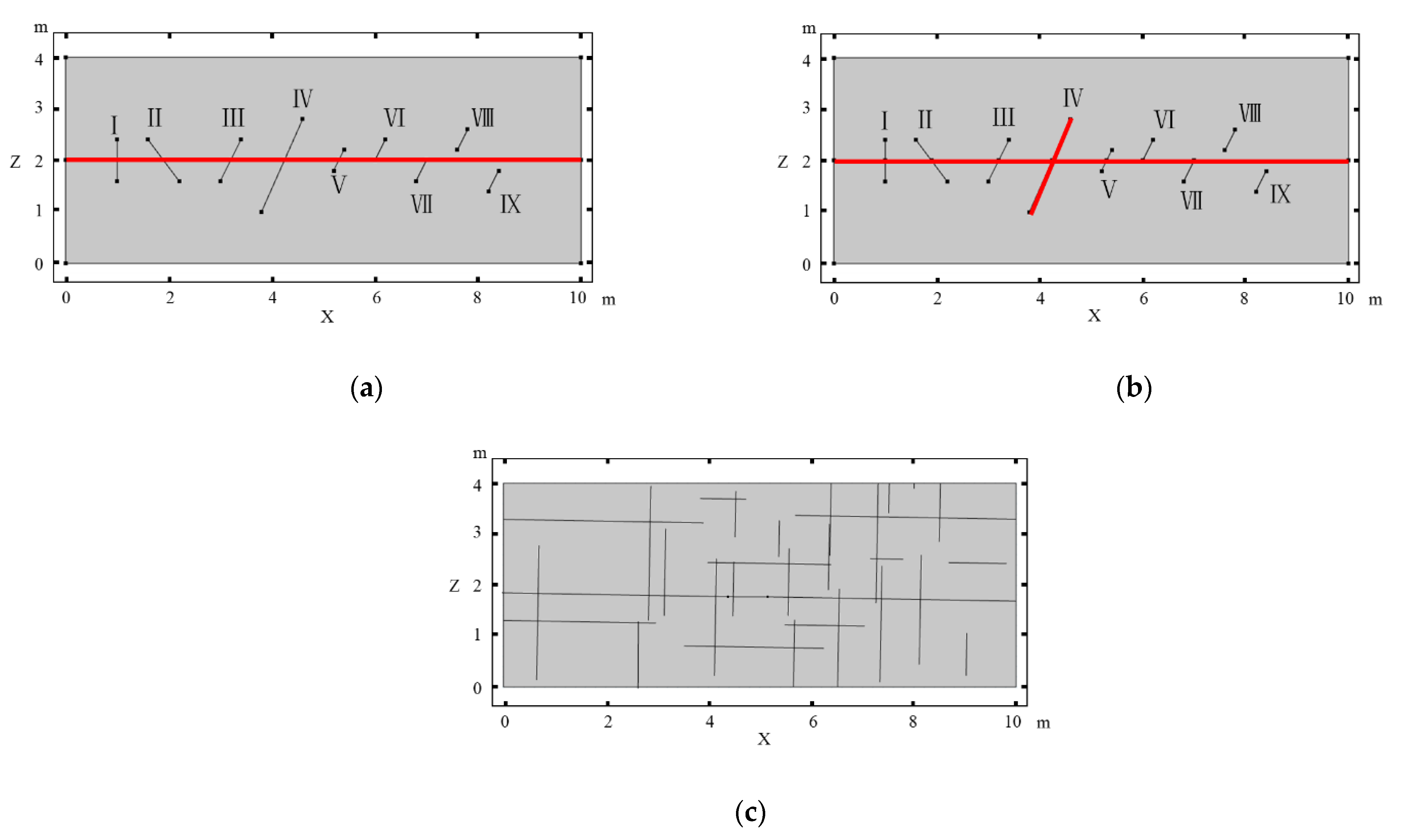
In addition to the model with one horizontal fracture, multiple intersecting fractures with different sizes and angles to the horizontal fracture were considered. Considering the presence of multiple sets of fractures in natural carbonate rocks, complex fracture network models were randomly generated with two sets of orthogonal fractures. The vertical and horizontal set of fractures obeys normal distribution with an average length of 1.47 m and 2.27 m, respectively. The the number of the two sets fractures is 19 and 10, respectively. Figure 2 shows the topology of fractures used for different scenarios.
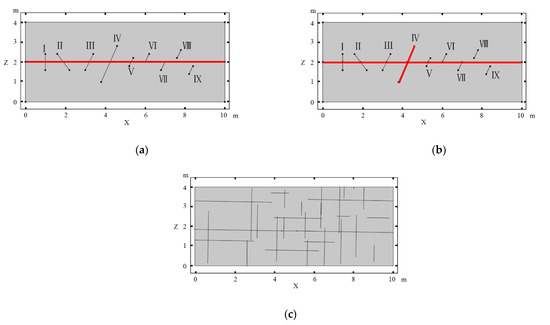
Figure 2.
Topology of intersecting fractures used for the numerical models. Red lines indicate fractures with an aperture of 1.1 × 10−5 m. (a) Intersecting fracture set 1 and set 3, (b) intersecting fracture set 2, (c) fracture network model.
The simulation scenarios are listed in Table 1. The fracture permeability () is proportional to b2 (b represents the fracture aperture). Parameter is ~1 × 10−11 m2 and 1 × 10−13 m2 when the fracture aperture (b) is 1.1 × 10−5 m and 1.1 × 10−6 m, respectively. Cases 1, 2, and 3 were used to investigate the influence of the magnitude of the porosity heterogeneity. Cases 3, 4, and 5 were employed to analyze the characteristic length of the matrix porosity heterogeneity. Cases 6, 7, and 8 were used to study the intersecting fractures. Case 9 considered a higher permeability of intersecting fractures and Cases 10 and 11 were used to investigate the complex fracture network. In Cases 10 and 11, the flow direction was horizontal and vertical, respectively.

Table 1.
Parameters of the simulation scenarios.
3.2. Model Setup
The model was simulated with a rectangular two-dimensional (2D) domain of 10 m × 4 m. In Cases 1–10, fluid flows from left to right with a constant pressure difference of 5000 Pa, while a zero-flux boundary condition was imposed on the top and bottom boundaries. On the left boundary, the fluid concentration . In Case 11, fluid flows from top to bottom with a constant pressure difference of 5000 Pa, while a zero-flux boundary condition was imposed on the lateral sides. The mathematical equations in Section 2 were solved using the finite element method and COMSOL 5.3 Multiphysics simulator (COMSOL Inc., Stockholm, Sweden). The Darcy’s law interface, Transport of Diluted Species in the Porous Media interface, and custom partial differential equations were utilized for the mathematical models described in Section 2. COMSOL Multiphysics is a finite element analysis software package that is used in various physics and engineering applications. The mathematical models are discretized using the finite element method. The matrix domain is subdivided into triangular mesh with size of 0.052 m, and the grids were refined where fracture occurs with mesh size no more than 0.0004 m. The geometric topology in different scenarios is not the same, the number of domain cells ranges from 37,236 to 195,997, corresponding to 735 to 3812 boundary cells.
4. Results
4.1. Porosity Evolution under Different Matrix Heterogeneity Magnitudes
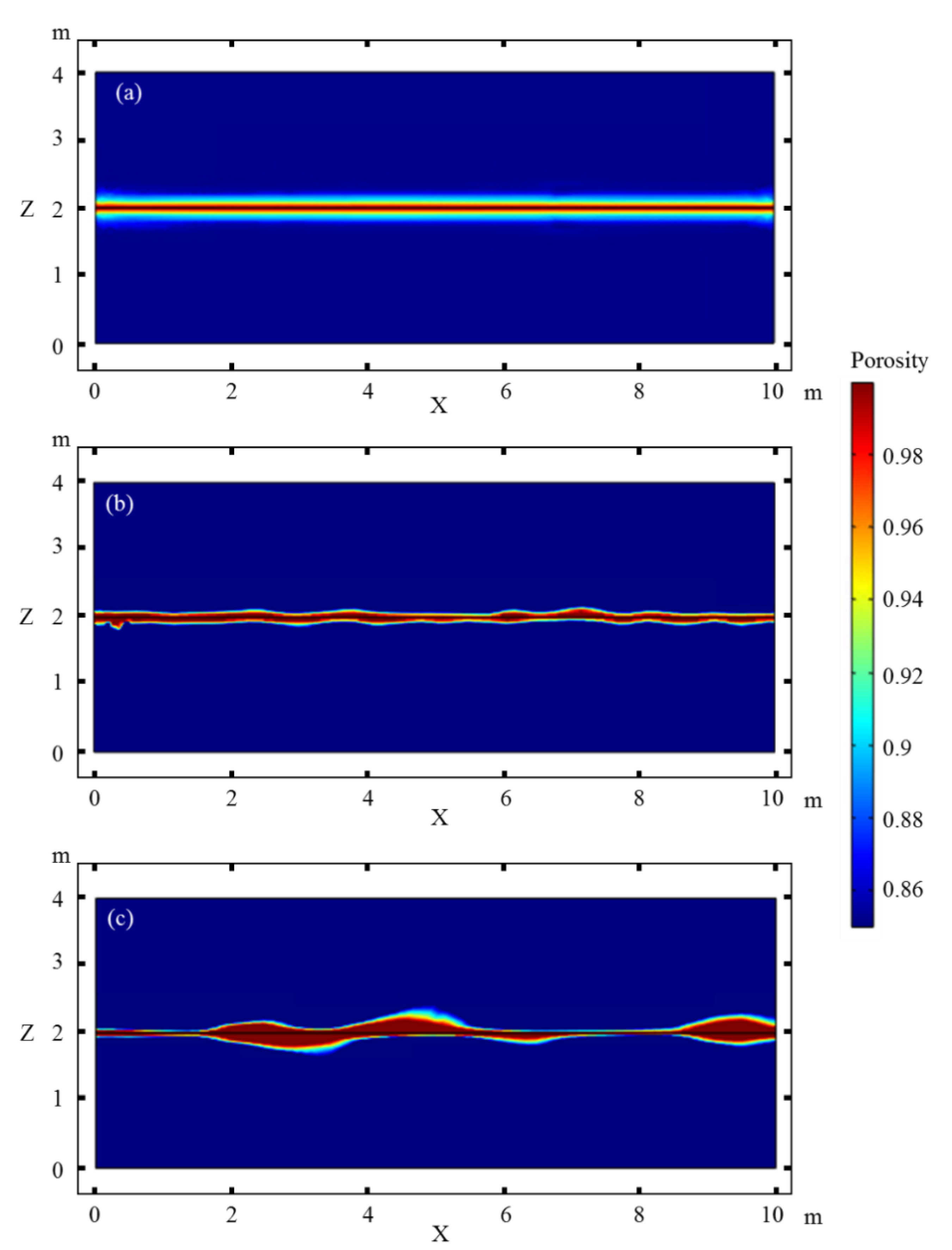
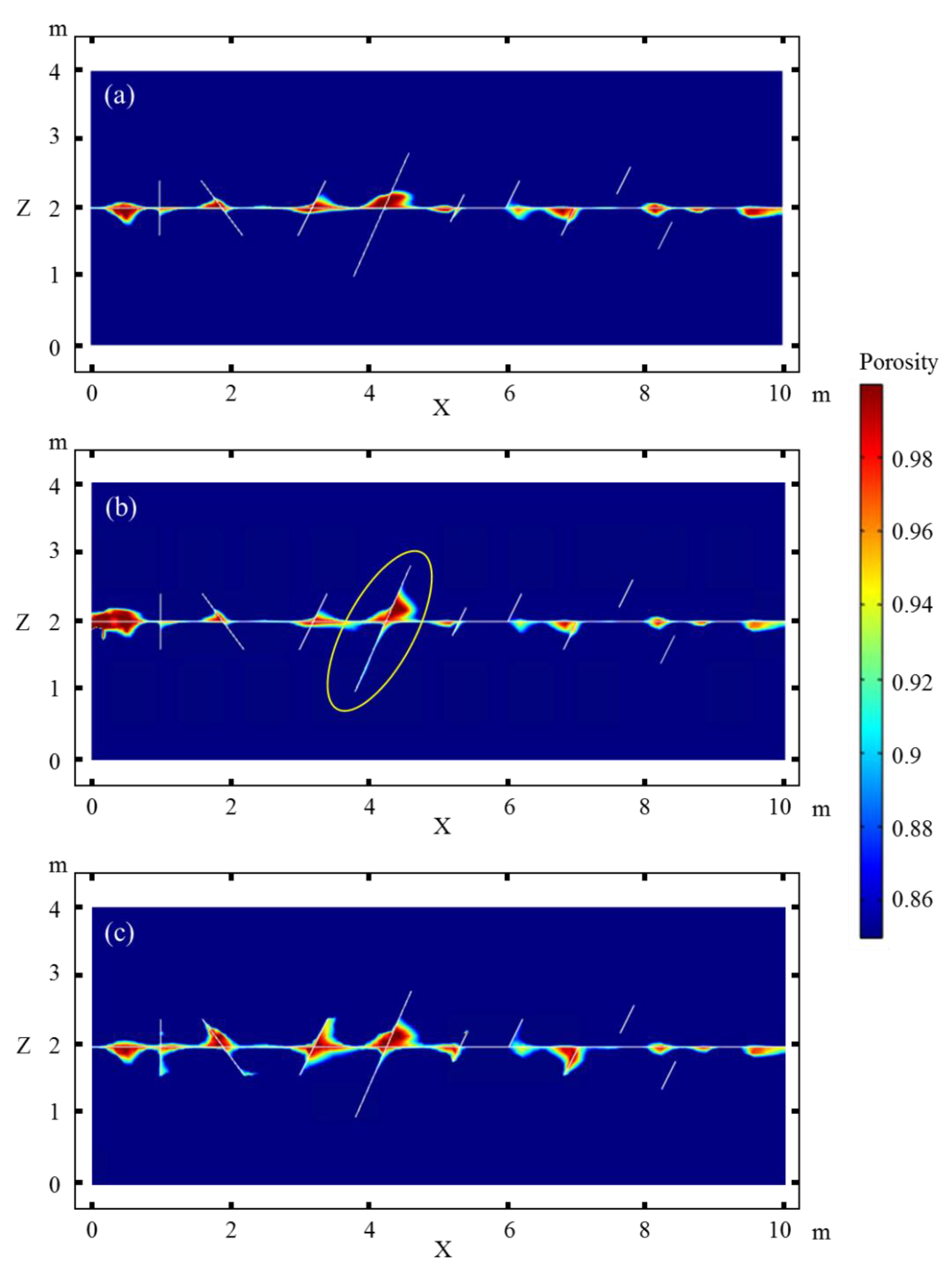
Figure 3 shows the effect of the magnitude of matrix porosity heterogeneity on the fracture dissolution and formation of beads along the fracture. In Case 1 with a homogeneous matrix, dissolution mainly occurs on both sides of the fracture, with an extension range of ~0.1 m. In Case 2 with a small heterogeneity, dissolution is affected by the distribution of the porosity and the dissolution extension on both sides of the horizontal fracture is asymmetrical. In Case 3 with a larger matrix heterogeneity, the dissolution notably differs along the fracture. In the area with higher initial porosity, the maximum height of the dissolution caves can reach 0.2 m, while it is negligible in the area with lower initial porosity.
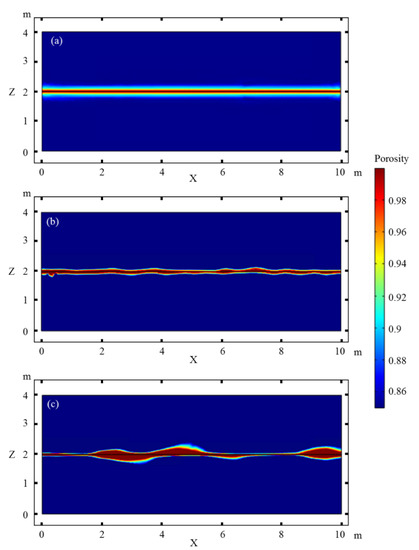
Figure 3.
Effect of the magnitude of matrix porosity heterogeneity on the dissolution along the horizontal fracture. (a) Homogeneity, (b) weak heterogeneity, (c) strong heterogeneity.
4.2. Porosity Evolution for Different Characteristic Lengths of the Matrix Porosity Heterogeneity
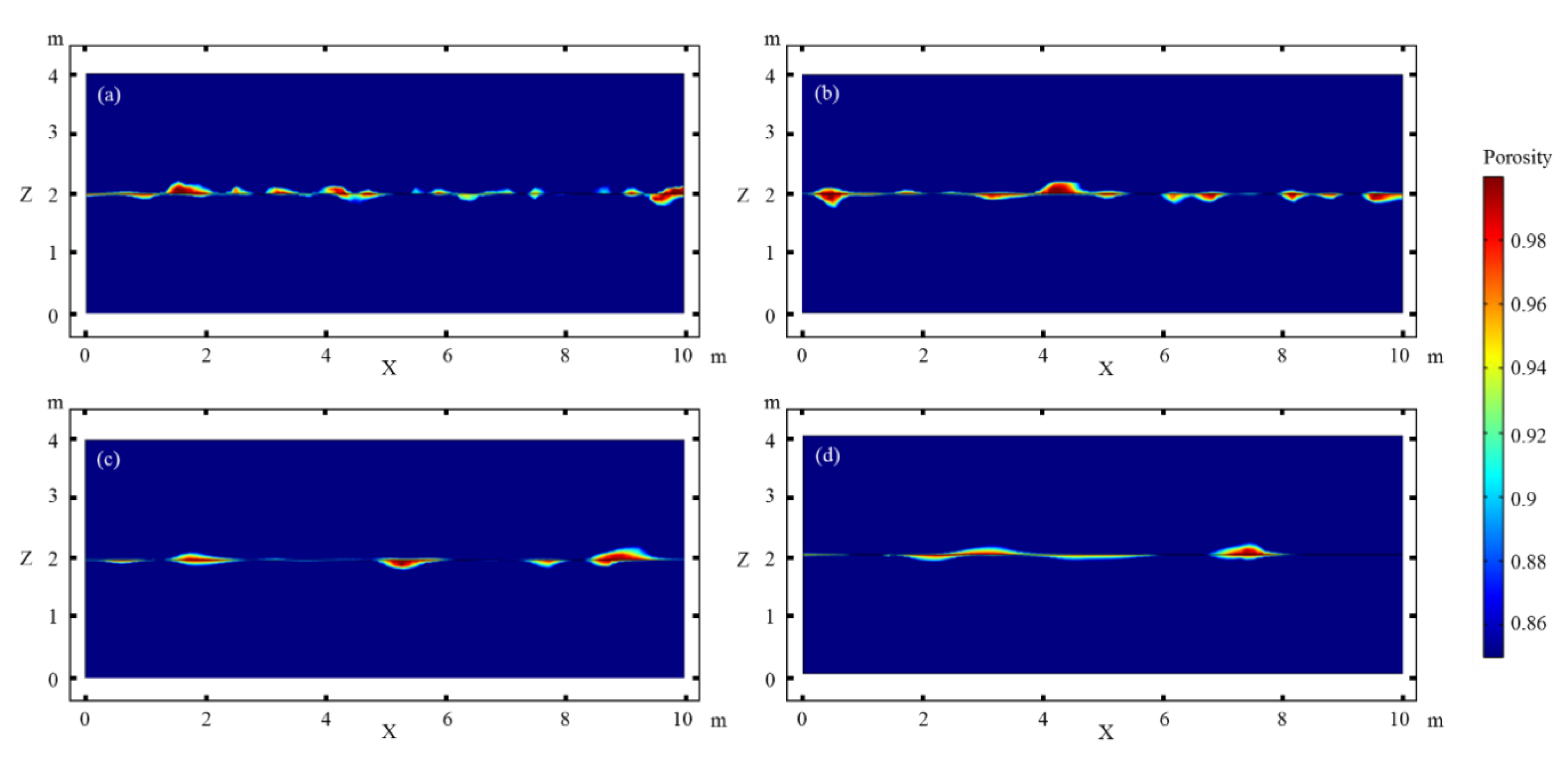
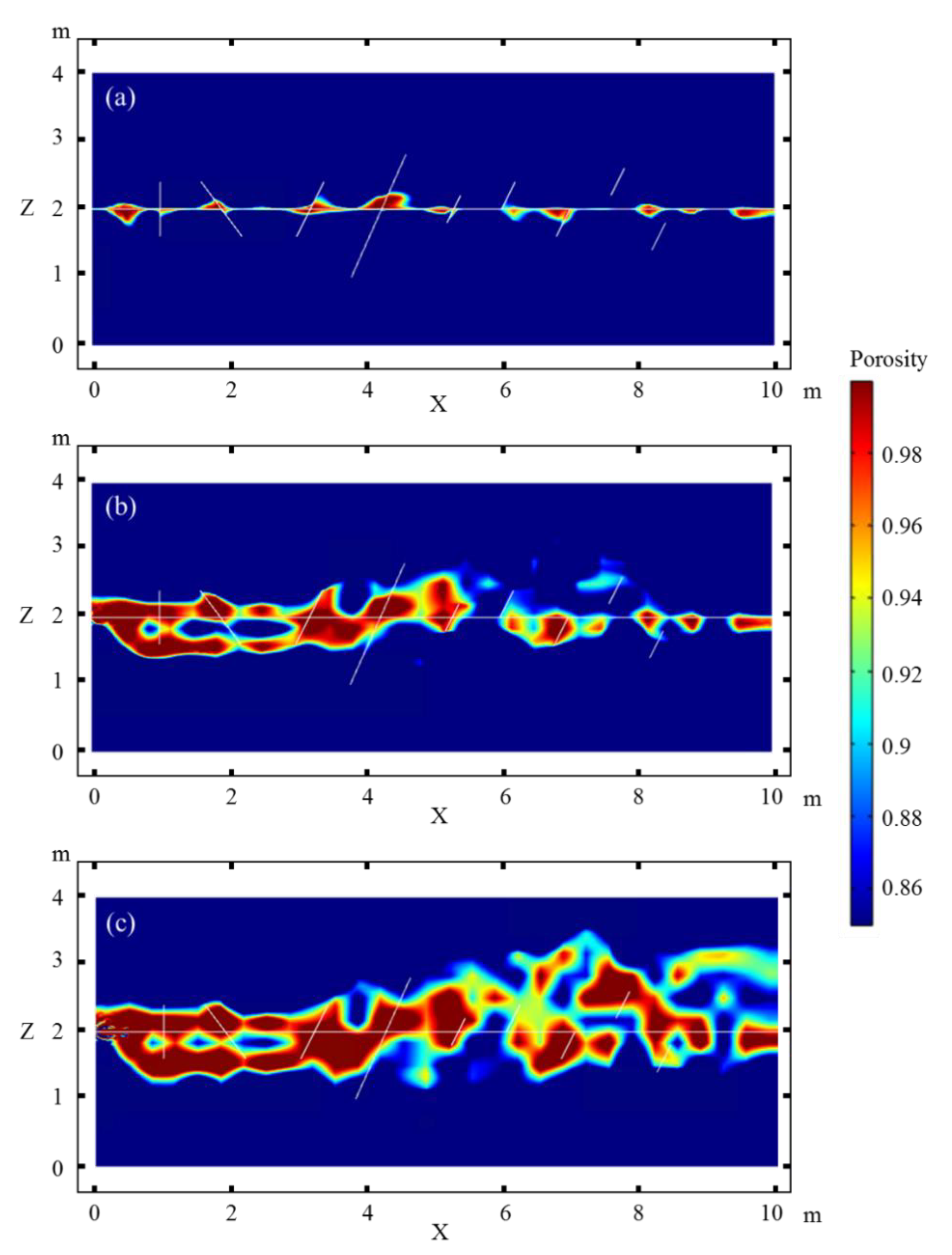
Figure 4 shows the influence of the characteristic length of the matrix porosity heterogeneity on the fracture dissolution and the formation of cavities along the fracture. The cavities are distributed along the fracture, but the sizes and shapes of the holes significantly differ. When the characteristic length is small (Figure 4a,b), the size of the cavities is small, with a maximum length of 0.9 m and maximum height of 0.2 m, and the extended length of cavities along the long axes is slightly larger than the short axes. When the characteristic length is large (Figure 4c,d), the cavities are larger and flatter, with a maximum length of 1.7 m and maximum height of 0.14 m, and the extended length of cavities along the long axes is significantly larger than the short axes. Although the cavities are smaller when the characteristic length is smaller, the number of holes is larger. The opposite is true for a larger characteristic length.
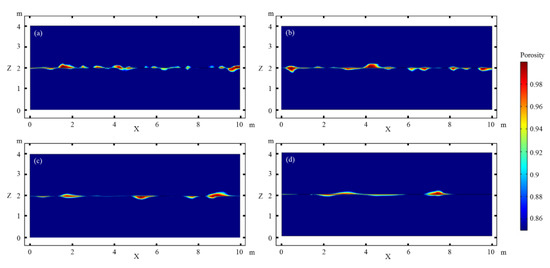
Figure 4.
Effect of the characteristic length of the matrix porosity heterogeneity on the dissolution along the horizontal fracture. (a–d) represent the results for a characteristic length of 0.2, 0.33, 0.5, and 1.0, respectively.
4.3. Porosity Evolution with Intersecting Fractures
Figure 5 shows the effects of cross fractures on the dissolution. Compared with the simulation results of the cases without intersecting fractures (Figure 3c and Figure 4b), caves form near the intersections of fractures, reflecting the porosity and permeability increase in this area. Based on the comparison of fractures I to V, the effect of the angle between the intersecting fractures on the formation of dissolved holes was studied. When the intersecting fracture (fracture I) is perpendicular to the horizontal fracture, the dissolution along the vertical fracture is very limited because it is perpendicular to the main flow direction. When the cross fractures approach the overall flow direction in the domain, the dissolution is enhanced. Note that the dissolution is strongly affected by the matrix heterogeneity and fractures increase the heterogeneity. For example, caves can form in high-porosity areas without fractures; however, large caves cannot be formed, even if there are fractures in the low-porosity areas.
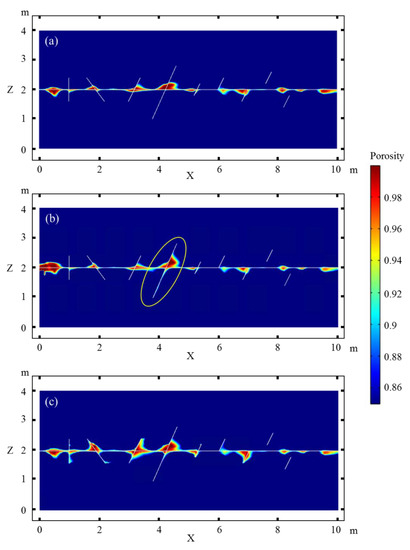
Figure 5.
Effects of intersecting fractures on the dissolution along the horizontal fracture. (a) Cross fracture set 1: the horizontal fracture aperture was set to and the cross fracture aperture was set to ; (b) cross fracture set 2: the apertures of the horizontal fracture and cross fracture IV were set to and all other cross fractures apertures were set to ; (c) cross fracture set 3: the horizontal fracture aperture was set to and the aperture of the cross fractures was set to .
Based on the difference of fracture IV between Figure 5a,b, the dissolution significantly improves along the fracture when the permeability of the secondary fracture is increased by two orders of magnitude, even in the area with a low matrix porosity in the lower part of fracture IV.
Figure 5a,c show the dissolution pattern under the influence of different magnitudes of permeability of the intersecting fracture. When the permeability of the cross fractures is increased by five orders of magnitude, the dissolution area along the intersecting fractures significantly increases. The size of the caves in fractures III, IV, V, and VII is more than one-fold enlarged. Note that the dissolution along the fractures is significantly enhanced if the fracture permeability is increased.
Figure 6 shows the formation of caves along the horizontal and the intersecting fractures for different magnitudes of the matrix permeability. The average permeability of the matrix in Figure 6b is one order of magnitude higher than that in Figure 6a, while it is two orders of magnitude higher in Figure 6c, which is close to the permeability of the cross fractures. In Figure 6a, the dissolved cavities are mainly limited to the vicinity of the joint of the horizontal and intersecting fractures and the cavities are sparsely distributed. When the average matrix permeability is increased by one order of magnitude (Figure 6b), the dissolution cavities on both sides of the horizontal fracture significantly increase in terms of the size and number. The maximum extension of cavities from the horizontal fracture reaches 0.7 m. With the increase in the matrix permeability, the effect of the fractures is weakened. This is especially notable in Figure 6c; the matrix permeability is further increased to be equivalent to that of the intersecting fractures. The domain of dissolution caves generally exceeds the intersecting fractures, with a maximum extension of cavities of 1 m from the horizontal fracture. Caves even form in the area near fractures VIII and IX, which are not connected to the horizontal fracture. In addition, with increasing matrix permeability, the caves connect and form a large cave system, which is similar to an underground river in the karst system.
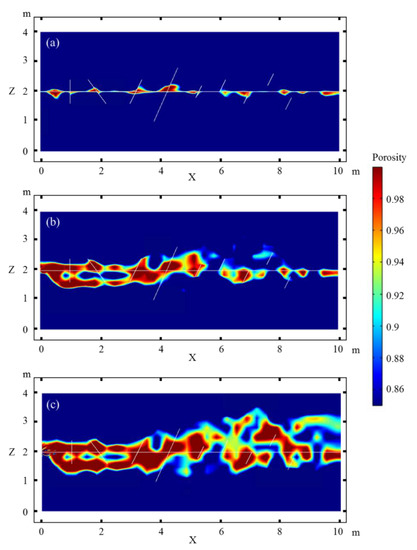
Figure 6.
Effect of the matrix porosity on the dissolution with intersecting fractures. The matrix permeability factor CK in (a), (b), and (c) is 1 × 10−13, 1 × 10−12, and 1 × 10−11 m2, respectively.
4.4. Porosity Evolution in Complex Fracture Networks
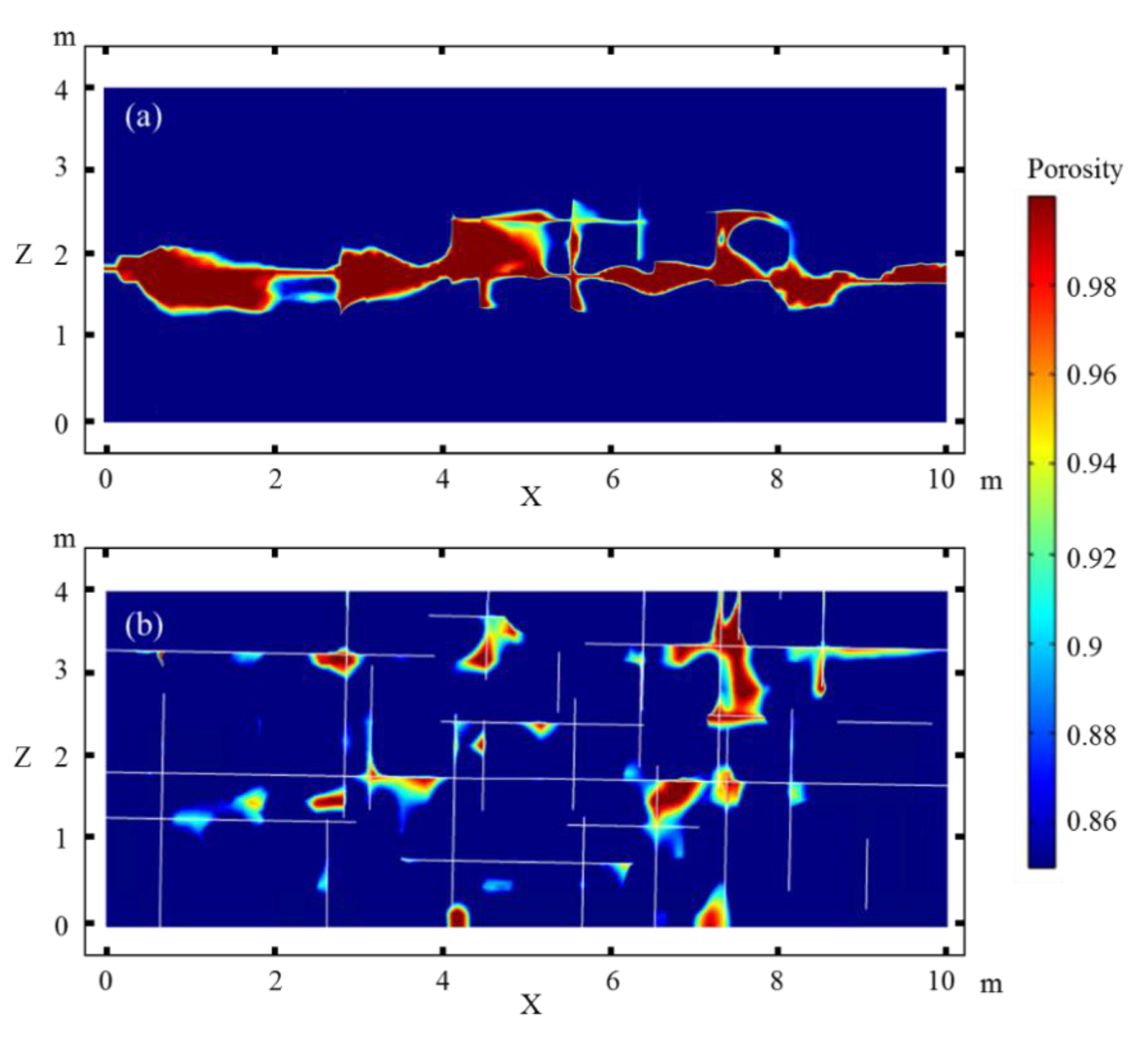
Figure 7 shows the simulation results for the porosity distribution at an injected pore volume (PV) of 7 PV. When the horizontal flow dominates the system (Figure 7a), dissolution mainly occurs along the horizontal fault/fracture, especially at the intersection of vertical and horizontal faults/fractures. The preferential flow caused by the vertical fissures allows the occurrence of dissolution pores and caves far away from the horizontal fault/fracture. Because of the effect of the matrix heterogeneity, not all matrix pores near the vertical fissures significantly interact with horizontal faults/fracture changes. When the fluids are injected through the vertical fractures (Figure 7b), the matrix porosity along most of the vertical fractures notably increases due to dissolution, especially that interacting with the upper boundary of the domain. The major axis of the caves tends to spread along the vertical y-axis. Dissolution around the intersection of the vertical and horizontal fractures is more likely to form larger caves. Similarly, the matrix heterogeneity limits the extension of the pores and caves when the initial porosity and permeability are poor and the dissolution caves show a T-shaped spread, whereas the dissolution has a much more widespread effect when the matrix is more permeable.
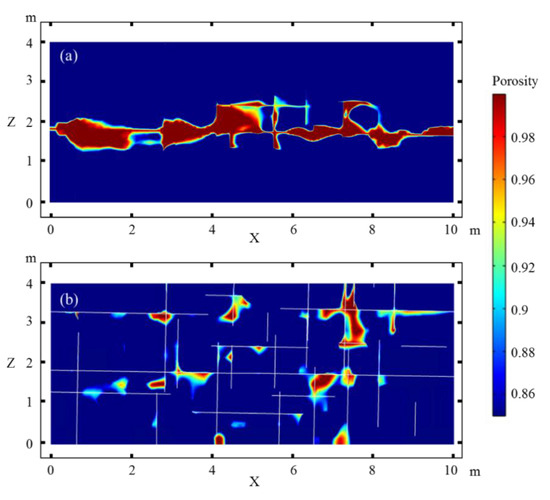
Figure 7.
Effects of a complex fracture network with different flow directions. (a) Horizontal flow, (b) vertical flow.
5. Discussion
5.1. Effect of the Magnitude of the Porosity Heterogeneity of the Matrix
To quantitatively estimate the shape parameters of the cavities, we conducted image analysis and determined the lengths, widths (heights), and volume fractions of the cavities. The images were filtered using the median filtering method and cavity objects were extracted with threshold segmentation. Finally, statistical analysis was performed to acquire the shape parameters of the cavities. All image processing was performed using ImageJ 1.51.
The statistical results for the characteristic parameters of the cavity shapes with different heterogeneity magnitudes are shown in Table 2. With the increase in the heterogeneity, the cavity volume significantly increases (2.54% to 4.63%). Horizontal fractures dominate the dissolution and distribution of cavities. The heterogeneity of the matrix on both sides of the fracture also has a significant effect on the shape of the cavities. With the enhancement of the heterogeneity, the dissolution space changes from uniform dissolution fractures to larger caves with greater size variation. These results show that the magnitude of the matrix heterogeneity has a significant impact on the formation and shape of the cavities.

Table 2.
Statistical cavity shape parameters for different heterogeneity magnitudes.
5.2. Effect of the Characteristic Length of the Matrix Porosity Heterogeneity
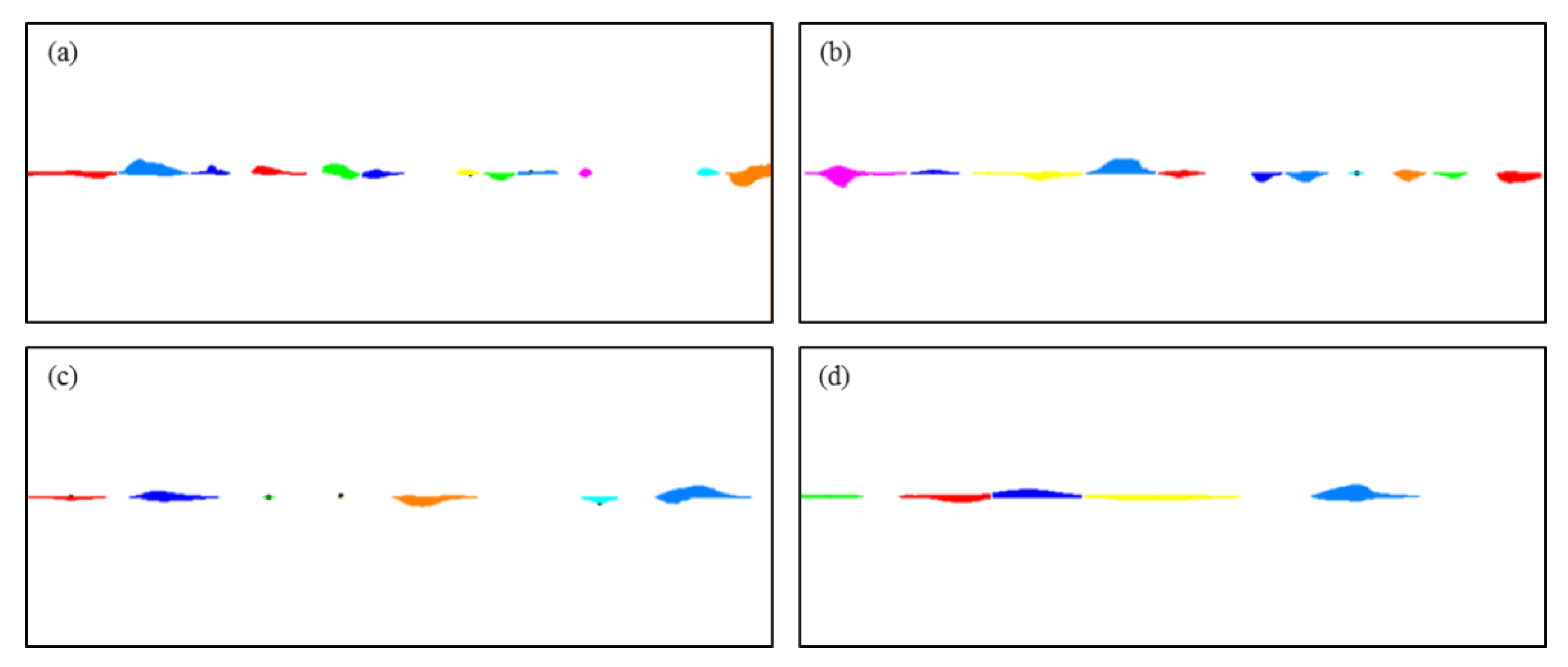
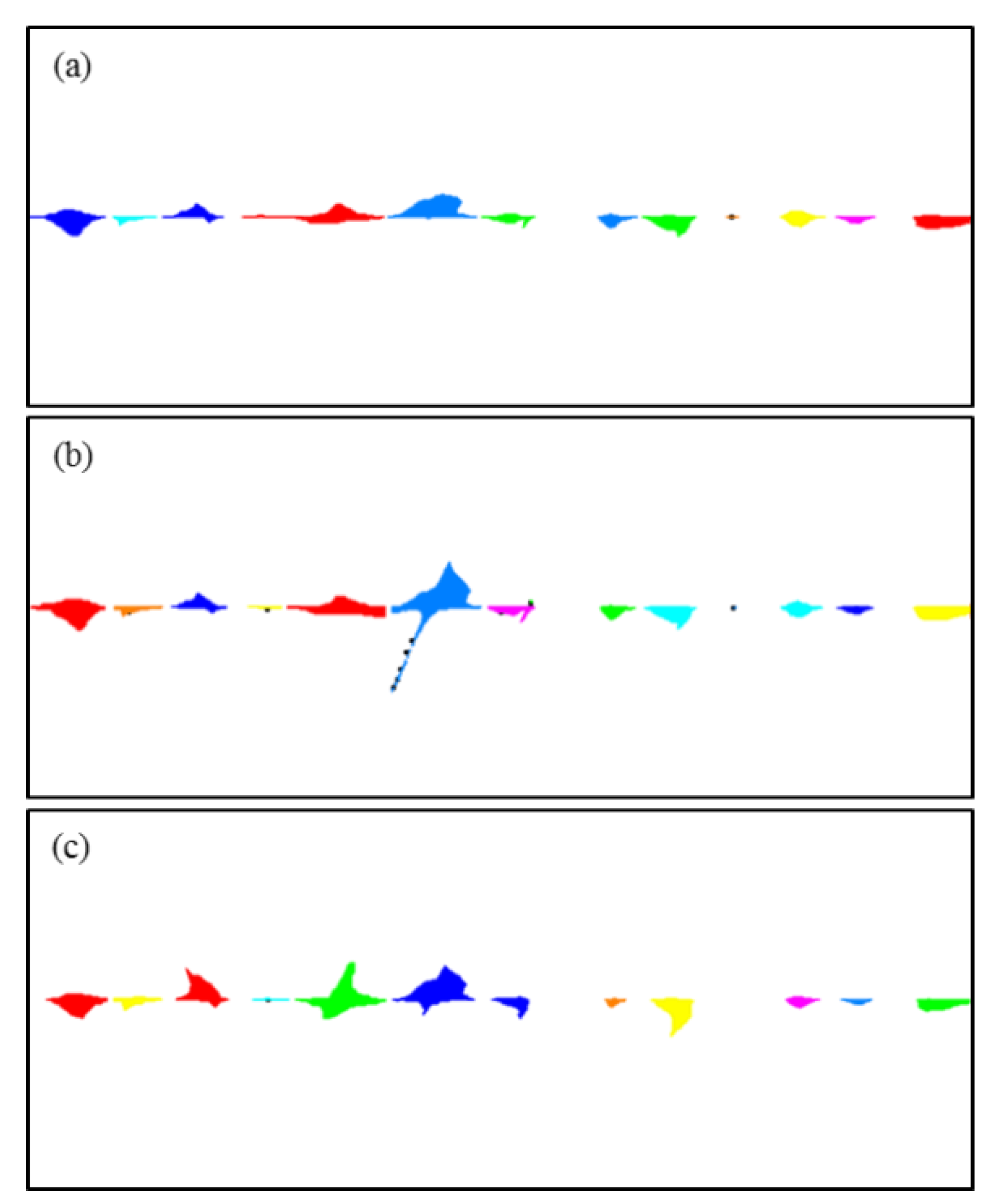
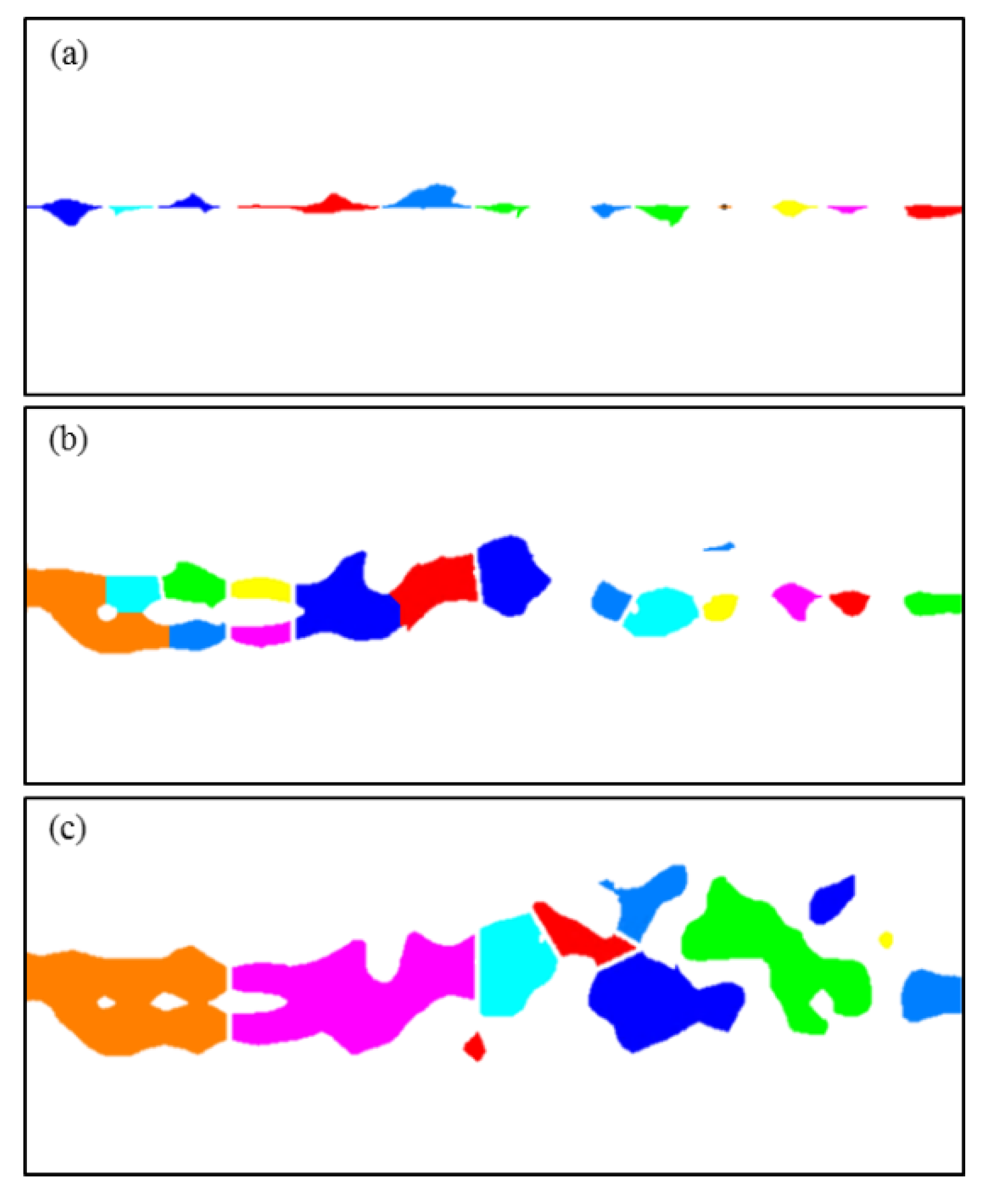
The images of the cavity distribution in Figure 4 were post-processed. The cavities were distinguished and separated, as shown in Figure 8.
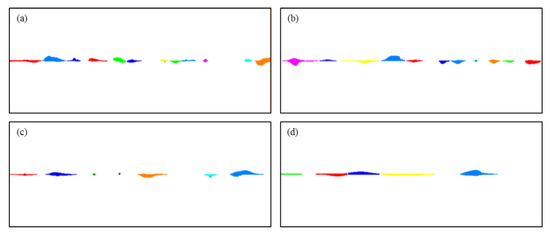
Figure 8.
Image processing results showing the cavity segmentation for different characteristic lengths. (a), (b), (c), and (d) represent the results for the characteristic lengths of 0.2, 0.33, 0.5, and 1.0, respectively. Different colors are used to visually differentiate the individual cavities.
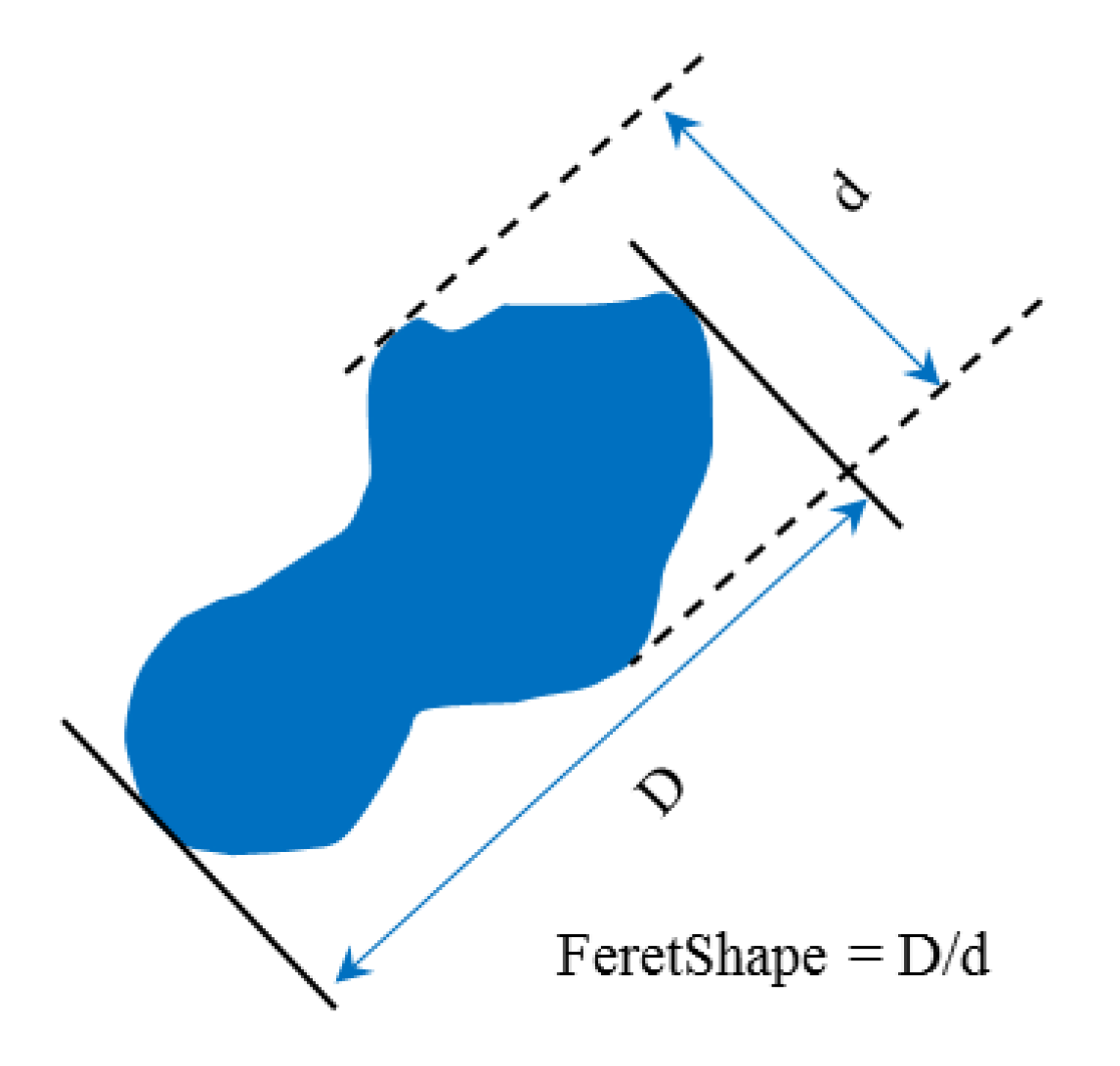
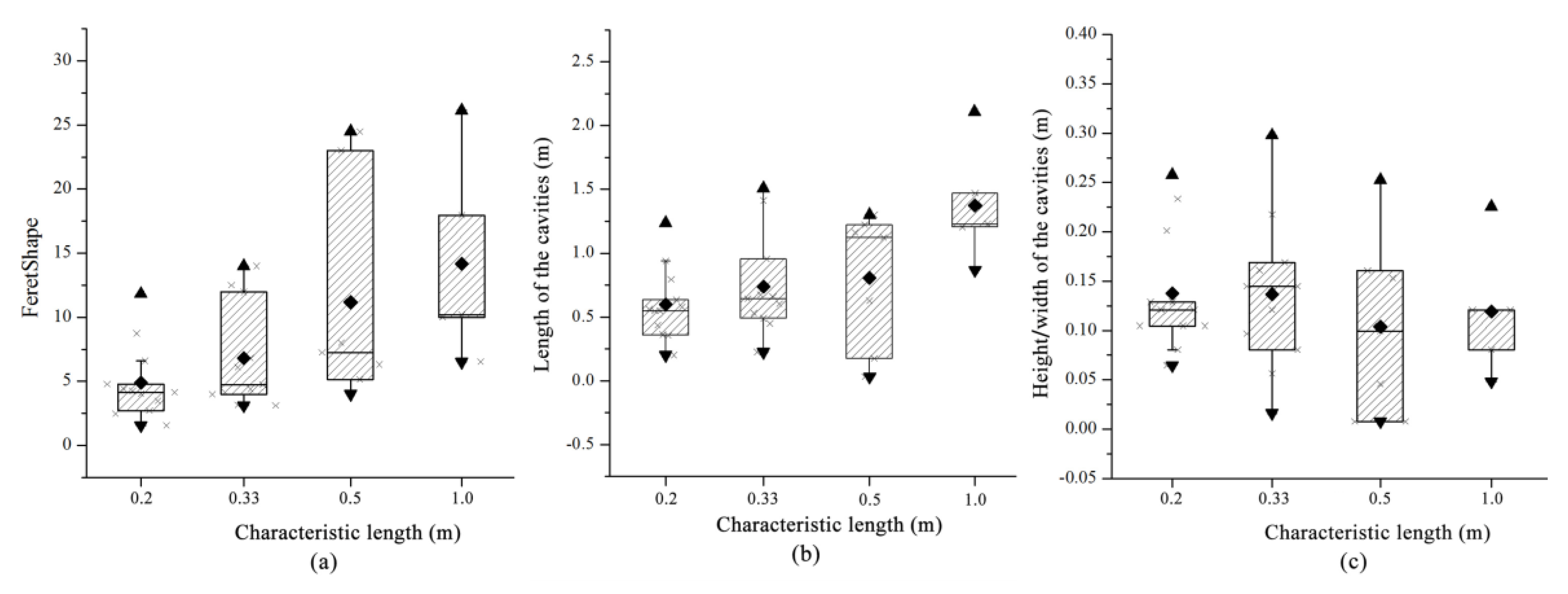
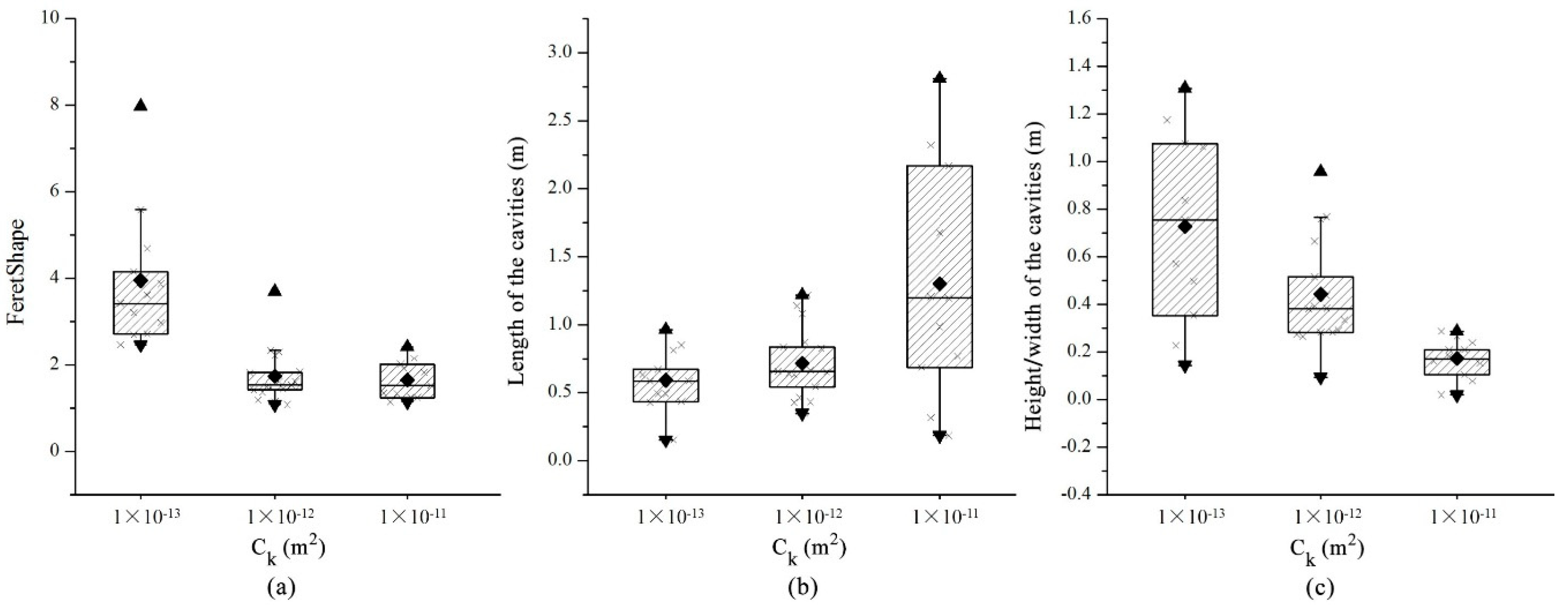
The statistical results for the characteristic parameters of the cavity shapes for different characteristic lengths are shown in Table 3. In this study, we introduced the FeretShape parameter to reflect the roundness of the cavities, which is defined by the maximum and minimum lengths (Figure 9). When the characteristic length is 0.2 m, the FeretShape ranges from 1.56 to 11.82, with an average of 4.91. The length of the cavities ranges from 0.20 to 1.24 m, with an average of 0.5 m. When the characteristic length is 0.33 m, the FeretShape ranges from 3.10 to 13.98, with an average of 6.80. The cavity length ranges from 0.22 to 1.51 m, with an average of 0.74 m. When the characteristic length increases to 0.5 and 1 m, the mean FeretShape increases to 11.16 and 14.15, respectively, and the average cavity length is 0.81 and 2.3 m, respectively. It can be concluded that the characteristic length has a significant influence on the roundness and size of the cavities. As the characteristic length increases, the FeretShape and length of the cavities increase (Figure 10a,b). The height/width of the cavities (d) is weakly correlated with the characteristic length. This is mainly due to the impact of the matrix heterogeneity. The matrix heterogeneity of different characteristic lengths differs; therefore, the average height/width of the cavities slightly varies, with an average height/width variation ranging from 0.10 to 0.14 m.

Table 3.
Statistical cavity shape parameters for different characteristic lengths.
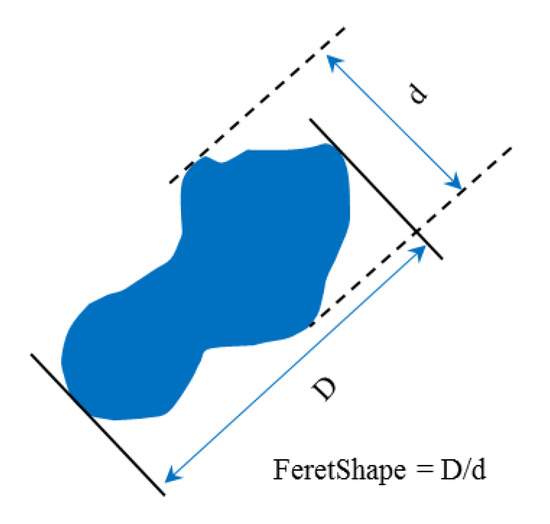
Figure 9.
Illustration of the FeretShape parameter.
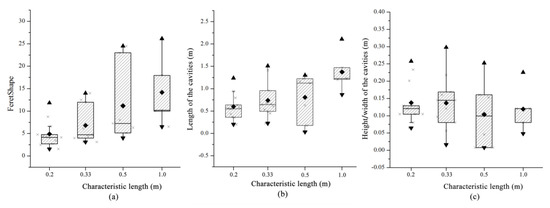
Figure 10.
Comparison of the shape parameters for different characteristic lengths. (a), (b), and (c) represent the statistical results of FeretShape, length of cavities, height/width of cavities with different characteristic lengths, respectively.
5.3. Effect of Cross Fractures
The images of the cavity distribution in Figure 5 were post-processed and the cavities were distinguished and separated, as shown in Figure 11.
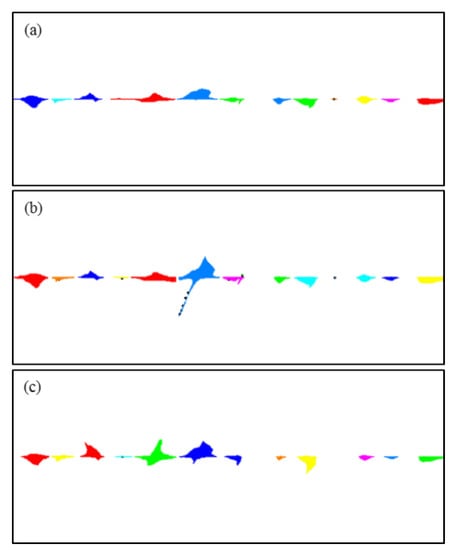
Figure 11.
Image processing results showing the cavity segmentation for different fracture permeabilities. (a) Cross fracture set 1: the horizontal fracture aperture was set to and the cross fracture aperture was set to ; (b) cross fracture set 2: the apertures of the horizontal fracture and cross fracture IV were set to and all other cross fracture apertures were set to ; (c) cross fracture set 1: the horizontal fracture aperture was set to and the cross fracture aperture was set to . Different colors are used to visually differentiate the individual cavities.
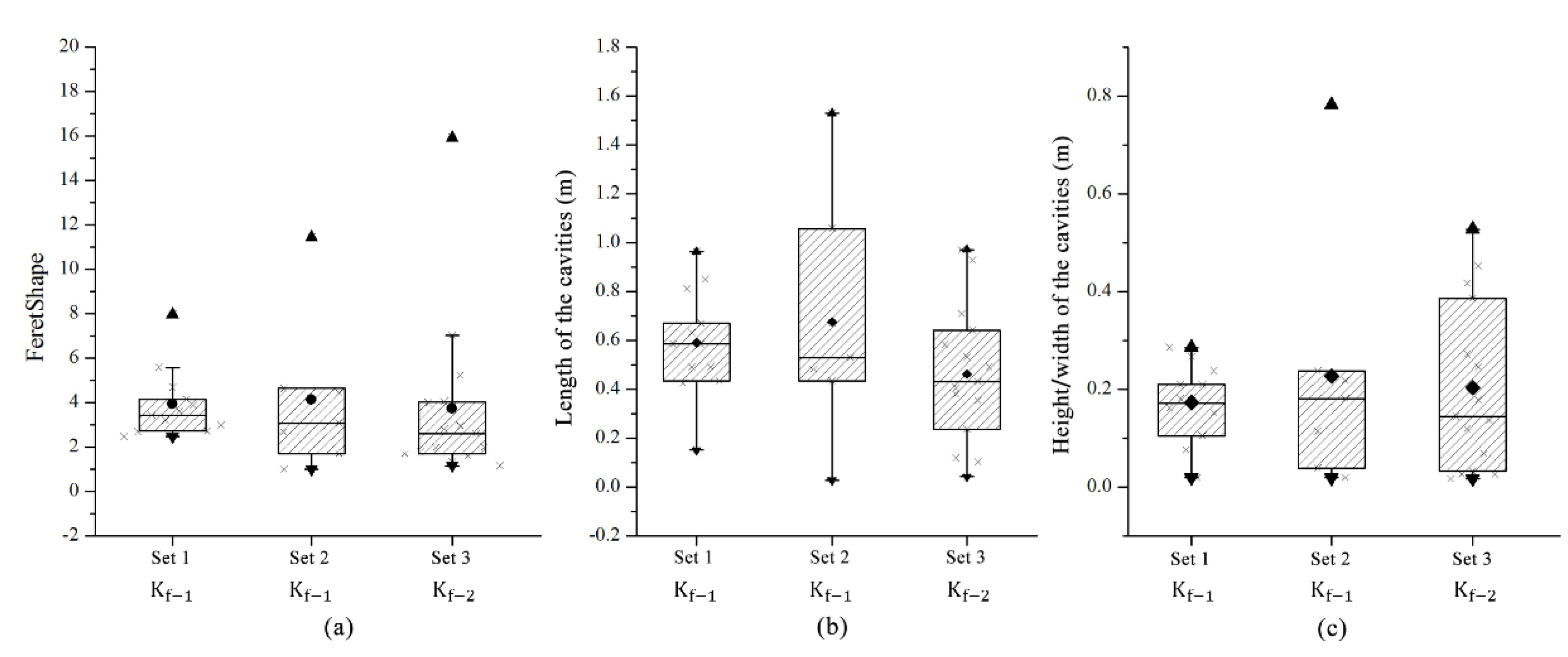
The statistical results for the morphology of the cavities with cross fractures are shown in Table 4 and Figure 12a,b. For cross fracture set 1, the FeretShape of the cavities ranges from 2.46 to 7.97, with an average value of 3.95. The cavity length ranges from 0.15 to 1.51 m, with an average of 0.65 m. The cavity width ranges from 0.019 to 0.29 m, with an average of 0.17 m. For cross fracture set 2, the FeretShape of the cavities is between 1 and 11.45, with an average value of 3.68. The cavity length is between 0.02 and 1.53 m, with an average of 0.56 m. The cavity widths are between 0.019 and 0.78 m, with an average of 0.19 m. Compared with the cross fracture set 1, the difference between the two scenarios is mainly reflected in the vicinity of cross fracture IV. The permeability of cross fracture IV in set 2 is the same as that of the horizontal fracture (1 × 10−11 m2) and the dissolution extends further along fracture IV. Therefore, the length and width of the cave near fracture IV significantly vary and the FeretShape increases to 11.45. Due to the increase in the fracture permeability, the cumulative injection volume (PV) of the cross fracture set 2 is slightly larger than that of set 1 during the same period. The cavity volume is larger (2.12% and 1.69% for sets 1 and 2, respectively). However, because the permeability of the other fractures, except for fracture IV, insignificantly changes, the average cavity dimensions (height, length, and FeretShape) are very similar.

Table 4.
Statistics parameters for different cross fracture networks.
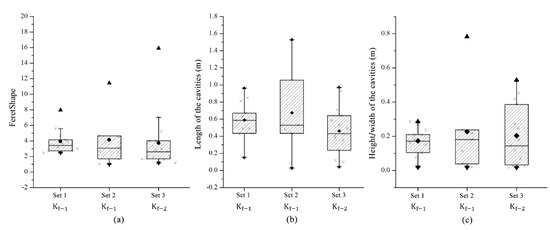
Figure 12.
Comparison of the shape parameters for different characteristic lengths. Parameter represents the condition under which the permeability of the cross fractures is 1 × 10−13 m2 and the aperture is 1.1 × 10−6 m; represents the condition under which the permeability of the cross fractures is 5 × 10−13 m2 and the aperture is 2.45 × 10−6 m. (a), (b), and (c) represent the statistical results of FeretShape, length of cavities, height/width of cavities with different cross fracture sets, respectively.
The statistical results for the pore morphology parameters for different cross fracture permeabilities are shown in Table 4 and Figure 12a,c. When the permeability of the cross fractures increases five-fold to 5 × 10−13 m2, the FeretShape ranges from 1.13 to 15.92, with an average value of 3.73. The cavity length ranges from 0.04 to 0.97, with an average of 0.46 m. The cavity width varies between 0.017 and 0.53 m, with an average of 0.20 m. The increase in the permeability of the cross fractures leads to an increase in the development height of the holes along the fractures and the difference between the length and width of the cavities decreases. Therefore, the mean value of the FeretShape slightly decreases (from 3.95 to 3.73). Due to the increase in the cross fracture permeability, the cumulative injected volume (PV) of the two fracture systems is very similar, but the cavity volume accounts for a slightly larger proportion when the cross fracture permeability is higher (2.03% larger than 1.69%).
The images of the cavity distribution in Figure 6 were post-processed and the cavities were distinguished and separated, as shown in Figure 13. The corresponding statistical results of the cavity morphology parameters for different matrix permeabilities are shown in Table 5 and Figure 14. When the matrix permeability increases, the cumulative injection volume (PV) significantly increases while the pressure difference remains constant. When the matrix permeability increased by one and two orders of magnitude, the PV increases 49- and 34-fold and the pore volume ratio increases 6- and 12-fold, respectively. When the matrix permeability increases by one order of magnitude (CK = −1 × 10−12 m2), the FeretShape ranges from 1.08 to 3.69, with an average of 1.74. The cavity length ranges from 0.35 to 1.22, with an average of 0.71 m. The cavity width varies between 0.094 and 0.77 m, with an average of 0.44 m. When the matrix permeability increases by two orders of magnitude (CK = −1 × 10−11 m2), the FeretShape varies between 1.14 and 2.41, with an average value of 1.65. The cavity length ranges from 0.31 to 2.81, with an average of 1.30 m. The cavity width of the pores is 0.14–1.31 m, with an average of 0.73 m. Therefore, the increase in the matrix permeability is conducive to the expansion of dissolution along different directions, effectively increasing the length and height/width of the cavities and reducing the difference between the long and short axes (D and d, respectively), leading to a decrease in the average value of the FeretShape.
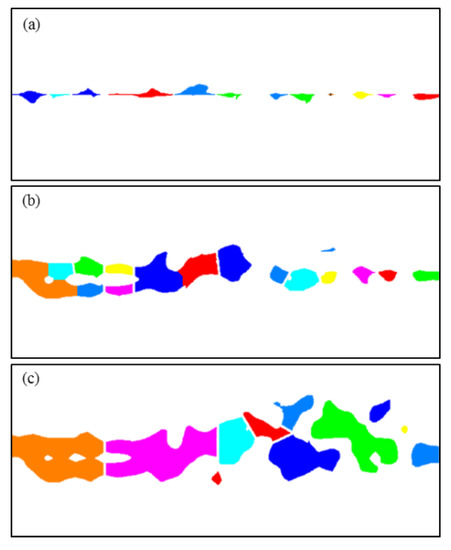
Figure 13.
Image processing results showing the cavity segmentation for different matrix permeabilities. The matrix permeability factor CK in (a), (b), and (c) is 1 × 10−13 m2, 1 × 10−12 m2, and 1 × 10−11 m2, respectively. Different colors are used to visually differentiate the individual cavities.

Table 5.
Statistics of the characteristic parameters for different cross fracture permeabilities.
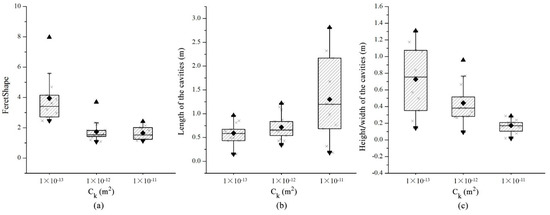
Figure 14.
Comparison of the characteristic parameters of the pore shape for different matrix permeabilities. (a), (b), and (c) represent the statistical results of FeretShape, length of cavities, height/width of cavities with different CK, respectively.
5.4. Cavity Formation in a Complex Fracture Network
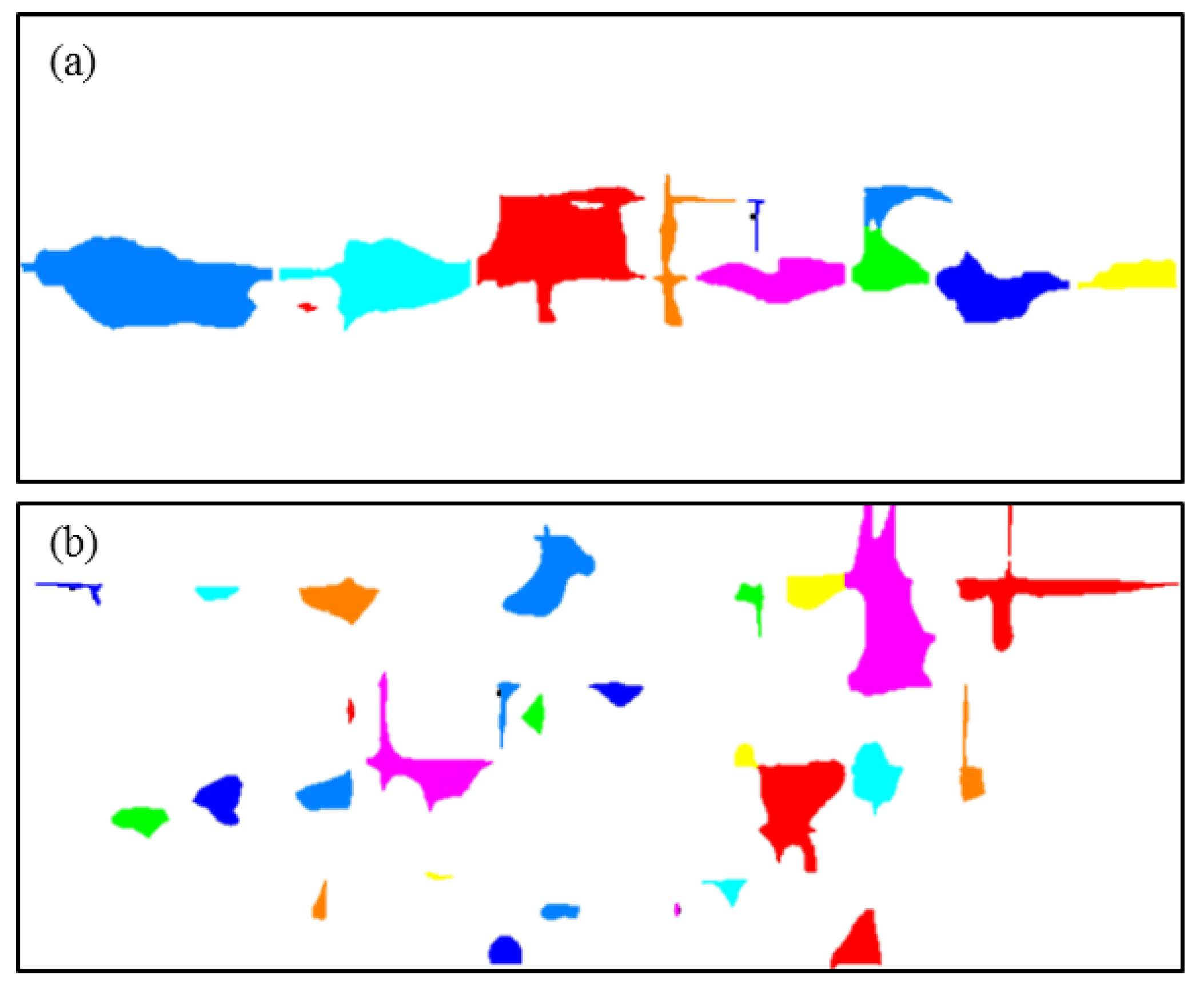
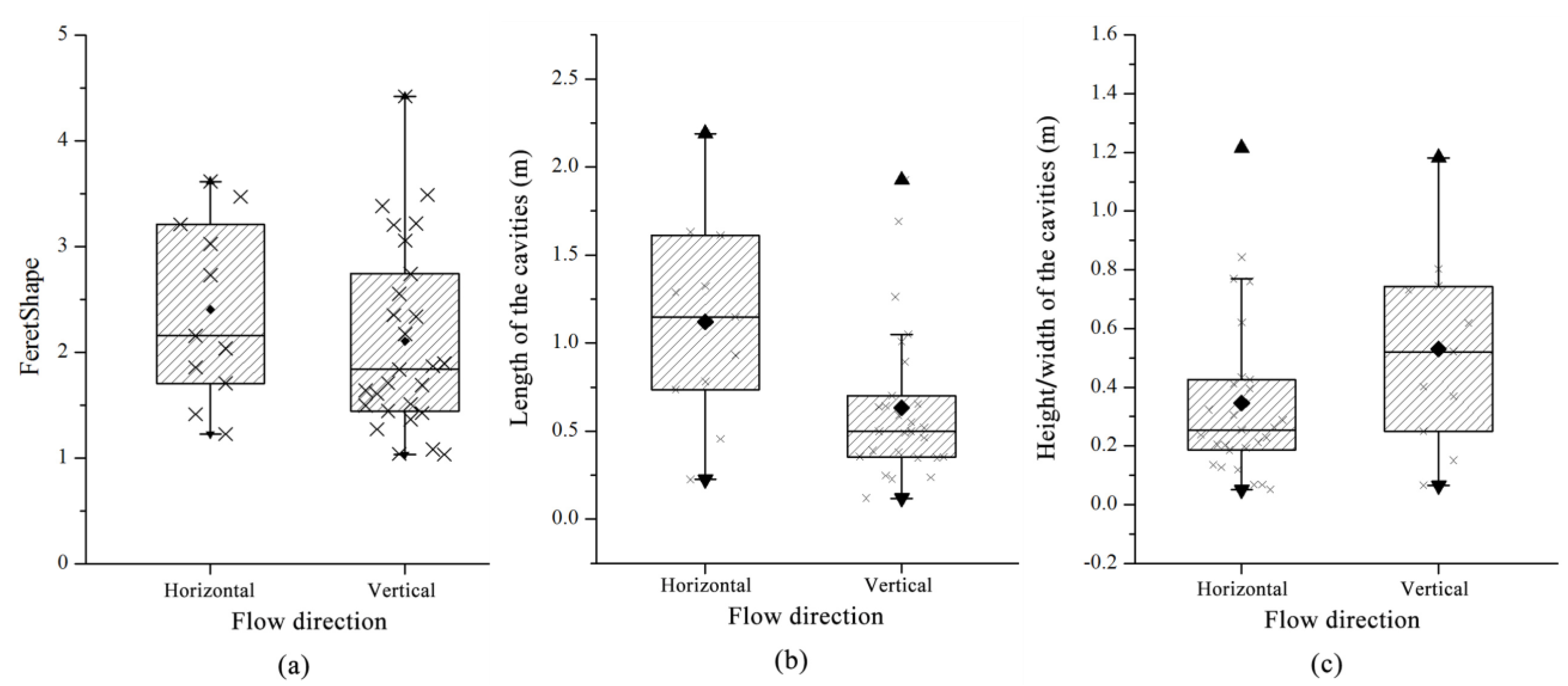
When the flow direction differed, the images of the cavity distribution in Figure 7 were post-processed and the cavities were distinguished and separated, as shown in Figure 15. The corresponding statistical results for the characteristic parameters of the pore morphology are shown in Table 6 and Figure 16. The topographic structures of the two scenarios are identical. When the volume of the injected fluid (PV) is the same, the differences between the two models reflect the hydraulic difference along the seepage directions such as the connectivity and actual preferential seepage pathways of the fluids. With respect to horizontal seepage, the volume of the dissolution holes accounts for ~9.86%, that is, it is slightly higher than that of vertical seepage (8.5%). The FeretShape ranges from 1.23 to 3.62, with an average of 2.41. The cavity length ranges from 0.23 to 2.19, with an average of 1.12 m. The width of the hole development varies between 0.065 and ~1.18 m, with an average of 0.53 m. When the seepage flow is mainly vertical, the FeretShape varies between 1.03 and 4.42, with an average of 2.11. The cavity length ranges from 0.12 to 1.93, with an average of 0.63 m. The width varies between 0.051 and 1.21 m, with an average of 0.35 m. Based on the combination with the spatial distribution of the dissolution caves corresponding to the two seepage directions in Figure 15, it can be seen that the caves are mainly distributed along the horizontal fracture when horizontal seepage is dominant and the number of caves is smaller. However, each cave is relatively large and the average FeretShape is larger. In the vertical seepage flow scenario, the caves mainly spread along multiple groups of orthogonal short and straight fractures and the number of caves is higher. However, the size and volume of the caves are relatively limited and the FeretShape of more than half of the caves is smaller than 2, leading to a smaller average FeretShape value.
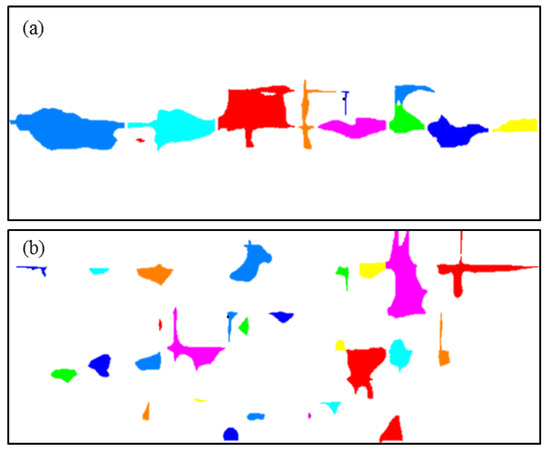
Figure 15.
Image processing results showing the cavity segmentation for different seepage directions. (a) Horizontal flow, (b) vertical flow. Different colors are used to visually differentiate the individual cavities.

Table 6.
Statistics of the characteristic parameters for different seepage directions.
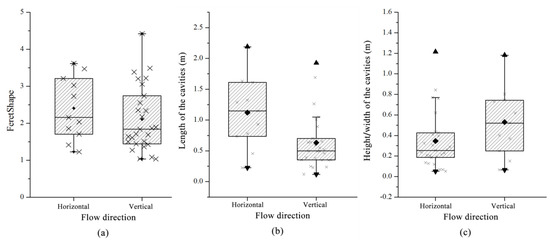
Figure 16.
Comparison of the characteristic parameters of the pore shape for different seepage directions. (a), (b), and (c) represent the statistical results of FeretShape, length of cavities, height/width of cavities with different flow directions, respectively.
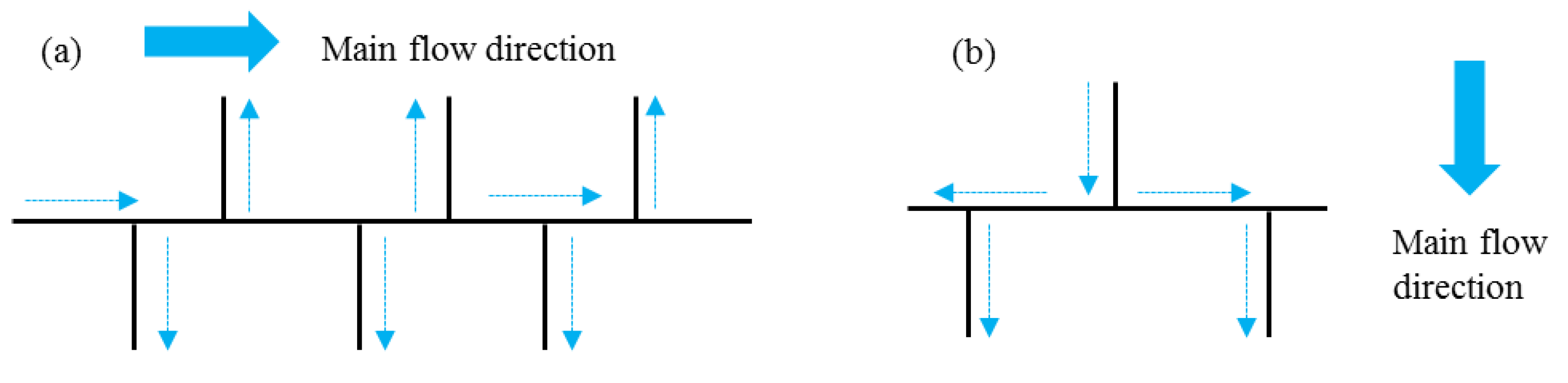
The preferential flow paths are closely related to the fracture network topology and flow direction [50]. When the main stream flows along a long fault/fracture with the majority of the flux in the horizontal fracture, as shown in Figure 17a, the secondary fractures are filled with unsaturated fluids, and dissolved mineral substances are transported to the external system through the long fault/fracture. The dissolution mainly occurs along the long fault/fracture and the local dissolution pores that formed along secondary fractures interact with the long fault/fracture. The bead-shaped wormhole or caves spread near the long fault/fracture. When the flow paths comprise a series of short fractures with similar lengths (Figure 17b), the fluids must migrate through more fractures to find a pathway with less resistance due to the lack of a single long and straight fracture acting as a preferential seepage path. The connectivity of the interacting fractures leads to dissolution in more paths and T-shaped dissolution pores or caves easily form at the intersection of the cross fractures. In contrast to the dissolution wormholes that spread along one main fracture, multiple seepage channels with dissolution phenomena can be observed in the case of the fracture network in Figure 7b and the major axis of the caves or wormholes is consistent with the vertical seepage direction. The vertical fractures developed in the right part of the model in Figure 7b, which have a better connectivity, are the optimal channels for fluid vertical seepage.
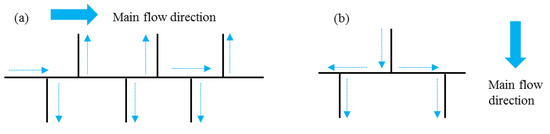
Figure 17.
Effect of the correlation between the topological structure of the fracture network and main direction of fluid flow. (a) Fluids flow along the long straight fracture, (b) seepage through multiple intersecting short fractures.
In general, the dissolution pores are dominated by preferential flow in the fractures, forming bead-shaped wormholes or caves along the seepage direction in the fractures, especially at intersecting fractures and more permeable positions. The phenomenon is similar with cave patterns under fracture networks summarized by Palmer et al., (1991) [51]. The scenarios that consider intersecting fractures (Figure 5 and Figure 6) and horizontal seepage condition in complex fracture network (Figure 7a) are consistent with the branch work patterns in the early stage of evolution history. The solutional caves spread based on the long main preferential pathway. The vertical seepage in complex fracture network (Figure 7b) is more likely to form the maze pattern with longer simulation time, where many orthogonal pathways give rise to solutional widening simultaneously. It illustrates that the impacts of matrix can be significantly alleviated when fracture network enhances the connectivity and seepage capacity of matrix-fracture system. The formation and evolution of cavities are dominated by fracture network topology.
The vertical and horizontal seepage scenarios depict the vertical seepage zone or deep phreatic caves and horizontal flow zone or water table caves in the karst system, respectively [52]. The former scenario leads to the formation of cavities with smaller sizes and FeretShape parameters along multiple sets of short and straight fractures, while the latter scenario leads to large caves and an underground river system along long and straight horizontal fractures.
6. Conclusions
In this study, a reactive transport model was established to simulate the cavern formation along fractures in carbonate rocks. The model combines the advantages of both equivalent continuum and discrete fractures and can be used to simulate the dissolution of carbonate rock mass and porosity evolution in a dual-medium system of matrix and fractures.
Different factors affecting the dissolution along fractures were considered in the simulation of matrix–fracture carbonate rocks including the magnitude of the porosity heterogeneity, characteristic length of the matrix porosity heterogeneity, intersecting fractures, and complex fracture network. The main results can be summarized as follows:
- (1)
- The magnitude of the matrix heterogeneity has a notable impact on the dissolution distribution along the fracture. Stronger heterogeneity results in a more significant difference in the cavity shape.
- (2)
- The characteristic length affects the size, shape, and roundness of beam-shaped wormholes. When the characteristic length is larger, the caves are larger and flatter. Although the caves are smaller when the characteristic length is smaller, the number of the holes is larger.
- (3)
- The existence of cross fractures enhances the dissolution area. Increasing the permeability of the cross fractures or matrix greatly improves the size of the beam-shaped wormholes, leading to the formation of an underground river in the karst system. The sizes of the cavities increase and the roundness (FeretShape) decreases with increasing permeability of the cross fractures.
- (4)
- A more complex fracture network leads to the development of more karst dissolution pores and caves. The topology of the fracture network and preferential flow dominate the distribution of caves but alleviate the effect of the matrix heterogeneity. The seepage along multiple sets of short and straight fractures leads to the formation of cavities with smaller sizes and FeretShape values, whereas the seepage along the long and straight horizontal fracture results in the formation of large caves and underground river systems.
Although this study demonstrates the impacts of matrix heterogeneity, cross fractures and complex fracture network on the formation of caves, limitations exist and further work is recommended. The cross fractures and fracture network used in this paper is set for theoretical analysis. The roughness and self-affine properties of natural fractures should be included for a more realistic scenario. Besides, the formation and morphology of cavities is a function of time. It is significant to evaluate the cavern evolution with time under different scenarios of spatial heterogeneity.
Author Contributions
R.D.: conceptualization, methodology, writing—original draft preparation. G.S.: conceptualization, resources, project administration. C.Y.: resources, data curation. Q.W.: resources, data curation. H.Z.: methodology, data curation. L.W.: software, methodology. Z.X.: writing—original draft preparation. Y.D.: conceptualization, writing—original draft preparation, project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by a Special Major Project on Petroleum study, China (2016ZX05053, 2017ZX05008003-021).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
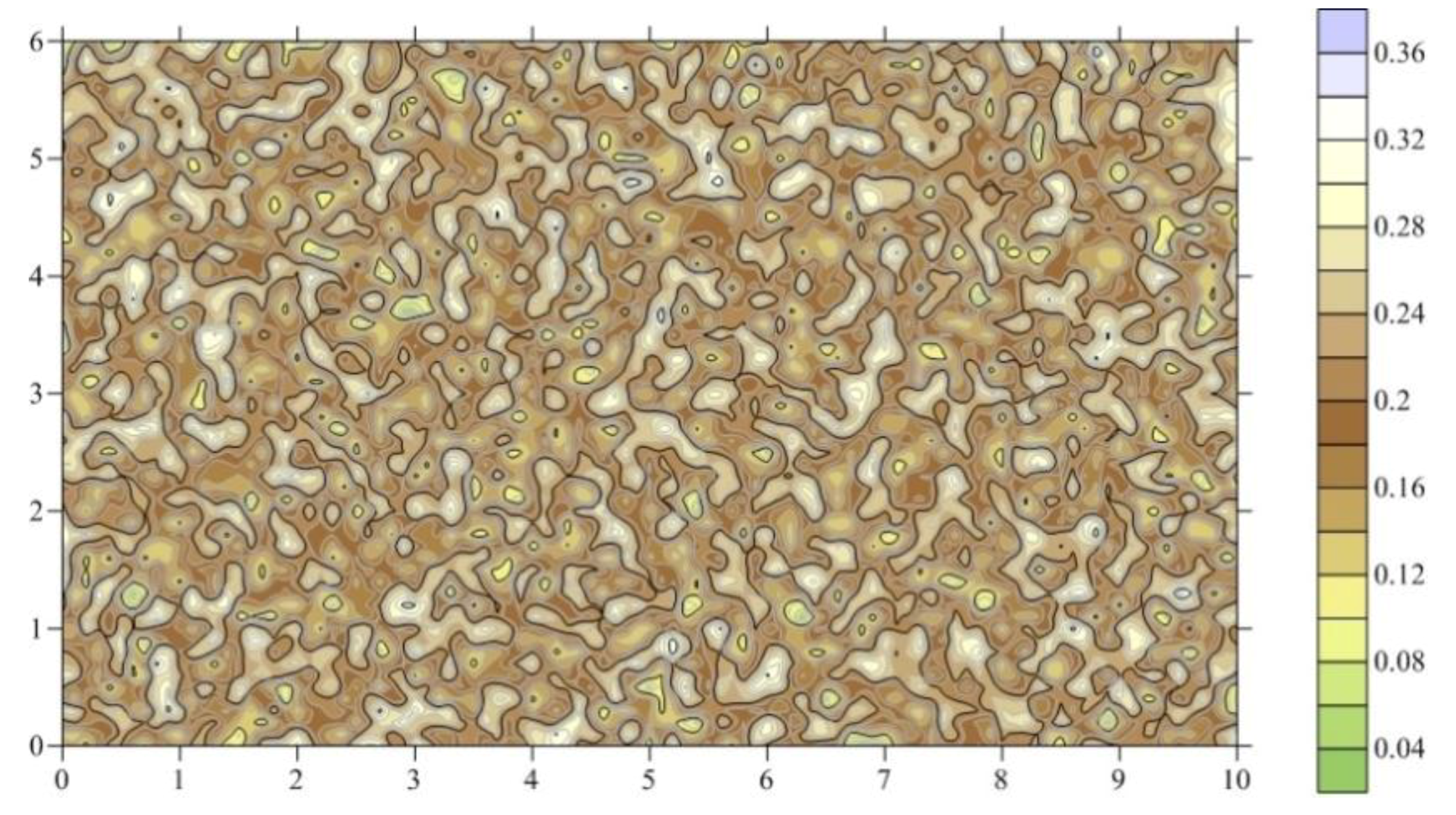
The validation of the mathematical models is tested in this part. The dissolution patterns of carbonate rocks with variable injected velocity of acidic fluids were simulated. The domain was 2 cm in width and 5 cm in height. A constant injection rate was set at the top of the domain, and the bottom was seemed as free flow boundary. The fluid was constrained within the domain by imposing zero flux boundary on the left and right sides. Similarly, the top and bottom boundary were set as constant concentration (C = 0.001 Ceq) and free discharge condition, respectively. The solute concentration was set as zero at initial state. The heterogeneity of matrix porosity and permeability was set according to Panga et al., (2005) [49]. The porosity was the sum of a mean value of and a random number . Here, was set as 0.2, and obeyed uniform distribution with interval of [−0.15, 0.15]. The porosity distribution was shown as Figure A1. The permeability is calculated by Equation (13).
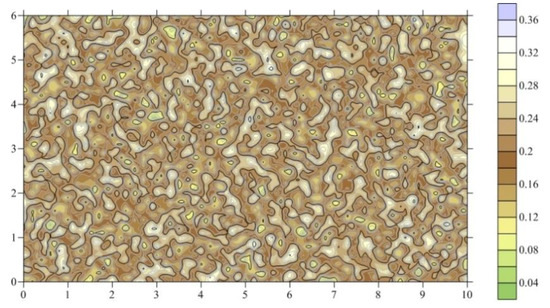
Figure A1.
Spitial distribution of porosity heterogeneity.
Figure A1.
Spitial distribution of porosity heterogeneity.
The validation results were shown in Figure A2. The dissolution pattern varied from face dissolution to uniform pattern when injection velocity increased. When the fluid migration was relatively slow with lower injection rate, like face dissolution pattern, the reactive transport process was mainly limited by convection. This led to a planar dissolution front where the medium behind it need to be dissolved completely first before the front moving forward. When the injection rate is relatively high, the fluid can spread throughout the domain simultaneously, and the reactive transport process was constrained by reaction, and dissolution occurred at different position, leading to uniform dissolution pattern. Wormhole pattern represented a scenario that the differential corrosion due to heterogeneity (Figure A2c). Both of the reaction and transport of solute influenced the evolution of carbonate minerals. The heterogeneity allowed preferential dissolution where porosity and pereability were relatively high and forming some preferential pathways.
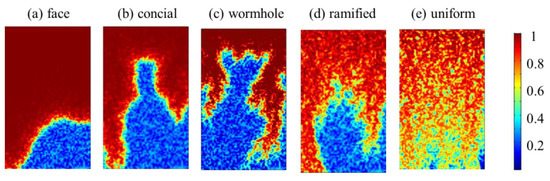
Figure A2.
Dissolution patterns under different injection velocity. (a) face dissolution, injection velocity , (b) concial dissolution with , (c) wormhole dissolution with , (d) ramified dissolution with , (e) uniform dissolution with .
Figure A2.
Dissolution patterns under different injection velocity. (a) face dissolution, injection velocity , (b) concial dissolution with , (c) wormhole dissolution with , (d) ramified dissolution with , (e) uniform dissolution with .
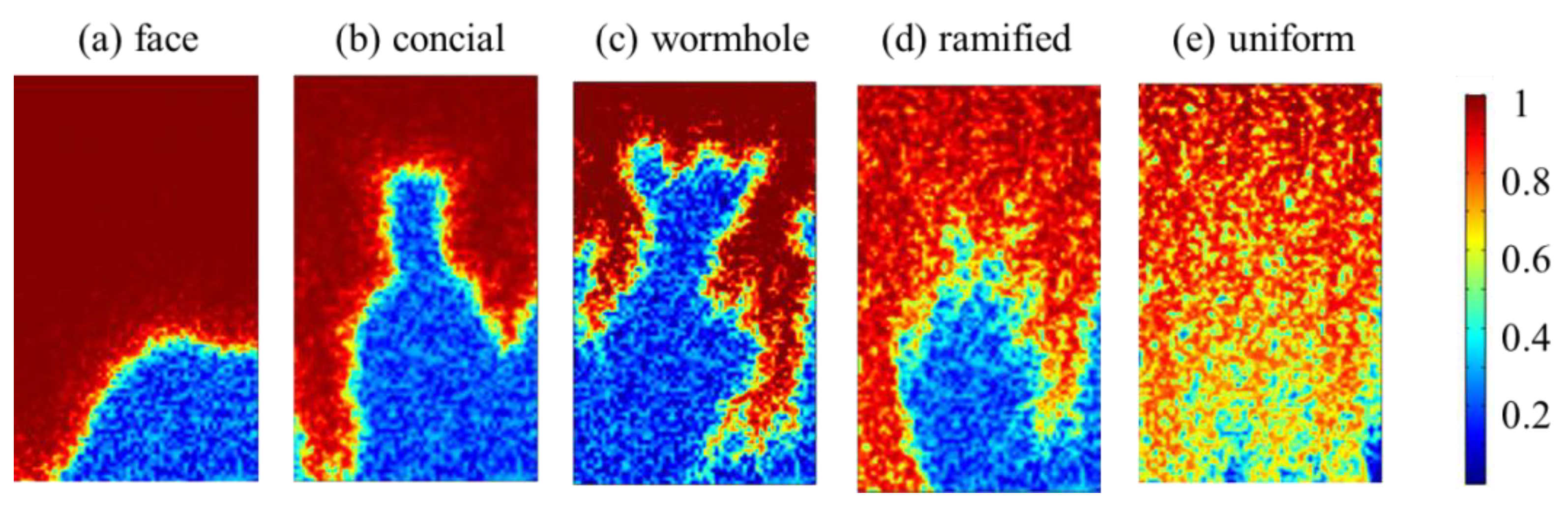
By utilizing the mathematical models stated in Section 2, different dissolution patterns varying from face dissolution to uniform pattern can be identified. The simulation results were similar with that reported by Panga et al., (2005) [49], whose work also discussed the formation of wormholes in carbonate acidization.
References
- Ford, D.; Williams, P. Karst Geomorphology and Hydrology; The Academic Division of Unwin Hyman Ltd.: London, UK, 1989; Volume 346. [Google Scholar]
- Al-Mumen, A.; Al-Habib, N.; Al-Anzi, E.; Al-Mutawa, M. Positive reactions in carbonate reservoir stimulation. Oilfield Rev. 2003, 15, 28–45. [Google Scholar]
- Burberry, C.M.; Jackson, C.A.-L.; Chandler, S.R. Seismic reflection imaging of karst in the Persian Gulf: Implications for the characterization of carbonate reservoirs. AAPG Bull. 2016, 100, 1561–1584. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, T.-G.; Li, M.; Yang, F.; Cheng, B. Biomarker geochemistry of crude oils and Lower Paleozoic source rocks in the Tarim Basin, western China: An oil-source rock correlation study. Mar. Pet. Geol. 2018, 96, 94–112. [Google Scholar] [CrossRef]
- Russel-Houston, J.; Gray, K. Paleokarst in the Grosmont Formation and reservoir implications, Saleski, Alberta, Canada. Interpretation 2014, 2, SF29–SF50. [Google Scholar] [CrossRef]
- Jiang, L.; Cai, C.; Worden, R.H.; Crowley, S.F.; Jia, L.; Zhang, K.; Duncan, I.J. Multiphase dolomitization of deeply buried Cambrian petroleum reservoirs, Tarim Basin, north-west China. Sedimentology 2016, 63, 2130–2157. [Google Scholar] [CrossRef]
- Jiang, L.; Worden, R.H.; Cai, C.F.; Shen, A.J.; He, X.Y.; Pan, L.Y. Contrasting diagenetic evolution patterns of platform margin limestones and dolostones in the Lower Triassic Feixianguan Formation, Sichuan Basin, China. Mar. Pet. Geol. 2018, 92, 332–351. [Google Scholar] [CrossRef]
- Tian, F.; Di, Q.; Jin, Q.; Cheng, F.; Zhang, W.; Lin, L.; Wang, Y.; Yang, D.; Niu, C.; Li, Y. Multiscale geological-geophysical characterization of the epigenic origin and deeply buried paleokarst system in Tahe Oilfield, Tarim Basin. Mar. Pet. Geol. 2019, 102, 16–32. [Google Scholar] [CrossRef]
- Lu, X.; Wang, Y.; Tian, F.; Li, X.; Yang, D.; Li, T.; Lv, Y.; He, X. New insights into the carbonate karstic fault system and reservoir formation in the Southern Tahe area of the Tarim Basin. Mar. Pet. Geol. 2017, 86, 587–605. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Zhang, J.; Wei, C.; Jiao, Y.; Wang, Q. Improved CRM Model for Inter-Well Connectivity Estimation and Production Optimization: Case Study for Karst Reservoirs. Energies 2019, 12, 816. [Google Scholar] [CrossRef]
- Tian, F.; Wang, Z.; Cheng, F.; Xin, W.; Fayemi, O.; Zhang, W.; Shan, X. Three-Dimensional Geophysical Characterization of Deeply Buried Paleokarst System in the Tahe Oilfield, Tarim Basin, China. Water 2019, 11, 1045. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Q.; Jia, C.; Liu, P.; Wang, Q.; Wang, D. Rate transient analysis for coupling Darcy flow and free flow in bead-string fracture-caved carbonate reservoirs. J. Pet. Sci. Eng. 2020, 195, 107809. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, X.; Chen, H. Seismic Characterization of Hypogenic Karst Systems Associated with Deep Hydrothermal Fluids in the Middle-Lower Ordovician Yingshan Formation of the Shunnan Area, Tarim Basin, NW China. Geofluids 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Mylroie, J.E.; Mylroie, J.R. Telogenetic limestones and island karst. In Coastal Karst Landforms; Lace, M.J., Mylroie, J.E., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 375–393. [Google Scholar]
- Garcia-Rios, M.; Luquot, L.; Soler, J.M.; Cama, J. Influence of the flow rate on dissolution and precipitation features during percolation of CO2-rich sulfate solutions through fractured limestone samples. Chem. Geol. 2015, 414, 95–108. [Google Scholar] [CrossRef]
- Deng, H.; Voltolini, M.; Molins, S.; Steefel, C.; DePaolo, D.; Ajo-Franklin, J.; Yang, L. Alteration and Erosion of Rock Matrix Bordering a Carbonate-Rich Shale Fracture. Environ. Sci. Technol. 2017, 51, 8861–8868. [Google Scholar] [CrossRef] [PubMed]
- Gray, F.; Anabaraonye, B.; Shah, S.; Boek, E.; Crawshaw, J. Chemical mechanisms of dissolution of calcite by HCl in porous media: Simulations and experiment. Adv. Water Resour. 2018, 121, 369–387. [Google Scholar] [CrossRef]
- Liu, P.; Yao, J.; Couples, G.D.; Ma, J.; Iliev, O. 3-D Modelling and Experimental Comparison of Reactive Flow in Carbonates under Radial Flow Conditions. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Szymczak, P.; Ladd, A.J.C. Wormhole formation in dissolving fractures. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Deng, H.; Steefel, C.; Molins, S.; DePaolo, D. Fracture Evolution in Multimineral Systems: The Role of Mineral Composition, Flow Rate, and Fracture Aperture Heterogeneity. ACS Earth Space Chem. 2018, 2, 112–124. [Google Scholar] [CrossRef]
- Roded, R.; Aharonov, E.; Holtzman, R.; Szymczak, P. Reactive flow and homogenization in anisotropic media. Water Resour. Res. 2020, 56, e2020WR027518. [Google Scholar] [CrossRef]
- Tansey, J.; Balhoff, M.T. Pore Network Modeling of Reactive Transport and Dissolution in Porous Media. Transp. Porous Media 2016, 113, 303–327. [Google Scholar] [CrossRef]
- Xiao, T.; Kweon, H.; McPherson, B.; Deo, M. Wormhole Generations in Indiana Limestone with CO2 Intrusion: Numerical Simulations Based on Core Flooding Experiments. Energy Fuels 2017, 31, 12487–12499. [Google Scholar] [CrossRef]
- Dávila, G.; Luquot, L.; Soler, J.M.; Cama, J. Interaction between a fractured marl caprock and CO2-rich sulfate solution under supercritical CO2 conditions. Int. J. Greenh. Gas Control 2016, 48, 105–119. [Google Scholar] [CrossRef]
- Fredd, C.N.; Fogler, H.S. Influence of transport and reaction on wormhole formation in porous media. AIChE J. 1998, 44, 1933–1949. [Google Scholar] [CrossRef]
- Soulaine, C.; Roman, S.; Kovscek, A.; Tchelepi, H.A. Mineral dissolution and wormholing from a pore-scale perspective. J. Fluid Mech. 2017, 827, 457–483. [Google Scholar] [CrossRef]
- Gong, X.; Hou, W.; Feng, D.; Luo, Q.; Yang, X. Modelling early karstification in future limestone geothermal reservoirs by mixing of meteoric water with cross-formational warm water. Geothermics 2019, 77, 313–326. [Google Scholar] [CrossRef]
- Gong, X.; Tóth, J.; Yang, X.; Yuan, B.; Feng, D. A numerical model in predicting the initial karst development in porous limestone. Environ. Earth Sci. 2018, 77, 295. [Google Scholar] [CrossRef]
- Romanov, D.; Dreybrodt, W. Evolution of porosity in the saltwater–freshwater mixing zone of coastal carbonate aquifers: An alternative modelling approach. J. Hydrol. 2006, 329, 661–673. [Google Scholar] [CrossRef]
- Deng, H.; Molins, S.; Steefel, C.; DePaolo, D.; Voltolini, M.; Yang, L.; Ajo-Franklin, J. A 2.5D Reactive Transport Model for Fracture Alteration Simulation. Environ. Sci. Technol. 2016, 50, 7564–7571. [Google Scholar] [CrossRef]
- Hill, A.D.; Zhu, D.; Dong, C.; Luna-Garcia, A.L. Computer Model Predicts Matrix Acidizing of Naturally Fractured Carbonate. J. Pet. Technol. 2001, 53, 20–25. [Google Scholar] [CrossRef]
- Dong, C.; Zhu, D.; Hill, A.D. Acid Penetration in Natural Fracture Networks. SPE Prod. Facil. 2002, 17, 160–170. [Google Scholar] [CrossRef]
- Dreybrodt, W.; Gabrovšek, F. Dynamics of wormhole formation in fractured limestones. Hydrol. Earth Syst. Sci. 2019, 23, 1995–2014. [Google Scholar] [CrossRef]
- Dreybrodt, W.; Gabrovšek, F. Basic processes and mechanisms governing the evolution of karst. Speleogenesis Evol. Karst Aquifers 2003, 1, 115–154. [Google Scholar]
- Gabrovšek, F.; Menne, B.; Dreybrodt, W. A model of early evolution of karst conduits affected by subterranean CO2 sources. Environ. Geol. 2000, 39, 531–543. [Google Scholar] [CrossRef]
- Gabrovšek, F.; Dreybrodt, W. Karstification in unconfined limestone aquifers by mixing of phreatic water with surface water from a local input: A model. J. Hydrol. 2010, 386, 130–141. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y.; Huang, N. Review: Mathematical expressions for estimating equivalent permeability of rock fracture networks. Hydrogeol. J. 2016, 24, 1623–1649. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: The roles of aperture, surface roughness, and number of intersections. Adv. Water Resour. 2016, 88, 53–65. [Google Scholar] [CrossRef]
- Kaufmann, G.; Romanov, D.; Hiller, T. Modeling three-dimensional karst aquifer evolution using different matrix-flow contributions. J. Hydrol. 2010, 388, 241–250. [Google Scholar] [CrossRef]
- Kaufmann, G. Modelling karst geomorphology on different time scales. Geomorphology 2009, 106, 62–77. [Google Scholar] [CrossRef]
- Kaufmann, G. Numerical models for mixing corrosion in natural and artificial karst environments. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Kaufmann, G. A model comparison of karst aquifer evolution for different matrix-flow formulations. J. Hydrol. 2003, 283, 281–289. [Google Scholar] [CrossRef]
- Kaufmann, G.; Braun, J. Karst Aquifer evolution in fractured, porous rocks. Water Resour. Res. 2000, 36, 1381–1391. [Google Scholar] [CrossRef]
- Liu, P.; Yao, J.; Couples, G.D.; Huang, Z.; Sun, H.; Ma, J. Numerical modelling and analysis of reactive flow and wormhole formation in fractured carbonate rocks. Chem. Eng. Sci. 2017, 172, 143–157. [Google Scholar] [CrossRef]
- Groves, C.G.; Howard, A.D. Early development of karst systems: 1. Preferential flow path enlargement under laminar flow. Water Resour. Res. 1994, 30, 2837–2846. [Google Scholar] [CrossRef]
- Dreybrodt, W.; Bühmann, D. A mass transfer model for dissolution and precipitation of calcite from solutions in turbulent motion. Chem. Geol. 1991, 90, 107–122. [Google Scholar] [CrossRef]
- Plummer, L.N.; Busenberg, E. The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90 °C, and an evaluation of the aqueous model for the systemCaCO3-CO2-H2O. Geochim. Cosmochim. Acta 1982, 46, 1011–1040. [Google Scholar] [CrossRef]
- Tao, J.; Wu, Y.; Elsworth, D.; Li, P.; Hao, Y. Coupled Thermo-Hydro-Mechanical-Chemical Modeling of Permeability Evolution in a CO2-Circulated Geothermal Reservoir. Geofluids 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Panga, M.K.R.; Ziauddin, M.; Balakotaiah, V. Two-scale continuum model for simulation of wormholes in carbonate acidization. AIChE J. 2005, 51, 3231–3248. [Google Scholar] [CrossRef]
- Aliouache, M.; Wang, X.; Jourde, H.; Huang, Z.; Yao, J. Incipient karst formation in carbonate rocks: Influence of fracture network topology. J. Hydrol. 2019, 575, 824–837. [Google Scholar] [CrossRef]
- Palmer, A.N. Origin and morphology of limestone caves. Geol. Soc. Am. Bull. 1991, 103, 1–21. [Google Scholar] [CrossRef]
- Ford, D.C.; Ewers, R.O. The development of limestone cave systems in the dimensions of length and depth. Can. J. Earth Sci. 1978, 15, 1783–1798. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).