In this work a cost-benefit optimization of WDS resilience is implemented and conducted for a real-world main line WDS of a city district. Therefore, a Mixed Integer Linear Program is derived based on graph-theoretical resilience assessment considering the WDS topology introduced by Herrera et al. [
12]. This resilience index considers both redundancy and robustness of the WDS. First, by considering all possible paths connecting demand and source nodes, the consequences of possible component failure or local contamination can be counteracted. Second, by ranking the paths by physical feasibility considering their hydraulic properties, the robustness of individual paths is accounted for. To do so, each path is assessed for its hydraulic resistance, computing the non-dimensional pressure loss of each edge making up the path, as derived by Lorenz et al. [
13]. In the following, the method of assessing and optimizing the main line WDS resilience is described in detail. This method is applicable to any WDS while yielding the best results when considering a main line WDS. In this work it is applied to a real-world main line WDS of a German city district.
2.1. Resilience Assessment
To assess the resilience, the real-world WDS is presented as a planar graph in which the pipes are represented as edges connecting source and consumer nodes. The set of these nodes is given as and , respectively, as well as the set of junction nodes , while the unified set is given as . The demand of a specific consumer node is given by , while the overall demand of the WDS is given by . The set of existing edges is given in a binary matrix of size in which an existing edge connecting node with node is represented by and all inexistent edges by . Since the direction of flow in a pipe is not fixed but depends on the actual pressure gradient, all edges are undirected. Therefore, the matrix describing the WDS is symmetric. Furthermore, there are no self-loops within the network, meaning there are no pipes starting and ending at the same node, and therefore its diagonal is strictly . Each edge has different characteristics, also presented in this matrix notation. Of interest for this work are the pipe diameters, lengths and roughness given in the matrices , , and , respectively.
When considering the addition of pipes, the edges representing them must be noted in a similar way. To consider the physical feasibility of the addition of a pipe, the current urban structure is of great importance as pipes cannot be laid between all nodes. Different studies show, and legal standards command, that infrastructures are highly parallel [
20,
21]. In general, there is a high parallelism between supply infrastructures, i.e., the water, energy and information and communications technology, and the urban transportation network, i.e., streets and pathways. Therefore, the addition of pipes is restricted by the urban transportation network embedded in the present urban structure. Information on the urban transportation system is mostly open access data and can for example be extracted from OpenStreetMap [
22]. With this data, the maximum possible edge matrix can be derived as
which is equally of size
and symmetrical. The edge characteristics of the added pipes can be written into the same matrices
,
, and
.
To assess the graph-theoretical resilience of the WDS, the overall resilience
is given as the sum of each consumer node’s resilience, as defined by Herrera et al. [
12]. To furthermore consider the demand and therefore the number of consumers depending on the demand fulfillment of a specific node, in this work it is proposed to weigh the resilience of each consumer node
by its relative water demand
.
This topology based resilience metric considers the hydraulic resistance
of each
-shortest path feeding the consumer node
from source
. As high hydraulic resistance paths have little impact on the resilience index, a maximum number of shortest paths to be considered,
, can be determined for the critical transfer node of the complete WDS, following the approach introduced by Lorenz et al. [
13]. The weight of the edges making up the shortest paths is, despite what the name might suggest, not its length but the hydraulic resistance of the pipe connecting the two nodes under consideration. Each path
connecting source node
and consumer node
can be represented by a two dimensional binary matrix
similar to the matrix
describing the network. In this matrix
sequence of nodes, part of the path starting at the source
and ending at the consumer node
is stored. Edges which are part of this path connecting two subsequently following nodes making up the path, have the value
while all other edges are of value
. In contrast to matrix
describing all pipes in a network, the matrix describing a specific path is not symmetrical, due to the direction of the path represented by the sequence of nodes connected by the edges making up the feeding path.
The physical considerations underlying the determination of the hydraulic resistance of each pipe is deduced by Lorenz et al. [
13]. Applying an order of magnitude analysis, it was derived that in the case of a WDS turbulent flow in hydraulic rough pipes can be assumed. The hydraulic resistance
of a path made up of pipes
represents the dimensionless pressure loss along this path and can be determined as follows.
Therefore, the pressure loss
along the path is related to the characteristic kinematic pressure given by the characteristic velocity
as well as to the density of the fluid in the pipes
, herein water. In the case of turbulent flow in hydraulic rough pipes, the friction factor
is given by Prandtl-Karman’s law as
[
23]. The calculation of hydraulic resistance can also be rewritten in matrix notation, making use of the representation of each shortest path for every consumer and source node in the five-dimensional matrix
.
2.2. Resilience Optimization
The resilience index introduced can be applied to assess the resilience of any WDS for which the network topology, as well as the pipe diameter, length, and roughness and the demand of all consumer nodes, is known. Therefore, present and further adaptations to the present WDS can be assessed. Adapting the WDS by adding pipes results in alternative feeding paths of different hydraulic resistance for different consumer nodes. These alternative feeding paths therefore impact the overall resilience differently, also depending on the weight of the consumer node being fed. As the problem of determining which pipe is best to add for maximum resilience enhancement rises to become a challenging combinatorial problem, it is useful to apply mathematical optimization in order to solve it.
The problem can be formulated as a maximization problem, as the resilience index of the WDS is to be maximized. The objective function is therefore the maximization of the resilience index.
This objective function considers the reciprocal of the hydraulic resistance of each path feeding a consumer node. This leads to a nonlinear optimization problem with a concave solution space, which are in general computationally expensive to solve. The formulation to find the shortest path in a network by a discrete optimization problem can also be easily implemented [
24]. Yet, in turn, finding the second, third and
-th shortest path is usually solved by heuristics, as for example by Yen’s K-shortest paths algorithm [
25]. This makes the formulation of all shortest paths
connecting a source and consumer node as an optimization problem infeasible for a dynamic graph, to the best of the authors knowledge. Identification or knowledge of all the shortest paths, in turn, is necessary to determine the hydraulic resistance as defined by Equation (2).
Taking into consideration the constraints on physical feasibility of a pipe addition to an existing WDS given by the parallelism of infrastructures, the possible addition of pipes is highly restricted compared to when considering a complete graph, i.e., a graph in which every pair of nodes is connected by an edge. Therefore, the calculation of all feeding paths in the maximum possible WDS, for each consumer node fed by any source, considering that all physically feasible pipes are added, is practicable for smaller networks. When calculating all possible feeding paths in a preprocessing step, the optimization problem can be rewritten as
where the hydraulic conductance
, i.e., the reciprocal of the hydraulic resistance, is already known for each path. The binary decision variable
permits the choice of the best possible feeding paths as part of the adapted WDS, and thereby the pipes to be added to the existing WDS for a set maximum length added.
Based on the linearized resilience optimization, taking into consideration only the single shortest path of each source-consumer node combination, conducted in [
13], the resulting Mixed Integer Linear Program considering the
-shortest paths is given in Equations (5)–(11). This optimization program relies on the following variables, sets and parameters, given in
Table 1,
Table 2 and
Table 3. It is implemented in Python using the Gurobi solver [
26]. For the preprocessing of the WDS, the python packages WNTR [
27] in combination with NetworkX [
28] are applied.
As described in
Table 1, two binary decision variables are introduced: on the one hand, choosing the pipes to be added to the existing WDS and therefore of similar form as the matrix describing the edges of the existing WDS,
; on the other hand, selecting the paths which are of the highest hydraulic conductance possible for the adapted WDS,
.
The unified node set
contains the source node set
as well as the consumer node set
and the junction node set
(see
Table 2). Each possible path connecting source and consumer nodes is also given in the path set
.
In addition to variables and sets, the optimization program relies on multiple parameters together with the sets which define the exact instance for an optimization, i.e., the unique optimization problem for which a specific optimization result can be achieved (see
Table 3). There are several parameters specific to the present WDS and its urban structure but also one parameter specific to the cost-benefit analysis conducted by this optimization program. This is the maximum allowed length for the sum of all pipes added
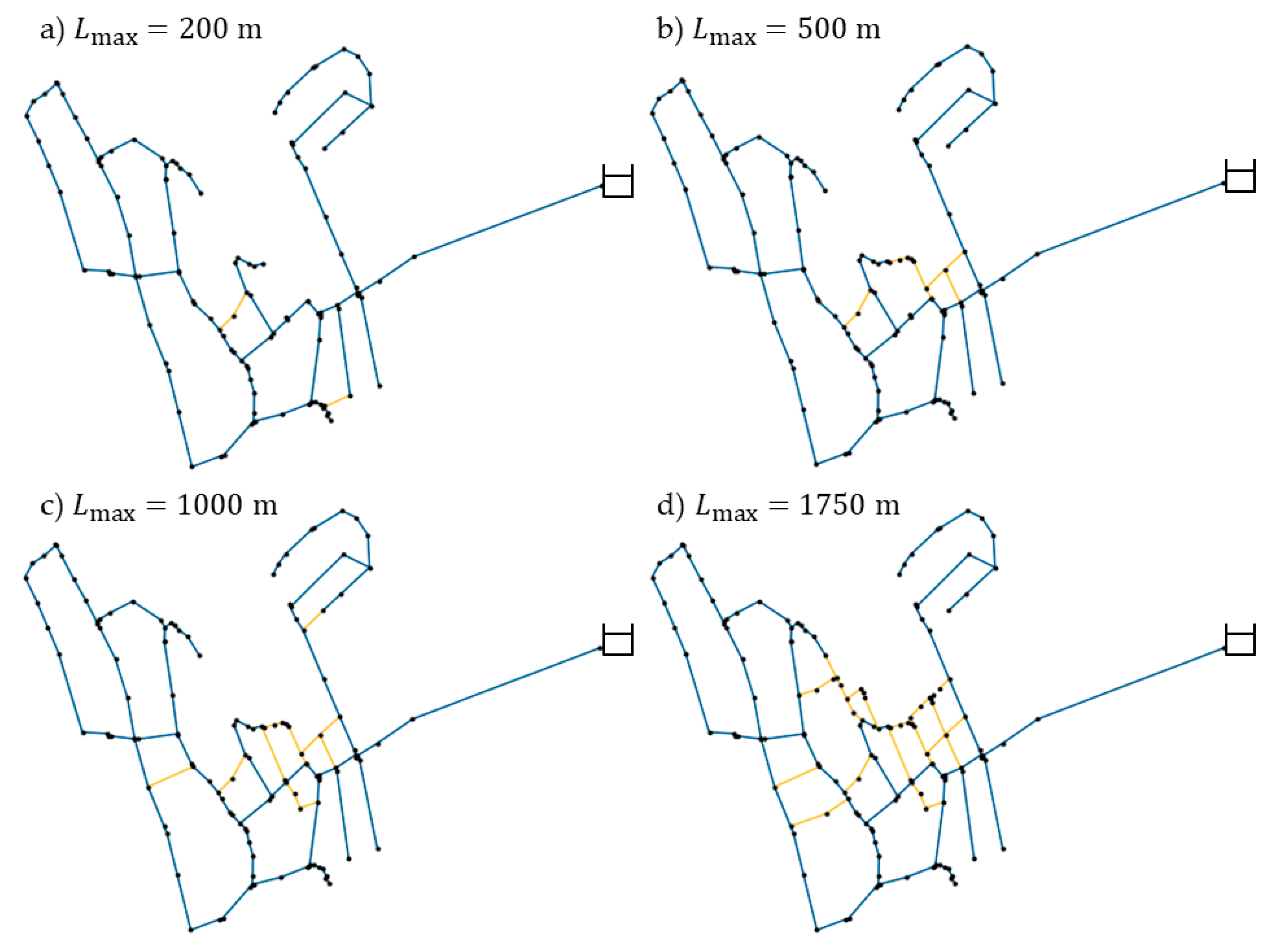
to determine the adapted WDS’s enhanced resilience under consideration of a specific investment budget, which can be varied as any positive real number including zero
. For a set pipe diameter, the costs are assumed to be linearly dependent on the overall pipe length added, since they consist of material costs and construction costs, both approximately proportional to the length of the pipe. Therefore, the variation of this Parameter
allows the determination of a Pareto front for the WDS’s resilience under varying maximum overall pipe lengths added to the existing WDS. This is shown in detail in the Results,
Section 3.
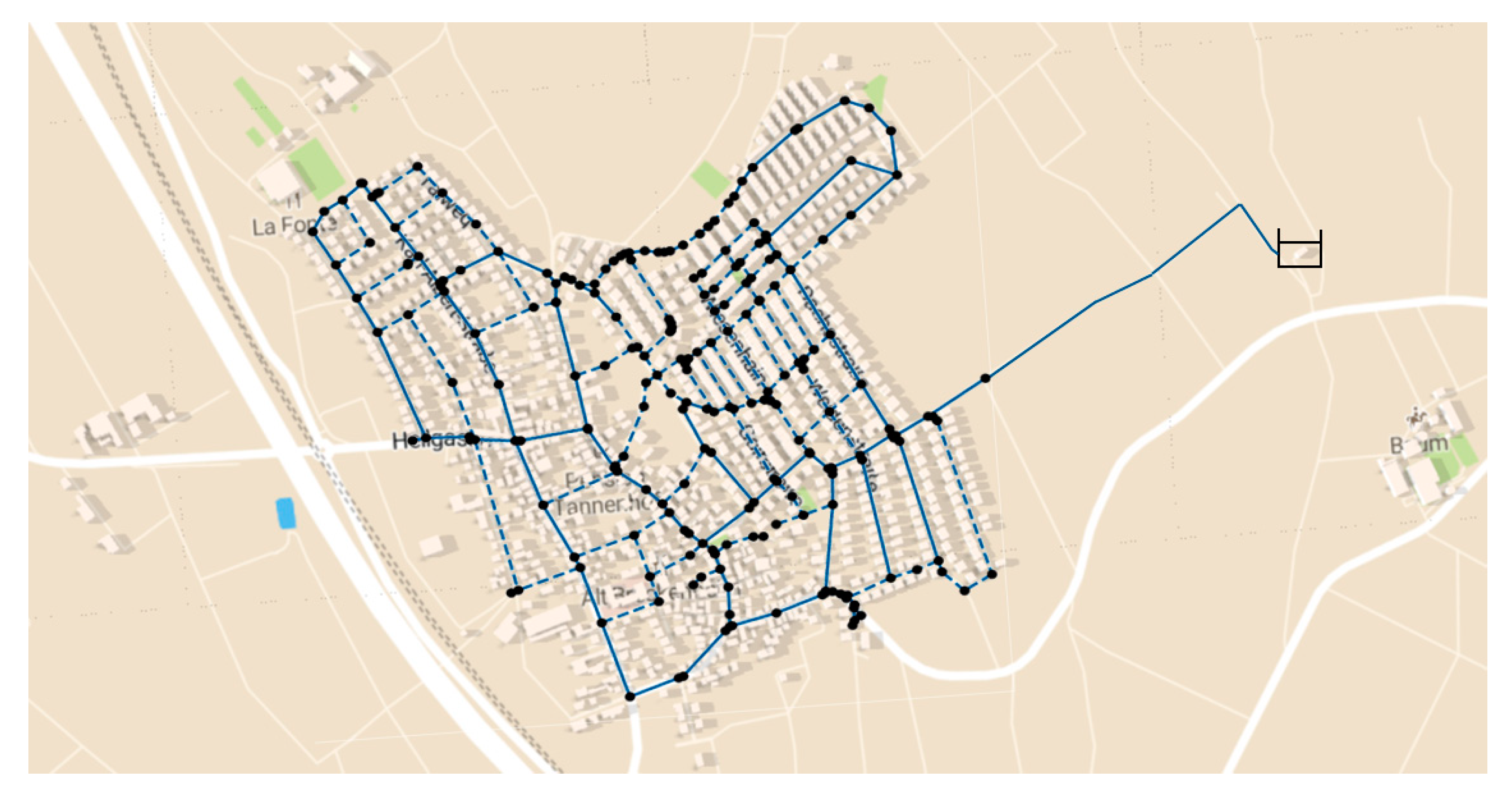
The remaining parameters of the optimization program are given by the existing WDS and the urban structure it is embedded in and are determined in the complex preprocessing of the optimization program. First, the main line WDS is determined from the existing overall WDS by making use of a cut-off criterion for the pipe diameter. This main line WDS is further processed by merging the demand of consumer nodes locally, i.e., , so that the overall demand is still true to the original WDS but the number of consumer nodes is reduced and therefore the computational expenses can be reduced in the subsequent optimization. For this main line WDS the edges are noted in the matrix . To determine the edges of the maximum possible WDS, OpenStreetMap data for the district containing the existing WDS are studied in combination with the existing WDS. By doing so all streets or pathways in which a pipe does not already lie are added as an edge to the existing WDS. This maximum possible WDS is represented by . For all possible additional edges, the important pipe characteristics, i.e., diameter, length and roughness, are chosen consistently to further diminish computational expenses. The length of the edges can be extracted from the OpenStreetMap data while diameter and roughness are chosen according to the typical pipe characteristics of newer pipes in the existing WDS. With this information, the hydraulic resistance of each edge in the maximum possible WDS can be determined.
Additionally, for this maximum possible WDS the critical transfer node and the maximum number of shortest paths to be considered in the resilience assessment of 1% accuracy can be determined. This limit of 1% accuracy can be adapted in the preprocessing. Subsequently, the -shortest paths for the existing WDS are heuristically identified, making use of Yen’s K-shortest path algorithm. For the maximum possible WDS ideally all possible paths with less hydraulic resistance than the highest hydraulic resistance path should be determined, as all these paths can increase the WDS’s resilience. Since this is computationally very expensive, a cut-off of -shortest paths for the maximum possible WDS has to be identified. This number varies with the size of the maximum possible WDS given by its consumer nodes and with the number of edges. The undertaken cut-off of the number of shortest paths considered for further optimization leads to limitation of the possible solution space but makes the problem feasible. Therefore, global optimization is only ensured if the feeding paths’ cut-off is worse than the already existing feeding paths. To further decrease computational expenses, this fact is made use of by cutting off the computation of any further feeding paths once the highest hydraulic resistance feeding path of the maximum possible WDS exceeds the highest hydraulic resistance feeding path of the existing WDS. To ensure that all -shortest paths of the existing WDS are considered in the optimization, the determined -shortest paths for the maximum possible WDS are complemented by all computed paths of the existing WDS which are not already part of the -shortest paths for the maximum possible WDS. The complemented -shortest paths for the maximum possible WDS is then used to calculate the conductance for each path.
Following, the optimization program, Equations (5)–(11) can be set up and solved. The objective is the maximization of resilience when a fixed length of overall pipe addition is allowed (Objective 5). The constraint linking the choice of pipes to be added to the existing WDS and therefore the shortest possible paths feeding a consumer node is given by Constraint 6. This constraint states that all edges making up a possible feeding path have to be part of either the existing WDS or have to be added to the WDS. The length of the sum of all added pipes is further restricted by twice the maximum length of the sum of all added pipes, as the undirected nature of the WDS allows for the addition of an edge connecting node
and
and vice versa (Constraint 7). This interrelation is stated in Constraint 8. Thoughts on the physical feasibility of the addition of pipes is given by Constraint 9, as pipes may only be added if they are part of the maximum possible WDS but not already part of the existing WDS. To pre-limit the pipes under consideration to be added to the existing WDS for a certain maximum cost of
, all pipes longer than
are directly eliminated from the set of pipes under consideration (Constraint 10). It is also ensured that only the best possible
-shortest paths of the adapted WDS are considered for the resilience assessment of the adapted WDS (Constraint 11).
subject to
As stated earlier, the global optimization of the solution highly depends on the computational capacities available in preliminary examination of the solution space during preprocessing, when determining the shortest paths of the maximum possible WDS. Therefore, the distinction between consumer nodes and junction nodes is of importance, as only nodes with a demand, i.e., consumer nodes, are considered in the customized resilience index introduced in Equation (1). Junction nodes do not have an external consumer, but only allow for flow to be distributed to the neighboring edges.
This optimization model assists decision-makers in how to adapt an existing main line WDS for optimal resilience improvement for a set investment budget, taking into consideration the physical feasibility of the solution. When calculated for different instances of the same WDS, but with different investment budgets in mind, a Pareto front for the cost-benefit analysis can be determined. This also allows for an analysis of the maximum achievable resilience for the present urban structure.