Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves
Abstract
1. Introduction
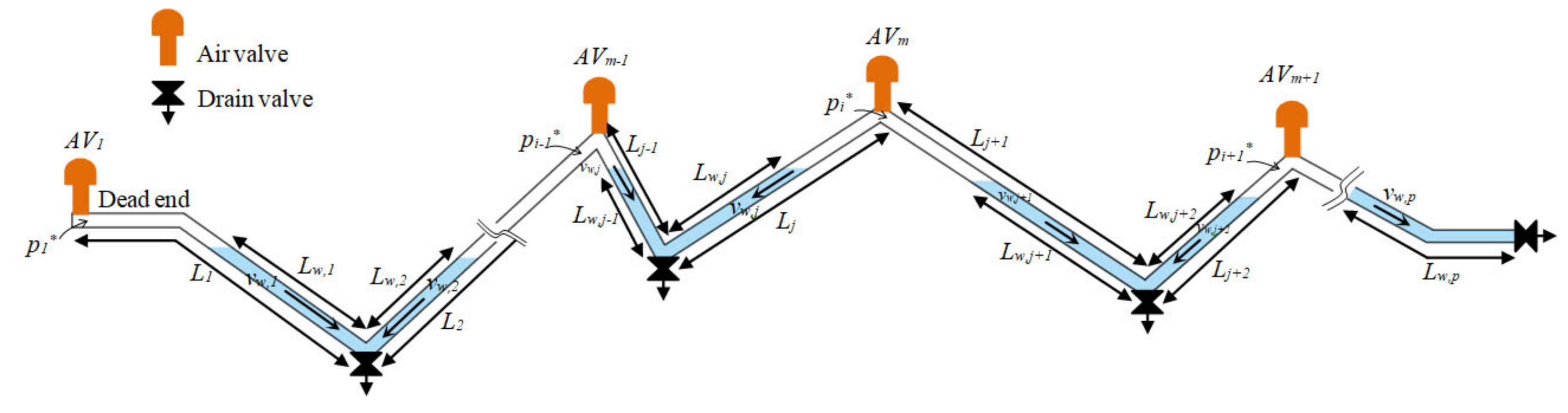
2. Mathematical Model
- Bernoulli´s equation:
- : water velocity, m/s.
- A: cross-sectional area of a pipeline, m2.
- : water flow, m3/s.
- : absolute pressure of trapped air pocket i, Pa.
- : atmospheric pressure (101,325 Pa).
- : water density at atmospheric conditions, kg/m3.
- : water column j, m.
- : gravity acceleration, 9.81 m/s2.
- : friction factor.
- : gravity term of the water column, m.: flow factor of the drain valve v, m3/s/m0.5.
- : internal pipe diameter of a pipeline, m.
- : drain valve loss, m.
- Piston formulation
- Polytropic equation
- : polytropic coefficient (dimensionless parameter).
- : air density at atmospheric conditions (1.205 kg/m3).
- : cross-sectional area of the air valve o for injecting air, m2.
- : air density of the entrapped air pocket i, kg/m3.
- : air velocity entering by the air valve o, m/s.
- Continuity equation of trapped air
- Air valve capacity formulation
- : injected air flow by the air valve o, m3/s.
- : admission coefficient of the air valve o.
3. Verification
3.1. Experimental Facility and Recorded Information
3.2. Equations
- Bernoulli’s equation for draining column 1
- 2.
- Piston-flow equation applied to air–water interface 1
- 3.
- Bernoulli’s equation for draining column 2
- 4.
- Piston-flow equation applied to air–water interface 2
- 5.
- Polytropic equation applied to air pocket 1
- 6.
- Continuity equation applied to air pocket 1
- 7.
- Air valve 1 capacity
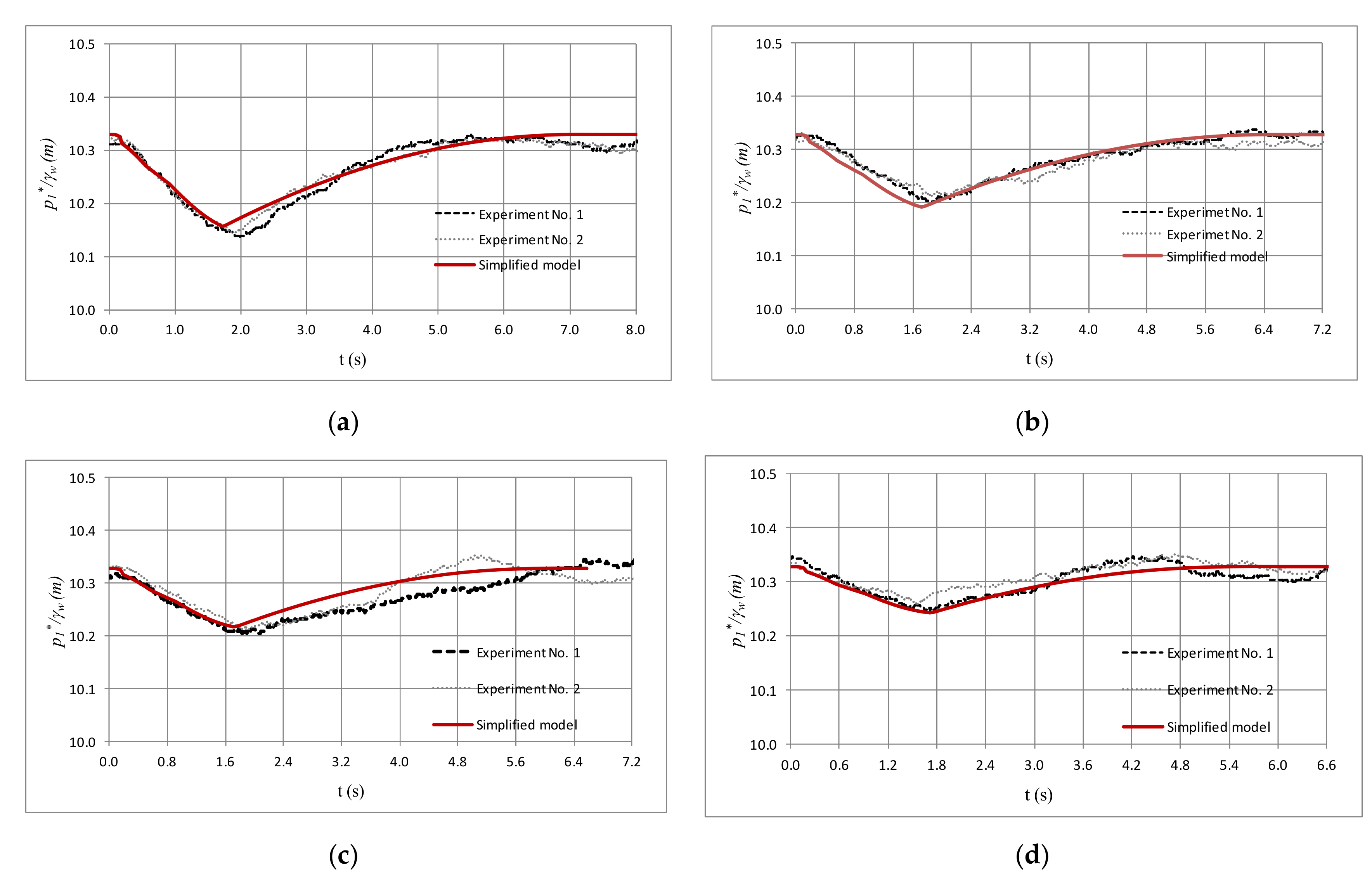
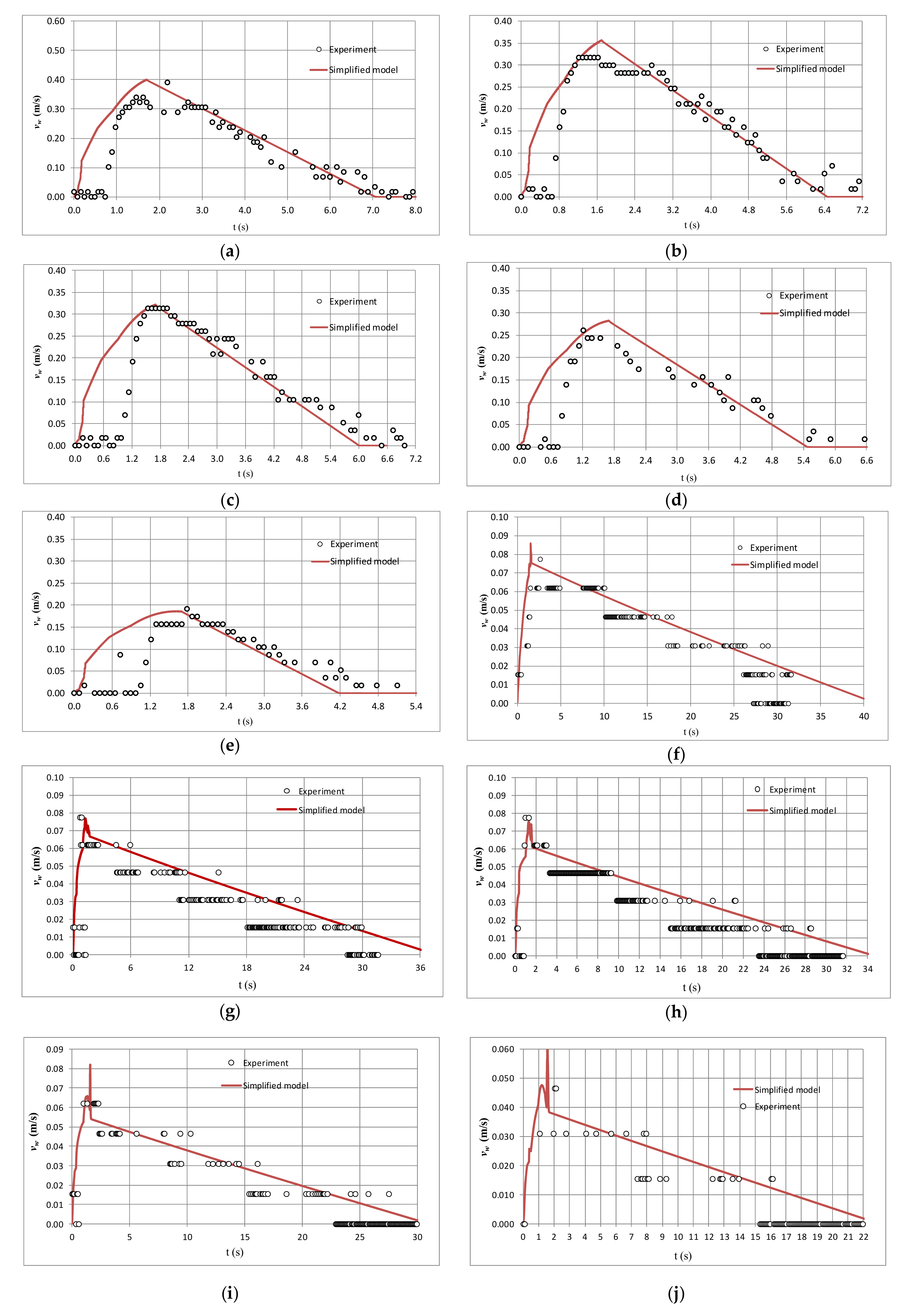
3.3. Comparison with Experimental Measurements
3.4. Comparison with an Inertial Model
4. Conclusions and Recommendations
Author Contributions
Funding
Conflicts of Interest
References
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Hydraulic Modeling during Filling and Emptying Processes in Pressurized Pipelines: A Literature Review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Iglesias-Rey, P.L.; Mora-Melia, D. Transient Phenomena during the Emptying Process of a Single Pipe with Water-Air Interaction. J. Hydraul. Res. 2019, 57, 318–326. [Google Scholar] [CrossRef]
- Tijsseling, A.; Hou, Q.; Bozkus, Z.; Laanearu, J. Improved One-Dimensional Models for Rapid Emptying and Filling of Pipelines. J. Press. Vessel Technol. 2016, 138, 031301. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Subatmospheric Pressure in a Water Draining Pipeline with an Air Pocket. Urban Water J. 2018, 15, 346–352. [Google Scholar] [CrossRef]
- Ramezani, L.; Karney, B.; Malekpour, A. Encouraging Effective Air Management in Water Pipelines: A Critical Review. J. Water Resour. Plan. Manag. 2016, 142, 04016055. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D. Experimental Investigation of Entrapped Air Pocket in a Partially Full Water Pipe. J. Hydraul. Res. 2013, 51, 469–474. [Google Scholar] [CrossRef]
- Carlos, M.; Arregui, F.J.; Cabrera, E.; Palau, C.V. Understanding Air Release through Air Valves. J. Hydraul. Eng. 2011, 137, 461–469. [Google Scholar] [CrossRef]
- American Water Works Association (AWWA). Manual of Water Supply Practices-M51: Air-Release, Air-Vacuum, and Combination Air Valves, 1st ed.; American Water Works Association: Denver, CO, USA, 2001. [Google Scholar]
- Bianchi, A.; Mambretti, S.; Pianta, P. Practical Formulas for the Dimensioning of Air Valves. J. Hydraul. Eng. 2007, 133, 1177–1180. [Google Scholar] [CrossRef]
- Ramezani, L.; Karney, B.; Malekpour, A. The Challenge of Air Valves: A Selective Critical Literature Review. J. Water Resour. Plan. Manag. 2016, 141, 04015017. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Experimental and Numerical Analysis of a Water Emptying Pipeline Using Different Air Valves. Water 2017, 9, 98. [Google Scholar] [CrossRef]
- Koppel, T.; Laanearu, J.; Annus, I.; Raidmaa, M. Using Transient Flow Equations for Modelling of Filling and Emptying of Large-Scale Pipeline. In Proceedings of the 12th Annual Conference on Water Distribution Systems Analysis (WDSA), Tucson, AZ, USA, 12–15 September 2010; American Society of Civil Engineers: Reston, VA, USA, 2010. [Google Scholar]
- Laanearu, J.; Annus, I.; Koppel, T.; Bergant, A.; Vučkovič, S.; Hou, Q.; van’t Westende, J.M.C. Emptying of Large-Scale Pipeline by Pressurized Air. J. Hydraul. Eng. 2012, 138, 1090–1100. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Rigid Water Column Model for Simulating the Emptying Process in a Pipeline Using Pressurized Air. J. Hydraul. Eng. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Closure to “Rigid Water Column Model for Simulating the Emptying Process in a Pipeline Using Pressurized Air”. J. Hydraul. Eng. 2020, 146, 07020002. [Google Scholar]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. A Parametric Sensitivity Analysis of Numerically Modelled Piston-Type Filling and Emptying of an Inclined Pipeline with an Air Valve. In Proceedings of the 13th International Conference on Pressure Surges, Bordeaux, France, 14–16 November 2018; BHR Group: Bordeaux, France, 2018. [Google Scholar]
- Vasconcelos, J.G.; Wright, S.J. Rapid Flow Startup in Filled Horizontal Pipelines. J. Hydraul. Eng. 2008, 134, 984–992. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Klaver, P.R.; Lautenbach, D.J. Flow Regime Transition Simulation Incorporating Entrapped Air Pocket Effects. Urban Water J. 2015, 6, 488–501. [Google Scholar] [CrossRef]
- Wang, L.; Wang, F.; Lei, X. Investigation on Friction Models for Simulation of Pipeline Filling Transients. J. Hydraul. Res. 2018, 56, 888–895. [Google Scholar] [CrossRef]
- Malekpour, A.; Karney, B.W.; Nault, J. Physical Understanding of Sudden Pressurization of Pipe Systems with Entrapped Air: Energy Auditing Approach. J. Hydraul. Eng. 2016, 142, 04015044. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Mora-Meliá, D.; Salgueiro, Y. Quasi-static Flow Model for Predicting the Extreme Values of Air Pocket Pressure in Draining and Filling Operations in Single Water Installations. Water 2020, 12, 664. [Google Scholar] [CrossRef]
- Wylie, E.; Streeter, V. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Graze, H.R.; Megler, V.; Hartmann, S. Thermodynamic Behaviour of Entrapped Air in an Air Chamber. In Proceedings of the 7th International Conference on Pressure Surges and Fluid Transients in Pipelines and Open Channels, Harrogate, UK, 16–18 April 1996. [Google Scholar]
- León, A.; Ghidaoui, M.; Schmidt, A.; García, M. A Robust Two-equation Model for Transient-mixed Flows. J. Hydraul. Res. 2010, 48, 44–56. [Google Scholar] [CrossRef]
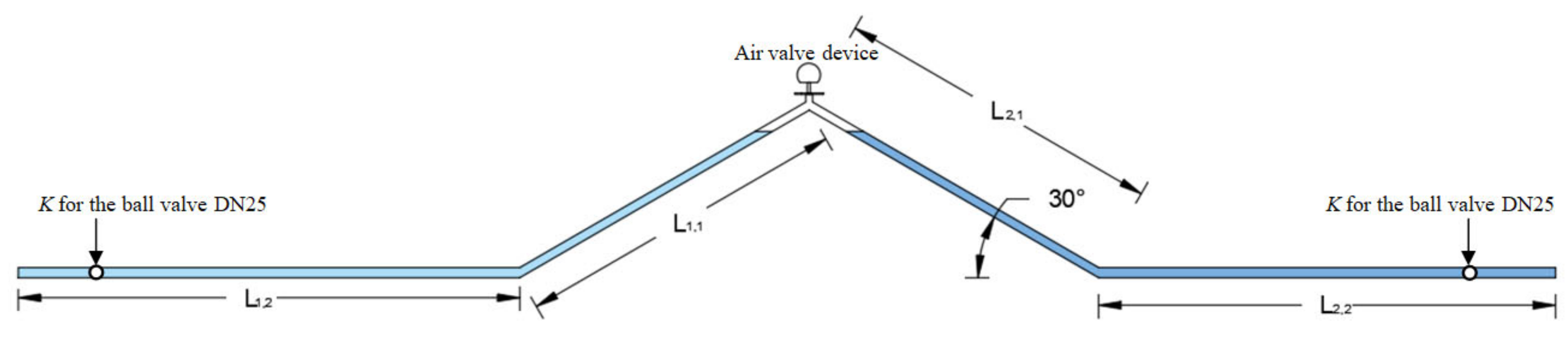

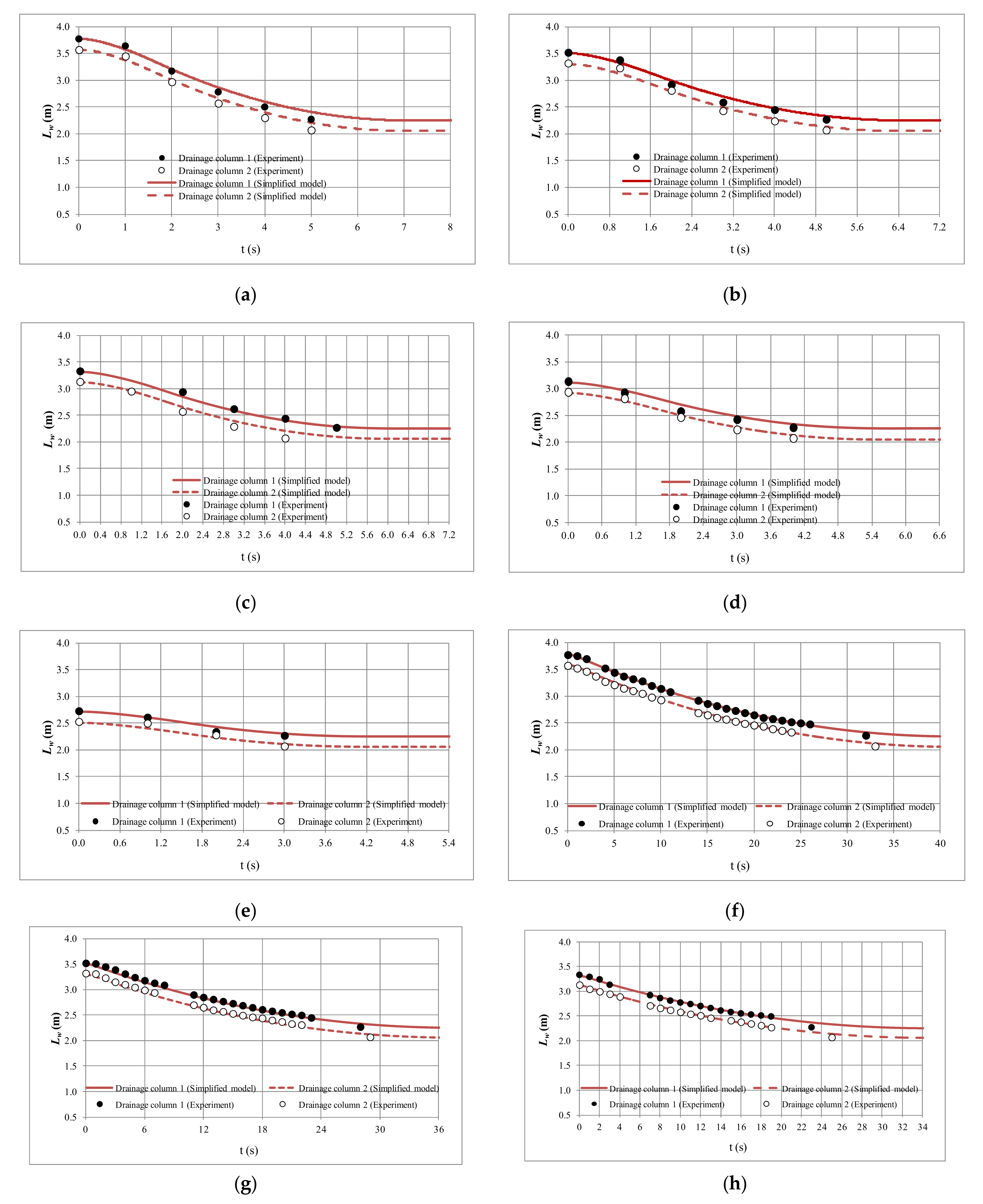
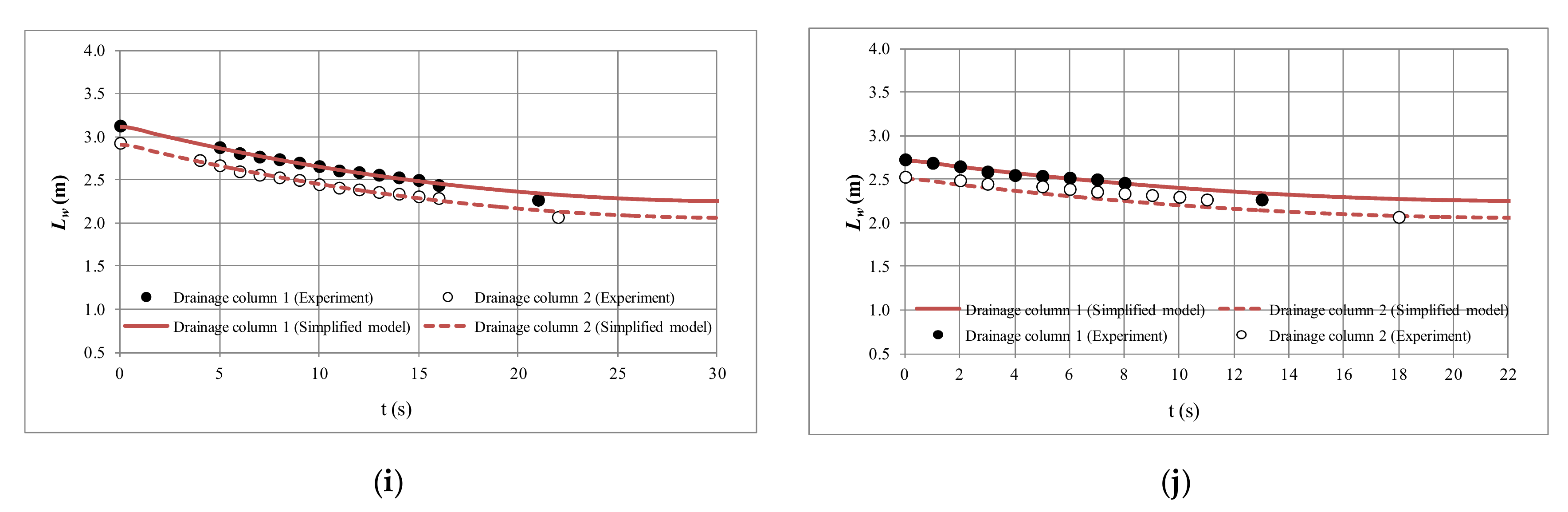
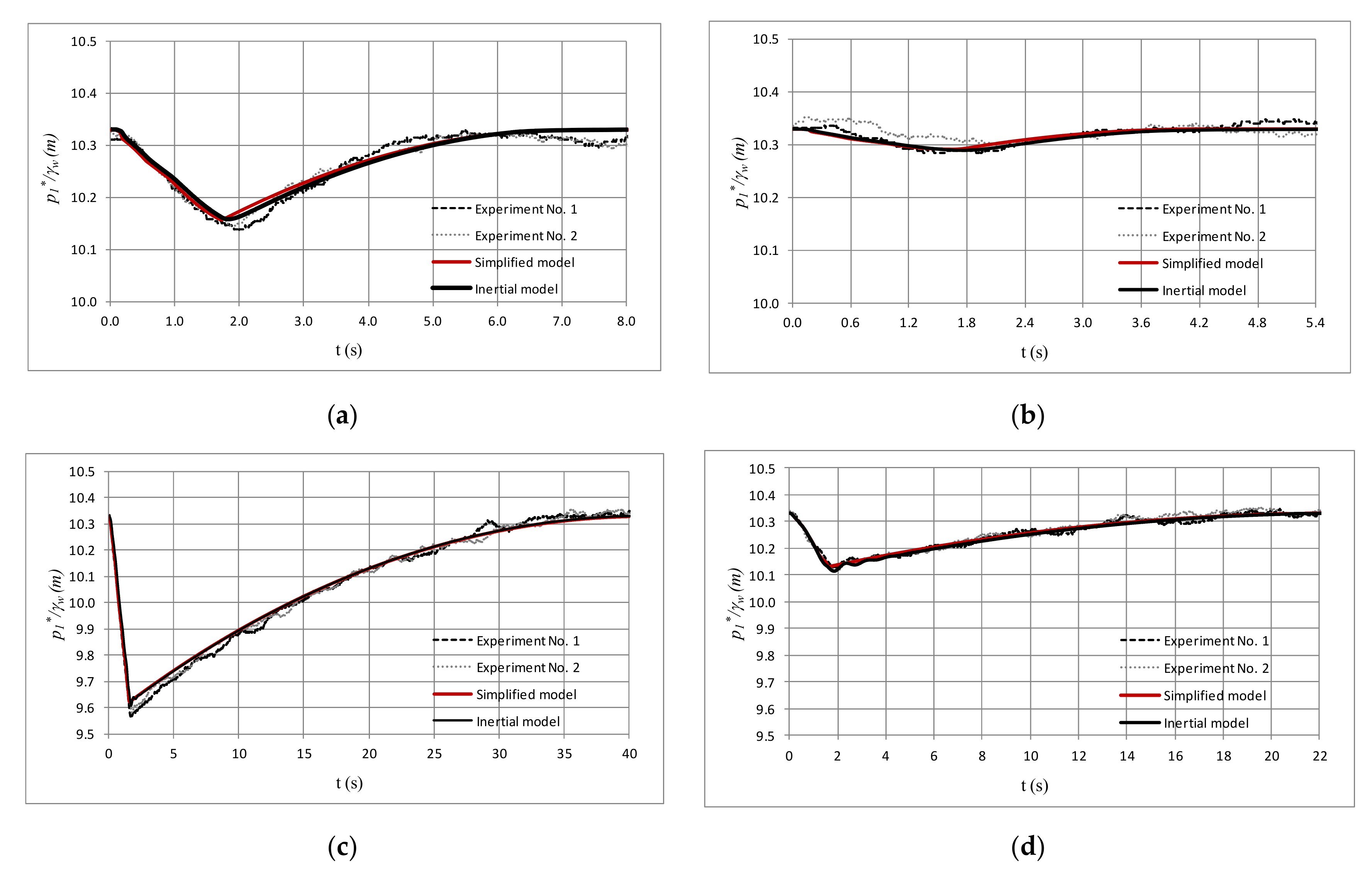
| Run No. | Air Pocket Size (m) | K × 103 (m3/s/m0.5) | f | Air valve Device | ||
|---|---|---|---|---|---|---|
| Model | Orifice Size (mm) | Cadm (-) | ||||
| 1 | 0.001 | 1.4 | 0.018 | D040 | 9.375 | 0.375 |
| 2 | 0.540 | |||||
| 3 | 0.920 | |||||
| 4 | 1.320 | |||||
| 5 | 2.120 | |||||
| 6 | 0.001 | S050 | 3.175 | 0.303 | ||
| 7 | 0.540 | |||||
| 8 | 0.920 | |||||
| 9 | 1.320 | |||||
| 10 | 2.120 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Quiñones-Bolaños, E.E.; Gatica, G.; Coronado-Hernández, J.R. Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves. Water 2020, 12, 2544. https://doi.org/10.3390/w12092544
Coronado-Hernández ÓE, Fuertes-Miquel VS, Quiñones-Bolaños EE, Gatica G, Coronado-Hernández JR. Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves. Water. 2020; 12(9):2544. https://doi.org/10.3390/w12092544
Chicago/Turabian StyleCoronado-Hernández, Óscar E., Vicente S. Fuertes-Miquel, Edgar E. Quiñones-Bolaños, Gustavo Gatica, and Jairo R. Coronado-Hernández. 2020. "Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves" Water 12, no. 9: 2544. https://doi.org/10.3390/w12092544
APA StyleCoronado-Hernández, Ó. E., Fuertes-Miquel, V. S., Quiñones-Bolaños, E. E., Gatica, G., & Coronado-Hernández, J. R. (2020). Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves. Water, 12(9), 2544. https://doi.org/10.3390/w12092544








