A Homogeneous Dataset for Rainfall Trend Analysis in the Calabria Region (Southern Italy)
Abstract
1. Introduction
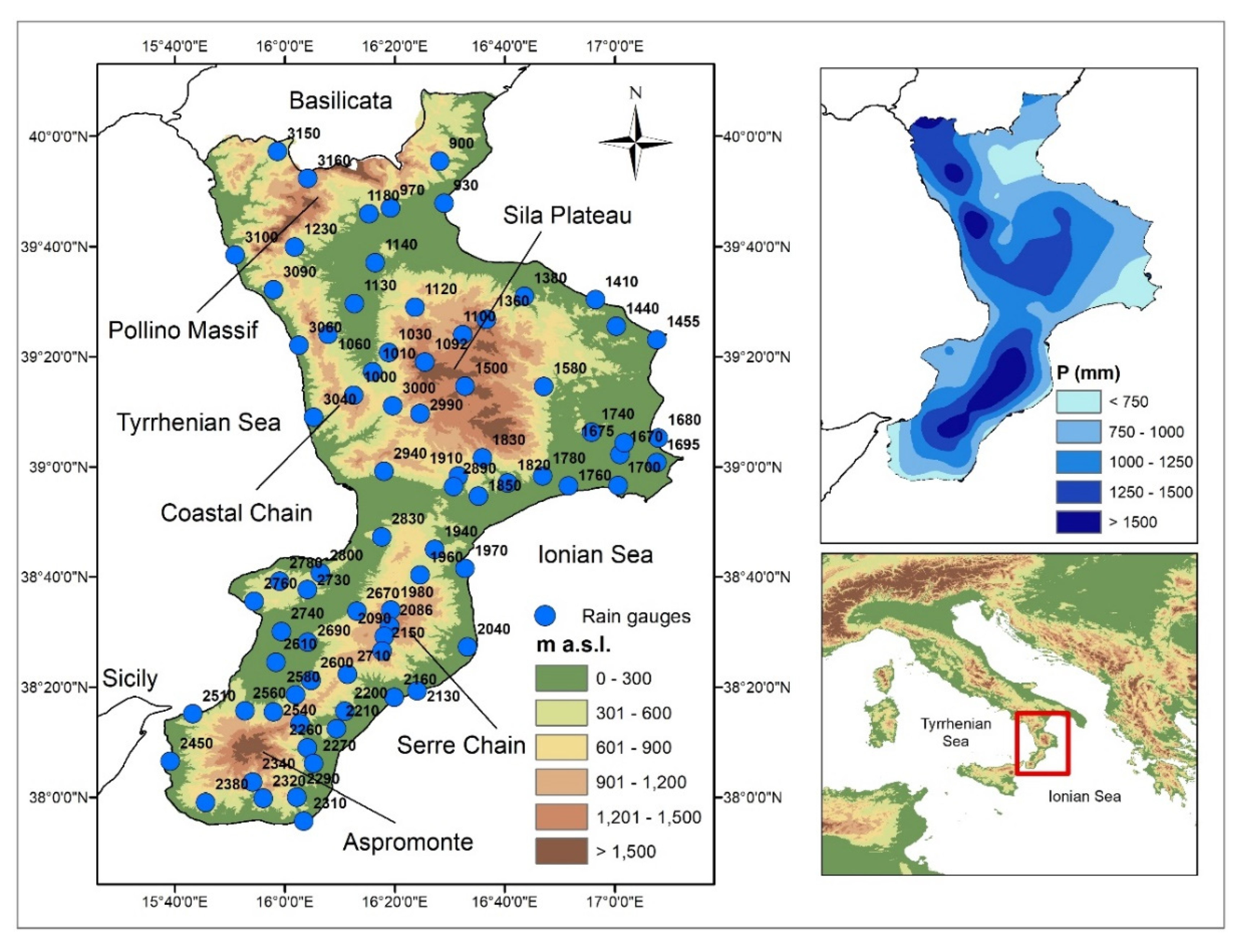
2. Study Area and Data
3. Methods
3.1. Homogenization Procedure
3.2. Trend Analysis
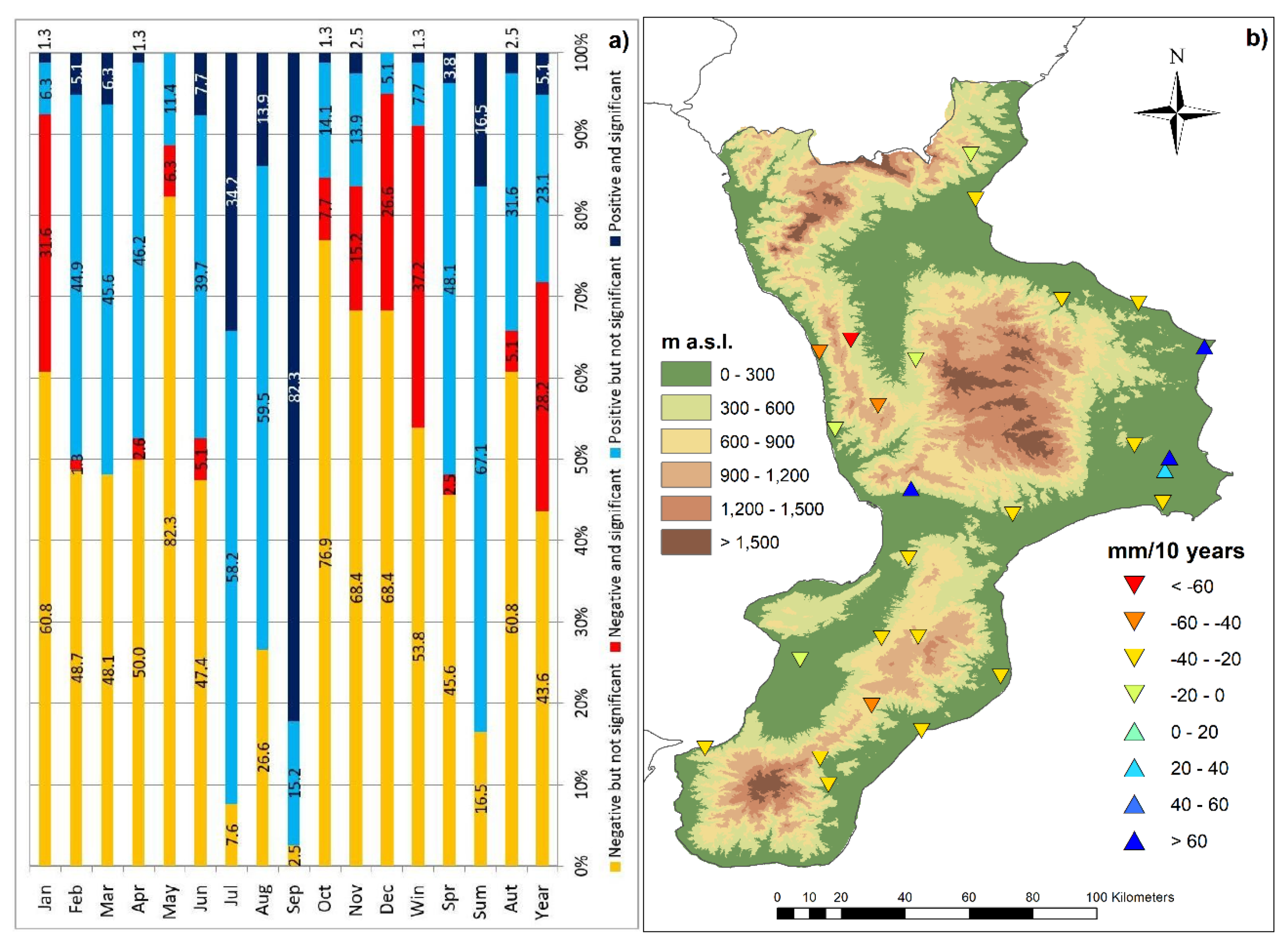
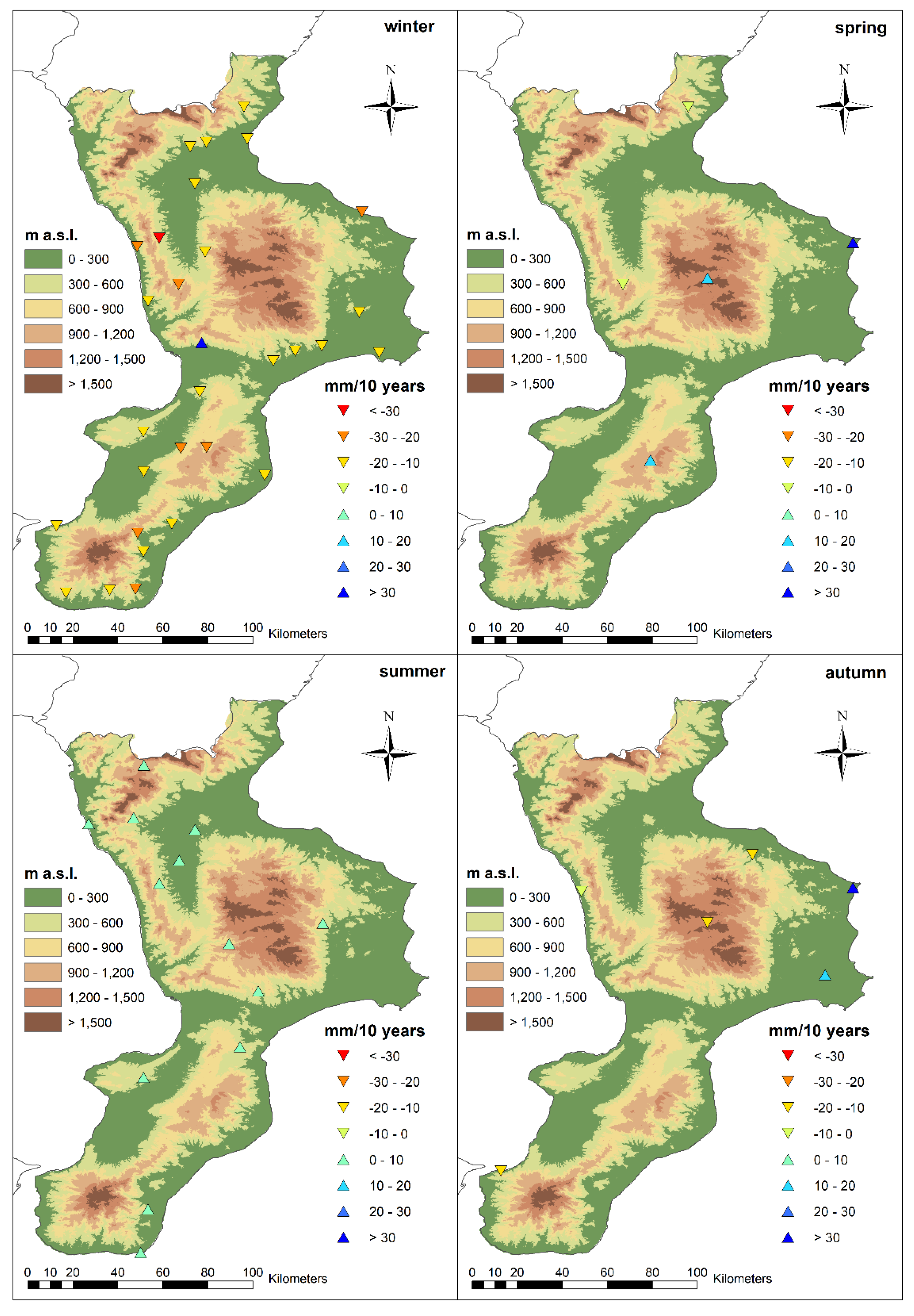
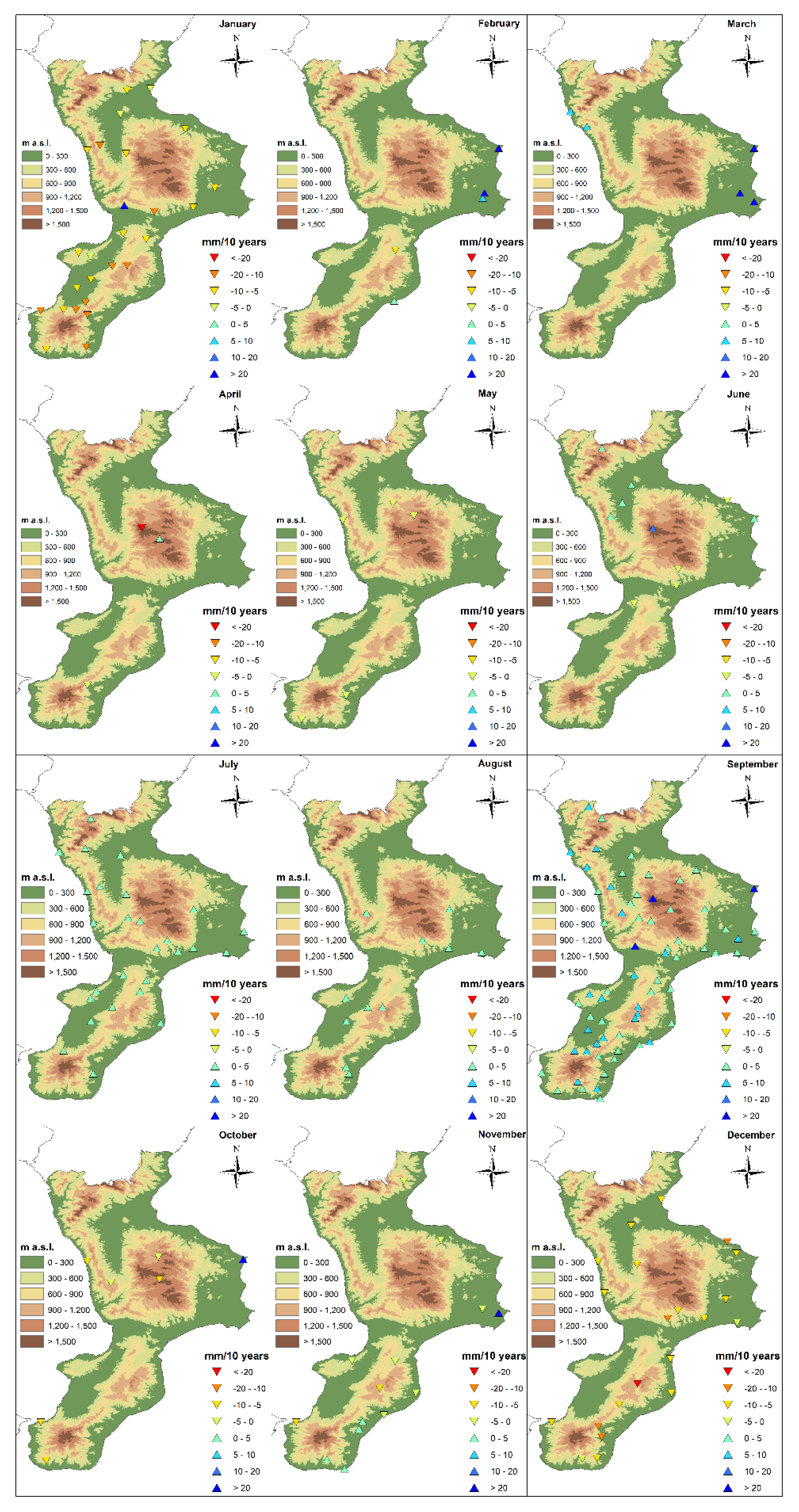
4. Results
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Elmeddahi, Y.; Mahmoudi, H.; Issaadi, A.; Goosen, M.F.A.; Ragab, R. Evaluating the effects of climate change and variability on water resources: A case study of the Cheliff basin in Algeria. Am. J. Eng. Appl. Sci. 2016, 9, 835–845. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Gaudio, R. Spatial and temporal variability of daily precipitation concentration in the Sardinia region (Italy). Int. J. Climatol. 2019, 39, 5006–5021. [Google Scholar] [CrossRef]
- del Rio, S.; Herrero, L.; Fraile, R.; Penas, A.P. Spatial distribution of recent rainfall trends in Spain (1961–2006). Int. J. Climatol. 2011, 31, 656–667. [Google Scholar]
- Caloiero, T.; Caloiero, P.; Frustaci, F. Long-term precipitation trend analysis in Europe and in the Mediterranean basin. Water Environ. J. 2018, 32, 433–445. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Maheras, P.; Tolika, K.; Anagnostopoulou, C.; Vafiadis, M.; Patrikas, I.; Flocas, H. On the relationships between circulation types and changes in rainfall variability in Greece. Int. J. Climatol. 2001, 24, 1695–1712. [Google Scholar] [CrossRef]
- Altin, T.B.; Barak, B. Changes and trends in total yearly precipitation of the Antalya District, Turkey. Procedia Soc. Behav. 2014, 120, 586–599. [Google Scholar] [CrossRef]
- Shohami, D.; Dayan, U.; Morin, E. Warming and drying of the eastern Mediterranean: Additional evidence from trend analysis. J. Geophys. Res. 2011, 116, D22101. [Google Scholar] [CrossRef]
- Ziv, B.; Saaroni, H.; Pargament, R.; Harpaz, T.; Alpert, P. Trends in rainfall regime over Israel, 1975–2010, and their relationship to large-scale variability. Reg. Environ. Chang. 2014, 14, 1751–1764. [Google Scholar] [CrossRef]
- Scorzini, A.R.; Leopardi, M. Precipitation and temperature trends over central Italy (Abruzzo Region): 1951–2012. Theor. Appl. Climatol. 2019, 135, 959–977. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Lee, H.S.; Zardi, D. Analysis of Rainfall Trends and Extreme Precipitation in the Middle Adriatic Side, Marche Region (Central Italy). Water 2019, 11, 1948. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Trend detection of annual and seasonal rainfall in Calabria (Southern Italy). Int. J. Climatol. 2011, 31, 44–56. [Google Scholar] [CrossRef]
- Diodato, N. Climatic fluctuations in southern Italy since 17th century: Reconstruction with precipitation records at Benevento. Clim. Chang. 2007, 80, 411–431. [Google Scholar] [CrossRef]
- Piccarreta, M.; Capolongo, D.; Boenzi, F. Trend analysis of precipitation and drought in Basilicata from 1923 to 2000 within a Southern Italy context. Int. J. Climatol. 2004, 24, 907–922. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Climatol. 2016, 126, 113–129. [Google Scholar] [CrossRef]
- Coscarelli, R.; Gaudio, R.; Caloiero, T. Climatic trends: An investigation for a Calabrian basin (southern Italy). In The Basis of Civilization–Water Science? Rodda, J.C., Ubertini, L., Eds.; IAHS Publ: Wallingford, UK, 2004; pp. 255–266. [Google Scholar]
- Montaldo, N.; Sarigu, A. Potential links between the North Atlantic Oscillation and decreasing precipitation and runoff on a Mediterranean area. J. Hydrol. 2017, 553, 419–437. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Gaudio, R.; Leonardo, G.P. Precipitation trend and concentration in the Sardinia region. Theor. Appl. Climatol. 2019, 137, 297–307. [Google Scholar] [CrossRef]
- Della-Marta, P.M.; Collins, D.; Braganza, K. Updating Australia’s high quality annual temperature dataset. Aust. Meteorol. Mag. 2004, 53, 75–93. [Google Scholar]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Precipitation variability and change in the Calabria region (Italy) from a high resolution daily dataset. Int. J. Climatol. 2012, 32, 57–73. [Google Scholar] [CrossRef]
- Mamara, A.; Argiriou, A.A.; Anadranistakis, M. Homogenization of mean monthly temperature time series of Greece. Int. J. Climatol. 2013, 33, 2649–2666. [Google Scholar] [CrossRef]
- Conrad, V.; Pollak, C. Methods in Climatology; Harvard University Press: Cambridge, MA, USA, 1950. [Google Scholar]
- Alexandersson, H. A homogeneity test applied to precipitation data. Int. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Craddock, J.M. Methods of comparing annual rainfall records for climatic purposes. Weather 1979, 34, 332–346. [Google Scholar] [CrossRef]
- Caussinus, H.; Mestre, O. New mathematical tools and methodologies for relative homogeneity testing. In Proceedings of the Seminar for Homogenization of Surface Climatological Data, Budapest, Hungary, 6–12 October 1996. [Google Scholar]
- Szentimrey, T. Multiple Analysis of Series for homogenization (MASH). In Proceedings of the Second Seminar for Homogenization of Surface Climatological Data, Budapest, Hungary, 9–13 November 1998. [Google Scholar]
- Szentimrey, T. Manual of Homogenization Software MASHv3.02; Hungarian Meteorological Service: Budapest, Hungary, 2007. [Google Scholar]
- Szentimrey, T. Development of MASH homogenization procedure for daily data. In Proceedings of the Fifth Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 29 May–2 June 2006. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Caloiero, T.; Callegari, G.; Cantasano, N.; Coletta, V.; Pellicone, G.; Veltri, A. Bioclimatic analysis in a region of southern Italy (Calabria). Plant Biosyst. 2016, 150, 1282–1295. [Google Scholar] [CrossRef]
- Guijarro, J.A. User’s Guide to Climatol. An R Contributed Package for Homogenization of Climatological Series. Report State Meteorological Agency; Balearic Islands Office: Palma de Mallorca, Spain, 2014. Available online: http://www.climatol.eu/climatol-guide.pdf (accessed on 23 June 2020).
- Yazici, C.; Yozgatligil, C.; Batmaz, I. A simulation study on theperformances of homogeneity tests applied in meteorological studies. In Proceedings of the ICACM—International Conference on Applied and Computational Mathematics, Ankara, Turkey, 3–6 October 2012. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Publishing Company: New York, NY, USA, 1962. [Google Scholar]
- Fioravanti, G.; Piervitali, E.; Desiato, F. A new homogenized daily data set for temperature variability assessment in Italy. Int. J. Climatol. 2019, 39, 5635–5654. [Google Scholar] [CrossRef]
- Piccarreta, M.; Pasini, A.; Capolongo, D.; Lazzari, M. Changes in daily precipitation extremes in the Mediterranean from 1951 to 2010: The Basilicata region, southern Italy. Int. J. Climatol. 2013, 33, 3229–3248. [Google Scholar] [CrossRef]
| ID | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Year | Win | Spr | Sum | Aut |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 900 | −4.5 | −1.2 | −1.7 | −0.9 | −1.5 | −1.2 | 0.0 | 0.6 | 0.4 | −0.2 | −6.3 | −4.0 | −16.8 | −13.4 | −6.3 | 0.9 | −5.1 |
| 930 | −4.5 | −0.7 | 1.9 | −0.1 | −1.5 | 0.0 | 0.2 | 0.0 | 1.2 | −2.5 | −2.4 | −6.4 | −22.3 | −17.4 | −2.0 | 0.2 | −4.0 |
| 970 | −5.4 | −0.6 | 1.5 | −0.9 | −1.7 | −0.4 | 0.7 | 0.0 | 0.4 | 0.0 | −1.8 | −4.0 | −9.1 | −11.9 | −2.0 | 0.5 | −1.5 |
| 1000 | −7.6 | −5.0 | −1.3 | −3.0 | −2.7 | −0.6 | 0.1 | 1.1 | 5.5 | −4.6 | 1.1 | −6.8 | −50.0 | −22.2 | −9.7 | −0.1 | 0.0 |
| 1010 | −0.9 | −2.6 | −0.7 | −1.8 | −1.3 | 0.2 | 0.3 | 0.0 | 3.1 | −3.0 | −1.5 | −4.0 | −11.1 | −9.7 | −3.3 | 1.0 | −0.9 |
| 1030 | −5.0 | −1.9 | 0.9 | 0.0 | −0.9 | 0.4 | 0.4 | 0.5 | 4.5 | −2.9 | −0.3 | −6.0 | −17.2 | −14.4 | 1.6 | 2.3 | −1.0 |
| 1060 | −16.1 | −8.0 | −3.0 | 1.5 | −2.7 | 1.4 | 0.9 | 0.0 | 6.6 | −5.5 | −7.8 | −7.8 | −64.6 | −45.1 | −4.3 | 5.2 | −13.1 |
| 1092 | 25.3 | 5.5 | 31.5 | −23.9 | −5.6 | 11.1 | −5.4 | −5.3 | 20.6 | −16.2 | −10.7 | −13.6 | 17.9 | −10.4 | 24.5 | −2.4 | −8.0 |
| 1100 | −7.4 | −1.3 | 5.1 | 0.9 | −2.7 | −1.1 | 0.2 | 0.6 | 2.2 | −3.8 | −3.3 | 0.8 | −12.9 | −9.6 | 4.5 | 0.8 | −7.7 |
| 1120 | −2.2 | −2.3 | 3.6 | 1.1 | −2.2 | 0.0 | 0.3 | 0.2 | 2.8 | −1.0 | −2.4 | −3.9 | 3.5 | −6.6 | 3.9 | 0.9 | −1.4 |
| 1130 | −1.5 | −0.9 | 0.4 | 1.2 | −0.5 | 0.9 | 0.2 | 0.2 | 3.2 | −1.5 | −1.6 | −2.1 | 4.7 | −5.6 | 1.7 | 2.9 | 0.7 |
| 1140 | −4.0 | −2.8 | 0.4 | −0.2 | −0.3 | 1.0 | 0.7 | 0.0 | 3.6 | −2.2 | −3.2 | −6.9 | −12.3 | −13.4 | −0.5 | 4.0 | −3.2 |
| 1180 | −3.3 | −1.4 | 1.3 | 0.2 | −1.1 | 0.3 | 0.5 | 0.2 | 1.5 | −0.1 | −2.9 | −2.6 | −8.7 | −12.8 | 0.6 | 0.8 | −1.0 |
| 1230 | −1.0 | −1.7 | 0.3 | 0.9 | −0.1 | 1.0 | 1.6 | 0.3 | 6.3 | −3.5 | 1.0 | −5.1 | 9.3 | −6.4 | 1.7 | 4.6 | 4.4 |
| 1360 | −2.0 | 0.6 | 2.8 | 0.0 | −1.2 | −0.1 | 0.0 | 0.3 | 3.3 | −2.4 | −3.6 | −1.6 | 0.1 | −8.6 | 4.2 | 0.1 | −8.0 |
| 1380 | −7.3 | 0.0 | 1.3 | −1.3 | −0.6 | 0.0 | 0.0 | 0.0 | 3.3 | −2.8 | −7.3 | −4.9 | −35.1 | −5.5 | −2.6 | 1.2 | −13.1 |
| 1410 | −3.0 | −3.3 | −2.3 | −1.0 | −1.1 | −0.8 | 0.0 | 0.0 | 2.0 | −2.8 | −2.9 | −10.8 | −39.0 | −22.0 | −3.3 | −1.7 | −2.8 |
| 1440 | −0.3 | 0.7 | 3.4 | −0.4 | −1.4 | −0.5 | 0.0 | 0.0 | 1.8 | −1.0 | −5.8 | −6.7 | −17.3 | −9.0 | 0.7 | 0.2 | −0.1 |
| 1455 | 16.4 | 35.7 | 35.3 | 2.3 | 3.3 | 2.5 | −0.2 | 0.0 | 40.4 | 54.4 | 42.0 | −10.7 | 238.6 | 58.6 | 46.9 | −1.7 | 151.3 |
| 1500 | −9.2 | 0.2 | 7.7 | 4.4 | −2.3 | −0.5 | 0.7 | 1.6 | 3.5 | −8.9 | −7.0 | 0.2 | −26.6 | −12.8 | 16.5 | 3.3 | −17.4 |
| 1580 | −4.0 | 0.8 | 0.6 | 0.8 | −0.8 | 0.3 | 0.4 | 0.9 | 2.9 | −0.3 | −6.1 | −4.9 | −4.2 | −1.0 | 2.7 | 3.2 | −5.6 |
| 1670 | −3.1 | 6.3 | 1.0 | 1.6 | −1.4 | 0.0 | 0.0 | 0.0 | 5.7 | −4.2 | 15.4 | −10.9 | 27.0 | −0.1 | 4.4 | −0.9 | 16.6 |
| 1675 | −4.6 | 34.6 | 43.2 | −3.4 | 3.3 | 0.6 | 0.1 | −2.0 | −3.2 | 4.9 | 46.8 | −20.8 | 158.7 | 62.7 | 40.0 | −8.2 | 48.6 |
| 1680 | −2.3 | 0.0 | 1.5 | 0.1 | 0.0 | 0.0 | 0.1 | 0.0 | 1.6 | 0.1 | −3.2 | −2.6 | 0.3 | −8.3 | 3.9 | 0.9 | 0.7 |
| 1695 | 10.4 | 25.6 | 48.9 | −6.0 | 1.3 | 0.6 | −0.1 | −0.2 | −6.7 | 29.6 | 34.9 | −23.2 | 51.5 | 44.7 | 32.7 | −4.5 | 38.9 |
| 1700 | −3.3 | −1.3 | −1.9 | 0.2 | −0.3 | −0.1 | 0.2 | 0.0 | 2.8 | −1.2 | −4.4 | −4.8 | −30.8 | −10.8 | −0.7 | 0.4 | −5.6 |
| 1740 | −6.3 | 0.4 | −0.5 | 0.2 | −0.9 | −0.4 | 0.0 | 0.0 | 4.0 | −0.4 | −5.2 | −6.3 | −26.7 | −12.3 | −0.9 | −0.5 | −2.6 |
| 1760 | −1.7 | 0.3 | 0.7 | −0.7 | −0.8 | −0.1 | 0.1 | 0.0 | 2.5 | −0.2 | −5.1 | −4.5 | −7.5 | −5.8 | 0.2 | 0.5 | −4.7 |
| 1780 | −6.5 | 0.3 | 1.1 | 0.0 | 0.4 | −0.5 | 0.6 | 0.6 | 3.7 | 1.2 | −1.8 | −7.0 | −5.1 | −16.8 | 2.3 | 1.8 | 2.7 |
| 1820 | −5.2 | −2.3 | 0.0 | 1.2 | −0.7 | 0.0 | 0.5 | 0.0 | 1.9 | 0.3 | −5.7 | −4.8 | −17.7 | −12.7 | 1.5 | 1.3 | −5.7 |
| 1830 | −3.1 | −1.0 | 0.2 | 1.8 | −1.0 | −2.3 | 1.6 | 2.0 | 3.8 | −2.2 | −5.5 | −6.8 | −7.3 | −12.1 | −0.8 | 3.0 | −5.1 |
| 1850 | −4.9 | −2.0 | −0.1 | −0.6 | −0.6 | −0.8 | 0.2 | 0.5 | 3.7 | −3.9 | −3.5 | −4.0 | −20.6 | −15.0 | −1.6 | 1.0 | −3.4 |
| 1910 | −4.5 | 2.1 | −2.5 | 0.0 | 0.3 | −0.6 | 1.4 | 1.1 | 3.7 | −2.7 | −2.2 | −10.5 | −15.0 | −8.6 | −2.2 | 3.7 | −2.5 |
| 1940 | −8.3 | 1.6 | −0.7 | 0.5 | 0.8 | 0.0 | 0.8 | 0.7 | 3.6 | −4.4 | −0.9 | −1.9 | −23.3 | −8.2 | 0.1 | 2.3 | −6.1 |
| 1960 | −3.6 | −6.2 | −2.8 | 0.4 | −0.4 | −0.6 | 0.9 | 0.6 | 4.9 | −3.7 | −7.1 | −3.2 | −11.6 | −10.8 | −1.7 | 1.0 | −5.8 |
| 1970 | −2.6 | 0.6 | 0.6 | 0.2 | −0.1 | −0.3 | 0.1 | 0.0 | 2.4 | −2.7 | −4.4 | −5.1 | −4.7 | −6.3 | 1.1 | 0.1 | −2.4 |
| 1980 | −11.1 | −4.5 | −4.9 | 0.7 | −1.5 | −0.8 | 0.5 | 2.0 | 6.3 | −2.6 | −7.0 | −7.7 | −32.5 | −22.6 | −3.2 | 0.2 | −0.5 |
| 2040 | −0.9 | 0.5 | 0.9 | −0.2 | −0.2 | 0.0 | 0.0 | 0.0 | 4.6 | −1.8 | −6.7 | −9.8 | −30.6 | −10.4 | 0.8 | 0.3 | −7.7 |
| 2086 | −3.9 | −0.3 | 5.6 | 3.9 | −0.6 | 0.9 | 0.7 | 0.6 | 5.3 | −2.4 | −6.6 | −25.3 | −12.8 | −11.4 | 13.6 | 2.6 | −8.2 |
| 2090 | −7.3 | −7.3 | −0.6 | −0.7 | −0.4 | −0.8 | 0.9 | 0.5 | 6.1 | −5.1 | −10.7 | −7.6 | −4.9 | −7.0 | −1.1 | 1.4 | −10.5 |
| 2130 | −0.4 | 4.6 | −1.2 | −0.7 | −0.8 | 0.0 | 0.0 | 0.0 | 5.7 | −6.4 | 3.2 | −0.2 | 6.6 | 8.2 | −2.6 | 1.7 | 3.4 |
| 2150 | −6.2 | −5.6 | −4.4 | 0.1 | −0.3 | −0.2 | 0.9 | 0.8 | 3.2 | −2.8 | −7.6 | −7.2 | −23.4 | −14.2 | −6.4 | 1.5 | −6.3 |
| 2160 | −0.7 | −0.1 | −1.2 | −0.8 | −1.1 | −0.3 | 0.0 | 0.0 | 2.7 | −0.8 | −5.9 | −4.1 | −24.0 | −6.5 | −3.7 | −1.2 | −3.4 |
| 2200 | −5.4 | −1.5 | −1.2 | −1.1 | −0.2 | 0.0 | 0.0 | 0.1 | 4.2 | 0.5 | −6.7 | −4.8 | −14.2 | −13.0 | −1.8 | 0.9 | 0.4 |
| 2210 | −3.4 | 1.8 | 0.6 | 0.7 | −0.7 | 0.1 | 0.1 | 0.0 | 3.8 | 1.7 | −6.6 | −4.4 | 0.7 | −7.0 | 1.0 | 1.4 | 4.8 |
| 2230 | −10.8 | −1.7 | −1.2 | −4.7 | −1.0 | 0.7 | 0.0 | 0.4 | 4.9 | −4.6 | −8.7 | −13.8 | −37.3 | −29.2 | −4.9 | 2.5 | −12.6 |
| 2260 | −7.2 | 0.9 | −1.5 | −2.4 | −1.6 | 0.0 | 0.0 | 0.2 | 0.9 | −1.6 | −5.0 | −10.3 | −34.6 | −15.5 | −6.7 | 1.4 | −6.7 |
| 2270 | −2.3 | 0.9 | 2.5 | 0.8 | −0.2 | 0.1 | 0.1 | 0.6 | 3.9 | −1.0 | −6.0 | −4.9 | −12.5 | −6.8 | 0.8 | 2.4 | −2.8 |
| 2290 | −13.3 | 3.9 | −3.1 | −1.4 | −1.4 | 0.0 | 0.0 | 0.0 | 6.0 | −5.5 | −2.4 | −8.0 | −29.8 | −24.4 | −8.1 | 0.8 | −5.7 |
| 2310 | −2.1 | 0.4 | 0.4 | 0.3 | −0.5 | 0.0 | 0.0 | 0.0 | 3.3 | 1.2 | −5.8 | −2.5 | −6.9 | −0.2 | −0.6 | 1.0 | −3.8 |
| 2320 | 2.3 | −2.1 | 1.3 | −0.3 | −1.0 | 0.0 | 0.0 | 0.0 | 3.8 | 2.3 | −10.5 | −4.8 | −14.7 | −12.4 | −1.3 | 0.1 | −5.1 |
| 2340 | −6.1 | 4.8 | 4.8 | 1.1 | −0.8 | 0.1 | 0.3 | 0.3 | 5.8 | −2.0 | 0.5 | −0.8 | 10.7 | 5.5 | 8.1 | 1.6 | 11.1 |
| 2380 | −8.3 | −3.0 | −0.5 | −0.4 | −1.9 | 0.1 | 0.0 | 0.0 | 4.0 | −6.2 | −1.9 | −3.7 | −21.9 | −13.1 | −2.1 | 0.4 | −5.5 |
| 2450 | −0.8 | 0.2 | 1.6 | 0.0 | −0.3 | 0.0 | 0.1 | 0.0 | 3.0 | 1.5 | −1.5 | −1.7 | 6.5 | −1.7 | 1.8 | 0.8 | 1.6 |
| 2510 | −10.8 | −0.7 | −2.6 | 0.3 | −1.9 | 0.0 | 0.4 | −0.6 | 3.2 | −8.7 | −7.1 | −7.6 | −30.8 | −19.9 | −3.0 | 1.2 | −12.3 |
| 2540 | −12.0 | 4.7 | −0.2 | 3.4 | −2.3 | 0.7 | 0.1 | −0.6 | 5.8 | −4.2 | −1.8 | −3.8 | −3.8 | −12.9 | 4.3 | 1.5 | −3.4 |
| 2560 | −8.1 | 3.2 | −1.7 | −3.0 | −0.6 | −0.8 | 1.2 | 0.9 | 7.8 | −3.3 | −0.3 | −3.5 | 5.3 | −4.0 | −4.8 | 2.4 | 3.4 |
| 2580 | −16.8 | 8.9 | −6.2 | −1.8 | −2.0 | 0.1 | 0.0 | 0.0 | 9.0 | −5.6 | −0.3 | −8.0 | −11.9 | −4.8 | −9.3 | 0.4 | −1.7 |
| 2600 | −2.9 | −0.1 | −2.5 | −2.5 | −2.4 | 0.0 | 0.3 | 0.5 | 6.1 | −2.0 | −2.5 | −2.8 | −18.4 | −8.1 | −6.6 | 2.4 | −3.5 |
| 2610 | −5.2 | 3.6 | 1.3 | −0.6 | −0.6 | −0.7 | 0.3 | 0.0 | 6.2 | −0.1 | −2.5 | −3.8 | 4.1 | −4.8 | 1.7 | 2.0 | 2.5 |
| 2670 | −11.1 | 0.2 | −2.6 | 0.2 | −0.9 | −1.2 | 1.8 | 1.5 | 3.3 | −2.6 | −4.5 | −4.4 | −28.7 | −21.9 | −1.2 | 2.6 | −0.4 |
| 2690 | −6.0 | −3.0 | −1.4 | 0.6 | −0.6 | 0.0 | 0.9 | 1.5 | 3.6 | −1.4 | −1.1 | −4.0 | −10.1 | −16.5 | 1.2 | 2.2 | 1.7 |
| 2710 | −5.8 | 1.4 | −1.7 | −3.4 | −2.3 | −1.0 | 0.0 | 0.4 | 4.8 | 0.5 | −6.0 | −9.5 | −54.5 | −15.5 | −6.1 | −0.5 | 2.7 |
| 2730 | −4.7 | −0.9 | −0.6 | −0.5 | −0.2 | 0.0 | 1.0 | 1.3 | 5.1 | −1.3 | −1.4 | −4.1 | −3.0 | −12.5 | −0.8 | 3.8 | 1.9 |
| 2740 | −3.6 | 0.5 | −0.3 | −0.1 | −0.6 | −0.6 | 0.2 | 0.2 | 3.7 | −2.8 | −1.4 | −1.8 | −12.7 | −6.8 | −1.1 | 0.9 | −0.1 |
| 2760 | −2.5 | 1.9 | 0.8 | 2.2 | −0.3 | −1.1 | 0.4 | 0.9 | 3.7 | −1.5 | −2.6 | −2.7 | −2.9 | −4.7 | 3.2 | 0.3 | 0.5 |
| 2780 | −8.0 | 2.5 | 3.6 | 2.6 | −1.6 | 0.0 | 0.0 | 0.0 | 5.7 | −0.1 | −1.1 | −1.9 | 3.6 | −13.2 | 5.9 | 3.1 | 5.2 |
| 2800 | −1.2 | 1.0 | 2.1 | −1.1 | −0.3 | −0.2 | 0.6 | 0.5 | 4.1 | −2.3 | −3.2 | −1.9 | 3.6 | −3.2 | 2.0 | 2.1 | −1.8 |
| 2830 | −7.4 | 1.0 | −0.2 | −0.6 | 0.6 | −1.6 | 1.0 | 0.2 | 5.2 | −2.3 | −2.8 | −3.0 | −25.3 | −15.3 | 1.0 | −1.4 | 1.3 |
| 2890 | −11.7 | 0.2 | −1.5 | 1.7 | −0.5 | −0.2 | 0.4 | 0.0 | 6.8 | −4.3 | −2.7 | −4.0 | −3.9 | −17.1 | 1.6 | 2.3 | 3.8 |
| 2940 | 48.1 | 22.5 | 27.5 | −10.6 | 7.2 | 5.1 | −0.4 | −1.6 | 21.7 | −5.3 | 8.7 | 14.5 | 202.8 | 97.7 | 37.7 | −4.0 | 35.3 |
| 2990 | 1.0 | 5.5 | 2.4 | −1.7 | −1.1 | 0.6 | 0.9 | 0.9 | 3.6 | −4.2 | 0.2 | −1.9 | 15.2 | 9.4 | 2.3 | 4.8 | −2.2 |
| 3000 | −4.0 | −1.5 | −0.3 | −1.3 | −2.4 | −0.3 | 0.7 | 0.1 | 4.3 | −3.5 | −1.0 | 2.0 | −6.5 | −13.1 | −3.0 | 2.2 | 0.0 |
| 3040 | −3.5 | −0.4 | −0.4 | −0.1 | −1.1 | −0.2 | 0.3 | 0.2 | 4.1 | −2.3 | −2.7 | −5.3 | −19.8 | −14.0 | −3.8 | 0.9 | −2.2 |
| 3060 | −9.0 | −3.1 | −0.3 | −1.3 | −4.6 | −0.2 | 0.6 | 0.0 | 3.5 | −6.4 | −3.1 | −9.5 | −40.7 | −23.7 | −6.0 | 0.8 | −8.4 |
| 3090 | −2.0 | −0.4 | 6.8 | 1.1 | −2.8 | 0.6 | 0.5 | −0.9 | 7.5 | −2.4 | −0.8 | −0.8 | 10.9 | −6.4 | 7.0 | 0.8 | 0.1 |
| 3100 | −0.8 | 3.5 | 5.8 | 0.9 | −1.5 | 1.0 | 0.7 | 0.0 | 5.1 | −0.7 | 0.7 | −2.5 | 1.3 | −4.8 | 3.7 | 3.9 | 4.0 |
| 3150 | −2.7 | −1.6 | 5.6 | 0.8 | −3.5 | −0.3 | 0.6 | −1.9 | 5.3 | −7.0 | 1.2 | −5.4 | −20.4 | −6.6 | 0.8 | −1.5 | −1.3 |
| 3160 | −3.8 | −1.4 | −0.9 | 1.6 | −0.1 | 1.4 | 1.2 | 0.8 | 4.5 | −0.2 | 0.6 | −3.9 | 4.4 | −12.3 | 3.0 | 4.9 | 4.7 |
| ID | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Year | Win | Spr | Sum | Aut |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 900 | −9.0 | −0.8 | −3.6 | −0.8 | −2.5 | −1.8 | 0.8 | 1.5 | 1.0 | −1.0 | −8.3 | −8.2 | −27.6 | −18.4 | −7.5 | 0.5 | −6.7 |
| 930 | −6.6 | −1.6 | 0.3 | −0.9 | −2.7 | −0.6 | 0.9 | 0.4 | 0.1 | −3.8 | −3.1 | −7.7 | −23.9 | −17.8 | −2.8 | 0.9 | −5.6 |
| 970 | −5.0 | −1.1 | 1.7 | −1.2 | −2.0 | −0.6 | 1.3 | 0.3 | 0.3 | 0.4 | −1.8 | −3.8 | −6.6 | −10.9 | −2.2 | 0.9 | −1.2 |
| 1000 | −8.0 | −4.7 | −0.1 | −3.3 | −3.7 | −1.5 | 0.4 | 1.5 | 3.9 | −4.2 | 0.4 | −10.2 | −49.7 | −25.8 | −8.9 | −0.5 | 0.6 |
| 1010 | −0.7 | −3.0 | 0.0 | −1.7 | −1.6 | 0.4 | 0.8 | 0.1 | 2.7 | −2.5 | −1.4 | −5.9 | −7.2 | −7.5 | −2.9 | 1.3 | −0.6 |
| 1030 | −4.9 | −1.8 | 1.3 | 0.5 | −1.9 | −0.1 | 1.1 | 0.9 | 3.9 | −3.2 | −1.4 | −7.7 | −14.5 | −14.0 | 0.4 | 1.7 | −0.5 |
| 1060 | −20.8 | −10.2 | −1.3 | 1.9 | −4.7 | 2.1 | 3.3 | 0.3 | 5.6 | −7.0 | −10.3 | −11.3 | −67.4 | −45.9 | −3.1 | 5.6 | −12.4 |
| 1092 | 15.6 | 10.5 | 43.0 | −19.7 | −5.0 | 14.4 | −9.9 | −4.6 | 18.9 | −13.7 | −14.3 | −12.7 | −19.4 | −8.9 | 18.9 | −9.9 | −27.2 |
| 1100 | −8.9 | −2.2 | 4.3 | 1.5 | −4.7 | −0.1 | −0.1 | 1.7 | 1.4 | −3.5 | −6.6 | −4.1 | −11.8 | −13.2 | 3.0 | 1.9 | −8.1 |
| 1120 | −1.5 | −2.1 | 4.6 | 2.1 | −2.4 | 0.2 | 0.4 | 0.8 | 3.8 | −0.7 | −4.0 | −4.0 | 9.0 | −5.3 | 4.9 | 1.2 | −0.6 |
| 1130 | −0.8 | −0.8 | 0.7 | 1.6 | −0.7 | 1.0 | 1.1 | 0.9 | 3.4 | −1.1 | −1.3 | −3.5 | 4.0 | −4.7 | 1.8 | 3.0 | 1.3 |
| 1140 | −3.3 | −2.0 | 0.4 | 0.0 | −0.7 | 1.4 | 1.6 | 0.8 | 2.8 | −1.5 | −3.1 | −8.4 | −11.7 | −11.6 | −0.6 | 3.8 | −2.6 |
| 1180 | −3.8 | −1.5 | 1.2 | −0.1 | −1.2 | 0.2 | 0.1 | 0.2 | 1.2 | −0.5 | −3.0 | −3.9 | −7.3 | −9.9 | 0.4 | 0.8 | −2.7 |
| 1230 | −0.2 | −2.1 | 1.9 | 0.6 | −0.6 | 1.1 | 3.0 | 1.8 | 6.9 | −2.3 | 0.7 | −8.9 | 9.8 | −5.3 | 2.5 | 5.9 | 5.7 |
| 1360 | −4.0 | −1.5 | 2.8 | 1.4 | −2.0 | 0.1 | 0.2 | 1.0 | 5.7 | −5.6 | −9.7 | −1.9 | 3.6 | −5.1 | 4.1 | 0.9 | −9.1 |
| 1380 | −11.7 | 0.4 | 0.9 | −1.5 | −2.5 | −0.4 | 0.6 | 1.6 | 6.6 | −8.7 | −12.4 | −7.0 | −39.9 | −6.7 | −4.0 | 1.8 | −15.2 |
| 1410 | −4.7 | −5.5 | −4.5 | −1.8 | −3.3 | −2.5 | 0.3 | 0.0 | 2.4 | −3.9 | −4.2 | −9.7 | −39.2 | −24.7 | −9.0 | −2.2 | −5.9 |
| 1440 | −2.7 | 1.7 | −2.2 | 1.0 | −2.1 | −1.1 | 1.3 | 0.6 | 5.7 | −2.7 | −3.0 | −8.4 | −14.6 | −7.9 | −2.8 | 0.7 | 1.8 |
| 1455 | 23.1 | 41.3 | 33.8 | 8.1 | 6.4 | 5.4 | −6.8 | −2.1 | 36.0 | 65.4 | 42.8 | −8.7 | 228.1 | 55.9 | 43.8 | −5.1 | 138.8 |
| 1500 | −11.6 | −3.6 | 6.3 | 4.5 | −2.2 | 0.0 | 1.8 | 2.1 | 2.7 | −8.6 | −10.4 | −8.8 | −24.4 | −20.4 | 14.3 | 4.1 | −17.4 |
| 1580 | −7.1 | 2.6 | −1.9 | 2.5 | −1.6 | −0.1 | 1.6 | 1.1 | 5.2 | −2.6 | −7.4 | −5.3 | −4.2 | −5.9 | 0.9 | 2.6 | −7.0 |
| 1670 | −2.8 | 9.2 | 0.0 | 3.2 | −2.2 | −0.3 | 0.7 | −0.5 | 10.2 | −5.1 | 12.3 | −7.2 | 29.8 | 3.0 | 1.5 | −0.2 | 17.4 |
| 1675 | 4.6 | 46.7 | 41.0 | −2.6 | −0.9 | 0.1 | −0.2 | −14.8 | −14.8 | 10.8 | 51.1 | −23.0 | 192.3 | 53.6 | 34.0 | −12.8 | 47.6 |
| 1680 | −2.0 | −0.6 | 1.5 | 0.9 | 0.2 | −0.2 | 1.2 | 0.1 | 3.1 | −1.1 | −4.4 | −2.9 | −3.3 | −7.7 | 3.2 | 1.1 | −2.7 |
| 1695 | 16.3 | 34.2 | 47.1 | −12.9 | −5.4 | 0.6 | −5.2 | −6.0 | −13.6 | 36.2 | 39.8 | −20.6 | 113.4 | 38.1 | 21.9 | −10.3 | 60.1 |
| 1700 | −3.8 | −1.7 | −2.1 | 0.6 | −0.2 | −1.3 | 1.3 | 0.2 | 4.5 | −5.5 | −7.4 | −5.2 | −31.9 | −12.1 | −1.8 | 0.3 | −9.4 |
| 1740 | −7.9 | 0.6 | −2.1 | 1.0 | −1.0 | −1.8 | 0.6 | 0.1 | 6.8 | −4.9 | −6.7 | −8.1 | −25.9 | −15.7 | −2.2 | −1.1 | −2.7 |
| 1760 | −1.4 | 1.7 | 1.5 | −0.3 | −0.9 | −1.0 | 1.1 | 0.5 | 2.4 | −2.4 | −8.8 | −5.0 | −7.9 | −5.7 | 0.3 | 0.6 | −7.9 |
| 1780 | −9.5 | 1.1 | 1.3 | 0.6 | −0.4 | −0.8 | 2.2 | 1.1 | 4.8 | 0.5 | −3.0 | −8.7 | −2.6 | −15.9 | 2.3 | 2.3 | 2.4 |
| 1820 | −7.0 | −2.6 | −3.1 | 2.4 | −0.4 | −0.1 | 2.1 | −0.5 | 2.2 | −2.6 | −6.0 | −9.2 | −15.7 | −17.1 | 0.2 | 1.6 | −7.9 |
| 1830 | −5.5 | −1.2 | −1.4 | 1.5 | −1.6 | −2.3 | 3.4 | 2.0 | 2.2 | −2.6 | −5.2 | −6.8 | −10.7 | −11.1 | −1.9 | 3.0 | −5.4 |
| 1850 | −4.1 | −3.2 | −1.5 | −1.0 | −0.6 | −1.5 | 0.9 | 1.5 | 3.2 | −3.9 | −5.5 | −5.7 | −22.1 | −15.4 | −2.9 | 1.0 | −6.1 |
| 1910 | −2.3 | 2.2 | −1.9 | −0.1 | −0.4 | −0.8 | 3.1 | 1.4 | 2.5 | −2.0 | −3.2 | −8.6 | −15.3 | −6.1 | −3.7 | 3.7 | −3.0 |
| 1940 | −7.4 | −0.2 | −2.1 | 0.0 | 0.2 | −0.4 | 1.4 | 1.1 | 4.8 | −6.0 | −3.6 | −6.0 | −27.5 | −13.1 | −0.7 | 2.3 | −7.4 |
| 1960 | −1.7 | −7.0 | −2.7 | −1.8 | −0.7 | −1.1 | 1.5 | 1.0 | 7.9 | −6.4 | −7.7 | −2.7 | −12.5 | −10.2 | −3.1 | 1.5 | −6.4 |
| 1970 | −0.1 | 0.0 | 0.9 | 0.7 | 0.1 | −0.6 | 0.6 | −0.1 | 4.7 | −4.3 | −2.9 | −6.3 | −0.2 | −4.8 | 1.5 | 0.0 | −1.7 |
| 1980 | −9.9 | −6.0 | −4.5 | 2.0 | −2.0 | −1.6 | 1.6 | 2.4 | 7.0 | −3.4 | −10.5 | −7.0 | −24.3 | −22.5 | −2.7 | 1.8 | −5.6 |
| 2040 | −0.9 | −1.3 | −0.5 | 0.2 | −0.6 | −0.5 | 0.4 | 0.1 | 8.9 | −6.3 | −11.4 | −10.9 | −23.4 | −11.5 | −0.4 | 0.2 | −7.6 |
| 2086 | −4.2 | −3.7 | 3.3 | 6.4 | −0.5 | 0.4 | 1.2 | 1.3 | 4.6 | −3.0 | −13.7 | −18.1 | −13.0 | −15.2 | 11.1 | 3.0 | −12.3 |
| 2090 | −6.6 | −11.4 | −4.7 | 0.0 | −0.9 | −1.9 | 1.4 | 0.9 | 6.7 | −8.3 | −18.9 | −9.9 | −16.9 | −12.5 | −2.5 | 0.5 | −21.2 |
| 2130 | 2.2 | 5.9 | 0.2 | −0.6 | −1.5 | −0.1 | 0.9 | 1.3 | 10.7 | −12.2 | 0.5 | 0.5 | 4.7 | 8.4 | −3.2 | 2.0 | −1.0 |
| 2150 | −10.2 | −7.1 | −7.5 | 0.8 | −0.9 | −2.2 | 1.3 | 1.0 | 4.5 | −4.8 | −9.9 | −12.2 | −44.1 | −32.6 | −10.0 | 0.4 | −10.4 |
| 2160 | 0.3 | −2.7 | −2.1 | −0.7 | −1.0 | −0.9 | 0.0 | 0.1 | 5.4 | −3.9 | −11.7 | −5.5 | −26.7 | −6.6 | −4.3 | −1.2 | −9.5 |
| 2200 | −4.9 | −3.0 | −2.2 | −0.2 | −0.2 | −0.6 | 0.2 | 1.2 | 8.3 | −2.6 | −7.1 | −6.2 | −15.0 | −13.8 | −2.9 | 0.9 | −1.0 |
| 2210 | −2.6 | 0.9 | 0.3 | 0.9 | −0.8 | −0.1 | 1.1 | 0.4 | 8.5 | −0.8 | −5.5 | −6.8 | 2.3 | −8.7 | 0.9 | 1.4 | 3.0 |
| 2230 | −10.1 | −4.5 | −1.7 | −3.2 | −1.5 | 0.8 | 0.1 | 1.3 | 5.1 | −9.1 | −10.2 | −15.4 | −37.8 | −30.8 | −5.6 | 2.2 | −15.8 |
| 2260 | −8.2 | −0.5 | −3.4 | −2.7 | −2.1 | −0.5 | 0.9 | 1.3 | 3.7 | −6.3 | −5.9 | −12.4 | −33.1 | −19.8 | −8.6 | 1.8 | −7.5 |
| 2270 | −2.4 | −3.7 | 1.7 | 0.9 | −1.4 | −0.7 | 0.4 | 1.7 | 6.8 | −5.9 | −6.5 | −6.6 | −14.8 | −10.7 | 0.0 | 1.4 | −5.9 |
| 2290 | −15.4 | 3.0 | −4.2 | −2.1 | −2.9 | 0.0 | 0.2 | 1.2 | 6.9 | −11.9 | −3.3 | −9.2 | −27.8 | −21.4 | −8.7 | 1.3 | −8.8 |
| 2310 | −2.4 | −0.1 | −0.3 | 0.1 | −0.8 | 0.0 | 0.4 | 0.6 | 4.2 | −2.1 | −6.3 | −1.7 | −6.9 | −2.7 | −0.9 | 0.9 | −3.9 |
| 2320 | 1.8 | −4.8 | −0.5 | −1.7 | −1.5 | −0.6 | 0.2 | −0.2 | 4.2 | −0.5 | −14.0 | −5.7 | −18.6 | −11.8 | −2.0 | −0.4 | −9.7 |
| 2340 | −10.9 | 7.6 | 3.3 | 1.2 | −0.6 | 0.2 | 0.6 | 0.4 | 5.1 | −8.6 | 5.8 | −2.1 | 9.0 | 2.0 | 6.0 | 1.1 | 5.1 |
| 2380 | −7.1 | −2.7 | −1.3 | −0.9 | −2.3 | 0.0 | 0.0 | 1.2 | 4.8 | −13.4 | −2.6 | −4.1 | −23.0 | −11.7 | −4.0 | 1.4 | −10.9 |
| 2450 | −0.3 | −0.5 | 1.7 | 0.3 | −0.2 | −0.2 | 0.4 | −0.1 | 4.2 | 1.2 | −1.9 | −1.5 | 5.2 | −1.8 | 1.8 | 0.1 | 3.6 |
| 2510 | −10.3 | −1.1 | −2.6 | 0.4 | −2.2 | 0.2 | 1.9 | −0.7 | 1.2 | −8.4 | −6.4 | −7.3 | −32.8 | −18.9 | −4.1 | 1.5 | −12.9 |
| 2540 | −15.6 | 6.5 | −2.4 | 3.3 | −3.9 | 1.0 | −0.7 | −0.5 | 4.4 | −15.1 | −4.8 | −2.9 | −26.9 | −11.3 | 0.1 | −0.4 | −15.3 |
| 2560 | −6.2 | 1.0 | −2.9 | −4.4 | −1.8 | −2.3 | 2.3 | 2.9 | 8.5 | −4.3 | 0.6 | −4.1 | 6.1 | −3.9 | −10.3 | 3.8 | 4.8 |
| 2580 | −13.8 | 10.5 | −5.3 | −1.6 | −4.9 | 0.6 | −0.6 | 0.2 | 7.8 | −9.2 | −3.2 | −8.6 | −13.9 | −5.3 | −10.6 | −0.7 | −3.6 |
| 2600 | −1.5 | 0.5 | −1.8 | −2.7 | −3.0 | −1.3 | 1.5 | 1.2 | 5.1 | −3.9 | −4.3 | −3.3 | −12.3 | −7.1 | −7.0 | 1.6 | −4.1 |
| 2610 | −3.4 | 1.3 | 2.1 | 0.5 | −0.7 | −3.3 | 2.2 | 1.3 | 6.8 | 1.0 | −2.3 | −2.8 | 5.2 | −4.1 | 0.6 | −0.1 | 4.6 |
| 2670 | −12.0 | −6.1 | −2.7 | −0.2 | −2.7 | −2.3 | 2.5 | 2.2 | 3.2 | −3.1 | −4.9 | −10.7 | −35.4 | −27.0 | −2.8 | 2.4 | −5.2 |
| 2690 | −5.8 | −3.3 | −1.1 | 1.4 | −1.5 | −1.7 | 0.4 | 2.7 | 2.8 | −1.9 | −1.3 | −5.9 | −8.7 | −14.4 | −0.3 | 0.9 | −0.1 |
| 2710 | −3.8 | −1.5 | −3.2 | −3.6 | −4.4 | −3.1 | 0.3 | −0.3 | 6.0 | −0.4 | −10.7 | −8.6 | −56.5 | −15.4 | −10.9 | −3.3 | −4.8 |
| 2730 | −3.6 | −1.7 | −0.3 | −0.3 | −1.1 | −0.4 | 2.4 | 2.2 | 6.2 | −2.0 | −1.7 | −5.3 | −3.8 | −12.6 | −1.3 | 3.8 | 3.2 |
| 2740 | −3.8 | −0.1 | −0.3 | 0.4 | −1.1 | −2.4 | 0.3 | 1.5 | 4.0 | −3.2 | −1.4 | −2.6 | −12.0 | −6.3 | −0.9 | −0.3 | 0.3 |
| 2760 | −2.7 | 1.0 | 0.5 | 2.6 | −2.5 | −2.2 | 0.7 | 1.1 | 4.6 | −1.3 | −3.9 | −4.1 | −8.0 | −6.1 | 0.4 | −0.4 | 0.0 |
| 2780 | −6.9 | 2.6 | 3.9 | 2.9 | −2.0 | 0.2 | 1.0 | 2.1 | 6.0 | 2.1 | −0.9 | −3.9 | 4.7 | −11.2 | 5.3 | 3.3 | 7.8 |
| 2800 | −1.0 | 0.7 | 2.4 | −1.3 | −0.4 | −1.6 | 2.5 | 1.2 | 4.4 | −1.8 | −3.9 | −3.4 | 2.0 | −2.9 | 1.7 | 3.1 | −1.9 |
| 2830 | −6.7 | −0.1 | 0.3 | 0.3 | 0.9 | −3.7 | 1.6 | 1.1 | 6.5 | −1.5 | −3.1 | −3.6 | −19.7 | −15.3 | 1.4 | −0.9 | 1.9 |
| 2890 | −11.6 | 1.9 | −3.4 | 1.8 | −0.8 | 0.2 | 1.6 | 1.1 | 7.6 | −2.9 | −1.1 | −3.1 | −1.4 | −12.6 | −1.5 | 3.0 | 4.9 |
| 2940 | 53.4 | 28.7 | 33.6 | −7.4 | 10.4 | −0.9 | −4.9 | −2.7 | 19.8 | −6.3 | 12.8 | −4.4 | 202.0 | 107.3 | 37.4 | −7.3 | 32.8 |
| 2990 | 0.0 | 2.4 | 2.6 | −1.9 | −0.8 | 0.9 | 1.3 | 1.4 | 2.8 | −4.7 | 0.1 | −2.5 | 13.0 | 8.7 | 2.1 | 3.7 | −1.7 |
| 3000 | −4.0 | −3.7 | −0.3 | −1.1 | −2.7 | −1.2 | 1.4 | 1.0 | 4.0 | −3.3 | −1.2 | −0.3 | −5.2 | −7.8 | −3.9 | 1.1 | 0.3 |
| 3040 | −4.9 | −1.0 | −0.6 | −0.8 | −2.2 | −2.4 | 0.5 | 1.1 | 3.7 | −2.3 | −2.8 | −7.0 | −18.0 | −12.0 | −4.7 | −0.9 | −1.7 |
| 3060 | −8.9 | −2.8 | −0.1 | −2.0 | −5.6 | −1.1 | 1.8 | 0.1 | 3.6 | −5.4 | −4.3 | −10.6 | −39.1 | −21.3 | −7.0 | 1.1 | −6.0 |
| 3090 | −0.4 | −0.3 | 6.8 | 1.4 | −3.2 | −0.1 | 2.4 | −1.2 | 7.9 | −2.4 | −1.4 | −2.1 | 15.1 | −2.1 | 6.7 | 1.0 | 4.3 |
| 3100 | −0.5 | 3.2 | 4.5 | 1.2 | −2.0 | 0.4 | 2.1 | 0.6 | 5.3 | 0.1 | −0.1 | −2.8 | 3.0 | −1.4 | 3.2 | 3.1 | 5.1 |
| 3150 | −3.5 | −5.3 | 4.4 | 0.1 | −4.2 | −0.8 | 1.3 | −2.1 | 2.9 | −6.5 | 0.8 | −6.1 | −6.1 | −8.9 | −2.2 | −1.9 | −1.1 |
| 3160 | −5.4 | −1.9 | 0.4 | 2.2 | −0.3 | 2.2 | 2.2 | 1.1 | 3.9 | 0.0 | 1.4 | −6.5 | 3.4 | −11.8 | 3.4 | 5.5 | 5.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caloiero, T.; Filice, E.; Coscarelli, R.; Pellicone, G. A Homogeneous Dataset for Rainfall Trend Analysis in the Calabria Region (Southern Italy). Water 2020, 12, 2541. https://doi.org/10.3390/w12092541
Caloiero T, Filice E, Coscarelli R, Pellicone G. A Homogeneous Dataset for Rainfall Trend Analysis in the Calabria Region (Southern Italy). Water. 2020; 12(9):2541. https://doi.org/10.3390/w12092541
Chicago/Turabian StyleCaloiero, Tommaso, Eugenio Filice, Roberto Coscarelli, and Gaetano Pellicone. 2020. "A Homogeneous Dataset for Rainfall Trend Analysis in the Calabria Region (Southern Italy)" Water 12, no. 9: 2541. https://doi.org/10.3390/w12092541
APA StyleCaloiero, T., Filice, E., Coscarelli, R., & Pellicone, G. (2020). A Homogeneous Dataset for Rainfall Trend Analysis in the Calabria Region (Southern Italy). Water, 12(9), 2541. https://doi.org/10.3390/w12092541





