Applicability of Kinematic Wave Model for Flood Routing under Unsteady Inflow

Abstract

This study implemented kinematic wave and dynamic wave approximation of flood routing for a prismatic rectangular channel. The results of the two methods were compared by differences in maximum flow depth, and the applicability of kinematic wave equation was discussed. The influences of hydraulic and geometrical factors on the applicability of kinematic wave equation were considered. It was found that a portion of the numerical results violated existing criteria used to indicate the applicability of kinematic wave equation, particularly when geometrical and hydraulic factors were considered together. This is because the characteristics of upstream inflow were rarely or incompletely considered in these criteria. Therefore, the present study proposed a new criterion. The theoretical influence of all factors was considered using three parameters, namely, ${KF}_0^2$, ${\eta }_{ts}/T_0^{\prime }$ and $Q_{bottom}/Q_{peak}$ ($K, F_0, {\eta }_{ts}, T_0^{\prime }, Q_{bottom}$, and $Q_{peak}$ represent the kinematic wave number, Froude number, the time span of discharge exceeding 90% of maximum discharge in hydrograph, wave travel time in the channel, base flow discharge, and peak discharge, respectively, while the subscript 0 represent the value of reference discharge). The influences of these three parameters were illustrated by the momentum equation of one-dimensional Saint-Venant equation. The numerical results showed that the value of ${\eta }_{ts}/T_0^{\prime } {\left(K{F}_0^2\right)}^D$ could be used to determine the relative error ${\xi }_h$ of kinematic wave equation. In addition, for each $Q_{bottom}/Q_{peak}$ the value of ${\eta }_{ts}/T_0^{\prime } {\left({KF}_0^2\right)}^D$ used to depict the same relative error ${\xi }_h$ was different. This new criterion was validated using two real case studies, and it showed a good performance.

1. Introduction

Flood disasters have historically resulted in huge damage to human societies, and have therefore been a persistent focus of research [1]. Many studies have attempted to simulate the flood routing process, and a wide range of flood routing methods have been proposed [2]. Among these approaches, the one-dimensional (1-D) Saint-Venant equation (SVE) has been very popular. The 1-D SVE considers the conservation of mass and momentum of flow and can be applied to a variety of domains [3,4]. Under specific conditions, some terms in the momentum equation of the SVE can be neglected, thereby allowing the characteristics of kinematic, diffusive, gravity, and dynamic waves to be derived accordingly [5,6]. Among these simplifications, kinematic wave approximation (KWA) is the simplest and has been a focus of many studies [7]. The inertia and pressure terms of the momentum equation are omitted in KWA, while the gravity term is immediately equal to the resistance. For this reason, KWA is computationally efficient and solvable. However, the KWA neglects the diffusive characteristics of flood propagation, resulting in no attenuation occurring in the model, which appears unrealistic. Therefore, some limitations to KWA remain, and a study on the applicability of KWA is meaningful.

Different criteria have been proposed by many researchers. Ponce et al. [8,9] utilized linear stability theory to transform the 1-D SVE to a linear form. By introducing a small perturbation in the steady uniform flow, the flow velocity u and the flow depth $h$ were assumed to be a superposition of the unsteady perturbation and the steady state of flow. The applicable domains of each wave type were defined by the Froude number of the steady uniform flow $F_0$. and the dimensionless wave period of unsteady component of motion $\tau$. Following the analysis of Ponce et al. [9], Lamberti and Pilati [10] took an additional parameter, the relative wave period, into consideration. Due to the lack of a method to depict the characteristics of flood routing along the channel in the above analysis, Tsai [11] introduced dimensionless wave velocity and the dimensionless logarithmic decrement, which were calculated in terms of different Froude numbers. These two parameters were used to depict the applicability of KWA along the channel. Venutelli [12] discussed the depiction of wave characteristics by group speed, phase speed, and wave amplitude in terms of different friction parameters, Froude number, and Courant number, thereby confirming the findings of Ponce and Simons [8].

The nondimensionalization of the 1-D SVE allows the use of the modulus of each term in the momentum equation to identify which term can be neglected. As illustrated by Woolhiser and Liggett [13], dynamic wave approximation (DWA) considers uniform lateral inflow. The kinematic wave number $K$ (equal to $S_0{L}_0/(h_0{F}_0^2)$ where $S_0$ and $L_0$ represent the slope and river length, $h_0$ represent the flow depth of reference discharge) is defined in the dimensionless momentum equation. The applicability of KWA has been assessed under different kinematic wave number $K$ and Froude $F_0$ (equal to $V_0/\sqrt{g{h}_0}$ when $V_0$ represent the flow velocity of reference discharge and $g$ is acceleration of gravity (9.8 $\mathrm{m}/{\mathrm{s}}^2$), and it was found that KWA performs well when $K > 20$. Morris and Woolhiser [14] extended the applicability of the parameter by Woolhiser and Liggett [13] to ${KF}_0^2 > 5$. The same parameter was used by Vieira [15], who considered the condition of shallow water flow. Ferrick [5] found that the system equation can be obtained by differentiating the continuity equation with respect to $x$ and differentiating the momentum equation with respect $x$ and $t$. Each type of wave can then be derived by four parameters. Moussa and Bocquillon [16] combined the two types of approach, namely, linear stability analysis and the dimensionless form of 1-D SVE. The applicability domains of each wave type were determined in the $F_0^2-{Tu}_0{S}_{f0}/h_0$ diagram ($u_0 {\mathrm{and} S}_{f0}$represent velocity and friction slope of referenced discharge, respectively and $T$ is the wave period). This combined approach was also utilized by Moramarco and Singh [6] in a study, which explored a condition in which channel slope exceeds 1% is suitable for KWA.

Some limitations of the above criteria remain. First, within linear stability analysis, inflow experiences a very small perturbation in comparison to initial steady state, and the nonlinear characteristics of dynamic waves are ignored. Such simplifications may be questionable under a condition of large disturbance produced upstream. Past studies used this type of criterion more frequently for overland flow or other shallow water analyses in which the unsteady portion was infinitesimal. Second, the criterion derived from dimensionless analysis of the momentum equation depends highly on a steady state, whereas the upstream boundary is rarely a focus. Third, the parameters used for the criterion combined several variables, resulting in uncertainty in the contribution of any single variable. In addition, some other variables, such as the base flow, used to depict the characteristics of the upstream inflow, which would influence the flood routing, have been incompletely considered.

Admittedly, the work of Moramarco et al. [17,18] overcame some of the limitations mentioned above. However, some more detailed aspects remain unexplored. First, the effects of the characteristics of the upstream boundary condition have been incompletely considered. Reference discharge defined by Moramarco et al. [18] was stable, thereby restricting variation in the shape of discharge of upstream inflow. In other words, the approach does not allow any single variable to influence upstream inflow, thereby resulting in incomplete analysis. Second, the contribution of each single variable to DWA or KWA was not considered separately. The contributions of these variables to the differences between KWA and DWA require further discussion. Third, the main focus of the study by Moramarco et al. [18] was on the characteristics of the upstream boundary, while the influence of geometry was restricted to the setting of several conditions with the aim of obtaining different kinematic numbers. Therefore, there remains insufficient consideration of these geometrical factors and the joint impacts of the characteristics of upstream inflow and geometrical factors.

The present study aimed to identify a more detailed criterion for the applicability of KWA and proposed a new criterion to extend the scope of application of KWA. The second-order two-step Lax–Wendroff numerical method [17,19] was utilized to obtain the numerical solutions of DWA applied to flood routing while the method provided by Chen and Capart [7] was utilized to obtain the analytical solution of KWA. The main concerns of the present study were shown as follows.

First, the influence of the shape of upstream inflow discharge on the applicability of KWA were considered. Different categories of upstream inflow were determined by the four parameters of the Pearson type III distribution, and influence of each parameter was discussed. The analysis on the applicability of KWA included the influence of single variables. Second, the joint impact of geometrical and hydraulic factors was considered. Third, these variables were linked with the variations in other parameters selected by previous studies, including kinematic wave number and Froude number. Fourth, a new criterion was proposed to efficiently evaluate the applicability of KWA, and the reliability of KWA was assessed by application to a real case study.

2. Methods

The present study used DWA and KWA to simulate unsteady flow in a rectangular prismatic channel. The assumptions used to build the governing equations were: (1) the transverse and vertical variations in characteristics of flow in the channel were ignored, (2) hydrodynamic pressure in the cross-section followed the rule of hydrostatic distribution, (3) there was no lateral inflow, and (4) compressibility and inhomogeneity of flow were not considered [20].

2.1. Dynamic Wave and Kinematic Wave Theory

With consideration of a prismatic rectangular channel, the DWA in 1-D SVE [20] can be expressed as follows:

$$\frac{\partial A}{\partial t}+\frac{\partial Q}{\partial x}=0$$

(1)

$$\frac{\partial Q}{\partial t}+\frac{\partial Q^2/A}{\partial x}+\frac{1}{2}gB\frac{\partial h^2}{\partial x}=gA(S_0-S_f)$$

(2)

where $A$ is cross-section area, $Q$ is discharge, $g$ is gravity acceleration, $B$ is the width of the rectangular channel, $h$ is the water depth of flow $S_0$ is the bed slope, $S_f$ is the friction slope expressed by the Manning equation, and $x$. and $t$ are used to describe the spatial and temporal directions, respectively.

Equation (1) describes the continuity conservation, and the physical meaning of the equation is that the mass difference between inflow and outflow in the specific reach $\Delta x$. equals the variation of mass in this reach during period $\Delta t$. Equation (2) describes momentum conservation. The first two terms of the left-hand side of this equation represent inertia, whereas the third term represents hydrodynamic pressure. The right-hand term represents gravity and friction.

The KWA is a simplified form of the 1-D SVE in which the inertia and pressure terms are ignored. The momentum equation can be regarded as the equilibrium between gravity and friction, and can be expressed as:

$$S_0=S_f$$

(3)

Under this condition, the relationship between discharge and water depth can be expressed by a single valued function and Chézy formula is taken into consideration, which can be expressed as:

$$Q=AC\sqrt{R{S}_0}$$

(4)

where $R$ is the hydraulic radius and $C$ is the Chezy coefficient.

2.2. The Accuracy Measurement

The difference between KWA and DWA should be evaluated to quantify the applicability of the KWA. Past studies have focused on the maximum flow depth along the channel for predicting a flood routing process since this is an indicator of whether a channel can accommodate upstream inflow and whether the residence communities adjacent the river would be influenced by the flood [18]. This factor was used when the DWA was regarded as the benchmark and is calculated as:

$${\xi }_h\left(x^{*}\right)=\frac{{h_{\max }^{kw}|}_{x^{*}}-{h_{\max }^{dy}|}_{x^{*}}}{{h_{\max }^{dy}|}_{x^{*}}}\times 100\%$$

(5)

where $x^{*}$ represents the different dimensionless locations along the channel and $h_{\max }^{kw}{|}_{x^{*}}$ and $h_{\max }^{dy}{|}_{x^{*}}$ represent the maximum water depth at the location $x^{*}$ derived from KWA and DWA, respectively.

2.3. The Calculating Method

The present study obtained solutions for DWA by the second-order two-step Lax–Wendroff method [17,19]. Under this numerical technique, the boundary value was determined by the characteristic method, whereas internal values were calculated using a two-step process in which the value of time step $\left(n + 1\right)\Delta t$. is calculated from the value of $n\Delta t$. Based on Equations (1) and (2), these two steps can be expressed as shown below.

The first step is implemented to obtain the intermediate value of $\left(n + \frac{1}{2}\right)\Delta t$:

$$A_{j+1/2}^{n+1/2}=\frac{A_j^n+A_{j+1}^n}{2}-\frac{\Delta t}{2\Delta x}(Q_{j+1}^n-Q_j^n)$$

(6)

$$\begin{array}{c}{Q}_{j+1/2}^{n+1/2}=\frac{Q_j^n+Q_{j+1}^n}{2}-\frac{\Delta t}{2\Delta x}((\frac{Q^2}{A}+\frac{1}{2}gB{h}^2{)}_{j+1}^n-(\frac{Q^2}{A}+\frac{1}{2}gB{h}^2{)}_j^n)\\ +\frac{\Delta t}{4}((gA(S_0-S_f){)}_{j+1}^n+(gA(S_0-S_f){)}_j^n)\end{array}$$

(7)

where the superscript $n$. represent the time point and subscript $j$ represent the space point.

Following the same procedure, the value of $\left(n + \frac{1}{2}\right)\Delta t$. in the spatial step $\left(j - \frac{1}{2}\right)\Delta x$ was derived.

The second step is then implemented to obtain the value of $\left(n + \frac{1}{2}\right)\Delta t$:

$$A_j^{n+1}=A_j^n-\frac{\Delta t}{\Delta x}(Q_{j+1/2}^{n+1/2}+Q_{j-1/2}^{n+1/2})$$

(8)

$$\begin{array}{c}{Q}_j^{n+1}=Q_j^n-\frac{\Delta t}{\Delta x}((\frac{Q^2}{A}+\frac{1}{2}gB{h}^2{)}_{j+1/2}^{n+1/2}+(\frac{Q^2}{A}+\frac{1}{2}gB{h}^2{)}_{j-1/2}^{n+1/2})\\ +\frac{\Delta t}{2}((gA(S_0-S_f){)}_{j+1/2}^{n+1/2}-(gA(S_0-S_f){)}_{j-1/2}^{n+1/2})\end{array}$$

(9)

From Equations (6)–(9), one can derive the value $A_j^{n+1}$ by the values $A_{j-1}^n$, $A_j^n$, and $A_{j+1}^n$, in the same approach as for $Q_j^{n+1}$.

The characteristic method and boundary condition were used together when considering the boundary value. The characteristics of DWA were calculated from Equations (1) and (2), whereas the DWA was expressed through the simplified form represented by Equations (3) and (4). The current study considered subcritical flow and the downstream boundary condition was necessary for DWA.

The characteristics of DWA can be expressed as:

$$\frac{dx}{dt}=\frac{Q}{A}\pm c$$

(10)

where $c$ represents the relative wave celerity and equals $\sqrt{gA/B}$. Following each characteristic, the 1-D SVE can be transformed to characteristic equation as follows:

$$\frac{dQ}{dt}-(\frac{Q}{A}\mp c)\frac{dA}{dt}=gA(S_0-S_f)$$

(11)

In subcritical flow, Equation (10) can be used to derive $dx/dt=Q/A+ c > 0$ while $dx/dt=Q/A- c < 0$. The line $dx/dt=Q/A- c < 0$ can intersect with the upstream boundary which is represented by the line $x = 0$. The value of $\left(n + 1\right)\Delta t$ on the upstream boundary can then be related to the value of $n\Delta t$ through Equation (11). When the upstream boundary condition is provided, discharge $Q$. and cross-section area $A$ of the upstream boundary can be determined. The same approach was adopted to identify the downstream boundary end.

The analytical solution can be obtained for KWA following the method provided by Chen and Capart [7]. Although the KWA only express the kinematic characteristics of the fluid and the damping effect is ignored by it, the maximum discharge remains stable along the river in case the shock wave by the maximum discharge happens beyond the simulated river length. Because of the single value relationship between discharge and area in KWA, the maximum flow depth by KWA depends only on the discharge, which means the maximum flow depth can be determined by the upstream boundary condition.

In the analytical solution of KWA, following the method by Chen and Capart [7], the site, where the shock happens in the wave front in the condition of zero flow rate of initial condition, can be calculated as follows.

$$x_F(t)=\frac{\beta m^{\frac{1}{\beta }}}{\beta -1}\times \frac{{\displaystyle {\int }_0^{t}Q(t)dt}}{Q{(t)}^{1/\beta }}$$

(12)

$$Q=\beta A^m$$

(13)

where $x_F\left(t\right)$ is the place where shock is in the wave front, $\beta$ and $m$ are the fitting coefficients in the relationship between discharge and wetted cross section. In addition, the assumption of dry bed in Equation (12) may contradict with the following designed tests. However, it can be expected that the nonzero flow rate of initial condition would result in the further downstream shock position, which makes the maximum discharge conveying along the simulated river length without the influence of shock wave [21].

Following the method by Stilmant et al. [21], the condition when the single shock happens in the wave front is as follows.

$$\frac{{\frac{dQ}{dt}|}_{t=t_0}{\displaystyle {\int }_0^{t_0}Q(t)-Q_{0}dt}}{{(Q(t_0)-Q_0)}^2}\le c(t_0)\frac{c(t_0)(A(t_0)-A_0)-(Q(t_0)-Q_0)}{(Q(t_0)-Q_0){\frac{dc}{dQ}|}_{t=t_0}}$$

(14)

It should be noted that Equations (12)–(14) were used in the analytical solution of KWA, while the numerical solution of DWA did not consider the shock, which is beyond the scope of the present study.

The upstream boundary was assumed to a specific discharge hydrograph following the Pearson type III distribution. This kind of distribution was widely used by other researchers as the upstream boundary condition [18,20]. Besides, the form of the discharge can easily be adjusted by the parameters inside the distribution, which make the flow hydrograph fulfill our requirements. It can be expressed as:

$$Q(t)=Q_{bottom}+(Q_{peak}-Q_{bottom}){\left(\frac{t}{T_{peak}}\right)}^{\frac{1}{\alpha -1}}\exp \left(\frac{1-t/T_{peak}}{\alpha -1}\right)$$

(15)

where $Q_{bottom}$ is baseflow and also represents the initial state of flow in the channel, $Q_{peak}$ is the peak flow of upstream inflow, $T_{peak}$ is the time to peak of upstream inflow, and $\alpha$ is a parameter which determines the steepness of the rise and fall in upstream inflow. These four parameters in Equation (15) determine the shape of the upstream inflow.

From Equations (14) and (15), when water wave was conveyed by the maximum discharge and its nearby interval, the single shock wave would happen in the wave front.

The downstream boundary condition for the DWA was assumed to be a zero-flow-depth gradient and to follow Equation (16)

$${\frac{dh}{dx}|}_{x=L}=0$$

(16)

Considering the significant effect of the downstream boundary condition, a location far enough was used for analysis to avoid this effect.

2.4. Numerical Tests

The applicability of KWA is influenced by two broad categories of factors, namely hydraulic factors and geometrical factors. Hydraulic factors include the characteristics of upstream inflow and the initial state. Four parameters representing hydraulic factors were in Equation (15), namely, base discharge $Q_{bottom}$, peak discharge $Q_{peak}$, time to peak flow $T_{peak}$, and the coefficient $\alpha$, whereas geometrical factors include slope $S_0$ and the Manning roughness coefficient $n$. Notably, 17 tests were designed for the identification of each hydraulic factor (

Table 1. Characteristics of each numerical experiment for identification of the influence of each hydraulic factor (for all simulated tests, $L=60 \mathrm{km}$, $S_0=0.0002$, $n=0.01$, and $B=100 \mathrm{m}$).

No.	Qpeak(m3 s−1)	Qbottom(m3 s−1)	Tpeak(h)	α
1	150	100	8	1.1
2	250	100	8	1.1
3	350	100	8	1.1
4	400	100	8	1.1
5	500	100	8	1.1
6	500	150	8	1.1
7	500	250	8	1.1
8	500	350	8	1.1
9	500	400	8	1.1
10	500	100	10	1.1
11	500	100	12	1.1
12	500	100	14	1.1
13	500	100	16	1.1
14	500	100	8	1.15
15	500	100	8	1.20
16	500	100	8	1.25
17	500	100	8	1.30

), whereas nine tests for geometrical factors were implemented and the details are illustrated in a later section. Moreover, after the identification of the influence of each factor, the joint impacts of each group of factors were assessed. In all numerical tests, $\Delta t=30 \mathrm{s}$ and $\Delta x=300 \mathrm{m}$ were used, and it can be verified that the Courant condition was satisfied.

It can be identified by Equation (12) that the shock wave of the maximum discharge in all simulated tests for KWA would not influence the final results of KWA, which means that the characteristic of no attenuation of KWA is valid in the simulated river.

To allow for a comparison with other criteria proposed by previous studies, the reference discharge was regarded as the average discharge of the upstream inflow as according to Moramarco et al. [18]:

$$Q_0=\frac{{\displaystyle {\int }_0^{T}Q(t)dt}}{T}$$

(17)

where $Q_0$ is the reference flow discharge.

The parameters selected by previous studies can be calculated for each test according to the reference discharge by Equation (17), such as kinematic wave number $K$, Froude number $F_0$, friction slope $S_{f0}$, flow depth $h_0$, flow velocity $V_0$, and wave travel time in the channel $T_0^{\prime }$.

In addition, under a Pearson type III distribution, there would be a very gradual variation in discharge at the beginning or end of a comparable period. During this period, the upstream inflow can be ignored and the flow in a channel can be regarded as uniform. Therefore, the starting and end points of the discharge were defined as 0.1% of the difference between base discharge and peak discharge, and the time from the starting point to the peak $T_{pr}$ and wave period $T$ should be calculated accordingly.

3. Results and Analysis

3.1. The Influence of the Hydraulic Factors

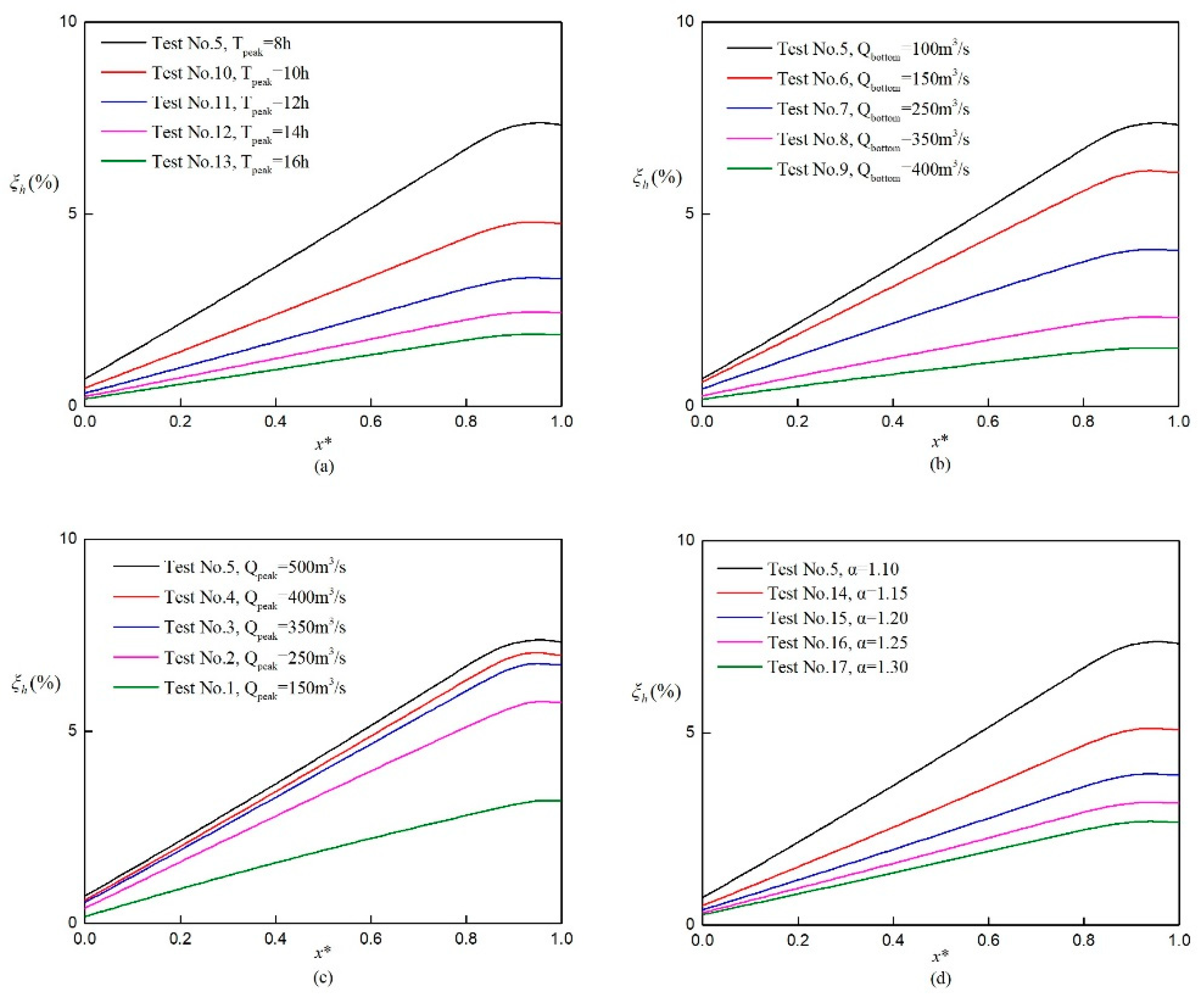
Figure 1 illustrates the influence of hydraulic factors on the relative error ${\xi }_h$ of KWA, including $Q_{peak}{, Q}_{bottom}{, T}_{peak}, \mathrm{and} \alpha$.

Although the results showed that the maximum relative error ${\xi }_h$ values of the selected tests were below 10%, these errors increased under other situations. These tests clearly showed a flattening effect on ${\xi }_h$ near the downstream boundary. This flattening effect resulted from the downstream boundary condition, which the current study selected as a zero-flow-depth gradient. A change in this downstream boundary condition would result in a different effect near the downstream end [18]. Therefore, the last 10% of the channel length was ignored, and instead $0.9·x^{*}$ was regarded as the downstream end. Furthermore, the relative error ${\xi }_h$ increased along the channel due to the existence of attenuation in DWA. Experiments by Moramarco et al. [18] similarly illustrated this phenomenon.

The effect of each parameter on the relative error ${\xi }_h$ is shown in Figure 1. The relative error ${\xi }_h$ decreased with increasing $T_{peak}$ (see Figure 1a). Moreover, the reduction in performance of the relative error ${\xi }_h$ was illustrated by increased $Q_{bottom}$, decreased $Q_{peak}$, and increased $\alpha$.

A more gradual variation in the upstream inflow resulted in a reduction of the relative error ${\xi }_h$ as according to the variation of $Q_{peak}{, Q}_{bottom}{, T}_{peak}, \mathrm{and} \alpha$. From test No. 5 to No. 9, $Q_{bottom}$ increased gradually from 100 to 400${ \mathrm{m}}^3/\mathrm{s}$, which means the difference of $Q_{peak}$ and $Q_{bottom}$ decreased in the situation that the time to peak discharge remain constant. Therefore, the flow rising limb of the hydrograph are becoming gradual from test No. 5 to No. 9. Consequently, the corresponding relative error ${\xi }_h$ decreased gradually from 7.3% to 1.5%. The similar behavior can be seen in decreased $Q_{peak}$ and increased $T_{peak}$ while there is something different for increased $\alpha$. $T_{peak}$ and the difference between $Q_{peak}$ and $Q_{bottom}$ will not change with the increased $\alpha$. However, the time zone near the maximum discharge would become gradual as $\alpha$ increases. This behavior would also result in decreased relative error.

This phenomenon can be explained by the momentum equation of SVE (Equation (2)), which can be transformed as (see Appendix A):

$$Q=Q_s\times \sqrt{1-\frac{1}{S_0}\frac{\partial h}{\partial x}-\frac{1}{S_{0}g}\frac{\partial V}{\partial t}-\frac{V}{S_{0}g}\frac{\partial V}{\partial x}}$$

(18)

where $V$ is the flow velocity and $Q_s$ is the steady discharge, which was defined in Appendix A.

The aim to reduce the relative error ${\xi }_h$ is mainly finding a situation in which less attenuation can occur in DWA. The reduction of the last three terms in the root of Equation (18) can achieve such a result. The gradual variation in upstream inflow formed by $Q_{peak}{, Q}_{bottom}{, T}_{peak}, \mathrm{and} \alpha$ would result in a decrease in the last three terms of the root of Equation (18). The gradual variation in upstream inflow clearly resulted in a decrease in the partial derivative of $V$ with respect to $t$. The variation in the other two partial derivatives with respect to $x$ could be identified with consideration of the numerical technique used. The numerical method described above showed that the point $M_{j=1}^{n+1}$ was a specific average form of point $N_{j-1}^n$, $P_j^n$ (see Figure 2), and $R_{j+1}^n$ ($n$ and $j$ are the temporal and spatial directions, respectively ). When gradual variation in upstream inflow results in a reduction in the difference between $N_{j-1}^n$ and $X_{j-1}^{n+1}$, the difference between $M_j^{n+1}$ and $X_{j-1}^{n+1}$ should also decrease. The points $P_j^n$ and $R_{j+1}^n$ would be influenced by the earlier point on the time line $n - 1$, which would promote the reduction in the difference between $M_{j = 1}^{n + 1}$ and $X_{j-1}^{n+1}$. For the other site j, the similar performance should be expected. Therefore, a gradual increase in the variation of upstream inflow resulted by any single variable of $Q_{peak}{, Q}_{bottom}{, T}_{peak}, \mathrm{and} \alpha$ would reduce the relative error ${\xi }_h$.

The influence of the four parameters of upstream inflow was considered separately in above analysis. A consideration of the joint influence of the four parameters required a parameter to be proposed to identify which inflow gradually varied. While the relative error ${\xi }_h$ at the downstream end was regarded as a measure of the accuracy of KWA, more attention could be placed on maximum discharge of inflow. For this reason, the present study focused on discharge exceeding 90% of the maximum discharge and the time span ${\eta }_{ts}$ of this region was calculated for each upstream boundary condition (see

Table 2. Time span for each test when discharge exceeded 90% of peak discharge.

Test No.	$0.9 {\mathbf{Q}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$	${\mathbf{\eta }}_{\mathit{t}\mathit{s}} \left(\mathbf{h}\right)$
1	135	4.28
2	225	3.05
3	315	2.78
4	360	2.7
5	450	2.62
6	450	2.82
7	450	3.38
8	450	4.57
9	450	5.98
10	450	3.27
11	450	3.93
12	450	4.57
13	450	5.23
14	450	3.20
15	450	3.70
16	450	4.13
17	450	4.53

).

A clear illustration of the combined influence of the four parameters, $Q_{peak}{, Q}_{bottom}{, T}_{peak}, \mathrm{and} \alpha$, was obtained by extracting the value of relative error from Figure 1 (see

Table 3. The relative error (%) by maximum flow depth for the entire 17 tests.

	${\mathit{x}}^{*}$	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
No.
1		0.18	0.54	0.90	1.24	1.58	1.90	2.21	2.52	2.81	3.09
2		0.40	1.00	1.60	2.20	2.79	3.38	3.97	4.54	5.11	5.64
3		0.54	1.22	1.91	2.59	3.28	3.98	4.67	5.36	6.05	6.66
4		0.61	1.30	2.01	2.72	3.43	4.15	4.88	5.60	6.33	6.95
5		0.71	1.43	2.15	2.89	3.63	4.39	5.15	5.92	6.70	7.29
6		0.63	1.25	1.87	2.49	3.12	3.74	4.37	4.99	5.61	6.08
7		0.45	0.88	1.31	1.74	2.16	2.57	2.98	3.38	3.76	4.05
8		0.27	0.53	0.78	1.02	1.26	1.50	1.72	1.94	2.15	2.31
9		0.18	0.35	0.52	0.68	0.83	0.98	1.13	1.27	1.41	1.50
10		0.48	0.95	1.42	1.90	2.39	2.88	3.38	3.88	4.38	4.76
11		0.34	0.67	1.00	1.34	1.68	2.02	2.37	2.72	3.06	3.32
12		0.25	0.50	0.74	0.99	1.24	1.49	1.75	2.00	2.25	2.43
13		0.19	0.38	0.57	0.76	0.95	1.15	1.34	1.53	1.72	1.86
14		0.50	1.01	1.51	2.03	2.54	3.07	3.60	4.14	4.68	5.08
15		0.39	0.78	1.17	1.57	1.96	2.37	2.78	3.19	3.60	3.90
16		0.32	0.64	0.96	1.28	1.60	1.93	2.27	2.60	2.93	3.17
17		0.27	0.54	0.81	1.08	1.36	1.63	1.91	2.20	2.48	2.68

). From tests No. 5 to No. 17, the higher time span of discharge exceeding 90% of maximum discharge ${\eta }_{ts}$ always indicate the higher relative error ${\xi }_h$ for any x^* (see Table 2 and Table 3), except for tests No. 8 and No. 12 in which the time span was the same but ${\xi }_h$ of test No. 8 exceeded that of test No. 12 at $x^{*}< 0.5$, whereas the relative error of test No. 12 exceeded that of No. 8 at all other sites. This phenomenon resulted from higher bottom discharge in test No. 8, as reflected in the high values of variables in points, $P_j^n$ and $R_{j+1}^n$, when $n = 0$ (see Figure 2), which would restrict the attenuation of DWA, particularly when this bottom discharge was close to peak discharge. After the gradual attenuation of peak discharge along the channel, bottom discharge became increasingly closer to peak discharge, indicating an increase in the restriction of attenuation of DWA. Therefore, the intersection of the two lines between test No. 8 and test No. 12 in ${\xi }_h-x^{*}$ diagram was expected and the second parameter, $Q_{bottom}/Q_{peak}$, should be considered to illustrate the effect of bottom discharge.

Table 3 shows that test No. 1 to No. 4 did not follow the rule of higher ${\eta }_{ts}$ with higher reliability of KWA at the beginning of the channel when compared with other tests. This phenomenon can be explained by Equation (18). A decrease in peak discharge resulted in a reduction in the last term in the root of Equation (18). For this reason, the attenuation of DWA continually decreased and the applicability of KWA improved, and the third parameter, $Q_{peak}$, was considered.

In general, the applicability of KWA could be determined by the three parameters, ${\eta }_{ts}$, $Q_{bottom}/Q_{peak}$, and $Q_{peak}$, when only hydraulic factors were considered. The promotion of the applicability of KWA was indicated by an increased ${\eta }_{ts}$, decreased $Q_{bottom}/Q_{peak}$, and decreased $Q_{peak}$.

3.2. The Influence of Geometrical Factors

The geometrical factors, the Manning coefficient $n$ and slope $S_0$, which would influence the applicability of KWA, were tested. The variations in each of these factors were tested separately to identify their individual influence while hydraulic factors were kept stable. The results are illustrated in Figure 3.

Figure 3a,b clearly shows a reduction in the relative error ${\xi }_h$ with a decreased Manning coefficient and increased slope. Figure 3c shows a more intuitive approach to illustrate the variation in relative error ${\xi }_h$ at the downstream end resulting from geometrical factors.

Under a condition of stabilization of the hydraulic factors of the upstream inflow, the relative error ${\xi }_h$ at the downstream end occurred under a large Manning coefficient with a small slope (see Figure 3c). The effect of the increased slope was offset by a decreased Manning coefficient, resulting in the isoline of ${\xi }_h$ in Figure 3c. Figure 3c shows that the gradient of the isolines of relative error in $n-S_0$ diagram continuously increased with decreasing slope, indicating that the effect of slope would become increasingly more important than the Manning coefficient as slope decreased. In contrast, the influence of the Manning coefficient would become increasingly important while the slope remained steep. The reason for the variation in the relative error ${\xi }_h$ with variation in slope and the Manning coefficient can be obtained by the momentum equation of 1-D SVE, which would illustrate later.

3.3. Identification of Other Criteria for Kinematic Wave Approximation

The focuses of existing criteria were sometimes on overland flow in which the upstream boundary condition was ignored and lateral inflow, such as rainfall, was considered [3,13]. Previous studies [12] were also interested in small perturbation of the steady state inflow. Although Moramarco et al. [18] recognized the limitation of previous studies by considering the influence of the upstream boundary, the parameters selected were the same as in previous studies. In addition, reference discharge was defined as the average discharge expressed by Equation (17), whereas the characteristics were calculated in steady uniform flow of the reference discharge. The prevailing criteria were selected, such as ${KF}_0^2{T/T}_0^{\prime }$ in Ponce et al. [9] and ${TV}_0{S}_{f0}{/h}_0$ in Moussa and Bocquillon [16], and the criterion considered the upstream boundary condition as in Moramarco et al. [18], as the reference criteria and its validity was discussed.

As according to Ponce et al. [9], the criteria which indicate the bound of 95% accuracy were as follows:

$$K{F}_0{}^2\frac{T}{T_0^{\prime }}>257$$

(19)

where $K$ is the kinematic wave number, $F_0$ is the Froude number of reference discharge, $T$ is the wave period, and $T_0^{\prime }$ is the response time of the channel.

As according to Moussa and Bocquillon [16], the following criterion which indicate the bound of 95% accuracy can be derived:

$$\frac{T{V}_0{S}_{f0}}{h_0}\ge 79 \mathrm{and} F_0<0.93$$

(20)

where $V_0{, S}_{f0}{, \mathrm{and} h}_0$ represent the velocity, friction slope, and flow depth of reference discharge, respectively.

Moramarco et al. [18] demonstrated a decrease in the relative error ${\xi }_h$ with increasing kinematic wave number and ${T/T}_0^{\prime }$, and when ${KF}_0^2>25$ and $K<30$, the relative error ${\xi }_h$ fell below 10% for any wave period.

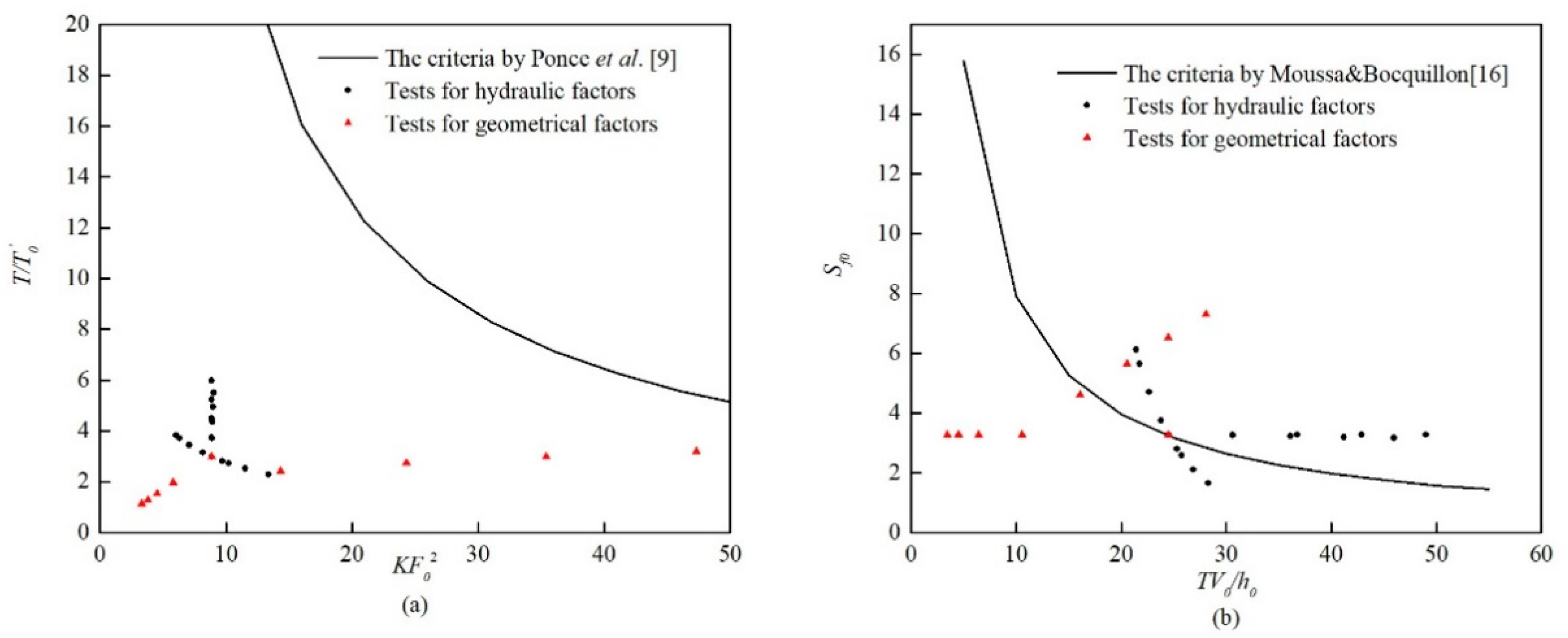
Each test could be identified by these criteria. In Figure 4a, the tests for the effects of variations in hydraulic factors and geometrical factors are illustrated separately in the ${KF}^2-{ T/T}_0^{\prime }$ diagram, with the line of criterion by Ponce et al. [9] used for comparison. It is clear that the position of each numerical test was below the line of Ponce et al. [9]. The relative error ${\xi }_h$ values of tests for hydraulic factors and geometrical factors ranged from 1.5% to 7.3% and from 7.3% to 52%, respectively. Therefore, the criterion of Ponce et al. [9] resulted in the relative error ${\xi }_h$ falling far below 1.5%. The numerical tests showed that the decreased relative error ${\xi }_h$ resulting from each geometrical factor was due to the contribution of the ${KF}_0^2{T/T}_0^{\prime }$. Therefore, the applicability of KWA due to each geometrical factor followed the criterion of Ponce et al. [9]. However, the influence of the hydraulic factors $Q_{bottom}{, T}_{peak}, \mathrm{and} \alpha$ followed the criterion of Ponce et al. [9], whereas the influence of $Q_{peak}$ did not. When considering all hydraulic factors and geometrical factors together, the resulting relative error ${\xi }_h$ was not equivalent along the line ${KF}_0^2{T/T}_0^{\prime }$. In addition, the higher value of ${KF}_0^2{T/T}_0^{\prime }$ in some tests could not be regarded as a lower relative error ${\xi }_h$, particularly when one test was for hydraulic factors and the other was for geometrical factors. Therefore, the criterion of Ponce et al. [9] appeared unreasonable when considering the upstream boundary condition.

To illustrate the criterion of Moussa and Bocquillon [16], two dimensionless parameters were selected as the coordinate axis, as shown in Figure 4b. The restriction of the Froude number is not depicted in the figure, whereas all numerical tests satisfied the limitation. The results of numerical tests clearly fell on both sides of the line of the criterion by Moussa and Bocquillon [16]. Therefore, the criterion by Ponce et al. [9] appeared to be more restrictive than that by Moussa and Bocquillon [16]. Moramarco et al. [18] came to the same conclusion. By calculating the parameter ${TV}_0{S}_{f0}{/h}_0$ for each numerical test following the criterion by Moussa and Bocquillon [16], it was found that the variation in relative error ${\xi }_h$ according to each geometrical factor followed the criterion of Moussa and Bocquillon [16]. However, certain abnormal phenomena could be expected when considering hydraulic factors. While the peak discharge increased with increasing relative error ${\xi }_h$, the value of ${TV}_0{S}_{f0}{/h}_0$ unexpectedly increased. Therefore, both the rules of Moussa and Bocquillon [16] and Ponce et al. [9] faced similar uncertainties.

Although the numerical results of each test were similar to results obtained by Moramarco et al. [18], the criterion followed was too limiting. A definite formula to evaluate the applicability of KWA does not exist, and instead an inequality ($K{F}_0{}^2>25$) with 90% accuracy was present. In addition, some conditions were not considered in the analysis of KWA, such as the initial state of the channel (the base discharge used in the present paper). Under circumstances in which real cases were of a sufficient complexity that not all parameters satisfied the criterion, the application of KWA would cause some confusion.

In general, the existing criterion of KWA could, to some degree, be used to illustrate variation in relative error ${\xi }_h$. However, some situations exist in which these criteria would be questionable.

3.4. Improvement to the Criterion for Kinematic Wave Approximation

The most original approach for considering the reliability of KWA involves reducing the extra terms of DWA to be sufficiently small compared to the kinematic wave to be ignored. The dimensionless form of the 1-D SVE would be better to determine which term can be ignored. Each variable was substituted as follows.

$$h^{*}=h/h_0,V^{*}=V/V_0,x^{*}=x/L_0,t^{*}=t{V}_0/L_0$$

(21)

where $h^{*}{ \mathrm{and} V}^{*}$ are the dimensionless flow depth and flow velocity, respectively, $L_0$ is channel length, and $h_0$ and $V_0$ are the flow depth and flow velocity of the reference discharge, respectively.

Under the expression of the dimensionless variables in Equation (21), the dimensionless form of the momentum equation in 1-D SVE could be expressed as follows.

$$\frac{\partial V^{*}}{\partial t^{*}}+V^{*}\frac{\partial V^{*}}{\partial x^{*}}+\frac{1}{F_0{}^2}\frac{\partial h^{*}}{\partial x^{*}}=\frac{S_0{L}_0}{h_0{F}_0{}^2}(1-\frac{V^{*}{}^2}{h^{*}})$$

(22)

Under situations in which the kinematic wave number in Equation (22) far exceeded the value of the three terms on the left-hand side of Equation (22), DWA would approach KWA. Therefore, the value of kinematic wave number and the three terms at the left-hand side of Equation (22) can be used to determine the applicability of KWA. Clearly, the direct calculation for each partial derivative would be somewhat difficult, and therefore, some parameters, which can be regarded as indicators of these terms, were selected. Considering the relative error ${\xi }_h$ as being the determined value, the reference discharge was selected as the peak discharge of upstream inflow. In addition, the top-most area of the upstream inflow determined the maximum flow depth along the channel. Therefore, the gradient of the top-most area of the upstream inflow representing the influence of a partial derivative of velocity with respect to $t$ and the indirect impact on the partial derivative of velocity with respect to $x$ should be considered. Therefore, ${\eta }_{ts}$ was used. Furthermore, the bottom discharge of upstream inflow also influenced the partial derivative of velocity with respect to $x$. Therefore, the present study considered $Q_{bottom}/Q_{peak}$. The aforementioned three parameters (${KF}_0^2, {\eta }_{ts}, \mathrm{and} Q_{bottom}/Q_{peak}$) represent the effects of the kinematic number and the three terms in left-hand side of Equation (22).

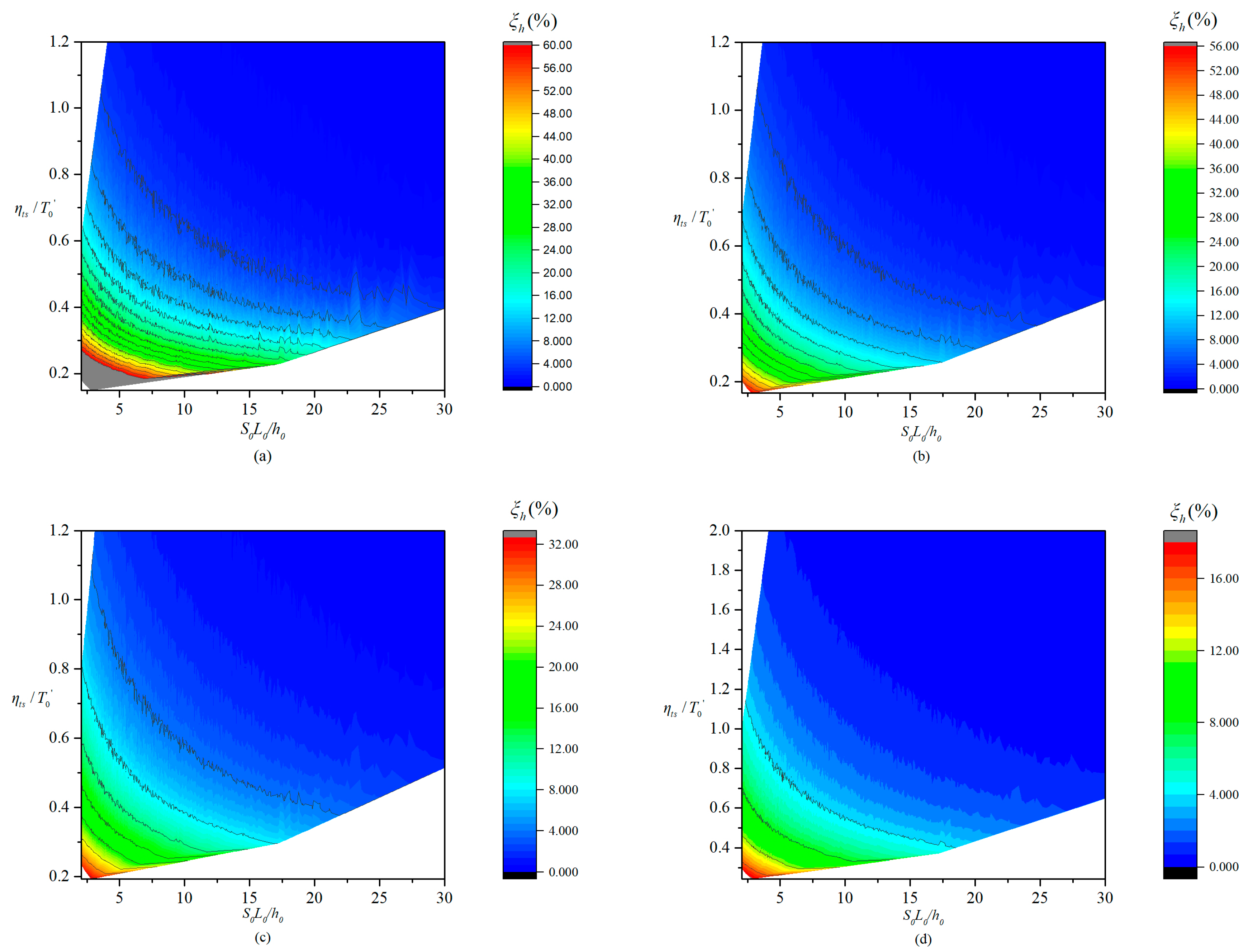
Some adjustments were made to these three parameters to obtain the dimensionless form, and the expressions used were $S_0{L}_0{/h}_0$ (which equals ${KF}_0^2$), ${\eta }_{ts}{/T}_0^{\prime }$, and $Q_{bottom}/Q_{peak}$. The relative error ${\xi }_h$ for different values of these three parameters were calculated to facilitate a good illustration of the influence of these three parameters on the applicability of KWA (see Figure 5). The variation in hydraulic factors and geometrical factors were considered together. The numerical tests were designed so that $Q_{peak} = [300, 400, 500]$, $T_{peak} = [8 \mathrm{h}, 10 \mathrm{h}, 12 \mathrm{h}]$, and $\alpha$ varied from 1.1 to 1.5 with an interval of 0.05, $n$ varied from 0.01 to 0.05 with an interval of 0.002, $S_0$ varied from 0.0002 to 0.0008 with an interval of 0.0001, and channel width and length were 100 m and 60 km, respectively.

The isolines of relative error ${\xi }_h$ could be defined for each $Q_{bottom}/Q_{peak}$ (see Figure 5) while the x-axis was ${KF}_0^2$ and y-axis was ${\eta }_{ts}{/T}_0^{\prime }$. In other words, while there was a definite $Q_{bottom}/Q_{peak}$, the value of ${KF}_0^2$ and ${\eta }_{ts}{/T}_0^{\prime }$ could be used to define the applicability of KWA. In addition, changes in $Q_{bottom}/Q_{peak}$ resulted in changes in the values of ${KF}_0^2$ and ${\eta }_{ts}{/T}_0^{\prime }$, which were used to define a definite relative error ${\xi }_h$. Figure 5 also shows that the isolines fluctuated within a narrow range. This is because that the parameter ${\eta }_{ts}{/T}_0^{\prime }$ was not so extremely accurate to express the steepness of the upper area in the discharge hydrograph. Time span ${\eta }_{ts}$ was calculated by intercepting the upper 10% area of the discharge hydrograph, whereas it was also possible to use the 5% boundary of this area to determine it. In addition, variation in the factors $\alpha$ and $T_{peak}$ would result in an occasional situation in which the higher time span of the upper 10% of the discharge hydrograph was with the lower time span of the upper 5% of the discharge hydrograph. Although many factors were responsible for different values of ${\eta }_{ts}{/T}_0^{\prime }$ and ${KF}_0^2$, this isoline could not be absolutely straight. Therefore, these errors can be ignored due to their insignificant influence and because the patterns expressed in Figure 6 remained clear. In addition, the time span calculated in the upper 10% of the discharge hydrograph was found available to represent the steepness of the hydrograph under most situations.

The present study did not consider variation in channel width and length. The influence of channel width would be similar to that of the Manning coefficient and would only result in a change to the Froude number. The influence of channel length was considered in both $S_0{L}_0{/h}_0$ and ${\eta }_{ts}{/T}_0^{\prime }$. To avoid redundant calculations, the influences of these two parameters were only verified in Figure 6.

Figure 6 shows that for a definite $Q_{peak}$ under different channel lengths and widths, the isolines also formed with small fluctuations. It is reasonable to deduce that this characteristic would be shown for other $Q_{peak}$. For this reason, it can be concluded that the influence of channel length and width were considered in the parameters $S_0{L}_0{/h}_0$ and ${\eta }_{ts}{/T}_0^{\prime }$, and the results shown in Figure 5 were valid for other channel widths and lengths.

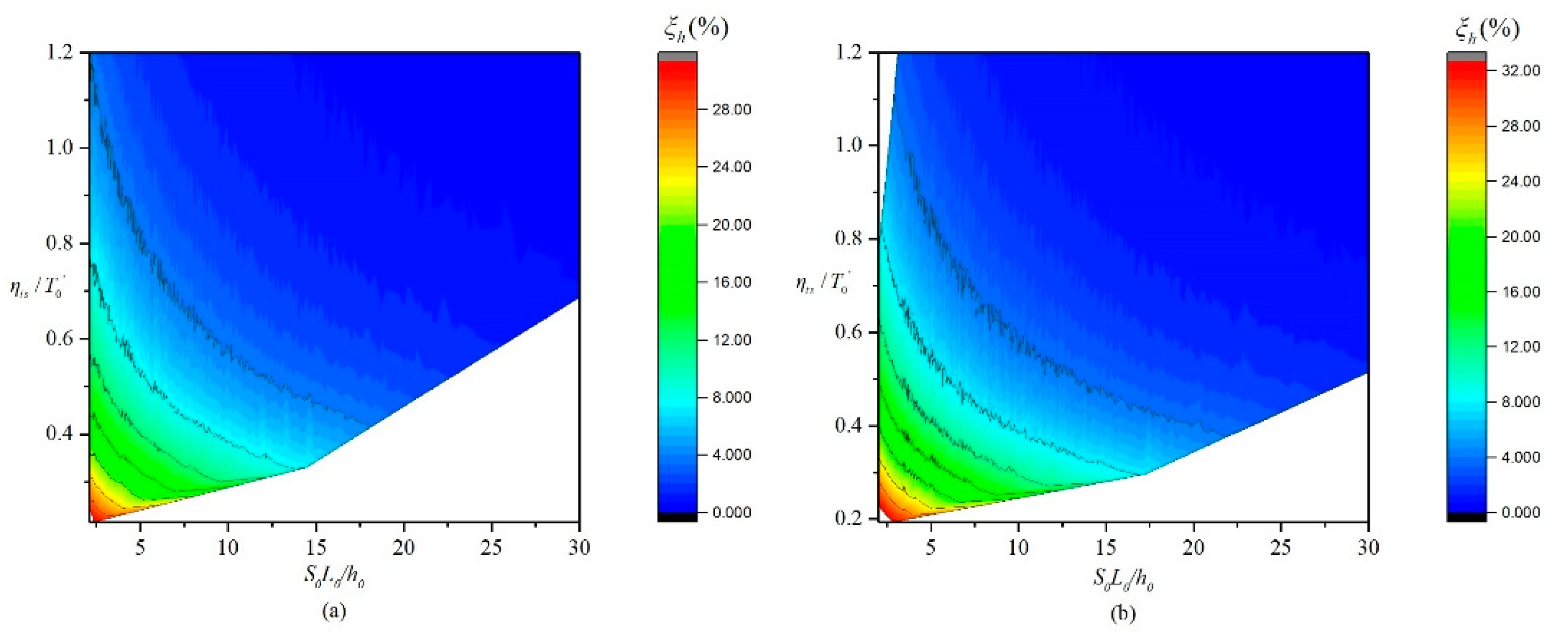
As shown in Figure 7a, the points in the isolines were extracted for each $Q_{bottom}/Q_{peak}$ when the relative error ${\xi }_h$ was equal to 4%, 8%, and 12% to better illustrate the variations in isolines for each $Q_{bottom}/Q_{peak}$.

An increase in $Q_{bottom}/Q_{peak}$ resulted in the isoline of the relative error ${\xi }_h$ moving left. Under this situation, the original position in the diagram showed a reduced relative error ${\xi }_h$, indicating that relative error decreases for higher $Q_{bottom}/Q_{peak}$. The fitting line was drawn for each group of points shown in Figure 7a to depict the relationship expressed by each group of points.

Table 4. The fitting relationship for each group of points ($y$ represents ${\eta }_{ts}{/T}_0^{\prime }$ and $x$ represents $h_0{/(S}_0{L}_0)$).

	${\mathbf{\xi }}_{\mathit{h}}=4\%$	${\mathbf{\xi }}_{\mathit{h}}=8\%$	${\mathbf{\xi }}_{\mathit{h}}=12\%$
Qbottom/Qpeak = 0	y = 2.0 x0.5	y = 1.35 x0.45	y = 1.05 x0.42
Qbottom/Qpeak = 0.2	y = 1.95 x0.52	y = 1.25 x0.48	y = 0.95 x0.46
Qbottom/Qpeak = 0.4	y = 1.88 x0.52	y = 1.16 x0.48	y = 0.82 x0.45
Qbottom/Qpeak = 0.6	y = 1.74 x0.5	y = 0.96 x0.45	y = 0.62 x0.39

shows the fitting relationship of each group of points.

Figure 7a and Table 4 show that the relationship for the definite relative error ${\xi }_h$ between ${\eta }_{ts}{/T}_0^{\prime }$ and ${1/KF}_0^2$ (which equals to $h_0{/(S}_0{L}_0)$) can be generalized to ${y = Cx}^D$. With results of any case falling within the upper area of this line, the relative error ${\xi }_h$ would be below the corresponding value. The parameter ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^D$ could be used to define the expression of the isolines of the corresponding relative error ${\xi }_h$. The corresponding value of this parameter was equal to the value $C$ for each case shown in Table 4. Table 4 shows that the value of $D$ varied in a small range for each relative error ${\xi }_h$, which complicated this criterion. This criterion could be made more practical by adjusting the value of $D$ to a constant for each relative error ${\xi }_h$ (see

Table 5. Adjustment made to the fitting relationship for each group of points ($y$ represents ${\eta }_{ts}{/T}_0^{\prime }$ and $x$ represents $h_0{/(S}_0{L}_0)$).

	${\mathbf{\xi }}_{\mathit{h}}=4\%$	${\mathbf{\xi }}_{\mathit{h}}=8\%$	${\mathbf{\xi }}_{\mathit{h}}=12\%$
Qbottom/Qpeak = 0	y = 2.3 x0.5	y = 1.6 x0.48	y = 1.3 x0.46
Qbottom/Qpeak = 0.2	y = 2.05 x0.5	y = 1.35 x0.48	y = 1.02 x0.46
Qbottom/Qpeak = 0.4	y = 1.95 x0.5	y = 1.2 x0.48	y = 0.89 x0.46
Qbottom/Qpeak = 0.6	y = 1.85 x0.5	y = 1.07 x0.48	y = 0.72 x0.46

).

The line shown in Table 5 was slightly higher than the original line shown in Table 4, as illustrated in Figure 7b–d. These lines were adjusted to be higher than most of the corresponding groups of points (see Figure 7b–d). Therefore, the relative error ${\xi }_h$ expressed by these lines in Table 5 was smaller than that of the original lines shown in Table 4, which facilitated the indication of the relative error ${\xi }_h$ of the corresponding isolines.

The criterion shown in Table 5 was more practical to apply. The exponent of $x$ was constant for the definite relative error with any value of $Q_{bottom}/Q_{peak}$. In addition, only the ratio between $y$ and $x^D$ changed for each $Q_{bottom}/Q_{peak}$. For a relative error of 4%, the parameter ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^{0.5}$ was calculated for each case, and the ratio between $y$ and $x^{0.5}$ listed in Table 5 would be the standard to evaluate ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^{0.5}$ for cases in which a reliable KWA was obtained. Interpolation was used to obtain the ratio between $y$ and $x^{0.5}$ when $Q_{bottom}/Q_{peak}$ was between two values shown in Table 5.

3.5. The Application of the New Criterion

A river reach of the Tiber River, Central Italy, which was used in the study by Moramarco et al. [18], was also used in the present study. The river reach is regarded as a rectangular prismatic channel and

Table 6. The geometrical characteristics of the river reach in the Tiber river, Central Italy.

Width (m)	Length (km)	${\mathit{S}}_0$	$\mathit{n}$
45	23.1	0.0014	0.04

shows the characteristics of the geometry of this reach. Two flood processes which occurred in this river reach were selected.

Table 7. The hydraulic characteristics of the upstream inflow.

Case	${\mathit{Q}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}} ({\mathbf{m}}^3 {\mathbf{s}}^{-1})$	${\mathit{h}}_0 \left(\mathbf{m}\right)$	${\mathit{V}}_0 (\mathbf{m}/\mathbf{s})$	${\mathit{T}}_0^{\prime } \left(\mathbf{h}\right)$	${\mathbf{\eta }}_{\mathit{t}\mathit{s}}\left(\mathbf{h}\right)$
1	210.5	2.75	1.7	2.52	1.22
2	483.8	4.66	2.3	1.85	2.40

shows the corresponding characteristics of the upstream inflow.

All values of $Q_{bottom}/Q_{peak}$ in these two cases fell far below 0.2, and could therefore be regarded as 0. The parameter ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^D$ was calculated for each case (see

Table 8. The results of the parameter ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^D$ for each case.

Case	${\mathbf{\eta }}_{\mathit{t}\mathit{s}}{/\mathit{T}}_0^{\prime }\mathit{·}{{(\mathit{K}\mathit{F}}_0^2)}^{0.5}$	${\mathbf{\eta }}_{\mathit{t}\mathit{s}}{/\mathit{T}}_0^{\prime }\mathit{·}{{(\mathit{K}\mathit{F}}_0^2)}^{0.48}$	${\mathbf{\eta }}_{\mathit{t}\mathit{s}}{/\mathit{T}}_0^{\prime }\mathit{·}{{(\mathit{K}\mathit{F}}_0^2)}^{0.46}$
1	1.66	1.58	1.51
2	3.40	3.27	3.15

). For case 1, the value of ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^{0.48}$ approximated to the corresponding quotient in Table 5, indicating that the relative error ${\xi }_h$ of case 1 was slightly higher than 8%. In addition, in the same way, the relative error ${\xi }_h$ of case 2 was below 4%. The maximum flow discharges for these two cases at the downstream end were 184.4 and 460.9 m³ s⁻¹, respectively, and the corresponding flow depths were calculated as 2.54 and 4.52 m, respectively, under an assumption of steady uniform flow. Therefore, the relative error ${\xi }_h$ values could be calculated for both cases and were equal to 8.4% and 3.2%, respectively, indicating that the new criterion was reliable.

Some factors would influence the relative errors ${\xi }_h$ in these two cases. First, the measured results at the downstream end were used to calculate the relative error ${\xi }_h$. In addition to some other uncertainties, the attenuation in reality along the channel would be higher than that of DWA, whereas the geometry of the reality would be more complicated. Therefore, the calculated relative error ${\xi }_h$ would be much higher. Second, since uniform flow was assumed to calculate the maximum flow depth, the influence of the dynamic wave was ignored. In addition, the slightly lower maximum flow depth at the downstream end was expected, and therefore, the calculated relative error ${\xi }_h$ was lower. This criterion can be considered applicable since it was an estimation of the reliability of KWA in comparison to DWA.

4. Conclusions

The present study compared the influence of hydraulic and geometrical factors on relative error ${\xi }_h$ of KWA, which used to indicate the applicability of KWA. Numerical tests used in the present study were designed to quantify the influence of each factor. These tests were identified by existing criteria, and considering deficiencies of these criteria, a new criterion was proposed. In addition, this new criterion was validated in two real cases. The present study made the following conclusions.

First, factors which influenced the relative error ${\xi }_h$ could be divided into two broad categories, namely, hydraulic factors and geometrical factors. Although upstream inflow was expressed by a Pearson type III curve, its shape was determined by $Q_{bottom}{, Q}_{peak}{, T}_{peak}, \mathrm{and} \alpha$. These factors were regarded as hydraulic factors. The geometrical factors considered included the Manning coefficient and slope. The variation in each factor was calculated using numerical tests, and the result showed that relative error ${\xi }_h$ decreased with decreasing $Q_{peak}$ and Manning’s coefficient and with increasing $Q_{bottom}$, $T_{peak}$, $\alpha$, and slope.

Second, the current study identified the existing criteria by the results of the numerical tests, and the criteria by Ponce et al. [9], Moussa and Bocquillon [16], and Moramarco et al. [18] were selected. It was found that the criterion of Ponce et al. [9] had an extremely restrictive border for a kinematic wave. However, the parameters of the Ponce et al. [9]’s criterion used to indicate the applicability of KWA did not vary monotonically with relative error ${\xi }_h$. Part of the numerical results satisfied the criterion of Moussa and Bocquillon [16], indicating that this criterion was not as restrictive as that of Ponce et al. [9], although their criteria all set a bound of 95% accuracy. Besides, similar uncertainties exist for both criteria. The comparison of the relative error ${\xi }_h$ between each numerical test in the present study followed the criterion of Moramarco et al. [18]. However, Moramarco et al. [18] proposed no concise formula to depict the applicability of KWA, which reduced the practicality of this criterion.

Third, when considering the deficiencies of the existing criteria, a new method to evaluate the applicability of KWA was proposed in the present study. Three parameters used to depict the applicability of a kinematic wave, ${KF}_0^2$, ${\eta }_{ts}{/T}_0^{\prime }$, and $Q_{bottom}/Q_{peak}$, were derived based on the dimensionless form of 1-D SVE and the numerical results. While $Q_{bottom}/Q_{peak}$ was definite, the value of ${\eta }_{ts}{/T}_0^{\prime }·{{(KF}_0^2)}^D$ could be used to determine the relative error ${\xi }_h$. In addition, the exponent $D$ was different for different relative errors ${\xi }_h$ (see Table 5). This new criterion was applied to two real case studies, and it showed a good performance.

The present study focused on the relative error ${\xi }_h$, which used to indicate the applicability of KWA. The contribution of each factor was discussed and a new criterion was proposed. Considering that the comparison between KWA and DWA was restricted to maximum flow depth, and since maximum flow depth is only one of numerous characteristics of the flood routing, some restrictions in the use of this criterion remain. However, the maximum flow depth of flood routing is very important as it is an indicator of whether a river will overflow the channel and whether communities adjacent the river would be influenced. Therefore, this criterion is of practicable value.