Anisotropy in the Free Stream Region of Turbulent Flows through Emergent Rigid Vegetation on Rough Beds
Abstract
:1. Introduction
2. Experimental Program
2.1. Flume Set-Up and Bed Sediments
2.2. Experimental Procedure
3. Results and Discussion
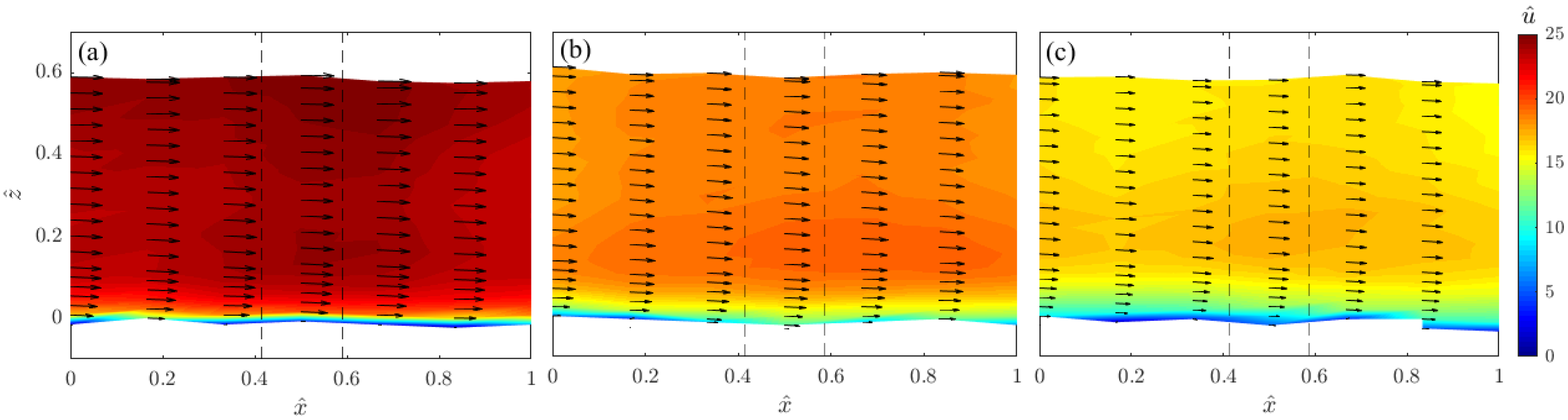
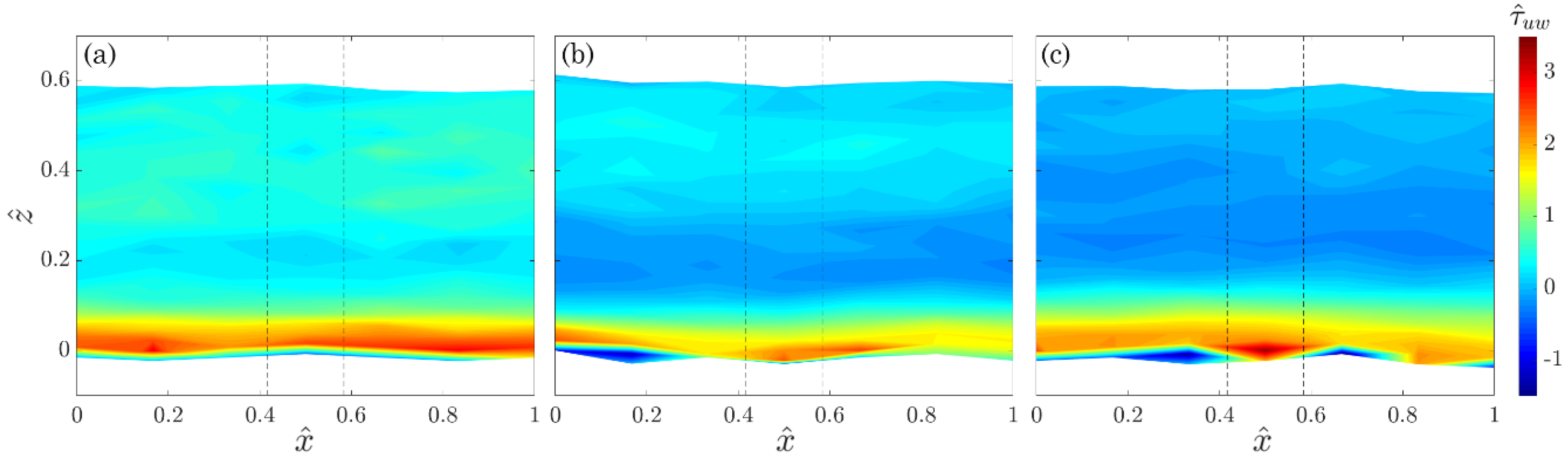
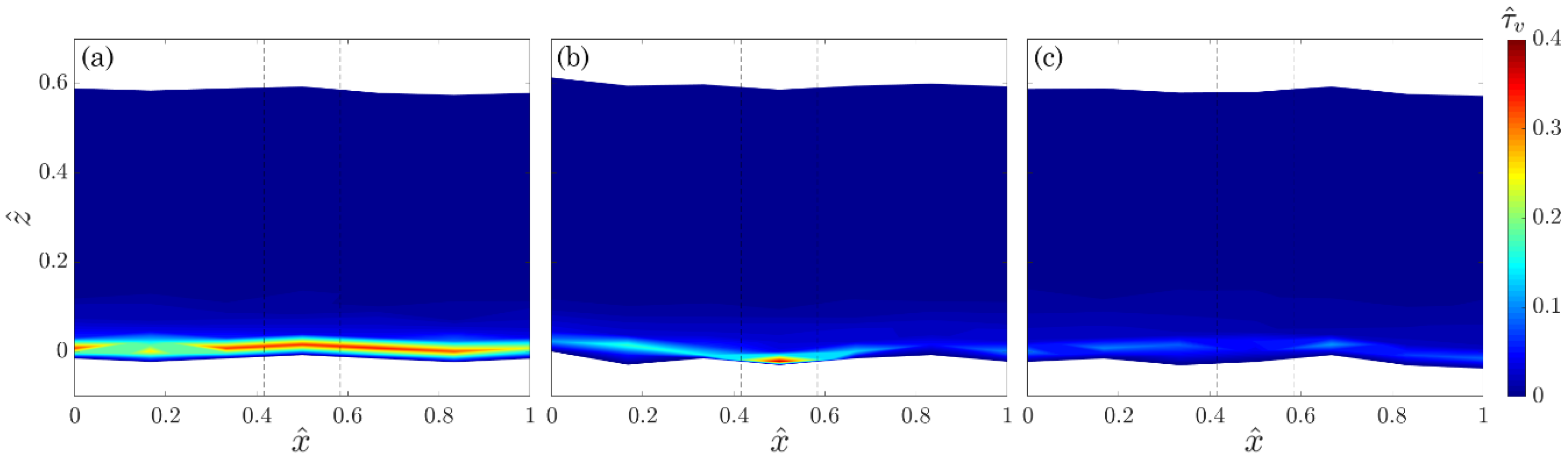
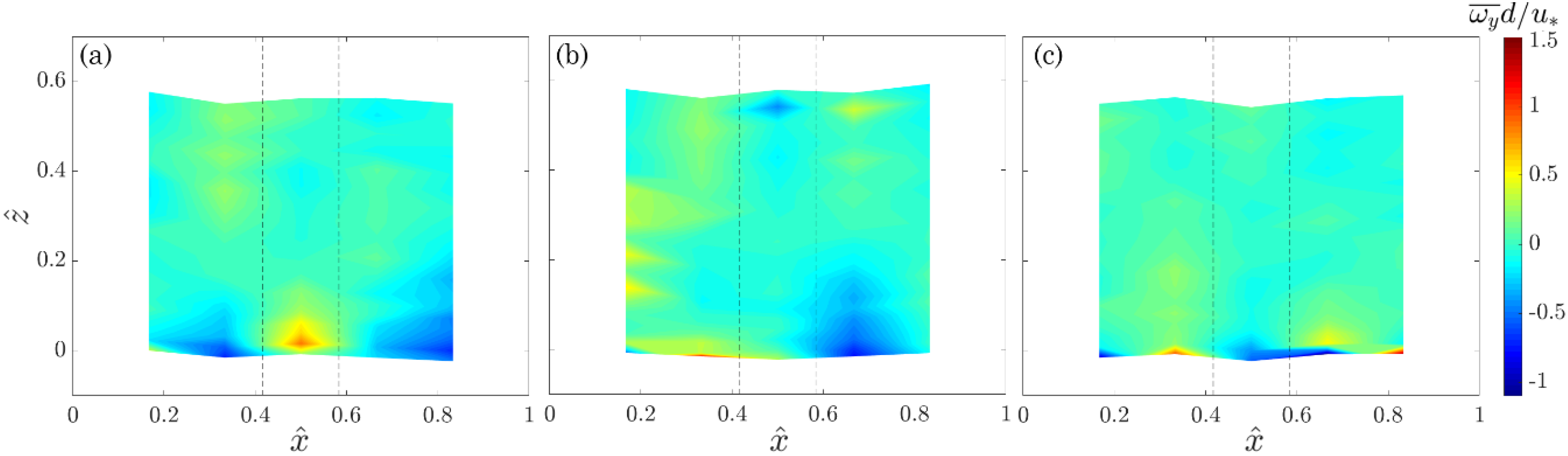
3.1. Time-Averaged Flow
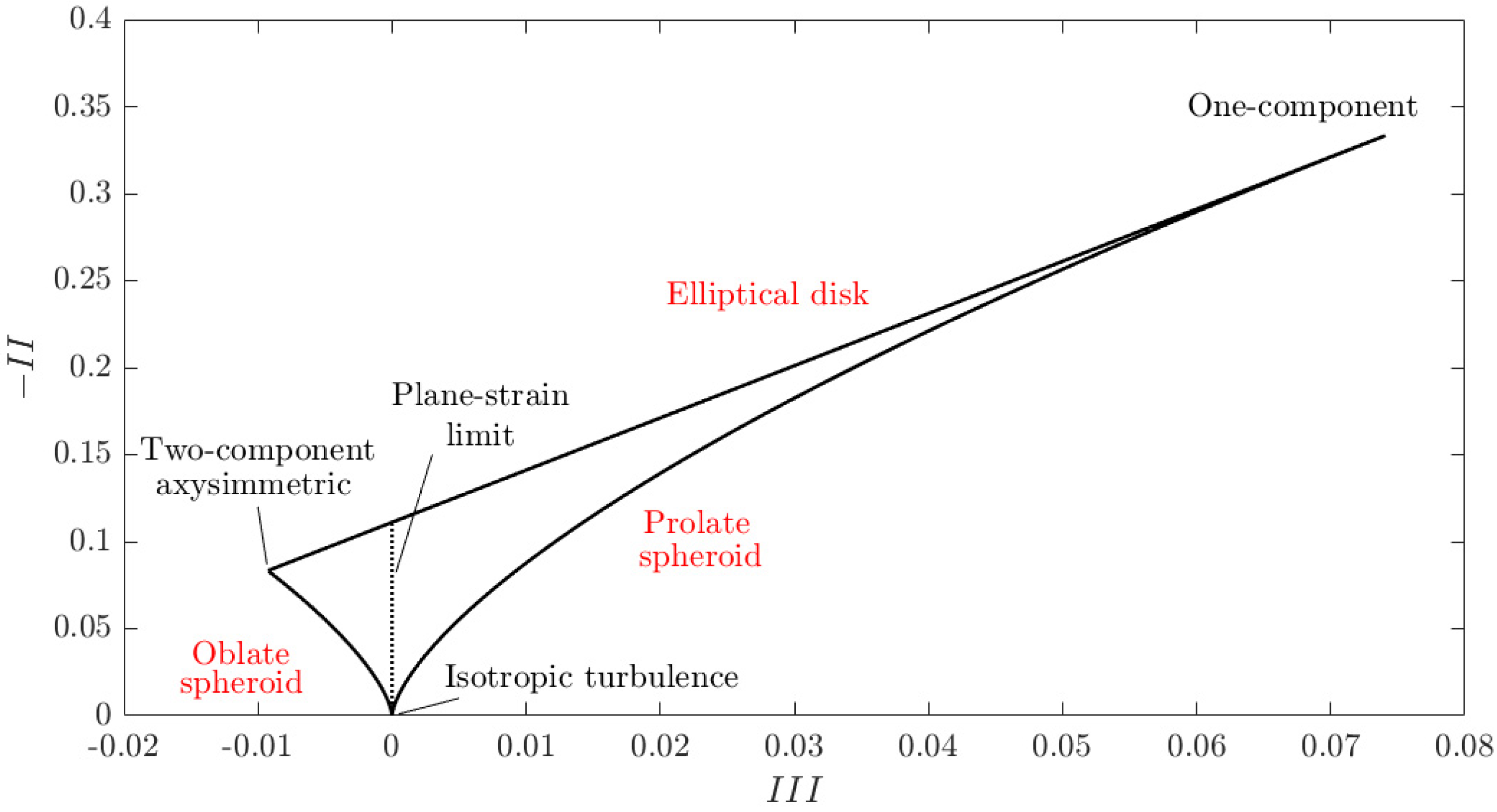
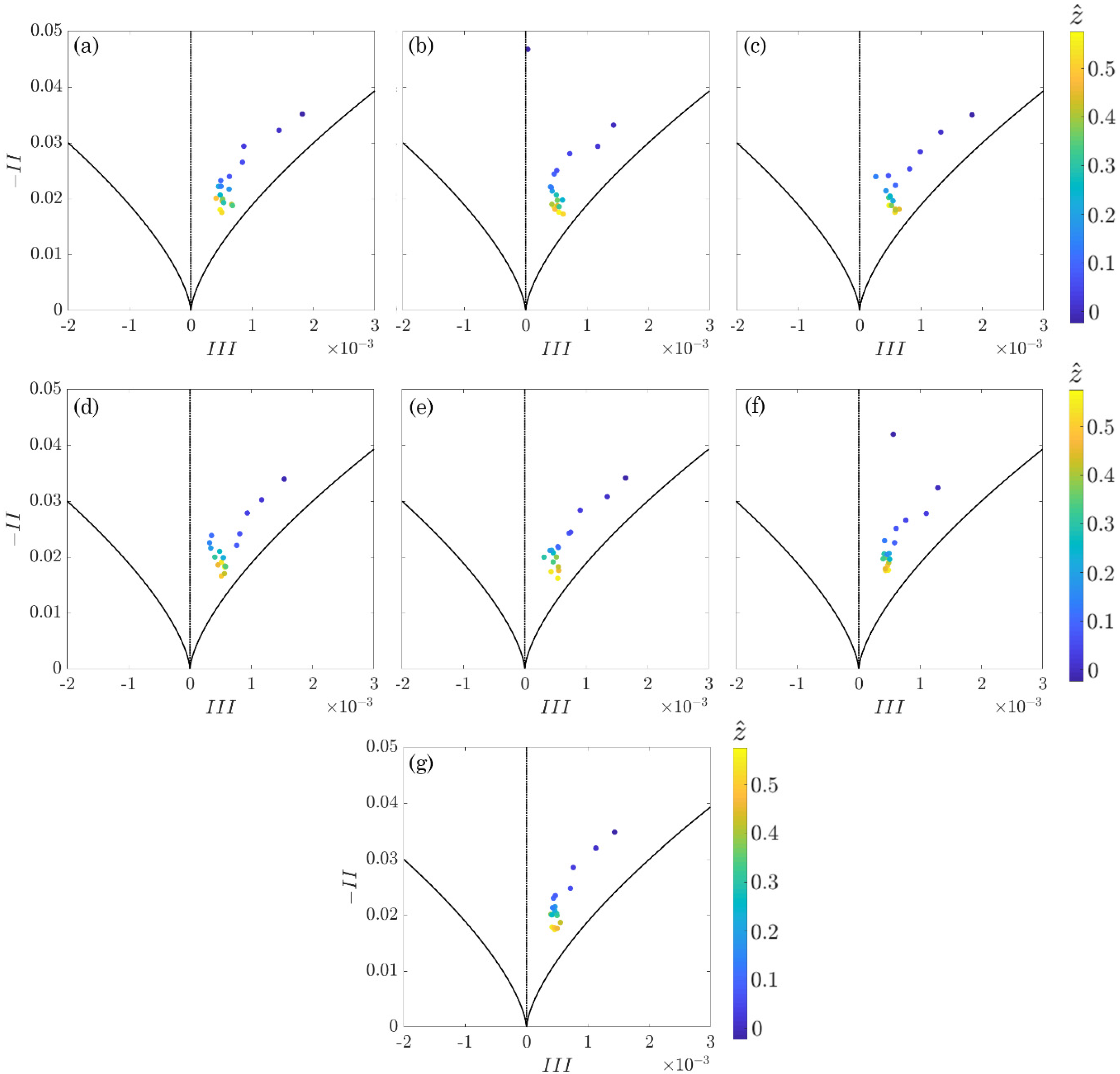
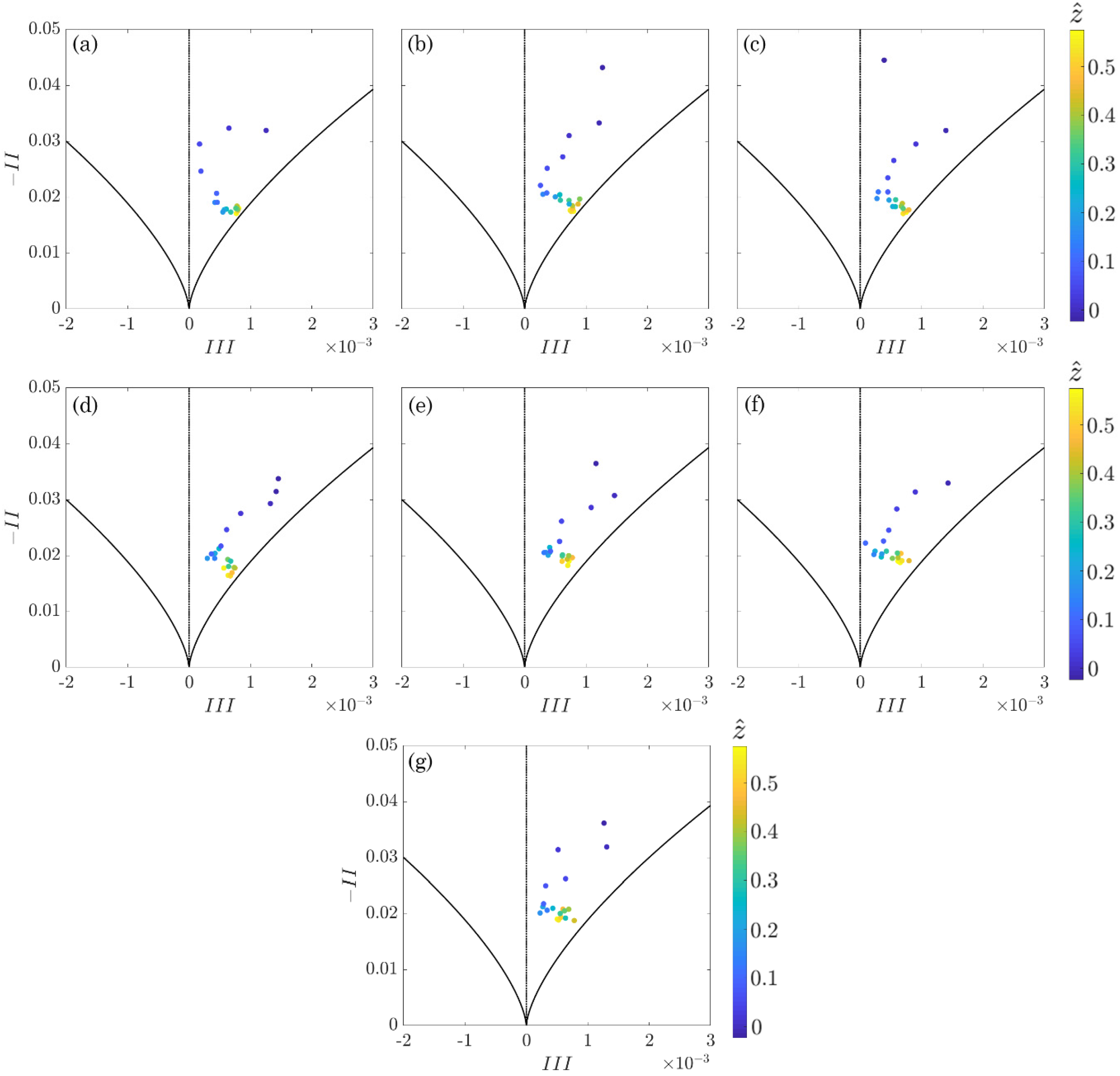
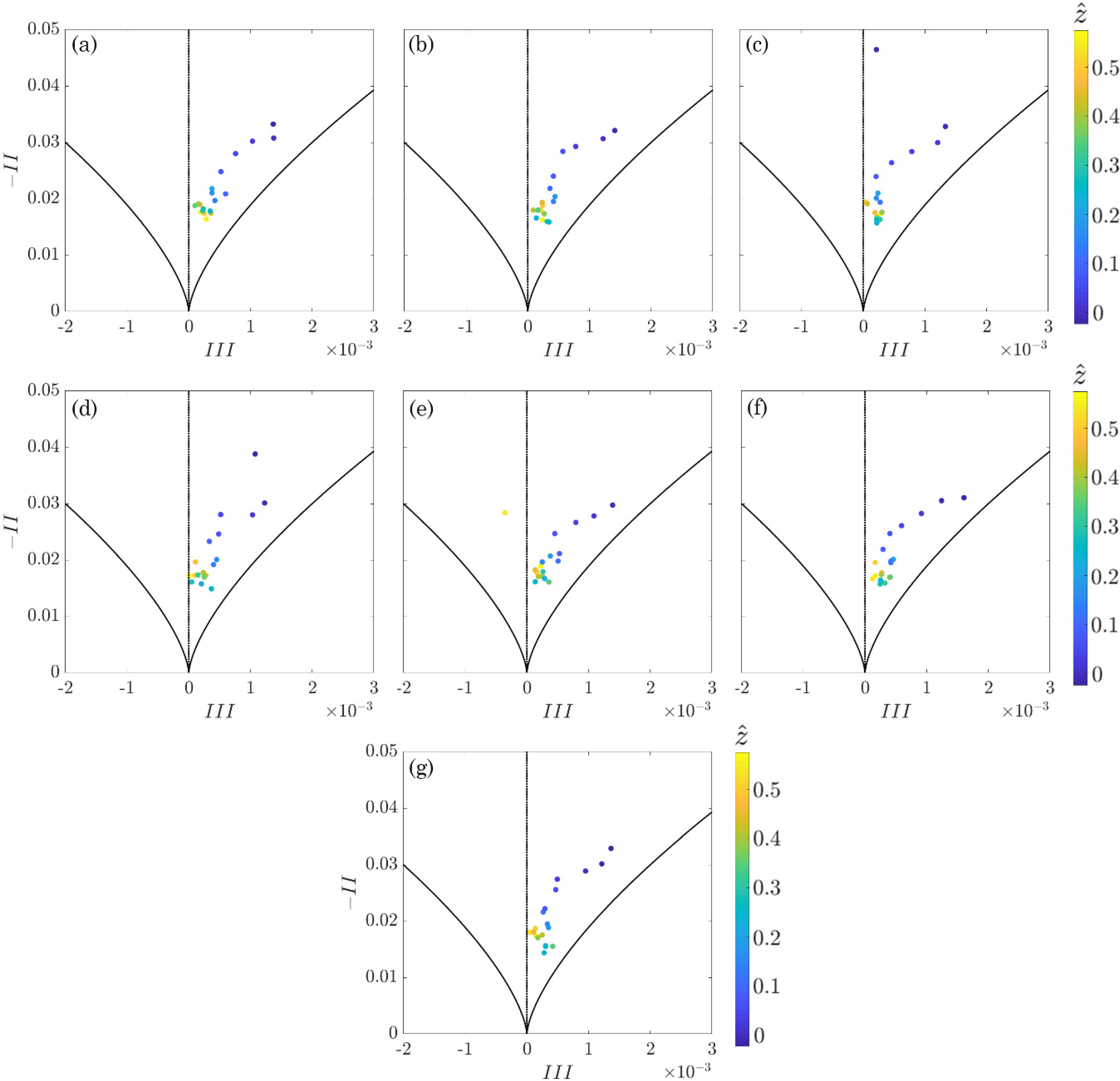
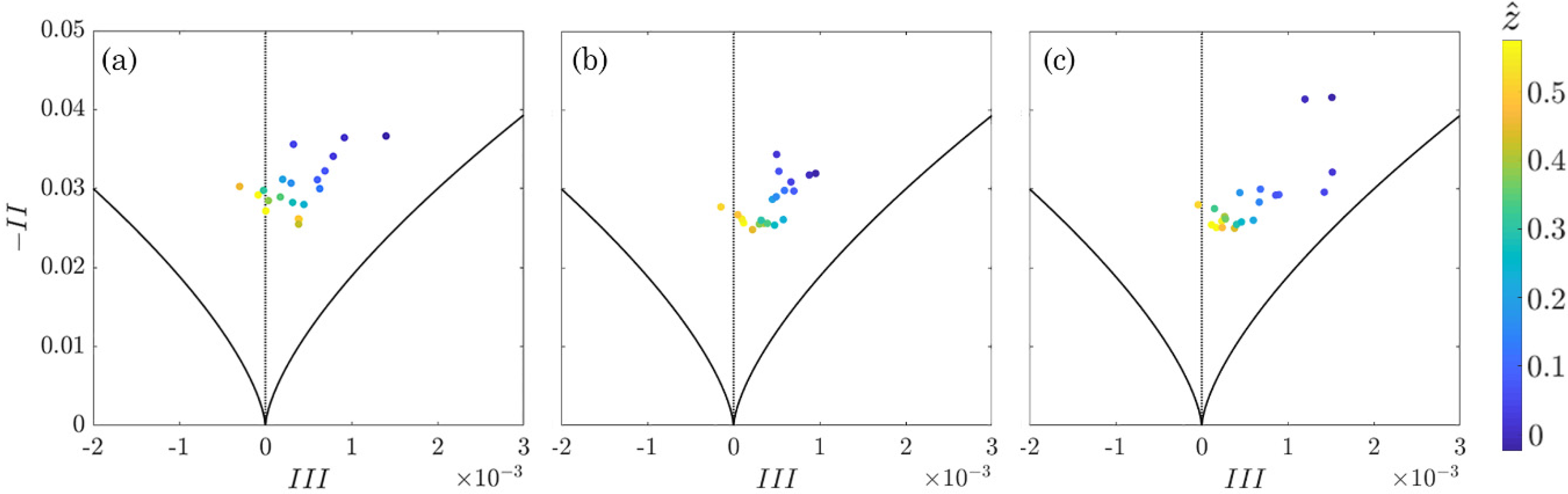
3.2. Anisotropy Invariant Maps
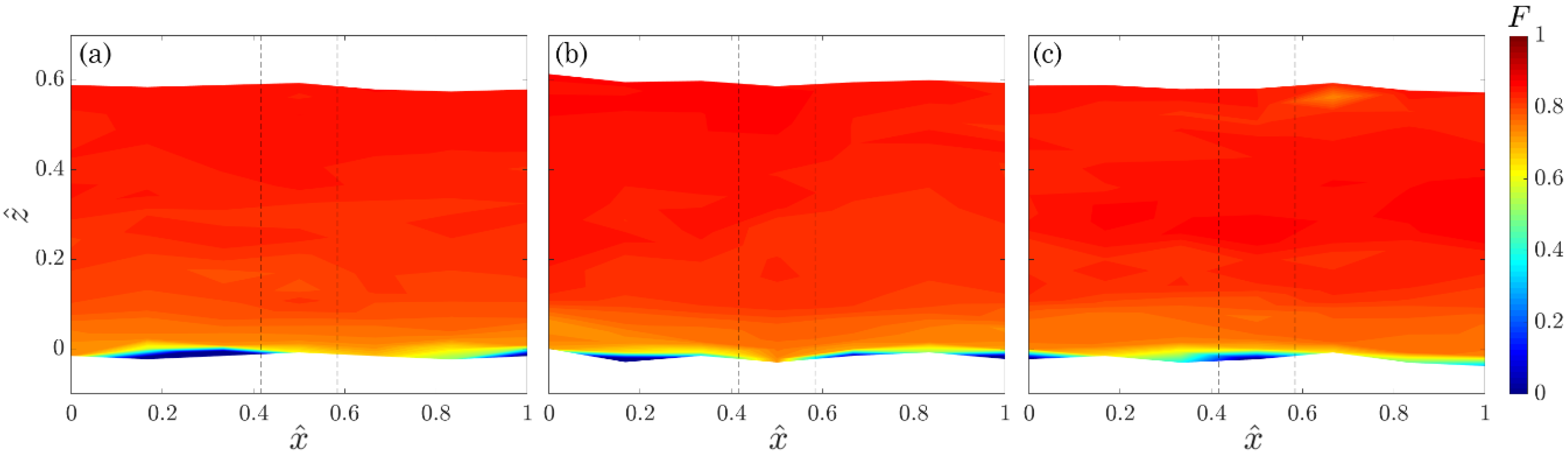
3.3. Anisotropic Invariant Function
3.4. New Research Prospects
4. Conclusions
- Two different zones were characterized along the flume centerline: a convergent flow zone between two stems and toward the flume centerline; a retarded flow zone owing to a divergent flow downstream of the stems. Owing to the bed roughness, a near-bed flow heterogeneity was found, activating the fluid streaks to have motions alternatively in both clockwise and counterclockwise directions. Here, the Reynolds shear stresses increase with a high gradient, but at the crest level they become negligible and the viscous stresses reach their maximum values. However, the quite uniform streamwise distribution of both and reveal that they were not influenced by the position of vegetation stems.
- The analysis of the AIMs revealed that the combined effect of vegetation and bed roughness causes the evolution of the turbulence from the quasi-three-dimensional isotropy (the stress ellipsoid is like a sphere) to a prolate spheroid axisymmetric turbulence. This kind of turbulence anisotropy is kept also near the bed surface. This particular pattern is also confirmed by the contours of the anisotropic invariant function.
- The topographical configuration of the bed surface has a strong impact on the turbulent characteristics of the flow. In fact, on the uphill stretches, the anisotropic invariant function indicates a strong two-dimensional turbulence, since one velocity component is limited by the bed surface. Instead, on the downhill stretches, the anisotropic invariant function reveals that the turbulence can develop in the three directions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Ben Meftah, M.; De Serio, F.; Mossa, M. Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 2014, 26, 065102. [Google Scholar] [CrossRef]
- Caroppi, G.; Gualtieri, P.; Fontana, N.; Giugni, M. Vegetated channel flows: Turbulence anisotropy at flow–rigid canopy interface. Geosciences 2018, 8, 259. [Google Scholar] [CrossRef] [Green Version]
- Rowiński, P.M.; Västilä, K.; Aberle, J.; Järvelä, J.; Kalinowska, M.B. How vegetation can aid in coping with river management challenges: A brief review. Ecohydrol. Hydrobiol. 2018, 18, 345–354. [Google Scholar] [CrossRef] [Green Version]
- Caroppi, G.; Västilä, K.; Järvelä, J.; Rowiński, P.M.; Giugni, M. Turbulence at water-vegetation interface in open channel flow: Experiments with natural-like plants. Adv. Water Resour. 2019, 127, 180–191. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Franca, M.J.; Ferreira, R.M. Turbulent flows within random arrays of rigid and emergent cylinders with varying distribution. J. Hydraul. Eng. 2016, 142, 04016022. [Google Scholar] [CrossRef]
- Schoelynck, J.; De Groote, T.; Bal, K.; Vandenbruwaene, W.; Meire, P.; Temmerman, S. Self-organised patchiness and scale dependent bio-geomorphic feedbacks in aquatic river vegetation. Ecography 2012, 35, 760–768. [Google Scholar] [CrossRef]
- Bearman, P.W.; Zdravkovich, M.M. Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 1978, 89, 33–47. [Google Scholar] [CrossRef]
- Nezu, I.; Sanjou, M. Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2008, 2, 62–90. [Google Scholar] [CrossRef]
- Yang, W.; Choi, S.U. A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 2010, 48, 466–475. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, T. Numerical analysis of turbulent open-channel flow over a vegetation layer using a k-ε turbulence model. J. Hydrosci. Hydraul. Eng. 1994, 11, 57–67. [Google Scholar]
- Nepf, H. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Righetti, M.; Armanini, A. Flow resistance in open channel flows with sparsely distributed bushes. J. Hydrol. 2002, 269, 55–64. [Google Scholar] [CrossRef]
- Choi, S.U.; Kang, H. Numerical investigations of mean flow and turbulence structures of partly-vegetated open-channel flows using the Reynolds stress model. J. Hydraul. Res. 2006, 44, 203–217. [Google Scholar] [CrossRef]
- Poggi, D.; Krug, C.; Katul, G.G. Hydraulic resistance of submerged rigid vegetation derived from first-order closure models. Water Resour. Res. 2009, 45, W10442. [Google Scholar] [CrossRef]
- Gualtieri, P.; De Felice, S.; Pasquino, V.; Doria, G. Use of conventional flow resistance equations and a model for the Nikuradse roughness in vegetated flows at high submergence. J. Hydrol. Hydromech. 2018, 66, 107–120. [Google Scholar] [CrossRef] [Green Version]
- Maji, S.; Hanmaiahgari, P.R.; Balachandar, R.; Pu, J.H.; Ricardo, A.M.; Ferreira, R.M. A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels. Water 2020, 12, 1218. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Bed roughness effects on the turbulence characteristics of flows through emergent rigid vegetation. Water 2020, 12, 2401. [Google Scholar] [CrossRef]
- Emory, M.; Iaccarino, G. Visualizing turbulence anisotropy in the spatial domain with componentality contours. Cent. Turbul. Res. Annu. Res. Briefs 2014, 123–138. [Google Scholar]
- Sarkar, S.; Ali, S.Z.; Dey, S. Turbulence in Wall-Wake Flow Downstream of an Isolated Dunal Bedform. Water 2019, 11, 1975. [Google Scholar] [CrossRef] [Green Version]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef] [Green Version]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- De Serio, F.; Ben Meftah, M.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2018, 120, 98–113. [Google Scholar] [CrossRef]
- Padhi, E.; Penna, N.; Dey, S.; Gaudio, R. Near-bed turbulence structures in water-worked and screeded gravel-bed flows. Phys. Fluids 2019, 31, 045107. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; Gaudio, R. Turbulent Flow Field around Horizontal Cylinders with Scour Hole. Water 2020, 12, 143. [Google Scholar] [CrossRef] [Green Version]
- Ricardo, A.M.; Koll, K.; Franca, M.J.; Schleiss, A.J.; Ferreira, R.M.L. The terms of turbulent kinetic energy budget within random arrays of emergent cylinders. Water Resour. Res. 2014, 50, 4131–4148. [Google Scholar] [CrossRef]
- Lumley, J.L.; Newman, G.R. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 1977, 82, 161–178. [Google Scholar] [CrossRef] [Green Version]
- Dey, S.; Ravi Kishore, G.; Castro-Orgaz, O.; Ali, S.Z. Turbulent length scales and anisotropy in submerged turbulent plane offset jets. J. Hydraul. Eng. 2019, 145, 04018085. [Google Scholar] [CrossRef]
- Choi, K.S.; Lumley, J.L. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 2001, 436, 59–84. [Google Scholar] [CrossRef]
- Penna, N.; Padhi, E.; Dey, S.; Gaudio, R. Structure functions and invariants of the anisotropic Reynolds stress tensor in turbulent flows on water-worked gravel beds. Phys. Fluids 2020, 32, 055106. [Google Scholar] [CrossRef]
- Pu, J.H.; Hussain, A.; Guo, Y.K.; Vardakastanis, N.; Hanmaiahgari, P.R.; Lam, D. Submerged flexible vegetation impact on open channel flow velocity distribution: An analytical modelling study on drag and friction. Water Sci. Eng. 2019, 12, 121–128. [Google Scholar] [CrossRef]
- Lucas, J.; Lutz, N.; Lais, A.; Hager, W.H.; Boes, R.M. Side-channel flow: Physical model studies. J. Hydraul. Eng. 2017, 05015003, 1–11. [Google Scholar] [CrossRef]
- Vidal, A.; Nagib, H.M.; Schlatter, P.; Vinuesa, R. Secondary flow in spanwise periodic in-phase sinusoidal channels. J. Fluid Mech. 2018, 851, 288–316. [Google Scholar] [CrossRef]
- Pu, J.H.; Pandey, M.; Hanmaiahgari, P.R. Analytical modelling of sidewall turbulence effect on streamwise velocity profile using 2D approach: A comparison of rectangular and trapezoidal open channel flows. J. Hydro-Environ. Res. 2020. [Google Scholar] [CrossRef]
- Pu, J.H.; Lim, S.Y. Efficient numerical computation and experimental study of temporally long equilibrium scour development around abutment. Environ. Fluid Mech. 2014, 14, 69–86. [Google Scholar] [CrossRef] [Green Version]
- Pu, J.H. Turbulent rectangular compound open channel flow study using multi-zonal approach. Environ. Fluid Mech. 2019, 19, 785–800. [Google Scholar] [CrossRef] [Green Version]
- Afzalimehr, H.; Maddahi, M.R.; Sui, J.; Rahimpour, M. Impacts of vegetation over bedforms on flow characteristics in gravel-bed rivers. J. Hydrodyn. 2019, 31, 986–998. [Google Scholar] [CrossRef]
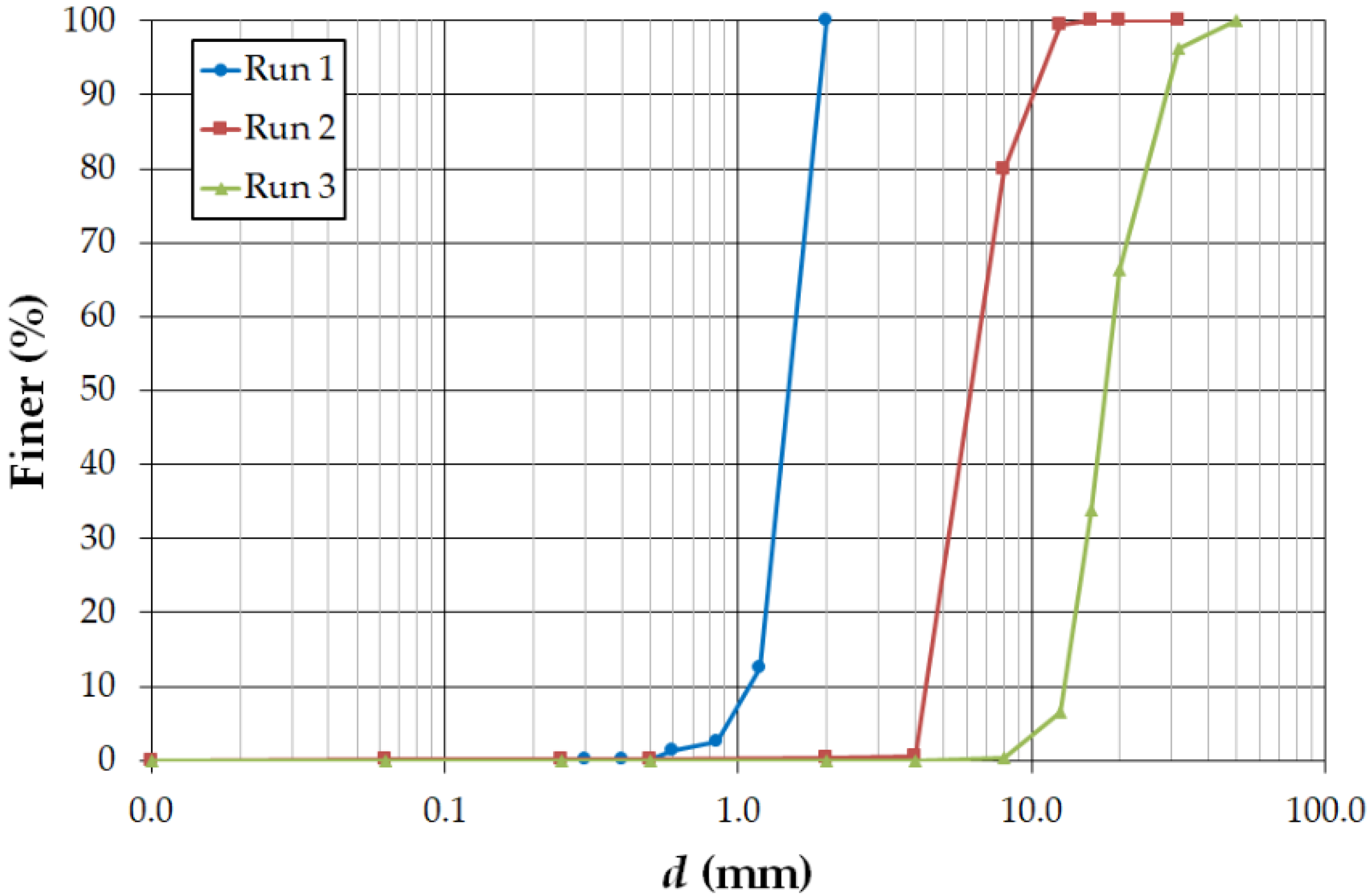
| Run | d50 (mm) | u* (m s−1) | T (°C) | ν (m2 s) | Re* | Red |
|---|---|---|---|---|---|---|
| 1 | 1.53 | 0.017 | 21.70 | 9.63 × 10−7 | 54 | 6231 |
| 2 | 6.49 | 0.022 | 21.44 | 9.69 × 10−7 | 295 | 6192 |
| 3 | 17.98 | 0.028 | 20.80 | 9.83 × 10−7 | 1024 | 6104 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Anisotropy in the Free Stream Region of Turbulent Flows through Emergent Rigid Vegetation on Rough Beds. Water 2020, 12, 2464. https://doi.org/10.3390/w12092464
Penna N, Coscarella F, D’Ippolito A, Gaudio R. Anisotropy in the Free Stream Region of Turbulent Flows through Emergent Rigid Vegetation on Rough Beds. Water. 2020; 12(9):2464. https://doi.org/10.3390/w12092464
Chicago/Turabian StylePenna, Nadia, Francesco Coscarella, Antonino D’Ippolito, and Roberto Gaudio. 2020. "Anisotropy in the Free Stream Region of Turbulent Flows through Emergent Rigid Vegetation on Rough Beds" Water 12, no. 9: 2464. https://doi.org/10.3390/w12092464
APA StylePenna, N., Coscarella, F., D’Ippolito, A., & Gaudio, R. (2020). Anisotropy in the Free Stream Region of Turbulent Flows through Emergent Rigid Vegetation on Rough Beds. Water, 12(9), 2464. https://doi.org/10.3390/w12092464






