State of the Art and Recent Advancements in the Modelling of Land Subsidence Induced by Groundwater Withdrawal
Abstract
1. Introduction
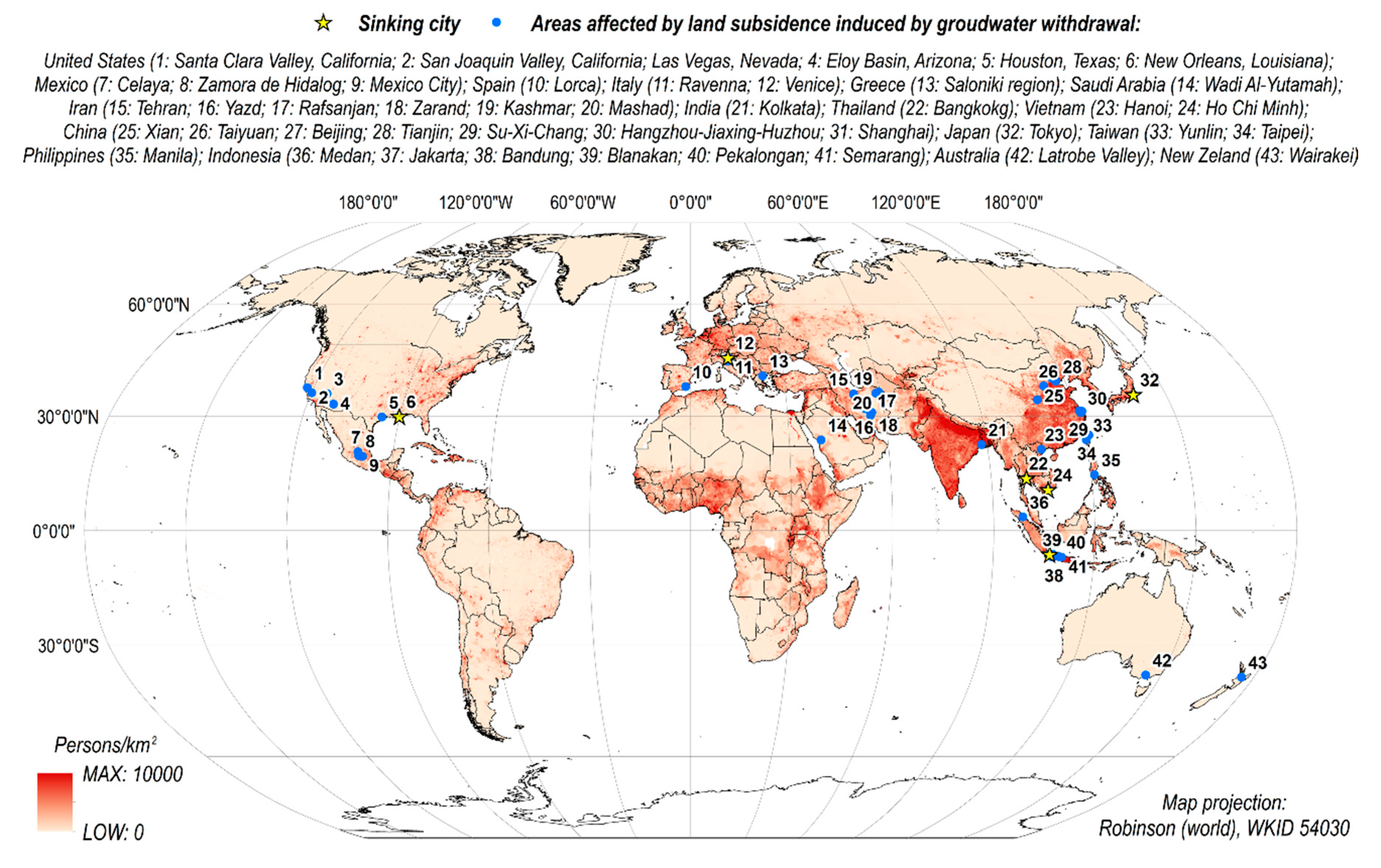
2. Groundwater Withdrawal-Induced Land Subsidence as a Global Problem
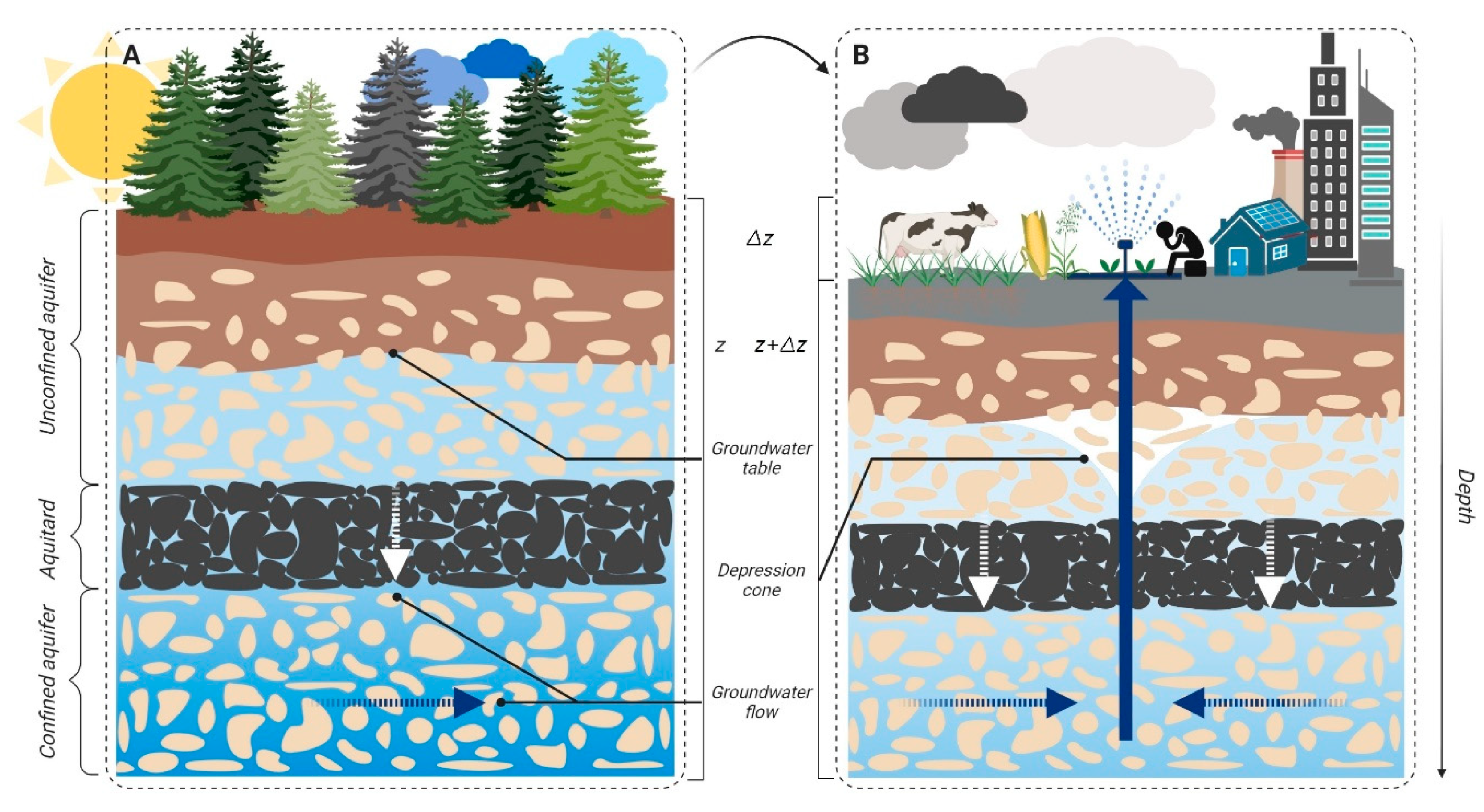
3. Geomechanics of Aquifer Response to Groundwater Withdrawal
3.1. Groundwater Depletion
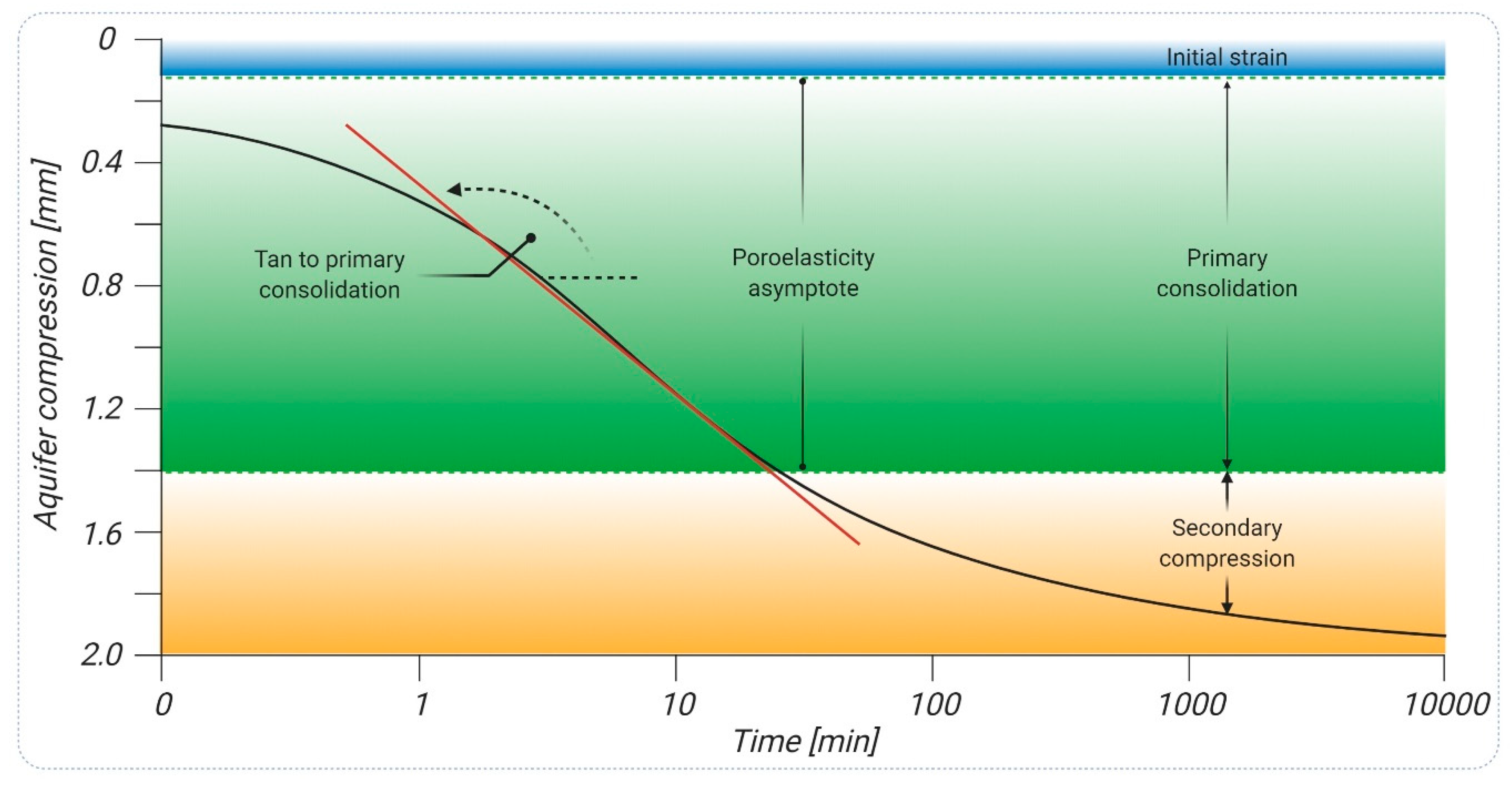
3.2. Aquifer Compaction
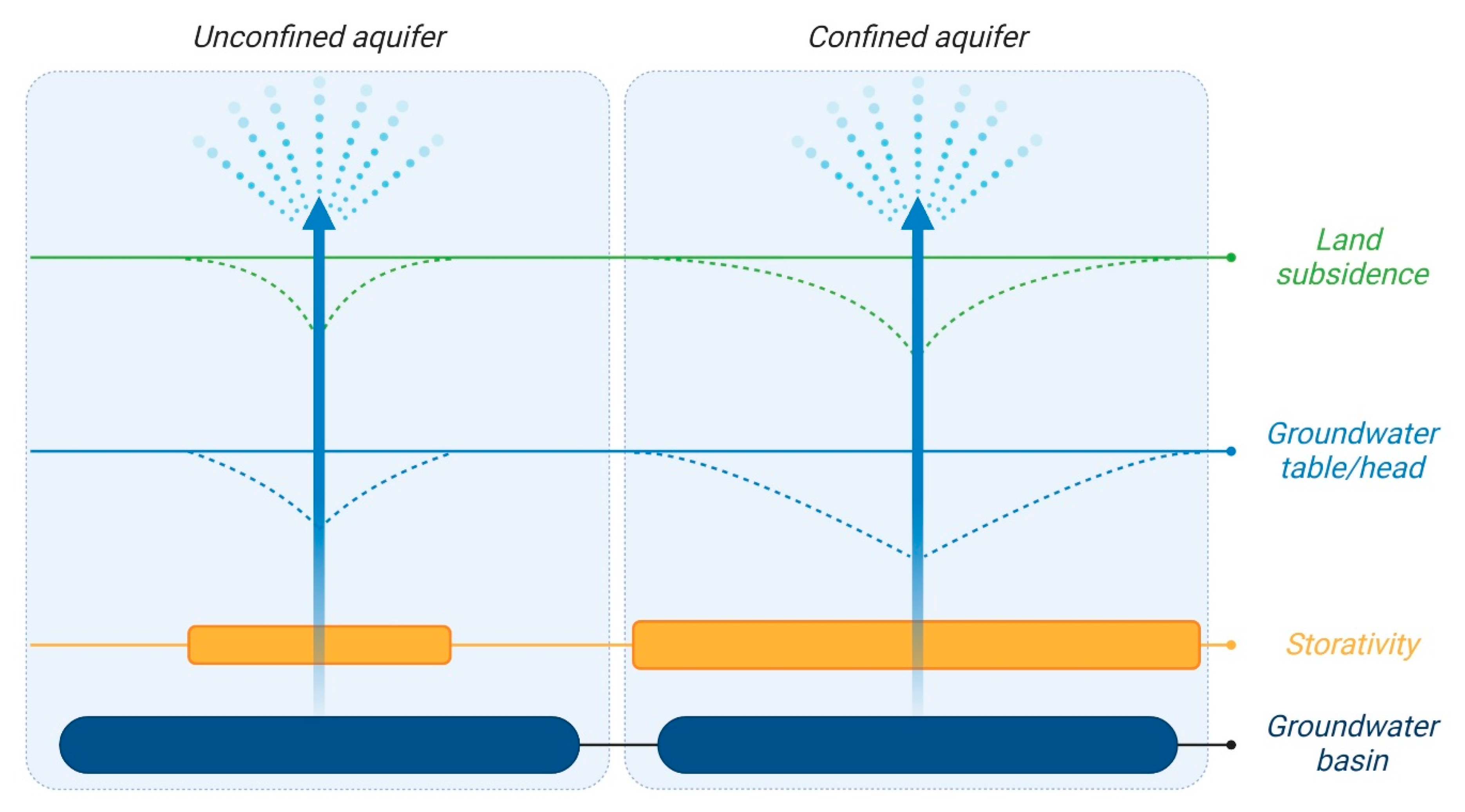
3.3. Groundwater System Response to Groundwater Head Changes Over Time
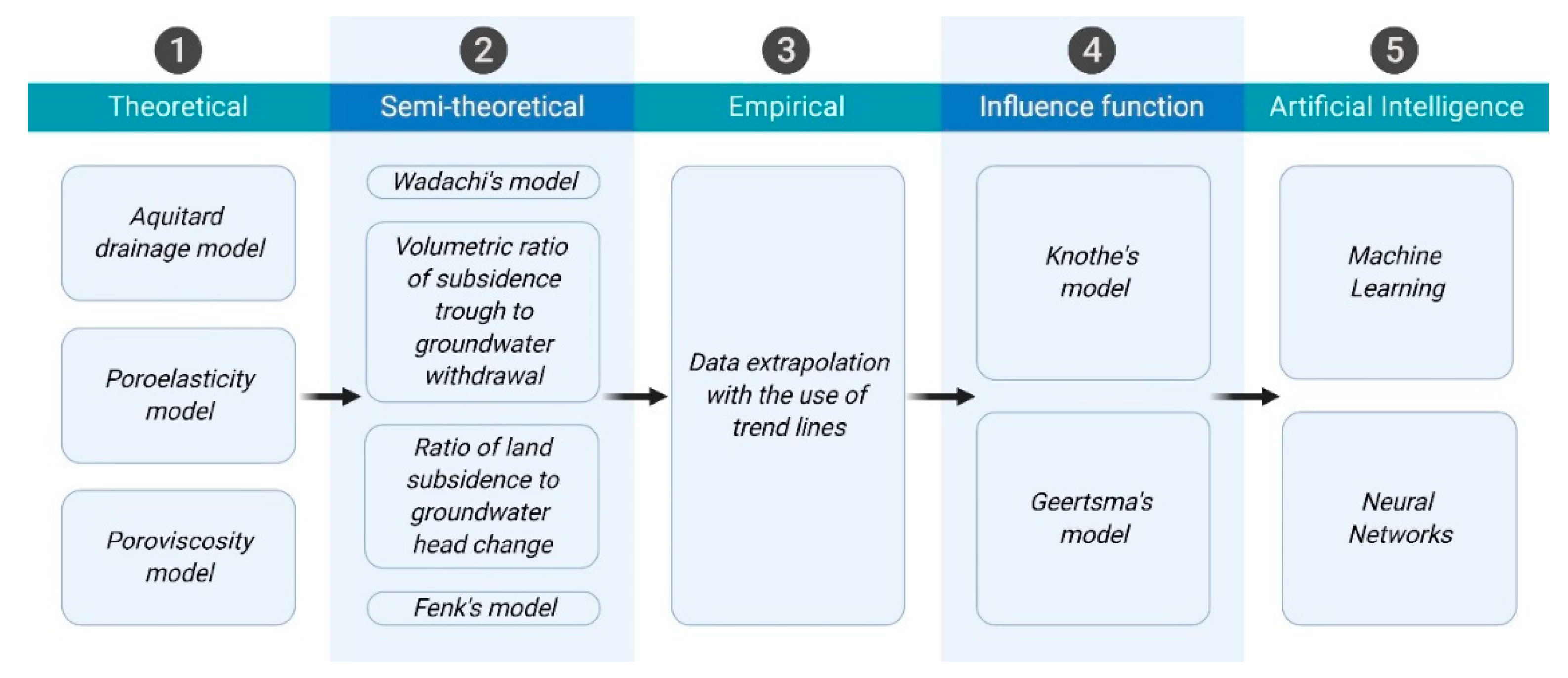
4. Simulation of Land Subsidence Due to Groundwater Withdrawal
4.1. Theoretical Methods
4.1.1. Aquitard Drainage Model
4.1.2. Poroelasticity Model
4.1.3. Poroviscosity Model
4.2. Semi-Theoretical Methods
4.2.1. Wadachi’s Model
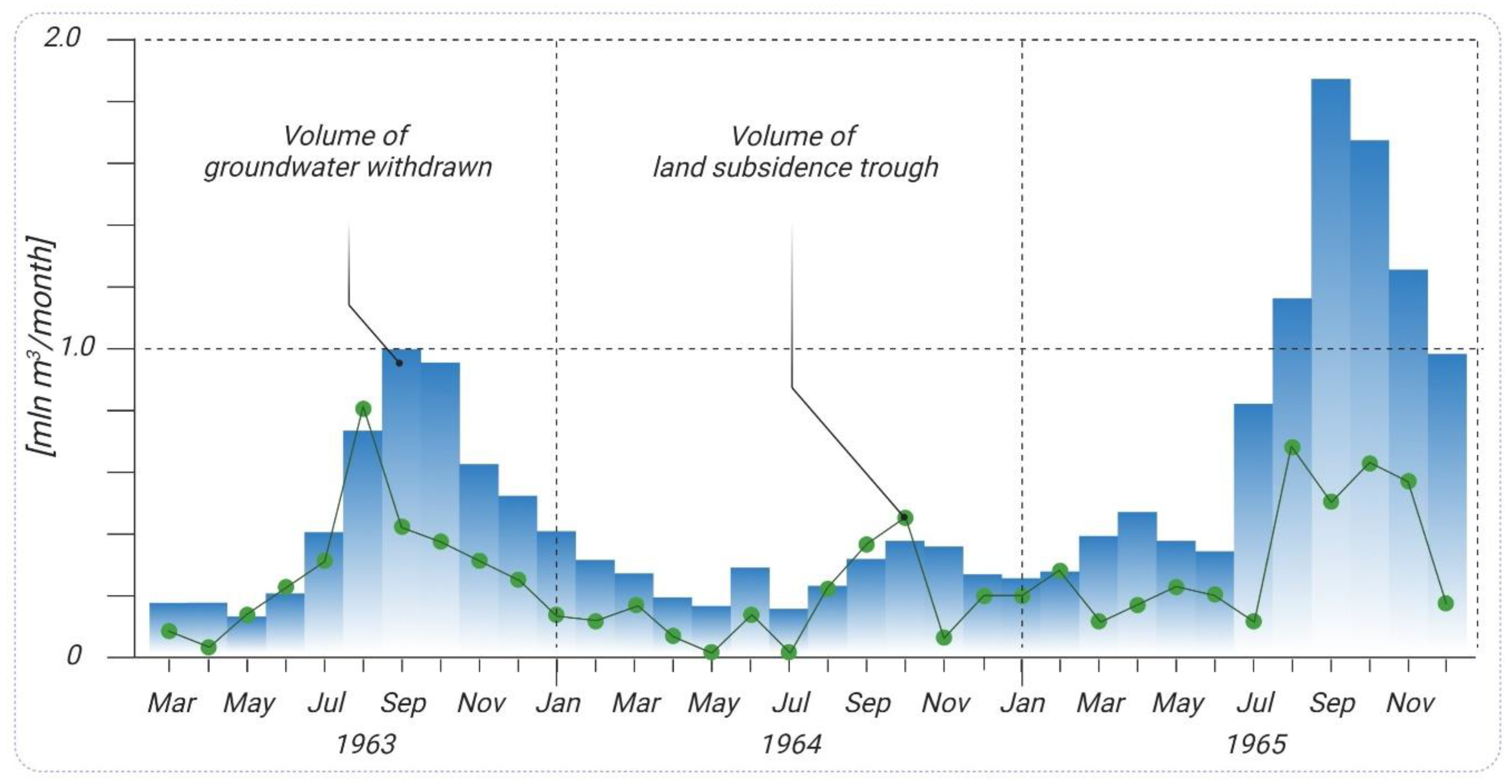
4.2.2. The Volumetric Ratio of Land Subsidence Trough to Groundwater Withdrawal
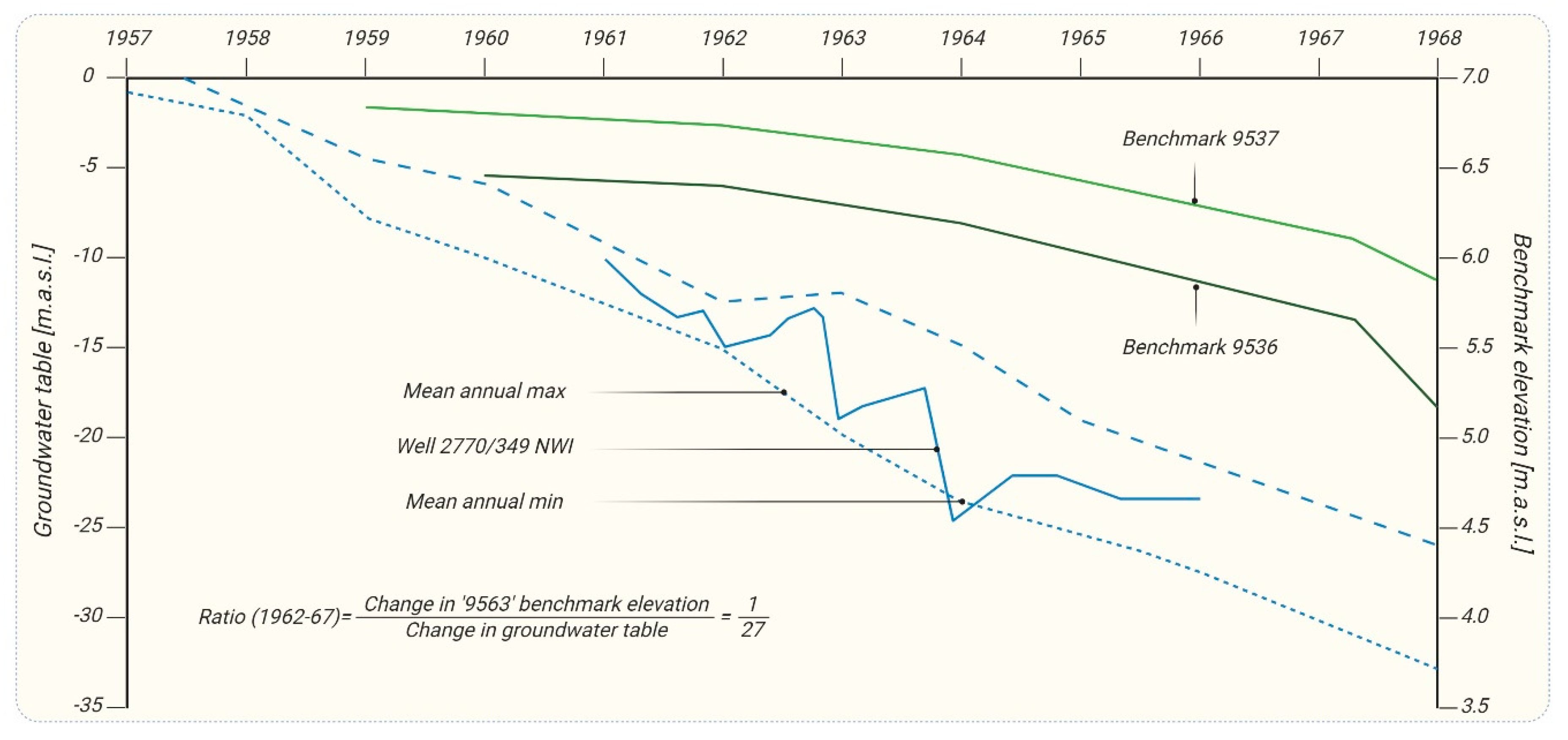
4.2.3. The Ratio of Land Subsidence to Groundwater Head Change
4.2.4. Fenk’s Model
4.3. Empirical Methods
4.4. Influence Function Methods
4.4.1. Knothe’s Model
4.4.2. Geertsma’s Model
4.5. AI Methods
5. InSAR as a Supportive Tool for Groundwater Withdrawal-Related Subsidence Prediction Models
5.1. Application of InSAR Data in Groundwater Withdrawal-Related Subsidence Issues
- structural boundaries of aquifer systems (e.g., tectonic faults);
- the spatio-temporal distribution of land surface displacements and hydrogeological heterogeneity of aquifer system;
- values of storage coefficients and hydraulic conductivity of the aquifer system.
5.1.1. Structural Limits of the Aquifer
5.1.2. Spatio-Temporal Distribution of Land Subsidence and Heterogeneity of Groundwater System
5.1.3. Estimation of the Aquifer Storativity and the Groundwater Head Variations
5.2. InSAR Limitations in Groundwater-Induced Land Displacement Studies
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gambolati, G.; Ricceri, G.; Bertoni, W.; Brighenti, G.; Vuillermin, E. Mathematical Simulation of the Subsidence of Ravenna. Water Resour. Res. 1991, 27, 2899–2918. [Google Scholar] [CrossRef]
- Ortega-Guerrero, A.; Rudolph, D.L.; Cherry, J.A. Analysis of Long-Term Land Subsidence near Mexico City: Field Investigations and Predictive Modeling. Water Resour. Res. 1999, 35, 3327–3341. [Google Scholar] [CrossRef]
- Ehlen, J.; Haneberg, W.C.; Larson, R.A.; Holzer, T.L.; Galloway, D.L. Impacts of Land Subsidence Caused by Withdrawal of Underground Fluids in the United States. In Humans as Geologic Agents; Geological Society of America: Boulder, CO, USA, 2007; Volume 16, pp. 87–99. [Google Scholar] [CrossRef]
- Teatini, P.; Ferronato, M.; Gambolati, G.; Gonella, M. Groundwater Pumping and Land Subsidence in the Emilia-Romagna Coastland, Italy: Modeling the Past Occurrence and the Future Trend. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Shi, X.Q.; Xue, Y.Q.; Ye, S.J.; Wu, J.C.; Zhang, Y.; Yu, J. Characterization of Land Subsidence Induced by Groundwater Withdrawals in Su-Xi-Chang Area, China. Environ. Geol. 2007, 52, 27–40. [Google Scholar] [CrossRef]
- Allis, R.; Bromley, C.; Currie, S. Update on Subsidence at the Wairakei-Tauhara Geothermal System, New Zealand. Geothermics 2009, 38, 169–180. [Google Scholar] [CrossRef]
- Mahmoudpour, M.; Khamehchiyan, M.; Nikudel, M.R.; Ghassemi, M.R. Characterization of Regional Land Subsidence Induced by Groundwater Withdrawals in Tehran, Iran. Geopersia 2013, 3, 49–62. [Google Scholar] [CrossRef]
- Erkens, G.; Bucx, T.; Dam, R.; De Lange, G.; Lambert, J. Sinking Coastal Cities. Proc. Int. Assoc. Hydrol. Sci. 2015. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; De Linage, C.R.; Rodell, M. Satellites Measure Recent Rates of Groundwater Depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Whittaker, B.N.; Reddish, D.J. Subsidence: Occurrence, Prediction, and Control; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Gambolati, G.; Teatini, P. Geomechanics of Subsurface Water Withdrawal and Injection. Water Resour. Res. 2015, 51, 3922–3955. [Google Scholar] [CrossRef]
- Wade, C.M.; Cobourn, K.M.; Amacher, G.S.; Hester, E.T. Policy Targeting to Reduce Economic Damages From Land Subsidence. Water Resour. Res. 2018, 54, 4401–4416. [Google Scholar] [CrossRef]
- Herrera, G.; Tomás, R.; Monells, D.; Centolanza, G.; Mallorquí, J.J.; Vicente, F.; Navarro, V.D.; Lopez-Sanchez, J.M.; Sanabria, M.; Cano, M. Analysis of Subsidence Using TerraSAR-X Data: Murcia Case Study. Eng. Geol. 2010, 116, 284–295. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, Y.; Liu, M.; Wang, R.; Wang, H. Research of Features Related to Land Subsidence and Ground Fissure Disasters in the Beijing Plain. Proc. Int. Assoc. Hydrol. Sci. 2015. [Google Scholar] [CrossRef]
- Béjar-Pizarro, M.; Ezquerro, P.; Herrera, G.; Tomás, R.; Guardiola-Albert, C.; Ruiz Hernández, J.M.; Fernández Merodo, J.A.; Marchamalo, M.; Martínez, R. Mapping Groundwater Level and Aquifer Storage Variations from InSAR Measurements in the Madrid Aquifer, Central Spain. J. Hydrol. 2017, 547, 678–689. [Google Scholar] [CrossRef]
- Pratt, W.E.; Johnson, D.W. Local Subsidence of the Goose Creek Oil Field. J. Geol. 1926, 34, 577–590. [Google Scholar] [CrossRef]
- Shah, T. Groundwater and Human Development: Challenges and Opportunities in Livelihoods and Environment. Water Sci. Technol. 2005, 51, 27–37. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional Land Subsidence Accompanying Groundwater Extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Amitrano, D.; Di Martino, G.; Iodice, A.; Mitidieri, F.; Papa, M.N.; Riccio, D.; Ruello, G. Sentinel-1 for Monitoring Reservoirs: A Performance Analysis. Remote Sens. 2014, 6, 10676–10693. [Google Scholar] [CrossRef]
- Bozzano, F.; Esposito, C.; Franchi, S.; Mazzanti, P.; Perissin, D.; Rocca, A.; Romano, E. Understanding the Subsidence Process of a Quaternary Plain by Combining Geological and Hydrogeological Modelling with Satellite InSAR Data: The Acque Albule Plain Case Study. Remote Sens. Environ. 2015, 168, 219–238. [Google Scholar] [CrossRef]
- Ezquerro, P.; Herrera, G.; Marchamalo, M.; Tomás, R.; Béjar-Pizarro, M.; Martínez, R. A Quasi-Elastic Aquifer Deformational Behavior: Madrid Aquifer Case Study. J. Hydrol. 2014, 519, 1192–1204. [Google Scholar] [CrossRef]
- Ezquerro, P.; Guardiola-Albert, C.; Herrera, G.; Fernández-Merodo, J.A.; Béjar-Pizarro, M.; Bonì, R. Groundwater and Subsidence Modeling Combining Geological and Multi-Satellite SAR Data over the Alto Guadalentín Aquifer (SE Spain). Geofluids 2017. [Google Scholar] [CrossRef]
- Bonì, R.; Cigna, F.; Bricker, S.; Meisina, C.; McCormack, H. Characterisation of Hydraulic Head Changes and Aquifer Properties in the London Basin Using Persistent Scatterer Interferometry Ground Motion Data. J. Hydrol. 2016, 540, 835–849. [Google Scholar] [CrossRef]
- Bonì, R.; Meisina, C.; Cigna, F.; Herrera, G.; Notti, D.; Bricker, S.; McCormack, H.; Tomás, R.; Béjar-Pizarro, M.; Mulas, J.; et al. Exploitation of Satellite A-DInSAR Time Series for Detection, Characterization and Modelling of Land Subsidence. Geosciences 2017, 7, 25. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Hooper, A.J. A Multi-Temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D.; Garduño-Monroy, V.H.; Muñiz-Jauregui, J.A.; García-Hernández, O.H.; Jiménez-Haro, A. Wide-Area InSAR Survey of Surface Deformation in Urban Areas and Geothermal Fields in the Eastern Trans-Mexican Volcanic Belt, Mexico. Remote Sens. 2019, 11, 2341. [Google Scholar] [CrossRef]
- Farolfi, G.; Del Soldato, M.; Bianchini, S.; Casagli, N. A Procedure to Use GNSS Data to Calibrate Satellite PSI Data for the Study of Subsidence:An Example from the North-Western Adriatic Coast (Italy). Eur. J. Remote. Sens. 2019, 1–10. [Google Scholar] [CrossRef]
- Morishita, Y.; Lazecky, M.; Wright, T.J.; Weiss, J.R.; Elliott, J.R.; Hooper, A. LiCSBAS: An Open-Source Insar Time Series Analysis Package Integrated with the LiCSAR Automated Sentinel-1 InSAR Processor. Remote Sens. 2020, 12, 424. [Google Scholar] [CrossRef]
- European Space Agency. Sentinel-1—Missions—Sentinel. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-1 (accessed on 21 March 2020).
- Poland, J.F. Guidebook to Studies of Land Subsidence Due to Ground-Water Withdrawal; UNESCO: Paris, France, 1984. [Google Scholar]
- Tomas, R.; Herrera, G.; Cooksley, G.; Mulas, J. Persistent Scatterer Interferometry Subsidence Data Exploitation Using Spatial Tools: The Vega Media of the Segura River Basin Case Study. J. Hydrol. 2011, 400, 411–428. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2012, 3, 322–329. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.H.; Van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global Depletion of Groundwater Resources. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Wada, Y.; Bierkens, M.F.P. Sustainability of Global Water Use: Past Reconstruction and Future Projections. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Allison, M.; Yuill, B.; Törnqvist, T.; Amelung, F.; Dixon, T.; Erkens, G.; Stuurman, R.; Jones, C.; Milne, G.; Steckler, M.; et al. Global Risks and Research Priorities for Coastal Subsidence. Eos 2016, 97. [Google Scholar] [CrossRef]
- Hu, B.; Chen, X.; Zhang, X. Using Multisensor SAR Datasets to Monitor Land Subsidence in Los Angeles from 2003 to 2017. J. Sens. 2019. [Google Scholar] [CrossRef]
- Castellazzi, P.; Arroyo-Domínguez, N.; Martel, R.; Calderhead, A.I.; Normand, J.C.L.; Gárfias, J.; Rivera, A. Land Subsidence in Major Cities of Central Mexico: Interpreting InSAR-Derived Land Subsidence Mapping with Hydrogeological Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 102–111. [Google Scholar] [CrossRef]
- Jones, C.E.; An, K.; Blom, R.G.; Kent, J.D.; Ivins, E.R.; Bekaert, D.P. Anthropogenic and Geologic Influences on Subsidence in the Vicinity of New Orleans, Louisiana. J. Geophys. Res. Solid Earth 2016. [Google Scholar] [CrossRef]
- Thoang, T.T.; Giao, P.H. Subsurface Characterization and Prediction of Land Subsidence for HCM City, Vietnam. Eng. Geol. 2015, 199, 107–124. [Google Scholar] [CrossRef]
- Pirouzi, A.; Eslami, A. Ground Subsidence in Plains around Tehran: Site Survey, Records Compilation and Analysis. Int. J. Geo-Eng. 2017. [Google Scholar] [CrossRef]
- Aobpaet, A.; Cuenca, M.C.; Hooper, A.; Trisirisatayawong, I. InSAR Time-Series Analysis of Land Subsidence in Bangkok, Thailand. Int. J. Remote Sens. 2013, 34, 2969–2982. [Google Scholar] [CrossRef]
- Guo, L.; Gong, H.; Zhu, F.; Zhu, L.; Zhang, Z.; Zhou, C.; Gao, M.; Sun, Y. Analysis of the Spatiotemporal Variation in Land Subsidence on the Beijing Plain, China. Remote Sens. 2019, 11, 1170. [Google Scholar] [CrossRef]
- Jafari, F.; Javadi, S.; Golmohammadi, G.; Karimi, N.; Mohammadi, K. Numerical Simulation of Groundwater Flow and Aquifer-System Compaction Using Simulation and InSAR Technique: Saveh Basin, Iran. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Rahmawati, N.; Vuillaume, J.F.; Purnama, I.L.S. Salt Intrusion in Coastal and Lowland Areas of Semarang City. J. Hydrol. 2013, 494, 146–159. [Google Scholar] [CrossRef]
- Faunt, C.C.; Sneed, M.; Traum, J.; Brandt, J.T. Water Availability and Land Subsidence in the Central Valley, California, USA. Hydrogeol. J. 2016, 24, 675–684. [Google Scholar] [CrossRef]
- Maps—UNESCO Land Subsidence International Initiative. Available online: https://www.landsubsidence-unesco.org/maps/ (accessed on 2 June 2020).
- Center for International Earth Science Information Network—CIESIN—Columbia University. Gridded Population of the World, Version 4 (GPWv4): Population Density, Revision 11; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2018. [CrossRef]
- Hole, J.K.; Bromley, C.J.; Stevens, N.F.; Wadge, G. Subsidence in the Geothermal Fields of the Taupo Volcanic Zone, New Zealand from 1996 to 2005 Measured by InSAR. J. Volcanol. Geotherm. Res. 2007, 166, 125–146. [Google Scholar] [CrossRef]
- Chaussard, E.; Wdowinski, S.; Cabral-Cano, E.; Amelung, F. Land Subsidence in Central Mexico Detected by ALOS InSAR Time-Series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar] [CrossRef]
- Hu, R.L.; Yue, Z.Q.; Wang, L.C.; Wang, S.J. Review on Current Status and Challenging Issues of Land Subsidence in China. Eng. Geol. 2004, 76, 65–77. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.; Li, X.; Wang, R.; Chen, B.; Dai, Z.; Teatini, P. Land Subsidence Due to Groundwater Withdrawal in the Northern Beijing Plain, China. Eng. Geol. 2015, 193, 243–255. [Google Scholar] [CrossRef]
- Qin, H.; Andrews, C.B.; Tian, F.; Cao, G.; Luo, Y.; Liu, J.; Zheng, C. Groundwater-pumping optimization for land-subsidence control in Beijing plain, China. Hydrogeol. J. 2018, 26, 1061–1081. [Google Scholar] [CrossRef]
- Why Indonesia’s Government Is Moving Capital from Jakarta to a “Strategic Location” in Borneo. Available online: https://www.telegraph.co.uk/news/2019/08/26/indonesias-government-reveals-location-new-capital-jakarta-sinks/ (accessed on 2 June 2020).
- Sinking Basilica in Mexico City. Available online: https://www.usgs.gov/media/images/sinking-basilica-mexico-city (accessed on 2 June 2020).
- Earth Fissure in Residential Area of Chandler Heights, Arizona, AZGS. Available online: https://azgs.arizona.edu/photo/earth-fissure-residential-area-chandler-heights-arizona (accessed on 2 June 2020).
- International Hydrological Programme. Available online: http://www.unesco.org/new/en/natural-sciences/environment/water/ihp/about-ihp/ (accessed on 9 April 2020).
- Tenth International Symposium on Land Subsidence. Available online: https://www.tisols2020.org/tisols2020 (accessed on 9 April 2020).
- Tison, L.J. Land Subsidence: Proceedings of the Tokyo Symposium, September, 1969, Tokyo, Japan; IAHS-UNESCO, The University of Virginia: Charlottesville, VA, USA, 1970. [Google Scholar]
- Johnson, A.I. Land Subsidence Symposium. Eos 1977, 58, 302. [Google Scholar] [CrossRef]
- Johnson, A.I.; Carbognin, L.; Ubertini, L. Land Subsidence. In Proceedings of the 3rd International Symposium, Venice, Italy, 19–25 March 1984; IAHS Publication: Wallingford, UK, 1986. [Google Scholar]
- Johnson, A.I. Proceedings of the Fourth International Symposium on Land Subsidence, Houston, TX, USA; IAHS Press, Institute of Hydrology: Wallingford, Oxfordshire, UK, 1991. [Google Scholar]
- Barends, F.B.J.; Brouwer, F.J.J.; Schröder, F.H. Land Subsidence: Natural Causes, Measuring Techniques, the Groningen Gasfields. In Proceedings of the Fifth International Symposium on Land Subsidence, The Hague, The Netherlands, 16–20 October 1995; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Carbognin, L.; Gambolati, G.; Johnson, A. Land Subsidence: Proceedings of the Sixth International Symposium on Land Subsidence, Ravenna, Italia, 24–29 September 2000; C.N.R: Roma, Italia, 2000. [Google Scholar]
- Zhang, A.; Gong, S.; Carbognin, L.; Johnson, A.I.; Arnold, I. Proceedings of the Seventh International Symposium on Land Subsidence, Held in Shanghai, China; Shanghai Institute of Geological Survey: Shanghai, China, 2005. [Google Scholar]
- Carreón-Freyre, D.; Cerca, M.; Galloway, D.L.; Silva-Corona, J.J.; International Association of Hydrological Sciences. Land Subsidence, Associated Hazards and the Role of Natural Resources Development; International Association of Hydrological Sciences: Wallingford, UK, 2010; Volume 339. [Google Scholar]
- Daito, K.; Galloway, D.L. Preface: Prevention and Mitigation of Natural and Anthoropogenic Hazards Due to Land Subsidence. Proc. Int. Assoc. Hydrol. Sci. 2015, 372, 555–557. [Google Scholar] [CrossRef][Green Version]
- Konikow, L.F. Long-Term Groundwater Depletion in the United States. Ground Water 2014, 53, 2–9. [Google Scholar] [CrossRef] [PubMed]
- Gleeson, T.; Alley, W.M.; Allen, D.M.; Sophocleous, M.A.; Zhou, Y.; Taniguchi, M.; Vandersteen, J. Towards Sustainable Groundwater Use: Setting Long-Term Goals, Backcasting, and Managing Adaptively. Ground Water 2012, 50, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Landes, A.A.L.; Aquilina, L.; De Ridder, J.; Longuevergne, L.; Page, C.; Goderniaux, P. Investigating the respective impacts of groundwater exploitation and climate change on wetland extension over 150 years. J. Hydrol. 2014, 509, 367–378. [Google Scholar] [CrossRef]
- De Marsily, G.; DeLay, F.; Gonçalves, J.; Renard, P.; Teles, V.; Violette, S.; Renard, P. Dealing with spatial heterogeneity. Hydrogeol. J. 2005, 13, 161–183. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, A.J. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Fetter, C.W. Applied Hydrogeology, 4th ed.; Waveland Press: Long Grove, IL, USA, 2018. [Google Scholar]
- Balkhair, K.S. Aquifer Parameters Determination for Large Diameter Wells Using Neural Network Approach. J. Hydrol. 2002, 265, 118–128. [Google Scholar] [CrossRef]
- Schad, H.; Teutsch, G. Effects of the Investigation Scale on Pumping Test Results in Heterogeneous Porous Aquifers. J. Hydrol. 1994, 159, 61–77. [Google Scholar] [CrossRef]
- Kaczmaryk, A.; DeLay, F. Interference pumping tests in a fractured limestone (Poitiers—France): Inversion of data by means of dual-medium approaches. J. Hydrol. 2007, 337, 133–146. [Google Scholar] [CrossRef]
- Jacob, C.E. On the Flow of Water in an Elastic Artesian Aquifer. Trans. Am. Geophys. Union 1940, 21, 574. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155. [Google Scholar] [CrossRef]
- Terzaghi, K. Principles of Soil Mechanics: IV-Settlement and Consolidation of Clay. Eng. News-Rec. 1925, 95, 742–746. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1943. [Google Scholar] [CrossRef]
- Cooper, H.H. The Equation of Groundwater Flow in Fixed and Deforming Coordinates. J. Geophys. Res. 1966, 71, 4785–4790. [Google Scholar] [CrossRef]
- Hoffmann, J.; Zebker, H.A.; Galloway, D.L.; Amelung, F. Seasonal Subsidence and Rebound in Las Vegas Valley, Nevada, Observed by Synthetic Aperture Radar Interferometry. Water Resour. Res. 2001, 37, 1551–1566. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Y.; Wu, J.-C.; Ye, S.; Wei, Z.-X.; Li, Q.-F.; Yu, J. Characteristics of aquifer system deformation in the Southern Yangtse Delta, China. Eng. Geol. 2007, 90, 160–173. [Google Scholar] [CrossRef]
- Theis, C.V. The Relation between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Ground-water Storage. Trans. Am. Geophys. Union 1935, 16, 519. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A Generalized Graphical Method for Evaluating Formation Constants and Summarizing Well-field History. Eos Trans. Am. Geophys. Union 1946, 27, 526. [Google Scholar] [CrossRef]
- Pool, D.R.; Eychaner, J.H. Measurements of Aquifer-Storage Change and Specific Yield Using Gravity Surveys. Ground Water 1995, 33, 425–432. [Google Scholar] [CrossRef]
- Gehman, C.L.; Harry, D.L.; Sanford, W.E.; Stednick, J.D.; Beckman, N.A. Estimating Specific Yield and Storage Change in an Unconfined Aquifer Using Temporal Gravity Surveys. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Poland, J.F.; Davis, G.H. Land Subsidence Due to Withdrawal of Fluids. Landslides 1969, 2, 187–270. [Google Scholar] [CrossRef]
- Chilingarian, G.V.; Donaldson, E.C.; Yen, T.F. Subsidence Due to Fluid Withdrawal. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1996, 33. [Google Scholar] [CrossRef]
- Wilson, A.M.; Gorelick, S. The Effects of Pulsed Pumping on Land Subsidence in the Santa Clara Valley, California. J. Hydrol. 1996, 174, 375–396. [Google Scholar] [CrossRef]
- Amelung, F.; Galloway, D.L.; Bell, J.W.; Zebker, H.A.; Laczniak, R.J. Sensing the Ups and Downs of Las Vegas: InSAR Reveals Structural Control of Land Subsidence and Aquifer-System Deformation. Geology 1999, 27, 483–486. [Google Scholar] [CrossRef]
- Lu, Z.; Danskin, W.R. InSAR Analysis of Natural Recharge to Define Structure of a Ground-Water Basin, San Bernardino, California. Geophys. Res. Lett. 2001, 28, 2661–2664. [Google Scholar] [CrossRef]
- Schmidt, D.A.; Bürgmann, R. Time-Dependent Land Uplift and Subsidence in the Santa Clara Valley, California, from a Large Interferometric Synthetic Aperture Radar Data Set. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Chaussard, E.; Bürgmann, R.; Shirzaei, M.; Fielding, E.J.; Baker, B. Predictability of Hydraulic Head Changes and Characterization of Aquifer-System and Fault Properties from InSAR-Derived Ground Deformation. J. Geophys. Res. Solid Earth 2014, 119, 6572–6590. [Google Scholar] [CrossRef]
- Hammond, W.C.; Burgette, R.J.; Johnson, K.M.; Blewitt, G. Uplift of the Western Transverse Ranges and Ventura Area of Southern California: A Four-Technique Geodetic Study Combining GPS, InSAR, Leveling, and Tide Gauges. J. Geophys. Res. Solid Earth 2018, 123, 836–858. [Google Scholar] [CrossRef]
- Hu, X.; Lu, Z.; Wang, T. Characterization of Hydrogeological Properties in Salt Lake Valley, Utah, Using InSAR. J. Geophys. Res. Earth Surf. 2018, 123, 1257–1271. [Google Scholar] [CrossRef]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.J.; Baker, B. Remote Sensing of Ground Deformation for Monitoring Groundwater Management Practices: Application to the Santa Clara Valley During the 2012–2015 California Drought. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Riley, F.S. Analysis of borehole extensometer data from central California, in Land Subsidence, vol. 2, edited by L. K. Tison. Int. Assoc. Sci. Hydrol. 1969, 89, 423–431. [Google Scholar]
- Borchers, J.W.; Association of Engineering Geologists. Sacramento Section.; Association of Engineering Geologists. Subsidence Committee. Land Subsidence Case Studies and Current Research: Proceedings of the Dr. Joseph F. Poland Symposium on Land Subsidence; California Water Foundation: Sacramento, CA, USA, 1998. [Google Scholar]
- Helm, D.C. One-Dimensional Simulation of Aquifer System Compaction. Water Resour. Res. 1975, 11, 465–478. [Google Scholar] [CrossRef]
- Helm, D.C. One-dimensional Simulation of Aquifer System Compaction near Pixley, California: 2. Stress-Dependent Parameters. Water Resour. Res. 1976, 12, 375–391. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Freeze, R.A. The Role of Aquitards in Multiple-Aquifer Systems. Trans. Am. Geophys. Union 1972, 53, 743. [Google Scholar] [CrossRef]
- Gambolati, G.; Freeze, R.A. Mathematical Simulation of the Subsidence of Venice: 1. Theory. Water Resour. Res. 1973, 9, 721–733. [Google Scholar] [CrossRef]
- Narasimhan, T.N.; Witherspoon, P.A. Numerical Model for Land Subsidence in Shallow Groundwater Systems. In Proceedings of the Second International Symposium on Land Subsidence, Anaheim, CA, USA, 13–17 December 1976. [Google Scholar]
- Neuman, S.P.; Preller, C.; Narasimhan, T.N. Adaptive Explicit-implicit Quasi Three-dimensional Finite Element Model of Flow and Subsidence in Multiaquifer Systems. Water Resour. Res. 1982, 18, 1551–1561. [Google Scholar] [CrossRef]
- Helm, D.C. Field-Based Computational Techniques for Predicting Subsidence Due to Fluid Withdrawal. GSA Rev. Eng. Geol. 1984. [Google Scholar] [CrossRef]
- Helm, D.C. COMPAC: A Field-Tested Model to Simulate and Predict Subsidence Due to Fluid Withdrawal. Aust. Geomech. 1986. [Google Scholar] [CrossRef]
- Pope, J.P.; Burbey, T.J. Multiple-Aquifer Characterization from Single Borehole Extensometer Records. Ground Water 2004, 42, 45–58. [Google Scholar] [CrossRef]
- Liu, Y.; Helm, D.C. Inverse Procedure for Calibrating Parameters That Control Land Subsidence Caused by Subsurface Fluid Withdrawal: 1. Methods. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Liu, Y.; Helm, D.C. Inverse Procedure for Calibrating Parameters That Control Land Subsidence Caused by Subsurface Fluid Withdrawal: 2. Field Application. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hung, W.C.; Hwang, C.; Liou, J.C.; Lin, Y.S.; Yang, H.L. Modeling Aquifer-System Compaction and Predicting Land Subsidence in Central Taiwan. Eng. Geol. 2012, 147, 78–90. [Google Scholar] [CrossRef]
- Prudic, D.E. Documentation of a Computer Program to Simulate Stream-Aquifer Relations Using a Modular, Finite-Difference Ground-Water Flow Model. U.S. Geol. Surv. 1989. [Google Scholar] [CrossRef]
- McDonald, M.G.; Harbaugh, A.W. A Modular Three-Dimensional Finite-Difference Groundwater Flow Model. U.S. Geol. Surv. 1984. [Google Scholar] [CrossRef]
- Larson, K.J.; Basagaoglu, H.; Mariño, M. Numerical Simulation of Land Subsidence in the Los Banos-Kettleman City Area, California; Contrib.—Univ. California, Water Resource Center: Irvine, CA, USA, 2001. [Google Scholar]
- Hanson, R.T.; Anderson, S.R.; Pool, D.R. Simulation of Ground-Water Flow and Potential Land Subsidence, Avra Valley, Arizona. U.S. Geol. Surv. 1990. [Google Scholar] [CrossRef]
- Hanson, R.T.; Benedict, J.F. Simulation of Ground-Water Flow and Potential for Land Subsidence, Upper Santa Cruz Basin, Arizona. U.S. Geol. Surv. 1994. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hudnut, K.W.; Ingebritsen, S.E.; Phillips, S.P.; Peltzer, G.; Rogez, F.; Rosen, P.A. Detection of Aquifer System Compaction and Land Subsidence Using Interferometric Synthetic Aperture Radar, Antelope Valley, Mojave Desert, California. Water Resour. Res. 1998, 34, 2573–2585. [Google Scholar] [CrossRef]
- Nishikawa, T.; Rewis, D.L.; Martin, P. Numerical Simulation of Ground-Water Flow and Land Subsidence at Edwards Air Force Base, Antelope Valley, California. U.S. Geol. Surv. 2001. [Google Scholar] [CrossRef]
- Kasmarek, M.C.; Strom, E.W. Hydrogeology and Simulation of Ground-Water Flow and Land-Surface Subsidence in the Chicot and Evangeline Aquifers, Houston Area, Texas. U.S. Geol. Surv. 2002. [Google Scholar] [CrossRef]
- Don, N.C.; Hang, N.T.M.; Araki, H.; Yamanishi, H.; Koga, K. Groundwater Resources Management under Environmental Constraints in Shiroishi of Saga Plain, Japan. Environ. Geol. 2006, 49, 601–609. [Google Scholar] [CrossRef]
- Leake, S.A. Interbed Storage Changes and Compaction in Models of Regional Groundwater Flow. Water Resour. Res. 1990, 26, 1939–1950. [Google Scholar] [CrossRef]
- Leake, S.A. Simulation of Vertical Compaction in Models of Regional Ground-Water Flow; International Association of Hydrological Sciences: Wallingford, UK, 1991; pp. 565–574. [Google Scholar] [CrossRef]
- Hoffmann, J.; Leake, S.A.; Galloway, D.L.; Wilson, A. MODFLOW-2000 Ground-Water Model—User Guide to the Subsidence and Aquifer-System Compaction (SUB) Package. U.S. Geol. Surv. 2003. [Google Scholar] [CrossRef]
- Harbaugh, B.A.W.; Banta, E.R.; Hill, M.C.; Mcdonald, M.G. MODFLOW-2000, The U.S. Geological Survey Modular Graound-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process. U.S. Geol. Surv. 2000. [Google Scholar] [CrossRef]
- Harbaugh Arlen, W. MODFLOW-2005, The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process. U.S. Geol. Surv. 2005. [Google Scholar] [CrossRef]
- Faunt, C.C. Groundwater Availability of the Central Valley Aquifer, California. U.S. Geol. Surv. 2010. [Google Scholar] [CrossRef]
- Deng, X.; Li, F.; Zhao, Y.; Li, S. Regulation of Deep Groundwater Based on MODFLOW in the Water Intake Area of the South-to-North Water Transfer Project in Tianjin, China. J. Hydroinformatics 2018, 20, 989–1007. [Google Scholar] [CrossRef]
- Leake, S.A.; Galloway, D.L. MODFLOW Ground-Water Model—User Guide to the Subsidence and Aquifer-System Compaction Package (SUB-WT) for Water-Table Aquifers. U.S. Geol. Surv. 2007. [Google Scholar] [CrossRef]
- Leake, S.A.; Galloway, D.L. Use of the SUB-WT Package for MODFLOW to Simulate Aquifer-System Compaction in Antelope Valley, California, USA; International Association of Hydrological Sciences: Wallingford, UK, 2010. [Google Scholar]
- Al-Sittawy, M.; Gad, S.; Fouad, R.; Nofal, E. Assessment of Soil Subsidence Due to Long-Term Dewatering, Esna City, Egypt. Water Sci. 2019, 33, 40–53. [Google Scholar] [CrossRef][Green Version]
- Kooi, H.; Yuherdha, A.T. Updated Subsidence Scenarios Jakarta MODFLOW SUB-CR Calculations for Sunter, Daan Mogot and Marunda; Deltares: Delft, The Netherlands, 2018. [Google Scholar]
- Vassena, C.; Giudici, M.; Ponzini, G. Modelling Land Subsidence Induced by Exploitation of a Multi-Layered Aquifer in Milan (Italy). Acta Universitatis Carolinae Geol. 2002, 46, 641–644. [Google Scholar]
- Verruijt, A. Elastic Storage of Aquifers. In Flow through Porous Media; De Wiest, R.J.M., Ed.; Academic Press: New York, NY, USA, 1969; pp. 331–376. [Google Scholar]
- Kumpel, H.J. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology. Geophys. J. Int. 2002, 150, 828–829. [Google Scholar] [CrossRef][Green Version]
- Ingebritsen, S.E.; Sanford, W.E. Groundwater in Geologic Processes; Cambridge University Press: Cambridge, UK, 1998; p. 536. [Google Scholar] [CrossRef]
- Hsieh, P.A. Deformation-Induced Changes in Hydraulic Head During Ground-Water Withdrawal. Ground Water 1996, 34, 1082–1089. [Google Scholar] [CrossRef]
- Burbey, T.J.; Helm, D.C. Modeling Three-Dimensional Deformation in Response to Pumping of Unconsolidated Aquifers. Environ. Eng. Geosci. 1999, 199–212. [Google Scholar] [CrossRef]
- Burbey, T.J. Stress-Strain Analyses for Aquifer-System Characterization. Ground Water 2001, 39, 128–136. [Google Scholar] [CrossRef]
- Burbey, T.J. The Influence of Faults in Basin-Fill Deposits on Land Subsidence, Las Vegas Valley, Nevada, USA. Hydrogeol. J. 2002, 10, 525–538. [Google Scholar] [CrossRef]
- Helm, D.C. Horizontal Aquifer Movement in a Theis-Thiem Confined System. Water Resour. Res. 1994, 30, 953–964. [Google Scholar] [CrossRef]
- Li, J. Transient Radial Movement of a Confined Leaky Aquifer Due to Variable Well Flow Rates. J. Hydrol. 2007, 333, 542–553. [Google Scholar] [CrossRef]
- Kim, J.-M.; Parizek, R.R. A Mathematical Model for the Hydraulic Properties of Deforming Porous Media. Ground Water 1999, 37, 546–554. [Google Scholar] [CrossRef]
- Aichi, M.; Tokunaga, T. Poroelastic Modeling to Assess the Effect of Water Injection for Land Subsidence Mitigation. Proc. Int. Assoc. Hydrol. Sci. 2015. [Google Scholar] [CrossRef]
- Li, J.; Helm, D.C. Using an analytical solution to estimate the subsidence risk caused by ASR applications. Environ. Eng. Geosci. 2001, 7, 67–79. [Google Scholar] [CrossRef]
- Li, J. A nonlinear elastic solution for 1-D subsidence due to aquifer storage and recovery applications. Hydrogeol. J. 2003, 11, 646–658. [Google Scholar] [CrossRef]
- Jackson, J.D.; Helm, D.C.; Brumley, J.C. The Role of Poroviscosity in Evaluating Land Subsidence Due to Groundwater Extraction from Sedimentary Basin Sequences. Geofis. Int. 2004, 43, 689–695. [Google Scholar]
- Taylor, D.W. Fundamentals of Soil Mechanics. Soil Sci. 1948, 66, 161. [Google Scholar] [CrossRef]
- Jeng, D.I. A Three-Dimensional Model of Poroviscous Aquifer Deformation. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2005. [Google Scholar]
- Jiang, L.; Helm, D. A General Formulation for Saturated Aquifer Deformation under Dynamic and Viscous Conditions. In Land Subsidence. Proceedings to the International Symposium, The Hague, 1995; International Association of Hydrological Sciences: Wallingford, UK, 1995; Volume 234, pp. 323–332. [Google Scholar] [CrossRef]
- Li, J.; Helm, D.C. Numerical Formulation of Dynamic Behavior within Saturated Soil Characterized by Elasto-Viscous Behavior with an Application to Las Vegas Valley. In Computer Method and Advances in Geomechanics, Proceedings of the 9th International Conference of the International Association for Computer Method and Advances in Geomechanics, Wuhan, China 2–7 November 1997; Yuan, J.X., Ed.; CRC Press: Boca Raton, FL, USA, 1997; pp. 911–916. [Google Scholar]
- Schwartz, F.W.; Zhang, H. Fundamentals of Ground Water; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Yamaguchi, R. Change of Water Level of a Deep Weel in the University of Tokyo. Tokyo Univ. Earthq. Res. Inst. Bull. 1969, 47, 1093–1111. [Google Scholar]
- Shibasaki, T.; Shindo, T. The Hydrologic Balance in the Land Subsidence Phenomena. In IASH/UNESCO Tokyo Symposium on Land Subsidence; Tison, L.J., Ed.; International Association of Hydrological Sciences: Wallingford, UK, 1969; pp. 201–215. [Google Scholar]
- Hwang, J.M.; Wu, C.M. Land Subsidence Problems in Taipei Basin. In Proceedings of the Tokyo Symposium on Land Subsidence; International Association of Scientific Hydrology and UNESCO: Tokyo, Japan, 1969; pp. 21–34. [Google Scholar]
- Wolkersdorfer, C.; Thiem, G. Ground Water Withdrawal and Land Subsidence in Northeastern Saxony (Germany). Mine Water Environ. 1999, 18, 81–92. [Google Scholar] [CrossRef]
- Kenselaar, F.; Quadvlieg, R. Trend-Signal Modelling of Land Subsidence. In The 10th FIG International Symposium on Deformation Measurements, California, USA; Metropolitan Water District: Los Angeles, CA, USA, 2001; pp. 336–345. [Google Scholar]
- Guzy, A.; Ahmed, A.W.; Malinowska, A. Spatio-Temporal Distribution of Land Subsidence and Water Drop Caused by Underground Exploitation of Mineral Resources. In International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management; SGEM World Science: Wien, Austria, 2018. [Google Scholar] [CrossRef]
- Malinowska, A.; Hejmanowski, R.; Dai, H.y. Ground Movements Modeling Applying Adjusted Influence Function. Int. J. Min. Sci. Technol. 2020, 30, 243–249. [Google Scholar] [CrossRef]
- Brown, K.; Trott, S. Groundwater Flow Models in Open Pit Mining: Can We Do Better? Mine Water Environ. 2014, 33, 187–190. [Google Scholar] [CrossRef]
- Fokker, P.A.; Orlić, B. Semi-Analytic Modelling of Subsidence. Math. Geol. 2006, 38, 565–589. [Google Scholar] [CrossRef]
- Ren, G.; Buckeridge, J.; Li, J. Estimating Land Subsidence Induced by Groundwater Extraction in Unconfined Aquifers Using an Influence Function Method. J. Water Resour. Plan. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Sroka, A.; Hejmanowski, R. Subsidence Prediction Caused by the Oil and Gas Development. In Proceedings of the 3rd/12th FIG Symposium, Baden, Germany, 22–24 May 2006. [Google Scholar]
- Knothe, S. Equation of the Subsidence Profile. Arch. Min. Metall. 1953, 1, 22–38. [Google Scholar]
- Knothe, S. Observations of Surface Movements under Influence of Mining and Their Theoretical Interpretation. In Proceedings of the European Congress on Ground Movement, Leeds, UK, 9–12 April 1957; pp. 210–218. [Google Scholar]
- Diaz-Fernandez, M.E.; Álvarez-Fernández, M.I.; Álvarez-Vigil, A.E. Computation of influence functions for automatic mining subsidence prediction. Comput. Geosci. 2010, 14, 83–103. [Google Scholar] [CrossRef]
- Burbey, T.J.; Zhang, M. Inverse Modeling Using PS-InSAR for Improved Calibration of Hydraulic Parameters and Prediction of Future Subsidence for Las Vegas Valley, USA. Proc. Int. Assoc. Hydrol. Sci. 2015. [Google Scholar] [CrossRef][Green Version]
- Hejmanowski, R. Modeling of time dependent subsidence for coal and ore deposits. Int. J. Coal Sci. Technol. 2015, 2, 287–292. [Google Scholar] [CrossRef]
- Fokker, P.A.; Van Thienen-Visser, K. Inversion of double-difference measurements from optical leveling for the Groningen gas field. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 1–9. [Google Scholar] [CrossRef]
- Zoccarato, C.; Ferronato, M.; Teatini, P. Formation compaction vs land subsidence to constrain rock compressibility of hydrocarbon reservoirs. Géoméch. Energy Environ. 2018, 13, 14–24. [Google Scholar] [CrossRef]
- Hoffmann, J.; Galloway, D.L.; Zebker, H.A. Inverse modeling of interbed storage parameters using land subsidence observations, Antelope Valley, California. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- McGovern, S.; Kollet, S.; Bürger, C.M.; Schwede, R.L.; Podlaha, O.G. Novel basin modelling concept for simulating deformation from mechanical compaction using level sets. Comput. Geosci. 2017, 148, 2–848. [Google Scholar] [CrossRef]
- Feng, X.-T.; Hudson, J.A. Specifying the information required for rock mechanics modelling and rock engineering design. Int. J. Rock Mech. Min. Sci. 2010, 47, 179–194. [Google Scholar] [CrossRef]
- Witkowski, W.T.; Hejmanowski, R. Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir. Appl. Sci. 2020, 10, 3287. [Google Scholar] [CrossRef]
- Truplett, T.; Yurchak, D. Determination of Intensity Functions for Predicting Subsidence from Coal Mining, Potash Mining, and Groundwater Withdrawal Using the Influence Function Technique. In Proceedings of the 6th. International FIG Symposium on Deformation Measurements: Measurement, Modeling and Prediction, Hannover, Germany, 24–18 February 1998; pp. 761–773. [Google Scholar]
- Hejmanowski, R. Prediction of surface subsidence due to oil- or gasfield development. In Proceedings of the 5th International Symposium on Land Subsidence FISOLS’95, The Hague, The Netherlands, 16–20 October 1995; pp. 291–300. [Google Scholar]
- Hejmanowski, R. Prognozowanie Deformacji Górotworu i Powierzchni Terenu Na Bazie Uogólnionej Teorii Knothego Dla Złóż Surowców Stałych, Ciekłych i Gazowych; IGSMiE PAN: Krakow, Poland, 2001. [Google Scholar]
- McCann, G.D.; Wilts, C.H. A Mathematical Analysis of the Subsidence in the Long Beach—San Pedro Area; California Institute of Technology: Pasadena, CA, USA, 1951. [Google Scholar]
- Geertsma, J. A Basic Theory of Subsidence Due to Reservoir Compaction: The Homogeneous Case. Verhandelingen van het Koninklijk Nederlands Geologisch-Mijnbouwkundig—Kundig Genoot. 1973, 28, 43–62. [Google Scholar]
- Gambolati, G. A Three-Dimensional Model to Compute Land Subsidence. Hydrol. Sci. Bull. 1972, 17, 219–226. [Google Scholar] [CrossRef]
- Fokker, P.A.; Osinga, S. On the Use of Influence Functions for Subsidence Evaluation. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, 17–20 June 2018; American Rock Mechanics Association (ARMA): Alexandria, VA, USA; pp. 1–10. [Google Scholar]
- Bekendam, R.F.; Pottgens, J.J. Ground Movements over the Coal Mines of Southern Limburg, the Netherlands, and Their Relation to Rising Mine Waters. In Land Subsidence, Proceedings of the Fifth International Symposium on Land Subsidence, The Hague, The Netherlands, 16–20 October 1995. [Google Scholar] [CrossRef]
- Lary, D.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Lee, S.; Hyung-Sup, J. (Eds.) Machine Learning Techniques Applied to Geoscience Information System and Remote Sensing; MDPI: Basel, Switzerland, 2019. [Google Scholar] [CrossRef]
- Lee, S.; Park, I.; Choi, J.-K. Spatial Prediction of Ground Subsidence Susceptibility Using an Artificial Neural Network. Environ. Manag. 2011, 49, 347–358. [Google Scholar] [CrossRef]
- Matano, F.; Sacchi, M.; Vigliotti, M.; Ruberti, D. Subsidence Trends of Volturno River Coastal Plain (Northern Campania, Southern Italy) Inferred by SAR Interferometry Data. Geoscience 2018, 8, 8. [Google Scholar] [CrossRef]
- Bui, D.T.; Dou, J.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Lee, S. Land Subsidence Susceptibility Mapping in South Korea Using Machine Learning Algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef]
- Kim, K.D.; Lee, S.; Oh, H.J.; Choi, J.K.; Won, J.S. Assessment of Ground Subsidence Hazard near an Abandoned Underground Coal Mine Using GIS. Environ. Geol. 2006, 50, 1183–1191. [Google Scholar] [CrossRef]
- Pradhan, B.; Abokharima, M.H.; Jebur, M.N.; Tehrany, M.S. Land subsidence susceptibility mapping at Kinta Valley (Malaysia) using the evidential belief function model in GIS. Nat. Hazards 2014, 73, 1019–1042. [Google Scholar] [CrossRef]
- Hu, B.; Zhou, J.; Wang, J.; Chen, Z.; Wang, D.; Xu, S. Risk assessment of land subsidence at Tianjin coastal area in China. Environ. Earth Sci. 2009, 59, 269–276. [Google Scholar] [CrossRef]
- Oh, H.-J.; Lee, S. Assessment of ground subsidence using GIS and the weights-of-evidence model. Eng. Geol. 2010, 115, 36–48. [Google Scholar] [CrossRef]
- Tang, Y.-Q.; Cui, Z.-D.; Wang, J.; Yan, L.-P.; Yan, X.-X. Application of grey theory-based model to prediction of land subsidence due to engineering environment in Shanghai. Environ. Geol. 2007, 55, 583–593. [Google Scholar] [CrossRef]
- Oh, H.-J.; Ahn, S.-C.; Choi, J.-K.; Lee, S. Sensitivity analysis for the GIS-based mapping of the ground subsidence hazard near abandoned underground coal mines. Environ. Earth Sci. 2010, 64, 347–358. [Google Scholar] [CrossRef]
- Choi, J.-K.; Kim, K.-D.; Lee, S.; Won, J.-S. Application of a fuzzy operator to susceptibility estimations of coal mine subsidence in Taebaek City, Korea. Environ. Earth Sci. 2009, 59, 1009–1022. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Aryal, J.; Gholaminia, K. A new GIS-based technique using an adaptive neuro-fuzzy inference system for land subsidence susceptibility mapping. J. Spat. Sci. 2018, 1–17. [Google Scholar] [CrossRef]
- Tan, Z.; Li, P.; Yan, L.; Deng, K. Study of the Method to Calculate Subsidence Coefficient Based on SVM. Procedia Earth Planet. Sci. 2009, 1, 970–976. [Google Scholar] [CrossRef]
- Hejmanowski, R.; Witkowski, W.T. Suitability assessment of artificial neural network to approximate surface subsidence due to rock mass drainage. J. Sustain. Min. 2015, 14, 101–107. [Google Scholar] [CrossRef]
- Zamanirad, M.; Sarraf, A.; Sedghi, H.; Saremi, A.; Rezaee, P. Modeling the Influence of Groundwater Exploitation on Land Subsidence Susceptibility Using Machine Learning Algorithms. Nat. Resour. Res. 2019, 29, 1127–1141. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.; Li, X.; Li, Y.; Su, X.; Guo, G. Comprehensive analysis and artificial intelligent simulation of land subsidence of Beijing, China. Chin. Geogr. Sci. 2013, 23, 237–248. [Google Scholar] [CrossRef]
- European Space Agency. ERS—ESA Earth Online. European Space Agency—Earth Online. 2014. Available online: https://earth.esa.int/web/guest/missions/esa-operational-eo-missions/ers (accessed on 20 April 2020).
- Canadian Space Agency. RADARSAT Constellation Mission—Canada.ca. Available online: https://www.asc-csa.gc.ca/eng/satellites/radarsat/default.asp (accessed on 22 March 2020).
- Covello, F.; Battazza, F.; Coletta, A.; Lopinto, E.; Fiorentino, C.; Pietranera, L.; Valentini, G.; Zoffoli, S. COSMO-SkyMed an existing opportunity for observing the Earth. J. Geodyn. 2010, 49, 171–180. [Google Scholar] [CrossRef]
- European Space Agency. TSX (TerraSAR-X)—eoPortal Directory—Satellite Missions. Available online: https://earth.esa.int/web/eoportal/satellite-missions/t/terrasar-x (accessed on 22 March 2020).
- De Luca, C.; Cuccu, R.; Elefante, S.; Zinno, I.; Manunta, M.; Casola, V.; Rivolta, G.; Lanari, R.; Casu, F. An On-Demand Web Tool for the Unsupervised Retrieval of Earth’s Surface Deformation from SAR Data: The P-SBAS Service within the ESA G-POD Environment. Remote. Sens. 2015, 7, 15630–15650. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Mapping Land Subsidence in Urban Areas Using Esa’s G-POD and the P-SBAS Insar Technique: Examples in Asia, South America And North Africa. In Proceedings of the Mediterranean and Middle-East Geoscience and Remote Sensing Symposium (M2GARSS), Tunis, Tunisia, 9–11 March 2020; pp. 223–226. [Google Scholar] [CrossRef]
- Foumelis, M.; Papadopoulou, T.; Bally, P.; Pacini, F.; Provost, F.; Patruno, J. Monitoring Geohazards Using On-Demand and Systematic Services on Esa’s Geohazards Exploitation Platform. In Proceedings of the 2019 International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2019; pp. 5457–5460. [Google Scholar]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Space Phys. 1989, 94, 9183. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar Interferometry and Its Application to Changes in the Earth’s Surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry, Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 120. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Space Phys. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Zhou, X.; Chang, N.-B.; Li, S. Applications of SAR Interferometry in Earth and Environmental Science Research. Sensors 2009, 9, 1876–1912. [Google Scholar] [CrossRef] [PubMed]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote. Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote. Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric sar images. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Interferometric Point Target Analysis for Deformation Mapping. In Proceedings of the International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2003; Volume 7, pp. 4362–4364. [Google Scholar] [CrossRef]
- Minh, D.H.T.; Hanssen, R.F.; Rocca, F. Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives. Remote Sens. 2020, 12, 1364. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hoffmann, J. The Application of Satellite Differential SAR Interferometry-Derived Ground Displacements in Hydrogeology. Hydrogeol. J. 2007, 15, 133–154. [Google Scholar] [CrossRef]
- Canuti, P.; Casagli, N.; Farina, P.; Marks, F.; Feretti, A.; Menduni, G. Land Subsidence in the Arno River Basin Studied through SAR Interferometry. In Land Subsidence, Proceedings of the Seventh International Symposium on Land Subsidence, Shanghai, China, 23–28 October; Shanghai Institute of Geological Survey: Shanghai, China, 2005; Volume 1, pp. 407–416. [Google Scholar]
- Bawden, G.W.; Thatcher, W.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic Contraction across Los Angeles after Removal of Groundwater Pumping Effects. Nature 2001, 412, 812–815. [Google Scholar] [CrossRef]
- Bell, J.W.; Amelung, F.; Ferretti, A.; Bianchi, M.; Novali, F. Permanent scatterer InSAR reveals seasonal and long-term aquifer-system response to groundwater pumping and artificial recharge. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Buckley, S.M. Land Subsidence in Houston, Texas, Measured by Radar Interferometry and Constrained by Extensometers. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Cigna, F.; Osmanoglu, B.; Cabral-Cano, E.; Dixon, T.; Ávila-Olivera, J.A.; Garduño-Monroy, V.H.; DeMets, C.; Wdowinski, S. Monitoring land subsidence and its induced geological hazard with Synthetic Aperture Radar Interferometry: A case study in Morelia, Mexico. Remote. Sens. Environ. 2012, 117, 146–161. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. Sar monitoring of progressive and seasonal ground deformation using the permanent scatterers technique. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef]
- Haghighi, M.H.; Motagh, M. Ground surface response to continuous compaction of aquifer system in Tehran, Iran: Results from a long-term multi-sensor InSAR analysis. Remote. Sens. Environ. 2019, 221, 534–550. [Google Scholar] [CrossRef]
- Qu, F.; Lu, Z.; Kim, J.-W. New faults detection by multi-temporal InSAR over Greater Houston, Texas. In Proceedings of the International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2017; pp. 71–74. [Google Scholar] [CrossRef]
- Hernandez-Marin, M.; Burbey, T.J. Fault-controlled deformation and stress from pumping-induced groundwater flow. J. Hydrol. 2012, 428, 80–93. [Google Scholar] [CrossRef]
- Zhou, L.; Guo, J.; Hu, J.; Li, J.; Xu, Y.; Pan, Y.; Shi, M. Wuhan Surface Subsidence Analysis in 2015–2016 Based on Sentinel-1A Data by SBAS-InSAR. Remote. Sens. 2017, 9, 982. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, H.; Chen, B.; Li, J.; Gao, M.L.; Zhu, F.; Chen, W.; Liang, Y. InSAR Time-Series Analysis of Land Subsidence under Different Land Use Types in the Eastern Beijing Plain, China. Remote Sens. 2017, 9, 380. [Google Scholar] [CrossRef]
- Gao, M.-L.; Gong, H.; Chen, B.; Li, X.; Zhou, C.; Shi, M.; Si, Y.; Chen, Z.; Duan, G. Regional Land Subsidence Analysis in Eastern Beijing Plain by InSAR Time Series and Wavelet Transforms. Remote Sens. 2018, 10, 365. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, H.; Zhang, Y.; Warner, T.; Wang, C. Spatiotemporal Evolution of Land Subsidence in the Beijing Plain 2003–2015 Using Persistent Scatterer Interferometry (PSI) with Multi-Source SAR Data. Remote Sens. 2018, 10, 552. [Google Scholar] [CrossRef]
- Rezaei, A.; Mousavi, Z. Characterization of land deformation, hydraulic head, and aquifer properties of the Gorgan confined aquifer, Iran, from InSAR observations. J. Hydrol. 2019, 579. [Google Scholar] [CrossRef]
- Bonì, R.; Herrera, G.; Meisina, C.; Notti, D.; Béjar-Pizarro, M.; Zucca, F.; González, P.J.; Palano, M.; Tomás, R.; Fernández, J.; et al. Twenty-year advanced DInSAR analysis of severe land subsidence: The Alto Guadalentín Basin (Spain) case study. Eng. Geol. 2015, 198, 40–52. [Google Scholar] [CrossRef]
- Jiang, L.; Bai, L.; Zhao, Y.; Cao, G.; Wang, H.; Sun, Q. Combining InSAR and Hydraulic Head Measurements to Estimate Aquifer Parameters and Storage Variations of Confined Aquifer System in Cangzhou, North China Plain. Water Resour. Res. 2018, 54, 8234–8252. [Google Scholar] [CrossRef]
- Chen, J.; Knight, R.; Zebker, H.A.; Schreuder, W.A. Confined aquifer head measurements and storage properties in the San Luis Valley, Colorado, from spaceborne InSAR observations. Water Resour. Res. 2016, 52, 3623–3636. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.L.; Longuevergne, L.; Rivera, A. Assessing Groundwater Depletion and Dynamics Using GRACE and InSAR: Potential and Limitations. Ground Water 2016, 54, 768–780. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, P.; Longuevergne, L.; Martel, R.; Rivera, A.; Brouard, C.; Chaussard, E. Quantitative mapping of groundwater depletion at the water management scale using a combined GRACE/InSAR approach. Remote Sens. Environ. 2018, 205, 408–418. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote. Sens. 2018, 10, 829. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzy, A.; Malinowska, A.A. State of the Art and Recent Advancements in the Modelling of Land Subsidence Induced by Groundwater Withdrawal. Water 2020, 12, 2051. https://doi.org/10.3390/w12072051
Guzy A, Malinowska AA. State of the Art and Recent Advancements in the Modelling of Land Subsidence Induced by Groundwater Withdrawal. Water. 2020; 12(7):2051. https://doi.org/10.3390/w12072051
Chicago/Turabian StyleGuzy, Artur, and Agnieszka A. Malinowska. 2020. "State of the Art and Recent Advancements in the Modelling of Land Subsidence Induced by Groundwater Withdrawal" Water 12, no. 7: 2051. https://doi.org/10.3390/w12072051
APA StyleGuzy, A., & Malinowska, A. A. (2020). State of the Art and Recent Advancements in the Modelling of Land Subsidence Induced by Groundwater Withdrawal. Water, 12(7), 2051. https://doi.org/10.3390/w12072051





