Improving SWAT Model Calibration Using Soil MERGE (SMERGE)
Abstract
1. Introduction
2. Watersheds Examined
3. Datasets Used
3.1. SWAT Model Input
3.2. Other Soft Data
4. Methodology
4.1. SWAT Model Setup
4.2. Simulation Series
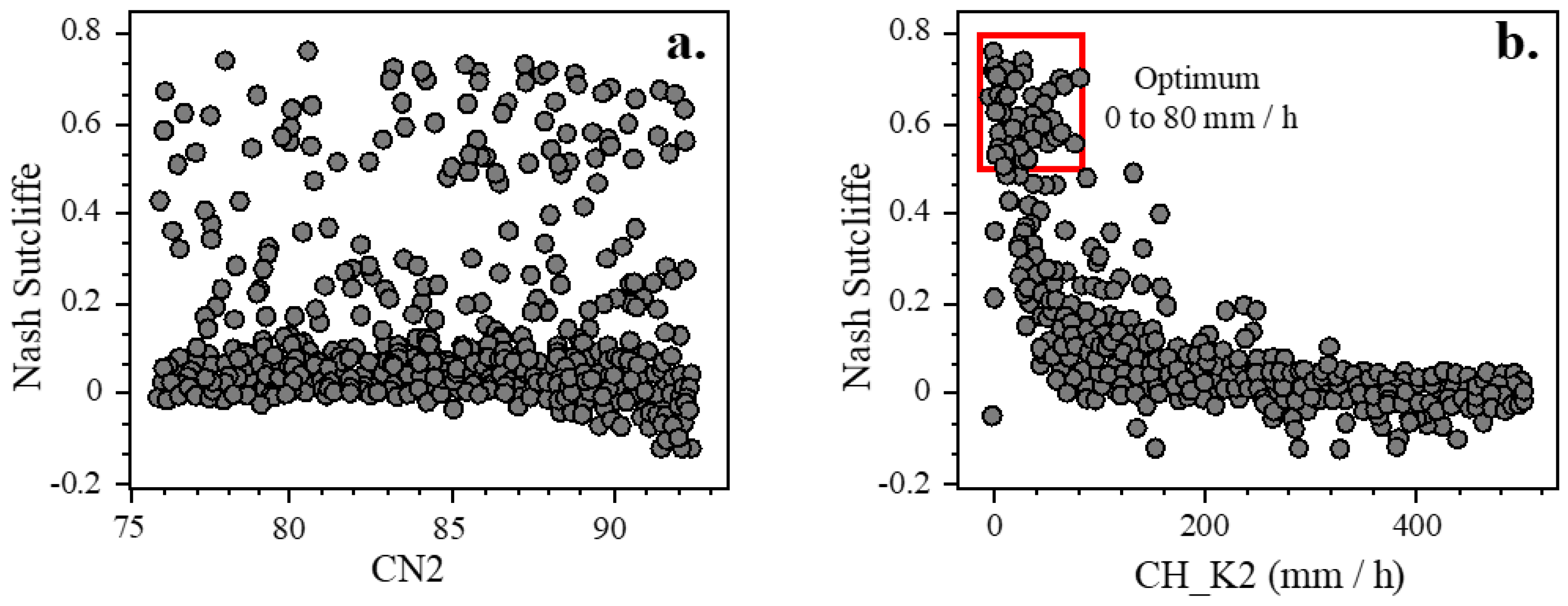
4.2.1. Global Simulation Series
4.2.2. Individual Year-By-Year Series
4.2.3. Final Calibration Year-By-Year Series
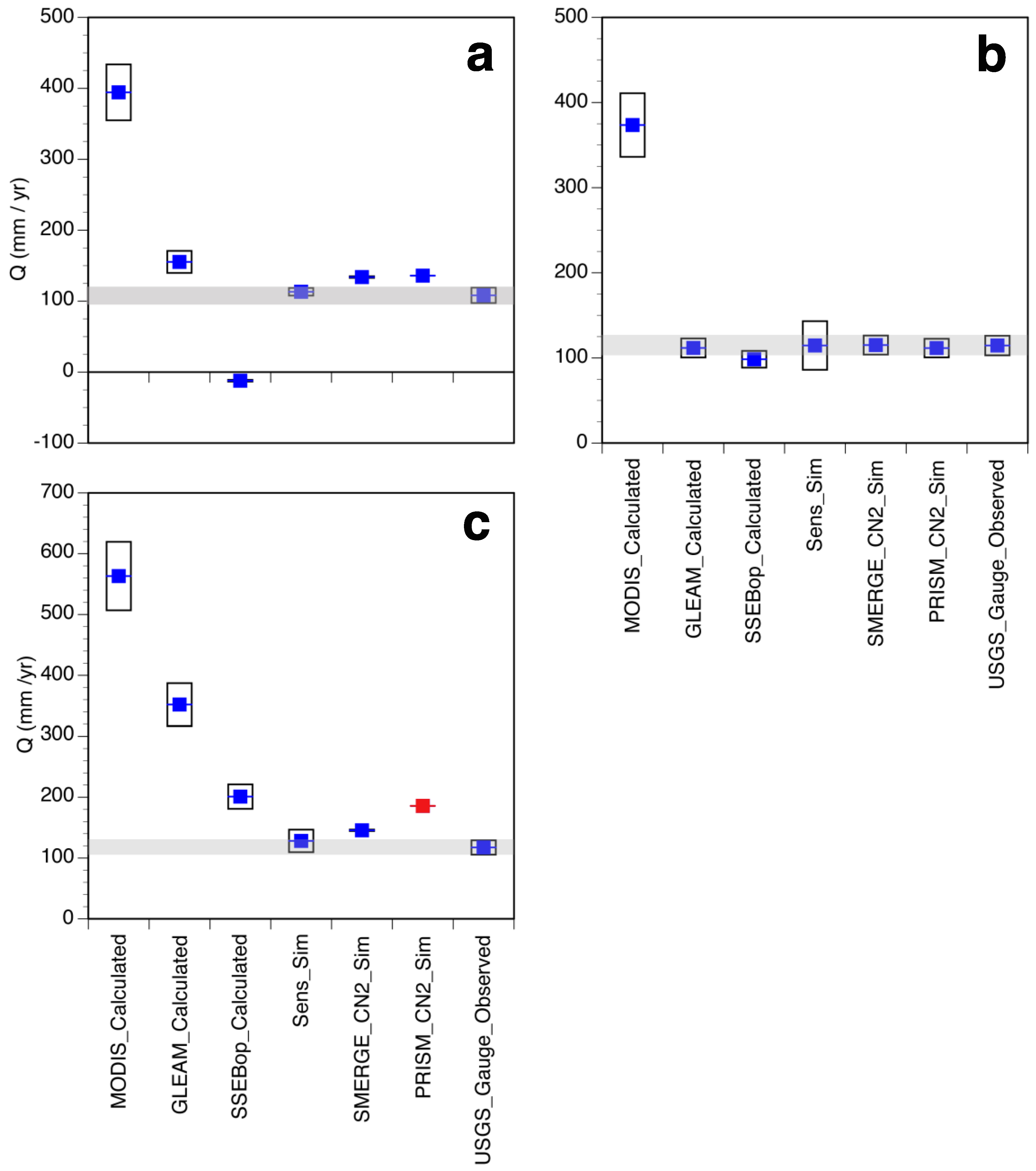
4.3. Mass Balance Calculations
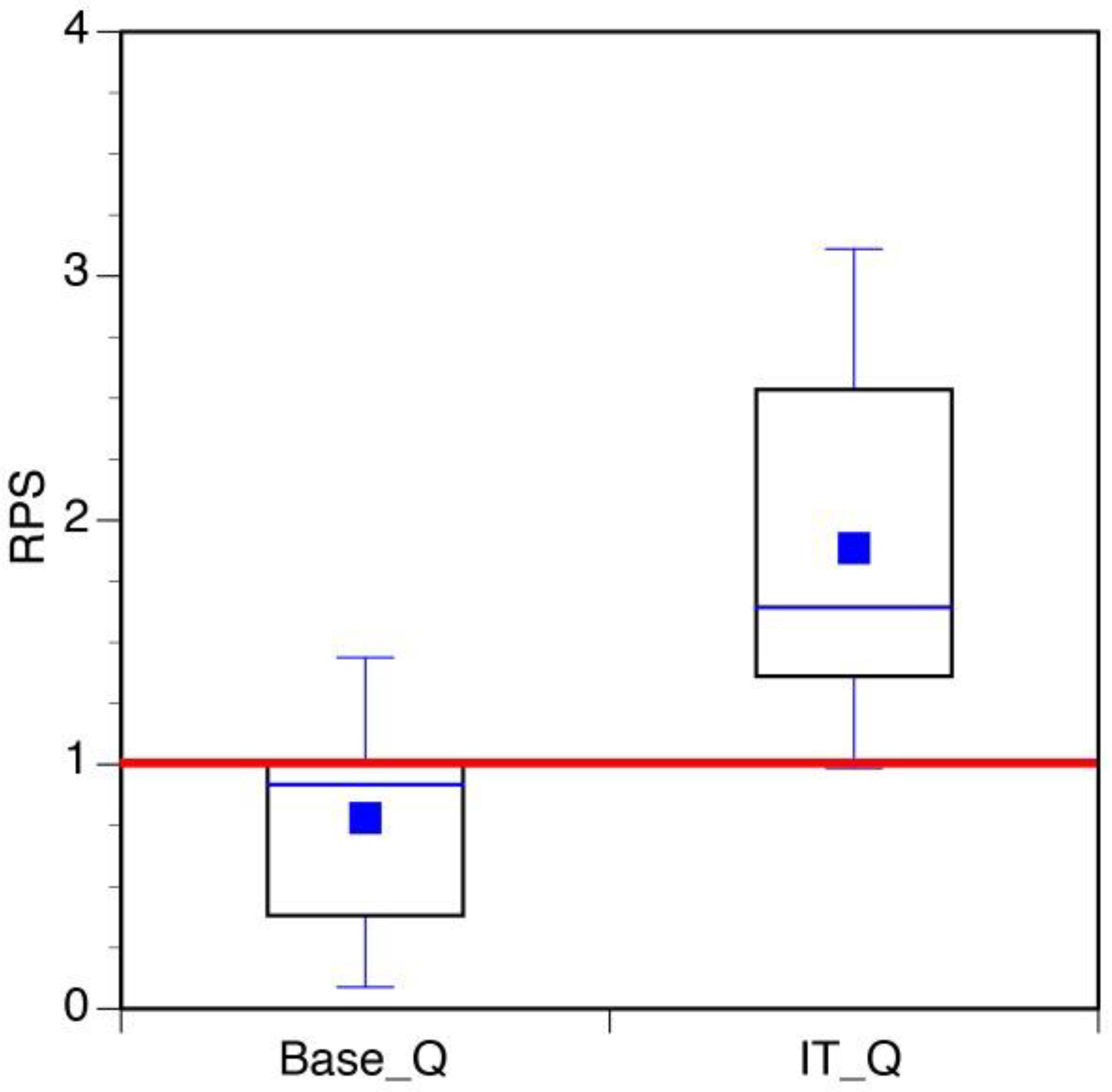
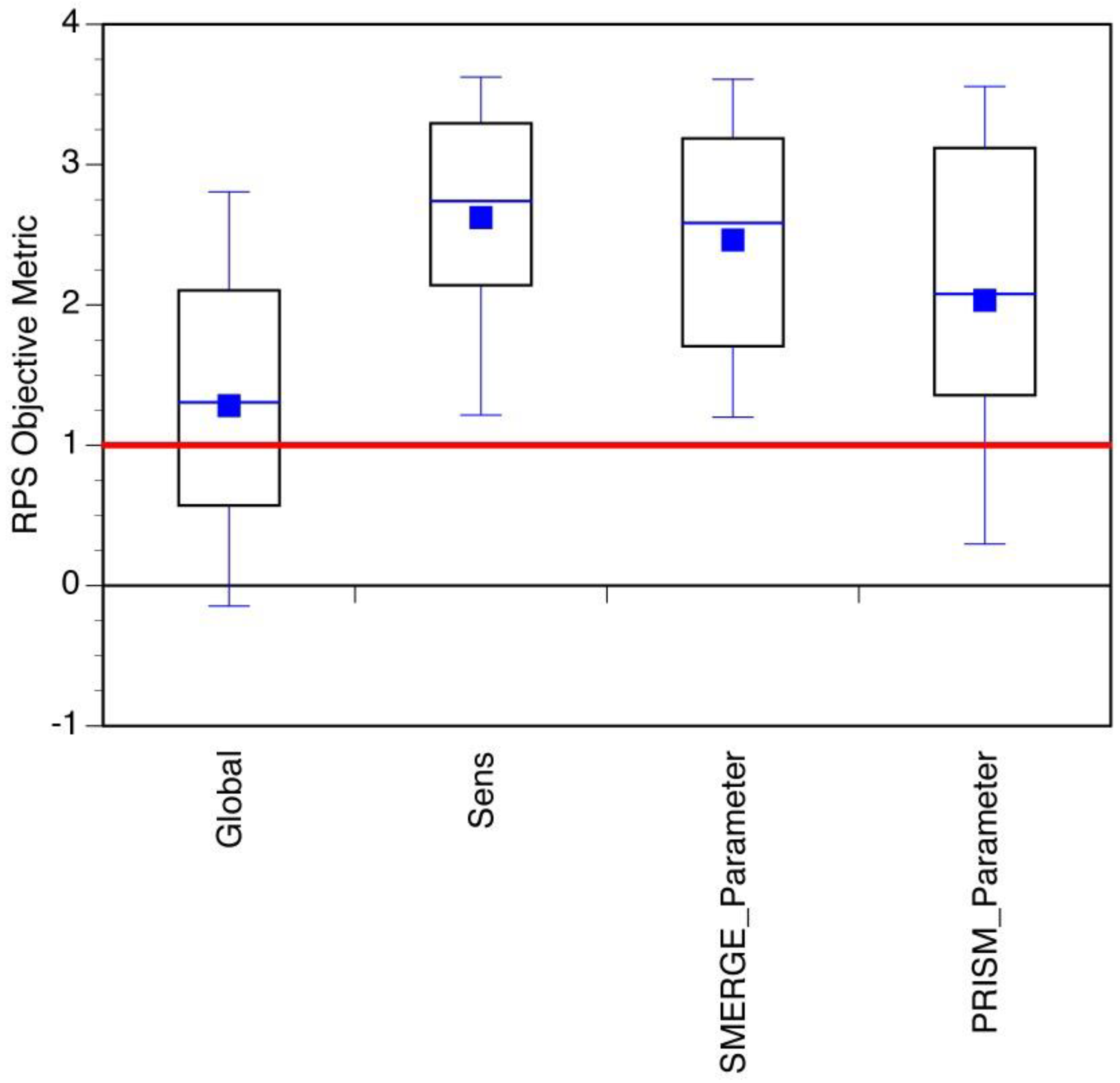
5. Results
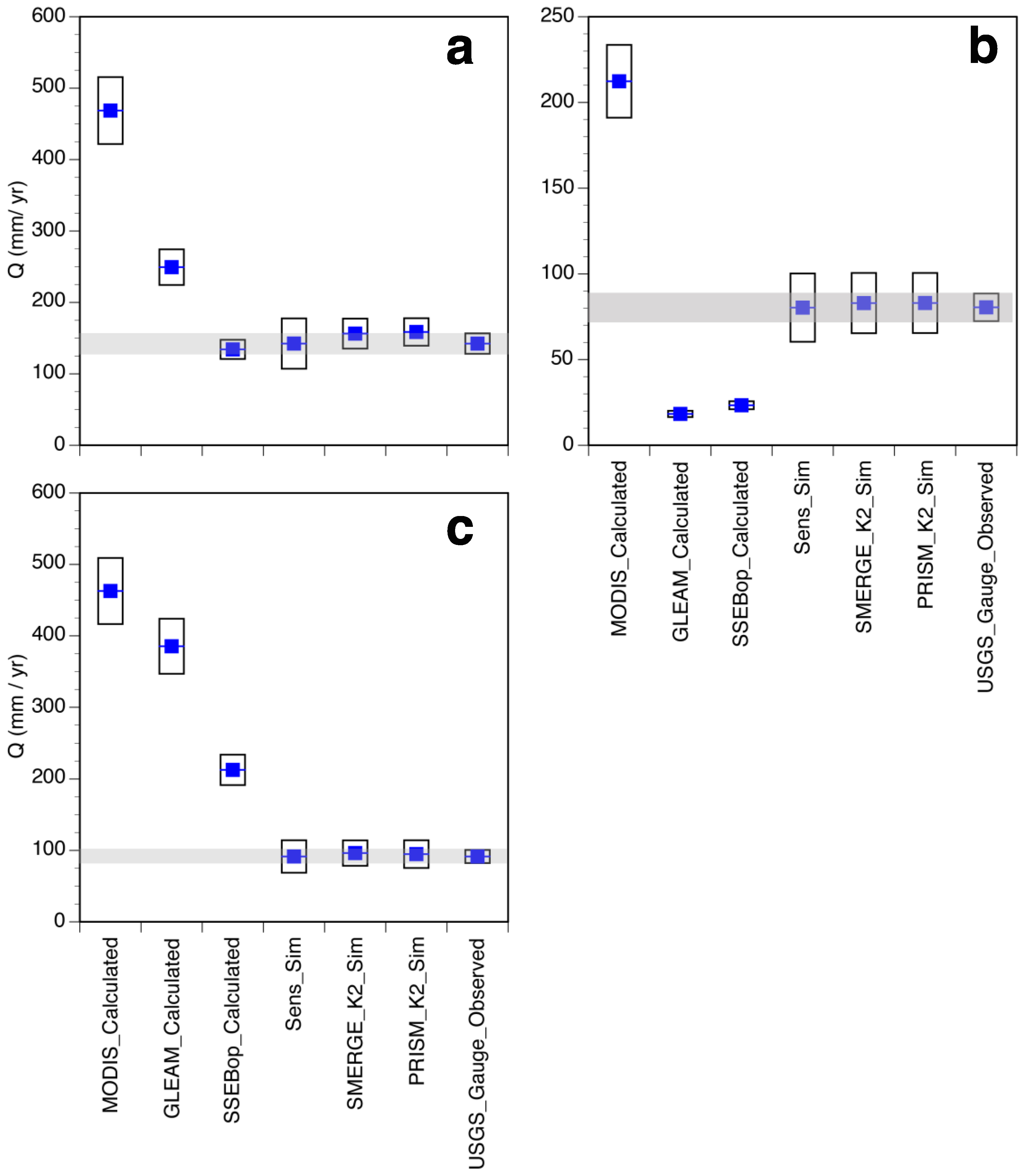
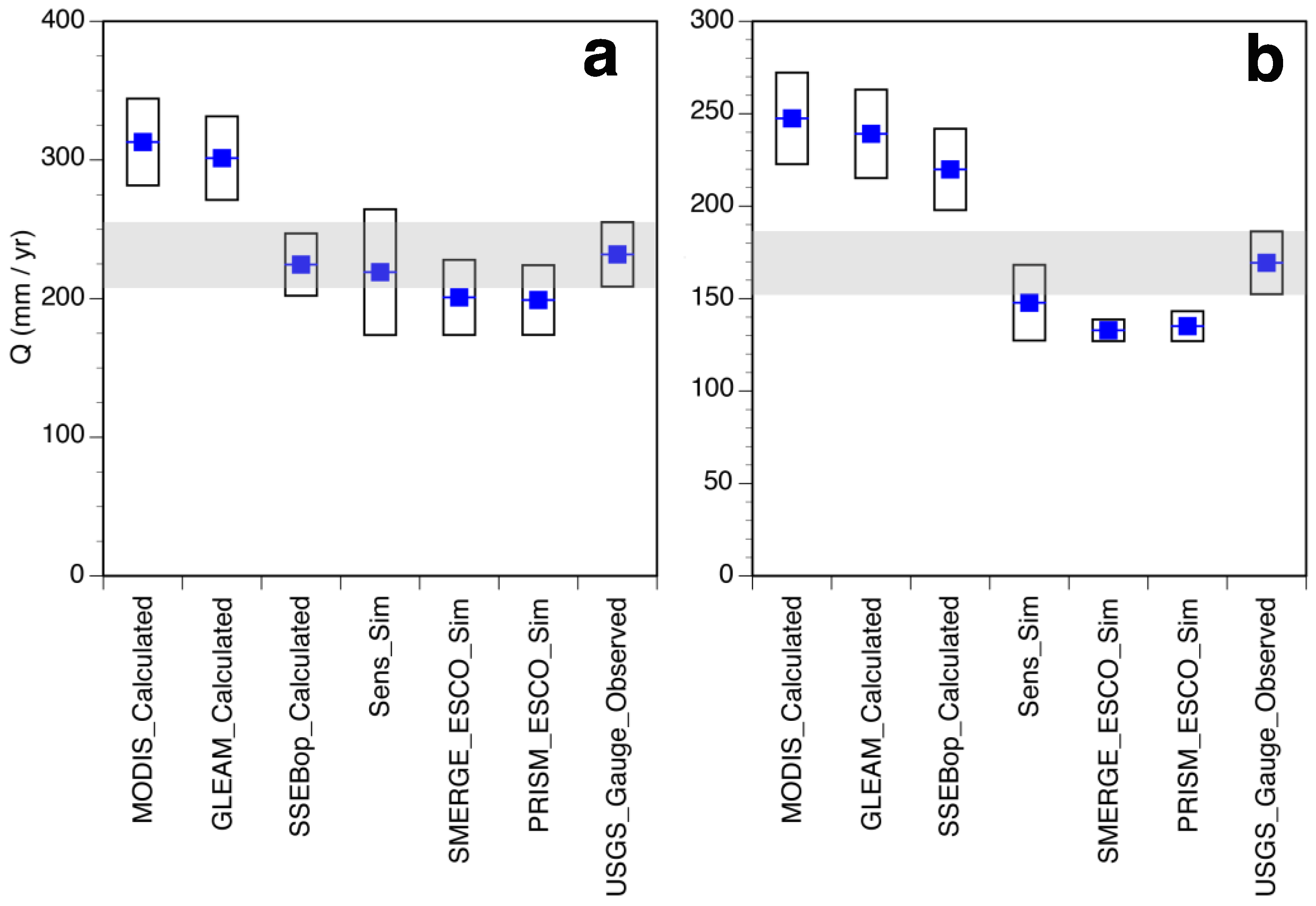
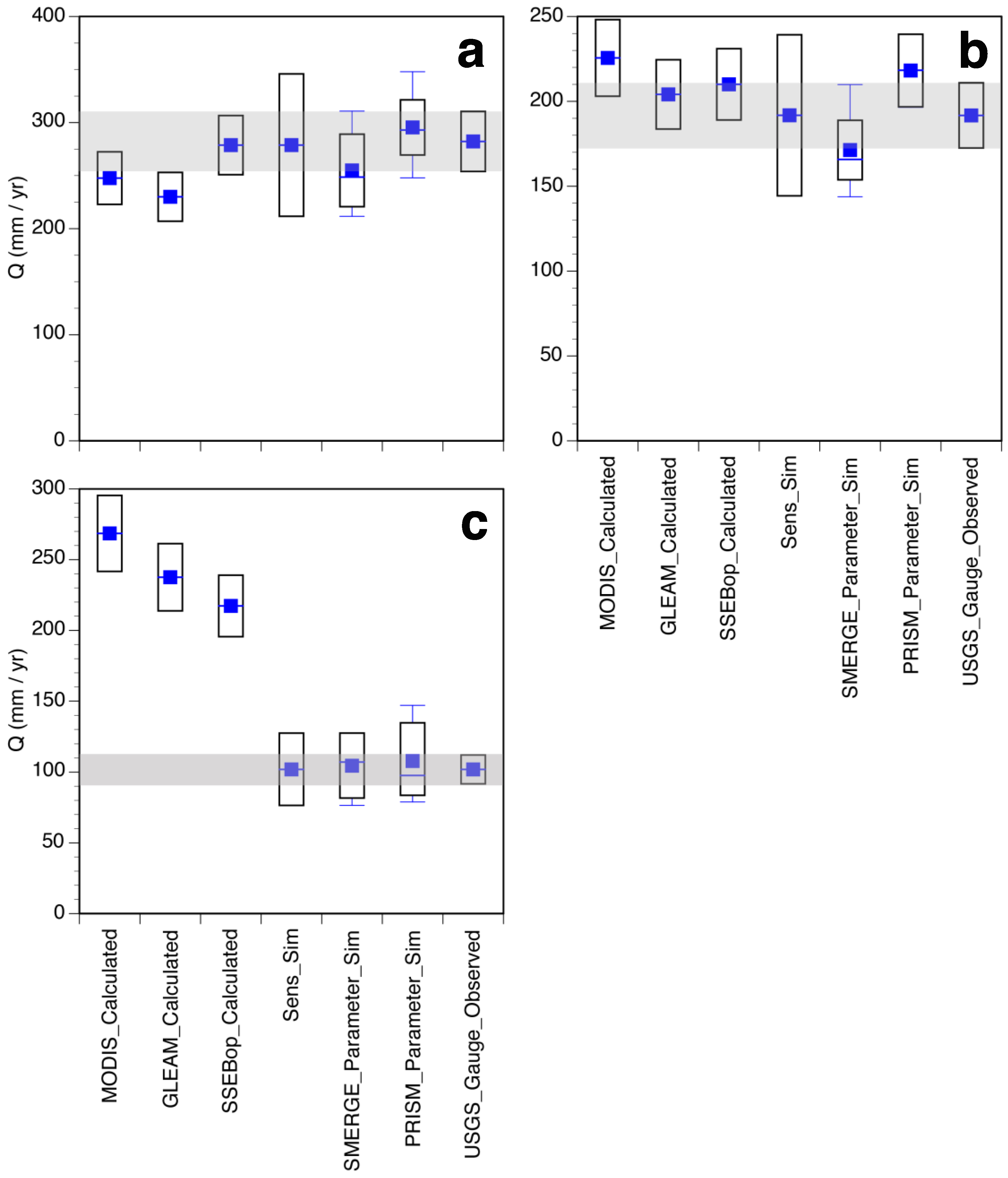
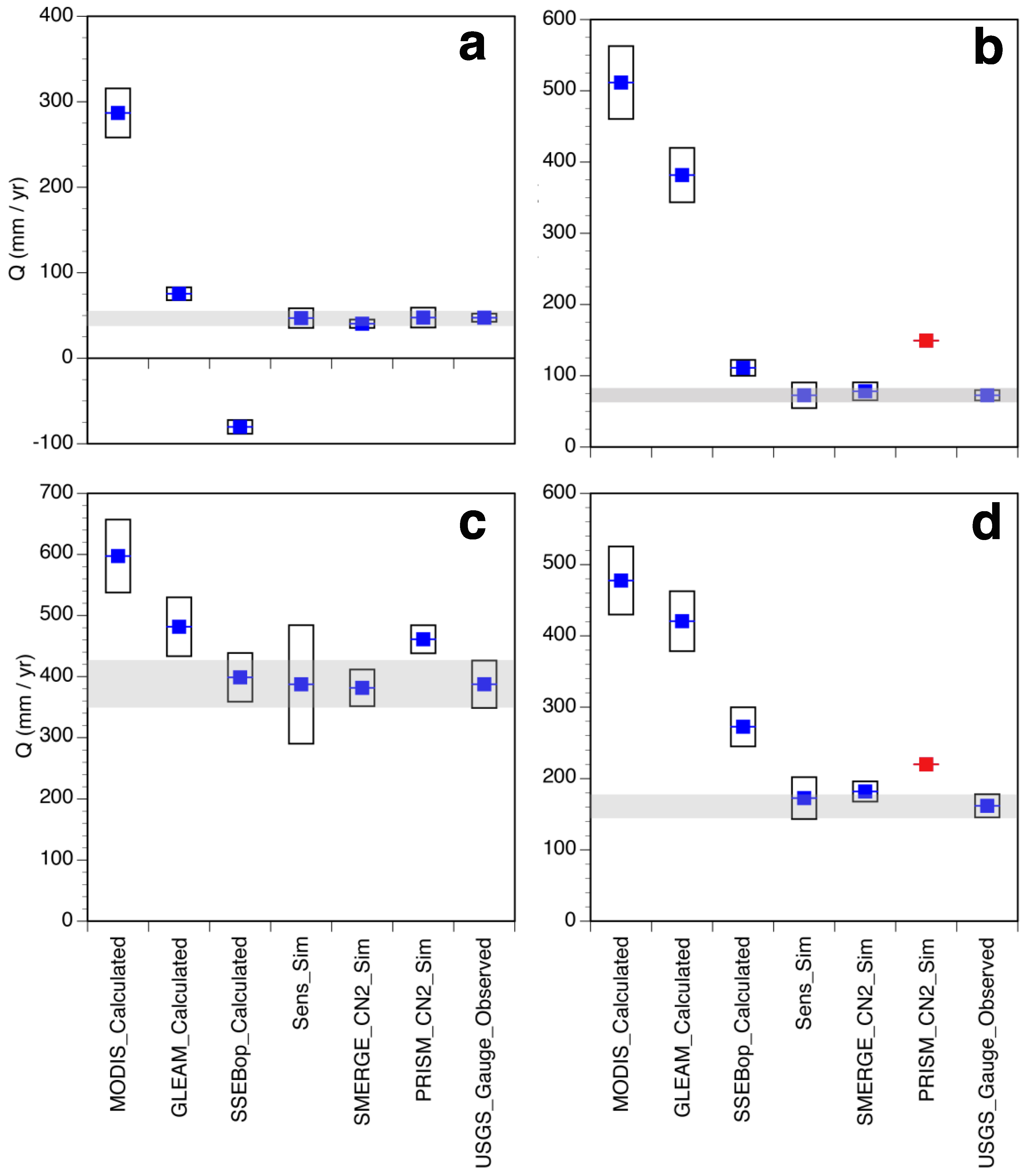
5.1. SWAT Simulations
5.2. Mass Balance Comparisons
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Zeiger, S.J.; Hubbart, J.A. A SWAT model validation of nested-scale contemporaneous streamflow, suspended sediment and nutrients from a multiple-land-use watershed of the central USA. Sci. Total Environ. 2016, 572, 232–243. [Google Scholar] [CrossRef] [PubMed]
- Akay, H.; Kocyigit, M.B.; Yanmaz, A.M. Effect of using multiple stream gauging stations on calibration of hydrologic parameters and estimation of hydrograph of ungauged neighboring basin. Arab. J. Geosci. 2018, 11, 282. [Google Scholar] [CrossRef]
- Xie, H.; Longuevergne, L.; Ringler, C.; Scalon, B.R. Calibration and evaluation of a semi-distributed watershed model of Sub-Saharan Africa using GRACE data. Hydrol. Earth Syst. Sci. 2012, 9, 3083–3099. [Google Scholar] [CrossRef]
- Qiao, L.; Herrmann, R.B.; Pan, Z. Parameter uncertainty reduction for SWAT using GRACE, streamflow, and groundwater table data for the Lower Missouri River Basin. J. Am. Water Resour. Assoc. 2013, 49, 343–358. [Google Scholar] [CrossRef]
- Kundu, D.; Vervoort, R.W.; van Ogtrop, F.F. The value of remotely sensed surface soil moisture for model calibration using SWAT. Hydrol. Process. 2017, 31, 2764–2780. [Google Scholar] [CrossRef]
- Nilawar, A.P.; Calderella, C.P.; Lakhankar, T.Y.; Waikar, M.L. Satellite soil moisture validation using hydrological SWAT Model: A case study of Puerto Rico, USA. Hydrology 2017, 4, 45. [Google Scholar] [CrossRef]
- Azimi, S.; Dariane, A.B.; Modanesi, S.; Bauer-Marschallinger, B.; Bindlish, R.; Wagner, W.; Massari, C. Assimilation of Sentinel 1 and SMAP—Based satellite soil moisture retrievals into SWAT hydrological model: The impact of satellite revisit time and product spatial resolution on flood simulations in small basins. J. Hydrol. 2020, 581, 124367. [Google Scholar] [CrossRef]
- Abiodun, O.O.; Guan, H.; Post, V.E.A.; Batelaan, O. Comparison of MODIS and SWAT evapotranspiration over a complex terrain at different spatial scales. Hydrol. Earth Syst. Sci. 2018, 22, 2775–2794. [Google Scholar] [CrossRef]
- Rajib, A.; Merwade, V.; Yu, Z. Rationale and efficacy of assimilating remotely sensed potential evapotranspiration for reduced uncertainty of hydrologic models. Water Resour. Res. 2018, 54, 4615–4637. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Improving alpine summertime streamflow simulations by incorporation of evapotranspiration data. Water 2019, 11, 112. [Google Scholar] [CrossRef]
- Fallatah, O.A.; Ahmed, M.; Cardace, D.; Boving, T.; Akanda, A.S. Assessment of modern recharge to arid region aquifers using an integrated geophysical, geochemical, and remote sensing approach. J. Hydrol. 2019, 569, 600–611. [Google Scholar] [CrossRef]
- Milewski, A.; Seyoum, W.M.; Elkadiri, R.; Durham, M. Multi-scale hydrologic sensitivity to climatic and anthropogenic changes in Northern Morocco. Geosciences 2020, 10, 13. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, D. Data assimilation for distributed hydrological catchment modeling via ensemble Kalman filter. Remote Sens. Environ. 2010, 33, 678–690. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Liu, Y. ESA CCI Soil moisture assimilation in SWAT for improved hydrological simulation in Upper Huai River Basin. Adv. Meteorol. 2018, 7301314. [Google Scholar] [CrossRef]
- Patil, A.; Ramsankaran, R. Improved streamflow simulations by coupling soil moisture analytical relationship in EnKF based hydrological data assimilation framework. Adv. Water Resour. 2018, 121, 173–188. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Starks, P.J.; Moriasi, D.N. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture. Adv. Water Resour. 2011, 34, 526–536. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Estimating hydrologic budgets for three Illinois watersheds. J. Hydrol. 1996, 176, 57–77. [Google Scholar] [CrossRef]
- Xu, C.Y. Climate change and hydrologic models: A review of existing gaps and recent research developments. Water Resour. Manag. 1999, 13, 369–382. [Google Scholar] [CrossRef]
- Berger, K.P.; Entekhabi, D. Basin hydrologic response relations to distributed physiographic descriptors and climate. J. Hydrol. 2001, 247, 169–182. [Google Scholar] [CrossRef]
- Lettenmaier, D.P. Observations of the Global Water Cycle—Global Monitoring Networks. In Encyclopedia of Hydrologic Sciences; Anderson, M.G., McDonnell, J.J., Eds.; J. Wiley and Sons Publishers: Hoboken, NJ, USA, 2005; Volume 5, pp. 2719–2732. [Google Scholar]
- Tobin, K.J.; Crow, W.T.; Dong, J.; Bennett, M.E. Validation of a new soil moisture product Soil MERGE or SMERGE. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3351–3365. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006 [Data set]; NASA EOSDIS Land Processes DAAC. 2017. Available online: https://doi.org/10.5067/MODIS/MOD16A2.006 (accessed on 21 April 2020).
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006 [Data set]; NASA EOSDIS Land Processes DAAC. 2015. Available online: https://doi.org/10.5067/MODIS/MOD15A2H.006 (accessed on 21 April 2020).
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual; Texas Water Resource Institute Report TR-192; Texas Water Resource Institute: College Station, TX, USA, 2002; Available online: https://swat.tamu.edu/media/1294/swatuserman.pdf (accessed on 1 March 2020).
- Williams, J.R. Flood routing with variable travel time or variable storage coefficients. Trans. ASABE 1969, 12, 100–103. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, L.; Siber, R.; Bogner, K. Modeling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for SWAT application to the Chaoche Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Uniyal, B.; Jha, M.K.; Verma, A.K. Parameter identification and uncertainty analysis for simulating streamflow in a river basin of Eastern India. Hydrol. Process. 2015, 29, 3744–3766. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Satellite precipitation products and hydrologic applications. Water Int. 2014, 39, 360–380. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Galdos, F.V.; Alvarex, C.; Garcia, A.; Revilla, J.A. Estimated distributed rainfall interception using a simple conceptual model and Moderate Resolution Imaging Spectroradiometer (MODIS). J. Hydrol. 2012, 468, 213–228. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and groundwater recharge from stream flow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modeling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Fu, C.; James, A.L.; Yao, H. Investigations of uncertainty in SWAT hydrologic simulations: A case study of a Canadian Shield catchment. Hydrol. Process. 2015, 29, 4000–4017. [Google Scholar] [CrossRef]
- Her, Y.; Chaubey, I. Impact of the numbers of observations and calibration parameters on equifinality, model performance, and output and parameter uncertainity. Hydrol. Process. 2015, 29, 4220–4237. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V. Improving soil moisture accounting and streamflow prediction in SWAT by incorporating a modified time-dependent Curve Number method. Hydrol. Process. 2016, 30, 603–624. [Google Scholar]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiski, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multi-temporal analysis of TRMM-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]


| Basin | Size (sq. km.) | Subbasins | Elevation (m) | Dominant Soil Texture | Dominant Land Cover |
|---|---|---|---|---|---|
| Bird Creek (BC) | 2360 | 31 | 177 to 403 | Loam | Rangeland/Grass |
| Black Vermillion (BV) | 1071 | 31 | 338 to 468 | Clay Loam | Agricultural |
| Chickaskia (CH) | 4892 | 33 | 295 to 608 | Silt Loam | Agricultural |
| Little Arkansas (LA) | 3402 | 33 | 409 to 544 | Silt Loam | Agricultural |
| Little Nemaha (LN) | 2061 | 31 | 274 to 444 | Clay | Agricultural |
| Mill Creek (MC) | 832 | 29 | 291 to 488 | Silt Clay Loam | Rangeland/Grass |
| Ninnescah (NI) | 2049 | 35 | 446 to 637 | Loamy Sand | Agricultural |
| Walnut (WN) | 4855 | 33 | 330 to 512 | Silt Loam | Rangeland/Grass |
| Description | Nash Sutcliffe (NS) | Mass Balance Error | Relative Performance Scale (RPS) |
|---|---|---|---|
| Perfect | 1.00 | 0% | 4.00 |
| Very Good | 0.75 | 10% | 3.00 |
| Good | 0.65 | 15% | 2.00 |
| Satisfactory | 0.50 | 25% | 1.00 |
| Unacceptable | <0.50 | >25% | <1.00 |
| Parameter | Name | Low | High |
|---|---|---|---|
| CN2 | Initial SCS runoff curve number for moisture condition II | 35 | 95 |
| ALPHA_BF | Baseflow Alpha Factor | 0 | 1 |
| GW_DELAY | Groundwater delay time (days) | 30 | 450 |
| CH_N2 | Manning’s “n” value for the main channel | 0 | 0.3 |
| CH_K2 | Effective hydraulic conductivity in main channel alluvium (mm/h) | 0 | 500 |
| CH_N1 | Manning’s “n” value for the tributary channels | 0 | 0.3 |
| CH_K1 | Effective hydraulic conductivity in tributary channel alluvium (mm/h) | 0 | 300 |
| OV_N | Manning’s “n” value for overland flow | 0.01 | 0.6 |
| SURLAG | Surface runoff lag coefficient | 1 | 34 |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur (mm H2O) | 0 | 5000 |
| SOL_AWC | Available water capacity of the soil layer (mm H2O/mm soil) | −0.2 | 0.4 |
| ESCO | Soil evaporation compensation factor | 0 | 1 |
| GW_REVAP | Groundwater “revap” coefficient | 0.02 | 0.2 |
| REVAPMN | Threshold depth of water in the shallow aquifer for “revap” or percolation to the deep aquifer to occur (mm H2O) | 0 | 500 |
| CANMX | Maximum canopy storage (mm H2O) | 0 | 100 |
| EPCO | Plant uptake compensation factor | 0 | 1 |
| SFTMP | Snowfall temperature (°C) | −5 | 5 |
| SMTMP | Snow melt base temperature (°C) | −5 | 5 |
| SMFMX | Melt factor for snow on June 21 (mm H2O/°C-day) | 0 | 10 |
| SMFMN | Melt factor for snow on Dec 21 (mm H2O/°C-day) | 0 | 10 |
| TIMP | Snow pack temperature lag factor | 0.01 | 1 |
| SOL_K | Saturated hydraulic conductivity (mm/h) | −0.8 | 0.8 |
| SOL_BD | Moist bulk density (g/cm3) | −0.5 | 0.6 |
| Basin | Variable Parameters | Non-Variable Parameters |
|---|---|---|
| BC | CN2, ALPHA_BF, CH_N2, OV_N | SOL_BD, GWQMN, ESCO |
| BV | CN2, CH_K2, OV_N, ESCO | CH_N2, ALPHA_BF, SOL_AWC |
| CH | CN2, CH_N2, CH_K2, OV_N, ESCO | ALPHA_BF |
| LA | CN2, CH_N2, CH_K2, OV_N, SOL_BD | ALPHA_BF, SMTMP |
| LN | CN2, OV_N, SOL_AWC, ESCO, SOL_BD | SMFMN |
| MC | CN2, CH_K2, ESCO | CH_N2, OV_N, SMTMP |
| NI | CN2, CH_N2, CH_K2, OV_N, SOL_BD | SMTMP |
| WN | CN2, CH_K2, OV_N, ESCO | ALPHA_BF, CH_N2, SOL_AWC |
| Parameter | BC | BV | CH | LA | LN | MC | NI | WN |
|---|---|---|---|---|---|---|---|---|
| ALPHA_BF | 0.112 | 0.0444 | 0.073 | 0.0427 | 0.012 | 0.033 | 0.0572 | |
| GW_DELAY | 252 | 136 | 43.6 | 81.4 | 105 | 443 | 166 | 189 |
| CH_N2 | 0.255 | 0.221 | 0.267 | 0.065 | ||||
| CH_K2 | 39.0 | 3.20 | ||||||
| CH_N1 | 0.184 | 0.0091 | 0.300 | 0.084 | 0.049 | 0.254 | 0.044 | 0.242 |
| CH_K1 | 11.0 | 297 | 239 | 83.8 | 73.9 | 275 | 123 | 190 |
| OV_N | 0.582 | |||||||
| SURLAG | 6.16 | 12.6 | 16.3 | 9.03 | 4.84 | 7.02 | 20.5 | 3.92 |
| GWQMN | 1967 | 2342 | 3517 | 2287 | 117 | 2167 | 4707 | 4552 |
| SOL_AWC | 0.268 | 0.370 | 0.352 | 0.0031 | 0.384 | −0.125 | 0.114 | |
| ESCO | 0.043 | 0.865 | 0.186 | |||||
| GW_REVAP | 0.118 | 0.056 | 0.077 | 0.068 | 0.159 | 0.191 | 0.177 | 0.026 |
| REVAPMN | 353 | 66.2 | 337 | 468 | 492 | 19.2 | 138 | 72.7 |
| CANMX | 0.514 | 0.405 | 0.396 | 0.255 | 0.322 | 0.368 | 0.470 | 0.691 |
| EPCO | 0.863 | 0.435 | 0.736 | 0.743 | 0.058 | 0.894 | 0.254 | 0.346 |
| SFTMP | −2.38 | −4.25 | −4.32 | 2.33 | −0.245 | −0.735 | −1.56 | 0.905 |
| SMTMP | −0.845 | 1.24 | 2.96 | 0.975 | 0.765 | 4.51 | 4.98 | −2.69 |
| SMFMX | 0.095 | 6.46 | 0.965 | 7.46 | 1.40 | 3.38 | 9.49 | 9.70 |
| SMFMN | 5.45 | 0.665 | 6.78 | 0.305 | 5.65 | 4.95 | 4.29 | 7.57 |
| TIMP | 0.869 | 0.579 | 0.587 | 0.795 | 0.735 | 0.156 | 0.671 | 0.689 |
| SOL_K | 0.294 | −0.418 | 0.257 | 0.036 | −0.401 | −0.310 | −0.015 | 0.434 |
| SOL_BD | −0.142 | 0.339 | −0.092 | −0.096 | 0.281 |
| Parameter | BC | BV | CH | LA | LN | MC | NI | WN |
|---|---|---|---|---|---|---|---|---|
| CN2 | 60–84 | 76–92.4 | 72–88 | 68–84 | 68–84 | 70–88 | 45.9–80 | 76–90.3 |
| ALPHA_BF | 0.035–0.139 | 0–0.3 | ||||||
| CH_N2 | 0.015–0.04 | 0–0.3 | 0–0.3 | 0–40 | 0–40 | 10–30 | ||
| CH_K2 | 0–20 | 0–40 | 0–40 | 0.01-0.6 | 0.01–0.6 | 0.4–0.6 | ||
| OV_N | 0.01–0.60 | 0.01–0.6 | 0.01–0.6 | 0.01–0.6 | −0.2–0.4 | |||
| ESCO | 0–1.0 | 0–1.0 | 0–1.0 | 0–1.0 | 0–1.0 | |||
| SOL_BD | −0.5–0.6 | −0.5–0.6 | −0.5–0.6 |
| SMERGE 2.0 | ||||||||
| Parameter | BC | BV | CH | LA | LN | MC | NI | WN |
| CN2 | 0.618 | 0.457 | 0.658 | 0.240 | 0.361 | 0.727 | 0.791 | 0.725 |
| ALPHA_BF | 0.266 | |||||||
| CH_N2 | 0.114 | −0.116 | 0.290 | 0.399 | 0.179 | |||
| CH_K2 | 0.191 | 0.324 | 0.345 | 0.129 | −0.150 | 0.437 | ||
| OV_N | 0.342 | 0.246 | 0.015 | −0.437 | −0.237 | 0.231 | ||
| SOL_AWC | 0.048 | |||||||
| ESCO | −0.301 | −0.251 | −0.707 | |||||
| SOL_BD | −0.450 | −0.075 | 0.041 | |||||
| PRISM | ||||||||
| Parameter | BC | BV | CH | LA | LN | MC | NI | WN |
| CN2 | 0.462 | 0.515 | 0.499 | 0.293 | 0.347 | 0.662 | 0.539 | 0.440 |
| ALPHA_BF | 0.297 | |||||||
| CH_N2 | 0.031 | −0.121 | −0.052 | 0.329 | 0.321 | |||
| CH_K2 | 0.512 | 0.346 | 0.577 | −0.124 | −0.255 | 0.227 | ||
| OV_N | 0.201 | 0.172 | −0.092 | −0.493 | −0.433 | 0.033 | ||
| SOL_AWC | −0.247 | |||||||
| ESCO | −0.384 | −0.572 | −0.651 | |||||
| SOL_BD | −0.336 | −0.219 | 0.058 | |||||
| Parameter | BC | BV | CH | LA |
| CN2 | 67.1 to 83.9 (76.7) | 77.9 to 89.7 (84.5) | 75.4 to 85.6 (81.5) | 69.0 to 83.2 (75.8) |
| ALPHA_BF | 0.035 to 0.127 (0.092) | |||
| CH_N2 | 0.016 to 0.060 (0.033) | 0.044 to 0.206 (0.104) | 0.065 to 0.180 (0.112) | |
| CH_K2 | 1.5 to 10.5 (7.7) | 4.7 to 15.5 (10.1) | 2.6 to 17.7 (9.6) | |
| OV_N | 0.022 to 0.591 (0.365) | 0.101 to 0.441 (0.303) | 0.206 to 0.572 (0.381) | 0.274 to 0.585 (0.396) |
| ESCO | 0.456 to 0.868 (0.612) | |||
| SOL_BD | −0.431 to 0.443 (0.008) | |||
| Parameter | LN | MC | NI | WN |
| CN2 | 69.8 to 82.8 (77.8) | 70.7 to 85.2 (77.7) | 47.9 to 76.3 (68.0) | 76.6 to 90.1 (84.7) |
| CH_N2 | 0.018 to 0.283 (0.164) | |||
| CH_K2 | 4.0 to 23.1 (11.5) | 2.2 to 24.0 (13.4) | 10.4 to 25.1 (16.8) | |
| OV_N | 0.301 to 0.581 (0.410) | 0.211 to 0.578 (0.387) | 0.407 to 0.591 (0.519) | |
| SOL_AWC | −0.172 to 0.362 (0.089) | |||
| ESCO | 0.583 to 0.959 (0.756) | 0.171 to 0.981 (0.639) | ||
| SOL_BD | −0.422 to 0.588 (0.0175) | −0.389 to 0.523 (0.065) |
| Basin | Year | Product | CN2 | CH_K2 | ESCO |
|---|---|---|---|---|---|
| BC | 2017 | SMERGE 2.0 | 78.5 | ||
| BC | 2017 | PRISM | 82.5 | ||
| BV | 2016 | SMERGE 2.0 | 84.4 | 6.7 | |
| BV | 2016 | PRISM | 84.2 | 6.6 | |
| BV | 2017 | SMERGE 2.0 | 81.0 | 4.1 | |
| BV | 2017 | PRISM | 80.2 | 3.5 | |
| BV | 2018 | SMERGE 2.0 | 81.8 | 4.7 | |
| BV | 2018 | PRISM | 83.3 | 5.8 | |
| CH | 2016 | SMERGE 2.0 | 81.2 | ||
| CH | 2016 | PRISM | 81.6 | ||
| CH | 2017 | SMERGE 2.0 | 80.5 | ||
| CH | 2017 | PRISM | 80.1 | ||
| CH | 2018 | SMERGE 2.0 | 80.1 | ||
| CH | 2018 | PRISM | 83.7 | ||
| LA | 2016 | SMERGE 2.0 | 12.8 | ||
| LA | 2016 | PRISM | 17.2 | ||
| LA | 2017 | SMERGE 2.0 | 7.1 | ||
| LA | 2017 | PRISM | 7.6 | ||
| LA | 2018 | SMERGE 2.0 | 8.0 | ||
| LA | 2018 | PRISM | 15.7 | ||
| LN | 2016 | SMERGE 2.0 | 0.824 | ||
| LN | 2016 | PRISM | 0.798 | ||
| LN | 2017 | SMERGE 2.0 | 0.726 | ||
| LN | 2017 | PRISM | 0.761 | ||
| LN | 2018 | SMERGE 2.0 | 0.798 | ||
| LN | 2018 | PRISM | 0.810 | ||
| MC | 2016 | SMERGE 2.0 | 79.5 | 0.693 | |
| MC | 2016 | PRISM | 85.1 | 0.943 | |
| MC | 2017 | SMERGE 2.0 | 77.5 | 0.602 | |
| MC | 2017 | PRISM | 84.3 | 0.907 | |
| MC | 2018 | SMERGE 2.0 | 74.1 | 0.453 | |
| MC | 2018 | PRISM | 81.1 | 0.764 | |
| NI | 2016 | SMERGE 2.0 | 62.4 | ||
| NI | 2016 | PRISM | 67.1 | ||
| NI | 2018 | SMERGE 2.0 | 65.0 | ||
| NI | 2018 | PRISM | 78.9 | ||
| WN | 2016 | SMERGE 2.0 | 85.0 | ||
| WN | 2016 | PRISM | 89.2 | ||
| WN | 2017 | SMERGE 2.0 | 81.3 | ||
| WN | 2017 | PRISM | 82.1 | ||
| WN | 2018 | SMERGE 2.0 | 80.3 | ||
| WN | 2018 | PRISM | 85.5 |
| Model Run #1 | Model Run #2 | p Value | Degree of Significance |
|---|---|---|---|
| Global_Q | Sens_Q | 0.0001 | Highly Significant |
| Global_Q | SMERGE_Parameter | 0.0001 | Highly Significant |
| Global_Q | PRISM_Parameter | 0.0309 | Significant |
| Sens_Q | SMERGE_Parameter | 0.5269 | Not Significant |
| Sens_Q | PRISM_Parameter | 0.0659 | Not Significant |
| SMERGE_Parameter | PRISM_Parameter | 0.1452 | Not Significant |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tobin, K.J.; Bennett, M.E. Improving SWAT Model Calibration Using Soil MERGE (SMERGE). Water 2020, 12, 2039. https://doi.org/10.3390/w12072039
Tobin KJ, Bennett ME. Improving SWAT Model Calibration Using Soil MERGE (SMERGE). Water. 2020; 12(7):2039. https://doi.org/10.3390/w12072039
Chicago/Turabian StyleTobin, Kenneth J., and Marvin E. Bennett. 2020. "Improving SWAT Model Calibration Using Soil MERGE (SMERGE)" Water 12, no. 7: 2039. https://doi.org/10.3390/w12072039
APA StyleTobin, K. J., & Bennett, M. E. (2020). Improving SWAT Model Calibration Using Soil MERGE (SMERGE). Water, 12(7), 2039. https://doi.org/10.3390/w12072039





