The Effects of Hydraulic Jumps Instability on a Natural River Confluence: The Case Study of the Chiaravagna River (Italy)
Abstract
1. Introduction
2. Materials and Methods
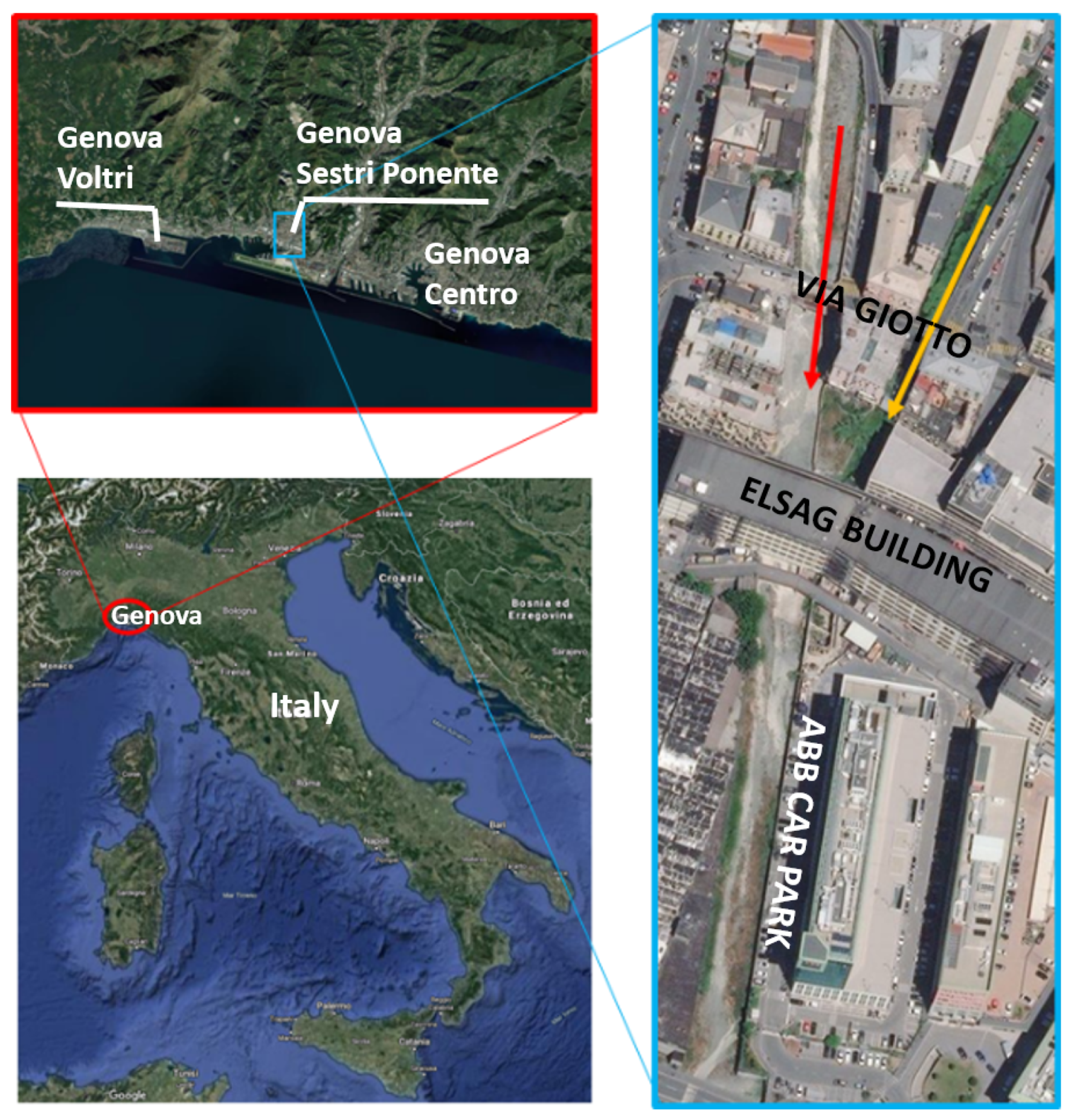
2.1. Study Area
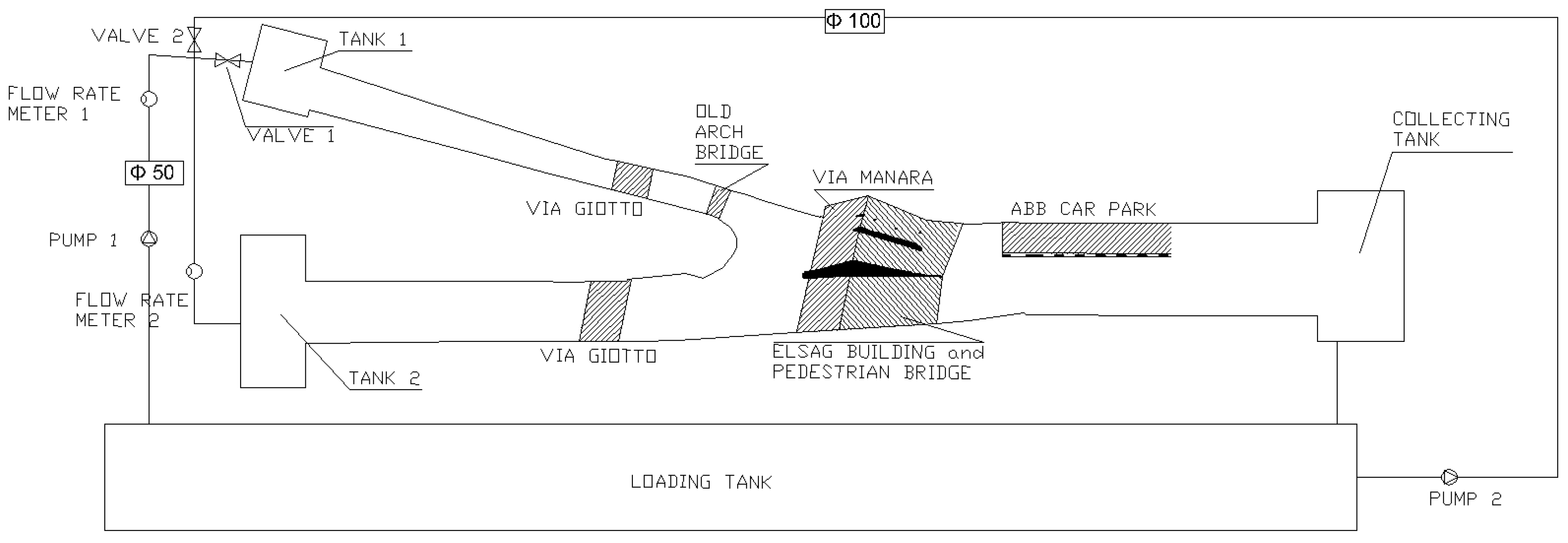
2.2. Physical Model Description
- two separate inlet channels, about 50 m long at the prototype scale, with a rectangular section with constant width that connects the feeding tanks (separated for Chiaravagna and Ruscarolo) to the actual model (sections 0–15, sections 0–33);
- a reach of about 60 m of the Chiaravagna River upstream of the confluence and including the via Giotto bridge and two weirs (sections 15–13.5);
- a reach of about 60 m of the Ruscarolo Creek upstream of the confluence and including the via Giotto bridge, the arched stone footbridge and a weir (section 31–30.1);
- a reach of about 70 m where the confluence insists, which includes the crossing of Via Manara, the reach below the ELSAG building cover, divided in three barrel-vaults, and a weir downstream of the building itself (sections from 13.5 and 30.1 to 12);
- a final reach of about 65 m downstream the ELSAG building where a car park area is located on the left bank (sections 12–11).
2.2.1. Measuring Techniques and Data Analysis
2.2.2. Experimental Conditions
3. Results
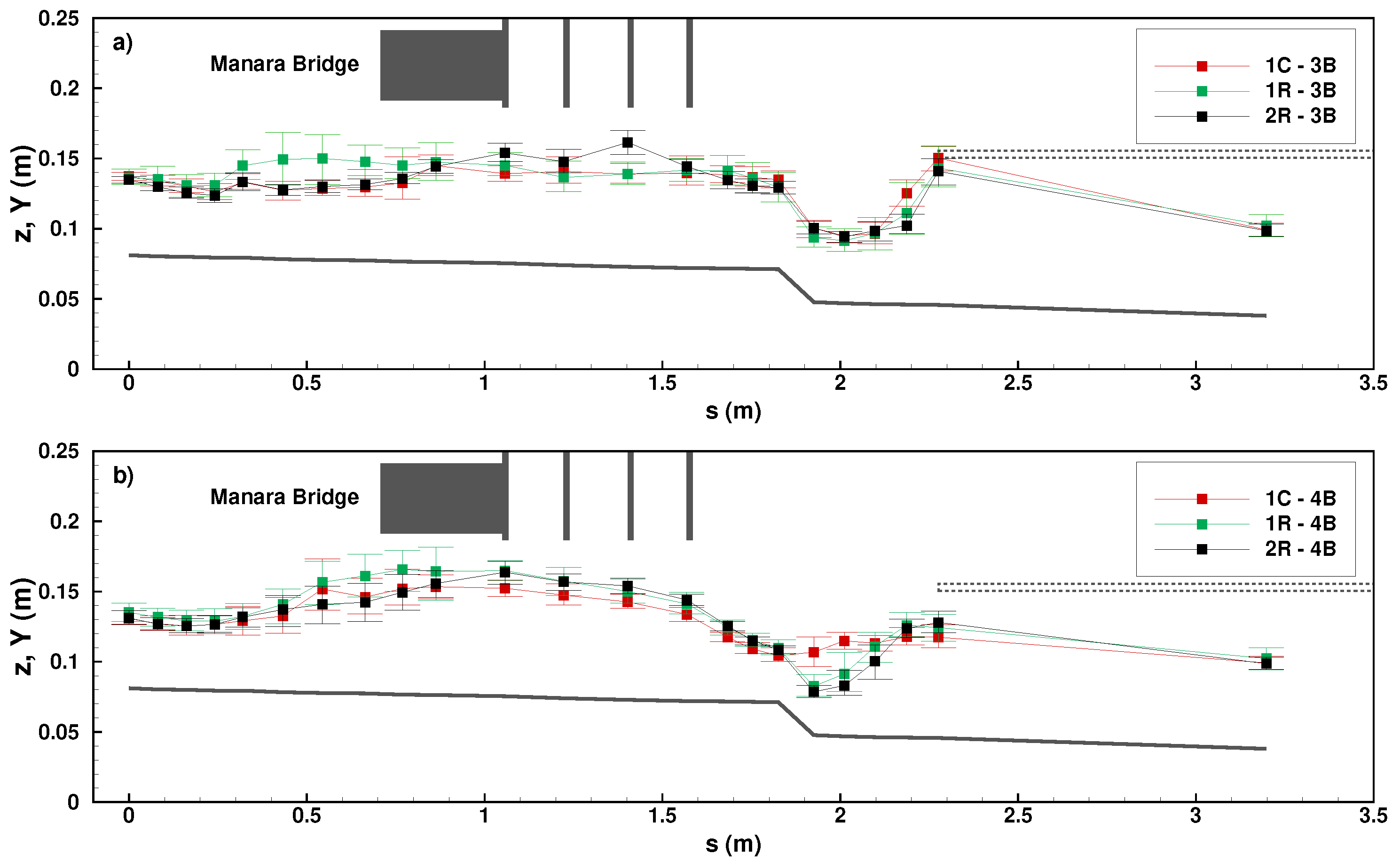
3.1. Free Surface Local Measurements and Longitudinal Profiles for the Design Discharge
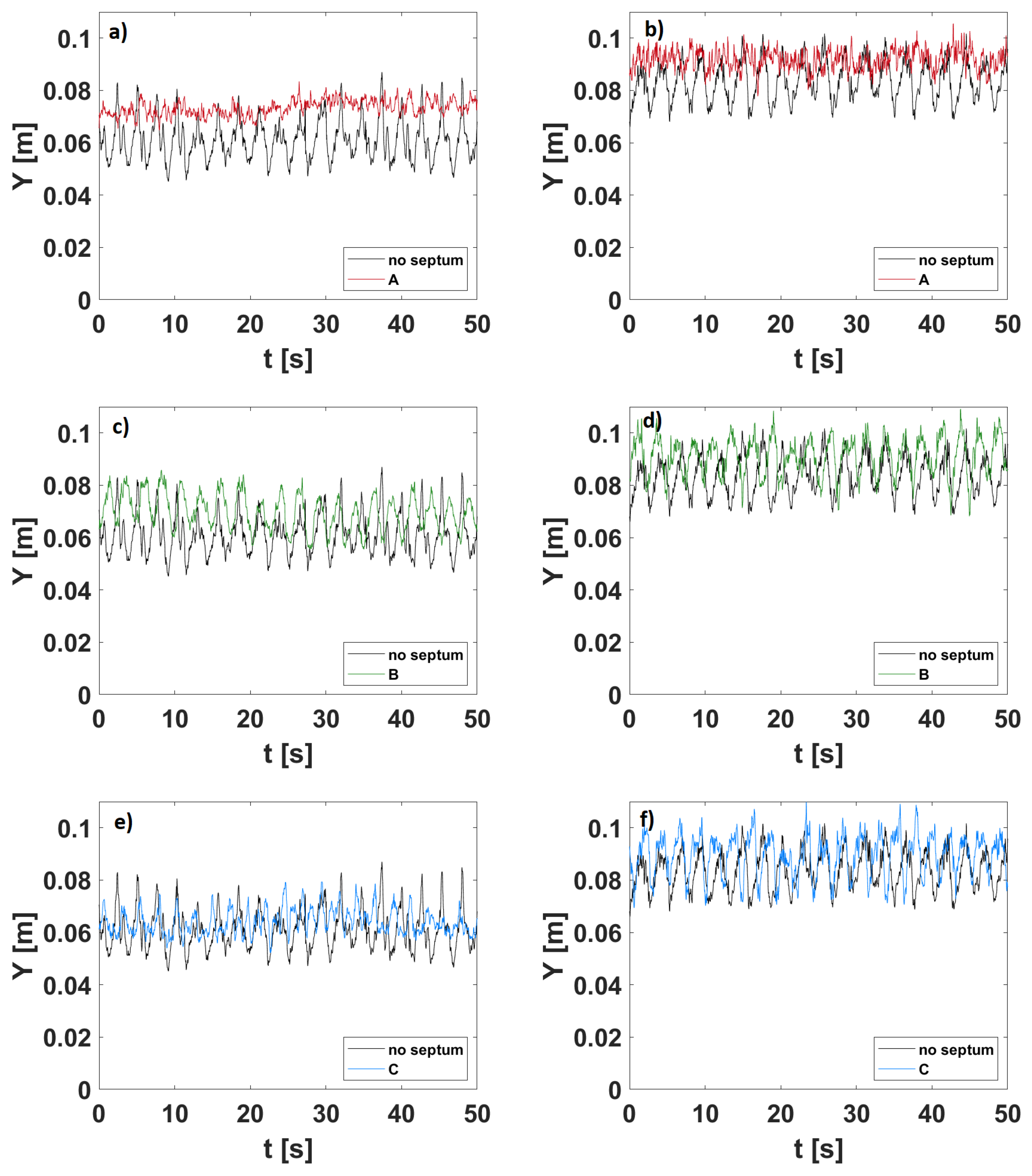
3.2. Time Velocity Distributions
4. Discussion
4.1. The Onset of the Free Surface Instability
4.2. The Effect of the Central Dyke in Damping the Velocity and Free Surface Oscillations
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| PSD | Power Spectral Density |
| Foude number | |
| Strouhal number |
References
- Hager, W.H. Energy Dissipators and Hydraulic Jump; Springer Science & Business Media: Berlin, Germany, 2013; Volume 8. [Google Scholar]
- Endreny, T.; Lautz, L.; Siegel, D. Hyporheic flow path response to hydraulic jumps at river steps: Flume and hydrodynamic models. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Wildhaber, Y.S.; Michel, C.; Epting, J.; Wildhaber, R.; Huber, E.; Huggenberger, P.; Burkhardt-Holm, P.; Alewell, C. Effects of river morphology, hydraulic gradients, and sediment deposition on water exchange and oxygen dynamics in salmonid redds. Sci. Total Environ. 2014, 470, 488–500. [Google Scholar] [CrossRef]
- Grant, S.B.; Gomez-Velez, J.D.; Ghisalberti, M. Modeling the effects of turbulence on hyporheic exchange and local-to-global nutrient processing in streams. Water Resour. Res. 2018, 54, 5883–5889. [Google Scholar] [CrossRef]
- Bakhmeteff, B.A. The hydraulic jump in terms of dynamic similarity. Trans. Am. Soc. Civ. Eng. ASCE 1936, 61, 145–162. [Google Scholar]
- Rouse, H.; Siao, T.T.; Nagaratnam, S. Turbulence characteristics of the hydraulic jump. J. Hydraul. Div. 1958, 84, 1–30. [Google Scholar]
- Bélanger, J. Notes sur l’Hydraulique; Ecole Royale des Ponts et Chaussées: Paris, France, 1841; Volume 1842, p. 223. [Google Scholar]
- Henderson, F.M. Open Channel Flow; Macmillan Co., Inc.: New York, NY, USA, 1966. [Google Scholar]
- Chanson, H. Development of the Bélanger equation and backwater equation by Jean-Baptiste Bélanger (1828). J. Hydraul. Eng. 2009, 135, 159–163. [Google Scholar] [CrossRef]
- Chanson, H. Momentum considerations in hydraulic jumps and bores. J. Irrig. Drain. Eng. 2012, 138, 382–385. [Google Scholar] [CrossRef]
- Lennon, J.; Hill, D. Particle image velocity measurements of undular and hydraulic jumps. J. Hydraul. Eng. 2006, 132, 1283–1294. [Google Scholar] [CrossRef]
- Long, D.; Rajaratnam, N.; Steffler, P.M.; Smy, P.R. Structure of flow in hydraulic jumps. J. Hydraul. Res. 1991, 29, 207–218. [Google Scholar] [CrossRef]
- Hager, W.H.; Bretz, N.V. Hydraulic jumps at positive and negative steps. J. Hydraul. Res. 1986, 24, 237–253. [Google Scholar] [CrossRef]
- Chanson, H.; Brattberg, T. Experimental study of the air–water shear flow in a hydraulic jump. Int. J. Multiph. Flow 2000, 26, 583–607. [Google Scholar] [CrossRef]
- Chanson, H. Convective transport of air bubbles in strong hydraulic jumps. Int. J. Multiph. Flow 2010, 36, 798–814. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Chanson, H. Turbulence and aeration in hydraulic jumps: Free-surface fluctuation and integral turbulent scale measurements. Environ. Fluid Mech. 2013, 13, 189–204. [Google Scholar] [CrossRef]
- Wang, H.; Chanson, H. Experimental study of turbulent fluctuations in hydraulic jumps. J. Hydraul. Eng. 2015, 141, 04015010. [Google Scholar] [CrossRef]
- Montano, L.; Felder, S. An experimental study of air–water flows in hydraulic jumps on flat slopes. J. Hydraul. Res. 2019, 1–11. [Google Scholar] [CrossRef]
- Valero, D.; Viti, N.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water 2019, 11, 36. [Google Scholar] [CrossRef]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical simulation of hydraulic jumps. Part 2: Recent results and future outlook. Water 2019, 11, 28. [Google Scholar] [CrossRef]
- Jesudhas, V.; Balachandar, R.; Bolisetti, T. Numerical study of a symmetric submerged spatial hydraulic jump. J. Hydraul. Res. 2019, 1–15. [Google Scholar] [CrossRef]
- Jesudhas, V.; Balachandar, R.; Wang, H.; Murzyn, F. Modelling hydraulic jumps: IDDES versus experiments. Environ. Fluid Mech. 2020, 1–21. [Google Scholar] [CrossRef]
- Mossa, M. On the oscillating characteristics of hydraulic jumps. J. Hydraul. Res. 1999, 37, 541–558. [Google Scholar] [CrossRef]
- Mossa, M.; Tolve, U. Flow Visualization in Bubbly Two-Phase Hydraulic Jump. Trans. ASME 1998. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free-surface fluctuations in hydraulic jumps: Experimental observations. Exp. Therm. Fluid Sci. 2009, 33, 1055–1064. [Google Scholar] [CrossRef]
- Kramer, M.; Valero, D. Turbulence and self-similarity in highly aerated shear flows: The stable hydraulic jump. Int. J. Multip. Flow 2020, 103316. [Google Scholar] [CrossRef]
- Chanson, H.; Gualtieri, C. Similitude and scale effects of air entrainment in hydraulic jumps. J. Hydraul. Res. 2008, 46, 35–44. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]


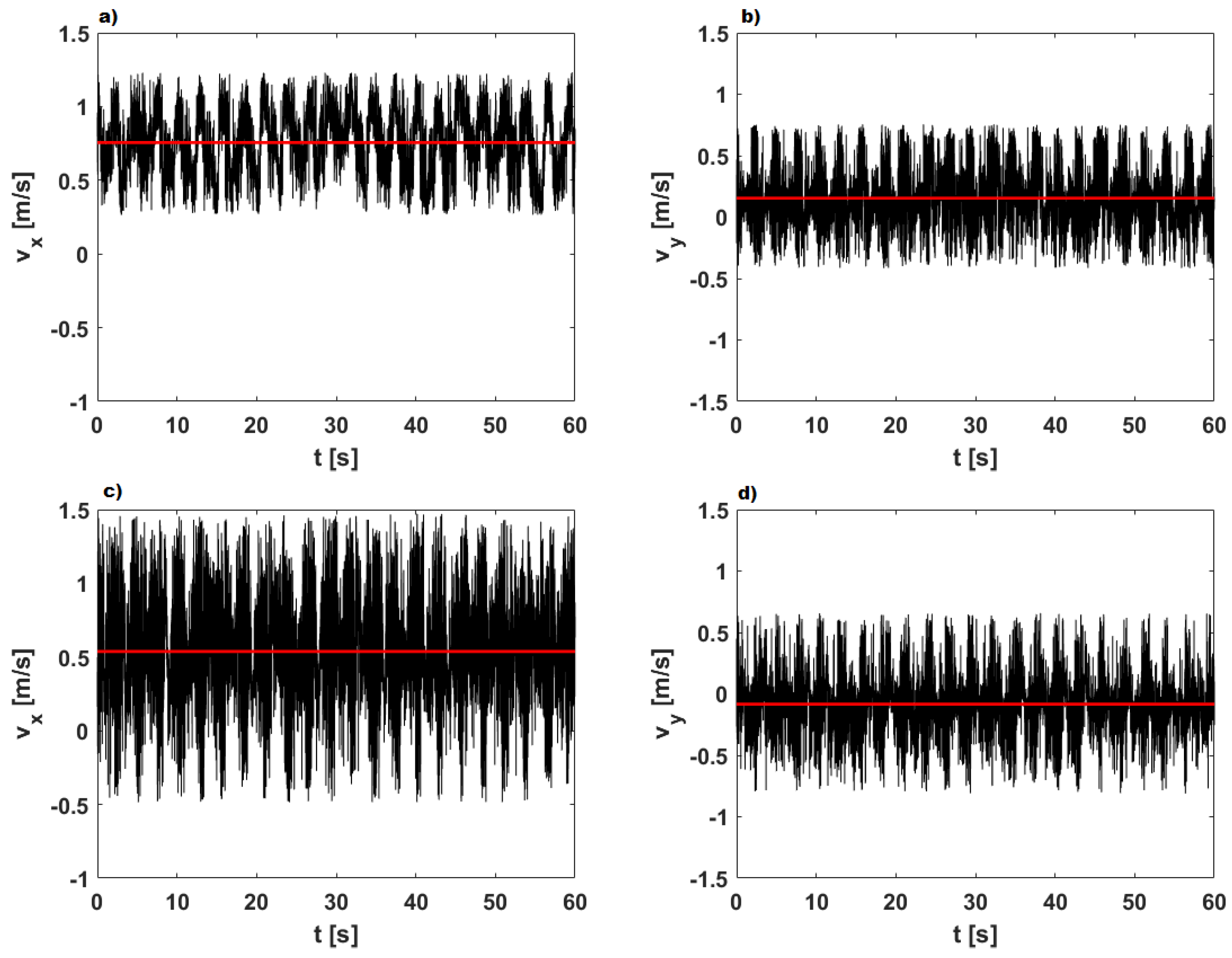
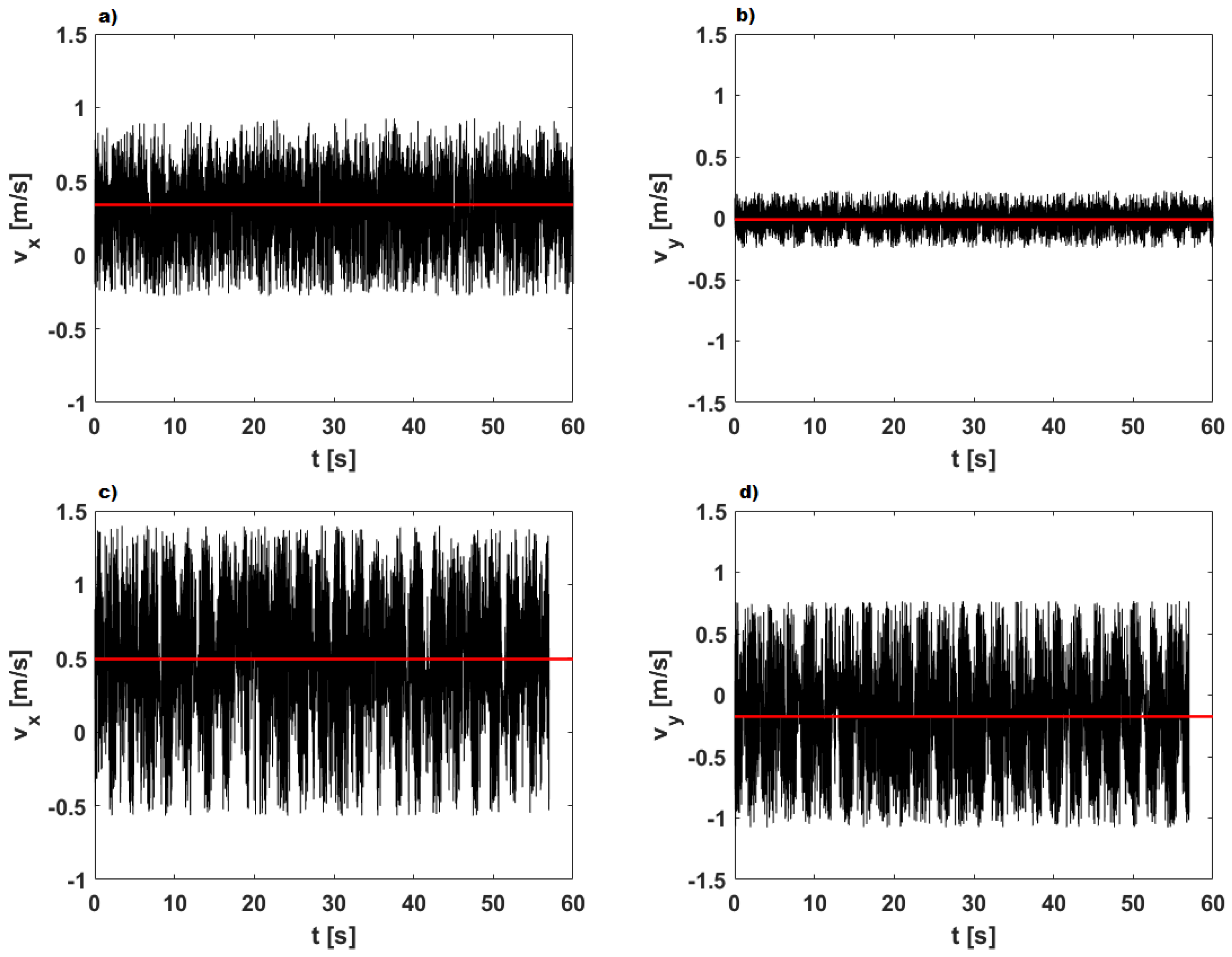
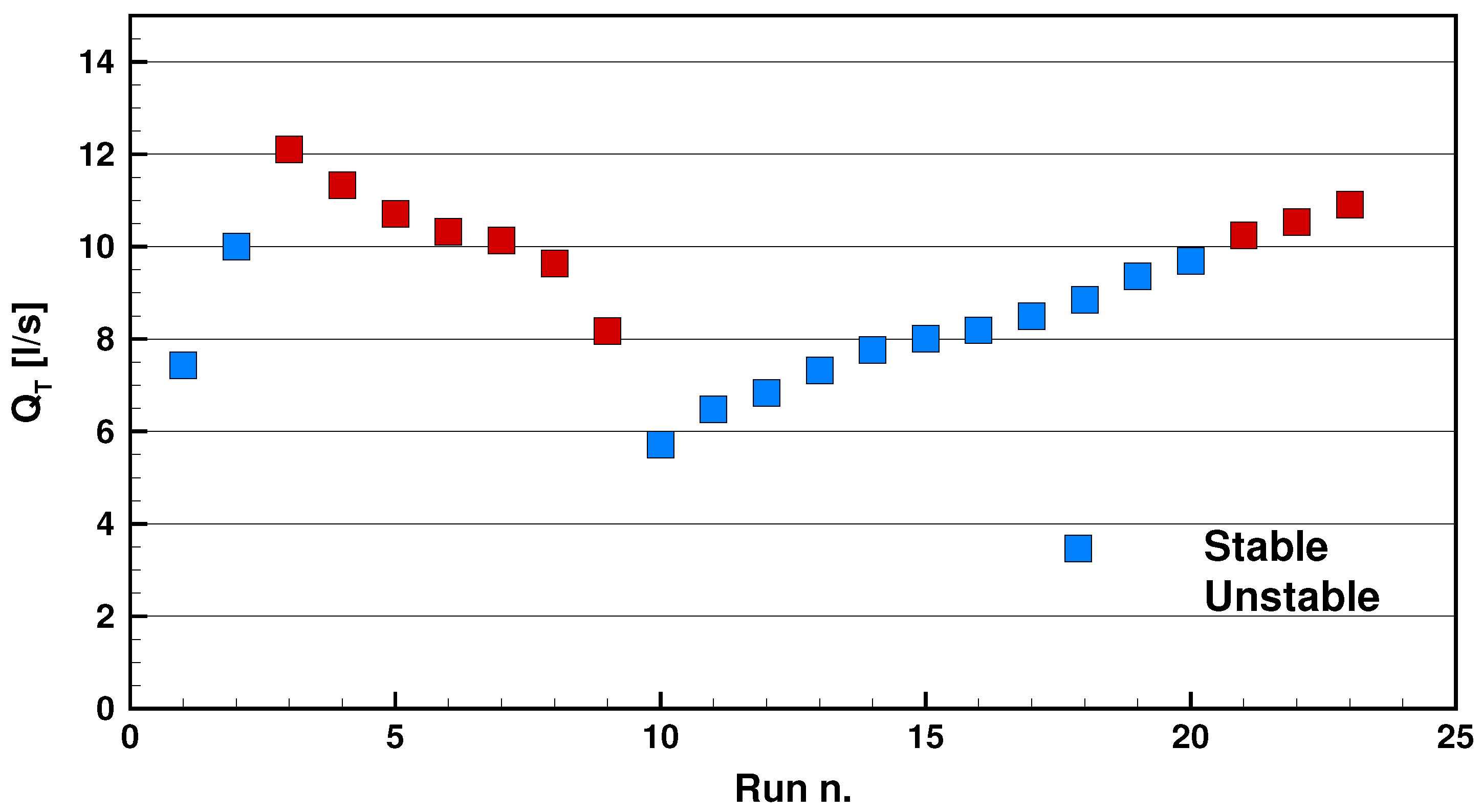


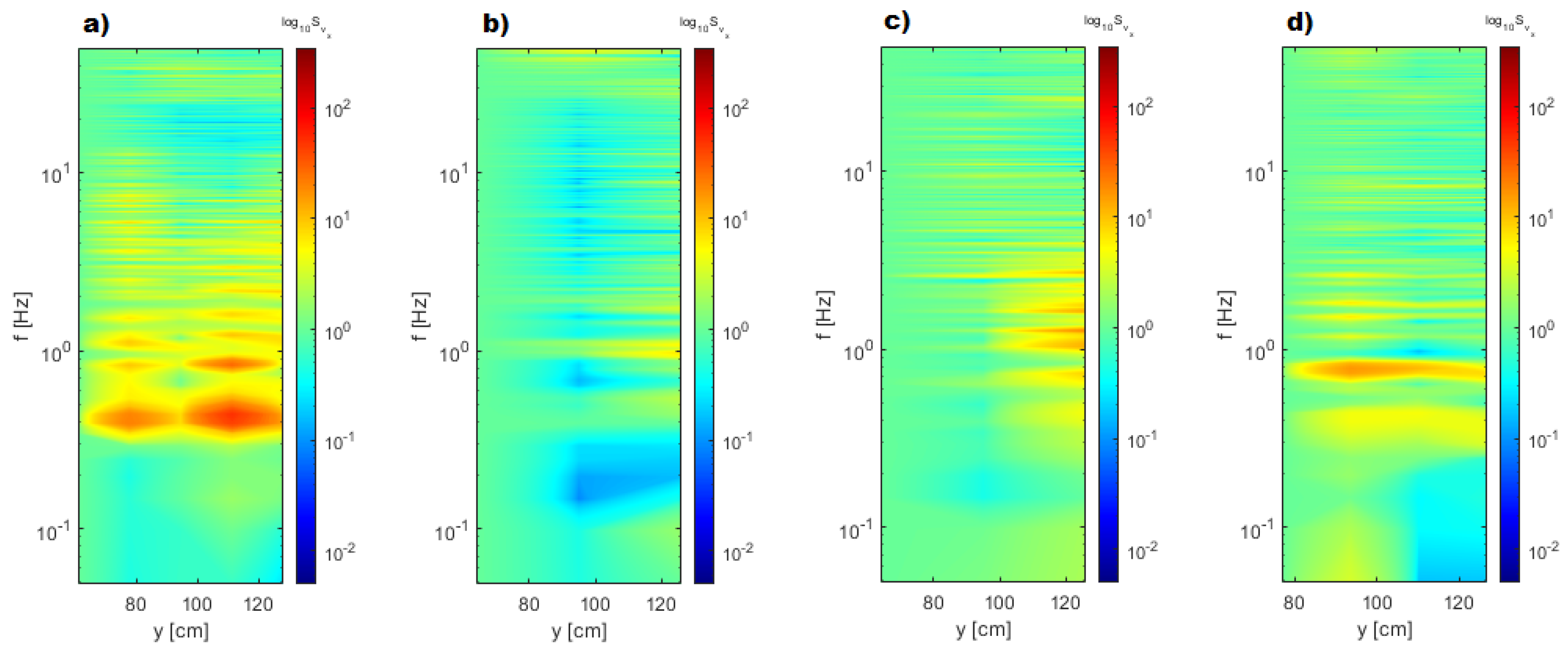
| RUN n. | (L/s) | (L/s) | (L/s) | (L/s) | (m) | (m) | Stability | ||
|---|---|---|---|---|---|---|---|---|---|
| 1C | 28.15 | 7.32 | 0.26 | 35.47 | 0.0427 | 0.0220 | 1.8349 | 2.49 | unstable |
| 1R | 24.98 | 10.48 | 0.42 | 35.47 | 0.0367 | 0.0250 | 2.04 | 2.95 | unstable |
| 2R | 24.98 | 10.48 | 0.42 | 35.47 | 0.0381 | 0.0250 | 1.93 | 2.95 | unstable |
| A | 24.98 | 10.48 | 0.42 | 35.47 | 0.0380 | 0.0250 | 1.94 | 2.95 | unstable |
| B | 24.98 | 10.48 | 0.42 | 35.47 | 0.0380 | 0.0250 | 1.94 | 2.95 | unstable |
| C | 24.98 | 10.48 | 0.42 | 35.47 | 0.0380 | 0.0250 | 1.94 | 2.95 | unstable |
| 1 | 5.93 | 1.88 | 0.25 | 7.43 | 0.0178 | 0.0078 | 1.43 | 2.42 | stable |
| 2 | 7.93 | 2.61 | 0.26 | 10.00 | 0.0231 | 0.0094 | 1.30 | 2.54 | stable |
| 3 | 9.58 | 3.20 | 0.26 | 12.11 | 0.0302 | 0.0102 | 1.05 | 2.74 | unstable |
| 4 | 9.00 | 2.94 | 0.26 | 11.33 | 0.0274 | 0.0098 | 1.14 | 2.68 | unstable |
| 5 | 8.53 | 2.74 | 0.26 | 10.71 | 0.0254 | 0.0093 | 1.21 | 2.71 | unstable |
| 6 | 8.20 | 2.66 | 0.26 | 10.32 | 0.0241 | 0.0092 | 1.26 | 2.65 | unstable |
| 7 | 8.04 | 2.64 | 0.26 | 10.13 | 0.0235 | 0.0092 | 1.28 | 2.65 | unstable |
| 8 | 7.65 | 2.50 | 0.26 | 9.64 | 0.0221 | 0.0091 | 1.34 | 2.56 | unstable |
| 9 | 6.48 | 2.14 | 0.26 | 8.17 | 0.0189 | 0.0081 | 1.43 | 2.58 | unstable |
| 10 | 5.40 | 1.80 | 0.26 | 6.83 | 0.0171 | 0.0077 | 1.39 | 2.34 | stable |
| 11 | 6.48 | 2.16 | 0.26 | 8.19 | 0.0189 | 0.0082 | 1.43 | 2.57 | stable |
| 12 | 4.53 | 1.50 | 0.26 | 5.72 | 0.0163 | 0.0070 | 1.25 | 2.26 | stable |
| 13 | 5.14 | 1.68 | 0.26 | 6.48 | 0.0165 | 0.0075 | 1.39 | 2.29 | stable |
| 14 | 5.81 | 1.90 | 0.26 | 7.32 | 0.0170 | 0.0077 | 1.51 | 2.48 | stable |
| 15 | 6.15 | 2.03 | 0.26 | 7.76 | 0.0178 | 0.0079 | 1.49 | 2.55 | stable |
| 16 | 6.35 | 2.10 | 0.26 | 8.01 | 0.0183 | 0.0080 | 1.47 | 2.58 | stable |
| 17 | 6.74 | 2.21 | 0.26 | 8.50 | 0.0195 | 0.0083 | 1.42 | 2.58 | stable |
| 18 | 7.02 | 2.30 | 0.26 | 8.85 | 0.0200 | 0.0086 | 1.43 | 2.55 | stable |
| 19 | 7.44 | 2.41 | 0.26 | 9.36 | 0.0210 | 0.0088 | 1.40 | 2.59 | stable |
| 20 | 7.70 | 2.51 | 0.26 | 9.69 | 0.0216 | 0.0091 | 1.39 | 2.55 | stable |
| 21 | 8.15 | 2.63 | 0.26 | 10.24 | 0.0229 | 0.0092 | 1.35 | 2.66 | unstable |
| 22 | 8.37 | 2.72 | 0.26 | 10.53 | 0.0241 | 0.0093 | 1.28 | 2.68 | unstable |
| 23 | 8.66 | 2.83 | 0.26 | 10.91 | 0.0255 | 0.0094 | 1.22 | 2.74 | unstable |
| Configuration | Longitudinal Profile | Maximum Oscillation Amplitude | Mean Oscillation Amplitude |
|---|---|---|---|
| 1C | 3B | 22.6% | 10.8% |
| 1R | 3B | 33.2% | 16.4% |
| 2R | 3B | 13.9% | 8.2% |
| 1C | 4B | 24.1% | 11.9% |
| 1R | 4B | 30.3% | 14.5% |
| 2R | 4B | 24.5% | 11.1% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Leo, A.; Ruffini, A.; Postacchini, M.; Colombini, M.; Stocchino, A. The Effects of Hydraulic Jumps Instability on a Natural River Confluence: The Case Study of the Chiaravagna River (Italy). Water 2020, 12, 2027. https://doi.org/10.3390/w12072027
De Leo A, Ruffini A, Postacchini M, Colombini M, Stocchino A. The Effects of Hydraulic Jumps Instability on a Natural River Confluence: The Case Study of the Chiaravagna River (Italy). Water. 2020; 12(7):2027. https://doi.org/10.3390/w12072027
Chicago/Turabian StyleDe Leo, Annalisa, Alessia Ruffini, Matteo Postacchini, Marco Colombini, and Alessandro Stocchino. 2020. "The Effects of Hydraulic Jumps Instability on a Natural River Confluence: The Case Study of the Chiaravagna River (Italy)" Water 12, no. 7: 2027. https://doi.org/10.3390/w12072027
APA StyleDe Leo, A., Ruffini, A., Postacchini, M., Colombini, M., & Stocchino, A. (2020). The Effects of Hydraulic Jumps Instability on a Natural River Confluence: The Case Study of the Chiaravagna River (Italy). Water, 12(7), 2027. https://doi.org/10.3390/w12072027








