An Improved Meshless Divergence-Free PBF Framework for Ocean Wave Modeling in Marine Simulator
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
1.2.1. Spectrum-Based Approaches
1.2.2. Physics-Based Methods
1.3. Our Contributions
2. Fluid Simulation
2.1. Governing Equations
2.2. Discretization of the Continuum Domain
2.3. Constant Density Constraints
2.4. Divergence-Free Velocity Constraints
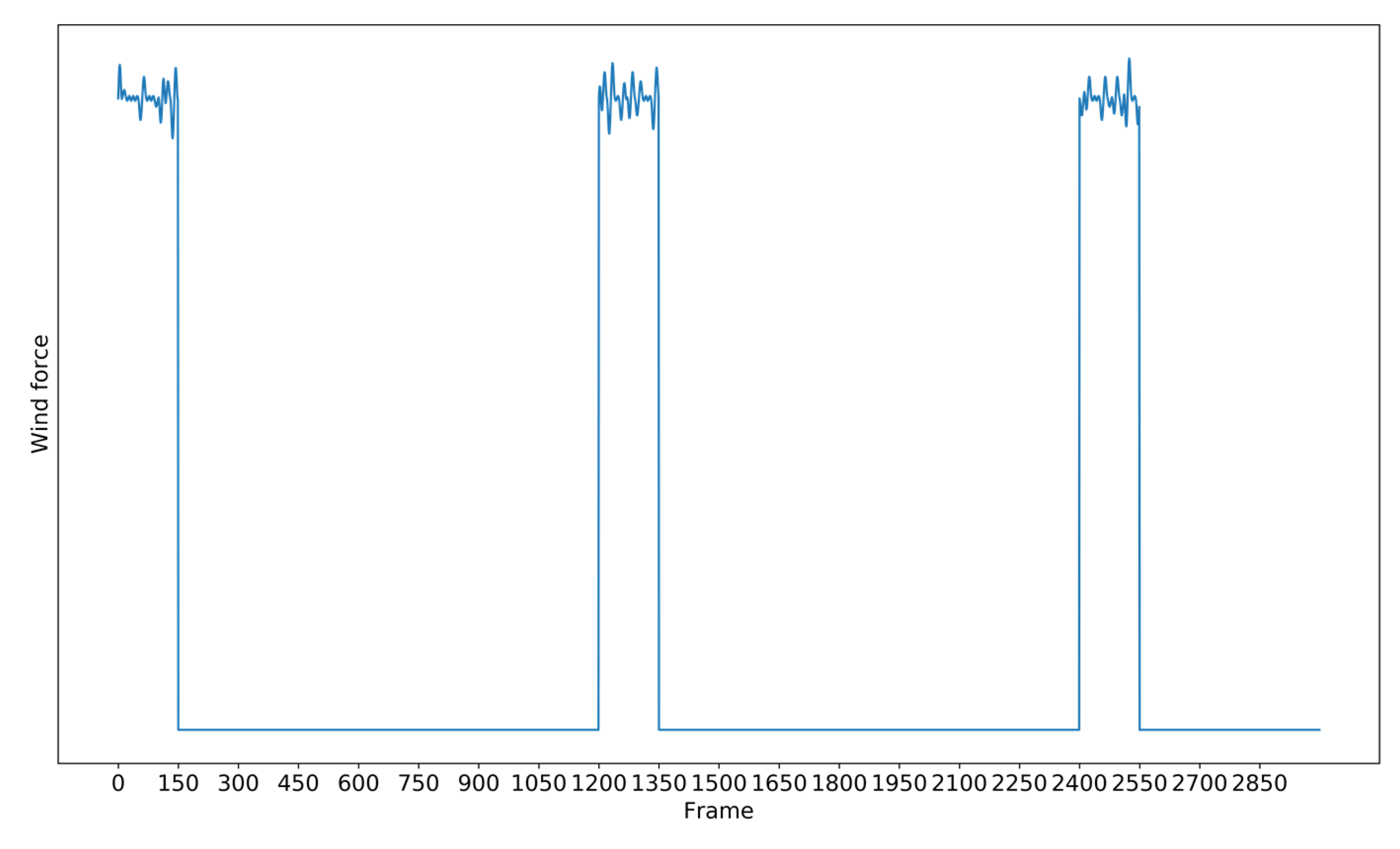
3. Wind Field Modeling
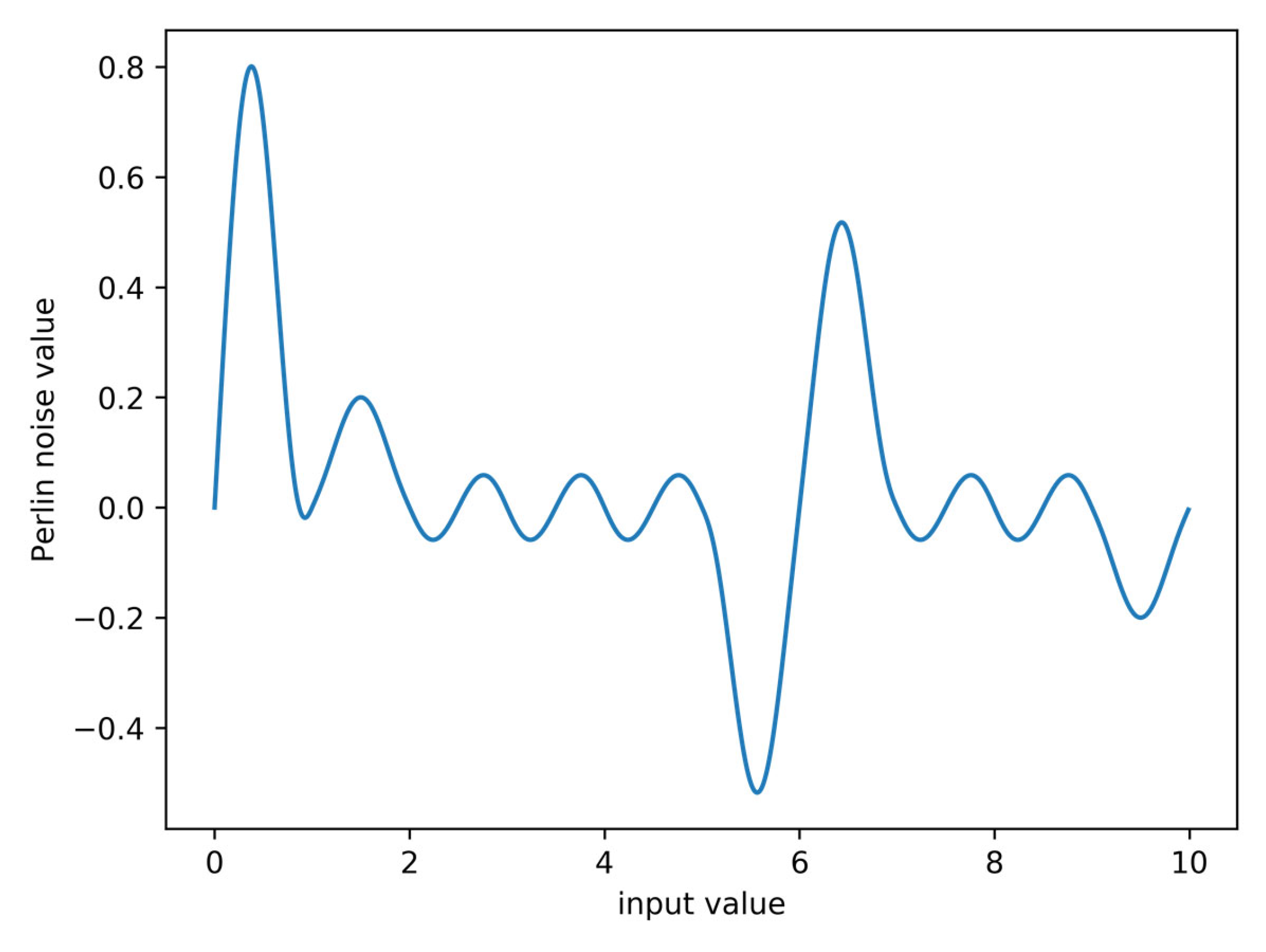
3.1. Stochastic Wind Field Based on Perlin Noise
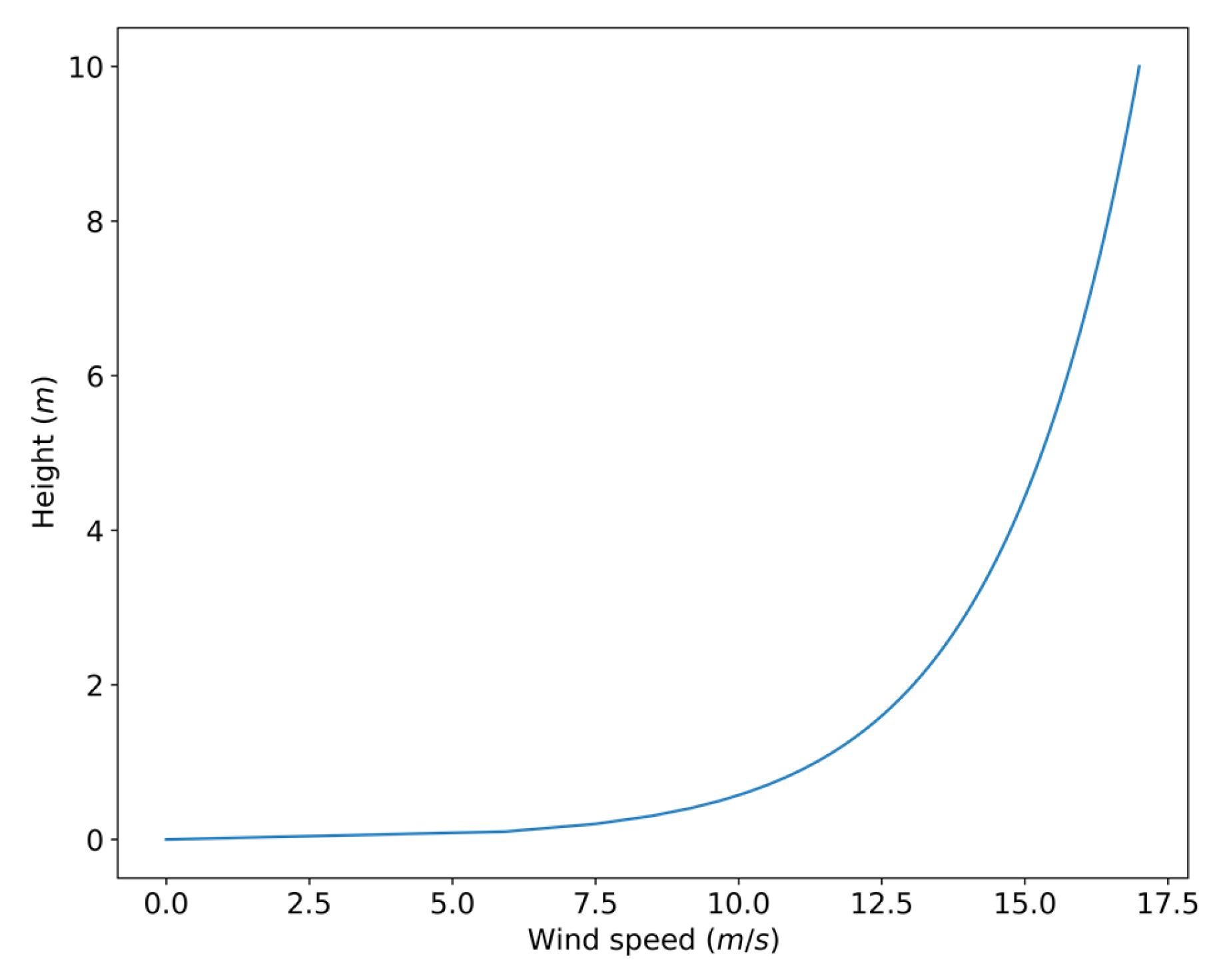
3.2. Wind Profile in the Vertical Direction
4. Results and Discussion
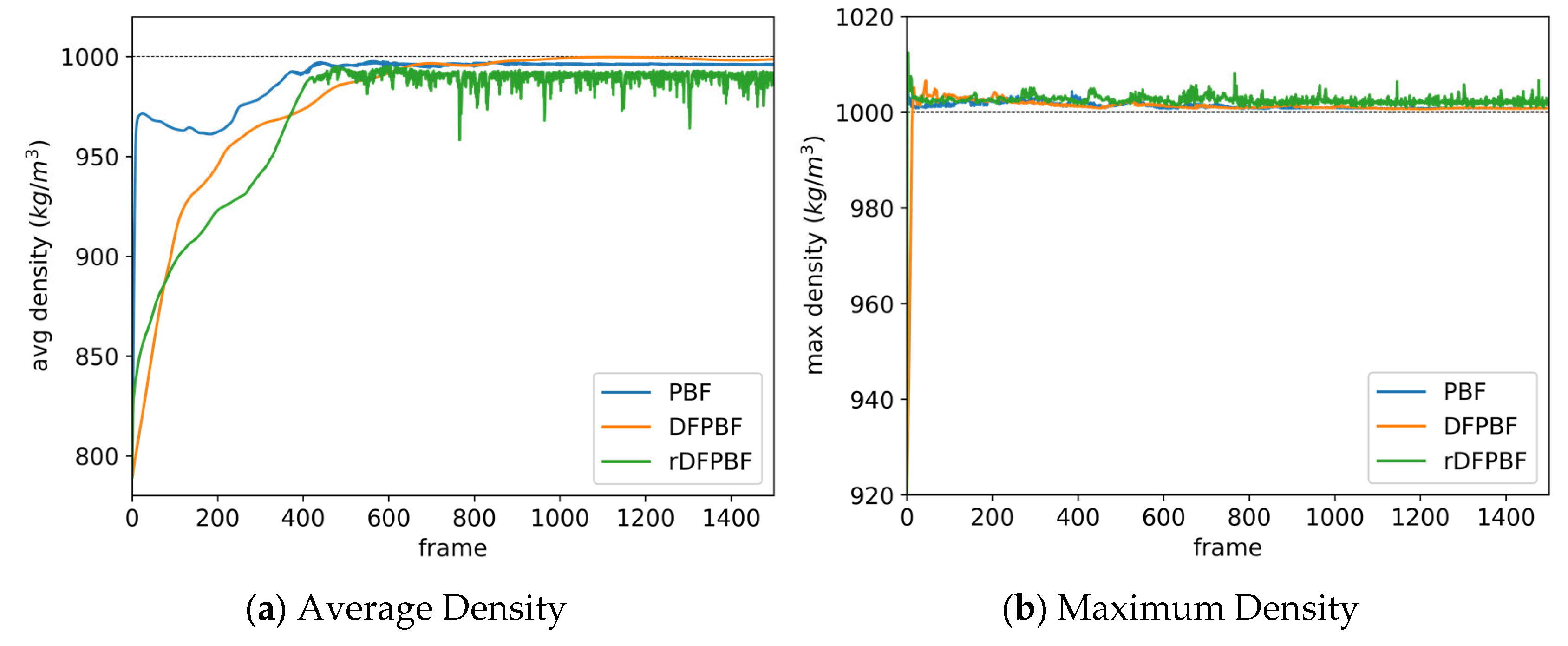
4.1. Performance of DFPBF
4.2. Wind Field Simulation Results
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A: Calculation Flow of the Constant Density Solver
| Algorithm A1 Constant Density Solver |
| 1: for i in particles: |
| 2: compute factor |
| 3: while and : |
| 4: for i in particles: |
| 5: compute density |
| 6: compute density constraint |
| 7: compute |
| 8: for i in particles: |
| 9: compute |
| 10: for i in particles: |
| 11: apply relaxation position update: |
| 12: update and |
Appendix B: Calculation Flow of the Divergence-Free Solver
| Algorithm A2 Divergence-Free Solver |
| 1: compute divergence-free velocity constraint |
| 2: while and : |
| 3: for i in particles: |
| 4: compute |
| 5: for i in particles: |
| 6: compute |
| 7: for i in particles: |
| 8: apply relaxation position update: |
| 9: update and |
Appendix C: Calculation Flow of the Wind Field
| Algorithm A3 Apply Wind Force |
| 1: if : |
| 2: |
| 3: if : |
| 4: for i in particles: |
| 5: generate stochastic wind field |
| 6: compute reference wind velocity |
| 7: apply wind profile model |
| 8: update velocity |
| 9: step += 1 |
Appendix D: Calculation Flow of the DFPBF framework
| Algorithm A4 DFPBF Simulation Loop |
| 1: for i in particles: |
| 2: apply gravity |
| 3: update position |
| 4: for i in particles: |
| 5: searching neighboring particles |
| 6: apply constant density solver |
| 7: for i in particles: |
| 8: update velocity |
| 9: apply artificial viscosity |
| 10: apply wind force |
| 11: apply divergence-free solver |
References
- Tessendorf, J. Simulating Ocean Water; 2004 Course Notes; ACM SIGGRAPH: Los Angeles, CA, USA, 2004. [Google Scholar]
- Pierson, W.J., Jr.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Horvath, C.J. Empirical directional wave spectra for computer graphics. In Proceedings of the 2015 Symposium on Digital Production, Los Angeles, CA, USA, 8 August 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 29–39. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergänzung Deut. Hydrogr. Z. 1973, 12, 1–95. [Google Scholar]
- Fréchot, J. Realistic simulation of ocean surface using wave spectra. In Proceedings of the First International Conference on Computer Graphics Theory and Applications, Setúbal, Portugal, 25–28 February 2006; Springer: Berlin/Heidelberg, Germany, 2007; pp. 76–83. [Google Scholar]
- Bouws, E.; Günther, H.; Rosenthal, W.; Vincent, C.L. Similarity of the wind wave spectrum in finite depth water: 1. Spectral form. J. Geophys. Res. Oceans 1985, 90, 975–986. [Google Scholar] [CrossRef]
- Lee, N.; Baek, N.; Ryu, K.W. A real-time method for ocean surface simulation using the TMA model. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2009, 1, 25–26. [Google Scholar]
- Kitaigordskii, S.A.; Krasitskii, V.P.; Zaslavskii, M.M. On Phillips’ theory of equilibrium range in the spectra of wind-generated gravity waves. J. Phys. Oceanogr. 1975, 5, 410–420. [Google Scholar] [CrossRef] [Green Version]
- Hughes, S.A. The TMA Shallow-Water Spectrum Description and Applications; Tech. Rep. CERC-84-7; Coastal Engineering Research Center: Vicksburg, MS, USA, 1984. [Google Scholar]
- Chen, L.; Jin, Y.; Yin, Y. Ocean wave rendering with whitecap in the visual system of a maritime simulator. J. Comput. Inf. Technol. 2017, 25, 63–76. [Google Scholar] [CrossRef] [Green Version]
- Irving, G.; Guendelman, E.; Losasso, F.; Fedkiw, R. Efficient simulation of large bodies of water by coupling two and three dimensional techniques. ACM Trans. Graph. 2006, 25, 805–811. [Google Scholar] [CrossRef]
- Chentanez, N.; Müller, M. Real-time Eulerian water simulation using a restricted tall cell grid. ACM Trans. Graph. 2011, 30, 82. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific Publishing Company: Singapore, 2003. [Google Scholar]
- Stam, J.; Fiume, E. Depicting fire and other gaseous phenomena using diffusion processes. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995; Mair, S.G., Cook, R., Eds.; Association for Computing Machinery: New York, NY, USA, 2003; pp. 129–136. [Google Scholar]
- Müller, M.; Charypar, D.; Gross, M. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation, San Diego, CA, USA, 26–27 July 2003; Eurographics Association: Goslar, Germany, 2003; pp. 154–159. [Google Scholar]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Becker, M.; Teschner, M. Weakly compressible SPH for free surface flows. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; Eurographics Association: Goslar, Germany, 2007; pp. 209–218. [Google Scholar]
- Solenthaler, B.; Pajarola, R. Predictive-corrective incompressible SPH. ACM Trans. Graph. 2009, 28, 40. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Liu, N.; Li, S.; Wang, H.; Wang, G. Local poisson SPH for viscous incompressible fluids. Comput. Graph. Forum 2012, 31, 1948–1958. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y.M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Asai, M.; Aly, A.M.; Sonoda, Y.; Sakai, Y. A stabilized incompressible SPH method by relaxing the density invariance condition. J. Appl. Math. 2012, 2012, 139583. [Google Scholar] [CrossRef]
- Ihmsen, M.; Cornelis, J.; Solenthaler, B.; Horvath, C.; Teschner, M. Implicit incompressible SPH. IEEE Trans. Vis. Comput. Graph. 2013, 20, 426–435. [Google Scholar] [CrossRef]
- Bender, J.; Koschier, D. Divergence-free smoothed particle hydrodynamics. In Proceedings of the 14th ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 7–9 August 2015; Eurographics Association: Goslar, Germany, 2015; pp. 147–155. [Google Scholar]
- Cornelis, J.; Bender, J.; Gissler, C.; Ihmsen, M.; Teschner, M. An optimized source term formulation for incompressible SPH. Visual Comput. 2019, 35, 579–590. [Google Scholar] [CrossRef]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Macklin, M.; Müller, M. Position based fluids. ACM Trans. Graph. 2013, 32, 104. [Google Scholar] [CrossRef]
- Bodin, K.; Lacoursière, C.; Servin, M. Constraint fluids. IEEE Trans. Vis. Comput. Graph. 2012, 18, 516–526. [Google Scholar] [CrossRef]
- Kang, N.; Sagong, D. Incompressible SPH using the divergence-free condition. Comput. Graph. Forum. 2014, 33, 219–228. [Google Scholar] [CrossRef]
- Müller, M.; Solenthaler, B.; Keiser, R.; Gross, M. Particle-based fluid-fluid interaction. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 29–31 July 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 237–244. [Google Scholar]
- Ihmsen, M.; Bader, J.; Akinci, G.; Teschner, M. Animation of air bubbles with SPH. In Proceedings of the International Conference on Computer Graphics Theory and Applications, Vilamoura, Algarve, Portugal, 5–7 March 2011; Institute for Systems and Technologies of Information, Control and Communication: Setubal, Portugal, 2011; pp. 225–234. [Google Scholar]
- Ihmsen, M.; Akinci, N.; Akinci, G.; Teschner, M. Unified spray, foam and air bubbles for particle-based fluids. Visual Comput. 2012, 28, 669–677. [Google Scholar] [CrossRef]
- Macklin, M.; Müller, M.; Chentanez, N.; Kim, T.Y. Unified particle physics for real-time applications. ACM Trans. Graph. 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Gissler, C.; Band, S.; Peer, A.; Ihmsen, M.; Teschner, M. Approximate air-fluid interactions for SPH. In Proceedings of the 13th Workshop on Virtual Reality Interaction and Physical Simulation, Lyon, France, 23–24 April 2017; Eurographics Association: Goslar, Germany, 2017; pp. 29–38. [Google Scholar]
- Akinci, N.; Ihmsen, M.; Akinci, G.; Solenthaler, B.; Teschner, M. Versatile rigid-fluid coupling for incompressible SPH. ACM Trans. Graph. 2012, 31, 62. [Google Scholar] [CrossRef]
- Bender, J.; Koschier, D.; Kugelstadt, T.; Weiler, M. A micropolar material model for turbulent SPH fluids. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 28–30 July 2017; Association for Computing Machinery: New York, NY, USA, 2017; p. 4. [Google Scholar]
- Bender, J.; Koschier, D.; Kugelstadt, T.; Weiler, M. Turbulent Micropolar SPH fluids with foam. IEEE Trans. Vis. Comput. Graph. 2018, 25, 2284–2295. [Google Scholar] [CrossRef]
- Losasso, F.; Talton, J.O.; Kwatra, N.; Fedkiw, R. Two-way coupled SPH and particle level set fluid simulation. IEEE Trans. Vis. Comput. Graph. 2008, 14, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Ihmsen, M.; Orthmann, J.; Solenthaler, B.; Kolb, A.; Teschner, M. SPH Fluids in Computer Graphics; EG2014–STARs: Strasbourg, France, 2014. [Google Scholar]
- Perlin, K. Improving Noise. ACM Trans. Graph. 2002, 21, 681–682. [Google Scholar] [CrossRef]
- Bowers, J.; Wang, R.; Wei, L.Y.; Maletz, D. Parallel Poisson disk sampling with spectrum analysis on surfaces. ACM Trans. Graph. 2010, 29, 166. [Google Scholar] [CrossRef]
- Li, H.; Ren, H.; Qiu, S.; Wang, C. Physics-Based Simulation of Ocean Scenes in Marine Simulator Visual System. Water 2020, 12, 215. [Google Scholar] [CrossRef] [Green Version]

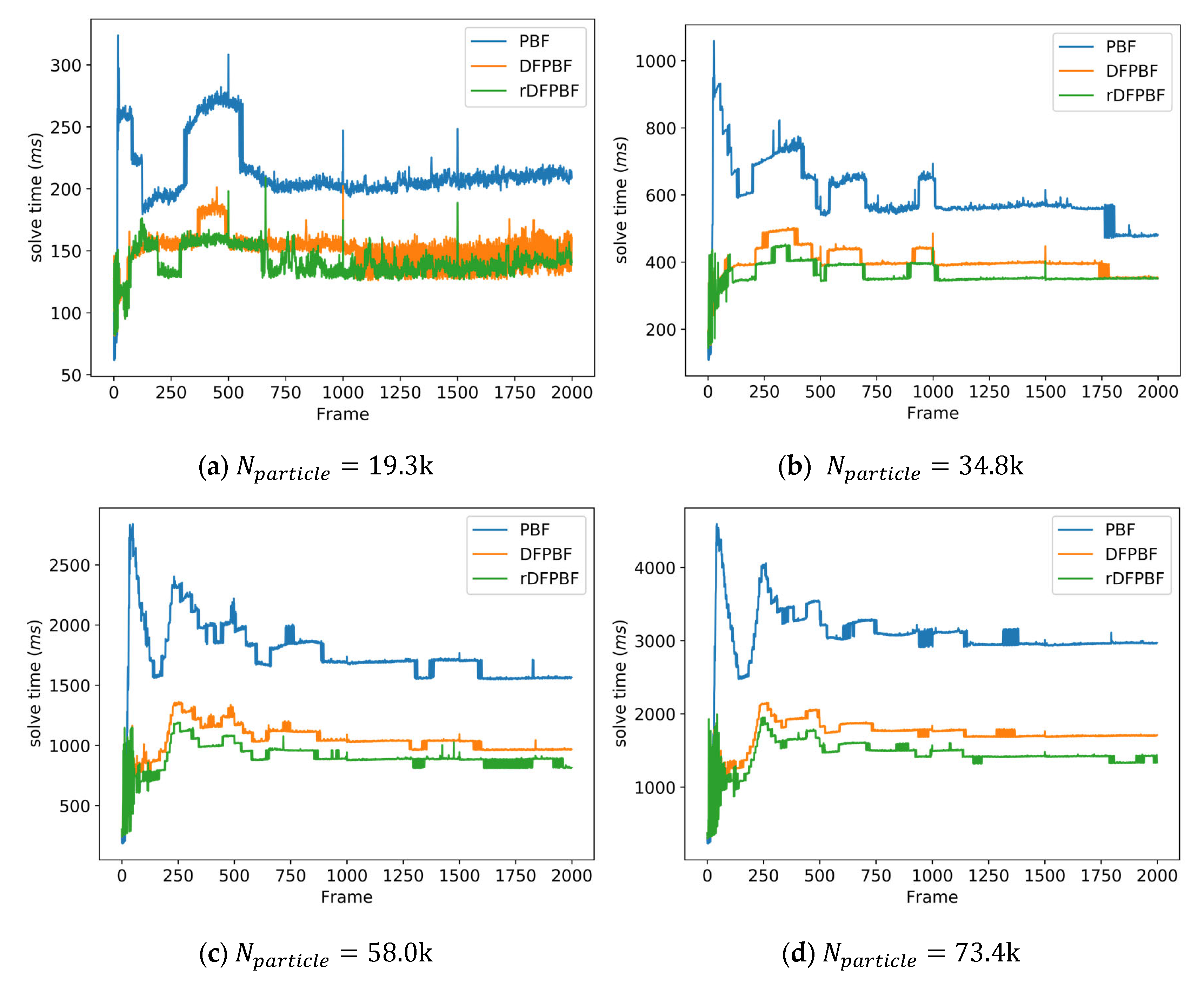
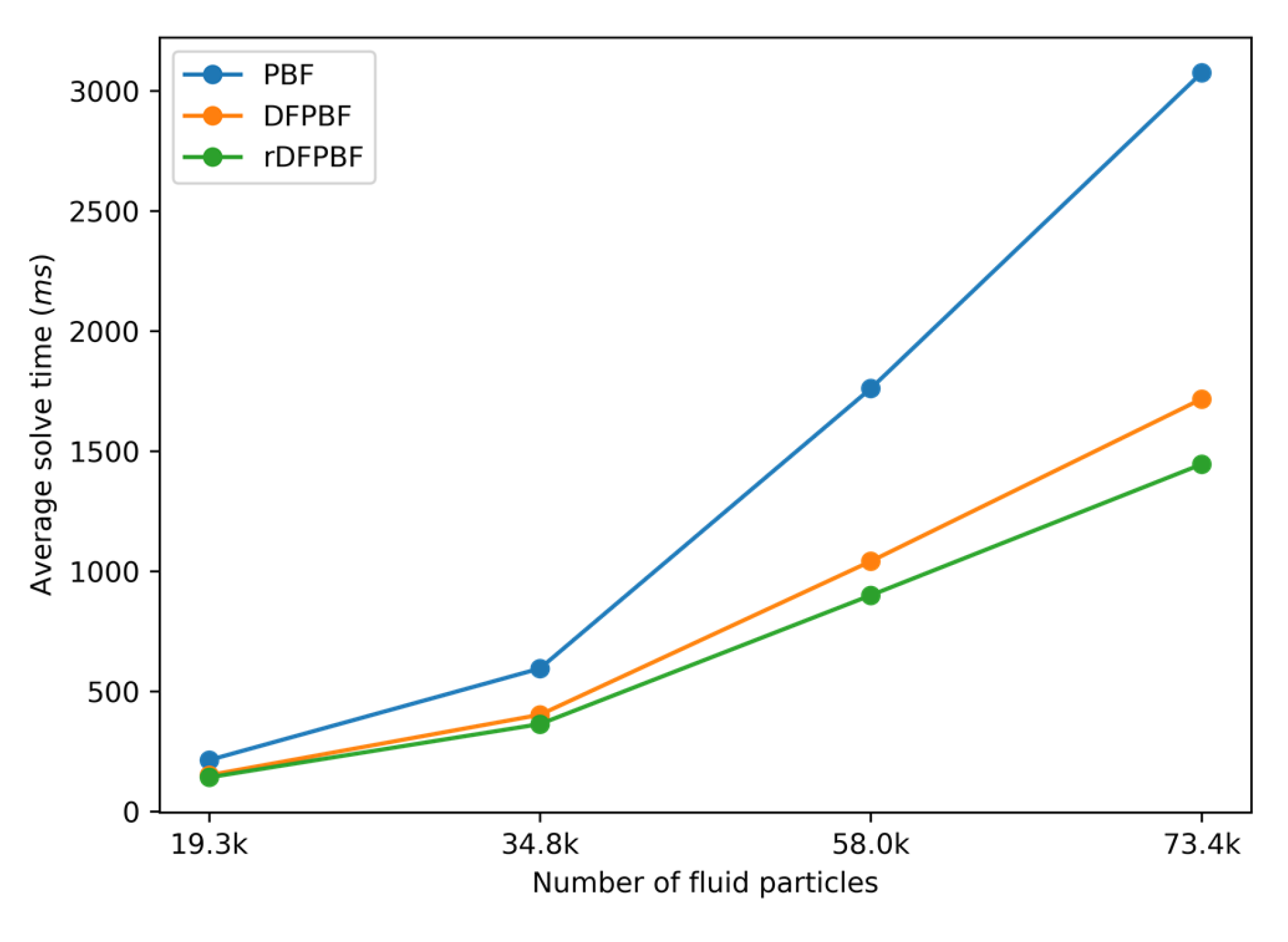
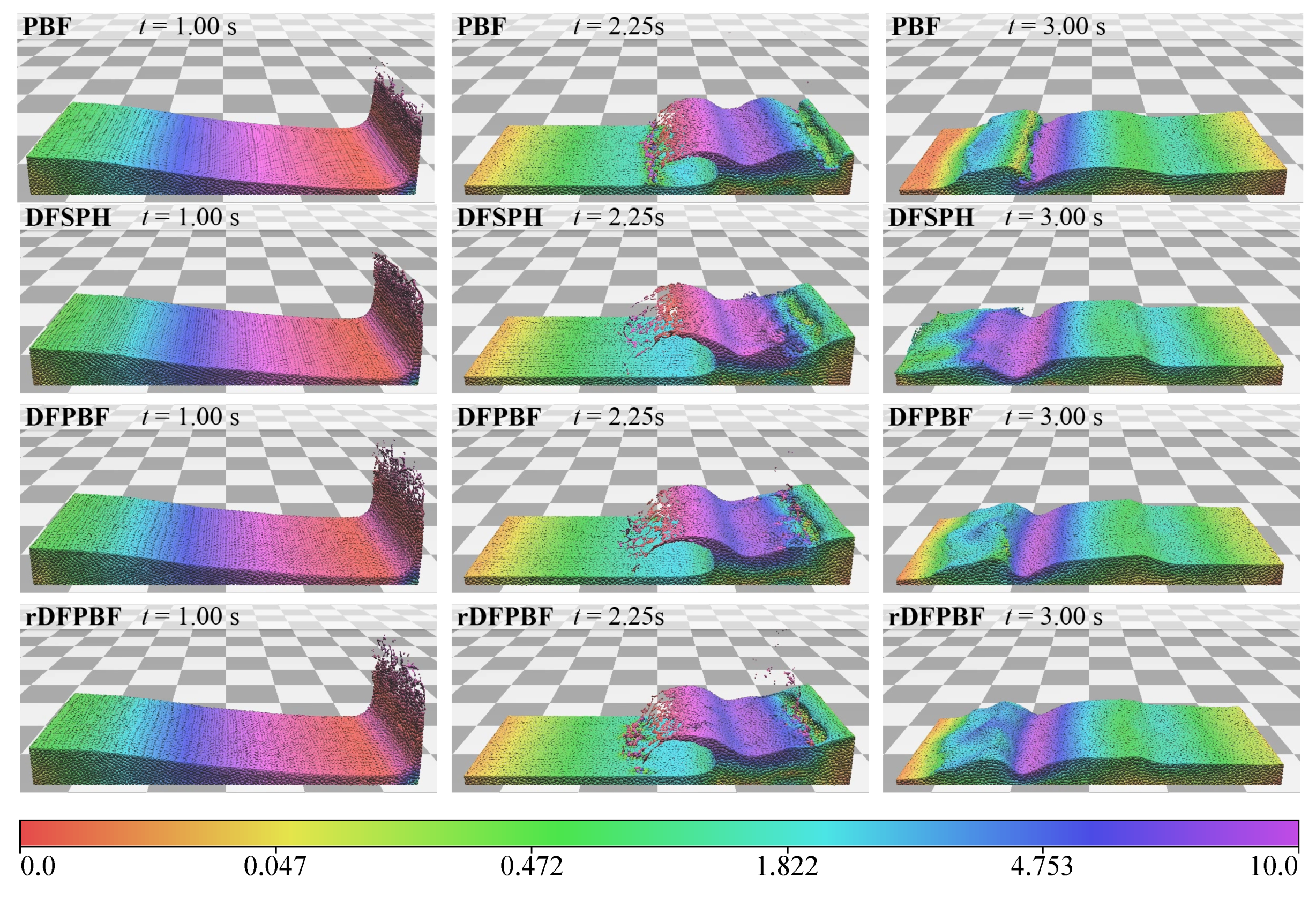
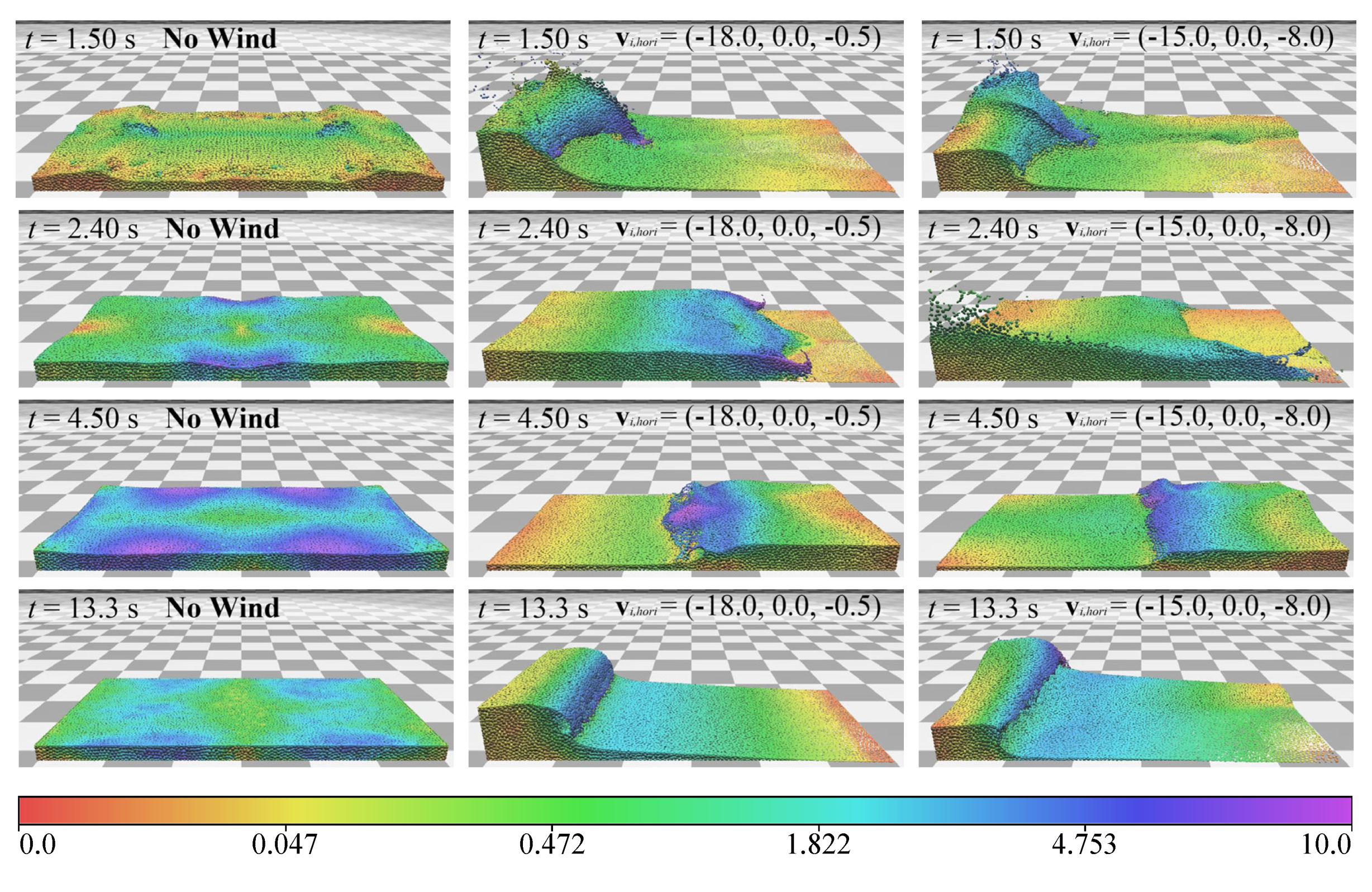
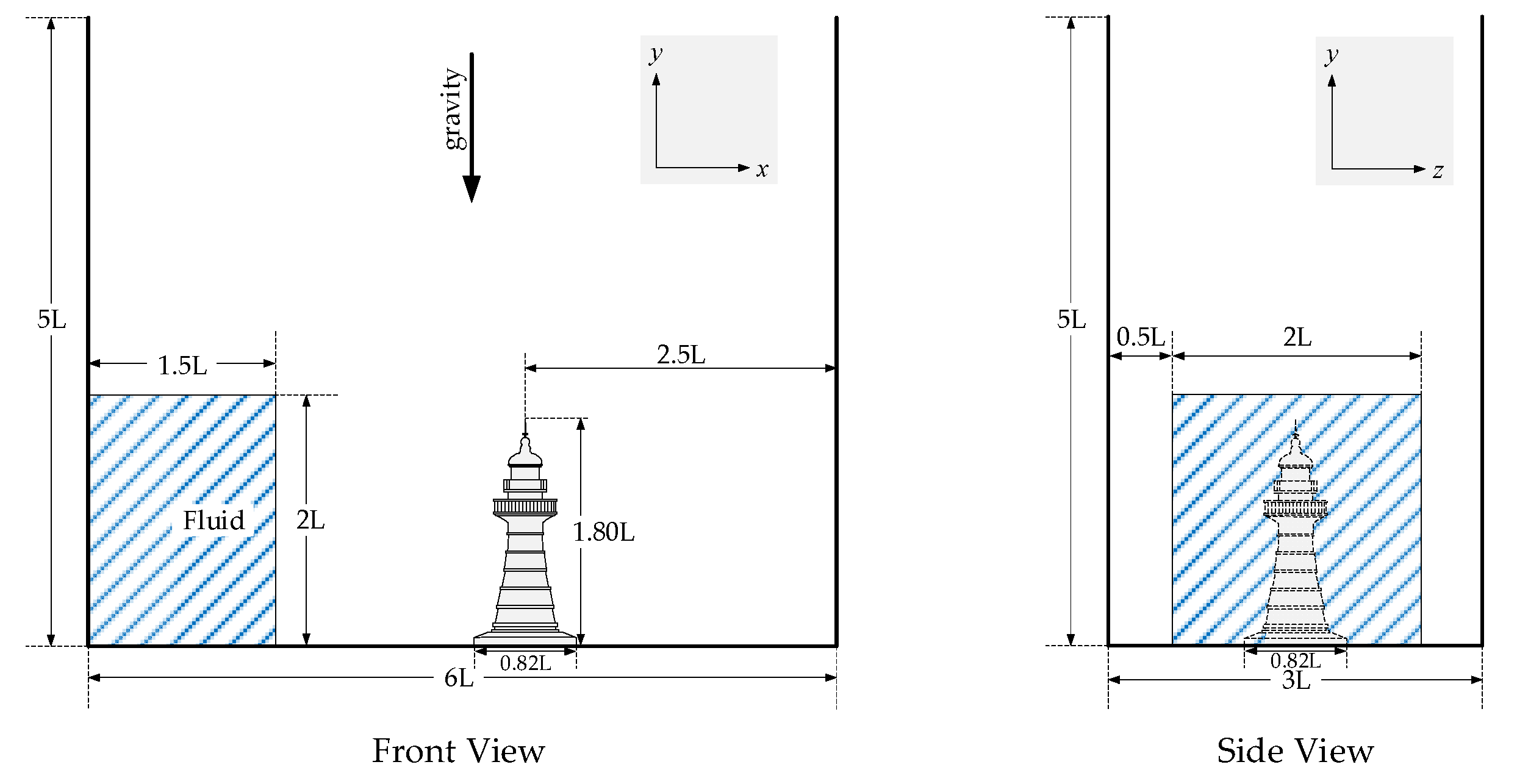
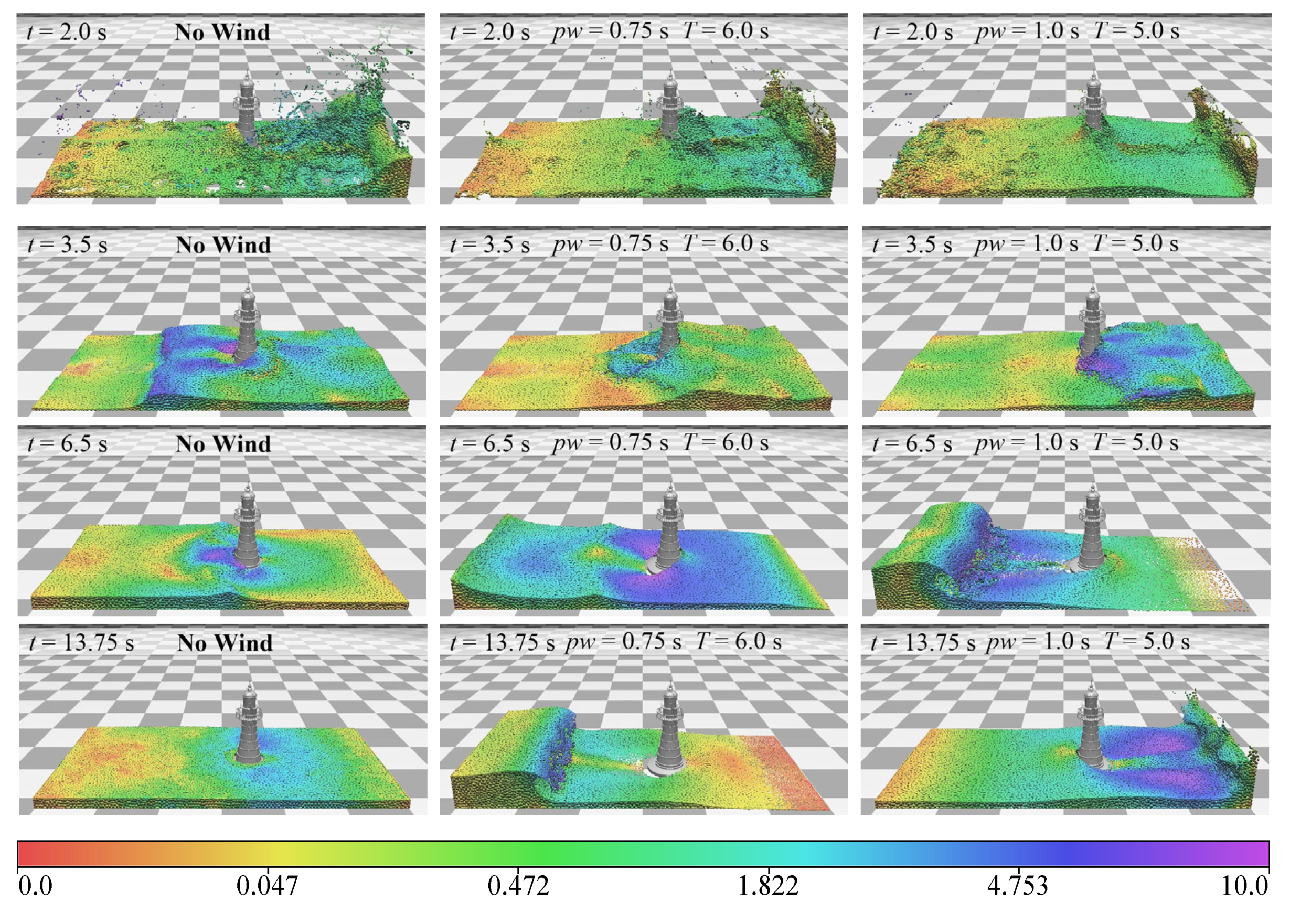
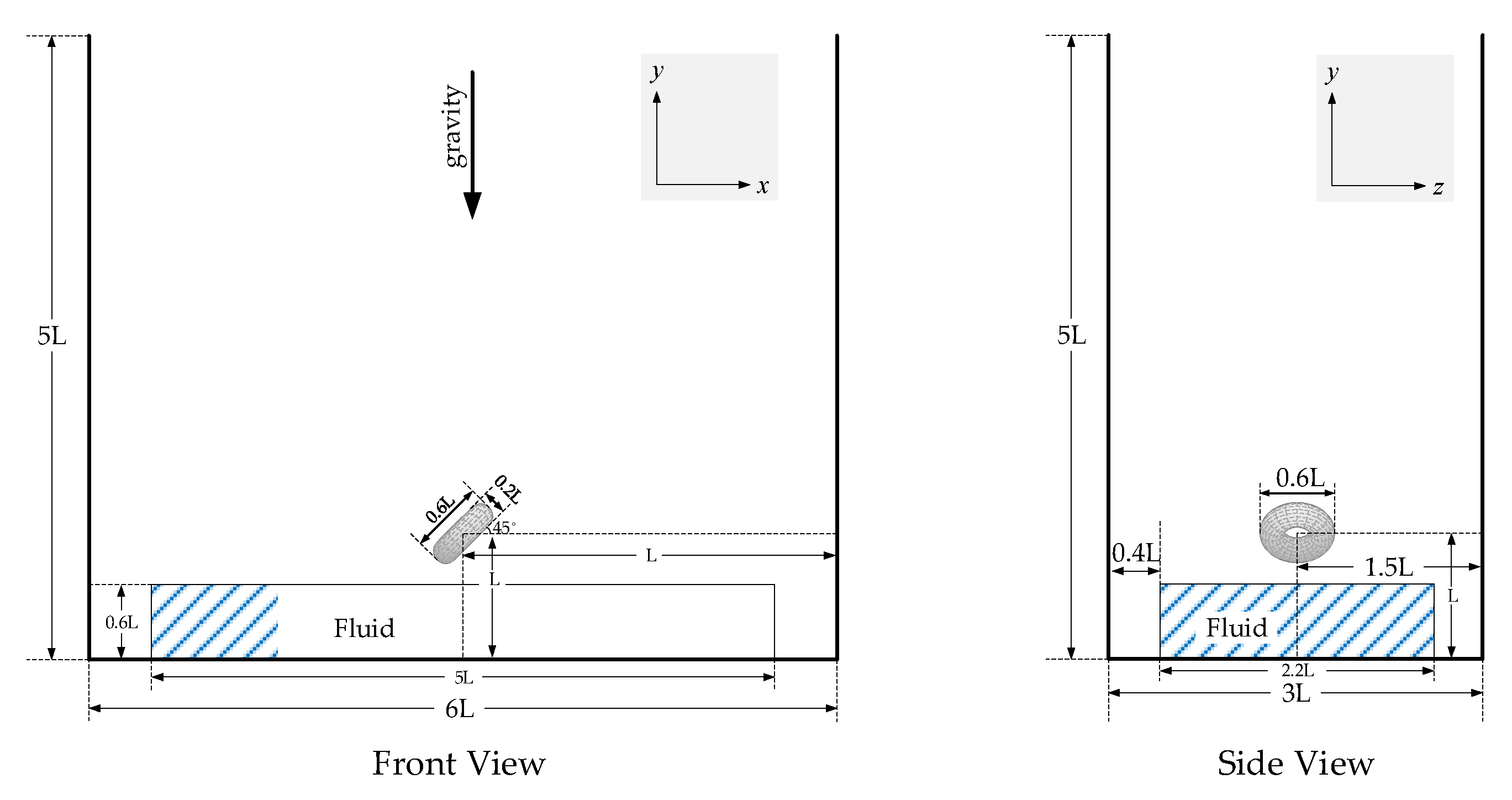
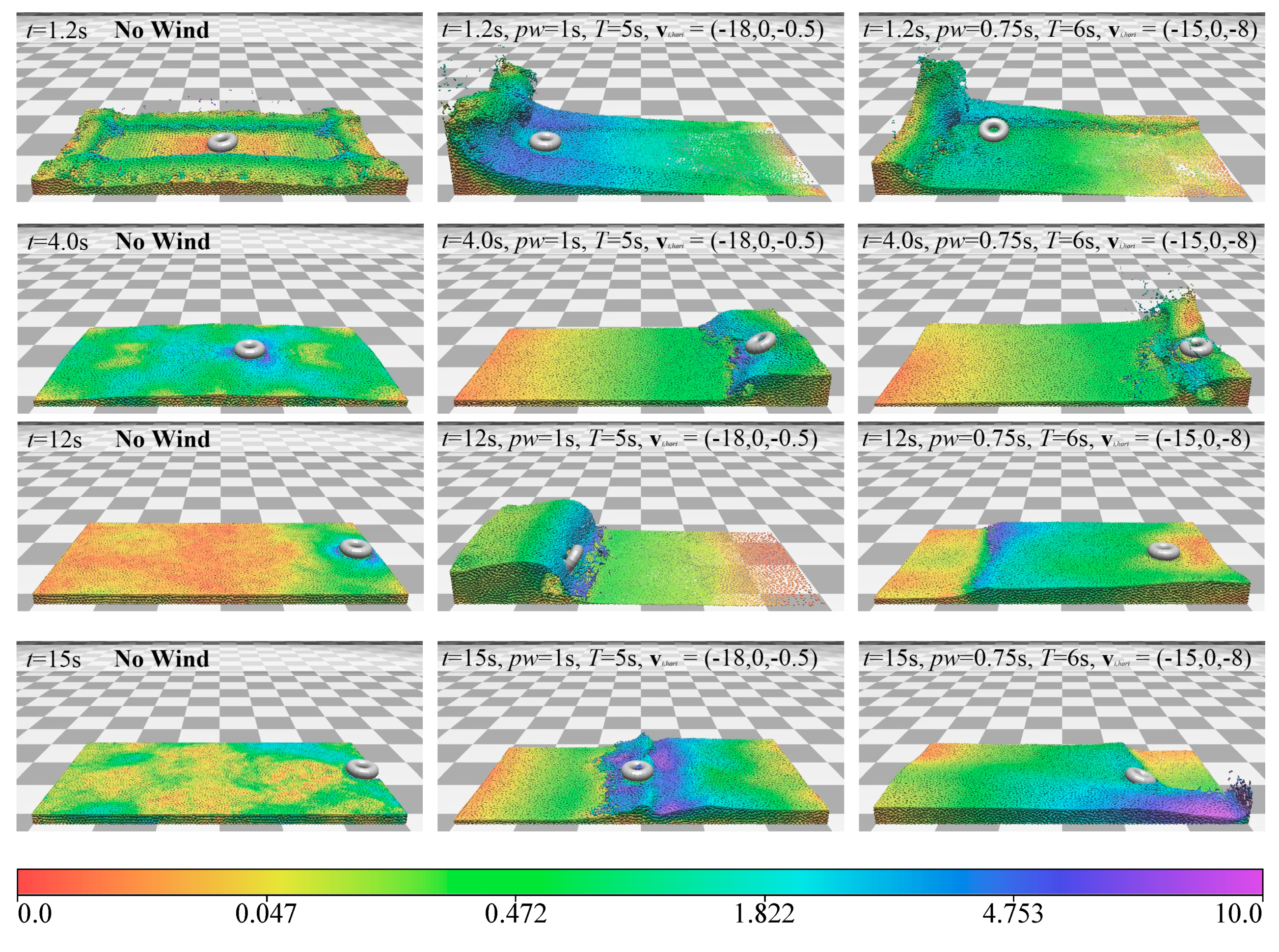
| Method | Compressibility: 0.01% | Compressibility: 0.001% | ||||
|---|---|---|---|---|---|---|
| Density Solver | Velocity Solver | Total | Density Solver | Velocity Solver | Total | |
| PBF | 9.7 | 0 | 9.7 | 15.8 | 0 | 15.8 |
| DFPBF | 9.4 | 1.3 | 10.7 | 15.4 | 1.3 | 16.7 |
| rDFPBF | 6.9 | 1.5 | 8.5 | 10.6 | 1.5 | 12.1 |
| Particle Number | Block Size | PBF (ms) | RPBF (ms) | rDFPBF (ms) |
|---|---|---|---|---|
| 19.3k | 5L × 0.3L × 2L | 213.24 | 150.41 | 141.39 |
| 34.8k | 5L × 0.5L × 2L | 594.73 | 401.90 | 363.10 |
| 58.0k | 5L × 0.8L × 2L | 1760.28 | 1040.89 | 899.35 |
| 73.4k | 5L × 1.0L × 2L | 3074.52 | 1716.63 | 1444.79 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Ren, H.; Duan, X.; Wang, C. An Improved Meshless Divergence-Free PBF Framework for Ocean Wave Modeling in Marine Simulator. Water 2020, 12, 1873. https://doi.org/10.3390/w12071873
Li H, Ren H, Duan X, Wang C. An Improved Meshless Divergence-Free PBF Framework for Ocean Wave Modeling in Marine Simulator. Water. 2020; 12(7):1873. https://doi.org/10.3390/w12071873
Chicago/Turabian StyleLi, Haijiang, Hongxiang Ren, Xingfeng Duan, and Chang Wang. 2020. "An Improved Meshless Divergence-Free PBF Framework for Ocean Wave Modeling in Marine Simulator" Water 12, no. 7: 1873. https://doi.org/10.3390/w12071873
APA StyleLi, H., Ren, H., Duan, X., & Wang, C. (2020). An Improved Meshless Divergence-Free PBF Framework for Ocean Wave Modeling in Marine Simulator. Water, 12(7), 1873. https://doi.org/10.3390/w12071873




