1. Introduction and Background
The sky-jump spillway was built for the first time in France in 1930 on the Dordogne’s hydraulic scheme [
1]. Rhone and Peterka [
2] studied and improved the design of this type of spillway, which today is commonly used in dams when the speed of the water, in the final stretch of the chute if adequately high [
3]. With this type of hydraulic structure, it is possible both to dissipate the energy and direct the jet to a certain area of the riverbed [
4]. In fact, the water jet can be directed to the most convenient area and also can be mixed as much as possible with the air along its path to the riverbed. In such a way, the jet loses some of its energy and, if the sky-jump spillway was properly designed, the local scour does not compromise the safety of the dam.
Determining the position of the scour basin during the design stage allows to control the impact zone. The shape and size of the scour basin depend on both the geometrical configuration of the flip bucket and the operating flow rates. Furthermore, the plunge pool water level upstream of impact location is important regarding riverbed scour. The water level range can be from 3 m [
5] to 8 m [
6].
Three options are available in order to minimize the damage: (a) To completely avoid scour; (b) to design the spillway so that the scour occurs far away from dam foundation and abutments; and (c) to limit the scour extent [
7].
Different bucket types are used to achieve an optimal combination with the chute end layout to reach an appropriate impact location of the jet into the plunge pool. When the flow discharge is small, the flip bucket works as a stilling basin and a hydraulic jump appears on it. In this condition the flow passing the sill falls close to bucket foundation might jeopardize the bucket stability. When the spillway is unregulated, the type of bucket with a drainage channel is used to avoid choking at the small discharge which could endanger dam stability. In this type of bucket, the hydraulic jump does not occur for relatively small discharge, so that a free jet emerges [
8].
However, it is important to notice that the hydraulic jump might be used to dissipate the energy for small discharges before the jump occurs, and remaining energy would be easy to dissipate as the falling height from the lip is usually low. In this way, the hydraulic jump inside the flip bucket might be useful to dissipate most of the flow energy in the range of low discharges.
An inadequate flip bucket could jeopardize the downstream area of the dam, as well as the dam itself. Hence there is a need to evaluate the geometric characteristics of the scour basin based on the features of both the water flow to be evacuated and the flip bucket. The first thing that is needed to be able to predict the position of the scour basin is to determine the flow rate for the initiation of the jet flow, which allows to establish with sufficient approximation the position of the scour basin at its extreme closest to the spillway.
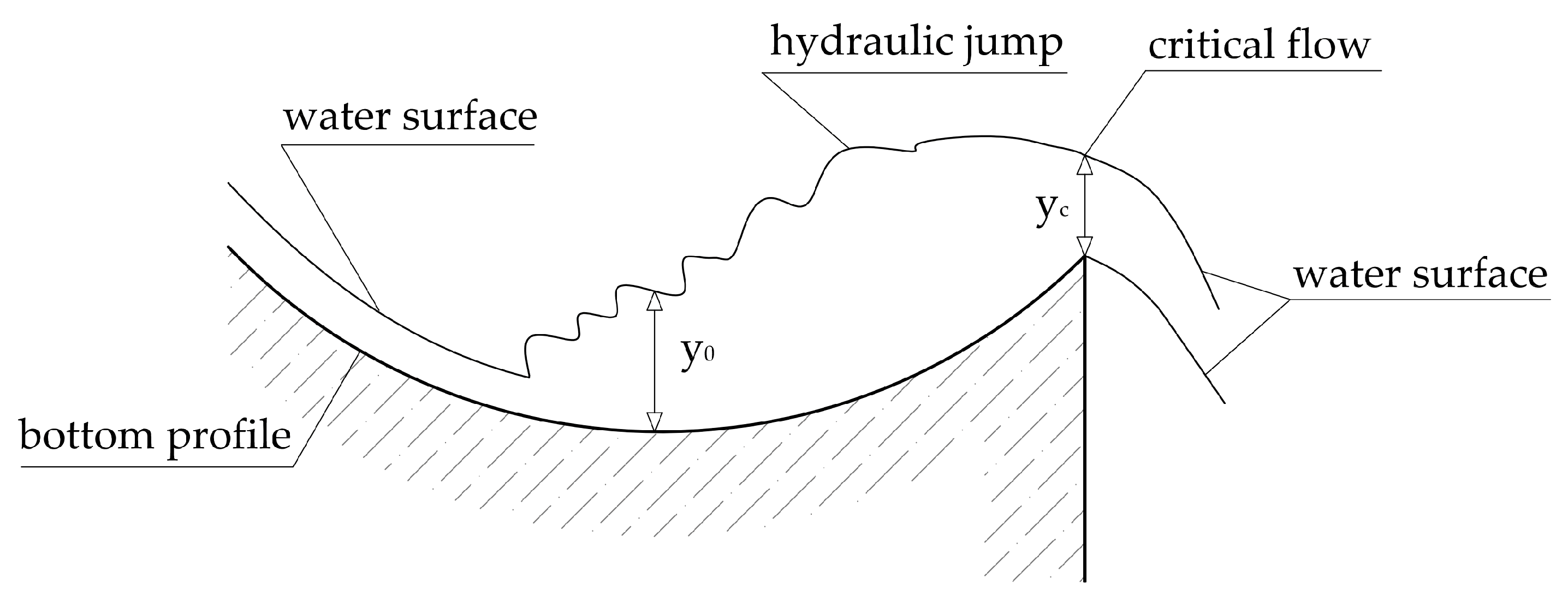
Rouve [
9] concluded that for a low flow rate range, the jet does not form, and the flip bucket works as a stilling basin ended with an overflow weir. The flow of water arrives through the chute to the flip bucket in supercritical regime and produces a hydraulic jump when contacting the water mass on the flip bucket, which is under subcritical regime. As the flow increases, the hydraulic jump moves towards the lip of the bucket, which is working as an overflow weir, until the flow rate for the initiation of the jet flow
Qi (with increasing flow) is reached. The hydraulic jump is then dragged out of the flip bucket, the jet flow occurs and the water if thrown out. The jet flow is maintained, with the sky-jump operating in supercritical regime, until reaching the maximum flow rate. Later on, as the flow rate descends, until the flow rate is reduced to the flow rate for the finishing of the jet flow
Qf (with decreasing flow). A hydraulic jump is then re-established on the flip bucket, which works again as a stilling basin. Therefore, a hysteresis phenomenon occurs, since the flow rates for the initiation and finishing of the jet flow,
Qi and
Qf, are different, being
Qi slightly higher than
Qf.
The hysteresis phenomenon has been studied, both experimentally [
10,
11] and theoretically [
12,
13], by several authors [
14,
15]. The formulas obtained by these authors were developed for flat approach channels, setting obstacles or deflectors at their end, but without considering the effect of the curvature of the flip bucket.
Abecasis and Quintela [
16,
17] obtained formulas for determining
Qi and
Qf. They applied the momentum Equation to the control volume between two sections, the first located upstream of the obstacle, with a flow depth
y0, and the second on the obstacle, where a section with the critical flow depth
yc was assumed. The formula obtained for
Qf, neglecting the horizontal component of the friction resistance, considering uniform velocity, parallel flow, and assuming a linear distribution of the hydrostatic pressure in the initial and final sections of the control volume, was:
where,
y0 is the flow depth and
F0 the Froude number both in the initial section, upstream of the obstacle, and
z is the vertical height of the obstacle, equivalent to the depth of the flip bucket.
Applying the momentum Equation again, but assuming a pressure on the upstream face of the obstacle, exerted by a critical flow depth
yc, they obtained the formula for the initiation of the jet flow:
Muskatirovic and Batinic [
18] applied the momentum theorem, assuming a hydrostatic distribution on the upstream face of the obstacle, with flow depth
y0, and a hydrostatic distribution over the obstacle corresponding to the critical flow depth
yc. The formula obtained for the end of the jet flow was:
For the initiation of the jet flow, they combined the Equation of the hydraulic jump with the Bernoulli’s Equation, obtaining the following relationship:
Heller, Hager, and Minor [
19] applied the momentum theorem by considering a baffle with height
z at the end of a channel. For the end of the jet flow they proposed:
and for the initiation:
Our research was focused on the development of a new formula that includes the effect of the curvature of the flip bucket on the initiation of the jet flow, and also the proposal of a new conceptual framework that leads to a novel procedure for the direct determination and analysis of the flow rate for the initiation of the jet flow.
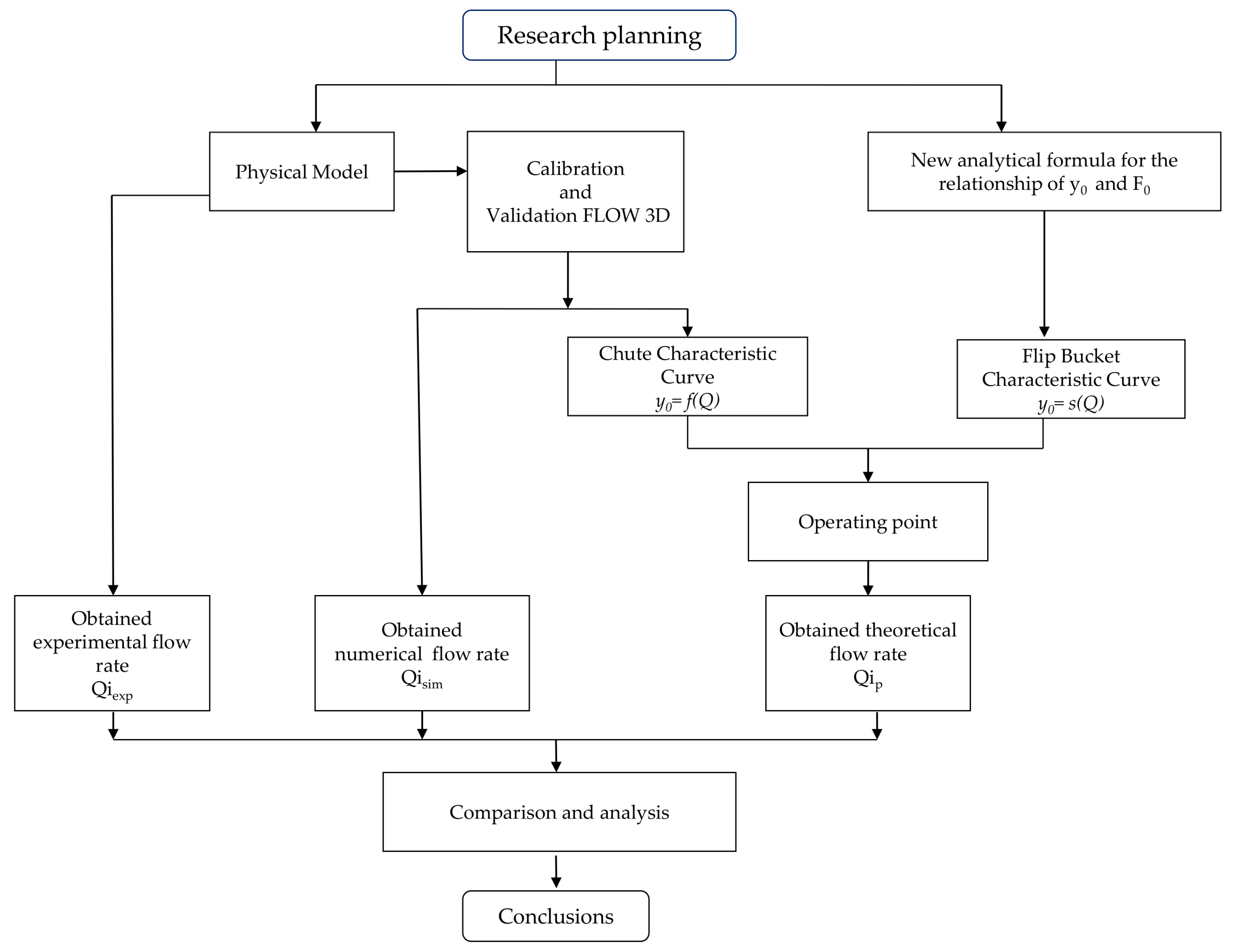
2. General Approach
To take into account the effect of the flip bucket’s radius of curvature a new formula was deduced, that incorporates this parameter by applying the momentum Equation. This formula establishes a relationship between the flow depth y0 and the number of Froude F0 at the lowest point of the flip bucket that must be met for jet flow to initiate, and it is the relationship that allows to determine the flow rate for the initiation of the jet flow.
The spillway is considered a system consisting of two elements: The chute and the flip bucket. For each of these elements, it is possible to define a characteristic curve that link the flow depth at the lowest point of the flip bucket y0 and the flow rate Q. The flow rate for the initiation of the jet flow Qi, and the corresponding flow depth y0i are given by the point of intersection of both characteristic curves. The approach is analogous to that of determining a pump operating point, when the system consists of the pump, or group of pumps, and the pipe. The characteristic curves link the pump head or head loss and the pumped flow.
The flow rate for the initiation of the jet flow must simultaneously satisfy the flip bucket characteristic curve, ratio between y0 and Q (which can be determined from the relationship between z/y0 and F0 obtained by the momentum Equation), and the chute characteristic curve, which expresses the ratio between y0 and the flow rate Q compatible with the energy loss that occurs along the channel, for being physically feasible.
The
chute characteristic curve y0 =
f(
Q) may be constructed point to point by applying the Bernoulli theorem to successive sections of the chute, or by using a Computational Fluid Dynamic numerical model. We followed the second option, using the commercial software Flow3D. Three different tools were used along the workflow: Experimental work at the hydraulic laboratory, numerical Computational Fluid Dynamic modeling, and analytical deduction based on the momentum theorem (
Figure 1). An empirical flow rate for the initiation of the jet flow was obtained from the physical models at the laboratory. The results of these laboratory tests were used to calibrate and validate the numerical models performed with Flow3D, regarding the flow characteristics along the chute. Once validated, Flow3D models served to elaborate the
chute characteristic curves and to determine the
flow rate for the initiation of the jet flow in the absence of air within the flow.
Later on, the proposed theoretical formula, obtained by means of the momentum theorem, allowed to elaborate the flip bucket characteristic curve, taking into consideration the curvature of the bucket. The flow rate for the initiation of the jet flow was determined at the operating point, intersection of both characteristic curves of the chute and the flip bucket.
The work ends up comparing and analyzing the three flow rates for the initiation of the determined jet flow: Experimental or empirical, numerical, and analytical or theoretical, in order to discuss the validity of the proposed methodology and formula.
3. New Formula for The Initiation of the Jet Flow
The flip bucket operates like a weir and presents a hydraulic jump for low flow rates, so it is not possible to define a clear flow depth
y0 at the lowest point of the flip bucket (
Figure 2). As the supercritical flow from the chute increases, the hydraulic jump moves towards the lip of the flip bucket until the energy of the flow is enough to completely sweep the hydraulic jump out of the flip bucket and the jet flow occurs. When the stream of water jumps, the flow regime is supercritical all along the chute–bucket system. Therefore, the flow depth
y0 at the lowest point of the flip bucket is determined by the upstream conditions, with control section at the ogee crest of the spillway.
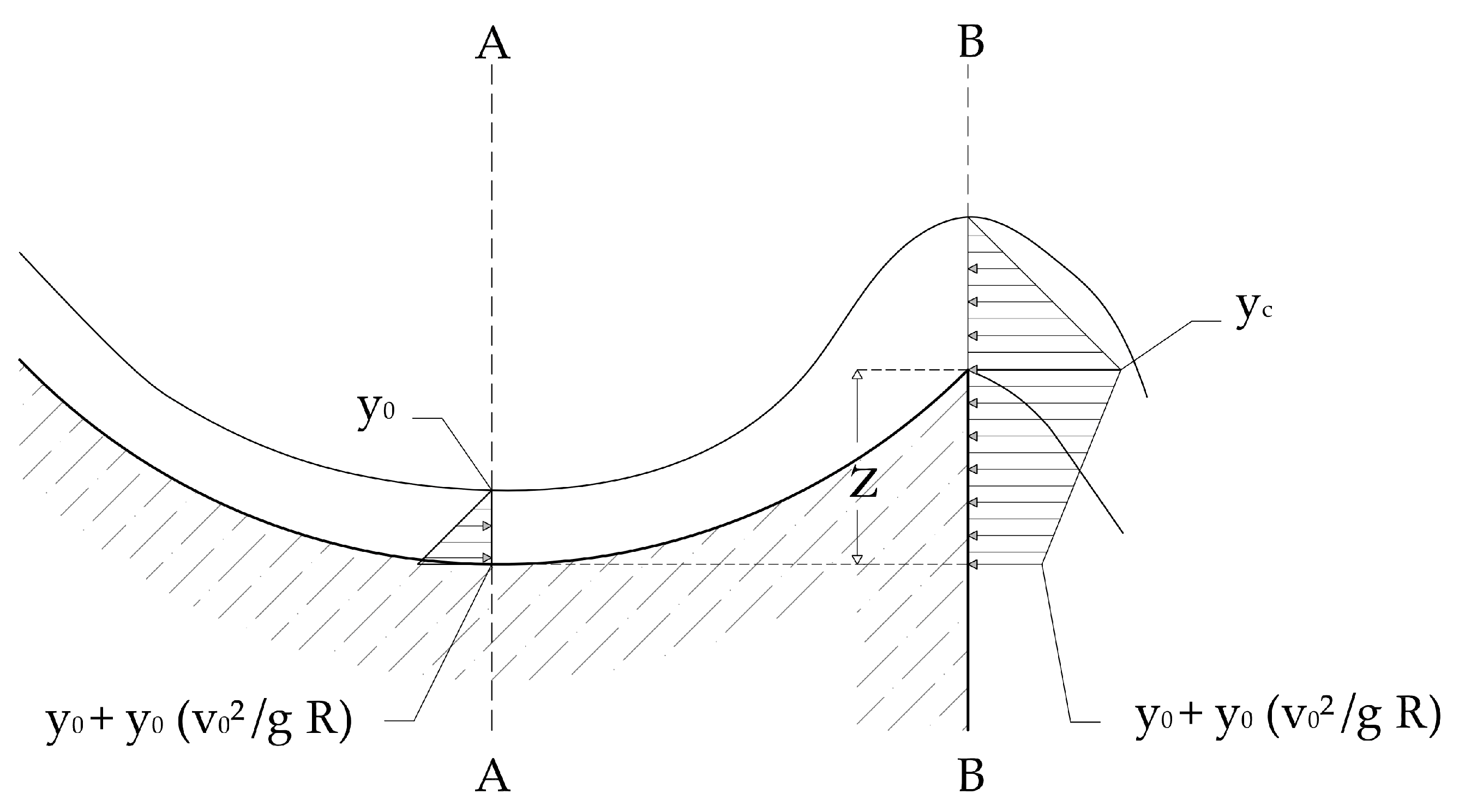
We apply the momentum theorem in the horizontal direction [
20]. The considered control volume is between the two vertical sections: (A) Passing through the lowest point of the flip bucket and (B) containing the lip (
Figure 3). We accept, as Heller et al. [
19], critical flow on the lip of the flip bucket before the jet flow occurs, since it is working as a weir, with a regimen change from subcritical to supercritical.
In section (A), y0 is the flow depth at the bottom of the flip bucket, where the corresponding speed is v0. In section (B) the flow is critical (depth yc) and the corresponding speed vc. The radius of curvature R and depth of the flip bucket z are also relevant parameters.
In the initial section (A), the hydrostatic pressure was considered plus the increase of the dynamic pressure due to the curvature of the flow in the flip bucket [
21]. For simplicity, linear distribution was assumed. The resulting force on section (A) is:
In the final section (B), the hydrostatic pressure corresponding to the critical flow depth on the flip bucket’s lip was assumed. The horizontal component of the resulting pressures on the flip bucket was determined considering, for simplicity, a linear distribution of pressure between the lowest point and the lip of the flip bucket. These pressures are applied to the vertical projection of the flip bucket, resulting the force:
Neglecting the horizontal component of friction resistance, considering uniform velocity and parallel flow, and applying the momentum Equation, we obtained Equation (9):
being
q the unit flow rate and
g the gravity acceleration. This Equation (9) can be expressed in a different and more compact way using the Froude number at the initial section (A)
F0, and the parameter
z/y0. For that, we divide Equation (9) by
y0 and substitute for:
and the resulting formula is:
Equation (13) includes the effect of the curvature of the flip bucket by means of the parameter R: Flip bucket radius of curvature. It is a novelty related to the previous existing formulas. It can be observed that the obtained formula differs from that of Abecasis and Quintela (Equation (1)) just in the negative term of the second member of the equality, that includes the radius as a parameter. This term approaches zero when increasing the radius and, at the limit, it becomes zero, as befits a straight bucket, without curvature, which is the hypothesis adopted by Abecasis and Quintela.
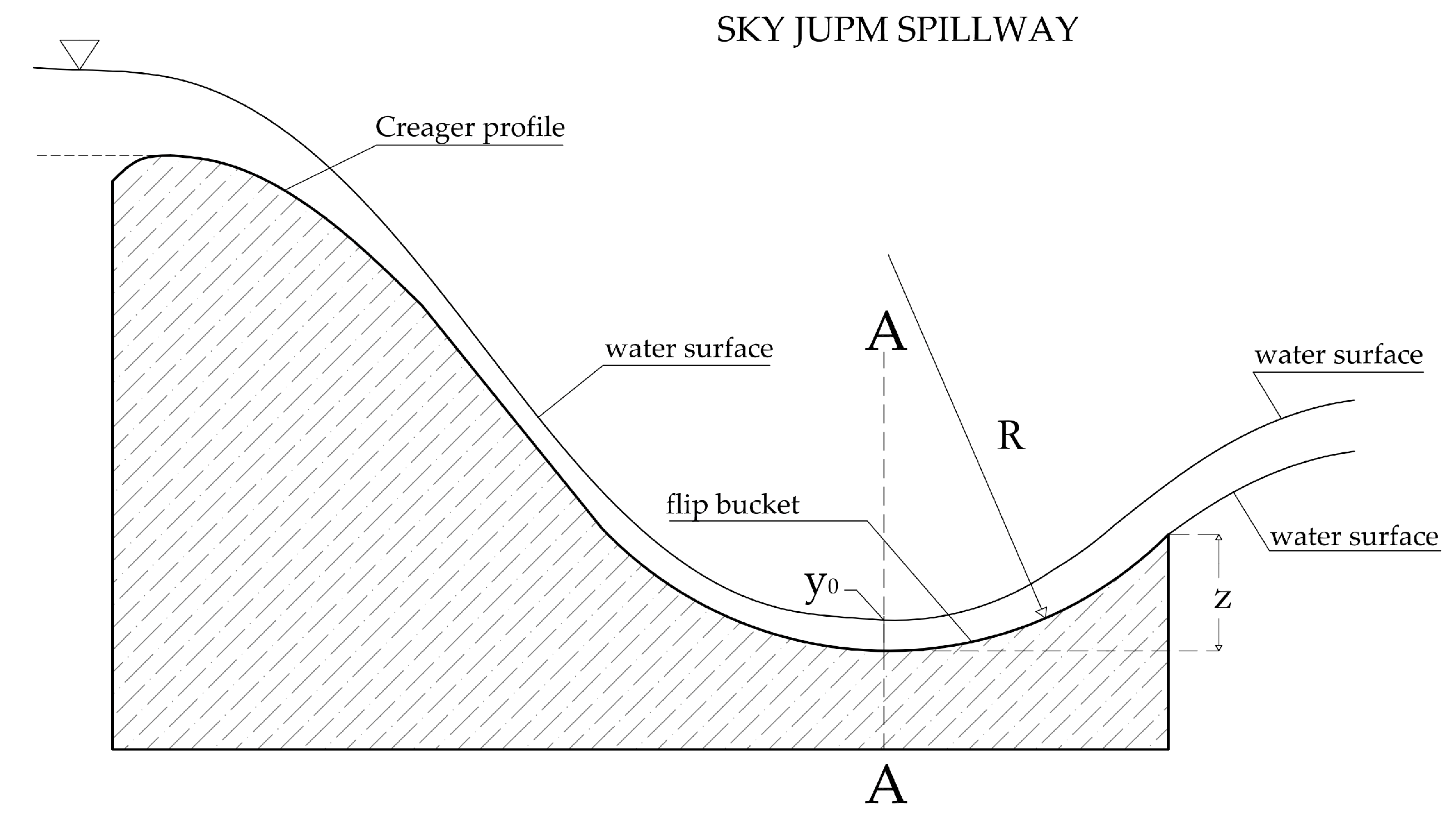
4. The Method of the Characteristic Curves
The sky-jump spillway can be considered as a system made up of two elements: The chute and the flip bucket. The lowest point of the bucket deflector (Section A;
Figure 4) was defined as the limit between them. It is analogous to a pumping system, consisting of a pump, or group of pumps, and the pump piping. In this analogy, the chute and the pump piping might be considered analogous elements, since the frictional force, along with the gravity force, dominates the behavior in both elements. The flip bucket and the pump group might also be considered analogous. In both cases, energy is required for water elevation. In the case of the group of pumps it is provided by the engines; in the case of the flip bucket the energy is provided by the water stream coming from the chute.
Like in the case of a pumping system, there is an operating point for the chute–bucket system. The operating point is the intersection of the characteristic curves of the elements of the system: Chute and flip bucket. Both characteristic curves express a relationship between the flow depth at the lowest point of the flip bucket y0 and the flow rate Q. The operating point defines the flow rate for the initiation of the jet flow and the flow depth at the lowest point of the flip bucket at that instant.
The
characteristic curve of the flip bucket can be obtained by applying the momentum Equation at the instant of initiation of the jet flow, using the new proposed formula (Equation (13)). It establishes a relationship between the parameter
z/y0, where
z is the depth of the flip bucket, and the Froude number
F0 at the lowest point of the bucket. This Equation can also be expressed as a function of the unit flow rate
q and the flow depth at the lowest point of the flip bucket
y0, taking into consideration Equations (10)–(12):
The function y0 = s(q) can be built point by point using Equation (14), under the hypothesis of cylindrical flip bucket and neglecting the effect of the flow aeration. This is the curve we call flip bucket characteristic curve.
The chute characteristic curve y0 = f(q) can be built using a CFD numerical model with greater accuracy than using Bernoulli theorem. We determined the value of y0 for different unit flow rates q using the commercial CFD code Flow3D.
Jet flow initiates when the operation conditions of the chute and the flip bucket are physically compatible, at the intersection of both characteristic curves: The operating point. It provides the flow rate for the initiation of the jet flow and the flow depth at the lowest point of the bucket deflector at that instant.
5. Experimental Work with Physical Models
The testing channel (
Figure 5 and
Figure 6) has a width of 2.46 m, is 1.3 m high, and 13.7 m long. It is divided into three functional areas. The first zone is for water supply and dissipation of its energy. The second is the testing area: 2.46 m wide and 6.37 m long. The testing area is filled with sand up to a height of 0.5 m, and is limited upstream by a wall. The sky-jump spillway is positioned in the middle of that wall. In the third and final zone of the testing channel there is a decant pond to prevent any dragged material to reach the tank, which is under the laboratory floor. On the left side of the channel, in the direction of the flow, there is a glass window 4.6 m long and 1.1 m high, which allows the visual inspection of the test and also to take photographs and video recording.
The water inlet to the model is regulated by a motorized valve. The flow rate was measured at two locations: Upstream, by means of an ultrasonic flow meter positioned in the supply pipe, and downstream, using a thin-plate rectangular weir located in the return channel that takes water to the tank. Two ultrasonic level probes based on the pulse-eco method, positioned upstream and downstream of the sky-jump spillway, were used for the recording of the water levels. The hardware specifications of the ultrasonic flow meter and the ultrasonic level probe are shown in the (
Table 1).
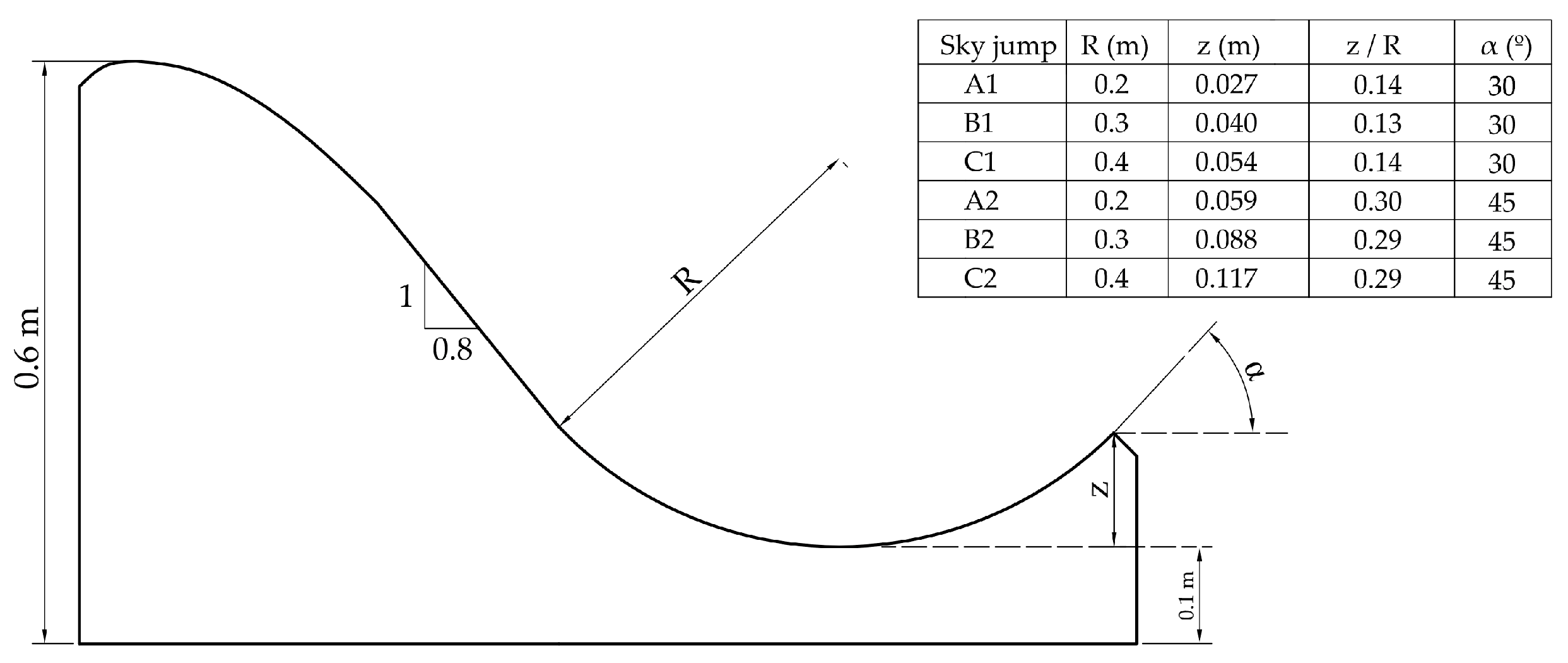
Six cement-made sky-jump spillways were built (
Figure 7). The design followed the criteria specified by the United States Bureau of Reclamation [
22]. The spillway has a Creager profile. The slopes of the physical model are vertical upstream and 0.8H:1.0V downstream; the height
H is 0.6 m; and the distance between the bottom of the flip bucket and elevation spillway is 0.5 m; it is 0.4 m wide. Three different values of radius of curvature
R were modeled: 0.2 m, 0.3 m, and 0.4 m; and also three different values of exit angle of flip bucket α: 15°, 30°, and 45°. The radius of curvature and the flip angle allow to determine
z, depth of the flip bucket, using the geometric relation
z =
R (1 − cos α). In order to inspect and measure the water depth, the sides of the physical models were built with methacrylate.
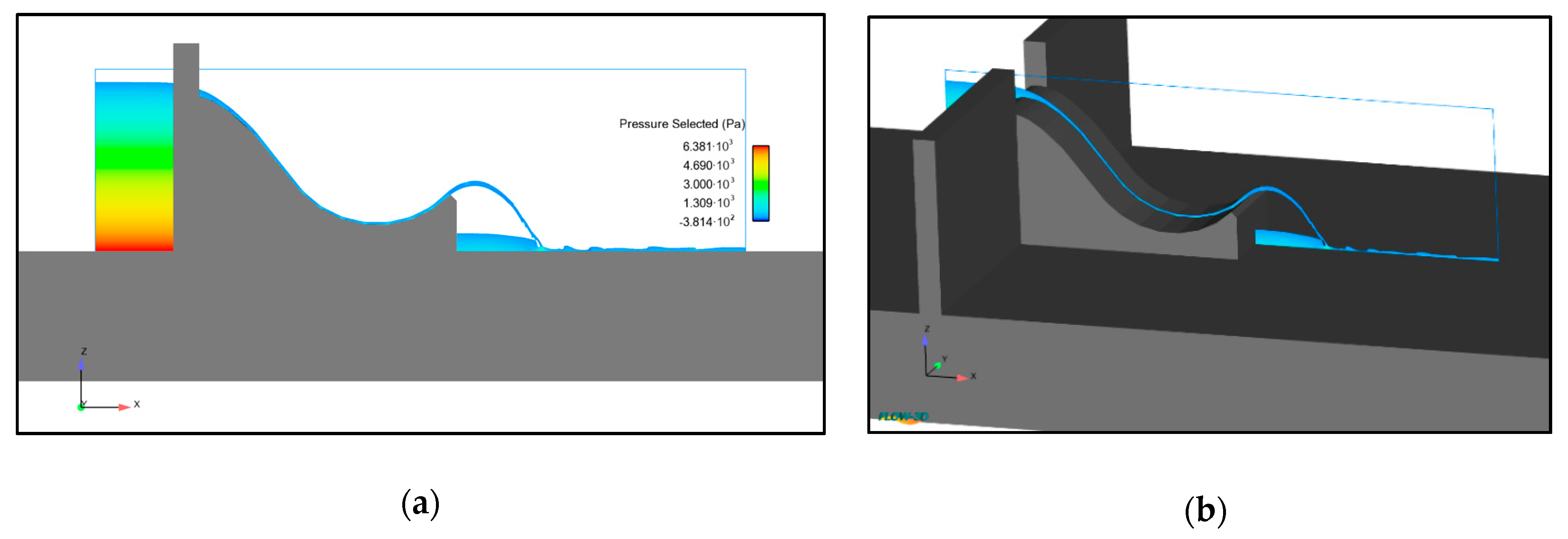
A protocol was followed for the experimental determination of the flow rate for the initiation of the jet flow. The level of the reservoir was maintained 0.04 m below the ogee crest threshold to allow the flow to stabilize before allowing the specified flow rate to enter the spillway. Every flow rate was maintained during 10 min flowing along the spillway. After that, if the jet flow did not occur, the procedure was repeated with the next higher flow rate discharge, and so on until the jet flow occurred. The flow rate for the initiation of the jet flow was measured for every geometrical configuration. The flow depth at the lowest point of the flip bucket could only be measured with sufficient accuracy for the sky-jump spillway with radius of curvature of 0.4 m and flip angle of 45° (C2). For the rest of the physical models the depth of water was too small. It was possible to differentiate for the case C2 an intensely aerated area, in the upper part of the flow, from a predominantly liquid area in the lower part (
Figure 8).
The experimental results (
Table 2) are later in this paper compared with the results obtained applying the proposed
method of the characteristic curves, using the new formula for the characteristic curve of the flip bucket, and with the results obtained from the CFD numerical model (Flow3D), described in the following section. The CFD numerical model was calibrated and validated with the experimental data of the physical model C2.
6. Numerical Models: Chute Characteristic Curve and Flow Rate for The Initiation of the Jet Flow
Every physical model was also modelled numerically. As above mentioned, the
chute characteristic curve was obtained point by point by means of the CFD numerical modeling code Flow3D. This software solves Reynolds–Navier–Stokes averaged Equations (RANS) in three dimensions along with the FAVOR and VOF algorithms for solid contouring and free surface tracking respectively [
23]. Due to a finite difference approach, Flow3D requires the resolution of structured meshes. The software uses the Fractional Area/Volume Obstacle Representation (FAVOR) method, developed by Hirt and Sicilian [
24]. This preprocessor is a tool that allows to represent a solid obstacle in a control volume. Control volumes with dead spaces are assumed empty, and value 1 is assigned, and volumes with geometry are assumed solid volumes and a value of 0 is assigned. The Volume of Fluid (VOF) method is described by Nichols and Hirt [
25], Nichols et al. [
26], and Hirt and Nichols [
27]. This method is similar to FAVOR; it defines whether a cell is empty, full, or partially filled with water. Cells without fluid have a value equal to 0. The filled cells have value equal to 1, and between 0 and 1 those partially filled.
The software Flow3D solves in three directions the mass continuity Equation (Equation (15)) and the momentum Equations (Equations (16)–(18)) besides the volume of fluid (VOF) Equation, that ensures that proper boundary conditions are applied at the free surface (Equation (19)). For Cartesian coordinates (
xi,
xj,
xz) and for incompressible fluid (fluid density constant), these Equations are:
where
t is time,
ρ is fluid density,
p is pressure, (
ui,
uj,
uk) are velocity component in Cartesian coordinates (
xi,
xj,
xk),
Ai is fractional area in the
i-direction,
Aj and
Ak are similar area fractions in the
j and
k direction, respectively, (
Gxi,
Gxj,
Gxk) are body acceleration and (
fxi,
fxj,
fxk) are viscous acceleration. In Equation (19)
A is the average flow area,
U is the average velocity and
F is the volume flow function. When the cell is filled with fluid, the value of
F is 1, and when it is empty,
F is 0.
The fluid-dynamic variables at a point in space are made up of a series of fluctuations of different scales, for this reason, the analysis of the turbulence is carried out from a statistical point of view, that is, with average velocity and intensity of “Reynolds averaged” fluctuations. This consideration helps solve the closure problem. For the numerical solution of turbulent flows, the Reynolds-Averaged Navier–Stokes Equations are applied, which supplies the turbulence kinetic energy k and the rate of turbulent energy dissipation Ɛ to achieve Reynolds stresses and the turbulent kinematic viscosity.
A quantitative verification, as defined in Jakeman et al. [
28] and in Blocken et al. [
29], was made for this numerical study, using the available data from Paul Guy Chanel [
30].
The turbulence model used in this study is the RNG
k-ε [
31], which usually provides better performance for swirling flows than standard
k-ε model [
32,
33]. Its formulation is represented in Equations (20) and (21):
where
µ is dynamic viscosity,
µt is turbulent dynamic viscosity and
Pk is production of turbulence kinetic energy. The remaining terms
C1ε,
C2ε, σk and
σε are model parameters whose values can be found in Yakhot et al. [
31]. Finally, the turbulence viscosity can be computed using the parameter
Cµ = 0.085 in the Equation (22):
The numerical model is implemented by importing the geometry of the entire physical model. A domain of 2.3 m long and 1 m high was defined. Although Flow3D is inherently a 3D software, it was considered a small thickness in the Y direction, transverse to the model section, in such a way that the behavior of the flow could be studied in 2D (
Figure 9), since the analyzed phenomenon is essentially two-dimensional.
The flow depths corresponding to the flow rate for the initiation of the jet flow for every modelled case are in the order of millimeters for most of the cases.
The boundary conditions must accurately represent those of the physical phenomenon: Two boundary conditions are fixed for each Cartesian plane: For the plane (XY) the atmospheric pressure and the wall condition are considered, for the plane (YZ) the hydrostatic pressure distribution and the output are defined, for the plane (XZ) the symmetrical smooth walls (free-slip/symmetry) are defined.
The numerical model was calibrated and validated using the experimental data corresponding to the 0.4 m radius of curvature and flip angle of 45° (C2). The test with the smallest flow rate was used to calibrate the roughness of the chute, and the test with the larger flow rate was used to validate the value obtained in the calibration. The flow depth with and without the intensely aerated upper area of the flow were separately considered.
The numerical simulation was started with the Mesh-sensitivity analysis and calibration of the Flow3D model. The measured value of the flow depth without the intensely aerated area (y0 exp) was used, since the proposed analytical formula does not consider the effect of aeration, and the purpose is to compare both results.
The absolute roughness of the chute was used as the calibration parameter. The roughness of the smooth cement is between 0.03 mm and 0.50 mm [
21]. We developed numerical models with 0.03 mm, 0.10 mm, 0.25 mm, and 0.50 mm.
The available experimental data refer to the 0.4 m flip bucket’s radius and lip angle of 45° (C2), for which we have two flow depth data at the lowest point of the flip bucket and the two related flow rates.
Mesh-sensitivity analysis, categorized as part of the quantitative verification, was performed diminishing the cell size, until changes were not reported in the results (
Table 3). However, the results with a 1 mm mesh were computationally unfeasible and a trade-off between computational time and accuracy was made.
The cell with the size of 1.25 mm was adopted because it restores the same water depth value observed experimentally and it also was computationally feasible. Then, different absolute roughness values were considered, as indicated in the (
Table 3), checking if the jet flow occurred.
Roughness was set to 0.03 mm and a cell size of 1.25 mm was adopted, because they restore the same water depth value experimentally observed (
Table 4).
This absolute roughness is compatible with the surface of sanded concrete of the physical models. The calibration results were then validated. For that, the flow rates obtained experimentally and numerically that produce the same flow depth at the lowest point of the flip bucket were compared, without considering the intensely aerated area. Validation was performed for an experimental flow rate of 43.56 L/s (
Table 5).
The relative error between flow rates observed and obtained from the numerical models is in the order of 5% in calibration and lower in validation. It is in accordance with the expected error in the numerical model [
23] and in the laboratory test.
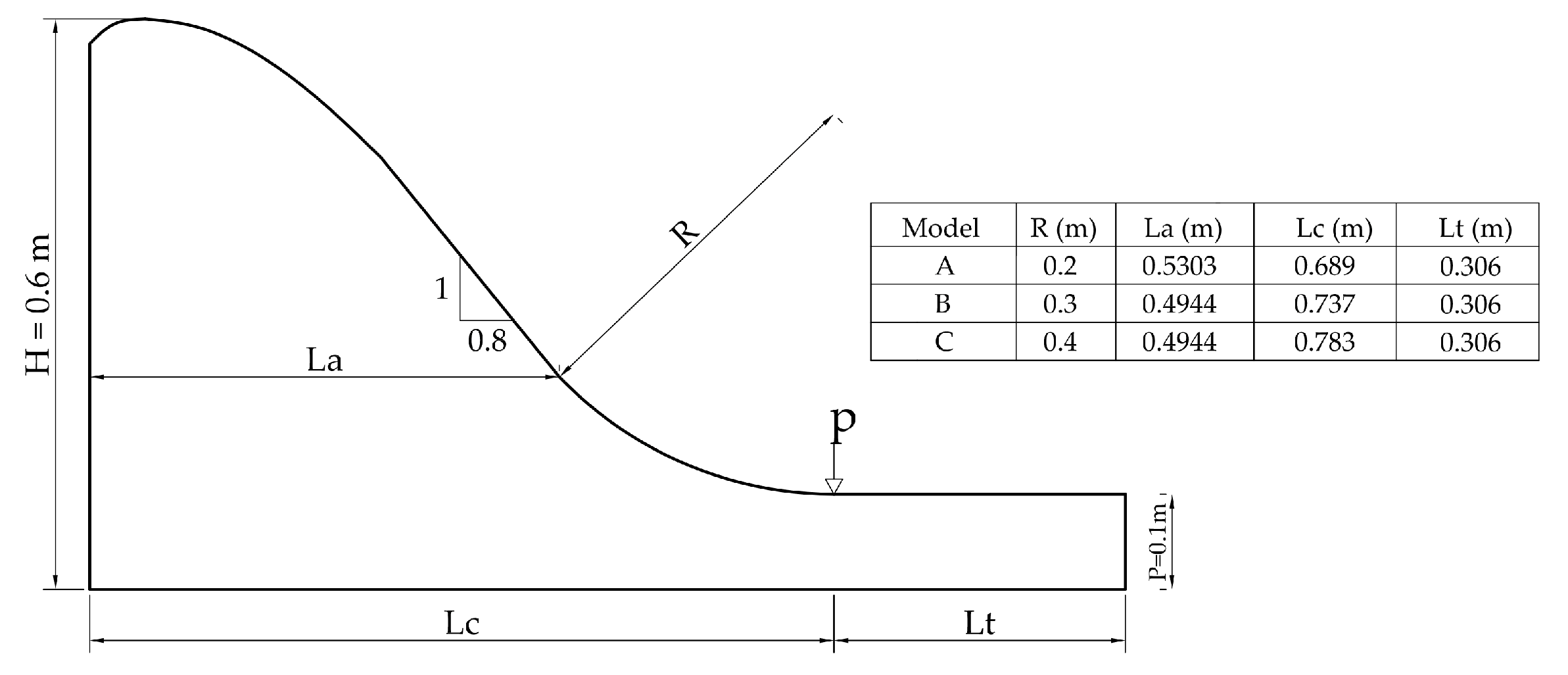
Once the numerical model was calibrated and validated, it was used for two purposes: (a) To build the
chute characteristic curve; (b) to determine the flow rate for the initiation of the jet flow; both for the different laboratory-tested geometric configurations. For the first purpose, three spillways, corresponding to each considered radius, were numerically modeled (
Figure 10). As expected, the differences between the curves of the three cases were minimal, since they only differ slightly on the initial curved part (
Table 6). The
chute characteristic curve was obtained by interpolation from the points defined by numerical modeling, (
Figure 11), where the fixed parameters are: total height
H of 0.6 m and distance
P from the bottom of the flip bucket to the ground of 0.1 m; variable parameters are: radius of curvature
R, horizontal distance
La from the upstream vertical wall to the point where the straight part of the chute ends, horizontal distance
Lc from the upstream vertical wall and measurement point “p”, and horizontal distance
Lt between the measurement point “p” and the flip bucket’s lip. The part of the flip bucket downstream point “p” has no influence on the chute flow, due to the supercritical regime.
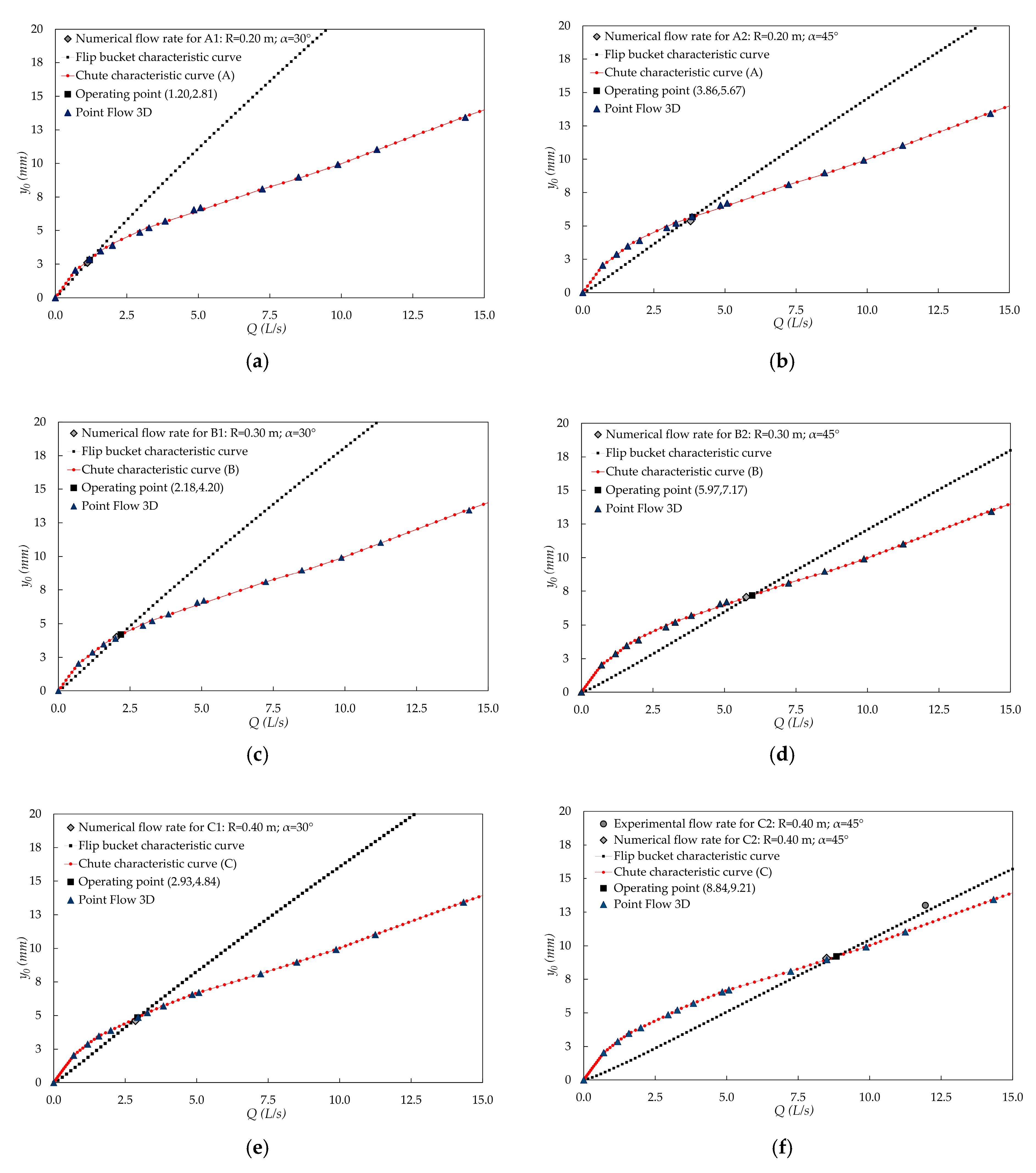
The flow rate for the initiation of the jet flow was determined for each of the six laboratory-tested geometric configurations, using the numerical model, by trial and error, increasing the flow discharge in small steps until the jet flow occurred (
Figure 12;
Table 7).
7. Results and Discussion
The main purpose of this research is to define and validate a methodology that allows to determine the flow rate for the initiation of the jet flow of a sky-jump spillway, taking into account the effect of the radius of curvature R of the flip bucket.
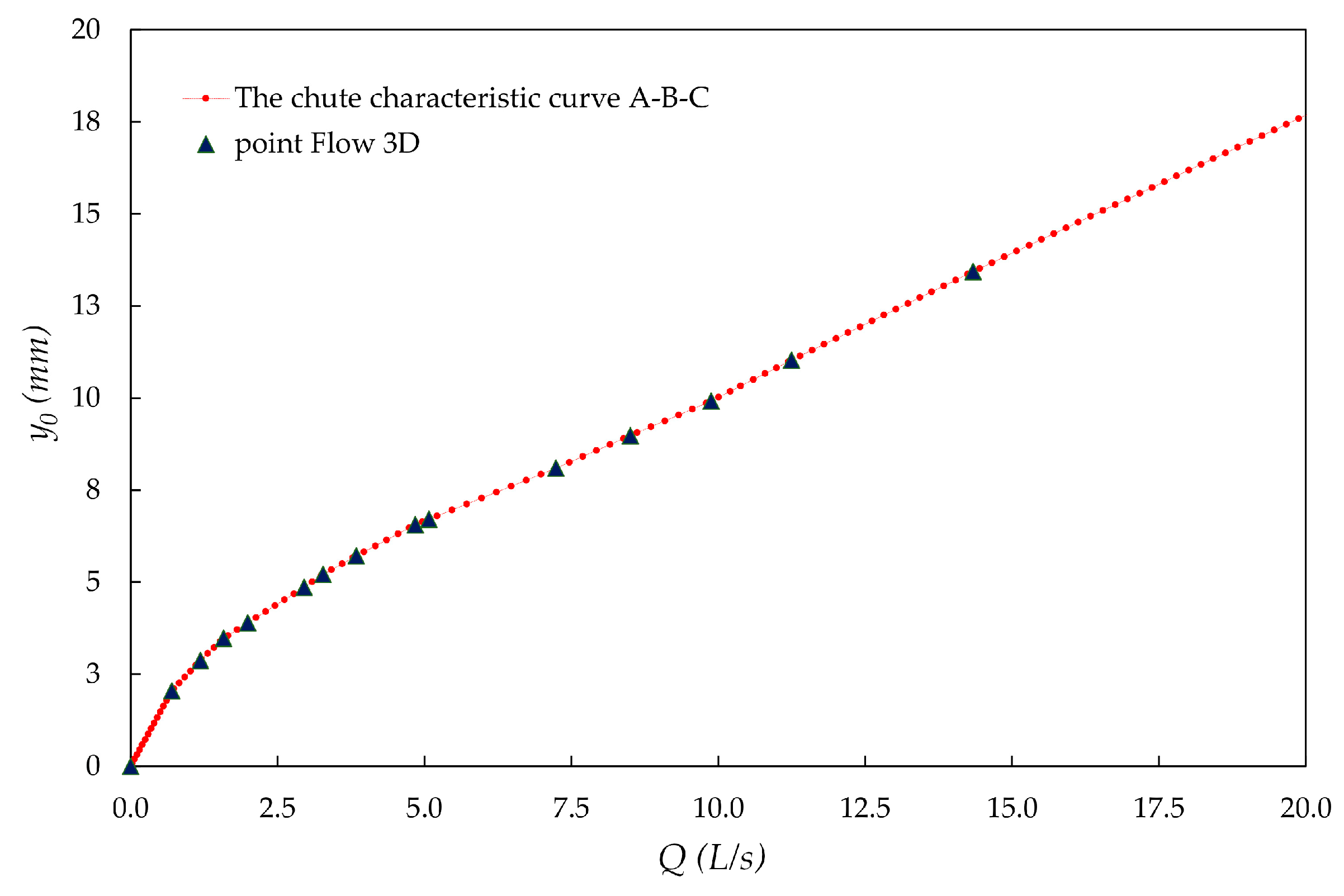
According to the proposed methodology, the flow rate for the initiation of the jet flow is the abscissa of the operating point at the intersection of two curves, the flip bucket characteristic curve and the chute characteristic curve.
The
flip bucket characteristic curve was built point by point using the proposed analytical formula (Equation (13)), that includes the effect of the flip bucket curvature. The
chute characteristic curve was built also point by point using the results of the numerical simulations performed with Flow3D. The operating point was identified for each geometrical configuration considered for the spillway. This way the flow rate
Qip and flow depth
y0ip were determined, and compared to the results of the numerical simulation (
Qisim, y0i sim) and to the values experimentally observed (
Qiexp, y0i exp). The main results of the different phases of the research are summarized in (
Table 8).
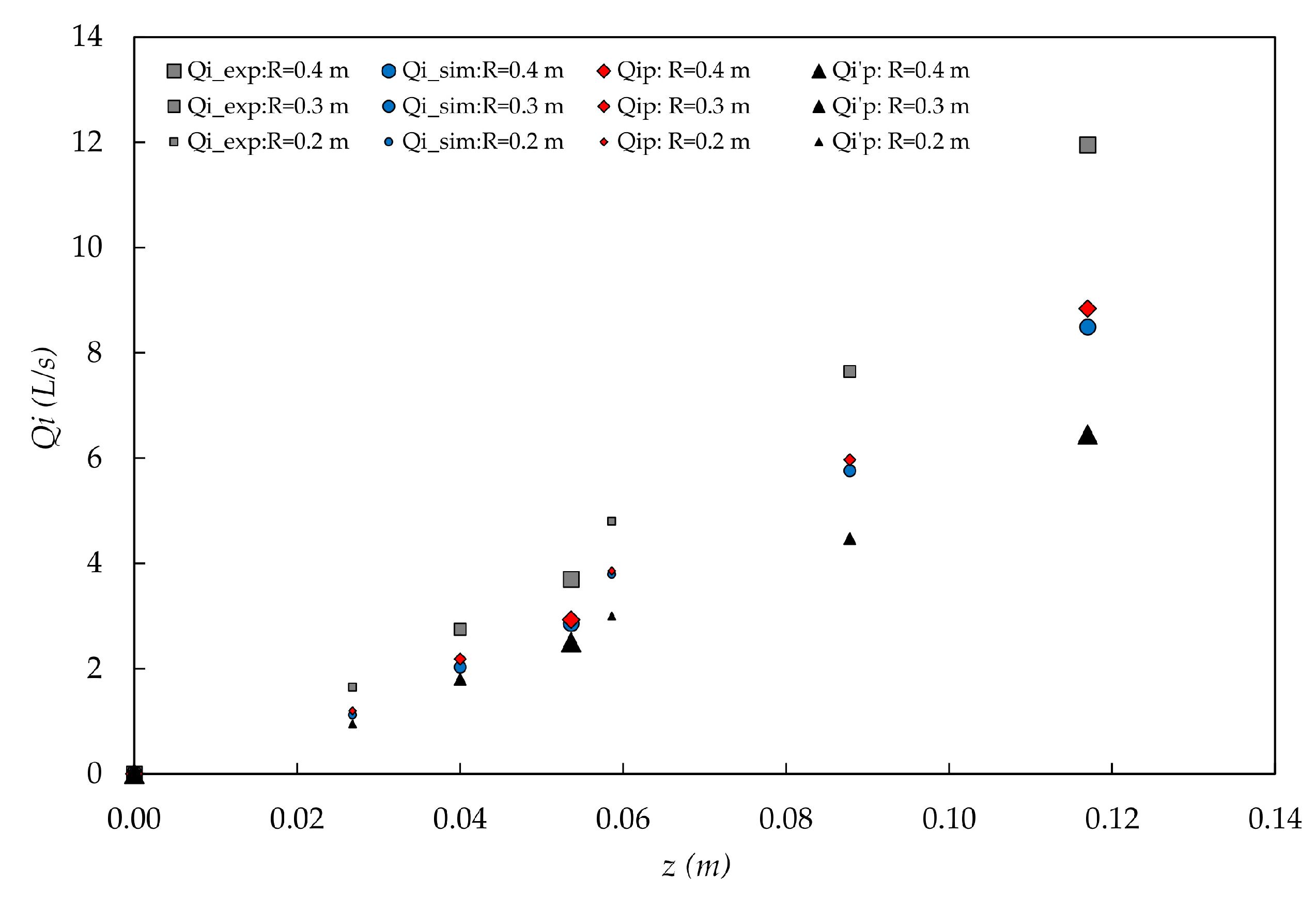
The flow rates for the initiation of the jet flow obtained by means of the proposed methodology and analytical formula and those obtained by numerical simulation are quite similar, while the values experimentally obtained are somewhat higher. The oscillation of ±0.75 L/s in the flow rates supplied to the physical model does not allow to explain the observed differences. It should be emphasized that both the proposed formula and the Flow3D numerical model do not include the effect of flow aeration, which is present on the physical model tests. This fact might explain the differences observed. If this was the reason, the effect of aeration would be to increase the flow rate for the initiation of the jet flow. In the tests performed the increase was around 26% (
Table 9). A greater increase might be expected at prototype size, due to the higher degree of aeration of the flow as compared to the laboratory size.
Let us now consider the differences between the flow depths at the lower point of the flip bucket obtained using the proposed methodology and formula and those obtained by numerical modeling. It is observed that by increasing the flow rate, the relative error decreases. For the flow rate, the MAE value is 0.15 L/s, the MRE is 4.20%, and the relative error reaches 6.88%. Similarly, for the flow depth it is observed that the MAE is 0.19 mm, and the absolute error does not exceed 0.29 mm; moreover, the MRE is 4.12% and relative error slightly exceeds 7%. For the proposed methodology and formula, it can be said in short, that the mean errors are less than 5%, related to the values obtained by numerical modeling.
Error is generally greater for small values of the flow rate for the initiation of the jet flow. Some uncertainty should be expected due to the markedly sharp angle of the characteristic curves of chute and flip bucket at the intersection point (
Figure 13). A small change in any of the two parameters involved may cause a significant variation in the other one, and so in the
chute-flip bucket system. The high sensitivity of the system to small alterations might explain the difficulty to accurately measure the flow rate for the initiation of the jet flow and the corresponding water depth at the lower point of the flip bucket.
It is observed that the flow rate for the initiation of the jet flow increases with the depth z of the flip bucket. It should be expected z to be the parameter with greater influence in the jet flow triggering. The supercritical flow stream, coming from the chute, must have enough energy to push the water mass out of the flip bucket. The water in the flip bucket has a depth z plus the height of water necessary to discharge over the lip, which acts as a weir before the jet flow occurs. On the other hand, it should be noticed that when the obstacle is not a simple wall, but a flip bucket with a certain radius of curvature, the geometric configuration of the flip bucket would be expected to influence the overspill conditions, and therefore to affect the flow rate for the initiation of the jet flow. The influence of the flip bucket curvature is included into the formula through the parameter R, radius of curvature of the flip bucket.
The effect of the radius of curvature of the flip bucket on the flow rate for the initiation of the jet flow can be easily analyzed by comparing the flow rate for the initiation of the jet flow obtained using the proposed formula with the actual
R radius of each flip bucket and that obtained with the same formula considering an infinite radius, equivalent to the absence of curvature. The goodness of the result is assessed by comparison with the results of the numerical simulations performed with Flow3D, since the influence of aeration is present in physical models (
Figure 14).
It was determined the difference between the flow rate for the initiation of the jet flow obtained by numerical simulation, and the values obtained by applying the proposed analytical formula with real radius and infinite radius, at the limit (without curvature). For infinite radius the term of the formula containing the radius becomes zero in Equation (13). Considering the results of the numerical models as the reference, the Mean Absolute Error and the Mean Relative Error were determined (
Table 10). It is noted that the Relative Error that is committed considering the complete proposed formula, with the term that includes the radius, does not exceed 8%, while if the proposed formula is considered by removing that term, the Relative Error reaches 24%. Consequently, the inclusion of radius in the formulation is relevant.
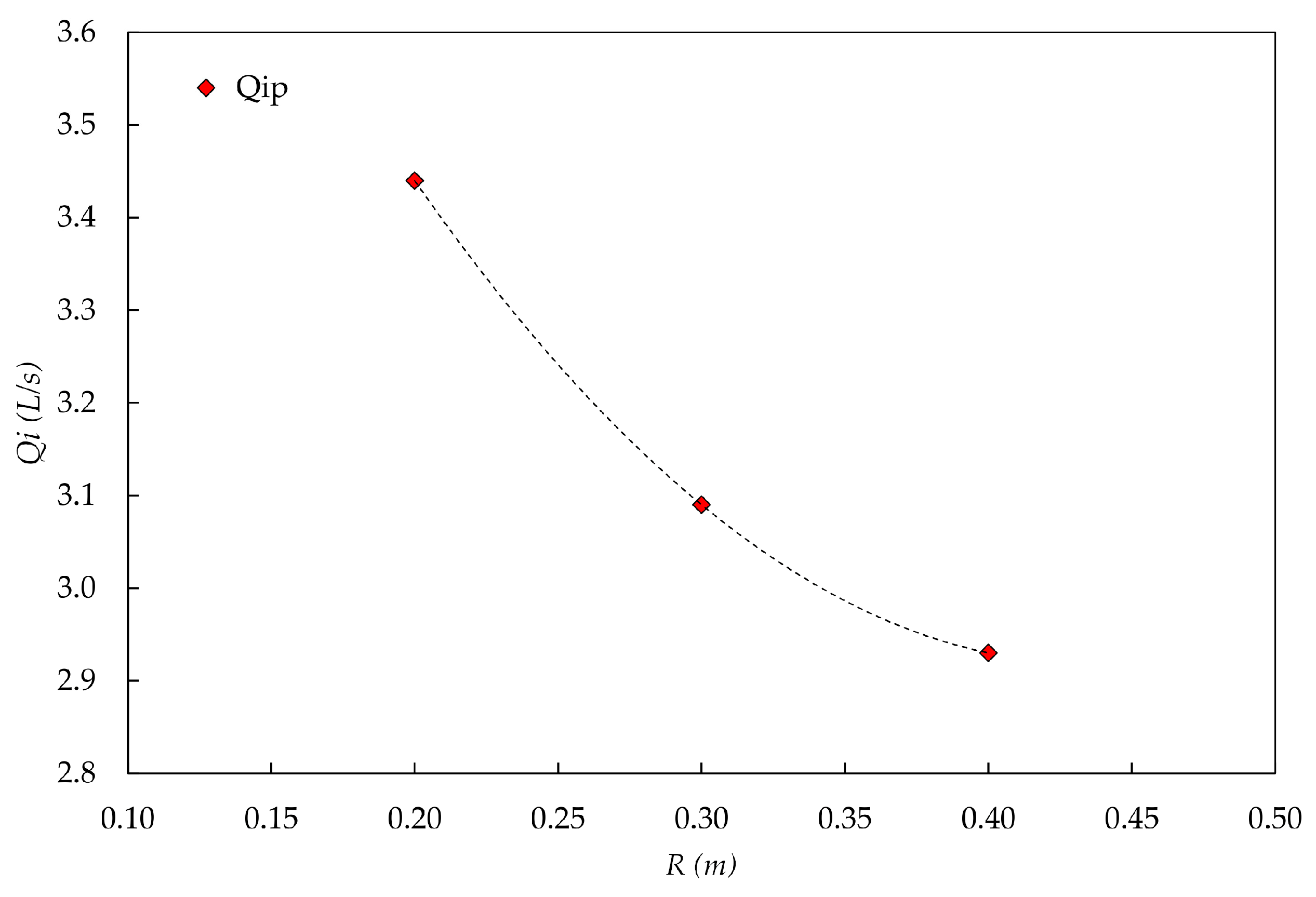
For the purpose of quantifying the influence of the radius on the flow rate for the initiation of the jet flow, the proposed methodology and formula were applied to three flip buckets with radius 0.2 m, 0.3 m, and 0.4 m, keeping the
z parameter fixed with value of 0.054 m (
Table 11). It was observed that, for the same
z value, the flow rate for the initiation of the jet flow increased as the radius was reduced, or, equivalently, as the flip angle was increased (
Figure 15). The increase in flow rate was 17.4% when the radius is halved, from 0.4 to 0.2 m. In accordance, the error due to neglecting the effect of the curvature of the flip bucket increases by decreasing the radius, in fact, the Relative Error increased from 12.97% to 25.87% when the radius was reduced by half, from 0.4 m to 0.2 m.
It is interesting to compare the flow rate for the initiation of the jet flow obtained through the proposed methodology and formula, which includes the effect of the curvature of the flip bucket, with those obtained using the formulas previously proposed by various authors. The
flip bucket characteristic curve is usually expressed as a relationship between parameter
z/y0 and the Froude number
F0, both at the lowest point of the flip bucket (Equations (1)–(6)). It can also be expressed as a relationship between
y0 and the unit flow rate for the initiation of the jet flow
q (
Table 12). This is useful for quantifying the flow rate for the initiation of the jet flow using the proposed
method of the characteristic curves.
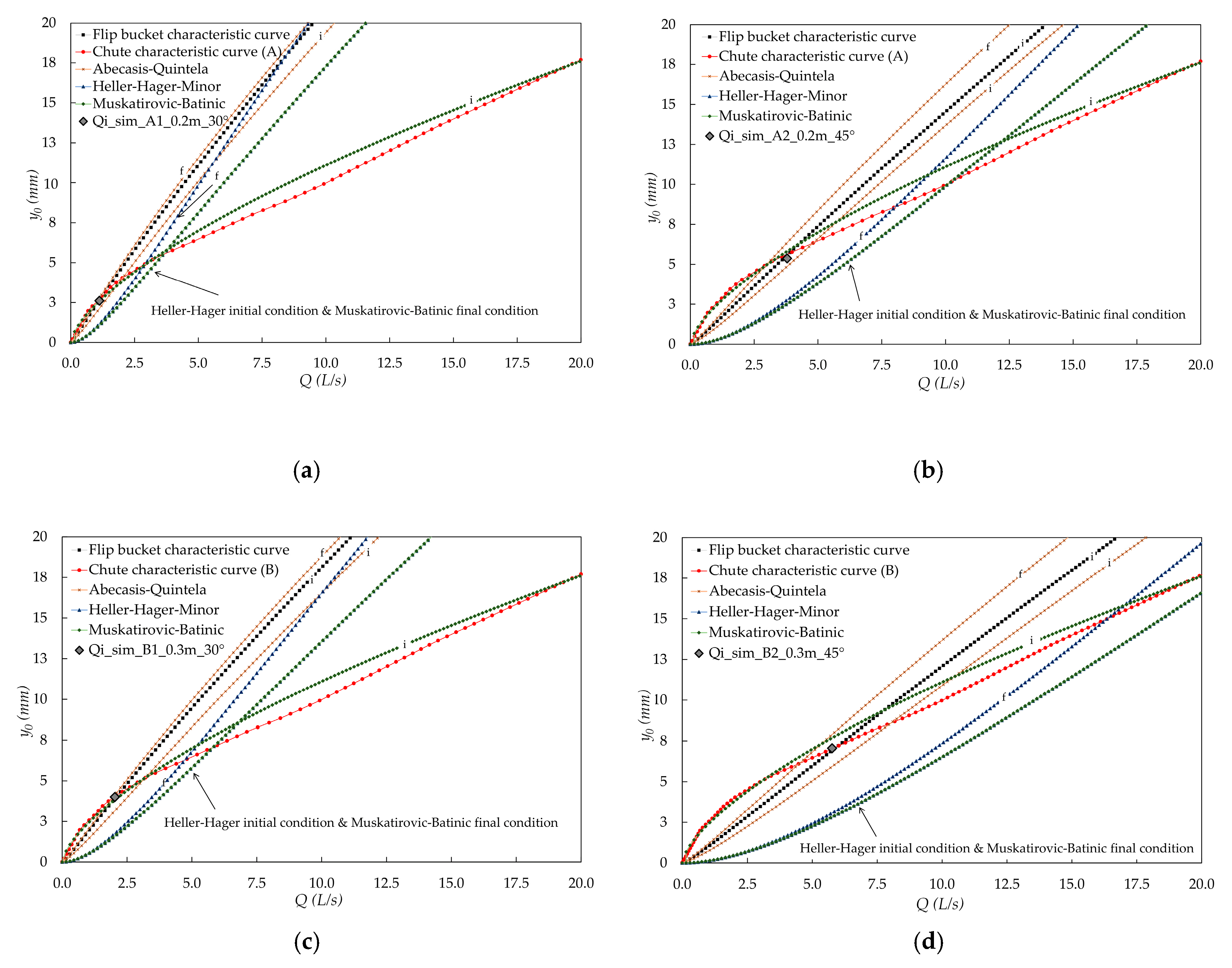
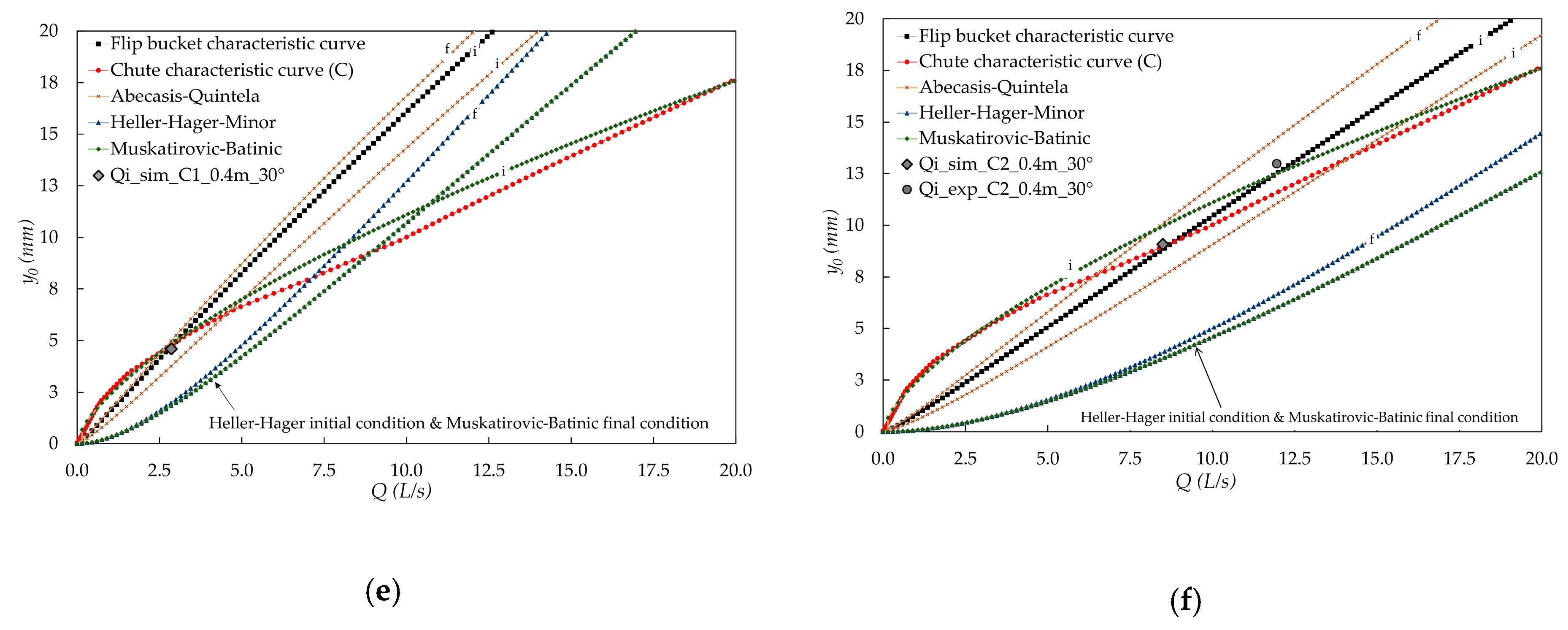
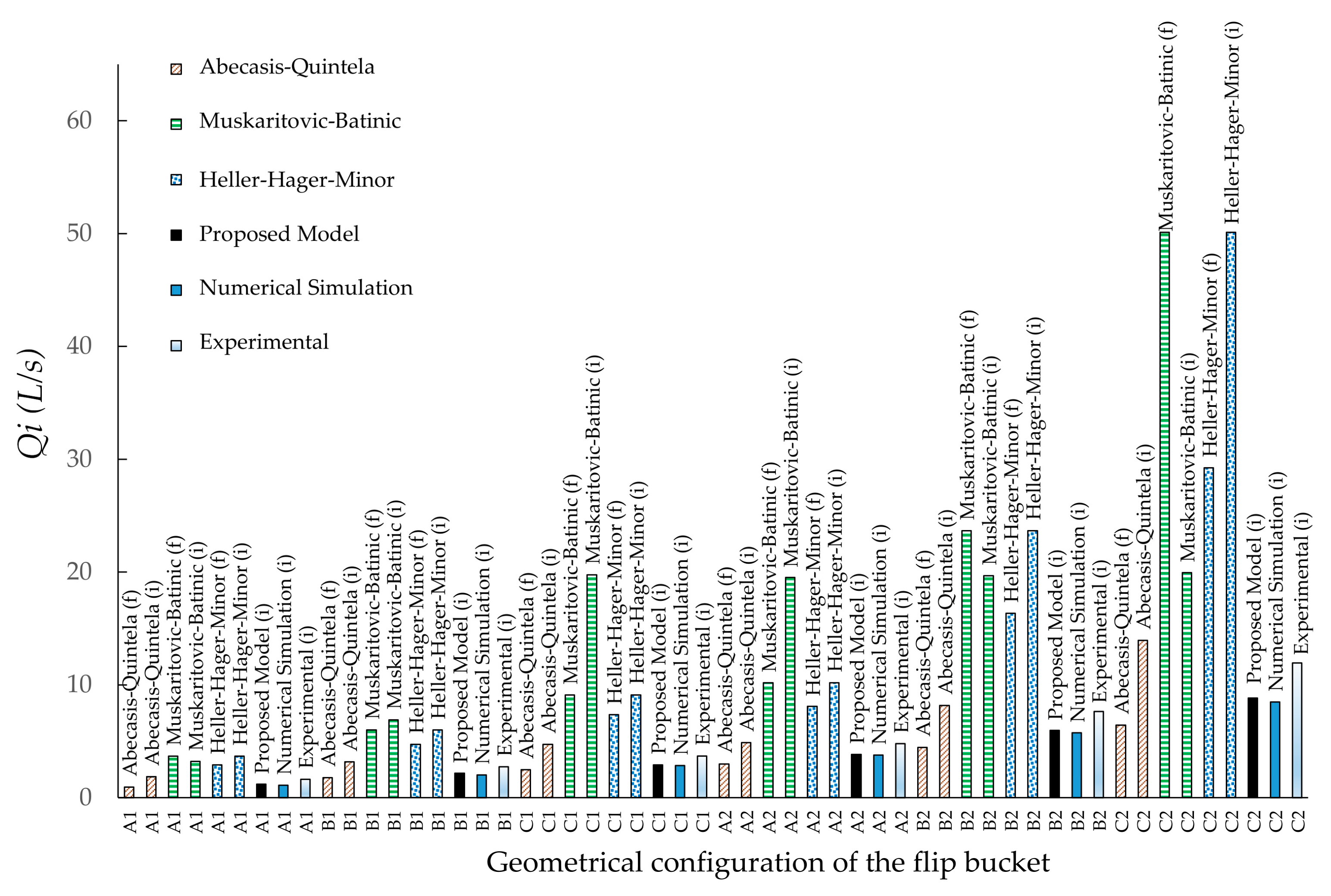
The
flip bucket characteristic curve was built point by point, and the previously determined
chute characteristic curve was used, and both were drawn for each geometrical configuration of the flip bucket, using the formula of different authors (
Figure 16). The operating points were obtained at the intersection of the characteristic curves, and therefore the flow rate for the initiation of the jet flow and the flow depth at the lowest point of the flip bucket for that flow rate (
Table 13;
Figure 17). It is noted that the proposed formula provides the best prediction for the flow rate for the initiation of the jet flow in all cases, taking as reference the one obtained by numerical modeling, followed by the formula of Abecasis and Quintela [
16,
17]. The obtained results using the formulas of the rest of the authors differ significantly, showing great dispersion.
8. Conclusions
The flip bucket might be used as a stilling basin in the range of low discharges. In some cases, it might be advisable to delay the initiation of the jet flow. This way, the dissipation of most of the energy would occur inside the flip bucket, by means of the hydraulic jump, for low discharges, which are the most frequent working condition.
For the jet flow, the energy is fully dissipated through the impact with the riverbed, which implies lower erosion control for the lower range of discharges. If a pre-excavated stilling basin is considered, it should be larger, and therefore more expensive, if jet flow occurs for low discharges.
In order to minimize the scour basin, and increase the distance between the bucket toe and the impact point, the flow rate for initiation of the jet flow should be as high as possible. It implies a longer impact distance, something beneficial for the spillway, and for the dam if it is in the vicinity of the flip bucket.
Determining the position of the erosion basin downstream of a sky-jump spillway allows to control the impact area. Its shape and size depend on both the geometrical configuration of the flip bucket and the operating flow rates. Knowing the flow rate for the initiation of the jet flow is of interest, since it allows to establish the position of the impact area closest to the spillway, and usually to the dam itself.
This study proposes a methodology that allows to determine the flow rate for the initiation of the jet flows by the intersection of two curves, by analogy with a pumping system: The chute characteristic curve and the flip bucket characteristic curve. For the latter a new formula is proposed that incorporates the effect of the curvature of the flip bucket. The flow rate for the initiation of the jet flow obtained with the proposed methodology and formula are similar to the value obtained by numerical modeling, with differences less than 5%. Experimentally obtained flow rates are somewhat higher, possibly due to the influence of the aeration of the water stream.
Accurate determination of this flow rate is difficult, as small variations of any of the parameters involved might imply a relatively significant change in the flow rate for the initiation of the jet flow. This is explained graphically by the chute and flip bucket characteristic curves, which form very sharp angles at the intersection.
The curvature of the flip bucket was found to affect significantly the flow rate for the initiation of the jet flow, although it is not the most influential parameter. In the cases that were studied, the RE that is committed considering the complete proposed formula, with the term that includes the radius, does not exceed 8%, while if the proposed formula is considered by removing that term, the RE reaches 24%. Consequently, the inclusion of radius in the formulation is relevant, which justifies the interest of using the proposed new formula. It was observed that, being constant the depth of the flip bucket (z), the flow rate for the initiation of the jet flow increases as the radius is reduced or, equivalently, by increasing the throwing angle. The increase is 17.4% when the radius is halved, from 0.4 to 0.2 m. In line with this, the error made, without considering the effect of the curvature of the flip bucket, increases, by decreasing the radius, from a RE of 12.97% to 25.87% when the radius is reduced by half, from 0.4 m to 0.2 m.
The flow rate for initiation of the jet flow is determined during the design of the flip bucket, and we have shown that it depends not only on the depth of the flip bucket (z), but also on the bucket radius. If the designer desires a high flow rate for the initiation of the jet flow, a high lip angle and the minimum radius compatible with flow conditions should be specified at the design stage. The here proposed formula should be used for considering the effect of the bucket radius. The proposed method of the characteristic curves might be used for determining the flow rate for the initiation of the jet flow. It is a decision of the designer to choose where to dissipate the low and frequent discharge flows: in the riverbed or inside the flip bucket. The decision should me made taking into consideration the geological characterization of the riverbed and the flow depth in the impact area, and also the need and cost of implementing a pre-excavated basin.
It is necessary to carry out additional research on the influence of flow aeration on the value of the flow rate for the initiation of the jet flow.