Numerical 3D Model Development and Validation of Curb-Cut Inlet for Efficiency Prediction
Abstract
:1. Introduction
2. Materials and Methods
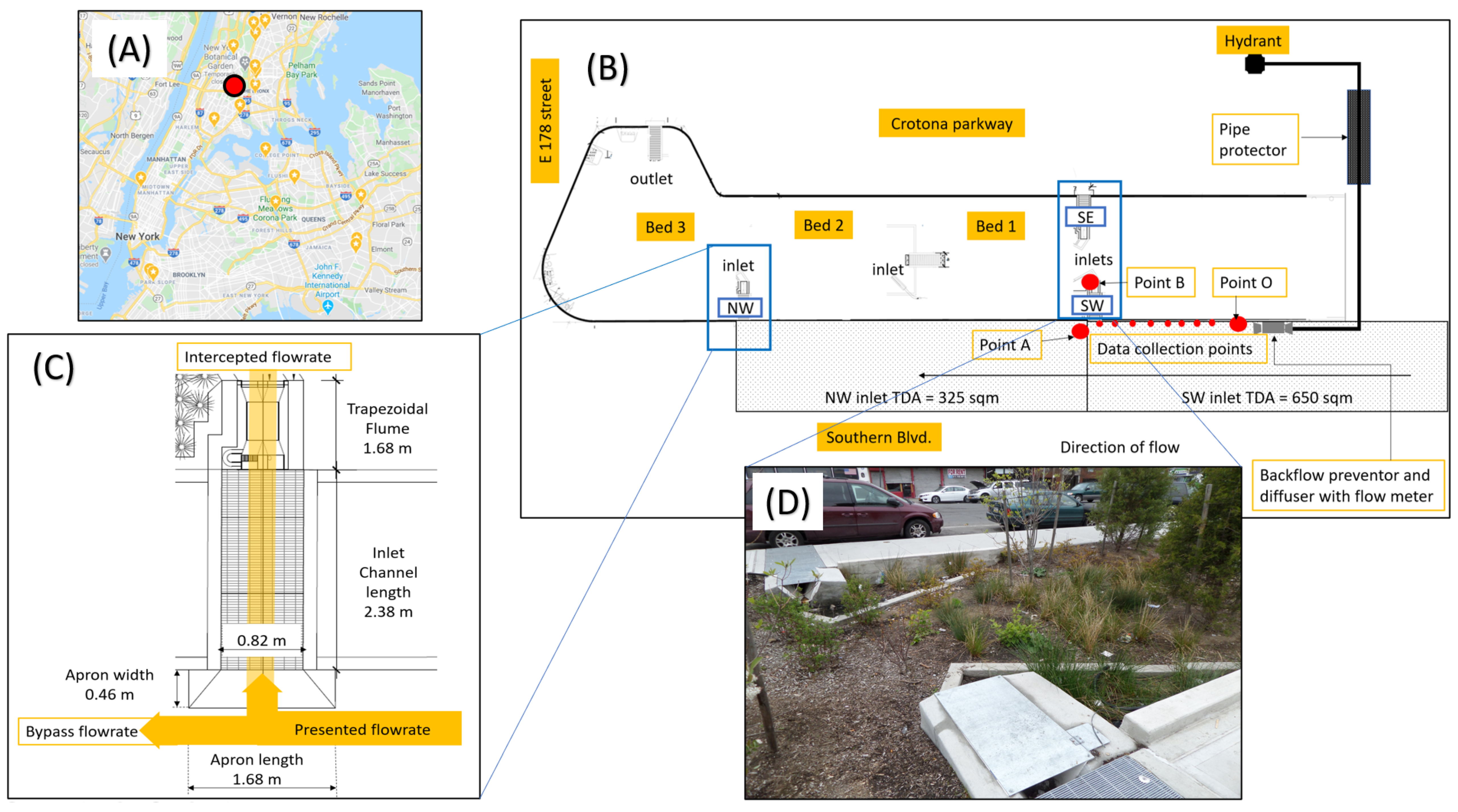
2.1. Site Characteristics
2.2. Fieldwork
2.2.1. Field Survey
2.2.2. Field Experiments Using a Hydrant Test
2.2.3. Selection of Flow Rates for Field Experiment
- Q—inflow (CMS),
- K—conversion factor from English to metric units = 0.0028,
- C—dimensionless runoff coefficient = 0.9 for impervious street [5],
- I—precipitation intensity (mm/hr), and
- A—drainage area (0.0325 ha for the NW inlet and 0.065 ha for the SW inlet).
2.3. CFD Model Development
2.3.1. Discretization and Surface Tracking Codes
2.3.2. Turbulence Model Selection
2.3.3. Time Step and Initial Condition
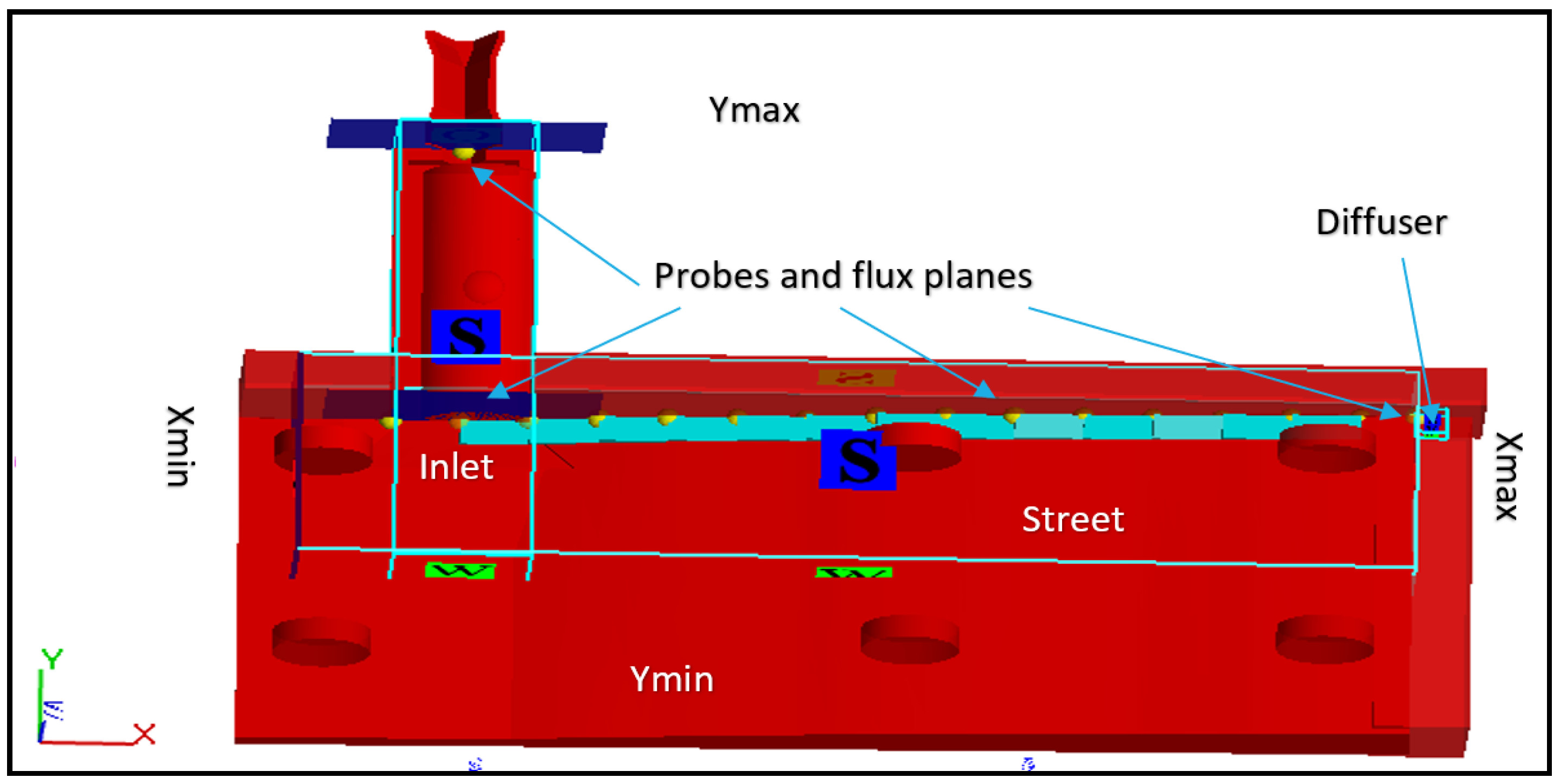
2.3.4. Mesh Size Selection and Definition of Boundary Conditions
2.4. Grid Analysis
2.5. Definition of Boundary Conditions
2.6. Replicating Inlet Clogging
2.7. Surface Roughness
2.8. Inlet Performance Metric
2.9. Convergence Assessment
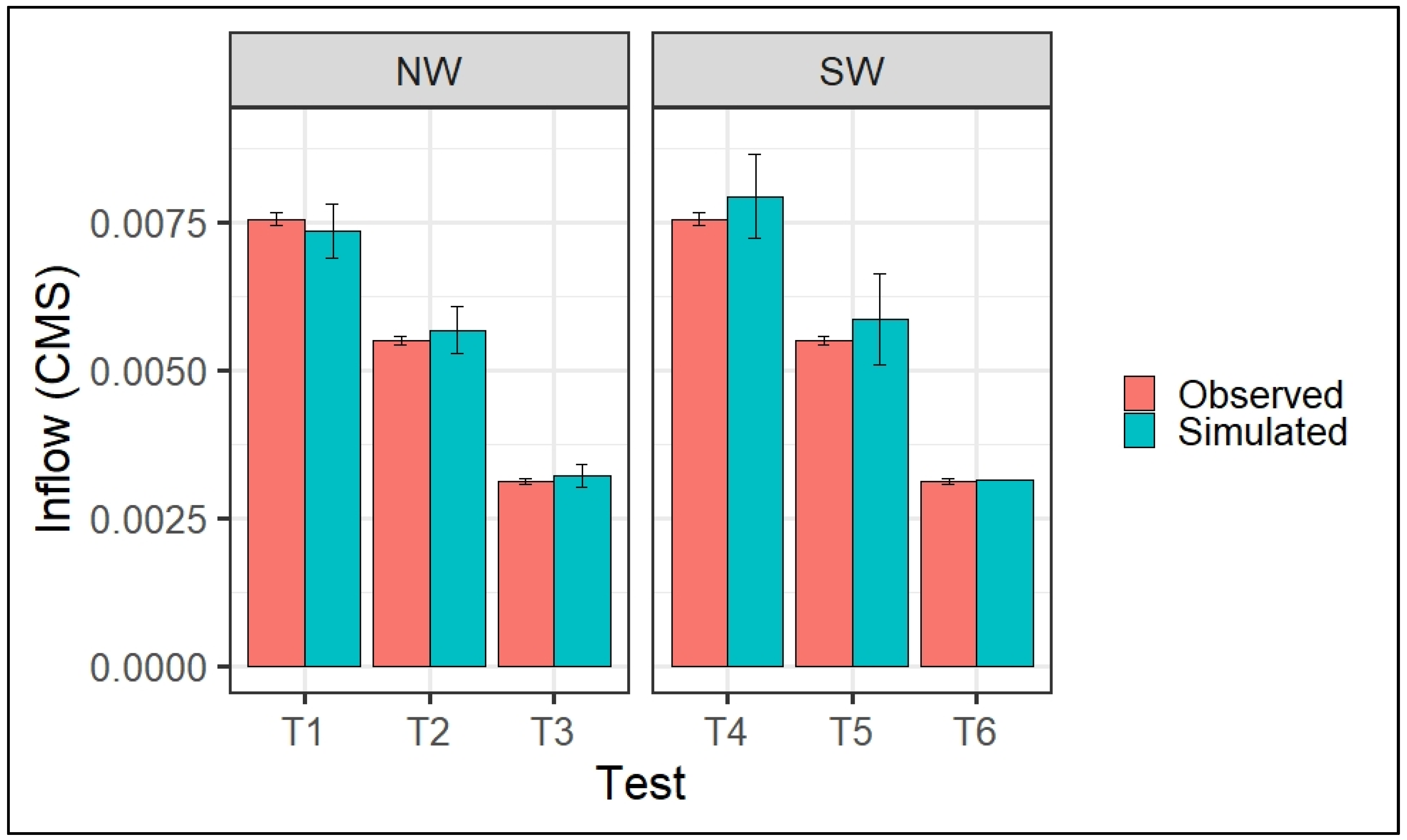
3. Validation Results
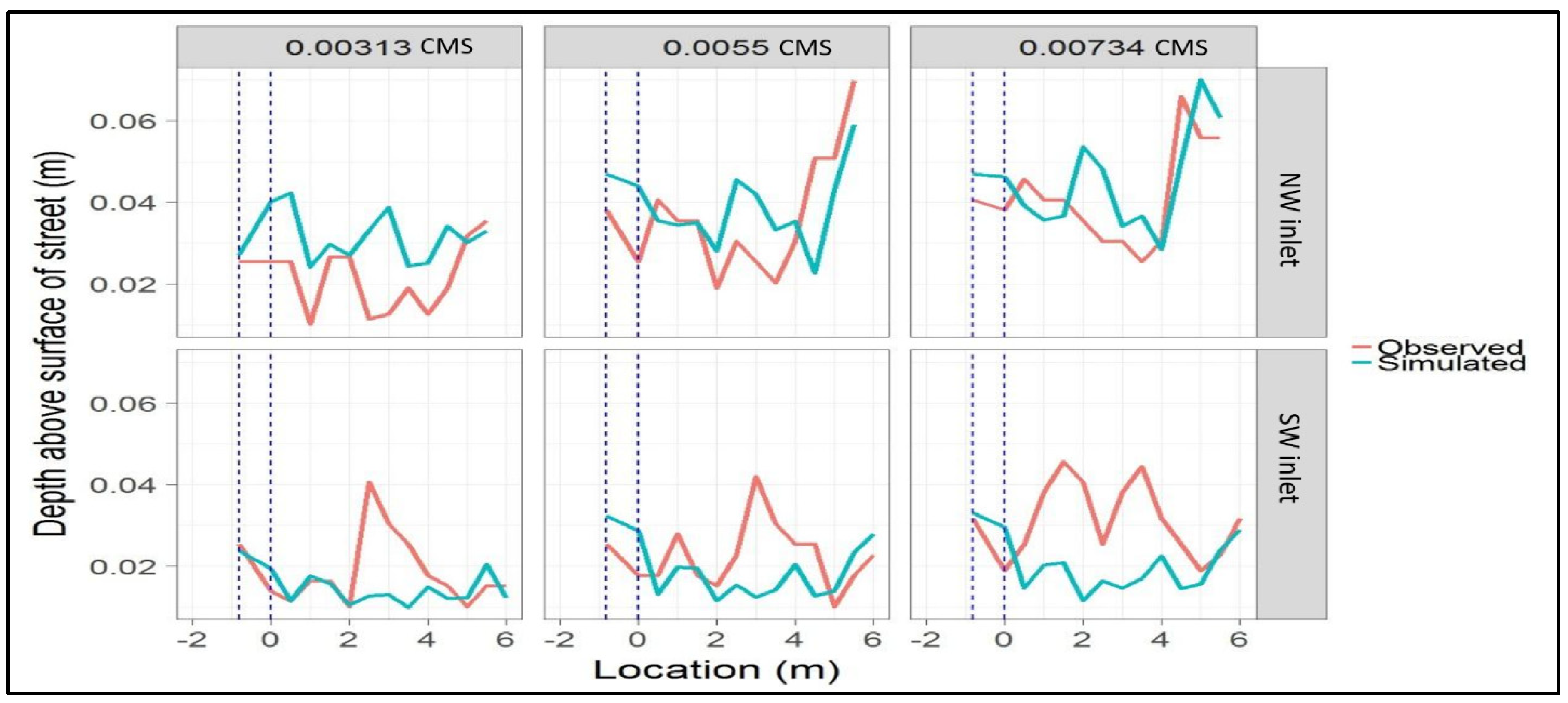
3.1. Qualitative Validation
3.2. Quantitative Validation
4. Scenarios for Sensitivity Analysis
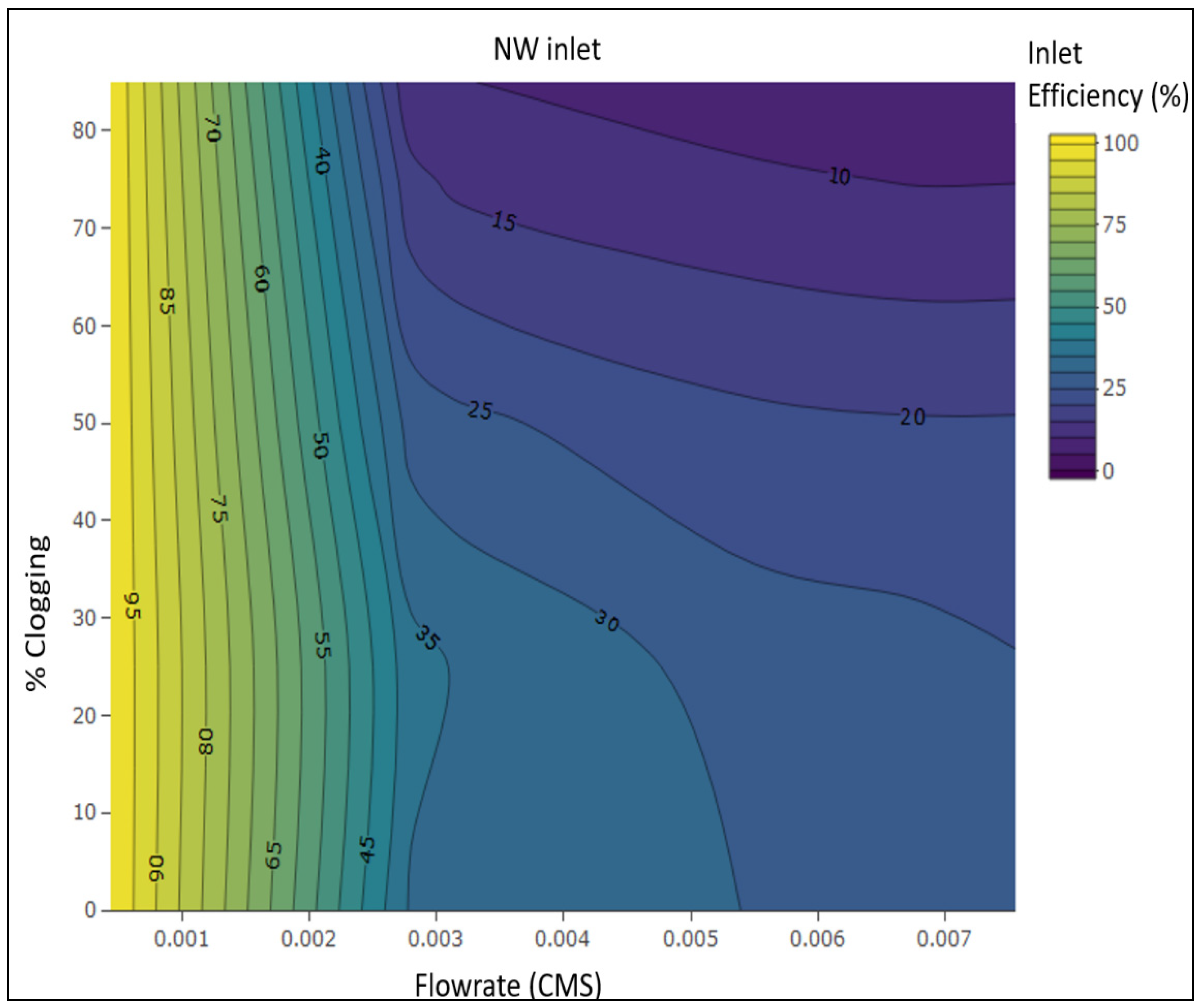
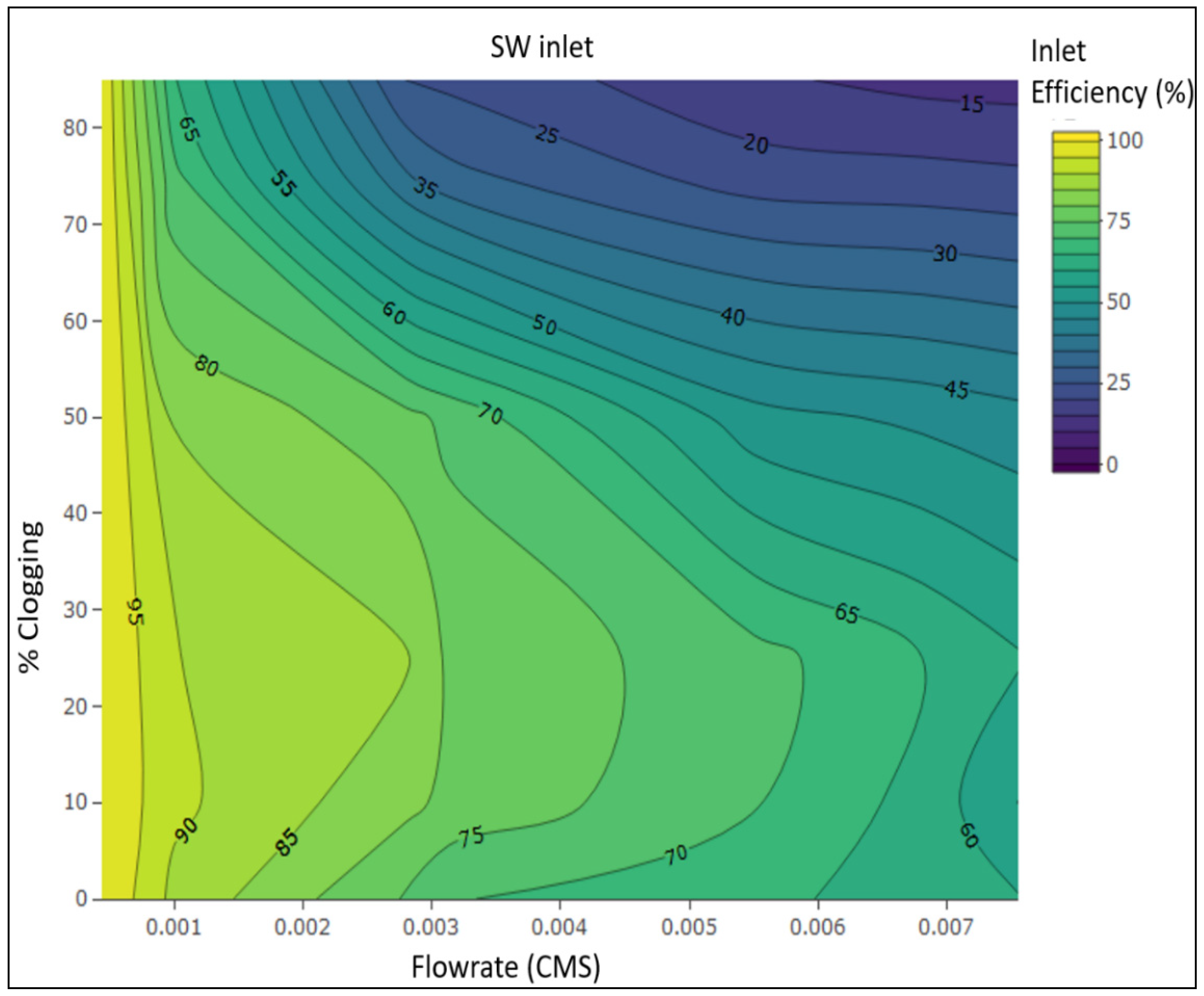
4.1. Effect of Flow Rate on Inlet Efficiency
4.2. Effect of Clogging on Inlet Efficiency
5. Sensitivity Analysis Results
5.1. Effect of Flow Rate on Inlet Efficiency
5.2. Effect of Inlet Clogging on Inlet Efficiency
6. Discussion
6.1. Possible Sources of Error in Model Validation
6.1.1. Velocity Measurements
6.1.2. Survey Data
6.1.3. Differences in Street Slope and Apron Slope
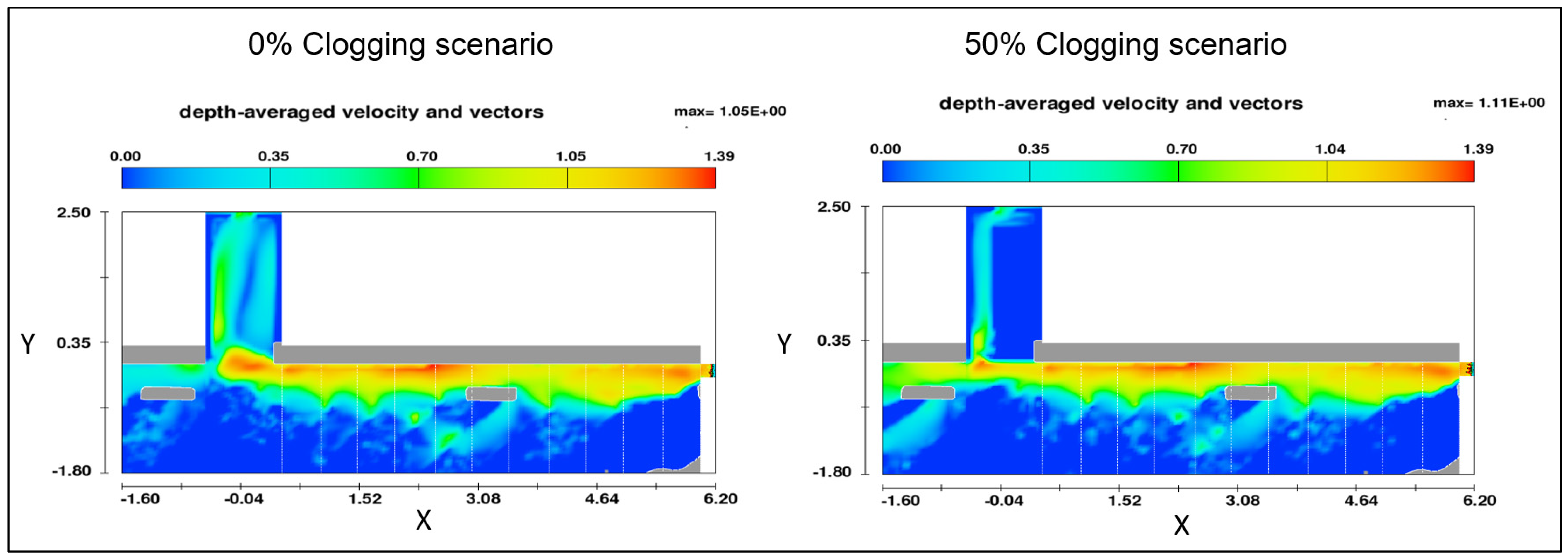
6.2. Effect of Inlet Hydraulics on Inlet Efficiency
6.2.1. Inlet Hydraulics—Effect of Upstream Velocity and Its Effect on Formation of Inlet Clogging
6.2.2. Effect of Upstream and Downstream Flow Condition on Inlet Efficiency
6.3. Model Application—Effect of Inlet Clogging on the Stage-Discharge Curve of Flume Fitted into the Inlet
7. Conclusions
Design Implications
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Results of Error Analysis
| # Cells | Modeled Inflow (CMS) | Observed Inflow (CMS) | Relative Error (%) | Modeled Inlet Efficiency (%) | Observed Inlet Efficiency (%) | Absolute Error (%) |
|---|---|---|---|---|---|---|
| 596311 | 0.00535 | 0.00552 | -3.07971 | 14.39000 | 11.95000 | 2.44000 |
| 397833 | 0.00553 | 0.00553 | 0.05134 | 11.98535 | 11.95000 | 0.03535 |
| 227896 | 0.00558 | 0.00552 | 1.08696 | 15.45000 | 11.95000 | 3.50000 |
| 198032 | 0.00586 | 0.00552 | 6.15942 | 15.87000 | 11.95000 | 3.92000 |
| 194635 | 0.00590 | 0.00552 | 6.88406 | 16.00000 | 11.95000 | 4.05000 |
| 162023 | 0.00600 | 0.00552 | 8.69565 | 18.28000 | 11.95000 | 6.33000 |
| 93754 | 0.00660 | 0.00552 | 19.56522 | 26.23000 | 11.95000 | 14.28000 |
Appendix A.2. Additional Validation Parameters
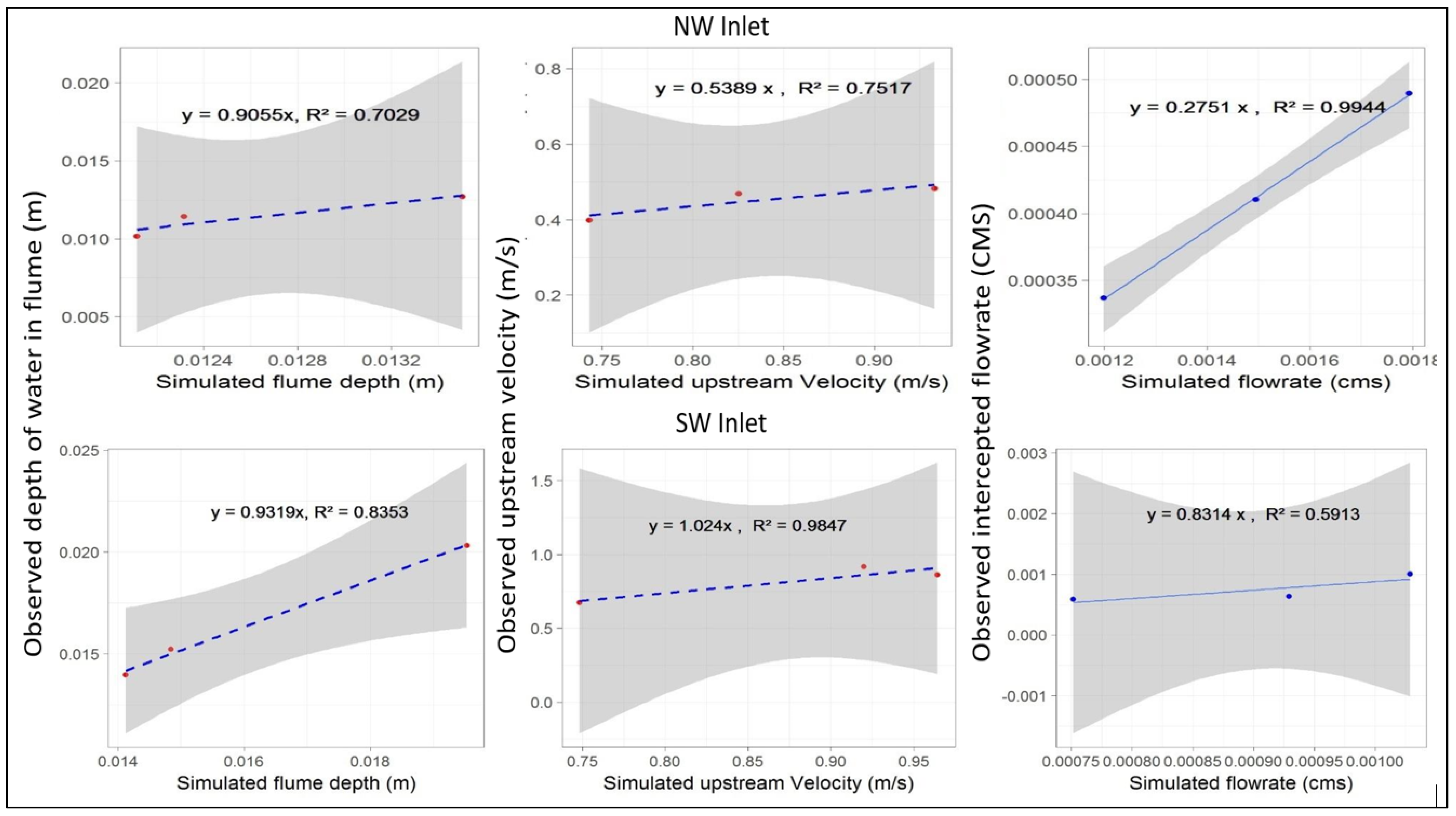
Appendix A.3. Site Photographs

Appendix A.4. Additional Explanation on Effect of Upstream and Downstream Flow Condition on Inlet Efficiency
- F—Froude number (unitless),
- V—the average velocity upstream of the inlet (m/s),
- G—acceleration due to gravity (m/s2),
- D—depth of flow upstream of the inlet (m),

References
- Muller, M. Adapting to climate change. Environ. Urban. 2016, 19, 99–113. [Google Scholar] [CrossRef] [Green Version]
- Palermo, S.A.; Zischg, J.; Sitzenfrei, R.; Rauch, W.; Piro, P. Parameter Sensitivity of a Microscale Hydrodynamic Model. In New Trends in Urban Drainage Modelling; Mannina, G., Ed.; UDM 2018; Green Energy and Technology; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Palla, A.; Colli, M.; Candela, A.; Aronica, G.T.; Lanza, L.G. Pluvial flooding in urban areas: The role of surface drainage efficiency. J. Flood Risk Manag. 2018, 11, S663–S676. [Google Scholar] [CrossRef]
- Catalano De’Sousa, M.R.; Montalto, F.A.; Gurian, P. Evaluating green infrastructure stormwater capture performance under extreme precipitation. J. Extrem. Events 2016, 3. [Google Scholar] [CrossRef]
- Brown, S.A.; Schall, J.D.; Morris, J.L.; Doherty, C.L.; Stein, S.M.; Warner, J.C. Urban Drainage Design Manual: Hydraulic Engineering Circular No. 22, 3rd ed.; Federal Highway Administration: Washington, DC, USA, 2016.
- Hammons, M.A.; Holley, E.R. Hydraulic Characteristics of Flushed Depressed Curb Inlets and Bridge. Drains; Texas Department of Transportation: Austin, TX, USA, 1995. Available online: https://library.ctr.utexas.edu/digitized/texasarchive/phase2/1409-1.pdf (accessed on 30 June 2017).
- Izzard, C.F. Tentative Results on Capacity of Curb Opening Inlets. 1950. Available online: http://onlinepubs.trb.org/Onlinepubs/hrbresearchrpts/1950/11B-004.pdf (accessed on 30 June 2017).
- Russo, B.; Gómez, M.; Tellez, J. Methodology to estimate the hydraulic efficiency of non-tested continuous transverse grates. J. Irrig. Drain. Eng. 2013, 139, 864–871. [Google Scholar] [CrossRef]
- Leitão, J.P.; Simões, N.E.; Pina, R.D.; Ochoa-Rodriguez, S.; Onof, C.; Marques, A.S. Stochastic evaluation of the impact of sewer inlets’ hydraulic capacity on urban pluvial flooding. Stoch. Environ. Res. Risk Assess. 2016, 31, 1907–1922. [Google Scholar] [CrossRef]
- Carbone, M.; Garofalo, G.; Piro, P. Comparison between CFD and surface overflow rate models to predict particulate matter separation in unit operations for combined sewer overflows. J. Environ. Eng. 2014, 140, 1–12. [Google Scholar] [CrossRef]
- Giovanni, M. New analytical formulation of De Marchi’s model for a zero-height side weir. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Durga Rao, K.H.V.; Pillai, C.R.S. Study of flow over side weirs under supercritical conditions. Water Resour. Manag. 2007, 22, 131–143. [Google Scholar] [CrossRef]
- Uyumaz, A.; Smith, R.H. Design procedure for flow over side weirs. J. Irrig. Drain. Eng. 1991, 117, 79–90. [Google Scholar] [CrossRef]
- Delkash, M.; Bakhshayesh, B.E. An Examination of Rectangular Side Weir Discharge Coefficient Equations under Subcritical Condition. Int. J. Hydraul. Eng. 2014, 3, 24–34. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Djordjevic, S.; Saul, A.J.; Tabor, G.R.; Blanksby, J.; Galambos, I.; Sabtu, N.; Sailor, G. Experimental and numerical investigation of interactions between above and below ground drainage systems. Water Sci. Technol. 2013, 67, 535–542. [Google Scholar] [CrossRef]
- Fang, X.; Jiang, S.; Alam, S.R. Numerical simulations of efficiency of curb-opening inlets. J. Hydraul. Eng. 2010, 136, 62–66. [Google Scholar] [CrossRef]
- Gomez, M.; Recasens, J.; Russo, B.; Martinez-Gomariz, E. Assessment of inlet efficiency through a 3D simulation: Numerical and experimental comparison. Water Sci. Technol. 2016, 74, 1926–1935. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S. Numerical Simulation of Shallow Flow through Curb Cut Inlets at Various Longitudinal and Cross Slope. Ph.D. Thesis, Lamar University, Beaumont, TX, USA, 2007. Unpublished work. [Google Scholar]
- Lopes, P.; Leandro, J.; Carvalho, R.F.; Russo, B.; Gómez, M. Assessment of the ability of a volume of fluid model to reproduce the efficiency of a continuous transverse gully with grate. J. Irrig. Drain. Eng. 2016, 142. [Google Scholar] [CrossRef] [Green Version]
- Senior, M.; Scheckenberger, R.; Bishop, B. Modeling catchbasins and inlets in SWMM. J. Water Manag. Modeling 2018. [Google Scholar] [CrossRef] [Green Version]
- Hager, W.H. Lateral outflow over side weir. J. Hydraul. Eng. 1987, 113, 491–504. [Google Scholar] [CrossRef] [Green Version]
- Michelazzo, G.; Oumeraci, H.; Paris, E. Laboratory study on 3D flow structures induced by zero-height side weir and implications for 1D modeling. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Mohammed, A.Y. Numerical analysis of flow over side weir. J. King Saud Univ. Eng. Sci. 2015, 27, 37–42. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Manivannan, D.; Satyanarayana, T. Discharge coefficient of rectangular side weirs. J. Irrig. Drain. Eng. 1994, 120, 814–819. [Google Scholar] [CrossRef]
- Catalano De’Sousa, M.R.; Miller, S.M.; Dorsch, M.; Montalto, F.A. Green Infrastructure as a Climate Change Resiliency Strategy in Jamaica Bay, NY. In Prospects for Resilience: Loss, Recovery and the Future of New York City’s Jamaica Bay; Sanderson, E.W., Solecki, W.D., Waldman, J.R., Parris, A.S., Eds.; Island Press: Washington, DC, USA, 2016; Chapter 9; p. 287. [Google Scholar]
- NYC Green Infrastructure Annual Report. NYC Environmental Protection, 2012. Available online: https://www1.nyc.gov/assets/dep/downloads/pdf/water/stormwater/green-infrastructure/gi-annual-report-2012.pdf (accessed on 30 June 2017).
- Mays, L. Stormwater Collection Systems Design Handbook; McGraw Hill Professional: New York, NY, USA, 2001; ISBN1 007138278X. ISBN2 9780071382786. [Google Scholar]
- NYC-DEP. Chapter 4: Precipitation, watershed, and tide gate analysis. In NYC Wastewater Resiliency Plan; City of New York DEP: New York, NY, USA, 2013. [Google Scholar]
- NOAA. NOAA Atlas 14; Volume 10, Version 3.0.; 2017. Available online: https://hdsc.nws.noaa.gov/hdsc/pfds/pfds_map_cont.html (accessed on 31 January 2019).
- FLOW-3D® (Version 11.2.0) [Computer software]; Flow Science, Inc: Santa Fe, NM, USA, 2017.
- Savage, B.M.; Johnson, M.C. Flow over ogee spillway: Physical and numerical model case study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]
- Hirt, C.; Sicilian, J. A porosity technique for the definition of obstacles in rectangular cell meshes. In Proceedings of the Fourth International Conference on Numerical Ship Hydrodynamics, National Academy of Sciences, Washington, DC, USA, 24–27 September 1985. [Google Scholar]
- Gholami, A.; Akhtari, A.A.; Minatour, Y.; Bonakdari, H.; Javadi, A.A. Experimental and Numerical Study on Velocity Fields and Water Surface Profile in a Strongly-Curved 90° Open Channel Bend. Eng. Appl. Comput. Fluid Mech. 2014, 8, 447–461. [Google Scholar] [CrossRef] [Green Version]
- Morvan, H.; Knight, D.; Wright, N.; Tang, X.; Crossley, A. The concept of roughness in fluvial hydraulics and its formulation in 1D, 2D and 3d numerical simulation models. J. Hydraul. Res. 2010, 46, 191–208. [Google Scholar] [CrossRef]
- Souders, D.T.; Hirt, C.W. Modeling Roughness Effects in Open Channel Flows; Flow Science, Inc. Technical Note (FSI-02-TN60); Available online: https://flowvisioncfd.com/webhelp/fven_30904/index.html?models_turb_literature.htm (accessed on 30 June 2017).
- CFD-101. 2011. Available online: https://www.flow3d.com/resources/cfd-101/numerical-issues/relaxation-and-convergence-criteria/ (accessed on 10 July 2018).
- Policy Analysis Report. City and County Of San Francisco, Budget and Legislative Analyst’s Office, 2018. Available online: https://sfbos.org/sites/default/files/BLA_Report_Street_Cleaning_Cost_Survey_062518.pdf (accessed on 31 January 2019).
- Guo, J.C.Y.; MacKenzie, K. Hydraulic Efficiency of Grate and Curb Opening Inlets under Clogging Effect; Report No. CDOT-2012-3; 2012. Available online: https://www.codot.gov/programs/research/pdfs/2012/inlets.pdf (accessed on 30 June 2017).
- Azimi, H.; Shabanlou, S.; Salimi, M.S. Free surface and velocity field in a circular channel along the side weir in supercritical flow conditions. Flow Meas. Instrum. 2014, 38, 108–115. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Ghazaw, Y.M. Design and analysis of a canal section for minimum water loss. Alex. Eng. J. 2011, 50, 337–344. [Google Scholar] [CrossRef]
- Mosetti, F. Froude number. In Beaches and Coastal Geology. Encyclopedia of Earth Science; Springer: Boston, MA, USA, 1982. [Google Scholar]




| Physical Characteristics | Validation |
|---|---|
| Street width, curb to crown | 3.5 m |
| Length of inlet | 0.82 m |
| Opening depth of inlet | 0.154 m |
| Upstream (U/S) gutter depression (apron) length | 0.425 m |
| Downstream (D/S) apron length | 0.425 m |
| Apron width | 0.445 m |
| NW inlet upstream street slopes (Sx, SL) | 1.50%, 1.18% |
| SW inlet upstream street slopes (Sx, SL) | 1.15%, 1.30% |
| Inlet | Flow Rate Tested at the Field (CMS) | Peak Flow Rate Calculated Based on the Rain Intensity Q (CMS) | The Nearest Equivalent to 15-min Duration Rain Intensity (mm/hr) | Corresponding Return Period (Years) |
|---|---|---|---|---|
| SW | 0.0090 | 0.01032 | 63 | 1 |
| NW | 0.0055 | 0.00516 | 63 | 1 |
| 0.0068 | 0.00614 | 75 | 2 | |
| 0.0075 | 0.00778 | 95 | 5 | |
| 0.0090 | 0.00909 | 111 | 10 |
| Inlet | Test | Simulated Inflow (CMS) | Observed Inflow (CMS) | Relative Error—Inflow Flowrate (%) | Simulated Intercepted Flow (CMS) | Observed Intercepted Flow (CMS) | Relative Error—Intercepted Flowrate (%) | Modeled Inlet Efficiency (%) | Observed Inlet Efficiency (%) |
|---|---|---|---|---|---|---|---|---|---|
| NW | T1 | 0.00735 | 0.00736 | −0.13 | 0.00179 | 0.00049 | −265.30 | 24.35 | 6.65 |
| NW | T2 | 0.00567 | 0.00566 | 0.17 | 0.00150 | 0.00041 | −265.85 | 26.45 | 7.24 |
| NW | T3 | 0.00322 | 0.00330 | −2.42 | 0.00120 | 0.00034 | −252.94 | 37.26 | 10.30 |
| SW | T4 | 0.00794 | 0.00755 | −5.16 | 0.00103 | 0.00108 | −4.62 | 12.97 | 14.30 |
| SW | T5 | 0.00586 | 0.00552 | −6.15 | 0.00093 | 0.00066 | 40.90 | 15.87 | 11.95 |
| SW | T6 | 0.00315 | 0.00314 | −0.31 | 0.00075 | 0.00057 | 31.57 | 23.80 | 18.15 |
| NW | T1 | 0.01212 | 0.01016 | −19.24 | 0.93313 | 0.48263 | −93.34 | 0.48263 | −93.34 |
| NW | T2 | 0.01232 | 0.01143 | −7.75 | 0.82539 | 0.46904 | −75.97 | 0.46904 | −75.97 |
| NW | T3 | 0.01350 | 0.01270 | −6.31 | 0.74312 | 0.39904 | −86.22 | 0.39904 | −86.22 |
| SW | T4 | 0.01953 | 0.02032 | 3.88 | 0.91998 | 0.91575 | −0.46 | 0.91575 | −0.46 |
| SW | T5 | 0.01484 | 0.01524 | 2.62 | 0.96437 | 0.86207 | −11.86 | 0.86207 | −11.86 |
| SW | T6 | 0.01412 | 0.01397 | −1.07 | 0.74851 | 0.67295 | −11.22 | 0.67295 | −11.22 |
| Flow Rate (CMS) | Selection Reference |
|---|---|
| 0.00044 | Observed inlet capacity during precipitation event dated July 29,2019 |
| 0.001 | Interpolation |
| 0.0028 | Interpolation |
| 0.0033 | Hydrant test |
| 0.0055 | Hydrant test and intensity corresponding to 15 min duration, 1-year return period with NW inlet |
| 0.0068 | Interpolation |
| 0.00755 | Hydrant test and intensity corresponding to 15 min duration, 5-year return period with the NW inlet, and less than 1-year return period for the SW inlet |
| Clogging Conditions | Flow Rate (CMS) | Total for NW Inlet | Total for SW Inlet | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.00044 | 0.001 | 0.0028 | 0.0031 | 0.0055 | 0.0068 | 0.00755 | |||
| 0% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
| 10% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
| 25% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
| 50% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
| 75% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
| 90% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
| Total | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 42 | 42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shevade, L.J.; Lo, L.J.; Montalto, F.A. Numerical 3D Model Development and Validation of Curb-Cut Inlet for Efficiency Prediction. Water 2020, 12, 1791. https://doi.org/10.3390/w12061791
Shevade LJ, Lo LJ, Montalto FA. Numerical 3D Model Development and Validation of Curb-Cut Inlet for Efficiency Prediction. Water. 2020; 12(6):1791. https://doi.org/10.3390/w12061791
Chicago/Turabian StyleShevade, Leena Jaydeep, L. James Lo, and Franco A. Montalto. 2020. "Numerical 3D Model Development and Validation of Curb-Cut Inlet for Efficiency Prediction" Water 12, no. 6: 1791. https://doi.org/10.3390/w12061791
APA StyleShevade, L. J., Lo, L. J., & Montalto, F. A. (2020). Numerical 3D Model Development and Validation of Curb-Cut Inlet for Efficiency Prediction. Water, 12(6), 1791. https://doi.org/10.3390/w12061791





