Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Study Area
2.2. Methods
2.2.1. Data Analysis
2.2.2. Mann–Kendal (M–K) Test
2.2.3. Application of the Copula Theory
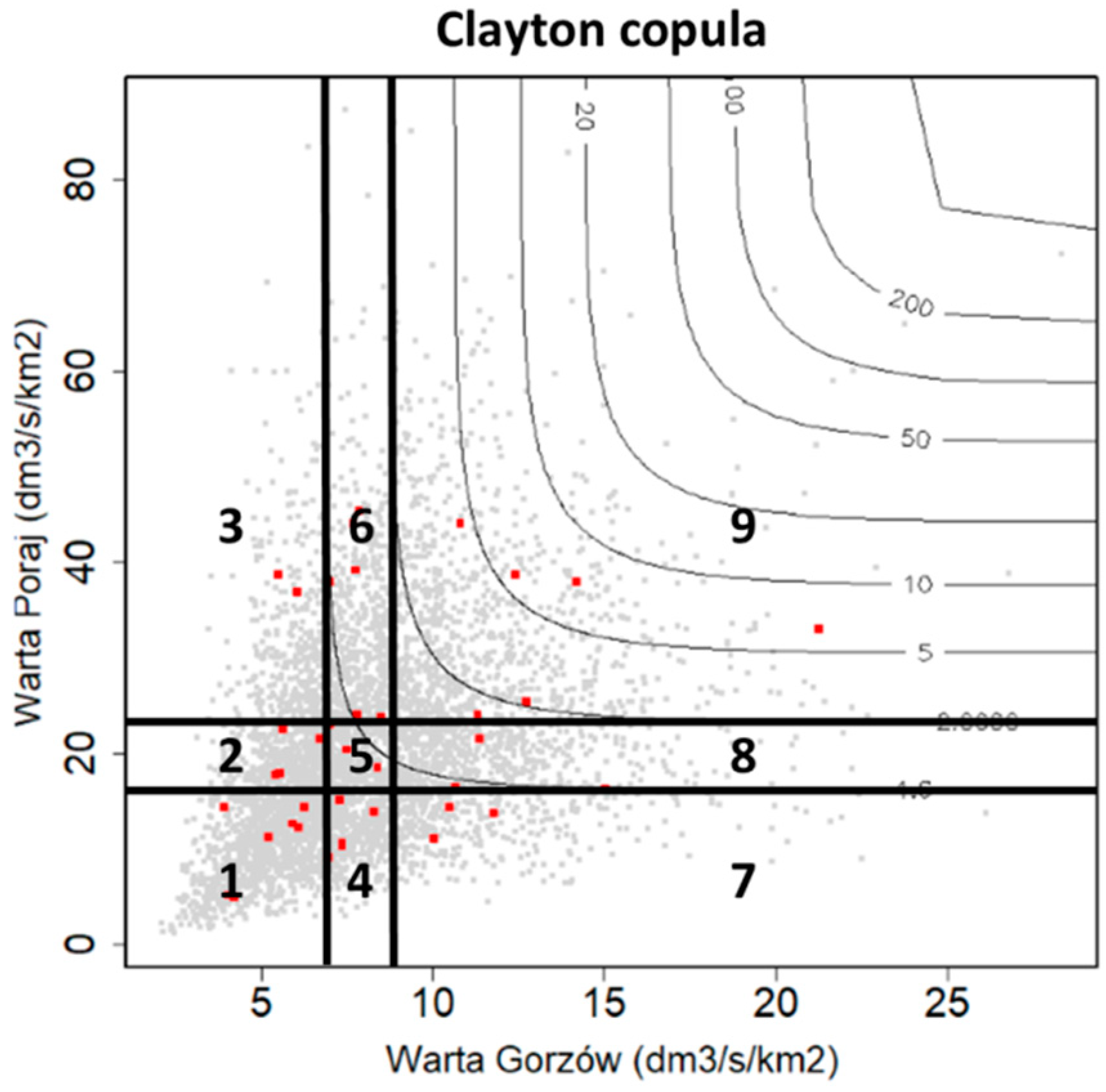
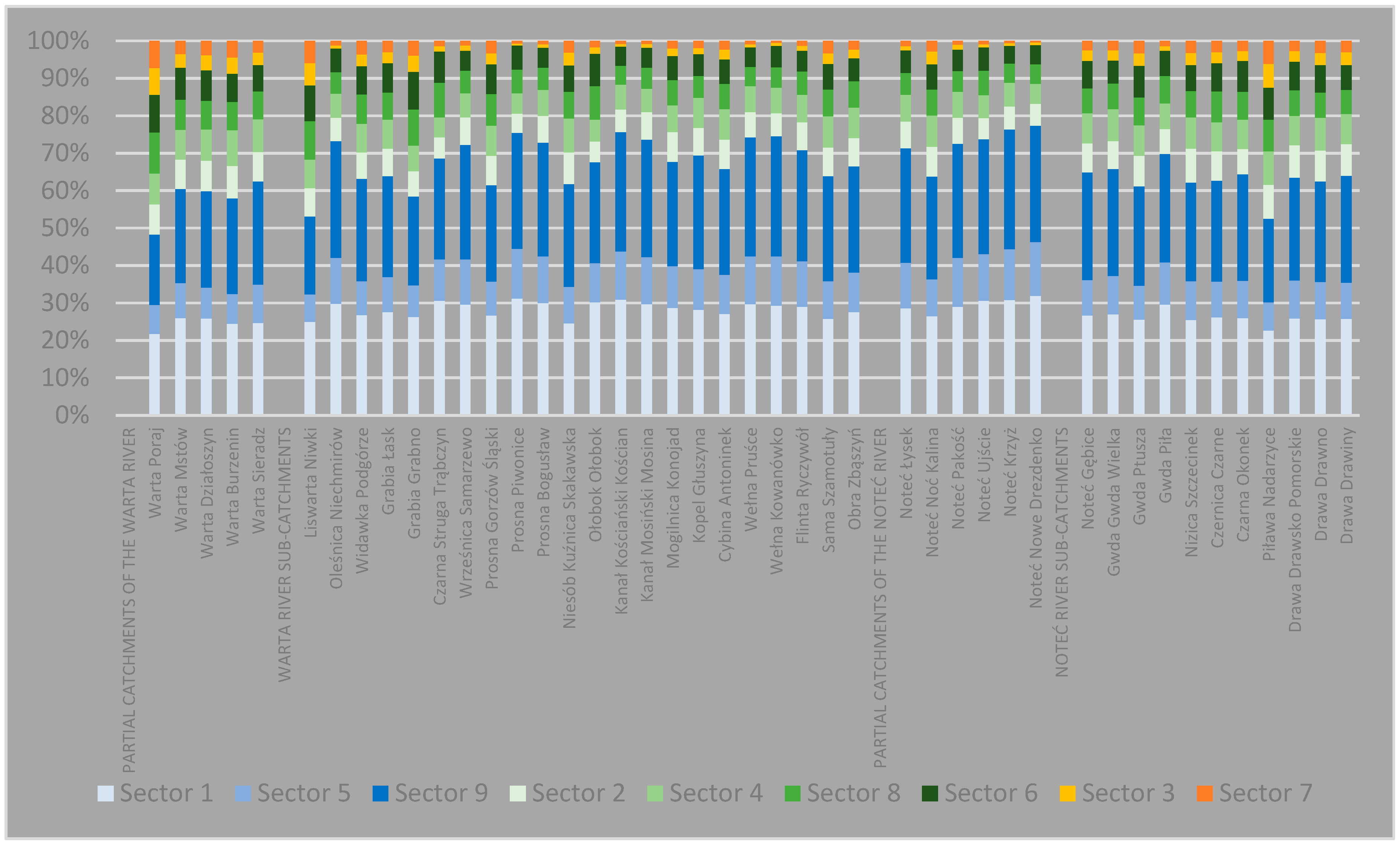
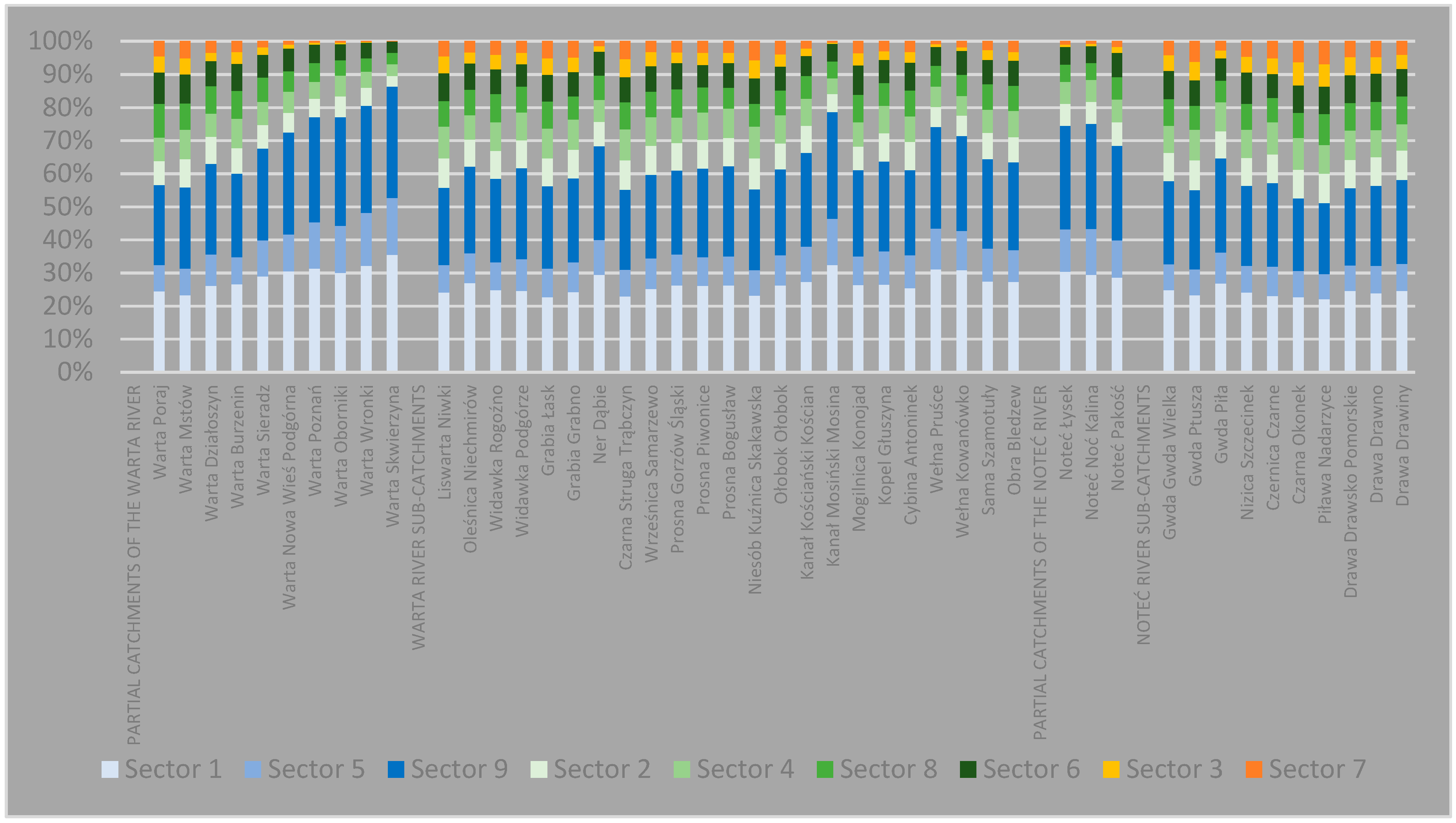
- Sector 1: LHqG–LHqR (X ≤ G62.5%, Y ≤ R62.5%);
- Sector 5: MHqG–MHqR (G62.5% < X ≤ G37.5%, R62.5% < Y ≤ R37.5%);
- Sector 9: HHqG–HHqR (X > G37.5%, Y > R37.5%);
- Sector 2: LHqG–MHqR (X ≤ G62.5%, R62.5% < Y ≤ R37.5%);
- Sector 3: LHqG–HHqR (X ≤ G62.5%, Y > R37.5%);
- Sector 4: MHqG–LHqR (G62.5% < X ≤ G37.5%, Y ≤ R62.5%);
- Sector 6: MHqG–HHqR (G62.5% < X ≤ G37.5%, Y > R37.5%);
- Sector 7: HHqG–LHqR (X > G37.5%, Y ≤ R62.5%);
- Sector 8: HHqG–MHqR (X > G37.5%, R62.5% < Y ≤ R37.5%).
- Probable MAXq with a probability of occurrence of <62.5% was designated as LHq;
- Probable MAXq with a probability of occurrence in a range >62.5% and <37.5% was designated as MHq;
- Probable MAXq with a probability of occurrence >37.5% was designated as HHq.
3. Results
3.1. Mann–Kendall (M–K) Test
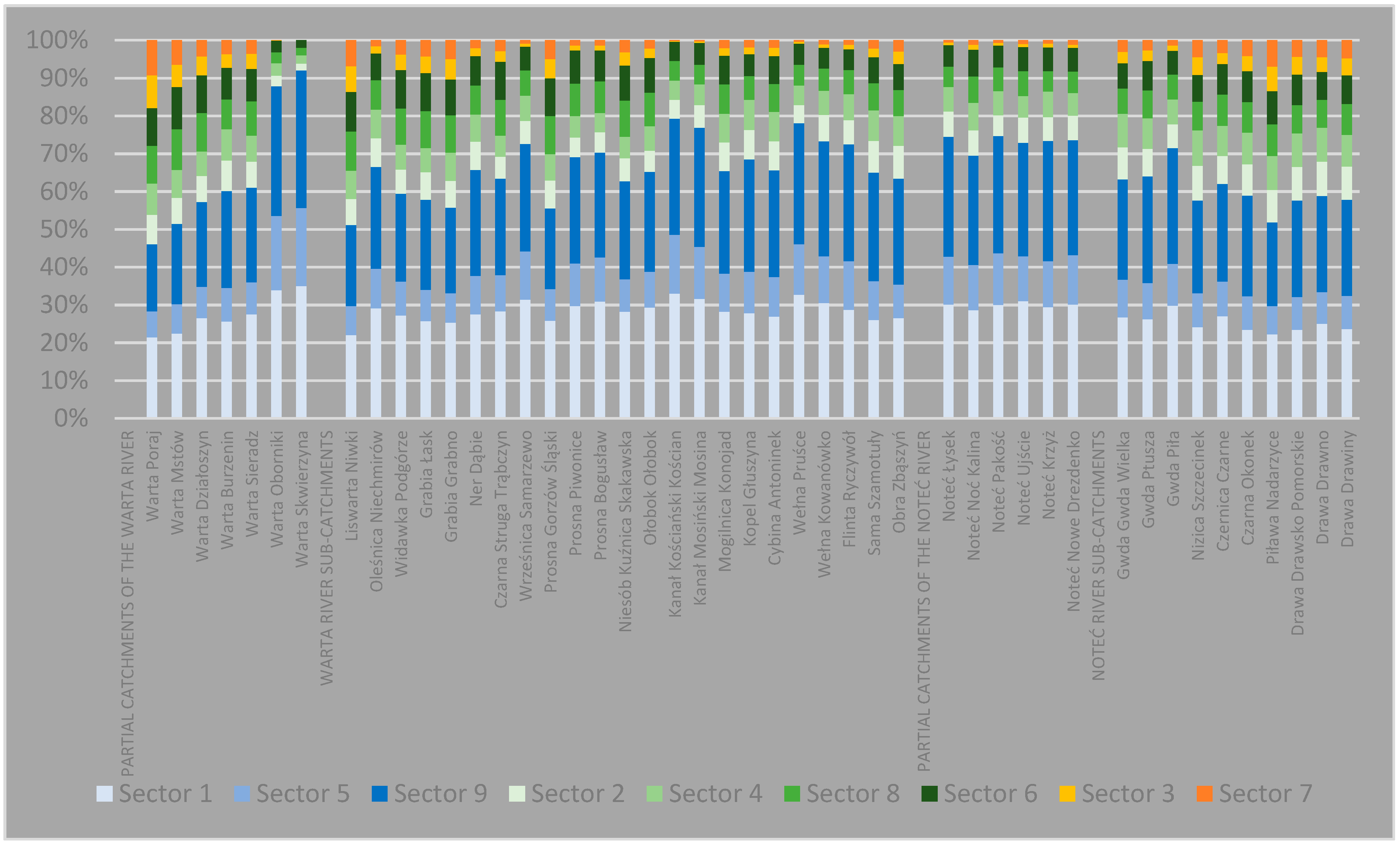
3.2. Synchronous Occurrence of Specific Runoffs
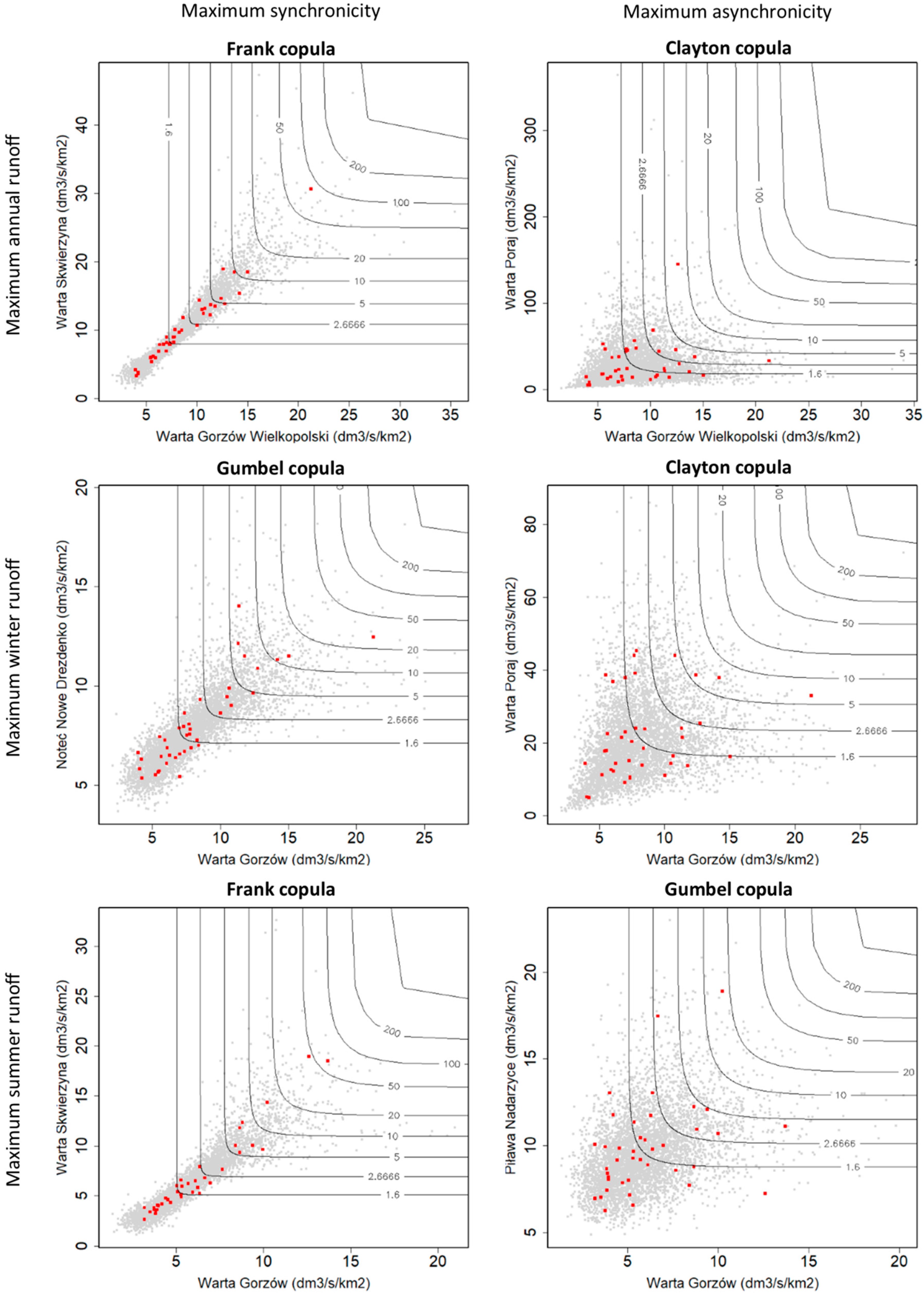
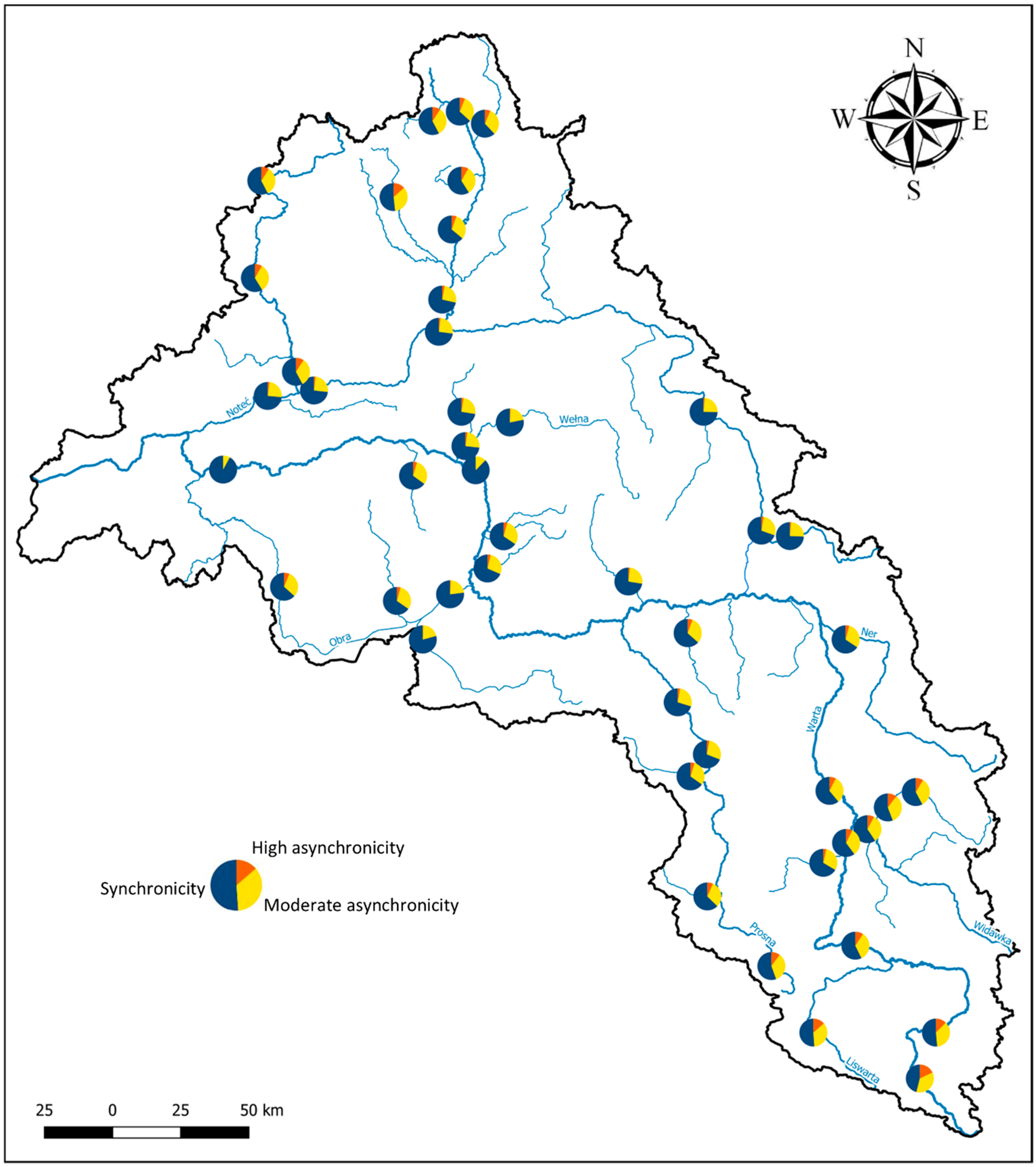
3.2.1. Annual Maximum Specific Runoff (AMAXq)
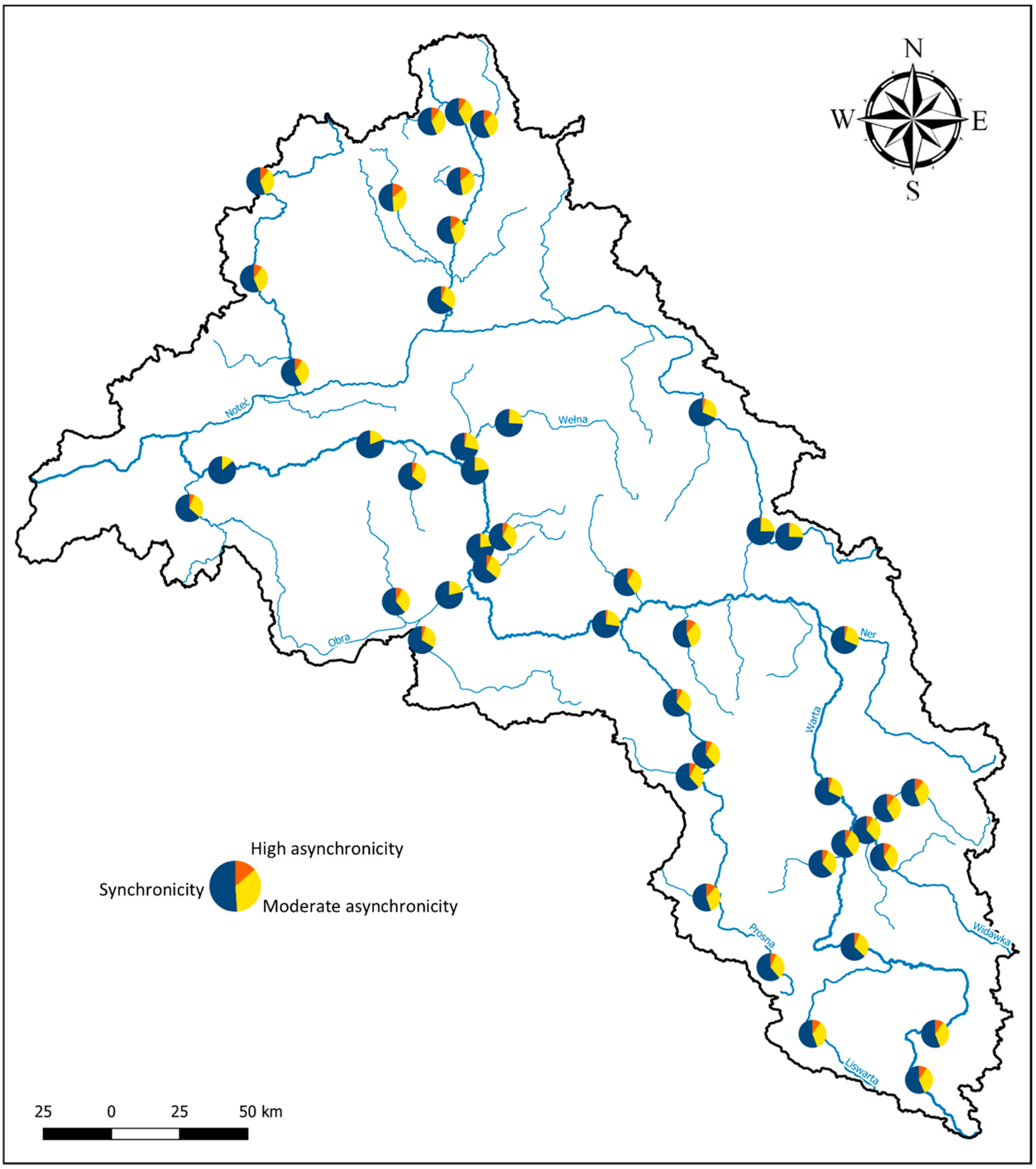
3.2.2. Winter Maximum Specific Runoff (WMAXq) (November–April)
3.2.3. Summer Maximum Specific Runoff (SMAXq) (May–October)
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| No.* | River | Gauge | Maximum | ||
|---|---|---|---|---|---|
| Annual | Winter Half-Year | Summer Half-Year | |||
| 2 | Warta | Poraj | −1.54 | −1.92 | −1.55 |
| 3 | Warta | Mstów | −0.52 | −0.92 | −0.36 |
| 5 | Warta | Działoszyn | −1.43 | −1.72 | −1.57 |
| 6 | Warta | Burzenin | −1.18 | −1.51 | −1.46 |
| 7 | Warta | Sieradz | −1.01 | −1.31 | −1.20 |
| 8 | Warta | Nowa Wieś Podgórna | −2.30 | −2.34 | −0.62 |
| 9 | Warta | Poznań | −2.02 | −2.13 | −0.93 |
| 10 | Warta | Oborniki | −1.89 | −2.00 | −0.83 |
| 11 | Warta | Wronki | −2.11 | −2.11 | −0.96 |
| 12 | Warta | Skwierzyna | −1.90 | −2.02 | −0.94 |
| 13 | Warta | Gorzów Wielkopolski | −1.64 | −1.60 | −1.08 |
| 14 | Liswarta | Niwki | 0.43 | −0.55 | −0.69 |
| 16 | Oleśnica | Niechmirów | −1.26 | −1.21 | −0.92 |
| 17 | Widawka | Szczerców | −3.32 | −3.95 | −2.60 |
| 18 | Widawka | Rogoźno | −2.69 | −2.84 | −1.46 |
| 19 | Widawka | Podgórze | −1.07 | −1.07 | −1.13 |
| 20 | Grabia | Łask | −1.54 | −1.90 | −0.29 |
| 21 | Grabia | Grabno | 0.12 | −0.09 | −0.44 |
| 23 | Ner | Dąbie | −1.82 | −2.06 | −0.98 |
| 26 | Czarna Struga | Trąbczyn | 0.31 | 0.27 | −1.15 |
| 27 | Wrześnica | Samarzewo | −1.22 | −0.63 | −0.96 |
| 28 | Prosna | Gorzów Śląski | −0.48 | −0.21 | −1.95 |
| 29 | Prosna | Mirków | −1.99 | −2.11 | −2.57 |
| 30 | Prosna | Piwonice | −1.50 | −1.60 | −1.61 |
| 31 | Prosna | Bogusław | −1.76 | −1.71 | −1.58 |
| 32 | Niesób | Kuźnica Skakawska | −0.57 | −0.44 | −1.48 |
| 33 | Ołobok | Ołobok | 0.72 | 0.59 | −1.11 |
| 34 | Kanał Kościański | Kościan | −1.78 | −1.32 | −1.31 |
| 35 | Kanał Mosiński | Mosina | −0.64 | −0.01 | −1.05 |
| 36 | Mogilnica | Konojad | −0.34 | −0.02 | −0.65 |
| 37 | Kopel | Głuszyna | 0.14 | 0.93 | 0.31 |
| 38 | Cybina | Antoninek | −0.05 | 0.41 | −0.63 |
| 40 | Wełna | Pruśce | −1.32 | −0.91 | −1.33 |
| 41 | Wełna | Kowanówko | −0.98 | −0.54 | −1.74 |
| 42 | Flinta | Ryczywół | −1.06 | −0.33 | −2.07 |
| 43 | Sama | Szamotuły | −0.96 | −0.44 | −1.06 |
| 44 | Obra | Zbąszyń | −1.36 | −1.36 | −2.69 |
| 45 | Obra | Bledzew | −2.23 | −2.47 | −0.75 |
| 47 | Noteć | Łysek | −1.25 | −0.93 | −0.69 |
| 48 | Noteć | Noć Kalina | −0.35 | −0.26 | −0.29 |
| 49 | Noteć | Pakość | −1.51 | −1.26 | −0.47 |
| 50 | Noteć | Ujście 1 | −1.67 | −1.43 | −2.07 |
| 52 | Noteć | Krzyż | −1.88 | −1.62 | −2.18 |
| 53 | Noteć | Nowe Drezdenko | −1.46 | −1.34 | −2.04 |
| 54 | Noteć | Gębice | −2.24 | −1.79 | −3.34 |
| 55 | Gąsawka | Żnin | −2.23 | −2.07 | −2.05 |
| 57 | Gwda | Gwda Wielka | −0.52 | −0.30 | 0.08 |
| 58 | Gwda | Ptusza | 0.54 | 0.99 | 0.58 |
| 59 | Gwda | Piła | −0.73 | −0.24 | −1.89 |
| 60 | Nizica | Szczecinek | −0.71 | −0.69 | −0.37 |
| 61 | Czernica | Czarne | −1.12 | −1.00 | −1.00 |
| 62 | Czarna | Okonek | −0.72 | −0.38 | −0.84 |
| 63 | Piława | Nadarzyce | −1.33 | −0.73 | −1.58 |
| 64 | Piława | Zabrodzie | −2.56 | −2.40 | −2.47 |
| 65 | Dobrzyca | Wiesiółka | −2.25 | −1.98 | −2.11 |
| 68 | Drawa | Drawsko Pomorskie | −0.94 | −0.98 | −0.35 |
| 69 | Drawa | Drawno | −1.52 | −1.00 | −1.46 |
| 70 | Drawa | Drawiny | −0.90 | −0.79 | −1.91 |
| No. | River | Gauge | ANNUAL (XI–X) MAXIMA | WINTER (XI–IV) MAXIMA | SUMMER (V–X) MAXIMA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S * (%) | MA * (%) | HA * (%) | S * (%) | MA * (%) | HA * (%) | S * (%) | MA * (%) | HA * (%) | |||
| 2 | Warta | Poraj | 46.10 | 35.96 | 17.94 | 48.26 | 37.32 | 14.42 | 56.64 | 33.98 | 9.38 |
| 3 | Warta | Mstów | 51.46 | 36.16 | 12.38 | 60.46 | 32.40 | 7.14 | 55.88 | 34.20 | 9.92 |
| 5 | Warta | Działoszyn | 57.26 | 33.50 | 9.24 | 59.86 | 32.32 | 7.82 | 62.98 | 31.02 | 6.00 |
| 6 | Warta | Burzenin | 60.18 | 32.54 | 7.28 | 57.90 | 33.36 | 8.74 | 60.00 | 33.22 | 6.78 |
| 7 | Warta | Sieradz | 61.02 | 31.48 | 7.50 | 62.48 | 31.04 | 6.48 | 67.66 | 28.34 | 4.00 |
| 8 | Warta | Nowa Wieś Podgórna | - | - | - | - | - | - | 72.48 | 25.32 | 2.20 |
| 9 | Warta | Poznań | - | - | - | - | - | - | 77.16 | 21.92 | 0.92 |
| 10 | Warta | Oborniki | 87.82 | 12.10 | 0.08 | - | - | - | 77.12 | 22.06 | 0.82 |
| 11 | Warta | Wronki | - | - | - | - | - | - | 80.58 | 19.04 | 0.38 |
| 12 | Warta | Skwierzyna | 92.06 | 7.94 | 0.00 | - | - | - | 86.38 | 13.56 | 0.06 |
| 14 | Liswarta | Niwki | 51.12 | 35.22 | 13.66 | 53.14 | 35.02 | 11.84 | 55.74 | 34.6 | 9.66 |
| 16 | Oleśnica | Niechmirów | 66.5 | 29.96 | 3.54 | 73.26 | 24.76 | 1.98 | 62.18 | 31.18 | 6.64 |
| 18 | Widawka | Rogoźno | - | - | - | - | - | - | 58.52 | 33.04 | 8.44 |
| 19 | Widawka | Podgórze | 59.46 | 32.74 | 7.80 | 63.14 | 30.14 | 6.72 | 61.74 | 31.42 | 6.84 |
| 20 | Grabia | Łask | 57.82 | 33.52 | 8.66 | 63.90 | 30.20 | 5.90 | 56.20 | 33.76 | 10.04 |
| 21 | Grabia | Grabno | 55.80 | 33.88 | 10.32 | 58.40 | 33.30 | 8.30 | 58.62 | 32.08 | 9.30 |
| 23 | Ner | Dąbie | 65.70 | 30.12 | 4.18 | - | - | - | 68.36 | 28.50 | 3.14 |
| 26 | Czarna Struga | Trąbczyn | 63.46 | 30.92 | 5.62 | 68.58 | 28.60 | 2.82 | 55.18 | 33.96 | 10.86 |
| 27 | Wrześnica | Samarzewo | 72.56 | 25.76 | 1.68 | 72.24 | 25.16 | 2.60 | 59.70 | 32.78 | 7.52 |
| 28 | Prosna | Gorzów Śląski | 55.60 | 34.32 | 10.08 | 61.44 | 32.34 | 6.22 | 61.00 | 32.44 | 6.56 |
| 30 | Prosna | Piwonice | 69.08 | 28.18 | 2.74 | 75.44 | 23.30 | 1.26 | 61.60 | 31.32 | 7.08 |
| 31 | Prosna | Bogusław | 70.30 | 27.04 | 2.66 | 72.78 | 25.42 | 1.80 | 62.30 | 31.14 | 6.56 |
| 32 | Niesób | Kuźnica Skakawska | 62.70 | 30.66 | 6.64 | 61.76 | 31.68 | 6.56 | 55.24 | 33.58 | 11.18 |
| 33 | Ołobok | Ołobok | 65.22 | 30.12 | 4.66 | 67.56 | 29.04 | 3.40 | 61.38 | 31.06 | 7.56 |
| 34 | Kanał Kościański | Kościan | 79.24 | 20.34 | 0.42 | 75.62 | 22.82 | 1.56 | 66.34 | 29.24 | 4.42 |
| 35 | Kanał Mosinski | Mosina | 76.94 | 22.30 | 0.76 | 73.58 | 24.58 | 1.84 | 78.66 | 20.60 | 0.74 |
| 36 | Mogilnica | Konojad | 65.40 | 30.52 | 4.08 | 67.72 | 28.22 | 4.06 | 61.12 | 31.58 | 7.30 |
| 37 | Kopel | Głuszyna | 68.52 | 27.82 | 3.66 | 69.42 | 27.02 | 3.56 | 63.76 | 30.62 | 5.62 |
| 38 | Cybina | Antoninek | 65.58 | 30.20 | 4.22 | 65.82 | 29.20 | 4.98 | 61.10 | 32.44 | 6.46 |
| 40 | Wełna | Pruśce | 78.08 | 21.04 | 0.88 | 74.26 | 24.04 | 1.70 | 74.12 | 24.18 | 1.70 |
| 41 | Wełna | Kowanówko | 73.32 | 24.62 | 2.06 | 74.56 | 24.10 | 1.34 | 71.38 | 25.76 | 2.86 |
| 42 | Flinta | Ryczywół | 72.54 | 25.08 | 2.38 | 70.84 | 26.58 | 2.58 | - | - | - |
| 43 | Sama | Szamotuły | 64.98 | 30.50 | 4.52 | 63.90 | 29.90 | 6.20 | 64.38 | 30.08 | 5.54 |
| 44 | Obra | Zbąszyń | 63.40 | 30.36 | 6.24 | 66.48 | 28.86 | 4.66 | - | - | - |
| 45 | Obra | Bledzew | - | - | - | - | - | - | 63.44 | 30.72 | 5.84 |
| 47 | Noteć | Łysek | 74.48 | 24.16 | 1.36 | 71.32 | 26.18 | 2.50 | 74.44 | 23.84 | 1.72 |
| 48 | Noteć | Noć Kalina | 69.56 | 27.90 | 2.54 | 63.78 | 29.96 | 6.26 | 75.14 | 23.42 | 1.44 |
| 49 | Noteć | Pakość 2 | 74.66 | 23.96 | 1.38 | 72.54 | 25.18 | 2.28 | 68.40 | 28.20 | 3.40 |
| 50 | Noteć | Ujście 1 | 72.94 | 25.22 | 1.84 | 73.74 | 24.54 | 1.72 | - | - | - |
| 52 | Noteć | Krzyż | 73.36 | 24.72 | 1.92 | 76.30 | 22.40 | 1.30 | - | - | - |
| 53 | Noteć | Nowe Drezdenko | 73.56 | 24.42 | 2.02 | 77.30 | 21.58 | 1.12 | - | - | - |
| 54 | Noteć (Zachodni) | Gębice | - | - | - | 64.88 | 29.78 | 5.34 | - | - | - |
| 57 | Gwda | Gwda Wielka | 63.24 | 30.74 | 6.02 | 65.74 | 29.04 | 5.22 | 57.72 | 33.36 | 8.92 |
| 58 | Gwda | Ptusza | 63.98 | 30.54 | 5.48 | 61.20 | 32.10 | 6.70 | 55.02 | 33.20 | 11.78 |
| 59 | Gwda | Piła | 71.52 | 25.68 | 2.80 | 69.78 | 27.62 | 2.60 | 64.70 | 30.20 | 5.10 |
| 60 | Nizica | Szczecinek | 57.68 | 33.16 | 9.16 | 62.20 | 31.32 | 6.48 | 56.30 | 34.34 | 9.36 |
| 61 | Czernica | Czarne | 62.06 | 31.66 | 6.28 | 62.64 | 31.44 | 5.92 | 57.22 | 32.94 | 9.84 |
| 62 | Czarna | Okonek | 58.96 | 32.94 | 8.10 | 64.42 | 30.22 | 5.36 | 52.56 | 34.12 | 13.32 |
| 63 | Piława | Nadarzyce | 51.82 | 34.78 | 13.40 | 52.46 | 35.02 | 12.52 | 51.16 | 35.18 | 13.66 |
| 68 | Drawa | Drawsko Pomorskie | 57.60 | 33.34 | 9.06 | 63.46 | 31.04 | 5.50 | 55.64 | 34.20 | 10.16 |
| 69 | Drawa | Drawno | 58.82 | 32.86 | 8.32 | 62.50 | 31.06 | 6.44 | 56.36 | 33.96 | 9.68 |
| 70 | Drawa | Drawiny | 57.86 | 32.88 | 9.26 | 64.00 | 29.58 | 6.42 | 58.14 | 33.56 | 8.30 |
References
- Budyko, M.I. The Heat Balance of the Earth’s Surface; U.S. Department of Commerce: Washington, DC, USA, 1958.
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. On the importance of including vegetation dynamics in Budyko’s hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 983–995. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; McVicar, T.R. Assessing climate change induced modification of Penman potential evaporation and runoff sensitivity in a large water-limited basin. J. Hydrol. 2012, 464, 352–362. [Google Scholar] [CrossRef]
- Greve, P.; Gudmundsson, L.; Orlowsky, B.; Seneviratne, S.I. The Budyko framework beyond stationarity. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 6799–6830. [Google Scholar] [CrossRef] [Green Version]
- Carmona, A.M.; Poveda, G.; Sivapalan, M.; Vallejo-Bernal, S.M.; Bustamante, E. A scaling approach to Budyko’s framework and the complementary relationship of evapotranspiration in humid environments: Case study of the Amazon River basin. Hydrol. Earth Syst. Sci. 2016, 20, 589–603. [Google Scholar] [CrossRef] [Green Version]
- Du, L.; Rajib, A.; Merwade, V. Large scale spatially explicit modeling of blue and green water dynamics in a temperate mid-latitude basin. J. Hydrol. 2018, 562, 84–102. [Google Scholar] [CrossRef]
- Sklar, A. Fonction de re’ partition a’ n dimensions et leurs marges; Publications de L’Institute de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Pitera, M. Application of the Copula Function in Finance and Statistics, with Special Regard to the Valuation of Instruments Based on Credit Risk and Debt Instruments. Master’s Thesis, Jagiellonian University, Kraków, Poland, 2010. (In Polish). [Google Scholar]
- Kharoubi-Rakotomalala, C.; Maurer, F. Copulas in Finance Ten Years Later. J. Appl. Bus. Res. 2013, 29, 1555–1566. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; You, J. The joint probability distribution of runoff and sediment and its change characteristics with multi-time scales. J. Hydrol. Hydromech. 2014, 62, 218–225. [Google Scholar] [CrossRef] [Green Version]
- Zhou, N.Q.; Zhao, L.; Shen, X.P. Copula-based Probability Evaluation of Rich-Poor Runoff and Sediment Encounter in Dongting Lake Basin. Sci. Geogr. Sin. 2014, 34, 242–248. (In Chinese) [Google Scholar] [CrossRef]
- You, Q.; Jiang, H.; Liu, Y.; Liu, Z.; Guan, Z. Probability Analysis and Control of River Runoff–sediment Characteristics based on Pair-Copula Functions: The Case of the Weihe River and Jinghe River. Water 2019, 11, 510. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Yu, Z.; Li, G.; Ju, Q. Nonstationary Multivariate Hydrological Frequency Analysis in the Upper Zhanghe River Basin, China. Water 2018, 10, 772. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Gu, S.X.; Zhang, T. Synchronous-Asynchronous Encounter Probability Analysis of High-Low Runoff for Jinsha River, China, using Copulas. MATEC Web Conf. 2018, 246, 01094. [Google Scholar] [CrossRef]
- Plewa, K.; Perz, A.; Wrzesiński, D.; Sobkowiak, L. Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water 2019, 11, 1292. [Google Scholar] [CrossRef] [Green Version]
- Perz, A.; Plewa, K. Synchronous Occurrence of Mean Water Levels of Coastal Lakes and the Baltic Sea. Bad. Fizjogr. Ser. A Geogr. Fiz. 2019, A70, 65–82. (In Polish) [Google Scholar]
- Fan, L.L.; Wang, H.R.; Wang, C.; Lai, W.L.; Zhao, Y. Exploration of Use of Copulas in Analysing the Relationship between Precipitation and Meteorological Drought in Beijing, China. Adv. Meteorol. 2017, 43, 1–11. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Q.; Singh, V.P.; Cui, Y. Copula-based evaluations of drought variations in Guangdong, South China. Nat Hazards 2011, 59, 1533–1546. [Google Scholar] [CrossRef]
- Okoński, B. Radial Growth of Pedunculate Oak and European Ash on Active River Terraces. Hydrologic and Climatic Controls. Infrastruct. Ecol. Rural Areas 2017, III/1, 1075–1091. [Google Scholar] [CrossRef]
- Kaniecki, A. Poznań. History of the City Written with Water; Wydawnictwo PTPN: Poznań, Poland, 2005. (In Polish) [Google Scholar]
- Sobkowiak, L. Changes in water relations in the area of Poznań. In Waters of the Greater Poland Region; Choiński, A., Ed.; Wydawnictwo Naukowe UAM: Poznań, Poland, 2019. (In Polish) [Google Scholar]
- Łabędzki, L.; Kanecka-Geszke, E.; Bąk, B.; Słowińska, S. Estimation of Reference Evapotranspiration Using the FAO Penman-Monteith Method for Climatic Conditions of Poland; Institute of Technology and Life Sciences: Falenty, Poland, 2011; Available online: https://www.intechopen.com/books/evapotranspiration/estimation-of-reference-evapotranspiration-using-the-fao-penman-monteith-method-for-climatic-conditi (accessed on 8 May 2020). [CrossRef] [Green Version]
- Woś, A. Climate of Poland in the Second Half of the 20th Century; Wydawnictwo Naukowe UAM: Poznań, Poland, 2010. (In Polish) [Google Scholar]
- Kundzewicz, Z.W.; Chałupka, M. Low Flows of the River Warta, Poland—Risk and Uncertainty Aspects. Modelling and Management of Sustainable Basin-Scale Water Resource Systems (Proceedings of a Boulder Symposium, July 1995); IAHS Publ.: Wallingford, UK, 1995; No. 231. [Google Scholar]
- Szwed, M.; Karg, G.; Pińskwar, I.; Radziejewski, M.; Graczyk, D.; Kędziora, A.; Kundzewicz, Z.W. Climate change and its effect on agriculture, water resources and human health sectors in Poland. Nat. Hazards Earth Syst. Sci. 2010, 10, 1725–1737. [Google Scholar] [CrossRef]
- Kozek, M. Spatial Variability of Low Flows in the Upper Warta River Catchment. Acta Sci. Pol. Formatio Circumiectus 2018, 17, 67–76. [Google Scholar] [CrossRef]
- Kozek, M.; Tomaszewski, E. Selected Characteristics of Hydrological Drought Progression in the Upper Warta River Catchment. Acta Sci. Pol. Formatio Circumiectus 2018, 17, 77–87. [Google Scholar] [CrossRef]
- Wrzesiński, D. The Seasonal Structure of the River Runoff in Selected Catchments of the Warta River Drainage Basin. Quaest. Geogr. 2000, 21, 97–110. [Google Scholar]
- Wrzesiński, D. Parametrization of Base Flows of the Warta Drainage Basin. Physiogr. Res. West. Pol. Ser. A Phys. Geogr. 2001, 52, 148–191. (In Polish) [Google Scholar]
- Jokiel, P. Seasonal and long-term variability of water balance elements in Central Poland. In Water Resources of Central Poland at the Beginning of the 21st Century; Jokiel, P., Ed.; Wydawnictwo UŁ: Łódź, Poland, 2004. (In Polish) [Google Scholar]
- Graczyk, D.; Kundzewicz, Z.W.; Szwed, M. Variability of change in the flow of the river Warta 1822–1994. In Detecting Changes of Climate and Hydrological Processes; Kundzewicz, Z.W., Radziejewski, M., Eds.; Wydawnictwo Sorus, Research Center for Agricultural and Forest Environment: Poznan, Poland, 2002. (In Polish) [Google Scholar]
- Ilnicki, P.; Farat, R.; Górecki, K.; Lewandowski, P. Impact of climatic change on river discharge in the driest region of Poland. Hydrol. Sci. J. 2014, 59, 1117–1134. [Google Scholar] [CrossRef] [Green Version]
- Miler, A.T. Variability of the Warta River water discharge in the city of Poznań as influenced by the Jeziorsko reservoir. Arch. Environ. Prot. 2015, 41, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Wrzesiński, D.; Perz, A. Trends in river runoff changes. In Waters of the Greater Poland Region; Choiński, A., Ed.; Wydawnictwo Naukowe UAM: Poznań, Poland, 2019. (In Polish) [Google Scholar]
- Wrzesiński, D. Impact of Man-Made Processes on the River Flow with Special Attention Paid to Extreme Phenomena: The Case of The Kiełbaska and Widawka River Catchments. Physiogr. Res. West. Pol. Ser. A Phys. Geogr. 1996, 47, 127–141. (In Polish) [Google Scholar]
- Wrzesiński, D. Detection of changes in the hydrological regime of the Warta in the Poznań profile over the years 1822-2005. In River Outflow and Its Regional Conditions; Wrzesiński, D., Ed.; Bogucki Wydawnictwo Naukowe: Poznań, Poland, 2010. (In Polish) [Google Scholar]
- Kałuża, T.; Sroka, Z.; Lewandowska, J. Impact of Decreasing the Normal Damming Level of the Jeziorsko Reservoir on Low Flows in the Warta River. Acta Sci. Pol. Formatio Circumiectus 2017, 16, 107–122. [Google Scholar] [CrossRef] [Green Version]
- Wrzesiński, D.; Sobkowiak, L. Detection of changes in flow regime of rivers in Poland. J. Hydrol. Hydromech. 2018, 66, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Ilnicki, P.; Górecki, K.; Melcer, B. Eutrophication of Rivers in the Warta Catchment in 1992–2002; University of Life Sciences: Poznań, Poland, 2008. (In Polish) [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Pasławski, Z.; Koczorowska, J.; Olejnik, K. Average Outflow in the Warta River Catchment. Water Manag. 1972, 6, 214–218. (In Polish) [Google Scholar]
- Wrzesiński, D.; Perz, A. Detection of Changes in the Flow Regime of Rivers in Poland. Physiogr. Res. West. Pol. Ser. A Phys. Geogr. 2016, 67, 289–304. [Google Scholar] [CrossRef] [Green Version]
- Dynowska, I. Types of River Regimes in Poland. Zeszyty Naukowe UJ, Prace Geograficzne 28; Wydawnictwo UJ: Kraków, Poland, 1971. (In Polish) [Google Scholar]
- Orsztynowicz, J. Groundwater Outflow of Polish Rivers. Water Manag. 1973, 5, 168–173. (In Polish) [Google Scholar]
- Paszczyk, J.L. The Role of Groundwater in the River Outflow and the Water Balance of Poland; Wydawnictwo UMCS: Lublin, Poland, 1975. (In Polish) [Google Scholar]
- Gutry-Korycka, M. Structure of Poland’s Natural Water Balance (1931–1960. Prace i Studia Geograficzne, 7, Studia Hydrologiczne; Wydawnictwo UW: Warszawa, Poland, 1985. (In Polish) [Google Scholar]
- Tomaszewski, E. Seasonal Changes of the Groundwater Outflow in Poland in 1971–1990. Acta Geogr. Lodz. 2001, 79. (In Polish) [Google Scholar]
- Bogdanowicz, R. Hydrological Conditions of Transport of Selected Nitrogen and Phosphorus Compounds by the Oder and Vistula Rivers and the Przymorze Rivers to the Baltic Sea; Wydawnictwo UG: Gdańsk, Poland, 2004. (In Polish) [Google Scholar]
- Dynowska, I. Regime of River Flow Sheet: 32.3. In Atlas of the Republic of Poland; IG PZ PAN: Warsaw, Poland, 1994. (In Polish) [Google Scholar]
- Rotnicka, J. A Typology of Hydrological Periods for Use in River Regime Studies. Quaest. Geogr. 1993, 15/16, 77–95. [Google Scholar]
- Kendall, M. Rank Correlation Methods; Griffin & Co.: London, UK, 1975. [Google Scholar]
- Önöz, B.; Bayazit, M. The power of statistical tests for trend detection. Turk. J. Eng. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Partal, T.; Küçük, M. Long-term trend analysis using discrete wavelet components of annual precipitations measurements in Marmara region (Turkey). Phys. Chem. Earth Parts A/B/C 2006, 31, 1189–1200. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Flood Frequency Analysis Using Copula with Mixed Marginal Distributions; Water Resources Research Report, Report No: 055; The University of Western Ontario: London, ON, Canada, 2007. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–722. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer Series in Statistics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Chen, L.; Guo, S.L. Copulas and Its Application in Hydrology and Water Resources; Springer Water; Springer: Singapore, 2019. [Google Scholar]
- Genest, C.; Favre, A.-C. Everything you always wanted to know about copula Modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.-P. Statistical inference procedure for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Ozga-Zielińska, M.; Brzeziński, J.; Ozga-Zieliński, B. Rules for Calculating the Maximum Annual Flows with a Specified Probability of Exceedance in Designing Hydrotechnical Facilities; Long Flow Measurement Series; Wydawnictwo IMGW: Warsaw, Poland, 1999. (In Polish) [Google Scholar]
- Kuchment, L.S.; Demidov, V.N. On the application of copula theory for determination of probabilistic characteristics of springflood. Russ. Meteorol. Hydrol. 2013, 38, 263–271. [Google Scholar] [CrossRef]

| No. | River | Gauge | Catchment Area A (km2) | Total Flow H (mm) | Groundwater Flow | Flow Variability (Cv) | Flow Irregularity | Type of River Regime * | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm) | (%) | Daily | Annual | Min | Max | |||||||
| 1 | Warta | Kręciwilk | 66 | 384 | 262 | 68.2 | 0.610 | 0.226 | 0.205 | 0.548 | 44 | 1 |
| 2 | Warta | Poraj | 390 | 233 | 125 | 56.3 | 0.881 | 0.379 | 0.295 | 0.838 | 101 | 1 |
| 3 | Warta | Mstów | 988 | 205 | 123 | 60.3 | 0.761 | 0.317 | 0.250 | 0.579 | 71 | 2 |
| 4 | Warta | Bobry | 1800 | 193 | 124 | 66.1 | 0.668 | 0.317 | 0.457 | 0.573 | 245 | 2 |
| 5 | Warta | Działoszyn | 4088 | 192 | 132 | 66.8 | 0.647 | 0.265 | 0.234 | 0.552 | 35 | 2 |
| 6 | Warta | Burzenin | 5437 | 186 | 125 | 67.0 | 0.630 | 0.274 | 0.252 | 0.599 | 35 | 2 |
| 7 | Warta | Sieradz | 8140 | 177 | 125 | 67.7 | 0.599 | 0.248 | 0.204 | 0.495 | 27 | 2 |
| 8 | Warta | Nowa Wieś Podgórna | 20,763 | 146 | 95 | 64.7 | 0.612 | 0.277 | 0.281 | 0.527 | 29 | 2 |
| 9 | Warta | Poznań | 25,126 | 128 | 87 | 64.3 | 0.621 | 0.295 | 0.267 | 0.518 | 29 | 2 |
| 10 | Warta | Oborniki | 26,789 | 135 | 87 | 64.1 | 0.626 | 0.296 | 0.278 | 0.489 | 30 | 2 |
| 11 | Warta | Wronki | 30,684 | 129 | 83 | 64.5 | 0.636 | 0.309 | 0.249 | 0.503 | 25 | 2 |
| 12 | Warta | Skwierzyna | 31,268 | 127 | 88 | 66.2 | 0.620 | 0.303 | 0.254 | 0.505 | 25 | 2 |
| 13 | Warta | Gorzów Wielkopolski | 52,186 | 127 | 97 | 74.0 | 0.520 | 0.264 | 0.251 | 0.408 | 17 | 2 |
| 14 | Liswarta | Niwki | 218 | 221 | 114 | 52.4 | 0.931 | 0.249 | 0.336 | 0.431 | 168 | 2 |
| 15 | Liswarta | Kule | 1557 | 159 | 93 | 56.0 | 0.869 | 0.297 | 0.345 | 0.607 | 115 | 2 |
| 16 | Oleśnica | Niechmirów | 592 | 132 | 56 | 42.1 | 1.362 | 0.443 | 0.399 | 0.721 | 312 | 3 |
| 17 | Widawka | Szczerców | 721 | 249 | 207 | 83.1 | 0.410 | 0.250 | 0.350 | 0.670 | 34 | 2 |
| 18 | Widawka | Rogoźno | 1268 | 208 | 170 | 74.7 | 0.524 | 0.244 | 0.302 | 0.525 | 31 | 1 |
| 19 | Widawka | Podgórze | 2354 | 186 | 128 | 65.9 | 0.689 | 0.260 | 0.327 | 0.491 | 54 | 1 |
| 20 | Grabia | Łask | 472 | 180 | 96 | 53.4 | 1.061 | 0.305 | 0.393 | 0.575 | 192 | 3 |
| 21 | Grabia | Grabno | 811 | 165 | 82 | 48.3 | 1.110 | 0.329 | 0.334 | 0.523 | 115 | 3 |
| 22 | Nieciecz | Widawa | 242 | 131 | 48 | 36.9 | 1.468 | 0.542 | 0.918 | 0.716 | 10,267 | 3 |
| 23 | Ner | Dąbie | 1712 | 189 | 113 | 55.5 | 0.720 | 0.275 | 0.378 | 0.417 | 116 | 2 |
| 24 | Kiełbaska | Kościelec | 476 | 167 | 127 | 67.8 | 0.547 | 0.223 | 0.333 | 0.486 | 34 | 2 |
| 25 | Powa | Posoka | 332 | 113 | 44 | 38.6 | 1.335 | 0.434 | 0.658 | 0.861 | 3550 | 3 |
| 26 | Czarna Struga | Trąbczyn | 423 | 115 | 40 | 34.2 | 1.434 | 0.489 | 0.813 | 0.721 | 3043 | 3 |
| 27 | Wrześnica | Samarzewo | 360 | 93 | 37 | 39.0 | 1.329 | 0.545 | 0.593 | 0.684 | 278 | 3 |
| 28 | Prosna | Gorzów Śląski | 164 | 171 | 92 | 53.9 | 1.358 | 0.270 | 0.307 | 0.703 | 407 | 2 |
| 29 | Prosna | Mirków | 1255 | 130 | 64 | 47.7 | 1.018 | 0.286 | 0.380 | 0.541 | 156 | 2 |
| 30 | Prosna | Piwonice | 2938 | 123 | 68 | 52.1 | 0.959 | 0.316 | 0.386 | 0.574 | 127 | 2 |
| 31 | Prosna | Bogusław | 4304 | 118 | 61 | 49.5 | 0.968 | 0.342 | 0.356 | 0.579 | 131 | 2 |
| 32 | Niesób | Kuźnica Skakawska | 246 | 123 | 67 | 52.4 | 1.052 | 0.283 | 0.401 | 0.717 | 554 | 3 |
| 33 | Ołobok | Ołobok | 447 | 115 | 47 | 41.6 | 1.287 | 0.386 | 0.445 | 0.547 | 550 | 3 |
| 34 | Kanał Kościański | Kościan | 1247 | 98 | 43 | 44.6 | 1.004 | 0.506 | 0.870 | 0.603 | 334 | 3 |
| 35 | Kanał Mosinski | Mosina | 2492 | 78 | 40 | 51.2 | 1.021 | 0.513 | 0.727 | 0.546 | 244 | 3 |
| 36 | Mogilnica | Konojad | 663 | 77 | 26 | 33.1 | 1.440 | 0.653 | 0.704 | 0.797 | 1325 | 3 |
| 37 | Kopel | Głuszyna | 369 | 105 | 36 | 36.3 | 1.288 | 0.532 | 0.594 | 0.611 | 705 | 3 |
| 38 | Cybina | Antoninek | 171 | 107 | 58 | 54.5 | 0.936 | 0.442 | 0.834 | 0.541 | 1707 | 3 |
| 39 | Główna | Wierzenica | 222 | 102 | 38 | 37.5 | 1.185 | 0.593 | 0.670 | 0.679 | 1800 | 3 |
| 40 | Wełna | Pruśce | 1130 | 95 | 52 | 52.7 | 1.032 | 0.556 | 0.681 | 0.747 | 410 | 3 |
| 41 | Wełna | Kowanówko | 2597 | 107 | 53 | 50.7 | 1.068 | 0.550 | 0.638 | 0.774 | 182 | 3 |
| 42 | Flinta | Ryczywół | 276 | 75 | 35 | 46.5 | 1.170 | 0.522 | 0.883 | 0.555 | 728 | 3 |
| 43 | Sama | Szamotuły | 395 | 85 | 38 | 43.3 | 1.362 | 0.673 | 0.802 | 0.945 | 1025 | 3 |
| 44 | Obra | Zbąszyń | 1291 | 111 | 56 | 53.1 | 0.842 | 0.431 | 0.730 | 0.407 | 158 | 3 |
| 45 | Obra | Bledzew | 2618 | 111 | 60 | 56.0 | 0.657 | 0.339 | 0.537 | 0.320 | 49 | 2 |
| 46 | Paklica | Międzyrzecz | 279 | 114 | 64 | 56.2 | 0.615 | 0.256 | 0.692 | 0.359 | 166 | 2 |
| 47 | Noteć | Łysek | 306 | 89 | 43 | 49.6 | 1.126 | 0.568 | 0.814 | 0.773 | 11,100 | 3 |
| 48 | Noteć | Noć Kalina | 440 | 99 | 54 | 54.1 | 0.977 | 0.470 | 0.559 | 0.627 | 334 | 3 |
| 49 | Noteć | Pakość 2 | 1620 | 110 | 63 | 59.5 | 0.979 | 0.588 | 0.562 | 0.878 | 131 | 2 |
| 50 | Noteć | Ujście 1 | 6308 | 94 | 53 | 56.0 | 0.719 | 0.437 | 0.472 | 0.432 | 52 | 2 |
| 51 | Noteć | Ujście 2 | 11,255 | 132 | 97 | 73.3 | 0.462 | 0.268 | 0.253 | 0.292 | 11 | 2 |
| 52 | Noteć | Krzyż | 12,610 | 134 | 98 | 72.9 | 0.451 | 0.261 | 0.255 | 0.275 | 11 | 2 |
| 53 | Noteć | Nowe Drezdenko | 15,970 | 144 | 116 | 78.1 | 0.394 | 0.216 | 0.202 | 0.270 | 9 | 2 |
| 54 | Noteć (Western) | Gębice | 182 | 109 | 55 | 54.8 | 0.926 | 0.519 | 0.747 | 0.742 | 393 | 2 |
| 55 | Gąsawka | Żnin | 148 | 116 | 66 | 55.5 | 0.952 | 0.544 | 0.787 | 0.671 | 1713 | 3 |
| 56 | Łobżonka | Wyrzysk | 635 | 127 | 60 | 49.6 | 0.880 | 0.400 | 0.480 | 0.470 | 352 | 2 |
| 57 | Gwda | Gwda Wielka | 426 | 259 | 205 | 79.2 | 0.525 | 0.282 | 0.259 | 0.363 | 23 | 2 |
| 58 | Gwda | Ptusza | 2052 | 174 | 122 | 69.3 | 0.378 | 0.186 | 0.183 | 0.246 | 10 | 2 |
| 59 | Gwda | Piła | 4704 | 181 | 144 | 77.6 | 0.353 | 0.177 | 0.218 | 0.244 | 8 | 2 |
| 60 | Nizica | Szczecinek | 161 | 165 | 104 | 63.9 | 0.761 | 0.339 | 0.539 | 0.381 | 2280 | 2 |
| 61 | Czernica | Czarne | 411 | 211 | 147 | 69.9 | 0.597 | 0.270 | 0.191 | 0.487 | 18 | 2 |
| 62 | Czarna | Okonek | 104 | 113 | 61 | 53.5 | 0.993 | 0.331 | 0.440 | 0.648 | 209 | 2 |
| 63 | Piława | Nadarzyce | 347 | 232 | 205 | 88.1 | 0.283 | 0.153 | 0.277 | 0.230 | 10 | 1 |
| 64 | Piława | Zabrodzie | 1368 | 178 | 151 | 84.1 | 0.330 | 0.190 | 0.240 | 0.270 | 8 | 1 |
| 65 | Dobrzyca | Wiesiółka | 892 | 161 | 128 | 82.3 | 0.401 | 0.207 | 0.218 | 0.445 | 11 | 2 |
| 66 | Głomia | Dobrzyca | 569 | 157 | 95 | 60.4 | 0.717 | 0.272 | 0.379 | 0.553 | 164 | 2 |
| 67 | Drawa | Stare Drawsko | 67 | 201 | 104 | 51.4 | 1.064 | 0.476 | 0.478 | 0.655 | 240 | 3 |
| 68 | Drawa | Drawsko Pomorskie | 609 | 215 | 161 | 71.1 | 0.554 | 0.236 | 0.289 | 0.334 | 22 | 2 |
| 69 | Drawa | Drawno | 1267 | 226 | 184 | 81.4 | 0.384 | 0.189 | 0.238 | 0.253 | 10 | 2 |
| 70 | Drawa | Drawiny | 3298 | 205 | 182 | 88.9 | 0.280 | 0.123 | 0.194 | 0.233 | 6 | 1 |
| 71 | Mierzęcka Struga | Mierzęcin | 533 | 104 | 83 | 79.5 | 0.500 | 0.223 | 0.426 | 0.305 | 69 | 2 |
| 72 | Miała | Chełst | 292 | 136 | 108 | 79.6 | 0.372 | 0.201 | 0.362 | 0.269 | 44 | 1 |
| Copula Family | ||||
|---|---|---|---|---|
| Clayton | ||||
| Gumbel–Hougaard | ||||
| Frank |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perz, A.; Sobkowiak, L.; Wrzesiński, D. Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland. Water 2020, 12, 1782. https://doi.org/10.3390/w12061782
Perz A, Sobkowiak L, Wrzesiński D. Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland. Water. 2020; 12(6):1782. https://doi.org/10.3390/w12061782
Chicago/Turabian StylePerz, Adam, Leszek Sobkowiak, and Dariusz Wrzesiński. 2020. "Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland" Water 12, no. 6: 1782. https://doi.org/10.3390/w12061782
APA StylePerz, A., Sobkowiak, L., & Wrzesiński, D. (2020). Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland. Water, 12(6), 1782. https://doi.org/10.3390/w12061782





