A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach
Abstract
1. Introduction
- To apply data preprocessing techniques to denoise water consumption time series and select best model input scenario.
- To evaluate the performance of an adaptive neuro fuzzy inference system (ANFIS) to predict mid-term municipal water demand based on several time intervals of water consumption.
- To apply a hybrid crow search algorithm and artificial neural network (CSA-ANN) to evaluate the results of the ANFIS model.
- To increase the predicting range and reduce the uncertainty of outcomes for urban water demands by testing different hyperparameters, such as the various types and orders of the wavelet denoising technique and different kinds and numbers of membership functions of the ANFIS technique.
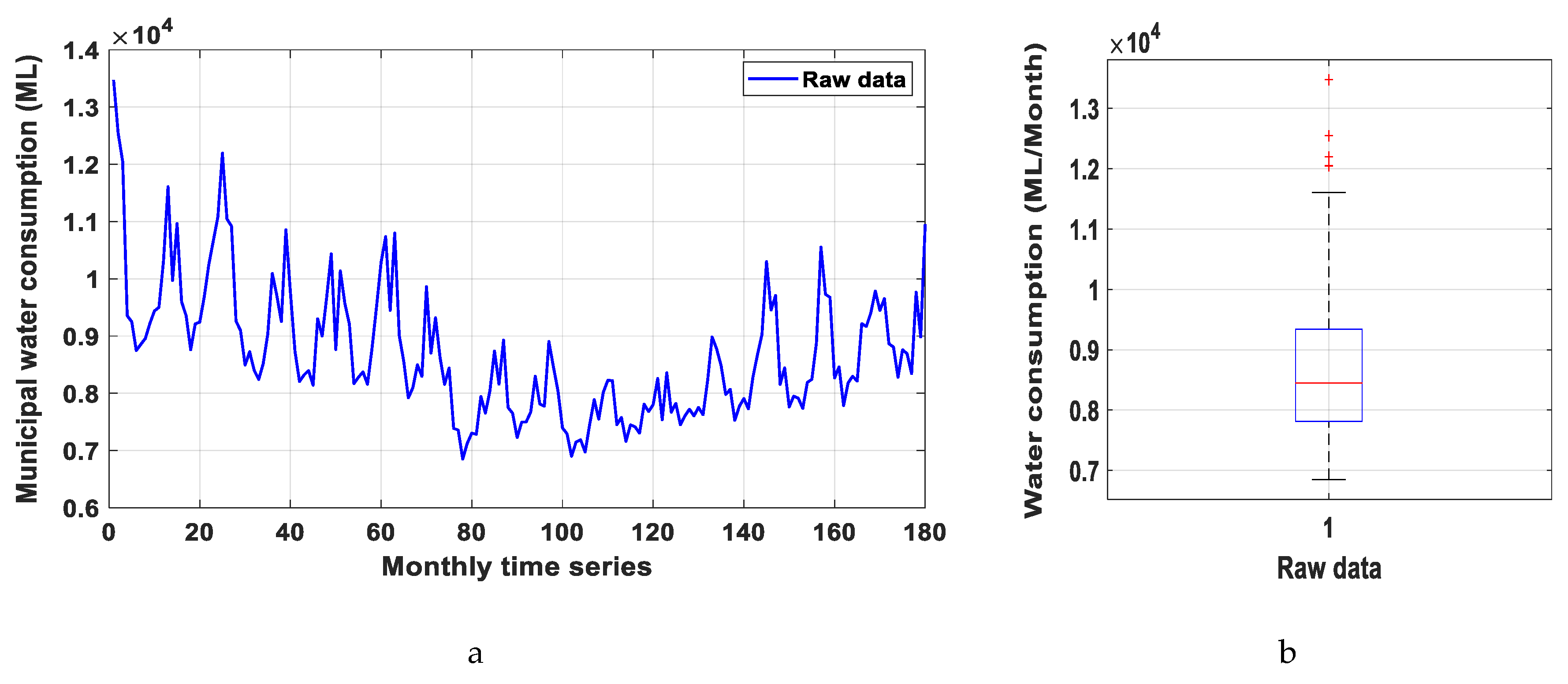
2. Study Area and Data Set
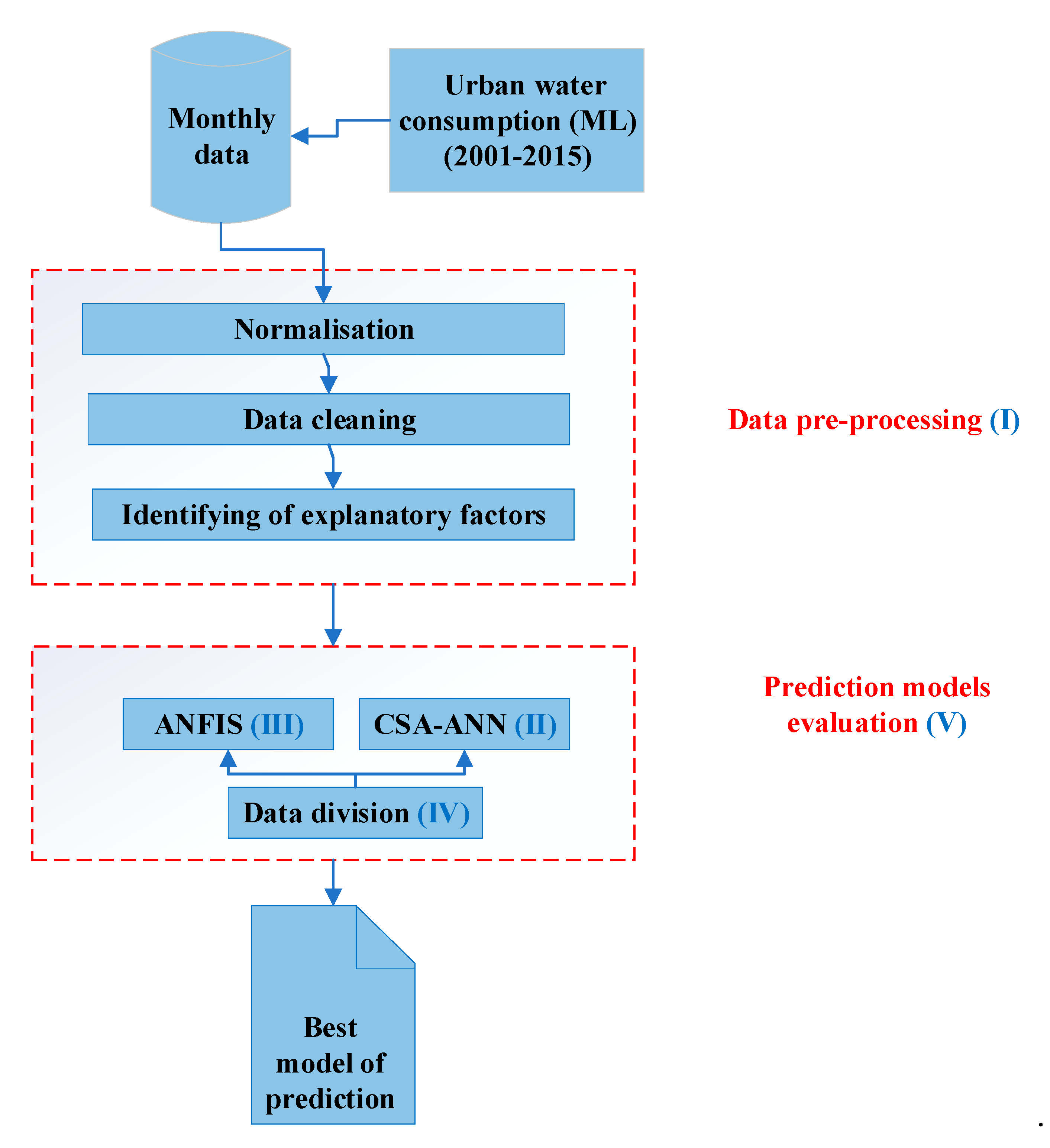
3. Methodology
3.1. Data Preprocessing
3.1.1. Normalization
3.1.2. Data Cleaning
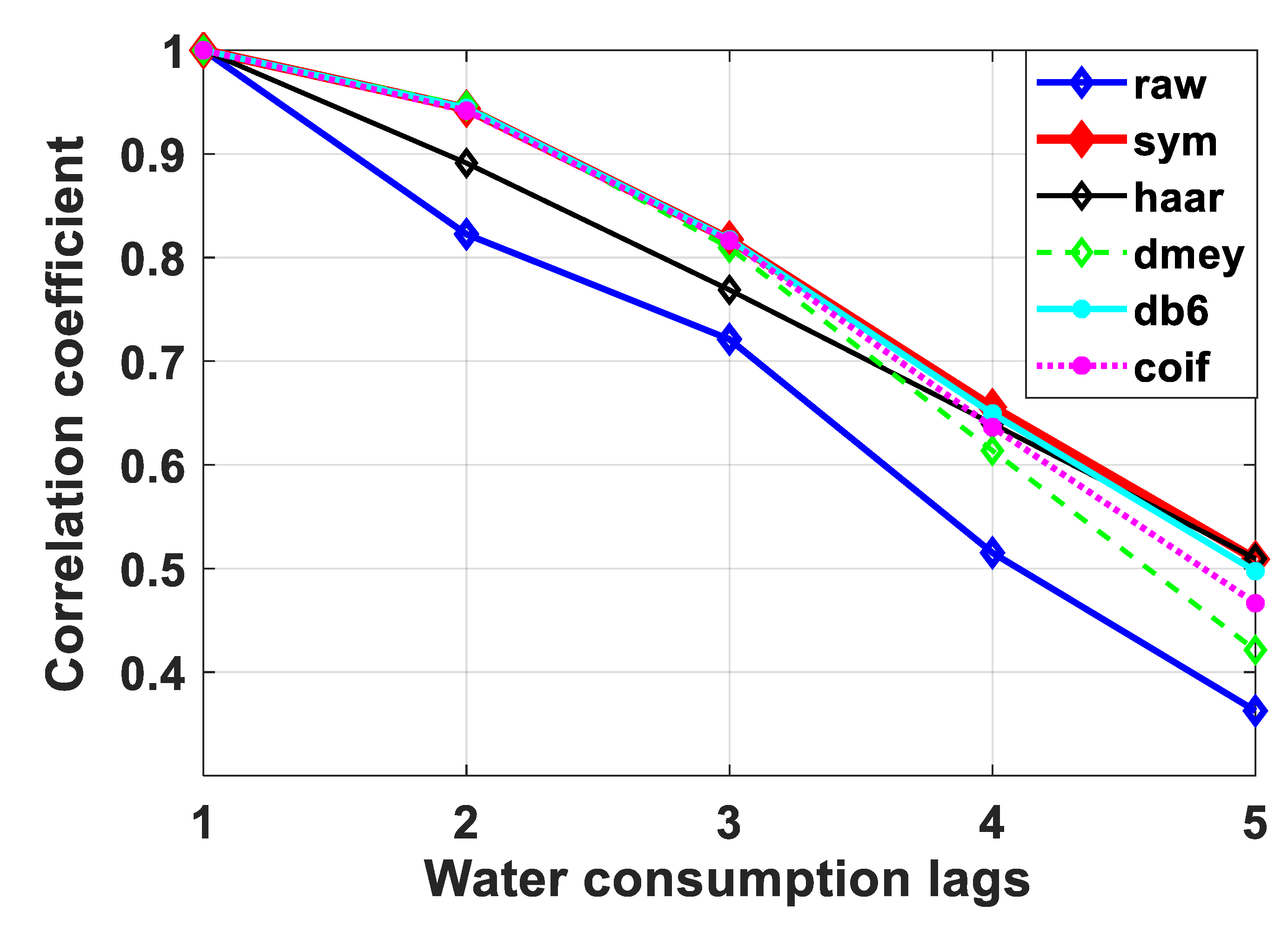
Wavelet Transform
3.1.3. Identifying of Explanatory Factors
3.2. Hybrid Metaheuristic Algorithm–Artificial Neural Network
3.2.1. Artificial Neural Networks (ANNs)
3.2.2. Crow Search Algorithm (CSA)
3.2.3. Combined Crow Search Algorithm-Based Artificial Neural Network
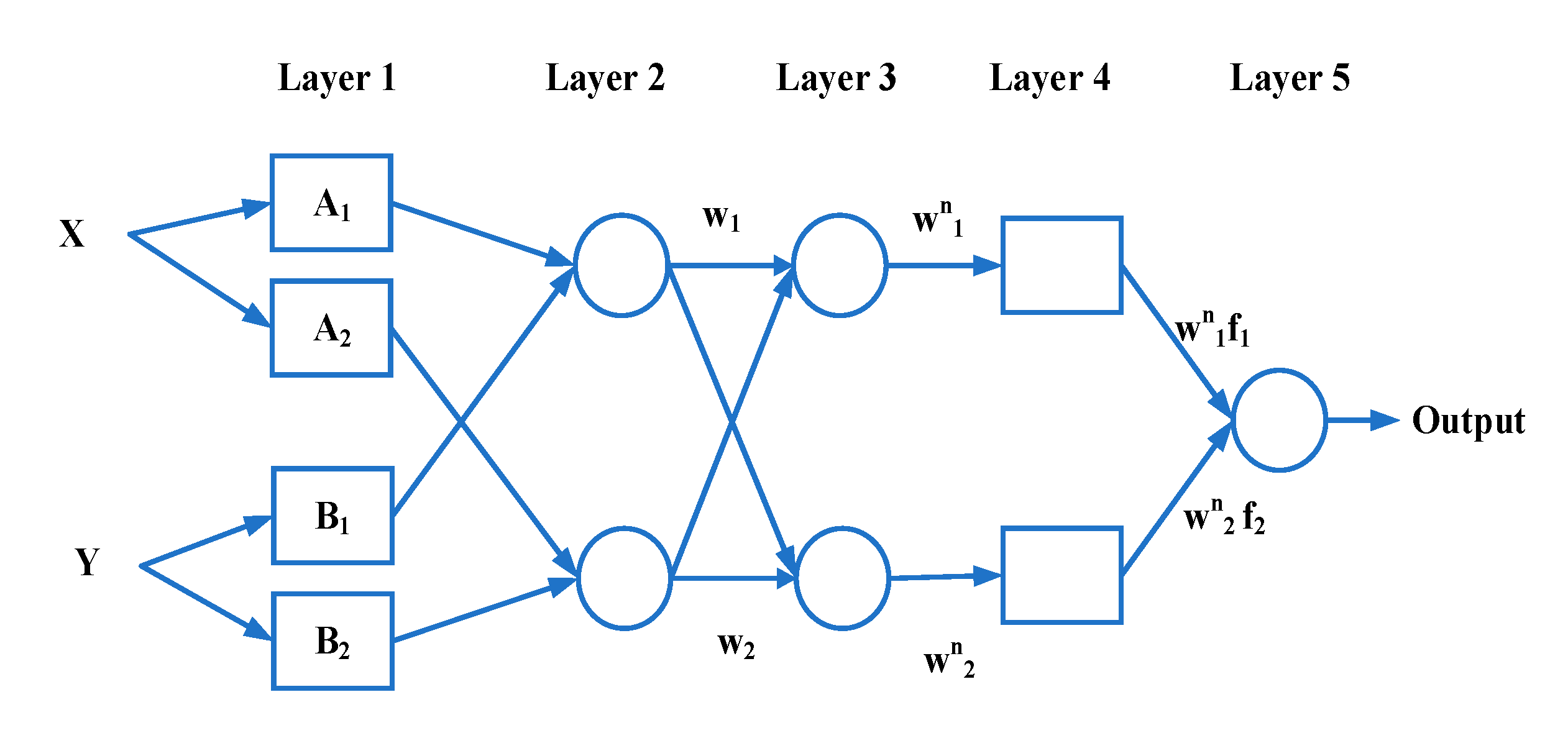
3.3. Adaptive Neuro Fuzzy Inference System (ANFIS)
3.4. Data Division
3.5. Model Performances Criteria
4. Results and Discussion
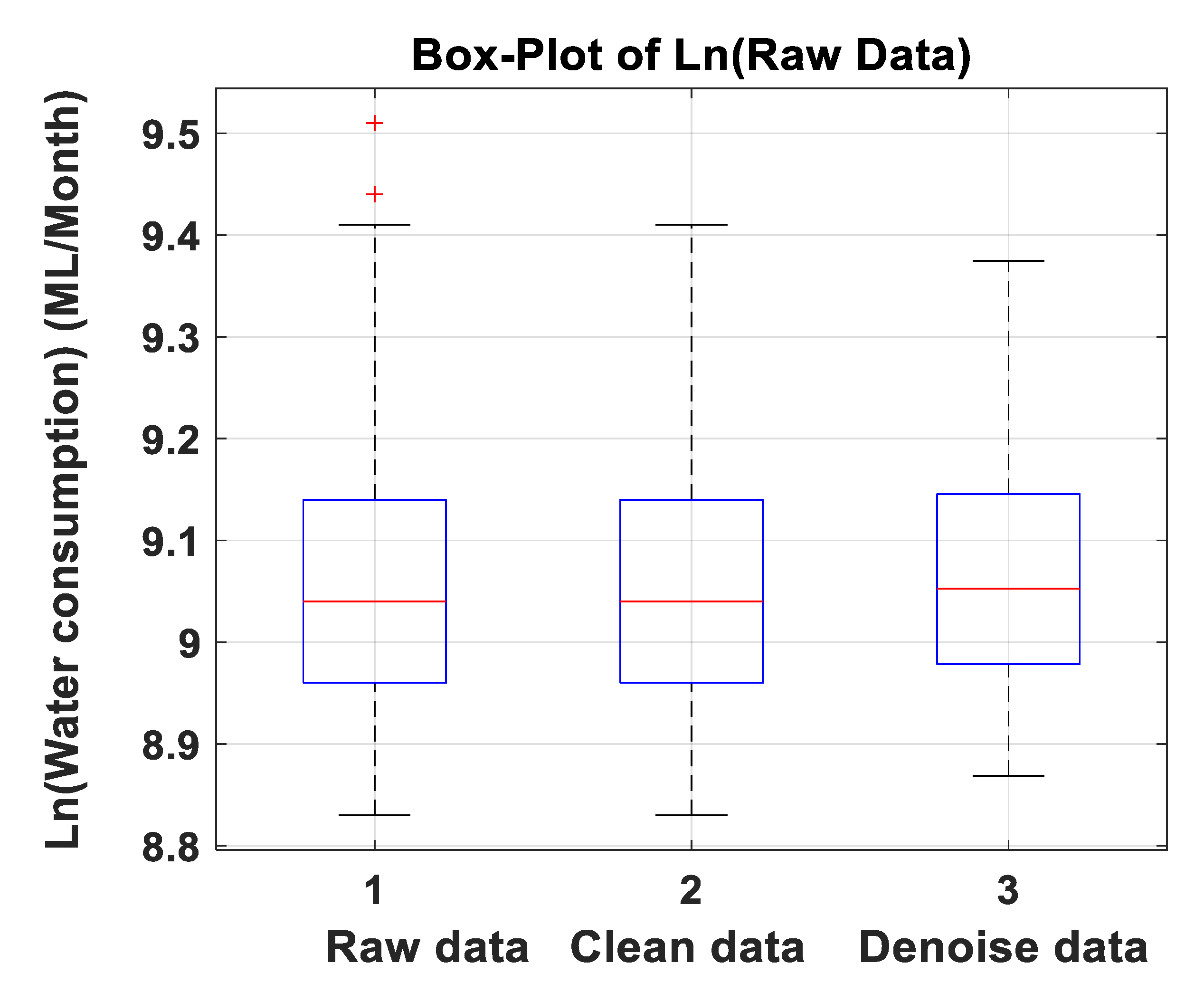
4.1. Data Preprocessing Analysis
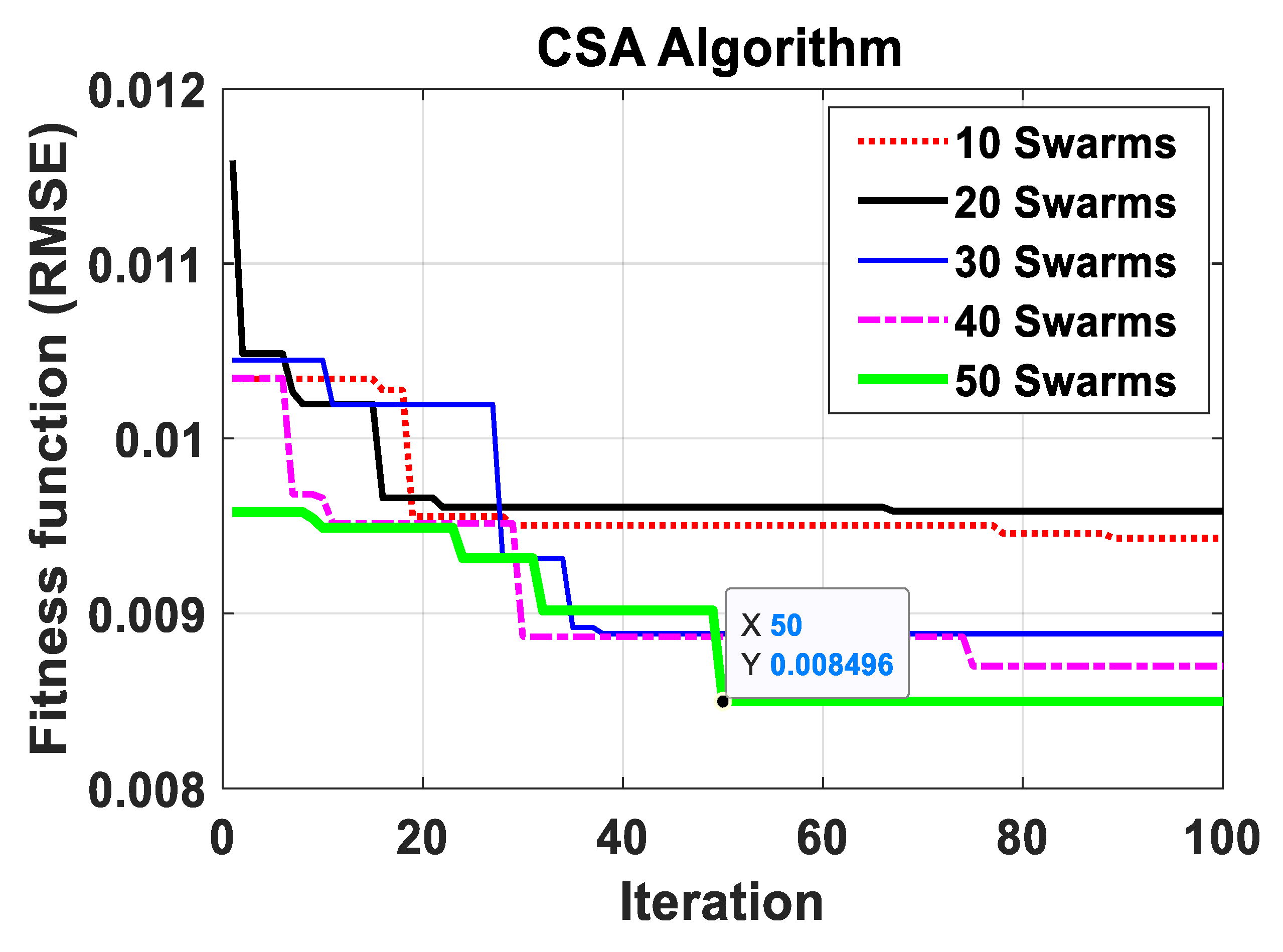
4.2. Preparation and Configuration of the Techniques
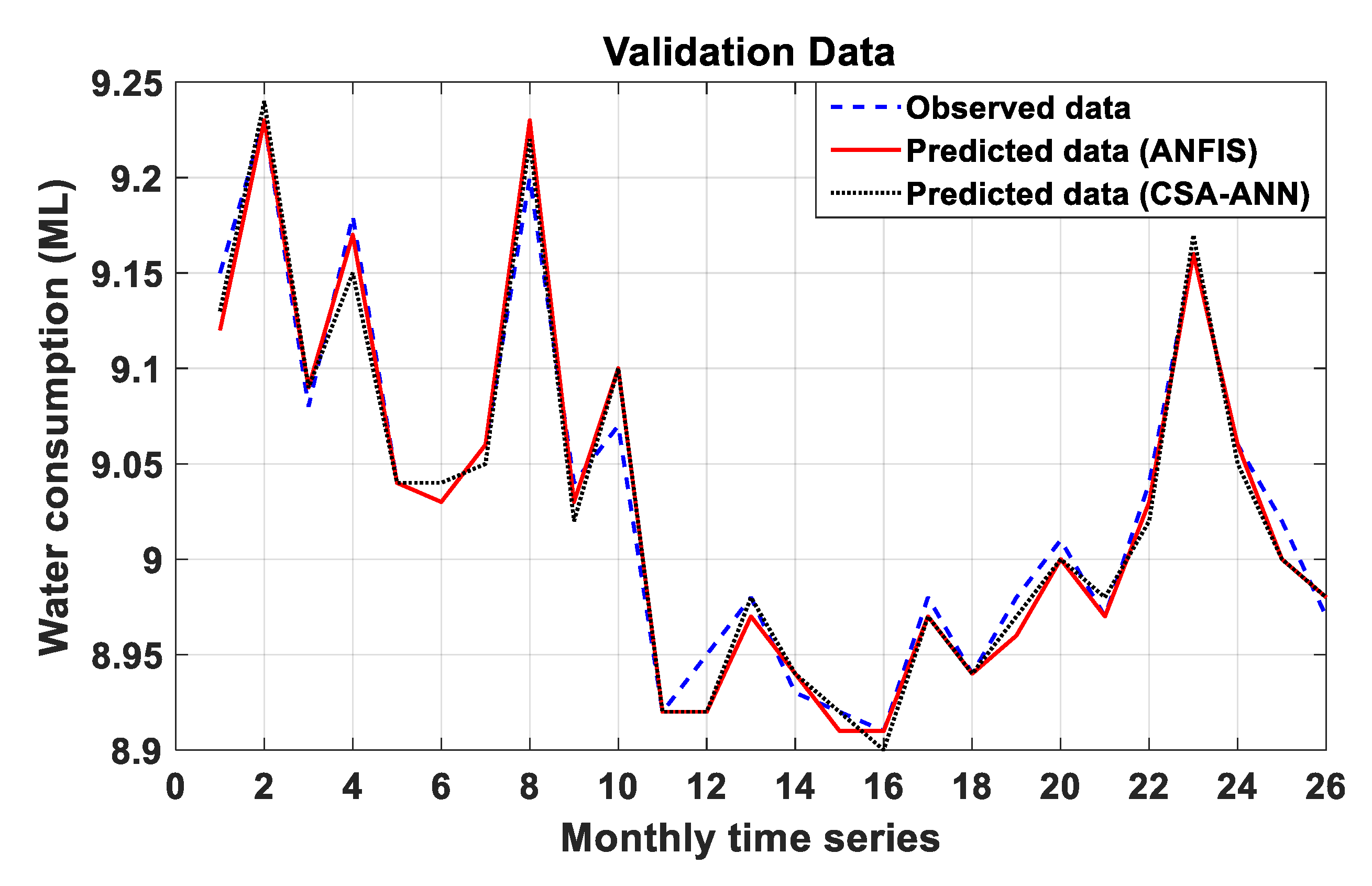
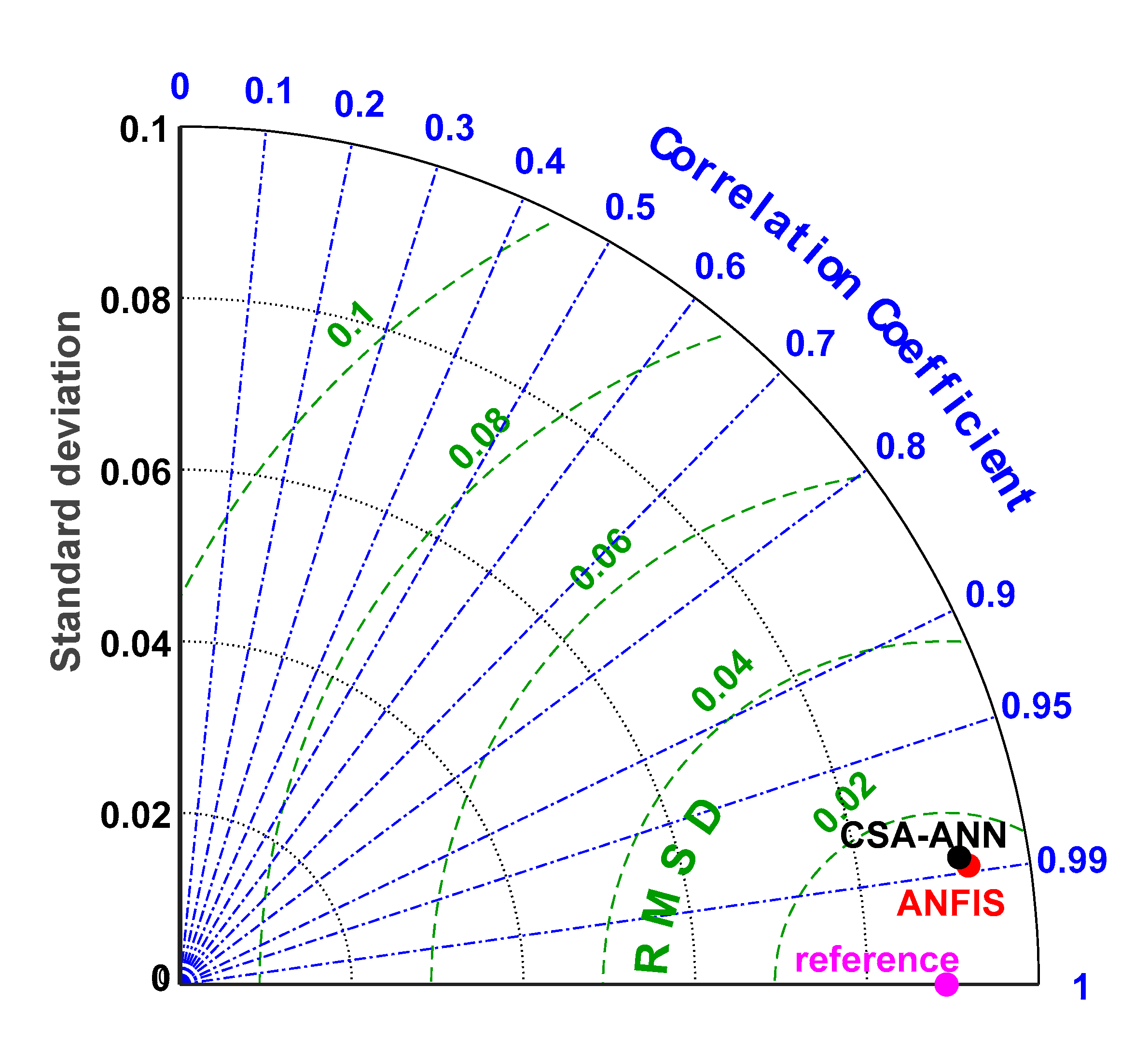
4.3. Evaluating and Comparing the Performance of the Techniques
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mashhadi Ali, A.; Shafiee, M.E.; Berglund, E.Z. Agent-based modeling to simulate the dynamics of urban water supply: Climate, population growth, and water shortages. Sustain. Cities Soc. 2017, 28, 420–434. [Google Scholar] [CrossRef]
- Hashim, K.S.; Hussein, A.H.; Zubaidi, S.L.; Kot, P.; Kraidi, L.; Alkhaddar, R.; Shaw, A.; Alwash, R. Effect of Initial Ph Value on The Removal of Reactive Black Dye from Water by Electrocoagulation (EC) Method. J. Phys. Conf. Ser. 2019, 1294, 1–6. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Chowdhury, R.K. A Comparative Assessment of Variable Selection Methods in Urban Water Demand Forecasting. Water 2018, 10, 419. [Google Scholar] [CrossRef]
- Omran, I.I.; Al-Saati, N.H.; Hashim, K.S.; Al-Saati, Z.N.; Kot, P.; Khaddar, R.A.; Al-Jumeily, D.; Shaw, A.; Ruddock, F.; Aljefery, M. Assessment of heavy metal pollution in the Great Al-Mussaib irrigation channel. Desalin. Water Treat. 2019, 168, 165–174. [Google Scholar] [CrossRef]
- Hashim, K.S.; Al-Saati, N.H.; Hussein, A.H.; Al-Saati, Z.N. An Investigation into The Level of Heavy Metals Leaching from Canal-Dreged Sediment: A Case Study Metals Leaching from Dreged Sediment. In Proceedings of the First International Conference on Materials Engineering & Science, Istanbul, Turkey, 8–9 August 2018; pp. 12–22. [Google Scholar]
- Hashim, K.S.; Kot, P.; Zubaidi, S.L.; Alwash, R.; Al Khaddar, R.; Shaw, A.; Al-Jumeily, D.; Aljefery, M.H. Energy Efficient Electrocoagulation Using Baffle-Plates Electrodes for Efficient Escherichia Coli Removal from Wastewater. J. Water Process. Eng. 2020, 33, 1–7. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Gharghan, S.K.; Ahmed, M.S.; Hashim, K. A Method for Predicting Long-Term Municipal Water Demands Under Climate Change. Water Resour. Manag. 2020, 34, 1265–1279. [Google Scholar] [CrossRef]
- Anele, A.; Todini, E.; Hamam, Y.; Abu-Mahfouz, A. Predictive Uncertainty Estimation in Water Demand Forecasting Using the Model Conditional Processor. Water 2018, 10, 475. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H.; Ortega-Martorell, S. A Novel approach for predicting monthly water demand by combining singular spectrum analysis with neural networks. J. Hydrol. 2018, 561, 136–145. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.H.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A., 2nd; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 313. [Google Scholar] [CrossRef]
- de Souza Groppo, G.; Costa, M.A.; Libânio, M. Predicting water demand: A review of the methods employed and future possibilities. Water Supply 2019. [Google Scholar] [CrossRef]
- Mouatadid, S.; Adamowski, J. Using extreme learning machines for short-term urban water demand forecasting. Urban. Water J. 2016, 14, 630–638. [Google Scholar] [CrossRef]
- Toth, E.; Bragalli, C.; Neri, M. Assessing the significance of tourism and climate on residential water demand: Panel-data analysis and non-linear modelling of monthly water consumptions. Environ. Model. Softw. 2018, 103, 52–61. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-Term Water Demand Forecast Based on Deep Learning Method. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Peña-Guzmán, C.; Melgarejo, J.; Prats, D. Forecasting Water Demand in Residential, Commercial, and Industrial Zones in Bogotá, Colombia, Using Least-Squares Support Vector Machines. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Firat, M.; Turan, M.E.; Yurdusev, M.A. Comparative analysis of fuzzy inference systems for water consumption time series prediction. J. Hydrol. 2009, 374, 235–241. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple Random Forests Modelling for Urban Water Consumption Forecasting. Water Resour. Manag. 2017, 31, 4715–4729. [Google Scholar] [CrossRef]
- Nguyen-ky, T.; Mushtaq, S.; Loch, A.; Reardon-Smith, K.; An-Vo, D.-A.; Ngo-Cong, D.; Tran-Cong, T. Predicting water allocation trade prices using a hybrid Artificial Neural Network-Bayesian modelling approach. J. Hydrol. 2018, 567, 781–791. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Gharghan, S.K.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M. Short-Term Urban Water Demand Prediction Considering Weather Factors. Water Resour. Manag. 2018, 32, 4527–4542. [Google Scholar] [CrossRef]
- Karami, H.; Farzin, S.; Jahangiri, A.; Ehteram, M.; Kisi, O.; El-Shafie, A. Multi-Reservoir System Optimization Based on Hybrid Gravitational Algorithm to Minimize Water-Supply Deficiencies. Water Resour. Manag. 2019, 33, 2741–2760. [Google Scholar] [CrossRef]
- Meshram, S.G.; Ghorbani, M.A.; Deo, R.C.; Kashani, M.H.; Meshram, C.; Karimi, V. New Approach for Sediment Yield Forecasting with a Two-Phase Feedforward Neuron Network-Particle Swarm Optimization Model Integrated with the Gravitational Search Algorithm. Water Resour. Manag. 2019, 33, 2335–2356. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Nigussie, T.A. Monthly water demand prediction using wavelet transform, first-order differencing and linear detrending techniques based on multilayer perceptron models. Urban. Water J. 2018, 15, 177–181. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. A multi-scale relevance vector regression approach for daily urban water demand forecasting. J. Hydrol. 2014, 517, 236–245. [Google Scholar] [CrossRef]
- Candelieri, A. Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Candelieri, A.; Archetti, F. Global optimization in machine learning: The design of a predictive analytics application. Soft Comput. 2018, 23, 2969–2977. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Zhang, R.; Wang, S.; Cheng, C.-T. Operation rule derivation of hydropower reservoir by k-means clustering method and extreme learning machine based on particle swarm optimization. J. Hydrol. 2019, 576, 229–238. [Google Scholar] [CrossRef]
- González Perea, R.; Camacho Poyato, E.; Montesinos, P.; Rodríguez Díaz, J.A. Optimisation of water demand forecasting by artificial intelligence with short data sets. Biosyst. Eng. 2019, 177, 59–66. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Nigussie, T.A. Monthly Water Consumption Prediction Using Season Algorithm and Wavelet Transform–Based Models. J. Water Resour. Plan. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Shabani, S.; Candelieri, A.; Archetti, F.; Naser, G. Gene Expression Programming Coupled with Unsupervised Learning: A Two-Stage Learning Process in Multi-Scale, Short-Term Water Demand Forecasts. Water 2018, 10, 142. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A Probabilistic Short-Term Water Demand Forecasting Model Based on the Markov Chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Pacchin, E.; Alvisi, S.; Franchini, M. A Short-Term Water Demand Forecasting Model Using a Moving Window on Previously Observed Data. Water 2017, 9, 172. [Google Scholar] [CrossRef]
- Bata, M.t.H.; Carriveau, R.; Ting, D.S.K. Short-Term Water Demand Forecasting Using Nonlinear Autoregressive Artificial Neural Networks. J. Water Resour. Plan. Manag. 2020, 146. [Google Scholar] [CrossRef]
- Rahim, M.S.; Nguyen, K.A.; Stewart, R.A.; Giurco, D.; Blumenstein, M. Machine Learning and Data Analytic Techniques in Digital Water Metering: A Review. Water 2020, 12, 294. [Google Scholar] [CrossRef]
- Bayatvarkeshi, M.; Mohammadi, K.; Kisi, O.; Fasihi, R. A new wavelet conjunction approach for estimation of relative humidity: Wavelet principal component analysis combined with ANN. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Seo, Y.; Kwon, S.; Choi, Y. Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology 2018, 5, 54. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H. Short-Term Water Demand Prediction in Residential Complexes: Case Study in Columbia City, USA. In Proceedings of the 11th International Conference on Developments in eSystems Engineering (DeSE), Cambridge, UK, 2–5 September 2018; pp. 31–35. [Google Scholar]
- Zubaidi, S.L.; Al-Bugharbee, H.; Muhsen, Y.R.; Hashim, K.; Alkhaddar, R.M.; Hmeesh, W.H. The Prediction of Municipal Water Demand in Iraq: A Case Study of Baghdad Governorate. In Proceedings of the 2019 12th International Conference on Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019; pp. 274–277. [Google Scholar]
- Eggimann, S.; Mutzner, L.; Wani, O.; Schneider, M.Y.; Spuhler, D.; Moy de Vitry, M.; Beutler, P.; Maurer, M. The Potential of Knowing More: A Review of Data-Driven Urban Water Management. Environ. Sci. Technol. 2017, 51, 2538–2553. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Shi, X.; Hong, Y. Wavelet-Nonlinear Cointegration Prediction of Irrigation Water in the Irrigation District. Water Resour. Manag. 2019, 33, 2941–2954. [Google Scholar] [CrossRef]
- Shah, S.; Ben Miled, Z.; Schaefer, R.; Berube, S. Differential Learning for Outliers: A Case Study of Water Demand Prediction. Appl. Sci. 2018, 8, 2018. [Google Scholar] [CrossRef]
- CWW. City West Water Annual Report 2018; CWW: Melbourne, Australia, 2018; p. 136. [Google Scholar]
- MW. Corporate Plan 2016/17 to 2020/21; MW: Melbourne, Australia, 2017; p. 39. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 6th ed.; Pearson Education, Inc.: Boston, MA, USA, 2013. [Google Scholar]
- Kossieris, P.; Makropoulos, C. Exploring the Statistical and Distributional Properties of Residential Water Demand at Fine Time Scales. Water 2018, 10, 1481. [Google Scholar] [CrossRef]
- Okkan, U.; Ali Serbes, Z. The combined use of wavelet transform and black box models in reservoir inflow modeling. J. Hydrol. Hydromech. 2013, 61, 112–119. [Google Scholar] [CrossRef]
- Dohan, K.; Whitfield, P.H. Identification and characterization of water quality transients using wavelet analysis. I. Wavelet analysis methodology. Water Sci. Technol. 1997, 36, 325–335. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Ali, J.A. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227. [Google Scholar] [CrossRef]
- Al-Sulttani, A.O.; Ahsan, A.; Hanoon, A.N.; Rahman, A.; Daud, N.N.N.; Idrus, S. Hourly yield prediction of a double-slope solar still hybrid with rubber scrapers in low-latitude areas based on the particle swarm optimization technique. Appl. Energy 2017, 203, 280–303. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Abou El Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Shalaby, A.S. Application of the Crow Search Algorithm for Economic Environmental Dispatch. In Proceedings of the 19th International Middle East Power Systems Conference (MEPCON), Shibin Al Kawm, Egypt, 19–21 December 2017; pp. 78–83. [Google Scholar]
- Díaz, P.; Pérez-Cisneros, M.; Cuevas, E.; Avalos, O.; Gálvez, J.; Hinojosa, S.; Zaldivar, D. An Improved Crow Search Algorithm Applied to Energy Problems. Energies 2018, 11, 571. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Fathy, A. A novel approach based on crow search algorithm for optimal selection of conductor size in radial distribution networks. Eng. Sci. Technol. Int. J. 2017, 20, 391–402. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Ismail, M. A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications. Sensors 2016, 16, 1043. [Google Scholar] [CrossRef]
- Mutlag, A.; Mohamed, A.; Shareef, H. A Nature-Inspired Optimization-Based Optimum Fuzzy Logic Photovoltaic Inverter Controller Utilizing an eZdsp F28335 Board. Energies 2016, 9, 120. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Jawad, A.M.; Jawad, H.M.; Ismail, M. Adaptive Neural Fuzzy Inference System for Accurate Localization of Wireless Sensor Network in Outdoor and Indoor Cycling Applications. IEEE Access 2018, 6, 38475–38489. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Comparison of different heuristic and decomposition techniques for river stage modeling. Environ. Monit. Assess. 2018, 190, 392. [Google Scholar] [CrossRef] [PubMed]
- Moayedi, H.; Mehrabi, M.; Kalantar, B.; Abdullahi Mu’azu, M.A.; Rashid, A.S.; Foong, L.K.; Nguyen, H. Novel hybrids of adaptive neuro-fuzzy inference system (ANFIS) with several metaheuristic algorithms for spatial susceptibility assessment of seismic-induced landslide. Geomat. Nat. Hazards Risk 2019, 10, 1879–1911. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
- Pallant, J. SPSS Survival Manual: A Step by Step Guide to Data Analysis Using IBM SPSS; Open University Press/McGraw-Hill: Aotearoa, New Zealand, 2016. [Google Scholar]
| Water Consumption (ML) | Wmax | Wmin | Wmean | WStd. | N |
|---|---|---|---|---|---|
| Training set | 9.37 | 8.87 | 9.0658 | 0.1132 | 123 |
| Testing set | 9.29 | 8.87 | 9.0651 | 0.1124 | 26 |
| Validation set | 9.23 | 8.91 | 9.0317 | 0.0910 | 26 |
| ANFIS mf Type | RMSE (ML) Values Based on Number of mfs | ||
|---|---|---|---|
| Three | Five | Seven | |
| tri | 0.0164 | 0.0843 | 0.8749 |
| trap | 0.0184 | 0.0321 | 1.8151 |
| gbell | 0.014 | 0.0382 | 1.1892 |
| gauss | 0.0142 | 0.0281 | 1.0938 |
| gauss2 | 0.0139 | 0.0299 | 1.6956 |
| pi | 0.0192 | 0.052 | 1.8252 |
| dsig | 0.0239 | 0.0364 | 1.5997 |
| psig | 0.0239 | 0.0385 | 1.5997 |
| Technique | MAE | CE | MARE |
|---|---|---|---|
| ANFIS | 0.0109 | 0.974 | 0.001105 |
| CSA-ANN | 0.0118 | 0.971 | 0.001359 |
| ANN (stand-alone) | 0.0192 | 0.923 | 0.002132 |
| Case | Sum of Squares | df | Mean Square | F | Significance Value (Sig.) |
|---|---|---|---|---|---|
| Between groups | 0.000 | 2 | 0.000 | 0.009 | 0.991 |
| Within groups | 0.651 | 75 | 0.009 | - | - |
| Total | 0.651 | 77 | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubaidi, S.L.; Al-Bugharbee, H.; Ortega-Martorell, S.; Gharghan, S.K.; Olier, I.; Hashim, K.S.; Al-Bdairi, N.S.S.; Kot, P. A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach. Water 2020, 12, 1628. https://doi.org/10.3390/w12061628
Zubaidi SL, Al-Bugharbee H, Ortega-Martorell S, Gharghan SK, Olier I, Hashim KS, Al-Bdairi NSS, Kot P. A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach. Water. 2020; 12(6):1628. https://doi.org/10.3390/w12061628
Chicago/Turabian StyleZubaidi, Salah L., Hussein Al-Bugharbee, Sandra Ortega-Martorell, Sadik Kamel Gharghan, Ivan Olier, Khalid S. Hashim, Nabeel Saleem Saad Al-Bdairi, and Patryk Kot. 2020. "A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach" Water 12, no. 6: 1628. https://doi.org/10.3390/w12061628
APA StyleZubaidi, S. L., Al-Bugharbee, H., Ortega-Martorell, S., Gharghan, S. K., Olier, I., Hashim, K. S., Al-Bdairi, N. S. S., & Kot, P. (2020). A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach. Water, 12(6), 1628. https://doi.org/10.3390/w12061628








