1. Introduction
A storm surge is the abnormal variation of sea level caused by extreme meteorological conditions, such as high wind and low pressure [
1]. It is a complex phenomenon involving interactions among waves, wind, tide and current. The set-up caused by waves breaking may contribute to the rise of water level during storm surges. However, the generation, propagation and nonlinear behaviors of waves are also related to the tidal phase and the current driven by tide and wind. A number of theoretical and numerical studies on storm surges in coastal oceans have been carried out, and have considered the roles of interactions among surges, waves, current and the meteorological condition in various ways. Prandle and Wolf [
1] examined the mechanism of interaction between surge and tide in the Thames River, and suggested that the surge tends to peak during the flood. Tang et al. [
2] confirmed that the quadratic bottom friction is significant in the wave–current interaction, and theoretically proved that the interaction substantially reduces the water levels, compared with those obtained without consideration of the wave–current interaction. Mastenbroek et al. [
3] and Moon [
4] studied the effects of waves on storm surge in terms of wind stress variation due to waves. However, these studies did not consider the influence of mass and momentum transport caused by wave propagation during storm surges.
The momentum transport due to waves can be represented by the wave radiation stress proposed by Longuethiggins and Stewart [
5], which can be derived from the wave energy. However, the waves in oceans are often random and obtaining the energy distribution of random waves is difficult. With the development of random wave models based on the action balance equations [
6], simulating random waves and considering the momentum transport due to random waves has become feasible. Combining a tide model and a wave model (simulating waves nearshore (SWAN) [
7]), Kim et al. [
8] and Kim et al. [
9] studied the effects of tide and waves on surges in terms of radiation stress. Their studies indicated that the radiation stress could contribute up to 40% of the peak surge water level on the coasts of Korea and Japan during typhoons. By coupling a finite volume ocean model (finite volume community ocean model (FVCOM)) [
10] and an unstructured-grid wave model (SWAVE) [
11], Yoon and Jun [
12] set up a wave-surge coupled model for the south coast of Korea, considering the land dissipation effects on the wind as well as the wave-induced surface drag and the radiation stress. Recently, Marsooli et al. [
13] developed a 3D model using the sECOM (estuarine and coastal ocean model) and the MDO (Mellor–Donelan–Oey wave model) with the consideration of radiation stress. Liu et al. [
14] studied the inundation in New York City caused by Hurricane Sandy, 2012, using the model coupled with tide, wind, and waves. These studies paved a way to examine the influence of waves on the coastal storm surges.
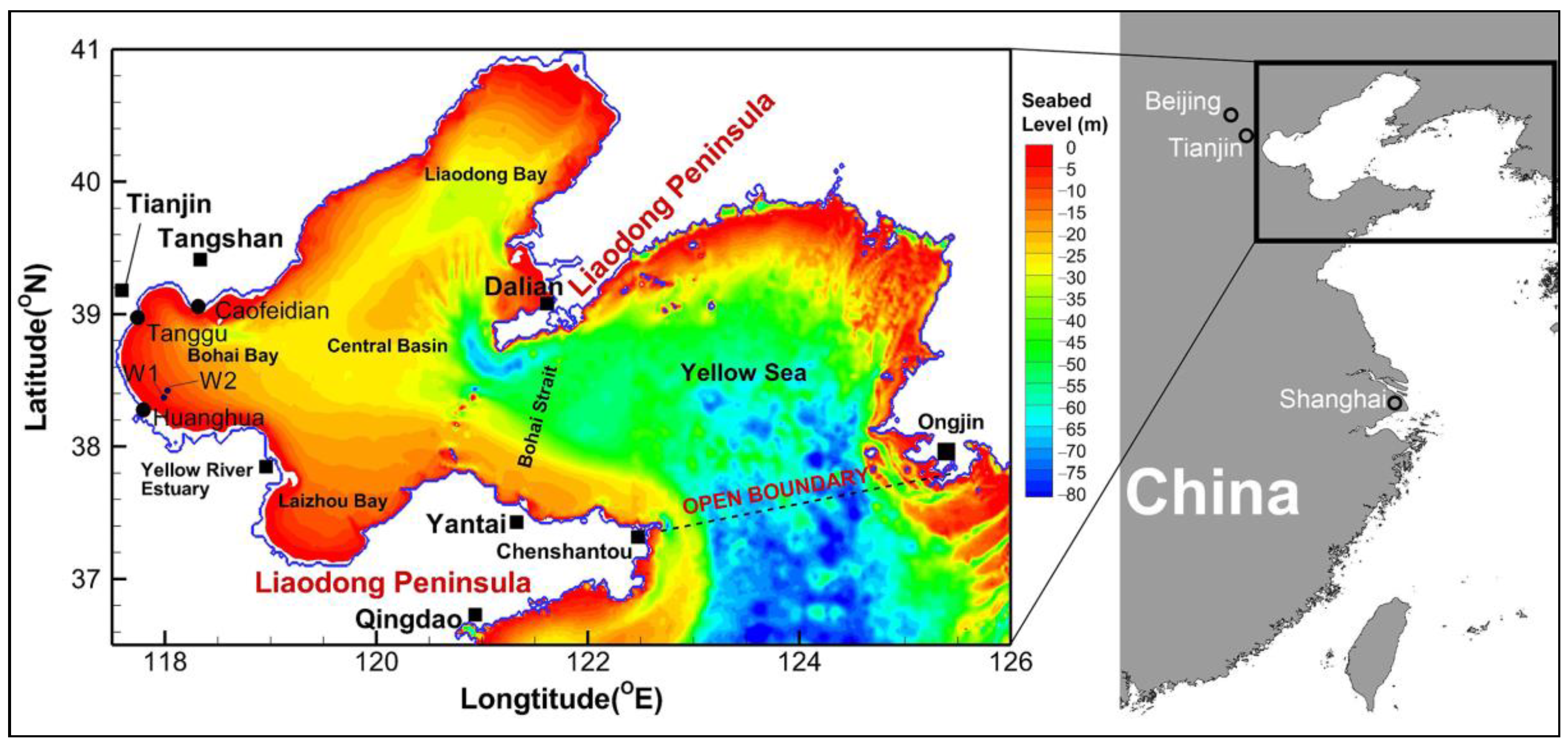
The Bohai Sea is an inner sea, located in Northern China, which suffers from frequent storm surges. It consists of Liaodong Bay, Bohai Bay, Laizhou Bay and the central basin (
Figure 1). The Bohai Sea coast is characterized by a gently varying seabed, which together with its semi-enclosed nature, makes it vulnerable to storm surges [
15,
16,
17]. The Bohai Sea is influenced by continental climate and temperate monsoon. Generally, the wind in winter is stronger than that in summer [
18,
19] and the annually averaged significant wave height (
Hs) is ~0.6 m [
20]. As a populated zone in the north and the northeast of China, the region around the Bohai Sea is experiencing a fast social and economic development, with several important ports and metropolises located there. Because of the social and economic importance of this area, the disasters caused by the frequent storm surges that result from the Bohai Sea climatic and physical characteristics have attracted the attention of researchers, the public and the government.
Thus, to protect the coast from flood damage, many studies have simulated the storm surges in the Bohai Sea to investigate their characteristics. Most of these studies have calculated the surge level without considering the effect of waves [
21,
22,
23,
24,
25]. However, the wave set-up (or set-down) may be obvious, as the water depth in the Bohai Sea is shallow and its bathymetry varies slowly, with an average depth of approximately 18 m and an averaged tidal amplitude of about 2 m. Moreover, the wave propagation is significantly affected by the currents and water depth variations due to flood and ebb tides, thereby altering the transport of mass and momentum induced by waves. Under these conditions, waves are one of the important factors influencing the water movements in this region, and the fluxes of mass and momentum caused by the waves probably have important impacts on the currents and surges. Therefore, it is necessary to quantitatively examine the contribution of waves to the surge in the Bohai Sea, as ignoring the effects of waves on the surge may be problematic in some regions [
8,
9]. Moreover, previous studies have also suggested that the storm surges in the south of Bohai Bay and Laizhou Bay are more serious [
15,
16,
17,
24,
26]. However, to the best of our knowledge, there is no study examining the detailed reasons for higher surges in these regions.
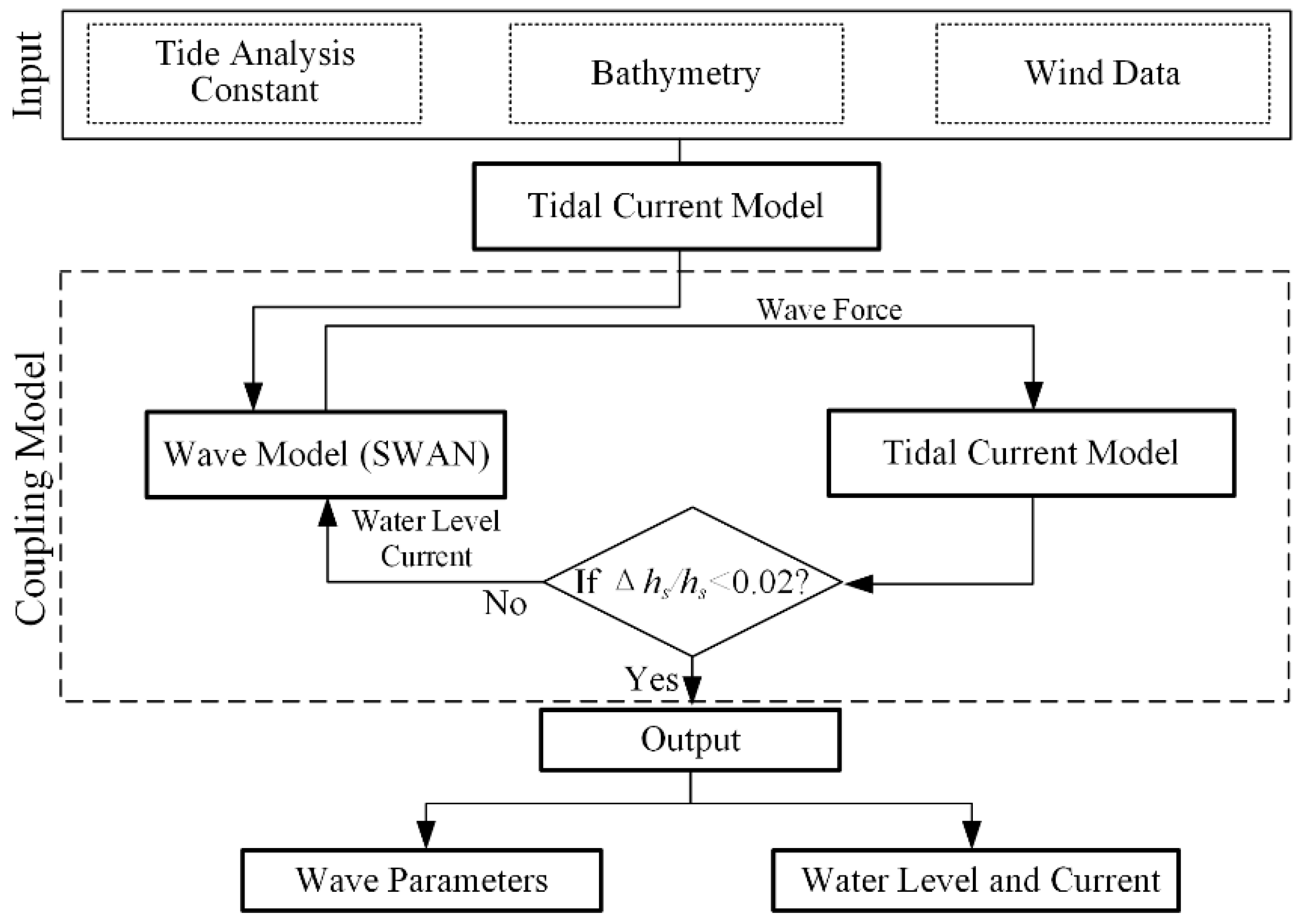
In this study, we aim to further understand the role of waves on storm surges in the Bohai Sea using a coupled model that includes tide, wind and waves. The objectives of the study are to: (i) analyze the interactions among tide, waves and current during surge events and discuss the role of these interactions on the occurrence of higher surges in a part of the Bohai Sea; and (ii) quantify the contribution of waves to the surge in such semi-enclosed seas and determine the need to include the effects of waves, tide and wind in surge prediction in such semi-enclosed inner seas.
Section 2 gives a detailed description of the model used in this study and presents the validation results.
Section 3 shows the results of the surge simulations. In that section, the surge distributions, the wave induced currents and the comparisons between the surges at different tidal phases are examined.
Section 4 discusses the advantages and the limits of this study and proposes possible directions for future studies. Finally,
Section 5 summarizes the main findings of this study.
3. Results
3.1. Surge Distribution
To study the surge distribution and the wave effects on the surge in the offshore region, simulation results of the surge of September 2010 in the Bohai Sea and in the north Yellow Sea were analyzed in detail.
Figure 6a,b show the storm surge at the time when the surge in the south part of the Bohai Sea peaks without (run 6) and with (run 4) consideration of wave forces, respectively. The highest surge occurs along the west and south coasts of the Bohai Sea, i.e., the Bohai Bay and the Laizhou Bay, and a serious surge mainly occurs near Huanghua and the Yellow River estuary, where there is a region with shallow water depth even during high tide. The negative storm surge is found in the Liaodong Bay, located in the northern Bohai Sea.
Figure 6c shows the surge difference between runs 4 and 6, which represents the wave-induced set-up (or set-down). It can be seen that the contribution of the wave is obvious in the region near the Yellow River estuary, the south coast of the Bohai Bay and the west and south coast of the Laizhou Bay. Moreover, the wave-induced set-up also occurs near the Luan River estuary. In the central region of the Bohai Sea, the waves mainly contribute to the set-down. In the north part of the Liaodong Bay, the wave-induced set-up is obvious, which indicates that the calculation without consideration of waves (run 6) may overestimate the negative surge and underestimate the water level in the shallow water region.
The wave effects on the surge are more obvious in the shallow water region. Under the influence of waves, the water level tends to rise in the onshore region and decrease in the offshore region. Generally, the wave-induced set-up and set-down in the Bohai Sea range from −0.1 to 0.3 m with the maximum value occurring near the Yellow River estuary and in the Laizhou Sea. In these regions, the wave set-up can be up to 12.5% of the maximum surge. Under north wind conditions, the positive surge occurs in the south of the Bohai Sea and the negative surge occurs in the Liaodong Bay. Compared to the calculations with waves, calculations without waves overestimate the water level decrease caused by the storm in the upwind direction, while they underestimate the water level increase in the downwind direction.
3.2. Wave-Induced Current and High Surges
The surge changes in
Figure 6 are due to the mass transport caused by waves. In this subsection, the wave-induced currents are calculated by subtracting the currents driven by tide and wind (run 6) from the results that consider tide, wind and waves (run 4).
Figure 7a,b show the currents at the time when the surge in the south part of the Bohai Sea peaks (same time as for
Figure 6). Evidently, in the offshore region, the general flow patterns of runs 4 and 6 are similar. There is a circulation in the central basin of the Bohai Sea in both runs. This similarity is confirmed by the small differences in currents between runs 4 and 6 shown in
Figure 7c.
The main differences between the two runs appear in onshore regions, especially near the Yellow River estuary, the Luan River estuary, and the west and east coasts of the Liaodong Bay. In these regions, the longshore currents could explain the differences. Indeed, under north wind conditions, the longshore currents in the Liaodong Bay and near the Luan River estuary are almost southward. The longshore currents transport water to the regions that suffer from severe surges, resulting in water accumulating in those regions and a water level relatively higher than that only driven by tides.
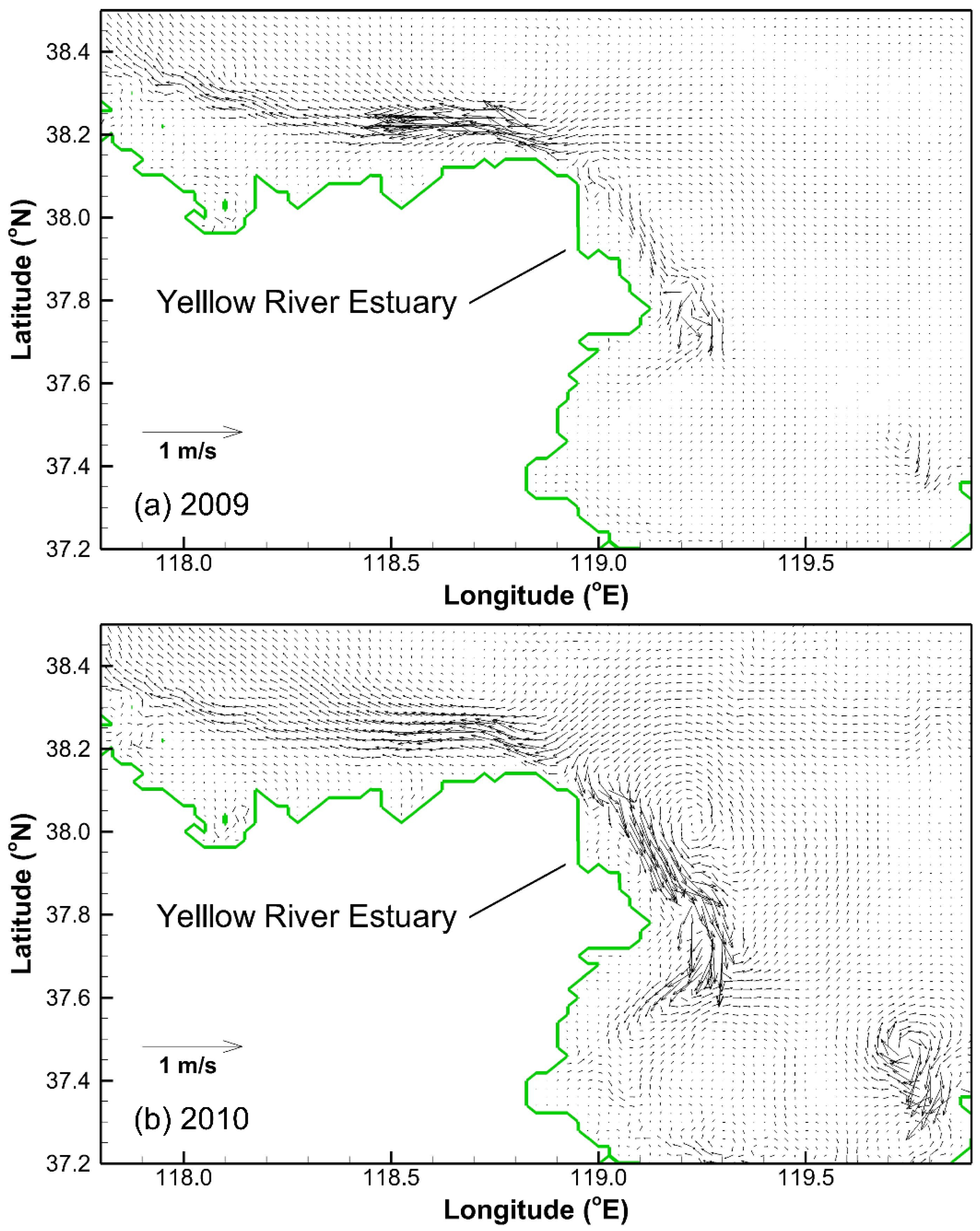
Figure 8 shows the strong longshore currents occurring near the Yellow River estuary at the time when the surges in the south part of the Bohai Sea peaks in 2009 and 2010. The longshore currents in this region are directed towards the south of the Bohai Bay and to the west of the Laizhou Bay. Following the currents, the water is transported from the Yellow River estuary to the south of the Bohai Bay and to the west of the Laizhou Bay, and is accumulated in the shallow water regions of the two bays, resulting in a rise in the water levels. This phenomenon corresponds to the higher surges near the Yellow River estuary, the south of the Bohai Bay and the south and west of the Laizhou Bay.
Based on the comparison of the flow patterns without and with the consideration of waves, and the difference of set-ups in runs 4 and 6, we infer that the formation of the longshore currents is due to radiation stress. In the wave model, the wave breaking is taken into account [
7], which contributes to the gradient of wave energy and produces a wave force.
Figure 9a,b present the distributions of wave forces at the times when the surge in the south part of the Bohai Sea peaks in 2009 and 2010, respectively. It can be seen that the distributions of wave forces during the two storm surges are similar, with the maximum wave force occurring near the Yellow River estuary in the two cases.
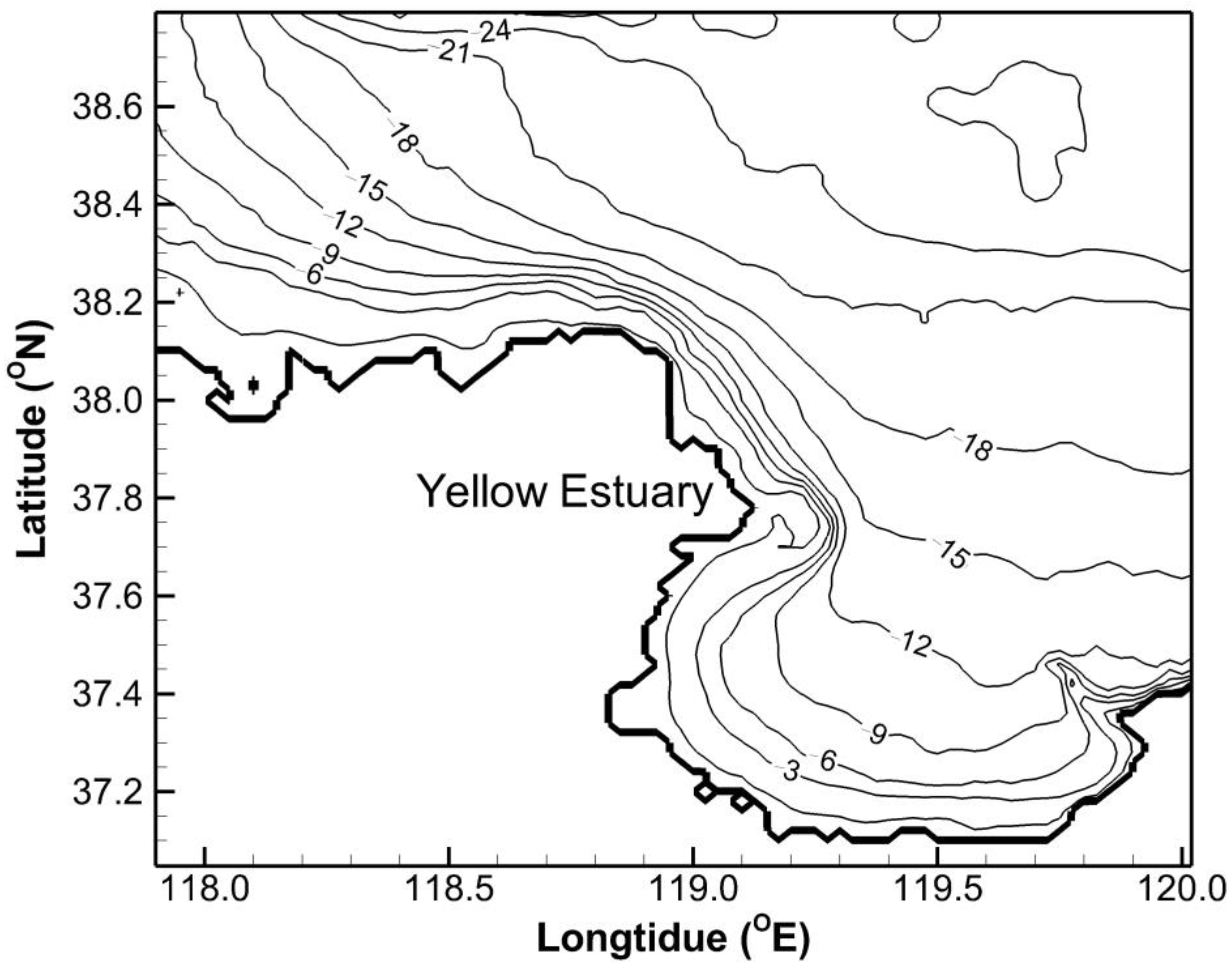
The seabed slope near the Yellow River estuary is rather steep, whereas the seabed slopes in the east and west of the estuary are mild (see
Figure 10). As waves from the central basin of the Bohai Bay propagate on the steep seabed, they break quickly in the shallow water area and generate a large gradient of radiation stress that results in significant wave forces near the Yellow River estuary. However, the wave forces on the west and the south of the estuary are weaker due to the milder slopes. Under these conditions, more water is pushed towards the Yellow River estuary resulting in higher water levels near the estuary than in its south-eastern and north-western parts. This also leads to the relatively strong longshore currents, transporting water from the Yellow River estuary to the south of the Bohai Bay and the west of the Laizhou Bay. This is one of the reasons for the higher surges occurring in the south of the Bohai Bay and the west of the Laizhou Bay than that in other parts of these bays.
The water depth becomes gradually shallower from north to south both in the south of the Bohai Bay and in the Laizhou Bay (
Figure 1). This bathymetry pattern produces gradual variations of the wave energies and unidirectional wave forces in the two regions (
Figure 9). Under the drive of the unidirectional wave forces, the wave-induced currents are southward, further accumulating water in the south of the Bohai Bay and in the Laizhou Bay. Therefore, the water levels additionally rise, which is another reason for the higher surges in these two regions. A similar situation also occurs in the north of the Liaodong Bay. The wave force there is also unidirectional due to the mild slope, but is northward. Under these conditions, the wave-induced currents are northward, opposite to the wind-induced currents. Therefore, the wave-induced currents mitigate the negative surge happening there. This explains the lower negative surge in the north of the Liaodong Bay when considering the wave effects. However, in the central basin, the situation is different as the bathymetry is undulating, especially in the region close to the Bohai Strait (
Figure 1), producing random directions of wave forces. With this pattern, the wave force cannot continuously push the water in one direction and thus has no significant effect on the surge in the central basin, as indicated in
Figure 6c.
3.3. Relationships between Tide and Surge
The dominant tidal component in the Bohai Sea is M2. For most of the coast around the Bohai Sea, the tidal height ranges from 0 to 2.5 m. Due to flood and ebb tides, the water depth changes significantly when the amplitude of the tide is large enough, which may significantly affect the wave deformation and propagation in shallow water.
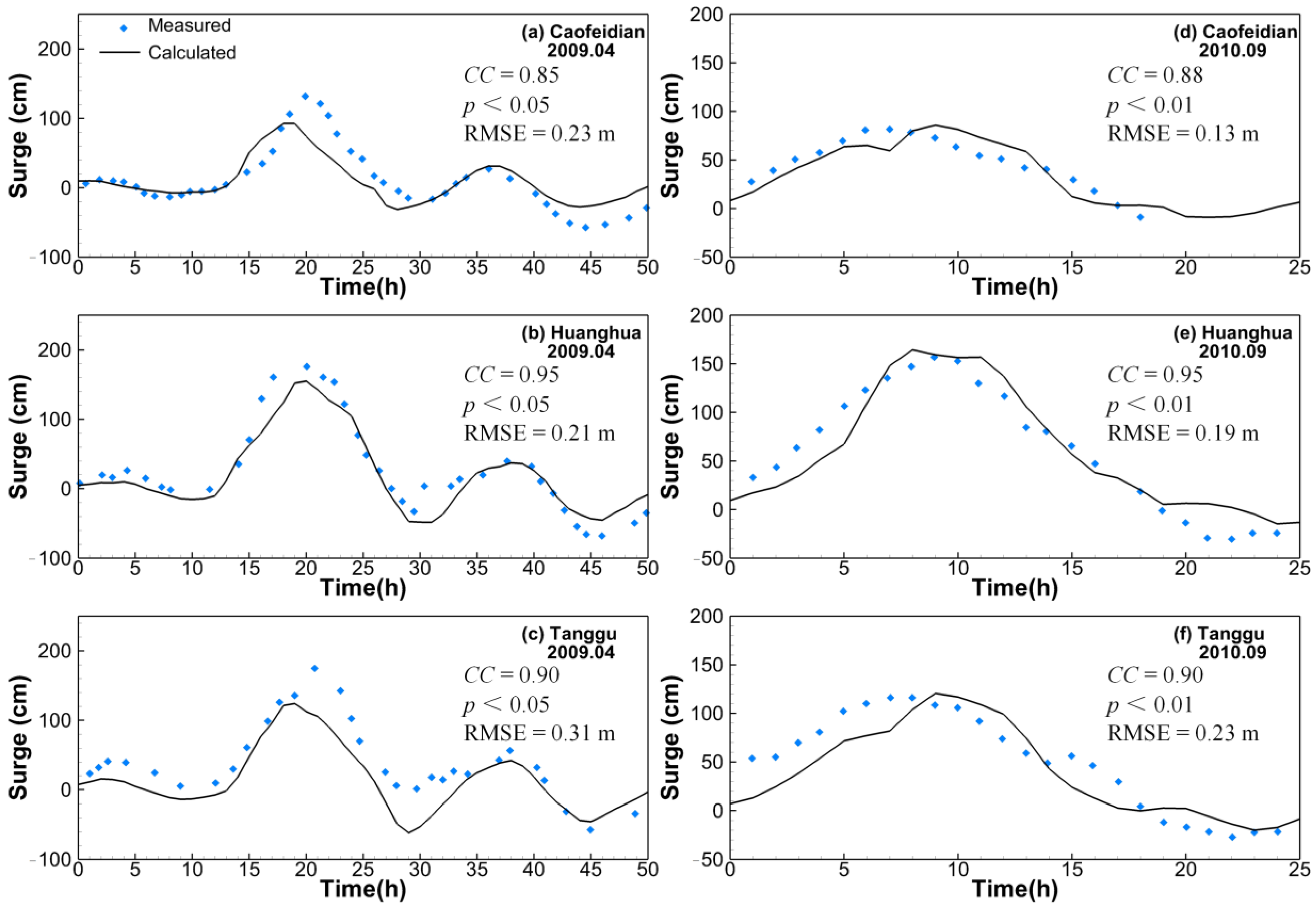
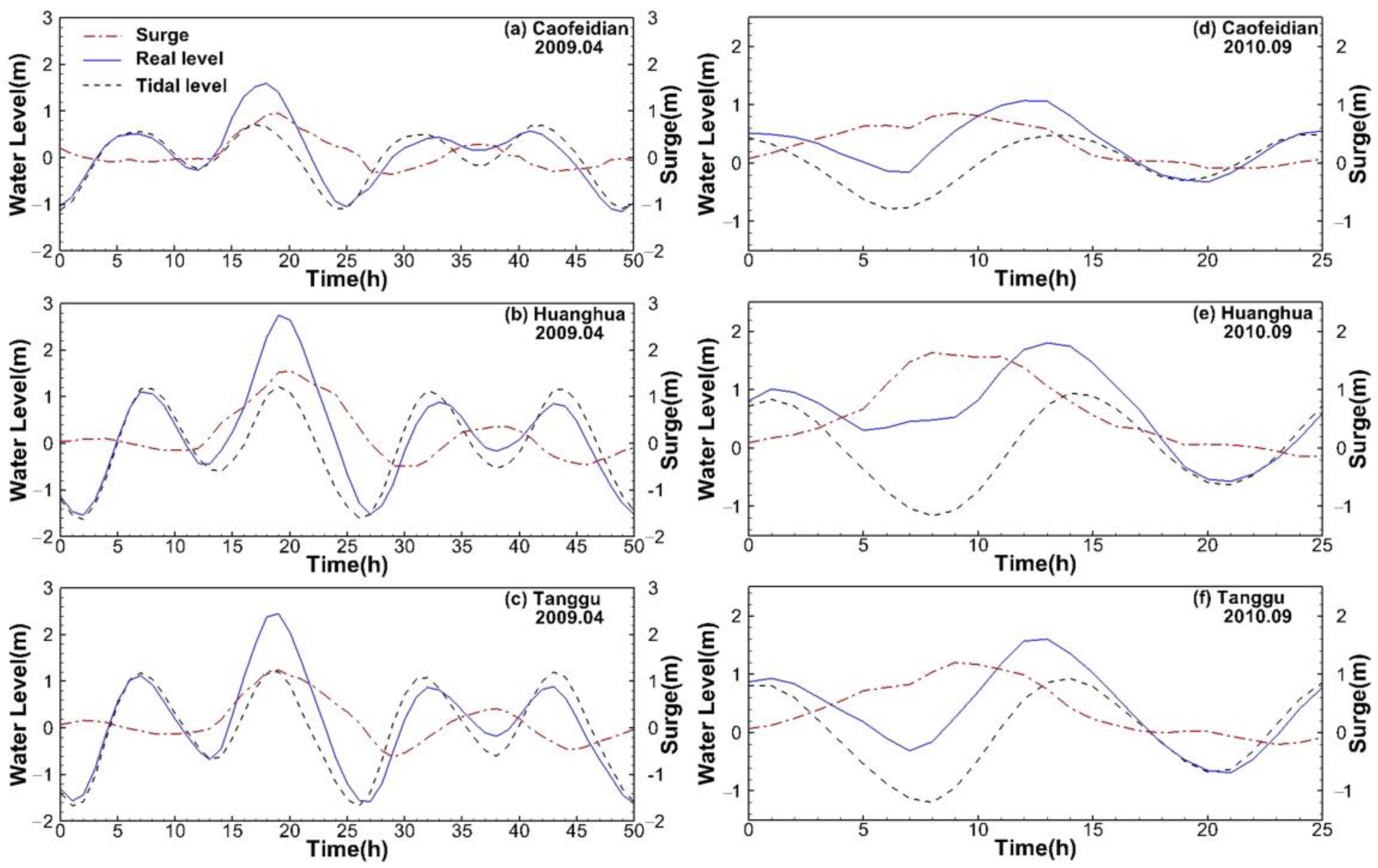
The storm surge events occurring on 13 April 2009 and on 21 September 2010 were simulated using runs 2, 3, 4 and 6, and were analyzed to study the effects of tide on the storm surges and its interaction with waves. The peak surges of the two events occurred during different tidal phases. The peak surge of the event beginning on 13 April 2009 occurred at high tide and that of the event beginning on 21 September 2010 occurred at rising tide (see
Figure 11).
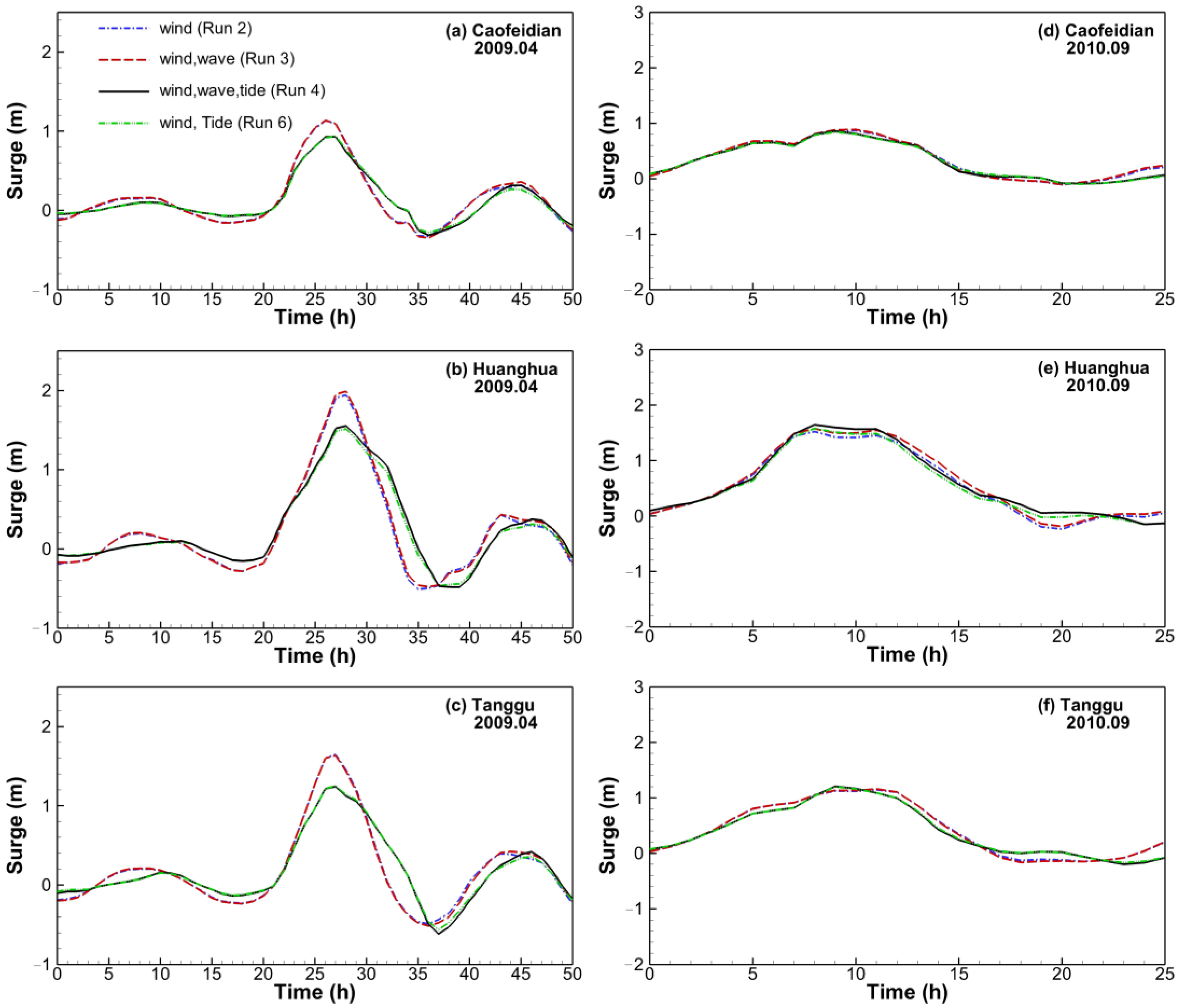
Figure 12a–c show the variations of the surges during the storm on 13 April 2009. By comparing the surge levels with tides to those without tides, it can be seen that the peak surges are significantly reduced when considering the influence of the tide, especially at Huanghua and Tanggu. This indicates that methods used to forecast or hindcast the peak water level of a storm surge occurring at high tide by adding the water levels driven by wind (and wave) (i.e., run 2 or run 3) to those driven by tide (run 1) are not suitable for the Bohai Sea. This can be explained by two reasons. Firstly, M
2, which is the dominant tidal component in the Bohai Sea, has a wavelength (~600 km) of approximately twice the spatial scale (~300 km) of the Bohai Sea [
41]. When the western coast of the Bohai Bay experiences high tide, the water level in the central part of the Bohai Sea and the Bohai Strait is relatively low. Under these conditions, the gravity force hinders the inflow of water from the central basin of the Bohai Sea to the western part of the Bohai Sea. This explains that the peak surges calculated by considering the tide in run 4 are lower than those without tides in runs 2 and 3. Secondly, an increase and decrease of water depth caused by flood and ebb tides is related to wave deformation in shallow water regions. As mentioned above, wave deformation in shallow water regions causes a significant set-up, which raises the water level in the coastal region. However, during high tide, water depth is higher, weakening the wave deformation near the coast and thereby also the longshore currents. If the surge is calculated without considering tidal effects, the water depth at the coast is lower than the real hydrodynamic conditions in which waves propagate. Due to the underestimation of water depth, the modelled wave deformation is overestimated and thereby the calculated set-up becomes more obvious in the coastal region. By comparing the water depth at the three locations, it can be found that the water depths at Huanghua and Tanggu are smaller than that at Caofeidian (
Figure 1). The model results show that the tidal amplitudes at Huanghua and Tanggu are larger than that at Caofeidian. As a result, for the surge of 2009, the differences between the peak surge values calculated by runs 3 and 4 vary with the location (
Figure 12a–c), with significant differences at Huanghua and Tanggu and a lower difference at Caofeidian.
In contrast, the peak surges at Caofeidian, Huanghua and Tanggu during the storm of September 2010 occurred at rising tide. At this time, the water depths at the three locations were shallower. Under these conditions, the water from the central basin of the Bohai Sea could flow easily into the western Bohai Bay as the water level in the Bohai Bay was equal to or lower than that in the central basin of the Bohai Sea. This explains that the peak surge values calculated under run 2 are similar to those calculated under run 4 (
Figure 12d–f). However, it can still be seen that the calculated surges under run 4 are slightly larger than those under runs 2 and 3. This can be attributed to the fact that runs 2 and 3 underestimate longshore currents and set-up led by the wave deformation in the regions of shallow water, where the water depth is overestimated.
The analysis above shows that the tide is an important factor determining the surge. The flood and ebb tides alter the hydrodynamic conditions in which waves propagate and influence the development of the surge. Ignoring tides can lead to overestimation of the surge at rising or high tide, but also to its underestimation at falling or low tide, and therefore, the tide should be considered for surge prediction in the Bohai Sea.
4. Discussion
In this study, we develop a numerical model that couples wave and tidal current models. Both sub-models have been calibrated and the results show that both of them are accurate enough for applications in the Bohai Sea. The validation of the coupled model against field measurements indicates that it is capable of capturing the characteristics of the surge with the effects of waves being considered. This study focuses on the surge caused by cold air invasions from the north but ignores the contributions by the gradient of air pressure that can also contribute to the surge. During cold air invasions, the gradient of air pressure is relatively low [
24]. As the Bohai Sea is semi-enclosed and shallow, with an average depth of 18 m, the effects of the air pressure gradient would be negligible compared to those of wind stress [
29,
42,
43]. Therefore, it is reasonable to ignore the air pressure and focus on the effect of wind and its interaction with wave and tide. This could not be ignored in the cases of a typhoon, which creates a large pressure gradient. However, the Bohai Sea seldom suffers from typhoons due to its high latitude.
The comparison between the calculations with (run 4) and without (run 6) waves shows that the waves affect the surge in such a semi-enclosed shallow sea. A limitation of the study is that the effect of waves on water movement are represented by the radiation stress, which is related to the spatial distribution of wave energy. In fact, the wave stress is derived from linear theory [
6]. However, the water depth in the Bohai Sea is very shallow and it varies significantly in some regions. Under this condition, the wave behavior usually becomes nonlinear, which is related to Stokes drift and non-hydrostatic pressure, both of which are ignored in this study [
44,
45]. Moreover, the model used in this study is two-dimensional and it cannot well represent the water flows in the vertical direction caused by the waves in onshore regions, which have a significant effect on the surge. This can also partly explain the small discrepancies between the simulated and observed surges (
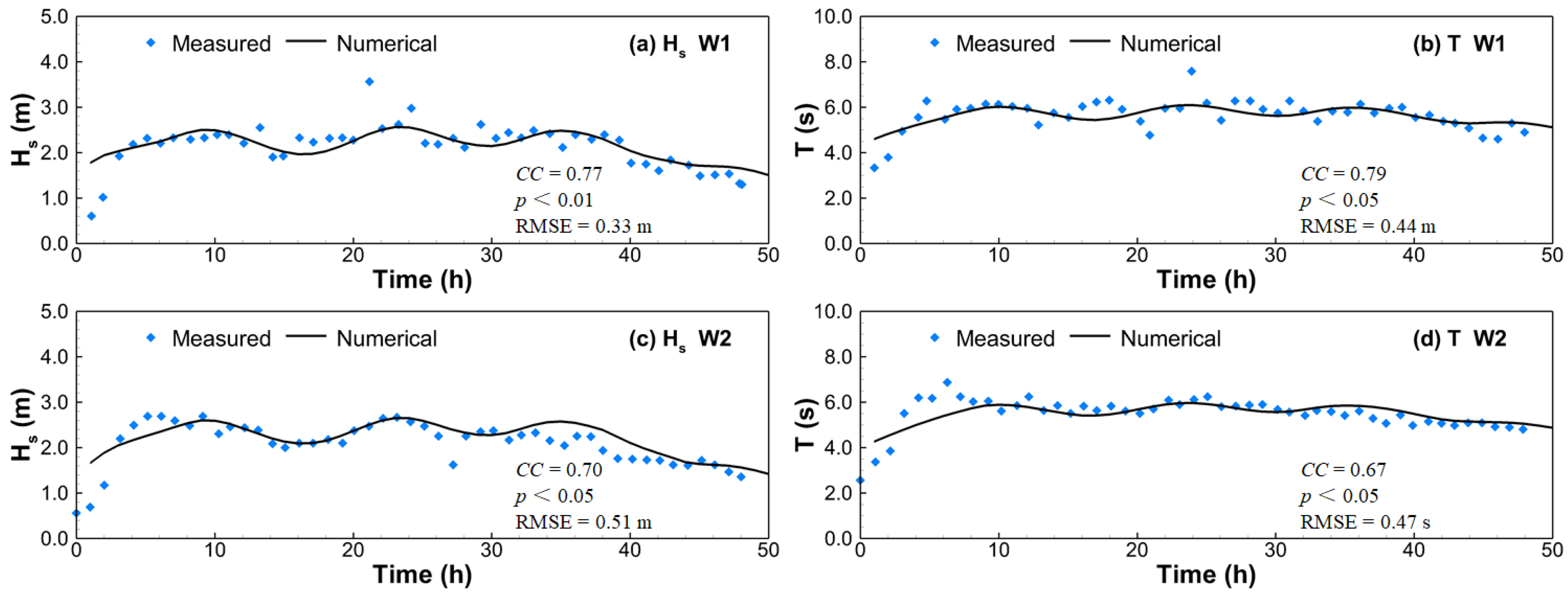
Figure 5). Future studies should examine and quantify the effect of nonlinear wave behavior on storm surges using a more detailed three-dimensional numerical model.
The case study in this paper, while relatively simple, demonstrates that interactions among waves, tide and current can be important and quantifies the contribution of the wave force on the surge magnitude in the Bohai Sea. By comparing the currents with and without the effects of the wave force, we find that the wave-induced longshore current is a main contributor to the surge around the Yellow River estuary. The result analysis shows that the topography of the seabed is an important factor influencing the wave propagation and deformation, which thereby determines the longshore current and water accumulation. This fact indicates that the higher surges in the south part of the Bohai Bay is the combined results of the topography in these regions and the stronger north wind in the Bohai Sea.
Moreover, by analyzing the model-simulated results of the two surge cases, for which the peak surges occurred at different tidal phases, we uncover the effect of tides on waves and surge. This implies that simply adding the water level rise caused by wind to the tidal water level is not generally suitable to precisely forecast or hindcast the surges in some situations. In shallow seas such as the Bohai Sea, such a method tends to overestimate the peak water level when it occurs at high tide, especially in shallow waters with mild seabed slopes. This method may be able to calculate the real water levels and surges in deep water regions, when the peak surge occurs at lower tide, but it still underestimates the water level in the shallow waters. Therefore, our results show that it is important to take the mutual influences of tide, wind and waves into account to evaluate the risk of a storm surge.
5. Conclusions
In this study, we developed and validated a storm surge model coupling the effects of waves, tide and current, which can improve both our understanding of storm surges and their distributions, and the evaluation of risks linked to storm surges in the Bohai Sea. We summarize the main findings of the study as follows:
The model results show that the wave-induced surge is stronger in shallow waters and could be ignored in offshore regions. Generally, the wave-induced set-down contributes up to 12% of the storm surge and it is in the range of −0.1 to −0.3 m with the maximum occurring near the Yellow River estuary and in the Laizhou Bay.
Under the drive of a north wind, the positive surge takes place in the south of the Bohai Sea and the negative surge takes place in the Liaodong Bay. In the upwind direction, calculations ignoring wave contribution can overestimate the water level decrease caused by a storm.
The longshore currents caused by wave breaking and energy dissipation are important contributors to the surges in shallow water regions. Under north wind conditions, the steep gradient of bathymetry near the Yellow River estuary contributes to the large gradient of wave energy and stronger wave force in this region, pushing the water towards the Yellow River estuary and raising the water level there. This higher water level generates longshore currents flowing into the south of the Bohai Bay and the west of the Laizhou Bay, and thereby amplifying the storm surges in these two regions.
The gently varying seabed in the south of the Bohai Bay and the Laizhou Bay is another factor contributing to the surges in these two bays. With such bathymetry, the wave force in the two bays is unidirectional. Therefore, their water can be continuously driven to the southern shallow water regions, resulting in higher surges in their coastal regions.
Tide also influences the formation of the surge. The flood and ebb tides have significant effects on the wind-induced flows from the outer sea to the bays and on the wave deformation that generates wave set-up and longshore currents along the coast. All of these factors influence the mass transport in the coast. Therefore, it is improper to forecast or hindcast the surges by simply adding the water level rise caused by wind to the tidal water level. The mutual influences of tide, wind and waves should be considered to evaluate the risks of storm surges in such a semi-enclosed shallow sea.