1. Introduction
Humanitarian emergency situations arise when natural or man-made hazards bring serious disruptions to a society, causing widespread human suffering, and stretch the community’s coping mechanisms to a breaking point [
1]. Damages to local water systems or mass migration in some cases may lead to a lack of water to meet the community’s basic needs. Insufficient quantity of water for consumption and hygiene, together with poor water quality, underlies most public health problems such as transmission of diarrheal diseases during crisis situations [
2]. Therefore, it is critical for humanitarian relief organizations to provide water of safe drinking quality and in adequate volume to support lives and hygiene in the community [
2,
3,
4]. For humanitarian water provision, disinfection is an essential step to produce water of safe drinking quality as it aims to inactivate disease-causing microorganisms in water.
There are a variety of water disinfection methods for application in the context of a humanitarian emergency (referred to as “the field” hereinafter) such as water boiling, chlorination, ultraviolet disinfection, etc. [
5]. However, free (or breakpoint) chlorination is usually the method of choice because chlorine is relatively easy to obtain, apply, measure, and it can inactivate most viral and bacterial pathogens in a rapid and cost-effective manner, in addition to leaving a residual protection in the water [
6,
7,
8].
Despite the various advantages of free chlorination in the field, a key challenge for its effective application is finding the appropriate doses to achieve protective residual at a target storage time at the point of use [
7]. Storage time is typically 24 h, assuming water is fetched daily. Within the 24-h storage time, the free chlorine residuals (FCR) need to meet both recommended health-derived and aesthetic objectives [
9]. This creates the challenge because chlorine is a strong oxidant and may react with a variety of constituents (i.e., metals, organics, ammonia, etc.) in water; hence, its concentration decays over time at a rate that depends on various factors [
10]. Some of these factors include quality of the treated water, water temperature, initial chlorine dose, and/or the reaction container (details of which are discussed later).
Field conditions set humanitarian water treatment apart from conventional treatment contexts. In the latter, chlorination is achieved in engineered tanks and pipelines under relatively stable environmental conditions. In humanitarian water treatment, chlorination may take place in locations ranging from centralized water tanks to decentralized collection and storage containers (e.g., buckets, jerrycans, etc.) at the point of collection or point of use in a humanitarian context [
9]. The treated water may often be subjected to elevated temperatures [
11], which accelerates chemical reactions in the water, leading to higher FCR decay rates [
11,
12,
13]. For FCR verifications, pool testers and several other measuring devices are often used, and the results are less consistent compared to those resulting from using a colorimeter because pool testers require operators’ personal judgement [
8]. The limitation of imprecise readings with the field instruments makes it challenging to obtain key information (i.e., chlorine demand, FCR decay data, etc.) Both the environmental conditions and instrumentation in humanitarian contexts add uncertainties to initial chlorine dose prediction.
To guide chlorination application in humanitarian contexts, varied international guidelines and research studies provide recommendations on the initial doses based on source water characteristics. A comparison of the recommendations is provided in
Table 1.
Based on the comparison of listed recommendations, there are four points to be noted. Firstly, the descriptive based guidelines are comprehensive, which allow for most people to execute. However, the bleach solution may have degraded [
18], and no information was included in the guidelines for FCR verification. This can lead to underdose of water. Secondly, several guidelines use turbidity (or cloudiness of the water) as a quantifiable indicator of water quality and use it for deciding the chlorine dose. Turbidity is an optical property of a suspension mainly attributed to the presence of suspended particles and can be measured with simple devices like a turbidity tube in the field [
19]. Arguably, suspended matter may not be the best indicator of chemical properties of dissolved compounds in water. Gallandat et al. [
20] suggest that kaolin clay-based turbidity has no impact on chlorine decay kinetics. Thus, it shows that the type of turbidity matters in terms of how it affects chlorine demand. Ali et al. [
11] explored relationships between FCR decay and water quality in 220 unique samples and concluded that ambient air temperature and water conductivity show potential direct relationships with decay kinetics, while other water parameters including turbidity only accounted for about 25% of the variance in their data. To this end, parameters directly related to chlorine demand inducing compounds such as natural organic matter (NOM) (e.g., UV absorbance, dissolved or total organic carbon, etc.) could be a better metric to use [
12]. Thirdly, several recommendations suggest verifying FCR at 30 min after dosing but do not consider chlorine decay for longer storage time [
6,
15]. Sometimes, it may be impractical to reach the recommended minimum FCR value of 0.2 mg/L for 24 h storage time [
11]. Based on the assumption that households fetch their water daily, to ensure effective residual protection, dose recommendations should evaluate FCR decay during storage to up to 24 h. Lastly, the values recommended by different guidelines vary, and it may create confusion for humanitarian staff in guideline selection.
To tackle the series of challenges present in determination of the adequate chlorine dose, a predictive tool, which uses the obtainable information in the field to rapidly and accurately estimate chlorine decay kinetics would be of use towards determining the appropriate initial dose for achieving safe free chlorination objectives. This paper examines several water parameters including NOM, water temperature, and 30-min chlorine demand and their impacts on chlorine decay kinetics. Model parameters from two of the chlorine decay kinetic models examined were found able to be calibrated with the above-mentioned water parameters. While chlorine decay models were typically calibrated with real chlorine decay data, the time constraint in the field limited the application of the models. Being able to calibrate model parameters with easily measurable water parameters allows the application of these models due to the substantial reduction in time requirement for calibration.
3. Materials and Methods
The development of a chlorine dose predictive tool contained three main stages: (1) establishment of base relationships between the model parameters and selected water quality parameters using synthetic water (i.e., “brown bottle” tests), (2) verification of the base findings in scaled up systems (i.e., 20-L jerrycans), (3) verification of the models by conducting chlorine decay tests on water from three different natural sources.
To evaluate the relations between chlorine decay kinetics and the selected water quality parameters, synthetic water with different amounts of added humic acid (Sigma-Aldrich) and under different temperature settings were dosed with chlorine, and the decay of FCR were monitored over a duration of 24 h. Selected models from Wu [
24] were used to fit the decay data, and correlation analysis was conducted between the estimated decay constant term and water parameters, including organics (by measuring ultraviolet absorbance at wavelength of 254 nm (UVA
254)), temperature, and 30-min chlorine demand. A total of 64 chlorine decay tests, in both 125-mL glass brown bottles (Fisher Scientific, Canada) and 20-L plastic jerrycans (ULINE, Seattle, WA, USA) were conducted from August 2019 to January 2020.
3.1. Apparatus Preparation
The containers used in the tests were either 125-mL brown bottles or 20-L jerrycans. The brown bottles were used for testing bulk chlorine decay, which means factors other than the characteristics of the tested water were minimized. The jerrycans were used to simulate chlorination in the field, and the results were compared to those obtained from bulk chlorine decay tests.
All glassware involved in the experiments were treated according to the Environmental Technology Verification Protocol before the test [
28]. This cleaning protocol involves using Fl-70 detergent and chlorine solution with 10–20 mg/L available chlorine to remove the chlorine demand-inducing substances (i.e., adsorbed organics) on the inner surface of glassware.
3.2. Synthetic Water Preparation
Synthetic water was prepared in batches prior to testing. Humic acid (Sigma-Aldrich) was added to the Milli-Q water based on the relationship described by Equation (2) to achieve specific readings of UVA
254, representing the amount of natural organic content in the water. This relationship was determined and used for the stock humid acid in the Public Health and Environmental Engineering (PH2E) laboratory at the University of Victoria (Victoria, Canada). The prepared water was then distributed into three 2-L Erlenmeyer flasks for temperature adjustments.
where
is the water UVA
254 value measured in cm
−1, and
is the concentration of humic Acid measured in mg/L.
3.3. Temperature Control
The test water was placed in three different incubators set at 10, 20, and 30 °C respectively to reach the designed temperature. For tests in jerrycans, a water bath was set up to keep the water temperature at 30 °C.
Figure 1 illustrates the experimental setup of the tests.
3.4. Chlorine Stock Solution Preparation
Chlorine stock solution was prepared by diluting commercially available bleach solution using Milli-Q water to reach a concentration of approximately 600 mg/L available chlorine. The strength of the stock chlorine solution was verified (HACH Method 8209) at least three times prior to each use. For each test, the stock solution was dosed to a separate container with Milli-Q water, parallel to the one with actual test water for dose verification.
3.5. Matrix for Test Conditions
The first stage of the study involves conducting a series of 24-h chlorine decay tests under various organics and temperature conditions.
Figure 2 illustrates the matrix for the tested conditions inspired by the approach adopted by Gallandat et al. [
20].
These 24-h decay tests were conducted in 125-mL brown bottles with synthetic water, incubated at the designed temperature. Chlorine residual readings were performed at 5, 10, 15, 20, 25, 30, 35, 40, and 45 min and 1, 2, 4, 20, and 24 h after dosing. These frequent readings increased the resolution of the chlorine decay curve, especially for the rapid decay phase in the first 30 min. The second stage of the test was to conduct the same chlorine decay tests in 20-L jerrycans, which simulated the conditions of field water chlorination in a similar fashion to the setup used by Gallandat et al. [
20]. The final stage of the test was to use water from three water sources, to verify the relationships developed in the first two stages.
For chlorine dose selection, the 2 mg/L and 4 mg/L for clear and turbid water, respectively, were tested based on current recommendations [
8,
28,
29]. Additionally, 1 mg/L was selected to examine a lower dose condition, which was a typical dose recorded in the South Sudan refugee camps [
11].
For UVA
254 settings, the selections were based on several studies, which determined the UVA
254 value of numerous water sources (e.g., river and reservoir) ranging from 0.0 to 0.8 cm
−1 [
30,
31,
32], with the value for most cases found below 0.3 cm
−1. Therefore, the selected values of 0.05, 0.10, 0.20, 0.30 cm
−1 represented most cases studied.
As for the temperature settings, 10, 20, and 30 °C were used to represent temperate climate conditions, room temperature conditions, and hot climate conditions, respectively. Even though specific values were selected to construct the test matrix, once the relationships between parameters were determined, any condition in between the extreme values tested could be interpolated and determined.
3.6. Natural Water Samples Preparation
Three water samples, representing three natural water types, were obtained for verifying the developed model. Water from an observation well located in the University of Victoria was used to represent groundwater. Water from the source reservoir, which supplies Victoria’s drinking water, was selected to represent surface water. In addition, water from a pond located in a local golf course was tested to examine cases of more contaminated surface water. The sampled water was carried to the laboratory immediately and tested for turbidity, pH, UVA254, and ammonia concentration. The water was then incubated and tested at 30 °C for chlorine decay. All the water quality parameters were tested again before chlorine dosing.
3.7. Data Analysis
All three selected models were fitted to test data in MATLAB (R2019a) using the least squares method. Pearson’s correlation analysis between parameters were conducted in Excel (2020) using its built-in Data Analysis toolbox.
4. Results
Overall, all models except first order model achieved satisfactory fitting on all 64 data sets, which were chlorine decay data in synthetic test water. The R
2 distribution from data fitting for all five models are demonstrated in the box and whisker plot (
Figure 3).
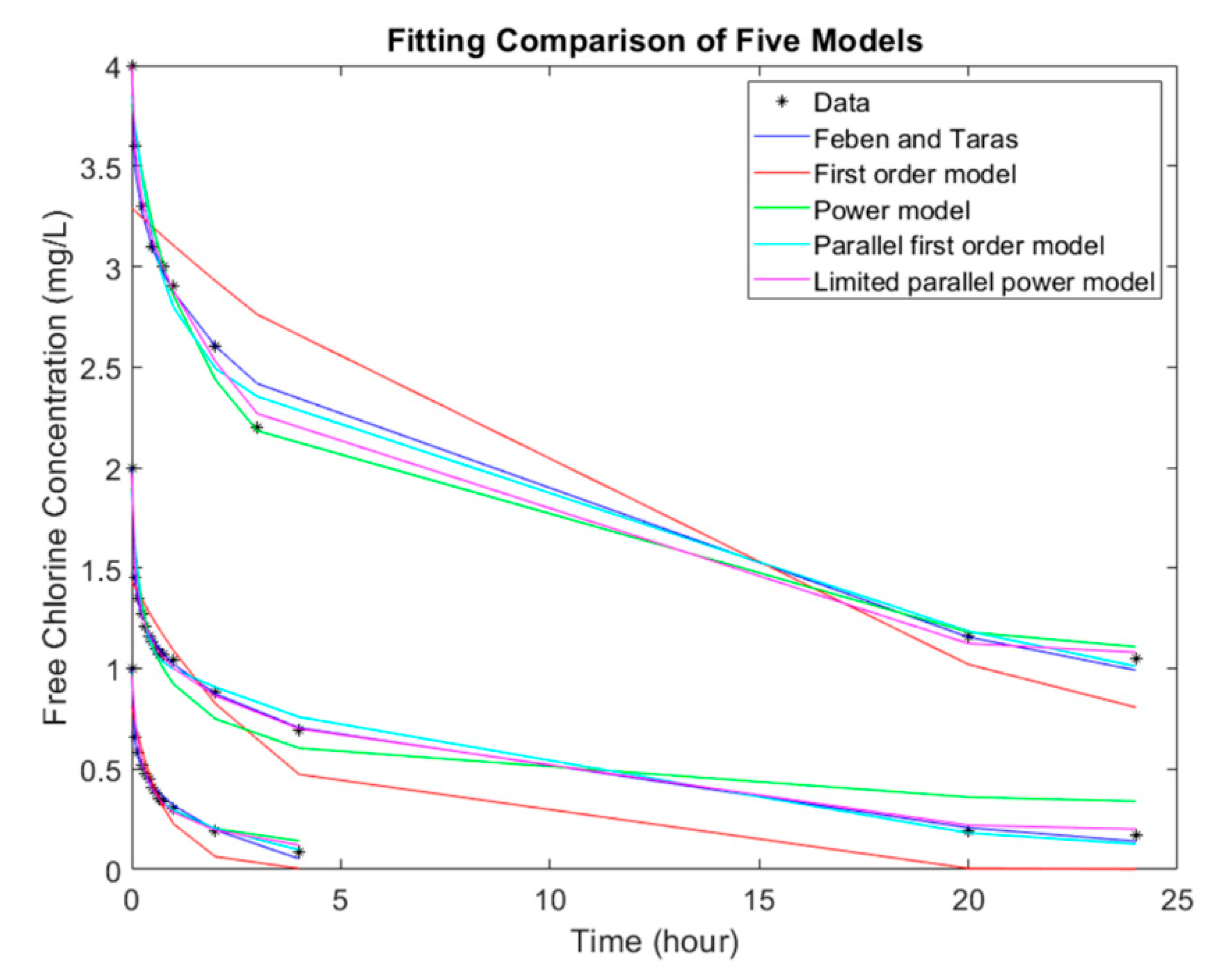
Figure 4 shows three randomly selected representative tests from the experiments and the regression curves from the five models to demonstrate their fitness. As shown in the results, the different available chlorine decay models in literature, except for first order model, can describe chlorine decay behavior very well, with 100% of the regression achieved an R
2 value above 0.9. The selection of models should be based primarily on model simplicity and the difficulty in model parameters calibration.
4.1. Correlation and Mathematical Relations
Pearson’s correlation analysis was conducted between estimated decay rate of the 36 bulk decay tests and their corresponding water quality parameters. The results from the analysis are shown in
Table 3. Based on the results, UVA
254 and 30-min chlorine demand of water appear to have significant impacts on chlorine decay rates. Feben and Taras’s empirical model and first order model were selected for further analysis because of their simplicity and the higher correlation values obtained between their
values and the water parameters. Due to the structures of these two models, water chemistry directly and solely impacts the
value in the equation, leading to high correlations between
and water parameters. For the rest of the models, the impacts from additional model parameters (i.e.,
in power models,
in parallel models) likely lower the correlations between k and water parameters.
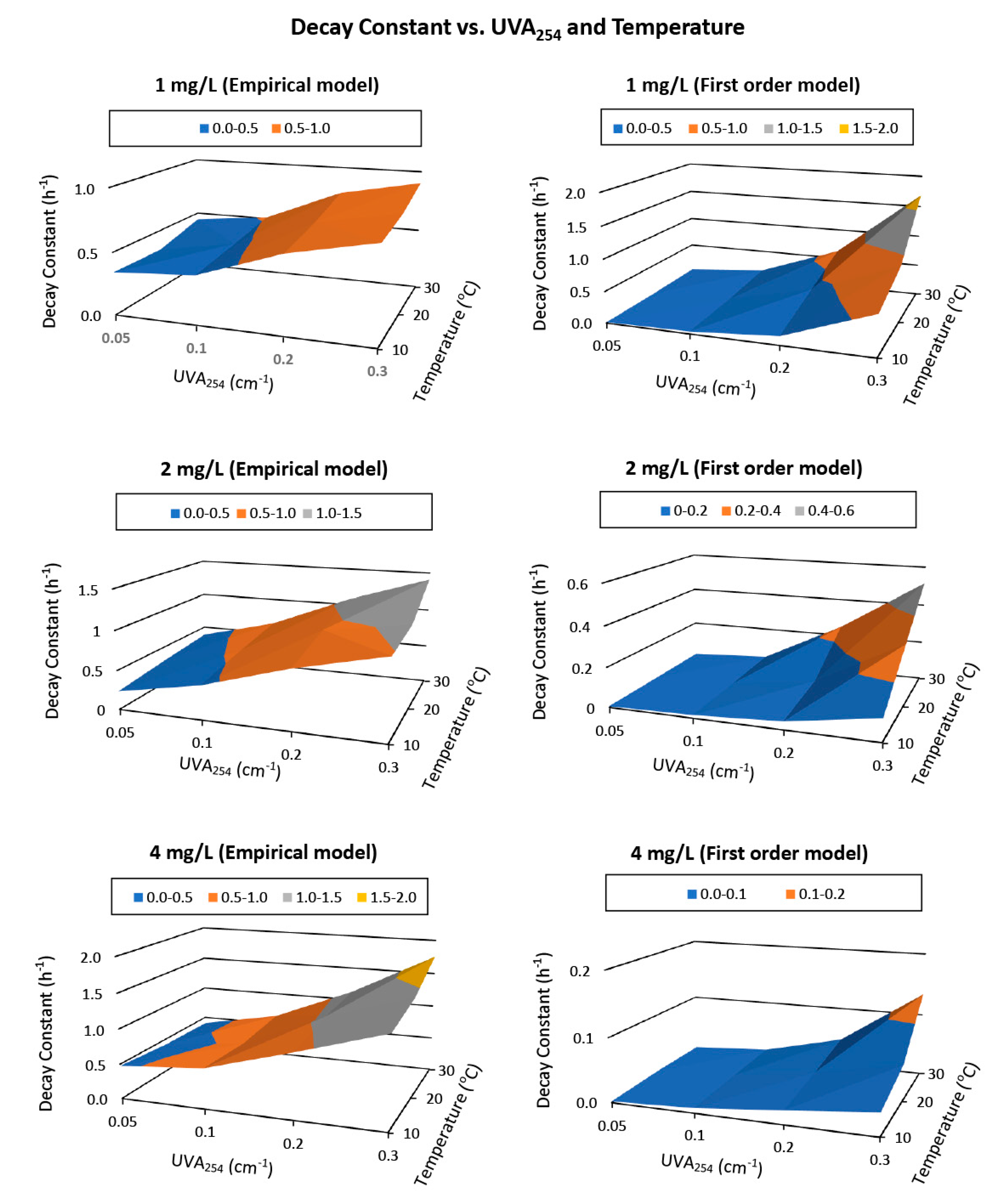
Model parameters from both Feben and Taras’s empirical model and first order model showed mathematical relationships with water’s UVA
254 value and the temperature (
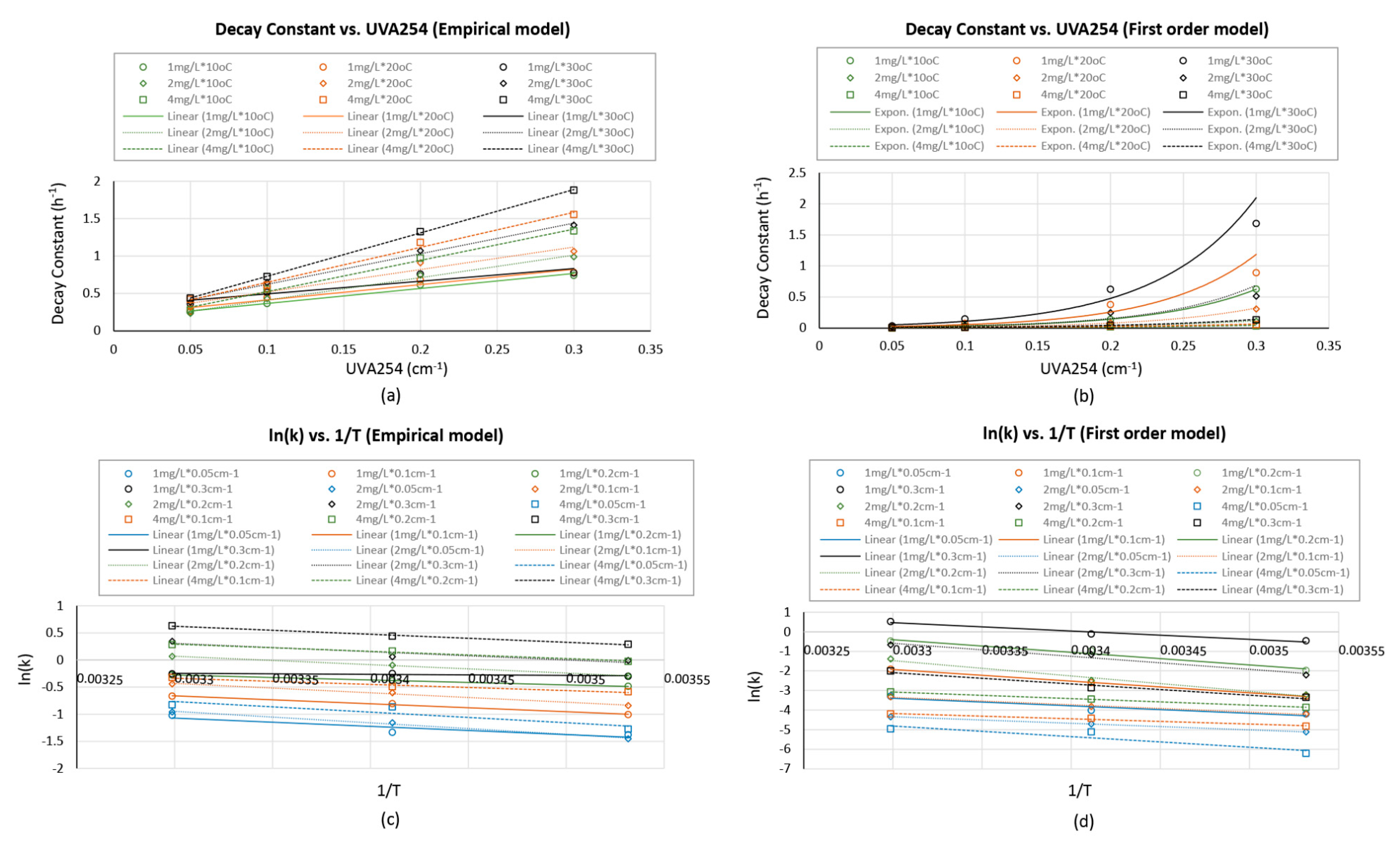
Figure 5). The decay constants for Feben and Taras’s empirical model and first order model increased linearly and exponentially with the increase in UVA
254, respectively (
Figure 6). Both models’ decay constants followed Arrhenius relationship with the water temperature, specifically, the linear relationship between the natural log of decay constant and the reciprocal of water temperature in Kelvin (
Figure 6). When the water parameters were determined in the field, the ‘
’ value could be estimated based on the identified relations.
4.2. Decay Kinetics and Water Chlorine Demand
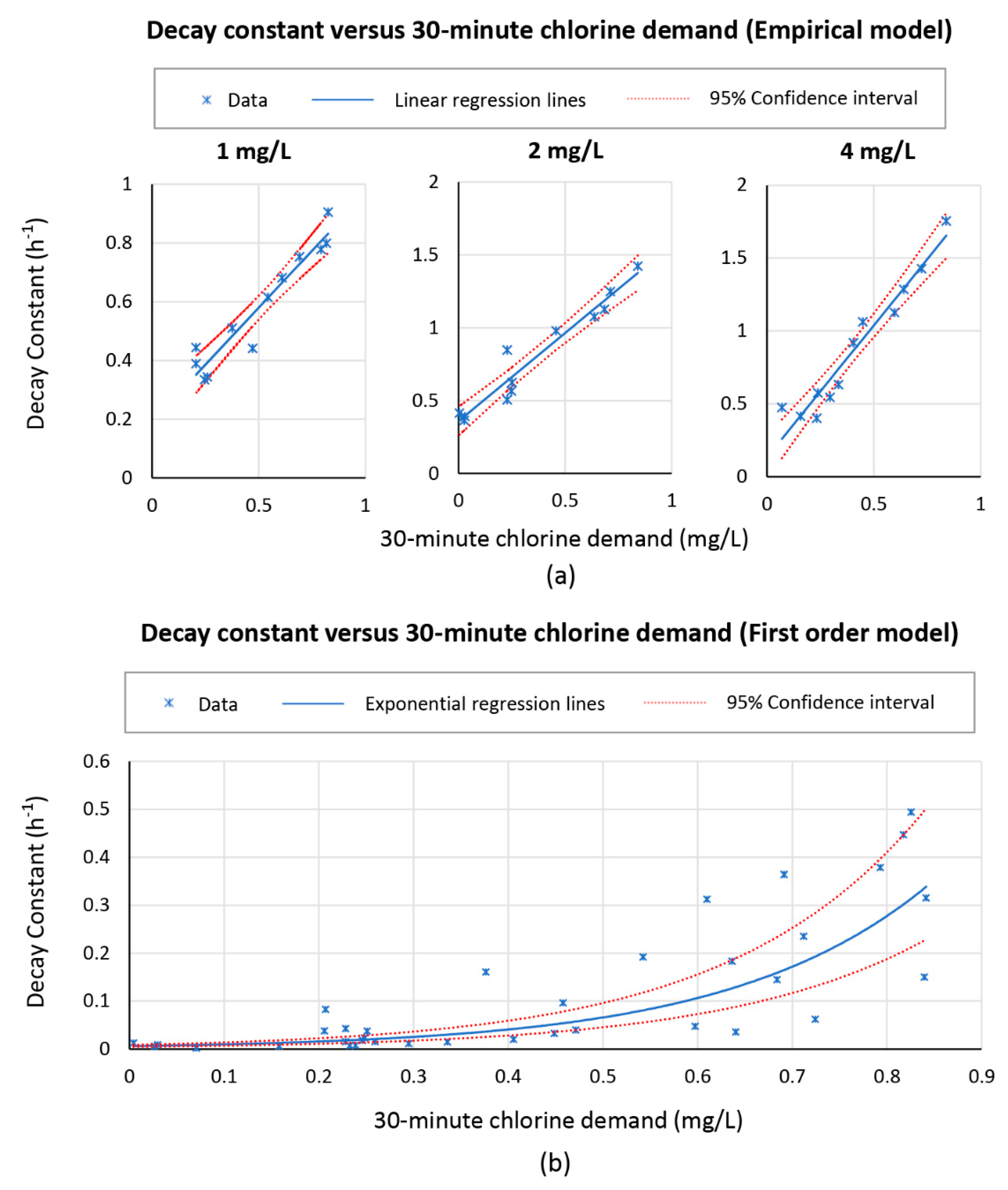
The relations between decay constants estimated from data fitting and the 30-min chlorine demand of the tested water are shown in
Figure 7. For Feben and Taras’s empirical model and a specific initial dose, the decay constant followed linearly with the 30-min chlorine demand. For the first order model, since the fast decay phase (data before 30 min) was excluded from the analysis, the initial dose changed from 1, 2, and 4 mg/L to the corresponding measured residual value at 30 min for each of the decay tests. Therefore, all the cases were plotted in the same figure. The relation between the two parameters was not obvious for all dose cases for first order model. However, generally, an exponential trend could be observed.
4.3. Quality Control
Four replicates were conducted for quality control purpose for the 36 bulk water tests. The four tests were selected randomly, and measured FCR were compared between the original and the replicates. Of the 36 FCR measurements in the four tests, the average error was 1% (−1% to 5%). For the eight replicates conducted for the 20-L jerrycans, the 96 measurements were all within 10% of the values from the initial tests.
4.4. Verification
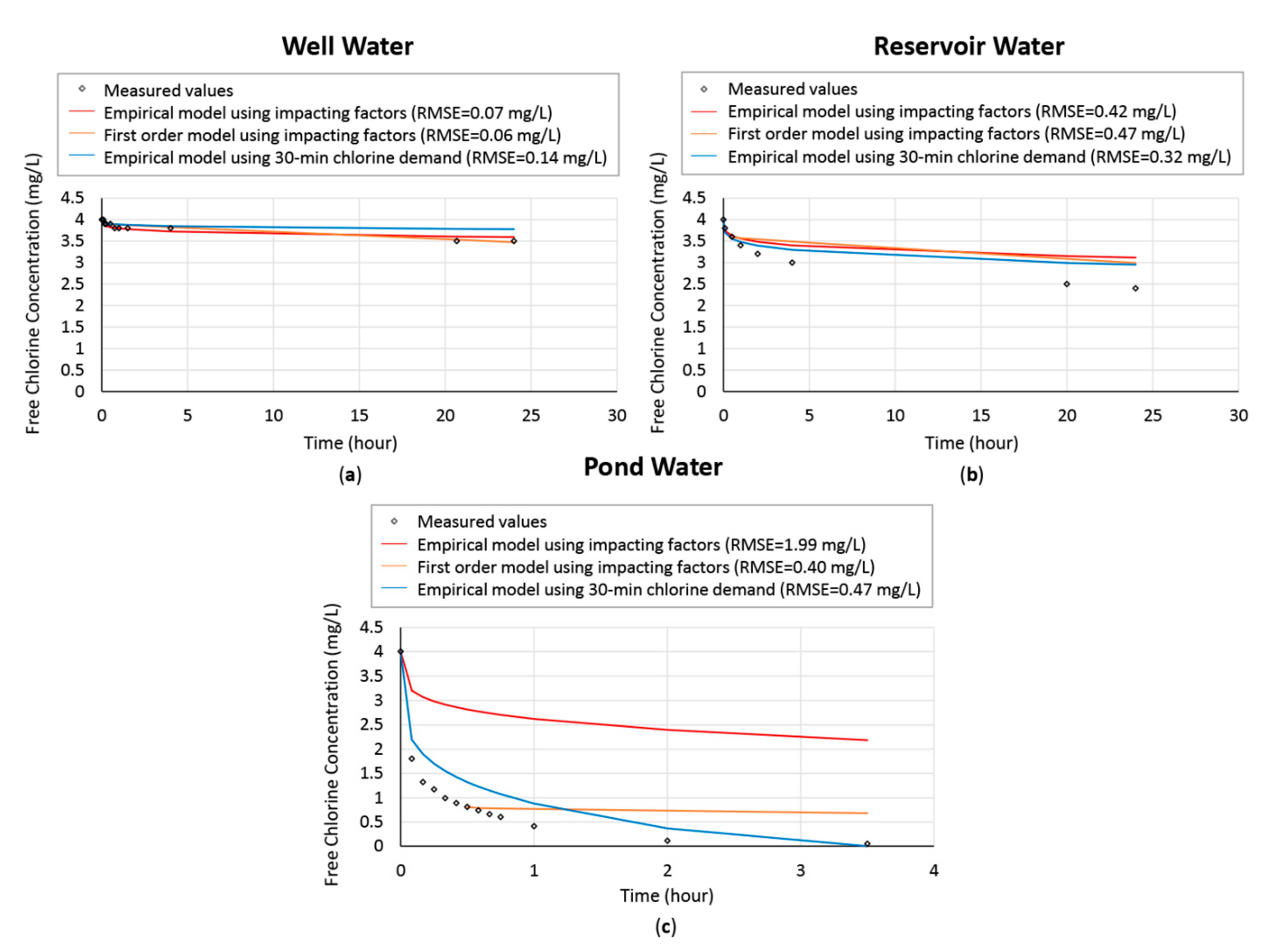
Water quality data of the three natural water samples obtained in Victoria were summarized in
Table 4 below. These values were measured right before the water was dosed with chlorine. The three water samples were dosed with a pre-determined dose of 4 mg/L chlorine, and the chlorine decay curves were predicted using the developed methods and compared with the actual measurements. A comparison of the predicted chlorine decay curves and actual decay curve can be seen in
Figure 8.
The two models with different methods for model parameter calibration performed similarly in prediction of chlroine decay for well water. Feben and Taras’s empirical model with the decay constant calibrated based on water’s 30-min chlorine demand could best capture the trend of chlorine decay with a relatively small root mean square error value for both reservoir water and pond water.
It can be seen in the case of well water that even though the turbidity of the water is higher (due to suspended mineral particles) than the other two water samples, the chlorine consumption is the lowest among the three water samples. This further proves that turbidity is a less ideal proxy for chlorine decay in comparison to UVA254 and 30-min chlorine demand.
5. Discussion
Traditionally, chlorine decay models need to be calibrated with extensive decay data for them to be able to describe chlorine decay in a water sample. This calibration requirement limits the application of chlorine decay models in contexts of humanitarian emergencies where data is usually unavailable and a rapid change of source water quality demands frequent model re-calibration.
This study showed that for simple model structures (Feben and Taras’s empirical model and first order model), model parameters showed high correlations with water quality parameters. The two models explored in the study could be calibrated using either actual water quality parameters (UVA254 and temperature) or using the 30-min chlorine demand, which is a proxy for the chlorine decay property of the water. This process substantially reduces the calibration requirement of the models, allowing the application of the chlorine decay models in humanitarian treatment contexts. The proposed model calibration methods also serve humanitarian field staff involved in water supply interventions by addressing the inadequacies and inconsistencies of current “rule-of-thumb” for chlorine dosing.
5.1. Model Calibration Using Impacting Factors and Their Mathematical Relations
Feben and Taras’s empirical model contains two parameters, decay constant “
” and power term “
”, to be determined from regression analysis. To evaluate relations between decay constant “
” and impacting factors, the influence from the power term “
” needs to be minimized. After the initial model fitting, “
” values generated from fitting the experimental data varied from 0.12 to 0.32, with 50% of the values located between 0.2 and 0.26. A second round of model fitting set the “
” value fixed at 0.22 (the average value from the first round) to remove the influence from “
”. As a result, the median R
2 value decreased from 0.988 to 0.960. The decay constant term was found linearly related to the change in water’s organic content under all doses and temperature conditions but with different slope. The
) over
plot (
Figure 6, plot c) showed linear relations between natural log of decay constant and the reciprocal of temperature in Kelvin. This verified the Arrhenius-type relationship. The slopes of the lines were very similar for all doses and organic content combinations with an average value of 1397
. Based on this result, the decay constant at a certain temperature from 10 °C to 30 °C can be estimated according to Equation (3) when the decay constant is known for the same water at any known temperature from 10 to 30 °C.
The analysis for the first order model was similar to those for the Feben and Taras’s empirical model; the decay constant increased with the increase in water organic content and water temperature. The relationships between the UVA
254 value and the decay constant under all three initial dosages conditions and all temperature settings were exponential. The four points for an initial dose of 1 mg/L in water with 0.2 and 0.3 cm
−1 for the 20- and 30-degree curves in
Figure 6 (plot b) did not follow the exponential trend, because the chlorine residual was completely reacted before 24 h, and the decay kinetics for the entire period was not able to be calculated. This also meant that the initial chlorine was not sufficient to maintain a chlorine residual of greater than 0.2 mg/L for 24 h for the tested conditions. Otherwise, all chlorine decay kinetics increased exponentially with the increase in water organics content. For impacts from temperature, the
) over
plot (
Figure 6, plot d) showed similar slopes of the regression lines for all doses and organic content combinations with an average value of 4818
. The values of the slope were less consistent in the case of first order model compared to those of Feben and Taras’s empirical model. Equation (4) can be used to adjust the
k value for first order model based on the water’s temperature.
5.2. Model Calibration Using 30-min Chlorine Demand
It was not feasible to calibrate the first order model with
using 30-min chlorine demand information because a large error was observed in the regression shown in
Figure 7 (plot b). Additionally, since the trend was exponential, the decay constant could increase to an unrealistic level as the chlorine demand increased further. Calibrating Feben and Taras’s empirical model with 30-min chlorine demand was feasible since the relations between estimated chlorine decay term and 30-min chlorine demand of water were linear. Feben and Taras’s empirical model calibrated with water’s 30-min chlorine demand produced the best prediction of chlorine decay in the natural water tested. This was likely due to the fact that 30-min chlorine demand incorporated other factors impacting chlorine decay, including temperature and chlorine consuming constituents. Thirty-min chlorine demand is also easily obtainable in the field. One disadvantage was that the relations between decay constant and measured 30-min chlorine demand for different initial doses differed, which did not permit the chlorine decay rate estimation at intermittent doses. Currently, only relations for chlorine doses of 1, 2, and 4 mg/L were determined.
For achieving a minimum FCR of 0.2 mg/L at 24 h of storage time, the maximum decay constant term was determined for the three doses. Corresponding maximum 30-min chlorine demand of the water can be determined based on the identified relationships shown in
Figure 7 (plot a). For an initial dose of 1, 2, and 4 mg/L chlorine, the 30-min chlorine demand of the water cannot exceed 0.26, 0.44, and 0.97 mg/L, respectively, to meet the FCR objective.
5.3. Discussion on Discovered Relations
Chlorine decay constant was observed to follow linear relationships with the UVA
254 in the water. Humic acids mostly contain organics with aromatic compounds, and the dominate reactions between chlorine and the aromatic compounds are electrophilic substitution followed by stepwise substitutions [
33]. An increase in humic acid concentration increases the available sites for the reactions. A linear increase in the UVA
254 of water leads to linear increase in chlorine consumption demonstrated by the consumption term
, in Feben and Taras’s empirical model.
We hypothesized that humic substances and temperature were the two main factors impacting the slow decay phase, and the results from reservoir and pond water showed that there were more substances in the water leading to higher chlorine decay in the slow decay phase. Potential mechanisms include chlorine consumption from ammonia, chloramines, and other organics such as fulvic acids.
From tests in the study, the 24-h chlorine consumption ranged from 0.5 mg/L to 4 mg/L depending on the UVA254 values. However, the turbidity of all test water was below 10 NTU. This again suggested that turbidity was indeed not an adequate indicator for chlorine decay in test water in the study.
5.4. Impacts from Storage Container
For all 16 tests conducted in the jerrycans, the chlorine decay kinetics were similar to those from tests in brown bottles under the same organics and temperature conditions. This implies that chlorine reactions in (new/clean) jerrycans can be treated as bulk water decay. Within 24 h, there were insignificant impacts from the environmental factors such as radiation and evaporation on chlorine decay. Additional chlorine reduction is possible in the field due to chlorine demand on the inner surface of the jerrycans. Frequent cleaning of the storage container can reduce chlorine demand from the containers and reduce the risk of water re-contamination [
34].
5.5. Additional Chlorine Reduction Mechanisms
The organics and temperature-calibrated model underpredicted the decay rate of chlorine in surface water sources where additional chlorine consuming substances might be present. Either a coagulation/flocculation pre-treatment was needed before applying the predictive tool, or more chlorine reduction reactions need to be researched to expand the tool’s applications.
5.6. Outlook
Ultimately, the discovered approach will be delivered through a user interface (e.g., spreadsheet and/or smartphone app). The models with their calibration methods can be built at the backstage. All the users need to do is to input the water parameters measured, and the tool automatically calculates and outputs the feasible initial doses for maintaining a 0.2 mg/L chlorine residual for 24 h of storage time. A preliminary tool (
Supplementary Material File S2) is attached for demonstration.
Verification and refinement of the tool will need to be conducted in field test. The robustness of the tool can be verified in varied contexts, with different source water as well as in different water treatment/distribution methods.
6. Conclusions
This study proves the possibility of chlorine decay model calibration using actual water parameters (UVA254, temperature, and 30-min chlorine demand) in the field, and this strategy satisfies the need for a practice-oriented, emergency-adapted dose prediction approach. With the discovered relations between chlorine decay model parameters and water parameters, humanitarian field staff can determine the appropriate initial chlorine dose for achieving FCR objectives by measuring several obtainable field water quality parameters.
Thirty-min chlorine demand was shown able to reflect actual chlorine decay kinetics. Together with the fact that it can be easily obtained in the field, it is recommended that 30-min chlorine demand be used as an indicator for chlorine dose design instead of using turbidity. Based on the relations discovered in the study, for an initial dose of 1, 2, and 4 mg/L chlorine, the 30-min chlorine demand of the water cannot exceed 0.26, 0.44, and 0.97 mg/L, respectively, for achieving a minimum FCR of 0.2 mg/L at 24 h of storage. The 30-min chlorine demand incorporates impacts such as UVA254 and temperature on chlorine decay kinetics. The exact values of the parameters were not required to be determined. Only 30-min chlorine demand is needed to evaluate if the initial doses were feasible for the test water in field.
To develop the tool for finding the appropriate initial dose, Feben and Taras’s empirical model can be used as the basic model. The power term “n” in the equation can be set fixed at 0.22, and the decay term “k” can be estimated with an embedded formula based on the three mathematical relations developed for the three initial doses in the study. The three doses, 1, 2, and 4 mg/L, can be evaluated at once on whether they are able to reach 0.2 mg/L FCR at 24 h based on the input value of 30-min chlorine demand. Doses able to achieve the objective are output for the humanitarian staff.