Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting
Abstract
:1. Introduction
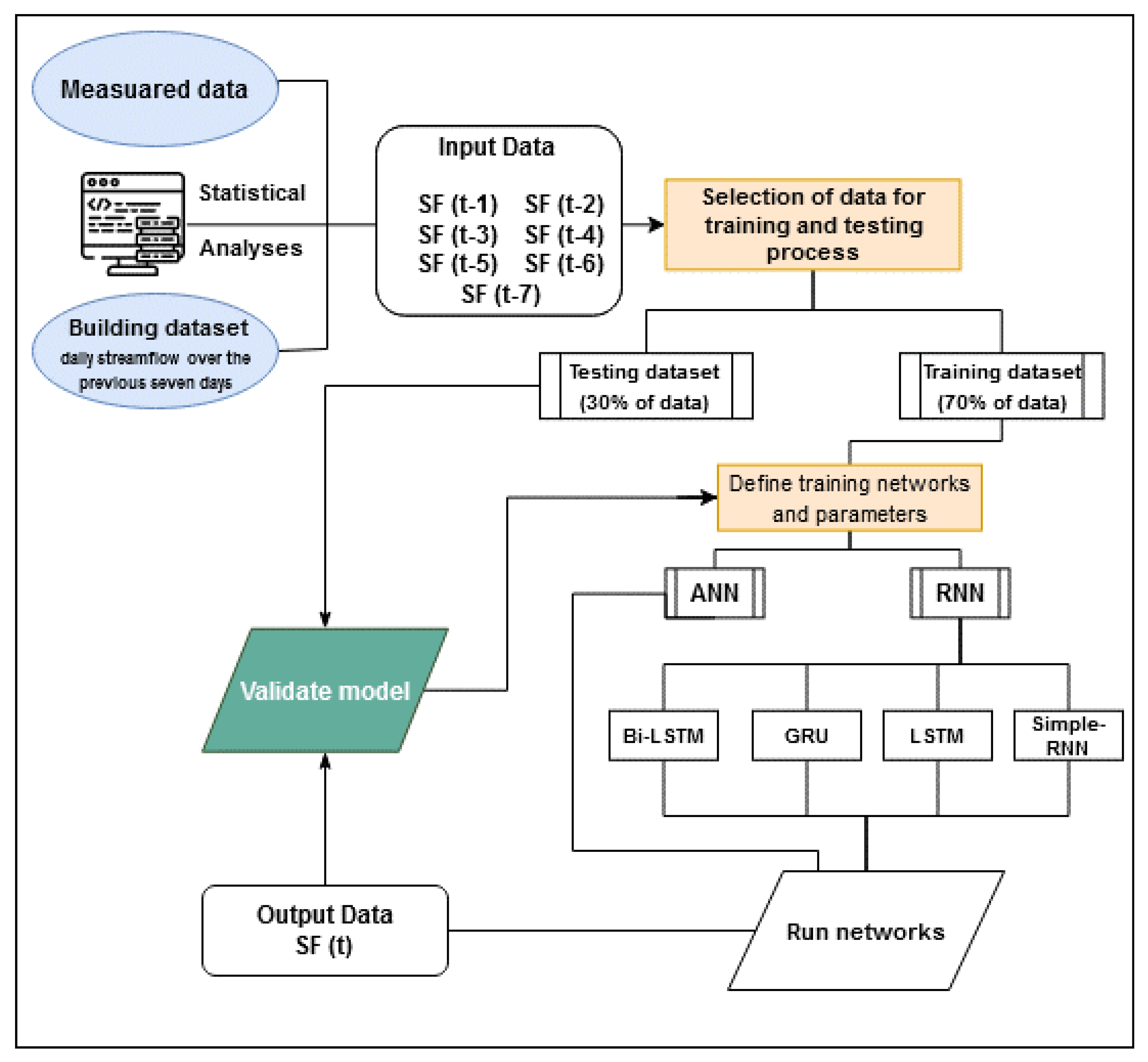
2. Materials and Methods
2.1. Study Area and Data
2.2. Artificial Neural Network (ANN)
2.3. Recurrent Neural Networks (RNN)
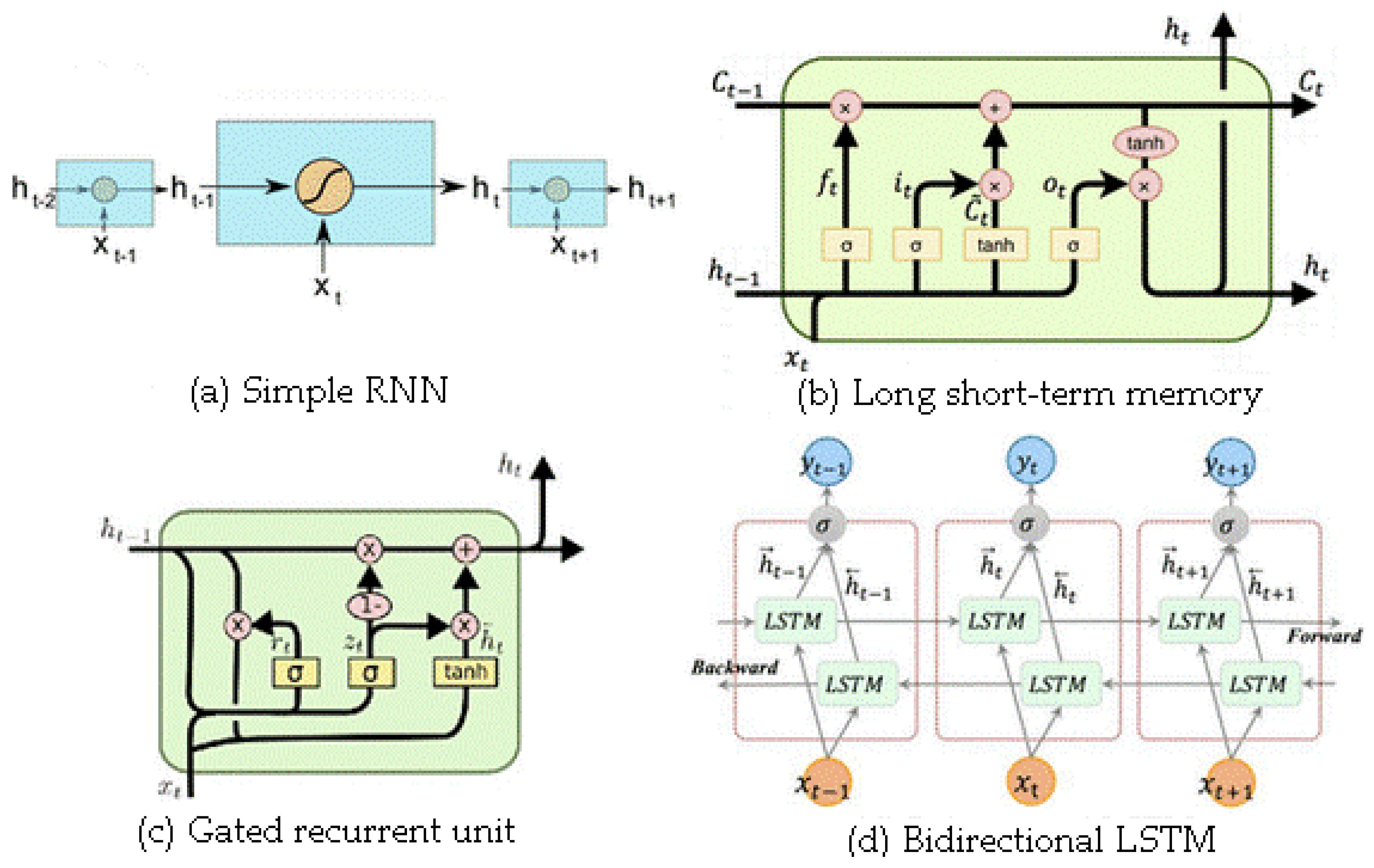
2.3.1. Simple Recurrent Neural Network (Simple RNN)
2.3.2. Long Short-Term Memory (LSTM)
2.3.3. Gated Recurrent Unit (GRU)
2.3.4. Bidirectional LSTM (Bi-LSTM)
2.4. Open-Source Software and Codes
2.5. Evaluation Criteria
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hamlet, A.F.; Lettenmaier, D.P. Columbia River Streamflow Forecasting Based on ENSO and PDO Climate Signals. J. Water Resour. Plan. Manag. 1999, 125, 333–341. [Google Scholar] [CrossRef]
- Ghumman, A.R.; Ghazaw, Y.M.; Sohail, A.R.; Watanabe, K. Runoff forecasting by artificial neural network and conventional model. Alex. Eng. J. 2011, 50, 345–350. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y. Learning Deep Architectures for AI by Yoshua Bengio; Now Publishers: Montréal, QC, Canada, 2009; Volume 2. [Google Scholar] [CrossRef]
- Elumalai, V.; Brindha, K.; Sithole, B.; Lakshmanan, E. Spatial interpolation methods and geostatistics for mapping groundwater contamination in a coastal area. Environ. Sci. Pollut. Res. 2017, 21, 11601–11617. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.N.; Raju, K.S.; Sathish, T. River Flow Forecasting using Recurrent Neural Networks. Water Resour. Manag. 2004, 18, 143–161. [Google Scholar] [CrossRef]
- Pan, T.-Y.; Wang, R.-Y.; Lai, J.-S. A deterministic linearized recurrent neural network for recognizing the transition of rainfall–runoff processes. Adv. Water Resour. 2007, 30, 1797–1814. [Google Scholar] [CrossRef]
- Firat, M. Comparison of Artificial Intelligence Techniques for river flow forecasting. Hydrol. Earth Syst. Sci. 2008, 12, 123–139. [Google Scholar] [CrossRef] [Green Version]
- Sattari, M.T.; Yurekli, K.; Pal, M. Performance evaluation of artificial neural network approaches in forecasting reservoir inflow. Appl. Math. Model. 2012, 36, 2649–2657. [Google Scholar] [CrossRef]
- Sattari, M.T.; Apaydin, H.; Ozturk, F. Flow estimations for the Sohu Stream using artificial neural networks. Envron. Earth Sci. 2011, 66, 2031–2045. [Google Scholar] [CrossRef]
- Chen, P.-A.; Chang, L.-C.; Chang, L.-C. Reinforced recurrent neural networks for multi-step-ahead flood forecasts. J. Hydrol. 2013, 497, 71–79. [Google Scholar] [CrossRef]
- Sattari, M.T.; Pal, M.; Apaydin, H.; Ozturk, F. M5 model tree application in daily river flow forecasting in Sohu Stream, Turkey. Water Resour. 2013, 40, 233–242. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Liu, F.; Xu, F.; Yang, S. A Flood Forecasting Model Based on Deep Learning Algorithm via Integrating Stacked Autoencoders with BP Neural Network. In Proceedings of the 2017 IEEE Third International Conference on Multimedia Big Data (BigMM), Laguna Hills, CA, USA, 19–21 April 2017; pp. 58–61. [Google Scholar] [CrossRef]
- Esmaeilzadeh, B.; Sattari, M.T.; Samadianfard, S. Performance evaluation of ANNs and an M5 model tree in Sattarkhan Reservoir inflow prediction. ISH J. Hydraul. Eng. 2017, 11, 1–10. [Google Scholar] [CrossRef]
- Amnatsan, S.; Yoshikawa, S.; Kanae, S. Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand. Water 2018, 10, 1614. [Google Scholar] [CrossRef] [Green Version]
- Chiang, Y.-M.; Hao, R.-N.; Zhang, J.-Q.; Lin, Y.-T.; Tsai, W.-P. Identifying the Sensitivity of Ensemble Streamflow Prediction by Artificial Intelligence. Water 2018, 10, 1341. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Peng, Q.; Lin, J.; Wang, D.; Liu, X.; Zhuang, J. Simulating Reservoir Operation Using a Recurrent Neural Network Algorithm. Water 2019, 11, 865. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Guo, S.; Xu, C.-Y.; Chang, F.-J.; Yin, J. Improving the Reliability of Probabilistic Multi-Step-Ahead Flood Forecasting by Fusing Unscented Kalman Filter with Recurrent Neural Network. Water 2020, 12, 578. [Google Scholar] [CrossRef] [Green Version]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef] [Green Version]
- Kao, I.-F.; Zhou, Y.; Chang, L.-C.; Chang, F.-J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, T.; Zhang, C.; Sun, N. Data Pre-Analysis and Ensemble of Various Artificial Neural Networks for Monthly Streamflow Forecasting. Water 2018, 10, 628. [Google Scholar] [CrossRef] [Green Version]
- Anonymous. Karaman Province Government, Statistics of Agricultural Section. Available online: https://karaman.tarimorman.gov.tr/ (accessed on 15 March 2019). (In Turkish)
- Anonymous. Mevlana Development Agency, Ermenek District Report 2014. Available online: http://www.mevka.org.tr/Yukleme/Uploads/DsyHvaoSM719201734625PM.pdf (accessed on 15 March 2019). (In Turkish).
- DSI. Available online: http://www.dsi.gov.tr/dsi-resmi-istatistikler (accessed on 15 March 2019). (In Turkish)
- Ghaffarinasab, N.; Ghazanfari, M.; Teimoury, E. Hub-and-spoke logistics network design for third party logistics service providers. Int. J. Manag. Sci. Eng. Manag. 2015, 11, 1–13. [Google Scholar] [CrossRef]
- Anonymous. Ermenek Dam and Hydroelectricity Facility Catalogue; The Ministry of Energy and Natural Resources: Karaman, Turkey, 2019. (In Turkish)
- Gao, C.; Gemmer, M.; Zeng, X.; Liu, B.; Su, B.; Wen, Y. Projected streamflow in the Huaihe River Basin (2010–2100) using artificial neural network. Stoch. Environ. Res. Risk Assess. 2010, 24, 685–697. [Google Scholar] [CrossRef]
- Li, F.; Johnson, J.; Yeung, S. Cource Notes. Lecture 4—1 April 12, 2018. Available online: http://cs231n.stanford.edu/slides/2018/cs231n_2018_lecture04.pdf (accessed on 20 May 2019).
- Schmidhuber, J. System Modeling and Optimization. The Technical University of Munich (TUM) Habilitation Thesis. 1993. Available online: http://people.idsia.ch/~juergen/onlinepub.html (accessed on 20 May 2019).
- Graves, A.; Mohamed, A.-R.; Hinton, G.; Graves, A. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Witten, I.; Frank, E.; Hall, M.; Pal, C. Data Mining. In Practical Machine Learning Tools and Techniques, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2016; p. 654. ISBN 9780128042915. [Google Scholar]
- Cui, Z.; Member, S.; Ke, R.; Member, S.; Wang, Y. Deep Stacked Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction. In Proceedings of the UrbComp 2017: The 6th International Workshop on Urban Computing, Halifax, NS, Canada, 14 August 2017; 2017; pp. 1–12. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder–Decoder Approaches. In Proceedings of the SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 7 October 2014; pp. 103–111. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- The Effect of Dropout on the Network Structure. Available online: https://blog.faradars.org/ (accessed on 20 May 2019).
- Ashcroft, M. Advanced Machine Learning. Available online: https://www.futurelearn.com/courses/advanced-machine-learning/0/steps/49552 (accessed on 20 May 2019).
- Train/Val Accuracy. Available online: http://cs231n.github.io/neural-networks-3/#accuracy (accessed on 20 May 2019).
- Chiew, F.; Stewardson, M.J.; McMahon, T. Comparison of six rainfall-runoff modelling approaches. J. Hydrol. 1993, 147, 1–36. [Google Scholar] [CrossRef]
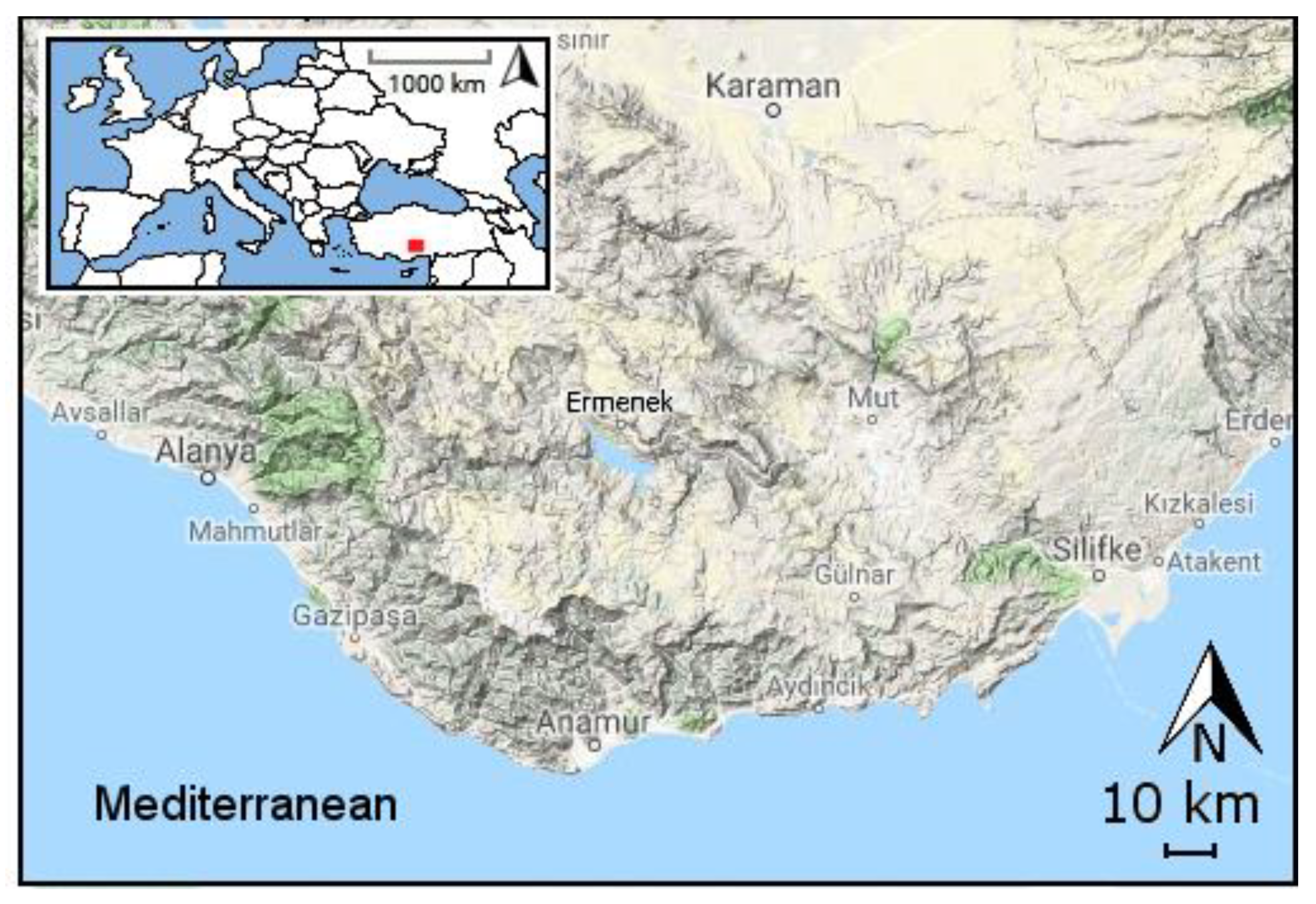
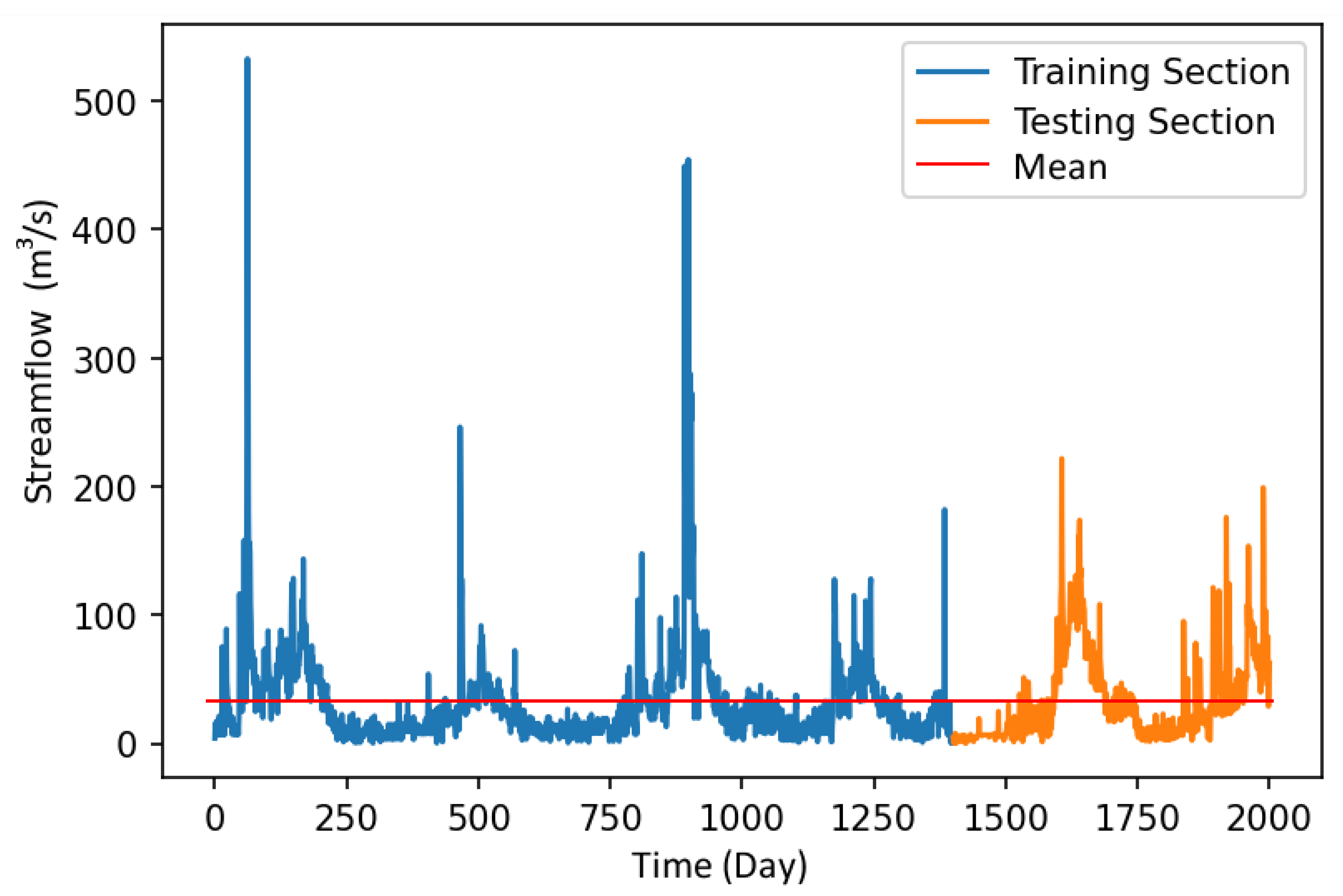


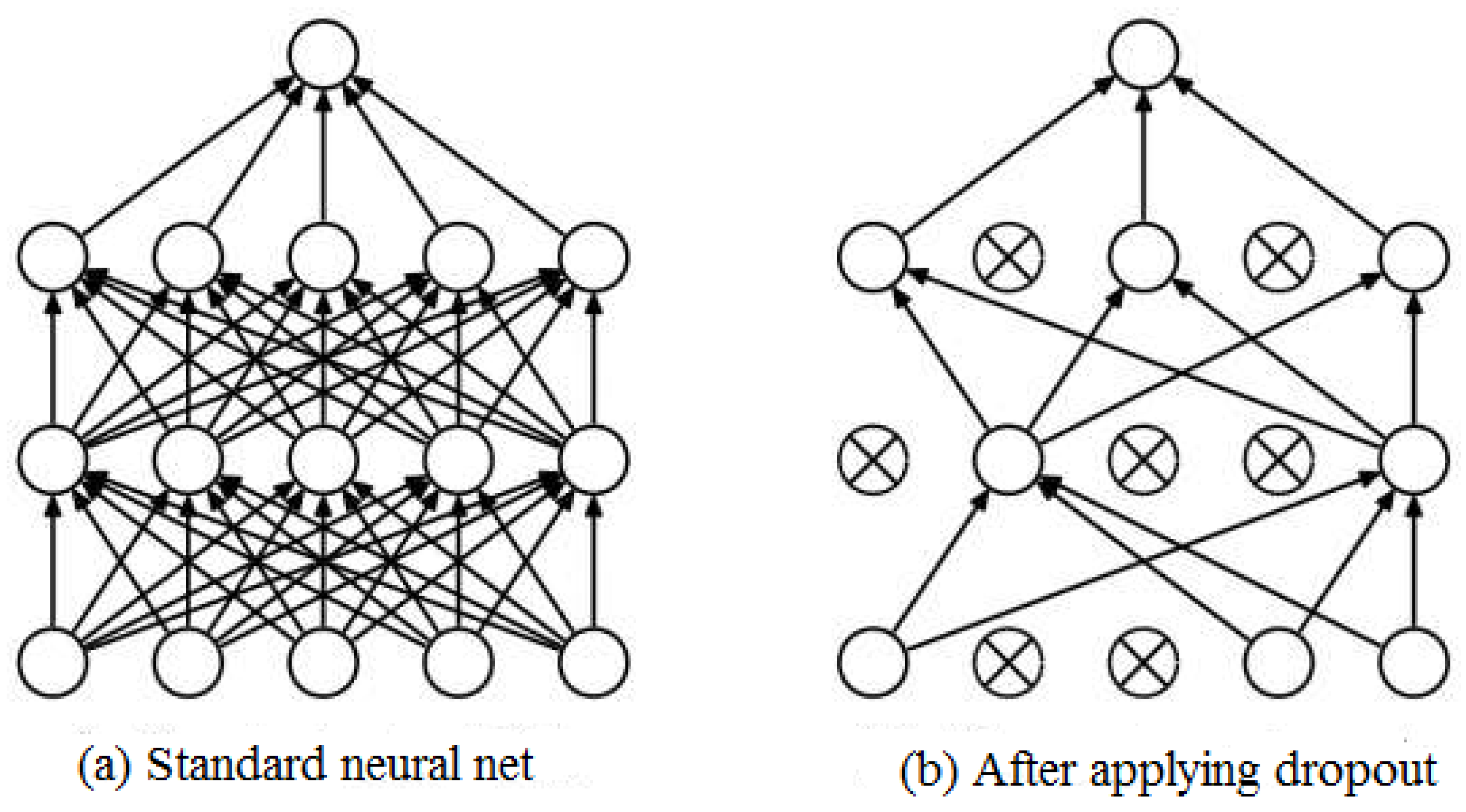


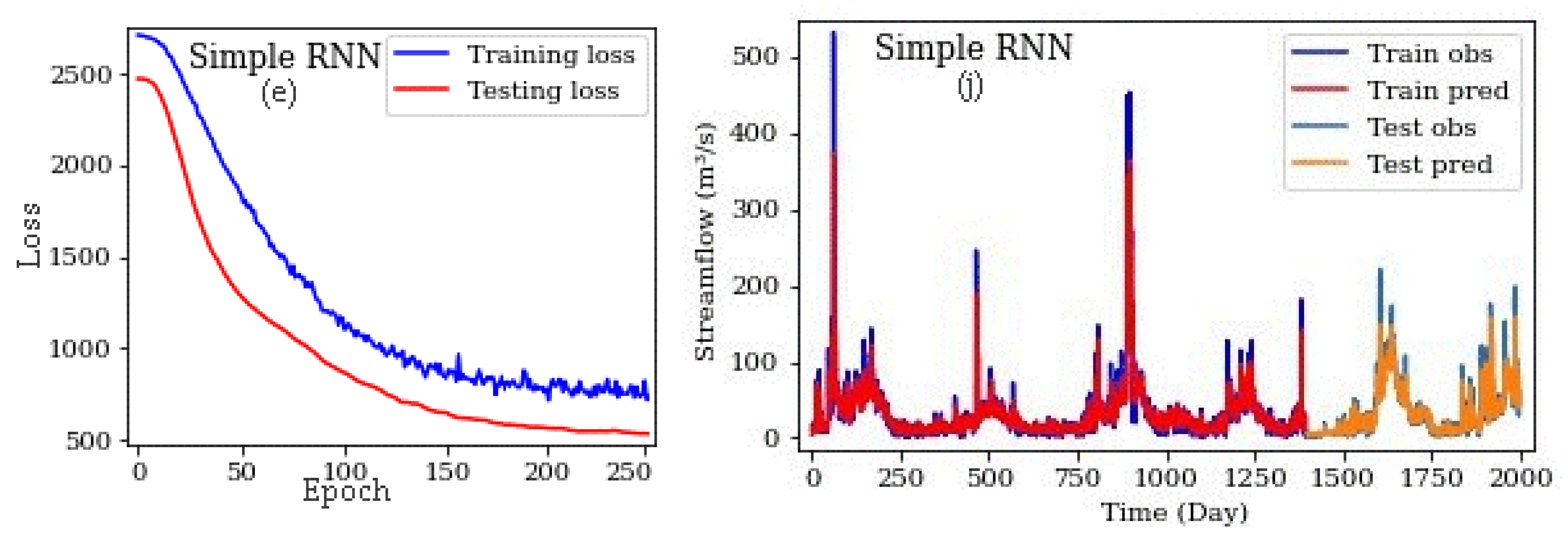
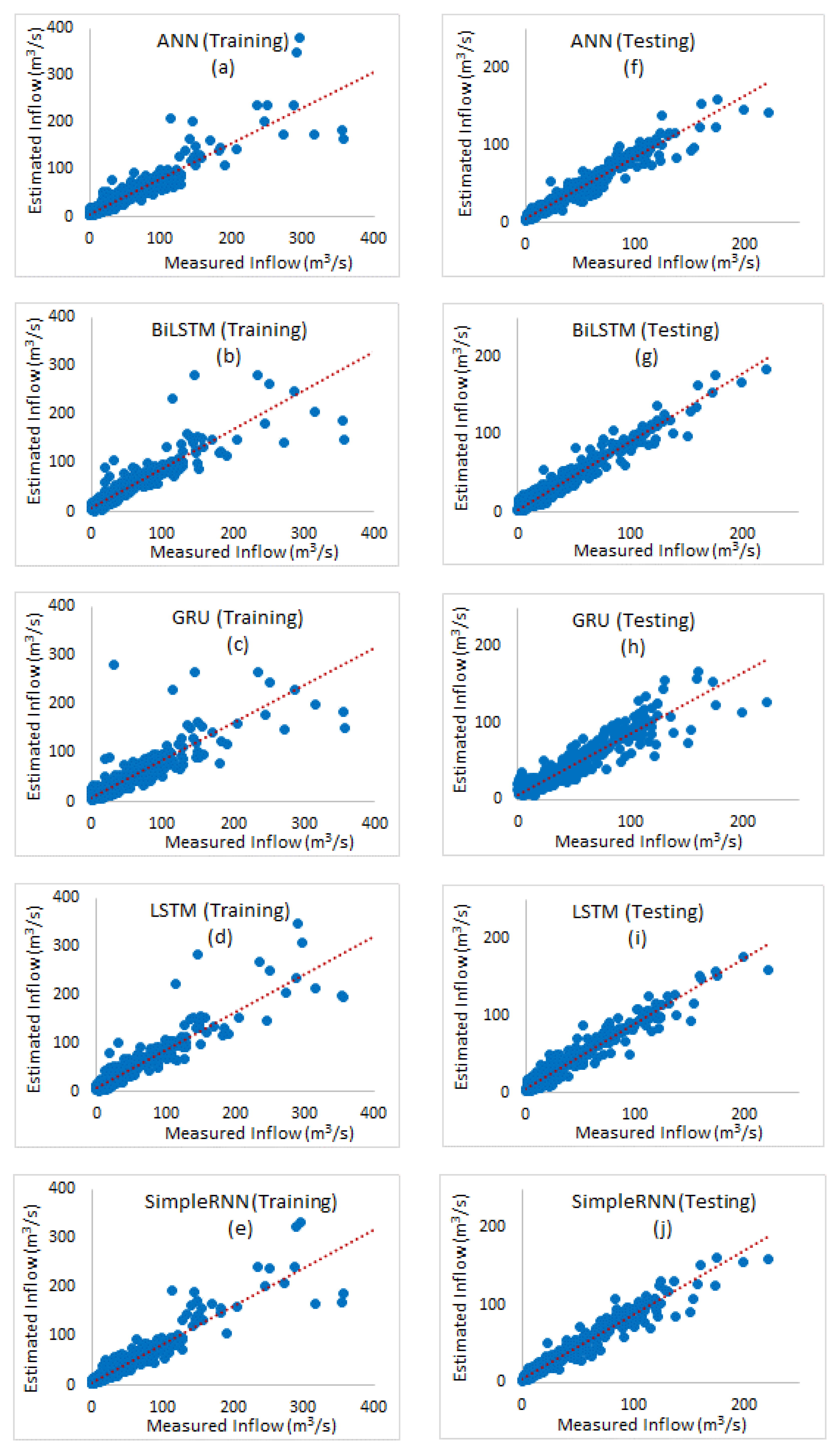
| Variable | Min | Max | Mean | Std. Deviation |
|---|---|---|---|---|
| Streamflow (m3/s) | 0.04 | 532.76 | 33.21 | 39.32 |
| Rainfall (mm/day) | 0.0 | 52.00 | 1.40 | 4.57 |
| Method | Lr | Decay | Epoch | Run Time | CC | NS | RMSE | MAE | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |||||
| ANN | 1 × 10−3 | 1 × 10−2 | 100 | 0:00:09 | 0.8 | 0.8 | 0.24 | 0.1 | 35.73 | 33.4 | 23.37 | 24.13 |
| 1 × 10−3 | 1 × 10−2 | 300 | 0:00:29 | 0.82 | 0.82 | 0.43 | 0.36 | 30.91 | 28.86 | 19.56 | 19.65 | |
| 1 × 10−3 | 1 × 10−2 | 500 | 0:00:51 | 0.86 | 0.85 | 0.73 | 0.72 | 21.11 | 18.71 | 10.51 | 10.35 | |
| Bi-LSTM | 1 × 10−4 | 1 × 10−3 | 100 | 0:02:45 | 0.83 | 0.83 | 0.64 | 0.56 | 33.7 | 29.19 | 21.24 | 20.81 |
| 1 × 10−4 | 1 × 10−2 | 300 | 0:07:29 | 0.88 | 0.84 | 0.68 | 0.61 | 24.65 | 23.43 | 15.35 | 15.31 | |
| 1 × 10−4 | 1 × 10−2 | 500 | 0:10:37 | 0.88 | 0.86 | 0.78 | 0.73 | 19.11 | 18.2 | 9.52 | 10.1 | |
| GRU | 1 × 10−4 | 1 × 10−2 | 100 | 0:00:47 | 0.84 | 0.8 | 0.41 | 0.36 | 31.33 | 28.16 | 20.32 | 19.92 |
| 1 × 10−2 | 1 × 10−2 | 300 | 00:02.0 | 0.9 | 0.85 | 0.82 | 0.72 | 17.55 | 18.7 | 8.93 | 10.63 | |
| 1 × 10−4 | 1 × 10−3 | 500 | 00:03.1 | 0.9 | 0.85 | 0.77 | 0.67 | 19.58 | 20.12 | 11.67 | 12.46 | |
| LSTM | 1 × 10−4 | 1 × 10−3 | 100 | 0:00:53 | 0.85 | 0.81 | 0.5 | 0.41 | 26.98 | 28.89 | 18.53 | 18.78 |
| 1 × 10−4 | 1 × 10−3 | 300 | 0:02:17 | 0.89 | 0.84 | 0.76 | 0.64 | 20.1 | 21.16 | 12.15 | 13.15 | |
| 1 × 10−4 | 1 × 10−2 | 500 | 0:03:37 | 0.87 | 0.87 | 0.74 | 0.74 | 20.75 | 17.92 | 10.22 | 9.98 | |
| Simple RNN | 1 × 10−4 | 1 × 10−3 | 100 | 0:00:30 | 0.8 | 0.83 | 0.36 | 0.31 | 32.63 | 29.25 | 21.74 | 21.21 |
| 1 × 10−4 | 1 × 10−3 | 300 | 0:01:09 | 0.85 | 0.86 | 0.71 | 0.71 | 21.94 | 18.31 | 10.71 | 10.11 | |
| 1 × 10−4 | 1 × 10−3 | 500 | 0:01:46 | 0.87 | 0.85 | 0.69 | 0.65 | 20.81 | 21.16 | 13.4 | 14.35 | |
| Prediction Methods | Observed | |||||||
|---|---|---|---|---|---|---|---|---|
| Statistic | ANN | Bi-LSTM | GRU | LSTM | Simple RNN | Train Data | Test Data | All Data |
| Min (m3/s) | 2.40 | 2.16 | 4.74 | 1.73 | 1.76 | 0.09 | 0.04 | 0.04 |
| Max (m3/s) | 158.45 | 182.93 | 167.07 | 175.63 | 160.69 | 532.76 | 221.64 | 532.76 |
| Mean (m3/s) | 32.05 | 34.57 | 34.14 | 33.93 | 32.67 | 32.42 | 34.99 | 33.21 |
| Stdev (m3/s) | 28.8 | 31.3 | 29.7 | 30.6 | 30.2 | 40.9 | 35.2 | 39.3 |
| N. of instances | 600 | 600 | 600 | 600 | 600 | 1400 | 600 | 2000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.-W. Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting. Water 2020, 12, 1500. https://doi.org/10.3390/w12051500
Apaydin H, Feizi H, Sattari MT, Colak MS, Shamshirband S, Chau K-W. Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting. Water. 2020; 12(5):1500. https://doi.org/10.3390/w12051500
Chicago/Turabian StyleApaydin, Halit, Hajar Feizi, Mohammad Taghi Sattari, Muslume Sevba Colak, Shahaboddin Shamshirband, and Kwok-Wing Chau. 2020. "Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting" Water 12, no. 5: 1500. https://doi.org/10.3390/w12051500
APA StyleApaydin, H., Feizi, H., Sattari, M. T., Colak, M. S., Shamshirband, S., & Chau, K.-W. (2020). Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting. Water, 12(5), 1500. https://doi.org/10.3390/w12051500








