Spatiotemporal Water Yield Variations and Influencing Factors in the Lhasa River Basin, Tibetan Plateau
Abstract
1. Introduction
2. Materials and Methods
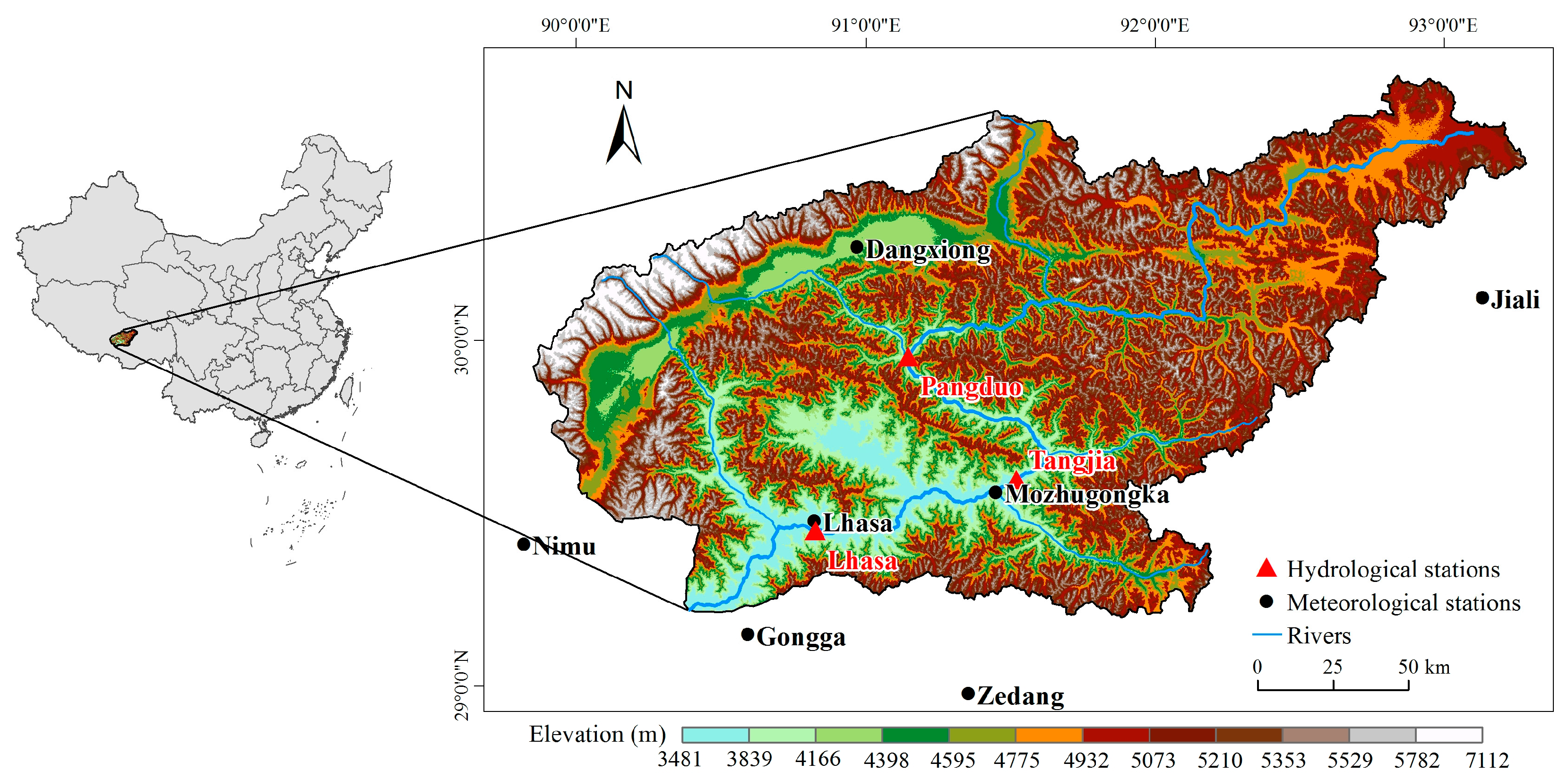
2.1. Study Area
2.2. Seasonal Water Yield Model
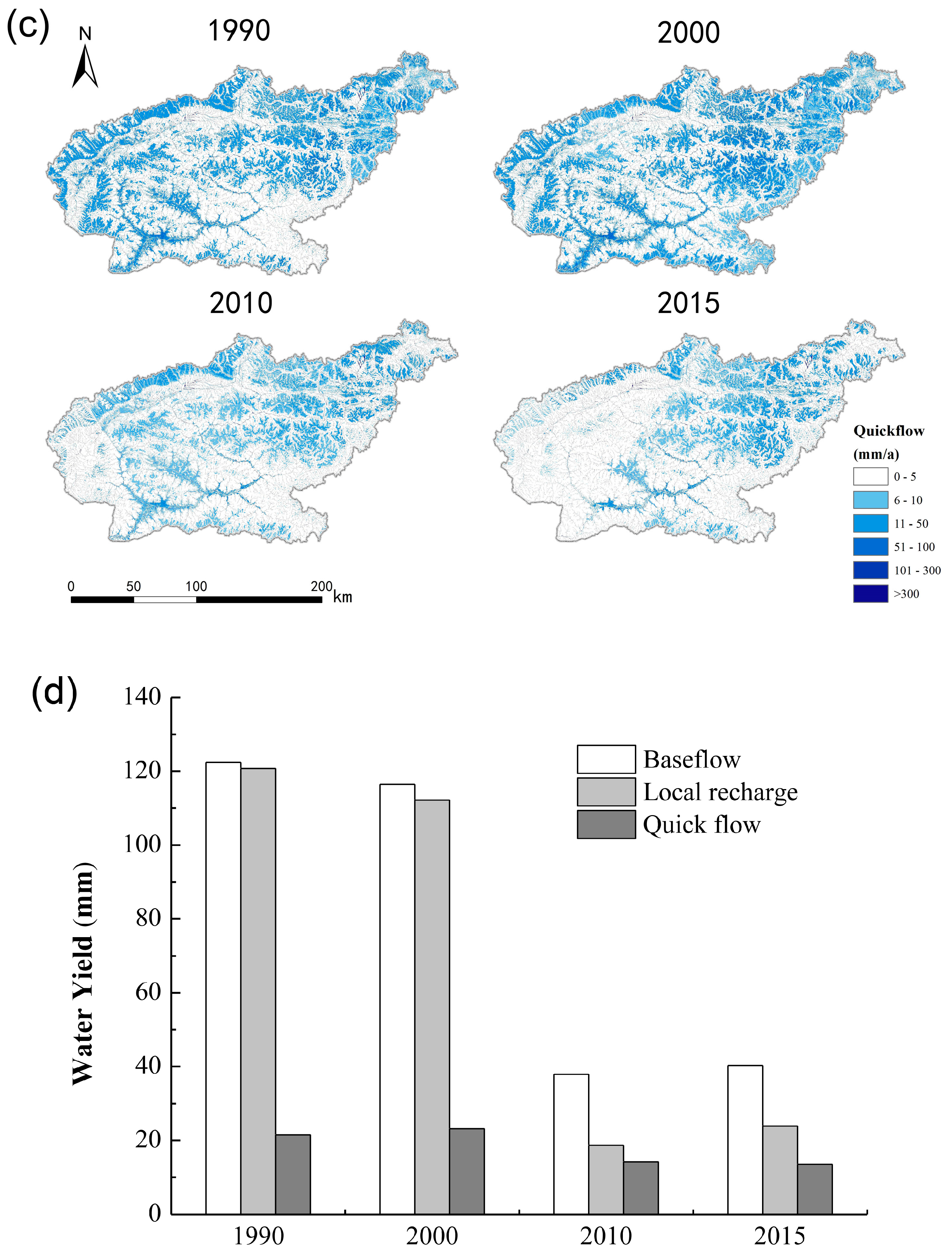
2.2.1. Quick Flow
2.2.2. Local Recharge
2.2.3. Baseflow
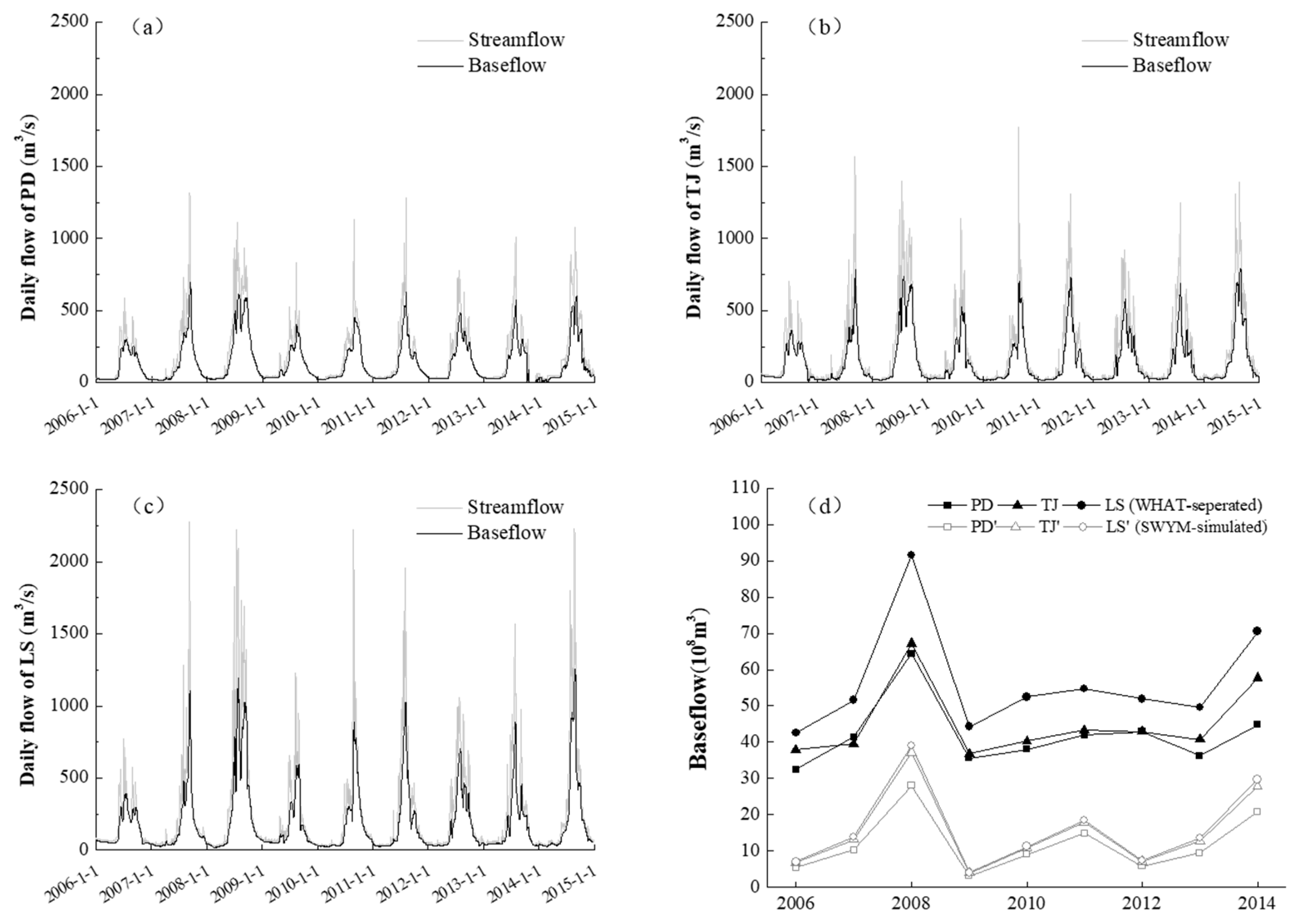
2.3. Baseflow Separation
2.4. Sensitivity Analysis: Morris Screening Method
2.5. Quantifying Relative Contributions of Influencing Factors
2.6. Data Sources
3. Results
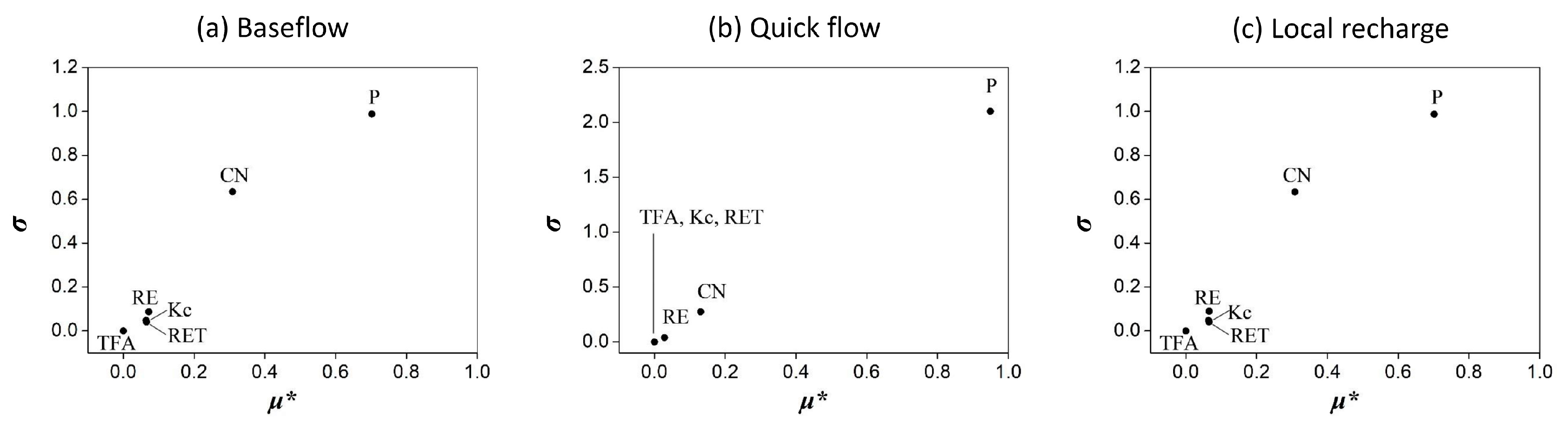
3.1. Sensitivity Analysis and Model Validation
3.2. Changing Trends of Influencing Factors
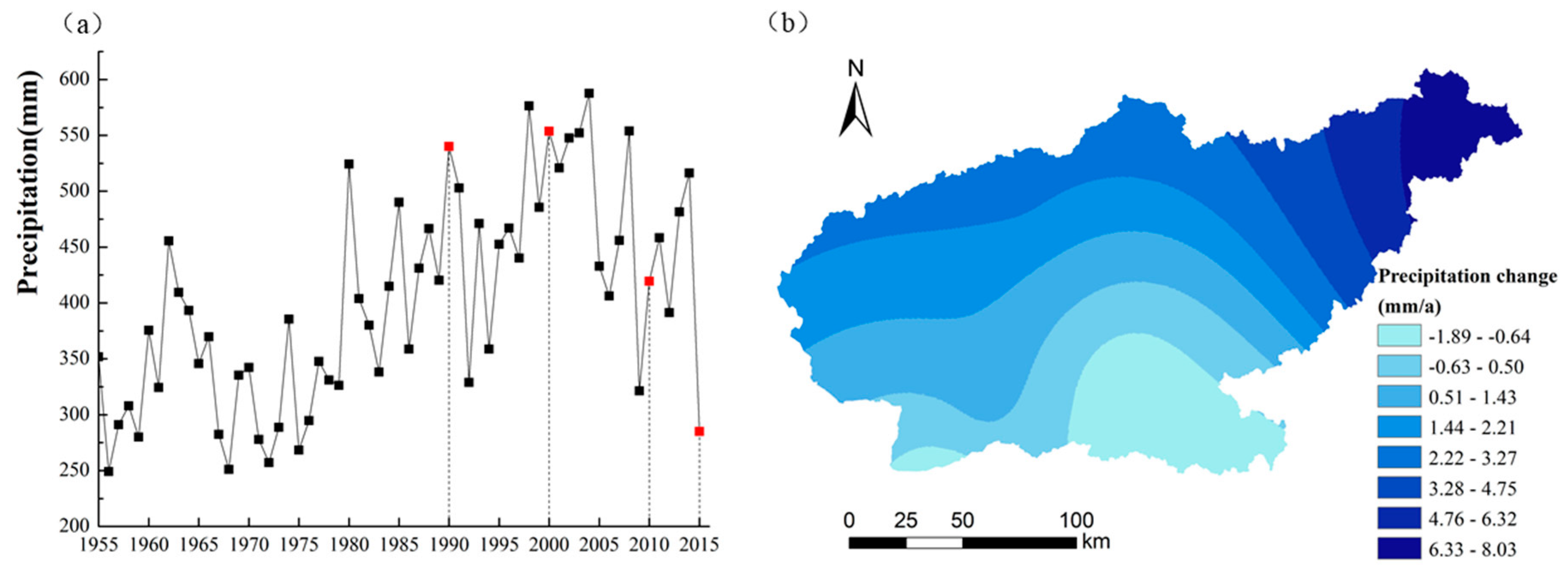
3.2.1. Precipitation
3.2.2. Land Cover
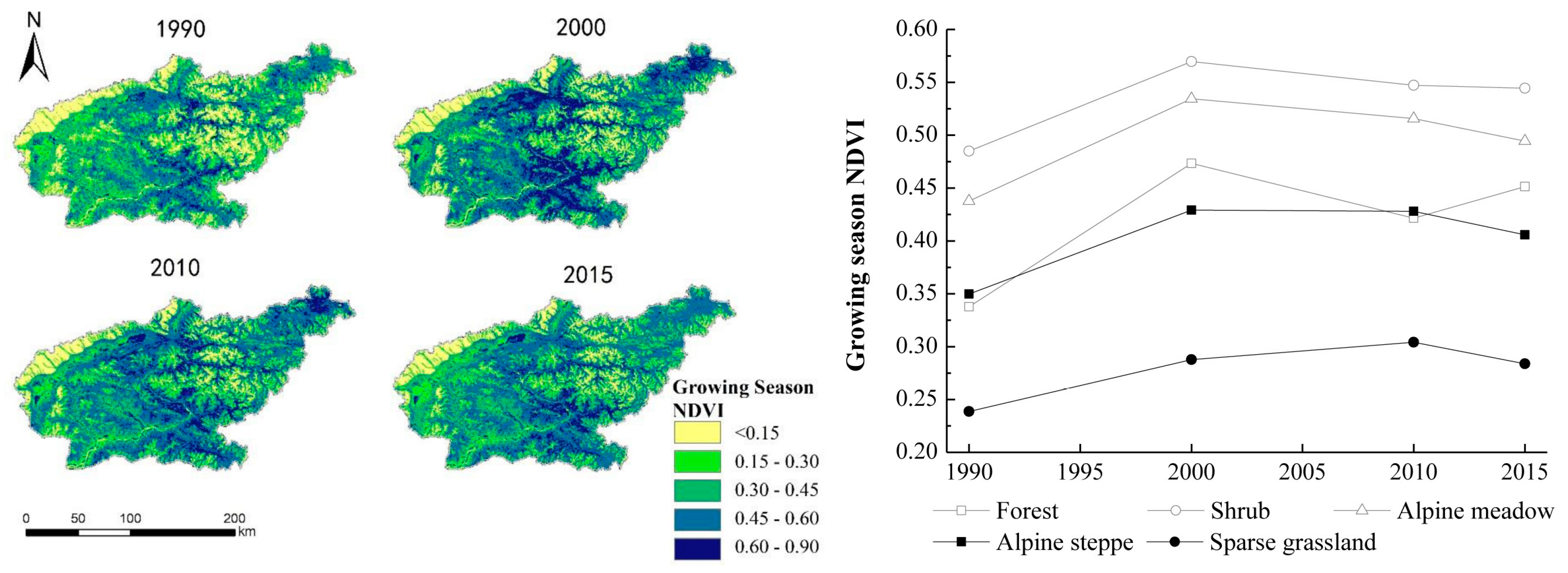
3.2.3. Normalized Difference Vegetation Index (NDVI)
3.3. Water Yield Change
3.4. Relative Contributions of Influencing Factors
4. Discussion
4.1. Model Performance and Uncertainties
4.2. Driving Force Analysis: Climate Change and Human Activities in Combination
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fan, M.; Shibata, H. Spatial and temporal analysis of hydrological provision ecosystem services for watershed conservation planning of water resources. Water Resour. Manag. 2014, 28, 3619–3636. [Google Scholar] [CrossRef]
- Muthuwatta, L.; Amarasinghe, U.A.; Sood, A.; Lagudu, S. Reviving the “Ganges Water Machine”: Where and how much? Hydrol. Earth Syst. Sci. 2017, 12, 9741–9763. [Google Scholar] [CrossRef]
- Qin, J.; Ding, Y.J.; Han, T.D.; Liu, Y.X. Identification of the factors influencing the baseflow in the permafrost region of the Northeastern Qinghai-Tibet Plateau. Water 2017, 9, 666. [Google Scholar] [CrossRef]
- Maliehe, M.; Mulungu, D.M.M. Assessment of water availability for competing uses using SWAT and WEAP in South Phuthiatsana catchment, Lesotho. Phys. Chem. Earth 2017, 100, 305–316. [Google Scholar] [CrossRef]
- Yao, Y.; Zheng, C.; Andrews, C.; Zheng, Y.; Zhang, A.; Liu, J. What controls the partitioning between baseflow and mountain block recharge in the Qinghai-Tibet Plateau? Geophys. Res. Lett. 2017, 44, 8352–8358. [Google Scholar] [CrossRef]
- Sharp, R.; Tallis, H.T.; Ricketts, T.; Guerry, A.D.; Wood, S.A.; Chaplin-Kramer, R.; Nelson, E.; Ennaanay, D.; Wolny, S.; Olwero, N.; et al. VEST 3.3.3. User’s Guide. 2016. Available online: http://data.naturalcapitalproject.org/nightly-build/invest-users-guide/html/ (accessed on 21 May 2020).
- Mandle, L.; Wolny, S.; Hamel, P.; Project, N.C.; Helsingen, H.; WWF-Myanmar; Bhagabati, N.; Dixon, A.; WWF-US. Natural Connections: How Natural Capital Supports Myanmar’s People and Economy. 2016. Available online: https://www.worldwildlife.org/publications/natural-connections-how-natural-capital-supports-myanmar-s-people-and-economy (accessed on 21 May 2020).
- Santhi, C.; Allen, P.M.; Muttiah, R.S.; Arnold, J.G.; Tuppad, P. Regional estimation of base flow for the conterminous United States by hydrologic landscape regions. J. Hydrol. 2008, 351, 139–153. [Google Scholar] [CrossRef]
- Ahiablame, L.; Sheshukov, A.Y.; Rahmani, V.; Moriasi, D. Annual baseflow variations as influenced by climate variability and agricultural land use change in the Missouri River Basin. J. Hydrol. 2017, 551, 188–202. [Google Scholar] [CrossRef]
- Zomlot, Z.; Verbeiren, B.; Huysmans, M.; Batelaan, O. Spatial distribution of groundwater recharge and base flow: Assessment of controlling factors. J. Hydrol. Reg. Stud. 2015, 4, 349–368. [Google Scholar] [CrossRef]
- Jiang, C.; Li, D.Q.; Wang, D.W.; Zhang, L.B. Quantification and assessment of changes in ecosystem service in the Three-River Headwaters Region, China as a result of climate variability and land cover change. Ecol. Indic. 2016, 66, 199–211. [Google Scholar] [CrossRef]
- Wang, H.; Sun, F.; Xia, J.; Liu, W. Impact of LUCC on streamflow based on the SWAT model over the Wei River basin on the Loess Plateau in China. Hydrol. Earth Syst. Sci. 2017, 21, 1–30. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Shi, X.; Zhu, C.; Bohn, T.; Su, F.; Pan, M.; Sheffield, J.; Lettenmaier, D.; Wood, E. Water Budget Record from Variable Infiltration Capacity (VIC) Model. In Algorithm Theoretical Basis Document for Terrestrial Water Cycle Data Records. 2010. Available online: http://hydrology.princeton.edu/~mpan/academics/uploads/content/articles/Water_Cycle_MEaSUREs_ATBD_Combined_v1.0.pdf (accessed on 21 May 2020).
- Sun, F.; Mejia, A.; Che, Y. Disentangling the Contributions of Climate and Basin Characteristics to Water Yield across Spatial and Temporal Scales in the Yangtze River Basin: A Combined Hydrological Model and Boosted Regression Approach. Water Resour. Manag. 2019, 33, 3449–3468. [Google Scholar] [CrossRef]
- Scordo, F.; Lavender, T.; Seitz, C.; Perillo, V.; Rusak, J.; Piccolo, M.; Perillo, G. Modeling water yield: Assessing the role of site and region-specific attributes in determining model performance of the InVEST Seasonal Water Yield Model. Water 2018, 10, 1496. [Google Scholar] [CrossRef]
- Yang, S.Q.; Zhao, W.W.; Liu, Y.X.; Wang, S.; Wang, J.; Zhai, R.J. Influence of land use change on the ecosystem service trade-offs in the ecological restoration area: Dynamics and scenarios in the Yanhe watershed, China. Sci. Total Environ. 2018, 644, 556–566. [Google Scholar] [CrossRef]
- Redhead, J.W.; Stratford, C.; Sharps, K.; Jones, L.; Ziv, G.; Clarke, D.; Oliver, T.H.; Bullock, J.M. Empirical validation of the InVEST water yield ecosystem service model at a national scale. Sci. Total Environ. 2016, 569, 1418–1426. [Google Scholar] [CrossRef]
- Sánchez-Canales, M.; López Benito, A.; Passuello, A.; Terrado, M.; Ziv, G.; Acuña, V.; Schuhmacher, M.; Elorza, F.J. Sensitivity analysis of ecosystem service valuation in a Mediterranean watershed. Sci. Total Environ. 2012, 440, 140–153. [Google Scholar] [CrossRef]
- Hamel, P.; Guswa, A.J. Uncertainty analysis of a spatially explicit annual water-balance model: Case study of the Cape Fear basin, North Carolina. Hydrol. Earth Syst. Sci. 2015, 19, 839–853. [Google Scholar] [CrossRef]
- Pan, T.; Zou, X.T.; Liu, Y.J.; Wu, S.H.; He, G.M. Contributions of climatic and non-climatic drivers to grassland variations on the Tibetan Plateau. Ecol. Eng. 2017, 108, 307–317. [Google Scholar] [CrossRef]
- Liu, X.D.; Chen, B.D. Climatic warming in the Tibetan plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Y.J.; Shan, P.; Zhao, C.L.; Wang, C.X.; Deng, H.B. Snow cover dynamics in and around the Shangri-La County, southeast margin of the Tibetan Plateau, 1974–2012: The influence of climate change and local tourism activities. Int. J. Sust. Dev. World 2015, 22, 156–164. [Google Scholar] [CrossRef]
- Kang, S.C.; Xu, Y.W.; You, Q.L.; Flügel, W.A.; Pepin, N.; Yao, T.D. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 015101. [Google Scholar] [CrossRef]
- Xu, Z.X.; Gong, T.L.; Li, J.Y. Decadal trend of climate in the Tibetan Plateau—Regional temperature and precipitation. Hydrol. Process. 2008, 22, 3056–3065. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, Y.J.; Dong, J.W.; Fu, Y.; Zhu, J.T.; Zhang, G.L.; Jiang, Y.B.; Tian, L.; Zhang, X.Z.; Zhang, T. Elevation-dependent relationships between climate change and grassland vegetation variation across the Qinghai-Xizang Plateau. Int. J. Climatol. 2015, 35, 1638–1647. [Google Scholar] [CrossRef]
- Wang, P.; Lassoie, J.P.; Morreale, S.J.; Dong, S.K. A critical review of socioeconomic and natural factors in ecological degradation on the Qinghai-Tibetan Plateau, China. Rangel. J. 2015, 37, 1–9. [Google Scholar] [CrossRef]
- Tibet Autonomous Region Water Resources Planning Survey Design Institute. Integrated Planning for the Lhasa River Basin 2000–2020; Tibet Autonomous Region: Tibet, China, 2002. (In Chinese) [Google Scholar]
- Lim, K.J.; Engel, B.A.; Tang, Z.X.; Choi, J.; Kim, K.S.; Muthukrishnan, S.; Tripathy, D. Automated Web Gis based hydrograph analysis tool, WHAT. J. Am. Water Resour. Assoc. 2005, 41, 1407–1416. [Google Scholar] [CrossRef]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Ahiablame, L.; Chaubey, I.; Engel, B.; Cherkauer, K.; Merwade, V. Estimation of annual baseflow at ungauged sites in Indiana USA. J. Hydrol. 2013, 476, 13–27. [Google Scholar] [CrossRef]
- Eckhardt, K. A comparison of baseflow indices, which were calculated with seven different baseflow separation methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Combalicer, E.; Lee, S.; Ahn, S.; Kim, D.; Im, S. Comparing groundwater recharge and base flow in the Bukmoongol small-forested watershed, Korea. J. Earth Syst. Sci. 2008, 117, 553–566. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–417. [Google Scholar]
- Zhang, C.; Chu, J.G.; Fu, G.T. Sobol’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China. J. Hydrol. 2013, 480, 58–68. [Google Scholar] [CrossRef]
- McRae, G.J.; Tilden, J.W.; Seinfeld, J.H. Global sensitivity analysis—A computational implementation of the Fourier Amplitude Sensitivity Test (FAST). Comput. Chem. Eng. 1982, 6, 15–25. [Google Scholar] [CrossRef]
- Neumann, M.B. Comparison of sensitivity analysis methods for pollutant degradation modelling: A case study from drinking water treatment. Sci. Total Environ. 2012, 433, 530–537. [Google Scholar] [CrossRef] [PubMed]
- Redhead, J.W.; May, L.; Oliver, T.H.; Hamel, P.; Sharp, R.; Bullock, J.M. National scale evaluation of the InVEST nutrient retention model in the United Kingdom. Sci. Total Environ. 2018, 610, 666–677. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Zhan, C.S.; Song, X.M.; Xia, J.; Tong, C. An efficient integrated approach for global sensitivity analysis of hydrological model parameters. Environ. Model. Softw. 2013, 41, 39–52. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K. Improving the Morris method for sensitivity analysis by scaling the elementary effects. In Proceedings of the 19th European Symposium on Computer Aided Process Engineering, Cracow, Poland, 14–17 June 2009. [Google Scholar]
- Zhang, L.; Wu, B.F.; Li, X.S.; Xing, Q. Classification system of China land cover for carbon budget. Acta Ecol. Sin. 2014, 34, 7158–7166. (In Chinese) [Google Scholar]
- United States Department of Agriculture (USDA). Chapter 7 Hydrologic Soil Groups, Part 630 Hydrology. In National Engineering Handbook; 2007. Available online: https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=22526.wba (accessed on 21 May 2020).
- Guo, X.J.; Cui, P.; Zhuang, J.Q.; Liu, Y.H.; Zhang, J. SCS Model and Its application to rainfall-runoff in debris activity region—A case from Jiangjiagou watershed of Yunnan province. J. Soil Water Conserv. 2010, 30, 225–228. (In Chinese) [Google Scholar]
- Zhou, C.N.; Ren, S.M.; Yan, M.J. Application of SCS model to simulate rainfall-runoff relationship in Wenyu river basin in Beijing. Trans. CSAE 2008, 24, 87–90. (In Chinese) [Google Scholar]
- The Food and Agriculture Organization of the United Nations (FAO). Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. 1998. Available online: http://www.fao.org/3/x0490e/x0490e00.htm (accessed on 21 May 2020).
- Sun, P.S.; Liu, S.R.; Liu, J.T.; Liu, C.W.; Lin, Y.; Jiang, H. Derivation and validation of leaf area index maps using NDVI data of different resolution satellite imageries. Acta Ecol. Sin. 2006, 26, 3826–3834. [Google Scholar]
- Bagstad, K.J.; Cohen, E.; Ancona, Z.H.; McNulty, S.G.; Sun, G. The sensitivity of ecosystem service models to choices of input data and spatial resolution. Appl. Geogr. 2018, 93, 25–36. [Google Scholar] [CrossRef]
- Sahle, M.; Saito, O.; Fürst, C.; Yeshitela, K. Quantifying and mapping of water-related ecosystem services for enhancing the security of the food-water-energy nexus in tropical data–sparse catchment. Sci. Total Environ. 2019, 646, 573–586. [Google Scholar] [CrossRef]
- Watson, K.B.; Galford, G.L.; Sonter, L.J.; Koh, I.; Ricketts, T.H. Effects of human demand on conservation planning for biodiversity and ecosystem services. Conserv. Biol. 2019, 33, 942–952. [Google Scholar] [CrossRef]
- Pan, T.; Wu, S.H.; Liu, Y.J. Relative contributions of land use and climate change to water supply variations over Yellow River source area in Tibetan Plateau during the past three decades. PLoS ONE 2015, 10, e0123793. [Google Scholar] [CrossRef]
- Su, C.H.; Fu, B.J. Evolution of ecosystem services in the Chinese Loess Plateau under climatic and land use changes. Glob. Planet. Chang. 2013, 101, 119–128. [Google Scholar] [CrossRef]
- Falcucci, A.; Maiorano, L.; Boitani, L. Changes in land-use/land-cover patterns in Italy and their implications for biodiversity conservation. Landsc. Ecol. 2007, 22, 617–631. [Google Scholar] [CrossRef]
- Nelson, E.; Sander, H.; Hawthorne, P.; Conte, M.; Ennaanay, D.; Wolny, S.; Manson, S.; Polasky, S. Projecting global land-use change and its effect on ecosystem service provision and biodiversity with simple models. PLoS ONE 2010, 5, e14327. [Google Scholar] [CrossRef]
- Polasky, S.; Nelson, E.; Pennington, D.; Johnson, K.A. The impact of land-use change on ecosystem services, biodiversity and returns to landowners: A case study in the state of Minnesota. Environ. Resour. Econ. 2011, 48, 219–242. [Google Scholar] [CrossRef]
- Intergovernmental Platform on Biodiversity and Ecosystem Services (IPBES). Summary for Policymakers of the Global Assessment Report on Biodiversity and Ecosystem Services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. 2019. Available online: https://ipbes.net/global-assessment (accessed on 21 May 2020).
- Intergovernmental Platform on Biodiversity and Ecosystem Services (IPBES). The IPBES Regional Assessment Report on Biodiversity and Ecosystem Services for Asia and the Pacifc. 2018. Available online: https://ipbes.net/assessment-reports/asia-pacific (accessed on 21 May 2020).
- Intergovernmental Panel on Climate Change (IPCC). Chapter 1 Framing and Context. In Global Warming of 1.5°C; 2018; Available online: https://www.ipcc.ch/sr15/ (accessed on 21 May 2020).
- Xu, H.J.; Wang, X.P.; Zhang, X.X. Alpine grasslands response to climatic factors and anthropogenic activities on the Tibetan Plateau from 2000 to 2012. Ecol. Eng. 2016, 92, 251–259. [Google Scholar] [CrossRef]
- Chen, B.X.; Zhang, X.Z.; Tao, J.; Wu, J.S.; Wang, J.S.; Shi, P.L.; Zhang, Y.J.; Yu, C.Q. The impact of climate change and anthropogenic activities on alpine grassland over the Qinghai-Tibet Plateau. Agric. For. Meteorol. 2014, 189, 11–18. [Google Scholar] [CrossRef]
- Reed, M.S.; Stringer, L.C. Land Degradation, Desertification, and Climate Change: Anticipating, Assessing, and Adapting to Future Change; Routledge: London, UK, 2016. [Google Scholar]
- Tibet Autonomous Region Statistics Bureau. Tibet Statistical Yearbook; China Statistics Press: Beijing, China, 2015. [Google Scholar]
- Dong, Q.M.; Zhao, X.Q.; Wu, G.L.; Chang, X.F. Optimization yak grazing stocking rate in an alpine grassland of Qinghai-Tibetan Plateau, China. Environ. Earth Sci. 2015, 73, 2497–2503. [Google Scholar] [CrossRef]
- Harris, R.B. Rangeland degradation on the Qinghai-Tibetan plateau: A review of the evidence of its magnitude and causes. J. Arid Environ. 2010, 74, 1–12. [Google Scholar] [CrossRef]
| No. | Parameters | Definition | Range | Unit |
|---|---|---|---|---|
| 1 | Precipitation (P) | Average annual precipitation | (50, 500) | mm |
| 2 | Reference evapotranspiration (RET) | Potential evaporation of a hypothetical vegetation with an abundant water supply | (50, 500) | mm |
| 3 | Curve number (CN) | An empirical parameter used in hydrology for predicting direct runoff or infiltration from rainfall excess | (10, 100) | - |
| 4 | Crop/vegetation coefficient (Kc) | Properties of plants used in predicting evapotranspiration | (0.1, 1) | - |
| 5 | Threshold flow accumulation (TFA) | The number of upstream cells that must flow into a cell before it is considered part of a stream | (1000, 10000) | - |
| 6 | Rain events (RE) | Average number of monthly rain events | (2, 20] | - |
| Name | Data Type | Resolution | Time Availability | Source |
|---|---|---|---|---|
| Precipitation | Excel | - | 1955–2015, monthly | China Meteorological Data Service Center |
| Land cover | Raster | 30 m | 1990, 2000, 2010, 2015 | Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences |
| NDVI | Raster | 250 m | 1990, 2000, 2010, 2015 | Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences |
| Stream flow | Excel | - | 2006–2014, daily | China Institute of Water Resources and Hydropower Research |
| DEM | Raster | 30 m | 2015 | Geospatial Data Cloud (http://www.gscloud.cn/) |
| Soil texture | Raster | 1 km | - | Harmonized World Soil Database (http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/zh/) |
| CN | Excel | - | - | USDA (United States Department of Agriculture) handbook [42] |
| Kc | Excel | - | - | FAO (Food and Agriculture Organization of the United Nations) guidelines [45] |
| Reference evapotranspiration | Raster | 1 km | Monthly | CGIAR CSI dataset (https://cgiarcsi.community/) |
| Land Cover Type | 1990 | 2000 | 2010 | 2015* | Area Change in Land Cover between 1990 and 20151 | Proportion Change in Land Cover between 1990 and 2015 |
|---|---|---|---|---|---|---|
| Forest | 80.01 | 80.21 | 80.73 | 80.75 | 0.74 | 0.92% |
| Shrub | 5077.63 | 5077.64 | 5077.72 | 5065.31 | −12.33 | −0.24% |
| Alpine meadow | 8561.66 | 8562.13 | 8561.94 | 8682.04 | 120.38 | 1.41% |
| Alpine steppe | 7629.94 | 7631.09 | 7613.59 | 7702.02 | 72.09 | 0.94% |
| Sparse grassland | 7388.28 | 7400.13 | 7401.72 | 7152.10 | −236.19 | −3.20% |
| Farmland | 613.00 | 598.68 | 584.79 | 583.83 | −29.17 | −4.76% |
| Barren land | 2098.49 | 2104.65 | 2105.12 | 2108.88 | 10.39 | 0.50% |
| Artificial surface | 90.29 | 102.97 | 117.59 | 164.87 | 74.57 | 82.59% |
| Water | 174.65 | 174.42 | 188.70 | 231.07 | 56.42 | 32.30% |
| Snow/Glaciers | 964.57 | 946.62 | 946.62 | 860.31 | −104.26 | −10.81% |
| Time Period | 1990–2000 | 2000–2010 | 2010–2015 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Influencing Factor | ΔP | ΔL | ΔN | ΔP | ΔL | ΔN | ΔP | ΔL | ΔN |
| Δ Baseflow | 22.80 | −0.09 1 | −25.78 | −76.68 | 0.06 | −3.46 | 1.77 | −0.88 | 1.97 |
| Δ Local Recharge | 22.81 | −0.09 | −28.91 | −90.74 | 0.08 | −3.96 | 4.21 | 2.71 | −0.67 |
| Δ Quick flow | 1.58 | 0.03 | 0.00 | −8.93 | 0.01 | 0.00 | −0.61 | −0.03 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Yan, Y.; Zhu, J.; Jin, T.; Liu, G.; Wu, G.; Stringer, L.C.; Dallimer, M. Spatiotemporal Water Yield Variations and Influencing Factors in the Lhasa River Basin, Tibetan Plateau. Water 2020, 12, 1498. https://doi.org/10.3390/w12051498
Lu H, Yan Y, Zhu J, Jin T, Liu G, Wu G, Stringer LC, Dallimer M. Spatiotemporal Water Yield Variations and Influencing Factors in the Lhasa River Basin, Tibetan Plateau. Water. 2020; 12(5):1498. https://doi.org/10.3390/w12051498
Chicago/Turabian StyleLu, Huiting, Yan Yan, Jieyuan Zhu, Tiantian Jin, Guohua Liu, Gang Wu, Lindsay C. Stringer, and Martin Dallimer. 2020. "Spatiotemporal Water Yield Variations and Influencing Factors in the Lhasa River Basin, Tibetan Plateau" Water 12, no. 5: 1498. https://doi.org/10.3390/w12051498
APA StyleLu, H., Yan, Y., Zhu, J., Jin, T., Liu, G., Wu, G., Stringer, L. C., & Dallimer, M. (2020). Spatiotemporal Water Yield Variations and Influencing Factors in the Lhasa River Basin, Tibetan Plateau. Water, 12(5), 1498. https://doi.org/10.3390/w12051498





