1. Introduction
Evaporation and freezing of droplets are two interesting areas with many applications. Evaporation of droplets is important in, e.g., spray cooling [
1], surface coating [
2], ink-jet printing [
3], and droplet based biosensing [
4]. For freezing droplets, the applications are found mainly when dealing with icing on wind turbines [
5], airplane wings [
6], and roads [
7]. Since icing is a big problem for these areas, effective icing prevention methods have been developed, but a lot is still unknown about the ice itself. One way in improving these existing icing prevention systems is to go back a few steps and start with a single freezing water droplet. Due to the complex nature of the flow within droplets, a wide range of temperatures, from freezing temperatures to heating temperatures, have to considered to increase the understanding of the flow behavior. This is the motivation for performing this comparative study between freezing and evaporating droplets.
To the author’s best knowledge, not many studies have been performed studying the internal flow within the droplets for freezing of water droplets. Kavanami et al. [
8] used a numerical model considering both surface tension and the density maximum at 277 K. The results were also validated with experiments. They found that both natural and Marangoni convection are important mechanisms for the internal flow. Karlsson et al. [
9] modeled the inner flow when internal natural convection was included and excluded (i.e., only conduction from the surface) in the model and the result was validated with existing experimental data. Karlsson et al. [
10] performed experiments by releasing droplets on a cold surface and the inner flow was captured by using Particle Image Velocimetry (PIV). The flow field in the center of the droplet was visualized and the magnitude and direction of the velocities were derived.
The evaporation of sessile droplets has been studied thoroughly both experimentally and numerically [
11,
12,
13,
14,
15]. A similar setup as in the experiments performed in this study was done by Erkan and Okamoto [
16] and Erkan [
17], where liquid droplets were released with different impact velocities onto a dry (and later, also heated) sapphire plate. The flow inside the droplet was investigated using time-resolved PIV, and a laser created a laser sheet illuminating a plane parallel to the surface. The radial velocity distribution during the early phase of spreading inside the droplets was compared to an analytical as well as a numerical model and both were proven to show similar results. However, none of the models could reproduce all of the experimental results in detail.
An interesting study of the internal flow within droplets impacting on a surface was performed by Kumar et al. [
18] using the same ray-tracing algorithm as in this work proposed by Kang et al. [
19] to account for the image distortion at the droplet boundary. The vortices caused by the impact to the surface were traced and the vortex strength was computed. The internal flow was also studied by Thokchom et al. [
20,
21] using PIV in externally heated sessile droplets confined in a narrow gap between two glass plates. The benefit of using a “Hele–Shaw” droplet is in the optics since no image correction has to be done and the surface flow is seen. The experiments yielded that an alteration in the free surface temperature changes the fluid flow profile inside the droplet and consequently also the deposition pattern of solute particles on the substrate. The heat sources were an IR light and a heating element that was moved along the droplet surface to create different effects. The measured velocity profiles were in qualitatively agreement with numerical simulations.
In a recent study by Zhao et al. [
22], the full velocity field in evaporating sessile droplets was captured. Instead of correcting the raw PIV data as done in this work, the Scheimpflug principle was applied. This is a mapping method used to eliminate the perspective effects and therefore the flow near the droplet surface can be studied. This method is very useful when studying evaporating droplets, but when working with freezing droplets this method will not work properly because of the positioning of the camera. Since the camera is placed underneath the droplet, the frost layer and the created ice during freezing will make it impossible for the camera to retrieve good images of the freezing process. This is one of the reasons the method by Kang et al. [
19] was used in the freezing experiments in the current study. For easier comparison, the same method was also applied in the evaporation experiments.
In this work, the effects of Marangoni convection on evaporating and freezing droplets were studied and the results from the two different processes were compared to each other. The effects of Marangoni convection on evaporating droplets has been studied before. To exemplify, Hu and Larson [
23] concluded from numerical simulations that a thermally driven Marangoni flow should be visible in an evaporating water droplet, but this is not as easy to visualize in experiments. One possible reason for this can be surfactant contaminants [
23,
24]. Xu and Luo [
25] showed that, even though this is partially true, the surface tension and the surface temperature change nonmonotonously along the liquid surface due to a stagnation point at the droplet surface. Kita et al. [
26] induced a Marangoni flow in pure water drops by creating a temperature gradient on the drop using infrared thermography. They found that, to initiate a Marangoni flow as two similar vortices, a temperature gradient along the liquid–air interface of about 2.5 K (
C) is necessary and to maintain them the temperature difference has to be about 1.5 K (
C). The main consensus is that Marangoni convection is small for water droplets [
24,
27], but can be induced [
26]. This motivates also a comparison between heated evaporating droplets and freezing droplets since it has been shown that the Marangoni convection plays an important role for the flow in the beginning of the freezing process, but after a while natural convection takes over [
10]. This is not as clear when studying evaporation of droplets, and this paper discusses the different effects in the droplets.
Hence, in this study, the aim was to investigate and compare the inner flow when droplets are released on a cold and warm surface and to reveal if natural convection and/or Marangoni convection have a noticeable influence on the flow within the droplets.
2. Method
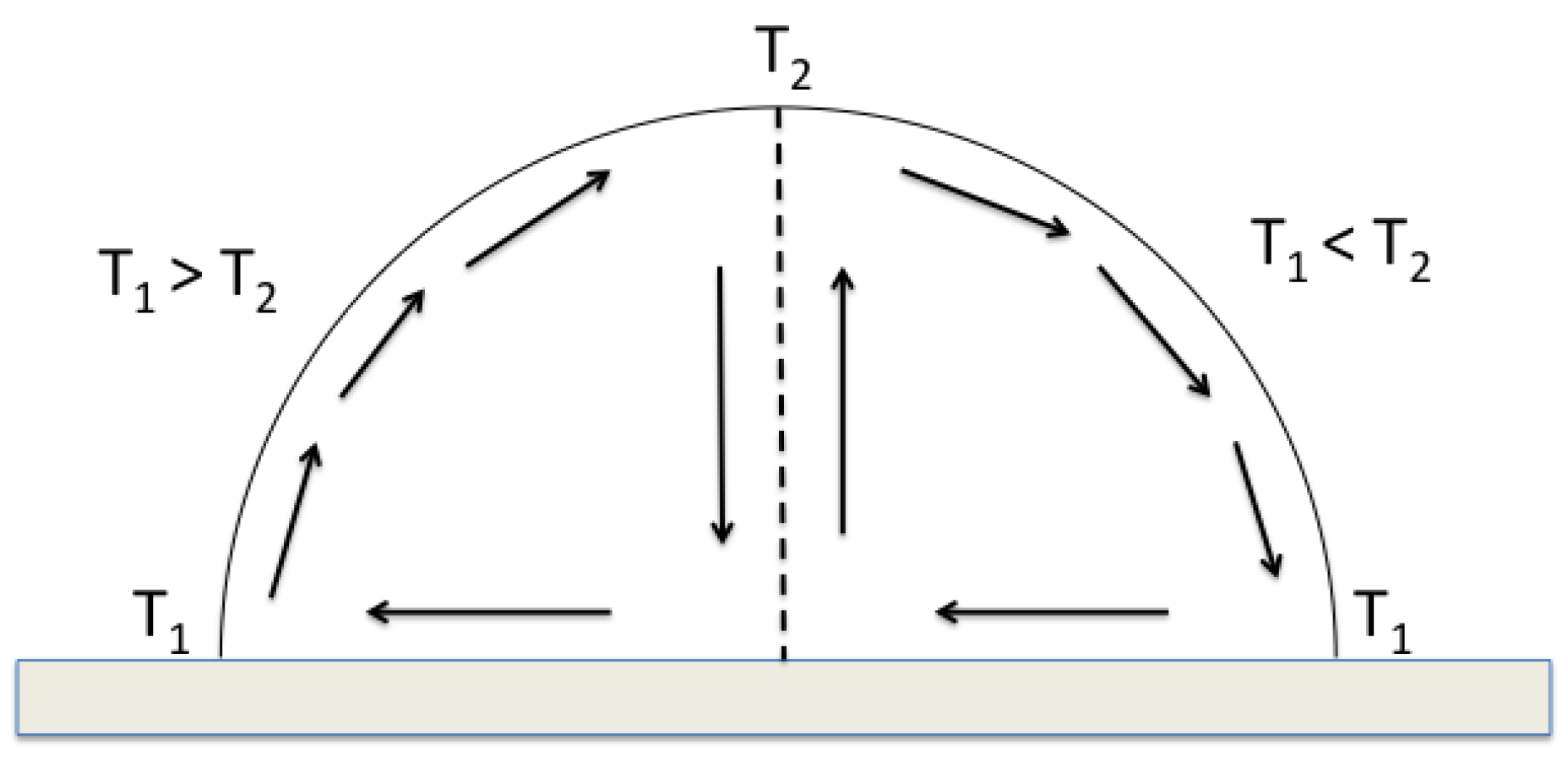
To facilitate the presentation of the results, a schematic image of the direction of Marangoni flow for a constant gradient is shown in
Figure 1. The Marangoni flow when
>
is seen to the left in the figure, i.e., the flow within an evaporating droplet, and the Marangoni flow when
<
is seen to the right, i.e., the flow within a freezing water droplet.
A similar setup and experimental procedure were used for the freezing and evaporating droplets. When these differ from one another, it is clearly stated in the text.
2.1. Experimental Setup
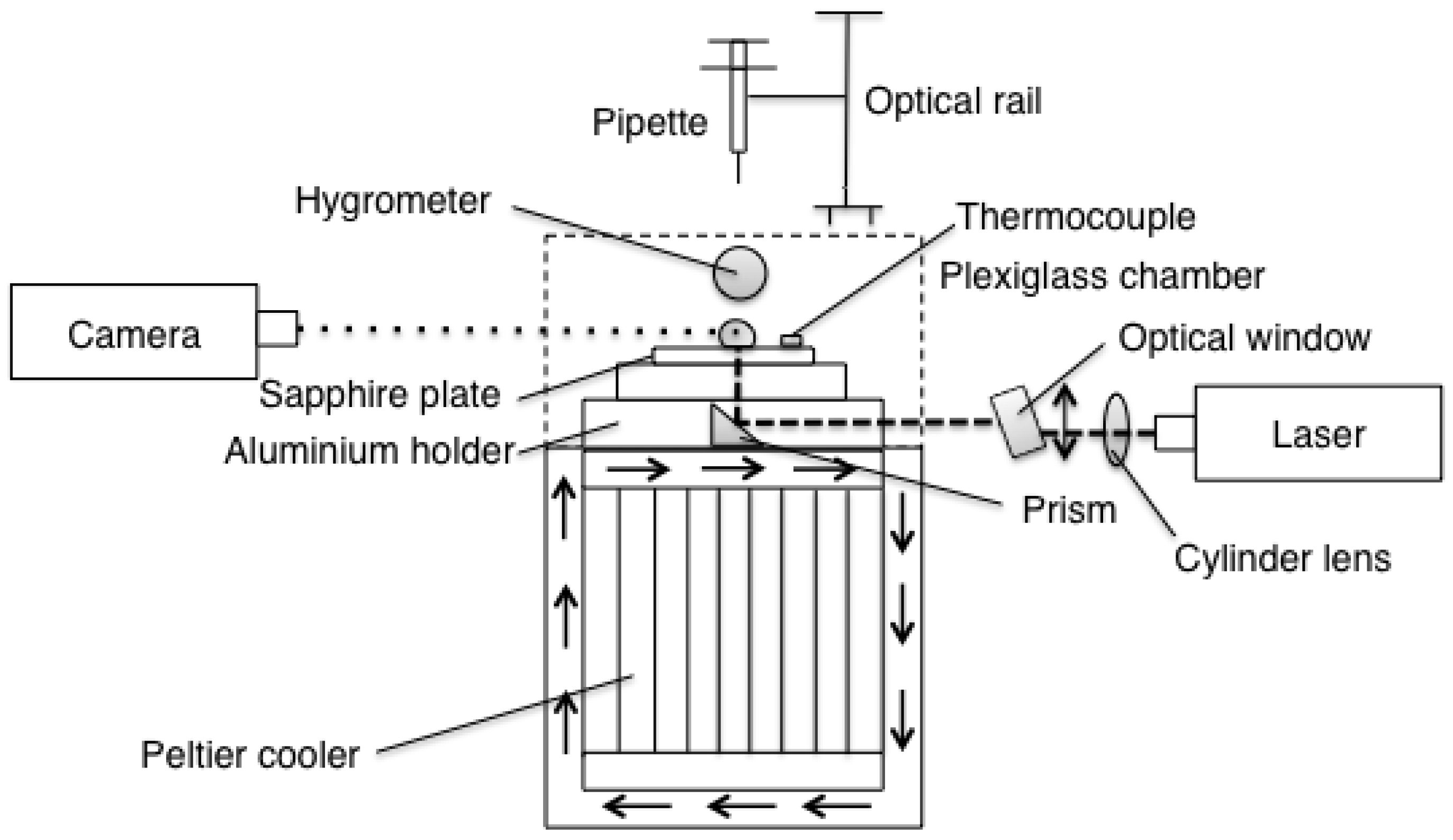
Droplets were gently deposited on a sapphire plate (aluminum oxide, Al
O
) using a pipette. The sapphire plate measured 0.0508 m (2
) in diameter, 0.005 m thick, and was chosen due to its high thermal conductivity in combination with its transparency. The pipette was a ThermoFisher Finnpipette F1 1–10
L, and it was kept in place by an optical rail to create repeatable deposition of the droplets in each experiment. The sapphire plate was resting on an aluminum holder that was heated using a Peltier element. The Peltier element was placed with its warm side up during the heating experiments and its cold side up during the freezing experiments. It was submerged in a box with either warm or cold circulating water depending on which experiment was performed (closed system, connected to a tank water held at
T = 295.85 K ± 0.98 K and
T = 277.05 K ± 1.3 K, respectively). The laser light was guided underneath the droplet using a prism that was put inside a central hole in the aluminum holder and a tunnel inside the holder allowed the light to pass through to the droplet. To protect the setup from disturbances in the room, a PMMA (plexiglass) chamber was put around the sapphire plate. Four holes was made in the chamber; one on top for the pipette to be able to release the droplets, one on the right side to allow the laser light to pass through to the prism, one on the left side to enable the camera to record the experiments and one on the back where the hygrometer was mounted. The sapphire plate was cleaned using Propanol (
) and deionized (DI) water using lens paper before each experiment. A schematic diagram of the experimental setup can be seen in
Figure 2. In both heating and freezing experiments, the liquid used was DI water kept at room temperature,
= 294.25 K ± 1.4 K. The seeding particles in the freezing experiments were chosen due to its good qualities when working with water. However, these particles did not work well in the heating experiments since the droplets collapsed as they reached the surface after the release from the pipette. Therefore, new particles were chosen for the heating experiments.
Table 1 presents details of the seeding particles for each setup. The Stokes number,
, was calculated for a “worst-case scenario” for both setups to determine if the particles was suitable for these experiments (see
Table 1). Since both have a
« 1, the conclusion is that the particles follow the flow well. Based on the guidelines, the amount of particles in the water was continuously evaluated to reach the recommended particles per interrogation area. The resulting concentration of particles for both setups can be found in
Table 1.
The temperature of the air and the humidity inside the chamber were monitored using a hygrometer and the temperature of the sapphire plate was measured using a thermocouple of K-type. The laser was a continuous 50 mW 532 nm Nd:YAG (Altechna Co Ltd., Vilnius, Lithuania) connected to a half wave-plate, a polarizing beam splitter (cube) and a beam dump. These components were used to adjust the amount of light transmitted through the droplet. A cylinder lens assembly from Dantec Dynamics created and focused the light sheet to a thickness of <0.0004 m. A 0.012-m-thick window placed on a rotation table was used to fine tune the position of the sheet to the center of the droplet (up and down to be able to adjust the light sheet to move sideways in the droplet) (see
Figure 2). The motivation for guiding the laser light from underneath the droplet was the advantage of the plane surface reducing the light scatter. This arrangement also allows a good view of the symmetry line of the droplet. For the freezing setup, a CMOS camera (IDS
Eye) with a spatial resolution of 1280 × 1024 pixels and pixel size 5.3·10
× 5.3·10
together with a Navitar long distance microscope captured images of the particles. For the heating setup a similar CMOS camera (IDS UI-3140CP-M-GL Rev.2) was used with the same spatial resolution and microscope mounted, but with pixel size 4.8·10
× 4.8·10
m
. Details about the specific sampling rates can be found in
Table 2. The height from which the droplets were released was measured to be 0.0021 m and the velocity as the droplet hit the surface was calculated to be 0.052 m/s for the heating experiments and 0.0039 m and 0.077 m/s, respectively, for the freezing experiments.
2.2. Experimental Procedures
The following statements can briefly summarize the experimental procedures:
Heating
The heating of the surface started.
At = 313.15, 323.15 or 333.15 K (visually determined from the computer screen):
- -
The pipette was filled with the DI water and seeding particle suspension.
- -
The camera and the laser were switched on.
- -
The laser sheet was fine tuned to the center of the droplet (while the droplet was still hanging from the pipette).
- -
Finally, the droplet was released.
The camera and laser light were turned off after about 60 s after the droplet has hit the surface.
The surface was cleaned and a new experiment could begin.
Freezing
The cooling of the surface started.
At = 261.15 K or 265.15 (visually determined from the computer screen), the pressurized air was switched on and turned off again when RH was around 50%. This took about 60 s.
The pipette was filled with the DI water and seeding particle suspension.
The camera and the laser were switched on. The position of the light sheet was fined tuned to the center of the droplet (while the droplet was still hanging from the pipette).
The droplet was released when reached 265.15 K (or 261.15 K) again (visually determined from the computer screen), which occurred approximately 30 s from when the pressurized air was switched off.
The cooling was turned off when the droplet was completely frozen.
The surface was cleaned and dried when > 273.15 K and at = 277.15 K a new experiment could begin.
In the freezing experiments, it was found that a roughness on the surface was necessary to initialize the freezing process without delay. Due to the smoothness of the sapphire plate, this roughness was added by producing frost on the surface. This layer was generated by letting pressurized air pass through a container filled with water and this humidified air was then guided into the closed chamber surrounding the experimental setup. The temperature of the surface and air and the relative humidity inside the chamber were monitored to produce a layer of frost as similar as possible during each freezing (see
Table 2 for details about the conditions for the frost). A longer discussion of how this frost layer can be found in the work of Karlsson et al. [
10].
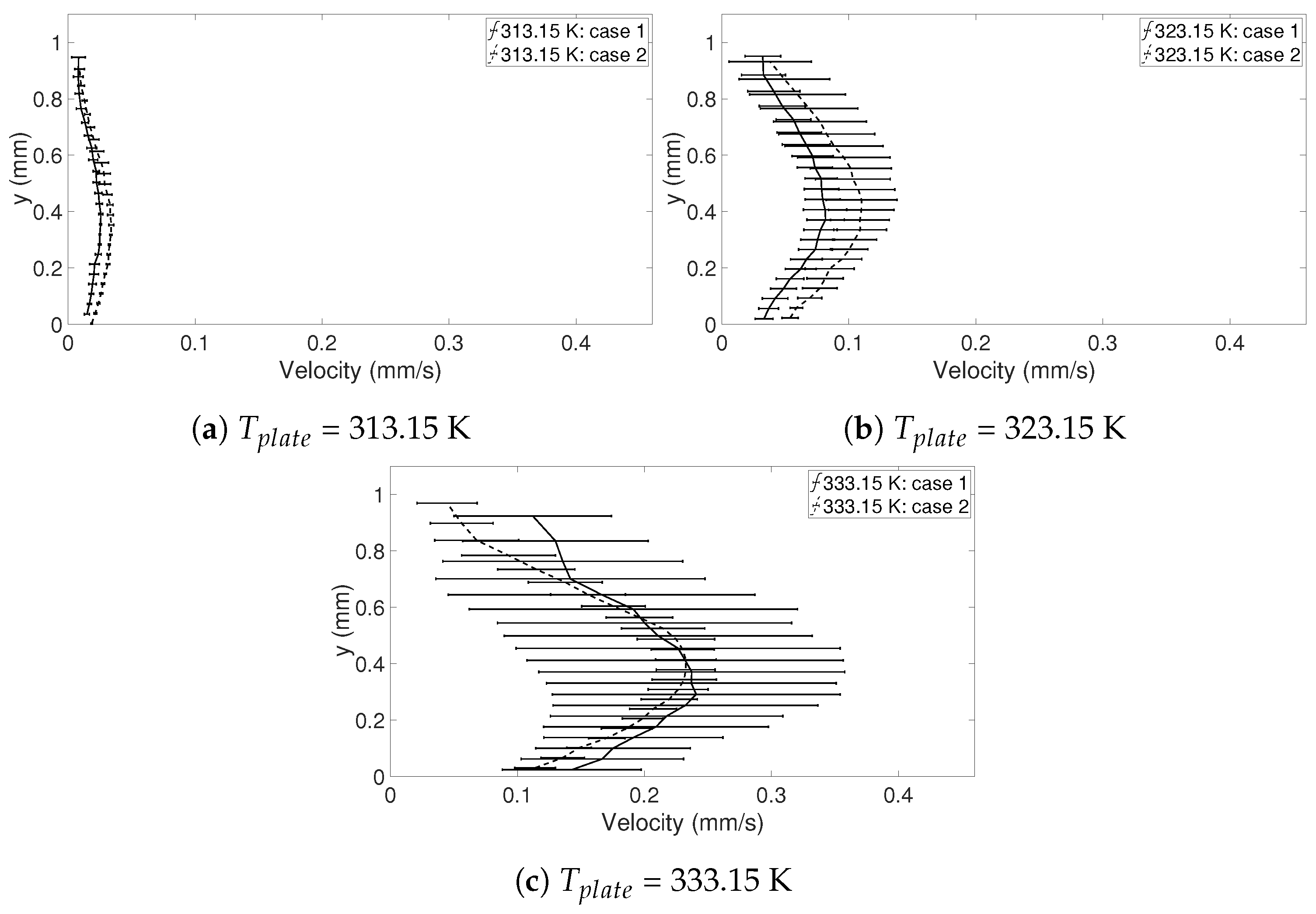
The result of the evaporation experiments is based on six evaporating droplets with a similar geometry, i.e., droplets with approximately same heights and radii, when
= 313.15, 323.15, and 333.15 K. These are presented in
Table 3. Two freezing droplets (when
= 261.15 and 265.15 K) are also included in this table.
2.3. Uncertainty Analysis
The uncertainties introduced during the measurements can be divided into two categories: systematic (bias) and random errors. The systematic errors usually arise from the measuring equipment and the random errors are usually due to unknown or unpredictable changes in the experiments [
28].
Similar to the experiments performed by Karlsson et al. [
10], the main sources of the systematic errors can be found in the pipette technique, i.e., the mixing of seeding particles in the water, the reading of the measurements instruments, and the positioning of the camera. Since these errors are introduced in each experiment, they may be difficult to detect and therefore have a large impact on the result. However, careful planning and execution of experiments can minimize these errors. Normally, the correlation error is 0.1 pixel [
29].
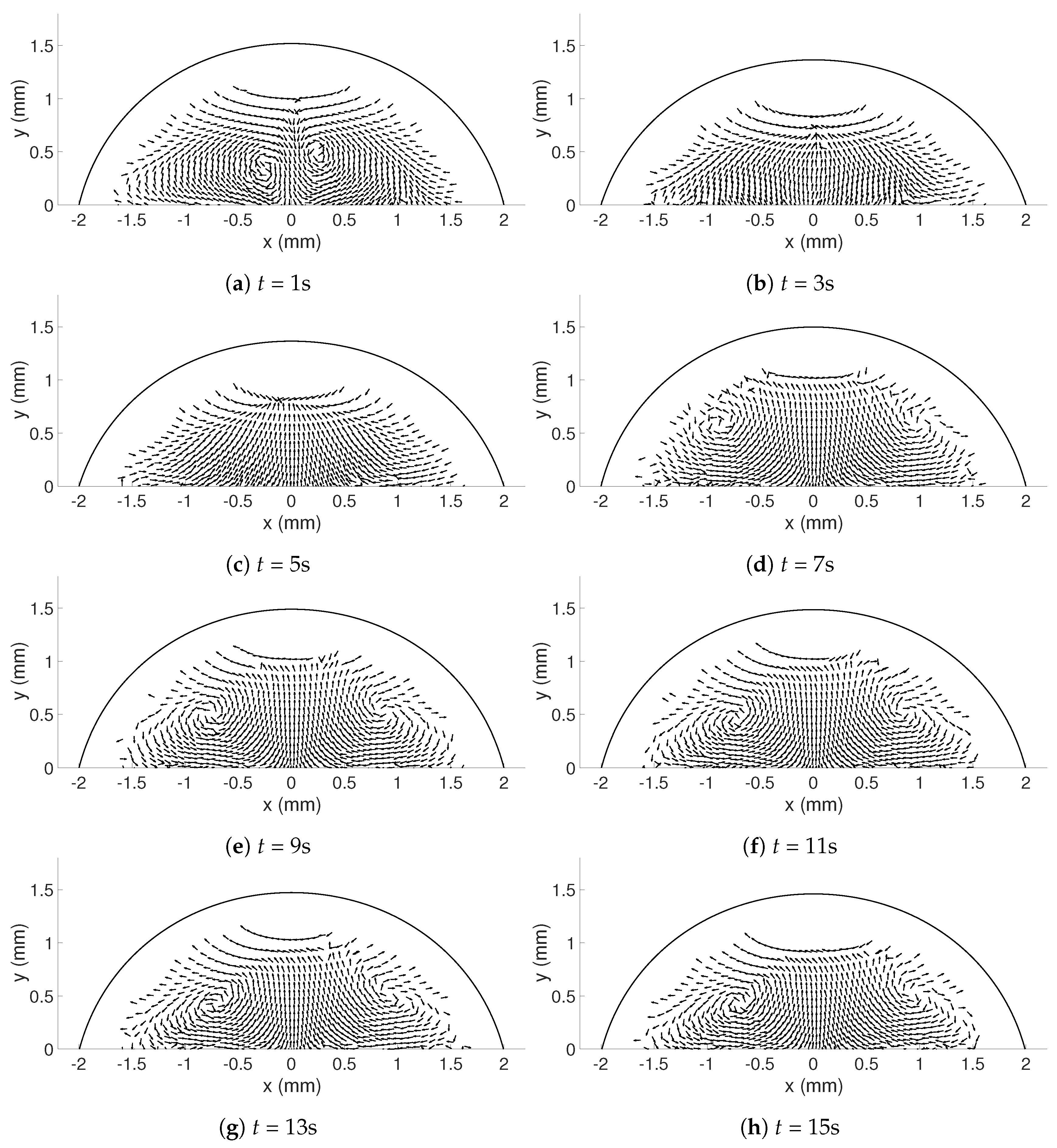
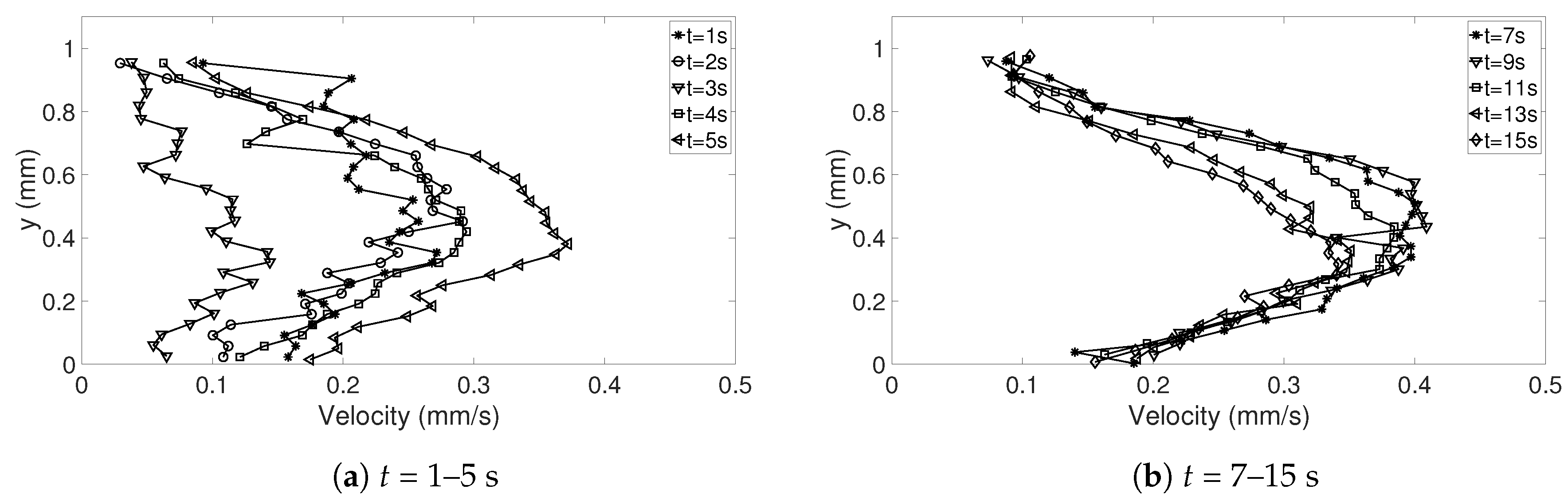
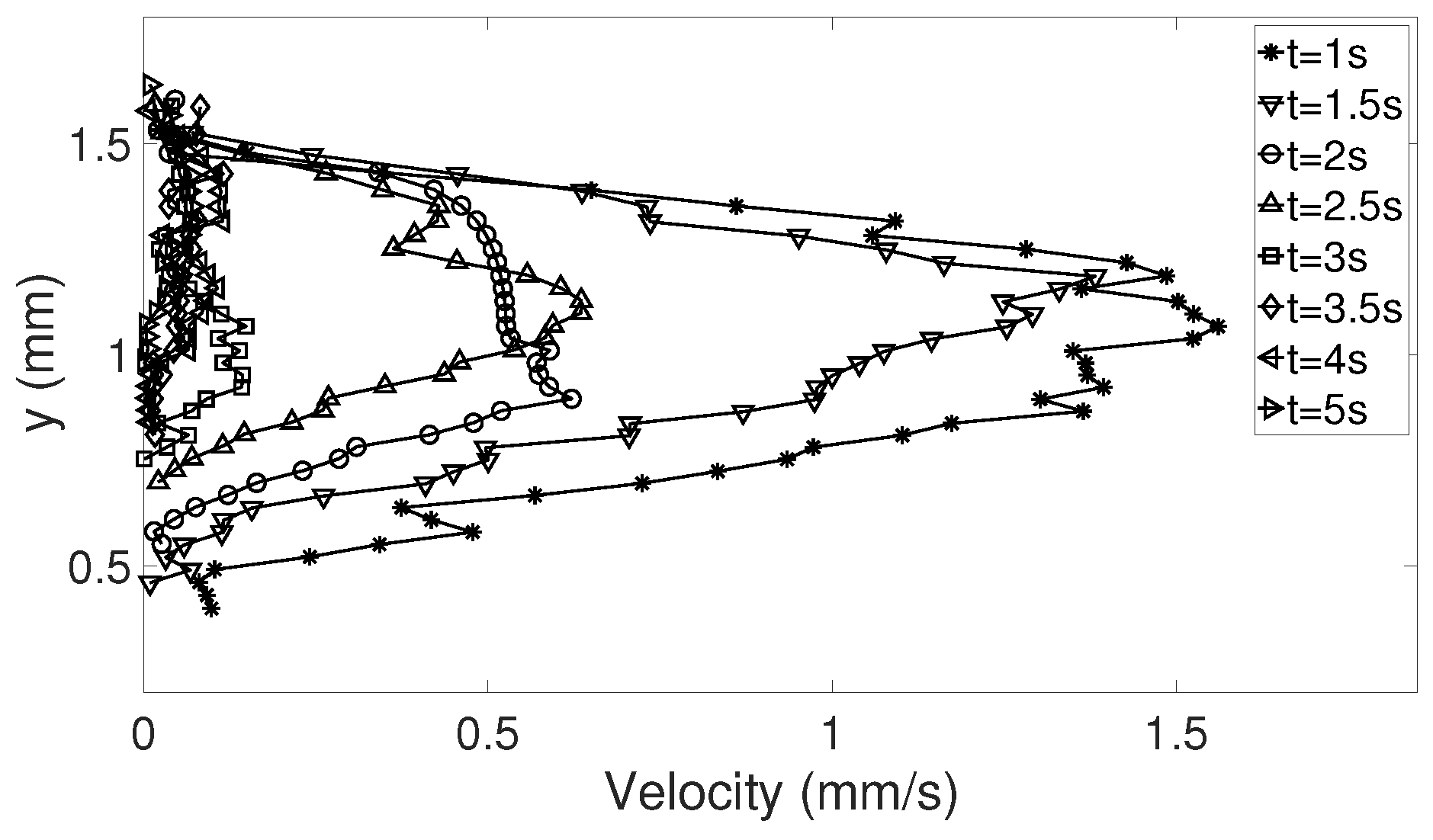
The random errors can mainly be found in the release of the droplet, resulting in droplets with different geometries and different initial internal flows (
t < 5 s). To get an estimate of the random errors, a repeatability test can be performed (see [
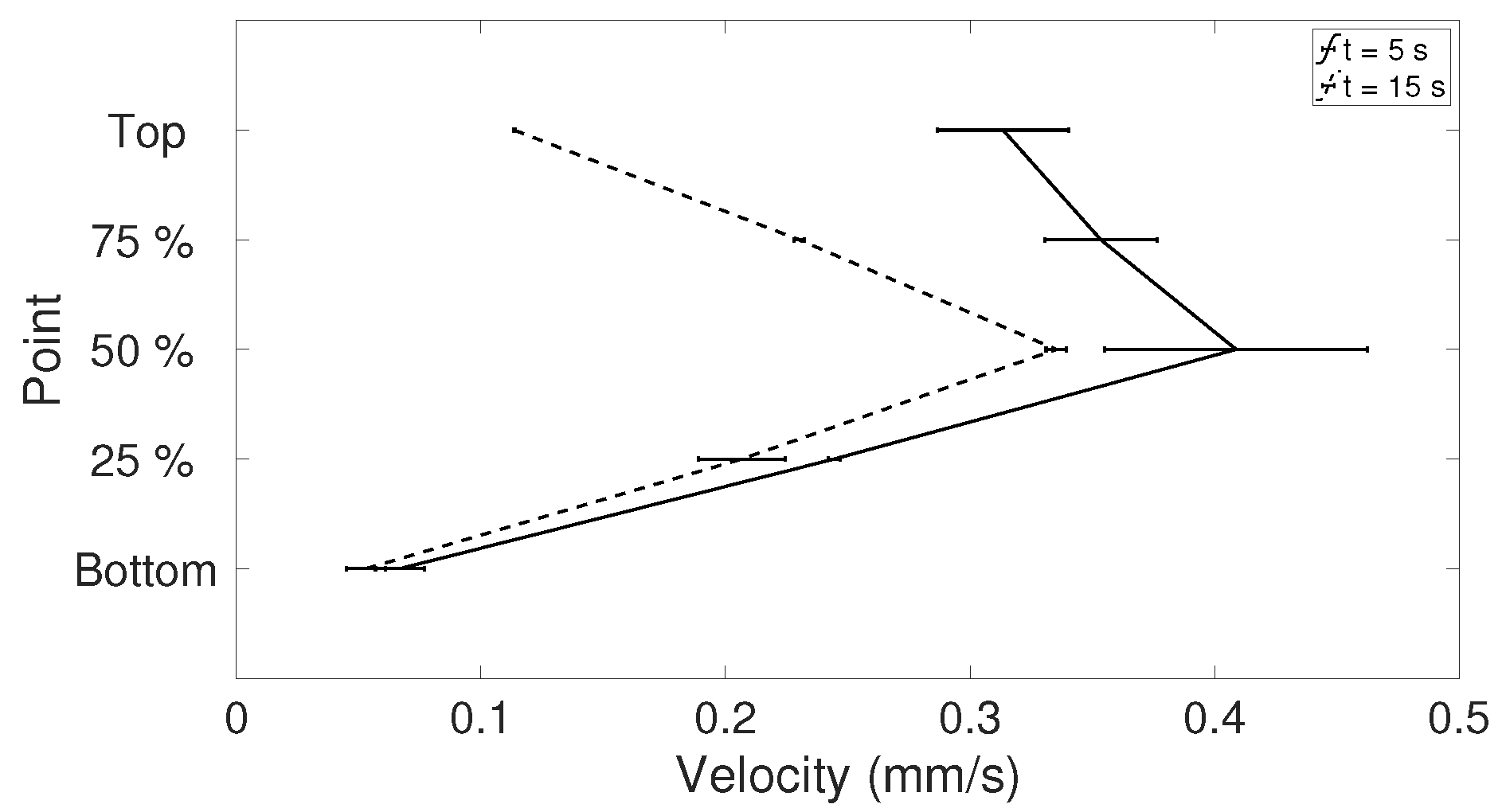
28]). Ten experiments for
= 333.15 K were considered (see
Table 4 for details about the droplets), where the magnitude of the corrected velocities in the y-direction along the symmetry line between bottom and apex of the droplet was studied. Since the droplets varied in height, the interesting points is what happened at just above the heated surface, i.e., the lowest value of the corrected dataset and at the top of the corrected data in each case. In addition, the points at 25%, 50%, and 75% above the heated surface were determined. To get an estimate of the variations in the velocities along the symmetry line in the beginning of evaporation and as the flow settled in the droplet, the times studied were
t = 5 and 15 s. The specific time
t = 5 s was chosen because the shift in flow direction (see
Section 3.2.1) had occurred for all 10 cases in this investigation; before this time the flow would be more difficult to evaluate. In
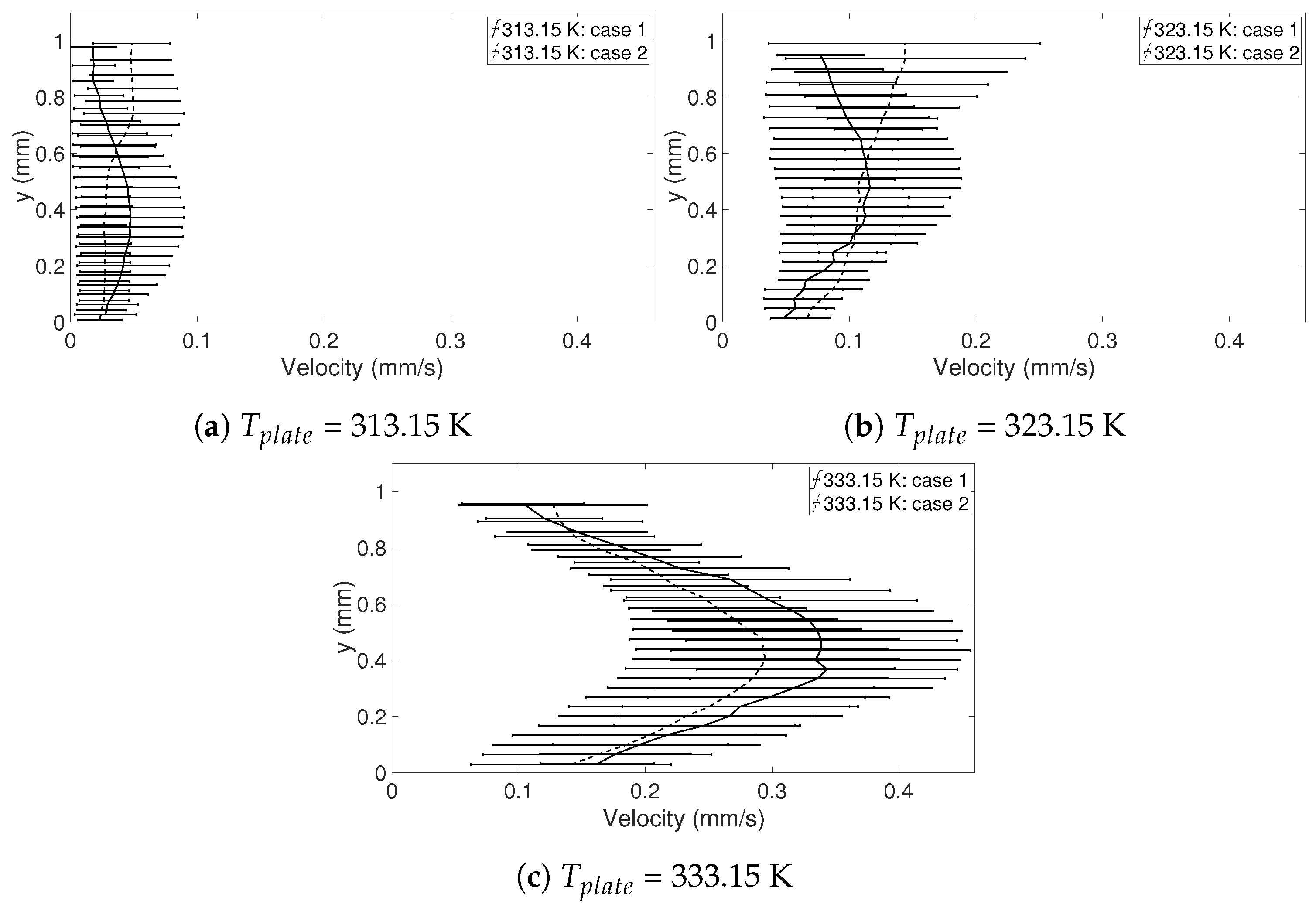
Table 5, the precision errors with a 95% confidence interval for the five points chosen are shown and it can be seen that the errors are below, or mostly well below 5.5%, suggesting that the random errors are relatively small regarding the velocities on the symmetry line, especially for when
t = 15 s. This can also be seen in
Figure 3, where the mean velocity in the five points is shown together with the precision error presented using error bars. This means that the velocities in the droplet are in fact comparable in each case despite their differences in geometry, and the six selected droplets in
Table 3 can be used in the further study.
4. Conclusions
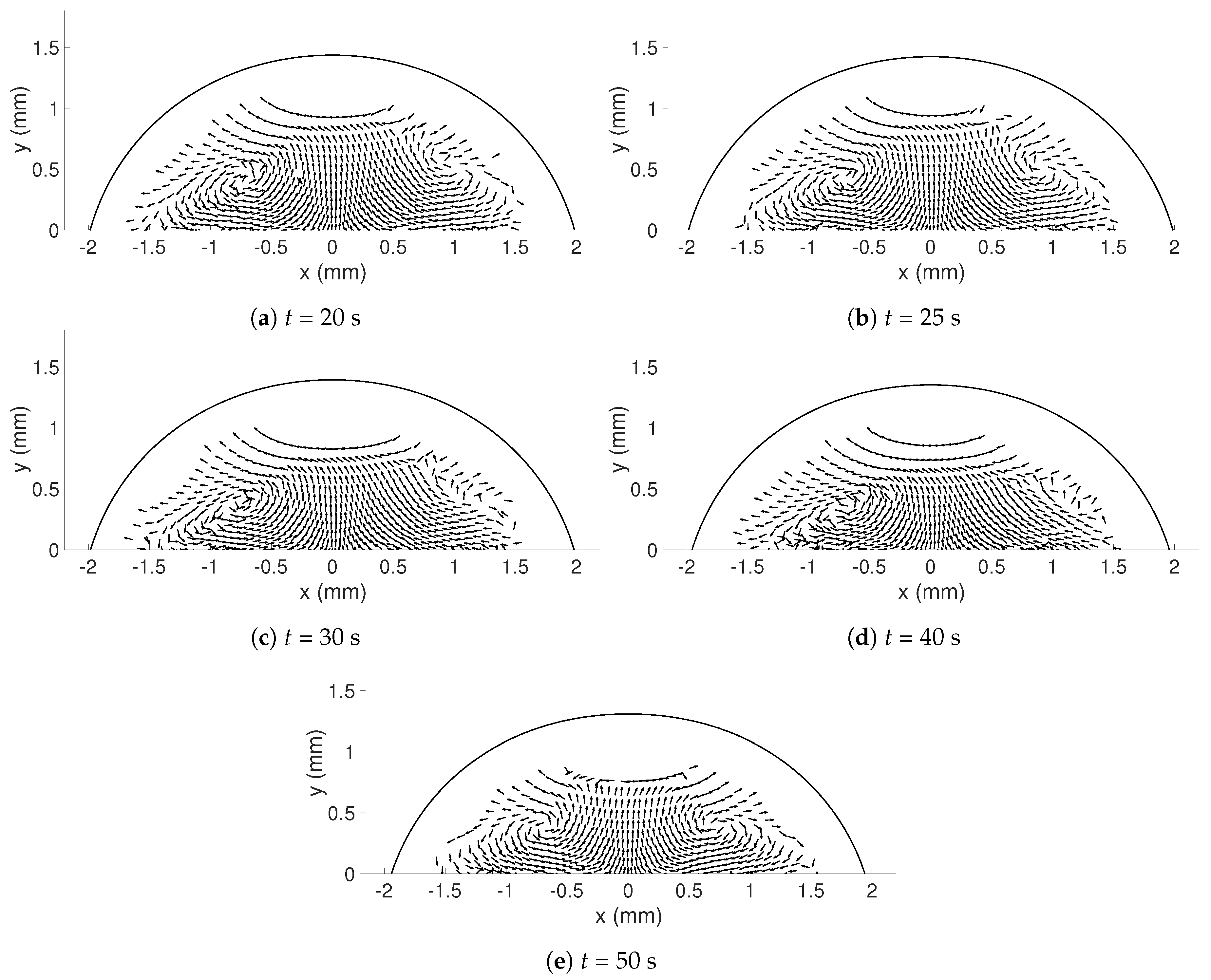
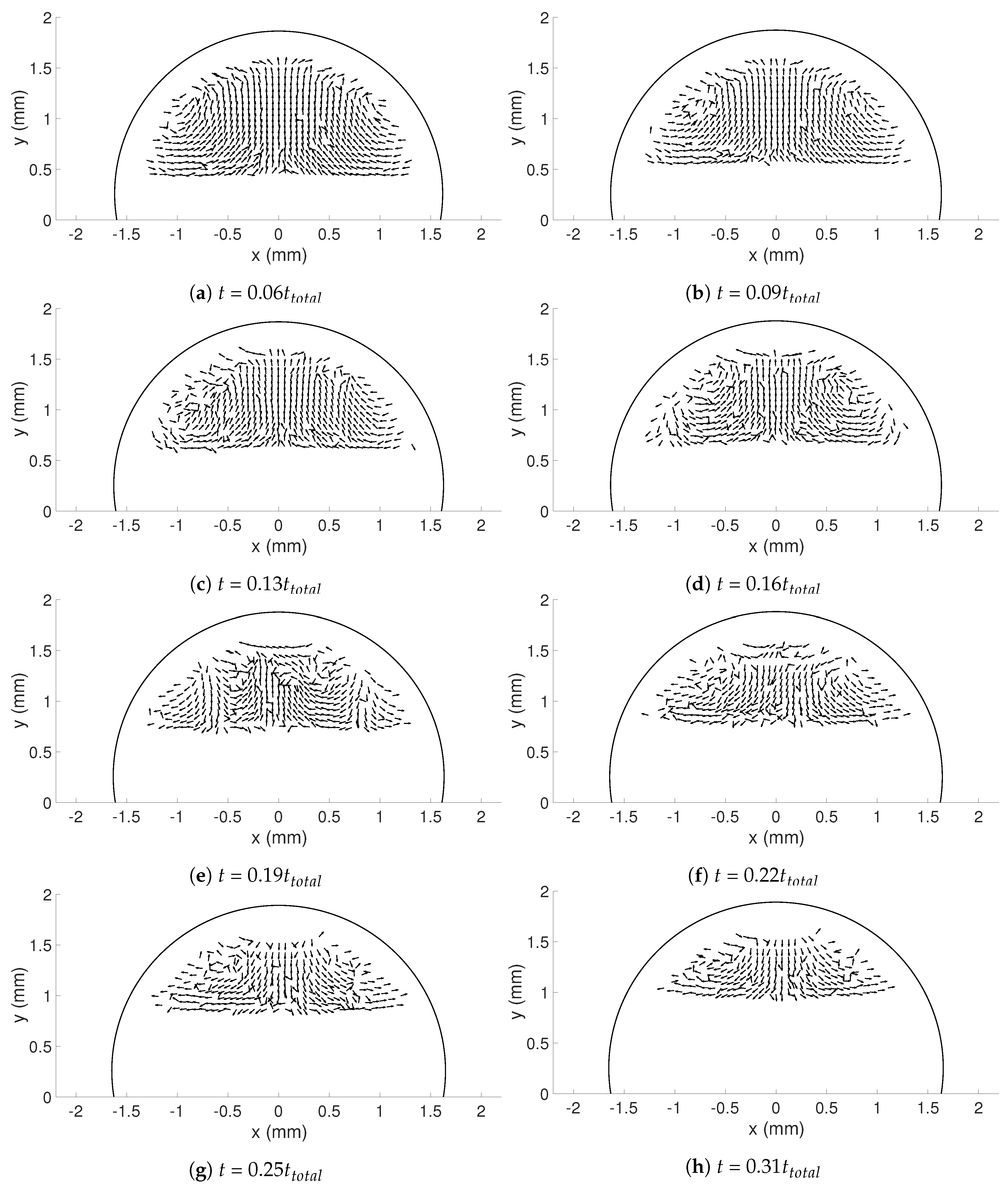
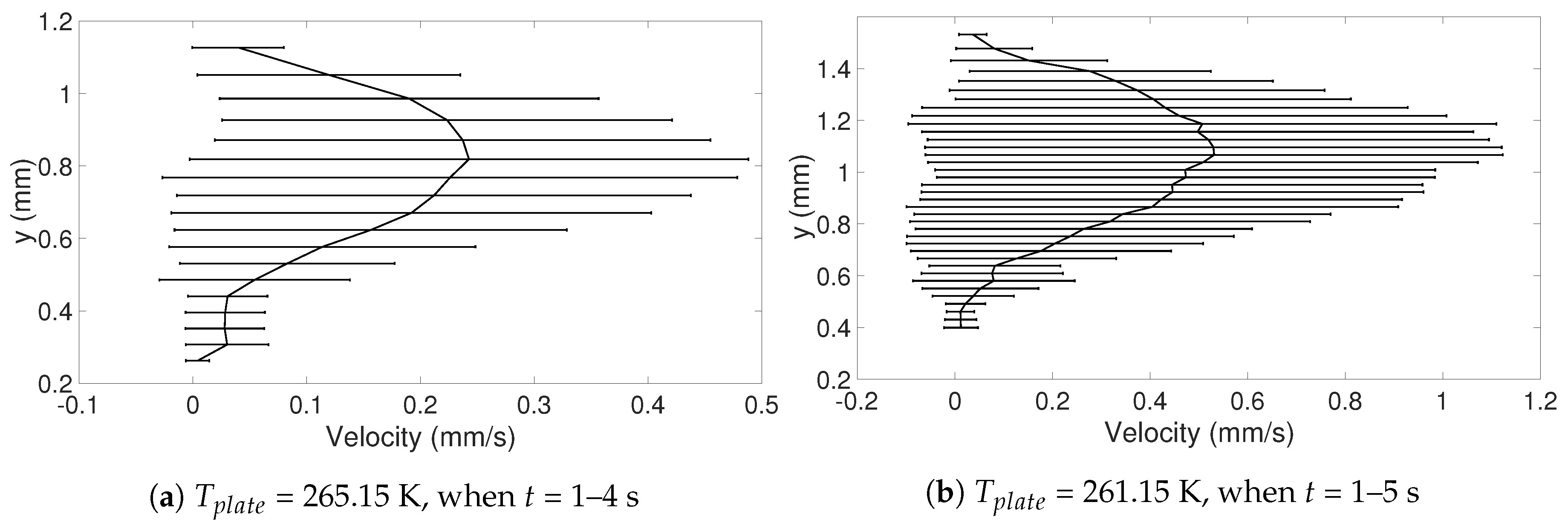
In this study, the internal flow in freezing and evaporating water droplets was investigated using Particle Image Velocimetry and a comparison between the two cases was performed. Three heating and two cooling temperatures were studied where the aim was to reveal if natural convection and/or if Marangoni effects influences the flow within the droplets. Due to the low viscosity in heated droplets, the early flow within these droplets might be influenced by the release of the droplet. For freezing droplets, the viscosity is high in the water and therefore the internal flow is not influenced by the release of the droplet, the movement is only due to freezing and T. During evaporation, within 15 s after the release of the droplet to the surface, a form of “steady-state” occurs since the conditions in and around the droplet are not changing significantly. As for the freezing droplets, a shift in flow direction occurs early in evaporation. This might be due to the Marangoni effects, but it could not be concluded in this work. Two other explantations could be due to the temperature differences caused by the heated surface or because of the force created as the droplets impact the heated surface, pushing the water up along the curved surface. In the freezing droplets, the flow is similar between the two temperatures and shows a typical “Marangoni flow”-behavior, suggesting that the Marangoni effects influence the early flow within freezing droplets. However, the shift in direction of the flow and the magnitude of the velocities differ between the two cases. When comparing the velocities during freezing and evaporation, it was found that a warmer heating surface yields higher velocities and a larger spread in velocities compared to a colder heating temperature, although the highest velocities and the largest spread in velocities was found when the temperature of the cooling surface was below zero.