1. Introduction
Due to intensified human activities and growth in living standards, many cities around the world are facing challenges of critically deteriorating water quality [
1,
2]. Water quality is a description of the chemical, physical, and biological characteristics of water with respect to its suitability for intended uses [
3,
4]. Reliable forecasting of water quality allows for the identification of future contaminant problems, and/or the initiation of effective countermeasures to prevent water pollution and protect public health. In China, the South-to-North Water Diversion Project is a major undertaking designed to resolve water shortage problems in northern China. The east route of the project uses an old artificial canal, known as the Grand Canal, which extends from Beijing to Hangzhou, as a diversion structure. Unlike some natural rivers, this artificial canal is usually characterized by a slow flow rate and irregular changes in water flow, as the canal occasionally opens and closes sluices to transfer a large amount of water. The water quality of the Grand Canal is a critical problem for the water diversion project, and predicting the degree of pollution along the canal is essential to guarantee water quality safety. In the past, a lot of forecasting models have been used in natural rivers, and they performed very well [
5,
6]. These models usually focused on only dissolved oxygen or the turbidity and salinity of water, but gave less attention to organic pollutants and nutrients pollutants [
7,
8]. Several previous studies have examined the spatial and temporal variations in water quality along the Grand Canal [
9,
10]. However, predicting water quality in the canal and this area has been comparatively scarce; even more rare and difficult is forecasting water quality using data with different measurement frequencies.
Many research efforts over the past decade have been aimed at developing and improving water quality prediction models [
11,
12]. Statistical models of time series data have become particularly popular in water quality [
13,
14]. A popular and widely used one is the autoregressive integrated moving average (ARIMA) model, which has already shown its capability in water quality prediction [
5]. Statistical modeling of water quality possesses many advantages, including simplification of complex of relations between water quality indicators, and the identification of similar temporal and spatial characteristics patterns among water quality indicators [
15,
16]. However, accurately describing nonlinear characteristics of a data series is a significant shortcoming of the approach, because the statistical models are usually based on temporal linear correlations within the modeled dataset.
To overcome this shortage, machine learning is widely used to address a range of nonlinear prediction problems, recently including the prediction of water quality [
17,
18,
19]. A support vector machine (SVM) is a typical model that represents an advanced form of machine learning and shows remarkable performance. SVM is well-known for its ability to improve classification and regression analysis [
20,
21]. Using kernel techniques as a part of a time series prediction provides for a more accurate estimation of the data, even where the data series are nonlinear, non-stationary, and not characterized a priori [
22]. In the recent years, the particle swarm optimization (PSO) algorithm has been applied to the optimization approach [
23]. It is also a good way to optimize model parameters when using SVM models [
24].
Currently, hybrid models have been extensively applied in a wide range of fields including environmental pollution forecasting and hydrology [
25,
26,
27]. Wavelet analysis is also a popular recent approach to data analysis and can distinguish between noise and useful signals information. Wavelet analysis is able to capture the non-stationary characteristics of data series and has been applied successfully to forecasting activities [
28]. Najah et al. [
28] used wavelet analysis and Adaptive Neuro-Fuzzy Inference System to predict the electrical conductivity, the total dissolved solids and turbidity in a river. Liu and colleagues made dissolved oxygen prediction in crab culture based on wavelet analysis and least squares support vector machine [
29]. However, there is a lack of studies on other water quality indicators, as well as in the different hydrological environment.
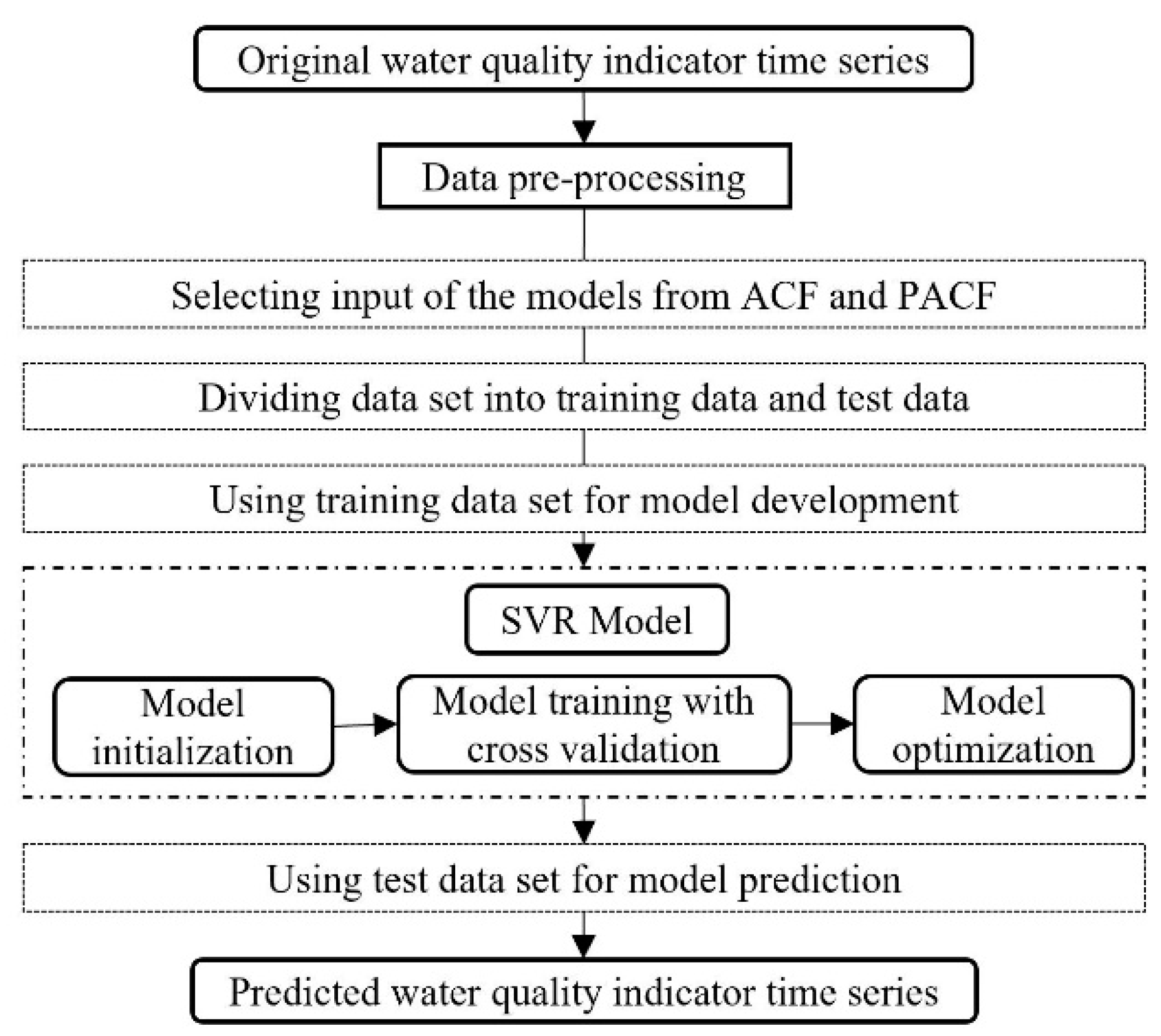
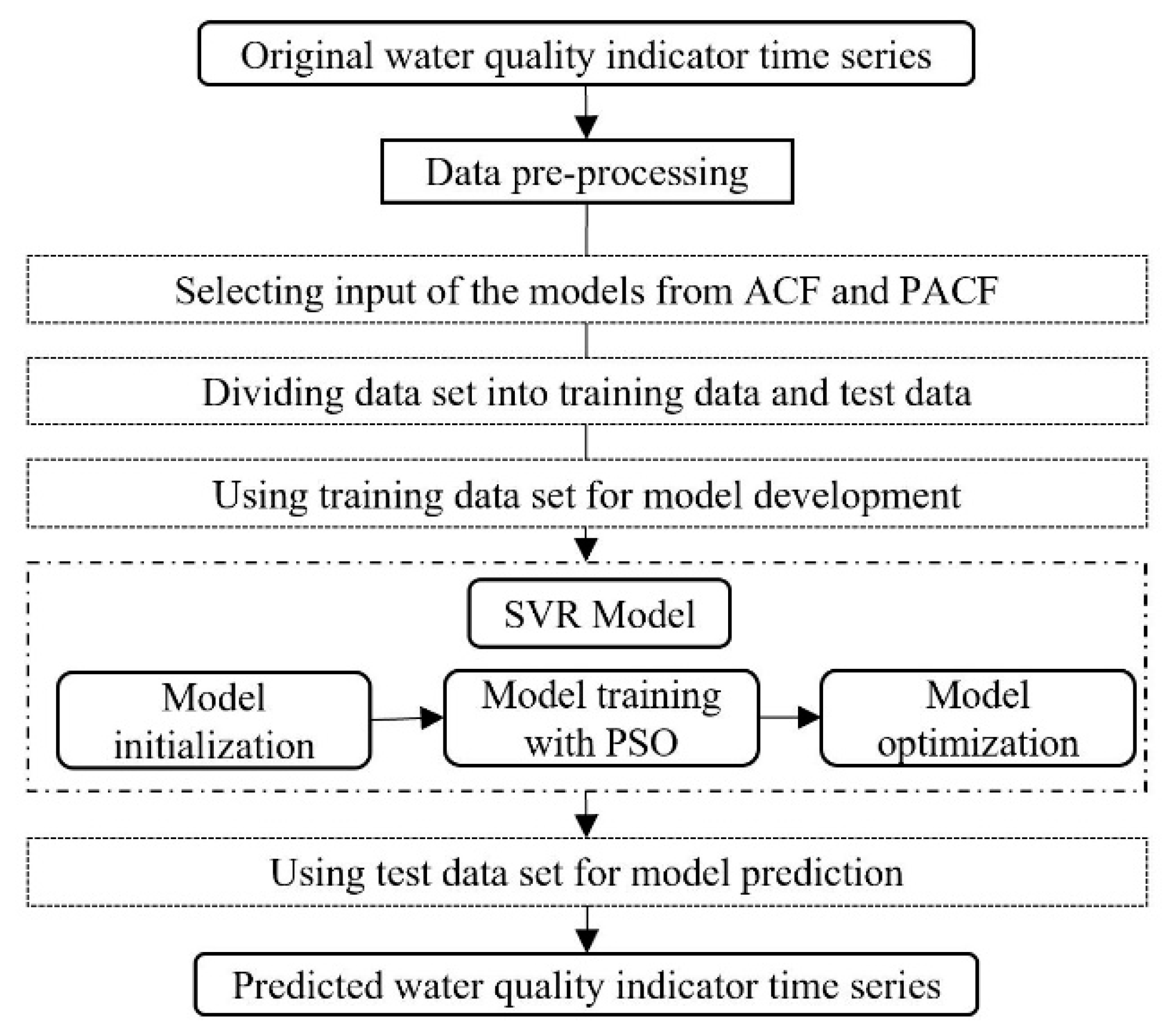
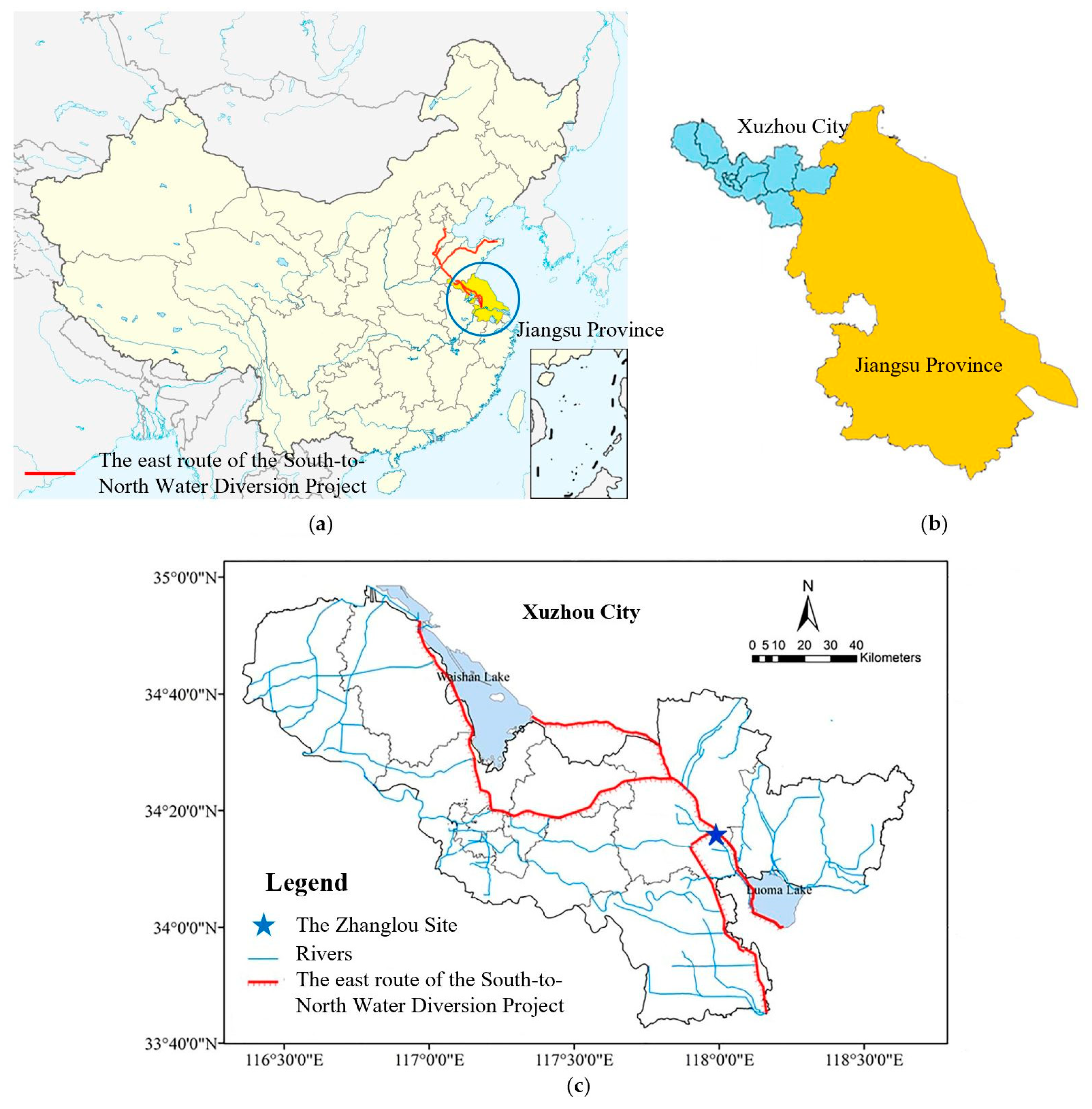
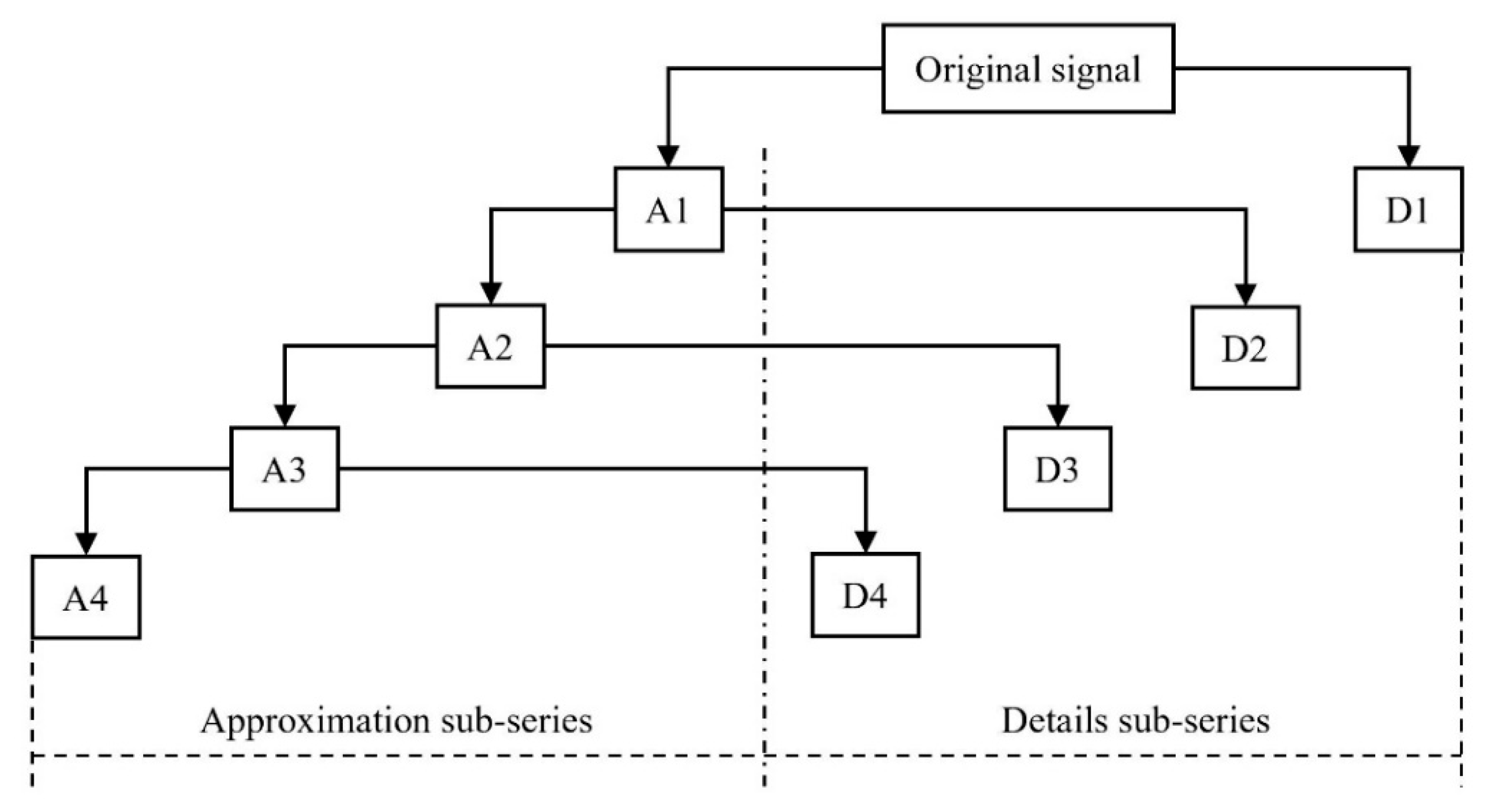
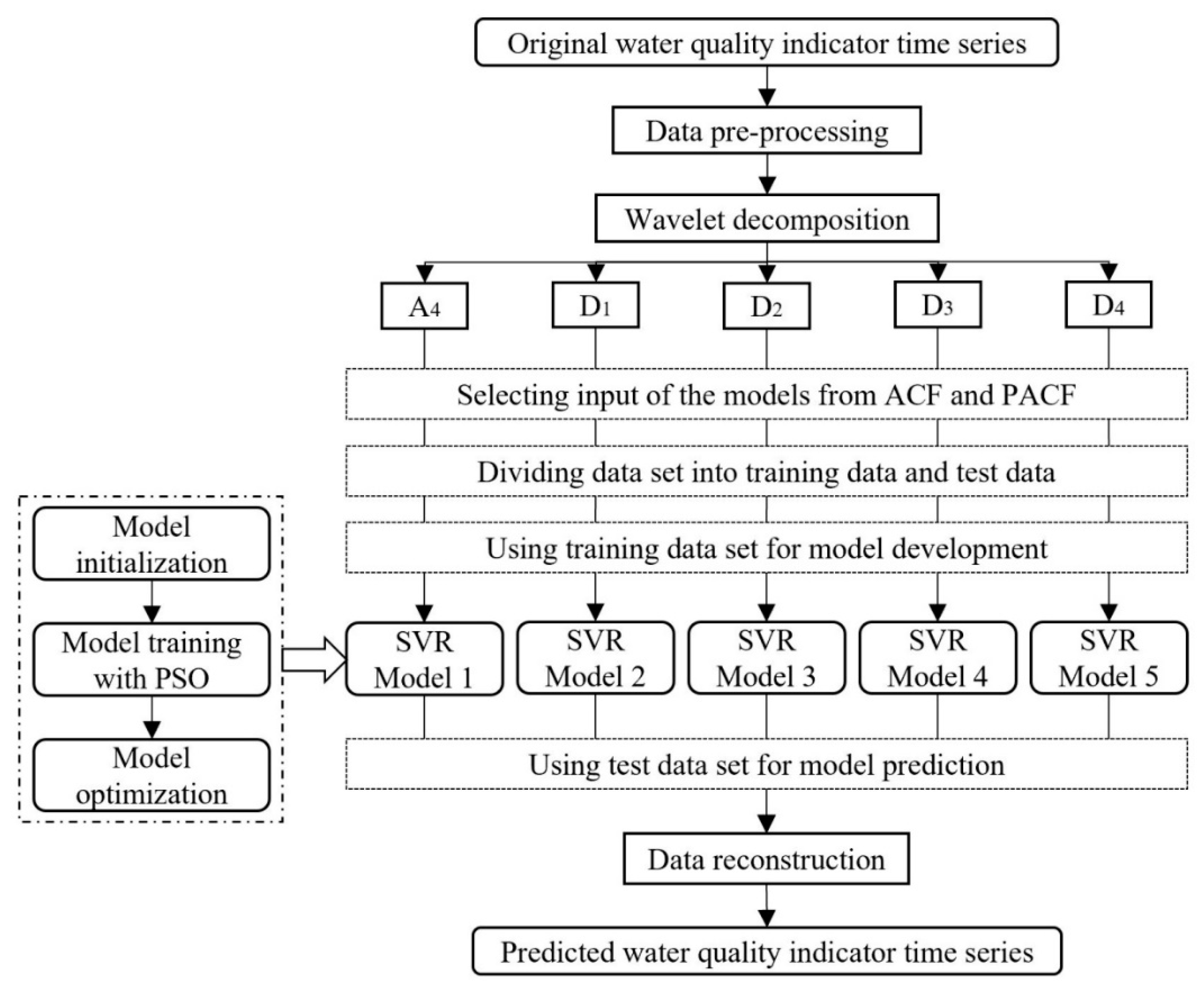
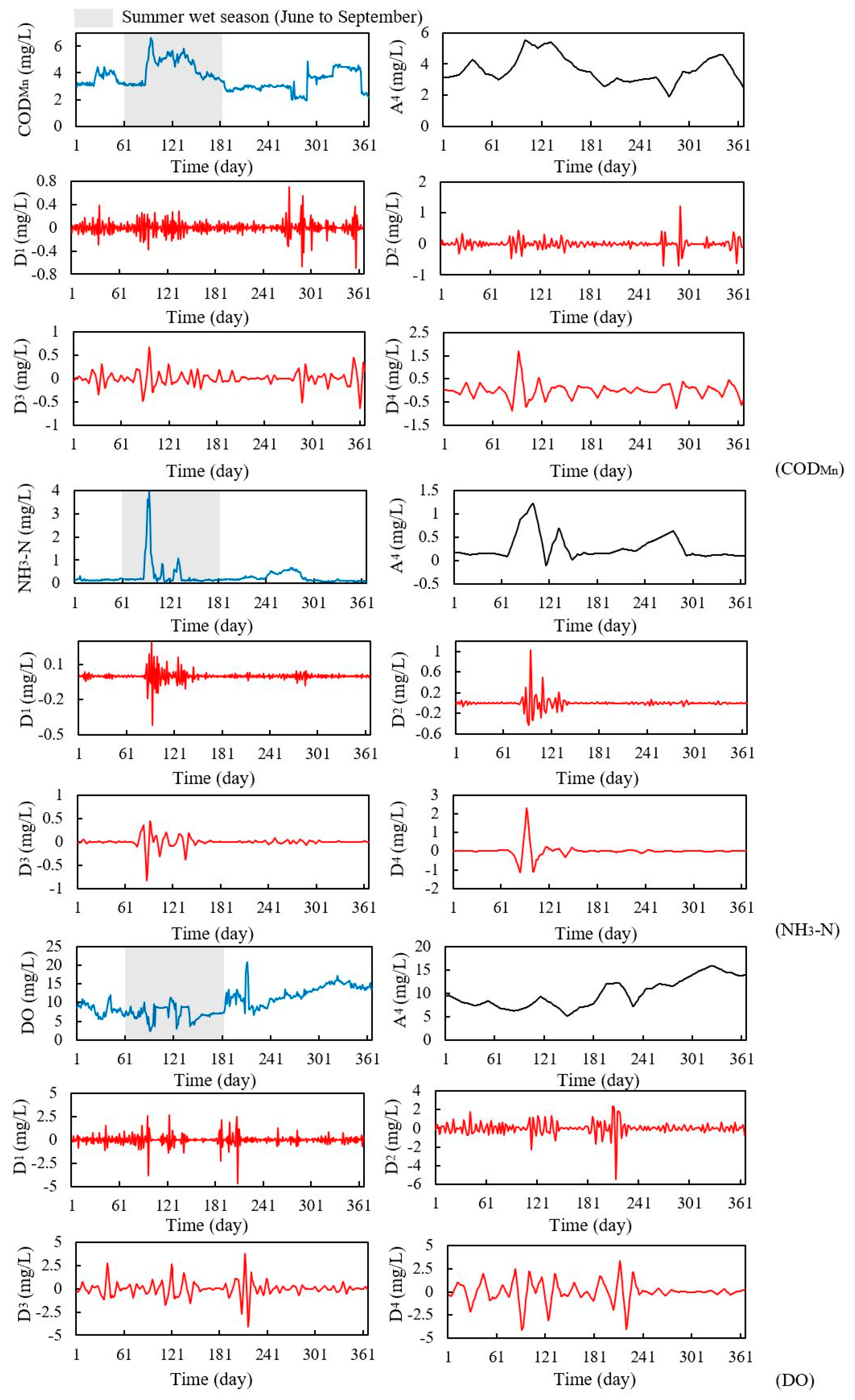
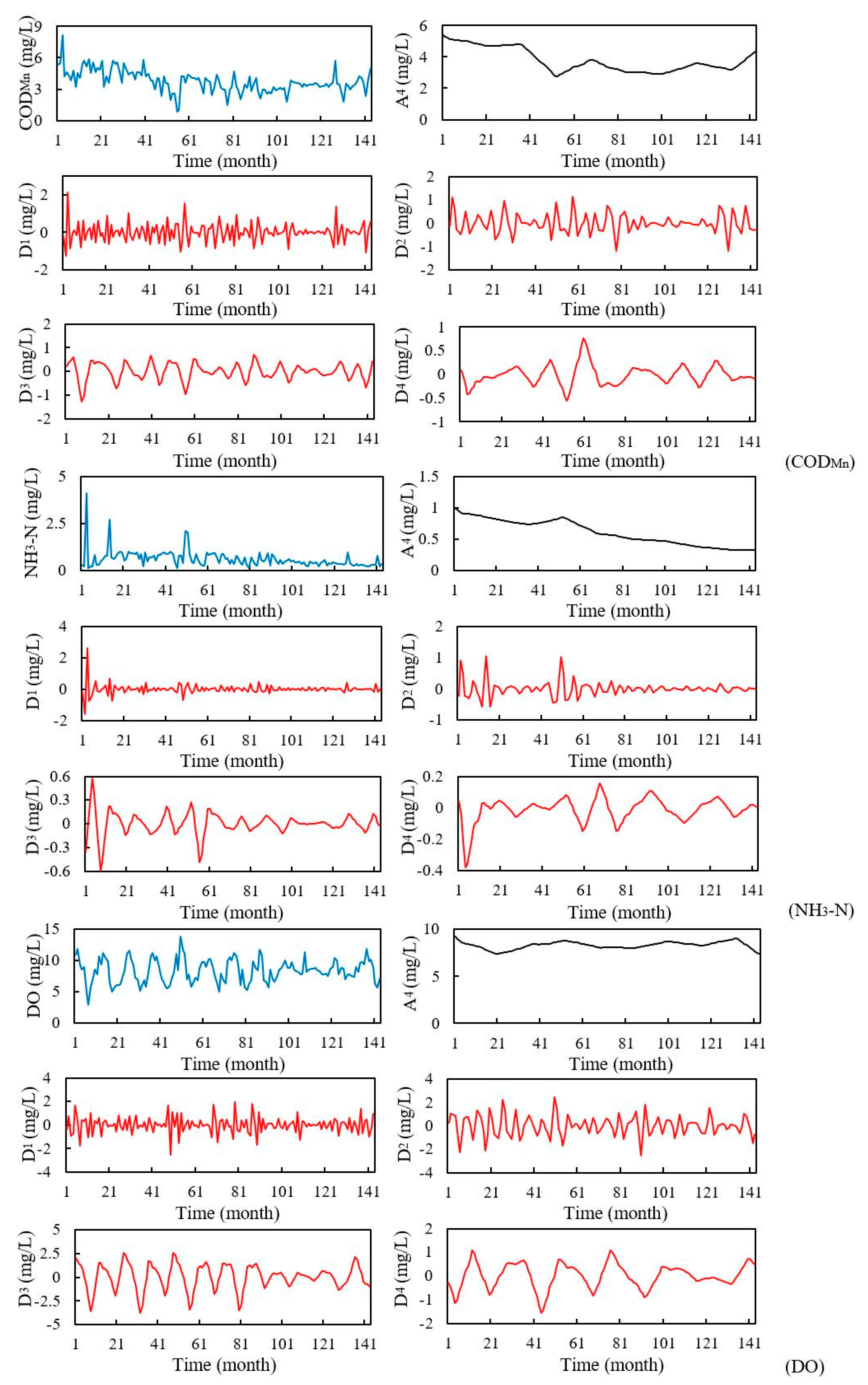
With the important position of the Grand Canal in the water diversion project and the national requirements of monitoring the water quality to guarantee water safety, this study tried to examine the efficiency of a hybrid model in predicting three organic pollutants and nutrients water quality indicators for this manually controlled canal. In this study, a wavelet analysis-support vector regression approach with particle swarm optimization algorithms (WA-PSO-SVR) over different time scales was established. The analyzed data include: (1) daily data collected over a period of one year (1 April 2015 to 1 March 2016), and (2) monthly data obtained over a period of about twelve years (January 2005 to November 2016). Three water quality indicators were modeled, including chemical oxygen demand determined by KMnO4 (CODMn), ammonia nitrogen (NH3-N), and dissolved oxygen (DO). The performance of the models developed for both time scales were compared and assessed. In addition, to assess the potential advantages of using the WA-PSO-SVR model, its results were compared to the results from a simple support vector regression with particle swarm optimization model (PSO-SVR) and a standalone SVR model, which were developed for the datasets.
This research demonstrates the reliability and suitability of the hybrid model in forecasting water quality indicators in situations. The results are helpful for (1) providing an effective method of water quality prediction for water diversion in the region towards better governance policies in daily management, (2) adding more research materials for the hybrid model applied in different water quality indicators and hydrological environment, and (3) contributing to the fields of non-linear water quality data prediction modeling over different time scales.
4. Discussion
Because of the requirement of daily water transfer management, an available forecasting model is essential to environmental governance. This model is mainly established for general changing trend prediction helping long-term water pollution control, but not for giving accurate forecasting of emergency or sudden changes caused by accident events, such as flooding or pollution leaks.
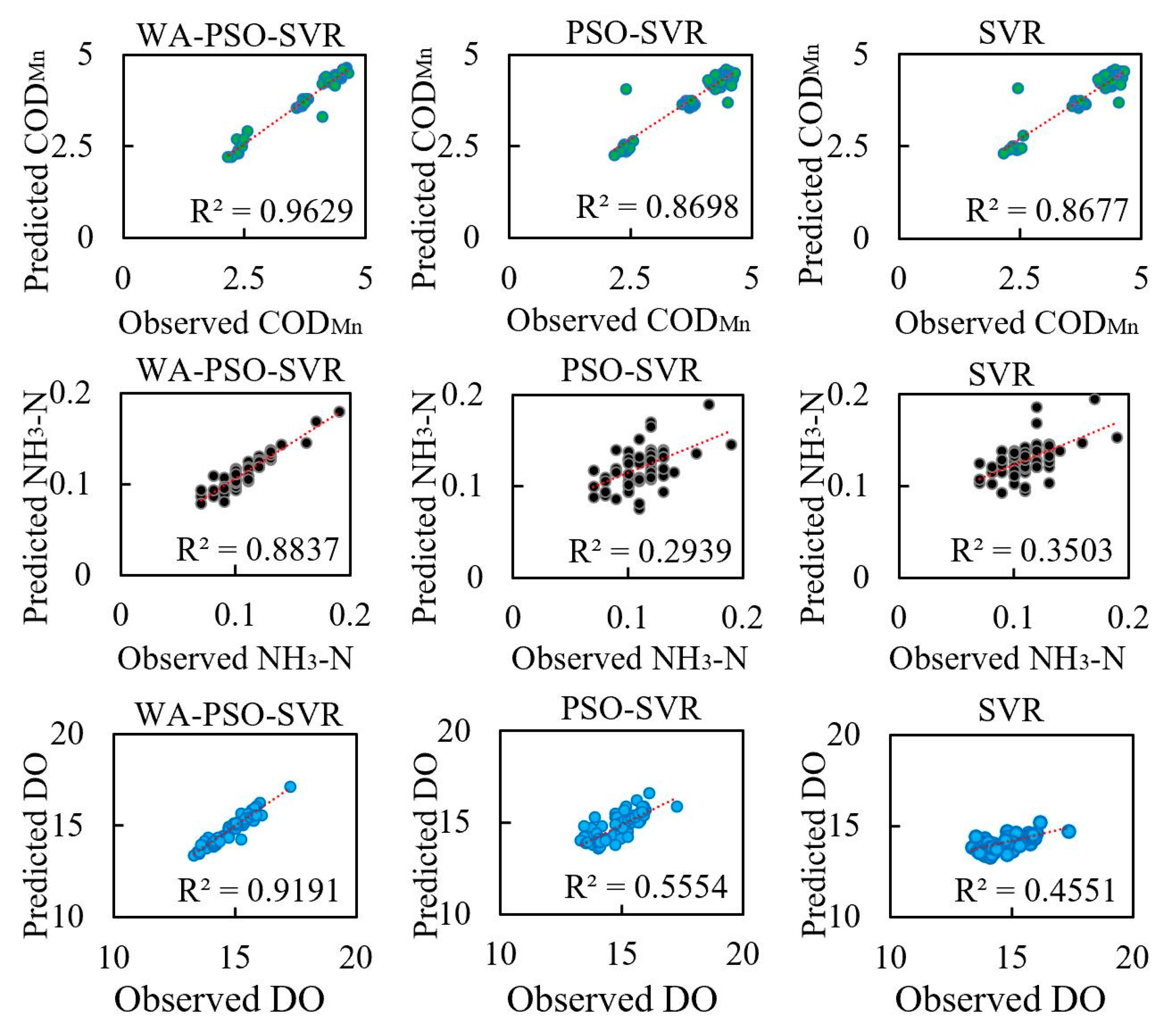
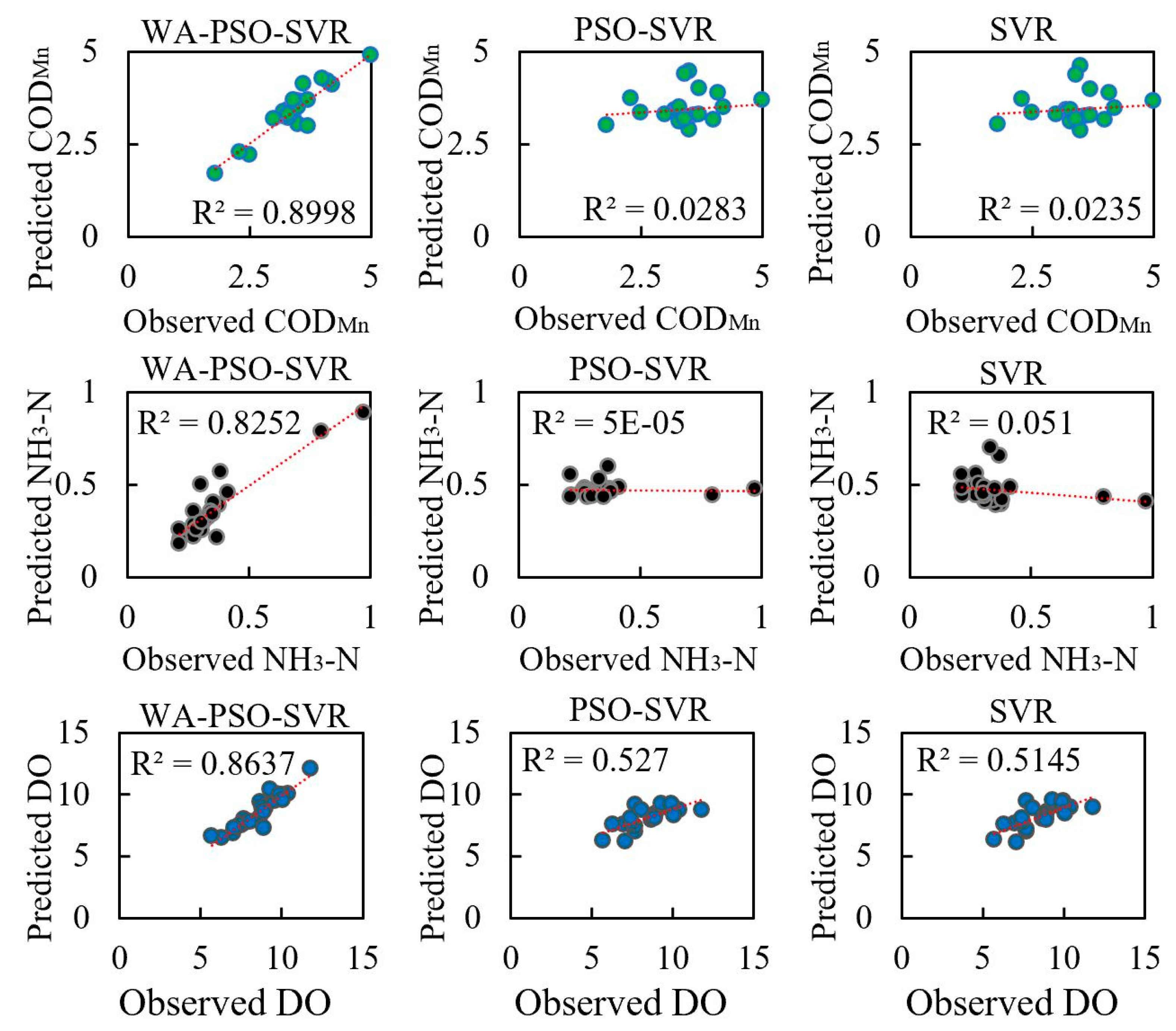
Regardless of whether daily or monthly time series data were predicted, the WA-PSO-SVR models produced more accurate results for the three analyzed water quality indicators. The hybrid modeling approach demonstrated to be a reliable approach for water quality prediction. Besides the similar studies that have been done for DO in the river and pond or the turbidity and salinity of water [
7,
8,
29], this study showed that the hybrid structure could be applied in more fields. During this study, the performance of the WA-PSO-SVR models was better when modeling daily data than monthly data, indicating that wavelet analysis, when applied to short-term forecasting, would produce more accurate results. Previous studies led to similar conclusions in that hourly machine learning models outperformed daily models when making DO predictions using wavelet-neural network models [
26].
As mentioned above, of the six time series related to the three water quality indicators, only the daily NH
3-N and monthly COD
Mn series were stationary. However, the accuracy of the WA-PSO-SVR modeling results was uncorrelated to whether the time series were stationary. For daily NH
3-N and monthly COD
Mn prediction, the hybrid models generated satisfying results, whereas both the PSO-SVR and SVR produced unreliable results for them, as determined by negative NSE values. The PSO-SVR and SVR have given satisfactory performances in some other studies [
21]; however, these results showed a possibility that the hybrid model was more suitable for stationary data than the PSO-SVR and SVR models in this situation. Similar to the stationarity of the data series, when comparing the WA-PSO-SVR and other two models, the model performances were also unrelated to the distribution of data. Wavelet analysis could increase the accuracy of prediction, which was independent of Skewness and Kurtosis values.
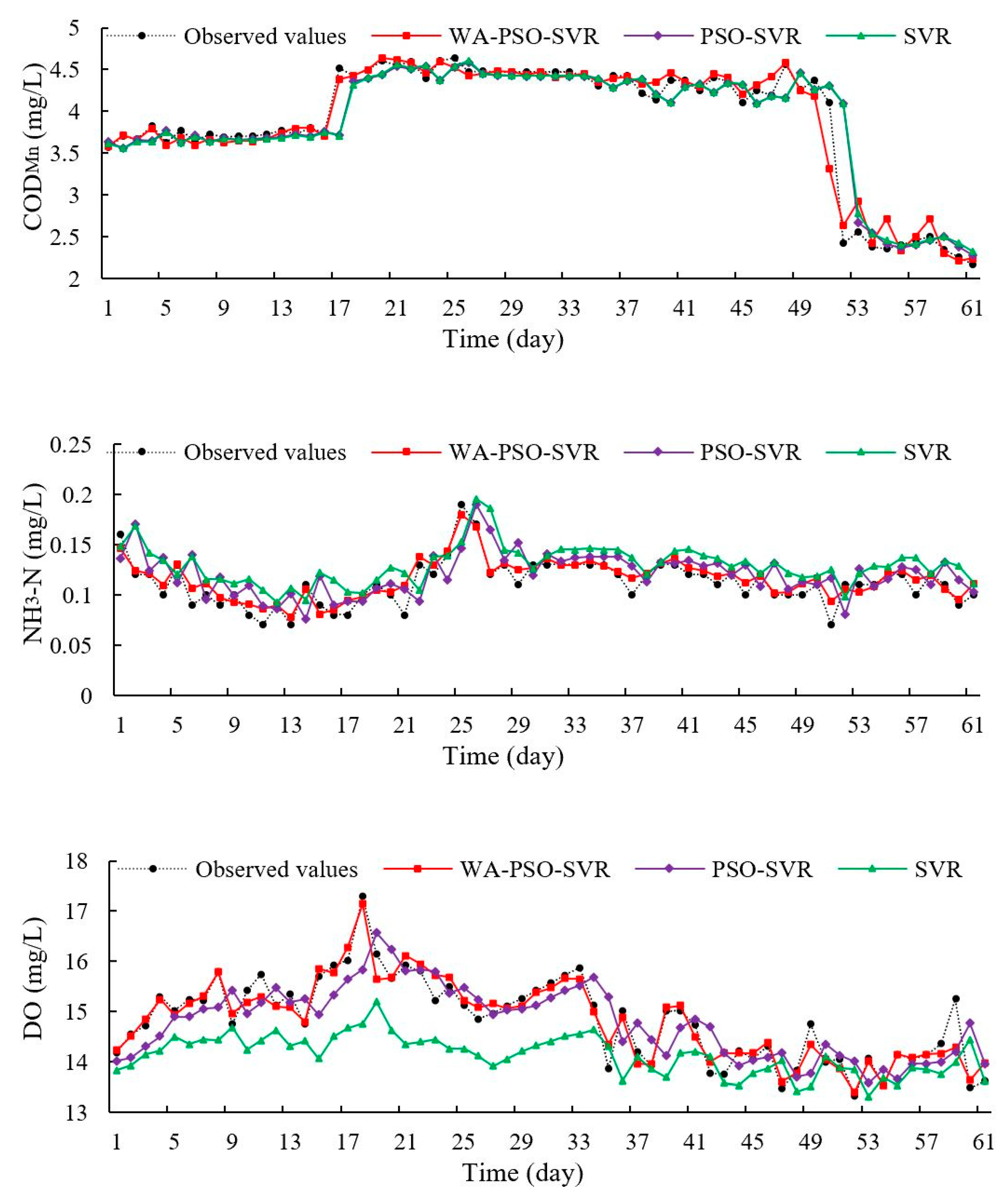
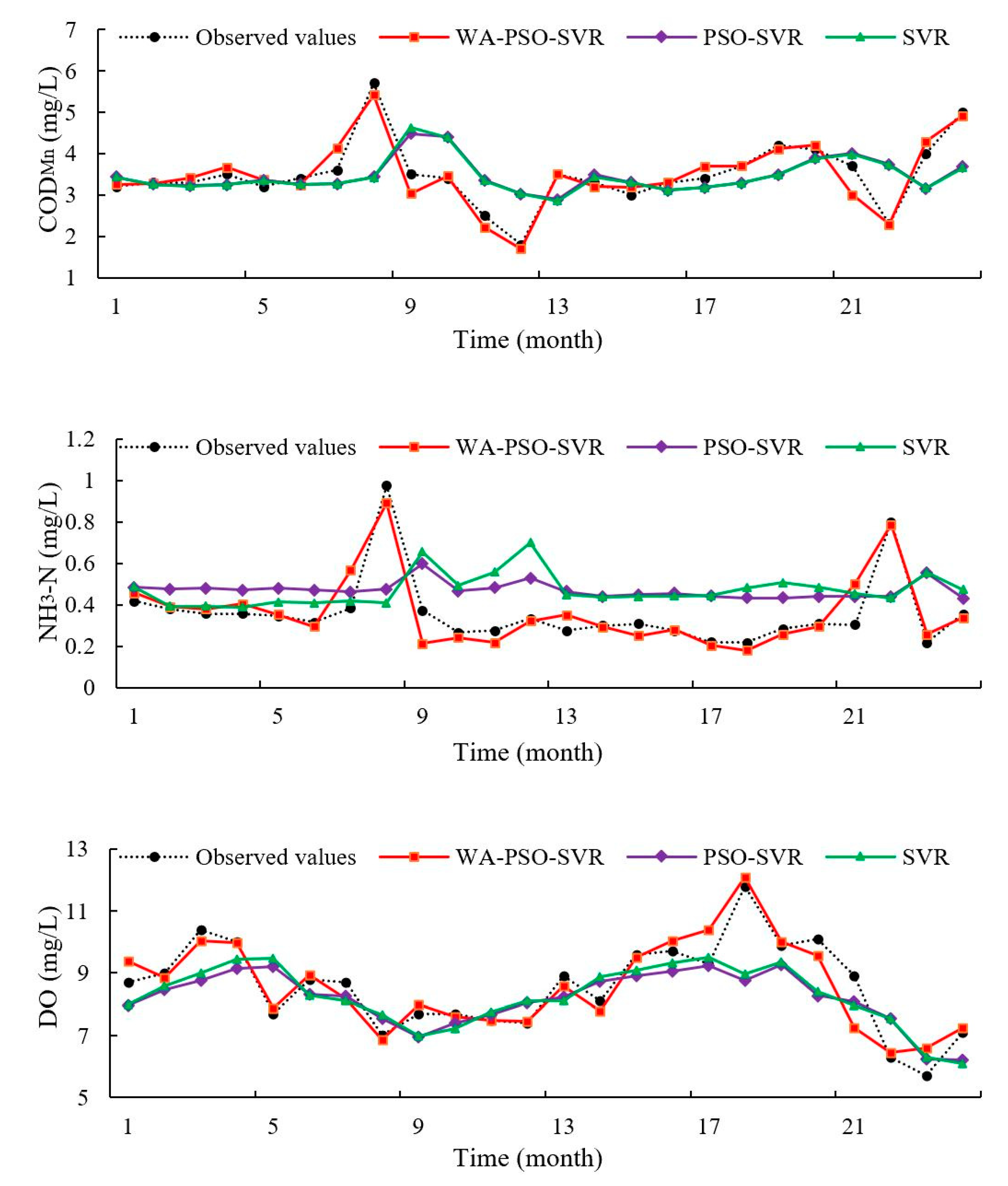
The PSO-SVR and SVR curves of observed and predicted values showed that there was a one-step lag in predicted values (
Figure 5 and
Figure 8). However, these models could effectively re-create changes in parameter trends relatively accurately. This phenomenon has occurred in some studies [
7,
26]. Usually, it means that the models had some drawbacks and deficient ability to provide accurate extreme values. This may be caused by a lack of sufficient input information by considering only autocorrelation of data series. A good way to solve this deficiency is by using a hybrid decomposition structure [
7,
27]. In this study, the hybrid WA-PSO-SVR models demonstrated their ability to predict extreme values through time.
Moreover, regardless of the time scale modeled (i.e., daily or monthly data), the estimation of COD
Mn was extremely good with the highest NSE values, followed closely by DO, and NH
3-N was the worst. However, when comparing the RMSE and MAPE values, the results were different. NH
3-N had the lowest RMSE, but DO had the lowest MAPE. In general, the prediction of NH
3-N was more difficult. The NH
3-N models always had larger MAPE and lower NSE among three indicators. This is related to the distribution of the data series. Although all of the original six data series did not have a normal distribution, two NH
3-N series had larger absolute values of Skewness and Kurtosis among them, indicating that they were far from normal distribution than other series. Highly skewed and imbalanced data is a reason that could lead to the poor performance of these models [
48].
Because there are many indicators that can be used to assess the level of water quality pollution, the prediction of water quality may rely on either multiple and single variable models. However, multivariable models do not always perform better than single variable models because of strong statistical autocorrelations of the water quality indicators [
6]. In this study, all models were developed based on their autocorrelation, including models of sub-series decomposed from wavelet analysis. The WA-PSO-SVR modeling results illustrate that these simple models with a single variable had the ability to provide reliable and accurate predictive outcomes. However, previous research has found that models that do not consider autocorrelation can also produce good estimations [
19]. Thus, the cross-correlation between indicators or the spatial correlation between a single parameter collected at different sample points is important. How these correlations influence a model’s performance should be studied in the future.
However, as mentioned above, this approach leads to the limitation that the models were based on historical trends of data series, and they were hard to give early warnings of abnormal values which indicate the happening of emergent events. Models to be used for an emergency response is required to account for all of the mechanisms and factors [
49]. The warning system for water transfer is another topic that needs to be studied next.
5. Conclusions
The prediction of water quality is important in monitoring the changing trends of water quality and managing water transfer better. A reliable predicting model can help the decision makers to do daily management and reduce the adverse consequences resulting from the potential deteriorating water quality. Therefore, in this study, a hybrid WA-PSO-SVR structure was developed to predict daily and monthly water quality parameters in a canal. This hybrid model was successfully applied to simulate the time series of three water quality indicators at Zhanglou Site along the Grand Canal. In light of the results obtained above, the following general conclusions were drawn.
First, wavelet analysis is an efficient method to improve the performance of machine learning models. The accuracy of models increased in all situations. Regardless of whether the times series were stationary, the WA-PSO-SVR model always produced the best predictions. In contrast, the PSO-SVR and standalone SVR models occasionally produced results exhibiting lower NSE values, indicating that they were less reliable in this case. The hybrid model also had a strong ability to track fluctuations in parameter trends and to predict extreme values. Second, a comparison of the performances of all models developed for both daily and monthly data showed that daily or short-term predictions were better than the longer predictions. With regards to the daily WA-PSO-SVR models, the NSE values of CODMn, NH3-N, and DO reached up to 0.9627, 0.8433, and 0.9190, respectively, indicating that the models were available to provide satisfactory predictions. Third, among the three indicators in this study, CODMn and DO were effectively predicted for both daily and monthly timeframes, but NH3-N showed the worst performances, as the data series much deviated to normal distribution. Finally, this study shows that the prediction of water quality indicators using only a data series (i.e., without considering other indicators) is possible. The autocorrelation of series data can identify statistically significant lagged data and be used to construct appropriate predictive models for daily management purposes.
This study provided a reliable method to track the changing trends of water quality in a canal. The results presented in this study contribute to the knowledge for both short-term and long-term water quality predictions which actively support environmental monitoring tasks. In particular, the hybrid model would be applied in the east route of the South-to-North Water Diversion Project, and is expected to help the decision makers to take timely actions towards a better water diversion operation and environmental management, by predicting water quality more accurately.