A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds
Abstract
:1. Introduction
1.1. The CN Model Framework
1.2. Effect of Slope on CN and Runoff Estimation
2. Materials and Methods
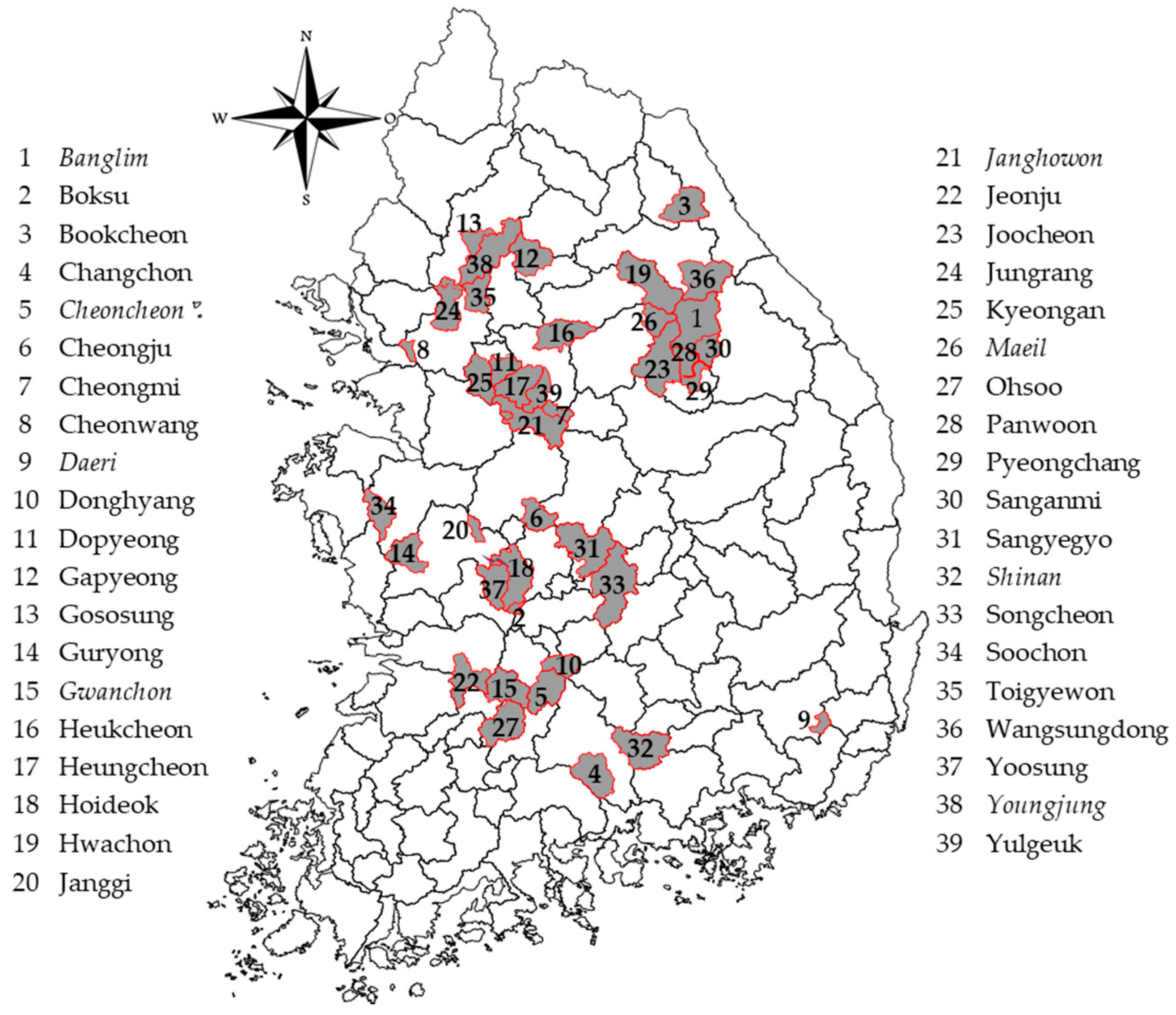
2.1. Study Area Description and Climate
2.2. Data Collection and Interpretation
2.3. Slope-Adjusted Curve Number Considerations and Development
2.4. Steps of Slope-Adjusted CN Parameter Optimization
- Data pertaining to 39 watersheds in which 1779 rainstorms events occurred provided the known values of the rainstorm events, P; the observed runoff, Qo; and the optimized CNs for each watershed. The least squares nonlinear orthogonal distance regression objective function in Origin Pro 9.6 software produced the optimized CN values from the following equation.
- To optimize parameter b in Equation (9), the CNs obtained for the 39 watersheds from Equation (10) were divided into two sets, those of 31 watersheds (1402 rainstorm–runoff events) for calibration and those of 8 watersheds (377 rainstorm-runoff events) for validation. For calibration, the optimized CNs in step 1 were set as the target values challenging the right side of Equation (9) using the nonlinear regression least squares Levenberg–Marquardt algorithm in SPSS v.25 software. To take into account the individual watersheds’ effects on parameter b optimization, the leave-one-out (LOOV) technique was adopted. The average of 31 calibrations repetitions was the value of b = 7.125. This led to recasting the proposed CNIIα as
3. Statistical Analysis for Model Performance Evaluation
4. Results and Discussion
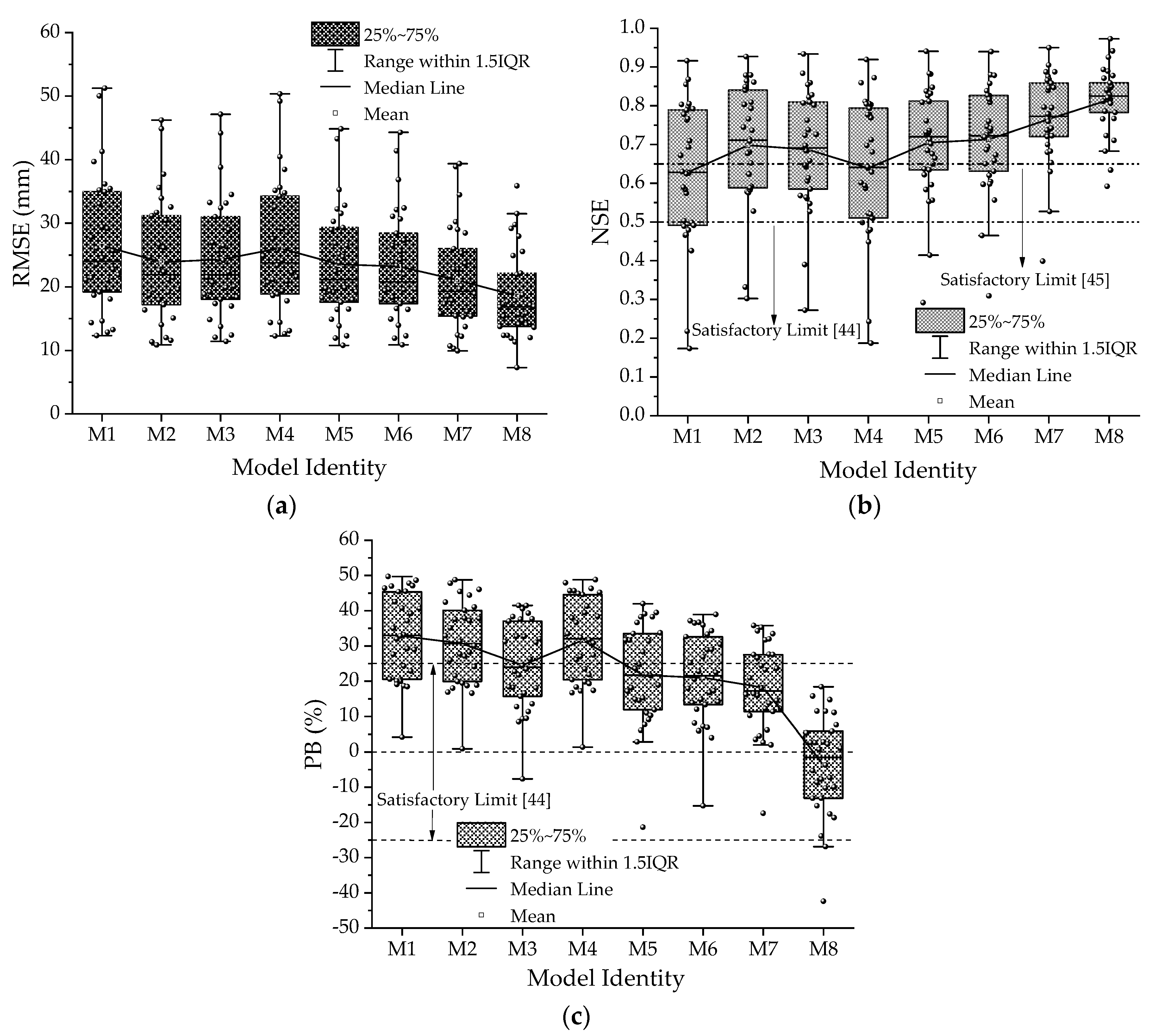
4.1. Models’ Analysis Based on Descriptive Statistics
4.2. Model Performance Evaluation in Watersheds Used for Calibration
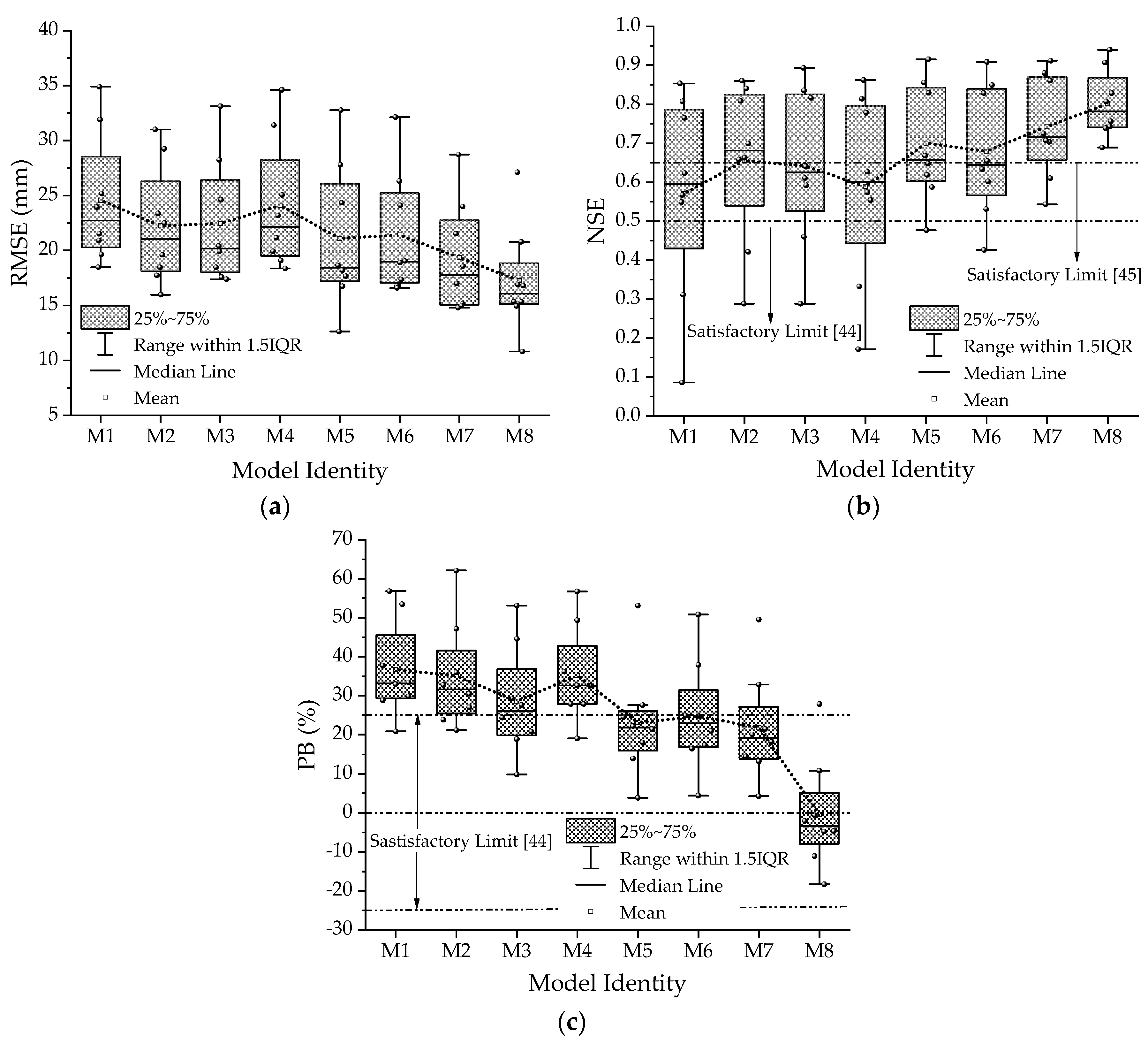
4.3. Models’ Performance Evaluation in Watersheds Used for Validation
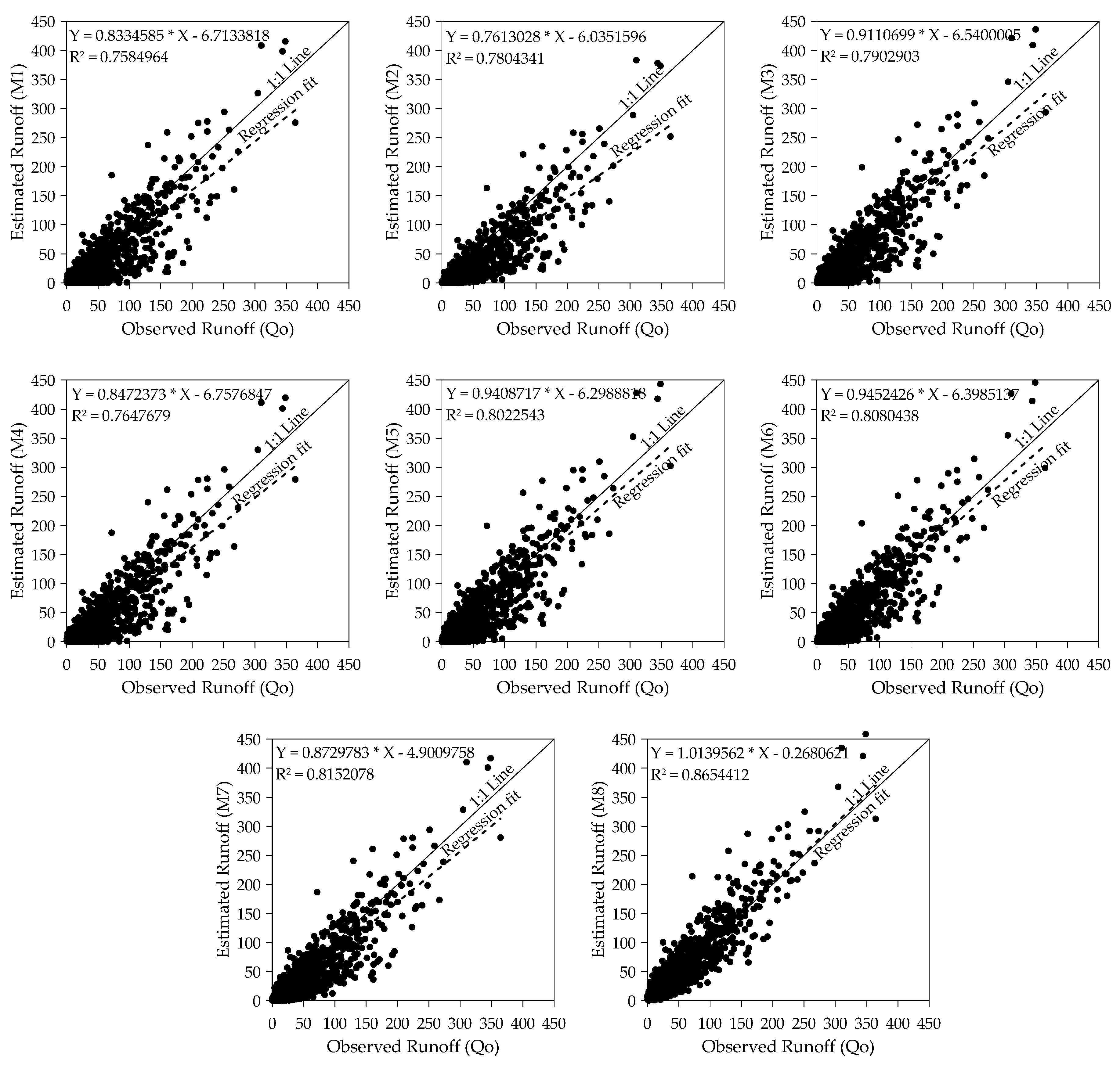
4.4. Overall Performance of Models and Comparison Based on 1:1 Plot
5. Conclusions and Practical Implications
Author Contributions
Funding
Conflicts of Interest
References
- Muche, M.E.; Hutchinson, S.L.; Hutchinson, J.S.; Johnston, J.M. Phenology-adjusted dynamic curve number for improved hydrologic modeling. J. Environ. Manag. 2019, 235, 403–413. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.H.; Ward, T.J.; Woodward, D.E.; Van Mullem, J.A. ASCE EWRI Task Committee Report on State of the Practice in Curve Number Hydrology; ASCE: Reston, VA, USA, 2009; Volume 106. [Google Scholar]
- Fan, F.; Deng, Y.; Hu, X.; Weng, Q. Estimating composite curve number using an improved SCS-CN method with remotely sensed variables in Guangzhou, China. Remote Sens. 2013, 5, 1425–1438. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; van Dijk, A.I.; de Roo, A.; Dutra, E.; Fink, G.; Orth, R.; Schellekens, J. Global evaluation of runoff from ten state-of-the-art hydrological models. Hydrol. Earth Sys. Sci. 2017, 21, 2881–2903. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, R.H.; Theurer, F.D.; Rezaeianzadeh, M. Understanding the basis of the curve number method for watershed models and TMDLs. J. Hydrol. Eng. 2019, 24, 06019003. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z.; Chow, M.F. Urban flood depth estimate with a new calibrated curve number runoff prediction model. IEEE Access 2020, 8, 10915–10923. [Google Scholar] [CrossRef]
- Pandit, A.; Heck, H.H. Estimations of soil conservation service curve numbers for concrete and asphalt. J. Hydrol. Eng. 2009, 14, 335–345. [Google Scholar] [CrossRef]
- Stewart, D.; Canfield, E.; Hawkins, R. Curve number determination methods and uncertainty in hydrologic soil groups from semiarid watershed data. J. Hydrol. Eng. 2012, 17, 1180–1187. [Google Scholar] [CrossRef]
- Tedela, N.H.; McCutcheon, S.C.; Rasmussen, T.C.; Hawkins, R.H.; Swank, W.T.; Campbell, J.L.; Adams, M.B.; Jackson, C.R.; Tollner, E.W. Runoff curve numbers for 10 small forested watersheds in the mountains of the eastern United States. J. Hydrol. Eng. 2012, 17, 1188–1198. [Google Scholar] [CrossRef] [Green Version]
- Ajmal, M.; Waseem, M.; Ahn, J.-H.; Kim, T.-W. Runoff estimation using the NRCS slope-adjusted curve number in mountainous watersheds. J. Irrig. Drain. Eng. 2016, 142, 04016002. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, G.; Wang, N.; Luo, L. Initial abstraction ratio in the SCS-CN method in the Loess Plateau of China. Trans. ASABE 2011, 54, 163–169. [Google Scholar] [CrossRef]
- D’Asaro, F.; Grillone, G. Empirical investigation of curve number method parameters in the Mediterranean area. J. Hydrol. Eng. 2012, 17, 1141–1152. [Google Scholar] [CrossRef]
- D’Asaro, F.; Grillone, G.; Hawkins, R.H. Curve number: Empirical evaluation and comparison with curve number handbook tables in Sicily. J. Hydrol. Eng. 2014, 19, 04014035. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.K.; Berndtsson, R.; Jain, M.K.; Pandey, R.P. Development of a modified SMA based MSCS-CN model for runoff estimation. Water Res. Manag. 2015, 29, 4111–4127. [Google Scholar] [CrossRef]
- Ajmal, M.; Kim, T.-W. Quantifying excess stormwater using SCS-CN–based rainfall runoff models and different curve number determination methods. J. Irrig. Drain. Eng. 2015, 141, 04014058. [Google Scholar] [CrossRef]
- Baltas, E.; Dervos, N.; Mimikou, M. Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Sys. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef] [Green Version]
- Sharpley, A.; Williams, J. Epic—Erosion/Productivity Impact Calculator: I. Model Documentation. II: User Manual; Technical Bulletin, No. 1768 1990; United State Department of Agriculture: Washington, DC, USA, 1990.
- Williams, J.R.; Izaurralde, R.C.; Steglich, E.M. Agricultural policy/environmental extender model. Theor. Doc. Version 2008, 604, 2008–2017. [Google Scholar]
- Huang, M.; Gallichand, J.; Wang, Z.; Goulet, M. A modification to the soil conservation service curve number method for steep slopes in the Loess Plateau of China. Hydrol. Process. 2006, 20, 579–589. [Google Scholar] [CrossRef]
- Deshmukh, D.S.; Chaube, U.C.; Hailu, A.E.; Gudeta, D.A.; Kassa, M.T. Estimation and comparision of curve numbers based on dynamic land use land cover change, observed rainfall-runoff data and land slope. J. Hydrol. 2013, 492, 89–101. [Google Scholar] [CrossRef]
- Ebrahimian, M.; Nuruddin, A.A.B.; Soom, M.A.B.M.; Sood, A.M.; Neng, L.J. Runoff estimation in steep slope watershed with standard and slope-adjusted curve number methods. Pol. J. Environ. Stud. 2012, 21, 1191–1202. [Google Scholar]
- Mishra, S.K.; Chaudhary, A.; Shrestha, R.K.; Pandey, A.; Lal, M. Experimental verification of the effect of slope and land use on scs runoff curve number. Water Res. Manag. 2014, 28, 3407–3416. [Google Scholar] [CrossRef]
- Williams, J.; Izaurralde, R. The APEX model. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Williams, J.; Kannan, N.; Wang, X.; Santhi, C.; Arnold, J. Evolution of the SCS runoff curve number method and its application to continuous runoff simulation. J. Hydrol. Eng. 2012, 17, 1221–1229. [Google Scholar] [CrossRef]
- Fang, H.; Cai, Q.; Chen, H.; Li, Q. Effect of rainfall regime and slope on runoff in a gullied loess region on the Loess Plateau in China. Environ. Manag. 2008, 42, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Garg, V.; Nikam, B.R.; Thakur, P.K.; Aggarwal, S. Assessment of the effect of slope on runoff potential of a watershed using NRCS-CN method. Int. J. Hydrol. Sci. 2013, 3, 141–159. [Google Scholar] [CrossRef]
- Slattery, M.C.; Bryan, R.B. Hydraulic conditions for rill incision under simulated rainfall: A laboratory experiment. Earth Surf. Process. Landf. 1992, 17, 127–146. [Google Scholar] [CrossRef]
- Govers, G. A field study on topographical and topsoil effects on runoff generation. Catena 1991, 18, 91–111. [Google Scholar] [CrossRef]
- Fox, D.; Bryan, R.; Price, A. The influence of slope angle on final infiltration rate for interrill conditions. Geoderma 1997, 80, 181–194. [Google Scholar] [CrossRef]
- Van de Giesen, N.; Stomph, T.J.; de Ridder, N. Surface runoff scale effects in west African watersheds: Modeling and management options. Agric. Water Manag. 2005, 72, 109–130. [Google Scholar] [CrossRef]
- Joel, A.; Messing, I.; Seguel, O.; Casanova, M. Measurement of surface water runoff from plots of two different sizes. Hydrol. Process. 2002, 16, 1467–1478. [Google Scholar] [CrossRef]
- Stomph, T.; De Ridder, N.; Steenhuis, T.; Van de Giesen, N. Scale effects of hortonian overland flow and rainfall-runoff dynamics: Laboratory validation of a process-based model. Earth Surf. Process. Landf. 2002, 27, 847–855. [Google Scholar] [CrossRef]
- Esteves, M.; Lapetite, J.M. A multi-scale approach of runoff generation in a sahelian gully catchment: A case study in Niger. Catena 2003, 50, 255–271. [Google Scholar] [CrossRef]
- Lal, M.; Mishra, S.; Pandey, A.; Pandey, R.; Meena, P.; Chaudhary, A.; Jha, R.K.; Shreevastava, A.K.; Kumar, Y. Evaluation of the soil conservation service curve number methodology using data from agricultural plots. Hydrogeol. J. 2017, 25, 151–167. [Google Scholar] [CrossRef]
- Mah, M.; Douglas, L.; Ringrose-Voase, A. Effects of crust development and surface slope on erosion by rainfall. Soil Sci. 1992, 154, 37–43. [Google Scholar] [CrossRef]
- Kowalik, T.; Walega, A. Estimation of CN parameter for small agricultural watersheds using asymptotic functions. Water 2015, 7, 939–955. [Google Scholar] [CrossRef] [Green Version]
- Lian, H.; Yen, H.; Huang, C.; Feng, Q.; Qin, L.; Bashir, M.A.; Wu, S.; Zhu, A.-X.; Luo, J.; Di, H. CN-China: Revised runoff curve number by using rainfall-runoff events data in China. Water Res. 2020, 177, 115767. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Im, E.-S.; Hur, J.; Shim, K.-M. Added value of very high resolution climate simulations over South Korea using WRF modeling system. Clim. Dyn. 2019, 54, 173–189. [Google Scholar] [CrossRef]
- Isik, S.; Kalin, L.; Schoonover, J.E.; Srivastava, P.; Lockaby, B.G. Modeling effects of changing land use/cover on daily streamflow: An artificial neural network and curve number based hybrid approach. J. Hydrol. 2013, 485, 103–112. [Google Scholar] [CrossRef]
- Mishra, S.K.; Jain, M.K.; Suresh Babu, P.; Venugopal, K.; Kaliappan, S. Comparison of AMC-dependent CN-conversion formulae. Water Res. Manag. 2008, 22, 1409–1420. [Google Scholar] [CrossRef]
- McCutcheon, S.; Tedela, N.; Adams, M.; Swank, W.; Campbell, J.; Hawkins, R.; Dye, C. Rainfall-Runoff Relationships for Selected Eastern us Forested Mountain Watersheds: Testing of the Curve Number Method for Flood Analysis; West Virginia Division of Forestry: Charleston, WV, USA, 2006. [Google Scholar]
- NRCS (Natural Resources Conservation Service). National Engineering Handbook Section-4, Part 630, Hydrology; NRCS: Washington, DC, USA, 2001.
- Lal, M.; Mishra, S.K.; Pandey, A. Physical verification of the effect of land features and antecedent moisture on runoff curve number. Catena 2015, 133, 318–327. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Harmel, R.; Smith, P.; Migliaccio, K.; Chaubey, I.; Douglas-Mankin, K.; Benham, B.; Shukla, S.; Muñoz-Carpena, R.; Robson, B.J. Evaluating, interpreting, and communicating performance of hydrologic/water quality models considering intended use: A review and recommendations. Environ. Model. Softw. 2014, 57, 40–51. [Google Scholar] [CrossRef]
- Van Mullem, J. Runoff and peak discharges using Green-Ampt infiltration model. J. Hydraul. Eng. 1991, 117, 354–370. [Google Scholar] [CrossRef]
- King, K.W.; Arnold, J.; Bingner, R. Comparison of Green-Ampt and curve number methods on Goodwin Creek watershed using SWAT. Trans. ASAE 1999, 42, 919. [Google Scholar] [CrossRef]
- Walega, A.; Salata, T. Influence of land cover data sources on estimation of direct runoff according to SCS-CN and modified SME methods. Catena 2019, 172, 232–242. [Google Scholar] [CrossRef]
- Hawkins Richard, H. Curve Number Method: Time to Think Anew? J. Hydrol. Eng. 2014, 19, 1059. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. Identification of the SCS-CN parameter spatial distribution using rainfall-runoff data in heterogeneous watersheds. Water Res. Manag. 2013, 27, 1737–1749. [Google Scholar] [CrossRef]
- Soulis, K.X. Estimation of SCS curve number variation following forest fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
| Parameters | |||
|---|---|---|---|
| Model Identity | λ | CN (CNIIα) | Model Expression |
| M1 | 0.20 | *NEH-4 Tables | Equations (1) and (2) |
| M2 | 0.05 | NEH-4 Tables | Equations (1)–(3) |
| M3 | 0.20 | Sharpley and Williams [17] | Equations (1), (2) and (5) |
| M4 | 0.20 | Huang et al. [19] | Equations (1), (2) and (7) |
| M5 | 0.20 | Ajmal et al. [10] | Equations (1), (2) and (8) |
| M6 | 0.20 | Proposed | Equations (1), (2) and (12) |
| M7 | 0.05 | Proposed | Equations (1)–(3) and (12) |
| M8 | 0.01 | Proposed | Equations (1), (2) and (12) |
| Performance Rating | NSE [44] | NSE [45] | PB (%) |
|---|---|---|---|
| Very good | 0.75 < NSE ≤ 1.00 | 0.90 < NSE ≤ 1.00 | −10 < PB < +10 |
| Good | 0.65 < NSE ≤ 0.75 | 0.80 ≤ NSE ≤ 0.90 | ±10 ≤ PB < ±15 |
| Satisfactory | 0.50 < NSE ≤ 0.65 | 0.65 ≤ NSE < 0.80 | ±15 ≤ PB < ±25 |
| Unsatisfactory | NSE ≤ 0.50 | NSE ≤ 0.65 | PB ≥ ±25 |
| Calibration Watersheds (1402 Rainstorm–Runoff Events) | ||||||
|---|---|---|---|---|---|---|
| Parameter/Model | Mean | Minimum | First Quartile (Q1) | Median | Third Quartile (Q3) | Maximum |
| P | 80.96 | 12.10 | 39.92 | 59.09 | 98.27 | 519.68 |
| Qo | 38.60 | 0.17 | 8.23 | 19.61 | 49.04 | 348.46 |
| M1 | 25.57 | 0.00 | 1.49 | 6.13 | 27.03 | 415.63 |
| M2 | 23.56 | 0.00 | 1.14 | 7.26 | 25.79 | 383.27 |
| M3 | 28.79 | 0.00 | 1.30 | 7.95 | 32.94 | 436.28 |
| M4 | 26.06 | 0.00 | 1.52 | 6.31 | 28.33 | 419.65 |
| M5 | 30.06 | 0.00 | 1.35 | 8.83 | 35.39 | 443.28 |
| M6 | 30.26 | 0.00 | 1.23 | 9.38 | 35.34 | 445.73 |
| M7 | 28.98 | 0.00 | 2.54 | 10.77 | 34.57 | 417.11 |
| M8 | 39.67 | 0.53 | 7.93 | 20.13 | 49.30 | 458.55 |
| Validation Watersheds (377 Rainstorm–Runoff Events) | ||||||
| P | 75.22 | 20.52 | 40.97 | 57.05 | 86.95 | 376.86 |
| Qo | 35.03 | 0.24 | 8.30 | 19.10 | 43.20 | 364.38 |
| M1 | 22.04 | 0.00 | 1.48 | 6.35 | 20.35 | 294.27 |
| M2 | 19.85 | 0.00 | 0.85 | 5.55 | 19.93 | 265.59 |
| M3 | 24.75 | 0.00 | 1.52 | 6.27 | 25.99 | 309.31 |
| M4 | 22.49 | 0.00 | 1.39 | 6.63 | 21.48 | 296.26 |
| M5 | 26.48 | 0.00 | 2.03 | 7.87 | 30.12 | 309.72 |
| M6 | 26.07 | 0.00 | 1.71 | 6.66 | 29.04 | 314.48 |
| M7 | 24.98 | 0.00 | 2.10 | 9.43 | 26.71 | 293.91 |
| M8 | 34.77 | 0.87 | 7.70 | 17.91 | 40.12 | 325.07 |
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | |
|---|---|---|---|---|---|---|---|---|
| Performance Criteria | NSE [44] | |||||||
| 0.75 < NSE ≤ 1.00 | 14 | 15 | 14 | 14 | 14 | 14 | 20 | 30 |
| 0.65 < NSE ≤ 0.75 | 3 | 10 | 7 | 3 | 10 | 12 | 13 | 6 |
| 0.50 < NSE ≤ 0.65 | 10 | 9 | 13 | 13 | 11 | 9 | 4 | 2 |
| NSE ≤ 0.50 | 12 | 5 | 5 | 9 | 4 | 4 | 2 | 1 |
| NSE [45] | ||||||||
| 0.90 < NSE ≤ 1.00 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 5 |
| 0.80 ≤ NSE ≤ 0.90 | 6 | 12 | 12 | 8 | 11 | 11 | 11 | 20 |
| 0.65 ≤ NSE < 0.80 | 10 | 12 | 8 | 8 | 11 | 13 | 19 | 11 |
| NSE ≤ 0.65 | 22 | 14 | 18 | 22 | 15 | 13 | 6 | 3 |
| PB (%) | ||||||||
| −10 < PB < +10 | 1 | 1 | 5 | 1 | 5 | 6 | 6 | 19 |
| ±10 ≤ PB < ±15 | 0 | 0 | 3 | 0 | 6 | 5 | 8 | 9 |
| ±15 ≤ PB < ±25 | 10 | 11 | 12 | 10 | 13 | 12 | 12 | 7 |
| PB ≥ ±25 | 28 | 27 | 19 | 28 | 15 | 16 | 13 | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajmal, M.; Waseem, M.; Kim, D.; Kim, T.-W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, 12, 1469. https://doi.org/10.3390/w12051469
Ajmal M, Waseem M, Kim D, Kim T-W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water. 2020; 12(5):1469. https://doi.org/10.3390/w12051469
Chicago/Turabian StyleAjmal, Muhammad, Muhammad Waseem, Dongwook Kim, and Tae-Woong Kim. 2020. "A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds" Water 12, no. 5: 1469. https://doi.org/10.3390/w12051469







