Detecting Pattern Anomalies in Hydrological Time Series with Weighted Probabilistic Suffix Trees
Abstract
:1. Introduction
2. Related Work
2.1. Time Series Pattern Anomaly Detection
2.2. PST-Based Anomaly Detection
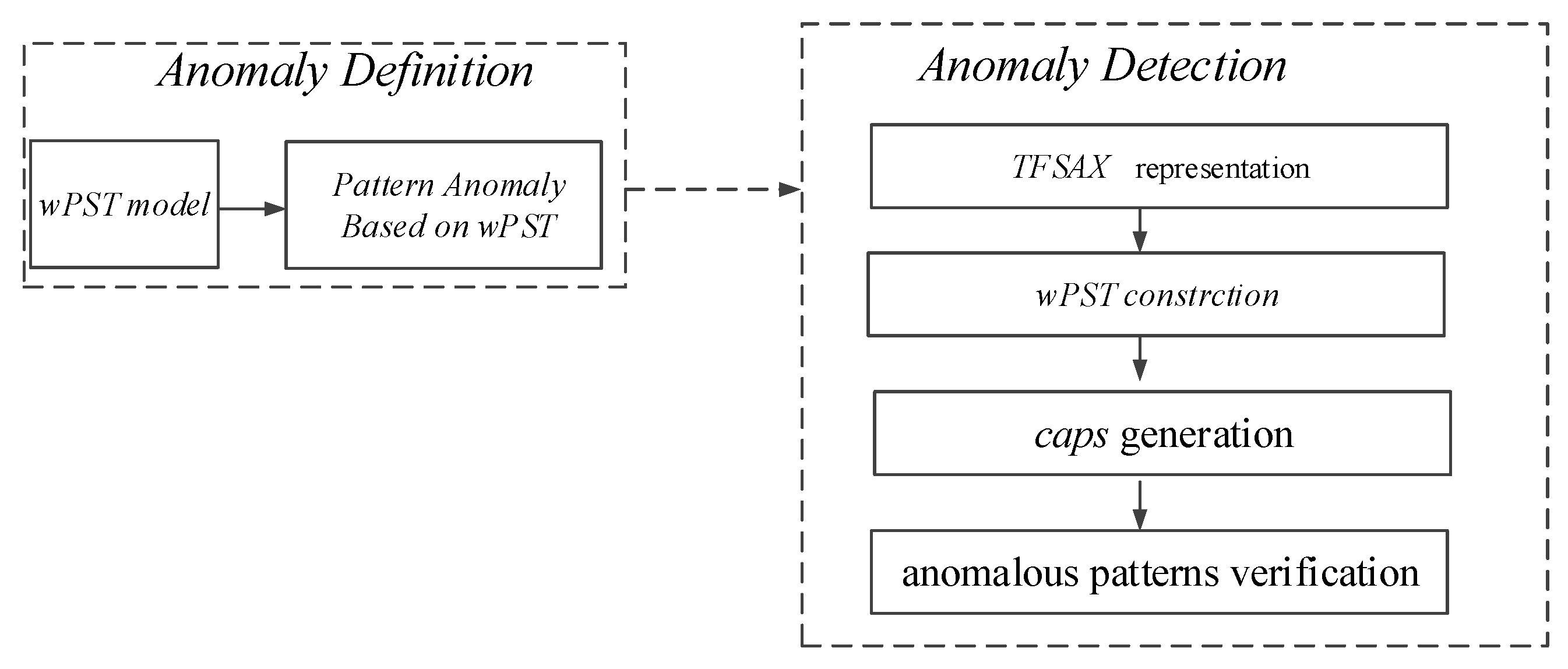
3. A Novel Time Series Anomaly Detection Approach TFSAX_wPST
3.1. Time Series Pattern Anomaly Based wPST Model
- (1)
- Pr (σ|s) < Prmin and
- (2)
- occ_num(σ) ≤ MinCt,
3.2. TFSAX_wPST Algorithm
3.2.1. TFSAX Representation
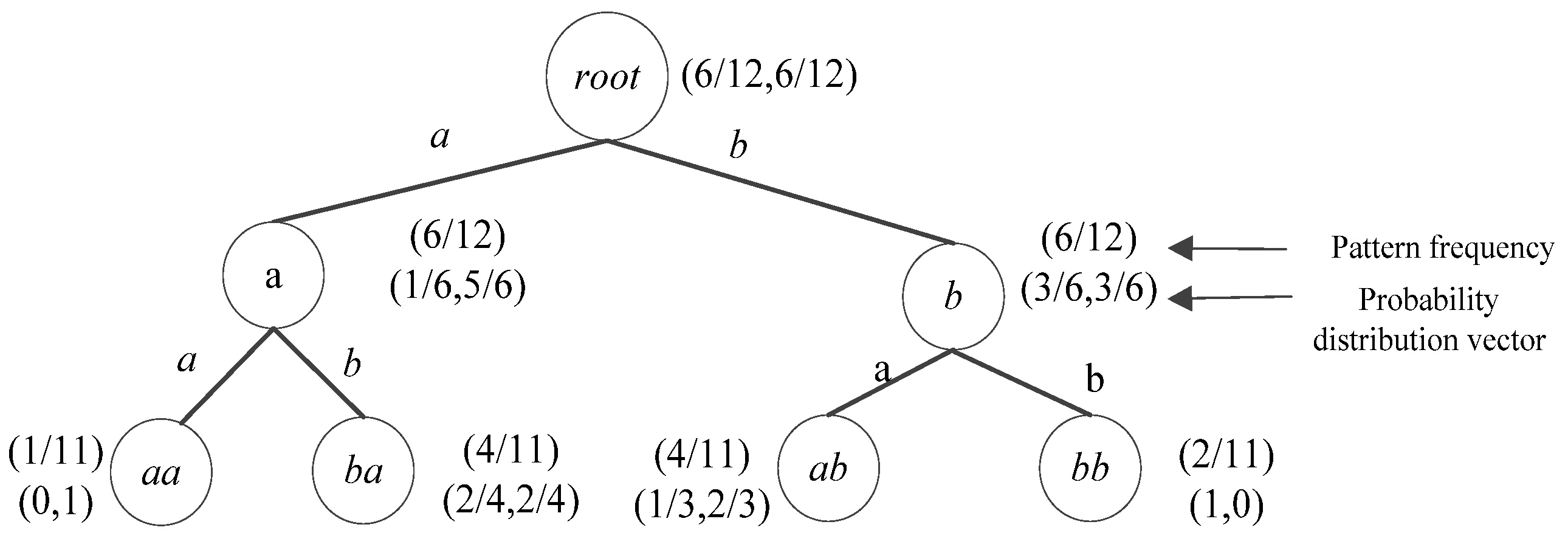
3.2.2. wPST Construction
| Algorithm 1wPST construction. Build_wPST(S,H) |
| Input: Sequence S, Maximum depth H |
| Output: wPST T |
| 1. Initialize: T← root; k = 0; |
| 2. k = 1, S1← {σ |σ∈Σ ∧ occ_count(σ) > 0} |
| 3. HM1← HASHMAP(S1) |
| 4. While k≤ H Do |
| 5. Foreach (s′∈Sk) |
| 6. Abefore[|Σ|], Aafter[|Σ|]←0; |
| 7. For i = 1 to len(s) –k + 1 |
| 8. ForEach (s[i,i + k−1] ∈ S) |
| 9. If s[i,i + k−1] ∈ HMk.keys then |
| 10. Update(occ_times(s[i,i + k−1])); |
| 11. ForEach(σ∈Σ | |σ′∈Σ) |
| 12. If (s[i + k] =σ) then Update(Aafter(s[i + k])); |
| 13. If (s[i−1] =σ′) then Update(Abefore(s[i−1])); |
| 14. ForEach (s′∈ Sk) |
| 15. T.Add(represent(u, s′)); |
| 16. w(represent(u, s′)) = occ_times(s′)/(len(S)-k); |
| 17. ForEach (σ∈Σ) |
| 18. compute Pr(σ|s′) using Aafter; |
| 19. smooth Pr(σ|s′); |
| 20. Mine_candidate_Anomaly (T, MinCt, Prmin); |
| 21. HMk + 1← HASHMAP(Sk + 1); |
| 22. Return T |
3.2.3. Candidate Anomalies Pattern Set Generation
| Algorithm 2 Candidate anomaly pattern mining. Mine_Candidate_Anomaly (wPST T, int MinCt, real Prmin) |
| Input: wPST T, MinCt, Prmin |
| Output: candidate pattern anomaly set cpas |
| 1. Initialize: cpas←∅ |
| 2. ForEach represent(u,X) ∈T |
| 3. occ_times(u).Cal(); Pr (suffix(u)). Cal (); |
| 4. If (occ_times(u) < MinCt || Pr (u) < Prmin) |
| 5. caps.Add(represent(u,X)); |
| 6. caps.Add(descendants (represent(u,X))); |
| 7. T.Prune(represent(u,X)); |
| 8. T.Prune(descendants (represent(u,X))); |
| 9. Return caps |
3.2.4. Pattern Anomalies Verification
| Algorithm 3 Anomalies Pattern Mining. Mine_Anomaly (CAPS caps) |
| Input: candidate pattern anomaly set caps |
| Output: pattern anomaly set aps |
| 1. Initialize: aps←∅ |
| 2. Pattern_Filter(caps); |
| 3. Pattern_Merge(caps); |
| 4. Pattern_Extend(caps); |
| 5. Pattern_Valid (aps); |
| 6. Pattern_Sort(aps); |
| 7. Return aps |
3.3. Algorithm Analysis
4. Case Studies
4.1. NWIS Dataset
4.1.1. Research Area
4.1.2. TFSAX Representation
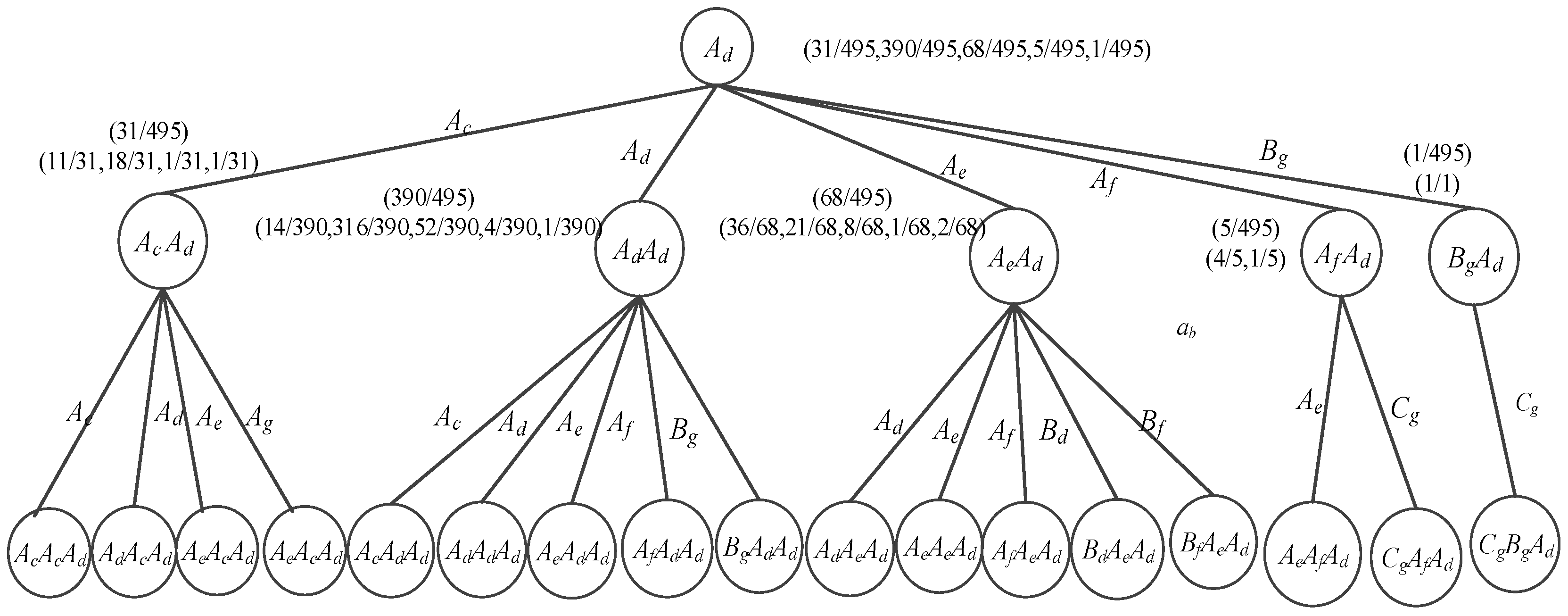
4.1.3. wPST Construction
4.1.4. Detection Results and Analysis
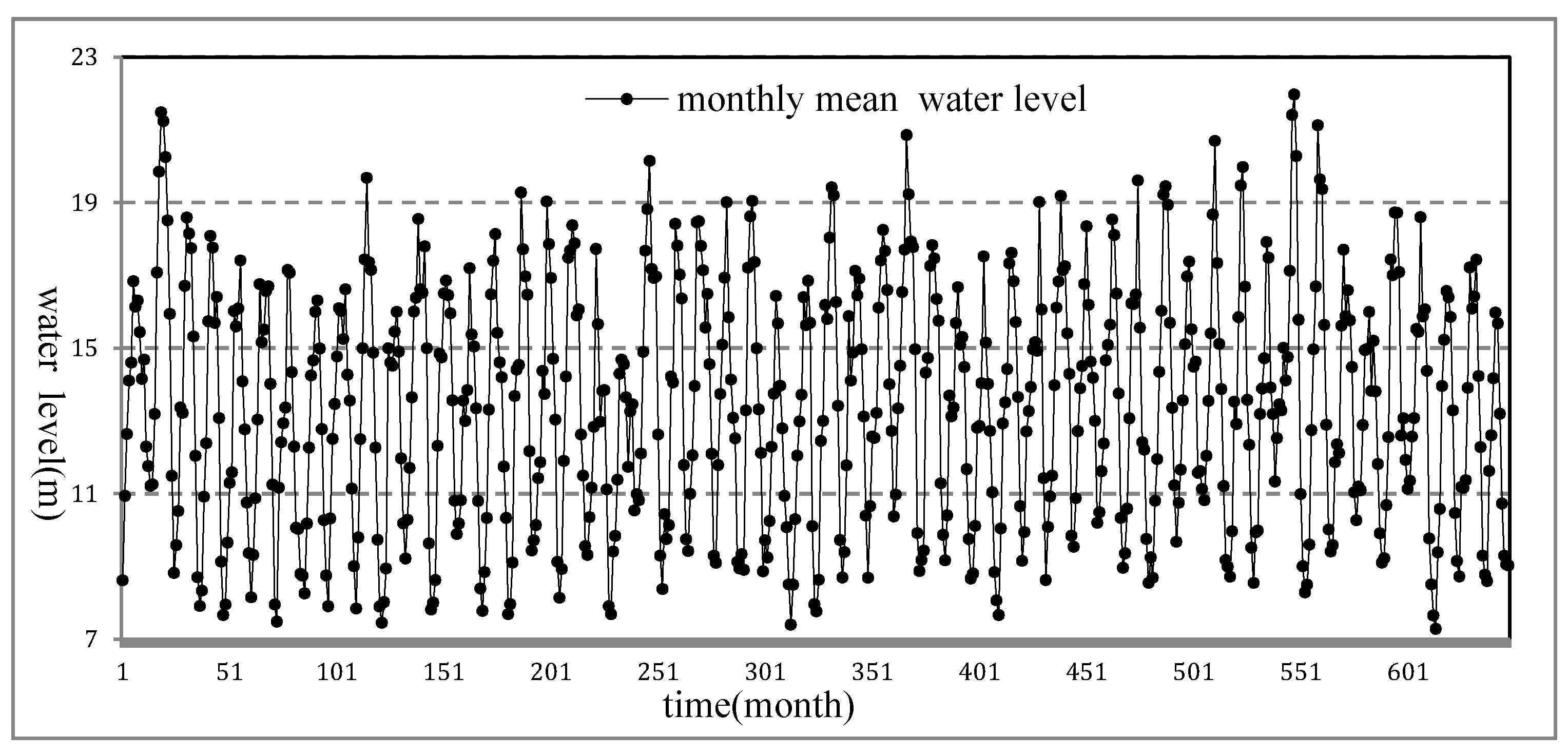
4.2. Poyang Lake Data Set
4.2.1. Research Area
4.2.2. TFSAX Representation
4.2.3. wPST Construction
4.2.4. Detection Results and Analysis
4.3. Analysis and Discussion
4.3.1. Construction Algorithm Comparison
4.3.2. Anomaly Detection Results Comparison
4.3.3. Computational Complexity Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, L.; Wang, L. Recent advance in earth observation big data for hydrology. Big Earth Data 2018, 2, 86–107. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Wang, L.; Chen, F.; Liang, D. Scientific big data and digital earth. Chin. Sci. Bull. 2014, 59, 5066–5073. [Google Scholar] [CrossRef]
- Azimi, S.; Moghaddam, M.A.; Monfared, S.A. Anomaly Detection and Reliability Analysis of Groundwater by Crude Monte Carlo and Importance Sampling Approaches. Water Resour. Manag. 2018, 32, 4447–4467. [Google Scholar] [CrossRef]
- Rougé, C.; Ge, Y.; Cai, X. Detecting gradual and abrupt changes in hydrological records. Adv. Water Resour. 2013, 53, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, D.M. Identification of Outliers; Chapman and Hall: London, UK, 1980. [Google Scholar]
- Chandala, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. CSUR 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Gupta, M.; Gao, J.; Aggarwal, C.; Han, J. Outlier detection for temporal data. Synth. Lect. Data Min. Knowl. Discov. 2014, 5, 1–129. [Google Scholar] [CrossRef]
- USGS. Interagency Advisory Committee on Water Data. In Guidelines for Determining Flood Flow Frequency: Bulletin 17 B; U.S. Geological Survey, Office of Water Data Coordination: Reston, VA, USA, 1982. [Google Scholar]
- Stedinger, J.R.; Griffis, V.W. Flood frequency analysis in the united states: Time to update. J. Hydrol. Eng. 2008, 13, 199–204. [Google Scholar] [CrossRef] [Green Version]
- Chebana, F.; Daboniang, S.; Ouarda, T.B. Exploratory functional flood frequency analysis and outlier detection. Water Resour. Res. 2012, 48, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Sarraf, A.P. Flood outlier detection using PCA and effect of how to deal with them in regional flood frequency analysis via L-moment method. Water Resour. 2015, 42, 448–459. [Google Scholar] [CrossRef]
- Amin, M.T.; Rizwan, M.; Alazba, A.A. Comparison of mixed distribution with EV1 and GEV components for analyzing hydrologic data containing outlier. Environ. Earth Sci. 2015, 73, 1369–1375. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, Y.; Li, S.; Wan, D. Time series outlier detection based on sliding window prediction. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
- Ng, W.W.; Panu, U.S.; Lennox, W.C. Chaos based analytical techniques for daily extreme hydrological observations. J. Hydrol. 2007, 342, 17–41. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhu, Y.; Wan, D.; Yu, Y.; Cheng, X. Research on the Data-Driven quality control method of hydrological time series data. Water 2018, 10, 1712. [Google Scholar] [CrossRef] [Green Version]
- Nyeko-Ogiramoi, P.; Willems, P.; Ngirane-Katashaya, G. Trend and variability in observed hydrometer- orological extremes in the Lake Victoria basin. J. Hydrol. 2013, 489, 56–73. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Z.; Gong, L.; Zhu, L.; Liu, Z.; Cheng, X. A distributed anomaly detection system for in-vehicle network using HTM. IEEE Access 2018, 6, 9091–9098. [Google Scholar] [CrossRef]
- Van Vlasselaer, V.; Bravo, C.; Caelen, O.; Eliassi-Rad, T.; Akoglu, L.; Snoeck, M.; Baesens, B. APATE: A novel approach for automated credit card transaction fraud detection using network-based extensions. Decis. Support Syst. 2015, 75, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Golmohammadi, K.; Zaiane, O.R. Time series contextual anomaly detection for detecting market manipulation in stock market. In Proceedings of the International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015; pp. 1–10. [Google Scholar]
- Sultani, W.; Chen, C.; Shah, M. Real-world anomaly detection in surveillance videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6479–6488. [Google Scholar]
- Keogh, E.; Lin, J.; Fu, A. HOT SAX: Efficiently Finding the Most Unusual Time Series Subsequence. In Proceedings of the IEEE International Conference on Data Mining, Houston, TX, USA, 27–30 November 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 226–233. [Google Scholar]
- Candelieri, A. Clustering and support vector regression for water demand forecasting and anomaly detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, Y.; Wan, D.; Liu, H.; Zhao, Q. A Novel Symbolic Aggregate Approximation for Time Series. In Proceedings of the 13th International Conference on Ubiquitous Information Management and Communication, IMCOM 2019, Phuket, Thailand, 4–6 January 2019; Springer: Cham, Switzerland, 2019; pp. 805–822. [Google Scholar]
- Ding, Z.; Fei, M. An anomaly detection approach based on isolation forest algorithm for streaming data using sliding window. IFAC Proc. Vol. 2013, 46, 12–17. [Google Scholar] [CrossRef]
- Budalakoti, S.; Srivastava, A.N.; Otey, M.E. Anomaly detection and diagnosis algorithms for discrete symbol sequences with applications to airline safety. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 101–113. [Google Scholar] [CrossRef]
- Safin, A.M.; Burnaev, E. Conformal kernel expected similarity for anomaly detection in time-series data. Adv. Syst. Sci. Appl. 2017, 17, 22–33. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection for discrete sequences: A survey. IEEE Trans. Knowl. Data Eng. 2010, 24, 823–839. [Google Scholar] [CrossRef]
- Keogh, E.; Lonardi, S.; Chiu, B.Y. Finding surprising patterns in a time series database in linear time and space. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 550–556. [Google Scholar]
- Sun, P.; Chawla, S.; Arunasalam, B. Mining for Outliers in Sequential Databases. In Proceedings of the SIAM International Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006; 2006; pp. 94–105. [Google Scholar]
- Klerx, T.; Anderka, M.; Büning, H.K.; Priesterjahn, S. Model-based anomaly detection for discrete event systems. In Proceedings of the International Conference on Tools with Artificial Intelligence, Limassol, Cyprus, 10–12 November 2014; pp. 665–672. [Google Scholar]
- Zohrevand, Z.; Glasser, U.; Shahir, H.Y.; Tayebi, M.A.; Costanzo, R. Hidden Markov based anomaly detection for water supply systems. In Proceedings of the International Conference on Big Data, Washington, DC, USA, 5–8 December 2016; pp. 1551–1560. [Google Scholar]
- Pimentel MA, F.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–490. [Google Scholar] [CrossRef]
- Wan, D.; Xiao, Y.; Zhang, P.; Feng, J.; Zhu, Y.; Liu, Q. Hydrological time series anomaly mining based on symbolization and distance measure. In Proceedings of the 2014 IEEE International Congress on Big Data, Beijing, China, 27 June–2 July 2014; pp. 339–346. [Google Scholar]
- Zhang, P.; Leung, H.; Xiao, Y.; Feng, J.; Wan, D.; Li, W.; Leung, H. A New Symbolization and Distance Measure Based Anomaly Mining Approach for Hydrological Time Series. Int. J. Web Serv. Res. 2016, 13, 26–45. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Li, X.; Qian, H. Detection of Anomalies and Changes of Rainfall in theYellow River Basin, China, through Two Graphical Methods. Water 2018, 10, 15. [Google Scholar] [CrossRef] [Green Version]
- Ye, N. A markov chain model of temporal behavior for anomaly detection. In Proceedings of the 2000 IEEE Systems, Man, and Cybernetics Information Assurance and Security Workshop, West Point, NY, USA, 6–7 June 2000; Volume 166, p. 169. [Google Scholar]
- Ron, D.; Singer, Y.; Tishby, N. The power of amnesia: Learning probabilistic automata with variable memory length. Mach. Learn. 1996, 25, 117–149. [Google Scholar] [CrossRef] [Green Version]
- Bejerano, G.; Yona, G. Variations on probabilistic suffix trees: Statistical modeling and prediction of protein families. Bioinformatics 2001, 17, 23–43. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W. CLUSEQ: Efficient and effective sequence clustering. In Proceedings of the 19th International Conference on Data Engineering, Bangalore, India, 5–8 March 2003; pp. 101–112. [Google Scholar]
- Kholidy, H.A.; Yousof, A.M.; Erradi, A.; Abdelwahed, S.; Ali, H.A. A Finite Context Intrusion Prediction Model for Cloud Systems with a Probabilistic Suffix Tree. In Proceedings of the 2014 European Modelling Symposium, Pisa, Italy, 21–23 October 2014; pp. 526–531. [Google Scholar]
- Li, Y.; Thomason, M.; Parker, L.E. Detecting time-related changes in Wireless Sensor Networks using symbol compression and Probabilistic Suffix Trees. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, China, 18–22 October 2010; pp. 2946–2951. [Google Scholar]
- Farahani, I.V.; Chien, A.; King, R.E.; Kay, M.G.; Klenz, B. Time Series Anomaly Detection from a Markov Chain Perspective. In Proceedings of the 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 1000–1007. [Google Scholar]
- Keogh, E.; Chakrabarti, K.; Pazzani, M.; Mehrotra, S. Dimensionality Reduction for Fast Similarity Search in Large Time Series Databases. Knowl. Inf. Syst. 2000, 3, 263–286. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, S.; Guo, H.; Chen, G.; Jiang, T. Interactions of the Yangtze river flow and hydrologic processes of the Poyang Lake, China. J. Hydrol. 2007, 347, 90–100. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Ye, X. Dry/wet conditions monitoring based on TRMM rainfall data and its reliability validation over Poyang Lake Basin, China. Water 2013, 5, 1848–1864. [Google Scholar] [CrossRef]
- Han, J.; Jian, P.; Micheline, K. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2011. [Google Scholar]
- Ghafoori, Z.; Erfani, S.M.; Rajasegarar, S.; Karunasekera, S.; Leckie, C.A. Anomaly Detection in Non-stationary Data: Ensemble based Self-Adaptive OCSVM. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 25–29 July 2016. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]






| Symbol | Meaning (Water Level) |
|---|---|
| A | 5.46 ft–7.45 ft |
| B | 7.46 ft–9.43 ft |
| C | 9.46 ft–10.39 ft |
| D | 10.48 ft–13.44 ft |
| E | 13.48 ft−16.56 ft |
| Symbol | Trend Feature | Meaning |
|---|---|---|
| a | (−90°–−45°) | water level drops sharply |
| b | (−90°–−30°) | water level drops rapidly |
| c | (−30°–−5°) | water level drops slowly |
| d | (−5°–5°) | water level remains stable |
| e | (5°–30°) | water level rises slowly |
| f | (30°–45°) | water level rises rapidly |
| g | (45°–90°) | water level rises sharply |
| Symbol | Frequency | Symbol | Frequency | Symbol | Frequency | Symbol | Frequency | Symbol | Frequency |
|---|---|---|---|---|---|---|---|---|---|
| Eb | 1 | Cc | 3 | Ea | 5 | Bf | 11 | Bd | 33 |
| Ee | 1 | Cf | 3 | Dc | 5 | Af | 12 | Be | 37 |
| Ec | 1 | Eg | 3 | Df | 6 | Bb | 13 | Ae | 103 |
| Ab | 2 | Ag | 4 | Ba | 6 | Dg | 13 | Bc | 125 |
| Ef | 2 | Db | 4 | Ca | 9 | Da | 7 | Ac | 149 |
| De | 3 | Cb | 4 | Cg | 9 | Bg | 8 | Ad | 495 |
| Pattern | Subsequence | Corresponding Event Description |
|---|---|---|
| BgCcBa | 1 Dec 2010–3 Dec 2010 | Daily water level is +1.88, −0.3, −1.19 feet, respectively. |
| BgDeDfDgEfEaDaCb | 2 Feb 2011–9 Feb 2011 | Daily water level is +1.68, +0.24, +1.33/2, +1.53, + 1.39/2, −1.53, −2.42, −0.8 feet, respectively. |
| BfCgDeCaBc | 9 Mar 2011–12 Mar 2011 | Daily water level is +2.13, +0.36, −2.35, −0.53 feet, respectively. |
| CgDgDbDcDfDbDaBbBcBgCfCa | 27 Mar 2011–7 Apr 2011 | Daily water level is +3.38, +1.6, −0.86, −0.31, + 0.9, −0.65, −1.74, −0.7, −0.39, +1.09, +0.61, −1.25 feet, respectively. |
| BgBcBb | 23 Sep 2011–25 Sep 2011 | Daily water level is +2.34/2, −0.51, −0.72 feet, respectively. |
| AgBg | 21 Jan 2012–22 Jan 2012 2012.1.21–1.22 | Daily water level is +1.3, +1.1 feet, respectively. |
| AfCgDfDaBcBb | 18 Feb 2012–23 Feb 2012 | Daily water level is +0.67, +2.67, +0.79, −2.1, −0.99 feet, respectively. |
| BfBgBaBc | 26 Dec 2012–28 Dec 2012 | Daily water level is +0.65, +1.49, −1.55 feet, respectively. |
| AgCgCaBaCgDgEeEcEaDaCaBc | 7 Feb 2013–18 Feb 2013 | Daily water level is +1.87, +1.78, −1.06, −1.14, +3.19, +3.44, +0.26, −0.32, −1.59, −2.04, −1.47, −0.57 feet, respectively. |
| BgDgEgEaDcDcEfEaDaCaBc | 22 Feb 2013–2 Mar 2013 | Daily water level is +1.14, +2.86, +1.85, −1.14, −0.2, +1.31, −1.24, −2.1, −1.15, −0.46 feet, respectively. |
| CgDgEaDaCb | 24 Mar 2013–28Mar 2013 | Daily water level is +3.25, 3.18/2, −1.62, −2.66, −0.88 feet, respectively. |
| BgDgDaBbBc BgDgEgDaDaBb | 29 Apr 2013–9 May 2013 | Daily water level is +2.04, +1.91, −1.98, −0.88, −0.31, +1.05, +2.55, +2.09/2, −1.31, −2.68, −0.9 feet, respectively. |
| CgEgDaBa | 23 May 2013–26 May 2013 | Daily water level is +4.21, +2.1/2, −3.97, −1.41 feet, respectively. |
| BgDcBfDgDfDbDaBcDgDfDa | 3 Jun 2013–13 Jun 2013 | Daily water level is +3.03, −0.24, +0.78, +2.17, +0.57, −0.8, −1.7, 0.35, +2.42, +0.6, −3.46 feet, respectively. |
| BfCfDaDeCaDgDaBa | 3 Jul 2013–10 Jul 2013 | Daily water level is +0.52, +0.46, −1.25, +0.25, −1.2, +1.61, −1.16, −1.13 feet, respectively. |
| CgDgDfDaBa | 12 Jul 2013–16 Jul 2013 | Daily water level is +1.97, +1.2, +0.57, −2.76, −1.11 feet, respectively. |
| AgBgCaBb | 2013.7.31–8.3 | Daily water level is +1.01, +2.43, −1.52, −0.92 feet, respectively. |
| BgCgDgDgEb | 15 Aug 2013–19Aug 2013 | Daily water level is +2.22, +2.79, +1.27, +1.14 feet, respectively. |
| Symbol | Meaning (Water Level) |
|---|---|
| A | 7.28 m–8 m |
| B | 8.01 m–10.99 m |
| C | 11.03 m–15 m |
| D | 15.04 m–19 m |
| E | 19.01 m−21.96 m |
| Symbol | Trend Feature | Meaning |
|---|---|---|
| a | (−90°–−30°) | water level drops rapidly |
| b | (−30°–−5°) | water level drops slowly |
| c | (−5°–5°) | water level remains stable |
| d | (5°–30°) | water level rises slowly |
| e | (30°–90°) | water level rises rapidly |
| Symbol | Frequency | Symbol | Frequency | Symbol | Frequency | Symbol | Frequency |
|---|---|---|---|---|---|---|---|
| Aa | 12 | Bc | 5 | Cd | 28 | De | 82 |
| Ab | 9 | Bd | 31 | Ce | 101 | Ea | 4 |
| Ac | 1 | Be | 37 | Da | 50 | Eb | 3 |
| Ad | 4 | Ca | 89 | Db | 31 | Ed | 4 |
| Ba | 73 | Cb | 24 | Dc | 9 | Ee | 16 |
| Bb | 29 | Cc | 12 | Dd | 30 |
| Pattern | Subsequence | Corresponding Event Description |
|---|---|---|
| DeEeEeEbEaDaDaCa | Mar 1954–Dec 1954 | Extraordinary floods in the Yangtze River Basin, monthly mean water levels are 17.07, 19.84, 21.47, 21.23, 20.24, 18.5, 15.93, 11.48 m |
| AaAb | Dec 1958–Feb 1959 | Extreme drought season, monthly mean water levels are 7.95, 7.48, 11.16 m |
| Jan 1963–Oct 1963 | Drought year, monthly mean water levels are 7.89, 7.45, 8.01, 8.94, 14.99, 14.59, 14.51, 15.45, 15.99, 14.9 m, highest water level occurred in September | |
| Dec 1971–Mar 1972 | Extreme drought event, monthly mean water levels are 7.9, 7.68, 9.4, 9.83 m | |
| Dec 1979–Feb 1980 | Extreme drought event, monthly mean water levels are 7.96, 7.76, 8.63, 12.4 m | |
| AaAd | Jan 1965–Apr 1965 | Extreme drought event, monthly mean water levels are 7.81, 8, 8.62, 12.31 m |
| Jan 1968–Apr 1968 | Extreme drought event, monthly mean water levels are 7.68, 7.9, 9.1, 13.68 m | |
| Dec 2007–Mar 2008 | Extreme drought event, monthly mean water levels are 7.54, 7.72, 8.5, 8.62 m | |
| DbDeEeEbDaCa | Jul 1980–Oct 1980 | Flood events, monthly mean water levels are 18.03, 19.41, 19.19, 16.26 m |
| EeEaDaDcCa | Jul 1983–Oct 1983 | Flood events, monthly mean water levels are 20.85, 19.22, 17.9, 17.77 m |
| CcEeDa | Jun 1968–Aug 1968 | Flood events, monthly mean water levels are 14.53, 19.27, 17.71 m |
| CdCbCaCaCeCdBaBd | Jun 1972–Feb 1973 | Drought year with a gentle overall trend, monthly mean water levels are 14.68, 14.55, 13.64, 11.73, 13.25, 13.45, 10.53, 10.98, 10.81 m |
| BaBbAbBe | Dec 1986–Feb 1987 | Drought season, monthly mean water levels are 8.84, 8.06, 7.66, 8.34 m |
| DeEeEdEaDaBa | Jun 1998–Nov 1998 | Extreme flood event, monthly mean water levels are 17.12, 21.4, 21.96, 20.17, 15.77, 10.98 m |
| DeEeEaEbDaCa | Jun 1999–Nov 1999 | Flood events, monthly mean water levels are 16.69, 21.12, 19.63, 19.36, 15.63, 12.89 m |
| CaBaBaAbAbBe | Nov 2003–Mar 2004 | Extreme drought event, monthly mean water levels are 8.5, 7.65, 7.28, 9.38 m |
| EeEd | Jul 1996–Oct 1996 | Flood events monthly mean water levels are 19.46, 19.97 m |
| BdCeCcDe | Apr 1974–Jun 1974 | No rainy season, monthly mean water levels are 10.13, 14.21, 14.05, 15.6 m |
| BaBaBbBcBaBdBeBbBe | Sep 2006–May 2007 | Extreme drought year, monthly mean water levels are 10.72, 9.29, 9.05, 9.02, 8.06, 8.28, 10.6, 10.4, 10.98 m |
| Approach | Order | Numbers of Nodes | −Log-Likelihood |
|---|---|---|---|
| PST-based | 1 | 10 | −0.0152 |
| 2 | 46 | −0.0108 | |
| 5 | 138 | −0.0068 | |
| wPST-based | 1 | 10 | −0.0152 |
| 2 | 41 | −0.0108 | |
| 5 | 84 | −0.0068 |
| Approach | MinCt | FNR (Miss Rate) | FPR (False Alarm) |
|---|---|---|---|
| PST-Based (order = 5) | 1 | 25.2% | 64.9% |
| 2 | 22.7% | 42.5% | |
| 5 | 14.3% | 21.9% | |
| 10 | 12.5% | 37.6% | |
| wPST-Based (order = 5) | 1 | 12.6% | 25.6% |
| 2 | 8.4% | 10.9% | |
| 5 | 2.3% | 3.8% | |
| 10 | 5.3% | 8.4% |
| Algorithm | PST-based | HMM-based | OCSVM | FP_SAX-based | Distance-based | TFSAX_wPST | |
|---|---|---|---|---|---|---|---|
| Metric | |||||||
| Accuracy | 0.912 | 0.928 | 0.874 | 0.936 | 0.947 | 0.976 | |
| Precision | 0.926 | 0.922 | 0.896 | 0.927 | 0.935 | 0.964 | |
| Recall | 0.925 | 0.932 | 0.902 | 0.944 | 0.951 | 0.969 | |
| F1-score | 0.926 | 0.927 | 0.918 | 0.935 | 0.943 | 0.966 | |
| AUC | 0.924 | 0.931 | 0.915 | 0.938 | 0.949 | 0.971 | |
| Num | Time | Sequence Lengths | Total Length | FP_SAX-based | Distance-based | TFSAX_wPST |
|---|---|---|---|---|---|---|
| 1 | Jul–Aug | 62 | 3534 | 0.372 s | 0.324 s | 0.264 s |
| 2 | Jun–Aug | 92 | 5244 | 0.719 s | 0.708 s | 0.532 s |
| 3 | Jun–Sep | 122 | 6954 | 1.133 s | 1.012 s | 0.793 s |
| 4 | Jun–Oct | 153 | 8721 | 1.471 s | 1.274 s | 0.946 s |
| 5 | May–Oct | 184 | 10,488 | 2.641 s | 2.416 s | 1.387 s |
| 6 | Apr–Nov | 244 | 13,908 | 3.325 s | 2.782 s | 1.764 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Wan, D.; Zhao, Q.; Liu, H. Detecting Pattern Anomalies in Hydrological Time Series with Weighted Probabilistic Suffix Trees. Water 2020, 12, 1464. https://doi.org/10.3390/w12051464
Yu Y, Wan D, Zhao Q, Liu H. Detecting Pattern Anomalies in Hydrological Time Series with Weighted Probabilistic Suffix Trees. Water. 2020; 12(5):1464. https://doi.org/10.3390/w12051464
Chicago/Turabian StyleYu, Yufeng, Dingsheng Wan, Qun Zhao, and Huan Liu. 2020. "Detecting Pattern Anomalies in Hydrological Time Series with Weighted Probabilistic Suffix Trees" Water 12, no. 5: 1464. https://doi.org/10.3390/w12051464
APA StyleYu, Y., Wan, D., Zhao, Q., & Liu, H. (2020). Detecting Pattern Anomalies in Hydrological Time Series with Weighted Probabilistic Suffix Trees. Water, 12(5), 1464. https://doi.org/10.3390/w12051464





